Comparison of dust-layer heights from active and passive satellite sensors

Aerosol-layer height is essential for understanding the impact of aerosols on the climate system. As part of the European Space Agency Aerosol_cci project, aerosol-layer height as derived from passive thermal and solar satellite sensors measurements have been compared with aerosol-layer heights estimated from CALIOP measurements. The Aerosol_cci project targeted dust-type aerosol for this study. This ensures relatively unambiguous aerosol identification by the CALIOP processing chain. Dust-layer height was estimated from thermal IASI measurements using four different algorithms (from BIRA-IASB, DLR, LMD, LISA) and from solar GOME-2 (KNMI) and SCIAMACHY (IUP) measurements. Due to differences in overpass time of the various satellites, a trajectory model was used to move the CALIOP-derived dust heights in space and time to the IASI, GOME-2 and SCIAMACHY dust height pixels. It is not possible to construct a unique dust-layer height from the CALIOP data. Thus two CALIOP-derived layer heights were used: the cumulative extinction height defined as the height where the CALIOP extinction column is half of the total extinction column, and the geometric mean height, which is defined as the geometrical mean of the top and bottom heights of the dust layer. In statistical average over all IASI data there is a general tendency to a positive bias of 0.5–0.8 km against CALIOP extinction-weighted height for three of the four algorithms assessed, while the fourth algorithm has almost no bias. When comparing geometric mean height there is a shift of −0.5 km for all algorithms (getting close to zero for the three algorithms and turning negative for the fourth). The standard deviation of all algorithms is quite similar and ranges between 1.0 and 1.3 km. When looking at different conditions (day, night, land, ocean), there is more detail in variabilities (e.g. all algorithms overestimate more at night than during the day). For the solar sensors it is found that on average SCIAMACHY data are lower by −1.097 km (−0.961 km) compared to the CALIOP geometric mean (cumulative extinction) height, and GOME-2 data are lower by −1.393 km (−0.818 km).

1 Introduction

Aerosol is identified as an essential climate variable (ECV) by the Global Climate Observing System (GCOS, http://www.wmo.int/pages/prog/gcos/, last access: 7 May 2018). The aerosol-layer height (GCOS product A.10.3) is one of four aerosol parameters which is needed to enhance our understanding of the aerosols' role in the climate system. Furthermore a deeper insight is important for radiative budget analysis, studying chemical and physical interactions in the troposphere, weather forecast modelling, remote sensing and air quality initiatives. Ground-based methods (lidar) offer high accuracy and calibration benchmarks; however their geographical coverage is sparse. Hence, satellite observations of the aerosol-layer height are warranted and the quality of such a product needs to be assessed. As part of the European Space Agency (ESA) Climate Change Initiative (CCI, Hollmann et al., 2013) the Aerosol_cci (Popp et al., 2016) project has conducted a comparison between dust-type aerosol-layer heights from passive and active sensors to identify strengths and possible weaknesses in the estimate of this parameter.

Both active and passive methods may be used to estimate the aerosol-layer height. The Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP) on board the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) satellite (Winker et al., 2009, and https://www-calipso.larc.nasa.gov/) provides detailed vertical information with a vertical resolution of 30 m below 8.2 km and a horizontal footprint of 335 m. Passive solar and thermal infrared satellite instruments may provide global data on a daily basis with horizontal resolution of the order of tens of kilometres. For example, Vandenbussche et al. (2013) retrieved desert dust aerosol vertical profiles from Infrared Atmospheric Sounding Interferometer (IASI) measurements; Cuesta et al. (2015) described the three-dimensional distribution of a dust outbreak over eastern Asia, including dust height and also using IASI measurements; Sanders and de Haan (2013) used the O₂ A-band to retrieve aerosol-layer height from the Global Ozone Monitoring Experiment-2A (GOME-2A). Dust top height may also be estimated using stereo view techniques by either utilizing instruments with multi-angle capabilities (for example the Advanced Along Track Scanning Radiometer, AATSR, Virtanen et al., 2014) or by combining measurement from different sensors (see for example Merucci et al., 2016). For a comprehensive survey on the methodological approaches, technical and scientific challenges of the retrieval of aerosol height, we refer the reader to the recent review by Xu et al. (2018).

The aim of this work is to assess the different aerosol-layer height products from different algorithms for various solar (SCanning Imaging Absorption SpectroMeter for Atmospheric CHartographY, SCIAMACHY, GOME-2) and thermal (IASI) sensors by comparison with CALIOP. The Aerosol_cci project targeted dust-type aerosol for this study. The relatively unambiguous classification of dust by CALIOP and the availability of large dust events possibly avoid any biases due to aerosol misclassification in the aerosol height comparison.

Earlier studies (Capelle et al., 2014; Peyridieu et al., 2010, 2013) compared monthly averaged and gridded data, or investigated a specific episode (Vandenbussche et al., 2013; Cuesta et al., 2015). We perform a point-by-point comparison for selected episodes. Furthermore we account for differences in satellite overpass times using trajectory model analysis. Finally, for the first time, by utilizing data from GOME-2, SCIAMACHY and IASI with their respective spectral and spatial resolutions, results from the different passive infrared and solar algorithms are compared for the same dust episodes to identify strengths and weaknesses. Note that this work focuses on the comparison of dust-layer heights retrieved from active and passive sensors. Comparisons of aerosol dust amount are outside the scope of this work and is discussed elsewhere (Popp et al., 2016).

The remainder of the paper is organized as follows: in Sect. 2 the data and data analysis methods are presented. The results from the aerosol-layer height comparison are given in Sect. 3. The results are discussed in Sect. 4 and followed by the conclusions.

2 Data and methodology

To allow the inclusion of data from the SCIAMACHY instrument that ceased operation in 2012, four desert dust events in 2010 were selected (total 40 days):

• 18–27 March (10 days),

• 22 May–1 June (11 days),

• 1–12 July (12 days),

• 14–20 September (7 days).

The comparison focuses on the region between 0–40^∘ N and 80^∘ W–120^∘ E (see Fig. 2) and is mainly affected by dust from the Sahara but is also influenced by dust from the Middle East, India and western China.

2.1 Active instrument dust height retrievals – CALIOP

CALIPSO is the fourth of the six satellites in the A-Train satellite constellation. All six of the A-Train satellites cross the equator within a few minutes of one another at around 13:30 local time. CALIOP is part of the payload of the CALIPSO platform. The CALIOP laser produces simultaneous co-aligned pulses at 532 and 1064 nm that are used to measure the backscatter profile. The 532 nm pulse is linearly polarized. The return signal is polarized parallel and perpendicular to the outgoing plane and detected by two photomultiplier detectors. The CALIOP aerosol-typing algorithm uses layer-averaged depolarization and the 532 nm attenuated backscatter to classify the aerosol into one of six types: clean marine, dust, polluted continental, clean continental, polluted dust, smoke (Omar et al., 2009). Of the six types the dust aerosol is largely non-spherical, implying a relatively large depolarization ratio and hence relatively unambiguous classification. Numerous data products are available from CALIOP. We use the 5 km profile product from CALIOP data version V4-10. Only dust profiles with CALIOP cloud aerosol discrimination (CAD) values between −100 and −20 are included (Winker et al., 2013). Profiles containing polluted dust and water and ice clouds are excluded. Furthermore we only include dust layers that are continuous; thus, multilayered dust clouds are excluded from the analysis. The dust-layer height is estimated from the extinction coefficient at 532 nm (Extinction_Coefficient_532). The extinction coefficient is a retrieved quantity and we only include profiles for which the quality control flag Extinction_QC_Flag_532 equals 0 (unconstrained retrieval; initial lidar ratio unchanged during solution process) or 1 (constrained retrieval).

2.1.1 CALIOP dust-layer height

Aerosol-layer heights may be termed either “effective” or “real” heights. The effective layer height represents the height at which the total aerosol load should be placed in order to be representative of the radiative properties of this aerosol. The thickness of effective layers are typically assumed to be small, 500 m or 1 km. For climate impact studies effective layer height is an important parameter, as it, together with the aerosol optical depth, single-scattering albedo and phase function, allows quantitative estimates of the aerosols' direct radiative forcing. The real aerosol height may be described in terms of layer boundaries or by the full vertical profile. It is required for the understanding and characterisation of aerosol–cloud interactions, air quality and flight safety.

There is no unique way to calculate the height of a dust layer from CALIOP data. Possible methods include the following:

• Threshold: Calculate the cumulative extinction and set the height to where cumulative extinction is above a prescribed threshold.

• Cumulative extinction: Calculate the cumulative extinction and set the height to where the extinction column is half of the total extinction column.

• Geometric mean: Identify the top and bottom heights of the dust layer and set dust height to the mean of the two.

• Extinction weighted: Weigh the dust-layer height z_i for layer i with an appropriate parameter and calculate the weighted average, for example using the extinction coefficient β_i as in Koffi et al. (2012):

  $$\begin{array}{}\text{(1)}& {\displaystyle }{z}_{\text{CALIOP}}={\displaystyle \frac{\sum {\mathit{\beta }}_i{z}_i}{\sum {\mathit{\beta }}_i}}.\end{array}$$

In Fig. 1 the extinction-weighted and geometric mean CALIOP dust heights are plotted against the cumulative extinction CALIOP dust height for the days and region under study. The extinction-weighted and cumulative extinction methods (right plot) are fairly similar except below about 2.5 km, where the extinction-weighted method gives slightly larger heights. The geometric mean method (left plot) generally gives larger heights than the cumulative extinction method. The geometric mean method is purely geometrical. The cumulative extinction, threshold and extinction-weighted methods use the profile extinction information from CALIOP. Below we present results for one CALIOP height method that includes extinction information and one that is purely geometrical. The extinction-weighted and cumulative extinction methods are nearly the same, R²=0.9942; right plot Fig. 1. To avoid having to arbitrarily set a threshold for the threshold method, we thus present results below for the cumulative extinction and the geometric mean methods.

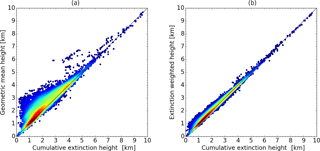
Figure 1 (a) The CALIOP cumulative extinction height versus the CALIOP geometric mean height. Linear regression ($y=ax+b$) gives a=0.882, b=0.6813, R²=0.941 and RMSE = 0.652 km. (b) The CALIOP cumulative extinction height versus the CALIOP extinction weighted height. Linear regression analysis gives a=0.9619, b=0.1597, R²=0.9942 and RMSE = 0.182 km.

It is noted that ambiguities in dust heights derived from CALIOP are larger for thick and optically dense dust layers. In these cases, the inversion of lidar profiles is less accurate for the lower part of these layers due to uncertainties in the lidar ratio for dust and multiple-scattering effects (see e.g. Cuesta et al., 2009, 2015). Multiple-scattering effects are neglected in the CALIOP operational products used here.

2.2 Passive instrument dust height retrievals

The dust-layer height was estimated from measurements by IASI and GOME-2 on board the MetOP-A satellite and SCIAMACHY on board Envisat. MetOP-A orbits in a sun-synchronous mid-morning orbit, crossing the equator at 09:30 local solar time in the descending node. Envisat was in a sun-synchronous polar orbit crossing the equator at 10:00 local solar time (MLST) in the descending node. The various dust height retrieval algorithms used in this study are summarized in Table 1 and described in more detail below.

Vandenbussche et al. (2013)2017Klüser et al. (2011, 2012)Banks et al. (2013)Peyridieu et al. (2010, 2013)Volz (1972, 1973)Capelle et al. (2014)Balkanski et al. (2007)Cuesta et al. (2015)Sanders and de Haan (2013)Lelli et al. (2017)

Table 1 Summary of dust height retrieval algorithms. See text for further details, including definitions of acronyms.

2.2.1 The IASI algorithm at BIRA-IASB: MAPIR

The Mineral Aerosol Profiling from Thermal Infrared (MAPIR) retrieval algorithm is an extensive technical and scientific improvement of the algorithm first published by Vandenbussche et al. (2013). Version 3.5 of the algorithm, fully described in Vandenbussche and De Mazière (2017), is used in this study.

The MAPIR retrieval scheme is based on the optimal estimation method (OEM, Rodgers, 2000), which iteratively adjusts a state vector composed of seven variables: the surface temperature (T_s) and the vertical profile of dust aerosol concentration, from 1 to 6 km height in steps of 1 km. The retrieval is performed only on cloud-free scenes (< 10 % cloud coverage in IASI level 2 cloud product). Unfortunately, the IASI cloud product seems to mislabel some intense dust clouds as meteorological clouds, removing that data from our analysis.

The a priori vertical profile of desert dust concentration is obtained from the LIdar climatology of Vertical Aerosol Structure for space-based lidar simulation studies (LIVAS) monthly $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ climatology derived from CALIOP data (Amiridis et al., 2015). The conversion from 532 nm extinction to particle number concentration is done using the cross section of the aerosol particles used in MAPIR. To account for the fact that CALIOP measurements are sparse, plausibly impacting the continuity of the climatology amongst adjacent $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ (the mean extinction in adjacent cells may come from measurements made for different days), we use a horizontal running mean over 25 cells (5 in latitude, 5 in longitude). The standard deviation for the dust aerosol vertical profile is set to 100 % at all altitudes and locations.

The dust aerosols in MAPIR are parameterized with a log-normal particle size distribution (PSD) with a median radius of 0.6 µm, geometric standard deviation of 2 corresponding to an effective size of 2 µm) and the refractive index from Massie (GEISA-HITRAN dust-like,  1994); Massie and Goldman (GEISA-HITRAN dust-like,  2003); Jacquinet-Husson et al. (GEISA-HITRAN dust-like,  2011).

After the retrievals, quality filters are undertaken. The retrievals are marked to be of good quality when

• the root mean square of spectral residuals is lower than 2 K over land and 1 K over oceans,

• the final fitted aerosol optical depth (AOD) at 10 µm is lower than 8 (otherwise the probability is extremely high that the scene was cloudy and unflagged as such).

The dust detection is computed a posteriori and based on the single criterion that the retrieved 10 µm AOD must be higher than 0.01. This is a very low threshold, and although it ensures that all dust scenes are indeed flagged, it might flag scenes where the aerosol presence is questionable. The AOD is obtained by vertical integration of the concentration profile and multiplication of the extinction coefficient at the desired wavelength. The mean height is obtained from the profile as a linear interpolation of the height that would separate the aerosol column into two identical partial columns (in other words, half the aerosols are below the mean height and half are above it).

2.2.2 IASI DLR algorithm – IMARS

The Infrared Mineral Aerosol Retrieval Scheme (IMARS) for IASI developed at DLR (Deutsches Zentrum für Luft-und Raumfahrt) combines dust and ice cloud remote sensing using principal component analysis (PCA) of the high-resolution IASI spectra (version 4.2). Bayesian inference is used for differentiating between dust and ice clouds (Klüser et al., 2011, 2012, 2015; Banks et al., 2013). The method may also be applied to volcanic ash retrievals (Klüser et al., 2015; Maes et al., 2016), with a focus on the very variable composition of the ash for which there is lack of reliable reports in the literature.

The retrieval uses spectral pattern matching between 8 and 12 µm in a subspace of the observation space, spanned by suited eigenvectors for inferring dust/ash properties from the observations. With this approach direct forward modelling of the infrared radiative transfer is avoided, as this would be strongly underdetermined due to the lack of information on surface emissivity (over deserts), atmospheric temperature, humidity profiles as well as detailed information on dust/ash composition, particle size and sphericity. The composition of dust/ash is assumed to be represented by linear combinations of typical dust composition mixtures (Klüser et al., 2015). For extreme cases not represented by these mixtures (e.g. very high calcite of gypsum content in dust aerosols), the retrieval will not be able to correctly characterize the dust/ash load. Dust optical properties used here have been calculated with traditional Mie theory, thus ignoring particle non-sphericity (see Klüser et al., 2015, 2016; Maes et al., 2016). One of the outputs of the DLR algorithm is the dust/ash emission temperature. Using a vertical temperature profile (standard atmosphere or model output), it is then converted to effective layer height (Klüser et al., 2015). De facto, the emission temperature is retrieved relative to the background, which implicitly delivers height information and not an absolute temperature.

The layer height is an effective emission height of a geometric thin (delta shape) dust layer. This makes its interpretation with regard to an averaged CALIPSO extinction profile non-intuitive. For optically thin dust layers the effective layer height is similar to the mean extinction of the profile; however, with growing dust AOD it moves further up in the profile (details depend on dust properties). Thus we expect a positive bias of the IMARS-layer height to the cumulative extinction height from CALIPSO.

2.2.3 IASI LMD algorithm

The LMD (Laboratoire de Météorologie Dynamique) method for the retrieval of dust characteristics from IASI observations was originally developed for application to the Atmospheric Infrared Sounder (AIRS) (Pierangelo et al., 2004, 2005) and then slightly modified as described in detail in Peyridieu et al. (2010, 2013) and in Capelle et al. (2014) for application to IASI. The method used to derive dust characteristics from IASI observations is a three-step physical algorithm based on a look-up table (LUT) approach. The first step constrains the atmospheric state (temperature and water profile) using 18 channels selected in the spectral range 4.5–14.5 µm and mostly sensitive to temperature and water profiles between 900 and 200 hPa and not, or almost not, sensitive to surface characteristics (temperature, emissivity). The second step simultaneously determines the 10 µm AOD, the dust-layer mean height and the surface temperature using eight channels localized in three window regions: 8–9, 10–12 and 4.6–4.7 µm. This selection of channels, both at short and long wavelengths, is aimed at decorrelating the contribution of AOD, height and surface temperature to the observed signal. The dust coarse-mode particle effective radius can be determined in a third step.

For each step, LUTs of IASI-simulated brightness temperatures are calculated using the forward coupled radiative transfer model 4A/OP-DISORT (available from http://4aop.noveltis.com,  Scott and Chédin, 1981). Entries to the model include AOD, height, surface pressure, surface temperature and emissivity, viewing angle, two refractive indices from Volz (1972, 1973) and Balkanski et al. (2007) and a set of 2311 atmospheric situations. These were selected using statistical methods from 80 000 radiosonde reports and stored in the Thermodynamic Initial Guess Retrieval (TIGR) climatological database (Chédin et al., 1985; Chevallier et al., 1998). The PSD is modelled by a monomodal log-normal distribution described by the effective radius (R_eff) and the standard deviation of the distribution σ_g. Following the results of previous sensitivity studies (Appendix A, Capelle et al., 2014; Pierangelo et al., 2005), fixed values are taken for the effective radius (R_eff=2.3 µm) and for the standard deviation of the size distribution (σ_g=0.65).

The aerosol vertical distribution is supposed to be concentrated within a single homogeneous layer. While this assumption cannot correctly describe observations that are in general more complex, the height retrieved here can be defined as an average weighted height for which half of the dust optical depth is below and half of the optical depth is above. This infrared optical equivalent to the real vertical profile is therefore appropriate for computing dust infrared forcing. It is worth noting that the resulting mean layer height corresponds to height above sea level. Several aspects of the retrieval algorithm, e.g. robustness in the aerosol model (size distribution, shape and refractive indices), possible contamination by other aerosol species, radiative transfer model bias removal or cloud mask including discrimination between clouds and aerosols, were investigated and details may be found, for example, in Pierangelo et al. (2004) and Capelle et al. (2014). The surface emissivity spectrum is supposed to be known and is read from a 0.5^∘ monthly grid retrieved from IASI (Capelle et al., 2012).

2.2.4 IASI LISA algorithm – AEROIASI

The IASI algorithm from LISA (Laboratoire Interuniversitaire des Systémes Atmosphériques), called AEROIASI, has been conceived to observe the three-dimensional distribution of desert dust plumes for each overpass of IASI, both over land and ocean (Cuesta et al., 2015). It derives vertical profiles of desert dust in terms of the extinction coefficient at 10 µm from individual thermal infrared spectra measured by IASI. It is a constrained least-squares fit method, based on explicit radiative transfer calculations, in which the vertical distribution and abundance of dust are iteratively adjusted in order to fit IASI observations. This approach uses auto-adaptive constraints for simultaneously adjusting the dust profile and surface temperature in order to offer particularly good adaptability for different atmospheric and surface conditions. This flexibility makes the aerosol retrieval possible for most cloud-free IASI pixels, both over ocean and land (even for bright surfaces and relatively low aerosol loads). The information on the vertical distribution of dust is mainly provided by their broadband radiative effect, which includes aerosol thermal emission depending on the height of the vertical profile of temperature (assuming local thermal equilibrium).

AEROIASI uses an a priori desert dust model (including dust microphysical properties) and meteorological profiles provided as inputs to the radiative transfer model. The line-by-line Karlsruhe Optimized and Precise Radiative transfer Algorithm (KOPRA,  Stiller, 2000) is used to simulate thermal infrared radiance spectra and the inversion module KOPRAFIT is used to compare them to those measured by IASI, for 12 selected spectral micro-windows in the atmospheric window between 8 and 12 µm. KOPRA accounts for light absorption, emission and single scattering by aerosols, using dust optical properties derived at each wavelength with a Mie code (Metzig, 1984), which is optimized as described in Deirmendjian et al. (1961) and Kerker (1969). The vertical grid of all profiles in the simulations is set between the surface and 9 km height a.s.l. (above mean sea level), with 1 km increments. For each pixel, we use atmospheric temperature profiles and first guesses of surface temperatures and water vapour profiles from ECMWF ERA-Interim reanalysis (Dee et al., 2011). For all seasons and locations, AEROIASI uses a unique a priori vertical profile of dust derived from CALIOP average dust profiles over the Sahara in the summer of 2011.

Once IASI spectra are fitted, a series of quality checks are performed in order to screen out cloudy measurements and aberrant retrievals. We exclude IASI pixels with derived surface temperatures below their ERA-Interim reanalyses counterparts by more than 10 K and those pixels exhibiting too-high root-mean-squared spectral residuals or horizontal variability with respect to their closest pixels. For each quality-checked retrieval, we derive a vertical profile of dust extinction coefficient (α₁₀ in km⁻¹) at 10 µm, the associated AOD (by vertical integration of the extinction profile), and mean and top heights of the observed dust layer. The mean height of the observed dust layer (the product used in the current paper) is defined as the height below which the integral of the extinction coefficient profile reaches 50 % of the AOD. Likewise, the height of the top of the dust layer is defined as the height below which the integral of the extinction coefficient profile reaches 95 % of the AOD. Indeed, AEROIASI provides valuable information, not only on the mean height of the dust layers but also on their vertical extent (i.e. layer-top heights and whether the layers reach the ground or are elevated).

In this study AEROIASI retrievals from version 2 of the algorithm are used. They mainly differ from the previous version described by Cuesta et al. (2015) in the a priori desert dust model and the surface emissivity database. Using these new databases, we obtain lower spectral residuals with respect to IASI measurements than with the previous version and higher adaptability for covering the large region analysed in this paper (i.e. the tropical dust belt). The climatological desert dust model consists of refractive indices, a single-mode log-normal particle size distribution and an a priori vertical profile of dust. Refractive indices are taken from field measurements of Saharan dust analysed by Di Biagio et al. (2014). The modal radius and width of the single-mode distribution are prescribed from average volume effective radius and width for the coarse mode derived from Saharan ground-based stations in June 2011 (for radii > 0.6 µm of the AERONET size distributions, http://aeronet.gsfc.nasa.gov, Dubovik et al., 2002). A unique first guess of dust vertical distribution (the same profile for all pixels and all seasons) is considered in the inversion, which is obtained from an average of CALIOP extinction vertical profiles for dust over the Sahara (during large dust outbreaks in late June 2011), scaled to particle concentration units (in order to set an a priori AOD at 10 µm of 0.03). Forward simulations include surface emissivity from a global monthly IASI-derived climatology over land (Paul et al., 2012) and a surface-temperature-dependent model over ocean (Newman et al., 2005).

2.2.5 GOME-2 KNMI algorithm

The deep oxygen lines (A band and/or B band) in the near infrared of the shortwave spectrum have traditionally been used for retrieval of the cloud height. In the absence of clouds, these bands contain information on the aerosol height (Wang et al., 2012). The algorithm developed at KNMI within the TROPOMI/Sentinel-5 Precursor programme (Veefkind et al., 2012) is based on the optimal estimation method and aims to derive the aerosol-layer height (Sanders and de Haan, 2013). This method has also been applied to Greenhouse gases Observing SATellite (GOSAT) and GOME-2 data within the ongoing ESA AeroPro study, in support of the Sentinel-4 development. The algorithm is sensitive to all aerosol types, including dust, biomass burning and industrial pollution plumes. Sensitivity analyses performed for the TROPOMI/Sentinel-5 Precursor Algorithm Theoretical Basis Document (ATBD) indicate that the aerosol-layer height can be derived with an accuracy of 0.5–1 km if the AOD is 0.3 or larger.

The algorithm uses the Determining Instrument Specifications and Analyzing Methods for Atmospheric Retrieval (DISAMAR) and simulation package developed at KNMI. In the set-up that is used in this work, the aerosol is modelled as a 50 hPa thick layer, for which the height and the aerosol optical depth are fitted. The single-scattering albedo of the aerosol particles is assumed to 0.95 and we apply a Henyey–Greenstein phase function with an asymmetry parameter of 0.7. A climatological value is used for the surface reflectance. Pressure-temperature profiles are obtained from the operational ECMWF forecast. The algorithm uses a fit window between 758 and 762 nm.

The algorithm is only applied to cloud-cleared scenes for which the UV aerosol index has a value exceeding 1.0, indicating the presence of absorbing aerosol layers. For the GOME-2 data used in this work, the cloud clearing is done based on the GOME-2 data itself, which may result in undetected subpixel cloudiness. It is noted that the size of the GOME-2 ground pixels is much larger than for the TROPOMI instrument, for which the algorithm has been designed.

2.2.6 SCIAMACHY IUP algorithm

The IUP (Institute of Environmental Physics) algorithm determines the aerosol layer height using top-of-atmosphere (TOA) reflectances R (defined as the sun-normalized radiances, weighted by the cosine of the solar zenith angle) in the oxygen A-band, that is, in the range 758–772 nm at the nominal spectral sampling 0.21 nm of SCIAMACHY, for a Gaussian instrument response function of 0.48 nm. The retrieval is based on the calculation of the weighting functions $W\left(h,b,\mathit{\tau }\right)=\partial R\left(h,b,\mathit{\tau }\right)/\partial \left(h,b,\mathit{\tau }\right)$, i.e. the Jacobians of R as function of the top and bottom altitude h, b and optical thickness τ of the aerosol layer. Upon linearization of the problem, the measured R in a gaseous absorption band can be written as a function of the desired h. Given that τ is inferred from an independent source, such as a non-absorbing channel outside the oxygen A-band, typically λ=758 nm, the retrieval can be further simplified assuming that either the aerosol layer originates at the ground (b=0 km) or is elevated (b ≠ 0 km). The latter assumption implies that the prior geometrical thickness is preserved when retrieving h. Either way, the problem is reduced to the calculation of W(h) (Rozanov, 2006; Rozanov et al., 2007) and the minimization of the difference between the forward-modelled and the measured reflectance, converging after ∼ 4 iterations on average, which delivers the height of the layer.

Information on the local non-spherical dust optical properties, encoded in the spectral scattering T-matrix (Dubovik et al., 2006), as well as on the single-scattering albedo and the aerosol extinction (box) profiles, are embedded in W(h). It has been assumed that these quantities are independent of height inside the aerosol layer. The HITRAN 2008 edition (Rothman et al., 2009) is used for the line intensities of the absorbing species (oxygen and water vapour) included in the forward problem. The full retrieval chain is implemented and carried out within the radiative transfer model SCIATRAN (Rozanov et al., 2014).

The selection of cloud-free SCIAMACHY pixels (60 × 40 km² of nominal footprint size) relies on the analysis of joint histograms of geometric cloud cover (CC < 0.1, from co-located 1 × 1 km² MEdium Resolution Imaging Spectrometer (MERIS) observations, Schlundt et al., 2011) and aerosol absorbing index (AAI > 1.0, de Graaf et al., 2005) for the area of interest. Surface reflectivity is taken from the MERIS-derived black-sky data set (Popp et al., 2011), which is the critical parameter for the accuracy of the retrieved h. An error of ±10 % in the a priori value of surface reflectivity can cause a bias of up to ±1 km for τ=0.25 and h>3.0 km. More details are given in Lelli et al. (2017) about the IUP algorithm as well as validation with independent measurements when it is applied to an elevated ash layer.

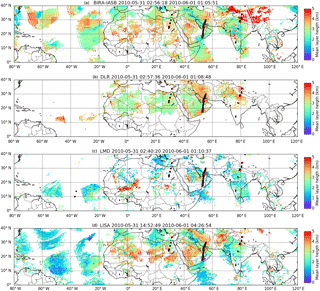
Figure 2 The IASI dust-layer height from the BIRA-IASB (a), DLR (b), LMD (c) and LISA (d) analysis. The CALIOP profiles identified as dust within 500 km and 5 h time differences from nearest IASI pixel are overlaid (red dots). The location of the CALIOP height after shifting to IASI overpass time is shown by the black dots. The time range (UTC) in the title gives the times of the first and last CALIOP points plotted.

2.3 Data selection and comparison methodology

The selection of data and the comparison between CALIOP and the other satellite instrument estimates of dust heights proceed through the following steps for each date listed at the beginning of Sect. 2:

• 1.

  Identify the CALIOP swaths that are within the region of interest.

• 2.

  Identify the closest CALIOP swath and IASI, GOME-2 and SCIAMACHY dust pixels in time and space. Due to the difference in the CALIPSO equator crossing time (13:30) and MetOP-A and Envisat equator crossing times (09:30 and 10:00), a maximum time difference of 5 h is allowed between CALIOP and IASI, GOME-2 and SCIAMACHY dust pixels in this step. To allow for possible movement of dust pixels between overpasses, pixels within 500 km were included for subsequent analysis. This allows for a maximum wind speed of 100 km h⁻¹.

• 3.

  For the CALIOP swaths from step 2, identify CALIOP dust profiles using the CALIOP dust flag and the CAD score. Calculate CALIOP cumulative extinction and geometric mean dust-layer heights.

• 4.

  Move CALIOP dust-layer heights from the previous step backward in time to the Metop-A and Envisat overpass times using the FLEXTRA trajectory model.

• 5.

  After moving the CALIOP dust heights backward in time they may still be at locations that are different from the IASI, GOME-2 and SCIAMACHY dust heights. A second co-location is thus made to co-locate the moved CALIOP dust heights with IASI, GOME-2 and SCIAMACHY dust heights. The maximum difference in distance is set to 20 km for IASI and 100 km for SCIAMACHY and GOME-2, reflecting the larger footprints of the latter two instruments.

• 6.

  Analysis of height differences including statistics.

In Fig. 2 examples of data from steps 1–5 are shown. The pixels identified as dust from IASI data by the BIRA-IASB (Royal Belgian Institute for Space Aeronomy; top plot, Fig. 2), DLR (second plot, Fig. 2), LMD (third plot, Fig. 2) and LISA (bottom plot, Fig. 2) algorithms are overlaid by CALIOP cumulative extinction heights, which are derived from profiles identified as dust (step 3, red dots) that are within the temporal and spatial requirements. CALIOP data are recorded after the IASI overpass. To account for possible movements of dust between the overpasses, the CALIOP dust heights were moved in longitude, latitude and height using the FLEXTRA model (step 4,  Stohl et al., 1995). FLEXTRA calculated mean wind trajectories with meteorological input data from the ECMWF. Here operational data with a 1^∘ latitude $\times \mathrm{1}{}^{\circ }$ longitude resolution, 91 vertical levels and a time resolution of 3 h were used. FLEXTRA does not include turbulence or loss processes. Quantification of trajectory errors is always difficult due to a general lack of ground-truth data. However, FLEXTRA has been quantitatively evaluated in the past. Comparisons of FLEXTRA trajectories driven with ECMWF data with balloon trajectories have revealed typical horizontal transport errors of about 20 % of the travel distance but with large variability from case to case (Baumann and Stohl, 1997; Stohl and Koffi, 1998; Riddle et al., 2006). Evaluation against meteorological tracers such as potential vorticity suggests errors of a similar magnitude (Stohl and Seibert, 1998). Thanks to improvements in the meteorological analysis data, slightly smaller errors may be assumed for more recent years, but the order of magnitude of the errors is likely still similar.

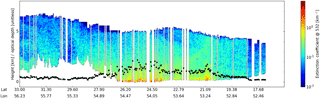
Figure 3 Curtain plot of the CALIOP extinction coefficient for heights identified as dust. The black dots are the column optical depth at 532 nm from CALIOP. The curtain is for the CALIOP data between 40 and 60^∘ E in the top plot of Fig. 2.

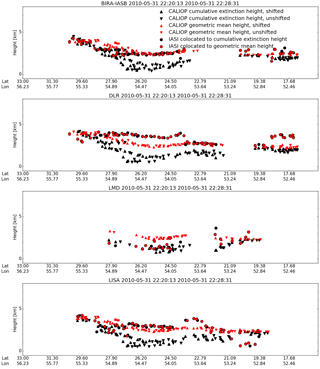
Figure 4 IASI dust-layer heights co-located to CALIOP cumulative extinction heights (black circles) and CALIOP geometric mean heights (red circles) for the same time and location as in Fig. 3. Also shown are shifted (upward triangles) and unshifted (downward triangles) CALIOP cumulative extinction and geometric mean heights.

The black dots in Fig. 2 are CALIOP dust height pixels that have been moved from their original location (red dots) to the nearest IASI pixel (step 5). As the cumulative extinction and geometric mean CALIOP dust heights are different they will be moved by FLEXTRA to different locations. An example of this is seen in Fig. 4, where the cumulative extinction (black circles) and geometric mean (red circles) heights from the passive instruments sometimes overlap (not moved or moved to same location and height) and sometimes do not overlap (moved to different location and/or height). It is also seen in the difference in the number of co-located points (Table 2). For the full data period the CALIOP dust heights were on average moved upwards by 0.015 (cumulative extinction) and 0.020 km (geometric mean), both with standard deviations of 0.25 km.

3 Results

The analysis steps 1–5 in Sect. 2.3 were performed for all days and algorithms. The number of dust pixels identified by the various algorithms after step 1 is given in Table 2. The number of pixels identified as dust by the various IASI algorithms vary by a factor of 4.6. The differences reflect the differences in dust detection methods and it is outside the scope of this study to further investigate the reasons for these differences. As expected the solar algorithms detect far fewer dust pixels due to only daytime coverage (factor of 2) and larger pixels size (factor of about 16). The difference between the two solar algorithms (KNMI and IUP) are due to differences in the constraints set to detect dust. In step 2 dust pixels are selected within a given time and distance from the CALIOP-detected dust pixels. This step reduces the number of IASI data points to between 0.58 and 1.8 % of those in step 1. The number of GOME-2 and SCIAMACHY points are reduced to 17.3 and 73.0 % respectively. The movement of CALIOP dust heights to the MetOp-A and Envisat overpass times and the final co-location of CALIOP heights and dust pixels gives the final number of dust heights to be compared to CALIOP dust heights; see values for step 5 in Tables 2 and 3.

Table 2 The number of data points (dust heights) at the data reducing step of the data analysis chain described in Sect. 2.3. Step number refers to the analysis steps as described in Sect. 2.3.

^a Numbers in parenthesis are data points in percentage relative to the total number in the previous analysis step. ^b Numbers in parenthesis are data points in percentage relative to the total number in analysis step number 2, for example $\mathrm{18.0}=\mathrm{2408}/\mathrm{13377}$ (column 2, row 4).

Inspection of IASI-retrieved dust heights shown in Fig. 2 reveal differences in dust detection and dust height between the various algorithms. While differences in dust detection is not the subject of this paper, we do, however, note that there are substantial differences in the pixels identified as containing dust by the various algorithms. In particular the DLR algorithm detects very little dust over the ocean regions; the BIRA-IASB and LISA algorithms detect dust over the ocean west of 40^∘ W and north of 20^∘ N, whereas the DLR and LMD algorithms do not detect dust in this region; for the example swath plots in Figs. 3 and 4 all algorithms except LMD detect dust north of about 28^∘ N. The BIRA-IASB algorithm's detection of dust over the Himalaya is due to retrievals being undertaken for all non-cloudy scenes, and the final result may never be a true zero due to the method used. These retrievals have a low AOD and their inclusion indicates that the AOD threshold for the dust flag may be too permissive. The differences in dust detection are the reason for the different number of pixels available for comparison with CALIOP.

For the example CALIOP swath shown in Fig. 3 the BIRA-IASB algorithm (red and black circles, Fig. 4) agrees reasonably with the CALIOP geometric mean heights (red triangles) and gives higher dust heights compared to the CALIOP cumulative extinction heights (black triangles). For the DLR algorithm the situation is similar, but the DLR algorithm generally gives larger dust heights. The LMD algorithm heights are generally similar to CALIOP cumulative extinction heights, while LISA algorithm heights are in better agreement with the geometric mean heights. For this transect, BIRA-IASB and LISA algorithms capture the rather monotonous decrease of dust-layer heights from about 4 km in altitude near 30^∘ N to 2 km in altitude at 19^∘ N depicted by CALIOP geometric mean heights. The LMD algorithm retrieves dust heights near 1.5 km at 24–27^∘ N, similar to the CALIOP cumulated extinction estimates. The behaviour for this single overpass is also present in the full IASI data set as shown in Figs. 5–6 and Table 3. However, note that there are substantial differences when comparing the passive methods with the CALIOP cumulative extinction and geometric mean methods. Overall, the CALIOP geometric mean method gives a larger CALIOP dust height (Table 4). Thus, the CALIOP minus passive instrument difference is smaller for the geometric mean method compared to the cumulative extinction method. The geometric mean method also gives slightly smaller standard deviations and more dust heights from the passive instrument within the CALIOP dust layer; see Table 3. This may point to a non-symmetrical vertical distribution of the aerosols, with more aerosol in the lower part of the layer, where IASI algorithms usually have less sensitivity (depending on surface temperature).

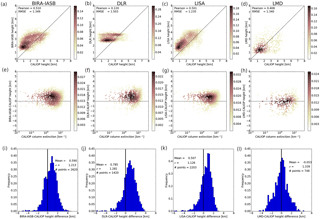
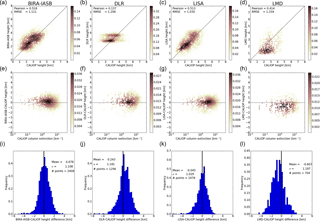
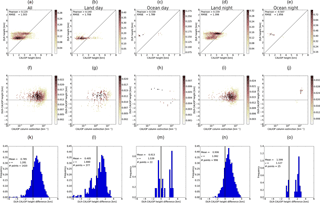
Figure 5 (a–d) The probability density, using kernel density estimation, of the CALIOP cumulative extinction height versus height from the various algorithms. Also given are the Pearson's correlation coefficient and root mean square error (RMSE). (e–h) The probability density, using kernel density estimation, of the difference between the passive algorithm and the CALIOP cumulative extinction heights versus the CALIOP column extinction. (i–l) Frequency distribution of the difference between the height from the various algorithms and the CALIOP cumulative extinction height. The mean and standard deviation (σ) together with the number data points are given in each plot. This information is also provided in Table 3. Data are shown for the BIRA-IASB (a, e, i), DLR (b, f, j), LISA (c, g, k) and LMD (d, h, l) algorithms.

Figure 6 Similar to Fig. 5 but for the CALIOP geometric mean height.

Table 3 The mean ± the standard deviation of the dust height difference between the passive sensors and CALIOP, and the number of co-located points. The inlay is the percentage of heights that are within the CALIOP layer. For BIRA-IASB, DLR, LISA and LMD statistics are given for all data and subgroups of data recorded during daytime and night-time and over land and ocean. For KNMI-GOME2 only day comparisons are possible, hence the lack of comparisons with CALIOP night overpasses. Also note that for KNMI-GOME2 the number of land and ocean pixels does not add up to the total due to some pixels covering coastal regions (mixed pixels).

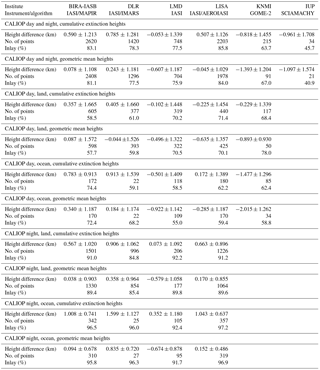
Table 4 CALIOP mean cumulative and geometric mean dust-layer height ±  standard deviation together with the dust-layer thickness ±  standard deviation. Statistics are given for the full data set and for subsets divided into land and ocean for day and night overpasses.

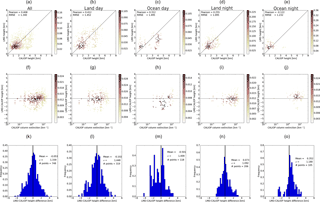
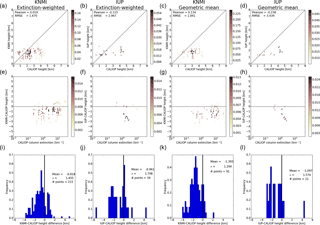
In the upper row of Fig. 5 the CALIOP cumulative extinction height is plotted against the dust heights from all IASI algorithms for all dates. Figure 6 is similar but for the CALIOP geometric mean height method. Also included in the plots are the Pearson's correlation coefficient and root mean square error (RMSE). In the centre rows of Figs. 5–6 the differences between the passive algorithms and CALIOP heights are shown against the CALIOP column extinction. In the upper and centre rows the colour indicates the density of points. The bottom rows of Figs. 5–6 show the frequency distribution of the difference between the dust heights from the various IASI algorithms and the CALIOP heights. Similar plots for the KNMI and IUP algorithms are shown in Fig. 7. For the IASI algorithms ocean-day, ocean-night, land-day and land-night data subsets are presented in Figs. A1–A4 for the CALIOP geometric mean heights and in Figs. A5–A8 for the CALIOP cumulative extinction heights. The mean and standard deviation and the number of data points are also listed in Table 3. It is noted that an analysis in terms of “bias” is only correct as a mean analysis when the difference distribution is at least symmetrical (if not Gaussian). This is not always the case, as shown, for example, for the ocean day subset in Fig. A8. Thus, while the mean of the difference may appear good the histogram sometimes shows something very different.

For the BIRA-IASB, LISA and LMD algorithms versus the CALIOP dust cumulative extinction (geometric mean) height, the Pearson's correlation coefficient is between 0.408 and 0.510 (0.414–0.518). It is smaller for the DLR, KNMI and IUP algorithms, being −0.115 to 0.120 (−0.238 to 0.137). For the IASI algorithms the RMSE is between 1.030 and 1.334 km when compared with the CALIOP geometric mean dust heights. It increases to 1.235–1503 km for the CALIOP cumulative extinction dust heights. For the KNMI and IUP algorithms the RMSE is larger, at 1.670–3.439 km. The rather large RMSE indicates the difficulty and uncertainty involved when comparing dust heights from very different sensors and data recorded at different times with large differences in footprint size. There appears to be no dependence on height differences on dust column extinction as shown in the centre rows of Figs. 5–7.

For the IASI algorithms both day and night-time data are included in Figs. 5–6. The mean height difference between the various algorithms and the CALIOP heights are given in Table 3. The BIRA-IASB mean height difference is 0.078 km (0.590 km) when compared with the CALIOP geometric mean (cumulative extinction) height. The DLR algorithm mean height difference of 0.243 km (0.785 km) is larger. However, it is noted that the DLR algorithm generally gives the altitude at two distinct modes (Fig. 5). For LMD the magnitude of the mean height difference is smallest when compared with the CALIOP cumulative extinction height, −0.053 km. It increases to −0.607 km when compared with the CALIOP geometric mean height. For the LISA algorithm the behaviour is similar to the BIRA-IASB and DLR algorithms with mean height differences of −0.045 km (geometric mean) and 0.507 km (cumulative extinction). Scatter plots in Figs. 5–6 (upper panels) reveal rather elongated clouds of points along (parallel to) the 1 : 1 straight line for BIRA-IASB and LISA with respect to the geometric mean (cumulative extinction) heights from CALIOP, whereas the point cloud is mainly localized below 2 km in altitude for LMD and above 2.5 km for DLR (this last one presents maxima of occurrences). The standard deviations are similar for the BIRA-IASB, DLR, LMD and LISA algorithms between 1.029–1.187 km (geometric mean) and 1.126–1.339 km (cumulative extinction), but are slightly lower for LISA, intermediate for BIRA-IASB and DLR, and to some extent greater for LMD.

Due to the larger footprint size of the solar sensors, fewer data points are available for dust height comparison of CALIOP with GOME-2 and SCIAMACHY. The statistics for all co-located GOME-2 and SCIAMACHY with CALIOP points are summarized in Fig. 7 and Table 3. Both algorithms give lower dust heights compared to CALIOP, with IUP being on average lower by −1.097 km (−0.961 km) compared to the CALIOP geometric mean (cumulative extinction) height and KNMI lower by −1.393 km (−0.818 km).

Figure 7 Similar to Figs. 5–6 but for the KNMI (a, e, i, c, g, k) and IUP (b, f, j, d, h, l) algorithms versus the CALIOP cumulative extinction (a, e, i, b, f, j,) and geometric mean (c, g, k, d, h, l) dust heights.

The features seen in the upper rows of Figs. 5–7 reveal that height differences may depend on region and time of day or other variables. It is well known that CALIOP daytime measurements are more noisy due to stray light from the sun. Thus, to investigate possible differences between night-time and daytime data the differences between CALIOP heights and the passive algorithm heights were calculated separately for night and day and also for land and ocean. For each IASI algorithm, plots similar to those in Figs. 5–6 for ocean-day, ocean-night, land-day and land-night data subsets are shown in Figs. A1–A4 for the CALIOP geometric mean heights and in Figs. A5–A8 for the CALIOP cumulative extinction heights. The results are also summarized in Table 3.

For BIRA-IASB the mean difference is similar over land during the day (0.087 km) and at night (0.038 km) when compared with the CALIOP geometric mean height. For the cumulative extinction height the mean difference increases from 0.357 km during the day to 0.567 km at night over land. Over the ocean the mean difference is somewhat larger during the day (0.340 km) than at night (0.094 km) for the geometric mean height, while it is the opposite for the cumulative extinction height, being 0.783 km (day) and 1.008 km (night). For DLR few data points are available over the ocean. Over land the mean difference is smaller for the daytime data than the night-time data, being −0.044 km (0.405 km) and 0.358 km (0.906 km) respectively for the geometric mean (cumulative extinction) height. For LMD the dust heights over land are found to be smaller than the CALIOP geometric mean (cumulative extinction) height during the day than at night, −0.496 km (−0.102 km) versus −0.579 km (0.073 km). Over the ocean the behaviour is similar, but the differences are somewhat larger; see Table 3. The magnitude of the mean LISA difference is larger during the day (−0.635 km) than at night (0.170 km) over land for the geometric mean height. For the cumulative extinction height the behaviour is the opposite, being −0.225 km during the day and 0.663 km at night. Over the ocean similar behaviour is observed. For nearly all comparisons the RMSE is smaller for the night-time data than the daytime data, most likely reflecting the lower noise in the CALIOP night-time data. These findings are further discussed and illustrated with plots in Appendix A. The KNMI-GOME-2 dust heights compare better with the CALIOP cumulative extinction (geometric mean) dust heights over land, with a difference of −0.229 km (−0.893 km), than over ocean, for which it is −1.477 km (−2.015 km; Table 3).

The four dust episodes investigated may have dust with different optical characteristics that may have an effect on the retrieved dust heights. The comparison was therefore further subdivided into four time periods representing the episodes. Investigations into the difference between the height from the various algorithms and the CALIOP cumulative extinction and geometric mean heights for the four episodes reveal no clear temporal variations.

For the full data set mean height differences vary between −0.607 and 0.243 km (geometric mean) and −0.053 and 0.785 km (cumulative extinction) for the IASI algorithms and −1.393 and −1.097 km (geometric mean) and −0.961 and −0.818 km (cumulative extinction) for the solar algorithms (Table 3). The percentage of retrieved heights from the passive sensors that are within the dust layer as seen by CALIOP, are given in Table 3. Here the CALIOP dust layer is the lowermost and uppermost heights identified as dust. For the IASI algorithms, between 75.9 and 85.8 % of the retrieved heights are within the CALIOP dust layer. The highest percentage is achieved by LISA at night over the ocean with up to 96.9 % (geometric mean) and 97.2 % (cumulative extinction) dust heights located within the CALIOP dust layer (for a subset of respectively 319 and 357 points).

The average CALIOP dust-layer thickness is 2.35 km over land during the day and 2.54 km over the ocean (Table 4). For the night the layer thickness is 3.55 km over land and 3.70 km over ocean. Thus, over land the dust-layer thickness is larger at night than during the day by about 1.12 and 1.16 km over the ocean. The dust layer over land is about 0.680–1.42 km higher than over ocean. It is lower by 0.52–1.02 km at night than during the day over the ocean. This is mainly caused by different regions being sampled at night-time and daytime overpasses. Most of the concurrent IASI and CALIOP night-time data are from the Persian Gulf and the Red Sea (lower dust height), while the daytime data are more evenly distributed over the study area.

4 Discussion

We have compared dust-layer heights from various passive sensors with CALIOP-derived heights. The CALIOP heights are considered the “true” values. However, the CALIOP heights are not unique as described in Sect. 2.1.1; thus we have used two different CALIOP-derived heights. For the cumulative extinction CALIOP height method, the lidar ratio is involved. This may be different for different regions and time of year, thus adding to the uncertainty in the comparison. The CALIOP analysis may also misclassify aerosol as discussed by Kim et al. (2013). The latter is largely avoided in this study by focusing on dust aerosol which has a relatively large depolarization ratio. Different methods used to calculate CALIOP heights are compared in Fig. 1. The RMSEs for the height methods are 0.652 and 0.182 km. These numbers should be kept in mind for the comparison results presented above.

While comparable, the heights retrieved from CALIOP and IASI are not the same quantities due to the instruments different sensitivities to various aerosol particle sizes and the assumptions of aerosol optical properties (lidar ratio, refractive index, particle shape) used in the retrieval. A full understanding of the reason for the differences requires a detailed algorithm comparison which is beyond the scope of this study. It is noted that infrared sensors have lower sensitivity to low dust height caused by the small temperature difference between the temperature of the surface and the temperature of the dust. For example, for the BIRA-IASB algorithm the lowest possible retrieval height is around 1.2 km due to low sensitivity to dust at a lower height. For the DLR algorithm a positive bias with respect to the CALIOP cumulative extinction height was predicted (Sect. 2.2.2). A positive bias between 0.0405 (day) and 0.906 km (night) is indeed found over land surfaces; see Table 3.

Overall the standard deviation of the difference between CALIOP heights and the passive sensor heights is smaller for the night-time data than for the daytime data (Table 3). This is most likely due to less noise in the CALIOP night-time data. Standard deviations are generally similar for ocean and land data, but there are differences for individual algorithms, indicating opportunities for future improvements.

There is quite a large difference between day and night over the ocean and all algorithms overestimate more at night than during the day over ocean (Table 3). Due to the differences in satellite overpass times, different regions are sampled for night-time and daytime overpasses. Most of the concurrent IASI and CALIOP night-time data are from the Persian Gulf and the Red Sea (lower dust height), while the daytime data are more evenly distributed over the study area. The differences seen between night-time and daytime data may thus be caused by differences in optical properties of the dust between the two regions, which is not accounted for by the retrieval algorithms.

The CALIOP heights are moved to the SCIAMACHY and GOME-2 overpass times. On average the vertical shift is small, being between 0.015 and 0.020 km with a standard deviation of 0.25 km. For individual data points the shift may be larger (compare shifted and unshifted black and red triangles in Fig. 4). This suggests that, when comparing data sets from satellite sensors with different overpass times, transport processes should be accounted for in the analysis. Moreover, the spatial resolutions of the IASI, GOME-2 and SCIAMACHY instruments are much coarser than CALIOP. The impact of differences in spatial resolution has not been investigated, but it is assumed to be small within large dust clouds as studied here.

It is not straightforward to estimate an uncertainty for the IASI height retrievals as this would require a sensitivity study that is beyond the scope of this work. A best-guess estimate would be that the uncertainty is of the order of 1–1.5 km. Vandenbussche et al. (2013) found that for low dust loads, the BIRA-IASB algorithm placed the aerosol layer 1–2 km above the CALIOP-retrieved layer. The algorithm has since undergone several revisions and improvements and the average overestimate for all data is 0.078 km (0.590 km) when compared with the CALIOP geometric mean (cumulative extinction) height. Possible reasons for this overestimate are discussed above. Vandenbussche et al. (2013) reported better agreement for moderate to higher dust loads compared to low dust loads. In the present study no effect of the dust load on dust height agreement appears to be present; see centre row plots of Figs. A1 and A5.

For monthly mean $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ gridded IASI data covering the period July 2007–June 2013, Capelle et al. (2014) reported a systematic IASI-CALIOP bias of 0.4 km with a standard deviation of 0.48 km over the ocean. Peyridieu et al. (2013) reported similar values for the same data set. In this study for LMD over ocean, a bias of −0.922 km (−0.501 km) against the CALIOP geometric mean (cumulative extinction) height is found for data recorded during the day overpasses with a standard deviation of 1.142 km (1.409 km). For the night overpasses the differences are −0.674 km (0.352 km) and the standard deviation 0.878 (1.180) (Table 3). One reason for the larger spread in this study may be the use of monthly and spatially averaged data by Peyridieu et al. (2013) and Capelle et al. (2014), while here the comparison is made on a pixel-by-pixel basis. Hence, extreme values are not averaged out.

Overall, for the IASI algorithms, two algorithms (BIRA-IASB and LISA) agree better with the CALIOP geometric mean height, while LMD agrees better with the CALIOP cumulative extinction height (Table 3). The DLR algorithm generally gives altitudes at two distinct modes but agrees better overall with the geometric mean height. This may indicate that the IASI algorithms do not provide the same height information. The BIRA-IASB and LISA algorithms retrieve an aerosol profile from which dust height is calculated. The LMD algorithm, however, uses single-layer aerosol in the retrieval, while DLR estimates the altitude from the retrieved dust layer temperature. The comparison with the two CALIOP heights suggests that the profile retrieval is generally more sensitive to the actual dust-layer vertical location. Both the BIRA-IASB and LISA algorithms use 1 km vertical steps, but with 1.5–2 degrees of freedom there is a significant correlation between the layers and therefore a low sensitivity to the actual high-resolution vertical distribution represented in the cumulative extinction height. Mean altitudes from those retrievals would then be something resembling geometric mean height. Contrary, the LMD algorithm, which places the aerosol in a single homogeneous layer, is more sensitive to the aerosol layer radiative effective height. It is also important to note that the sensitivity of the IASI algorithms does not only depend on aerosol load but also on the temperature profile.

The BIRA-IASB algorithm use CALIOP profiles as a priori which implies that the BIRA-IASB altitude data include information about the CALIOP data to which it is compared. However, the (monthly) a priori profile is averaged over a large spatial area ($\mathrm{5}{}^{\circ }\times \mathrm{5}{}^{\circ }$), therefore including measurements from different days and most probably even different dust events. Furthermore, the retrievals usually differ significantly from the a priori profile. Thus the a priori profile used for a single retrieval is only vaguely related to the exact CALIOP profile used for the validation. The LISA algorithm also uses an a priori profile of dust derived from a CALIOP climatology, but it is a unique a priori profile for all retrievals. Therefore, it is not related to the CALIOP measurements used in the validation.

It is noted that all IASI algorithms assume the dust particles to be spherical. Klüser et al. (2016) compared optical properties of spherical and non-spherical dust particles. They found the values of the dust single-scattering albedo to be different for spherical and non-spherical dust particles. This may potentially affect the dust height retrieval. It is beyond this study to investigate and quantify this effect.

The heights from the passive solar IUP-SCIAMACHY and KNMI-GOME-2 algorithms are generally low compared with the CALIOP height (Table 3). While IASI is mainly sensitive to the aerosol coarse mode, SCIAMACHY and GOME-2 are sensitive to both the fine and coarse modes. The height retrieved from these sensors depends on whether the surface albedo is retrieved simultaneously or not as shown by Sanders et al. (2015). They found that fixing the albedo in the retrieval gave a lower dust height than when retrieving both the albedo and the dust height. Fixing the albedo also gave better agreement with lidar measurements for the 16 scenes they analysed. Dubuisson et al. (2009) made sensitivity studies for the retrieval of aerosol height from POLarization and Directionality of the Earth's Reflectances (POLDER) and MERIS oxygen A-band measurements. They showed that aerosol height estimates vary with AOD, single-scattering albedo, aerosol phase function, aerosol-layer height, and the underlying surface albedo. For low surface albedo theoretical analysis gave errors of about ±0.5 and ±0.2 km for POLDER and MERIS respectively. A comparison between POLDER and CALIOP gave standard deviations less than about 0.55 km, consistent with the theoretical analysis. However, for parts of the three cases along the coast of Africa, the aerosol height was underestimated by up to 1–2 km. Dubuisson et al. (2009) attributed this to either a more complex vertical aerosol structure, including a layer near the surface, or the presence of low clouds under the aerosol layer. The theoretical sensitivity results of Dubuisson et al. (2009) was confirmed by Kokhanovsky and Rozanov (2010), whose modelling sensitivity study indicated aerosol heights within ±0.5 km if the aerosol single-scattering albedo used in the retrieval deviated by less then 0.01 from the actual value of 0.99. They also reported that the error increased with dust-layer-top height.

It must be stressed that the reported errors on dust height, based on synthetic sensitivity studies, are estimated with the assumption that either AOD, the optical model or the surface reflectance are perfectly known beforehand or are derived from independent instrument channels. For instance, Dubuisson et al. (2009) make first use of the official POLDER and MERIS AOD products, while focusing on dark ocean surfaces only. Then, they find the most accurate aerosol model (pure dust or a mixture with sea salt or biomass burning) by perturbing the reflectance in a non-absorbing channel. Conversely, the solar algorithms of this work have been designed to fit the oxygen spectrum to concurrently infer dust height and optical thickness together, so that AOD and height uncertainties cannot be decoupled and deviations of the assumed optical model and climatological surface reflectivity from the actual ones contribute to the overall error budget. As such, the evaluation of the presented dust cases can be regarded as a more comprehensive test bed for operational dust height retrievals.

Xu et al. (2017) combined oxygen A and B-band measurements from the Earth Polychromatic Imaging Camera (EPIC) on the Deep Space Climate Observatory (DSCOVR) to retrieve AOD and height, finding that 71.5 and 98.7 % aerosol heights were respectively within ±0.5 and ±1.0 km envelopes when compared to CALIOP for two overpasses of Saharan dust events over water only. Their reported rms error, in this case, amounts to 0.45 km, pointing to the advantage of adding the information concealed in the B-band to the retrieval .

Generally, we found the IUP-SCIAMACHY and KNMI-GOME-2 algorithm retrieved heights to be lower by -1.097 km (−0.961) and −1.393 km (−0.818) respectively when compared with CALIOP geometric mean (cumulative extinction) heights. For the KNMI-GOME-2 algorithm the underestimate is larger over ocean −2.015 km (−1.477) than over land −0.893 km (−0.229; Table 3). These differences are larger than those reported in the above-cited studies. Still, it is found that for KNMI-GOME-2 (IUP-SCIAMACHY) between 63.7–67–0 % (40.9–45.7 %) of the aerosol heights are within the CALIOP aerosol layer. For KNMI more of the retrieved heights are within the CALIOP aerosol layer over land than ocean (Table 3).

In general, possible reasons for the underestimation of layer height by the solar sensors are the local optical dust properties and the surface reflectivity assumed in the forward model. While it has been already demonstrated that a positive deviation of the true surface albedo from the assumed prior value leads to an underestimation of layer height (Sanders et al., 2015), the similar tendency of lower retrievals by GOME-2 and SCIAMACHY suggests that the influence of a wrongly prescribed aerosol model can be ruled out. This is because the KNMI/GOME-2 algorithm uses a Henyey–Greenstein phase function, whereas IUP-SCIAMACHY ingests spectrally resolved T-matrix calculations of the phase matrix representing aspherical dust particles (see Table 1).

To this end, we note that the algorithms of the solar spectrometers assume that satellite pixels are fully covered by dust. Because of their coarse footprint sizes, this condition frequently cannot be satisfied. The EPIC pixel size is 12 × 12 km² compared to 80 × 40 km² for GOME-2 and 30 × 60 km² for SCIAMACHY. Thus the results of Xu et al. (2017) are likely to be less affected by cloud contamination and aerosol inhomogeneities. A situation of partially aerosol-covered pixels implies that fewer oxygen molecules are shielded by the intervening scatterers, with the effect of increasing absorption inside the A-band sensed by the instruments. This effect is even more pronounced closer to the ground, where the majority of oxygen molecules reside. Since most of the information content on the height of the aerosol layer is carried by the in-band wavelengths of the A-band (about 760 nm) ratioed to the continuum (758 nm), it can be deduced that a dust pixel fraction smaller than 1 will lead to an additional underestimation of layer height.

We end the discussion by listing several questions left open by this study. These questions may broadly be divided into two sets: (1) questions requiring analysis of a larger data set to consolidate findings and (2) questions requiring a more detailed analysis to better understand the reasons for the differences. Some specific open questions are as follows:

• 1a.

  How will the results change when including other types of aerosol in the analysis?

• 1b.

  How will a larger data set in time and space affect the results?

• 1c.

  Could an optimal aerosol height algorithm covering all situations be developed?

• 2a.

  What are the physical reasons for the differences between the IASI algorithms?

• 2b:

  What are the physical reasons for the differences between the solar algorithms?

• 2c.

  What are the physical reasons for the differences between the quantities estimated by the IR and solar algorithms?

• 2d.

  How may synthetic data be used to understand and evaluate the various algorithms?

• 2e.

  Which pixel-level uncertainties can we estimate to the layer height results of each algorithm (based on studies 2a–2d)?

5 Conclusions

As part of the ESA Aerosol_cci project dust aerosol heights retrieved from passive infrared and solar sensors using different algorithms have been compared with two different CALIOP-derived dust-layer heights. The comparison was made on a pixel-by-pixel basis for the IASI, GOME-2 and SCIAMACHY sensors for four dust episodes in 2010. Time differences between the overpass of CALIOP and the passive sensors were accounted for by shifting the CALIOP heights to the location of the pixels of the passive sensors using the FLEXTRA trajectory model.

As it is not possible to construct a unique dust-layer height from CALIOP data, two CALIOP-derived layer heights were used: the cumulative extinction height, which is set to the height at which the CALIOP extinction column is half of the total extinction column, and the geometric mean height, which is defined as the geometrical mean of the top and bottom heights of the dust layer.

Four algorithms (BIRA-IASB, DLR, LMD, LISA) retrieved dust heights from IASI spectra. The mean difference between the IASI heights and the CALIOP geometric mean (cumulative extinction) heights was found to vary between −0.635 and 0.087 km (−0.225 and 0.405 km) over land during the day. For night-time overpasses the values were between −0.579 and 0.358 km (0.073 and 0.906 km). Over the ocean day differences were between −0.922 and 0.340 km (−0.501 and 0.913 km) and night-time differences were between −0.674 and 0.835 km (0.352 and 1.599 km). Standard deviations were between 1.322 and 1.572 km (1.448–1.665 km) over land during the day and decreased to 0.855–1.058 km (0.896–1.092 km) at night. Over the ocean the standard deviation decreased from 1.142 to 1.187 km (0.913–1.539 km) during the day to 0.486–0.878 km (0.637–1.180 km) at night.

Two of the IASI algorithms (BIRA-IASB and LISA) were found to agree better with the CALIOP geometric mean height (BIRA-IASB: 0.078 km, cumulative extinction 0.590 km; LISA: −0.045 km, 0.507 km), while the LMD algorithm agreed better with the CALIOP cumulative extinction height of −0.053 km (geometric mean: −0.607 km). This is believed to be caused by the differences in the aerosol profile used for the radiative transfer simulations: BIRA-IASB and LISA use and retrieve vertically extended and resolved profiles, while LMD place all the aerosols in one single homogeneous layer.

Far fewer data points were available for the solar sensors due to their larger pixel size and lack of night-time data. The heights retrieved from the solar sensors on average underestimate the CALIOP geometric mean (cumulative extinction) heights by −1.393 km (−0.818 km) (KNMI, GOME-2) and −1.097 km (−0.961 km) (IUP, SCIAMACHY). This may be caused by the large pixel size and the assumption in the retrieval that the pixels are fully covered by aerosol.

The IASI instrument was first flown in 2006 and was the first of several to be launched. Thus data from IASI have the potential to provide long global time series of ECVs. There is considerable variation between the IASI-retrieved dust heights. Nevertheless, if careful consideration is taken for differences in temporal and spatial characteristics of the observations, it might be feasible to construct a global data set of quality-controlled IASI-retrieved heights against CALIOP. The quality control will allow uncertainties on a pixel-by-pixel basis, which again may be used for sensitivity studies. This dust height data set may be used to further our understanding of dust on the climate system. However, several open questions should be answered to have a better understanding of the quantities measured and their accuracy. A list of open questions are given at the end of the discussion section and includes both studies requiring large data sets and time periods, and studies looking at algorithm specifics.

Finally, the various algorithms and instruments are different in their approaches to retrieving dust height. In the comparison with CALIOP no single algorithm is found as the best overall. Different methodologies may give best results in different locations and situations. Thus it seems fruitful to continue the development of all algorithms and encourage comparison exercises.

Appendix A: Additional figures

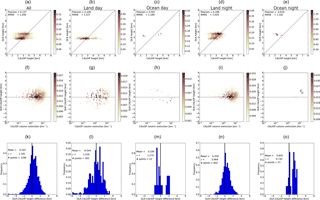
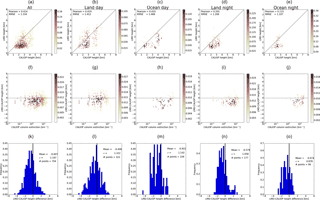
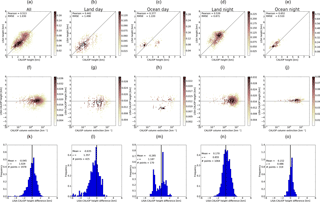
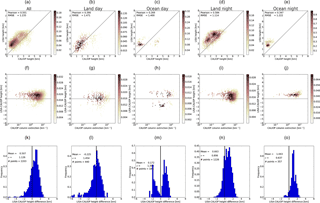
In Figs. A1–A4 statistics are shown for all data, and land-day, ocean-day, land-night and land-day subsets for all IASI dust height retrieval methods compared with the CALIOP geometric mean heights. Figures A5–A8 show similar data but using the CALIOP cumulative extinction heights.

The plots in Figs. A1–A8 reflect the findings presented in Table 3. The BIRA-IASB algorithm agrees well with the CALIOP geometric mean height over land for day and night (Fig. A1). Over ocean the agreement is better at night. It is noted that for the ocean-day subset the histogram is bimodal. When compared with the cumulative extinction height (Fig. A5), the BIRA-IASB dust height is overestimated over ocean during both day and night; the ocean day subset appears to be bimodal; and the agreement appears to be better over land during the day than at night, but this may in part be due to a bimodal histogram for the land day subset. This is reflected in the spread in the difference, which is smaller at night than during the day. For DLR (Figs. A2 and A6) there are few data points available over the ocean. Over land the DLR height data are clumped at a single height for the day subset and at two heights for the night-time data subset. For LMD (Figs. A3 and A7) the agreement is mono-modal for the land day, land night and ocean night subsets when compared with both the CALIOP cumulative extinction and geometric mean heights. For the ocean day subset a bimodal distribution may be present. Overall the agreement is better when compared with the cumulative extinction height. The LISA data (Figs. A4 and A8) also have a bimodal ocean day distribution compared with the CALIOP heights. For the ocean the mean difference with the CALIOP cumulative extinction height is significantly larger at night than during the day. This difference is nearly a factor of 2 smaller when compared with the geometric mean height. For land the magnitude of the difference is smallest when compared with the cumulative extinction height during the day and with the geometric mean height at night.

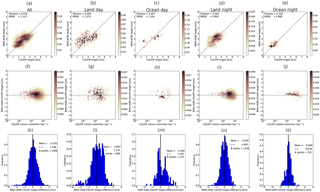
Figure A1 (a–e) Scatter plots of the CALIOP geometric mean height versus height from the BIRA-IASB algorithm. (f–j) Scatter plot of the difference between the BIRA-IASB and CALIOP heights versus the CALIOP column extinction. (k–o) Frequency distribution of the difference between the height from the BIRA-IASB algorithm and the CALIOP height. The mean and standard deviation of the normal distribution are given in each plot. (a, f, k) All data points. (b, g, l) CALIOP daytime data and IASI land pixels. (c, h, m) CALIOP daytime data and IASI ocean pixels. (d, i, n) CALIOP night-time data and IASI land pixels. (e, j, o) CALIOP night-time data and IASI ocean pixels.

Figure A2 Similar to Fig. A1 but for the DLR algorithm.

Figure A3 Similar to Fig. A1 but for the LMD algorithm.

Figure A4 Similar to Fig. A1 but for the LISA algorithm.

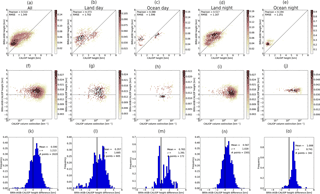
Figure A5 (a–e) Scatter plots of the CALIOP cumulative extinction height versus height from the BIRA-IASB algorithm. (f–j) Scatter plot of the difference between the BIRA-IASB and CALIOP heights versus the CALIOP column extinction. (k–o) Frequency distribution of the difference between the height from the BIRA-IASB algorithm and the CALIOP height. The mean and standard deviation of the normal distribution are given in each plot. (a, f, k) All data points. (b, g, l) CALIOP daytime data and IASI land pixels. (c, h, m) CALIOP daytime data and IASI ocean pixels. (d, i, n) CALIOP night-time data and IASI land pixels. (e, j, o) CALIOP night-time data and IASI ocean pixels.

Figure A6 Similar to Fig. A5 but for the DLR algorithm.

Figure A7 Similar to Fig. A5 but for the LMD algorithm.

Figure A8 Similar to Fig. A5 but for the LISA algorithm.