Instrument artifacts lead to uncertainties in parameterizations of cloud condensation nucleation

The concentrations of cloud condensation nuclei (CCN) modulate cloud properties, rainfall location and intensity, and climate forcings. This work assesses uncertainties in CCN measurements and the apparent hygroscopicity parameter (κ_app), which is widely used to represent CCN populations in climate models. CCN measurements require accurate operation of three instruments: the CCN instrument, the differential mobility analyzer (DMA), and the condensation particle counter (CPC). Assessment of DMA operation showed that varying the ratio of aerosol to sheath flow from 0.05 to 0.30 resulted in discrepancies between the κ_app values calculated from CCN measurements and the literature value. Discrepancies were found to increase from <1 % to 13 % for both sodium chloride and ammonium sulfate. The ratio of excess to sheath flow was also varied, which shifted the downstream aerosol distribution towards smaller particle diameters (for excess flow < sheath flow) or larger particle diameters (for excess flow > sheath flow) than predicted. For the CPC instrument, undercounting occurred at high concentrations, resulting in calculated κ_app lower than the literature values. Lastly, undercounting by CCN instruments at high concentration was also assessed, taking the effect of supersaturation on counting efficiency into account. Under recommended operating conditions, the combined DMA, CPC, and CCN uncertainties in κ_app are 1.2 % or less for 25 to 200 nm diameter aerosols.

1 Introduction

Aerosol–cloud interactions represent a major uncertainty in current predictions of the Earth's climate (IPCC, 2013). According to the well-known Köhler theory, an aerosol's potential to catalyze cloud droplet formation by activating as a cloud condensation nucleus (CCN) depends on its physical and chemical properties. For any given composition, the CCN activation potential of an aerosol increases as its diameter decreases. While the relationship between aerosol diameter and CCN activation is straightforward, the effect of composition on an aerosol's ability to participate in cloud formation is more complex (Petters and Kreidenweis, 2013; Ovadnevaite et al., 2011). Predicting the cloud forming capacity of various air masses based on the properties of the aerosol they contain is essential for evaluating relative contributions from pollution, continental background, and marine aerosol sources (Brooks and Thornton, 2018; Carslaw et al., 2013). Long-term CCN measurements are available from numerous locations globally (Schmale et al., 2018). However, understanding regional and temporal variability in CCN populations requires the ability to assess whether observed differences reflect true physical differences or simply variations in CCN sampling strategies.

Parameterizations of CCN activity that accurately prescribe CCN measurements are needed for climate models, cloud-resolving models, and air quality predictions (Morales Betancourt and Nenes, 2014; Betancourt et al., 2013; Chang et al., 2017; Crosbie et al., 2015; Karydis et al., 2012; Kawecki and Steiner, 2018). One parameterization was designed to represent the cloud droplet activation potential ambient aerosol masses of unknown composition with a single variable, kappa (κ), based on the dry aerosol's hygroscopicity or ability to uptake water and form a solution droplet (Petters and Kreidenweis, 2007). Various names and abbreviations have been given to κ throughout the literature: hygroscopicity parameter, single hygroscopicity parameter, κ (Petters and Kreidenweis, 2007; Carrico et al., 2008; Asa-Awuku et al., 2010; Moore et al., 2012b), CCN-derived κ, κ_CCN (Carrico et al., 2008; Petters and Kreidenweis, 2007), and the apparent hygroscopicity parameter κ_app (Sullivan et al., 2009; Collins et al., 2016; Petters and Kreidenweis, 2013). The term apparent hygroscopicity is favored by many because it emphasizes that fact that while CCN activation can often be predicted accurately by hygroscopic water uptake, they are different physical processes. It is possible for a compound to have high intrinsic hygroscopicity and low apparent hygroscopicity if it is poorly soluble in water (Sullivan et al., 2009).

Parameterizations of hygroscopicity that predate Petters and Kreidenweis (2007) exist as well. Winkler (1973) developed an equation for approximating the growth of an aerosol particle with relative humidity, based on the quantity and physical characteristics of the soluble species in the particle. Another approximation for the relationship between the equilibrium size of a particle and relative humidity was derived by Fitzgerald (1975), in which the soluble fraction and composition of the soluble component(s) are taken into account. Fitzgerald et al. (1982) derived a particle composition parameter using the mass fraction and physical properties of soluble material in a particle. Kreidenweis et al. (2005) determined that the critical activation diameter of dry aerosol particles can be calculated from simplified Köhler theory using the physical properties of water and the solute in a solution droplet. This parameterization has been used in CCN closure studies (Bougiatioti et al., 2009; Moore et al., 2011, 2012a). The earliest prediction of CCN concentrations for specific particle diameters and hygroscopicity used this parameterization as well (Mochida et al., 2006).

Once calculated, hygroscopicity parameters are useful tools for comparing CCN field measurements conducted in various regions and seasons and for making predictions about cloud formation, aerosol–cloud interactions in weather, and climate models. Values of κ_app can be used to compare the CCN results in field and laboratory studies, including sea spray aerosol. For example, aggregation of results from several mesocosm experiments and marine field studies found submicron (30–100 nm) κ_app for sea spray aerosol as low as 0.4 and as high as 1.3 (Collins et al., 2016). Another study, which included a survey of observational CCN data, reported that marine and continental aerosols could be described by κ_app values of 0.7±0.2 and 0.3±0.1, respectively (Andreae and Rosenfeld, 2008).

Several studies have examined the sensitivity of models to κ values derived from humidified tandem differential mobility analyzer (HTDMA) measurements. An analysis of the NASA Global Modeling Initiative chemical transport model (CTM) and the GEOS-Chem CTM (Karydis et al., 2012) found that cloud droplet number concentration is sensitive to κ in Arctic and remote regions, where background aerosol loadings are low. Another study (Morales Betancourt and Nenes, 2014) found that a ±50 % uncertainty range in the κ of secondary organic aerosols and particulate organic matter resulted in a cloud droplet number concentration uncertainty of up to 15 % and 16 %, respectively. Updating precipitation models with lab-derived κ values for specific inorganic and organic species may increase the accuracy of storm forecasts by providing better predictions of intense precipitation (Kawecki and Steiner, 2018). In terms of climate, Liu and Wang (2010) found that increasing the κ of primary organic aerosols from 0 to 0.1, and decreasing the κ of secondary organics aerosols from 0.14 to 0.07, resulted in an uncertainty in global secondary aerosol indirect forcing of 0.4 W m⁻² from preindustrial times to present day.

The sensitivity of weather and climate models to hygroscopicity parameters demonstrates the need for accurate measurements. In this study, we examine experimental uncertainties in CCN measurements and the resulting uncertainties in determination of κ_app. Differences in reported κ_app values may result from experimental artifacts rather any actual differences in an aerosol's ability to facilitate cloud formation. By systematically quantifying sources of experimental error, this study provides a framework for determining the significance of variations in CCN properties reported in multiple studies and defining the operating conditions that minimize instrumental artifacts.

2 Background

The Köhler equation relates water vapor saturation ratio at the surface of a wet droplet, s, to its radius at equilibrium (Rogers and Yau, 1989):

$$\begin{array}{}\text{(1a)}& {\displaystyle }& {\displaystyle }s=\left(\mathrm{1}-{\displaystyle \frac{b}{r^{\mathrm{3}}}}\right)\exp \left({\displaystyle \frac{a}{r}}\right),\text{(1b)}& {\displaystyle }& {\displaystyle }a={\displaystyle \frac{\mathrm{2}{\mathit{\sigma }}_{\mathrm{w}}{M}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{w}}\text{R}T}},\text{(1c)}& {\displaystyle }& {\displaystyle }b={\displaystyle \frac{\mathrm{3}i{m}_{\mathrm{s}}{M}_{\mathrm{w}}}{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}{M}_{\mathrm{s}}}},\end{array}$$

where s is the equilibrium saturation ratio of a solution droplet with radius r, σ_w is the surface tension of water, M_w is the molecular weight of water, R is the ideal gas constant, T is temperature in Kelvin, ρ_w is the density of water, and M_s is the molecular weight of the solute. The minimum saturation ratio that is required for spontaneous droplet growth, s_act, is therefore

$$\begin{array}{}\text{(2)}& {\displaystyle }{s}_{\mathrm{crit}}=\mathrm{1}+\sqrt{{\displaystyle \frac{\mathrm{4}{a}^{\mathrm{3}}}{\mathrm{27}b}}}.\end{array}$$

Petters and Kreidenweis (2007) reformulated the Köhler equation as κ-Köhler theory:

$$\begin{array}{ll}\text{(3a)}& {\displaystyle }& {\displaystyle }{s}_{\mathrm{crit}}=\exp \left(\sqrt{{\displaystyle \frac{\mathrm{4}{A}^{\mathrm{3}}}{\mathrm{27}{D}_{\mathrm{act}}^{\mathrm{3}}{\mathit{\kappa }}_{\mathrm{app}}}}}\right){\displaystyle }& {\displaystyle }\text{and}\\ \text{(3b)}& {\displaystyle }& {\displaystyle }A={\displaystyle \frac{\mathrm{4}{\mathit{\sigma }}_{\mathrm{lv}}{M}_{\mathrm{w}}}{\text{R}T{\mathit{\rho }}_{\mathrm{w}}}},\end{array}$$

where s_crit is the critical water vapor saturation ratio, D_act is the dry particle activation diameter, and κ_app is the apparent hygroscopicity parameter. Solving for κ_app yields

$$\begin{array}{}\text{(3c)}& {\displaystyle }{\mathit{\kappa }}_{\mathrm{app}}={\displaystyle \frac{\mathrm{4}{A}^{\mathrm{3}}{\mathit{\sigma }}_{\mathrm{lv}}^{\mathrm{3}}}{\mathrm{27}{T}^{\mathrm{3}}{D}_{\mathrm{act}}^{\mathrm{3}}{\ln }^{\mathrm{2}}\left(s_{\mathrm{crit}}\right)}}.\end{array}$$

The apparent hygroscopicity parameter can be calculated from experimental CCN results, for which the dry diameter and water vapor saturation ratio are known. For a chosen aerosol diameter, the activated fraction is the ratio of the concentration aerosols that activate as CCN to the total aerosol concentration:

$$\begin{array}{}\text{(4)}& {\displaystyle }\text{activated fraction}={\displaystyle \frac{\text{CCN concentration}}{\text{aerosol concentration}}}.\end{array}$$

Activated fraction data are fit with a sigmoid error function to determine the percent supersaturation at which 50 % of the particles have activated as CCN (activated fraction =0.50), which is considered the operationally defined critical percent supersaturation SS_crit (Rose et al., 2008). The critical saturation ratio s_crit can then be determined and entered into Eq. (4) in order to calculate κ_app for the near-monodisperse aerosol:

$$\begin{array}{}\text{(5)}& {\displaystyle }{s}_{\mathrm{crit}}=\mathrm{1}+{\displaystyle \frac{{\text{SS}}_{\mathrm{crit}}}{\mathrm{100}}}.\end{array}$$

Reporting κ_app as a function of diameter allows for the comparison of the cloud condensation nucleation abilities of multimodal aerosol populations, without overlooking differences that arise due to aerosol composition.

The apparent hygroscopicity parameter is related to chemical composition; therefore, the calculated κ_app of a pure substance should be constant across CCN experiments. However, discrepancies among κ_app values for a single chemical species have been observed. Experimental results for ammonium nitrate are inconsistent with reported values ranging from $\mathrm{0.577}\le {\mathit{\kappa }}_{\mathrm{app}}\le \mathrm{0.753}$ (Svenningsson et al., 2006). Also, large ranges are often observed for organic compounds, such as glutaric acid ($\mathrm{0.054}\le {\mathit{\kappa }}_{\mathrm{app}}\le \mathrm{0.16}$) and malonic acid ($\mathrm{0.199}\le {\mathit{\kappa }}_{\mathrm{app}}\le \mathrm{0.255}$) (Koehler et al., 2006; Pradeep Kumar et al., 2003; Hartz et al., 2006). Below we evaluate potential sources of uncertainties in CCN measurements and the resulting uncertainties in κ_app.

3 Artifacts derived from sized CCN measurements

CCN measurements used for calculating apparent hygroscopicity from monodisperse aerosol require accurate operation of three instruments: the CCN, the differential mobility analyzer (DMA), and the condensation particle counter (CPC). The setup for laboratory CCN experiments is shown in Fig. 1. First, a polydisperse population of aerosols is generated by an atomizer and dried using a desiccant tube packed with silica gel. A near-monodisperse flow is obtained through size selection in the DMA. The flow is then split between a CPC (which measures aerosol concentration) and a CCN counter (which measures the concentration of particles that activate as CCN at a given percent supersaturation). Instrument artifacts will first be assessed separately for the DMA, CPC, and CCN counter. In the concluding section of the paper (and Fig. 10), the overall uncertainty due to the combination of these is presented and discussed.

We note that this study considers sized CCN measurements, which may be used for the determination of κ_app. In contrast, a number of earlier CCN studies were conducted on the full ambient aerosol population without sizing the aerosol (Jennings et al., 1996; Hudson and Xie, 1998; Modini et al., 2015; Duan et al., 2017; Schmale et al., 2018; Leng et al., 2013). While useful, such studies do not produce the data required for accurate determination of κ_app from the CCN measurements.

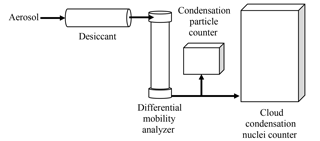
Figure 1 Experimental setup used for obtaining sized CCN and particle concentration measurements from an aerosol sample.

3.1 Artifacts derived from differential mobility analyzers

3.1.1 DMA operation and electrical mobility

DMAs used in atmospheric science include commercially available instruments from Grimm Aerosol Technik, TSI Incorporated, and MSP Corporation. They have also been custom-built by a number of research groups (Mei et al., 2011; Barmpounis et al., 2016; Jokinen and Makela, 1997; Seol et al., 2000). All models allow for the selection of particles through electrical mobility, the ability of a particle to move through a medium (such as air) while acted upon by an electrical field. The DMA size-selects near-monodisperse aerosol from a polydisperse aerosol source, as shown in Fig. 2 (modeled after the Vienna-type long DMA from Grimm Technologies). The electrical mobility Z_p of a particle with mobility diameter d_m can be calculated according to

$$\begin{array}{}\text{(6)}& {\displaystyle }{Z}_{\mathrm{p}}={\displaystyle \frac{ne{C}_{\mathrm{C}}\left(d_{\mathrm{m}}\right)}{\mathrm{3}\mathit{\pi }\mathit{\eta }{d}_{\mathrm{m}}}},\end{array}$$

where n is the number of charges on the particle (assumed to be one in this study), e is the elementary unit of charge, η is the gas dynamic viscosity, and C_C(d_m) is the Cunningham slip correction factor:

$$\begin{array}{}\text{(7)}& {\displaystyle }{C}_{\mathrm{C}}\left(d_{\mathrm{m}}\right)=\mathrm{1}+{\displaystyle \frac{\mathrm{2}\mathit{\lambda }}{d_{\mathrm{m}}}}\left({\mathit{\alpha }}_{\mathrm{CC}}+{\mathit{\beta }}_{\mathrm{CC}}\exp \left[-{\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{CC}}}{\mathrm{2}\mathit{\lambda }/d_{\mathrm{m}}}}\right]\right),\end{array}$$

where λ is the mean free path (DeCarlo et al., 2004). For the Vienna-type long DMA from Grimm Technologies, Inc. considered here, α_CC=1.246, β_CC=0.42, and γ_CC=0.86 (Grimm Aerosol Technik, 2009).

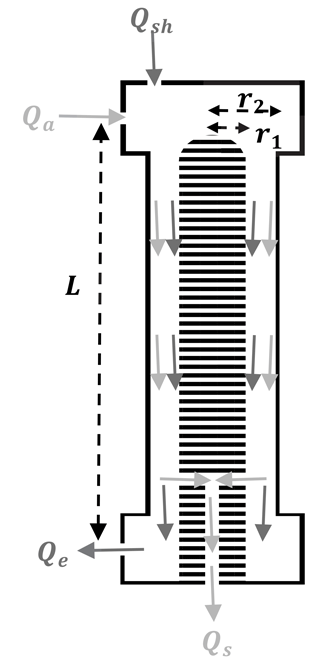
Figure 2 Simplified flow diagram of a DMA with an inner electrode radius r₁, outer electrode radius r₂, distance between aerosol inlet and sample outlet L, clean sheath air flow Q_sh, aerosol flow Q_a, excess air flow Q_e, and sample air flow Q_s.

Particle-laden flow enters the DMA through the aerosol inlet (flow Q_a) and travels down the DMA column (inner radius r₁, outer radius r₂) with the clean air sheath flow Q_sh. Positively charged particles are attracted by the negatively charged inner electrode, to which voltage V₀ has been applied. Ideally, selection of a voltage allows only particles of a specific mobility diameter to exit the DMA through the sample flow Q_s. All particles with a larger diameter (lower Z_p) or smaller diameter (higher Z_p) will exit the DMA through the excess flow Q_e. In other words, Q_s would ideally consist only of aerosols with diameters equal to, or very nearly equal to, the selected diameter.

In reality, the aerosol flow that leaves the DMA through Q_s is polydisperse with a mobility distribution determined by instrumental parameters. A triangular approximation has been chosen as a model for this distribution, as particle inertia is negligible for the diameters considered in this study (Stratmann et al., 1997; Mamakos et al., 2007). The probability that a particle at the aerosol inlet will exit with the sampling flow is defined by transfer function $f\left(Z_{\mathrm{p}},Z_{\mathrm{p},\mathrm{mid}}\right)$:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }f\left(Z_{\mathrm{p}},Z_{\mathrm{p},\mathrm{mid}}\right)={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{TF}}}{\mathrm{2}{\mathit{\beta }}_{\mathrm{TF}}}}\left(\left|{\displaystyle \frac{Z_{\mathrm{p}}}{Z_{\mathrm{p},\mathrm{mid}}}}-\left(\mathrm{1}+{\mathit{\beta }}_{\mathrm{TF}}\right)\right|\right.\\ \text{(8)}& {\displaystyle }& {\displaystyle }\left.+\left|{\displaystyle \frac{Z_{\mathrm{p}}}{Z_{\mathrm{p},\mathrm{mid}}}}-\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{TF}}\right)\right|-\mathrm{2}\left|{\displaystyle \frac{Z_{\mathrm{p}}}{Z_{\mathrm{p},\mathrm{mid}}}}-\mathrm{1}\right|\right),\end{array}$$

where Z_p, mid is the midpoint mobility of the transfer function, and α_TF and β_TF are flow-derived constants, defined as

$$\begin{array}{}\text{(9a)}& {\displaystyle }{\mathit{\alpha }}_{\mathrm{TF}}={\displaystyle \frac{Q_{\mathrm{s}}+Q_{\mathrm{a}}}{\mathrm{2}{Q}_{\mathrm{a}}}}\end{array}$$

and

$$\begin{array}{}\text{(9b)}& {\displaystyle }{\mathit{\beta }}_{\mathrm{TF}}={\displaystyle \frac{Q_{\mathrm{s}}}{Q_{\mathrm{sh}}}}.\end{array}$$

The midpoint and half-width of the transfer function are respectively calculated according to Knutson and Whitby (1975):

$$\begin{array}{}\text{(10a)}& {\displaystyle }{Z}_{\mathrm{p},\mathrm{mid}}={\displaystyle \frac{Q_{\mathrm{e}}+Q_{\mathrm{sh}}}{\mathrm{4}\mathit{\pi }L{V}_{\mathrm{0}}}}\ln \left({\displaystyle \frac{r_{\mathrm{2}}}{r_{\mathrm{1}}}}\right)\end{array}$$

and

$$\begin{array}{}\text{(10b)}& {\displaystyle }\mathrm{\Delta }{Z}_{\mathrm{p}}={\displaystyle \frac{Q_{\mathrm{a}}}{\mathrm{2}\mathit{\pi }L{V}_{\mathrm{0}}}}\ln \left({\displaystyle \frac{r_{\mathrm{2}}}{r_{\mathrm{1}}}}\right),\end{array}$$

where L is the distance between the DMA inlet and outlet.

3.1.2 κ_app artifacts arising from DMA flow ratios

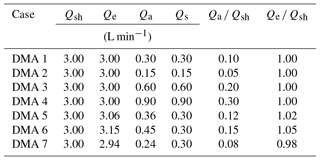
Next we assess the ramifications of the DMA transfer function for the derived κ_app. A lognormal theoretical aerosol number distribution was used to represent a polydisperse ambient aerosol population (Fig. 3a). This distribution was converted to an electrical mobility distribution using Eqs. (7) and (8), assuming that the aerosols in the distribution were spherical and singly charged. From the distribution, a series of single aerosol sizes were selected (25, 50, 100, and 200 nm diameter). For each aerosol size, the resulting DMA transfer functions were calculated for seven cases using Eq. (9) and the various parameters for DMA sheath, excess, aerosol, and sample flow listed in Table 1. These seven cases were chosen to represent possible measurement scenarios that may be encountered in a CCN experiment. The aerosol ∕ sheath ratio is varied in cases 1–4 in order to study the effects of chosen experimental parameters. Sheath flow is predetermined in some DMAs (for example, the Grimm Vienna DMA considered in this study), but can be varied in other instruments. The aerosol flow rate may also be selected in an experiment. Cases 5–7 vary the excess ∕ sheath ratio in order to take proper instrument operation into account. The excess and sheath flow should be identical, but small discrepancies may occur.

Table 1 Theoretical DMA flow test cases.

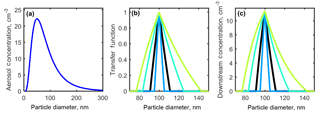
Figure 3 (a) A theoretical aerosol distribution generated using a lognormal function centered at 50 nm. (b) The transfer function calculated using Eq. (7). (c) Multiplying the distribution by the transfer function gives the downstream aerosol concentration (cm⁻³).

For example, the resulting DMA transfer functions for 100 nm aerosol conditions constrained by cases 1–4 are shown in Fig. 3b, in which an increase in Q_a ∕ Q_sh from 0.1 (black line) to 0.3 (green line) tripled the width of the number distribution, and decreasing Q_a ∕ Q_sh to 0.05 (blue line) from 0.10 halved the width of the number distribution. The result of applying the transfer functions shown in Fig. 3b to the distribution in Fig. 3a is shown in Fig. 3c.

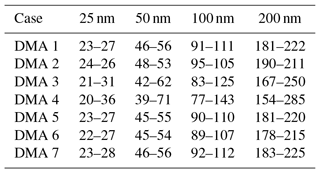
All downstream distributions for all seven DMA cases and all aerosol sizes are shown in Fig. S1 in the Supplement. DMA cases 1–4 represent experimental conditions in which the sheath and excess air flows are equal and the aerosol ∕ sheath flow ratio is varied. As Q_a ∕ Q_sh increases, the width of the number distribution measured downstream of the DMA increases, while the midpoint diameter remains constant. It was found that doubling the aerosol-to-sheath ratio doubled the width of the downstream number distribution for 25, 50, 100, and 200 nm particles. For example, when selecting 200 nm particles, increasing Q_a ∕ Q_sh from 0.10 to 0.20 increased the downstream diameter range from 181–222 nm (a spread of 41 nm) to 167–250 nm (a spread of 87 nm). The particle diameter ranges that would be observed downstream of the DMA are summarized in Table 2.

Table 2 Predicted downstream particle diameter range for each DMA case.

To assess the variations in CCN properties resulting from DMA uncertainties, the critical percent supersaturation was calculated for representative atmospheric aerosols. The value of SS_crit was calculated for each particle diameter using Eq. (3a), using literature values for apparent hygroscopicity of 0.61 for ammonium sulfate and 1.28 for sodium chloride (Clegg et al., 1998). It should be noted that this analysis considers two homogeneous aerosol distributions of hygroscopic salts. Real aerosol distributions tend to be mixtures of many species, and the shape of the number distribution can vary among species.

To test how uncertainties in DMA diameter translate to uncertainties in κ_app, the activation of particles downstream of the DMA was assessed. First, for each case and diameter (25, 50, 100, and 200 nm) the critical saturation ratio s_crit was calculated for each particle diameter range downstream from the DMA using Eq. (3a). These critical saturation ratios were converted to critical percent supersaturation SS_crit and used to calculate the activated fraction (AF) for the aerosol particles downstream from the DMA for percent supersaturations $\mathrm{0.01}<\text{SS}<\mathrm{1.5}$, using the equation

$$\begin{array}{}\text{(11)}& {\displaystyle }\text{AF}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}+\text{erf}\left({\displaystyle \frac{\text{SS}-{\text{SS}}_{\mathrm{crit}}}{\mathit{\sigma }\sqrt{\mathrm{2}}}}\right)),\end{array}$$

where the standard deviation σ was equal to 1∕100 of SS_crit. The small σ ∕ SS_crit ratio was chosen in order to generate accurate activated fraction curves for each particle diameter.

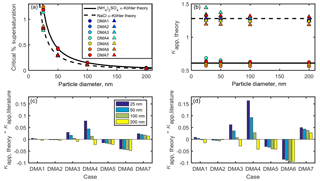
Figure 4 (a) Critical supersaturation of ammonium sulfate and sodium chloride particles calculated for DMA cases 1–7 for sodium chloride (triangles) and ammonium sulfate (circles). Ammonium sulfate and sodium chloride curves from κ-Köhler theory are shown for comparison. (b) Apparent hygroscopicity κ_app for DMA cases 1–7. (c) DMA-flow-derived artifacts in ammonium sulfate κ_app are shown for each DMA case. (d) DMA-flow-derived artifacts in sodium chloride κ_app are shown for each DMA case.

The activated fraction curve for each selected diameter (25, 50, 100, and 200 nm) was then calculated as the sum of the number-weighted activated fractions of each particle diameter downstream from the DMA. For example, for a selected diameter of 25 nm, the downstream diameters ranged from 23 to 27 nm for DMA case 1 and from 20 to 36 nm in DMA case 4. The equation used for this calculation is

$$\begin{array}{}\text{(12)}& {\displaystyle }{\text{AF}}_{\mathrm{weighted}}={\sum }_i{\displaystyle \frac{n_i}{n_{\mathrm{total}}}}{\text{AF}}_i,\end{array}$$

where AF_i is the activated fraction calculated using Eq. (12) and $\frac{n_i}{n_{\mathrm{total}}}$ is the fraction of particle downstream from the DMA of diameter i.

This calculation was repeated for each selected diameter (25, 50, 100, and 200 nm), each DMA case (1–7), and percent supersaturation (0.01–1.5) in order to construct activation curves for each selected diameter and DMA case. As an example, in Fig. S2, the shape and position of each activated fraction curve vary with the DMA flow ratios. As the aerosol ∕ sheath ratio increases, the activated fraction curve flattens out (DMA case 4). The critical percent supersaturation SS_crit was then determined for each activation curve as the percent supersaturation, for which AF =0.50. These results are shown in Fig. 4a for ammonium sulfate and sodium chloride. Equation (4) was then used to calculate κ_{app, theory} for each DMA case and selected diameter, as shown in Fig. 4b. Discrepancies between κ_{app, theory} calculated in this study and literature values (hereafter referred to as “κ_app artifacts”) are shown for both compounds in Fig. 4c–d.

The largest κ_app artifact was found in DMA case 4 (in which the aerosol ∕ sheath ratio was the highest) for both ammonium sulfate and sodium chloride aerosols. The artifact for 25 nm ammonium sulfate aerosol in DMA case 4 was 0.08, or ∼13 % of the literature value used for ${\mathit{\kappa }}_{\mathrm{app}}^{{\left({\mathrm{NH}}_{\mathrm{4}}\right)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$, while the artifact for 25 nm sodium chloride in DMA case 4 was 0.16, or ∼13 % of the literature value used for ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$. Artifacts were also high for DMA case 6 ($-\mathrm{0.041}\le {\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}^{{\left({\mathrm{NH}}_{\mathrm{4}}\right)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}\le -\mathrm{0.048}$) and DMA case 7 ($\mathrm{0.014}\le {\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}^{{\left({\mathrm{NH}}_{\mathrm{4}}\right)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}\le \mathrm{0.024}$), in which sheath and excess flow were unequal. This result demonstrates that artifacts may still occur when low aerosol ∕ sheath flow ratios are chosen (0.15 and 0.08 for DMA cases 6 and 7, respectively) due to small differences between sheath and excess flow rates (5 % and 2 % for DMA cases 6 and 7, respectively).

κ_app artifacts were larger for sodium chloride ($-\mathrm{0.10}\le {\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}^{\mathrm{NaCl}}\le \mathrm{0.16}$) than for ammonium sulfate ($-\mathrm{0.05}\le {\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}^{{\left({\mathrm{NH}}_{\mathrm{4}}\right)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}\le \mathrm{0.08}$) across the DMA cases. As our results show, when two or more compounds are compared, the more hygroscopic compound will have larger κ_app artifacts.

This analysis was also applied to the range of apparent hygroscopicity values Svenningsson et al. (2006) reported for ammonium nitrate $\mathrm{0.577}\le {\mathit{\kappa }}_{\mathrm{app}}\le \mathrm{0.753}$, with a mean value of 0.670. If 0.670 is assumed to be the true κ_app for ammonium nitrate, then the sample ∕ sheath ratio used to determine κ_app (1.2–2.0 L min⁻¹) could lead to an experimental kappa as low as 0.665 or as high as 0.674, which would not fully explain the actual experimental range. This assessment ignores possibility of under- or overcounting, which could introduce additional errors.

In addition to the errors discussed above, accuracy in CCN measurements depends on the accuracy of the instrument calibration. Specifically, accurate determination of the percent supersaturation set points within the CCN instrument is dependent on accurate sizing of aerosols entering the CCN, and therefore is dependent on the DMA sizing during CCN calibration. CCN calibrations were performed using two standard compounds, ammonium sulfate and sodium chloride, as described in detail in Rose et al. (2008). Fortunately, if the calibration procedure described by Rose is followed and an optimal DMA aerosol-to-sheath ratio is employed, the uncertainties will be minimal. Specifically, this analysis shows that an aerosol ∕ sheath ratio of 1 : 10 or 1 : 20 (case 1 or 2, respectively) is recommended for all CCN calibrations. This will result in κ_app uncertainties of less than 1 % for all dry sizes (25–200 nm). However, if CCN calibrations are performed using a DMA operated with less-than-ideal aerosol-to-sheath ratios, substantial errors will be introduced. Analysis of the impact of DMA uncertainties on CCN calibrations is discussed in detail in the Supplement. In the worst case scenario amongst the cases evaluated here (case 4), the resulting uncertainty in κ_app is 15 %.

3.1.3 Effect of double and triple charges on particles

During normal operation, the Grimm DMA employs a bipolar charger (also known as a neutralizer) to charge aerosol particles through the capture of gaseous ions. The analysis in Sect. 3.1.2 assumes that each particle carries a single (+1) charge. In reality, the methods used to charge particles prior to entering a DMA may impart two, three, or more charges to individual particles (Fuchs, 1963). The charge distribution resulting from a bipolar charger is roughly approximated using the Boltzmann law (Keefe et al., 1959). However, the Boltzmann law assumes symmetric aerosol particle charging (equal concentrations of negatively and positively charged particles). Deviation from symmetric charging is observed in regions of high ionizations, and this deviation becomes more pronounced as particle size increases (Hoppel and Frick, 1990). A more accurate estimation of stationary charge distribution has been calculated using an approximation formula for the charge distribution produced by a bipolar charger:

$$\begin{array}{}\text{(13)}& {\displaystyle }f\left(k\right)={\mathrm{10}}^{\left[{\sum }_{i=\mathrm{0}}^{i=\mathrm{5}}{a}_i\left(k\right){\left({\log }_{\mathrm{10}}{D}_{\mathrm{nm}}\right)}^i\right]},\end{array}$$

where f(k) is the fraction of particles carrying k charges, a_i(k) is the approximation coefficients determined using a least-squares regression analysis, and D_nm is the particle diameter in nanometers (Wiedensohler, 1988). The approximation coefficients only apply to particles with 0, ±1, and ±2 charges. In a separate study, Maricq (2008) determined approximation coefficients for poly (α-olefin) oligomer oil droplets with ±1, ±2, and ±3 charges. The approximation coefficients reported by these two studies were in excellent agreement for particles with a ±1 charge and in weak agreement for ±2 charges (+2 and −2 charging efficiencies were overestimated by 50 % and 100 %, respectively). Therefore, this analysis will use the approximation coefficients from Wiedensolher (1988) for particles with +1 and +2 charges and the approximation coefficient for particles with a +3 charge from Maricq (2008).

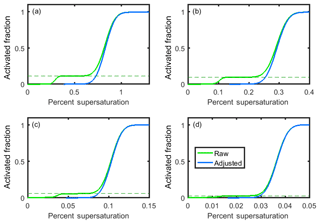
Figure 5 Theoretical raw (green) and adjusted (blue) activated fraction curves for (a) 25 nm (+1), 50 nm (+2), and 75 nm (+3) particles; (b) 50 nm (+1), 100 nm (+2), and 150 nm (+3) particles; (c) 100 nm (+1), 200 nm (+2), and 300 nm (+3) particles; and (d) 200 nm (+1), 400 nm (+2), and 600 nm (+3) particles. All particles are pure sodium chloride.

In order to assess the impact of multiple charges on κ_app, Eq. (14) and the approximation coefficients from Wiedensohler (1988) and Maricq (2008) were used to calculate the charge distribution of the representative aerosol population shown in Fig. 3a. The resulting charge distribution is shown in Fig. S6a. An increase in multiple charging is observed as particle diameter increases, though this is offset somewhat by the decrease in concentration with particle size above 50 nm.

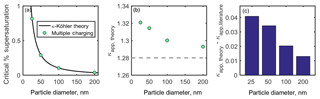
Figure 6 (a) Critical percent supersaturation of sodium chloride particles determined from activated fraction curves shown in Fig. 5. A κ-Köhler curve for sodium chloride is shown for comparison. (b) Theoretical κ_app for each particle diameter (gray dashed line indicates literature value for ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$). (c) Artifacts in κ_app resulting from multiple particle charges.

It follows that aerosols incorrectly sized due to double and triple charging will be passed from the DMA to the CCN counter and result in an additional uncertainty in the CCN measurements. To illustrate this, activated fraction curves were generated for 25, 50, 100, and 200 nm sodium chloride particle selection by the DMA (Fig. 5). The activation of sodium chloride is represented by sigmoid curves, for which the midpoint of each activation curve is the κ-Köhler-derived critical supersaturation of sodium chloride, and the standard deviation of each curve is 1∕10 of this value (consistent with the standard deviation ∕ midpoint ratio observed from our instrument's ammonium sulfate CCN calibration data). For each particle diameter, D, the observed activated fraction, AF${}_{D,\mathrm{weighted}}^{\mathrm{SS}}$, for each percent supersaturation SS was determined by weighting the activated fraction AF${}_{D,i}^{\mathrm{SS}}$ of each particle diameter and charge at that percent supersaturation by the fraction of particles of that diameter:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\text{AF}}_{D,\mathrm{weighted}}^{\mathrm{SS}}={\sum }_{i=\mathrm{1}}^{i=\mathrm{3}}\\ {\displaystyle }& {\displaystyle \frac{\text{concentration of particles with charge}i\text{and diameter}D}{\text{concentration of particles with charge}+\mathrm{1},+\mathrm{2},+\mathrm{3},\text{and diameter}D}}\\ \text{(14)}& {\displaystyle }& {\displaystyle }\cdot {\text{AF}}_{D,i}^{\mathrm{SS}}.\end{array}$$

The raw data shown in Fig. 5 (green curves) can be corrected for multiple charging by determining the fraction of particles with $>+\mathrm{1}$ charge from the lower plateau in each plot (dashed lines). The adjusted activated fraction for each percent supersaturation, AF_adjusted, is calculated using the equation

$$\begin{array}{}\text{(15)}& {\displaystyle }{\text{AF}}_{\mathrm{adjusted}}={\displaystyle \frac{{\text{AF}}_{\mathrm{raw}}-{\text{AF}}_{\mathrm{plateau}}}{\mathrm{1}-{\text{AF}}_{\mathrm{plateau}}}},\end{array}$$

where AF_raw is the raw activated fraction at that percent supersaturation, and AF_plateau is the activated fraction corresponding to the lower plateau (Rose, 2008). The adjusted activated fraction curves are shown in Fig. 5 (blue curves). These are in good agreement with the theoretical κ-Köhler-derived activation curves for sodium chloride (not shown).

Critical supersaturation was determined for each diameter by calculating the percent supersaturation at which the raw AF${}_{D,\mathrm{weighted}}^{\mathrm{SS}}=\mathrm{0.5}$. These critical supersaturations are shown in Fig. 6a, and the theoretical critical supersaturations calculated from κ-Kohler theory are shown for comparison. Equation (4) was used to calculate apparent hygroscopicity for each particle diameter, shown in Fig. 6b. A dashed line in Fig. 6b indicates the literature value for ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$. It is apparent that failing to account for multiply charged particles in the activated fraction curves shown in Fig. 5 leads to an overestimation of κ_app. Artifacts in κ_app are shown in Fig. 6c.

For the theoretical aerosol distribution used in this analysis (Fig. 3a), small, positive deviations from κ-Köhler theory and the literature value for ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$ were observed ($\mathrm{1}\le {\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}^{\mathrm{NaCl}}\le \mathrm{0.04}$, 1 %–3 % of ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$). As shown in the figure, κ_app artifacts resulting from unaccounted-for multiple charges decrease with particle diameter for this theoretical aerosol population. Greater κ_app artifacts would be expected for aerosol populations with more prevalent accumulation modes.

The aerosol ∕ sheath ratio within the DMA also modulates the effect of multiple charges on κ_app. As the aerosol ∕ sheath ratio increases, the transfer function broadens, allowing particles that are both larger and smaller than the selected diameter to exit the DMA. This in turn broadens the CCN activated fraction curve (Rose et al., 2008). The larger particles will activate as CCN at lower supersaturations than particles with the selected diameter, resulting in an increase in the activated fraction plateau due to multiply charged particles and a further decrease in the determined SS_crit. Petters et al. (2007) showed that CCN activated fraction curves are significantly skewed by multiply charged particles when the mode diameter of the aerosol population upstream of the DMA exceeds the critical diameter of the size-selected particles. In an example CCN activated fraction curve, Rose et al. (2008) demonstrated that a 1 : 6 ratio of doubly to singly charged particles resulted in an underestimation of the critical activation diameter by 2 %. Zhao-Ze and Liang (2014) also showed that multiply charged particles can introduce significant uncertainty into hygroscopicity calculations.

3.1.4 Additional artifacts resulting from DMA measurements

Several additional factors that may impact experimental κ_app are beyond the scope of this study, but are worth mentioning as they represent additional potential sources of error in some cases. First, volatile aerosols may partially evaporate inside the DMA, resulting in a decrease in particle size exiting the DMA. DMA sizing error due to aerosol volatility (defined as the ratio of sampled diameter to the selected diameter) increases with volatility, though sizing error can be decreased by increasing the sheath flow rate in the DMA. Conversely, hygroscopic aerosols may grow inside the DMA, resulting in larger particles existing in the DMA. Operationally, errors in DMA sizing due to hygroscopic growth can be mitigated if aerosols entering the DMA inlet are in wet metastable states (higher aerosol relative humidity at DMA inlet) and if DMA sheath flow rates are kept low (Khlystov, 2014).

Voltage shifts within the DMA (differences between the selected voltage and the actual voltage inside the DMA) can lead to discrepancies between selected and sampled particle diameters. Voltage shifts may result from a space-charge field generated by the motion of charges within the DMA. Particles charged by the bipolar neutralizer will either be attracted towards or repelled away from the inner column of the DMA, depending on whether they are positively or negatively charged. This charge separation creates a space-charge field that shifts the actual voltage within the DMA from the selected voltage. The impact of the space-charge field on the midpoint and spread of the DMA transfer function increases as particle mobility increases (as particle size decreases) and as particle concentration increases (Alonso and Kousaka, 1996; Alonso et al., 2000, 2001).

4 Artifacts derived from condensation particle counters

4.1 CPC operation at low concentration

The second instrument that must function accurately during CCN experiments is the CPC. CPC performance is characterized by the maximum counting efficiency (which may be influenced by the working fluid in the instrument) and the 50 % cutoff diameter (d₅₀), the particle diameter at which 50 % counting efficiency is observed, both of which can vary among commercially available models and even among individual CPCs (Heim et al., 2004). One study found that n-butanol CPCs (TSI, Inc. models 3772, 3775, and 3776) exhibited smaller d₅₀ values for silver particles than sodium chloride ($\mathrm{3.3}\mathrm{nm}\le d_{\mathrm{50}}^{\mathrm{Ag}}\le \mathrm{7.8}$ nm and $\mathrm{4.1}\mathrm{nm}\le d_{\mathrm{50}}^{\mathrm{NaCl}}\le \mathrm{14.7}$ nm) due to the more effective condensation of n-butanol on silver particles (Hermann et al., 2007).

Maximum counting efficiencies in that study varied from 88.9 % to 100.3 %. Another comparison of n-butanol CPCs (TSI Inc. models 3010 and 3022, Grimm Tech. Inc. model 5.403) found $\mathrm{3.1}\mathrm{nm}\le d_{\mathrm{50}}\le \mathrm{11.9}$ nm for sodium chloride aerosols (Heim et al., 2004). In another study, the counting efficiencies observed in measurements of tungsten oxide particles by different instruments of the same model (TSI 3025) varied from 88.9 % to 138.9 %, while $d_{\mathrm{50}}^{{\mathrm{NO}}_x}$ varied from 3.2 to 11.0 nm (Hameri et al., 2002).

While some issues can cause undercounting at all concentrations, the additional issue of uncounted particles due to the arrival of more than one particle in the detector's field of view at any time arises only at higher concentrations. The cutoff between low and high concentration is not exact and varies among instruments. CPC undercounting issues that arise even at relatively low concentrations (which one would expect to encounter under standard experimental conditions) will be discussed in this section. Concentration-dependent effects encountered at higher concentrations will be explored in Sect. 4.2.

Six counting efficiency curves were generated using sigmoidal distributions and the 50 % cutoff diameters and maximum counting efficiencies listed in Table 3. Chosen values represent d₅₀ values and maximum counting efficiencies reported in the literature under relatively low concentrations of 1000–4000 cm⁻³ (Hermann et al., 2007). The resulting sigmoidal distributions (Fig. 7a) were used to determine the counting efficiency of 25, 50, 100, and 200 nm particles.

Table 3 Values of 50 % cutoff diameter and maximum counting efficiency used in investigating κ_app artifacts for low particle concentrations measured by a CPC.

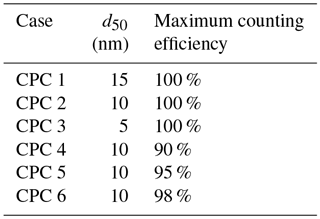
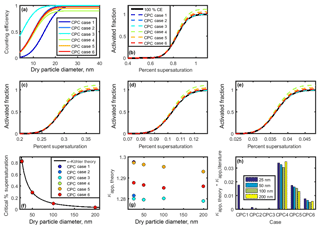
Figure 7 (a) Counting efficiency curves for CPC cases 1–6 (shown in Table 3). (b–e) CCN activated fraction curves for 25, 50, 100, and 200 nm NaCl, respectively. (f) Critical supersaturation calculated for each particle diameter. (g) Theoretical κ_app for each CPC case and particle diameter. (h) Artifacts in κ_app for each CPC case and particle diameter.

Next, κ_app was calculated from theoretical critical percent supersaturations for each chosen diameter. To do so, four sigmoid curves representing sodium chloride CCN activation (hereafter referred to as “activation curves”) for 25, 50, 100, and 200 nm were generated. The κ-Köhler SS_crit of sodium chloride was used as the midpoint of each activation curve, and 1∕10 of this value was used as the standard deviation (100 % CE, Fig. 7b–e). These values are consistent with the standard deviation ∕ midpoint ratio observed from our instrument's ammonium sulfate CCN calibration data.

Activation curves were then generated for CPC cases 1–6 by dividing the activated fraction for each dry particle diameter by the counting efficiency for that diameter. SS_crit was determined for each CPC case by finding the percent supersaturation at which the activated fraction =0.50. Results are summarized in Fig. 7f. Next, critical supersaturation was converted to saturation, and κ_{app, theory} was calculated for each diameter in each CPC case using Eq. (4) (see Fig. 7g). As above, κ_app artifacts were calculated by finding the difference between these results and the literature value of κ_app for sodium chloride (see Fig. 7h).

For the diameters studied, the effect of maximum counting efficiency on CPC concentration (and activated fraction) is greater than the effect of the the 50 % cutoff diameter. However, neither characteristic resulted in large κ_app artifacts. The largest κ_app artifact observed at low concentrations was 0.035 for CPC case 4, 2.4 % of the literature value for the apparent hygroscopicity factor for sodium chloride.

4.2 CPC operation at high concentration

Operation at high concentrations introduces an additional source of undercounting through particle coincidence at the CPC optical counter. For the TSI 3010 CPC, undercounting is observed for particle concentrations above 1×10⁴ cm⁻³. At 5×10⁴ cm⁻³, the detector saturates and cannot detect higher concentrations. By comparison, the TSI 3025 is effective at counting higher particle concentrations, of up to 2.5×10⁴ cm⁻³ (Hameri et al., 2002; Sem, 2002).

To model undercounting due to particle coincidence, four CPC counting curves (Fig. 8a) were generated using the equations in Table 4. Case 7 represents a CPC for which counting efficiency decreases with particle concentration, without reaching saturation. Cases 8–10 represent CPCs for which saturation is reached at 4×10⁴, 2×10⁴, and 1×10⁴ cm⁻³, respectively. These saturation concentrations are of similar magnitude to those observed from TSI 3010 concentration data. It should be noted that the CPC concentration in cases 7–10 levels off at the saturation concentration for each case.

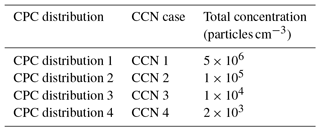
In order to assess the importance of undercounting in CPC cases 7–10, four theoretical aerosol distributions with a peak concentration at 50 nm were employed (Table 5, Fig. 8b). CPC distribution 1 represents a worst case scenario of similar magnitude to the highest particle concentrations measured during a coastal nucleation event (Hameri et al., 2002; Sem, 2002), while CPC distributions 2, 3, and 4 are lower in concentration (due to the lack of undercounting in CPC distributions 2, 3, and 4 as demonstrated in Fig. 6b; the remaining analysis for CPC operation at high concentration considers only CPC distribution 1.) CPC cases 8–10 were applied to CPC distribution 1 in order to determine the concentration measured by the CPC for 25, 50, 100, and 200 nm aerosols. The counting efficiency was then calculated for each case and aerosol diameter in CPC distribution 1.

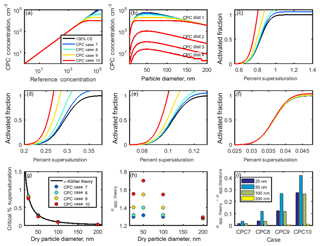
Figure 8 (a) Theoretical relationships between the reference aerosol concentration and CPC concentration. (b) Concentration-dependent counting efficiencies from (a) were applied to four theoretical aerosol distributions. (c–f) Activated fraction curves for CPC distribution 1 and particle diameters 25, 50, 100, and 200 nm NaCl aerosol, respectively. (g, h) Critical supersaturation and κ_app for each case. (i) Artifacts in κ_app for each case.

Table 4 Equations used to model the relationship between a reference or true aerosol concentration x (particles cm⁻³) and the concentration measured by a condensation particle counter y (particles cm⁻³).

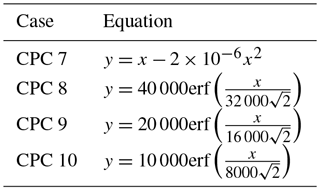
Sigmoidal activated fraction curves were generated for 25, 50, 100, and 200 nm sodium chloride aerosols. As in the low concentration cases, the midpoint of each 100 % CE curve was chosen to be equal to the κ-Köhler-derived SS_crit of sodium chloride at each dry diameter, and the standard deviation of each curve is equal to 1∕10 of the SS_crit. These activated fraction curves were adjusted using the counting efficiencies calculated in the previous step. In cases in which the activated fraction has increased due to undercounting by the CPC, the theoretical sigmoidal curve shifts to the left relative to the 100 % CE case (Fig. 8c–f). Thus, undercounting by the CPC effectively increases the reported activated fraction. As before, SS_crit was determined from each of these curves, and κ_{app, theory} was subsequently calculated using Eq. (4) (Fig. 8g–h).

κ_{app, theory} fell over a much wider range for 25, 50, and 100 nm particles (1.30–1.56, 1.32–1.70, and 1.30–1.55, respectively) than for 200 nm particles (1.28–1.29) due to the lower concentration of 200 nm particles in the chosen aerosol distribution, which resulted in a higher counting efficiency for these aerosols. In comparison, the largest range in κ_{app, theory} was observed for 50 nm aerosols, the peak diameter in this aerosol distribution.

A wider range in κ_{app, theory} was observed for the high-concentration CPC cases (7–10) compared to the low-concentration CPC cases (1–6). The lowest counting efficiency observed across the low-concentration cases was 89.9 % for 25 nm aerosol in case 4, while the lowest counting efficiency observed in the high-concentration cases was 18.0 % for 50 nm aerosol in case 10.

Artifacts in the apparent hygroscopicity parameter are shown in Fig. 8i. κ_app artifacts were the greatest for a CPC that becomes saturated at 20 000 particles cm⁻³ ($\mathrm{0.0131}\le {\mathit{\kappa }}_{\mathrm{app}}\le \mathrm{0.4206}$). The lower the concentration at which a CPC becomes saturated, the more quickly its counting efficiency will drop as concentration increases, resulting in increased activated fraction and increased apparent hygroscopicity. The magnitude of artifacts due to CPC undercounting depends on the saturation concentration of the CPC and the distribution of the aerosol population being studied.

5 Artifacts derived from cloud condensation nuclei instruments

Finally, the third instrument whose performance accuracy contributes to the overall certainty in CCN assessment is the CCN instrument itself. Several instruments have been implemented for measuring CCN concentrations over the last few decades. Older models include the continuous-flow parallel-plate diffusion chamber (Sinnarwalla and Alofs, 1973) and the Hudson CCN spectrometer (Hudson, 1989), which both employ an applied temperature gradient perpendicular to the aerosol flow. Newer models, such as the widely used Droplet Measurement Technologies cloud condensation nuclei counter (DMT CCN-100), operate with a streamwise temperature gradient and continuous laminar flow (Lance et al., 2006). The total flow through the DMT CCN-100 is 0.20–0.90 L min⁻¹, though the instrument is typically operated with a total flow of 0.50 L min⁻¹. The aerosol ∕ sheath ratio in the DMT CCN-100 is set by the user, and a ratio of 1 : 10 is commonly chosen. The following analysis considers the DMT CCN-100. According to the CCN-100 manual, the counting efficiency for this CCN instrument depends on concentration and supersaturation (Fig. 9a). The counting efficiency decreases rapidly with concentration at <0.2 % SS due to rapid water vapor depletion at these low supersaturations and falls off more slowly for >0.2 % SS (DMT CCN-100 manual).

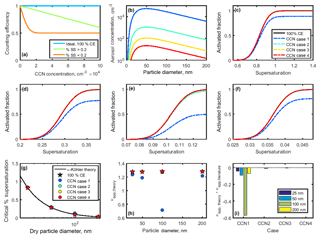
Figure 9 (a) Counting efficiencies of the DMT CCN-100 for specific supersaturations. (b) Lognormal aerosol distributions used to study CCN undercounting at high concentrations. (c–f) Activated fraction curves for 25, 50, 100, and 200 nm NaCl particles. Supersaturation-specific counting efficiencies from (a) applied to theoretical sigmoid curves for NaCl CCN activation. Activated fraction in the case of 100 % counting efficiency is shown for comparison. (g) Critical supersaturation for each case. (h) Theoretical κ_app calculated for each case. (i) Artifacts in κ_app artifacts for each case.

The counting efficiency of the DMT CCN-100 was tested for four lognormal aerosol distributions with peak concentrations at 50 nm and varying total concentrations (Table 5, Fig. 9b). Note that CCN cases 1–4 are identical to the aerosol distributions CPC distributions 1–4 used for the high-concentration CPC cases.

The counting efficiencies for each case were applied to theoretical sodium chloride sigmoidal activated fraction curves to produce normalized activated fraction curves (Fig. 9c–f). As above, the midpoint is set to the SS_crit of sodium chloride at each dry diameter, and the standard deviation is assumed to be 1∕10 of SS_crit. CCN undercounting effectively decreases the activated fraction, therefore shifting the activated fraction curve downwards and towards higher percent supersaturations. The opposite effect is observed when CPC undercounting occurs. Critical supersaturation was determined for each CCN case, as above (Fig. 9g). Values of SS_crit were then converted to saturation, and κ_{app, theory} was calculated using Eq. (4) (Fig. 9h).

Table 5 Total concentrations used in theoretical aerosol distribution for CPC operation at high concentration and CCN-derived κ_app artifacts.

Significant deviations from κ-Köhler theory were only observed in CCN case 1, with total aerosol concentration of 5×10⁶ particles cm⁻³ (Fig. 9g–i). The largest deviation for CCN case 1 was observed in 100 nm particles (${\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}=-\mathrm{0.57}$), due to the higher concentration of 100 nm particles compared to 25 and 200 nm particles and the lower percent supersaturation necessary for activation. The largest artifacts across CCN cases 2 and 3 were also observed for 100 nm particles, though no artifacts were observed for any particle diameter in CCN case 4 due to the much lower concentrations.

Sodium chloride is very hygroscopic. It should be noted that aerosols consisting of less hygroscopic compounds will activate at higher percent supersaturations (>0.2 % SS regime), which will lead to smaller κ_app artifacts when the same aerosol distribution and total aerosol concentration is considered. If a mixture was considered (for example, sodium chloride with a nonhygroscopic species such as soot) the results may also be different. The shape of the aerosol distribution must also be taken into account. A distribution with a narrower peak than the one generated for this analysis would be at risk for larger κ_app artifacts for any total aerosol concentration, and these artifacts would be greater at the peak diameter, while a broader distribution would result in less variation in κ_app artifacts for each particle diameter.

6 Counting statistics in CCN and CPC measurements

Though it is beyond the scope of this analysis, it should be mentioned that sampling at very low particle concentrations (<200 cm⁻³ total particle concentration) can introduce additional error into CCN and CPC measurements. This error can be mitigated by increasing scan times (Moore et al., 2010). For example, Moore et al. (2010) averaged CCN and particle concentrations over 5 s intervals for monodisperse particle concentrations <10 cm⁻³ and increased averaging time to 20 s intervals when the monodisperse particle concentration reached <6 cm⁻³.

7 Discussion

A comparison of the major instrument sources of error in CCN-derived κ_app is shown in Fig. 10. In addition, the best and worst case combination of errors, determined by additive error propagation, are also shown. DMA case 4, CPC case 4, CPC case 10, and CCN case 1 represent the operating conditions that resulted in the largest κ_app artifacts in this study. In DMA case 4, the aerosol ∕ sheath ratio of 0.30 resulted in a broadened aerosol distribution downstream of the DMA. Compared to DMA case 1, in which $Q_{\mathrm{a}}/Q_{\mathrm{sh}}=\mathrm{0.10}$, the downstream diameter range in DMA case 4 was 300 % higher for 25 nm particles, resulting in a spread of 20–36 nm. Similarly, the diameter ranges for the 50, 100, and 200 nm diameters were 220 %, 230 %, and 220 % wider than in case 1, respectively. Compared to the most ideal DMA case presented in this study (DMA case 2), in which $Q_{\mathrm{a}}/Q_{\mathrm{sh}}=\mathrm{0.05}$, the downstream diameter range in DMA case 4 was 700 % higher for 25 nm particles; the diameter ranges for the 50, 100, and 200 nm diameters were 540 %, 560 %, and 520 % wider than in case 2, respectively. The results demonstrate that limiting Q_a ∕ Q_sh to ≤0.10 will result in a narrow particle size distribution downstream of the DMA. Other studies have recommended employing DMA sample ∕ sheath ratios of 0.2 (Petters et al., 2007; Carrico et al., 2008; Moore et al., 2010) or 0.1 (Moore et al., 2010; Zhao-Ze and Liang, 2014) in order to minimize measurement aerosols due to transfer function broadening.

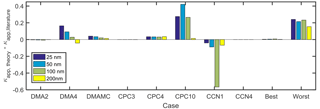
Figure 10 Comparison of κ_app artifacts derived from best and worst case scenarios for instrumental measurements for sodium chloride. Combined artifacts for the lowest-artifact cases (best: DMA case 2, CPC case 3, and CCN case 4) and the highest-artifact cases (worst: DMA case 4, multiple charging, CPC case 4, CPC case 8, and CCN case 1).

The effects of multiply charged particles on κ_app calculations were also quantified, as shown in Fig. 10. Small, positive κ_app artifacts (1 %–3 % of ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$) were observed when particles with +2 and +3 charges were not accounted for. This analysis considered a theoretical aerosol distribution in which most of the particles measure less than 100 nm in diameter. Actual aerosol distributions vary temporally and spatially and often include accumulation and coarse modes that would result in larger κ_app artifacts.

CPC case 4 represents κ_app artifacts (0.031–0.035) due to undercounting that arises from poor maximum CPC counting efficiency (90 %), which may be observed when using butanol as a working fluid while measuring the concentration of inorganic aerosols. In contrast, κ_app artifacts are negligible (<0.10 % of ${\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{NaCl}}$) in CPC case 3, in which maximum counting efficiency =100 %. CPC cases 8 and 10 (applied to the highest-concentration case, CPC distribution 1) represent undercounting at high concentration with CPCs for which saturation is observed at 4×10⁴ and 1×10⁴ cm⁻³, respectively. Counting efficiency drops off more rapidly with concentration in the latter case, resulting in κ_app artifacts that are highest at the peak of the aerosol distribution (0.1190 and 0.4206 for 50 nm aerosols in CPC cases 8 and 10, respectively). It should be noted that undercounting was only observed for one of the four upstream distributions studied, CPC distribution 1. No undercounting was observed when CPC cases 7–10 were applied to CPC distributions 2–4.

CCN case 1 represents CCN undercounting at high concentration (total aerosol concentration $=\mathrm{5}\times {\mathrm{10}}^{\mathrm{6}}$ cm⁻³). CCN undercounting is greatest for low supersaturation (<0.2 %) and high concentration, resulting in the lowest counting efficiency and highest κ_app artifacts (−0.57) for 100 nm aerosols in CCN case 1. The largest CCN-derived κ_app artifact observed outside of CCN case 1 was −0.01 for 100 nm aerosols in CCN case 2.

The combined artifacts for the cases in which the highest artifacts were observed (DMA case 4, multiple particle charging, CPC case 4, CPC case 10, CCN case 1) are 0.24, 0.21, 0.23, and 0.15 for 25, 50, 100, and 200 nm particles, respectively, as shown in Fig. 10. The combined artifacts for the lowest-artifact cases (DMA case 2, CPC case 3, and CCN case 4) are <0.008 except for all four particle diameters.

8 Conclusions

The sensitivity of weather and climate models to accuracy in CCN activation predictions has been demonstrated in other works. Possible sources of apparent hygroscopicity artifacts calculated from CCN measurements have been presented in this study. This analysis has focused on sodium chloride and ammonium sulfate aerosols, but it can be extended to other aerosol populations, including mixtures and field samples.

The greatest combined artifacts ($\mathrm{0.15}<{\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}<\mathrm{0.24}$, NaCl) occurred as a result of the combined issues of the highest DMA aerosol ∕ sheath ratio, uncorrected multiple particle charging, and undercounting by both CPC and CCN instruments. The lowest combined artifacts ($.0021<{\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}<\mathrm{0.0074}$, NaCl) occurred as a result of ideal operating conditions: lowest DMA ∕ sheath ratio, corrected multiple particle charging, and little to no undercounting.

The largest single-instrument artifacts ($-\mathrm{0.57}<{\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}<\mathrm{0.42}$ for sodium chloride) in this study arise from undercounting by either the CPC or CCN counter at high concentration. This problem occurs during attempts to measure aerosol concentrations of ∼10⁴ cm⁻³, which is much higher than the recommended concentration ranges for either instrument (CPC cases 7–10 and CCN case 4). Corrective action should be taken to dilute aerosol samples in order to avoid undercounting. It should be noted that these artifacts are for individual instruments and do not take combined operation of the CPC and CCN into account; when both instruments undercount, artifacts in κ_{app, artifact} are reduced.

Smaller single-instrument artifacts (${\mathit{\kappa }}_{\mathrm{app},\mathrm{artifact}}<\mathrm{0.04})$ were observed for the CPC cases in which 50 % cutoff diameter and maximum counting efficiency were varied. Given the chosen particle diameters (25, 50, 100, 200 nm), κ_app artifacts due to d₅₀ were minimal. The largest κ_app artifacts for a CPC counting at low concentration (0.031–0.035) were observed when the maximum counting efficiency was equal 0.90. This may represent a compositional mismatch between n-butanol as the working fluid and sodium chloride as the aerosol due to the poor solubility of the latter in the former. Individual n-butanol CPCs may exhibit higher maximum counting efficiencies for sodium chloride.

Uncertainty arising from the DMA depended greatly on the chosen aerosol and sheath settings. One set of DMA cases (cases 2–4) examined the effect of aerosol ∕ sheath ratio. By decreasing this ratio, a narrower near-monodisperse flow can be produced, which increases the accuracy of calculated κ_app. The κ_app artifacts for an aerosol ∕ sheath ratio of 0.10 were 0.65 % of κ_literature for 25 nm sodium chloride aerosols, 0.31 % for 50 nm, −0.17 % for 100 nm, and −1.2 % for 200 nm.

The second set of DMA cases (5–7) were designed to evaluate the effects of holding the sheath flow constant while varying the excess air flow by −2 %, +2 %, and +5 %. These resulted in shifts of ≤2 nm for 25 and 50 nm particles, ≤4 nm for 100 nm particles, and ≤7 nm for 200 nm particles. The downstream aerosol distribution was shifted towards larger particle diameters when sheath flow exceeded excess flow and towards smaller particle diameter when sheath flow was less than excess flow. When taking field measurements, the composition of the sample may vary with particle diameter, thereby introducing another source of error from a broader DMA distribution.

By extension, the issue of uncertain sizing by the DMA leads to added uncertainties in the CCN instrument calibrations, which are strongly dependent on the chosen aerosol-to-sheath ratio within the DMA. We recommend conducting all CCN calibrations with a DMA aerosol-to-sheath ratio of 1 : 10 or 1 : 20, which will reduce kappa uncertainties to less than 1 % for all dry sizes (25 to 200 nm).

Overall, under optimal operating conditions, where the DMA aerosol ∕ sheath ratio is 0.10 and excess ∕ sheath ratio is 1.0, and in the absence of undercounting by the CPC or CCN, uncertainties in κ_app are less than ±1.2 % for 25 to 200 nm particles. During sampling, when the DMA sample ∕ sheath ratio is reduced to 0.05, κ_app uncertainties decrease to ±0.58 %. Additionally, errors in the activated fraction (and therefore κ_app) resulting from the bipolar charge distribution can be corrected by determining the fraction of particles with multiple charges.

Apparent hygroscopicity parameter artifacts were calculated for two pure inorganic species in this study. This analysis could be used to estimate κ_app artifacts for ambient aerosol populations, which may result in a better understanding of the real differences among these populations. As discussed in the introduction, Collins et al. (2016) aggregated κ_app from several mesocosm and field studies for 30–100 nm sea spray aerosol ($\mathrm{0.4}<{\mathit{\kappa }}_{\mathrm{app}}^{\mathrm{SSA}}<\mathrm{1.3}$). The wide range of κ_app in these studies may be attributed to differences in composition, experimental artifacts, or a combination of the two. Quantification of experimental artifacts would facilitate interpretation of κ_app in aerosol populations and constrain the importance of composition in CCN activation. There has been a recent proliferation of CCN data availability from multiple researchers and multiple experimental setups. To maximize the utility of these studies and to compare cloud-activating properties of various ambient aerosol masses, it is essential that artifacts are considered in both CCN data collection and reporting of the data.

Appendix A

αCC, βCC, γCC	Empirically determined constants used to calculate Cunningham slip correction factor
Zp	Aerosol particle electrical mobility
CC	Cunningham slip correction factor
dm	Electrical mobility diameter
n	Number of charges on particle
e	Elementary unit of charge
η	Gas dynamic viscosity
λ	Mean free path
Qsh	Sheath flow
Qe	Excess air flow
Qa	Aerosol flow
Qs	Sample flow
κapp	Apparent hygroscopicity parameter
κapp, artifact	Apparent hygroscopicity parameter artifact
s	Equilibrium water vapor saturation
scrit	Critical saturation (50 % of aerosols active as cloud condensation nuclei)
A	Constant used in calculating κapp
σlv	Surface tension of water
T	Temperature
Dact	Activation diameter
SScrit	Critical percent supersaturation
αTF	Height of DMA transfer function
βTF	Half-width of DMA transfer function
$Z{{}^{\prime }}_{\mathrm{p}}$	Mobility of particle at DMA inlet
Zp, mid	Midpoint of transfer function
ΔZp	Half-width of transfer function
V0	Voltage selected at DMA
r1	DMA inner radius
r2	DMA outer radius
L	DMA length
d50	50 % cutoff diameter