Retrieval of aerosol microphysical and optical properties over land using a multimode approach

Polarimeter retrievals can provide detailed and accurate information on aerosol microphysical and optical properties. The SRON aerosol algorithm is one of the few retrieval approaches that can fully exploit this information. The algorithm core is a two-mode retrieval in which effective radius (r_eff), effective variance (v_eff), refractive index, and column number are retrieved for each mode; the fraction of spheres for the coarse mode and an aerosol layer height are also retrieved. Further, land and ocean properties are retrieved simultaneously with the aerosol properties. In this contribution, we extend the SRON aerosol algorithm by implementing a multimode approach in which each mode has fixed r_eff and v_eff. In this way the algorithm obtains more flexibility in describing the aerosol size distribution and avoids the high nonlinear dependence of the forward model on the aerosol size parameters. Conversely, the approach depends on the choice of the modes.

We compare the performances of multimode retrievals (varying the number of modes from 2 to 10) with those based on the original (parametric) two-mode approach. Experiments with both synthetic measurements and real measurements (PARASOL satellite level-1 data of intensity and polarization) are conducted. The synthetic data experiments show that multimode retrievals are good alternatives to the parametric two-mode approach. It is found that for multimode approaches, with five modes the retrieval results can already be good for most parameters. The real data experiments (validated with AERONET data) show that, for the aerosol optical thickness (AOT), multimode approaches achieve higher accuracy than the parametric two-mode approach. For single scattering albedo (SSA), both approaches have similar performances.

1 Introduction

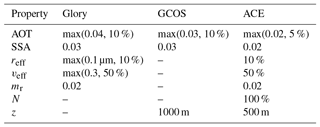
Aerosols such as dust, smoke, sulfate, and volcanic ash affect the Earth's climate by interaction with radiation (direct effect) and by modifying the properties of clouds (indirect effect). In order to reduce the large uncertainties in aerosol direct and indirect effects, satellite remote sensing is of crucial importance (Lee et al., 2009). Satellite data of intensity and polarization (polarized intensity) that observe a ground pixel under multiple viewing angles contain the richest set of information of aerosols in our atmosphere from a passive remote-sensing perspective (Kokhanovsky, 2015). To acquire useful knowledge based on these data, accurate retrievals of aerosols' microphysical and optical properties are essential. Here, aerosol microphysical properties include the particle effective radius, the effective variance, the refractive index, and the particle shape. Aerosol optical properties mainly include the (multispectral) aerosol optical thickness (AOT) and single scattering albedo (SSA). Accuracy requirements for (a subset of) these parameters are listed in Table 1.

Table 1 Accuracy requirements on aerosol properties from Mishchenko et al. (2004) as used for the Glory mission, Global Climate Observing System (GCOS), and the ACE study (https://acemission.gsfc.nasa.gov/documents/ACE_Report5_Aerosol_Science_v7.pdf, last access: 13 December 2018).

There are currently a number of aerosol retrieval algorithms available (Chowdhary et al., 2001; Hasekamp, 2010; Hasekamp and Landgraf, 2007) based on the use of multi-angle and multispectral measurements of intensity and polarization. These algorithms can be divided in two main groups: approaches based on lookup tables (LUTs) and full inversion approaches. Generally speaking, LUT approaches are faster but less accurate than full inversion approaches because LUT approaches choose the best fitting aerosol model from a discrete LUT. Full inversion approaches are more accurate but slower because they require radiative transfer (RT) calculations as part of the retrieval procedure. The LUT algorithms are, for example, the Laboratoire d'optique atmosphérique (LOA) LUT algorithm over ocean (Deuzé et al., 2000), the LOA LUT algorithm over land (Deuzé et al., 2001; Herman et al., 1997), and the SSA LUT algorithm (Waquet et al., 2016). The full inversion algorithms are, for example, the Generalized Retrieval of Aerosol and Surface Properties (GRASP) algorithm (Dubovik et al., 2011), the SRON aerosol algorithm (Di Noia et al., 2017; Hasekamp and Landgraf, 2007; Hasekamp et al., 2011; Stap et al., 2015; Wu et al., 2015, 2016), the Jet Propulsion Laboratory (JPL) algorithm (Xu et al., 2017), the Goddard Institute for Space Studies (GISS) algorithm (Waquet et al., 2009), and the microphysical aerosol properties from polarimetry (MAPP) algorithm (Stamnes et al., 2018). In addition, some additional aerosol retrieval approaches can be found in Sano et al. (2006), Cheng et al. (2011), Masuda et al. (2000), and Lebsock et al. (2007). It should be noted that of the full inversion approaches only the SRON aerosol algorithm and the GRASP algorithm have been applied at a global scale.

In this study, the SRON aerosol algorithm is used, which is a full inversion retrieval approach with the first guess generated by LUT retrieval. In the SRON aerosol algorithm, a damped Gauss–Newton iteration method is used to solve the nonlinear retrieval problem. Phillips–Tikhonov regularization is used as the regularization method. In the current version of the algorithm, it is based on a bimodal description of aerosols in fine and coarse modes, both described by a lognormal size distribution. The parameters that describe these two modes (for each mode r_eff, v_eff, refractive index, and column number and for the coarse mode additionally the fraction of spheres) are retrieved. A similar approach has been used by Waquet et al. (2009) and Stamnes et al. (2018). Other algorithms (GRASP, JPL) do not retrieve size parameters of each mode but instead describe aerosols with a larger number of modes with fixed size distribution. The column number of each mode is then a free parameter in the retrieval.

Both approaches have advantages and disadvantages. The bimodal approach may not be appropriate in situations in which aerosols contain more than two modes. Also, the retrieval of r_eff and v_eff for each mode makes the inversion problem highly nonlinear and hence more difficult to solve. Conversely, multimode approaches are expected to depend strongly on the assumed size distribution of each mode and the total number of modes used.

The aim of this paper is to compare the bimodal and multimodal approaches for the retrieval of aerosols from multi-angle polarimeter (MAP) data. For this purpose we extend the SRON algorithm with the capability to perform a multimode retrieval. We then compare the approaches for synthetic measurements and for real measurements of POLDER-3 on PARASOL.

This paper is organized as follows. Section 2 introduces the methodologies of the parametric two-mode retrieval and multimode retrievals. Section 3 describes the data sets and retrieval quality measures used in this study. Section 4 contains the synthetic data experiments. The real data experiments of multimode approaches are discussed in Sect. 5. Finally, the last section summarizes and concludes this study.

2 Methodology

2.1 Parametric two-mode retrieval

In this section, we first describe the methodology of the original SRON aerosol algorithm, which is referred to as a parametric two-mode retrieval. The inversion retrieval approach is aimed to invert a forward model equation:

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathit{y}=\mathbf{F}\left(\mathit{x}\right)+{\mathit{e}}_y.\end{array}$$

Here, y is the measurement vector containing the multispectral and multi-angle polarimetric measurements of PARASOL. e_y represents the measurement error. x contains parameters to be retrieved, which include aerosol properties and land or ocean properties. The forward model F(x), which describes the dependence between y and x, contains two parts: (1) microphysical properties to optical properties and (2) optical properties to the intensity vector (at the top of the atmosphere) through an atmospheric RT model. Nonspherical aerosols are modeled as a size–shape mixture of randomly oriented spheroids (Hill et al., 1984; Mishchenko et al., 1997). We use the Mie–T matrix–improved geometrical optics database by Dubovik et al. (2006) along with their proposed spheroid aspect ratio distribution for computing optical properties for a mixture of spheroids and spheres. For the RT model we refer to Landgraf et al. (2001), Hasekamp and Landgraf (2002), and Hasekamp and Landgraf (2005).

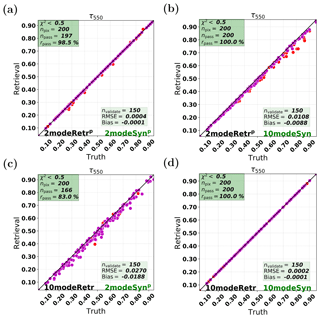
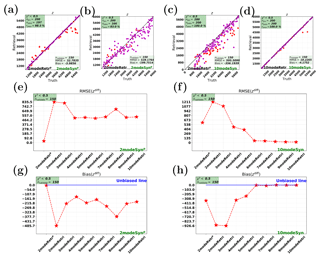
Figure 1 Synthetic retrievals: aerosol optical thickness (AOT) with the parametric two-mode retrieval (2modeRetr^p) and the 10-mode retrieval (10modeRetr). The red and magenta points represent n_pass and n_validate points, respectively. The measurements are the parametric two-mode synthetic measurement (2modeSyn^p) and the 10-mode synthetic measurement (10modeSyn). (a) 2modeRetr^p on 2modeSyn^p. (b) 2modeRetr^p on 10modeSyn. (c) 10modeRetr on 2modeSyn^p. (d) 10modeRetr on 10modeSyn.

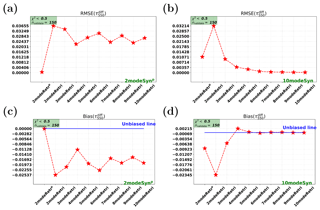
Figure 2 Synthetic retrievals for AOT: root-mean-square error (RMSE) and bias for the difference between the retrieved AOT and the true AOT. The x axis in each subplot represents 2modeRetr^p and different multimode retrieval cases (i.e., 2modeRetr, 3modeRetr, …, 10modeRetr). Panels (a, c) show RMSE and bias for the cases on 2modeSyn^p. Panels (b, d) show RMSE and bias for the cases on 10modeSyn.

In the parametric two-mode retrieval algorithm, the fine and coarse modes (denoted by superscript “f” or “c”) are characterized by the effective radius $r_{\mathrm{eff}}^{\mathrm{f};\mathrm{c}}$, the effective variance $v_{\mathrm{eff}}^{\mathrm{f};\mathrm{c}}$, the real and imaginary part of refractive index $m_{\mathrm{r}}^{\mathrm{f};\mathrm{c}}$ and $m_{\mathrm{i}}^{\mathrm{f};\mathrm{c}}$, the aerosol loading N^f;c, and the fraction of spheres $f_{\mathrm{sphere}}^{\mathrm{f};\mathrm{c}}$. The complex refractive index for each mode is $m^{\mathrm{f};\mathrm{c}}=m_{\mathrm{r}}^{\mathrm{f};\mathrm{c}}+i{m}_{\mathrm{i}}^{\mathrm{f};\mathrm{c}}$. In the latest SRON aerosol algorithm, m^f;c values are not directly retrieved (i.e., not in the state vector x), but constructed using $m^{\mathrm{f};\mathrm{c}}\left(\mathit{\lambda }\right)={\sum }_{k=\mathrm{1}}^{n_{\mathit{\alpha }}^{\mathrm{f};\mathrm{c}}}{\mathit{\alpha }}_k^{\mathrm{f};\mathrm{c}}{m}^{k,\mathrm{f};\mathrm{c}}\left(\mathit{\lambda }\right)$, where the mode component coefficients ${\mathit{\alpha }}_k^{\mathrm{f};\mathrm{c}}$ ($\mathrm{0}\le {\mathit{\alpha }}_k^{\mathrm{f};\mathrm{c}}\le \mathrm{1}$) are included in the retrieval state vector. m^k,f for the fine mode (or m^k,c for the coarse mode) is the fixed spectral-dependent complex refractive index spectra for some aerosol components, e.g., dust (DUST), water (H₂O), black carbon (BC), and inorganic matter (INORG). In this study, we set $n_{\mathit{\alpha }}^{\mathrm{f};\mathrm{c}}=\mathrm{2}$ and assume that the fine mode and the coarse mode are respectively composed by INORG+BC and DUST+INORG. Note that this assumption is flexible and can be updated according to the information content of the measurement. Also, spectra based on principal component analysis (PCA) can be used like in Wu et al. (2015).

To retrieve the state vector from the satellite measurements, a damped Gauss–Newton iteration method with Phillips–Tikhonov regularization is employed (Hasekamp et al., 2011). The inversion algorithm finds the solution $\widehat{\mathit{x}}$, which solves the minimization–optimization problem,

$$\begin{array}{}\text{(2)}& {\displaystyle }\widehat{\mathit{x}}=\underset{\mathit{x}}{\min }\left(\right|\left|{\mathbf{S}}_y^{-\frac{\mathrm{1}}{\mathrm{2}}}\right(\mathbf{F}\left(\mathit{x}\right)-\mathit{y}\left)\right|{|}^{\mathrm{2}}+\mathit{\gamma }\left|\right|{\mathbf{W}}^{-\frac{\mathrm{1}}{\mathrm{2}}}(\mathit{x}-{\mathit{x}}_{\mathrm{a}})\left|{|}^{\mathrm{2}}\right).\end{array}$$

Here, x_a is the a priori state vector, W is a weighting matrix, γ is a regularization parameter, and S_y is the measurement error covariance matrix. The weighting matrix W ensures that all state vector parameters range within the same order of magnitude (Hasekamp et al., 2011) and can be used to give some parameters more freedom in the inversion than others (similar to the prior covariance matrix in optimal estimation methods). Since the forward model F(x) is nonlinear with respect to x, the inversion for Eq. (2) is implemented iteratively. For each iteration step (e.g., step n), we approximate the forward model F(x) with

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathbf{F}\left(\mathit{x}\right)\approx \mathbf{F}\left({\mathit{x}}_n\right)+\mathbf{K}(\mathit{x}-{\mathit{x}}_n).\end{array}$$

Here, K is the Jacobian matrix (with $K_{ij}=\frac{\partial F_i}{\partial x_j}\left({\mathit{x}}_n\right)$), which contains the derivatives of the forward model with respect to each variable in the state vector x.

Based on the linear approximation (Eq. 3), the optimization problem (Eq. 2) can be reduced to

$$\begin{array}{}\text{(4)}& {\displaystyle }{\stackrel{\mathrm{̃}}{\mathit{x}}}_{n+\mathrm{1}}=\underset{\stackrel{\mathrm{̃}}{\mathit{x}}}{\min }\left(\right|\left|\stackrel{\mathrm{̃}}{\mathbf{K}}\right(\stackrel{\mathrm{̃}}{\mathit{x}}-{\stackrel{\mathrm{̃}}{\mathit{x}}}_n)-\stackrel{\mathrm{̃}}{\mathit{y}}|{|}^{\mathrm{2}}+\mathit{\gamma }\left|\right|\stackrel{\mathrm{̃}}{\mathit{x}}-{\stackrel{\mathrm{̃}}{\mathit{x}}}_a\left|{|}^{\mathrm{2}}\right),\end{array}$$

where $\stackrel{\mathrm{̃}}{\mathbf{K}}={\mathbf{S}}_y^{-\frac{\mathrm{1}}{\mathrm{2}}}{\mathbf{KW}}^{\frac{\mathrm{1}}{\mathrm{2}}}$, $\stackrel{\mathrm{̃}}{\mathit{x}}={\mathbf{W}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathit{x}$, and $\stackrel{\mathrm{̃}}{\mathit{y}}={\mathbf{S}}_y^{-\frac{\mathrm{1}}{\mathrm{2}}}(\mathit{y}-\mathbf{F}({\mathit{x}}_n\left)\right)$. The solution of Eq. (4) refers to Rodgers (2000) and Hasekamp et al. (2011) and is iterated by

$$\begin{array}{}\text{(5)}& {\displaystyle }{\stackrel{\mathrm{̃}}{\mathit{x}}}_{n+\mathrm{1}}=\mathrm{\Lambda }\stackrel{\mathrm{̃}}{\mathbf{G}}\stackrel{\mathrm{̃}}{\mathit{y}}+\stackrel{\mathrm{̃}}{\mathbf{A}}{\stackrel{\mathrm{̃}}{\mathit{x}}}_n+(\mathbf{I}-\stackrel{\mathrm{̃}}{\mathbf{A}}){\stackrel{\mathrm{̃}}{\mathit{x}}}_a,\end{array}$$

with the contribution matrix $\stackrel{\mathrm{̃}}{\mathbf{G}}=({\stackrel{\mathrm{̃}}{\mathbf{K}}}^T\stackrel{\mathrm{̃}}{\mathbf{K}}+\mathit{\gamma }\mathbf{I}{)}^{-\mathrm{1}}{\stackrel{\mathrm{̃}}{\mathbf{K}}}^T$ and the averaging kernel matrix $\stackrel{\mathrm{̃}}{\mathbf{A}}=\stackrel{\mathrm{̃}}{\mathbf{G}}\stackrel{\mathrm{̃}}{\mathbf{K}}$. Λ is a filter factor, which limits the step size for each iteration of the state vector. In this way, we use a Gauss–Newton scheme with reduced step size to avoid diverging retrievals (Hasekamp et al., 2011). The filter factor Λ shows values between 0 and 1.

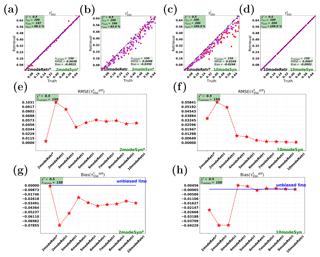
Figure 3 Synthetic retrievals for the AOT (at 550 nm) of all the fine modes (${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$). The left panels (i.e., a, b, e, g) and the right panels (i.e., c, d, f, h) are for cases on 2modeSyn^p and 10modeSyn, respectively. Panels (a–d) show the parametric two-mode retrieval (2modeRetr^p) and the 10-mode retrieval (10modeRetr). Panels (e, f) show RMSE and (g, h) show bias for different retrieval cases.

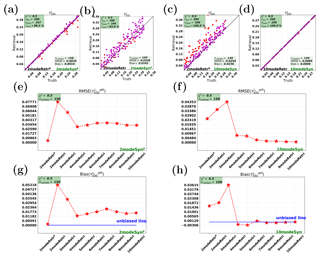
Figure 4 Synthetic retrievals for the AOT (at 550 nm) of all the coarse modes (${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{c}}$). Panels (a, b, e, g) and (c, d, f, h) show cases on 2modeSyn^p and 10modeSyn, respectively.

The regularization parameter γ and filter factor Λ in Eqs. (4) and (5) are chosen optimally (for each iteration) from different values for γ (10 values from 0.1 to 5) and for Λ (10 values from 0.1 to 1) by evaluating the goodness of fit using a simplified (fast) forward model.

2.2 Multimode retrieval

We now introduce the multimode SRON aerosol retrieval approach. In principle, the idea of the multimode approach is that instead of fitting the size distribution parameters (r_eff and v_eff) of two modes, one aims to fit the size distribution with a larger number of modes for which r_eff and v_eff are fixed. An expected advantage of this approach is that it makes the inversion problem more linear (r_eff and v_eff tend to make the inversion problem highly nonlinear). Furthermore, the multimode approach has more freedom in fitting different shapes of size distribution if the number of chosen modes is sufficiently large. Conversely, the multimode approach is expected to depend strongly on the assumed modes.

Table 2 Multimode retrieval definition.

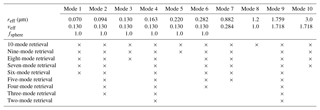
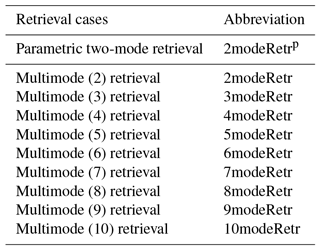
The performance of the multimode approach is expected to be better and better as the mode number increases. In this study, we take the 10-mode retrieval as the maximum mode number retrieval. All the multimode retrieval cases are defined as in Table 2. For example, for the five-mode retrieval case, the five modes used for retrieval are actually modes 2, 4, 6, 7, and 9 in the 10-mode retrieval. Here, the five modes correspond to those of Xu et al. (2017). The abbreviations for different retrieval cases used in this study are listed in Table 3, in which the parametric retrieval is denoted with a superscript “p”, i.e., 2modeRetr^p.

Table 3 Abbreviations for different retrieval cases.

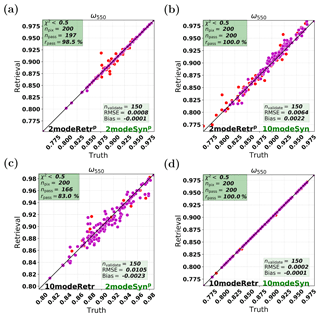
Figure 5 Synthetic retrievals: single scattering albedo (SSA) with the parametric two-mode retrieval (2modeRetr^p) and the 10-mode retrieval (10modeRetr). The red and magenta points represent n_pass and n_validate points, respectively. The measurements are the parametric two-mode synthetic measurement (2modeSyn^p) and the 10-mode synthetic measurement (10modeSyn). (a) 2modeRetr^p on 2modeSyn^p. (b) 2modeRetr^p on 10modeSyn. (c) 10modeRetr on 2modeSyn^p. (d) 10modeRetr on 10modeSyn.

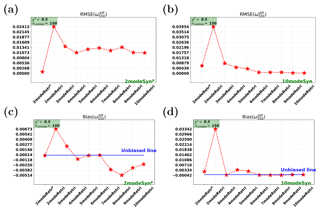
Figure 6 Synthetic retrievals for SSA: root-mean-square error (RMSE) and bias for the difference between the retrieved SSA and the true SSA. Panels (a, c) show RMSE and bias for the cases on 2modeSyn^p. Panels (b, d) show RMSE and bias for the cases on 10modeSyn.

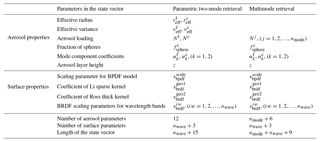
For multimode retrievals, the state vector x in Eqs. (1) and (2) is different from that in the parametric two-mode retrieval. The difference is shown in Table 4, which specifies the parameters in the state vector. In the multimode retrieval, since r_eff and v_eff are not retrieved for all modes, they are not included in x. The aerosol loading $N^j(j=\mathrm{1},\mathrm{2},\mathrm{\dots },n_{\mathrm{mode}})$ for all modes is retrieved and included in x. In principle, other aerosol parameters like the refractive index coefficients, the fraction of spheres, and the aerosol layer height can be retrieved for each mode independently. However, the measurement vector will not contain sufficient information to extract this information for each mode separately. Therefore, for the retrieval of these parameters we group the modes into two types – fine (i.e., modes 1–6 of Table 2 for the 10-mode case) and coarse (modes 7–10 of Table 2). For the refractive index coefficients, we fit one value for the fine modes and one value for the coarse modes. For the fraction of spheres, we only retrieve one value for the coarse modes and assume the fine modes consist only of spheres. (A recent study by Liu and Mishchenko, 2018, indicates that this assumption becomes unrealistic for an increasing fraction of carbonaceous aerosol in the fine mode.) For the aerosol layer height we fit one value that is assumed representative for all modes. These assumptions are similar to those in the parametric two-mode retrieval. According to Table 4, the number of aerosol parameters for the parametric two-mode retrieval and the multimode retrieval is respectively $n_{\mathit{\alpha }}^{\mathrm{f}}+n_{\mathit{\alpha }}^{\mathrm{c}}+\mathrm{8}$ and $n_{\mathrm{mode}}+n_{\mathit{\alpha }}^{\mathrm{f}}+n_{\mathit{\alpha }}^{\mathrm{c}}+\mathrm{2}$, where the fine- and coarse-mode component coefficients $n_{\mathit{\alpha }}^{\mathrm{f}}$ and $n_{\mathit{\alpha }}^{\mathrm{c}}$ are both set to 2 in this study.

Table 4 State vector for parametric two-mode retrieval and multimode retrieval.

In addition to the aerosol-related parameters, x in multimode retrievals also includes surface reflectance and polarization parameters in the same manner as the parametric two-mode retrieval. For surface models of the bidirectional reflectance distribution function (BRDF), we use the Ross–Li model (Li and Strahler, 1992; Ross, 1981) for the same settings as in Litvinov et al. (2011). For modeling surface bidirectional polarization distribution function (BPDF), a Fresnel model is used as introduced by Maignan et al. (2009). The surface parameters, to be retrieved in the state vector (see Table 4), are scaling parameters for the BPDF model ($x_{\mathrm{bpdf}}^{\mathrm{scale}}$), the coefficient of the Li sparse kernel ($x_{\mathrm{brdf}}^{\mathrm{geo}\mathrm{1}}$), the coefficient of the Ross thick kernel ($x_{\mathrm{brdf}}^{\mathrm{geo}\mathrm{2}}$), and the BRDF scaling parameters at each wavelength band ($x_{\mathrm{brdf}}^{iw}$, $iw=\mathrm{1},\mathrm{2},\mathrm{\dots },n_{\mathrm{wave}}$). The number of surface-related parameters in the state vector for all retrieval cases is n_wave+3. Therefore, the length of the state vector (i.e., the total number of aerosol- and surface-related parameters) is $n_{\mathit{\alpha }}^{\mathrm{f}}+n_{\mathit{\alpha }}^{\mathrm{c}}+n_{\mathrm{wave}}+\mathrm{11}$ for the parametric two-mode retrieval and is $n_{\mathrm{mode}}+n_{\mathit{\alpha }}^{\mathrm{f}}+n_{\mathit{\alpha }}^{\mathrm{c}}+n_{\mathrm{wave}}+\mathrm{5}$ for the multimode retrieval.

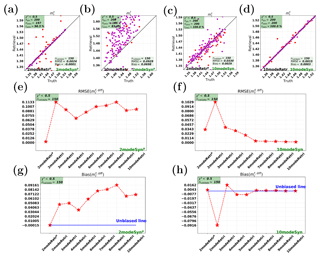
Figure 7 Synthetic retrievals for the real part of refractive index (at 550 nm) of the fine modes ($m_{\mathrm{r}}^{\mathrm{f}}$). Panels (a, b, e, g) and (c, d, f, h) show cases on 2modeSyn^p and 10modeSyn, respectively.

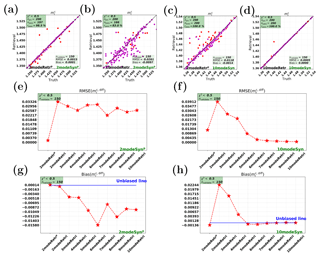
Figure 8 Synthetic retrievals for the real part of refractive index (at 550 nm) of the coarse modes ($m_{\mathrm{r}}^{\mathrm{c}}$). Panels (a, b, e, g) and (c, d, f, h) show cases on 2modeSyn^p and 10modeSyn, respectively.

Table 5 Prior values and weighting factors for the state vector in the parametric two-mode retrieval and the multimode retrieval. The prior value and weighting factor of aerosol loading N for each mode are further calculated based on Mie theory using the prior information of τ^f and τ^c from the table.

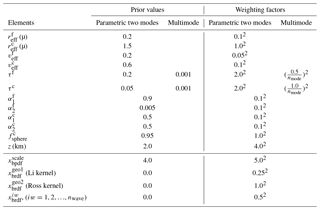
The inversion procedure of multimode retrievals is the same as described by Eqs. (3), (4), and (5). W is a diagonal matrix and its diagonal values are shown in Table 5. Note that the prior information of aerosol loading (N) is provided in terms of AOT.

2.3 Multimode retrieval of first guess

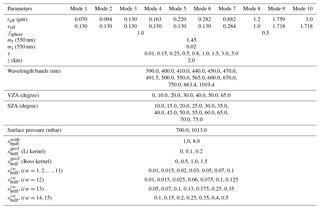
In the SRON aerosol algorithm, the first guess of x is obtained before the full inversion retrieval using a LUT, which is based on tabulated RT calculations for each of the 10 modes listed in Table 6 separately. The RT calculations are performed for different combinations of input parameters (as specified in Table 6), which are, for example, one single layer height, one value of the refractive index (different for fine and coarse modes), nine AOT (τ) values, 15 wavelength bands, seven viewing zenith angles (VZAs), 14 solar zenith angles (SZAs), two surface pressures, two values for the scaling parameter for the BPDF model, three values for the coefficient of the Li sparse kernel, four values for the coefficient of the Ross thick kernel, and seven values for the BRDF scaling parameters at each wavelength band.

Table 6 Parameters to create a 10-mode lookup table.

The precalculated LUT is used as input for an approximate forward model in the LUT retrieval. Here, the RT multiple scattering calculations, performed separately for the different modes, are combined using the method of Gordon and Wang (1994). Single scattering is computed exactly as its computational cost is negligible. Using the approximate forward model, a retrieval is performed using the same inversion method as for the full retrieval (Eqs. 3–5). The fit parameters are the aerosol column numbers of the 10 modes and the surface parameters. The result of the 10-mode LUT retrieval is also used for full retrievals with fewer than 10 modes (e.g., the parametric two-mode retrieval), by fitting the n_mode (n_mode<10) size distribution to the 10-mode size distribution coming from the LUT retrieval with the n_mode aerosol columns for the different modes as fit parameters.

3 Data and retrieval measures

3.1 PARASOL data

The satellite data used in this study for aerosol retrievals are from the Polarization and Directionality of Earth Reflectances-3 (POLDER-3) instrument (Deschamps et al., 1994; Fougnie et al., 2007), which was mounted on the PARASOL satellite (retired in 2013). The POLDER-3 instrument in space provided in-orbit multi-angle and multispectral photopolarimetric measurements of intensity and polarization. The PARASOL level-1 Collection 3 product data have been used in this study.

Each PARASOL image including 242 × 274 elements was made on a charge-coupled device (CCD) matrix array over a total view of 114^∘. Each ground pixel (6 km × 6 km) is measured under up to 16 angles. The intensity component (Stokes parameter I) was measured at nine bands and the polarization component (Stokes parameters Q and U) was measured at 490, 670, and 865 nm. PARASOL has a swath width of about 2400 km. The data from PARASOL have been used for aerosol retrievals in a number of studies (Dubovik et al., 2011; Hasekamp et al., 2011; Lacagnina et al., 2015, 2017; Stap et al., 2015). In previous studies using the SRON aerosol algorithm (Hasekamp et al., 2011; Lacagnina et al., 2015, 2017; Stap et al., 2015), four bands (i.e., 490, 670, 865, 1020 nm) were used. In this study, two more bands (440 and 565 nm) are added for retrievals.

In the SRON aerosol algorithm, we do not directly use Q and U in the measurement vector but use the degree of linear polarization (DoLP) as the polarization component (together with the intensity component I) in the measurement vector. Here, DoLP equals $\frac{\sqrt{Q^{\mathrm{2}}+U^{\mathrm{2}}}}{I}$. For our retrievals on PARASOL measurements, we assume an intensity error I_err=0.01 and the polarization error DoLP_err=0.007, in the diagonal matrix ${\mathbf{S}}_y^{\frac{\mathrm{1}}{\mathrm{2}}}$ in Eq. (4). Here the intensity error is the relative error, and the polarization error is the absolute error. I_err=0.01 holds for all POLDER bands except for the band 440 nm, where $I_{\mathrm{err}}^{\mathrm{440}}$ is set at 0.03 because the intensity measurements at 440 nm are usually considered less accurate than those at other bands (Dubovik et al., 2011; Fougnie et al., 2007). Note that in our study in principle the 0.01 for I_err and 0.007 for DoLP_err used underestimating the PARASOL errors but in our inversion approach only the relative dependence between intensity errors and DoLP errors is important. The absolute value is compensated for by the regularization parameter.

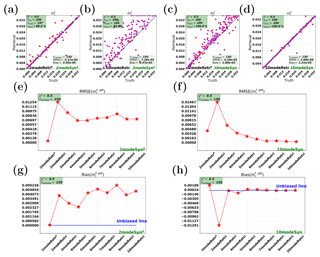
Figure 9 Synthetic retrievals for the imaginary part of refractive index (at 550 nm) of the fine modes ($m_{\mathrm{i}}^{\mathrm{f}}$). Panels (a, b, e, g) and (c, d, f, h) show cases on 2modeSyn^p and 10modeSyn, respectively.

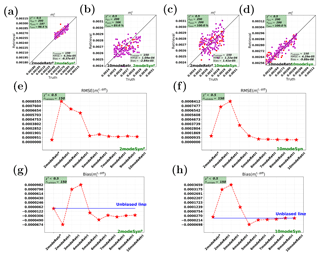
Figure 10 Synthetic retrievals for the imaginary part of refractive index (at 550 nm) of the coarse modes ($m_{\mathrm{i}}^{\mathrm{c}}$). Panels (a, b, e, g) and (c, d, f, h) show cases on 2modeSyn^p and 10modeSyn, respectively.

It should also be noted that higher-accuracy aerosol retrievals are to be expected for all parameters from instruments that have higher polarimetric accuracy, more scattering angles, and/or more spectral bands (e.g., Hasekamp and Landgraf, 2007; Mishchenko and Travis, 1997). Examples of such improved instruments are GLORY-APS (Mishchenko et al., 2007), MAIA (Diner et al., 2018), SPEXone (Hasekamp et al., 2018), and HARP-2 (Martins et al., 2017).

3.2 Meteorological data

During retrievals, some atmospheric and meteorological inputs are needed to be interpolated to each pixel (where there is a PARASOL measurement) at a specified time and a geographical location. The required atmospheric parameters and inputs are humidity, temperature, pressure, and height. In this study, we obtain this information from National Centers for Environmental Prediction (NCEP) reanalysis data (Kalnay et al., 1996).

3.3 AERONET data

In this study we focus on aerosol retrievals over land. We validate the retrieved AOT with AERONET (AErosol RObotic NETwork) level 2.0 data (quality assured) of AOT (Holben et al., 2001). The retrieved SSA is validated with AERONET level 1.5 (cloud screened and quality controlled) Almucantar retrieval inversion products (Dubovik et al., 2002) of SSA.

Figure 11 Synthetic retrievals for the central height (z) of the aerosol layer. Panels (a, b, e, g) and (c, d, f, h) show cases on 2modeSyn^p and 10modeSyn, respectively.

3.4 Retrieval measures

In a retrieval, it is a common approach to apply the goodness of fit (χ²) to decide whether the retrievals have successfully converged. The goodness of fit χ² for each pixel is calculated by

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathit{\chi }}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{n_{\mathrm{meas}}}}\sum _{i=\mathrm{1}}^{n_{\mathrm{meas}}}{\displaystyle \frac{(F_i-y_i{)}^{\mathrm{2}}}{S_y(i,i)}}.\end{array}$$

Here, n_meas is the total number of measurements (multi-angle and multispectral intensity and polarization) for each pixel. y_i represents the measurement (synthetic or real) and F_i represents the simulated measurement through the forward model. S_y(i,i) is the diagonal value of the measurement error covariance matrix, corresponding to the ith measurement.

We consider retrievals with ${\mathit{\chi }}^{\mathrm{2}}<{\mathit{\chi }}_{\max }^{\mathrm{2}}$ as valid retrievals. This filter rejects cases in which the forward model is not able to fit the measurements, i.e., because of cloud-contaminated pixels (Stap et al., 2015, 2016), corrupted measurements (Hasekamp et al., 2011), and cases in which the first guess state vector deviates too much from the truth. Based on χ², we define the pass rate $r_{\mathrm{pass}}=\frac{n_{\mathrm{pass}}}{n_{\mathrm{pix}}}$ to be the number of successful pixels (n_pass) over the number of all pixels (n_pix).

To evaluate the retrieved aerosol properties, two measures are used, which are the RMSE and the bias. The two measures are both with respect to the differences between the retrieved values and the reference values (AERONET for real measurements and the truth for synthetic measurements). Here the difference $x_{\mathrm{ipix}}^{\mathrm{diff}}\left[j\right]$ (at the ith pixel (ipix) for the jth variable in the state vector x) is computed by $x_{\mathrm{ipix}}^{\mathrm{diff}}\left[j\right]=x_{\mathrm{ipix}}^{\mathrm{retr}}\left[j\right]-x_{\mathrm{ipix}}^{\mathrm{true}}\left[j\right]$, where $x_{\mathrm{ipix}}^{\mathrm{retr}}$ represents the retrieved aerosol property for the pixel ipix, while $x_{\mathrm{ipix}}^{\mathrm{true}}$ represents the reference aerosol property.

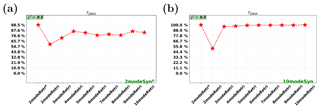
Figure 12 Synthetic retrievals: pass rates when χ²<0.5. (a) Retrievals on the parametric two-mode-based synthetic measurement (2modeSyn^p). (b) Retrievals on the 10-mode-based synthetic measurement (10modeSyn). The x axis in the subplot represents the parametric two-mode retrieval (2modeRetr^p) and different multimode retrieval cases (i.e., 2modeRetr, 3modeRetr, …, 10modeRetr).

For each aerosol property, the RMSE counts the overall retrieval errors for all pixels with $\sqrt{\frac{\mathrm{1}}{n_{\mathrm{pass}}}{\sum }_{\mathrm{ipix}=\mathrm{1}}^{n_{\mathrm{pass}}}\left(x_{\mathrm{ipix}}^{\mathrm{diff}}\right[j]{)}^{\mathrm{2}}}$. The bias is calculated by $\frac{\mathrm{1}}{n_{\mathrm{pass}}}{\sum }_{\mathrm{ipix}=\mathrm{1}}^{n_{\mathrm{pass}}}\left(x_{\mathrm{ipix}}^{\mathrm{diff}}\right[j\left]\right)$. The bias can be positive or negative, meaning the overestimation or the underestimation.

4 Synthetic retrievals

4.1 Synthetic measurements

To investigate the capability of multimode retrievals of aerosol microphysical and optical properties, we first perform synthetic data experiments. We can assess the capability of different retrieval setups by comparing the result of the retrieval to the truth that was used to create the synthetic measurement. The synthetic measurements are computed for the PARASOL wavelengths and 14 viewing angles, which is representative for PARASOL (Sect. 3.1).

The synthetic measurements are created pixel by pixel with two steps. (1) We generate aerosol modes based on assumed true aerosol properties of the effective radius r_eff, the effective variance v_eff, the fraction of spheres f_sphere, the aerosol loading N, the mode component coefficients α_k, and the aerosol height z. In this study, two sets of synthetic measurements are created. One set is created based on 10 aerosol modes. Each mode has fixed r_eff, v_eff as shown in Table 2. The other set is two-mode based. For this set, $r_{\mathrm{eff}}^{\mathrm{f}}$ and $r_{\mathrm{eff}}^{\mathrm{c}}$ are perturbed within [0.1, 0.3] and [0.65, 3.4], respectively. $v_{\mathrm{eff}}^{\mathrm{f}}$ and $v_{\mathrm{eff}}^{\mathrm{c}}$ are perturbed within [0.1, 0.3] and [0.4, 0.6], respectively. (2) Based on the generated aerosol modes, the forward model as discussed in Sect. 2.1 is used to generate the synthetic measurements. The assumed true aerosol properties for each pixel are generated stochastically.

For synthetic data experiments, we only consider noise-free retrievals; i.e., no noise is added to the generated synthetic measurements. In this way we focus the experiment on errors related to inconsistencies between the synthetic measurement and retrieval (i.e., different modes), and the capability of the retrieval algorithm itself (for consistent retrievals).

4.2 AOT

The synthetic retrievals for AOT are first evaluated. The abbreviations for different retrieval cases are summarized in Table 3. For synthetic retrievals, ${\mathit{\chi }}_{\max }^{\mathrm{2}}=\mathrm{0.5}$ is chosen as the threshold for χ² to define the successfully converged retrievals. Both consistent retrievals and inconsistent retrievals are tested. Consistent retrievals are retrievals for which the mode number for retrievals equals the mode number for creating synthetic measurements. Inconsistent retrievals are the cases when both mode numbers are not equal. Here, although the synthetic measurements do not contain noise, we use the values assumed in the retrieval procedure to compute the χ². Note that for consistent retrievals, in principle the χ² should be much smaller than 0.5 and should even be very close to 0 when the global minimum has been reached. This does obviously not hold for inconsistent retrievals in which a different number of modes have been used in the retrieval than in the creation of the synthetic measurements.

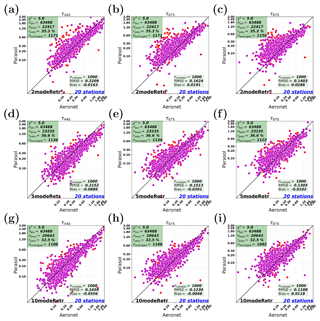
Figure 13 Real data retrievals of AOT among 2modeRetr^p, 5modeRetr, and 10modeRetr at different wavelengths. The red and magenta points represent n_averaged and n_validate points, respectively. Panels (a–c) show 2modeRetr^p at 440, 675, and 870 nm, respectively. Panels (d–f) show 5modeRetr at 440, 675, and 870 nm, respectively. Panels (g–i) show 10modeRetr at 440, 675, and 870 nm, respectively.

Figure 1 shows synthetic retrievals of AOT with the parametric two-mode retrieval (2modeRetr^p) and the 10-mode retrieval (10modeRetr). Both consistent retrievals (i.e., Fig. 1a and d) and inconsistent retrievals (i.e., Fig. 1b and c) are performed. To quantitatively evaluate the performances of different retrieval cases, RMSE and bias are indicated. For a fair comparison, RMSE and bias should be calculated for the same number of points. Thus a constant number n_validate (n_validate<n_pass) of points are selected to calculate RMSE and bias. In each retrieval case, the selected n_validate (n_validate is chosen at 150 here) points correspond to the points with the smallest n_validate number of χ². The total number of retrievals is n_pix (n_pix=200 here).

We first look at the performance of the consistent 10-mode synthetic retrieval, which is shown in Fig. 1d. The case is named 10modeRetr+10modeSyn. It shows that the retrieved AOT matches very well with the true AOT. The retrievals at all pixels can pass the strict filter χ²<0.5. Another consistent retrieval case, i.e., parametric two-mode retrieval on two-mode synthetic measurements (2modeRetr^p+2modeSyn^p), is shown in Fig. 1a, in which the AOT retrieval for r_pass (i.e., 98.5 %) pixels is also very accurate. Figure 1a and d show that both the 10-mode and the parametric two-mode retrievals have good capabilities of retrieving AOT for consistent synthetic measurements.

In addition to consistent retrievals, it is interesting to test the performances of inconsistent retrievals of AOT. This is because in reality, it is unknown how many modes the true atmosphere contains. For this purpose, inconsistent retrievals are also shown: parametric two-mode retrieval on 10-mode synthetic measurements (2modeRetr^p+10modeSyn) in Fig. 1b and 10-mode retrieval on two-mode synthetic measurements (10modeRetr+2modeSyn^p) in Fig. 1c. Although AOT retrievals in both inconsistent cases are not as good as those in consistent cases, there is still a good agreement between the retrieved total AOT and the true total AOT over different mode numbers. This shows that inconsistent retrievals are also capable of retrieving AOT.

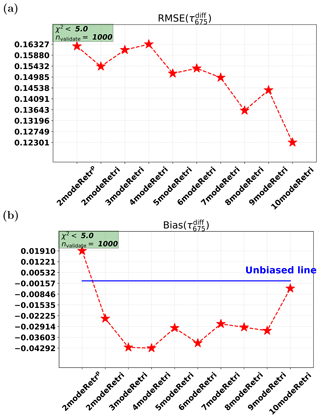
Figure 14 Real data retrievals for AOT: root-mean-square error (RMSE) and bias for the difference between PARASOL retrievals and AERONET data.

Next, we check the performances of other multimode (i.e., two-,three-, …, nine-mode) retrievals. Figure 2 shows the RMSE and the bias for all retrieval cases in the synthetic tests. The x axis in each subplot represents the parametric two-mode retrieval (2modeRetr^p) and different multimode retrieval cases (i.e., 2modeRetr, 3modeRetr, …, 10modeRetr). Figure 2a and c are for the cases on the two-mode measurements. It confirms that the parametric two-mode retrieval as the consistent case has the smallest RMSE and the smallest absolute bias (i.e., closest to zero) compared to inconsistent retrieval cases. Figure 2b and d show the cases on the 10-mode measurements. It can be found that the inconsistent retrieval for which $\mathrm{5}<n_{\mathrm{mode}}<\mathrm{10}$ has as good of a performance as the consistent retrieval (10modeRetr+10modeSyn). Actually, although three-, four-, and five-mode retrievals on the 10-mode measurements function a bit worse than the multimode retrievals with n_mode>5, their accuracy is better than the parametric two-mode retrieval on the 10-mode synthetic measurements. Therefore, we can conclude that multimode retrievals have more freedom to be compatible with inconsistent multimode measurements. Conversely, for inconsistent retrievals on two-mode synthetic measurements, the biases are larger than for the parametric two-mode retrieval on the 10-mode measurements.

4.3 AOT of the fine and coarse modes

It has been investigated that the multimode retrievals are capable of retrieving AOT (the total AOT over all modes) for both consistent and inconsistent cases. Since each retrieval case and each measurement case include two types of modes (i.e., the fine and coarse types), it is interesting to test multimode retrievals on the AOT over all fine modes (${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$) and the AOT over all coarse modes (${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{c}}$).

Figure 3 shows ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$. For consistent cases (Fig. 3a and d), the retrievals are accurate and nearly unbiased. For inconsistent cases (Fig. 3b and c), there are clear underestimations. This generally happens in inconsistent retrievals on the two-mode measurements, which can be seen in Fig. 3g (in which all the inconsistent retrievals show a negative bias). This does not happen for inconsistent retrievals on the 10-mode measurements, for which the parametric two-mode retrieval (2modeRetr^p), the fixed two-mode retrieval (2modeRetr), and the three-mode retrieval (3modeRetr) underestimate ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$; the four-mode retrieval (4modeRetr) and the five-mode retrieval (5modeRetr) slightly overestimate ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$; retrievals are almost unbiased for ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$ if n_mode>5. By checking the RMSE of all retrieval cases on the two-mode measurements (Fig. 3e) and the RMSE on the 10-mode measurements (Fig. 3f), retrievals have quite acceptable accuracies on both types of measurements if n_mode>3.

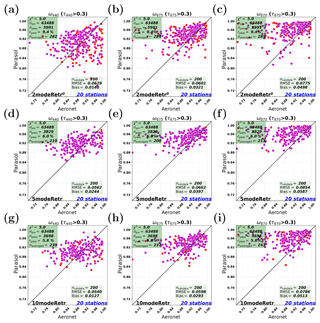
Figure 15 Real data retrievals of SSA among 2modeRetr^p, 5modeRetr, and 10modeRetr at different wavelengths. The red and magenta points represent n_averaged and n_validate points, respectively. Panels (a–c) show 2modeRetr^p at 440, 675, and 870 nm, respectively. Panels (d–f) show 5modeRetr at 440, 675, and 870 nm, respectively. Panels (g–i) show 10modeRetr at 440, 675, and 870 nm, respectively.

The total AOT of the coarse modes (${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{c}}$) is shown in Fig. 4. Compared to the underestimation in Fig. 3b and c for ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$, there is an overestimation for ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{c}}$, as shown in Fig. 4b and c. The reverse bias between ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{f}}$ and ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{c}}$ results in total AOT over all modes that is almost unbiased, as shown in Fig. 1. These offset effects can also be seen by comparing Figs. 4g and 3g or by comparing Figs. 4h and 3h. According to the RMSE shown in Fig. 4e and f, retrievals with n_mode>3 have good retrieval accuracy of ${\mathit{\tau }}_{\mathrm{550}}^{\mathrm{c}}$ on both synthetic measurements.

4.4 SSA

We also tested multimode retrievals of SSA. Figure 5 shows the parametric two-mode retrieval and the 10-mode retrieval for SSA while Fig. 6 shows the RMSE and the bias for different retrieval cases for the difference between the retrieved SSA and the true SSA.

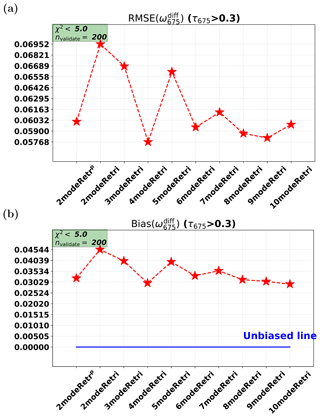
Figure 16 Real data retrievals for SSA: root-mean-square error (RMSE) and bias for the difference between PARASOL retrievals and AERONET data.

By comparing SSA for consistent retrieval cases (Fig. 5a and d), for the n_pass pixels (marked as red points), the match between the retrieved SSA and the true SSA in Fig. 5a is slightly worse than the match in Fig. 5d. This demonstrates the challenge in retrieving r_eff and v_eff in the parametric two-mode approach – even for a consistent setup – since r_eff and v_eff affect the derived SSA. For inconsistent retrievals however, we see that the parametric two-mode retrieval on the 10-mode synthetic measurements works better than vice versa. Although Fig. 5 shows different performances between the parametric two-mode retrieval (2modeRetr^p) and the 10-mode retrieval (10modeRetr), the accuracy and the bias in the four cases are quite good.

Figure 6b and d show the RMSE and bias comparisons among all retrieval cases on the 10-mode synthetic measurements. All retrievals for SSA except the fixed two-mode case are shown to be accurate and have small bias. On the two-mode synthetic measurements, the RMSEs (Fig. 6a) of multimode retrievals are a bit worse than the consistent SSA retrieval. For the bias on the two-mode synthetic measurement shown in Fig. 6c, it varies between 0 and −0.005. For the 10-mode synthetic measurements, multimode retrievals (if n_mode>4) and the parametric two-mode retrieval are virtually unbiased.

4.5 Refractive index

4.5.1 Real part of refractive index

As described in Sect. 2.2, for multimode retrievals we also use a separate refractive index for the fine and coarse modes. In this case, the fine-mode refractive index corresponds to mode numbers 1–6 in Table 2 and the coarse-mode refractive index to modes 7–10. Here we first test the retrievals of the real part of the refractive index for the fine modes and the coarse modes, i.e., $m_{\mathrm{r}}^{\mathrm{f}}$ and $m_{\mathrm{r}}^{\mathrm{c}}$ (at wavelength 550 nm), as respectively shown in Figs. 7 and 8.

For the consistent retrievals (2modeRetr^p+2modeSyn^p and 10modeRetr+10modeRetr), $m_{\mathrm{r}}^{\mathrm{f}}$ is retrieved with a small RMSE and nearly unbiased, as shown in Fig. 7a and d. Similarly, $m_{\mathrm{r}}^{\mathrm{c}}$ is also well retrieved in the consistent retrievals, which are shown in Fig. 8a and d. Actually, $m_{\mathrm{r}}^{\mathrm{c}}$ retrieval is shown better than $m_{\mathrm{r}}^{\mathrm{f}}$ retrieval, and 10-mode retrieval on 10-mode synthetic measurements is shown better than parametric two-mode retrieval on two-mode synthetic measurements.

For inconsistent retrieval cases, we first check the performances on the 10-mode measurements, i.e., the right panel of Figs. 7 and 8. It shows that the parametric two-mode retrieval and the multimode retrievals with n_mode>4 are capable of retrieving $m_{\mathrm{r}}^{\mathrm{f}}$ and $m_{\mathrm{r}}^{\mathrm{c}}$. However, this is not the case for retrievals on the two-mode measurements, i.e., the left panel in Figs. 7 and 8. $m_{\mathrm{r}}^{\mathrm{f}}$ is retrieved with overestimation, as shown in Fig. 7b and g. For the retrieval of $m_{\mathrm{r}}^{\mathrm{c}}$ (see Fig. 8b and g) an underestimation can be observed. It can be concluded that the parametric two-mode retrieval works better for the fine-mode real part of the refractive index than the multimode retrievals.

4.5.2 Imaginary part of refractive index

Next, we test the retrievals of the imaginary part of the refractive index. The fine-mode and coarse-mode cases (i.e., $m_{\mathrm{i}}^{\mathrm{f}}$ and $m_{\mathrm{i}}^{\mathrm{c}}$) are respectively shown in Figs. 9 and 10.

For consistent retrievals, $m_{\mathrm{i}}^{\mathrm{f}}$ is shown to be well retrieved for both the parametric two-mode case and the 10-mode case; see Fig. 9a and d. This is a result similar to that of the consistent retrievals of $m_{\mathrm{r}}^{\mathrm{f}}$ (Fig. 7a and d). However, for the coarse-mode case, the consistent retrievals of $m_{\mathrm{i}}^{\mathrm{c}}$ (Fig. 10a and d) do not look as good as the consistent retrievals of $m_{\mathrm{r}}^{\mathrm{c}}$ (Fig. 8a and d), especially for the consistent parametric two-mode case (Fig. 10a), in which there are some clear outliers. Based on these results, we conclude that for the consistent cases, (1) $m_{\mathrm{i}}^{\mathrm{f}}$ retrieval is better than $m_{\mathrm{i}}^{\mathrm{c}}$ retrieval; (2) 10-mode retrieval of $m_{\mathrm{i}}^{\mathrm{f}}$ and $m_{\mathrm{i}}^{\mathrm{c}}$ looks better than the parametric two-mode retrieval.

For inconsistent retrieval cases, the performances on the 10-mode synthetic measurements (see panels c, f, and h of Figs. 9 and 10) show that $m_{\mathrm{i}}^{\mathrm{f}}$ and $m_{\mathrm{i}}^{\mathrm{c}}$ can be well retrieved in the parametric two-mode and multimode retrievals with n_mode>4. This result is similar to what was shown for the inconsistent retrievals of $m_{\mathrm{r}}^{\mathrm{f}}$ and $m_{\mathrm{r}}^{\mathrm{c}}$ (see panels c, f, and h of Figs. 7 and 8), except for one difference; i.e., the parametric two-mode retrieval has clear overestimation when retrieving $m_{\mathrm{i}}^{\mathrm{f}}$, as shown in Fig. 9c or h. Now we check inconsistent retrievals on the two-mode measurements. For $m_{\mathrm{i}}^{\mathrm{f}}$ (see panels b, e, and g of Fig. 9), clear overestimation can be observed. For $m_{\mathrm{i}}^{\mathrm{c}}$ (see panels b, e, and g of Fig. 10), the multimode retrievals with n_mode>4 are quite accurate and only slightly underestimate $m_{\mathrm{i}}^{\mathrm{c}}$. We can therefore conclude that the multimode retrievals with n_mode>4 work slightly better than the parametric two-mode retrieval for the fine- and coarse-mode imaginary part of the refractive index.

4.6 Height

The retrievals of the central height z of the aerosol layer are shown in Fig. 11. It can be seen that z can be well retrieved in the consistent retrievals (RMSE < 50 m, bias ≈ −5 m), as shown in Fig. 11a and d.

For the inconsistent retrievals on the two-mode synthetic measurements, 4-, 5-, 6-, 7-, 9-, and 10-mode retrievals (RMSE ≈ 200 m, bias ≈ −200 m) perform better than other inconsistent cases, which are shown in Fig. 11b, e, and g. For inconsistent retrievals on the 10-mode synthetic measurements, the parametric two-mode retrieval performs with clear underestimation as shown in Fig. 11c (bias = −396.2 m), but multimode retrievals with n_mode>5 perform very well with high accuracy (RMSE < 20 m) and little bias, as shown in Fig. 11f and g. To summarize, for inconsistent retrievals, the RMSE is typically around 500 m and the bias is around 300 m.

Based on the results above, we conclude that the multimode retrievals with n_mode>5 are capable of retrieving the central height of the aerosol layer.

4.7 Pass rate of synthetic retrievals

The pass rate $r_{\mathrm{pass}}({\mathit{\chi }}^{\mathrm{2}}<{\mathit{\chi }}_{\max }^{\mathrm{2}},{\mathit{\chi }}_{\max }^{\mathrm{2}}=\mathrm{0.5})$ for the parametric two-mode retrieval (2modeRetr^p) and the multimode retrievals are shown in Fig. 12. In both Fig. 12a and b, the fixed two-mode retrieval (2modeRetr) has the smallest pass rate (r_pass ≈ 55 %) compared to the other retrieval cases. This is an indication that two fixed modes are not enough. Figure 12a shows retrievals on two-mode measurements (2modeSyn^p). The r_pass for retrievals with n_mode>2 are about 75 % to 90 %. The highest pass rate (up to 98.5 %) in Fig. 12a is reached by the parametric two-mode retrieval on two-mode synthetic measurements. Figure 12b shows the retrievals on 10-mode measurements (10modeSyn). The pass rates are high (95 % to 100 %) for all retrieval cases except for the two-fixed-mode retrieval.

5 Real data retrievals

5.1 Experimental setup

The synthetic experiments above have shown that multimode retrievals with n_mode>5 have the capability to retrieve aerosol optical and microphysical properties. Next, we test the performances of multimode retrievals on real data, i.e., PARASOL satellite data, as introduced in Sect. 3.1.

Table 7 AERONET stations for validation of PARASOL retrievals.

To validate PARASOL (satellite) retrievals, AERONET (ground-based) AOT and SSA data are used, as introduced in Sect. 3.3. AERONET measurements at 20 stations (listed in Table 7) in the year 2006 are used in this study to validate multimode retrievals on real data. To make PARASOL retrievals and AERONET data comparable, only the PARASOL retrievals within 20 km around each AERONET station are selected. The AERONET data are averaged within 2 h from PARASOL.

5.2 AOT: multimode retrievals versus parametric two-mode retrieval

In this section, the performances of multimode retrievals for AOT are compared to that of the parametric two-mode retrieval. Figure 13 shows real data retrievals of AOT among the parametric two-mode retrieval, the five-mode retrieval, and the 10-mode retrieval at three different wavelengths, i.e., 440, 675, and 870 nm, which are represented by the three columns in Fig. 13.

We first focus on the performances at 675 nm, i.e., Fig. 13b (2modeRetr^p), e (5modeRetr), and h (10modeRetr). The total number of PARASOL retrievals for the 20 AERONET stations is n_pix (n_pix=63 488 here). For real data retrievals, ${\mathit{\chi }}_{\max }^{\mathrm{2}}=\mathrm{5.0}$ is used as the filter for goodness of fit. The total number of pixels at which the retrieval passes ${\mathit{\chi }}^{\mathrm{2}}<{\mathit{\chi }}_{\max }^{\mathrm{2}}$ is n_pass. The number of red points shown in each figure is not n_pass, but n_averaged (n_averaged ≈ 1100 here), which represents the number of n_pass retrievals after daily averages. The magenta points represent the n_validate (n_validate=1000 here) best retrievals corresponding to the smallest χ², which is needed if we want to compare the different retrieval setups for the same number of measurements.

For real data retrievals, we set ${\mathit{\chi }}_{\max }^{\mathrm{2}}$ at 5.0, which means that we actually underestimated the assumed errors in the retrieval (otherwise the χ² would be around 1.0). The pass rates for the parametric two-mode retrieval and the multimode retrievals are between 32.5 % and 40.8 %. Comparing Fig. 13b, e, and h, the 10-mode retrieval performs the best with the smallest RMSE (0.1230) and the smallest absolute bias (0.0048). However, the parametric two-mode retrieval has the largest RMSE (0.1624) and the five-mode retrieval has the largest absolute bias (0.0301).

In addition to these three retrieval cases, we also perform multimode retrievals with different numbers of modes. The RMSE and the bias for all the retrieval cases (2–10 modes) are shown in Fig. 14. From Fig. 14a, it is seen that multimode retrievals generally have better agreement with AERONET than parametric two-mode retrieval, especially for the multimode retrievals with n_mode>4. From Fig. 14b, it can be found that the parametric two-mode retrieval has an overestimation (0.019) and all the multimode retrievals show an underestimation. The 10-mode retrieval is almost unbiased, with the smallest underestimation. Other multimode retrievals show larger underestimation (from 0.0235 to 0.0429).

Based on the results above, we can conclude that multimode retrievals generally work better for retrieving AOT than the parametric two-mode retrieval. However, multimode (except for 10-mode) retrievals have larger absolute bias than the parametric two-mode retrieval.

5.3 AOT: multimode retrievals for different wavelengths

Section 5.2 discussed the retrieval performances at 675 nm. It is interesting to see how the retrievals perform at other wavelengths. For this purpose, 440 and 870 nm are chosen to evaluate the results.

We compare the three sub-figures in each row of Fig. 13, e.g., Fig. 13g (440 nm), h (675 nm), and i (870 nm). It can be observed that for the 10-mode retrieval (10modeRetr) at 440, 675, and 870 nm, the RMSEs are respectively 0.1654, 0.1230, and 0.1188. For the five-mode retrieval (5modeRetr), the RMSEs are respectively 0.2152, 0.1513, and 0.1305. For the parametric two-mode retrieval (2modeRetr^p), the RMSEs are respectively 0.2209, 0.1624, and 0.1403. It can be therefore found that as the wavelength increases, the retrieval accuracy improves in an absolute sense. However, this is mainly caused by the fact that the AOT value itself decreases with wavelength.

Second, we check at 440 and 875 nm whether the conclusions at 675 nm hold. For this purpose, we look at the first and the third columns of Fig. 13. It can be seen that the RMSE decreases from the parametric two-mode retrieval to the five-mode retrieval to the 10-mode retrieval. This means that the retrieval accuracy at 440 nm (or 875 nm) improves as the mode number increases. Therefore, the conclusion at 675 nm also holds for other wavelengths.

5.4 SSA

Next we validate PARASOL retrievals of SSA with the AERONET-based SSA (described in Sect. 3.3). The AERONET SSA itself is not a result from a direct measurement but from an inversion procedure with different kinds of assumptions (Dubovik et al., 2002). The error in the AERONET SSA is at least 0.03 (Dubovik et al., 2002). The comparisons shown in this section should be interpreted taking this uncertainty into account.

Similarly to what was shown for AOT (Fig. 13), Fig. 15 shows SSA comparisons for the same retrieval setups as above (2modeRetr^p, 5modeRetr, and 10modeRetr) at 440, 675, and 870 nm. For SSA, it is usually difficult to retrieve it when AOT is small; thus in Fig. 15 the SSA retrievals when AOT is larger than 0.3 at the corresponding wavelength are shown.

We first check the tendency of the SSA accuracy for different wavelengths. By comparing RMSE in each row of Fig. 15, it can be found that the RMSE increases as the wavelength increases for all setups. Thus, PARASOL retrievals of SSA have a “decreasing accuracy” tendency as the wavelength increases. The reason is (again) that the AOT decreases with wavelength and the SSA retrieval becomes less accurate for decreasing AOT. The reverse is true for AOT retrievals as discussed in Sect. 5.3. Note that for the parametric two-mode retrieval, the RMSE at 675 nm (0.0601) in Fig. 15 is actually smaller than the RMSE at 440 nm (0.0629), but the difference is small.

Comparing RMSE in each column of Fig. 15, it can hardly be concluded which one among the different retrieval setups (2modeRetr^p, 5modeRetr, and 10modeRetr) compares best against AERONET. For example, the 10-mode retrieval performs better at 440 and 675 nm, but the parametric two-mode retrieval performs better at 870 nm. Different retrieval setups for SSA seem to have similar accuracies. This can be confirmed by Fig. 16a, in which RMSE values vary within a small interval (0.0577 to 0.0611) for most retrieval cases except for the fixed two-mode retrieval, the three-mode retrieval, and the five-mode retrieval. As for the bias (Fig. 16b), all the setups show an overestimation and the bias values in all the retrieval cases are quite similar (except for the fixed two-mode retrieval). Based on the comparison above, we can conclude that multimode retrievals have performances similar to those of the parametric two-mode retrieval for SSA.

For the PARASOL retrievals in this paper we did not retrieve the aerosol layer height but used a fixed value of 1 km. This resulted in better AOT retrievals. The reason for poor performance of aerosol height retrieval from PARASOL is probably the absence of near-UV polarization measurements in combination with the relatively poor polarimetric accuracy (Wu et al., 2016).

6 Discussions and conclusions

In this study we compared aerosol retrievals from Multi-Angle Polarimeter (MAP) data for different definitions of the retrieval state vector: (1) a two-mode definition in which the state vector includes aerosol properties for fine–coarse modes and land or ocean surface properties; (2) a multimode definition in which the state vector excludes the effective radius and the effective variance and only retrieves the aerosol column of each mode. For the purpose of this study we extended the SRON aerosol algorithm – which was based on a parametric two-mode approach – to include capability of a multimode retrieval. To evaluate the retrieval capability for different state vector definitions, the performances between multimode approaches and the parametric two-mode retrieval approach were compared on both synthetic measurements and real (PARASOL) measurements.

In synthetic experiments, the consistent retrievals (when the number of modes for retrievals equals the number of modes for creating synthetic measurements) show both the multimode and parametric two-mode approaches can reach high accuracy for most of the parameters, e.g., the AOT, the SSA, the refractive index, and the aerosol height. For inconsistent retrievals on 10-mode synthetic measurements, the multimode retrievals with n_mode>5 were shown to be capable of retrieving aerosol properties with sufficient accuracy, and they perform similar to the parametric two-mode retrievals. The good performances of multimode approaches indicate that multimode retrievals have good compatibility with different kinds of measurements.

It should be noted that the geometry used for the synthetic study in this paper is quite favorable as it assumes measurements in the principal plane. We also performed the same synthetic study for a much less favorable geometry (SZA = 20^∘, relative azimuth angle = 60^∘$/-\mathrm{120}$^∘). Although for the latter geometry, the performance is somewhat worse, the main conclusions from the synthetic study still hold for this geometry.

After synthetic experiments, real (PARASOL) data experiments were performed. Multimode retrievals of AOT were shown to compare better to AERONET than the parametric two-mode retrieval (e.g., RMSE 0.1230 over 0.1624). Here, we found that the agreement with AERONET improves with an increasing number of modes, with the 10-mode retrieval showing the best agreement with AERONET for AOT. For real data retrievals of SSA, both multimode and parametric two-mode retrievals have similar performances.

When comparing retrievals among different algorithms, it is important to realize that the performance of a given algorithm depends on a number of factors, the definition of the aerosol state vector being one of them. Other factors are the inversion approach (cost function, regularization strength, multiple versus single pixel), the accuracy of the forward model, and the surface reflection model. It is important to study the abovementioned aspects with an individual algorithm. However, now that the SRON algorithm has been extended to include an arbitrary number of fixed modes, it has become easier to compare to other algorithms using a similar state vector definition (Dubovik et al., 2011; Xu et al., 2017). This would be an important topic for future research.

The multimode approach provides an opportunity to make aerosol retrievals more computationally efficient. This is due to the fact that the effective radius and the effective variance are not retrieved in the multimode retrievals, thus the Mie–T matrix calculation for each mode can be fixed and precomputed as a function of refractive index. Then, there is no need to integrate over size distribution during the retrieval. Therefore, the most time-consuming part (as it is called many times) of the retrieval can be significantly accelerated.