Retrieval of convective available potential energy from INSAT-3D measurements: comparison with radiosonde data and their spatial–temporal variations

Convective available potential energy (CAPE) is a measure of the amount of energy available for convection in the atmosphere. The satellite-derived data over the ocean and land are used for a better understanding of the atmospheric stability indices. In this work, an attempt is made for the first time to estimate CAPE from high spatial and temporal resolution measurements of the INSAT-3D over the Indian region. The estimated CAPE from the INSAT-3D is comprehensively evaluated using radiosonde derived CAPE and ERA-Interim CAPE. The evaluation shows that the INSAT-3D CAPE reasonably correlated with the radiosonde derived CAPE; however, the magnitude of CAPE shows higher values. Further, the distribution of CAPE is studied for different instability conditions (different range of CAPE values) during different seasons over the Indian region. In addition, the diurnal and seasonal variability in CAPE is also investigated at different geographical locations to understand the spatial variability with respect to different terrains.

1 Introduction

Convective available potential energy (CAPE; Moncrieff and Miller, 1976) is a measure of convective potential in the atmosphere that incorporates the instability and moisture ingredients (Johns and Doswell, 1992). Climatology of CAPE provides valuable information for severe weather forecasting. CAPE can also be used as a potential indicator of climate change (Gettelman et al., 2002; DeMott and Randall, 2004; Riemann-Campe et al., 2008; Murugavel et al., 2012; Brooks, 2013). Variability in CAPE can also affect the temperature field in the upper troposphere (Gaffen et al., 1991; Dhaka et al., 2010). For example, Dhaka et al. (2010) studied the relationship between seasonal, annual, and large-scale variations in CAPE and the solar cycle on the temperature at 100 hPa pressure level using daily radiosonde data for the period 1980–2006 over the Indian region. They showed that the increase in CAPE was associated with the decrease in temperature at 100 hPa pressure level on all time scales.

The convective schemes in general circulation models use CAPE as a variable for calculating convective heating (e.g. Arakawa and Schubert, 1974; Moncrieff and Miller, 1976; Washington and Parkinson, 2005). Many of the cumulus parameterization schemes make use of CAPE in constructing closures (Donner and Phillips, 2003). The diurnal variation of CAPE is of primary importance for understanding the sensitivity of convection schemes in the model for producing the diurnal cycle of precipitation (Lee et al., 2007). The reliability of model-simulated temporal and spatial variations in CAPE is an important indicator of model performance, particularly in the tropics (Gettelman et al., 2002). Also, the seasonal and diurnal changes in CAPE are important for models to provide validation of their capacity to simulate future changes in the tropical climate. The above studies conclude that the estimation of CAPE is imperative, not only for assessing the conditional instability of the atmosphere and for the convective parameterization, but also for the studies related to climatic change.

Most of the earlier studies on CAPE are based on radiosonde observations. Globally, the radiosondes are launched twice a day, 00:00 and 12:00 UTC. This limits the studies that are available on CAPE at diurnal scales. It is also to be noted that the radiosonde observations are limited to land, and are very sparse over the oceans. Reanalysis datasets fill these gaps; however, their spatial resolution is poor and most of the time the data accuracy does not match with the standard techniques. Satellite observation is the only solution that has regular observations of CAPE with high spatial resolution across the globe. With the availability of satellite measurements, several studies were carried out on CAPE. Narendra Babu et al. (2010) studied the seasonal and diurnal variations in CAPE over land and oceanic regions using 1 year of observations from the FORMOSAT mission 3/Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC/FORMOSAT-3) Global Positioning System (GPS) Radio Occultation (GPS-RO). Santhi et al. (2014) estimated various stability indices using COSMIC GPS-RO profiles and the uncertainty in estimating these stability indices. They also studied the diurnal variation of these stability indices over Gadanki, India. In order to study the diurnal variation of stability indices, they integrated the data over a season as the occultations were sparse and hence not adequate to study on daily scale. This limitation of under sampling can be overcome by the use of geostationary satellites. These geostationary satellite measurements provide near-continuous monitoring of the atmosphere with better spatial coverage, which is helpful in nowcasting of convection (Koenig and de Coning, 2009). Siewert et al. (2010) discussed the advantages of the METEOSAT Second Generation (MSG) system in deriving the instability indices and to predict the convection initiation over Central Europe and South Africa. Using the MSG satellite measurements, de Coning et al. (2011) derived a new convection indicator, the combined instability index which can calculate the probability of convection over South Africa. They showed that the combined instability index can predict the convection better than the individual instability indices like K-index, total totals index etc. Jewett and Mecikalski (2010) developed an algorithm to derive convective momentum fluxes from the Geostationary Operational Environmental Satellite (GOES) measurements. The advantage of this algorithm is that it can be used in any convective environment.

Recently, the Indian Space Research Organization (ISRO) launched the Indian National Satellite System (INSAT-3D), which is a geostationary satellite that provides the profile of temperature and relative humidity with high temporal and spatial resolution. Several researchers evaluated the temperature and relative humidity measurements from the INSAT-3D. Mitra et al. (2015) evaluated the INSAT-3D temperature and moisture retrievals up to 100 hPa with GPS sonde observations for the period January–May 2014. They observed that the INSAT-3D measurements compare better with GPS sonde observations at middle levels (from 900 to 500 hPa). The assessment of the quality of temperature and water vapour obtained from the INSAT-3D with in situ, satellite, and reanalysis datasets by Venkat Ratnam et al. (2016) revealed that the INSAT-3D measurements agree well with the GPS sonde observations, satellite measurements, and reanalysis datasets below 25^∘ N. The temperature difference was 0.5 K, with a standard deviation of about 1 K, and for humidity, a dry bias (20 %–30 %) was observed between INSAT-3D and GPS sonde observations. Hence, these satellite measurements also suffer from some inherent shortcomings and have biases and random errors. Therefore, it is essential to evaluate the satellite products with conventional measurements to quantify the direct usability of these products.

The objective of the present study is to calculate CAPE from high spatial and temporal resolution measurements of INSAT-3D over the Indian region and its performance assessment. To date there are no studies utilizing such high-resolution data for such a long period to evaluate and understand the variability of CAPE. Hence, this study provides the direct usability of INSAT-3D datasets in the numerical weather prediction models for nowcasting of thunderstorms and for severe weather conditions, which is lacking over the Indian region. In this work, we first attempted to validate the estimated CAPE from the INSAT-3D measurements with that of radiosonde measurements over different stations in India. In general, there are many profiles that do not reach the ground level in the INSAT-3D measurements. Hence, different statistical indices are calculated to assess the detectability of INSAT-3D derived CAPE over these regions. Secondly, the diurnal variation of CAPE is studied at different regions in India. Finally, the seasonal mean CAPE is estimated over the Indian region. The paper is organized as follows. Section 2 provides the details of the datasets used. Section 3 discusses the methodology adopted to estimate the CAPE. Section 4 provides the results and discussion. Finally, summary of the present study is provided in Sect. 5.

2 Database

2.1 INSAT-3D

In the present study, 3 years (1 April 2014–31 March 2017) of measurements obtained from the INSAT-3D are used to estimate CAPE over the Indian region and assess the estimation against radiosonde measurements. The INSAT is a series of multipurpose geostationary satellites launched by the ISRO, India. The INSAT-3D, which is considered to be the advanced version of all the other INSAT series satellites, is a multipurpose geosynchronous spacecraft with main meteorological payloads (imager and sounder) launched on 26 July 2013. The main objective of the mission is to monitor the earth and ocean continuously and also provide data dissemination capabilities. The INSAT-3D also provides an operational, environmental and storm warning system to protect life and property.

The INSAT-3D spacecraft carries two meteorological payloads: (i) an imager (optical radiometer) provides high-resolution images of mesoscale phenomena in the visible and infrared (IR) spectral bands (0.55 to 12.5 µm) and (ii) a sounder has one visible and 18 IR (7 in long-wave IR, 5 in mid-IR, and 6 in short-wave IR) channels. The sounder measures the irradiance and provide profiles of temperature, water vapour, and integrated ozone over the Indian landmass and surrounding ocean every hour and over the whole of the Indian Ocean every 6 h with a spatial resolution of 0.1^∘. For the present study, temperature and water vapour data collected from the INSAT-3D sounder during the clear (cloud free) conditions are used. These datasets are interpolated to 0.25^∘ spatial resolution and are used to estimate the CAPE over the Indian region.

2.2 Radiosonde

The upper air radiosonde profiles are downloaded from the University of Wyoming website (http://weather.uwyo.edu/upperair/sounding.html, last access: 4 September 2017). Radiosonde data are usually available at 00:00 and 12:00 UTC regularly to monitor the thermodynamic state of the atmosphere by the National Weather Service. For the present study, the data collected from 20 stations (black dots in Fig. 1) for the period from 1 April 2014 to 31 March 2017 are used to assess the INSAT-3D estimated CAPE. The values of CAPE reported in this paper are taken directly from the data provided by the University of Wyoming.

Figure 1 The geographical map of India representing the 20 stations considered for the present study.

2.3 ERA-Interim reanalysis

The reanalysis datasets used in this study are from the ERA-Interim project (Dee et al., 2011). The ERA-Interim is the latest global atmospheric reanalysis produced by the European Centre for Medium-Range Weather Forecasts (ECMWF), which envisaged preparing a future reanalysis project that will span the entire twentieth century. The ERA-Interim data are available in near real-time from 1 January 1979 onwards. The ERA-Interim generates gridded data, including a large variety of surface parameters that describe the weather as well as land surface and ocean conditions at the 3-hourly and 6-hourly interval. The present study utilizes the CAPE derived from the ERA-Interim dataset. The data are extracted over the Indian region at 00:00 and 12:00 UTC for each day between 1 April 2014 and 31 March 2017. The spatial resolution of the data utilized is $\mathrm{0.25}{}^{\circ }\times \mathrm{0.25}{}^{\circ }$.

3 Estimation of CAPE

To calculate the CAPE, the vertical profiles of temperature and water vapour are taken from the INSAT-3D measurements. For many years, a debate has existed in the literature regarding the most meaningful way to calculate CAPE and how to interpret the result. The most important methods of calculating CAPE are (1) pseudoadiabatic CAPE, in which CAPE is estimated after assuming that all the condensate has fallen out of the air parcel, and (2) reversible CAPE, in which it is assumed that the condensate remains within the parcel. In the present study, the pseudoadiabatic algorithm is used to calculate CAPE. Further, CAPE is very sensitive to near-surface temperature and humidity (Gartzke et al., 2017), which are known to vary spatially. However, Venkat Ratnam et al. (2016) found that the variability of the atmospheric state within the INSAT-3D footprint sampled by the radiosonde had little bias over the Indian region. They also reported that the difference in temperature between INSAT-3D and ERA-Interim reanalysis datasets lies within 1 K and a dry bias of 5 %–10 % was found in the lower and mid-troposphere relative humidity when compared with the ERA-Interim reanalysis datasets. In this scenario, it is assumed that the spatial sampling mismatch may not affect much in the calculation of CAPE and hence are neglected in the present study. In addition, only cases with radiosonde profiles having CAPE greater than 0 J kg⁻¹ are included in the analysis. This threshold is used to eliminate the large number of zero CAPE values.

The integration of the buoyancy of the air parcel from the level of free convection (LFC) to equilibrium level (EL) gives the measure of CAPE.

$$\begin{array}{}\text{(1)}& \mathrm{CAPE}={\int }_{\mathrm{LFC}}^{\mathrm{EL}}{\displaystyle \frac{g\left(T_{\mathrm{vp}}-T_{\mathrm{ve}}\right)}{T_{\mathrm{ve}}}}\mathrm{d}Z,\end{array}$$

where T_vp is the virtual temperature of the air parcel, T_ve is the virtual temperature of the environment, and g is the acceleration due to gravity. The LFC is situated above the lifting condensation level (LCL) and at that level, the parcel temperature is greater than the environmental temperature. This is calculated by lifting the air parcel moist adiabatically. The EL is situated above the LFC and at this level, the parcel temperature is less than or equal to the environment temperature. At EL, the air parcel attains stability and the convection stops. Under stable environmental conditions, the LFC and EL will not be present. The procedure to estimate CAPE is similar to that discussed in Uma and Das (2017).

The error in estimating the CAPE is determined by applying the standard error propagation formula (Bevington and Robinson, 1992). The error in the CAPE calculation depends on the temperature and water vapour retrievals. In this study, an error of 5 % in the measured relative humidity and temperature corresponds to an error of 8 % in the calculated CAPE from the INSAT-3D measurements.

4 Results and discussion

A total of 3 years of data collected from the INSAT-3D measurements are utilized to estimate CAPE over the Indian region. These estimates are compared with the radiosonde derived CAPE at 00:00 and 12:00 UTC along with the ERA-Interim reanalysis CAPE data.

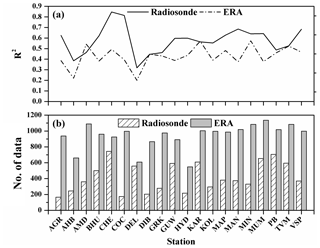
Figure 2 (a) Correlation coefficient in the comparison of INSAT-3D CAPE with radiosonde and ERA-Interim CAPE for 20 stations in India for the period April 2014 to March 2017. (b) Number of data points in the comparison of INSAT-3D CAPE with radiosonde and ERA-Interim CAPE.

4.1 Comparison of INSAT-3D CAPE with radiosonde and ERA-Interim CAPE

In this work, 20 stations are selected for which the radiosonde profiles are available during the study period (location shown in Fig. 1). Table 1 provide the details of the stations considered along with the total number of data available from INSAT-3D measurements during four seasons (winter: December to February; pre-monsoon: March to May; monsoon: June to September; and post-monsoon: October and November). Figure 2 shows the correlation coefficient along with the number of data points used in the analysis for the comparison between estimated CAPE from the INSAT-3D measurements, ERA-Interim CAPE, and radiosonde derived CAPE. Here, the comparison is performed only when the INSAT-3D and radiosonde CAPE as well as INSAT-3D and ERA-Interim CAPE are greater than zero. From this figure, it is noted that the INSAT-3D estimated CAPE shows better correlation with radiosonde CAPE compared to the ERA-Interim CAPE. In general, the coastal stations show a higher correlation coefficient than that of the other stations for the INSAT-3D estimated CAPE. All the coastal stations show a correlation higher than 0.6 except Trivandrum. The correlation coefficient is highest for Chennai 0.84 among all the stations. The correlation values are lower for the stations located near the foothills of Himalayas and northeastern (NE) regions of India. A weak correlation of 0.31 is found for Delhi. For the ERA-Interim data, INSAT-3D CAPE shows a lower correlation coefficient for all the stations except Amini Divi compared to radiosonde CAPE. Even in the ERA-Interim CAPE, the coastal stations show better correlation compared to other stations. The ERA-Interim CAPE shows a higher correlation for Minicoy and the correlation is minimum for Delhi. This result suggests that the INSAT-3D CAPE measurements agree well with the radiosonde measurements.

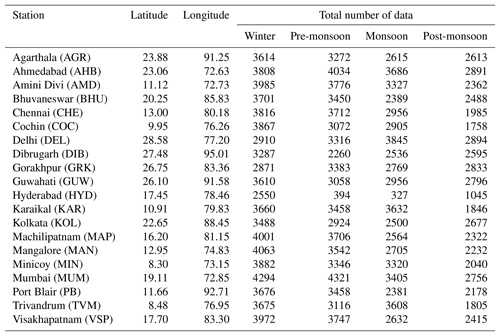
Table 1 The total number of data available during four seasons for the 20 stations for the period from April 2014 to March 2017.

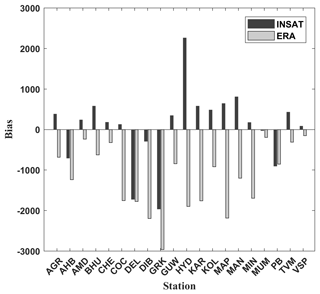
To elucidate the consistency of INSAT-3D estimated CAPE against the ERA-Interim CAPE, the bias in the measurements of INSAT-3D and ERA-Interim with the radiosonde is presented in Fig. 3. The bias evaluates the size of the difference between the two datasets. The positive (negative) value of bias indicates the overestimation (underestimation) of the satellite and reanalysis measurements. The INSAT-3D estimated CAPE shows small and positive bias for most of the stations considered in the study. Among all the stations, Hyderabad, Gorakhpur, and Delhi show higher bias, whereas Mumbai shows minimum bias. All the stations show positive bias except Ahmedabad, Dibrughar, Delhi, Gorakhpur, and Port Blair, where the bias is negative and Mumbai shows small negative bias. Whereas, the ERA-Interim CAPE shows negative bias for all the stations indicating the underestimation of CAPE compared to radiosonde measurements. Further, the bias in the estimation of CAPE in the ERA-Interim data is higher for most of the stations. Among all the stations, Gorakhpur shows the highest negative bias. From this, it is clear that the INSAT-3D (ERA-Interim) overestimated (underestimated) the CAPE compared to radiosonde measurements. From the above discussion, it can be concluded that the INSAT-3D provides better estimates over coastal regions compared to other regions and also a better comparison with the radiosonde measurements.

Figure 3 Bias in the comparison between INSAT-3D CAPE and ERA-Interim reanalysis CAPE with radiosonde for different stations in India for the period April 2014–March 2017.

4.2 Statistical indices in the estimation of CAPE from INSAT-3D measurements

To examine the capability of detection of the INSAT-3D sounder, the probability of detection (POD), false alarm ratio (FAR), critical success index (CSI), and accuracy (ACC) are computed on the basis of a contingency table (Table 2). A threshold value of zero is considered for CAPE to be estimated by the satellite measurements. The POD is a measure of the CAPE successfully identified by the satellite product, and FAR gives a proportional measure of the satellite product's tendency to estimate CAPE where none is observed; i.e. it gives the CAPE estimates that are incorrectly detected. CSI represents how well the estimated CAPE events correspond to the observed CAPE events. ACC measures the fraction of the correctness in the CAPE estimates. For a perfect satellite-based estimate, the values of POD, FAR, CSI, and ACC should be 1, 0, 1, and 1, respectively. These statistical indices can be calculated as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{POD}={\displaystyle \frac{A}{A+C}}\text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{FAR}={\displaystyle \frac{B}{A+B}}\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{CSI}={\displaystyle \frac{A}{A+B+C}}\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{ACC}={\displaystyle \frac{A+D}{A+B+C+D}}\end{array}$$

where A, B, C, and D represent hits, false alarms, misses, and correct negatives, respectively, as shown in contingency table (Table 2). Figure 4a–d shows the POD, FAR, CSI, and ACC calculated for the INSAT-3D estimated CAPE, respectively. Among all the stations, Mumbai shows higher POD whereas Hyderabad shows lower POD. This indicates that the INSAT-3D is unable to detect CAPE over Hyderabad. This may be due to lower availability of data and the inability to catch the short-lived convective storms frequently observed over this region. All the coastal stations show higher POD, CSI, and ACC. Cochin shows the highest CSI and ACC, whereas Agarthala and Kolkata have highest FAR. This indicates that the INSAT-3D product performs reasonably well with the higher POD, CSI, and ACC and lower FAR.

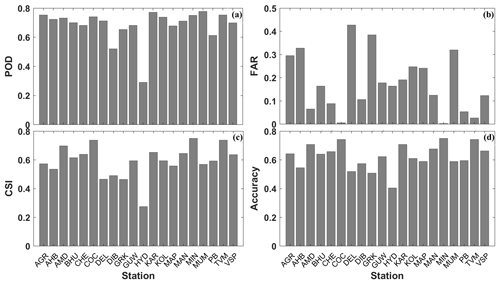
Figure 4 Statistical indices (a) POD, (b) FAR, (c) CSI and (d) ACC in the comparison between the INSAT-3D CAPE with radiosonde CAPE for 20 stations in India.

Table 2 Contingency table for the comparison of INSAT-3D estimated CAPE with radiosonde measured CAPE. The CAPE threshold is considered as 0 J kg⁻¹.

4.3 Distribution of CAPE over India

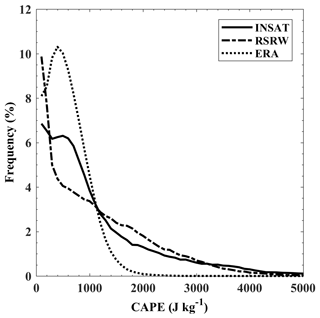
A summary of the frequency distribution of CAPE computed from the INSAT-3D, ERA-Interim and radiosonde measurements for the 20 stations are shown in Fig. 5. The distribution of CAPE shows higher occurrence for lower values. Thus, the CAPE distribution is shifted to lower values in all three of the measurements. The INSAT-3D estimated CAPE and ERA-Interim CAPE shows a similar kind of distribution compared to radiosonde CAPE. The distribution of the INSAT-3D estimated CAPE is higher (lower) in the range ∼300–1200 (1200–3000) J kg⁻¹ compared to the radiosonde measurements. The INSAT-3D estimated CAPE matches with the radiosonde CAPE above 3000 J kg⁻¹. The ERA-Interim CAPE distribution shows higher values below 1200 J kg⁻¹. However, the ERA-Interim distribution becomes negligible above 2000 J kg⁻¹. This also shows that for the higher values of CAPE, ERA-Interim underestimates the observations. This may be due to the fact that the spatial resolution of the reanalysis data is coarse compared to the observations. The figure shows that among the two distributions, the INSAT-3D distribution agrees well with the radiosonde distribution.

Figure 5 Distribution (%) of INSAT-3D, radiosonde and ERA-Interim reanalysis CAPE (J kg⁻¹) for all the stations considered in the study.

4.4 Seasonal variation of CAPE

In the present study, the INSAT-3D dataset is divided into four seasons, viz. winter, pre-monsoon, monsoon, and post-monsoon to understand the seasonal variations in CAPE over the Indian region. Figure 6a–d show the seasonal mean CAPE estimated from the INSAT-3D measurements during the period from April 2014 to March 2017 over the Indian region. During the winter season (Fig. 6a), the mean CAPE is below 500 J kg⁻¹ over the land regions. The mean CAPE is relatively higher over the west coast and Arabian Sea (AS) and parts of the northern Bay of Bengal (BoB). This relatively high CAPE over oceans and the western coastal regions may be due to the occurrence of depression and cyclone during the month of December over the oceanic regions. In the pre-monsoon season (Fig. 6b), higher values of CAPE (above 2000 J kg⁻¹) are observed over the AS, BoB, and central India (CI). The pre-monsoon depressions are regular during this time period over surrounding oceanic regions of India. This sustains for few days, which results in higher CAPE over these regions. Higher values of CAPE are the causative factors for frequent thunderstorms and deep convection over northern and central India. The Western Ghats have higher CAPE, which may be due to the orographically induced deep convection. CAPE is lower over southern peninsular India. Further, CI, northern India (NI), and the foothills of the Himalayas exhibit higher CAPE compared to other land regions. The northwestern parts of India show higher CAPE among other land regions. During the monsoon season (Fig. 6c), the east coast of India, AS, BoB, and the foothills of the Himalayas show relatively high CAPE than the other regions. During the post-monsoon period (Fig. 6d), the northern parts of AS and BoB, and the east and west coasts of India show higher values of CAPE and the southern peninsular and eastern regions show lower CAPE.

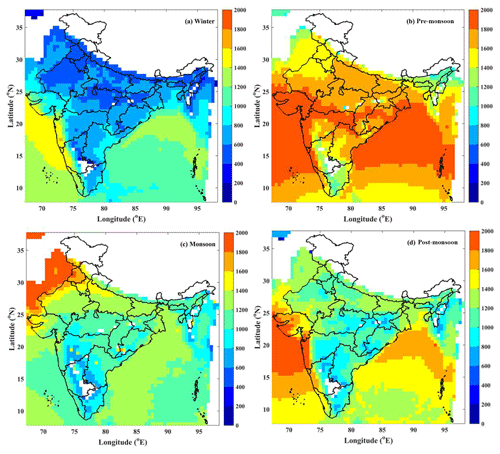
Figure 6 The distribution of CAPE (J kg⁻¹) during (a) winter, (b) pre-monsoon, (c) monsoon, and (d) post-monsoon from INSAT-3D data over the Indian region.

Further, the spatial distribution of CAPE estimated from the INSAT-3D is studied for different CAPE ranges. The spatial distribution of CAPE provides information on the distribution of extreme weather events over the study region. The estimated CAPE is divided into four categories: weak instability (< 500 J kg⁻¹), moderate instability (501–1500 J kg⁻¹), strong instability (1501–3000 J kg⁻¹), and extreme instability (> 3000 J kg⁻¹). The normalized anomaly distribution of CAPE in the four instability conditions during different seasons is provided over the Indian region as shown in Fig. 7. The spatial distribution of CAPE during weak, moderate, strong, and extreme instability conditions is shown in Fig. 7a–d, e–h, i–l, and m–p, respectively. The top panel is for the winter, second from the top is for the pre-monsoon, third from the top is for the monsoon and the bottom panel is for the post-monsoon season. Here, the negative (positive) anomaly indicates the increase (decrease) in CAPE. During winter, the response of weak instability (Fig. 7a) is much lower over the Indian subcontinent as well as the surrounding oceanic regions. However, the response of winter towards strong and extreme instability is observed over the BoB, the southeastern AS, and some parts of NI. The higher response may be due to the cyclones and depressions that occur over the oceanic regions during December. Over NI, strong westerlies are observed during the winter, which may result in a dry convection with higher CAPE.

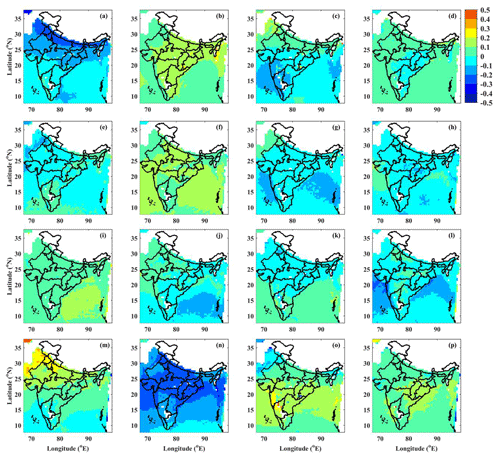
Figure 7 Frequency distribution (%) of CAPE in (a) weak, (b) moderate, (c) strong, and (d) extreme instability during the winter season. Panels (e–h) are the same as (a–d) except for the pre-monsoon season. Panels (i–l) are the same as (a–d) but for monsoon season. Panels (m–p) are the same as (a–d) except for post-monsoon season.

The response during pre-monsoon is observed to be higher for strong and extreme instability. The pre-monsoon season is considered to be summer over the Indian subcontinent and it is the favourable season for thunderstorms and deep convection. It can be easily observed in the figure that during extreme instability the whole Indian region is observed to have higher frequencies of CAPE. During monsoon season, the response to weak and moderate instability is higher compared to that for strong and extreme instability. It is observed that the Western Ghats and the surrounding oceanic regions have a higher frequency of weak and moderate instabilities compared to the other regions. The Western Ghats are generally dominated by the shallow clouds (e.g. Das et al., 2017; Utsav et al., 2017), which results in high response with weak instability, as deep convection does not predominantly occur over this region. The monsoon trough region (from the heat low in Pakistan to the BoB) has a higher response to strong instability. This trough (core low-pressure region) occurs during the monsoon, which results in heavy rainfall over the Indian subcontinent. Compared to the pre-monsoon, there is little response in strong instability conditions over the oceanic regions. This results in fewer occurrences of deep convection and cyclones (inhibited because of the presence of strong wind shear at 500 hPa) during the monsoon season. In the post-monsoon, the response is very similar to the pre-monsoon during the strong and extreme instability conditions. In the post-monsoon season, the wind flow over the Indian region is northeasterly, which results in more convection over the northwestern and southern peninsular Indian region. Usually, in October and November, deep depressions occur over the Bay of Bengal, due to which a higher frequency of CAPE is observed. In general, weak instability is predominant during the winter season. The moderate instability shows higher occurrence during post-monsoon compared to other seasons. The strong instability condition is more during the monsoon period, whereas the occurrence of extreme instability is higher during pre-monsoon months.

4.5 Diurnal variation of CAPE

Figure 8 shows hourly mean CAPE averaged for 3 years (2014–2017). A strong diurnal variation in the mean CAPE is observed over different parts of India. A clear land–sea contrast is also observed in the mean CAPE. The CAPE starts building up in the morning (05:30 LT = 00:00 UTC+05:30) over the oceans with land having low values of CAPE. The mean CAPE reaches its maximum at ∼12:00 LT over the oceans. However, the CAPE starts increasing after 09:00 LT over the land and reaches the maximum in the afternoon (between 13:00 and 14:00 LT) and decreases again thereafter. The land–sea contrast in the mean CAPE has disappeared in the evening. Again in the evening, the CAPE increases and a secondary maximum is observed at midnight over the oceans. Over the tropics, the Indian region is one of the active convective regions. The deep convective clouds form during the daytime over the Indian sub-continent due to solar insolation, which increases the lower tropospheric temperature, resulting in convective instability. Uma and Das (2016) have found the lower tropospheric humidity maximum in the afternoon and minimum in the evening. The surrounding oceanic regions found to peak in the late evening and at midnight. This indicates that the convection peaks in the late afternoon over the land region, and from the evening to midnight over the oceans. These results are consistent with the findings of Dutta and Rao (2001) and Dutta and Kesarkar (2004). These studies revealed that the maximum value of CAPE is observed during night-time over the BoB and the east coast of India. However, this secondary maximum is not observed over the land areas. In contrast, another maximum is observed around 17:00 LT over the east coast, west coast and northwestern regions of India.

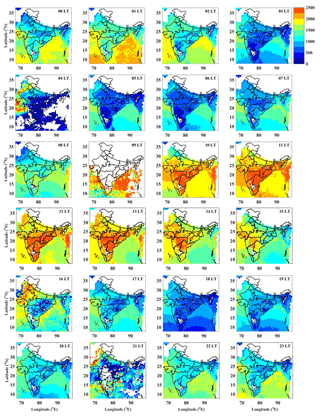
Figure 8 Hourly mean distribution of INSAT-3D CAPE (J kg⁻¹) during the period from 1 April 2014 to 31 March 2017 over the Indian region.

To observe the diurnal variation of CAPE over different parts of India, the study region is divided (by latitude for uniformity) into six sub-regions as provided in Raut et al. (2009). These regions are the Arabian Sea (AS; 8–20^∘ N, 65–72^∘ E), the Bay of Bengal (BoB; 8–20^∘ N, 80–90^∘ E), southern peninsular India (SP; 8–20^∘ N, 72–80^∘ E), central India (CI; 20–25^∘ N, 73–82^∘ E), northern India (NI; 25–35^∘ N, 73–80^∘ E), and northeastern India (NE; 24–29^∘ N, 90–96^∘ E). Figure 9 shows the diurnal variation of mean CAPE over these sub-regions during four seasons. From this figure, one can observe a bimodal distribution in the mean CAPE over the AS and BoB during the pre-monsoon and monsoon periods (Fig. 9a and b). The primary maximum is observed at night-time and the secondary maximum is observed in the afternoon over these regions. Uma and Das (2016) have also observed bimodal distribution in the relative humidity over the BoB and the Indian Ocean. They found maximum distribution at 12:00 and 15:00 LT, which is similar to that observed in the present study. During the Bay of Bengal Monsoon Experiment (BOBMEX) 1999, Dutta and Kesarkar (2004) observed that the CAPE is maximum at night-time rather than in the daytime. Further, the night-time maximum in the mean CAPE is observed around ∼00:00 LT over the BoB and AS during the pre-monsoon and monsoon periods. The bimodal distribution in mean CAPE is also observed over the AS and BoB during the post-monsoon season. However, the secondary maximum is not very prominent, as observed in the pre-monsoon and monsoon periods. The mean CAPE peaks in the afternoon hours over the AS and BoB during the winter season.

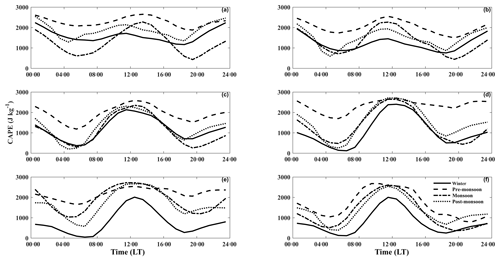
Figure 9 Diurnal variation of CAPE (J kg⁻¹) over the (a) AS, (b) BoB, (c) SP, (d) CI, (e) NI, and (f) NE regions of India during four seasons.

The SP region (Fig. 9c) also shows similar behaviour to that of oceans. The mean CAPE over the SP region maximizes in the afternoon hours. The secondary maximum is also observed at midnight (00:00 LT). The mean CAPE in the CI region (Fig. 9d) shows a bimodal distribution during the winter, monsoon, and post-monsoon seasons. The mean CAPE is at its maximum in the afternoon. The other maximum is during night-time. A noticeable difference is observed in the mean CAPE during the pre-monsoon season. During this period, the CAPE is nearly the same throughout the day. However, CAPE decreases a little and reaches a minimum in the early morning over the CI region. The mean CAPE in the NI region (Fig. 9e) shows a similar diurnal variation, as observed over the CI region. The mean CAPE shows little variation during the pre-monsoon months. The other three seasons show bimodal distribution as observed in other regions. However, the magnitude of the mean CAPE is higher in the NI region compared to the CI region. Further, the difference in mean CAPE between the primary and secondary maximum is relatively small compared to the other regions. The NE region (Fig. 9f) also shows a bimodal distribution in mean CAPE, with the primary maximum in the afternoon hours and the secondary maximum in the late-night during the winter, monsoon, and post-monsoon seasons. In addition to these two maxima, a third maximum is also observed over the NE region during the pre-monsoon season. The third maximum is observed at ∼09:00 LT over this region. The third maximum observed in the mean CAPE may be due to the occurrence of pre-monsoon thunderstorms known as Nor'westers during the morning over this region.

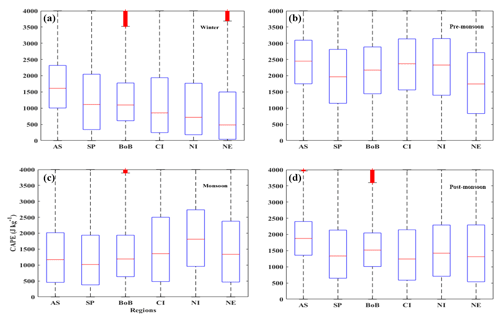
Figure 10 Box-plot analysis of CAPE (J kg⁻¹) during (a) winter, (b) pre-monsoon, (c) monsoon, and (d) post-monsoon from INSAT-3D data of six sub-regions over the Indian sub-continent.

Statistical analysis of CAPE is also attempted over these six regions to understand the variability during different seasons as shown in Fig. 10. The mean and standard deviation, along with a maximum to minimum range with a 25 %, 50 %, and 70 % occurrence are provided in the figure. During winter, the mean CAPE is higher (∼1600 J kg⁻¹) over the AS compared to that of the BoB (∼1000 J kg⁻¹). Over the land regions, the mean CAPE is found to be less than ∼1000 J kg⁻¹. The oceanic regions are found to have higher CAPE during winter compared to that of the continent. NI and NE have smaller CAPE during winter period. Winter is extremely dry over the Indian region except for the surrounding oceanic regions and southern peninsular India, where we observe cyclones and depressions during December, which bring more moisture and heavy rainfall, as discussed earlier. During pre-monsoon months, the mean CAPE is higher than ∼ 2000 J kg⁻¹ over all the regions concerned. The pre-monsoon depressions, thunderstorms, deep convection, and Nor'westers contribute to higher CAPE values over India and surrounding oceanic regions. During monsoon season, the mean CAPE is less than ∼1500 J kg⁻¹ over all of the regions except NI, where it is about ∼2000 J kg⁻¹. The shallow convection dominates during the monsoon season rather than deep convection, which results in lower CAPE values compared to that of the pre-monsoon. During post-monsoon, the mean value of CAPE is about ∼1200 J kg⁻¹ except AS where it is about ∼1800 J kg⁻¹ and at BoB where it is about ∼1500 J kg⁻¹. The northeastern monsoon dominates the Indian region during post-monsoon which results in deep convection resulting in relatively higher values of CAPE. Overall, the maximum CAPE is found in the pre-monsoon followed by the post-monsoon, monsoon, and winter over the Indian sub-continent.

5 Summary

The extreme weather events such as thunderstorms and tropical cyclones cause severe damage to lives and property, especially in the tropical regions. Convective available potential energy (CAPE) is a measure of the amount of energy available for convection in the atmosphere. Hence, CAPE can be used as a measure for the occurrence of these severe weather conditions. In the present study, we made an attempt for the first time to estimate CAPE from the INSAT-3D measurements and evaluate comprehensively over the Indian sub-continent. For this evaluation, 20 stations are selected in different parts of India and these estimates are evaluated against the radiosonde measurements collected from the Wyoming University along with the ERA-Interim data. The station based comparison shows that the INSAT-3D estimates match well with a higher correlation coefficient and lower bias in the radiosonde measurements. The correlation coefficient between INSAT-3D and radiosonde CAPE is higher than the one between INSAT-3D and ERA-Interim. Further, the INSAT-3D derived CAPE overestimate the radiosonde CAPE, whereas the ERA-Interim underestimate the radiosonde CAPE. The categorical statistics shows that the INSAT-3D can better represent the radiosonde measured CAPE. The distribution of CAPE is higher for lower values (< 1000 J kg⁻¹) in three of the datasets (radiosonde, INSAT-3D and ERA-Interim) for all the stations. The INSAT-3D and ERA-Interim estimated CAPE is higher than the radiosonde measurements in the lower ranges. The INSAT-3D estimated CAPE matches well with the radiosonde measurements above ∼3000 J kg⁻¹.

The spatial and temporal distribution of CAPE reveals that the weak instability is predominant during winter season, moderate instability is higher during post-monsoon, strong instability is more during monsoon period, and extreme instability is higher during pre-monsoon months. The diurnal variation in mean CAPE shows a bimodal distribution with a primary peak around midnight and a secondary peak in the afternoon for most of the regions and in different seasons. The seasonal mean CAPE shows that the land areas show lower CAPE during winter, whereas the oceans show the highest CAPE during pre-monsoon season. The higher values of CAPE over the oceanic regions may be due to higher occurrence of the tropical cyclones during the pre-monsoon season. Further, the northwestern parts of India show higher CAPE among other land regions. Overall, the INSAT-3D estimated CAPE is in close agreement with the radiosonde derived CAPE. As the INSAT-3D provides high temporal and spatial resolution data, hence it can be used for nowcasting and severe weather warnings in the numerical prediction models.