On the estimation of vertical air velocity and detection of atmospheric turbulence from the ascent rate of balloon soundings

Vertical ascent rate V_B of meteorological balloons is sometimes used for retrieving vertical air velocity W, an important parameter for meteorological applications, but at the cost of crude hypotheses on atmospheric turbulence and without the possibility of formally validating the models from concurrent measurements. From simultaneous radar and unmanned aerial vehicle (UAV) measurements of turbulent kinetic energy dissipation rates ε, we show that V_B can be strongly affected by turbulence, even above the convective boundary layer. For “weak” turbulence (here ε≲10⁻⁴ m² s⁻³), the fluctuations of V_B were found to be fully consistent with W fluctuations measured by middle and upper atmosphere (MU) radar, indicating that an estimate of W can indeed be retrieved from V_B if the free balloon lift is determined. In contrast, stronger turbulence intensity systematically implies an increase in V_B, not associated with an increase in W according to radar data, very likely due to the decrease in the turbulence drag coefficient of the balloon. From the statistical analysis of data gathered from 376 balloons launched every 3 h at Bengkulu (Indonesia), positive V_B disturbances, mainly observed in the troposphere, were found to be clearly associated with Ri≲0.25, usually indicative of turbulence, confirming the case studies. The analysis also revealed the superimposition of additional positive and negative disturbances for Ri≲0.25 likely due to Kelvin–Helmholtz waves and large-scale billows. From this experimental evidence, we conclude that the ascent rate of meteorological balloons, with the current performance of radiosondes in terms of altitude accuracy, can potentially be used for the detection of turbulence. The presence of turbulence complicates the estimation of W, and misinterpretations of V_B fluctuations can be made if localized turbulence effects are ignored.

1 Introduction

The vertical ascent rates V_B of meteorological balloons are mainly the combination of the free lift and fluctuations due to vertical air velocities and variations in atmospheric turbulence drag effects. Despite balloons' frequent use all over the world, few studies have tried to extract information from V_B. Most of these studies have focused on the estimation of the vertical air velocity because this parameter is very important for many meteorological applications (e.g., Wang et al., 2009) and for the characterization of internal gravity waves (e.g., McHugh et al., 2008). Evidence of internal gravity wave fluctuations in balloon ascent rates was reported by Corby (1957), Reid (1972), and Lalas and Einaudi (1980). Shutts et al. (1988) and Reeder et al. (1999) described large amplitude gravity waves in the stratosphere from the analyses of V_B.

However, the models or methods used for retrieving vertical air velocity from balloon ascent rates are often based on crude assumptions about atmospheric turbulence: it is either considered more or less uniform or neglected above the planetary boundary layer. Johansson and Bergström (2005) estimated the height of boundary layers from V_B considering that V_B is mainly affected by turbulence in convective boundary layers. In fact, the free stratified atmosphere usually reveals a “sheet and layer” structure (e.g., Fritts et al., 2003) consisting of more or less deep layers of turbulence (a few hundred meters) separated by quieter and generally statically stable regions. In such conditions, turbulence intensity, often quantified by turbulence kinetic energy dissipation rates, can vary over several orders of magnitude with height and can reach levels similar to those met in the convective atmospheric boundary layers (e.g., Luce et al., 2019).

In addition, most studies did not validate their estimations from concurrent measurements of vertical air velocities, making their models and hypotheses uncertain (e.g., McHugh et al., 2008; Gallice et al., 2011). Gallice et al. (2011) proposed a model to describe balloon ascent rates in the presence of free-stream turbulence. Even if the variations in the drag coefficient with altitude were taken into account, their expression of the drag coefficient was based on a mean turbulent state, and, thus, the model did not consider the possibility of localized layers of turbulence, as acknowledged by the authors. Wang et al. (2009) retrieved vertical air velocity from radiosondes and dropsondes assuming that turbulence has a negligible effect above the convective boundary layer such that the drag coefficient was nearly constant. Comparisons with wind profiler data (their Fig. 7) showed poor agreement. Most profiles revealed oscillations, indicative of gravity waves. McHugh et al. (2008) noted large (always positive) variations in balloon ascent rate around the tropopause over Hawaii and interpreted these localized peaks as strong increases in W due to mountain waves around their critical levels. Independent measurements could not validate this interpretation, and possible turbulence effects were not considered when interpreting observations. Houchi et al. (2015) used a model similar to Wang et al.'s (2009) model for statistical estimates of the vertical air velocity. The authors assumed that the balloon ascent rate is the sum of the ascent rate in still air and vertical air velocity.

Modeling the ascent of balloons is not an easy task, especially if the free-stream turbulence effects are not correctly taken into account. In the present work, we study the effects of turbulence on V_B from experimental data. For this purpose, vertical profiles of V_B are compared with profiles of turbulence kinetic energy (TKE) dissipation rate ε estimated from unmanned aerial vehicle (UAV) data and from 46.5 MHz middle and upper atmosphere (MU) radar data. These data were gathered during Shigaraki UAV-Radar Experiment (ShUREX) campaigns at the Shigaraki MU observatory (Kantha et al., 2017). In addition, the MU radar provided coincident estimates of vertical air velocities so that quantitative comparisons with V_B could be made. We found that a balloon is likely a good “W sensor” in the case of light turbulence only: under the conditions of our experiment, V_B is affected by turbulence and thus cannot be used for estimating W when ε≳10⁻⁴ m² s⁻³ (1 mW kg⁻¹). Therefore, a balloon is potentially more a “turbulence sensor” than a “W sensor”, and very large errors in W can arise if the presence of free-stream turbulence is not properly considered. Alternately, statistics on the occurrence of atmospheric turbulence could be made from balloon ascent rates if the contribution of air motion is accurately taken into account. This alternative purpose seems to be more achievable than retrieving W, except at stratospheric heights and during very calm tropospheric conditions, as shown by earlier studies, and likely during deep convective storms during which strong vertical motions are expected.

The effects of turbulence on the balloon ascent rate can be understood considering that this parameter in still air is given by (Gallice et al., 2011)

$$\begin{array}{}\text{(1)}& V_z=\sqrt{{\displaystyle \frac{\mathrm{8}Rg}{\mathrm{3}{c}_{\mathrm{D}}}}\left(\mathrm{1}-{\displaystyle \frac{\mathrm{3}{m}_{\mathrm{tot}}}{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{a}}{R}^{\mathrm{3}}}}\right)},\end{array}$$

where R is the radius of the volume-equivalent sphere, g is the acceleration of gravity, ρ_a is the air density, and m_tot is the total mass of the balloon–radiosonde system. The drag coefficient, c_D, depends on the Reynolds number associated with the balloon $Re={\mathit{\rho }}_{\mathrm{a}}{V}_{z}R/\mathit{\mu }$, where μ is the dynamic viscosity of air. The variation in c_D with Re for a perfect sphere in the absence of atmospheric turbulence and for various values of turbulence intensity T_u, defined as the ratio of the standard deviation of the incident air velocity fluctuations to the mean incident air velocity (e.g., Son et al., 2010), is shown in Fig. 1 of Gallice et al. (2011). c_D suddenly decreases by a factor 4 to 5 above a critical value of Re (called drag crisis) so that V_z can increase by a factor 2 or more. In the presence of atmospheric turbulence, the drag crisis is displaced toward lower values of Re so that c_D can be reduced when crossing a turbulent layer. Recently, Söder et al. (2019) compared a profile of Re with a profile of balloon ascent rate (their Fig. A1) and clearly showed the existence of a drag crisis about $Re\sim \mathrm{4}\times {\mathrm{10}}^{\mathrm{5}}$ in close agreement with the theoretical expectation for a sphere (Fig. 1 of Gallice et al., 2011). Gallice et al. (2011) proposed another (smoother) model from experimental data with a more realistic shape of balloons and with more complete consideration of the heat imbalance between balloon and atmosphere. Their drag curve presented qualitative similarities with the curves by Son et al. (2010) for a mean turbulent state of the atmosphere at T_u=6 % and T_u=8 %. The fact that the model proposed by Gallice et al. does not consider the variability of turbulence with height is likely a weak point because turbulence is generally confined to layers of variable depth in the troposphere and the stratosphere.

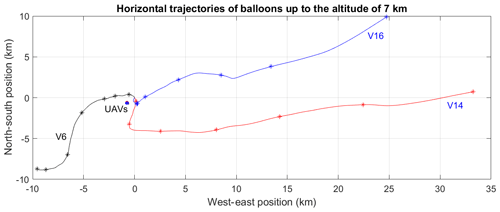
Figure 1 Horizontal trajectories of the meteorological balloons V6, V14 and V16. Each asterisk shows altitudes of 1 km, 2 km, etc., up to 7 km. The position (0, 0) corresponds to the location of the Shigaraki MU Observatory. The circular patterns of the UAV trajectories are also shown.

In Sect. 2, we briefly describe the methods used for retrieving the atmospheric parameters analyzed in the present study. In Sect. 3, we show comparison results between V_B, vertical velocity measured by MU radar, energy dissipation rate, and Richardson number profiles from three case studies selected from ShUREX2017. These comparisons clearly indicate that turbulence effects dominate the balloon ascent rate. The results of a statistical analysis from 376 balloons and based on the intimate relationship between turbulence and Richardson number Ri are shown in Sect. 4. They confirm that V_B is dominated by turbulence effects when Ri≲0.25. Finally, conclusions of this work are given in Sect. 5.

2 Methods

2.1 Estimation of V_B

Rubber balloons 200 g in weight and manufactured by TOTEX were equipped with Vaisala RS92SGPD radiosondes for pressure, temperature, relative humidity and horizontal wind measurements during ShUREX campaigns. Their ascent rate V_B was calculated from Δz∕Δt where z is the GPS altitude of the radiosondes and Δt=2 s. A 20 s rectangular window was applied to V_B to reduce the noise, likely due to pendulum effects, self-induced balloon motions and other potential causes. For the case studies, we focused on the data from the ground (384 m a.s.l. at MU Observatory) up to the altitude of 7.0 km a.s.l. This is primarily because (1) the datasets were originally processed for comparisons with data from UAVs, which did not fly above altitudes of a few kilometers; (2) a limited height range makes the description of individual turbulent events less tedious; (3) the increasing horizontal distance between the radar and balloons with height due to strong horizontal winds becomes an important factor of uncertainty when doing comparisons; and (4) the signal-to-noise ratio (SNR) of radar measurements statistically decreases with height in the troposphere and low SNR values produce additional uncertainties.

2.2 Detection of turbulence from TKE dissipation rate ε

The TKE dissipation rate ε is a key parameter describing the intensity of dynamic turbulence. It is thus well adapted for the present purpose, i.e., the identification of turbulent layers when the balloons were flying. Values of ε can be calculated from UAV data using two methods described by Luce et al. (2019). A direct estimate is obtained from one-dimensional (1D) spectra of streamwise wind fluctuation measurements. An indirect estimate is deduced from the temperature structure function parameter $C_{\mathrm{T}}^{\mathrm{2}}$ calculated from 1D temperature spectra. Similar levels of ε and $\mathit{\epsilon }(C_{\mathrm{T}}^{\mathrm{2}}$) give credence to the results since the two estimates are independent. In addition, consecutive profiles can be obtained during UAV ascents and descents, depending on the configuration of the flights. Therefore, both vertical profiles of ε and $\mathit{\epsilon }(C_{\mathrm{T}}^{\mathrm{2}}$) during ascents and descents will be shown when available.

The TKE dissipation rate can also be estimated from MU radar data using the variance σ² of Doppler spectrum peaks produced by turbulence. It is based on an empirical model proposed by Luce et al. (2018) and validated from comparisons with UAV-derived ε. The expression of the model is $\mathit{\epsilon }\left(\mathrm{MU}\right)={\mathit{\sigma }}^{\mathrm{3}}/L_{\mathrm{out}}$ where L_out∼60 m. In the present work, an estimate of ε(MU) at a given altitude z is obtained from an average of the values of σ² over a centered-in-time 2 min window (about 30 values since radar profiles were obtained every ∼4 s) around the time that the altitude z was reached by the radiosonde (see also Fig. 1 of Luce et al., 2018, for a schematic). This procedure should ensure that the estimates of ε are representative of those met by the balloons, assuming horizontal homogeneity over a distance at least equal to the horizontal distance separating the balloons and the radar (up to ∼30 km; see Sect. 3). The horizontal distance between UAV and balloon measurements did not exceed ∼10 km up to the altitude of ∼4.0 km. Considering that all the turbulent events analyzed in the present study persisted for more than 1 h and were likely associated with meso- or synoptic-scale dynamics, the procedure may appear unnecessary, but it is crucial for the vertical velocity (see Sect. 3).

Consequently, we have three independent estimates of ε in the vicinity of the balloon flights. The two UAV estimates are obtained from the ground up to ∼4.0 km and the radar estimates in the height range 1.27–7.0 km. The radar and UAV estimates overlap between 1.27 and ∼4.0 km and are complementary outside this range.

2.3 Estimation of vertical velocity profiles from radar data

Vertical velocities W can also be directly measured by Doppler spectra when the radar beam is vertical (e.g., Röttger and Larsen, 1990). Pseudo-vertical profiles of W were reconstructed in the same way as ε(MU) by averaging over a 2 min window centered on the time that the altitude z was reached by the radiosonde. This 2 min averaging was applied in order to reduce the statistical estimation errors and is suitable for detecting W fluctuations of periods significantly larger than 2 min.

As shown by, e.g., Muschinski (1996), Worthington et al. (2001) and Yamamoto et al. (2003), W can be biased by a few tens of centimeters per second or more because of refractivity–surface tilts produced by Kelvin–Helmholtz or internal gravity waves. However, this potential bias cannot explain the large differences of a few meters per second between W and the vertical air velocities deduced from V_B (see Sect. 3).

3 Case studies

Three balloon flights (hereafter called V6, V14 and V16, which correspond to UAV flight numbers SH14, SH29 and SH31, respectively) performed during ShUREX2017 on 18 and 26 June 2017 are analyzed in detail. Figure 1 shows the horizontal trajectories of the balloons up to the altitude of 7.0 km a.s.l. The nearly circular patterns of the UAV trajectories are also shown. The MU radar is at the position (0, 0).

The balloons were intentionally underinflated with respect to standard procedures in order to get a mean ascent rate of ∼2 m s⁻¹ similar to the vertical ascent rate of the UAVs. V6, V14 and V16 reached the altitude of 7.0 km a.s.l. within about 33, 52 and 53 min, respectively, and their mean vertical ascent rates were about 3.3, 2.1 and 2.1 m s⁻¹. V6 each drifted by less than 15 km southwestward when reaching the altitude of 7.0 km. V14 and V16 drifted by about 30 km mainly eastward due to the influence of the subtropical jet stream.

3.1 Analysis of the radar data

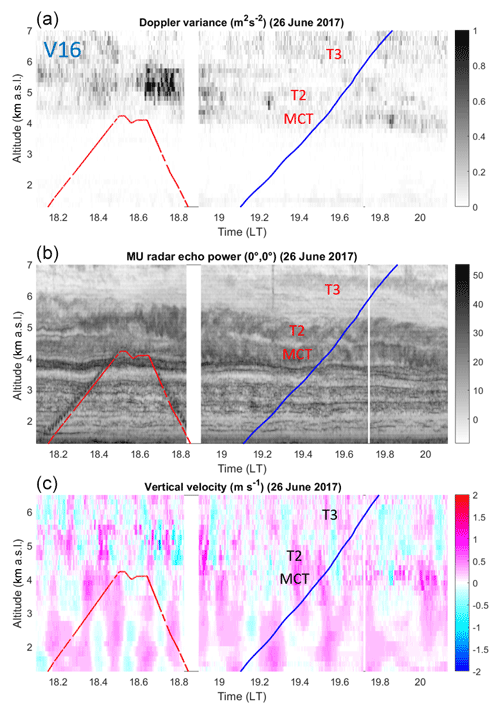
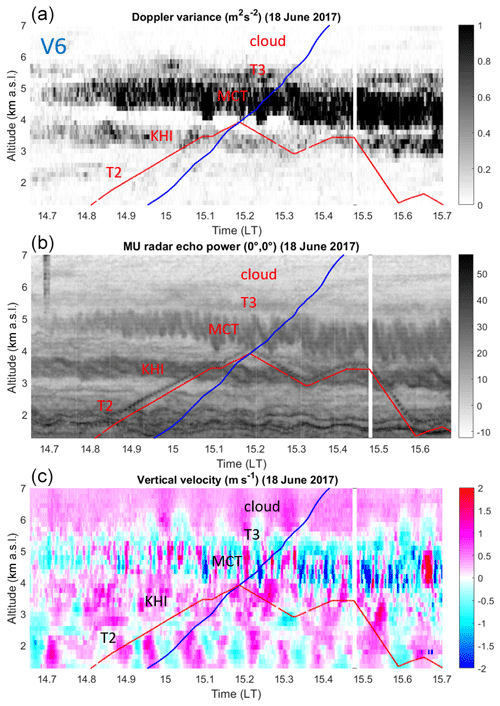
Time–height cross sections of MU radar Doppler variance σ² (m² s⁻²), echo power (dB) and vertical velocity (m s⁻¹) around the times of the UAV and balloon flights in the height range 1.27–7.0 km are shown in Figs. 2, 3 and 4 for V14, V16 and V6, respectively (they are not shown in time order for ease of the description made below). The red and blue lines indicate the altitude of the UAVs and balloons vs. time, respectively. For easy reference, the most prominent and persisting turbulent layers identified from enhanced Doppler variance (or ε(MU)) and UAV-derived ε are labeled. The source of these layers is sometimes recognizable from the morphology of the corresponding radar echoes in the high-resolution power images. When this is the case, the labels indicate the nature of the instabilities that gave rise to turbulence; otherwise the labels are “T1”, “T2”, etc. “KHI”, “MCT” and “CBL” refer to sheared-flow Kelvin–Helmholtz instability (e.g., Fukao et al., 2011), mid-level cloud-base turbulence (e.g., Kudo et al., 2015) and convective boundary layer, respectively. The presence of saturated air is also indicated by the label “cloud”. Note that enhanced σ² does not necessarily imply enhanced echoes (e.g., T1 in Fig. 2 and T2 in Fig. 4) because turbulence can sometimes produce faint echoes surrounded by enhanced echoes at their edges (e.g., McKelley et al., 2005). The CBL in Fig. 2 is only guessed because the CBL top only slightly exceeded the altitude of the first radar gate, but it was confirmed by the UAV observations.

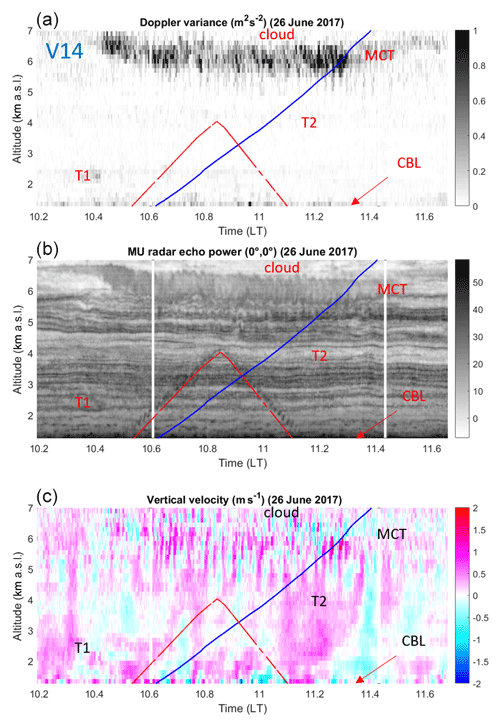
Figure 2 (a) Time–height cross section of variance of the Doppler spectrum peaks corrected from the beam-broadening effects obtained from MU radar measurements during balloon flight V14 and UAV flight SH29. The altitudes of V14 and SH29 vs. time are given by blue and red lines, respectively. (b) Same as top for radar echo power (dB) in range imaging mode. (c) Same as top for vertical velocity (m s⁻¹). The white vertical lines are due to radar stops. See, e.g., Luce et al. (2018) for more details about these figures. Labels refer to the location of turbulent layers.

The V14 case was characterized by weak turbulence except below ∼1.3 km (CBL) and above ∼5.0 km (MCT) (Fig. 2). The atmosphere was weakly turbulent between the CBL and MCT, but two events (T1 and T2) persisted around 2.3 km and between 4.0 and 4.5 km. The V16 case was also characterized by weak turbulence below 3.5–4.0 km and at least three well-defined layers associated with MCT and two instabilities within clouds (T2 and T3 in Fig. 3). The V6 case showed enhanced turbulence at almost all altitudes (Fig. 4), but distinct layers can be clearly noted: MCT around 5.0 km, KHI around 3.5 km (braided structures are clearly visible around 15:00 LT), and less intense events around 2.5 km (T2) and just above the cloud base (T3). Turbulent layers (T1) detected from UAV data below 1.27 km are not indicated on the figures.

Rapid W fluctuations (of a period of ∼1 min) are generally associated with MCT events. Nearly monochromatic oscillations of W likely due to ducted gravity waves can also be noted below 2.5–3.0 km during V16 and V6 (Figs. 3 and 4). Their periods are about 9 and 6 min, respectively. The amplitude of W did not exceed ∼0.5 m s⁻¹ except in the MCT layer during V6 where W fluctuated between ±2.0 m s⁻¹.

Figure 3 Same as Fig. 2 for SH31 and V16.

Figure 4 Same as Fig. 2 for SH14 and V6.

3.2 Profile comparisons

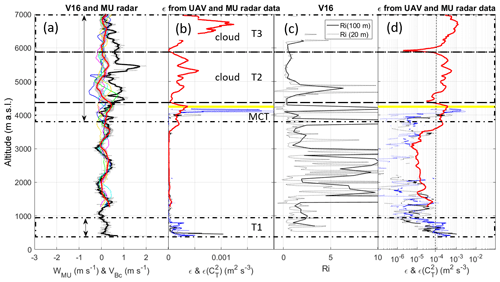
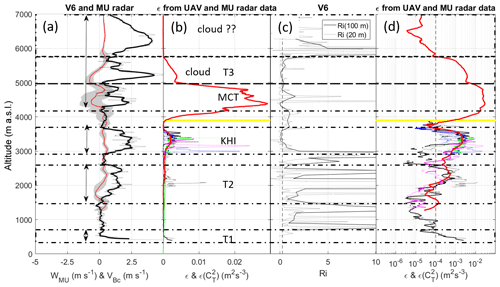
The results of comparisons between V_B and atmospheric parameter profiles are shown for V14, V16 and V6 in Figs. 5, 6 and 7, respectively. Panels (a) show vertical velocity profiles from MU radar data and radiosondes. Panels (b) and (d) show UAV- and radar-derived ε profiles in linear and logarithmic scales, respectively. Both representations are shown for ease of analysis. Panels (c) show Richardson number Ri profiles defined as $Ri=N^{\mathrm{2}}/S^{\mathrm{2}}$, where N is the Brunt–Väisälä frequency and S the vertical shear of horizontal wind, estimated from balloon data at 20 and 100 m resolution. Two vertical resolutions are used because Ri is scale-dependent (Balsley et al., 2008).

The balloon ascent rate in still air V_z was estimated from the difference between W and V_B when turbulence was weak and the Richardson number was high. V_z was found to be 1.8, 1.8 and 2.3 m s⁻¹ for V14, V16 and V6, respectively, and $V_{\mathrm{Bc}}=V_{\mathrm{B}}-V_z$ is shown in the figures. Indeed, the vertical fluctuations of V_Bc coincide well with those of W outside the labeled turbulent layers, indicating that the variations in balloon ascent rate are dominated by the vertical air motions when turbulence is “sufficiently weak”. This is particularly evident in Fig. 6 in the height range 1.3–3.8 km where the wavy fluctuations in W (of ∼0.5 m s⁻¹ in amplitude) coincide very well with those of V_Bc. Several radar estimates of W are shown for different time lags. Each time lag is a multiple of ∼9 min, which corresponds to the apparent period of the wave in the radar image (Fig. 3). The fluctuations of W and V_Bc are in phase. The W profile suggests that the oscillations still occurred above 3.8 km in the MCT layer. The V_Bc profile indicates enhanced values of up to +1.8 m s⁻¹ at 5.5 km that are clearly not related to vertical air motions.

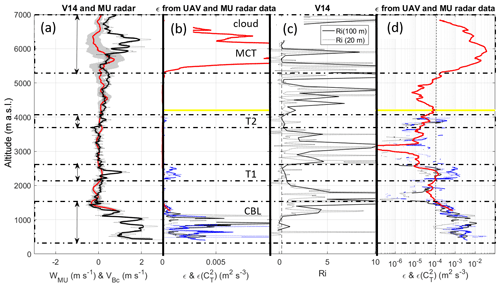
Figure 5 (a) Vertical profile of V_Bc (m s⁻¹) (solid black: smoothed; dotted black: raw) for V14 and W_MU (m s⁻¹) (red). The gray area shows the standard deviation of W_MU over the averaging time (2 min). The vertical arrows indicate the altitude ranges affected by turbulence. (b) Vertical profiles of TKE dissipation rates ε obtained from MU radar measurements (red) and UAV measurements during ascent and descent (black and blue) and using the direct and indirect methods (solid and dashed lines). The maximum altitude reached by the UAV is shown by the horizontal gray line. (c) Vertical profiles of Richardson numbers at a resolution of 20 m (dashed) and 100 m (solid). The vertical dashed line indicates Ri=0.25. (d) Same as (b) in log scale. The vertical dashed line indicates the value of $\mathit{\epsilon }={\mathrm{10}}^{-\mathrm{4}}$ m² s⁻³.

In contrast, wherever UAV- and radar-derived ε estimates are enhanced in the labeled height ranges, V_Bc is also enhanced and V_Bc and W strongly differ. Note that the UAV profiles of ε during ascents and descents are very similar and there is a good agreement with the radar-derived profiles obtained during the balloon flights. Therefore, we can reasonably assume that these profiles are representative of the turbulence conditions met by the balloons. In general, the height ranges of enhanced ε coincide with minima of Ri, close to the critical value of 0.25, as expected for shear-generated turbulence (e.g., KHI in Fig. 7), or even less than 0, expected for MCT. Ri is not necessarily small over the whole depth of the layers (e.g., around 6.0 km in Fig. 5) and is surprisingly high for the whole depth of T2 in Fig. 7, but the overall results remain consistent. A puzzling result can be noted above the cloud base (6.0 km) during V6 (Fig. 7, as indicated by “??”) where a strong increase in V_Bc (∼4 m s⁻¹) was neither associated with an increase in W nor an increase in turbulence according to MU radar observations. A slowdown of the balloon due to precipitation loading would rather be expected. This thus remains unexplained and, by default, we must invoke horizontal inhomogeneity of W and/or turbulence intensity over the horizontal distance between the radar and the balloon (∼10 km). Similar features were not observed in clouds during V14 and V16.

Figure 6 Same as Fig. 5 for V16.

Figure 7 Same as Fig. 5 for V6.

These case studies provide experimental evidence that turbulence can strongly increase the balloon ascent rate, very likely through the decrease in the drag coefficient. The observed V_Bc is thus the combination of turbulence effects and vertical air velocities. Because W fluctuations appear significantly weaker than V_Bc fluctuations, turbulence effects are likely dominant. On some occasions, an increase in V_Bc might be due solely to turbulence effects, as in T1 of V14 (Fig. 5) since W does not show any particular variations in the range of T1.

In the present cases, $\mathit{\epsilon }\sim {\mathrm{10}}^{-\mathrm{4}}$ m² s⁻³ seems to be a threshold below which turbulence does not seem to affect the balloon ascent rate significantly. However, this value is likely specific to the present observations and may not be applicable to other conditions.

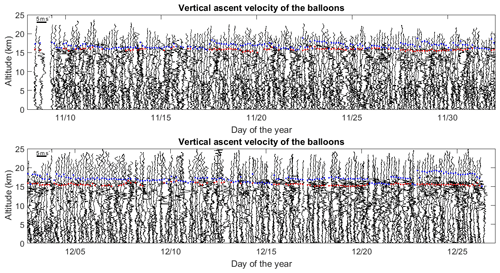
Figure 8 Vertical profiles of V_B from 376 consecutive balloons launched about every 3 h from 8 November to 27 December 2015 during the pre-YMC campaign at Bengkulu (102.26^∘ E, 3.79^∘ S; Indonesia); 0.5 d corresponds to 5 m s⁻¹, and each profile was shifted by about 0.125 d (1.25 m s⁻¹). The cold point temperature tropopause and a secondary temperature inversion of similar intensity at lower altitude are shown as blue and red dots, respectively.

4 Statistics

The case studies strongly suggest that increased balloon ascent rates are generally related to minimum values of the Richardson number (negative or smaller than ∼0.25 consistent with convective overturning or shear-generated instabilities in stratified conditions, respectively). This observation can be confirmed by analyzing the relationship between V_Bc and Ri from a large amount of data. For this purpose, we used data from 376 radiosondes launched every 3 h in Indonesia (Bengkulu, November–December 2015) during a preliminary Years of the Maritime Continent (YMC) campaign (e.g., Kinoshita et al., 2019). The choice of this dataset is arbitrary, but it ensures that the same type of balloons (TOTEX-TA 200) and radiosondes (RS92SGPD) were used with similar procedures of balloon inflation for all the datasets. Figure 8 shows all the V_B profiles with a slight offset for legibility. The balloons were inflated in order to get a mean ascent rate of 5 m s⁻¹ (free lift). During the period of observations, the tropical tropopause layer (TTL) was often characterized by a strong temperature inversion just above the cold point temperature (CPT) around the altitude of 16–17 km (blue dots in Fig. 8) and a secondary temperature inversion of similar intensity at slightly lower altitude (red dots). For ease of statistical analysis, we refer to altitude ranges 0–16.3 km as troposphere and altitude ranges above 17.2 km (up to the top of the radiosoundings) as stratosphere.

The profiles of V_B often display multiple peaks of variable widths in the troposphere especially in its upper part. In the stratosphere, the profiles are much smoother and show either weak variations or nearly monochromatic fluctuations undoubtedly due to internal gravity waves (Tsuda et al., 1994). Therefore, we suggest that the variations in V_B with height are primarily due to vertical air motions in the stratosphere and mainly due to turbulence effects in the troposphere. To assess this hypothesis, we analyzed the relationship between Ri and V_Bc (V_B corrected from the free lift). We calculated (moist) $Ri=N_m^{\mathrm{2}}/S^{\mathrm{2}}$, where $N_m^{\mathrm{2}}$ is the squared moist Brunt–Väisälä frequency using expression (5) of Kirshbaum and Durran (2004) at a vertical resolution of 50 m, a reasonable trade-off between 20 and 100 m used for the case studies. Because V_B seems to be weakly affected by turbulence in the stratosphere, the mean value of V_B for stratospheric heights, 〈V_B〉_ST, is expected to be a fair estimate of the ascent rate in still air (V_z), assuming that wave contribution is indeed removed after averaging and that other contributions are negligible. Thus, we have $V_{\mathrm{Bc}}=V_{\mathrm{B}}-\langle V_{\mathrm{B}}{\rangle }_{\mathrm{ST}}$. The value of 〈V_B〉_ST was calculated for each flight and removed from each profile of V_B in order to reduce the effects of variable mean ascent rates that may result from different balloon inflations. The mean value of 〈V_B〉_ST over the 376 flights was found to be precisely equal to the nominal value of 5 m s⁻¹.

First, the scatterplot of V_Bc vs. Ri shows a very significant maximum around and below the critical value of Ri_c∼0.25 in the troposphere (Fig. 9a). This is an indirect confirmation that V_Bc peaks are indeed due to turbulence (Fig. 9a), considering that small Ri values are generally associated with turbulence. Second, this increase is accompanied by a larger scatter. There is no similar tendency in the stratosphere (Fig. 9b) because Ri rarely dropped below Ri_c, in accordance with the absence of significant turbulence ascertained from the profiles of V_B. The increased variability of V_Bc with decreasing Ri in Fig. 9b should mainly be due to waves.

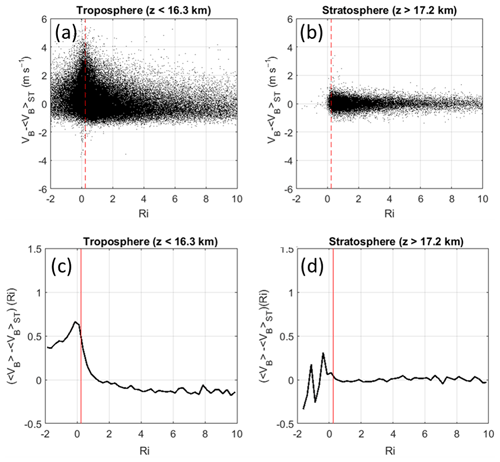
Figure 9 (a) Scatterplot of $V_{\mathrm{Bc}}=V_{\mathrm{B}}-\langle V_{\mathrm{B}}{\rangle }_{\mathrm{ST}}$ versus moist Ri for the troposphere. (b) Same as (a) for the stratosphere. (c) Mean values of V_Bc in Ri bands of 0.25 in width for the troposphere. (d) Same as (c) for the stratosphere. The vertical red lines show Ri_c=0.25.

In order to emphasize the tendency shown by Fig. 9a and b, averaged values of V_Bc in Ri value bands of 0.25 in width, 〈V_Bc〉, are shown in Fig. 9c and d, respectively. For Ri≳1, 〈V_Bc〉 is roughly constant but slightly negative: $\sim -\mathrm{0.2}$ m s⁻¹ (Fig. 9c) because 〈V_B〉_ST is likely not exactly the ascent rate in still air in the troposphere. This is not an important issue for the present purpose. When Ri drops below Ri_c, 〈V_Bc〉 increases by $\sim +\mathrm{0.9}$ m s⁻¹ and remains high when Ri<0 (Fig. 9a). The values for Ri<Ri_c are not reliable in the stratosphere (Fig. 9d) due to the lack of data. The results shown in Fig. 9c constitute a statistical confirmation of the observations reported in Sect. 3.

Figure 10 show V_Bc−〈V_Bc〉 vs. Ri for the troposphere. A larger scatter is observed between Ri=0 and Ri_c=0.25. The broadening of the scatter was attributed to turbulence by Houchi et al. (2015). However, the broadening cannot be explained by a decrease in the drag coefficient because it is necessarily due to both positive and negative vertical velocities. The broadening is thus more likely due to turbulent billows of scales much larger than the balloon size. In addition, Kelvin–Helmholtz (KH) waves can also produce updrafts and downdrafts of up to a few meters per second when Ri reaches Ri_c (see, e.g., Fukao et al., 2011). Therefore, the enhanced variability of V_Bc when Ri is small (Fig. 9a) is presumably the combination of turbulence effects and vertical air motion disturbances produced by large-scale billows and KH waves.

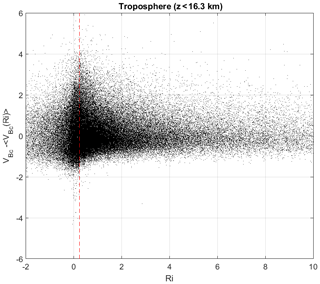
Figure 10 Same as Fig. 9a after removing the mean tendency shown by Fig. 9c for the troposphere. The vertical dashed line shows Ri_c=0.25.

Finally, it can be noted that the scatterplot of V_Bc−〈V_Bc〉 (Fig. 10) is not symmetrical about 0 for Ri>1 (for which turbulence is expected to be suppressed) and suggests peaks of V_B (without corresponding negative disturbances) even in the absence of turbulence. However, this result must be tempered by the fact that turbulence can be observed even if the estimation of Ri at a given resolution is not small (see, e.g., Fig. 7, T2). Measurement and estimation errors of temperature, humidity and winds cannot be discarded on some occasions and $N_m^{\mathrm{2}}$ may not be the appropriate parameter for all conditions. For all these reasons, this observation may not be indicative of more complex interactions between the balloon and the surrounding atmosphere.

5 Discussion and conclusions

We have found that the possibility of retrieving the vertical air velocity W from radiosonde ascent rate V_B highly depends on the turbulent state of the atmosphere. In turbulent layers generated by shear or convective instabilities, W cannot be measured because V_B is very likely affected by the decrease in the drag coefficient c_D of the balloon. In contrast, in the calm regions of the atmosphere, the fluctuations of V_B are dominated by the fluctuations of W. These conditions were probably met by, e.g., Corby (1957) and Reid (1972) and are most likely met in the lower stratosphere (Shutts et al., 1988; Reeder et al., 1999). This was also the case during the conditions analyzed by Wang et al. (2009) above the CBL. However, in light of our observations, we speculate that Wang et al. (2009) also detected turbulent layers: localized increases in V_B (up to ∼2 m s⁻¹) observed in the height range 8–10 km (their Fig. 1) may be attributed to turbulent layers. McHugh et al. (2008) interpreted isolated peaks of V_B of several meters per second of amplitude near the tropopause and at the jet-stream level in terms of W disturbances around critical levels associated with mountain waves. The absence of corresponding negative disturbances was explained by the three-dimensional nature of the flow. Even though our hypothesis remains speculative in the absence of additional and independent measurements of vertical air velocity, we suggest that turbulence effects may have also contributed to the observed increase in ascent rates since critical levels are generally associated with turbulence. A careful scrutiny of their Figs. 3–7 indicates that V_B increased at altitudes where the horizontal wind shear was enhanced and temperature gradient was close to adiabatic (so that Ri was likely small). Houchi et al. (2015) attributed the spread of the height increment “dz” probability density function to “turbulence”. The authors likely implicitly referred to advection by large-scale billows. The decrease in the drag coefficient due to turbulence can explain the upward-only motion anomaly noticed by the authors.

It turns out that V_B can also potentially be used for the detection of turbulence in the free atmosphere if the increase in V_B can be separated from the contribution of W. Turbulence is frequent in the free atmosphere but also very variable with height and generally distributed in layers, especially in stratified conditions. This feature was likely not well appreciated by Gallice et al. (2011). The authors themselves recognized that their model cannot work if localized turbulence – they proposed the example of turbulence generated by gravity wave breaking – occurs.

The amplitude of the V_B disturbances should depend on the variation in c_D with the Reynolds number, the intensity of turbulence and on the scales of turbulence with respect to the balloon size so that it might be difficult or even impossible to retrieve turbulence parameters solely from V_B measurements. However, further comparisons such as shown in Sect. 3 might be useful for establishing empirical rules on the turbulence detection threshold.