Retrieval of stratospheric aerosol extinction coefficients from sun-normalized Ozone Mapper and Profiler Suite Limb Profiler (OMPS-LP) measurements

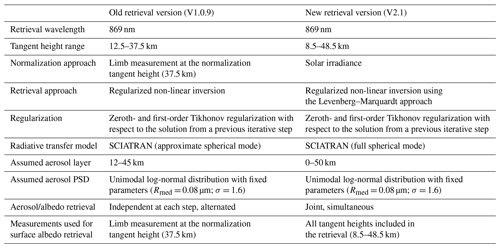
A new retrieval approach for obtaining vertical profiles of the aerosol extinction coefficient from measurements of scattered solar light in the limb-viewing geometry made by the Ozone Mapper and Profiler Suite Limb Profiler (OMPS-LP) instrument is presented.

In contrast to many other published limb-scatter retrievals, our new algorithm does not employ normalization by a limb measurement at an upper tangent height. Instead, the measured limb radiances are normalized to solar irradiance. The main advantage of this approach is an almost complete elimination of the dependence of the retrieval results on the prior aerosol extinction profile used in the retrieval. This makes the retrieval better suited for the analysis of observation scenes with highly elevated aerosol plumes, such as those that occurred after the Hunga Tonga–Hunga Ha′apai volcanic eruption in January 2022. The results from the new approach were compared to the vertical profiles of the aerosol extinction coefficients retrieved from the Stratospheric Aerosol and Gas Experiment III on the International Space Station (SAGE III/ISS) and the Optical Spectrograph and InfraRed Imaging System (OSIRIS). In general, agreement within 25 % between the different data products was observed in the 18–23 km altitude range, although larger differences were seen after very strong volcanic eruptions and wildfires. In comparison with OSIRIS, larger differences are seen at high southern latitudes (above 60° S). The new data product was used to investigate the evolution of the aerosol plume after the Hunga Tonga–Hunga Ha′apai volcanic eruption.

1 Introduction

Stratospheric aerosols directly influence the radiative budget of the Earth's atmosphere by scattering incident solar radiation back into space within the UV–Vis–NIR spectral range and by absorbing the radiation upwelling from the troposphere in the thermal-infrared spectral range. As discussed, for example, by Solomon et al. (2011), the presence of an increased amount of aerosol in the stratosphere leads to global cooling. Cooler temperatures increase the rate of the formation of ozone (O₃) (Groves et al., 1978; Groves and Tuck, 1979) and probably decrease the rate of the catalytic removal of O₃. In addition, stratospheric aerosols serve as nuclei for the formation of polar stratospheric clouds (PSCs) or directly provide surfaces for heterogeneous reactions releasing photolabile halogens (Cl₂, Br₂, and I₂ – noting that only small amounts of I reach the stratosphere) and interhalogens (BrCl, ICl, and IBr), which are photolyzed and yield halogen atoms. These react with O₃, generating halogen oxides. Aerosols also take up HNO₃, reducing the amount of NO_x. At sufficiently low NO_x levels, the ClO disproportionation reaction and the reaction of BrO with ClO participate in additional catalytic cycles, which lead to the formation of ozone holes in the polar regions (Solomon et al., 1986; Portmann et al., 1996; Tritscher et al., 2021). At high levels of aerosol loading, similar processes might also become significant at extrapolar latitudes. For example, a remarkable ozone loss of up to 18 Dobson units was identified at southern midlatitudes after the 2020 Australian wildfires (Solomon et al., 2023), while Evan et al. (2023) reported a decrease in stratospheric O₃ above the tropical southwestern Pacific and Indian Ocean regions of 5 % after the 2022 Hunga Tonga–Hunga Ha′apai eruption. However, as discussed by Zhu et al. (2023), the latter decrease was mainly caused by the injection of a large amount of water vapor, as well as the injection of ClO, which led to chlorine activation in heterogenic reactions. Thus, the ozone decrease reported by Evan et al. (2023) seems to be specific to the Hunga Tonga–Hunga Ha′apai eruption. Besides temperature and the amount of stratospheric ozone, global precipitation, sea-level pressure, circulation patterns, El Niño, and climate extremes have been reported to be affected by volcanic eruptions; see, e.g., Fyfe et al. (2013), Khodri et al. (2017), and Paik and Min (2018).

Despite its high scientific importance, the availability of information about stratospheric aerosols on a global scale is quite limited. One of the widely used characteristics of stratospheric aerosols, which is available from several spaceborne instruments currently in operation, is the stratospheric aerosol extinction coefficient. As discussed by several authors, this quantity can be used to calculate the radiative forcing due to stratospheric aerosols; see, e.g., Hansen et al. (2005), von Savigny et al. (2015), Kloss et al. (2020), and Malinina et al. (2021). Global vertical distributions of the stratospheric aerosol extinction coefficient can only be retrieved from spaceborne measurements. The most robust data come from solar occultation measurements as measured spectra are self-calibrated through exo-atmospheric measurements, and the corresponding retrievals do not use any strong assumptions in the forward modeling. Such measurements, for example, have been performed quasi-globally since 1979 by the Stratospheric Aerosol and Gas Experiment (SAGE) instrument series (McCormick, 1987; McCormick et al., 1989; Chu et al., 1997). Data products from occultation instruments are well suited for use as a validation source but suffer from relatively sparse spatial sampling and coverage. Much denser spatial sampling is provided by the aerosol extinction data retrieved from measurements of scattered solar light in the limb-viewing geometry made by the Optical Spectrograph and InfraRed Imaging System (OSIRIS) (Llewellyn et al., 2004), SCanning Imaging Absorption spectroMeter for Atmospheric CartograpHY (SCIAMACHY) (Burrows et al., 1995; Bovensmann et al., 1999), and Ozone Mapper and Profiler Suite Limb Profiler (OMPS-LP) (Flynn et al., 2014) instruments. In contrast to solar occultation measurements, the retrieval of aerosol extinction coefficients from limb-scatter radiances requires assumptions about the aerosol particle size distribution and aerosol amount around the normalization tangent height if this kind of normalization is applied; see, e.g., Rieger et al. (2015). Furthermore, limb-scatter radiance strongly depends on the reflectance of the troposphere and surface. In the nadir-viewing geometry, the aerosol extinction coefficient is retrieved from active remote sensing measurements performed by lidar instruments, such as the Cloud-Aerosol LIdar with Orthogonal Polarization (CALIOP) (Winker et al., 2009). Lidar retrievals also employ normalization to measurements at high altitudes, resulting in sensitivity to the aerosol at the normalization altitude. A major source of uncertainty for lidar instruments is a lack of knowledge regarding the lidar ratio; see, e.g., Young et al. (2013).

This study focuses on the retrieval of the aerosol extinction coefficient from spaceborne limb-scatter measurements. Although several algorithms for such retrievals have been successfully developed (Bourassa et al., 2012; von Savigny et al., 2015; Rieger et al., 2019; Malinina et al., 2021; Taha et al., 2021; Bourassa et al., 2023), all of them have been optimized to mitigate the influence of surface reflectance, and some also minimize errors arising from the usage of a fixed aerosol particle size distribution. In this study, we present a new algorithm to retrieve vertical distributions of the aerosol extinction coefficient from limb-scatter measurements made by the OMPS-LP instrument. The algorithm has been developed at the University of Bremen. One of its objectives is to minimize the influence of unknown aerosol loading at high altitudes. This is especially crucial in cases of volcanic eruptions that reach high altitudes, such as the Hunga Tonga–Hunga Ha′apai eruption of January 2022. The latter was the strongest volcanic eruption of the 21st century so far, with the highest volcanic plume observed in the satellite era, and it injected 0.4–0.9 Tg of SO₂ to altitudes of up to ∼ 32 km and a huge amount of water vapor to altitudes of up to ∼ 50 km; see, e.g., Carn et al. (2022), Carr et al. (2022), Duchamp et al. (2023), Legras et al. (2022), Millán et al. (2022), Proud et al. (2022), and Xia et al. (2024).

In addition to the OMPS-LP retrieval developed at the University of Bremen and described in this study, algorithms from NASA (Taha et al., 2021) and the University of Saskatchewan (Bourassa et al., 2023) also exist. An intercomparison of the extinction profiles generated by the three algorithms is not straightforward due to the different assumptions about particle size distribution used in the NASA retrieval and the tomographic approach employed in the retrieval developed by the University of Saskatchewan. This intercomparison is the subject of a dedicated study that is currently ongoing. The CALIOP aerosol extinction profile data (Young et al., 2018) are also available but are not used in this study. This is because of a very different measurement principle, a much smaller footprint in the cross-track direction (resulting in significantly sparser coverage), uncertainty from the lidar ratio, and a typically low signal-to-noise ratio in the stratosphere, which would make the interpretation of the obtained results and the attribution of the differences much more ambiguous compared to the selected datasets (OSIRIS and SAGE III/ISS). CALIOP data might be extremely valuable for comparison exercises dedicated to latitudes for which SAGE III/ISS data are not available (e.g., winter high latitudes) or regions where discrimination between aerosol types or between aerosols and cirrus clouds is essential (e.g., the tropical upper troposphere and lower stratosphere (UTLS)). Detailed comparisons of this kind are, however, outside the scope of this study.

The paper is structured as follows. In Sect. 2, the observational data used for the retrieval and comparisons are described. Section 3 presents a detailed description of the retrieval algorithm. The selection of the retrieval wavelength is justified in Sect. 4. The main advantages of the new retrieval algorithm are discussed in Sect. 5. Comparisons with independent data are discussed in Sect. 6. The application of the new dataset for tracing the evolution of the aerosol plume after the Hunga Tonga–Hunga Ha′apai eruption is presented in Sect. 7. Conclusions are presented in Sect. 8.

2 Measurement data

The Ozone Mapping and Profiler Suite (OMPS) was launched in October 2011 onboard the Suomi National Polar-orbiting Partnership (NPP) satellite, a joint venture of the NOAA and NASA (Flynn et al., 2014). The satellite flies in a sun-synchronous orbit with a 98.78° inclination at an altitude of about 800 km. The OMPS comprises three instruments: the Nadir Mapper (NM), the Nadir Profiler (NP), and the Limb Profiler (LP). In this study, only the measurements from the latter instrument, OMPS-LP, are used. The OMPS-LP instrument observes solar radiance scattered by the Earth's atmosphere, including that passing downward through the atmosphere and reflected back by the underlying surface. The radiance from the atmosphere enters the instrument through three slits pointing in the direction opposite to that of the satellite's flight. Using two-dimensional charge-coupled-device (CCD) detectors, measurements are made simultaneously in the altitude range from approximately 0 to 100 km, with a vertical sampling of 1 km. Because of unresolved calibration issues, only the measurements from the central slit are used in this study. The OMPS-LP instrument is a prism spectrometer covering the 280–1000 nm spectral range, with a spectral resolution increasing with wavelength from 1 nm in the UV range to about 30 nm in the near-IR region. The vertical field of view of each detector pixel is about 1.5 km. In this study, the Level-1G V2.6 data provided by NASA are used. This dataset contains both sun-normalized and unnormalized radiances.

The Stratospheric Aerosol and Gas Experiment (SAGE) III instrument has been operating since February 2017 onboard the International Space Station (ISS). The ISS flies at an altitude of ∼ 400 km, and its orbit has an inclination of 51.6°. The SAGE III/ISS instrument performs solar occultation measurements during sunrise and sunset. The aerosol extinction coefficients are provided at nine wavelengths: 384, 449, 520, 602, 676, 756, 869, 1021, and 1544 nm. The retrievals cover the range from the cloud top to about 45 km altitude at a vertical resolution of about 0.75 km. In this study, Level-2 V5.3 data from the SAGE III/ISS instrument were used. No cloud filtering was applied. Negative values in the SAGE III/ISS data were not filtered out to avoid creating a positive bias.

The Optical Spectrograph and InfraRed Imaging System (OSIRIS) instrument (Llewellyn et al., 2004) was launched in November 2001 onboard the Swedish Odin satellite. The satellite flies in a sun-synchronous orbit with a 98.78° inclination at an altitude of about 600 km. The instrument combines a grating UV–Vis spectrograph and an IR imager and observes the solar radiance scattered by the Earth's atmosphere, including that reflected by the underlying surface. The observations are conducted in the altitude range between about 0 and 100 km, with a vertical sampling of ∼ 2 km and a similar vertical resolution. The optical spectrograph, whose data were used in this study, measures the spectral radiance in the 280–800 nm range with a resolution of 1–2 nm. OSIRIS retrievals provide vertical profiles of the stratospheric aerosol extinction coefficient at a wavelength of 750 nm between about 8 and 40 km altitude, with a vertical resolution of about 2 km. In this study, OSIRIS cloud-cleared Level-2 data from V7.3 were used (Rieger et al., 2019). Because of issues identified by the University of Saskatchewan team with respect to the vertical profiles of the aerosol extinction coefficient retrieved after the Hunga Tonga–Hunga Ha′apai eruption, only data before January 2022 are considered.

3 Retrieval algorithm

In this section, a detailed description of the new OMPS-LP retrieval algorithm from the University of Bremen (V2.1) is presented. The retrieval approach is based on a regularized non-linear inversion.¹ This algorithm is similar to those employed for the retrieval of vertical distributions of atmospheric species by the University of Bremen team and many other authors, e.g., Glatthor et al. (2006), Livesey et al. (2006), Rozanov et al. (2011), Malinina et al. (2018), Rieger et al. (2019), Mettig et al. (2021), and Keppens et al. (2024). This kind of algorithm is also referred to as the global fit approach because all available spectral data are fitted together at once, with no separation into spectral and vertical steps.

In general, the following quadratic form needs to be minimized to obtain the solution (see, e.g., Rodgers, 2000):

$$\begin{array}{}\text{(1)}& \parallel \mathit{y}-\mathbf{F}\left({\mathit{x}}_{\mathrm{0}}\right)-\mathbf{K}(\mathit{x}-{\mathit{x}}_{\mathrm{0}}){\parallel }_{{\mathbf{S}}_y^{-\mathrm{1}}}+\parallel \mathit{x}-{\mathit{x}}_{\mathrm{0}}{\parallel }_{{\mathbf{S}}_{\mathrm{r}}},\end{array}$$

where x is the resulting state vector, i.e., the solution to be obtained; x₀ is the initial guess (a priori) state vector; $\mathbf{K}={\left.\frac{\mathit{\delta }\mathbf{F}\left(\mathit{x}\right)}{\mathit{\delta }\mathit{x}}\right|}_{\mathit{x}={\mathit{x}}_{\mathrm{0}}}$ is the Jacobian of the forward model operator, also referred to as the weighting function; y is the measurement vector constructed from the observed values; F(x₀) is the measurement vector simulated by the forward model assuming the initial guess atmospheric state; ${\mathbf{S}}_y^{-\mathrm{1}}$ is the noise covariance matrix; and S_r is the regularization matrix.

The state vector contains aerosol extinction coefficient values at altitude levels corresponding to the measurement tangent heights and the effective Lambertian surface albedo. The initial guess values for the aerosol profile are set in accordance with an arbitrary profile extracted from the SAGE II aerosol climatology published by Bingen et al. (2004). As the retrieval depends only weakly on the initial guess profile (see below), the selection of any particular profile is rather unimportant. For the effective surface albedo, the initial guess value is set to 0.5. The initial guess state vector is the same for all retrievals. The aerosol extinction coefficient and the scattering phase function are calculated employing Mie theory, assuming a spherical shape for the aerosol droplets. The optical properties of the aerosol particles are taken from the Optical Properties of Aerosols and Clouds (OPAC) database (Hess et al., 1998) for the “sulfate droplets” aerosol type. This aerosol type corresponds to background stratospheric aerosols (with a 75 % solution of H₂SO₄). The calculations are performed for a relative humidity of 0 % in the ambient air. A unimodal log-normal particle size distribution (PSD) with fixed parameters (a median radius, R_med, of 0.08 µm and a geometrical standard deviation, σ, of 1.6) is assumed for all calculations. The PSD parameters are taken from an arbitrary balloon-borne in situ measurement for background aerosol conditions reported by Deshler (2008). An aerosol layer between 0 and 50 km and an aerosol-free atmosphere above are assumed.

The measurement vector contains logarithms of limb radiance in the tangent height range of 8.5–48.5 km (with 1 km sampling), normalized by solar irradiance. This normalization approach is the main difference between the new retrieval and the previous version of the OMPS-LP retrieval from the University of Bremen (V1.0.9), published by Malinina et al. (2021), which used normalization by a limb measurement at an upper tangent height. As normalization by solar irradiance instead of the reference tangent height makes the retrievals more sensitive to surface reflectance, the approach for retrieving the effective Lambertian surface albedo was optimized as follows. In the new retrieval, the effective surface albedo is included in the state vector and retrieved simultaneously with the aerosol extinction coefficients. Measurements at all tangent heights in the 8.5–48.5 km range are used to retrieve the effective surface albedo. In contrast, the V1.0.9 approach performed alternating independent retrievals of the aerosol extinction coefficients and the effective surface albedo. The latter retrieval used only the limb measurement at the reference tangent height. In addition, the V2.1 approach is more sensitive to the quality of the radiative transfer modeling. For this reason, the fully spherical mode of the SCIATRAN radiative transfer model, CDIPI (the combined differential–integral approach involving the Picard iterative approximation), was used for forward modeling, rather than the approximate spherical mode (the combined differential–integral (CDI) approach) used in the V1.0.9 algorithm. A detailed description of the CDI and CDIPI modes of SCIATRAN can be found in Rozanov et al. (2000, 2001). We note that the use of solar normalization makes the retrieval more sensitive to the quality of the absolute calibration of the measurements. In particular, errors can be expected if the absolute calibration of the limb spectra differs from that of the solar irradiance spectra. Although absolute calibration errors are typically independent of the incoming signal, they might be redistributed differently by the retrieval among the retrieved parameters (the aerosol extinction coefficient and effective surface albedo in our case), depending on the observational geometry and surface reflectivity. This makes them difficult to identify. In the case of detector degradation, a drift in the data might be expected. Degradation of detectors is, however, more of an issue in the UV spectral range than in the near-IR range used in this study. For now, there are no indications of any issues with the absolute calibration of the OMPS-LP instrument or with degradation of the detectors.

The retrieval is performed for the relative changes in the aerosol extinction coefficient, $\left([x{]}_i-[x_{\mathrm{0}}{]}_i\right)/[x_{\mathrm{0}}{]}_i$, and the absolute changes in the effective surface albedo, [x]_j−[x₀]_j. In the formulas above, the square brackets denote the component-wise operation, i runs through all aerosol levels included in the retrieval, and j is the number assigned to the effective surface albedo component in the state vector. The regularization is based on the Tikhonov approach, containing the zeroth- and first-order terms:

$$\begin{array}{}\text{(2)}& {\mathbf{S}}_{\mathrm{r}}={\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}+{\mathit{\gamma }}^{-\mathrm{2}}{\mathbf{S}}_{\mathrm{d}}^T{\mathbf{S}}_{\mathrm{d}}.\end{array}$$

The zeroth-order Tikhonov term, ${\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}$, acts similarly to the a priori covariance matrix in the maximum a posteriori information method described by Rodgers (2000). The diagonal elements of the matrix S_a are set to 0.3 for the aerosol extinction coefficients and to 0.01 for the effective surface albedo. The off-diagonal elements are selected assuming a 1 km correlation radius for the aerosol extinction coefficients and no correlation between the aerosol extinction and the effective surface albedo. The matrix S_d in the first-order Tikhonov term is the first-derivative matrix. Detailed formulas for calculating the elements of the regularization matrices can be found in Rozanov et al. (2011). The Tikhonov parameter, γ, is set to 0.2. The noise covariance matrix is a diagonal matrix with diagonal elements corresponding to a signal-to-noise ratio of 200, independent of the tangent height. This value and the values of the Tikhonov parameters were selected empirically as a trade-off between the stability and sensitivity of the retrievals. Taking into account that the regularization strength is determined by the ratio of the noise covariance to the Tikhonov parameters, rather then the absolute values of these components, we prefer to use an empirical value for the signal-to-noise ratio instead of the reported measurement errors. This keeps the regularization strength similar for all retrievals.

The non-linearity of the inverse problem defined in Eq. (1) is accounted for by employing an iterative scheme. The Levenberg–Marquardt algorithm is used to obtain the final solution. At each iterative step, the solution of the non-linear inverse problem is written as follows (see, e.g., Rodgers, 2000 for details):

$$\begin{array}{}\text{(3)}& {\mathit{x}}_{i+\mathrm{1}}={\mathit{x}}_i+{\left[{\mathbf{K}}_i^T{\mathbf{S}}_y^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{r}}+\mathit{\lambda }{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}{\mathbf{K}}_i^T{\mathbf{S}}_y^{-\mathrm{1}}(\mathit{y}-\mathbf{F}({\mathit{x}}_i\left)\right),\end{array}$$

where i is the iteration number and λ is the Levenberg–Marquardt parameter with an initial guess of 1. We note that the regularization is done with respect to the solution from the previous iterative step rather than with respect to the initial guess atmospheric state. With that, a constraint on the magnitude and shape of the difference profile is applied only within a single iterative step, making the difference between the final solution and the initial guess state much less constrained. The iterative process stops if the aerosol extinction coefficient from two subsequent iterative steps does not change by more than 2 % between 15 and 28 km, or if the relative change in the total root-mean-square difference is below 0.001. The convergence criteria are selected empirically, taking into account the targeted precision of the retrieved aerosol extinction profiles of about 10 %. The results are rejected if the retrieval requires more than 100 iterations to converge. About 80 % of the retrieval runs converged within 17 iterations (histograms illustrating the number of iterations needed for the convergence are presented in Fig. S1 in the Supplement).

The averaging kernels, which describe the sensitivity of the retrieval to the true state, are calculated during the last (nth) iteration using the following formula:

$$\begin{array}{}\text{(4)}& \mathbf{A}={\left[{\mathbf{K}}_{n-\mathrm{1}}^T{\mathbf{S}}_y^{-\mathrm{1}}{\mathbf{K}}_{n-\mathrm{1}}+{\mathbf{S}}_{\mathrm{r}}+\mathit{\lambda }{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}{\mathbf{K}}_{n-\mathrm{1}}^T{\mathbf{S}}_y^{-\mathrm{1}}{\mathbf{K}}_{n-\mathrm{1}}.\end{array}$$

The most important settings used in the new OMPS-LP retrieval approach from the University of Bremen (V2.1) and those used in its precursor version (V1.0.9) are summarized in Table 1.

Table 1 Retrieval settings in the OMPS-LP V2.1 and V1.0.9 algorithms from the University of Bremen.

4 Optimization of the retrieval wavelength

The optimal wavelength for the OMPS-LP V2.1 aerosol retrieval from the University of Bremen is selected by (i) analyzing the possible contamination of the measured signal by interfering with the spectral signatures of other atmospheric constituents and (ii) investigating the sensitivity of limb-scatter measurements to the vertical distribution of stratospheric aerosols.

To investigate the potential influence of interfering absorbers, a measured or modeled atmospheric spectrum with a higher spectral resolution and finer sampling compared to OMPS-LP is required. To ensure that all relevant spectral signatures from all atmospheric constituents are taken into account and that their strength is representative of real observational conditions, we decided to analyze a measured spectrum rather than a modeled one. Suitable spectral information was provided by the SCIAMACHY spectrometer, which was onboard the European Envisat satellite from March 2002 to April 2012 and had a similar observational geometry to that of the OMPS-LP instrument. While the most recent version of the University of Bremen retrieval described in this study uses sun-normalized limb-scatter measurements, all previous retrieval versions, as well as most other limb-scatter stratospheric aerosol retrievals, use limb radiances normalized by a limb measurement at an upper tangent height (also referred to as the reference tangent height). For this reason, below we analyze the spectral behavior of both sun-normalized radiance and radiance normalized by the reference tangent height.

Figure 1 shows spectra of limb-scatter radiance at different tangent heights, normalized by a limb measurement at the reference tangent height of 35 km, as shown in panel (a), and by the solar irradiance spectrum, shown in panel (b). The spectra were obtained from the SCIAMACHY measurement performed on 7 January 2004 at 16:24:37 UTC, with the following tangent point ground coordinates: 26° S, 5° W. The vertical dashed lines mark the wavelengths of 675, 745, 869, and 997 nm, which were used by the NASA OMPS-LP V2.0 stratospheric aerosol extinction retrieval (Taha et al., 2021). The cyan shading marks the areas smeared by the spectral response function (SRF) of the OMPS-LP instruments. The width of each shaded area is selected as ± the FWHM (full width at half maximum) of the SRF. These widths were estimated using Fig. 1-3 in Rault et al. (2010) as 12, 16, 23, and 26 nm at 675, 745, 869, and 997 nm, respectively. Figure 1 reveals that the band centered at 675 nm touches, at its longwave edge, the O₂–B absorption band centered at 688 nm. A similar situation is observed for 745 nm. At this wavelength, the measurements might be affected by the strong absorption in the O₂–A band centered at 762 nm. The potential influence of oxygen absorption is similar for radiances normalized by a measurement at the reference tangent height and by the solar irradiance spectrum. The longwave edge of the band centered at 869 nm approaches the water vapor absorption band; however, the potential interference is rather small. It might be advantageous to slightly shift the wavelength band toward shorter wavelengths. However, due to the sparse spectral sampling of the Level-1 OMPS-LP data, this is not possible without including the water vapor band on its short-wavelength side. For reference tangent height normalization, a small spectral feature is present in the middle of the band, which is not observed for sun-normalized radiance. This is most probably an emission signature propagating from the measurement at the reference tangent height. At 997 nm, the measurements might be affected by water vapor absorption near the shortwave edge of the band. This influence seems to be stronger for sun-normalized radiance. The reason for this is a partial canceling of the tropospheric signal when using reference tangent height normalization. A strong increase in measurement noise toward longer wavelengths in the case of reference tangent height normalization is typical of SCIAMACHY. For the OMPS-LP instrument, the signal-to-noise ratio at 997 nm is about a factor of 2 lower than that at 869 nm. Because of the stronger overlap with absorption features of atmospheric gases and the lower signal-to-noise ratio compared to other wavelengths, we exclude the 997 nm wavelength from further consideration.

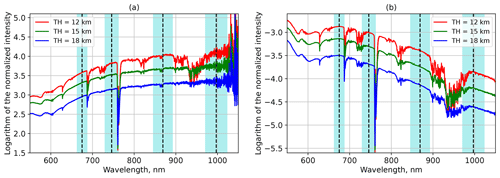
Figure 1 Spectra of limb-scatter radiance at different tangent heights (THs), normalized by a limb measurement at the reference tangent height (a) and by the solar irradiance spectrum (b). The dashed lines depict selected central wavelengths used by NASA's aerosol retrieval (675, 745, 869, and 997 nm). The cyan shading marks the ranges corresponding to ± the FWHM of the OMPS-LP instrument around the central wavelengths of NASA's aerosol retrieval.

To investigate the sensitivity of the OMPS-LP V2.1 aerosol retrieval to changes in the vertical distribution of the aerosol extinction coefficient, averaging kernels (see Eq. 4) obtained at different wavelengths were analyzed for an example OMPS-LP measurement performed on 6 January 2018 at 15:04:37 UTC, with the following tangent point ground coordinates: 51° S, 14° W. The results are presented in Fig. 2. The averaging kernels (AKs) for wavelengths of 675, 745, and 869 nm are presented in panel (a) of the figure. For clarity, only every third AK between 9.5 and 33.5 km is plotted. It can be seen that the AKs for 675 nm (red) are always smaller than those for 745 nm (green) and 869 nm (blue) and that they significantly degrade below 15 km altitude. This is evidence of a lower sensitivity of the retrieval at 675 nm compared to that at the other two wavelengths at all altitudes. At the lowest altitude shown in the figure (9.5 km), the AK for 675 nm is very small, and its peak is strongly displaced from the nominal altitude, which is an indication of a nearly complete loss of sensitivity below 10 km altitude. Comparing the AKs for 745 and 869 nm, we see that the former are only slightly lower than the latter at almost all altitudes (and even slightly higher above 30 km altitude). For both wavelengths, AKs peak at their nominal altitudes.

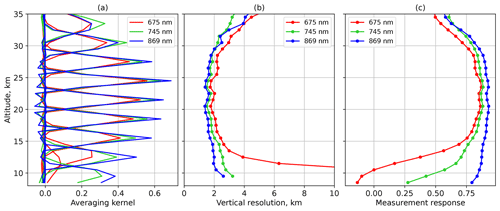
Figure 2 Characteristics of the OMPS-LP V2.1 aerosol extinction coefficient retrieval from the University of Bremen for different wavelengths. (a) Averaging kernels. (b) Vertical resolution. (c) Measurement response.

Figure 2b shows the vertical resolution of the retrieval for different wavelengths. It is calculated as the reciprocal of the diagonal elements of the AK matrix multiplied by the step of the retrieval's vertical grid (1 km in our case). Confirming the conclusions drawn from Fig. 2a, the vertical resolution of the retrieval at 675 nm is only a bit lower compared to that at the two other wavelengths down to 13.5 km altitude and starts to degrade rapidly below this altitude, exceeding the value of 10 km at an altitude level of 11.5 km. The vertical resolution of the retrieval at 745 nm is slightly worse than that at 869 nm below 30 km altitude, but it is slightly better above that altitude. A similar behavior is seen for the measurement response shown in Fig. 2c and calculated as the sum of the elements in the AK matrix rows. The measurement response for the retrieval at 869 nm is close to the ideal value of 1, with values greater than 0.75 below 31.5 km altitude. At both 675 and 745 nm, the measurement response starts to degrade at lower altitudes, crossing the 0.5 level at about 13 km altitude for the former wavelength and at about 10 km altitude for the latter wavelength.

From the discussion in this section, we consider the wavelength of 869 nm to be optimal for the retrieval of vertical profiles of the stratospheric aerosol extinction coefficient from limb-scatter measurements performed by the OMPS-LP instrument.

5 Main advantages of the new retrieval algorithm

Several advantages are associated with the normalization of limb radiance by solar irradiance, as implemented in the new V2.1 retrieval from the University of Bremen, compared to normalization by limb measurement at the reference tangent height, as used in the precursor V1.0.9 retrieval described by Malinina et al. (2021) and in other limb-scatter stratospheric aerosol retrievals (Bourassa et al., 2008; von Savigny et al., 2015; Taha et al., 2021). First, limb measurements at upper tangent heights generally have lower signal-to-noise ratios and are more contaminated by stray light compared to measurements at lower tangent heights. Thus, dividing all measurements by the measurement at an upper tangent height generally degrades the quality of all data used in the retrieval. Second, the presence of an unknown signal from aerosol scattering at the reference tangent height might bias the retrieval if the a priori aerosol content used in the forward model significantly differs from the real aerosol content. In addition, the reference tangent height is often used to estimate the effective Lambertian albedo of the underlying scene, and a wrong assumption about the aerosol scattering contribution at this tangent height might bias the retrieved value of the effective albedo, which might additionally bias the retrieved vertical profile of the aerosol extinction coefficient.

The increase in measurement noise when using the reference tangent height normalization approach is clearly seen in the example of SCIAMACHY measurements shown in Fig. 1. The spectra in panel (a) of the figure are obviously noisier compared to those in panel (b), especially for the longer wavelengths. Although results from SCIAMACHY cannot be directly transferred to other instruments, a degradation in measurement quality with increasing tangent height is rather common for limb-scatter observations.

To illustrate the dependence of the retrievals using different normalization approaches on the a priori aerosol extinction profile, we performed retrievals for three example measurements of OMPS-LP using three different a priori profiles: the standard one, one halved for all altitudes, and one doubled for all altitudes. The results of this investigation are shown in Fig. 3. We note that all results shown in this figure were obtained with the V2.1 retrieval using normalization to either the reference tangent height or solar irradiance; all other settings remained unchanged. The figure reveals that the results obtained using normalization to the reference tangent height (Fig. 3a–c) strongly depend on the a priori profile used in the retrieval. We note that the bulk effect comes from the scaling of the a priori profile at the altitude level corresponding to the reference tangent height – the results obtained by scaling the a priori profile only at and above the reference tangent height (as well as only below it) are shown in Fig. S2. In contrast, the retrieval results obtained using normalization to solar irradiance (Fig. 3d–f) are almost independent of the a priori profile. In this case, small deviations between the results obtained for different a priori profiles are only seen below about 12.5 km altitude. The results for altitudes above 30 km are shown in Fig. S3. For comparison, results obtained with the V1.0.9 retrieval (using the same Level-1 data as in V2.1) are shown in Fig. S4. The values for the effective surface albedo retrieved for different test cases are shown in Table S1 in the Supplement.

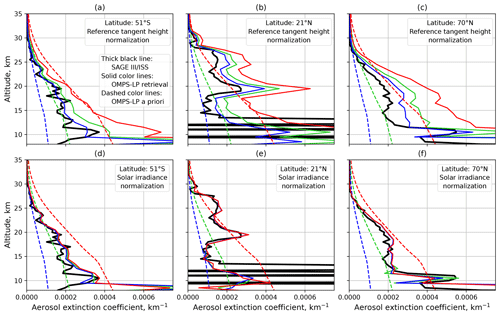
Figure 3 Dependence of the retrieval results on the a priori aerosol extinction profile for the University of Bremen retrieval using normalization to a limb measurement at the reference tangent height (a–c) and normalization to the solar irradiance spectrum (d–f). Comparisons are made for three example OMPS-LP measurements: (a, d) 6 January 2018 (15:04:37 UTC; 51° S, 14° W), (b, e) 22 January 2018 (10:20:45 UTC; 22° N, 43° E), and (c, f) 25 July 2018 (04:39:29 UTC; 70° N, 107° E).

The dependence of the V1.0.9 retrieval, which uses reference tangent height normalization, on the aerosol amount around the tangent height of the reference measurement results in retrieval artifacts if a strong aerosol plume resides in this altitude range. This effect is illustrated in Fig. 4, where retrieval results are presented for an OMPS-LP single orbit that occurred shortly after the Hunga Tonga–Hunga Ha′apai eruption (January 2022). We note that here and below we use the original V1.0.9 results rather than any adjustments of V2.1 to V1.0.9 settings. It can be seen from the figure that the V1.0.9 retrieval (Fig. 4a) shows unrealistically low values below the aerosol plume located in the reference tangent height region (38.5 km). As shown in Fig. 4b, this artifact is not present in the V2.1 retrieval, which uses normalization to solar irradiance. There is still a range of quite small values below the aerosol plume, as seen in panel (b) of the figure. For now, we cannot definitely say whether this represents a real minimum in aerosol extinction or a remaining retrieval artifact. It can also be seen from the figure that the V2.1 retrieval shows generally lower values than the V1.0.9 retrieval. As discussed below, these lower values are in better agreement with reference measurements, which demonstrates another advantage of the new approach.

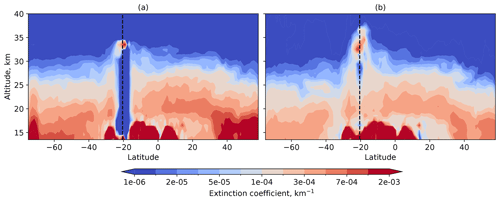
Figure 4 Aerosol extinction coefficient at 869 nm retrieved from OMPS-LP measurements during orbit 52974 on 17 January 2022. Panel (a) shows results from V1.0.9, which uses normalization to the reference tangent height. Panel (b) shows results from V2.1, which uses normalization to the solar irradiance spectrum. Dashed lines mark the location of the Hunga Tonga–Hunga Ha′apai volcano.

6 Comparison with other datasets

To assess the quality of the new retrieval and demonstrate the achieved improvement, the results of the OMPS-LP V2.1 and V1.0.9 retrievals were compared to the colocated data from SAGE III/ISS. The criteria for selecting colocated pairs of measurements included maximum differences of 5° in latitude, 10° in longitude, and 12 h. For this comparison, no cloud filtering was applied to either data product. The comparison of aerosol extinction coefficients obtained at 869 nm from both instruments for the year 2018 (arbitrarily selected) across different latitude bands is presented in Fig. 5. The relative difference was calculated as (OMPS-LP − SAGE_III) $/$ SAGE_III. The comparisons were carried out independently for SAGE III/ISS sunset measurements (solid lines) and SAGE III/ISS sunrise measurements (dashed lines). For clarity, the standard deviation of the differences is shown only for colocations with the SAGE III/ISS sunset measurements. The figure demonstrates that the V2.1 retrieval generally shows values lower than those from the V1.0.9 retrieval, significantly reducing the differences with the SAGE III/ISS results for most of the latitude bands. In the tropics, agreement with SAGE III/ISS data is similar for the results from both V2.1 and V1.0.9, with differences changing from mostly positive for V1.0.9 to mostly negative for V2.1. Across most of the latitude bands, the OMPS-LP V2.1 retrieval agrees within 25 % with SAGE III/ISS data in the 18–30 km altitude range. Only at high southern latitudes does the agreement start to degrade already above 27 km altitude (see Fig. 5a). In the lower stratosphere, good agreement is observed down to about 13 km altitude in the northern extratropics (about 16 km altitude for sunrise colocations at northern midlatitudes; see Fig. 5d and e), down to 15 km altitude at southern midlatitudes (Fig. 5b), and down to 8 (12) km altitude for sunset (sunrise) colocations at high southern latitudes (Fig. 5a).

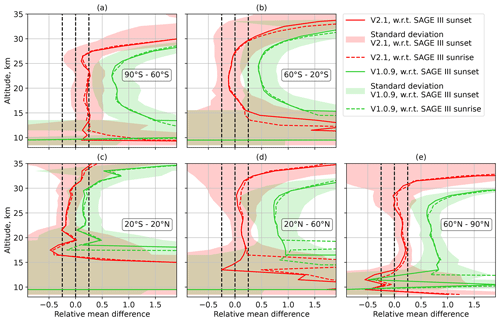
Figure 5 Comparison of OMPS-LP V2.1 and V1.0.9 retrieval results with colocated SAGE III/ISS data for 2018 across different latitude bands. The vertical dashed black lines mark the 0 % and ±25 % levels. Note that “w.r.t.” stands for “with respect to”.

Figure 6 presents the relative mean differences between the aerosol extinction coefficients at 869 nm retrieved from OMPS-LP and SAGE III/ISS observations for different years. Only V2.1 of the OMPS-LP retrieval is shown. The figure reveals that differences between OMPS-LP and SAGE III/ISS data are very similar for most of the years and latitude bands. Exceptions are seen in (i) the tropics and southern extratropics in 2022 (Fig. 6a–c), when the influence of the Hunga Tonga–Hunga Ha′apai eruption was the strongest; (ii) the southern extratropics (Fig. 6a and b) in 2020, likely explained by the strong aerosol pollution from Australian wildfires; and (iii) the high northern latitudes (Fig. 6e) in 2019, most probably because of the Raikoke eruption. In general, the differences during these anomalous years are more negative, indicating that the OMPS-LP V2.1 aerosol extinction product is lower than the SAGE III/ISS data when there is a higher aerosol load in the stratosphere.

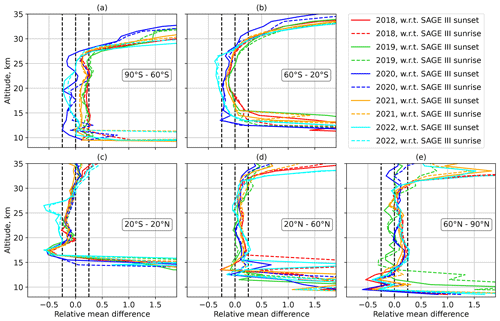
Figure 6 Comparison of the OMPS-LP V2.1 retrieval results with colocated SAGE III/ISS data for different years and different latitude bands. The vertical dashed black lines mark the 0 % and ±25 % levels.

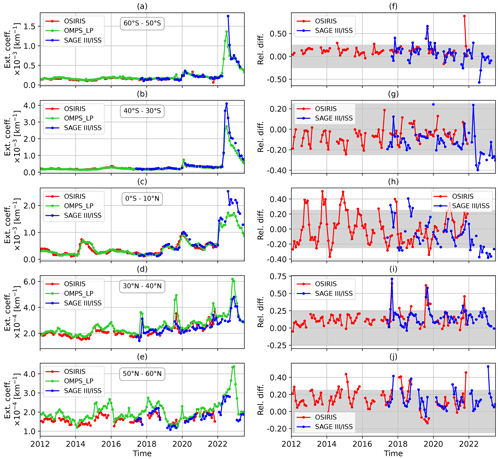
To evaluate the time evolution of the stratospheric aerosol extinction coefficients in more detail, monthly zonal-mean time series from OMPS-LP V2.1 retrievals were compared with the results from the SAGE III/ISS and OSIRIS instruments. A rough cloud filter was applied when calculating the monthly zonal-mean OMPS-LP V2.1 data by rejecting extinction coefficient values larger than 0.1. To perform the comparison, the OMPS-LP data were converted to a wavelength of 750 nm using the Ångström exponent, calculated for 750 and 869 nm using Mie theory. The calculations were performed assuming a fixed particle size distribution with a median radius of 0.08 µm and a standard deviation in logarithmic space of 1.6 (the same values as those used in the retrieval; see Sect. 3). This results in a constant conversion factor of 1.477 when transforming data from 869 to 750 nm. For SAGE III/ISS, the aerosol extinction coefficients at 756 nm were used without any adjustments. As mentioned in Sect. 2, the University of Saskatchewan team does not recommend the usage of OSIRIS data after 2021. For this reason, the comparison with OSIRIS is limited to the 2012–2021 period.

A comparison of the monthly zonal-mean aerosol extinction coefficients at 750 nm obtained from OMPS-LP (V2.1), OSIRIS, and SAGE III/ISS data at an altitude of 21.5 km is shown in Fig. 7 for different latitude ranges. Panels (a)–(e) show the extinction coefficient time series, while panels (f)–(j) depict the relative differences between the respective time series and OMPS-LP data, calculated as $\mathrm{2}\times \left(\text{OMPS-LP}-\text{instrument}\right)/\left(\text{OMPS-LP}+\text{instrument}\right)$. Generally, good agreement between the results from different instruments is observed, with relative differences occurring mostly within ±25 %, which is consistent with the results presented in Figs. 5 and 6. After the Hunga Tonga–Hunga Ha′apai eruption, the agreement between the OMPS-LP and SAGE III/ISS results is worse in the 40–30° S (Fig. 7b and g) and 0–10° N (Fig. 7c and h) latitude bands. Here, OMPS-LP values generally tend to be smaller than SAGE III/ISS results. In the 50–60° N latitude band (Fig. 7e and j), OMPS-LP shows increased aerosol loading at the beginning of 2023, which is not seen in the SAGE III/ISS data. This might be caused by the coarser sampling of the latter instrument. In general, OMPS-LP results in this latitude band are slightly higher than those from SAGE III/ISS and OSIRIS. We note that OMPS-LP retrievals in this latitude band have the strongest sensitivity to aerosol particle size distribution due to the small scattering angle. In the 30–40° N (Fig. 7d and i) and 0–10° N (Fig. 7c and h) latitude bands, OMPS-LP data seem to show a somewhat stronger seasonal cycle compared to both OSIRIS and SAGE III/ISS measurements, and the pattern of the relative difference seems to be dominated by the seasonal cycle. The observed difference in the seasonal cycle is most likely caused by the dependence of the retrieval error on the scattering angle. This dependence is associated with the assumption of a fixed aerosol particle size distribution. As expected, for small scattering angles, which occur at middle and high northern latitudes in the OMPS-LP observational geometry, this dependence is stronger, resulting in pronounced seasonal variation in the differences between the results from OMPS-LP and those from SAGE III/ISS and OSIRIS. We note that the OSIRIS instrument observes the atmosphere at a narrower range of scattering angles (60–120°) compared to OMPS-LP (25–160°).

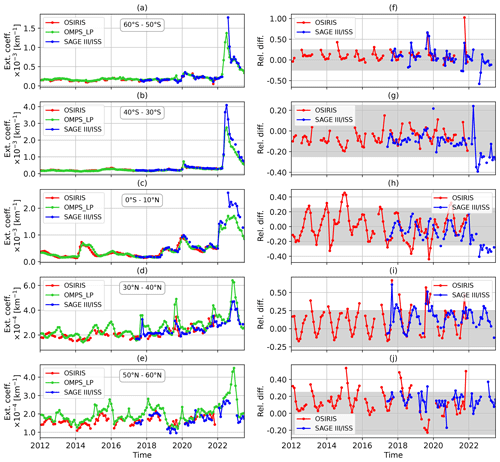
Figure 7 Comparison of monthly zonal-mean aerosol extinction coefficients at 750 nm from OMPS-LP V2.1, OSIRIS, and SAGE III/ISS data at an altitude of 21.5 km. (a–e) Aerosol extinction coefficient time series. (f–j) Relative differences. The rows show the results for different latitude bands: (a, f) 60–50° S, (b, g) 40–30° S, (c, h) 0–10° N, (d, i) 30–40° N, and (e, j) 50–60° N. Gray areas mark the ±25 % range. Ext. coeff.: extinction coefficient. Rel. diff.: relative difference.

To analyze the influence of seasonal variations, deseasonalized time series were also investigated. These were obtained by calculating the absolute anomalies of the time series (by subtracting the mean value for each month in the considered observation period from the corresponding monthly value) and then adding a mean value (specific to each instrument) calculated over all months in the observational period. The comparison results for the deseasonalized time series are presented in Fig. 8. The figure reveals that the differences are generally lower for the deseasonalized time series, especially in the 30–40° N latitude band (Fig. 8d and i). In contrast, the oscillating structure seen in the 0–10° N latitude band (Fig. 8c and h) before 2016 is not removed by the deseasonalizing procedure, indicating that these differences are most probably not related to seasonal variations. We note, however, that due to orbit drift, the Equator crossing time of OSIRIS changes over time. Therefore, depending on the time and latitude, measurements at either the ascending node or the descending node of the orbit (having quite different scattering angles) are performed in the illuminated part of the atmosphere. Occasionally, measurements at both the ascending and descending nodes might be performed in the illuminated part of the atmosphere, and their results are averaged in the data product. This might influence the efficiency of the deseasonalizing procedure.

Figure 8 Same as Fig. 7 but for deseasonalized time series.

Figure 9 presents an overview of the relative differences between the OMPS-LP V2.1 and OSIRIS data as a function of altitude and latitude. The differences were obtained by averaging all data from the 2012–2021 period. Below 60° latitude, in the altitude range between the tropopause and about 30 km altitude, the differences between the results from both instruments are mostly within 10 %. In contrast, higher differences are observed at latitudes above 60° below 20 km altitude in the Northern Hemisphere and throughout the entire altitude range (with a maximum around 30 km altitude) in the Southern Hemisphere. These differences might be related to the sampling issues of both instruments at high latitudes and to retrieval issues associated with high surface albedo and large solar zenith angles. As expected, high differences in the troposphere are observed due to the different treatments of clouds.

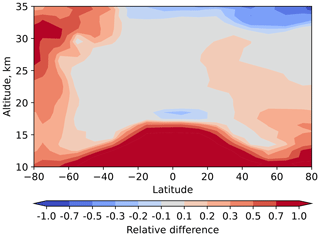
Figure 9 Comparison of zonal-mean aerosol extinction coefficients at 750 nm obtained from OMPS-LP V2.1 and OSIRIS data (2012–2021).

Relative differences between the OMPS-LP V2.1 and OSIRIS data are shown in Fig. 10 as functions of altitude and time for three different latitude ranges: southern midlatitudes (60–20° S), the tropics (20° S–20° N), and northern midlatitudes (20–60° N). Fig. 10a–c show the results for original time series, while Fig. 10d–f present the differences for deseasonalized time series. At southern midlatitudes (Fig. 10a and d), both datasets typically agree within 10 % in the altitude region between 20 and 27 km. Somewhat higher differences are seen for 2020, when stratospheric aerosol loading was increased as a result of Australian wildfires. Above 27 km altitude and below 20 km altitude, pronounced seasonal variations are seen in the relative differences, with areas of higher differences grouping around the gaps in OSIRIS observations during the austral winter months. Deseasonalizing the time series reduces the differences below 21 km altitude to less than 20 %, but it does not seem to have any effect above 27 km altitude. In the tropics (Fig. 10b and e), the results from OMPS-LP and OSIRIS observations typically agree within 10 %–20 % in the altitude region between 20 and 33 km. For the deseasonalized time series, the differences are slightly lower; however, the general picture remains almost the same. At northern midlatitudes (Fig. 10c and f), stronger seasonal oscillations are seen in the relative differences, with areas of higher differences mostly grouped around the gaps in OSIRIS observations during the boreal winter months. Somewhat higher differences are noted at the end of 2017 and the beginning of 2018 and are most likely associated with forest fires in British Columbia. For the deseasonalized time series, the differences are largely smoothed and do not show any pronounced peaks, with the exception of the last months of the time series. Overall, the OMPS-LP results are positively biased with respect to the OSIRIS data, but the relative differences do not typically exceed 20 % in the altitude range between 15 and 30 km.

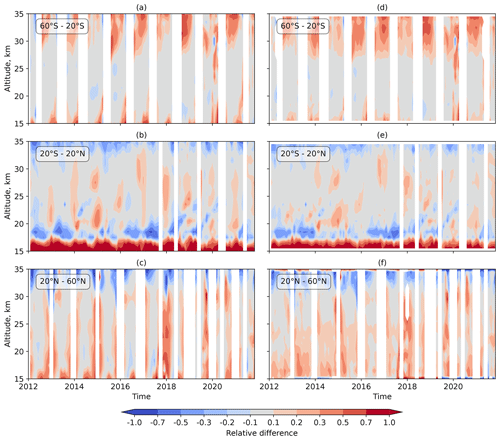
Figure 10 Relative differences in monthly zonal-mean aerosol extinction coefficients at 750 nm obtained from OMPS-LP V2.1 and OSIRIS data for different latitude ranges: (a, d) 60–20° S, (b, e) 20° S–20° N, and (c, f) 20–60° N. (a–c) Aerosol extinction coefficient time series. (d–f) Deseasonalized time series.

7 Evolution of the aerosol plume from the Hunga Tonga–Hunga Ha′apai eruption

In this section, the newly generated OMPS-LP V2.1 aerosol extinction coefficient product is used to investigate the evolution of the aerosol plume after the Hunga Tonga–Hunga Ha′apai eruption in January 2022. For this purpose, a dataset of zonal-mean aerosol extinction coefficients at 869 nm with an increased temporal resolution (10 d mean) was created. The altitude–time cross sections of the aerosol extinction coefficient for different latitude ranges are shown in Fig. 11a–c. In the tropics (Fig. 11a), the aerosol extinction coefficient increases right after the strongest Hunga Tonga–Hunga Ha′apai eruption, which occurred on 15 January 2022 (marked by the vertical dashed line in the panel). A significant perturbation in the vertical distribution of the extinction coefficient is seen up to about 33 km. It should be noted here that the extinction observed right after the eruption is strongly affected by the ash plume and ice clouds, which may result in high retrieval errors caused by a wrong assumption about the aerosol composition in the Mie scattering calculations of the forward model. In about one time step, i.e., 10 d, a strong increase in the aerosol extinction coefficient is observed, which is most probably caused by the creation of a significant amount of sulfate aerosol from the sulfur injected into the stratosphere by the volcanic eruption. As reported, for example, by Legras et al. (2022), ash and ice clouds were rapidly removed within the first day after the eruption, while the conversion of SO₂ to sulfates started immediately after the eruption. Thus, we can assume that from the second time bin after the eruption, the extinction by sulfate aerosols dominates, and the retrieval results are robust. It can be seen in Fig. 11a that the maximum of the extinction coefficient is observed between about 21 and 26 km. The plume remained stable until about the middle of April 2022 and then started sinking. Above about 22 km, the values relaxed quite rapidly to quasi-stationary levels, which are significantly higher than those observed before the eruption.

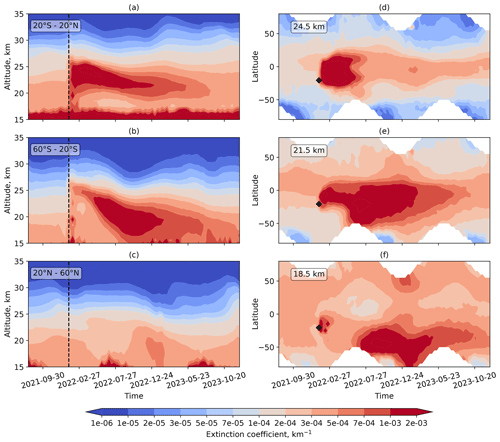
Figure 11 Evolution of the aerosol plume across different latitude bands and at different altitude levels. (a–c) 10 d zonal-mean aerosol extinction coefficients at 869 nm across different latitude bands: (a) 20° S–20° N, (b) 60–20° S, and (c) 20–60° N. The dashed black line marks the time of the strongest Hunga Tonga–Hunga Ha'apai eruption (15 January 2022). (d–f) 10 d zonal-mean aerosol extinction coefficients at 869 nm at different altitude layers: (d) 24.5, (e) 21.5, and (f) 18.5 km. A black rhombus marks the position of the Hunga Tonga–Hunga Ha′apai volcano and the date of its strongest eruption. OMPS-LP V2.1 data were used for all panels.

At southern midlatitudes, as shown in Fig. 11b, a similar immediate increase in the aerosol extinction coefficient is observed after the Hunga Tonga–Hunga Ha′apai eruption, as seen in the tropics. However, relatively few sulfate aerosols are observed 10–20 d after the eruption. A stronger increase in the aerosol extinction coefficient is seen only after the middle of April, when the aerosol plume in the tropics started sinking and was transported into the southern midlatitudes. Thereafter, the evolution of the plume was quite similar to that observed in the tropics. The plume sank, and the values near the upper boundary of the plume relaxed quite rapidly to quasi-stationary elevated values. At northern midlatitudes, as shown in Fig. 11c, no immediate response to the Hunga Tonga–Hunga Ha′apai eruption is observed. Elevated values have been observed at lower altitudes since November 2022, most likely caused by the transport of Hunga Tonga–Hunga Ha′apai aerosols from the tropics. As discussed below, this statement is confirmed by the evolution of the aerosol plume depicted in the latitude–time cross-section plot at 21.5 km altitude (Fig. 11e).

In Fig. 11d–f, the latitude–time cross sections of the aerosol extinction coefficient for different altitudes are shown. The latitude of the Hunga Tonga–Hunga Ha′apai volcano and the date of its strongest eruption are marked by a black rhombus. At 24.5 km altitude (Fig. 11d), large amounts of aerosols were created about 10 d after the eruption. The strongly elevated aerosol plume formed over the entire tropical region and partially penetrated into the southern subtropics. In the first 4 months after the eruption, the plume did not extend much in the latitudinal direction and resided mainly in the tropical region. Thereafter, the aerosol plume began to propagate to the southern midlatitudes. From June 2022, the aerosol extinction coefficient started to decrease rapidly, reaching a quasi-stationary elevated level at the end of July. In spring 2023, the plume began to disappear in the southern subtropics and at southern midlatitudes but remained stable until the end of the analyzed record (December 2023) in the tropics.

At 21.5 km altitude (Fig. 11e), the aerosol plume was localized in the tropics during the first 3 months after the eruption. In May 2022, the plume rapidly propagated southward and spread over the entire region of the southern midlatitudes. No propagation to the northern extratropics was seen until October 2022. Thereafter, the plume spread into the Northern Hemisphere.

At 18.5 km altitude (Fig. 11f), a strong increase in extinction is seen right after the eruption. Elevated values can only be observed until the end of March, before the concentration fell back to pre-eruption levels. From the beginning of June 2022, high aerosol amounts that propagated to the southern midlatitudes from the tropics at around 21.5 km altitude sank to 18.5 km altitude, leading to a strong increase in aerosol extinction across almost the entire Southern Hemisphere. These increased values resided at this altitude until May 2023. Thereafter, a relaxation process began. At the end of the analyzed period (December 2023), some increase in the aerosol extinction coefficient is still observed. In the Northern Hemisphere, increased values of the aerosol extinction coefficient are observed at the end of 2022 and the beginning of 2023. It is, however, unclear whether these values are related to the Hunga Tonga–Hunga Ha′apai eruption plume.

The results presented in this section are in good agreement with the findings of other studies on the evolution of stratospheric aerosols after the Hunga Tonga–Hunga Ha′apai volcanic eruption. For example, using ground-based lidar, Baron et al. (2023) observed a strong aerosol plume with a maximum just below 30 km on 21 January 2022 (5 d after the eruption) over the island of Réunion (21° S, 55° E). Within the next few days, aerosol plumes with altitudes decreasing to about 20 km were observed. This agrees with the aerosol extinction peak observed at altitudes of up to about 30 km and the increase in aerosols over the entire altitude range shortly after the eruption, as seen in Fig. 11a and b. Analyzing SAGE III/ISS data, Duchamp et al. (2023) reported a strong increase in aerosol extinction shortly after the eruption in the 30–10° S and 10° S–10° N latitude ranges, with peak altitudes ranging from 20 to 26 km. The maximum altitude of the plume remained stable until May–June 2022, after which the plume began descending. These findings are in agreement with the results presented in Fig. 11a. At southern midlatitudes (50–30° S), Duchamp et al. (2023) reported a strong increase in aerosol extinction starting around May 2022, with peak altitudes descending from about 24 to 18 km and the onset of relaxation occurring after January 2023. A very similar behavior is observed in Fig. 11b. In accordance with the plots presented by Taha et al. (2022), who analyzed the OMPS-LP data (NASA retrieval), the aerosol plume in the tropics resided between altitudes of about 19 and 26 km during the first 5 months after the eruption. No significant changes in its vertical extent or maximum altitude were observed. This agrees very well with our findings shown in Fig. 11a. Furthermore, Taha et al. (2022) showed that in the first 5 months, the plume was always south of 20° N and started propagating south of 30° S about 4 months after the eruption. This behavior also agrees well with our findings (Fig. 11d–f).

8 Conclusions

In this study, we have introduced a new retrieval algorithm developed to obtain vertical distributions of the aerosol extinction coefficient from limb-scatter measurements of the OMPS-LP instrument. The main change with respect to the algorithms used by other scientific groups, as well as with respect to the previous version of the University of Bremen retrieval, is the normalization of limb measurements by solar irradiance rather than by a limb measurement obtained at an upper tangent height. As normalizing to solar irradiance increases the sensitivity of the retrieval to the reflectance of the underlying scene, an optimized scheme for deriving the effective Lambertian surface albedo has been implemented.

The employed normalization approach makes the retrieval results from the OMPS-LP V2.1 algorithm almost independent of the prior profile of the aerosol extinction coefficient used in the retrieval. In contrast, adequate knowledge of the aerosol extinction at altitudes around the normalization tangent height is crucial for algorithms using normalization to a limb measurement at an upper tangent height. Furthermore, as the quality of limb measurements decreases with increasing tangent height and the influence of stray light increases, skipping the process of normalization to an upper tangent height enables us to extend the vertical range of the retrieval to 8.5–48 km, compared with the 12.5–37.5 km retrieval range of the previous version of the University of Bremen retrieval, published by Malinina et al. (2021). This makes the retrieval applicable to scenes with high aerosol plume elevation, as was the case after the Hunga Tonga–Hunga Ha′apai eruption in January 2022.

The new dataset of the OMPS-LP V2.1 aerosol extinction coefficient, covering the period from February 2012 to December 2023, was verified using data from the SAGE III/ISS solar occultation and OSIRIS limb-scatter instruments. Comparison of the newly generated OMPS-LP V2.1 data product with that of SAGE III/ISS shows good overall agreement, typically within 25 %, between 15 and 30 km. Similarly, the comparison with OSIRIS data generally shows good agreement in terms of temporal behavior and values. Within strong aerosol plumes, larger discrepancies between the data from different instruments (OMPS-LP, OSIRIS, and SAGE III/ISS) were identified. This is most probably related to the assumption about the aerosol particle size distribution used in the limb-scatter retrievals (OMPS-LP and OSIRIS), which was originally selected for background aerosol conditions and might be suboptimal for strong volcanic eruption conditions.

The OMPS-LP V2.1 aerosol extinction coefficient dataset was used to investigate the evolution of the aerosol plume after the Hunga Tonga–Hunga Ha′apai eruption. The perturbation of the aerosol layer is seen at altitudes of up to about 33 km. A strong increase in aerosol loading is seen at altitudes of up to 27 km. About 2 weeks after the eruption, the maximum aerosol absorption is seen in the tropics between 21 and 26 km altitude. About 4 months after the eruption, the aerosol plume started rapidly sinking. At higher altitudes (23–25 km), the plume mainly resided in the tropics, while at lower altitudes (around 18 km), the aerosol was transported southward and spread over almost the entire Southern Hemisphere. At higher altitudes, relaxation had already started, but by the end of the analyzed period (December 2023), the aerosol level in the tropics still remained elevated in comparison to the pre-eruption level.

The OMPS-LP V2.1 aerosol extinction coefficient dataset described in this paper is available for the scientific community via the web page of the University of Bremen (see the “Data availability” section below).