Impact of water uptake on fluorescence of atmospheric aerosols: insights from Mie–Raman–fluorescence lidar measurements

This study investigates the impact of water uptake by particles during hygroscopic growth on aerosol fluorescence properties, using multiwavelength Mie–Raman–fluorescence lidar measurements conducted at the ATmospheric Observation at LiLLe (ATOLL) observatory (Laboratoire d'Optique Atmosphérique, University of Lille) between 2021 and 2024. During certain episodes, we observed a systematic height-dependent decrease in the fluorescence backscattering coefficient within the well-mixed planetary boundary layer. This phenomenon begins at relatively low relative humidity (RH ∼ 50 %) simultaneously with a decrease in the particle depolarization ratio. However, the rapid growth of the aerosol backscattering coefficient at high RH is not mirrored by the same rate of fluorescence reduction. This distinct behavior suggests a nonlinear relationship between water uptake and fluorescence suppression, likely indicating that water-induced quenching effects operate independently of bulk hygroscopic growth. Furthermore, we demonstrate the capability to retrieve particle volume and surface area density from single-wavelength extinction coefficients during strong hygroscopic growth episodes, validated against full 3β+2α lidar measurements. The values of the conversion factors for urban aerosol and smoke at 355 and 532 nm, together with associated uncertainties, are presented.

1 Introduction

Atmospheric aerosols are the subject of intense study due to their role in the planet's radiation balance and their potential impact on the environment. To characterize the vertical distribution of aerosol loading, multiwavelength Mie–Raman and high-spectral-resolution lidars are widely used (e.g., Burton et al., 2012; Floutsi et al., 2023; Haarig et al., 2025, and references therein). Studies conducted over the past 2 decades have demonstrated significant progress in retrieving particle microphysical properties such as volume density, effective radius, and the complex refractive index (RI) from so-called 3β+2α observations, which include three aerosol backscattering, β, and two extinction, α, coefficients (Veselovskii et al., 2002; Kolgotin et al., 2018, 2023, 2025; Chang et al., 2022; Zhou et al., 2024).

The 3β+2α dataset is not always available. However, if the aerosol type is identified, the particle volume and surface area density can be estimated from the aerosol extinction coefficient at a single wavelength, λ, using corresponding extinction-to-volume and extinction-to-surface area conversion factors. This approach was proposed by Mamouri and Ansmann (2016, 2017) and further developed by Ansmann et al. (2021), where optical depths and column-integrated volumes provided by the network of sun photometers (AERONET) were used to determine conversion factors for pollution, smoke, and dust at various locations. Similarly, He et al. (2023) reported conversion factors for dust of different origins. However, the column-integrated values provided by AERONET do not account for the possible presence of different aerosol types at different altitudes. In contrast, multiwavelength lidar measurements allow for the retrieval of vertical profiles of particle volume and surface area density, enabling the calculation of conversion factors within specific height intervals that correspond to distinct aerosol types.

An important factor influencing the physical properties of aerosols is relative humidity (RH). Many aerosol types, such as sulfates, organic carbon, and sea salt, increase in size at high RH, accompanied by a simultaneous decrease in their complex refractive index. Lidars, with their capability to assess particle properties under ambient conditions at RH levels close to saturation, offer unique opportunities for studying the particle hygroscopic growth. Lidar measurements are typically used to determine the dependence of the aerosol backscattering coefficient on RH within well-mixed layers (Feingold and Morley, 2003; Fernández et al., 2015; Granados-Muñoz et al., 2015; Haarig et al., 2017; Navas-Guzmán et al., 2019; Chen et al., 2019; Pérez-Ramírez et al., 2021; Sicard et al., 2022; Miri et al., 2024). The use of aerosol extinction coefficients in hygroscopic growth studies is less common (Veselovskii et al., 2009; Dawson et al., 2020; Haarig et al., 2025) because β can be retrieved from lower altitudes and with greater accuracy compared to α. Multiwavelength lidar measurements further extend hygroscopic growth studies by enabling the analysis of particle volume, surface area, and the refractive index as a function of RH. This, in turn, allows for the evaluation of extinction-to-volume and extinction-to-surface area conversion factors in the presence of hygroscopic growth.

The addition of a fluorescence channel to Mie–Raman lidar (Veselovskii et al., 2020) opens new opportunities for particle characterization. If hygroscopic growth has no impact on aerosol fluorescence properties, fluorescence may serve as a proxy for evaluating the volume of dry aerosol. However, laboratory studies demonstrate that fluorescence can be suppressed (“quenched”) by interactions with other molecules through processes of collision and energy transfer (Lakowicz, 2006), leading to reduction in emission intensity. In particular, water molecules can efficiently quench fluorescence of organic fluorophores as reported by Dobretsov et al. (2014) and Maillard et al. (2021). Meanwhile, the extent to which such quenching occurs in atmospheric aerosols during hygroscopic growth remains an open question (Gast et al., 2025; Reichardt et al., 2025). Fluorescence quenching is expected to depend on aerosol composition, phase state, and the presence of organic coating, highlighting the need to analyze a diverse set of measurement episodes.

The Mie–Raman–fluorescence lidar has been operational at the ATmospheric Observation at LiLLe (ATOLL) instrumentation site at the Laboratoire d'Optique Atmosphérique, University of Lille, since 2020, accumulating a large volume of observations. In this paper, we focus on several episodes of hygroscopic growth within the planetary boundary layer (PBL), investigating potential evidence of fluorescence quenching by water uptake. Additionally, we analyze extinction-to-volume and extinction-to-surface area conversion factors in the presence of hygroscopic growth. We begin with a description of the lidar system and data analysis approach (Sect. 2). In Sect. 3, a numerical simulation is performed to investigate the behavior of particle volume and surface area density as a function of the particle extinction coefficient for different refractive indices and different particle size distribution parameters. In the first results section (Sect. 4), we present case studies demonstrating that, in certain episodes, water uptake leads to fluorescence quenching. In Sect. 5, we analyze the conversion factors in the presence of the particle hygroscopic growth. The paper concludes with a summary of our findings in the conclusion section.

2 Instrumentation and methodology

The multiwavelength Mie–Raman–fluorescence lidar LIlle Lidar AtmosphereS (LILAS) operates using a tripled Nd:YAG laser with a 20 Hz repetition rate and a pulse energy of 90 mJ at 355 nm. Backscattered light is collected by a 400 mm aperture Newtonian telescope. Detailed information on the system parameters and data analysis methodology can be found in our previous publications (e.g. Veselovskii et al., 2020). Measurements were performed primarily in the vertical direction. In cases where measurements were taken at an angle, this information is provided in the figure captions. LILAS is designed to detect elastic and Raman backscattering, enabling the so-called $\mathrm{3}\mathit{\beta }+\mathrm{2}\mathit{\alpha }+\mathrm{3}\mathit{\delta }$ data configuration. This includes three particle backscattering coefficients (β₃₅₅, β₅₃₂, β₁₀₆₄), two extinction coefficients (α₃₅₅, α₅₃₂), and three particle linear depolarization ratios (δ₃₅₅, δ₅₃₂, δ₁₀₆₄). Additionally, the water vapor mixing ratio (WVMR) is derived from the water vapor Raman measurements. The lidar also profiles the laser-induced fluorescence of aerosol particles within a spectral interval centered at 466 nm with 44 nm bandwidth. The fluorescence backscattering coefficient, β_F, and the fluorescence capacity, $G_{\mathrm{F}}=\frac{{\mathit{\beta }}_{\mathrm{F}}}{{\mathit{\beta }}_{\mathrm{532}}}$, calculated from these measurements facilitate aerosol classification, as described in Veselovskii et al. (2024).

The inversion of the 3β+2α lidar dataset enables the estimation of particle volume, V; surface area, S; and the refractive index, RI. In our study, we used the inversion algorithm described by Veselovskii et al. (2002). The solution search was performed within the following parameter ranges:

• a particle radius of 0.05 < r < 10 µm;

• the real part of the refractive index, 1.33 < m_R < 1.65;

• the imaginary part of the refractive index, 0 < m_I < 0.02.

The retrieval uncertainty for particle volume and surface density is estimated to be below 15 %, while it is ±0.05 for the real part of the refractive index. The uncertainty for the imaginary part is higher, reaching up to 50 %. Therefore, in the analysis of the presented measurements, only the real part of the refractive index is considered. Retrieved values of V and S along with the 3β+2α set enable the calculation of conversion factors for both aerosol extinction and backscattering coefficients, defined as $C_{\mathit{\alpha },\mathit{\lambda }}^V=\frac{V}{{\mathit{\alpha }}_{\mathit{\lambda }}}$, $C_{\mathit{\beta },\mathit{\lambda }}^V=\frac{V}{{\mathit{\beta }}_{\mathit{\lambda }}}$, $C_{\mathit{\alpha },\mathit{\lambda }}^S=\frac{S}{{\mathit{\alpha }}_{\mathit{\lambda }}}$, and $C_{\mathit{\beta },\mathit{\lambda }}^S=\frac{S}{{\mathit{\beta }}_{\mathit{\lambda }}}$. These factors allow for the estimation of V and S from a single extinction coefficient at wavelength λ, when the aerosol type is known.

To assess the effect of water uptake on fluorescence, we selected episodes where the PBL was well mixed, ensuring that aerosol composition and particle number density remained unchanged with height. A well-mixed layer was identified based on stable WVMR and potential temperature. The potential temperature was available from radiosonde measurements at the Herstmonceux (UK) and Beauvechain (Belgium) stations, located 160 and 80 km away from the observation site respectively. The relative humidity profiles were calculated using lidar-derived WVMR and temperature profiles from radiosonde data and from the Global Data Assimilation System (GDAS). Across all episodes analyzed in this work, the difference between RH profiles derived from radiosonde temperatures and temperatures from GDAS remained below 10 %.

Within the well-mixed PBL, relative humidity increases with height, leading to an increase in the aerosol extinction and backscattering coefficients. However, these coefficients respond differently to changes in RH. Water uptake reduces the particle refractive index, but the extinction coefficient is less sensitive to the refractive index changes than backscattering. As a result, during hygroscopic growth, α increases more rapidly with RH than β, causing the extinction-to-backscattering ratio (lidar ratio) to rise (Haarig et al., 2025).

Dependence of backscattering on RH can be either monotonic or deliquescent, when backscattering is unchanged up to a certain RH value, called the deliquescence point, where a phase transition occurs from solid to liquid (Carrico et al., 2003; Randriamiarisoa et al., 2006). For relative humidity exceeding the deliquescence value, the dependence of particle parameters, such as β, m_R, and r, on RH can be modeled relative to their values at some reference height, z_ref. In particular, for the backscattering coefficient, the simplified Hänel parameterization is commonly used (Hänel, 1976; Sheridan et al., 2001; Sicard et al., 2022):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathit{\beta }}{{\mathit{\beta }}_{\mathrm{ref}}}}={\left({\displaystyle \frac{\mathrm{1}-\mathrm{RH}}{\mathrm{1}-{\mathrm{RH}}_{\mathrm{ref}}}}\right)}^{-{\mathit{\gamma }}_{\mathit{\beta }}}.\end{array}$$

The subscript “ref” denotes the values of the parameters at the reference height z_ref; γ_β is the backscattering hygroscopic growth coefficient. The reference height is usually chosen at altitudes with low RH, where particles can be considered quasi-dry. However, for deliquescent particles, as mentioned, RH_ref should exceed the corresponding deliquescence point.

The size distribution of atmospheric aerosols is commonly described using a superposition of lognormal distributions, typically corresponding to three distinct modes: nucleation, accumulation, and coarse. Each mode can be characterized by its modal radius, r₀; standard deviation, σ; and number concentration, N. The increase in the modal radius with RH, assuming that σ is unchanged, can be parameterized as (Randriamiarisoa et al., 2006)

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{r_{\mathrm{0}}}{r_{\mathrm{0},\mathrm{ref}}}}={\left({\displaystyle \frac{\mathrm{1}-\mathrm{RH}}{\mathrm{1}-{\mathrm{RH}}_{\mathrm{ref}}}}\right)}^{-\mathit{\epsilon }},\end{array}$$

where ε is the size growth coefficient, which depends on the aerosol chemical composition. The volume of particles in the accumulation mode is predominant for urban aerosol and smoke, which are considered in this study. Thus, the volume of the particle relative to its value, V_ref, at the reference height is

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{V}{V_{\mathrm{ref}}}}={\left({\displaystyle \frac{r_{\mathrm{0}}}{r_{\mathrm{0},\mathrm{ref}}}}\right)}^{\mathrm{3}}={\left({\displaystyle \frac{\mathrm{1}-\mathrm{RH}}{\mathrm{1}-{\mathrm{RH}}_{\mathrm{ref}}}}\right)}^{-\mathrm{3}\mathit{\epsilon }}.\end{array}$$

The particle volume, modeled with Eq. (3), is hereafter denoted as V^mod. Assuming that total volume, V, is the sum of the volume of the dry particle and water uptake, the real part of the refractive index can be parameterized as (Randriamiarisoa et al., 2006; Raut and Chazette, 2008)

$$\begin{array}{}\text{(4)}& m_{\mathrm{R}}=m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}+\left(m_{\mathrm{R},\mathrm{ref}}-m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\right){\left({\displaystyle \frac{\mathrm{1}-\mathrm{RH}}{\mathrm{1}-{\mathrm{RH}}_{\mathrm{ref}}}}\right)}^{\mathrm{3}\mathit{\epsilon }},\end{array}$$

where $m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is the real part of the refractive index of water; the real part of the refractive index, modeled using Eq. (4), is hereafter denoted as $m_{\mathrm{R}}^{\mathrm{mod}}$. When the vertical profile of particle volume density retrieved from 3β+2α observations, V³⁺², is available, the ratio $\frac{V}{V_{\mathrm{ref}}}$ in Eq. (3) can be replaced by $\frac{V^{\mathrm{3}+\mathrm{2}}}{V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}}$, allowing us to calculate the m_R without the knowledge of the RH profile:

$$\begin{array}{}\text{(5)}& m_{\mathrm{R}}=m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}+\left(m_{\mathrm{R},\mathrm{ref}}-m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\right){\displaystyle \frac{V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}}{V^{\mathrm{3}+\mathrm{2}}}}.\end{array}$$

The real part of the refractive index, calculated using Eq. (5), is denoted as $m_{\mathrm{R}}^V$. The volume V³⁺² can only be retrieved for altitudes above the complete geometrical overlap height. Therefore, z_ref must be selected at or above this height. Recall also that Eqs. (3)–(5) are applicable only within a well-mixed layer. The real part of the RI at reference height, in Eqs. (4) and (5), can be selected from the values retrieved from 3β+2α observations, which is denoted as $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$. Further in the text, when calculating V^mod with Eq. (3), we use volume $V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}$ at the reference height as V_ref.

If water uptake does not alter the chemical composition and does not cause fluorescence quenching, the fluorescence signal should be proportional to the volume of dry particles. Thus, the variation in the fluorescence backscattering coefficient, β_F, relative to its value at the reference height, β_F,ref, allows for modeling m_R within the layers, where particle number density varies with height, assuming the particle type remains unchanged. If the number density of particles at heights z and z_ref is N and N_ref respectively, their ratio is $\frac{N}{N_{\mathrm{ref}}}=\frac{{\mathit{\beta }}_{\mathrm{F}}}{{\mathit{\beta }}_{\mathrm{F},\mathrm{ref}}}$. The real part of the RI calculated for a single particle is

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{m}_{\mathrm{R}}& ={\displaystyle \frac{m_{\mathrm{R},\mathrm{ref}}\frac{V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}}{N_{\mathrm{ref}}}+m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(\frac{V^{\mathrm{3}+\mathrm{2}}}{N}-\frac{V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}}{N_{\mathrm{ref}}}\right)}{\frac{V^{\mathrm{3}+\mathrm{2}}}{N}}}\\ & =m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}+\left(m_{\mathrm{R},\mathrm{ref}}-m_{\mathrm{R}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\right){\displaystyle \frac{V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}}{V^{\mathrm{3}+\mathrm{2}}}}{\displaystyle \frac{{\mathit{\beta }}_{\mathrm{F}}}{{\mathit{\beta }}_{\mathrm{F},\mathrm{ref}}}}.\end{array}\end{array}$$

The real part of the RI, modeled with Eq. (6), is denoted as $m_{\mathrm{R}}^F$.

Our approach to assessing the potential effect of water uptake on fluorescence involves analyzing episodes of strong hygroscopic growth within the well-mixed PBL. A decrease in fluorescence backscattering with height may indicate fluorescence quenching. Additionally, we compare the profiles of the real part of the refractive index, retrieved from 3β+2α observations, $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$, with the values $m_{\mathrm{R}}^{\mathrm{mod}}$, $m_{\mathrm{R}}^V$, and $m_{\mathrm{R}}^F$ obtained from Eqs. (4), (5), and (6) respectively. Agreement between $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$ and $m_{\mathrm{R}}^{\mathrm{mod}}$ would support the applicability of the assumption that the total particle volume results from the additive contributions of dry aerosol and water uptake. Consistency between $m_{\mathrm{R}}^{\mathrm{mod}}$ and $m_{\mathrm{R}}^V$ would further validate the RH profile used in the calculations. And, finally, a significant deviation of $m_{\mathrm{R}}^F$ from $m_{\mathrm{R}}^V$ at high RH could suggest the presence of fluorescence quenching.

3 Numerical simulation of the particle volume and surface density as a function of the extinction coefficient

We begin with a numerical simulation to explore the relationship between particle volume and surface area density, on one hand, and the extinction coefficient, on the other, for different particle sizes and refractive indices. In this simulation, we consider a set of lognormal particle size distributions (PSDs) for the number density n(r):

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\mathrm{d}n\left(r\right)}{\mathrm{d}\ln r}}={\displaystyle \frac{N}{(\mathrm{2}\mathit{\pi }{)}^{\mathrm{1}/\mathrm{2}}\ln \mathit{\sigma }}}\exp \left[-{\displaystyle \frac{(\ln r-\ln r_{\mathrm{0}}{)}^{\mathrm{2}}}{\mathrm{2}(\ln \mathit{\sigma }{)}^{\mathrm{2}}}}\right],\end{array}$$

where N is the total particle number (N=1 in all computations) and σ is the standard deviation. The modal radius, r₀, and ln σ varied within the [0.015–6.3] µm and the [0.43–0.936] intervals respectively. The particle extinction coefficient at 532 nm, α₅₃₂, was computed for spheres with the real and the imaginary parts of the refractive index within the ranges [1.3–1.7] and [0.00–0.03] respectively. In total, more than 10⁵ extinction coefficients were calculated using look-up tables (Kolgotin et al., 2023).

The results of the computations are summarized in Fig. 1, which shows particle volume and surface area density as a function of the extinction coefficient at 532 nm. To provide insight into the particle sizes corresponding to different α₅₃₂, the upper axis presents approximate values of the effective radius, r_eff. Among the numerous data points shown in Fig. 1, some of them represent the hygroscopic growth of specific aerosol types. To emphasize these points, we overlay lines depicting the hygroscopic growth of sulfate (SU) and organic carbon (OC) particles from the MERRA-2 model (Chin et al., 2002; Colarco et al., 2010). The particle parameters used in the computations, such as modal radius and the RI, are summarized in Table A1 for different relative humidities. The ln σ in Eq. (7) was set to 0.79 for OC and 0.71 for SU independent of RH.

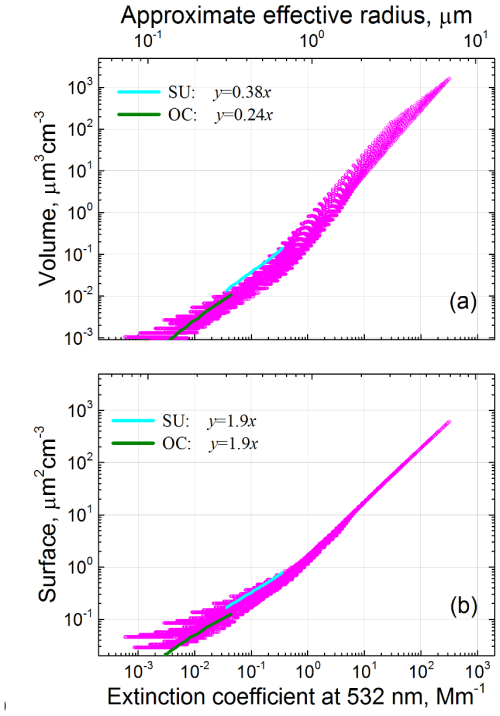
Figure 1 Modeled particle (a) volume and (b) surface area density as functions of the extinction coefficient at 532 nm. Cyan and green lines correspond to hygroscopic growth of sulfates (SU) and organic carbon (OC) particles from the MERRA-2 model. The particle parameters used in the computations are described in the text.

The ratio $V/{\mathit{\alpha }}_{\mathrm{532}}$ in Fig. 1a exhibits a tendency to increase with particle size, and for a given value of α₅₃₂ this ratio varies significantly, spanning up to an order of magnitude. However, for specific aerosol types, such as SU and OC, the dependence V(α₅₃₂), which characterizes particle hygroscopic growth, can be reasonably approximated by a linear fit: V=0.38α₅₃₂ and V=0.24α₅₃₂ respectively, where volume is expressed in µm³ cm⁻³ and the extinction coefficient in Mm⁻¹. These modeling results suggest that, even in the presence of hygroscopic growth, aerosol-type-specific conversion factors can still enable estimation of particle volume from the extinction coefficient. The variation in $S/{\mathit{\alpha }}_{\mathrm{532}}$ in Fig. 1b is significantly smaller compared to $V/{\mathit{\alpha }}_{\mathrm{532}}$ in Fig. 1a, and it decreases with particle size, allowing for a more accurate estimation of surface area density.

4 Results of observations

4.1 25 March 2022 – hygroscopic growth within the well-mixed PBL

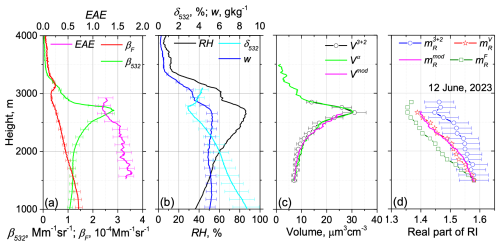
We begin with the episode on 25 March 2022, when the fluorescence backscattering remained relatively stable within the PBL. For this episode, measurements were performed at a 48° angle to horizon, and the height of complete geometrical overlap of the laser beam and the telescope's field of view is 700 m. As shown in Fig. 2, variations in WVMR within the 650–1750 m height range remain below 0.3 g kg⁻¹, while potential temperature deviations are within 1.5 K. These conditions indicate that the PBL is well mixed. The relative humidity increases with height from 35 % to 75 %, resulting in a 1.5-fold increase in β₅₃₂. Using parameterization (1), the backscattering growth coefficient, γ_β, is estimated to be 0.45 ± 0.1. This result is consistent with observed γ_β values for different aerosol types, as reported by Sicard et al. (2022). Specifically, for urban aerosols at 532 nm wavelength, γ_β ranges between 0.38 and 0.65, which aligns well with our findings. During hygroscopic growth, the particle depolarization ratio, δ₅₃₂, decreases with height from 10 % to 5 %, while the extinction Ångström exponent (EAE), calculated from α₃₅₅ to α₅₃₂, decreases from 1.4 to 0.9. The lidar ratios at 355 and 532 nm, S₃₅₅ and S₅₃₂, during hygroscopic growth increase from 44 ± 7 to 53 ± 8 sr and from 52 ± 8 to 69 ± 10 sr respectively. The fluorescence capacity at 700 m is G_F = 0.65 × 10⁻⁴, and according to the classification scheme in Veselovskii et al. (2024), this corresponds to urban aerosol. This classification is further supported by HYSPLIT backward-trajectory analysis, which indicates that the air masses at this altitude originated from Germany.

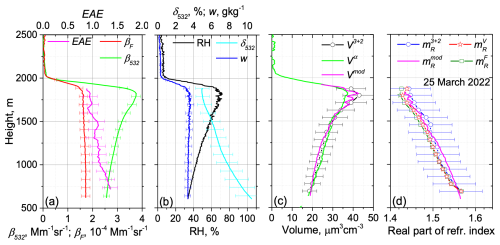
Figure 2 Vertical profiles of the particle parameters on 25 March 2022 for the 19:10–21:30 UTC period. (a) The backscattering coefficient, β₅₃₂; the fluorescence backscattering coefficient, β_F; and the Ångström exponent, EAE. (b) The particle depolarization ratio, δ₅₃₂; the water vapor mixing ratio, w; and the relative humidity, RH. (c) The particle volume, V³⁺², retrieved from 3β+2α observations; the volume V^α, calculated from the extinction coefficient α₅₃₂; and the volume V^mod, modeled with Eq. (3) using ε = 0.33. (d) The real part of the refractive index, $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$, retrieved from 3β+2α observations, along with the values $m_{\mathrm{R}}^{\mathrm{mod}}$, modeled with Eq. (4), and the values of $m_{\mathrm{R}}^V$ and $m_{\mathrm{R}}^F$ calculated from Eqs. (5) and (6) respectively. Measurements were performed at 48° to horizon.

The profile of particle volume, retrieved from 3β+2α observations, V³⁺², is presented in Fig. 2c, along with the corresponding conversion factors $C_{\mathit{\alpha },\mathrm{532}}^V$ and $C_{\mathit{\beta },\mathrm{532}}^V$, shown in Fig. 3a. The conversion factor $C_{\mathit{\alpha },\mathrm{532}}^V$ remains relatively stable during hygroscopic growth, with a deviation from the mean value of about 10 %. As shown in Fig. 2c, the volume, V^α, calculated from α₅₃₂ as $V^{\mathit{\alpha }}=C_{\mathit{\alpha },\mathrm{532}}^V\times {\mathit{\alpha }}_{\mathrm{532}}$, aligns well with V³⁺², when using a mean conversion factor $C_{\mathit{\alpha },\mathrm{532}}^V$ = 0.15 µm³ cm⁻³ Mm. On the other hand, the conversion factor $C_{\mathit{\beta },\mathrm{532}}^V$ exhibits higher variability (up to 20 %), as it is sensitive to changes in the refractive index. Figure 2c also displays the profile of V^mod, modeled using Eq. (3). The value $V_{\mathrm{ref}}^{\mathrm{3}+\mathrm{2}}$ is taken from inversion of 3β+2α measurements at reference height z_ref = 700 m. The size growth coefficient, ε, reported by Randriamiarisoa et al. (2006) for urban aerosol in Paris, was 0.26. However, for our observations a better fit with V³⁺² was achieved when using ε = 0.33.

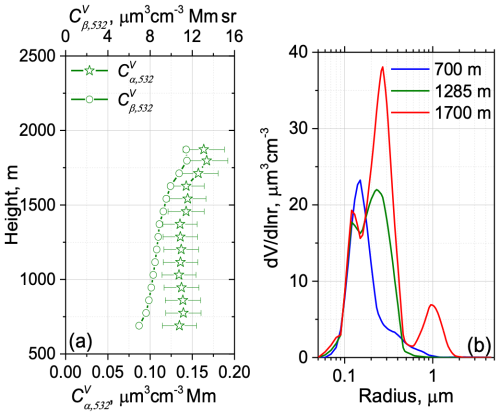
Figure 3 (a) Vertical profiles of extinction-to-volume, $C_{\mathit{\alpha },\mathrm{532}}^V$, and backscattering-to-volume, $C_{\mathit{\beta },\mathrm{532}}^V$, conversion factors on 25 March 2022. (b) The particle size distribution $\frac{\mathrm{d}V}{\mathrm{d}\ln r}$ at heights 700, 1285, and 1700 m.

The real part of the refractive index, $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$ , retrieved from 3β+2α observations, in Fig. 2d decreases with height from 1.57 to 1.44, and it agrees with the Hänel parameterization, $m_{\mathrm{R}}^{\mathrm{mod}}$, calculated with Eq. (4). The profiles of $m_{\mathrm{R}}^V$ and $m_{\mathrm{R}}^F$, calculated with Eqs. (5) and (6) respectively, align with $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$ within the uncertainty of retrieval. Thus, for this specific case, we see no evidence of fluorescence quenching by the water uptake.

The 3β+2α observations enable the estimation of key characteristics of the particle size distribution, at least for fine-mode particles. As the maximum available laser wavelength is 1064 nm, the retrievals exhibit decreasing sensitivity to particles with radii larger than approximately 2 µm (Veselovskii et al., 2009). The evolution of $\frac{\mathrm{d}V}{\mathrm{d}\ln r}$ with height is shown in Fig. 3b. At 700 m, the fine mode, with a maximum at r = 0.15 µm, is dominant. By 1700 m the maximum of the PSD shifts to approximately r = 0.25 µm due to hygroscopic growth. A small secondary maximum at r = 1.0 µm also appears; however we cannot conclusively determine whether it is a real feature or merely an artifact of the retrieval process. From this figure, we can conclude that, for the episode considered, the hygroscopic growth primarily affects fine-mode particles.

4.2 30–31 August 2022 – hygroscopic growth within a layer that is not well mixed

On 30–31 August 2022, an episode of pronounced hygroscopic growth was observed. The vertical profiles of the particle parameters, similar to those shown in Fig. 2, are presented in Fig. 4 for 30 August 2022. Complete geometrical overlap occurred at 1250 m; therefore, the extinction profiles and inversion results are available only above this height. The lidar ratios at 1250 m are S₃₅₅ = 57 ± 8 sr and S₅₃₂ = 51 ± 8 sr. The WVMR shows significant height variations within the 1250–2500 m range, indicating that this layer is not well mixed. The HYSPLIT backward-trajectory analysis indicates that the air masses below the 1000 m height originated from the north of Germany, while at higher altitudes they arrived from the Atlantic region and may have transported maritime particles. The relative humidity increases steadily with height and peaks at approximately 85 % near 1750 m. Above this level, RH gradually decreases. Within the 1000–2500 m range, aerosol particles undergo hygroscopic growth, and the peak in the backscattering coefficient, β₅₃₂, is consistent with the RH maximum at 1750 m. In contrast, both the Ångström exponent and the linear depolarization ratio exhibit distinct minima at this height. As previously noted, the aerosol layer is not well mixed, and the backscattering growth coefficient, γ_β, can only be derived within specific altitude ranges. For the lower range of 750–1000 m (45 % < RH < 55 %), γ_β is estimated as 0.6 ± 0.2. However, at higher altitudes, γ_β exhibits an increase. Specifically, within the 1300–1750 m range (65 % < RH < 85 %), the coefficient rises to 1.2 ± 0.3. This increase may be attributed to the presence of maritime aerosol. Additionally, the fluorescence capacity is low (G_F = 0.36 ± 0.05 at 750 m), suggesting a low content of organic particles.

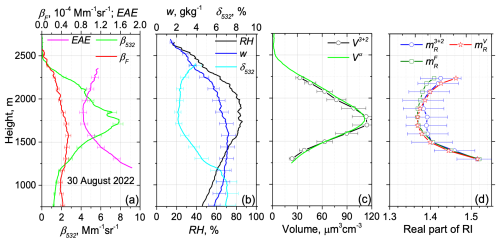
Figure 4 Similar to Fig. 2 but for the measurements on 30 August 2022 during the 19:30–20:30 UTC period.

The particle volume was retrieved from 3β+2α observations, allowing calculation of the conversion factors $C_{\mathit{\alpha },\mathrm{532}}^V$ and $C_{\mathit{\beta },\mathrm{532}}^V$, as shown in Fig. 5a. The deviation of $C_{\mathit{\alpha },\mathrm{532}}^V$ from its mean value is less than 15 %, while for $C_{\mathit{\beta },\mathrm{532}}^V$ the deviation is larger, about 30 %. The profile of the particle volume V^α calculated using the mean conversion factor $C_{\mathit{\alpha },\mathrm{532}}^V$ = 0.23 µm³ cm⁻³ Mm aligns well with V³⁺² in Fig. 4c.

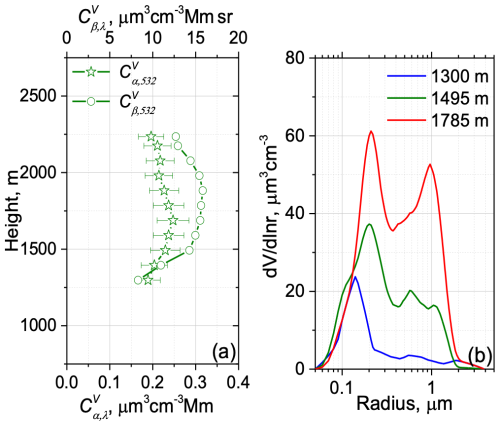
Figure 5 Similar to Fig. 3 but for the measurements on 30 August 2022 during the 19:30–20:30 UTC period.

The retrieved $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$ decreases with height from 1.52 to 1.39 within the 1250–1750 m range and then begins to increase above this level. The values of $m_{\mathrm{R}}^V$ and $m_{\mathrm{R}}^F$ calculated via Eqs. (5) and (6), as shown in Fig. 4d, agree with $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$ within the uncertainty of retrieval. Thus, in this episode, once again, water uptake does not exhibit a significant effect on the fluorescence signal.

The modification of the PSD during hygroscopic growth is shown in Fig. 5b. The maximum of the fine mode, within the 1300–1800 m range, shifts with height from r = 0.14 µm to r = 0.2 µm. Simultaneously, the second mode, centered near 1.0 µm, increases with height. This suggests that the aerosol mixture likely contains coarse hygroscopic particles, which could have a maritime origin.

4.3 Possibility of fluorescence quenching by the water uptake

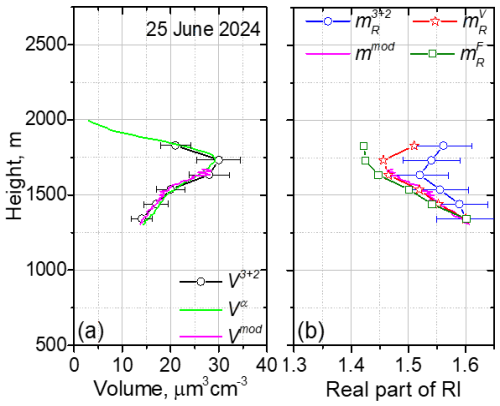
The assumption that fluorescence backscattering is independent of water uptake is crucial when using the fluorescence technique to study aerosol hygroscopic growth (Miri et al., 2024). However, in some episodes we observed a decrease in β_F with height within the well-mixed PBL, which may indicate possible fluorescence quenching. Two such episodes, on 11 May and 25 June 2024, are shown in Fig. 6. The complete geometrical overlap was achieved at 1030 and 1300 m respectively, with lidar ratios at these heights measured as follows: S₃₅₅ = 50 ± 7 sr and S₅₃₂ = 42 ± 6 sr on 11 May and S₃₅₅ = 46 ± 7 sr and S₅₃₂ = 49 ± 7 sr on 25 June 2024. In both cases, the PBL is well mixed, with variations in WVMR remaining below 0.2 g kg⁻¹. The air masses within the 500–2500 m range for both episodes originated from Germany. The fluorescence capacities at 750 m for these cases are 0.86 × 10⁻⁴ and 0.75 × 10⁻⁴ respectively, which are higher than for previous episodes. The backscattering growth coefficients, γ_β, on 11 May and 25 June 2024 are estimated as 0.4 ± 0.1 and 0.9 ± 0.2. In contrast to results in Fig. 2a, the fluorescence backscattering, β_F, decreases with height along with δ₅₃₂. This decrease begins at relatively low RH, and the rapid increase in β₅₃₂ at high RH is not accompanied by a similarly fast decrease in β_F.

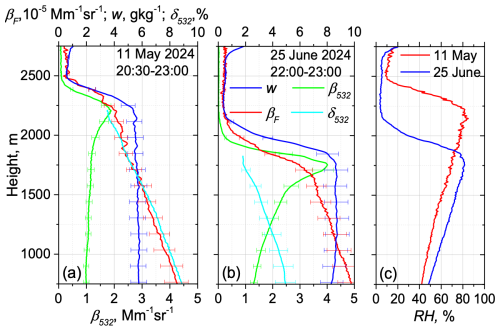
Figure 6 Vertical profiles of aerosol and fluorescence backscattering coefficients, β₅₃₂ and β_F, along with the water vapor mixing ratio, w, and the particle depolarization ratio, δ₅₃₂, measured on (a) 11 May 2024 and (b) 25 June 2024. (c) The relative humidity for the episodes considered.

Figure 7 Similar to Fig. 2 but for the measurements on 12 June 2023 for the 21:00–22:20 UTC period.

All episodes demonstrating the fluorescence quenching happened when urban aerosols presented within the PBL. Among these episodes, one of the most representative occurred on 12 June 2023. Corresponding profiles of particle parameters are shown in Fig. 7. Variations in WVMR and potential temperature within the 1000–2750 m range are small (below ±0.2 g kg⁻¹ and ±2 K respectively), indicating that the PBL is well mixed. The HYSPLIT backward-trajectory analysis indicates that the air masses within the 1000–3000 m height range originated from eastern Europe. The fluorescence capacity at 750 m is quite high (1.4 × 10⁻⁴), suggesting the presence of organic particles. The height of complete geometrical overlap is 1500 m, and the lidar ratios at this height are S₃₅₅ = 37 ± 6 sr and S₅₃₂ = 38 ± 6 sr.

Within the 1000–2700 m altitude range, the backscattering coefficient, β₅₃₂, shows a consistent positive response to RH, reaching its maximum value at 2700 m where RH peaks. The backscattering growth coefficient, γ_β, is determined to be 0.55 ± 0.1. Simultaneously, the observed increase in RH correlates with reduced fluorescence backscattering, suggesting potential fluorescence-quenching effects. The aerosol volume, V^α, derived from α₅₃₂ measurements shows good agreement with V³⁺², when applying a mean conversion factor $C_V^{\mathit{\alpha }}$ = 0.15 µm³ cm⁻³ Mm. The modeled volume profile, V^mod, calculated using Eq. (3) and ε = 0.33, similarly matches V³⁺² within the layer, where aerosols are presumed to be well mixed.

The real part of the refractive index, $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$, retrieved from 3β+2α observations, decreases from 1.58 to 1.45, within the 1500–2700 m altitude range. However, this observed decrease occurs at a lower rate compared to both $m_{\mathrm{R}}^{\mathrm{mod}}$ and $m_{\mathrm{R}}^V$ values, suggesting that the simplified model, which assumes additivity of dry aerosol and water uptake, may not be applicable to this episode. Furthermore, the values $m_{\mathrm{R}}^F$, derived using the fluorescence signal in Eq. (6), are systematically lower than both $m_{\mathrm{R}}^{\mathrm{mod}}$ and $m_{\mathrm{R}}^V$, providing additional evidence for potential fluorescence-quenching effects. A similar behavior of $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$, $m_{\mathrm{R}}^V$, and $m_{\mathrm{R}}^F$ was observed for the episodes shown in Fig. 6, with corresponding results presented in the Appendix (Figs. A1 and A2).

Figure 8 shows the PSDs for three episodes, discussed in this section. As the particles undergo hygroscopic growth, the fine mode shifts toward larger radii; however, the second mode at r = 1 µm, observed in Fig. 5b, is absent. This suggests that only fine particles undergo hygroscopic growth.

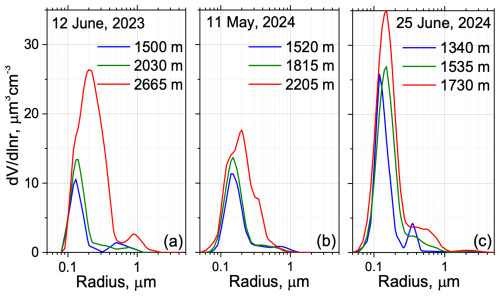
Figure 8 The particle size distribution, $\frac{\mathrm{d}V}{\mathrm{d}\ln r}$, at different heights for three case studies showing evidence of fluorescence quenching during hygroscopic growth: (a) 12 June 2023, (b) 11 May 2024, and (c) 25 June 2024.

To quantify fluorescence-quenching effects, we computed the relative reduction in fluorescence backscattering using

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }{\mathit{\beta }}_{\mathrm{F}}={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{F},\mathrm{ref}}-{\mathit{\beta }}_{\mathrm{F}}}{{\mathit{\beta }}_{\mathrm{F},\mathrm{ref}}}}.\end{array}$$

Figure 9a displays the normalized β₅₃₂ and fluorescence reduction Δβ_F as a function of RH for three observational periods: 25 March 2022, 12 June 2023, and 11 May 2024. For consistent comparison, β₅₃₂ values were normalized to the backscattering coefficient at RH_ref = 50 %, and Δβ_F values were calculated for the same RH_ref. These cases were selected based on two criteria: consistent β₅₃₂(RH) growth patterns across all events and distinctive variations in Δβ_F behavior between cases. As previously noted, the 25 March 2022 case showed no significant RH-dependent increase in Δβ_F. In contrast, during the other two episodes (12 June 2023 and 11 May 2024), Δβ_F exhibited a steady increase from baseline conditions, reaching a maximum reduction of ∼ 50 % at RH = 85 %. However, the rapid growth of β₅₃₂ at high RH is not mirrored by the same rate of increase in Δβ_F. This decoupling between hygroscopic backscattering growth and fluorescence suppression suggests that water uptake affects aerosol fluorescence through mechanisms beyond simple dilution effects.

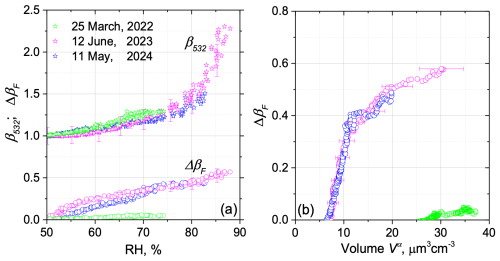
Figure 9 (a) The RH dependence of the normalized backscattering coefficient, β₅₃₂ (stars), and fluorescence reduction, Δβ_F (circles), for three case studies: 25 March 2022, 12 June 2023, and 11 May 2024. All values are normalized relative to RH = 50 % baseline conditions. (b) The relationship between fluorescence reduction Δβ_F and particle volume V^α, calculated from α₅₃₂, for the same three episodes.

To further investigate water uptake effects on fluorescence, Fig. 9b presents the relationship between fluorescence reduction Δβ_F and particle volume V^α, calculated from α₅₃₂, for the same three case studies as in Fig. 9a. On 12 June 2023 and 11 May 2024, Δβ_F demonstrates a sharp increase within the ∼ 5–12 µm³ cm⁻³ volume range and a subsequent plateau at higher volumes. These observations reveal two key findings: quenching starts at relatively low RH (before maximum hygroscopic growth), and the Δβ_F–volume relationship is nonlinear, disproving simple proportional dependence on water uptake. While aerosol-type dependence is evident, the specific particle composition driving this quenching behavior cannot yet be definitively identified from these measurements.

5 Conversion factors for smoke and urban particles

As demonstrated in the previous section, the volume density of urban aerosol, even in the presence of hygroscopic growth, can be estimated using a single extinction or backscattering coefficient and corresponding conversion factors. However, urban aerosol includes a variety of particle types (e.g. sulfates, soot), causing these conversion factors to vary across episodes. To quantify this variability and assess the resulting uncertainty in V and S calculations, we analyzed multiple episodes of urban aerosol within the PBL exhibiting hygroscopic growth. For each episode, conversion factors at 355 and 532 nm were derived from 3β+2α observations.

In addition to urban aerosols, we also examined smoke episodes. For smoke, hygroscopic growth events were rare, and our focus shifted to the vertical dependence of conversion factors in the lower and middle troposphere. Figure 10 presents the vertical profiles of the conversion factors, $C_{\mathit{\alpha },\mathrm{532}}^V$ and $C_{\mathit{\beta },\mathrm{532}}^V$, for 10 urban aerosol episodes involving hygroscopic growth, along with 6 smoke episodes observed between 2020 and 2024.

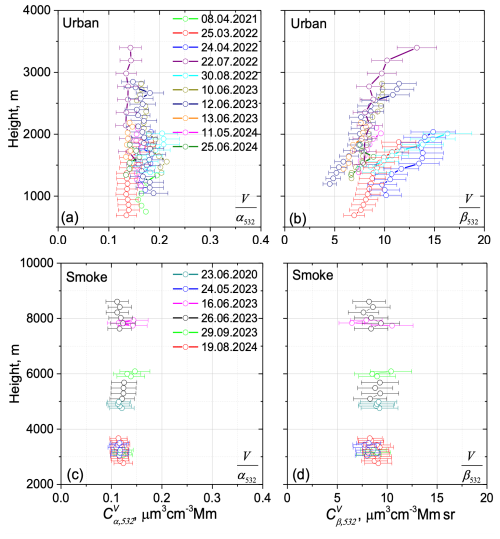
Figure 10 Height profiles of the extinction-to-volume, $C_{\mathit{\alpha },\mathrm{532}}^V$, and backscattering-to-volume, $C_{\mathit{\beta },\mathrm{532}}^V$, conversion factors in several measurement sessions for (a, b) urban aerosol and (c, d) smoke.

Table 1 Conversion factors for calculation of the volume and surface area of smoke and urban particles from the extinction and backscattering coefficients at 355 and 532 nm wavelengths.

For urban aerosol, the mean value of $C_{\mathit{\alpha },\mathrm{532}}^V$ is estimated to be 0.17 ± 0.04 µm³ cm⁻³ Mm. This contrasts with the higher value of 0.30  ± 0.08 µm³ cm⁻³ Mm reported by Mamouri and Ansmann (2017) for continental aerosol in Germany. It is interesting that extinction-to-surface area conversion factors $C_{\mathit{\alpha },\mathit{\lambda }}^S$, provided by Mamouri and Ansmann (2016) ($C_{\mathit{\alpha },\mathrm{355}}^S$ = 1.55 ± 0.46 and $C_{\mathit{\alpha },\mathrm{532}}^S$ = 2.8 ± 0.89 µm² cm⁻³ Mm), agree well with values in Table 1. In contrast to the extinction coefficient, the backscattering coefficient exhibits greater sensitivity to changes in the refractive index, leading to significantly stronger variations in $C_{\mathit{\beta },\mathrm{532}}^V$ compared to $C_{\mathit{\alpha },\mathrm{532}}^V$ (Fig. 10b). The mean value of $C_{\mathit{\beta },\mathrm{532}}^V$ is 10 ± 6 µm³ cm⁻³ Mm sr, corresponding to an unacceptably high uncertainty in volume estimation (up to 60 %). Consequently, for urban aerosols, reliable volume density retrievals should be based solely on the extinction coefficient.

For smoke, the mean conversion factor $C_{\mathit{\alpha },\mathrm{532}}^V$ is 0.13 ± 0.02 µm³ cm⁻³ Mm across all height ranges, which is very close to the value of 0.13 ± 0.08 µm³ cm⁻³ Mm reported by Ansmann et al. (2021) for aged smoke in AERONET measurements. The composition of smoke is less variable compared to urban aerosol, allowing for reliable volume estimations even based on the backscattering coefficient (Fig. 10d). The mean value of $C_{\mathit{\beta },\mathrm{532}}^V$ for smoke is 9 ± 1.5 µm³ cm⁻³ Mm sr, indicating comparable uncertainties in volume estimation from both extinction and backscattering coefficients for the analyzed episodes.

Table 1 summarizes the conversion factors for calculating particle volume and surface area density for the episodes presented in Fig. 10. The conversion factors $C_{\mathit{\beta },\mathit{\lambda }}^V$ and $C_{\mathit{\beta },\mathit{\lambda }}^S$ for urban aerosol are excluded due to their unacceptably high uncertainties. For aged smoke, we obtain $C_{\mathit{\alpha },\mathrm{532}}^S$ = 1.75 ± 0.4 µm² cm⁻³ Mm, which agrees well with the value 1.75 ± 0.25 µm² cm⁻³ Mm reported by Ansmann et al. (2021). These findings demonstrate that in numerous cases, both particle volume and surface density of smoke can be retrieved from either a single extinction coefficient or a single backscattering coefficient, which is particularly valuable when complete 3β+2α measurements are unavailable. It should also be noted that the extinction-to-volume conversion factors $C_{\mathit{\alpha },\mathrm{532}}^V$ for sulfate (SU) and organic carbon (OC), derived from Fig. 1a (0.38 and 0.24 µm³ cm⁻³ Mm respectively), are significantly higher than the corresponding values in Table 1. This discrepancy suggests that using just SU and OC is insufficient for accurately modeling urban aerosol and smoke, as these aerosols consist of complex mixtures of different particle types.

6 Conclusion

We analyzed Mie–Raman–fluorescence lidar observations during aerosol hygroscopic growth episodes to investigate water uptake effects on fluorescence backscattering, β_F. The well-mixed PBL serves as a convenient environment for such studies, since β_F should remain constant in the absence of water uptake effects. However, during certain episodes, we observed a systematic height-dependent decrease in β_F. This observed β_F reduction is difficult to explain solely by changes in aerosol composition and likely indicates fluorescence quenching. Notably, the decrease in β_F begins at relatively low RH (less than 50 %), coinciding with a reduction in the depolarization ratio. Interestingly, while β₅₃₂ shows rapid enhancement at high RH levels, this is not accompanied by an accelerated β_F decrease rate.

All fluorescence-quenching episodes have been observed within the well-mixed PBLs of urban aerosols. Fluorescence quenching exhibits strong dependence on aerosol composition, as evidenced by its absence in numerous episodes. However, we cannot yet identify the specific particle type responsible for this quenching effect in this study. It should also be mentioned that when fluorescence measurements are conducted using multiple discrete channels, the ratio of fluorescence backscattering coefficients between these channels remains unaffected by water uptake, even though each individual channel is influenced by it (see Fig. 10 in Veselovskii et al., 2025). This implies that the spectral signatures of fluorescence are preserved during hygroscopic growth.

The particle volume and surface area density, retrieved from 3β+2α measurements during analysis of hygroscopic growth episodes, were used to validate the feasibility of estimating these parameters from a single extinction coefficient. Our analysis shows that for urban aerosols, the uncertainty in V and S determination remains below 25 % when using α₅₃₂. Smoke particles demonstrate comparable uncertainties in V and S calculation. The conversion factors show a clear dependence on aerosol type, which can be effectively identified through fluorescence lidar measurements. These findings highlight the Mie–Raman–fluorescence lidar as a promising tool for aerosol characterization.

Appendix A

Table A1 Particle parameters from the MERRA-2 model. The modal radius of log-normal PSD along with the real and imaginary parts of the RI at 532 nm for sulfates (SU) and organic carbon (OC) for different values of RH.

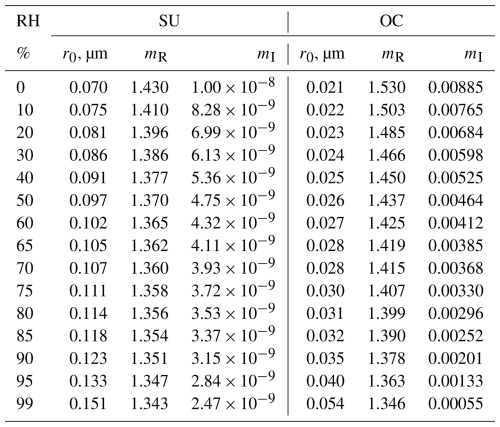
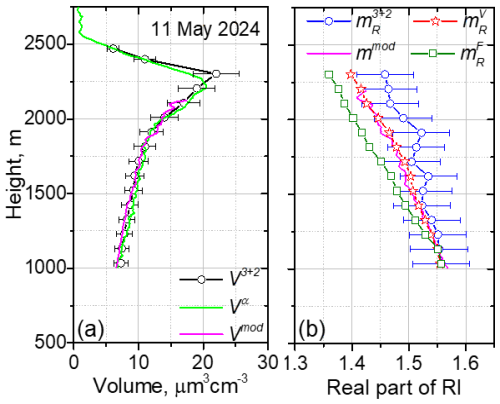
Figure A1 Vertical profiles of the particle parameters on 11 May 2024 for the 20:30–23:00 UTC period. (a) The particle volume, V³⁺², retrieved from 3β+2α observations; the volume V^α, calculated from the extinction coefficient, α₅₃₂; and the volume V^mod, modeled with Eq. (3). (b) The real part of the refractive index, $m_{\mathrm{R}}^{\mathrm{3}+\mathrm{2}}$, retrieved from 3β+2α observations, along with the values $m_{\mathrm{R}}^{\mathrm{mod}}$, modeled with Eq. (4), and the values of $m_{\mathrm{R}}^V$ and $m_{\mathrm{R}}^F$, calculated from Eqs. (5) and (6) respectively. Values of V^mod and $m_{\mathrm{R}}^{\mathrm{mod}}$ were calculated for ε=0.33.

Figure A2 Similar to Fig. A1 but for the measurements on 25 June 2024 for the 22:00–23:00 UTC period. Values of V^mod and $m_{\mathrm{R}}^{\mathrm{mod}}$ were calculated for ε = 0.52.