the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The Ozone Mapping and Profiler Suite (OMPS) Limb Profiler (LP) Version 1 aerosol extinction retrieval algorithm: theoretical basis
Robert Loughman
Pawan K. Bhartia
Zhong Chen
Philippe Xu
Ernest Nyaku
Ghassan Taha
The theoretical basis of the Ozone Mapping and Profiler Suite (OMPS) Limb Profiler (LP) Version 1 aerosol extinction retrieval algorithm is presented. The algorithm uses an assumed bimodal lognormal aerosol size distribution to retrieve aerosol extinction profiles at 675 nm from OMPS LP radiance measurements. A first-guess aerosol extinction profile is updated by iteration using the Chahine nonlinear relaxation method, based on comparisons between the measured radiance profile at 675 nm and the radiance profile calculated by the Gauss–Seidel limb-scattering (GSLS) radiative transfer model for a spherical-shell atmosphere. This algorithm is discussed in the context of previous limb-scattering aerosol extinction retrieval algorithms, and the most significant error sources are enumerated. The retrieval algorithm is limited primarily by uncertainty about the aerosol phase function. Horizontal variations in aerosol extinction, which violate the spherical-shell atmosphere assumed in the version 1 algorithm, may also limit the quality of the retrieved aerosol extinction profiles significantly.
- Article
(5606 KB) - Full-text XML
- BibTeX
- EndNote
Most of the aerosols found in the Earth's atmosphere occur in the planetary boundary layer, due to the wide variety of aerosol sources that exist at the surface (dust, smoke, sea salt, etc.). But a secondary peak in aerosol abundance typically occurs in the stratosphere (Junge et al., 1961a), extending from the tropopause to an altitude of approximately 30 km (Brock et al., 1995; Hamill et al., 1997). The stratospheric aerosol layer consists primarily of hydrated sulfuric acid (H2SO4) droplets (Toon and Pollack, 1973), generated by the oxidation of tropospheric sulfur dioxide (SO2) and carbonyl sulfide (OCS) that has entered the stratosphere through troposphere–stratosphere exchange processes (Holton et al., 1995). The stratospheric aerosol layer is enhanced by volcanic eruptions that inject SO2 into the stratosphere, creating a layer of H2SO4 droplets that spreads quickly in the horizontal directions (and much more slowly in the vertical direction), slowly dissipating over a period from months to several years. Volcanic eruptions also may inject ash particles directly into the stratosphere, and mineral dust from the ablation of meteors also can augment the stratospheric aerosol layer (Cziczo et al., 2001). Several competing influences therefore affect the stratospheric aerosol layer, including volcanic activity, stratosphere–troposphere exchange, stratospheric transport processes, gas-to-droplet conversion rates, and particle sedimentation. As a result, the stratospheric aerosol concentration varies widely in space and in time.
Aerosols in the stratosphere play key roles in the chemistry of that region, particularly including heterogeneous ozone destruction (Hofmann and Solomon, 1989; McCormick et al., 1995; Meinrat and Crutzen, 1997; Solomon, 1999). Monitoring stratospheric aerosols as a tracer for stratospheric air mass motion has also provided useful insight (Holton et al., 1995; Goering et al., 2001). The most significant climate impact of changes in the distribution of stratospheric aerosols occurs due to backscattering of solar radiation, which increases the planetary albedo and cools the troposphere (Robock, 2000; Kravitz et al., 2011; Ridley et al., 2014). The magnitude of this effect varies significantly with latitude, solar zenith angle, etc. (Deshler et al., 2008). A recent review of the observations and processes of stratospheric aerosol and how they impact the Earth's climate is presented in Kremser et al. (2016).
1.1 Occultation measurements
The primary global record of stratospheric aerosol abundance has been derived from solar occultation (SO) measurements. (This kind of data will be indicated as “solar occultation transmission (SOT)”, to avoid confusion with the notation for sulfur oxide gases.) The Stratospheric Aerosol Measurement (SAM)/Stratospheric Aerosol and Gas Experiment (SAGE) series of missions pioneered this technique, with the long-lived SAGE II instrument (1984–2005) providing a particularly valuable continuous data record (Russell and McCormick, 1989; McCormick and Veiga, 1992; Thomason et al., 1997). An overview of the large variation of stratospheric aerosol optical depth during the SAM/SAGE time period can be found in Fig. 1 of Thomason et al. (2008). These SOT measurements provide unmatched altitude resolution, precision, and accuracy for stratospheric aerosol monitoring: transmission profiles are produced on a 0.5 km grid with estimated vertical resolution of 0.7 km (SAGE, 2002). The SAGE aerosol extinction coefficient βa retrieval has targeted accuracy and precision = 5 %, and analysis of the version 4 product indicates accuracy and precision performance on the order of 10 % for the 15–25 km altitude range (Thomason et al., 2010). The Polar Ozone and Aerosol Measurement (POAM) satellite (Lucke et al., 1999) series has further provided SOT measurements in the polar regions. Comparison between POAM III and SAGE II data indicates relative differences of ±30 % in βa, with some hemispheric differences evident (Randall et al., 2001). The MAESTRO instrument also launched aboard the SCISAT satellite in 2003 (McElroy et al., 2007). This mission has provided aerosol extinction profiles based on SOT measurements, as described by Sioris et al. (2010) and McElroy (2016).
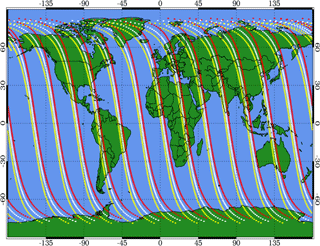
Figure 1Daily coverage provided by the OMPS LP instrument mounted on the SNPP satellite. The tangent point for the LOS corresponding to each observation is indicated, with red, white, and yellow circles depicting the left, center, and right slit observations, respectively.
The primary drawbacks of SOT observations made from a low Earth orbit are the limited number of profiles measurable (30 occultations per day) and the lack of flexibility concerning the locations monitored (which are determined entirely by the orbit of the satellite). In addition to SOT measurements, occultation measurements involving other sources of light are also possible. The SAGE III instrument also performs lunar occultations, but it does not produce βa profiles based on lunar occultation measurements (Thomason et al., 2010). The Global Ozone Monitoring by Occultation of Stars (GOMOS) instrument (Bertaux et al., 2010) has provided stellar occultation monitoring of the stratospheric aerosol layer (Vanhellemont et al., 2016). Since numerous bright stars can be used as the source of photons, this method offers the potential for increased geographic coverage as compared to SOT (but with a much dimmer source of light). Comparisons of GOMOS stellar occultation βa retrievals to SAGE II, SAGE III, and POAM III βa data indicate agreement at the 10–25 % level in the lower stratosphere (Vanhellemont et al., 2010).
The lack of global stratospheric βa profile measurements from SOT since the SAGE II, POAM III, and Meteor-3M SAGE III missions ended (in 2005, 2005, and 2006, respectively) has left a vacancy. Limb-scattering (LS) data have been combined with occultation data (Rieger et al., 2015) to produce a merged time series, which will aid in tracking the evolution of aerosol plumes from volcanic eruptions that contribute aerosol to the upper troposphere and lower stratosphere (UTLS) (Andersson et al., 2015). After an absence of over a decade, the recent installation of a SAGE III instrument on the International Space Station (Cisewski et al., 2014) in February 2017 promises to resume the valuable SOT data set for stratospheric βa monitoring.
1.2 Limb-scattering (LS) measurements
Several recent missions have provided LS measurements, including the Optical Spectograph and InfraRed Imaging System (OSIRIS) (Llewellyn et al., 2004), the Scanning Imaging Absorption spectroMeter for Atmospheric CartograpHY (SCIAMACHY) (Bovensmann et al., 1999), Meteor-3M SAGE III (Mauldin et al., 1998) (which made LS measurements in addition to occultation measurements), and the Ozone Mapping and Profiler Suite (OMPS) Limb Profiler (LP) (Flynn et al., 2006). These instruments measure profiles of the LS sunlight across the ultraviolet (UV), visible, and near-infrared (NIR) spectral regions.
As illustrated in Fig. 1 of Rault and Loughman (2013), LS measurements are possible throughout the entire sunlit hemisphere, permitting much better spatial coverage and sampling than SOT measurements. But LS retrievals of stratospheric βa are significantly more challenging, requiring radiative transfer (RT) models to simulate the diffuse radiation field, which must include all orders of atmospheric scattering as well as surface reflection. Careful tangent height registration of the measured radiance profiles (Moy et al., 2017) and cloud screening (Chen et al., 2016) are also required. The LS radiance is also susceptible to stray-light (SL) contamination (see Fig. 2 of Rault, 2005). Finally, the LS radiance depends upon both the scattering properties (especially the phase function) and the extinction coefficient for the aerosols, while occultation measurements are only sensitive to the latter property.
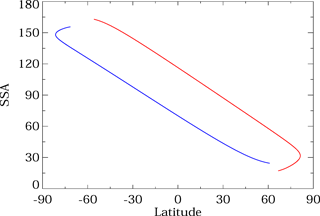
Figure 2The single-scattering angle (SSA, or Θ) as a function of latitude for the SNPP OMPS LP instrument. June and December solstice conditions are illustrated by the red and blue lines, respectively. Note that near-polar latitudes may be observed twice (during the ascending and descending nodes of the orbit), which provides useful diagnostic information.
Each LS mission team has developed its own methodology to retrieve stratospheric βa profiles from limb radiance measurements, but all of the retrieval algorithms involve the comparison of measured LS radiance profiles with simulated radiance profiles that are generated by a RT model. In the case of OSIRIS, the “color index” of measured LS radiances at 470 and 750 nm is compared to radiances calculated by the SASKTRAN (Bourassa et al., 2008a; Zawada et al., 2015) model. The evolution of βa during the OSIRIS mission has been investigated in a series of papers (Bourassa et al., 2007; Bourassa et al., 2010; Bourassa et al., 2012). Comparison between version 5 OSIRIS retrievals and the version 4 SAGE III record indicates agreement to within 10 % for βa in the 15–25 km altitude range (Bourassa et al., 2012). The retrieval of aerosol size information from OSIRIS data has also been investigated (Bourassa et al., 2008b; Rieger et al., 2014) to produce the version 6 OSIRIS aerosol product. The version 6 algorithm combines the infrared imager 1.53 µm channel with OSIRIS data to allow retrieval of both βa and aerosol mode radius, based on an assumed aerosol mode width value.
For the SCIAMACHY mission, the initial βa retrievals were performed by Taha et al. (2011), using a modified version of the algorithm under development for the eventual OMPS LP mission (Rault and Loughman, 2013). Ovigneur et al. (2011) present an approach to retrieve stratospheric aerosol number density from SCIAMACHY LS data in the O2 A-band. More recent work (Ernst et al., 2012; Ernst, 2013; Von Savigny et al., 2015) describes an approach that uses the color-index approach introduced by Bourassa et al. (2007). The global average difference between SAGE II (version 7) and SCIAMACHY (version 1.1) βa data is 10 %, with larger relative differences (up to 40 %) at specific latitudes and altitudes (Von Savigny et al., 2015). The SCIATRAN RT model (Rozanov et al., 2014) provides the radiance simulations in this case.
The SAGE III instrument that flew on the Meteor-3M satellite made LS measurements as a research product, from which retrievals of ozone (Rault, 2005) and aerosol (Rault and Loughman, 2007) were derived. These retrieval algorithms were the predecessors for the initial OMPS LP algorithm (Rault and Loughman, 2013), which used the Gauss–Seidel limb-scattering (GSLS) RT model described in Loughman et al. (2004) to provide the simulated radiances. Comparison to coincident SAGE II SOT data indicated bias < 5 % and precision = 25–50 % for βa retrievals from SAGE III LS data (Rault and Loughman, 2007).
The βa retrieval algorithm described by Rault and Loughman (2013) was applied to early OMPS LP observations. It was modified slightly to assess the aftermath of the Chelyabinsk bolide explosion, as documented by Gorkavyi et al. (2013). This paper describes the new OMPS LP Version 1 (V1) βa retrieval algorithm. Section 2 briefly describes the OMPS instruments (particularly the LP instrument) and the Suomi National Polar-Orbiting Operational Environmental Satellite System Preparatory Project (SNPP) satellite on which OMPS was initially installed. Section 3 focuses on the necessary radiance calculations, while Sect. 4 describes the retrieval algorithm in detail. Section 5 contains error analysis of the retrieved aerosol extinction profiles. Finally, a preliminary evaluation of the retrieval results is presented in Sect. 6. We conclude with a summary and description of proposed future work in Sect. 7.
The LP instrument is part of the Ozone Mapping and Profiler Suite (OMPS), whose primary purpose is to monitor the ozone layer. The LP instrument design was guided by the preceding Shuttle Ozone Limb Sounding Experiment (SOLSE) and Limb Ozone Retrieval Experiment (LORE) sensors (McPeters et al., 2000) and was built by Ball Aerospace Technology Corporation under contract from the Integrated Program Office. The instrument makes a series of simultaneous observations of the Earth's entire sunlit limb through three vertical slits, producing a set of three radiance profiles: the line of sight (LOS) for one set of observations (called the “center slit”) is oriented along the orbital track, while the other two sets (called the “left” and “right” slits) are offset by 4.25∘ from the orbital track. The ground track of the resulting sequence of observations is illustrated in Fig. 1.
OMPS LP is installed in a fixed orientation relative to the SNPP spacecraft, which is in a sun-synchronous orbit with a 13:30 ascending node and mean altitude of 833 km above the Earth's surface. As a result of this orientation, the single-scattering angle (Θ) observed by the LP instrument varies with latitude as shown in Fig. 2. Most notably, Northern Hemisphere observations (with latitude > 0∘) generally correspond to forward-scattered beams (Θ<90∘), while Southern Hemisphere observations (latitude < 0∘) correspond to backscattered beams (Θ > 90∘). As a result, the relative strength of the aerosol scattering signal is much larger in Northern Hemisphere OMPS LP measurements, as shown in Fig. 3: the aerosol phase function (Pa) increases by a factor of approximately 50 over the course of a typical orbit, as the SNPP satellite travels from its southernmost observation to its northernmost observation. (All observations for which the solar zenith angle at the tangent point θT<85∘ are processed by the OMPS LP V1 software.) The variation of the Pa at several latitudes over the course of a year due to the OMPS LP orbit is shown in Fig. 4.
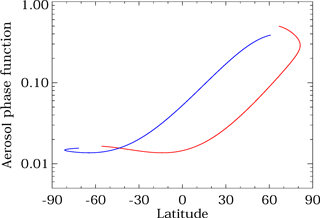
Figure 3The aerosol phase function (for the Θ values shown in Fig. 2) as a function of latitude for the SNPP OMPS LP instrument. June and December solstice conditions are illustrated by the red and blue lines, respectively. Due to the variation of the aerosol phase function with latitude and season, the SNPP OMPS LP observations are most sensitive to aerosols in the NH winter and least sensitive to those in the SH. The aerosol size distribution described in Table 1 for the V1 aerosol extinction retrieval algorithm is assumed.
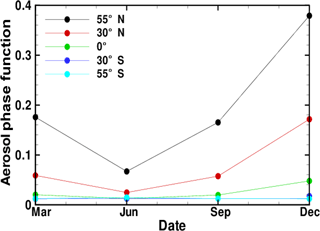
Figure 4 The seasonal variation of the aerosol phase function at several latitudes for the SNPP OMPS LP orbit. The aerosol size distribution described in Table 1 for the V1 aerosol extinction retrieval algorithm is assumed.
The OMPS LP instrument permits radiance observations for the 290–1000 nm wavelength range. Dispersion is provided by a prism, which provides images whose spectral resolution varies greatly with wavelength (from ≈1 nm in the UV to ≈ 30 nm in the NIR). At the wavelength of interest for the V1 βa retrieval algorithm (675 nm), the spectral resolution is 15 nm. For further information about the OMPS LP instrument characteristics, please consult Flynn et al. (2006), Rault and Loughman (2013), and Jaross et al. (2014).
3.1 The GSLS radiative transfer model
The GSLS RT model is built from the previous models described by Herman et al. (1994, 1995), as summarized in Loughman et al. (2004). The model atmosphere is specified by input pressure, temperature, absorbing gas number density, and βa profiles. Radiances are calculated using Rayleigh and Mie scattering cross sections at 675 nm, using the user-provided aerosol microphysical and optical properties. Ozone cross sections are averaged over the spectral width of the OMPS LP bandpass (15 nm). This approach is significantly faster than performing a full radiance convolution, and it produces radiance errors < 1 %. The viewing geometry is specified by the solar zenith angle and relative azimuth angle at the tangent point (TP) for the LOS, denoted by θT and ϕT, respectively, and illustrated in Fig. 5.
The GSLS model calculates radiances at several wavelengths λ and tangent heights h. For single-scattering (SS) calculations, the solar beam attenuation is calculated to each point along the LOS, including the curvature of the spherical atmosphere as well as the variation of solar zenith angle and solar beam attenuation along the LOS. The attenuation of the scattered beam along the LOS is also calculated accounting for the curvature of the atmosphere. Recent updates to the GSLS model described in Loughman et al. (2015) reduce SS radiance errors that were as great as 4 % in the Loughman et al. (2004) comparisons to the 0.3 % level.
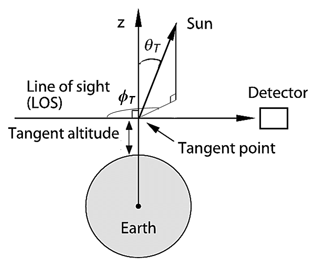
Figure 5Illustration of the limb-scattering viewing geometry, including definitions of the tangent altitude h and tangent point. The solar zenith angle and solar azimuth angle at the tangent point are indicated by θT and ϕT, respectively. Adapted from Fig. 1 of Griffioen and Oikarinen (2000). Note that a frequently committed error in the definition of ϕT (Griffioen and Oikarinen, 2000; Loughman et al., 2004; Bourassa et al., 2008b) has been corrected: a beam with Θ=0∘ (scattered exactly forward) has ϕT=0∘.
The multiple-scattered (MS) radiances observed by a LS instrument originate from illumination of the limb LOS by photons that have been scattered within the atmosphere or reflected by the underlying surface. These photons are scattered for the final time at some point along the limb LOS and then transmitted from that point to the observer. The diffuse upwelling radiance (DUR) from below the LOS provides the primary source of illumination that produces MS photons, containing the combined effects of molecular scattering, aerosol scattering, cloud scattering, and surface reflection. For the V1 βa retrieval, the DUR is estimated as described in Sect. 3.2.
The MS source function is calculated at one or more points along the LOS using the pseudo-spherical version of the RT model described by Herman et al. (1994, 1995). In the Loughman et al. (2004) GSLS model, the MS source functions were calculated only at the TP (solar zenith angle = θT). This was updated in Loughman et al. (2015) to calculate the MS source functions at multiple solar zenith angles along the LOS, increasing the accuracy of the MS radiances. Total radiance errors that had reached 10% in the Loughman et al. (2004) comparisons decrease to 1–3 % in the updated comparisons presented by Loughman et al. (2015).
The GSLS model described by Loughman et al. (2004) was used for retrieval applications on missions including SOLSE/LORE (Flittner et al., 2000), SAGE III (Rault, 2005; Rault and Taha, 2007; Rault and Loughman, 2007), GOMOS (Taha et al., 2008), SCIAMACHY (Taha et al., 2011), and OMPS LP (Rault and Loughman, 2013). These retrieval algorithms generally performed well despite the shortcomings of the Loughman et al. (2004) version of the GSLS model, but development of a more accurate version of the GSLS model was considered desirable to improve the algorithms further, as well as for the purpose of interpreting residuals (differences between measured radiances and radiances calculated for the desired model atmosphere). The Loughman et al. (2015) version of GSLS has therefore been implemented for the V1 algorithm described in this paper.
3.2 The diffuse upwelling radiance (DUR)
The horizontal extent of the limb LOS covers thousands of kilometers, and the underlying scene generally includes variable surface types, broken clouds at various locations and levels, etc. The current GSLS model lacks the capability to model the full complexity of such a scene, even if its properties were known. To estimate the DUR, the V1 βa retrieval algorithm uses a simple Lambertian model of the reflecting surface, characterized by its reflectivity R. Radiances simulated by the GSLS RT model using a Lambertian surface (placed at sea level) are used to estimate an effective scene reflectivity from a measurement, by tuning the value of R used in the GSLS model until the calculated radiance matches the measured value for a given set of viewing and illumination conditions.
The R value at which the calculations match the measurement is sometimes called the “Lambert-equivalent reflectivity”, or LER. It does not equal the true reflectivity of the surface, since the scene generally contains clouds, aerosols, etc. below the LOS that are not properly captured in the GSLS model atmosphere, and variations in terrain height are also ignored. This approach has been extensively used for nadir-viewing applications such as ozone profile retrievals from the SBUV satellite series and ozone total column retrievals from the TOMS satellite series (Heath et al., 1975), and it was suggested by Mateer et al. (1971). Approximate treatment of DUR in the V1 OMPS LP βa retrieval algorithm is justified by the relative insensitivity of the normalized radiances used by the βa retrieval to DUR, as demonstrated in Sect. 3.4.
Finally, note that the model atmosphere for the GSLS model used in the V1 βa retrieval algorithm is constrained to be one-dimensional (i.e., the atmospheric properties vary only with altitude). A two-dimensional SS version of GSLS (allowing atmospheric properties to vary along the LOS as well as with altitude) has recently been developed (Loughman et al., 2016), and a full MS version of this model is currently under development.
3.3 Aerosol properties
The LS radiance is affected by several aerosol properties. The V1 algorithm described in this paper employs assumptions for several of these properties in order to deduce the βa based on observations of the LS radiance I(λ, h).
3.3.1 Aerosol shape and optical properties
First, the stratospheric aerosols are assumed to be spherical droplets of sulfuric acid (H2SO4). Mie theory is used to calculate the aerosol scattering and extinction properties, based on the aerosol refractive index values given in Table 1. These assumptions exclude numerous processes that may contribute significantly to the stratospheric aerosols found at particular places and times (e.g., volcanic ash, meteoric dust, various tropospheric aerosols that enter the stratosphere). However, the assumption that “aged” aerosol in the Junge layer is dominated by such H2SO4 droplets agrees with observations dating back to the earliest studies of stratospheric aerosol (Junge et al., 1961b) and is assumed in all previous LS βa retrieval algorithms. The assumption is less supportable under “perturbed” stratospheric conditions (such as the immediate aftermaths of volcanic eruptions), as noted by Vernier et al. (2016), or at the upper and lower boundaries of the Junge layer, which may have more meteoric content above and more tropospheric aerosol near the tropopause.
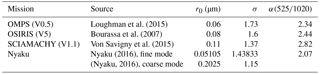
Table 1Aerosol optical properties and aerosol size distribution (ASD) assumed in the V1 OMPS LP aerosol extinction retrieval.

3.3.2 Aerosol size distribution (ASD)
In the V1 algorithm, the ASD is modeled as a bimodal lognormal (LN) distribution, as specified in Table 1. This ASD is defined by Eq. (1):
Five independent parameters are required to specify the shape of the bimodal LN ASD: two median radii (r1 and r2), two mode widths (σ1 and σ2), and one more parameter indicating the relative sizes of the aerosol concentration associated with each mode (N1, N2). In this work, the mode with the smaller median radius value (r1) is called the “fine mode”, while the other mode is the “coarse mode”. Therefore the relative sizes of the aerosol modes are described by the “coarse-mode fraction” fc = . (Changes in the absolute values of N1 and N2 alter the magnitude of the βa for a given distribution but do not change the shape of the ASD for a given fc value.)
The ASDs used in several other LS βa retrieval algorithms are given in Table 2. These properties have typically been taken from the long record of balloon-borne optical particle counter (OPC) data provided by T. Deshler's group at the University of Wyoming. But this data set indicates that the ASD varies considerably with time, location, and altitude. For example, the V1.1 SCIAMACHY ASD (Von Savigny et al., 2015) is taken from Fig. 3c in Deshler et al. (2008) (excluding the coarse mode). Bourassa et al. (2007) and Rieger et al. (2014) cite Deshler et al. (2003) as the source of the V5 OSIRIS ASD, which resembles Fig. 5b of that reference (again excluding coarse-mode particles). Nyaku (2016) uses the 2012–2013 data provided by the University of Wyoming website for Laramie as the basis of the bimodal LN ASD for sensitivity studies, as cited earlier in Loughman et al. (2015). Unfortunately, the OPC data corrections described by Kovilakam and Deshler (2015) occurred after the OSIRIS, SCIAMACHY, and Nyaku ASDs described in this paragraph were defined, so none of those ASDs reflect the corrected version of the OPC data.
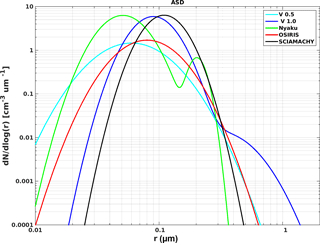
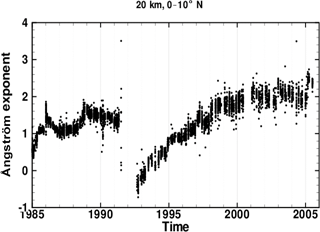
Figure 7 Ångström exponent α(525∕1020) derived from SAGE II SOT measurements during its measurement history. This picture corresponds to measurements at altitude 20 km for the 0–10∘ N latitude bin. Cases for which the measured aerosol extinction at 1020 nm km were excluded from this analysis (L. Thomason, private communication).
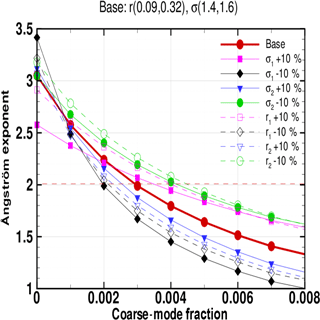
Figure 8 Variation of Ångström exponent α(525∕1020) with aerosol properties for the V1 OMPS LP aerosol extinction retrieval algorithm characteristics. Each curve shows the variation of (α(525∕1020) with fc for a given set of median radii and mode widths. In addition to the “base” curve (which uses the V1 characteristics listed in Table 1), several curves show how the value of α(525∕1020) changes as the values of , and σ2 (in Table 1) are perturbed by ±10 %.
The apparent lack of consistency in the stratospheric aerosol ASD poses a significant problem for efforts to retrieve βa from LS measurements, as discussed further in Sect. 5.2. A single-mode LN ASD is assumed in stratospheric βa retrievals by the V5 OSIRIS (Bourassa et al., 2007), V1.1 SCIAMACHY (Von Savigny et al., 2015), and intermediate V0.5 OMPS LP retrievals, as shown in Table 2. The assumed median radius (r0), mode width (σ), and resulting Ångström coefficient α(525∕1020) (defined below in Eq. 2) are shown in Table 2, and several single-mode and bimodal LN ASDs are shown in Fig. 6. Table 2 also includes the properties of the bimodal LN ASD analyzed by Nyaku (2016).
For the V1 OMPS LP βa retrieval algorithm, we introduce the added complexity of the bimodal LN ASD because it generally describes the properties of stratospheric aerosol observations better (Thomason and Peter, 2006). The fine- and coarse-mode properties of the V1 OMPS ASD (given in Table 1) were selected based on the data found in Table 1a of Pueschel et al. (1994). These observations were taken on 23 August 1991, in the aftermath of the eruption of Mt. Pinatubo, and are based on in situ measurements by impactor samplers flown on an ER-2 aircraft in the lower stratosphere. The intention of this choice was to keep the observed fine mode for stratospheric aerosols (with properties broadly similar to the single-mode LN ASDs shown in Table 2), while introducing the possibility of a coarse mode of larger aerosols. The recent eruption of Mt. Pinatubo causes fc=0.36 in the selected Pueschel et al. (1994) data, which is much larger than one would expect in the background stratosphere. Therefore the relative prominence of the coarse mode was reduced for the V1 OMPS LP βa algorithm by tuning the fc value, based on the following considerations drawn from the available stratospheric aerosol data record:
-
The SAGE satellite series (particularly SAGE II) provides a long-term record of βa profiles for stratospheric aerosols at several wavelengths. The βa wavelength variation can be expressed by the Ångström coefficient α, which is defined by Eq. (2) based on observations of βa at 525 and 1020 nm. The SAGE II zonal mean α value for the tropics at 20 km is shown in Fig. 7. Except for volcanically perturbed periods, the observed α value at this altitude is relatively constant at α≈2. This value tends to grow with altitude above the peak of the stratospheric aerosol layer, approaching α≈2.5 at 30 km.
-
Figure 8 shows how α varies with coarse-mode fraction fc, for fine- and coarse-mode fraction values in the vicinity of the V1 OMPS LP ASD values (r1, σ1, r2, and σ2 in Table 1). For these assumed fine- and coarse-mode properties, the value of α is extremely sensitive to fc. If one assumes that the fine and coarse modes are correctly specified, this implies that fc can be determined with great precision based on the observed value of α. The V1 OMPS LP βa retrieval algorithm uses fc=0.003 in conjunction with the Pueschel et al. (1994) values of , and σ2 to produce α=2.
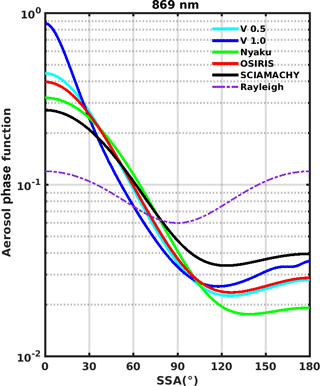
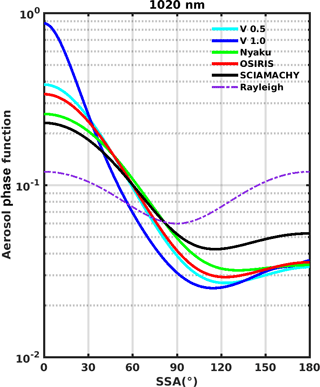
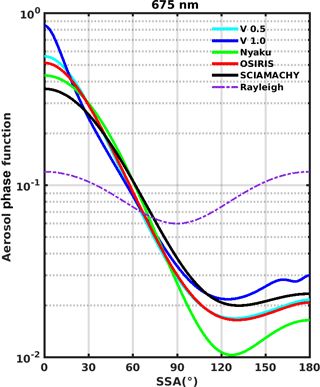
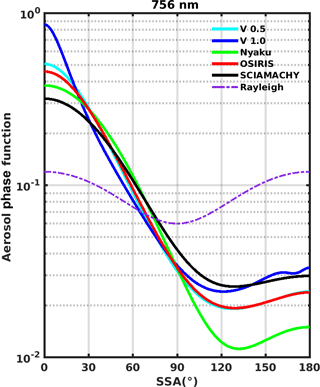
The differences among the V1 algorithm assumed Pa and the phase functions associated with other LS βa retrievals are shown in Figs. 9–12 for 675, 756, 869, and 1020 nm. To assess the sensitivity of the V1 ASD, we also present Fig. 13, in which , and σ2 in Table 1 are perturbed by 10% (while fc is also adjusted to maintain α≈2). This analysis shows the greatest percentage change in Pa (up to 30 %) for Θ>90∘ when σ1 is perturbed. Figure 13 also includes the Pa when r1, σ1, r2, and σ2 remain at their default values (shown in Table 1), but fc is varied: in one case fc=0.0012 (producing α=2.5), while in the other case fc=0.006 (producing α=1.5). As expected, the Pa becomes more “Rayleigh-like” as α increases, but the change in Pa is relatively modest (generally < 10 %) except for small scattering angles (Θ<30∘). The impact of the Pa is discussed further in Sect. 5.2.
3.4 Properties of altitude-normalized radiances (ANRs)
As explained in Sect. 4.1, the V1 algorithm uses ANRs rather than radiances to define the measurement vector y. The ANR is defined as , with the radiance at the tangent height h of interest divided by the radiance at a selected normalization tangent height hn>h. For the V1 algorithm, hn=40.5 km. In Fig. 14, ρ at 675 nm is calculated for a range of scattering angles using the V1 OMPS LP ASD. The βa, ozone, pressure, and temperature profiles are fixed for the radiance calculations shown in Fig. 14, in order to isolate the dependency of ρ on Θ and R. In Fig. 14, h and hn are 25.5 and 40.5 km, respectively.
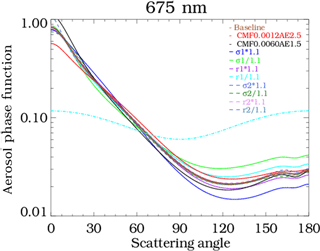
Figure 13Aerosol phase function sensitivity to perturbations of the aerosol size distribution, using the V1 aerosol size distribution as a baseline. Note that the ±10 % perturbations of , and σ2 also involved adjustments of fc to keep α≈2. Two other perturbations are shown, in which the values of , and σ2 remain at the V1 aerosol size distribution values, but fc is varied: CMF0.0012AE2.5 (red line) indicates that fc=0.0012 (producing α=2.5), and CMF0.0060AE1.5 (black line) indicates that fc=0.06 (producing α=1.5)
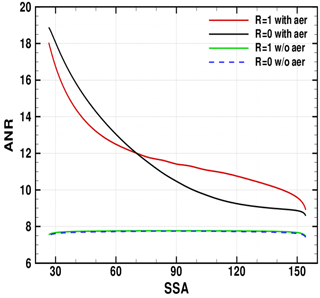
Figure 14Altitude-normalized radiances (ANR, or ρ) at 675 nm as a function of SSA (or Θ) under aerosol-free and aerosol conditions, with both non-reflecting (R=0) and perfectly reflecting (R=1) surface conditions. The values of h and hn are 25.5 and 40.5 km, respectively.
When aerosols are excluded from the model atmosphere, Fig. 14 shows that the ρ is insensitive to both Θ and R. But when aerosols are included, several effects emerge:
-
ρ is sensitive to Θ due to the strong variation of the Pa with Θ, as shown in Fig. 3. For cases in which R is low, the variation of ρ with Θ can be estimated by the variation of the phase function ratio Pa∕PR, in which the Pa is divided by the Rayleigh phase function PR. The phase function ratio varies with Θ as shown in Fig. 15.
-
ρ also shows some dependence on R when aerosols are included. However, this effect is relatively small compared to the effect of R on the radiance, which can reach 100 % at large values of R.
-
As noted above, ρ decreases with increasing Θ, showing similar behavior to the Pa∕PR ratio when the underlying scene is dark. But this decrease becomes more gradual for brighter scenes, in which the ρ dependence on Θ is flattened out. As the underlying scene becomes brighter, the limb radiance is influenced more by DUR. This upwelling radiation illuminates the LOS from a variety of directions, reducing the influence of the solar scattering angle Θ on ρ. As a result, ρ becomes less sensitive to the details of Pa(Θ) as R increases.
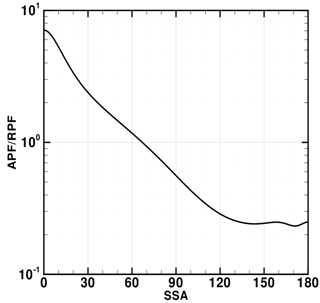
Figure 15The ratio of APF (or Pa) to RPF (or PR) as a function of SSA (or Θ) for the V1 OMPS LP aerosol size distribution. This ratio declines by a factor of ≈50 between forward (Θ=0∘) and backward (Θ=180∘) scattering conditions.
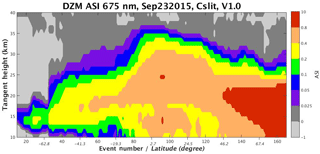
Figure 16Daily zonal mean aerosol scattering index (ASI, or y) measured by the SNPP OMPS LP instrument. This picture corresponds to center slit observations on 23 September 2015. The x axis is labeled with both the event number (solid) and tangent point latitude (italics). The color scale is nonlinear, designed to highlight relatively small y values in the SH.
4.1 Aerosol scattering index (ASI)
The V1 algorithm uses the ASI as its measurement vector y. The ASI is defined as , where ρm is the measured ANR and ρR is the ANR calculated assuming an aerosol-free (and therefore purely Rayleigh scattering) atmosphere bounded by a Lambertian reflecting surface of reflectivity R. The value of R is derived from 675 nm sun-normalized radiances measured at hn=40.5 km, as discussed in Sect. 3.4. The radiance calculation that determines R assumes that no aerosols are present along the LOS at hn=40.5 km, which forces y=0 at hn. We initially assume a climatological ozone profile to account for the weak ozone absorption at 675 nm. The ozone estimate is then updated at the final step of the retrieval, as described in Sect. 4.3.
For an optically thin LOS, the ANR is approximately the sum of ρa (the ANR due to aerosol scattering) + ρR (the ANR due to Rayleigh scattering). In that case, the measured ANR = , and therefore the ASI = . It is also true under these conditions that . However, under more general conditions the scattering contributions cannot be treated independently: attenuation of Rayleigh-scattered photons by aerosols (and vice versa) can cause y to become negative at some altitudes. This indicates that the aerosol attenuation effect has exceeded the aerosol scattering effect. This behavior can be seen in Fig. 16, particularly at the southern end of the orbit (where the OMPS LP aerosol signal is weakest). Figure 16 shows a strong hemispheric contrast in y, which simply reflects the variation of Pa with Θ.
Finally, note that use of y (and its dependence on ρ) is best suited for a circumstance in which an “aerosol-free” layer lies above the aerosols of interest. That implicit assumption is consistent with the fact that H2SO4 droplets evaporate completely in the 30–35 km altitude range, due to the warmer stratospheric temperatures at that level (Toon and Pollack, 1973). But use of y makes us unable to detect aerosol scattering that has a constant mixing ratio with height (relative to molecular scattering), so the contributions of other aerosol sources such as meteoric smoke (Hervig et al., 2009) require further investigation.
4.2 Inverse model
The V1 algorithm uses OMPS LP radiance measurements at a single wavelength (675 nm) to estimate the βa profile. This wavelength was selected primarily to provide aerosol information to the V2.5 ozone code that uses a wavelength triplet (consisting of 510, 600, and 675 nm) to retrieve the ozone profile (Kramarova et al., 2017). Since both βa and Pa have strong wavelength dependence in the stratosphere, aerosol profiles derived from a wavelength near the Chappuis ozone band are expected to minimize aerosol-related errors in the ozone retrieval.
Several additional advantages make selecting a wavelength near 700 nm optimal for OMPS LP aerosol retrievals. Wavelengths < 500 nm feature weak ozone absorption, but large Rayleigh scattering obscures the aerosol signal. OMPS LP also measures wavelengths longer than 675 nm, but these tend to be more affected by internal instrument SL. The OMPS LP instrument was designed and characterized primarily with the goal of ozone retrieval, and therefore successful characterization of SL at the longer wavelengths is an ongoing project. Longer wavelengths are also more sensitive to the highly uncertain ASD than 675 nm (see Figs. 10–12), making 675 nm attractive for βa retrievals.
The V1 algorithm uses the Chahine nonlinear relaxation method (Chahine, 1970) to obtain the βa from the OMPS LP measurements. Since ASI is roughly proportional to βa, we use ASI as the measurement vector y, which is updated iteratively as shown in Eq. (3), based on the notation of Rodgers (2000), Sect. 6.8:
The symbol represents the state vector (βa) at altitude zi after n iterations of the retrieval algorithm. The measurement vector represents the measured y at tangent height hi=zi. The GSLS RT model calculates the ASI vector at each iteration, using the βa profile given by . The iterative process is initialized with a nominal first-guess aerosol profile derived from 2000–2004 SAGE data (shown as Fig. 17), which does not vary with latitude or season. Figure 18 shows the daily zonal mean βa retrieved from the y values shown in Fig. 16. Note that the hemispheric asymmetry shown in the y figure is not repeated in the βa figure.
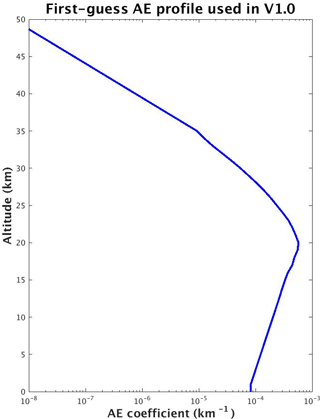
Figure 17The first-guess aerosol extinction (or AE) profile used in the V1 OMPS LP aerosol extinction retrieval algorithm.
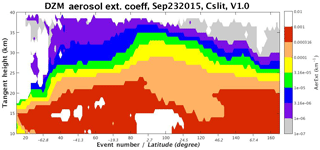
Figure 18Daily zonal mean aerosol extinction for center slit observations on 23 September 2015 (derived from the y measurements shown in Fig. 16).
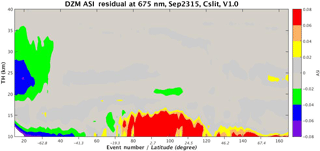
Figure 19Daily zonal mean aerosol scattering index (ASI, or y) residuals for center slit observations on 23 September 2015 (derived from the y measurements shown in Fig. 16).
The retrieval is constrained to limit changes within a single iteration: xi can increase by no more than a factor of 2, while decreases are limited to be a factor of 5 or less in each iteration. The algorithm executes just three iterations, which constrains the final solution at each altitude within the range of values . The retrieval algorithm sets xi to zero for observations with weak aerosol signals (where ). Data at altitudes for which a cloud has been detected by the algorithm described by Chen et al. (2016) are flagged. An example of the residual (difference between measured and calculated) y is presented in Fig. 19, which demonstrates general convergence to the ±2 % level except at altitudes < 15 km and for regions near the South Pole (where the SNPP OMPS LP aerosol signal is weakest).
4.3 Ozone correction
The V1 βa algorithm operates independently from the ozone retrieval algorithm (Kramarova et al., 2017). As noted in Sect. 4.1, a climatological ozone profile is assumed during the iterations of the βa retrieval. After those three iterations are complete, an approximate ozone correction is applied as follows. For λ1,λ2, and λ3=510, 600, and 675 nm, respectively, we define in terms of the measured radiance (Im) and the calculated radiance (Ic) at each wavelength:
Based on these three Y values, we define a three-parameter fit:
where σi = the ozone absorption cross section averaged over the OMPS LP bandpass centered at λi. The c parameter represents the sensitivity of the ozone slant column density with respect to the first guess and can be determined from Eq. (6):
The ozone-corrected value of Y at 675 nm is therefore denoted by Yc(λ3):
A similar correction is also applied to the value of Y at the normalization tangent height to obtain Yc (hn,λ3).
This section describes the most significant categories of uncertainty that we anticipate will limit the accuracy and precision of the V1 retrievals. Quantitative estimates of the anticipated error are provided when possible, but a full algorithm error budget is beyond the scope of this study. Unfortunately, many uncertainties are difficult to quantify for the full range of possible conditions.
To provide an overall context for assessing the significance of various error sources, we begin by detailing the process used to estimate the atmospheric number density profile used in the V1 βa retrieval algorithm. This profile is derived from the operational geopotential height product provided by the NASA Global Modeling and Assimilation Office (GMAO), which has reduced quality at altitudes above 35 km. The resulting uncertainty has been estimated by comparisons with the Modern-Era Retrospective analysis for Research and Analysis, Version 2 (MERRA-2) fields, which incorporate Microwave Limb Sounder (MLS) temperature profiles above 35 km (Gelaro et al., 2017). This comparison indicates both noise and bias at the 1–2 % level for calculation of radiances at h=40 km.
We therefore neglect error sources that exist below this 1–2 % “floor” level and concentrate on error sources that exceed that threshold. This criterion eliminates both stray light and random error associated with the OMPS LP measurements, which typically are < 1 %.
5.1 Uncertainty due to measurement errors
As defined in Sect. 4.1, our measurement vector y is influenced by four radiances (all at λ=675 nm): the measured radiance at the tangent height of interest hi and the normalization tangent height hn, and the calculated radiance (excluding aerosol from the model atmosphere) at the same tangent heights. The primary source of error in y appears to be the SL error at hn. OMPS LP stray light acts roughly as an additive effect (Jaross et al., 2014) and therefore affects the measured radiance at hn much more strongly than the other radiances that form y, due to the roughly exponential decrease of I with tangent height. Internal analysis suggests that this error is 1 %, and it therefore produces fractional error in . Stray-light error therefore becomes most significant at altitudes and latitudes where y is small (<0.1). As shown in Fig. 16, this condition is most likely to occur near the top of the Junge layer ( km) and/or near the South Pole (where SNPP OMPS LP provides unfavorable viewing conditions for βa retrieval, with large Θ producing small Pa values).
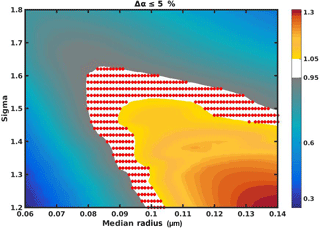
Figure 20Contour plot showing the ratio of the Ångström coefficient α for a given aerosol size distribution to the V1 aerosol size distribution α≈2. Cases for which this ratio is within ±5 % of 1 are highlighted in white. The coarse-mode properties are fixed in this example at the V1 aerosol size distribution values (r2=0.32 µm; σ2=1.6), while the fine-mode properties vary in the vicinity of the V1 aerosol size distribution values (r1=0.09 µm; σ1=1.4). Red circles indicate the individual cases calculated to create this figure.
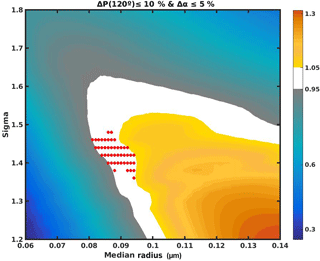
Figure 21The background contour plot is the same as in Fig. 20. This time, red circles appear only for cases in which the Ångström coefficient ratio is within ±5 % of 1 and the aerosol phase function is within ±10 % of the V1 aerosol size distribution value at Θ=60∘. Nearly every aerosol size distribution that satisfies the Ångström coefficient ratio criterion also satisfies the aerosol phase function criterion for this case.
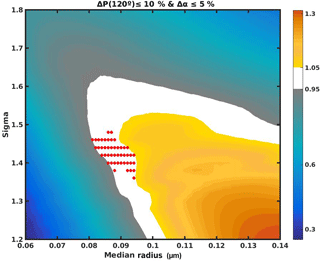
Figure 22Identical to Fig. 21 except that the aerosol phase function comparison is done for Θ=120∘. For this viewing geometry, the aerosol phase function criterion is much more useful in determining the aerosol size distribution properties: Note the smaller number of red circles (relative to Fig. 21), centered around the true values of r1 (0.09 µm) and σ1 (1.4).
5.2 Uncertainty due to radiative transfer limitations
The GSLS radiative transfer model used in the V1 OMPS LP βa retrieval algorithm contains several limitations that affect the retrieved βa profiles. The most significant issues are listed below, in order of priority.
-
Uncertainty in the aerosol scattering phase function Pa
As described in Sect. 3.3.2, we have selected a bimodal LN ASD to calculate the assumed Pa used in the V1 βa retrieval algorithm. However, we cannot expect that any single ASD will be correct for the full range of OMPS LP observations. And even if a single ASD were suitable, many plausible combinations of and fc exist that would fit the criterion stated in Sect. 3.3.2 (α≈2) equally well, as shown in Fig. 20. Whether these “plausible” ASDs produce significantly different Pa values depends strongly on Θ. As shown in Fig. 3, the Pa for backscattered directions varies much more strongly with Θ than the Θ=30–90∘ directions. The sensitivity of Pa to ASD for the cases shown in Fig. 20 is illustrated in Figs. 21–22.
Since ρa is approximately proportional to Pa for optically thin LOS, differences between the assumed and true Pa values map directly into βa errors in the V1 algorithm. Figure 22 therefore predicts that the OMPS LP βa retrievals for Θ=120∘ will be greatly affected by the assumed ASD in the retrieval, while Fig. 21 shows that the OMPS LP βa retrievals for Θ=60∘ will be nearly insensitive to the assumed ASD. The preceding analysis roughly estimates the possible error that may result in the V1 OMPS LP βa retrievals, but it provides no clear method to estimate the error in a single retrieval at a particular place, time, and altitude. This topic will be explored more thoroughly in a future publication.
-
Uncertainty due to LOS variation in atmospheric properties
As noted in Sect. 3.1, the RT model in the V1 OMPS LP βa retrieval assumes that the atmospheric properties vary only with altitude. This assumption is used to retrieve βa for each measured image, independent of the neighboring images. But the maps of retrieved βa values regularly feature large horizontal variations, particularly latitudinal variations (see Fig. 18). Many such features persist at particular latitude ranges for which stratospheric dynamics are known to cause steep horizontal gradients in βa at a given altitude.
The viewing geometry of OMPS LP (looking backwards along the sun-synchronous orbital track) exacerbates this problem, due to the zonal gradients in βa seen in Fig. 18, but LOS variations of atmospheric properties affect all limb-viewing retrieval methods. Past limb missions have developed a two-dimensional retrieval strategy that allows variation of the retrieved quantity both along the LOS and with altitude. The MLS (limb emission) mission (Livesey and Read, 2000) and OSIRIS (LS) mission (Zawada et al., 2015) have made notable progress in this area. The V1 OMPS LP algorithm remains a 1-D solution (with βa varying only with altitude). This assumption is likely to affect the retrieval most strongly at the edge of the tropics (where βa tends to have a large horizontal gradient), in the Northern Hemisphere (where y varies rapidly with Θ), and at the edges of a fresh volcanic cloud.
-
Uncertainty due to approximate treatment of DUR
The limb LOS is illuminated from above (overwhelmingly by direct solar radiation) and from below (by photons scattered within the underlying atmosphere and/or reflected by the underlying surface). The latter source of radiation is modeled as described in Sect. 3.2: A Lambertian surface is assumed to lie beneath the model atmosphere (which is not updated outside the range at which the βa is retrieved during the iteration process). This assumption allows one to determine R, the effective Lambertian surface reflectivity that is consistent with the measured radiance at hn=40.5 km.
This assumption provides a first-order estimate of the DUR, but this estimate will generally be imperfect for the following reasons:
- a.
The simple assumptions described above generally fail to represent the true conditions below a given LOS in multiple ways: the atmosphere will generally include clouds and aerosols below the LOS that are not included in the model atmosphere. The true bi-directional reflectance distribution model (BRDF) of the scene will also generally be non-Lambertian. In such cases, the upwelling radiation in the model calculation will have a different angular distribution than the upwelling radiation in the true atmosphere.
- b.
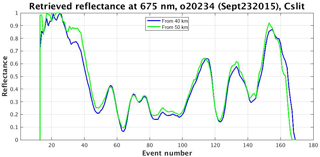
For an inhomogeneous underlying scene, the effective LER may also vary with h, due to the varying solid angle that contributes to I(h). The difference between LER (h=40 km) and LER (h=50 km) is typically slight (see Fig. 23), implying that this is a minor effect, but more research is needed to assess whether any systematic relationships exist.
5.3 Inverse model errors
This section includes several effects unrelated to the radiative transfer model that affect the V1 OMPS LP βa retrieval, again listed in order of priority.
-
Large aerosol extinction
As noted in Sect. 4.2, the algorithm limits possible variation of the retrieved βa value. As a result, the retrieval often “saturates” at the maximum allowed value when the βa is large relative to the first-guess profile. At higher extinction values, the retrieval will also be more influenced by inhomogeneity along the LOS, since the LS radiance will be more influenced by the LOS segment nearest the sensor (see item 3 below).
-
Cloud detection algorithm
The current cloud detection algorithm (Chen et al., 2016) detects clouds well, but it sometimes also flags fresh volcanic aerosols as clouds. Since retrieval of such aerosols is quite complicated for several reasons discussed earlier (LOS inhomogeneity, uncertainty about the appropriate Pa due to a mixture of aerosol types and shapes, etc.), we have not attempted to fix this error.
-
Poor convergence
The algorithm often does not converge well for scenes in which the y has large horizontal gradient. We believe that this occurs because of 2-D effects discussed earlier in Sect. 5.2, which produce an asymmetry in the LS radiance contribution function. Under optically thick conditions, the LS radiance will be influenced by the atmosphere near the satellite much more than the atmosphere far from the satellite at a given altitude. This effect is illustrated in Fig. 6c of Loughman et al. (2015). Fixing this problem will require the development of a 2-D aerosol algorithm.
5.4 Ozone correction errors
The 675 nm radiances used in the V1 OMPS LP βa retrieval algorithm lie within the Chappuis ozone absorption band, and therefore the βa estimate is influenced by possible differences between the true ozone profile and the ozone profile that is assumed in the calculation of in Eq. (3). We therefore apply the ozone correction described in Sect. 4.3 to reduce this source of error. This correction produces the largest percentage change in the retrieved βa value when the following conditions are met:
-
the a priori ozone concentration differs significantly from the true ozone concentration,
-
y is relatively small for a given βa value,
-
the βa value itself is small.
The first condition is most likely to occur for regions with highly variable ozone profiles. The second condition will prevail for regions that are viewed by OMPS LP at large Θ values, where the corresponding Pa value is small. The third condition occurs primarily in regions with low βa values, typically where sinking air prevails in the mid-stratospheric region.
The largest ozone corrections therefore typically appear near the South Pole, where minima for both the y and βa at a given altitude tend to occur, as shown in Figs. 16 and 18, respectively. The ozone profile also exhibits large variation in this region, partly due to the formation of the Antarctic spring ozone hole. Under these extreme conditions, the ozone correction produces changes in the retrieved βa value as large as 20 %. For a more typical case in the tropics, the βa changes by < 3 % when the ozone correction is applied.
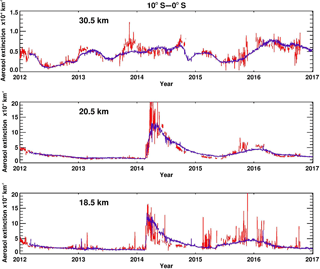
Figure 24OMPS LP V1 (blue line) and OSIRIS V5.07 (red line) retrieved aerosol extinction daily zonal means at selected altitudes from 2012 to 2016, at latitudes between 10 and 0∘ S. The OSIRIS data set reports aerosol extinction at 750 nm, so the OMPS aerosol extinction was converted from 674 to 750 nm by using the Ångström coefficient consistent with the aerosol size distribution assumed in the OMPS LP V1 algorithm.
In this section, we will only present an early qualitative evaluation of OMPS LP V1 βa data in comparison with profiles derived from OSIRIS LS radiances and Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO; Winker et al., 2009) backscattered lidar measurements. A detailed validation paper for the OMPS LP βa retrievals is in preparation.
Figure 24 shows OMPS LP V1 and OSIRIS V5.07 retrieved βa in the tropics. In general, the two data sets agree to within 25 %. OSIRIS daily means are noisier because of its relatively limited coverage, which provides fewer profiles for a given day than OMPS. Both OMPS and OSIRIS show enhanced aerosol values at 18.5 and 20.5 km following the tropical volcanic eruptions of Nabro (June 2011) and Kelut (February 2014). Transport of the plume associated with Calbuco (which erupted in the Southern Hemisphere in May 2015) is also evident. At 20.5 km, OMPS measurements are lower than OSIRIS during the peak of the Kelut plume, most likely caused by the retrieval's restriction on the number of iterations (see Sects. 4.2 and 5.3), although differences between the OMPS LP and OSIRIS coverage patterns can contribute to such differences. At 30.5 km, both instruments clearly show the quasi-biennial oscillation (QBO) signature of enhanced βa values during easterly shear conditions of the QBO (Trepte and Hitchman, 1992) during early 2012, 2013–2014, and 2016, caused by enhanced aerosol lofting. The lower values of βa in 2012 and 2015 are associated with westerly shear conditions of the QBO, causing downward aerosol transport.
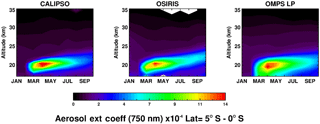
Figure 25Monthly zonal mean aerosol extinction profiles at 750 nm derived from CALIPSO, OSIRIS, and OMPS LP measurements during the aftermath of the Kelut eruption in 2014.
Figure 25 shows monthly zonal mean βa profiles at 750 nm derived from CALIPSO, OSIRIS, and OMPS LP measurements during 2014. This time series is averaged from 5 to 0∘ S, and altitudes 15–35 km are illustrated. CALIPSO data were provided by Vernier et al. (2011) and Vernier et al. (2015). The three instruments track Kelut injection of volcanic aerosol at 20 km and the upward lofting of the aerosol to higher altitudes (≈ 25 km) within a few months. The CALIPSO data are based on a series of narrow lidar swaths, so its coverage differs from OSIRIS and OMPS LP coverage. Vertical resolution differences might also explain some the differences seen among the three instruments.
The OMPS LP V1 aerosol extinction (βa) retrieval algorithm is summarized in this document. The V1 algorithm differs from the most recently published OMPS LP algorithm (given in Rault and Loughman, 2013) in several ways:
-
the βa profile is retrieved at a single wavelength, 675 nm;
-
the assumed ASD is bimodal lognormal, guided by the aerosol properties measured by Pueschel et al. (1994) with the coarse-mode fraction tuned to produce Ångström coefficient .
The main motivation for these changes was to produce a simpler algorithm that works with the best-characterized OMPS LP radiances. The resulting βa profiles are more stable and permit more straightforward analysis of the radiance residuals. Initial comparisons with coincident OSIRIS and CALIPSO βa data show similar spatial and temporal variation over the lifetime of the OMPS LP instruments.
The accuracy of the absolute value of the OMPS LP βa remains variable, primarily due to uncertainty about the appropriate ASD to be used. The V1 ASD selection was guided by the Ångström coefficient measured by SAGE II during volcanically quiescent periods. But the lack of contemporaneous global observations of the ASD presents a significant challenge for all LS βa retrievals, particularly for observations at Θ>90∘ (Southern Hemisphere conditions for OMPS LP). The recently launched ISS SAGE III instrument is capable of both SOT and LS observations, which should provide valuable information to reduce uncertainty in the Pa for stratospheric aerosols.
Future work to improve the OMPS LP βa algorithm will begin by adding consideration of additional wavelengths. Longer wavelengths are sensitive to lower tangent heights that typically saturate at 675 nm due to interference by Rayleigh scattering and are also more sensitive to small aerosol signals (such as OMPS LP encounters in the Southern Hemisphere). Additional wavelengths also will allow us to asses the self-consistency of the measured βa wavelength variation with the Mie theory prediction for the assumed ASD. A 2-D algorithm will also improve performance in the vicinity of large horizontal variations. The ability to allow the ASD to vary with height will also be valuable, given better ASD information.
The retrieved profiles produced by the V1 OMPS LP aerosol extinction retrieval algorithm are publicly available at the following site: https://ozoneaq.gsfc.nasa.gov/data/ozone/ (NASA, 2018).
The Suomi NPP daily files for the aerosol extinction product are labeled as “OMPS Limb Profiler –Suomi NPP – LP-L2–AER675-DAILY”.
The authors declare that they have no conflict of interest.
This paper includes material that first appeared at the 8th and 9th
Atmospheric Limb Workshops, which were hosted by Chalmers University
(Gothenburg, Sweden, September 2015) and the University of Saskatchewan
(Saskatchewan, Canada, June 2017), respectively. This research was supported
by NASA Goddard Space Flight Center through SSAI subcontracts 21205-12-043
and 21702-17-010. The authors recognize the contributions of the SAGE,
OSIRIS, SCIAMACHY, CALIPSO, and University of Wyoming teams to maintaining
high-quality stratospheric aerosol data, and particularly thank Larry
Thomason, Terry Deshler, Adam Bourassa, Landon Rieger, Christian von Savigny,
Alexei Rozanov, and Jean-Paul Vernier for helpful insights into the
stratospheric aerosol problem. Surendra Bhatta contributed significantly to
preparing the figures and references. The NASA, SSAI, and NOAA OMPS teams
supported this research and contributed many useful discussions, including
Larry Flynn, Matt DeLand, Jack Larsen, and Tong Zhu. Finally, several summer
research students contributed to studies that have improved this work,
including Nelson Ojeda, Ryan McCabe, and Ashley Orehek.
Edited by: Christian von Savigny
Reviewed by:
two anonymous referees
Andersson, S. M., Martinsson, B. G., Vernier, J. P., Friberg, J., Brenninkmeijer, C. A., Hermann, M., van Velthoven, P. F., and Zahn, A.: Significant radiative impact of volcanic aerosol in the lowermost stratosphere, Nat. Commun., 6, 7692, https://doi.org/10.1038/ncomms8692, 2015. a
Bertaux, J. L., Kyrölä, E., Fussen, D., Hauchecorne, A., Dalaudier, F., Sofieva, V., Tamminen, J., Vanhellemont, F., Fanton d'Andon, O., Barrot, G., Mangin, A., Blanot, L., Lebrun, J. C., Pérot, K., Fehr, T., Saavedra, L., Leppelmeier, G. W., and Fraisse, R.: Global ozone monitoring by occultation of stars: an overview of GOMOS measurements on ENVISAT, Atmos. Chem. Phys., 10, 12091–12148, https://doi.org/10.5194/acp-10-12091-2010, 2010. a
Boucher, O.: On aerosol direct shortwave forcing and the henyey-greenstein phase function, J. Atmos. Sci., 55, 128–134, 1998.
Bourassa, A. E., Degenstein, D. A., Gattinger, R. L., and Llewellyn, E. J.: Stratospheric aerosol retrieval with optical spectrograph and infrared imaging system limb scatter measurements, J. Geophys. Res.-Atmos., 112, D10217, https://doi.org/10.1029/2006JD008079, 2007. a, b, c, d, e
Bourassa, A. E., Degenstein, D. A., and Llewellyn, E. J.: Retrieval of stratospheric aerosol size information from OSIRIS limb scattered sunlight spectra, Atmos. Chem. Phys., 8, 6375–6380, https://doi.org/10.5194/acp-8-6375-2008, 2008a. a
Bourassa, A. E., Degenstein, D. A., and Llewellyn, E. J.: SASKTRAN: A spherical geometry radiative transfer code for efficient estimation of limb scattered sunlight, J. Quant. Spec. Rad. Trans., 109, 52–73, 2008b. a, b
Bourassa, A. E., Degenstein, D. A., Elash, B. J., and Llewellyn, E. J.: Evolution of the stratospheric aerosol enhancement following the eruptions of Okmok and Kasatochi: Odin-OSIRIS measurements, J. Geophys. Res., 115, D00L03, https://doi.org/10.1029/2009JD013274, 2010. a
Bourassa, A. E., Rieger, L. A., Lloyd, N. D., and Degenstein, D. A.: Odin-OSIRIS stratospheric aerosol data product and SAGE III intercomparison, Atmos. Chem. Phys., 12, 605–614, https://doi.org/10.5194/acp-12-605-2012, 2012. a, b
Bovensmann, H., Burrows, J. P., Buchwitz, M., Frerick, J., Noël, S., Rozanov, V. V., Chance, K. V., and Goede, A. P. H.: SCIAMACHY: Mission Objectives and Measurement Modes, J. Atmos. Sci., 56, 127–150, 1999. a
Brock, C. A., Hamill, P., Wilson, J. C., Jonsson, H. H., and Chan, K. R.: Particle Formation in the Upper Tropical Troposphere: A Source of Nuclei for the Stratospheric Aerosol, Science, 270, 1650–1653, https://doi.org/10.1126/science.270.5242.1650, 1995. a
Chahine, M.: Inverse problems in radiative transfer: A determination of atmospheric parameters, J. Atmos. Sci, 27, 960–967, 1970. a, b
Chen, Z., DeLand, M., and Bhartia, P. K.: A new algorithm for detecting cloud height using OMPS/LP measurements, Atmos. Meas. Tech., 9, 1239–1246, https://doi.org/10.5194/amt-9-1239-2016, 2016. a, b, c
Cisewski, M., Zawodny, J., Gasbarre, J., Eckman, R., Topiwala, N., Rodriguez-Alvarez, O., Cheek, D., and Hall, S.: The Stratospheric Aerosol and Gas Experiment (SAGE III) on the International Space Station (ISS) Mission, Proc. SPIE, 9241, 924107, https://doi.org/10.1117/12.2073131, 2014. a
Cziczo, D., Thomson, D., and Murphy, D.: Ablation, flux, and atmospheric implications of meteors inferred from stratospheric aerosol, Science, 291, 1772–1775, 2001. a
Deshler, T., Hervig, M. E., Hoffman, D. J., Rosen, J. M., and Liley, J. B.: Thirty years of in situ stratospheric aerosol size distribution measurements from Laramie, Wyoming (41∘ N), using balloon-borne instruments, J. Geophys. Res., 108, 4167, https://doi.org/10.1029/2002JD002514, 2003. a
Deshler, T., Hervig, M. E., Hofmann, D. J., Rosen, J. M., and Liley, J. B.: Measurements, importance, life cycle, and local stratospheric aerosol, Atmos. Res., 90, 223–232, 2008. a, b
Ernst, F.: Stratospheric aerosol extinction profile retrievals fro SCIAMACHY limb-scatter observations, (PhD thesis), University of Bremen, Bremen, 180 pp., 2013. a
Ernst, F., von Savigny, C., Rozanov, A., Rozanov, V., Eichmann, K.-U., Brinkhoff, L. A., Bovensmann, H., and Burrows, J. P.: Global stratospheric aerosol extinction profile retrievals from SCIAMACHY limb-scatter observations, Atmos. Meas. Tech. Discuss., 5, 5993–6035, https://doi.org/10.5194/amtd-5-5993-2012, 2012. a
Flittner, D. E., Bhartia, P. K., and Herman, B. M.: O3 profiles retrieved from limb scatter measurements: Theory, Geophys. Res. Lett., 27, 2601–2604, 2000. a
Flynn, L. E., Seftor, C. J., Larsen, J. C., and Xu, P.: The Ozone Mapping and Profiler Suite, Earth Science Satellite Remote Sensing, Volume 1: Science and instruments, edited by: Qu, J., Gao, W., Kafatos, M., Murphy, R. E., and Salomonson, V. V., 279–295, Tsinghua University Press, Beijing and Springer, Berlin Heidelberg New York, https://doi.org/10.1007/978-3-540-37293-6, 2006. a, b
Gelaro, R., McCarty, W., Suarez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a
Goering, M. A., Gallus Jr., W. A., Olsen, M. A., and Stanford, J. L.: Role of stratospheric air in a severe weather event: Analysis of potential vorticity and ozone, J. Geophys. Res., 106, 11813–11823, 2001. a
Gorkavyi, N., Rault, D. F., Newman, P. A., da Silva, A. M., and Dudorov, A. E.: New stratospheric dust belt due to the Chelyabinsk bolide, Geophys. Res. Lett., 40, 4734–4739, https://doi.org/10.1002/grl.50788, 2013. a
Griffioen, E. and Oikarinen, L.: LIMBTRAN: A pseudo three-dimensional radiative transfer model for the limb-viewing imager OSIRIS on the ODIN satellite, J. Geophys. Res., 105, 29717–29730, 2000. a, b
Hamill, P., Jensen, E. J., Russell, P. B., and Bauman, J. J.: The Life Cycle of Stratospheric Aerosol Particles, B. Am. Meteor. Soc., 7, 1395–1410, 1997. a
Heath, D. F., Krueger, A. J., Roeder, H. A., and Henderson, B. D.: Solar Backscatter Ultraviolet and Total Ozone Mapping Spectrometer (SBUV-TOMS) for Nimbus G, Opt. Eng., 14, 323–331, 1975. a
Herman, B. M., Caudill, T. R., Flittner, D. E., Thome, K. J., and Ben-David, A.: Comparison of the Gauss-Seidel spherical polarized radiative transfer code with other radiative transfer codes, Appl. Opt., 34, 4563–4572, 1995. a, b
Herman, B. M., Ben-David, A., and Thome, K. J.: Numerical techniques for solving the radiative transfer equation for a spherical shell atmosphere, Appl. Opt., 33, 1760–1770, 1994. a, b
Hervig, M. E., Gordley, L. L., Deaver, L. E., Siskind, D. E., Stevens, M. H., Russell III, J. M., Bailey, S. M., Megner, L., and Bardeen, C. G.: First Satellite Observations of Meteoric Smoke in the Middle Atmosphere, Geophys. Res. Lett., 36, L18805, https://doi.org/10.1029/2009GL039737, 2009. a
Hofmann, D. J. and Solomon, S.: Ozone destruction through heterogeneous chemistry following the eruption of El Chichón, J. Geophys. Res., 94, 5029–5041, 1989. a
Holton, J. R., Haynes, P. H., McIntyre, M. E., Douglass, A. R., Rood, R. B., and Pfister, L.: Stratosphere-troposphere exchange, Rev. Geophys., 33, 403–439, 1995. a, b
Jaross, G., Bhartia, P. K., Chen, G., Kowitt, M., Haken, M., Chen, Z., Xu, P., Warner, J., and Kelly, T.: OMPS Limb Profiler instrument performance assessment, J. Geophys. Res., 119, 4399–4412, https://doi.org/10.1002/2013JD020482, 2014. a, b
Junge, C. E., Chagnon, C. W., and Manson, J. E.: A world-wide stratospheric aerosol layer, Science, 133, 1478–1479, 1961a. a
Junge, C. E., Chagnon, C. W., and Manson, J. E.:Stratospheric aerosol layer,J. Meteorol., 18, 81–108, 1961b. a
Kovilakam, M. and Deshler, T.: On the accuracy of stratospheric aerosol extinction derived from in situ size distribution measurements and surface area density derived from remote SAGE II and HALOE extinction measurements, J. Geophys. Res.-Atmos., 120, 8426–8447, https://doi.org/10.1002/2015JD023303, 2015. a
Kramarova, N. A., Bhartia, P. K., Jaross, G., Moy, L., Xu, P., Chen, Z., DeLand, M., Froidevaux, L., Livesey, N., Degenstein, D., Bourassa, A., Walker, K. A., and Sheese, P.: Validation of ozone profile retrievals derived from the OMPS LP version 2.5 algorithm against correlative satellite measurements, Atmos. Meas. Tech. Discuss., https://doi.org/10.5194/amt-2017-431, in review, 2017. a, b
Kravitz, B., Robock, A., Bourassa, A., Deshler, T., Wu, D., Mattis, I., Finger, F., Hoffmann, A., Ritter, C., Bitar, L., Duck, T. J., and Barnes, J. E.: Simulation and observations of stratospheric aerosols from the 2009 sarychev volcanic eruption, J. Geophys. Res., 116, https://doi.org/10.1029/2010JD015501, 2011. a
Kremser, S., Thomason, L. W., von Hobe, M., Hermann, M., Deshler, T., Timmreck, C., Toohey, M., Stenke, A., Schwarz, J. P., Weigel, R., Fueglistaler, S., Prata, F. J., Vernier, J.-P., Schlager, H., Barnes, J. E., Antua-Marrero, J.-C., Fairlie, D., Palm, M., Mahieu, E., Notholt, J., Rex, M., Bingen, C., Vanhellemont, F., Bourassa, A., Plane, J. M. C., Klocke, D., Carn, S. A., Clarisse, L., Trickl, T., Neely, R., James, A. D., Rieger, L., Wilson, J. C., and Meland, B.: Stratospheric aerosol – observations, processes, and impact on climate, Rev. Geophys., 54, 278–335, https://doi.org/10.1002/2015RG000511, 2016. a
Livesey, N. J. and Read, W. G.: Direct retrieval of line-of-sight atmospheric structure from limb sounding observations, Geophys. Res. Lett., 27, 891–894, 2000. a
Llewellyn, E. J., Lloyd, N. D., Degenstein, D. A., Gattinger, R. L., Petelina, S. V., Bourassa, A. E., Wiensz, J. T., Ivanov, E. V., McDade, I. C., Solheim, B. H., McConnell, J. C., Haley, C. S., von Savigny, C., Sioris, C. E., McLinden, C. A., Griffioen, E., Kaminski, J., Evans, W. F., Puckrin, E., Strong, K., Wehrle, V., Hum, R. H., Kendall, D. J. W., Matsushita, J., Murtagh, D. P., Brohede, S., Stegman, J., Witt, G., Barnes, G., Payne, W. F., Piché, L., Smith, K., Warshaw, G., Deslauniers, D.-L., Marchand, P., Richardson, E. H., King, R. A., Wevers, I., McCreath, W., Kyrölä, E., Oikarinen, L., Leppelmeier, G. W., Auvinen, H., Mégie, G., Hauchecorne, A., Lefèvre, F., de La Nöe, J., Ricaud, P., Frisk, U., Sjoberg, F., von Schéele, F., and Nordh, L.: The OSIRIS instrument on the Odin spacecraft, Can. J. Phys., 82, 411–422, 2004. a
Loughman, R. P., Griffioen, E., Oikarinen, L., Postylyakov, O. V., Rozanov, A., Flittner, D. E., and Rault, D. F.: Comparison of radiative transfer models for limb-viewing scattered sunlight measurements, J. Geophys. Res., 109, D06303, https://doi.org/10.1029/2003JD003854, 2004. a, b, c, d, e, f, g, h
Loughman, R., Flittner, D., Nyaku, E., and Bhartia, P. K.: Gauss-Seidel limb scattering (GSLS) radiative transfer model development in support of the Ozone Mapping and Profiler Suite (OMPS) limb profiler mission, Atmos. Chem. Phys., 15, 3007–3020, https://doi.org/10.5194/acp-15-3007-2015, 2015. a, b, c, d, e, f, g
Loughman, R., Bhartia, P. K., Moy, L., Kramarova, N., and Wargan, K.: Using MERRA-2 analysis fields to simulate limb scattered radiance profiles for inhomogeneous atmospheric lines of sight: Preparation for data assimilation of OMPS LP radiances through 2D single-scattering GSLS radiative transfer model development, poster presented at the AGU Fall 2016 Meeting, San Francisco, California, December 2016, abstract no. A23C-0248, 2016. a
Loughman, R., Flittner, D., Nyaku, E., and Bhartia, P. K.: Gauss-Seidel limb scattering (GSLS) radiative transfer model development in support of the Ozone Mapping and Profiler Suite (OMPS) limb profiler mission, Atmos. Chem. Phys., 15, 3007–3020, https://doi.org/10.5194/acp-15-3007-2015, 2015.
Lucke, R. L., Korwan, D. R., Bevilacqua, R., Hornstein, J. S., Shettle, E. P., Chen, D. T., Daehler, M., Lumpe, J. D., Fromm, M. D., Debrestian, D., Neff, B., Squire, M., Konig-Langlo, G., and Davies, J.: The Polar Ozone and Aerosol Measurement (POAM) III instrument and early validation results, J. Geophys. Res., 104, 18785–18799, 1999. a
Mateer, C. L., Heath, D. F., and Krueger, A. J.: Estimation of Total Ozone from Satellite Measurements of Backscattered Ultraviolet Earth Radiance, J. Atmos. Sci., 28, 1307–1311, 1971. a
Mauldin, L. E., Salikhov, R., Habib, S., Vladimirov, A., Carraway, D., Petrenko, G., and Comella, J.: Meteor-3M-/Stratospheric Aerosol and Gas Experiment III (SAGE III), Proc. SPIE Int. Soc. Opt. Eng., 3501, 355–365, 1998. a
McCormick, M. P., Thomason, L. W., and Trepte, C. R.: Atmospheric effects of the Mt. Pinatubo eruption, Nature, 373–399, 1995. a
McCormick, M. P. and Veiga, R.: SAGE II measurements of early Pinatubo aerosols, Geophys. Res. Lett., 19, 155–158, https://doi.org/10.1029/91GL02790, 1992. a
McElroy, C. T.: UV-Visible-NIR Spectrophotometer on Canadian Science Satellite SCISAT, 615–638, in: Optical Payloads for Space Missions, edited by: Qian, S.-E., 2016. a
McElroy, C. T., Nowlan, C. R., Drummond, J. R., Bernath, P. F., Barton, D. V., Dufour, D. G., Midwinter, C., Hall, R. B., Ogyu, A., Ullberg, A., Wardle, D. I., Kar, J., Zou, J., Nichitiu, F., Boone, C. D., Walker, K. A., and Rowlands, N.: The ACE-MAESTRO instrument on SCISAT: description, performance, and preliminary results, Appl. Opt., 4341–4356, 2007. a
McPeters, R. D., Janz, S. J., Hilsenrath, E., Brown, T. L., Flittner, D. E., and Heath, D. F.: The retrieval of O3 profiles from limb scatter measurements: Results from the shuttle ozone limb sounding experiment, Geophys. Res. Lett., 27, 2597–2600, 2000. a
Meinrat, O. A. and Crutzen, P. J.: Atmospheric Aerosols: Biogeochemical Sources and Role in Atmospheric Chemistry, Science, 276, 1052–1058, https://doi.org/10.1126/science.276.5315.1052, 1997. a
Moy, L., Bhartia, P. K., Jaross, G., Loughman, R., Kramarova, N., Chen, Z., Taha, G., Chen, G., and Xu, P.: Altitude registration of limb-scattered radiation, Atmos. Meas. Tech., 10, 167–178, https://doi.org/10.5194/amt-10-167-2017, 2017. a
NASA: Ozone Multi-mission ozone measurements, available at: https://ozoneaq.gsfc.nasa.gov/data/ozone/, last access: 20 April 2018.
Nyaku, E.: Characterizing aerosol properties in the upper troposphere and stratosphere from limb scatter radiance, PhD. dissertation, Hampton University, 151 pp., 2016. a, b, c, d, e
Ovigneur, B., Landgraf, J., Snel, R., and Aben, I.: Retrieval of stratospheric aerosol density profiles from SCIAMACHY limb radiance measurements in the O2 A-band, Atmos. Meas. Tech., 4, 2359–2373, https://doi.org/10.5194/amt-4-2359-2011, 2011. a
Pueschel, R. F., Russell, P. B., Allen, D. A., Ferry, G. V., Snetsinger, K. G., Livingston, J. M., and Verma, S.: Physical and optical properties of the Pinatubo volcanic aerosol: Aircraft observations with impactors and a Sun-tracking photometer, J. Geophys. Res., 99, 12915–12922, https://doi.org/10.1029/94JD00621, 1994. a, b, c, d
Randall, C. E., Bevilacqua, R. M., Lumpe, J. D., and Hoppel, K. W.: Validation of POAM III aerosols: Comparison to SAGE II and HALOE, J. Geophys. Res., 106, 27525–27536, 2001. a
Rault, D. F.: Ozone profile retrieval from SAGE III limb scattering measurements, J. Geophys. Res., 110, D09309, https://doi.org/10.1029/2004JD004970, 2005. a, b, c
Rault, D. F. and Taha, G.: Validation of ozone profiles retrieved from Stratospheric Aerosol and Gas Experiment III limb scatter measurements, J. Geophys. Res., 112, D13309, https://doi.org/10.1029/2006JD007679, 2007. a
Rault, D. and Loughman, R. P.: The OMPS Limb Profiler Environmental Data Record Algorithm Theoretical Basis Document and Expected Performance, IEEE T. Geosc. Remote Sens., 51, 2505–2527, https://doi.org/10.1109/TGRS.2012.2213093, 2013. a, b, c, d, e, f, g
Rault, D. and Loughman, R.: Stratospheric and upper tropospheric aerosol retrieval from limb scatter signals, Proc. SPIE, 6745, 674509, https://doi.org/10.1117/12.737325, 2007. a, b, c
Ridley, D., Solomon, S., Barnes, J., Burlakov, V., Deshler, T., Dolgii, S., Herber, A. B., Nagai, T., Neely, R., Nevzorov, A., Ritter, C., Sakai, T., Santer, B. D., Sato, M., Schmidt, A., Uchino, O., and Vernier, J. P.: Total volcanic stratospheric aerosol optical depths and implications for global climate change, Geophys. Res. Lett., 41, 7763–7769, 2014. a
Rieger, L., Bourassa, A., and Degenstein, D.: Merging the osiris and sage ii stratospheric aerosol records, J. Geophys. Res., 120, 8890–8904, 2015. a
Rieger, L. A., Bourassa, A. E., and Degenstein, D. A.: Stratospheric aerosol particle size information in Odin-OSIRIS limb scatter spectra, Atmos. Meas. Tech., 7, 507–522, https://doi.org/10.5194/amt-7-507-2014, 2014. a, b
Robock, A.: Volcanic eruptions and climate, Rev. Geophys., 38, 191–219, 2000. a
Rodgers, C. D.: Inverse methods for atmosphere sounding: Theory and practice, World Scientific, Pub. 832, Singapore, 256 pp., 2000. a
Rozanov, V. V., Rozanov, A., Kokhanovsky, A. A., and Burrows, J. P.: Radiative transfer through terrestrial atmosphere and ocean: software package SCIATRAN, J. Quant. Spectrosc. Radiat. Transfer, 133, 13–71, 2014. a
Russell, P. B. and McCormick, M. P.: SAGE II aerosol data validation and initial data use: An introduction and overview, J. Geophys. Res., 94, 8335–8338, 1989. a
SAGE III Algorithm Theoretical Basis Document: Solar and Lunar Algorithm, Earth Observing System Project, available at: https://eospso.gsfc.nasa.gov/sites/default/files/atbd/atbd-sage-solar-lunar.pdf (last access: 15 April 2018), 2002. a
Sioris, C. E., Boone, C. D., Bernath, P. F., Zou, J., McElroy, C. T., and McLinden, C. A.: Atmospheric Chemistry Experiment (ACE) observations of aerosol in the upper troposphere and lower stratosphere from the Kasatochi volcanic eruption, J. Geophys. Res., 115, D00L14, https://doi.org/10.1029/2009JD013469, 2010. a
Solomon, S.: Stratospheric ozone depletion: A review of concepts and theory, Rev. Geophys., 37, 275–316, 1999. a
Taha, G., Jaross, G., Fussen, D., Vanhellemont, F., Kyrölä, E., and McPeters, R. D.: Ozone profile retrieval from GOMOS limb scattering measurements, J. Geophys. Res., 113, D23307, https://doi.org/10.1029/2007JD009409, 2008. a
Taha, G., Rault, D. F., Loughman, R. P., Bourassa, A. E., and von Savigny, C.: SCIAMACHY stratospheric aerosol extinction profile retrieval using the OMPS/LP algorithm, Atmos. Meas. Tech., 4, 547–556, https://doi.org/10.5194/amt-4-547-2011, 2011. a, b
Thomason, L. W. and Peter, T. (Eds.): Assessment of Stratospheric Aerosol Properties (ASAP), SPARC Report No. 4, WCRP-124, WMO/TD-No. 1295, http://www.atmosp.physics.utoronto.ca/SPARC/index.html, February, 2006. a
Thomason, L. W., Poole, L. R., and Deshler, T.: A global climatology of stratospheric aerosol surface area density deduced from Stratospheric Aerosol and Gas Experiment II measurements: 1984–1994, J. Geophys. Res., 102, 8967–8976, https://doi.org/10.1029/96JD02962, 1997. a
Thomason, L. W., Burton, S. P., Luo, B.-P., and Peter, T.: SAGE II measurements of stratospheric aerosol properties at non-volcanic levels, Atmos. Chem. Phys., 8, 983–995, https://doi.org/10.5194/acp-8-983-2008, 2008. a
Thomason, L. W., Moore, J. R., Pitts, M. C., Zawodny, J. M., and Chiou, E. W.: An evaluation of the SAGE III version 4 aerosol extinction coefficient and water vapor data products, Atmos. Chem. Phys., 10, 2159–2173, https://doi.org/10.5194/acp-10-2159-2010, 2010. a, b
Toon, O. B. and Pollack, J. B.: Physical properties of the stratospheric aerosols, J. Geophys. Res., 78, 7051–7056, 1973. a, b
Trepte, C. R. and Hitchman, M. H.: Tropical stratospheric circulation deduced from satellite aerosol data, Nature 355, 626–628, 1992. a
Vanhellemont, F., Mateshvili, N., Blanot, L., Robert, C. É., Bingen, C., Sofieva, V., Dalaudier, F., Tétard, C., Fussen, D., Dekemper, E., Kyrölä, E., Laine, M., Tamminen, J., and Zehner, C.: AerGOM, an improved algorithm for stratospheric aerosol extinction retrieval from GOMOS observations – Part 1: Algorithm description, Atmos. Meas. Tech., 9, 4687–4700, https://doi.org/10.5194/amt-9-4687-2016, 2016. a
Vanhellemont, F., Fussen, D., Mateshvili, N., Tétard, C., Bingen, C., Dekemper, E., Loodts, N., Kyrölä, E., Sofieva, V., Tamminen, J., Hauchecorne, A., Bertaux, J.-L., Dalaudier, F., Blanot, L., Fanton d'Andon, O., Barrot, G., Guirlet, M., Fehr, T., and Saavedra, L.: Optical extinction by upper tropospheric/stratospheric aerosols and clouds: GOMOS observations for the period 2002–2008, Atmos. Chem. Phys., 10, 7997–8009, https://doi.org/10.5194/acp-10-7997-2010, 2010. a
Vernier, J.-P., Fairlie, T. D., Deshler, T., Natarajan, M., Knepp, T., Foster, K., Wienhold, F. G., Bedka, K. M., Thomason, L., and Trepte, C.: In situ and space-based observations of the Kelud volcanic plume: The persistence of ash in the lower stratosphere, J. Geophys. Res. Atmos., 121, 11104–11118, https://doi.org/10.1002/2016JD025344, 2016. a
Vernier, J.-P., Fairlie, T. D., Natarajan, M., Wienhold, F. G., Bian, J., Martinsson, B. G., Crumeyrolle, S., Thomason, L. W., and Bedka, K. M.: Increase in upper tropospheric and lower stratospheric aerosol levels and its potential connection with Asian pollution, J. Geophys. Res., 120, 1608–1619, https://doi.org/10.1002/2014JD022372, 2015. a
Vernier, J.-P., Thomason, L. W., and Kar, J.: CALIPSO detection of an Asian tropopause aerosol layer, Geophys. Res. Lett., 38, L07804, https://doi.org/10.1029/2010GL046614, 2011. a
von Savigny, C., Ernst, F., Rozanov, A., Hommel, R., Eichmann, K.-U., Rozanov, V., Burrows, J. P., and Thomason, L. W.: Improved stratospheric aerosol extinction profiles from SCIAMACHY: validation and sample results, Atmos. Meas. Tech., 8, 5223–5235, https://doi.org/10.5194/amt-8-5223-2015, 2015. a, b, c, d, e
Winker, D. M., Vaughan, M. A., Omar, A. H., Hu, Y., Powell, K. A., Liu, Z., Hunt, W. H., and Young, S. A.: Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms, J. Atmos. Ocean. Tech., 26, 2310–2323, https://doi.org/10.1175/2009JTECHA1281.1, 2009. a
Zawada, D. J., Dueck, S. R., Rieger, L. A., Bourassa, A. E., Lloyd, N. D., and Degenstein, D. A.: High-resolution and Monte Carlo additions to the SASKTRAN radiative transfer model, Atmos. Meas. Tech., 8, 2609–2623, https://doi.org/10.5194/amt-8-2609-2015, 2015. a, b