Parameterizing cloud top effective radii from satellite retrieved values, accounting for vertical photon transport: quantification and correction of the resulting bias in droplet concentration and liquid water path retrievals

Droplet concentration (N_d) and liquid water path (LWP) retrievals from passive satellite retrievals of cloud optical depth (τ) and effective radius (r_e) usually assume the model of an idealized cloud in which the liquid water content (LWC) increases linearly between cloud base and cloud top (i.e. at a fixed fraction of the adiabatic LWC). Generally it is assumed that the retrieved r_e value is that at the top of the cloud. In reality, barring r_e retrieval biases due to cloud heterogeneity, the retrieved r_e is representative of smaller values that occur lower down in the cloud due to the vertical penetration of photons at the shortwave-infrared wavelengths used to retrieve r_e. This inconsistency will cause an overestimate of N_d and an underestimate of LWP (referred to here as the “penetration depth bias”), which this paper quantifies via a parameterization of the cloud top r_e as a function of the retrieved r_e and τ. Here we estimate the relative r_e underestimate for a range of idealized modelled adiabatic clouds using bispectral retrievals and plane-parallel radiative transfer. We find a tight relationship between $g_{\text{re}}=r_{\text{e}}^{\text{cloud top}}/r_{\text{e}}^{\text{retrieved}}$ and τ and that a 1-D relationship approximates the modelled data well. Using this relationship we find that g_re values and hence N_d and LWP biases are higher for the 2.1 µm channel r_e retrieval (r_e2.1) compared to the 3.7 µm one (r_e3.7). The theoretical bias in the retrieved N_d is very large for optically thin clouds, but rapidly reduces as cloud thickness increases. However, it remains above 20 % for τ<19.8 and τ<7.7 for r_e2.1 and r_e3.7, respectively. We also provide a parameterization of penetration depth in terms of the optical depth below cloud top (dτ) for which the retrieved r_e is likely to be representative.

The magnitude of the N_d and LWP biases for climatological data sets is estimated globally using 1 year of daily MODIS (MODerate Imaging Spectroradiometer) data. Screening criteria are applied that are consistent with those required to help ensure accurate N_d and LWP retrievals. The results show that the SE Atlantic, SE Pacific and Californian stratocumulus regions produce fairly large overestimates due to the penetration depth bias with mean biases of 32–35 % for r_e2.1 and 15–17 % for r_e3.7. For the other stratocumulus regions examined the errors are smaller (24–28 % for r_e2.1 and 10–12 % for r_e3.7). Significant time variability in the percentage errors is also found with regional mean standard deviations of 19–37 % of the regional mean percentage error for r_e2.1 and 32–56 % for r_e3.7. This shows that it is important to apply a daily correction to N_d for the penetration depth error rather than a time–mean correction when examining daily data. We also examine the seasonal variation of the bias and find that the biases in the SE Atlantic, SE Pacific and Californian stratocumulus regions exhibit the most seasonality, with the largest errors occurring in the December, January and February (DJF) season. LWP biases are smaller in magnitude than those for N_d (−8 to −11 % for r_e2.1 and −3.6 to −6.1 % for r_e3.7).

In reality, and especially for more heterogeneous clouds, the vertical penetration error will be combined with a number of other errors that affect both the r_e and τ, which are potentially larger and may compensate or enhance the bias due to vertical penetration depth. Therefore caution is required when applying the bias corrections; we suggest that they are only used for more homogeneous clouds.

1 Introduction

Clouds have a major impact on Earth's radiative balance (Hartmann et al., 1992) and small changes in their properties are predicted to have large radiative impacts (Latham et al., 2008). The amount of shortwave flux reflected by fully overcast warm (liquid water) clouds for a given sun and scattering angle, or the reflectance of a cloud, is primarily determined by the cloud optical depth (τ), which in turn can often be characterized by the liquid water path (LWP; the vertical integral of liquid water content) and the cloud droplet number concentration (N_d). For a given cloud updraft, N_d is determined by the number concentration and physicochemical properties of aerosols. Thus, couching cloud reflectance in terms of N_d links the cloud albedo to aerosol and microphysical effects via the Twomey (1974) effect, making N_d a very useful quantity to determine observationally. N_d can also influence cloud macrophysical feedbacks via its control on rain formation (Ackerman et al., 2004; Albrecht, 1989; Berner et al., 2013; Feingold et al., 2015; Stevens et al., 1998) and stratocumulus cloud top entrainment (Ackerman et al., 2004; Bretherton et al., 2007; Hill et al., 2009).

Satellite observations of clouds and N_d are immensely useful for studying clouds, cloud–aerosol interactions and for model evaluation since they afford large spatial and temporal coverage. A method to obtain N_d from passive satellite observations (Salomonson et al., 1998) of τ and the cloud droplet effective radius (r_e) for stratiform liquid clouds has been previously demonstrated (Bennartz, 2007; Bennartz and Rausch, 2017; Boers et al., 2006; Brenguier et al., 2000; Grosvenor and Wood, 2014; Han et al., 1998; Nakajima et al., 2001; Quaas et al., 2006; Szczodrak et al., 2001) and is described further below. For more details see the Grosvenor et al. (2018) review paper on this technique, which also describes the known sources of error. In cloudy environments, aerosol optical depth cannot be retrieved from satellites, making cloud property observations such as N_d and the cloud droplet effective radius (r_e) the only useful indicator of the influence of aerosol on clouds. An advantage of using N_d rather than r_e to study cloud–aerosol interactions is that r_e is also determined by the cloud water content and thus is a function of cloud macrophysical properties. N_d, in contrast, is only weakly controlled by cloud macrophysics, allowing some separation of microphysical and macrophysical effects.

However, retrievals of N_d from space are still somewhat experimental and there is a lack of comprehensive validation of the retrievals and the assumptions required. There is a need to characterize and quantify the associated errors; in this paper we focus on doing this for one source of N_d error using a 1-year N_d data set for stratocumulus clouds from MODIS.

2 The adiabatic N_d and LWP retrieval model and the vertical penetration depth bias

N_d and LWP are retrieved from passive satellite retrievals of r_e and τ using an adiabatic cloud model that is described below. However, as shown in Platnick (2000) and Bennartz and Rausch (2017), for a retrieval free from other error sources (e.g. those due to cloud heterogeneity), the retrieved r_e is representative of the r_e value lower down in the cloud due to the vertical penetration of photons at the shortwave-infrared (SWIR) wavelengths used to retrieve r_e. In contrast, the retrieved τ is comprised of contributions from the extinction coefficient β_ext(h), where h represents height from cloud base, throughout the whole cloud profile:

$$\begin{array}{}\text{(1)}& \mathit{\tau }=\underset{\mathrm{0}}{\overset{H}{\int }}{\mathit{\beta }}_{\mathrm{ext}}\left(h\right)\text{d}h.\end{array}$$

Here h=0 represents cloud base and h=H is cloud top. β_ext(h) is defined as

$$\begin{array}{}\text{(2)}& {\mathit{\beta }}_{\mathrm{ext}}\left(h\right)=\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{Q}_{\mathrm{ext}}\left(r\right)r^{\mathrm{2}}n\left(r\right)\text{d}r,\end{array}$$

where r is the droplet radius and n(r) is the droplet size number distribution within a cloud unit volume such that $N_{\text{d}}={\int }_{\mathrm{0}}^{\mathrm{\infty }}n\left(r\right)\text{d}r$. Q_ext(r) represents the ratio between the extinction and the geometric cross section of a given droplet and can be approximated by its asymptotic value of 2 (van de Hulst, 1957) since droplet radii are generally much larger than the wavelength of light concerned (typically 0.6 to 0.85 µm) such that the geometric optics limit is almost reached.

r_e and liquid water content (LWC) at a given height are, respectively, defined as

$$\begin{array}{}\text{(3)}& r_{\text{e}}\left(h\right)={\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{r}^{\mathrm{3}}n\left(r\right)\text{d}r}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{r}^{\mathrm{2}}n\left(r\right)\text{d}r}},\end{array}$$

and

$$\begin{array}{}\text{(4)}& \text{LWC}\left(h\right)={\displaystyle \frac{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\text{w}}}{\mathrm{3}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{r}^{\mathrm{3}}n\left(r\right)\text{d}r,\end{array}$$

where ρ_w is the density of liquid water. Combining Eqs. (3) and (4) and inserting into Eq. (2) gives

$$\begin{array}{}\text{(5)}& {\mathit{\beta }}_{\mathrm{ext}}\left(h\right)={\displaystyle \frac{\mathrm{3}{Q}_{\mathrm{ext}}}{\mathrm{4}{\mathit{\rho }}_{\text{w}}}}{\displaystyle \frac{\text{LWC}\left(h\right)}{r_{\text{e}}\left(h\right)}}.\end{array}$$

To determine the form of r_e(h) in the above equation in terms of L(h) and N_d(h) we can utilize the fact that the “k” value,

$$\begin{array}{}\text{(6)}& k={\left({\displaystyle \frac{r_{\text{v}}}{r_{\text{e}}}}\right)}^{\mathrm{3}},\end{array}$$

which is a measure of the width of the droplet size distribution (lower values indicate wider distributions), has been shown to be approximately constant in stratocumulus clouds (Martin et al., 1994; Painemal and Zuidema, 2011; Pawlowska et al., 2006). In this study we adopt a value of k=0.72, which is the value assumed by the MODIS retrieval (Zhang, 2013). r_v is the volume radius, defined as

$$\begin{array}{}\text{(7)}& r_{\text{v}}(h{)}^{\mathrm{3}}={\displaystyle \frac{\mathrm{1}}{N_{\text{d}}\left(h\right)}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{r}^{\mathrm{3}}n(r)\text{d}r={\displaystyle \frac{\mathrm{3}\text{LWC}\left(h\right)}{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\text{w}}{N}_{\text{d}}\left(h\right)}}=k{r}_{\text{e}}(h{)}^{\mathrm{3}},\end{array}$$

where we have used Eq. (4) to insert LWC and Eq. (6) to write r_v as a function of k and r_e. Now we utilize the assumptions that N_d(h) is constant with height and that LWC(h) is a constant fraction, f_ad, of the adiabatic LWC. The latter equates to

$$\begin{array}{}\text{(8)}& \text{LWC}\left(h\right)=f_{\text{ad}}{c}_{\text{w}}h,\end{array}$$

where c_w is the rate of increase of LWC with height (dLWC∕dz, with units kg m⁻⁴) for a moist adiabatic ascent and is referred to as the “condensation rate” in Brenguier et al. (2000), or the “water content lapse rate” in Painemal and Zuidema (2011). See Ahmad et al. (2013) for a derivation. c_w is a constant for a given temperature and pressure. Allowing these assumptions, using Eq. (7) to substitute for r_e in Eq. (5) and combining with Eqs. (1) and (8) we can write

$$\begin{array}{ll}\text{(9)}& {\displaystyle }{\mathit{\tau }}^{*}& {\displaystyle }=\underset{\mathrm{0}}{\overset{H^{*}}{\int }}{Q}_{\mathrm{ext}}{\left({\displaystyle \frac{\mathrm{3}{f}_{\text{ad}}{c}_{\text{w}}}{\mathrm{4}{\mathit{\rho }}_{\text{w}}}}\right)}^{\mathrm{2}/\mathrm{3}}{\left(N_{\text{d}}\mathit{\pi }k\right)}^{\mathrm{1}/\mathrm{3}}{h}^{\mathrm{2}/\mathrm{3}}\text{d}h{\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{3}{Q}_{\mathrm{ext}}}{\mathrm{5}}}{\left({\displaystyle \frac{\mathrm{3}{f}_{\text{ad}}{c}_{\text{w}}}{\mathrm{4}{\mathit{\rho }}_{\text{w}}}}\right)}^{\mathrm{2}/\mathrm{3}}{\left(N_{\text{d}}\mathit{\pi }k\right)}^{\mathrm{1}/\mathrm{3}}{H}^{*\mathrm{5}/\mathrm{3}}.\end{array}$$

At this stage, H^* is any arbitrary height above cloud base and τ^* is thus the optical depth between the cloud base and that height. H^* can be expressed as a function of r_e(H^*), k, N_d and some constants by using Eqs. (7) and (8). Then, given r_e(H^*) and τ^*, N_d can be calculated as follows:

$$\begin{array}{}\text{(10)}& N_{\text{d}}={\displaystyle \frac{\sqrt{\mathrm{5}}}{\mathrm{2}\mathit{\pi }k}}{\left({\displaystyle \frac{f_{\text{ad}}{c}_{\text{w}}{\mathit{\tau }}^{*}}{Q_{\mathrm{ext}}{\mathit{\rho }}_{\text{w}}{r}_{\text{e}}(H^{*}{)}^{\mathrm{5}}}}\right)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

Generally, when retrieving N_d it is assumed that the r_e obtained from satellite is representative of that from cloud top, i.e. $r_{\text{e}}\left(H^{*}\right)=r_{\text{e}}\left(H\right)$ (Bennartz, 2007; Painemal and Zuidema, 2011). This would then mean that τ^* is the full cloud optical depth (τ) as retrieved by the satellite and thus could be used in Eq. (10) above to obtain N_d. However, since the r_e obtained by satellite is actually equal to r_e(H^*) then ${\mathit{\tau }}^{*}<\mathit{\tau }$ and thus τ^* should be used in Eq. (10) instead of the retrieved τ; the problem lies in the fact that τ^* is unknown. However, in this paper we fit a simple function for τ^* as a function of τ based on radiative transfer (RT) modelling of a variety of idealized clouds.

Alternatively, Eq. (10) can be formulated using the retrieved τ over the full cloud depth (setting ${\mathit{\tau }}^{*}=\mathit{\tau }$) and the cloud top r_e (setting $r_{\text{e}}\left(H^{*}\right)=r_{\text{e}}\left(H\right)$). The problem then becomes one of estimating r_e(H) from the retrieved r_e(H^*). Here we formulate a parameterization of $r_{\text{e}}\left(H\right)/r_{\text{e}}\left(H^{*}\right)$ as a function of τ. Note that either the τ or r_e corrections should be applied to correct N_d, but not both together.

Then we estimate the error introduced in N_d retrievals for 1 year of MODIS data due to the usual assumptions of $r_{\text{e}}\left(H^{*}\right)=r_{\text{e}}\left(H\right)$ and ${\mathit{\tau }}^{*}=\mathit{\tau }$, on the assumption that there are no other biases affecting the r_e retrieval. We label this bias the “vertical penetration bias”.

The method of correcting r_e has the advantage over the τ correction since it also allows a correction to the retrieval of LWP. LWP can be estimated (Szczodrak et al., 2001) using

$$\begin{array}{}\text{(11)}& \mathrm{LWP}={\displaystyle \frac{\mathrm{5}}{\mathrm{9}}}{\mathit{\rho }}_w{r}_{\text{e}}\left(H\right)\mathit{\tau }.\end{array}$$

For a corrected LWP the cloud top r_e and the retrieved (total) τ values should be used. Since the retrieved r_e(H^*) is likely to be underestimated due to the vertical penetration depth bias, LWP would otherwise be underestimated and the correct value can be obtained by using the parameterized r_e(H) instead.

3 Data and methods

3.1 Calculation of τ and r_e corrections

In order to calculate

$$\begin{array}{}\text{(12)}& g_{\text{re}}={\displaystyle \frac{r_{\text{e}}\left(H\right)}{r_{\text{e}}\left(H^{*}\right)}},\end{array}$$

and

$$\begin{array}{}\text{(13)}& \text{d}\mathit{\tau }=\mathit{\tau }-{\mathit{\tau }}^{*},\end{array}$$

we have performed r_e retrievals on idealized clouds using a similar algorithm to that used for MODIS retrievals. We produced idealized clouds that span a large range of stratocumulus-like clouds as represented by combinations of N_d and LWP. We chose 41 values between N_d=10 and 1000 cm⁻³ that were equally spaced in log space and 91 values between LWP = 20 and 200 g m⁻² spaced equally in linear space. All of the possible combinations from this sampling were used to sample the 2-D (N_d, LWP) phase space. For each combination, discretized adiabatic model profiles following the form of those described in Sect. 1 (i.e. with a vertically constant N_d and LWC that increases linearly with height) were generated using $c_{\text{w}}=\mathrm{1.81}\times {\mathrm{10}}^{-\mathrm{6}}$ kg m⁻⁴, f_ad=0.8 and a vertical spacing of 1 m. The droplet size distributions at each height were represented by a modified gamma distribution with a k value of 0.72, i.e. representative of an effective variance of 0.1. One-dimensional RT calculations, assuming plane-parallel clouds, were performed on these profiles using DISORT (Stamnes et al., 1988) radiation code in order to simulate reflectances at wavelengths of 0.86, 2.1 and 3.7 µm, matching those measured by MODIS to retrieve τ and r_e over an ocean surface. Note that MODIS provides r_e retrievals using both 2.1 and 3.7 µm wavelengths, which are hereafter referred to as r_e2.1 and r_e3.7, respectively. The MODIS r_e3.7 retrieval requires a correction to account for the contribution to the observed radiance from thermal emission, which is based on the observed 11 µm radiance (King et al., 2015; Platnick and Valero, 1995; Platnick et al., 2017). We account for this in our retrievals by removing the thermal contribution during the RT calculation instead of via the 11 µm radiance, which should produce a consistent end result. The RT calculations were performed assuming a black surface, a clear atmosphere (i.e. gaseous absorption is neglected), using a solar zenith angle (SZA) of 20^∘ and a nadir viewing angle.

These reflectances were then used to retrieve τ and r_e values using the Nakajima and King (1990) bispectral method, as operationally used by MODIS. To do so, a lookup table was built from reflectances calculated for a range of clouds that were assumed to be plane-parallel in nature, as assumed for the operational MODIS retrievals; i.e. these clouds were uniform in the vertical and horizontal with infinite horizontal extent. Again, a black surface and a k value of 0.72 were assumed along with the same viewing geometry as for the RT calculations on the adiabatic clouds. A fixed depth of 1 km was assumed with cloud base at an altitude of 1 km and cloud top at 2 km, although the cloud depth has no major effect on the reflectances generated for a given τ and r_e. g_re was then calculated using the retrieved and model top r_e values. dτ was calculated by choosing the value from the model profile of τ, as measured from cloud top downwards, that corresponded to the location where the model profile r_e matched the retrieved r_e.

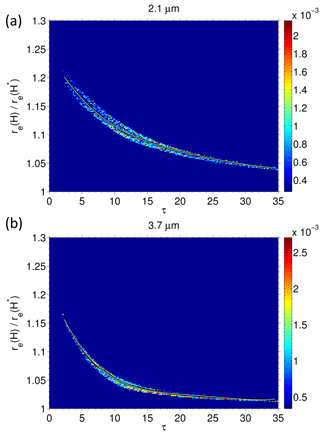
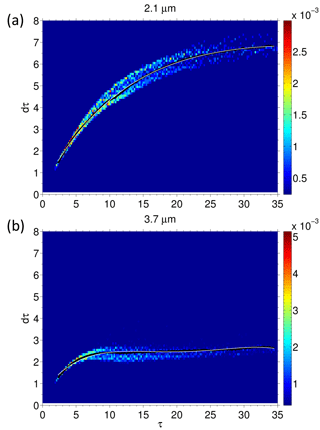
Figure 1 Two-dimensional histogram of g_re as a function of τ for a range of clouds (see text) for the 2.1 µm r_e retrieval (a) and the 3.7 µm retrieval (b). The black line is the median g_re in each τ bin after smoothing over τ interval windows of 0.2. The white line is the fit to the mean curve using Eq. (14).

Figure 1a shows a 2-D histogram of g_re values as a function of τ for the 2.1 µm retrieval. It shows that when plotted in this way g_re forms a fairly tight relationship with τ so that for a given τ only a small range of g_re values are possible. This suggests that the relationship can be parameterized based upon a 1-D relationship fitted to these data with little loss of accuracy. The median value of each τ bin is also plotted (after smoothing over τ windows of 0.2) and this is the relationship used in this paper. g_re is seen to decrease with τ with a gradient that decreases with τ. Similarly, Fig. 2 shows dτ vs. τ, which also shows a tight relationship that is suited to a 1-D parameterization. Fourth-order polynomial curves can be fitted (using the least squares method) to the median value relationships that take the form

$$\begin{array}{}\text{(14)}& g_{\text{re}}=a_{\mathrm{4}}{\mathit{\tau }}^{\mathrm{4}}+a_{\mathrm{3}}{\mathit{\tau }}^{\mathrm{3}}+a_{\mathrm{2}}{\mathit{\tau }}^{\mathrm{2}}+a_{\mathrm{1}}\mathit{\tau }+a_{\mathrm{0}},\end{array}$$

and

$$\begin{array}{}\text{(15)}& \text{d}\mathit{\tau }=b_{\mathrm{4}}{\mathit{\tau }}^{\mathrm{4}}+b_{\mathrm{3}}{\mathit{\tau }}^{\mathrm{3}}+b_{\mathrm{2}}{\mathit{\tau }}^{\mathrm{2}}+b_{\mathrm{1}}\mathit{\tau }+b_{\mathrm{0}}.\end{array}$$

Table 1 Coefficients for the fitting curve (Eq. 14) to estimate the median g_re value as a function of τ. The maximum absolute error between the fit and the median line is also shown.

Table 2 Coefficients for the fitting curve (Eq. 15) to estimate the mean dτ value as a function of τ. The maximum absolute error between the fit and the mean line is also shown.

The coefficients of these fits are given in Tables 1 and 2 along with the maximum errors for the fit (relative to the mean or median line) for the range shown. The curves (white lines in Figs. 1a and 2a) fit the mean data well with maximum absolute differences of 0.001 and 0.09, respectively, for the g_re and dτ curves. However, there will be some error when using this relationship (or the mean value relationship) due to the spread in the g_re and dτ values seen in the underlying histograms.

Figures 1b and 2b show the same results for the 3.7 µm retrieval. Again tight 1-D relationships are suggested. Here, though, g_re and dτ values are lower for a given τ and the curves are steeper at lower τ values, but flatten off much more rapidly. By τ=7.5 there is little dependence of dτ on τ and dτ saturates at a mean value of ∼ 2.6. The fit estimates for the curves (Eqs. 14 and 15 and Tables 1 and 2) again match the actual curves closely with a maximum absolute error in g_re and dτ of 0.003 and 0.14, respectively.

Figure 2 As for Fig. 1 except for dτ as a function of τ and using Eq. (15) for the white line.

3.2 MODIS data

For the MODIS data we use 1 year (2008) of MODIS Aqua data and follow a similar methodology to that used in Grosvenor and Wood (2014) in order to create a data set akin to the MODIS Level-3 (L3) product (King et al., 1997; Oreopoulos, 2005). We processed MODIS Collection 5.1 joint Level-2 (L2) swaths into $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid boxes. Joint L2 swaths are subsampled versions of the full L2 swaths (sampling every fifth 1 km pixel) that also contains fewer parameters. We process the data from L2 to L3 in order to allow the filtering out of data at high SZAs and to provide both r_e2.1 and r_e3.7 retrievals.

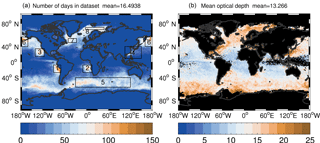
Figure 3 (a) Number of days in 2008 that fulfilled the criteria required to be counted as a valid N_d retrieval. See the text for details on the criteria. Various regions of interest are also denoted by the boxes and numbers. (b) Mean optical depth for data set with filtering criteria 1–7 applied (see text).

For this work we relax the screening methodology slightly from that used in Grosvenor and Wood (2014) since here we are interested in the effects of the vertical penetration N_d bias upon a more general global data set. We applied the following restrictions to each $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ sample that goes into the daily average (since multiple overpasses per day are possible) in order to attempt to remove some artifacts that may cause biases:

1. At least 50 joint L2 1 km resolution pixels from the MODIS swath that did not suffer from sunglint were required to have been sampled within each grid box.

2. At least 80 % of the available (non-sunglint) pixels were required to be of liquid phase based upon the “primary cloud retrieval phase flag”. Analysis was only performed on these pixels. A high cloud fraction helps to ensure that the clouds are not broken, since broken clouds are known to cause biases in retrieved optical properties due to photon scattering through the sides of clouds. Often retrievals of N_d are restricted to high cloud fraction fields for this reason (Bennartz, 2007; Painemal and Zuidema, 2011) and so we focus on such data points here.

3. The only pixels used were those remaining after (2) for which the “cloud mask status” indicated that the cloud mask could be determined, the “cloud mask cloudiness flag” was set to “confident cloudy”, successful simultaneous retrievals of both τ and r_e for the 2.1µm channel were performed and the cloud water path confidence from the MODIS L2 quality flags was designated as “very good confidence” (the highest level possible). This is a little different from the official MODIS L3 product where a set of cloud products are provided that are weighted using the quality assurance (QA) flags. Rather than weighting our L3-like product with the QA flags we have simply restricted our analysis to pixels with the highest confidence for water path.

4. The mean $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ cloud top height (CTH) is restricted to values lower than 3.2 km. This is done to avoid both deeper clouds for which N_d retrievals are likely to be problematic due to the increased likelihood of a breakdown of the assumptions required to estimate N_d, such as a constant fraction of the adiabatic value for LWC and vertically constant N_d, and increased retrieval issues due to cloud heterogeneity. CTH is calculated from the MODIS $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ mean cloud top temperature (CTT) and the sea surface temperature (SST) using the method of Zuidema et al. (2009). SST data were obtained from version 2 of the NOAA Optimum Interpolation (OI) Sea Surface Temperature data set (NOAA_OI_SST_V2) that provides weekly SST data at $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ resolution. This was interpolated to daily data on the assumption that SST does not vary significantly over sub-weekly timescales.

5. The mean $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ SZA was restricted to ≤ 65^∘ following the identification of biases in the retrieved τ, r_e and N_d at high SZAs (Grosvenor and Wood, 2014).

6. $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ grid boxes were rejected if the maximum sea-ice areal coverage over a moving 2-week window exceeded 0.001 %. The sea-ice data used were the daily $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ version of the “Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1” data set (Cavalieri et al., 1996).

7. Only $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ grid points with mean τ>5 were considered for the N_d data set due to larger uncertainties from instrument error and other sources of reflectance error for τ and r_e retrievals at low τ (Sourdeval et al., 2016; Zhang and Plantnick, 2011).

Following this screening, the $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ grid boxes associated with each MODIS Aqua overpass were averaged into daily mean values for ocean covered surfaces only. Figure 3a shows the number of days from the year of data examined in this study (year 2008) that fulfilled the above criteria and thus are likely to produce a good N_d retrieval. Regions with high numbers of days where useful N_d retrievals can be made have been selected for closer examination in this study; they are listed in Table 3 along with information on the mean and maximum numbers of days of good data. The permanent marine stratocumulus decks are among those selected, namely those in the SE Pacific off the western coast of S. America (Region no. 1), in the SE Atlantic off the western coast of southern Africa (Region no. 2), off the coast of California and the Baja Peninsula (Region no. 3), in the Bering Sea off the SW coast of Alaska (Region no. 6) and in the Barents Sea to the north of Scandinavia (Region no. 8). These regions are where the highest numbers of selected days occur with values ranging up to a maximum of 141 days (for the Bering Sea region). The Barents Sea region has the lowest maximum number of days out of this group, reflecting the fact that N_d retrievals cannot be made during a lot of the winter season in this region due to a lack of sunlight. The Southern Ocean (Region no. 5) and the NW Atlantic (Region no. 7) regions frequently produce stratocumulus, although it is often associated with the cold sectors of cyclones and so its location from day to day is more transient. These regions are also affected by high SZAs in the winter seasons, which also restricts the number of retrievals possible there. The East China Sea region (Region no. 4) produces the lowest mean and maximum numbers of days since the stratocumulus areas are mostly restricted to near the coast and occur mostly in the winter season.

N_d was calculated for both r_e2.1 and r_e3.7 using Eq. (10) from the $\mathrm{1}{}^{\circ }\times \mathrm{1}$^∘ daily mean τ, r_e and CTT. This was done by using the retrieved τ value in Eq. (10) along with both the retrieved r_e value (i.e. assuming that $r_{\text{e}}\left(H^{*}\right)=r_{\text{e}}\left(H\right)$ as is often assumed for N_d retrievals) and by estimating r_e(H^*) using the retrieved r_e along with the g_re values that were calculated as described above. This therefore gives N_d data sets for the “standard” method and a corrected method, allowing the differences between the two to be examined. A similar process was applied for the LWP retrieval.

4 Results

Following Eq. (10), the ratio between the uncorrected and corrected N_d values can be shown to be

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{N_{\text{d\hspace{0.17em}(uncorrected)}}}{N_{\text{d\hspace{0.17em}(corrected)}}}}={\left({\displaystyle \frac{r_{\text{e}}\left(H\right)}{r_{\text{e}}\left(H^{*}\right)}}\right)}^{\mathrm{5}/\mathrm{2}}=g_{\text{re}}^{\mathrm{5}/\mathrm{2}}.\end{array}$$

Figure 4 shows how the relative N_d bias varies as a function of retrieved τ when using an r_e that has been corrected using the g_re from Fig. 1 (mean curve, black line). At τ=5 the relative error is 46 % for the r_e2.1 retrieval and 28 % for the r_e3.7 retrieval. At higher τ the errors reduce rapidly but remain above 10 % for the r_e2.1 retrieval over the τ range shown. For the r_e3.7 retrieval the relative error drops below 10 % for $\mathit{\tau }>\sim \mathrm{13}$. Thus, the overall degree of error due to this effect will be determined by the distribution of τ for the regions of interest, which we take into consideration here using MODIS data for a representative N_d data set.

Alternatively, if the correction is formulated in terms of a correction to τ we obtain

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{N_{\text{d\hspace{0.17em}(uncorrected)}}}{N_{\text{d\hspace{0.17em}(corrected)}}}}={\left({\displaystyle \frac{\mathit{\tau }}{{\mathit{\tau }}^{*}}}\right)}^{\mathrm{1}/\mathrm{2}}={\left({\displaystyle \frac{\mathit{\tau }}{\mathit{\tau }-\text{d}\mathit{\tau }}}\right)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

The equation shows that, for a constant dτ, the relative N_d bias due to an uncorrected τ value would increase with decreasing τ as τ−dτ approaches zero.

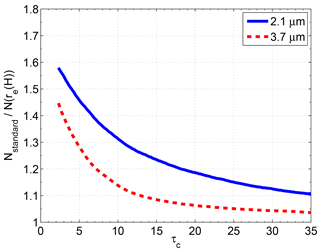
Figure 4 The ratios of N_d values from the standard MODIS calculation (using the retrieved r_e for $r_{\text{e}}^{*}$ in Eq. 10) to those from the corrected calculation (using the corrected r_e for $r_{\text{e}}^{*}$ as calculated from the retrieved value and g_re; the g_re values used are those shown by the black line in Fig. 1) vs. retrieved τ.

Figure 3b shows the time–mean τ for the data set as filtered by criteria 1–7 above, i.e. to replicate the type of filtering that would likely be performed for N_d retrievals. Table 3 lists the regional means of these time–mean values along with the regional means of the standard deviations of τ over time. It shows that the mean τ values of the tropical and subtropical regions are generally lower than those at higher latitudes. The East China Sea, Barents Sea, NW Atlantic and Southern Ocean regions exhibit the highest mean τ values out of those examined and so should be expected to show the lowest N_d biases due to the vertical penetration effect. The SE Atlantic region (and the region to the west of Africa in general) show low τ and can be expected to give high N_d biases. Table 3 also lists the fraction of days for which τ≤10 (f_τ≤10). τ=10 is the value above which N_d biases drop below 31 % for the 2.1 µm retrieval and below 14 % for r_e3.7 according to Fig. 4.

Thus f_τ≤10 indicates the fraction of days for which daily N_d biases will be greater than 31 % for that channel. The values in the table indicate that even in the least affected region (Barents Sea) this will occur for 21 % of the days. For the SE Atlantic and SE Pacific region the percentages rise to 69 % and 53 % of the days, respectively. Thus, the vertical penetration depth N_d bias is prevalent in all regions for which N_d data sets are likely to be used and particularly so in the subtropical stratocumulus regions where N_d retrievals have been widely used and studied.

Table 3 Regional statistics for the various marine stratocumulus regions shown in Fig. 3. Shown are the mean and maximum number of days that fulfill the screening criteria in order to be considered as useful N_d retrievals; the regional means and standard deviations (σ) of the time-averaged optical depths (τ) for the screened data set; and the regional mean of the fraction of days for which τ≤10 (f_τ≤10), which is calculated using only data from grid points for which the number of days with N_d data was ≥ 15.

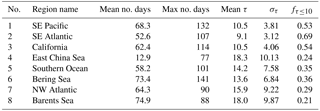
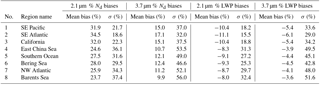
Table 4 Regional means of the predicted time–mean percentage biases in N_d and LWP due to the vertical penetration depth error and regional means of the relative (percentage) standard deviations (over time) of the percentage N_d and LWP biases (i.e. regional means of the values in Fig. 6 and the equivalent for LWP). Bias results are shown for both the 2.1 and the 3.7 µm r_e retrievals.

The overall bias is now estimated using 1 year of actual MODIS data in order to obtain a realistic distribution of τ values. However, it should be noted that the data set used is deliberately filtered in order to only retain data points that are likely to give useful N_d data, namely low liquid clouds with extensive 1^∘ × 1^∘ cloud fractions, i.e. predominately stratocumulus. This is done in order to assess biases for the types of clouds that N_d data sets will typically be used to study.

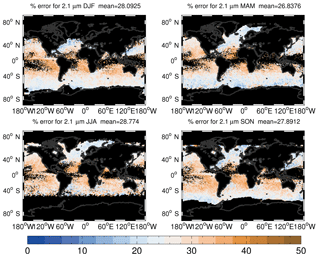
Figure 5 shows a map of the mean percentage biases and Table 4 gives the regional means of the values in the map. Considering firstly the biases for the r_e2.1 retrieval, the biases are highest in the tropics and subtropics. The regional mean bias is 34.5 % for the SE Atlantic region (Region no. 2), which is the stratocumulus region that seems to suffer the most. The biases are a little lower for the other major stratocumulus regions; e.g. for the SE Pacific region (Region no. 1) and the Californian region (Region no. 3) the mean biases are 32 %, although the biases increase further west, where the dominant cloud regime tends to shift towards trade cumulus clouds. The remaining regions all have mean biases of 24–28 %. The Barents Sea region (Region no. 8) has a value of only 23.7 %, representing the stratocumulus region with lowest mean bias. These results indicate higher τ values for the clouds in the East China Sea, Southern Ocean, Bering Sea, NW Atlantic and Barents Sea regions relative to the Californian and SE Pacific stratocumulus regions, with the SE Atlantic region exhibiting the lowest τ values. This is confirmed by the mean τ values shown in Table 3. The biases for the r_e3.7 retrieval display the same spatial patterns as for r_e2.1, but are significantly lower; the mean value in the region with the maximum bias (SE Atlantic, Region no. 2) is 17 % and in the region with the lowest bias (Barents Sea, Region no. 8) it is 10 %.

The regional mean LWP biases are also listed in Table 4. They are negative since an r_e underestimation from the vertical penetration effect leads to an LWP underestimate (see Eq. 11). The biases are also smaller in magnitude than for N_d due to the smaller sensitivity of LWP to r_e inherent in the latter equation. They are anticorrelated with the N_d biases such that the region with largest N_d bias (SE Atlantic) has the largest negative LWP bias of −11.1 %. The smallest magnitude bias occurs in that Barents Sea region (−8 %).

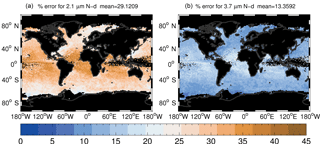
Figure 5 Maps of the annual mean percentage error for uncorrected N_d retrievals using a year (2008) of daily MODIS data that have been filtered to select data points in which N_d retrievals are favourable and therefore most likely to be used for N_d data sets (see text for details). The left plot shows the results for the r_e2.1 retrieval and the right for the r_e3.7 retrieval.

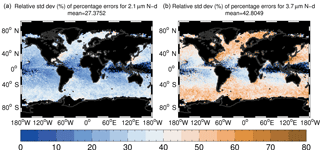
Figure 6 As for Fig. 5 except showing the relative (as a percentage) standard deviation of the percentage N_d bias over time, i.e. ${\mathit{\sigma }}_{\text{\%\hspace{0.17em}bias}}/\stackrel{\mathrm{‾}}{\text{\%\hspace{0.17em}bias}}$.

It is also useful to know how variable the biases are from day to day for a given point in space since this will determine how useful the application of a single offset bias correction might be for correcting N_d biases for daily data. Figure 6 shows the time variability of the bias in the form of the relative standard deviations (over time) of the percentage N_d biases. It reveals that the percentage bias in N_d generally has a larger relative standard deviation at latitudes above around 40^∘ with values typically ranging up to around 30–50 % (of the mean percentage N_d bias) for the 2.1 µm retrieval. Relative variability is greater for the 3.7 µm retrieval, perhaps due to the much lower mean percentage errors. Some of the selected regions show more variability than others, in particular the Barents Sea and East China Sea regions.

Table 4 gives the regional means of the relative standard deviations revealing values that range from approximately 20 to 40 % of the mean percentage biases for the 2.1 µm retrieval and 30–60 % for the 3.7 µm one. This shows that the application of a single annual mean offset bias correction is likely to lead to fairly large biases for the N_d estimates for individual days for regions where the mean N_d errors are significant. If daily data are used to determine relationships between cloud properties and N_d without correcting for the biases examined here then significant variability in N_d might be introduced that may affect those relationships via non-linear effects.

Figure 7 shows how the percentage N_d biases change with season for the r_e2.1 retrieval only. Interestingly, the highest biases tend to occur in the DJF season for the SE Pacific and SE Atlantic stratocumulus regions, indicating that τ values are lower in DJF for those seasons. The September–October–November (SON) season also generally produces higher biases than March–April–May (MAM) and June–July–August (JJA) for those regions, particularly for SE Pacific. For the East China Sea region the biases are lower in SON and DJF seasons than in the other seasons. We note that there are little data in this region for JJA since there are few low-altitude clouds with large regional liquid cloud fractions there in this season. Either the other regions do not show a large amount of seasonal variability or N_d data are only available for part of the year due to a lack of sunlight in the winter months.

Figure 7 Seasonal mean percentage N_d biases for the r_e2.1 retrieval only.

5 Discussion

There are some caveats to the results that we presented here that we now discuss. We have shown that, theoretically, the effect of retrieving a lower r_e than the cloud top r_e can be corrected for by simply replacing r_e with the parameterized cloud top version or by removing dτ from the observed τ. However, this rests upon the parameterizations being valid across all of the cloud types relevant for the N_d and LWP data sets. The relationships are based on the retrieved r_e for a range of clouds, although only for a nadir viewing angle and a SZA of 20^∘. Platnick (2000) showed that dτ has some dependence on viewing geometry and so the consideration of a wider range of view and SZAs should ideally be made.

In addition, a liquid water condensation rate (c_w) value of 1.81 × 10⁻⁶ kg m⁻⁴ was assumed for the model adiabatic clouds, which corresponds to a cloud temperature of 278 K at a pressure of 850 hPa. In reality, cloud temperatures and hence c_w will vary, mainly as a function of cloud temperature. We have performed sensitivity tests using a value of 1.0 × 10⁻⁶ kg m⁻⁴, which corresponds to a cloud temperature of 262 K. This is likely to be close to the coldest temperature attained by boundary layer clouds over the oceans that are coupled to the surface, which are generally the types of clouds for which the droplet concentration retrievals are applied. The results (not shown) reveal mean differences (across the τ values tested) in the mean dτ line (i.e. the white line in Fig. 2a) of 4.2 % (the maximum difference was 10 %) for the 2.1 µm retrieval and 3.6 % (maximum of 7.6 %) for the 3.7 µm one. For g_re the differences were of the opposite sign and much smaller, with mean differences in the median g_re line of −0.45 % (the most negative difference was −0.6 %) for the 2.1 µm retrieval and −0.3 % (−0.66 % was the most negative difference) for the 3.7 µm one. Therefore, the effect of c_w changes is relatively minor. These results would also apply for equivalent changes in the cloud adiabaticity (i.e. the value of f_ad).

The modelling of the idealized clouds and the correction rests on the assumption that r_e increases monotonically with height within the cloud (following the adiabatic assumption), but there is some suggestion that the development of precipitation-sized droplets might lead to larger droplets being preferentially found below cloud top (Chang and Li, 2002; Nakajima et al., 2010a, b; Suzuki et al., 2010). However, Zhang et al. (2012) found that MODIS retrievals of r_e performed on model-generated clouds were not significantly affected by the presence of precipitation. Also, during the VOCALS field campaign in the SE Pacific region, aircraft observations showed that r_e generally did increase with height up to cloud top (Painemal and Zuidema, 2011), indicating that this is not a problem at least for the near-coastal clouds tested. Further offshore the likelihood of precipitation increases as clouds become more cumulus-like and so for those clouds the issue may be greater and hence more caution should be exercised when interpreting the results presented here for such regions.

Evaporation effects related to entrainment also have the potential to reduce r_e, N_d and LWC near cloud top and hence negate some of the assumptions upon which the N_d retrievals rest. However, we argue that the entrainment effect upon r_e is likely to be minimal for two reasons: firstly, the evidence suggests that for stratocumulus clouds extreme inhomogeneous mixing occurs at cloud top, which reduces the LWC and N_d, but does not change r_e (Brenguier et al., 2011; Burnet and Brenguier, 2007; Painemal and Zuidema, 2011). Secondly, the results of Painemal and Zuidema (2011) indicate that entrainment occurs within approximately the first 0.5 optical depths from cloud top on average; the penetration depths calculated here are considerably larger than this for reasonably thick clouds (Fig. 2). The effect of the reduced N_d and LWC within the entrainment zone is not so clear-cut; this would negate the assumption of a vertically constant N_d and monotonically increasing LWC used to formulate the total τ. However, given the likely small τ contribution from the entrainment region relative to the total τ, this effect is likely to be small.

It is also clear that the suggested correction for the vertical penetration effect should only be applied to the retrievals of N_d with consideration of other bias sources. These other potential error sources are numerous and include r_e biases due to subpixel heterogeneity (Zhang and Plantnick, 2011; Zhang et al., 2016, 2012), 3-D radiative effects (Marshak et al., 2006), assumptions regarding the degree of cloud adiabaticity (Janssen et al., 2011; Merk et al., 2016), the choice of k value (Brenguier et al., 2011; Merk et al., 2016), the assumption of a vertically uniform N_d, the assumed droplet size distribution shape and width (Zhang, 2013), viewing geometry effects (Bennartz and Rausch, 2017; Di Girolamo et al., 2010; Grosvenor and Wood, 2014; Horváth, 2004; Kato and Marshak, 2009; Liang and Girolamo, 2013; Liang et al., 2009, 2015; Maddux et al., 2010; Várnai and Davies, 1999; Várnai and Marshak, 2007) and upper-level cloud and aerosol layers (Adebiyi et al., 2015; Bennartz and Harshvardhan, 2007; Davis et al., 2009; Haywood et al., 2004; Meyer et al., 2013; Sourdeval et al., 2013, 2016). These errors have the potential to bias N_d in a way that opposes the positive bias expected from the vertical penetration effect such that the overall biases may cancel out. Indeed, the largest source of error in N_d is likely that from r_e biases given the sensitivity of N_d to r_e in Eq. (10). MODIS r_e has generally been shown to be biased positively compared to aircraft observations (King et al., 2013; Painemal and Zuidema, 2011), which would lead to a negative N_d error when taken alone. Thus, the application of the correction described in this paper in isolation has the potential to enhance any negative bias in N_d caused by a positive r_e bias.

Our paper quantifies the vertical penetration bias in isolation to the other effects mentioned above. It should be questioned, though, whether the presence of cloud heterogeneity and other effects somehow prevent the effects of the vertical stratification from influencing the retrieved r_e, making it irrelevant. This could be a potential explanation for why it is often observed that r_e2.1 is larger than r_e3.7 (Zhang and Plantnick, 2011) in contrast to the direction expected from adiabatic clouds given the vertical penetration effect, since it is known that subpixel heterogeneity effects tend to cause a positive r_e2.1 bias relative to r_e3.7 (Zhang et al., 2012). We argue, though, that the vertical stratification effect occurs in addition to other effects (e.g. heterogeneity) with the latter cancelling out and often exceeding the former such that the positive difference between r_e2.1 and r_e3.7 would be even larger without the vertical stratification effect. The cancellation of biases may also explain why VOCALS aircraft measurements (Painemal and Zuidema, 2011) tended to show that r_e2.1 and r_e3.7 were very similar.

We also note that there are many situations when the expected result due to vertical stratification of r_e does occur (i.e. r_e3.7>r_e2.1), as demonstrated in Painemal et al. (2013) and Fig. 8. This shows ratios between r_e3.7 and r_e2.1 for an example MODIS scene in the SE Pacific stratocumulus region. Ratios using the uncorrected MODIS r_e values are shown, which shows that the ratio exceeds 1 for most of the stratocumulus cloud region (the clouds that adjoin the coast) with ratios ranging from around 1.1 to 1.2. In the more broken clouds the ratio is less than 1, which is likely a result of cloud heterogeneity. However, it would be expected that N_d retrievals would not be applied to such clouds. The figure also shows the ratios calculated using r_e3.7 and r_e2.1 values that have been corrected using the g_re factors. If the differences between r_e3.7 and r_e2.1 were caused by vertical stratification alone and our parameterization were correctly predicting the cloud top r_e for both MODIS channels, then this ratio should be equal to 1. This is the case for the clouds close to the coast, indicating that our parameterization is working well for these clouds. The ratios are a little higher than 1 further north and west (around 1.05–1.08) indicating that either our parameterization is not working correctly for these clouds or other factors are causing relative differences between r_e3.7 and r_e2.1 (e.g. subadiabaticity, cloud heterogeneity). Figure 9 shows the percentage of pixels for which r_e3.7>r_e2.1 for 90 days of MODIS SE Pacific observations divided into four different heterogeneity bins. Heterogeneity is characterized by the H_σ parameter (Liang et al., 2009), which is the standard deviation of the 250 m resolution 0.86 µm reflectance (R_0.86) divided by the mean R_0.86. It is clear that for many regions relative r_e values that are consistent with an adiabatic profile occur more than 50 % of the time, particularly when the cloud heterogeneity is low. This suggests that it may be possible to use H_σ to determine the situations in which the bias correction is more applicable. However, it is hard to definitively prove our argument within the scope of this study, particularly for more heterogeneous regions, since it would likely require computationally expensive 3-D RT modelling of known cloud fields (e.g. from LES models), followed by r_e and τ retrievals.

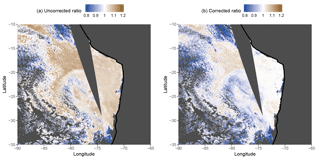
Figure 8 Ratios of r_e3.7 to r_e2.1 for a MODIS snapshot scene from the Southeast Pacific stratocumulus region from 16 June 2015. (a) Using uncorrected r_e values. (b) Using r_e values that have been corrected using the parameterizations for g_re (for both r_e3.7 and r_e2.1). A ratio of 1 is expected for the plot on the right if the relative differences between r_e3.7 and r_e2.1 are caused by vertical stratification alone and if the parameterization is correctly predicting the relative differences.

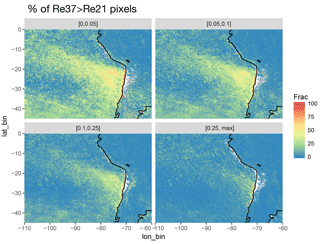
Figure 9 The percentage of pixels for which r_e3.7>r_e2.1 for 90 days (January, February and March of 2008) of 0.1^∘ resolution MODIS Collection 6 observations for the SE Pacific stratocumulus region. Only single layer liquid clouds are included and data points have been filtered to exclude τ<5 and partially cloudy pixels. The four panels are for four different bins of the heterogeneity parameter (the standard deviation of the 250 m resolution 0.86 µm reflectance divided by the mean reflectance) with bin ranges labelled in square brackets above the panels and the x and y axes in degrees longitude and latitude, respectively.

Painemal and Zuidema (2011) actually demonstrated that MODIS N_d agreed rather well with N_d from aircraft for the SE Pacific region despite a fairly large positive r_e bias; this was thought to be due to the fortuitous cancellation of (for N_d) the r_e bias with biases in the k parameter and f_ad. However, the agreement between aircraft and MODIS N_d seen in Painemal and Zuidema (2011) would deteriorate if a correction for the N_d bias due to the penetration depth effect discussed here were also applied. Table 4 indicates that the result would be a MODIS N_d underestimate of around 32 % (average for SE Pacific, Region no. 1) for the 2.1 µm retrieval, assuming perfect initial agreement. This indicates that another N_d bias may have been operating in order to give the good observed agreement.

The MODIS retrieval uses reflectances from both a visible and a SWIR wavelength channel, with the former being primarily determined by τ and the latter by r_e. However, a bispectral retrieval is used and so there is also some sensitivity of the retrieved τ to the SWIR reflectance, which will be representative of the r_e below cloud top due to the vertical penetration effect. This, combined with the fact that the MODIS forward retrieval model assumes a vertically uniform cloud, will result in the retrieved τ being biased relative to the real value (assuming the real cloud has an adiabatic profile). Figure 10 shows the difference between the retrieved and model profile τ; the bias is negative and smaller in magnitude than 5 % for the 3.7 µm retrieval. They are slightly larger for the 2.1 µm retrieval, but still lower in magnitude than 5 %, except at r_e ≲ 7 µm. Although it should be noted that some of this bias may be due to other causes related to the inconsistencies between the vertically uniform and adiabatic models rather than the r_e vertical penetration bias. Since the retrieved N_d is proportional to the square root of τ, this will lead to small N_d biases. Biases in LWP will be similar to those in τ since LWP is proportional to τ, but r_e biases are still likely to dominate (e.g. see Fig. 1). Thus, we have not pursued this further.

In this paper we have only considered retrievals over the ocean, although retrievals over land for τ and r_e are available for MODIS. MODIS surface albedo uncertainties are likely to be much higher over land than over the oceans (Bréon and Doutriaux-Boucher, 2005; King et al., 2004; Rosenfeld et al., 2004) since the surface albedo is much more variable over land. In addition, cloud masking is more difficult over land, particularly over non-vegetated surfaces, transitional areas between desert and vegetated surfaces and above high-altitude regions (Platnick et al., 2003). We have ignored land regions in order to avoid such complications and also because stratocumulus clouds are more prevalent over ocean regions (Klein and Hartmann, 1993; Wood, 2012). However, the results shown in this paper may still apply over land. The results of Rosenfeld et al. (2004) and Platnick et al. (2017) suggest that surface albedo uncertainties are more important at lower optical depths (≲ 5) and for the 2.1 µm retrieval (relative to the 3.7 µm one). Thus, for thicker clouds and the 3.7 µm retrieval land surface albedo issues may be less problematic.

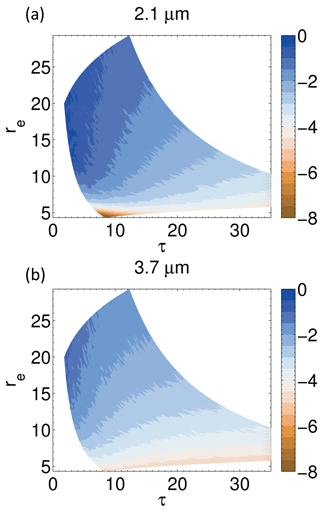
Figure 10 Percentage τ bias (retrieved vs. actual value from the input model profile) as a function of τ and r_e.

Finally, we note that the thermal emission correction for the MODIS r_e3.7 (see Sect. 3.1) retrieval has some uncertainty that should be considered; the uncertainty for this is included (combined with other uncertainties) in the MODIS Collection 6 pixel level uncertainty products (Platnick et al., 2017). It is possible that effects additional to those included, such as cloud heterogeneity and surface heterogeneity, may further increase the uncertainty beyond that estimated in the MODIS products, but these are currently not well documented.

6 Conclusions

We have described and quantified a positive bias in satellite retrievals of cloud droplet concentration (N_d) and liquid water path (LWP) that make use of the adiabatic cloud assumption to estimate these quantities from satellite-observed cloud optical depth (τ), effective radius (r_e) and cloud top temperature. We term the bias the “vertical penetration bias”. It arises due to the well-documented vertical penetration of photons with wavelengths in the shortwave-infrared range into the upper regions of clouds, so that r_e retrievals are representative of values some distance below cloud top (Bennartz and Rausch, 2017; Platnick, 2000) rather than being those at cloud top as assumed by the N_d and LWP retrievals. Here we quantified the optical depth as measured from cloud top downwards, dτ, at which the retrieved r_e equaled the actual r_e for adiabatic clouds covering a large range of total cloud optical depths and N_d values. We showed that knowledge of dτ allows a corrected N_d to be calculated by subtracting dτ from the observed τ and using that in the N_d retrieval instead of τ. We characterized dτ as functions of τ for the 2.1 and 3.7 µm r_e retrievals (r_e2.1 and r_e1.6, respectively) and found that a 1-D relationship approximates the modelled data well. dτ increases with τ and is larger for r_e2.1 than for r_e3.7 and so the vertical penetration N_d bias affects retrievals based on r_e2.1 more than those using r_e3.7. Similarly, we also parameterized the true cloud top effective radius (r_e(H)) as a function of the retrieved r_e and τ, allowing both a corrected N_d and LWP to be calculated by using r_e(H) instead of the retrieved value. Both the dτ and r_e correction methods give similar results for the N_d retrievals suggesting that the latter is preferable since it also allows for a correction to LWP. However, for some applications it may be useful to be able to parameterize dτ.

We quantified the vertical penetration N_d bias for 1-year N_d and LWP data sets. The corrections presented here suggest that N_d and LWP errors will increase as the τ value of the cloud scene gets lower. For many regions that are considered trustworthy for N_d and LWP retrievals (typically stratocumulus regions), there are high frequencies of low τ values and the N_d biases are significant. For example, for the SE Pacific and SE Atlantic regions clouds with τ≤10 (for which N_d errors are expected to be ≥ 31 % for r_e2.1 and ≥ 15 % for r_e3.7) occur, respectively, 53 and 69 % of the time on average. The mean r_e2.1 vertical penetration N_d biases for these regions were 32 and 35 %, respectively. Out of the stratocumulus regions examined, these two were the worst affected. For r_e3.7 the N_d biases were much smaller; for example, mean biases for the SE Pacific and SE Atlantic regions were 15 and 17 %, respectively. N_d biases were predicted to be worse for the tropical and subtropical regions than for higher latitudes. The time variability of the biases were also examined and were shown to be significant (regional mean standard deviations of 19–37 and 32–56 % for r_e2.1 and r_e3.7, respectively). This indicates that long-term averages of the vertical penetration N_d bias corrections are not useful for correcting N_d data over short timescales (e.g. daily N_d data). We also examined the seasonality of the N_d biases and showed that, for the stratocumulus regions, generally the DJF season was worst affected, followed by SON.

LWP biases were of a lower magnitude than those for N_d and were negative. The largest biases were again for the SE Atlantic region where the mean bias was −11.1 % and the smallest for the Barents Sea region (−8 %). Biases were also lower when using r_e3.7 with a maximum (most negative) bias of −6.1 %.

We caution that the correction for the N_d and LWP vertical penetration biases presented here should only be considered in combination with corrections for other biases that affect τ and r_e. Zhang et al. (2016) suggest a correction for the subpixel heterogeneity bias effect, but corrections may not currently exist for all biases and it is likely that some unidentified biases still exist. Therefore, we recommend that our correction is currently only applied to homogeneous cloud scenes in order to minimize possible entanglements with biases resulting from heterogeneity effects, which are not accounted for. Such conditions can be obtained by limiting retrievals to associated heterogeneity (H_σ) values (available in MODIS MYD06 Collection 6 products) to less than about 0.1. Otherwise N_d and LWP biases could be made worse, for example, in situations where the fortuitous cancellation of opposing errors leads to initially small N_d errors. The latter was suspected to have occurred for the comparison between MODIS N_d retrievals and in situ aircraft observations as presented in Painemal and Zuidema (2011). We showed that the SE Pacific, which is the region examined in that study, had a mean vertical penetration depth error of 32 %, suggesting that another unidentified N_d bias may have been operating in order to give good agreement.

Previous studies have shown that r_e3.7 is less prone to biases due to subpixel averaging (Zhang and Plantnick, 2011; Zhang et al., 2016, 2012). Thus, combined with the work presented here, this supports the conclusion that r_e3.7 likely represents a better choice for use in N_d and LWP retrievals.

For future work, it is recommended that additional characterization of dτ and g_re is performed for a range of viewing geometries in order to ensure that the results presented here are robust for all cloud retrievals. The use of 3-D radiative transfer calculations and simulated retrievals upon known LES model fields would also be useful for investigating how heterogeneity effects might interact with the vertical penetration effects. Further investigation into how the presence of precipitation affects our assumptions and results is also warranted.