Viscosity of erythritol and erythritol–water particles as a function of water activity: new results and an intercomparison of techniques for measuring the viscosity of particles

A previous study reported an uncertainty of up to 3 orders of magnitude for the viscosity of erythritol (1,2,3,4-butanetetrol)–water particles. To help reduce the uncertainty in the viscosity of these particles, we measured the diffusion coefficient of a large organic dye (rhodamine B isothiocyanate–dextran, average molecular weight $\sim \mathrm{70}\mathrm{000}\mathrm{g}{\mathrm{mol}}^{-\mathrm{1}})$ in an erythritol–water matrix as a function of water activity using rectangular-area fluorescence recovery after photobleaching (rFRAP). The diffusion coefficients were then converted to viscosities of erythritol–water particles using the Stokes–Einstein equation. In addition, we carried out new viscosity measurements of erythritol–water particles using aerosol optical tweezers. Based on the new experimental results and viscosities reported in the literature, we conclude the following: (1) the viscosity of pure erythritol is ${\mathrm{184}}_{-\mathrm{73}}^{+\mathrm{122}}$ Pa s (2 standard deviations); (2) the addition of a hydroxyl (OH) functional group to a linear C₄ carbon backbone increases the viscosity on average by a factor of ${\mathrm{27}}_{-\mathrm{5}}^{+\mathrm{6}}$ (2 standard deviations); and (3) the increase in viscosity from the addition of one OH functional group to a linear C₄ carbon backbone is not a strong function of the number of OH functional groups already present in the molecule up to the addition of three OH functional groups, but the increase in viscosity may be larger when the linear C₄ carbon backbone already contains three OH functional groups. These results should help improve the understanding of the viscosity of secondary organic aerosol particles in the atmosphere. In addition, these results show that at water activity>0.4 the rFRAP technique, aerosol optical tweezers technique, and bead-mobility technique give results in reasonable agreement if the uncertainties in the measurements are considered. At water activity<0.4, the mean viscosity values determined by the optical tweezers technique were higher than those determined by the bead-mobility and rFRAP techniques by 1–2 orders of magnitude. Nevertheless, the disagreement in viscosity measured using multiple techniques reported in this paper is smaller than reported previously.

1 Introduction

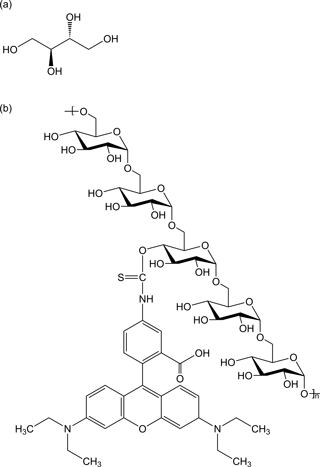
Table 1 The molar masses (M_w) and hydrodynamic radii (R_H) of erythritol and rhodamine B isothiocyanate–dextran (RBID), which are used as the matrix and diffusing fluorescent dye in this work, respectively.

Secondary organic aerosol (SOA) is produced by the oxidation of volatile organic compounds followed by the condensation of oxidation products (Hallquist et al., 2009). SOA contributes approximately 20 % to 70 % to the mass of fine aerosol particles, depending on location (Hallquist et al., 2009; Jimenez et al., 2009; Kanakidou et al., 2005; Zhang et al., 2007). Despite the abundance of SOA in the atmosphere, some physical and chemical properties of SOA remain poorly understood. An example is the diffusion of organic molecules within SOA particles (Cappa and Wilson, 2011; Mikhailov et al., 2009; Perraud et al., 2012; Reid et al., 2018; Vaden et al., 2011). Diffusion rates of organic molecules in SOA have implications for predicting the size and mass distribution of SOA particles (Lu et al., 2014; Saleh et al., 2013; Shiraiwa and Seinfeld, 2012; Zaveri et al., 2014, 2018). Diffusion rates of molecules in SOA also influence reaction rates (Berkemeier et al., 2016; Chu and Chan, 2017a, b; Gatzsche et al., 2017; Hinks et al., 2016; Houle et al., 2015; Kuwata and Martin, 2012; Li et al., 2015; Lignell et al., 2014; Liu et al., 2018; Steimer et al., 2015; Wang et al., 2015; Wong et al., 2015; Zhou et al., 2012), the long-range transport of pollutants (Bastelberger et al., 2017; Shrivastava et al., 2017; Zelenyuk et al., 2012), and optical properties of SOA particles (Adler et al., 2013; Robinson et al., 2014). Diffusion may also have implications for the ice-nucleating ability of SOA (Bodsworth et al., 2010; Ignatius et al., 2016; Ladino et al., 2014; Murray and Bertram, 2008; Schill et al., 2014; Wilson et al., 2012).

Diffusion limitations in SOA have been investigated through aerosol population mixing experiments, aerosol size change, and other approaches (Cappa and Wilson, 2011; Gorkowski et al., 2017; Liu et al., 2016; Perraud et al., 2012; Ye et al., 2016, 2018; Zaveri et al., 2018). In addition, researchers have used measurements of SOA viscosity together with the Stokes–Einstein equation to estimate diffusion rates of organics within SOA. The Stokes–Einstein equation is as follows:

$$\begin{array}{}\text{(1)}& D=k_{\mathrm{B}}T/\left(\mathrm{6}\mathit{\pi }\mathit{\eta }{R}_{\mathrm{H}}\right),\end{array}$$

where D is the diffusion coefficient (m² s⁻¹), k_B is the Boltzmann constant ($\mathrm{1.38}\times {\mathrm{10}}^{-\mathrm{23}}$ J K⁻¹), T is the temperature (K), η is the matrix viscosity (Pa s), and R_H is the hydrodynamic radius (m) of the diffusing species.

Researchers have investigated the viscosity of SOA in the atmosphere (Bateman et al., 2016, 2017; O'Brien et al., 2014; Pajunoja et al., 2016; Virtanen et al., 2010), the viscosity of SOA material generated in environmental chambers (Grayson et al., 2016; Pajunoja et al., 2014; Renbaum-Wolff et al., 2013; M. Song et al., 2015, 2016; Virtanen et al., 2011), the viscosity of compounds identified in SOA particles (Abramson et al., 2013; Bateman et al., 2015; Hosny et al., 2016), and the viscosity of simple proxies of SOA material (Marshall et al., 2016; Power et al., 2013). In addition, researchers have investigated the dependence of viscosity on molar mass and the number and type of functional groups (Grayson et al., 2017; Rothfuss and Petters, 2017; Y. C. Song et al., 2016). For example, Grayson et al. (2017) investigated the dependence of viscosity on the number of hydroxyl (OH) functional groups on a carbon backbone and found that viscosity increased, on average, by a factor of 22–45 following the addition of an OH functional group to linear C₃, linear C₄, branched C₅, and linear C₆ carbon backbones. However, the study by Grayson et al. (2017) revealed a large discrepancy between the viscosity of erythritol (1,2,3,4-butanetetrol) measured with the bead-mobility technique (Grayson et al., 2017) and measured with the aerosol optical tweezers technique (Y. C. Song et al., 2016) at ≤25 % relative humidity (RH). This led to uncertainties when predicting the effect of adding OH functional groups to a linear C₄ carbon backbone on viscosity. This also led to uncertainties regarding the viscosity of tetrols, which have been observed in ambient SOA particles and SOA particles generated in environmental chambers (Claeys, 2004; Edney et al., 2005; Surratt et al., 2006, 2010). An important formation pathway for tetrols is the hydrolysis of isoprene epoxidiol (IEPOX). IEPOX has been identified as a key intermediate during the oxidation of isoprene, an SOA precursor (Guenther et al., 2006; Surratt et al., 2010).

To help reduce the uncertainty in the viscosity of erythritol–water particles, we measured the diffusion coefficients of a large organic dye (rhodamine B isothiocyanate–dextran, referred to as RBID in the following; average molecular weight $\sim \mathrm{70}\mathrm{000}\mathrm{g}{\mathrm{mol}}^{-\mathrm{1}})$ in erythritol–water matrices as a function of water activity (a_w) using the rectangular-area fluorescence recovery after photobleaching (rFRAP) technique (Deschout et al., 2010). The diffusion coefficients were then converted to viscosities using the Stokes–Einstein equation (Eq. 1). RBID has a hydrodynamic radius that is more than 16 times larger than that of erythritol (Table 1 and Fig. 1). We assume that the viscosity of an erythritol–water particle can be accurately calculated from the diffusion coefficient of RBID and the Stokes–Einstein equation, since the Stokes–Einstein equation accurately predicts diffusion coefficients when the diffusing molecules are large in size relative to the matrix molecules and when the matrix viscosity is comparable to or less than 10⁴ Pa s (Chenyakin et al., 2017; Price et al., 2016), which is the case for erythritol–water particles (Grayson et al., 2017; Y. C. Song et al., 2016).

In addition to determining viscosities from the rFRAP diffusion measurements, we carried out new viscosity measurements for erythritol–water particles at a_w<0.1 using the aerosol optical tweezers technique. The new viscosity results from the rFRAP and the aerosol optical tweezers measurements were then used to update our understanding of the viscosity of erythritol–water particles and the effect of adding OH functional groups to a linear C₄ carbon backbone on viscosity. The new results also allowed us to perform an intercomparison between three techniques (rFRAP, aerosol optical tweezers, and bead mobility) used for measuring the viscosity of organic–water particles.

Figure 1 Molecular structures of (a) erythritol and (b) rhodamine B isothiocyanate–dextran (RBID) in neutral form. On average, n≈429.

2 Experimental method

2.1 rFRAP

As mentioned above, the rFRAP technique was used to measure diffusion coefficients of RBID in erythritol–water matrices as a function of a_w. The rFRAP experiments were similar to those described in Chenyakin et al. (2017). The current rFRAP experiments required thin films (30–50 µm thick) with a known a_w, containing erythritol, water, and trace amounts of RBID. Section 2.1.1 describes the preparation of the thin films. Section 2.1.2 describes the rFRAP technique and the extraction of diffusion coefficients from the rFRAP data.

2.1.1 Preparation of thin films containing erythritol, water, and trace amounts of RBID with a known a_w

The solubility of erythritol in water at 293 K is ∼38 wt % (Haynes, 2015), which corresponds to an a_w≈0.92, based on Raoult's law and assuming erythritol does not dissociate in water (Koop et al., 2011). In our experiments, all thin films were conditioned at a_w<0.92 and were therefore supersaturated with respect to crystalline erythritol. To prepare these supersaturated thin films, a bulk solution containing 20 wt % erythritol in water and 0.056 wt % (0.01 mmol L⁻¹) RBID was prepared gravimetrically. The prepared bulk solution was then filtered using a 0.45 µm Millex^®-HV syringe filter unit (Millipore Sigma Ltd., Etobikoe, ON, Canada) to eliminate solid impurities. Next, the solution was nebulized onto a siliconized hydrophobic glass slide (22×22 mm, VWR, Radnor, PA, USA), which had been rinsed with Milli-Q^® water (18.2 MΩ cm). This resulted in droplets with radii ranging from 100 to 185 µm on the hydrophobic glass slide. For most of the experiments, the slide holding the droplets was then transferred into a flow cell in an inflatable glove bag (Glas-Col, Terre Haute, IN, USA) for conditioning at a particular a_w. For some of the experiments, the slide holding the droplets was placed in a sealed container above a saturated inorganic salt solution with a known a_w. A handheld hygrometer (OMEGA, Norwalk, CT, USA) with an accuracy of ±2.5 % was used to measure the RH at the flow cell outlet and in the glove bag or above the bulk solutions. The a_w was calculated from the measured RH ($a_{\mathrm{w}}=\mathrm{RH}\left(\mathrm{\%}\right)/\mathrm{100})$ (Seinfeld and Pandis, 2006). The time used for conditioning droplets ranged from 21.5 to 96 h. See Sect. S1 and Table S1 in the Supplement for details. After conditioning the droplets at a particular a_w, thin films were formed by placing a second hydrophobic glass slide on top of the original glass slide supporting the droplets. A pair of aluminum spacers, with a thickness of 30–50 µm, were placed between the two slides to control the thickness of the thin films. A seal was formed between the two slides by lining the perimeter of one slide with high-vacuum grease prior to sandwiching the droplets. Figure S1 in the Supplement shows a schematic of the thin films used in the rFRAP experiment. The process of creating the thin films was carried out inside the inflated glove bag, to prevent the sample from being exposed to the uncontrolled RH in the room. After conditioning the droplets to a known a_w and creating the thin films, the concentration of RBID in the thin films ranged from 0.2 to 0.3 wt %. At this concentration, the fluorescence intensity of the thin films was proportional to the RBID concentration (Sect. S2 and Fig. S2 in the Supplement).

Even though all thin films were supersaturated with respect to crystalline erythritol, crystallization was not observed, likely because (1) the bulk solution was filtered to remove impurities and (2) the glass slides were highly hydrophobic, which reduced the possibility of heterogeneous nucleation of organic crystals (Bodsworth et al., 2010; Pant et al., 2004, 2006; Wheeler and Bertram, 2012; Yeung et al., 2009).

2.1.2 rFRAP technique and data extraction

In the rFRAP experiments, a confocal laser scanning microscope was used to photobleach RBID molecules in a small volume of the thin film. The photobleaching process occurs as follows. First, RBID molecules in the ground state absorb photons generated by the 543 nm laser and undergo an electronic transition from the ground state to the excited singlet state. Next, these excited molecules can either relax to the ground state via the emission of a photon (this process is fluorescence, which does not result in photobleaching) or undergo intersystem crossing from the excited singlet state to the excited triplet state. In the excited singlet or triplet state, RBID molecules may react with molecular oxygen, resulting in permanent destruction of the fluorophore (Song et al., 1995; Widengren and Rigler, 1996). After photobleaching, a gradual recovery of fluorescence within the photobleached region occurred due to the diffusion of unbleached fluorescent molecules from outside the bleached region into the bleached region. The diffusion coefficient of the fluorescent dye was determined by monitoring the time-dependent recovery of the fluorescence intensity using the same confocal laser scanning microscope used for photobleaching.

In this work, a Zeiss LSM510 confocal laser scanning microscope with a 10× objective and 0.30 numerical aperture was used. The pinhole was set at 120 µm. Photobleaching was performed using a helium–neon laser with an emission wavelength of 543 nm, at a power of 330 µW. The photobleached area ranged from 3×3 to 6×6 µm². The bleach parameters, including the number of iterations and scanning speed of the laser, were adjusted to obtain a reduction in fluorescence intensity of ∼30 % in the bleached region, as recommended by Deschout et al. (2010). After photobleaching, images were taken using the same laser at a power of 4 µW, at time intervals ranging from 2 to 30 s, depending on the speed of recovery of the fluorescence signal, with longer intervals used when the fluorescence recovery was slower. All experiments were performed at room temperature (292–294 K).

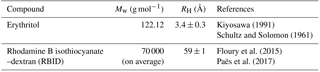
Figure 2 shows an example of a series of images recorded during an rFRAP experiment. All of the images recorded after photobleaching were normalized against an image captured prior to photobleaching, using ImageJ software. After normalization, the images were downsized from 512×512 pixels to 128×128 pixels by averaging pixels to reduce the level of noise (Chenyakin et al., 2017).

Figure 2 Images captured during an rFRAP experiment for thin erythritol–water films conditioned at $a_{\mathrm{w}}=\mathrm{0.023}\pm \mathrm{0.023}$. RBID concentration in the films was approximately 0.3 wt %. The red square in (a) indicates the region selected for photobleaching. Images (b–f) were recorded at 0, 360, 720, 1080, and 1440 s after photobleaching. Dimensions of the images and the red square are 60×60 and 6×6 µm², respectively.

The fluorescence intensity at position (x, y) and time t after photobleaching a rectangular area in a thin film can be described by the following equation (Deschout et al., 2010):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{F\left(x,y,t\right)}{F_{\mathrm{0}}\left(x,y\right)}}=\\ {\displaystyle }& {\displaystyle }B\left\{\mathrm{1}-{\displaystyle \frac{K_{\mathrm{0}}}{\mathrm{4}}}\left[\mathrm{erf}\left({\displaystyle \frac{x+\frac{l_x}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)-\mathrm{erf}\left({\displaystyle \frac{x-\frac{l_x}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)\right]\right.\\ \text{(2)}& {\displaystyle }& {\displaystyle }\left.\times \left[\mathrm{erf}\left({\displaystyle \frac{y+\frac{l_y}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)-\mathrm{erf}\left({\displaystyle \frac{y-\frac{l_y}{\mathrm{2}}}{\sqrt{r^{\mathrm{2}}+\mathrm{4}Dt}}}\right)\right]\right\},\end{array}$$

where F(x, y, t) is the fluorescence intensity at position (x, y) and time t after photobleaching, F₀(x, y) is the fluorescence intensity at position (x, y) prior to photobleaching, l_x and l_y are the lengths of the rectangular photobleached area, K₀ is related to the fraction of molecules photobleached in the bleach region, r is the resolution of the microscope, t is the time after photobleaching, and D is the diffusion coefficient of the fluorescent dye. B is a normalization constant, and “erf” is the error function.

Following the rFRAP experiments, individual images were fit to Eq. (2) using a Matlab script, with terms B and K₀ left as free parameters. The combined term of r²+4 Dt was also left as a free parameter. Due to the normalization of images to a pre-bleached image, B returned a value close to 1, as expected. From Eq. (2), a value for the combined term r²+4 Dt was obtained for each image taken after photobleaching. Next, r²+4 Dt was plotted as a function of time after photobleaching, and a straight line was fit to the plotted data. An example plot of r²+4 Dt versus t and a linear fit to the data are shown in Fig. 3. Diffusion coefficients were determined from the slope of the fitted line. The diffusion coefficient at each a_w reported in Sect. 3 is the average of at least four measurements.

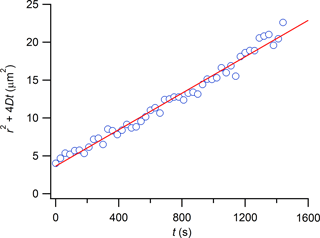
Figure 3 r²+4 Dt as a function of t for the diffusion of RBID in erythritol–water matrix with $a_{\mathrm{w}}=\mathrm{0.023}\pm \mathrm{0.023}$. RBID concentration in the conditioned films was approximately 0.3 wt %. The red line represents a linear fit to the data.

Cross-sectional views of the fluorescence intensity along the x axis for different times after photobleaching are shown in Fig. 4. The cross sections for the measured intensities (blue dots) were generated by averaging the normalized fluorescence intensities (F∕F₀) over the width of the photobleached region in the y direction, at each position x. Calculated cross sections of the fluorescence intensities (red lines) were generated from fits of Eq. (2) to the experimental data. The close agreement between the measured and calculated cross sections illustrates that Eq. (2) describes our experimental data well.

Equation (2) was derived by assuming no diffusion in the axial direction (i.e., z direction). Deschout et al. (2010) have shown that Eq. (2) gives accurate diffusion coefficients when the numerical aperture of the microscope is low (≤0.45) and the thickness of the films is small (≤120 µm), consistent with the numerical aperture of 0.30 and film thickness of 30–50 µm used in our experiments. Equation (2) also assumes that the only mechanism for recovery in the photobleached region is diffusion. An additional possible mechanism is reversible photobleaching (or photoswitching), where the fluorescent molecules convert between a fluorescent and a non-fluorescent state without being permanently photobleached (Fukaminato, 2011; Long et al., 2011; Sinnecker et al., 2005). To determine if reversible photobleaching was responsible for the recovery of fluorescence in the photobleached region, experiments with small droplets (10–30 µm in diameter) containing erythritol, water, and trace amounts of RBID (approximately 0.3 wt %) were carried out. In these experiments, we uniformly photobleached the entire droplet, resulting in ∼30 % reduction in fluorescence intensity. Uniform bleaching ensures that the diffusion of fluorescent RBID molecules will not result in a change in fluorescence intensity. After bleaching, the average fluorescence intensity of the entire droplet was monitored over time, as shown in Fig. S3 in the Supplement. The fluorescence intensity remained constant within the uncertainty of the measurements, indicating that reversible photobleaching was not an important mechanism in our rFRAP experiments.

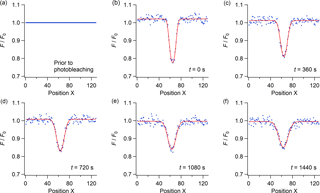
Figure 4 Cross-sectional view of the normalized fluorescence intensities (F∕F₀) along the x axis during an rFRAP experiment. Blue dots correspond to the measured data, while the red lines represent fits to the experimental data using Eq. (2). The sample films were conditioned at $a_{\mathrm{w}}=\mathrm{0.023}\pm \mathrm{0.023}$. RBID concentration in the conditioned films was approximately 0.3 wt % . Panel (a) shows the cross section prior to photobleaching. F∕F₀ equals 1 because the image was normalized against itself. Panels (b–f) show the cross sections at 0, 360, 720, 1080, and 1440 s after photobleaching, corresponding to frames (b–f) in Fig. 2.

2.2 Aerosol optical tweezers

The application of the aerosol optical tweezers technique to measure the viscosity of aerosol particles has been discussed in detail in previous publications (Bzdek et al., 2016; Y. C. Song et al., 2016) and will only be briefly reviewed here. Two optical traps are formed using a holographic optical tweezers instrument equipped with a laser at 532 nm (Laser Quantum Opus 3W). The holographic arrangement uses a spatial light modulator (Hamamatsu, X10468) to encode phase information into the expanded laser-light wavefront, creating an interference pattern in the trapping plane that resembles two tightly focused beams. Aerosol droplets are captured from a cloud of aerosol generated from a medical nebulizer and introduced into a RH-controlled trapping cell with the RH recorded by a capacitance probe (Honeywell, HIH-4202A). Typical particle diameters are 9–16 µm. Experiments were performed at room temperature of 293 K. Droplet sizes and refractive indices are inferred from the discrete wavelengths commensurate with whispering gallery modes (WGMs) that are observed in the Raman scattering fingerprints recorded from the two droplets. Particle size and refractive index are estimated from comparison with calculated WGM wavelengths using Mie scattering theory and can be determined with an accuracy of $<\pm \mathrm{2}\mathrm{nm}$ and $<\pm \mathrm{0.0005}$, respectively (Preston and Reid, 2013).

Following a conditioning period of many hours, identified by a steady droplet size over a period of tens of minutes, the particles are coalesced by manipulating the optical trap positions. Once brought into contact, the shape of the composite particle relaxes over a timescale of microseconds to hours, dependent on the viscosity. One of three methods is then chosen to infer particle viscosity from the shape relaxation based on the relaxation timescale:

1. For relaxation timescales of <1 ms (equivalent to viscosities <10 Pa s) (Power and Reid, 2014), the time dependence of the backscattered light intensity can be used to monitor the change in shape using a silicon photodetector (Thorlabs, DET 110) and oscilloscope (LeCroy, HDO 6034-MS). At timescales longer than this, the movement of the trapped particle relative to the laser beam focus (i.e., the relaxation in trapped position) contributes to the change in light-scattering signal and becomes convoluted with the change arising from the relaxation in shape. Thus, light-scattering measurements cannot be used for viscosities >10 Pa s (Bzdek et al., 2016).

2. For longer timescales, the relaxation in shape can be directly viewed from bright-field microscopy over a period spanning from 5–10 ms (equivalent to viscosities >10 Pa s) to as long as 10³ s (equivalent to viscosities ∼10⁷ Pa s) (Bzdek et al., 2016). Images are recorded by a camera (Dalsa Genie HM 640, CMOS) with 5–10 ms time resolution. The change in aspect ratio for the relaxing particle is determined and used to determine the relaxation time constant (Y. C. Song et al., 2016).

3. The disappearance followed by the reappearance of WGMs from the Raman spectrum from the coalesced dimer (recorded with 1 s time resolution) can be used to infer the slow disappearance of a spherical cavity on one side of the dimer and reemergence of a single spherical particle at the end of the relaxation process (Power et al., 2013). With a coarse time resolution of 1 s, this method should only be used to infer the viscosity when higher than 10⁴ Pa s (Power and Reid, 2014).

With three analysis methods, the optical tweezers technique can measure a wide range of viscosities, from 10⁻³ to >10⁹ Pa s. However, it should be noted that there are ranges where two techniques may overlap but have varying accuracy (e.g., bright-field imaging and Raman for viscosities 10⁴–10⁵ Pa s with relaxation times of 1–10 s).

3 Results and discussion

3.1 Diffusion coefficients in and viscosities of erythritol–water particles as functions of a_w measured by the rFRAP technique

Shown in Fig. 5a and listed in Table S2 (Supplement) are the measured diffusion coefficients of RBID in erythritol–water matrices as a function of a_w. The diffusion coefficient decreased by 2–3 orders of magnitude as a_w decreased from approximately 0.5 to 0. This decrease in the diffusion coefficients with a decrease in a_w is due to the plasticizing effect of water (Koop et al., 2011; Power et al., 2013).

The Stokes–Einstein equation and measured diffusion coefficients were used to calculate the viscosity of erythritol–water particles. It has been found that the Stokes–Einstein equation significantly underestimates the diffusion coefficients of small molecules such as water and ozone within a matrix containing larger molecules (Bastelberger et al., 2017; Davies and Wilson, 2016; Li et al., 2015; Marshall et al., 2016; Price et al., 2014; Shiraiwa et al., 2011). On the other hand, as discussed in Sect. 1, the Stokes–Einstein equation gives accurate diffusion coefficients when the diffusing species is similar in size to or larger than the matrix molecules and when the viscosity of the matrix is comparable to or lower than 10⁴ Pa s (Chenyakin et al., 2017; Price et al., 2016). Hence, in this study, we assume that the viscosity of erythritol–water particles can be accurately calculated using the measured RBID diffusion coefficient and the Stokes–Einstein equation, because RBID is much larger than the matrix molecules (Table 1) and the highest reported viscosity of erythritol in the literature is on the order of 10⁴ Pa s (Grayson et al., 2017; Y. C. Song et al., 2016).

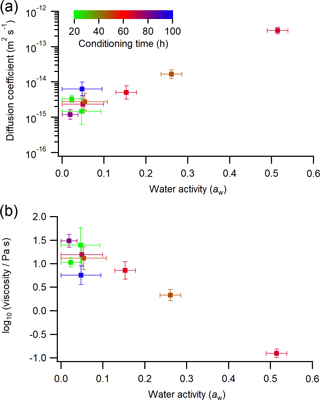
Figure 5 (a) The measured diffusion coefficients of RBID as a function of a_w. (b) The viscosity of erythritol–water particles as a function of a_w based on the measured RBID diffusion coefficients and the Stokes–Einstein equation. Results from rFRAP measurements are color-coded by the sample conditioning time prior to the rFRAP experiments. The color scale applies to both panels. Horizontal error bars indicate the upper and lower limits of a_w. Vertical error bars correspond to 2 standard deviations of diffusion coefficient (a) and log₁₀(viscosity ∕ Pa s) (b).

Figure 5b and Table S2 show the viscosity of erythritol–water particles (calculated using diffusion coefficients from Fig. 5a and the Stokes–Einstein equation) as a function of a_w. As a_w decreased from approximately 0.5 to 0, the viscosity increased from approximately $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{1}}$ to 5×10¹ Pa s. The symbols in Fig. 5 are color-coded by the time allowed to condition the samples to a particular a_w value before measuring the diffusion coefficient. The color scale in the top left corner applies to both panels (a, b). No clear trend is observed between the conditioning time and the diffusion coefficient or particle viscosity.

To further investigate the effect of the time used to condition the samples to a particular a_w value, in Fig. 6 the measured RBID diffusion coefficients in erythritol–water matrices are plotted as a function of conditioning time at a_w≤0.105. The data shown in Fig. 6 were taken from the data shown in Fig. 5a. Included as a secondary x axis is the sample conditioning time in multiples of τ_w, where τ_w is the characteristic time for water diffusion within the sample droplets used in the conditioning experiments (see Sect. S1 in the Supplement for details). Consistent with Fig. 5a, Fig. 6 illustrates that there is no clear trend between the diffusion coefficient and the time allowed for conditioning the samples prior to the diffusion measurements. Figure 6 also suggests that a sample conditioning time of ≥21.5 h, or ≥6.5 τ_w, was sufficient to reach near equilibrium between the RH used for conditioning and the a_w in particles.

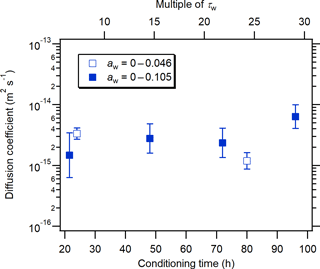
Figure 6 The diffusion coefficient of RBID as a function of the time allowed for conditioning erythritol–water particles at a_w=0–0.046 (open squares) and 0–0.105 (filled squares). The secondary (top) x axis represents the conditioning time expressed in multiples of τ_w (characteristic time for the diffusion of water molecules within the erythritol–water droplets). For the calculation of τ_w, the lower limit of a_w (i.e., 0) was taken, leading to maximum τ_w values of 3.3 h for droplets with a radius of 100 µm. Error bars represent 2 standard deviations of RBID diffusion coefficients.

3.2 Viscosity of erythritol–water particles as a function of a_w measured by the aerosol optical tweezers technique

Erythritol viscosity measurements using the aerosol optical tweezers technique are shown in Fig. 7. The viscosity of pure water at 293 K (Korson et al., 1969) is also included for comparison. The red circles represent the new aerosol optical tweezers measurements obtained in this work (also listed in Table S3 in the Supplement), based solely on bright-field images. The gray circles represent the viscosities reported in Y. C. Song et al. (2016). The new averaged viscosities reported here based on the aerosol optical tweezers technique are lower than those reported by Y. C. Song et al. (2016) at a_w<0.1, although the error bars (representing 2 standard deviations) overlap.

In the previous aerosol optical tweezers measurements at a_w<0.1 (Y. C. Song et al., 2016), the timescale for relaxation to a sphere was estimated from two methods: the change in coalesced particle shape as recorded by the bright-field images and the reappearance of WGMs in the Raman spectrum. Figure 8 shows an example of captured bright-field images as a function of time after the coalescence of two erythritol particles at $a_{\mathrm{w}}=\mathrm{0.04}\pm \mathrm{0.02}$. The relaxation to a spherical particle occurred within 56 ms, a timescale that is too short to be resolved by Raman spectral measurements (time resolution of 1 s; see Sect. 2.2). Therefore, previous erythritol viscosity measurements under dry conditions using the Raman spectral measurements (Y. C. Song et al., 2016) were compromised by the limited time resolution (1 s, equivalent to ∼10⁴ Pa s) and higher than those estimated from bright-field imaging, yielding an overestimate of the viscosity. Since the new aerosol optical tweezers measurements in this work are based solely on the bright-field images, they are more accurate than the previous results at a_w<0.1 as a consequence of the higher time resolution of the bright-field imaging measurements compared to the Raman spectroscopy measurements. The viscosity at $a_{\mathrm{w}}=\mathrm{0.22}\pm \mathrm{0.02}$ reported by Y. C. Song et al. (2016) was based on bright-field images alone, and those at a_w≥0.43 were based on backscattered light intensity (where viscosities were <10 Pa s; see Sect. 2.2).

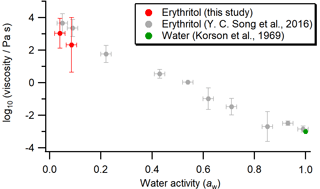
Figure 7 Viscosity of erythritol–water particles (on a log₁₀ scale) as a function of a_w, determined using the aerosol optical tweezers technique. Red circles represent experimental results from this study. Gray circles represent experimental results from Y. C. Song et al. (2016). The green circle represents the viscosity of pure water at 293 K (Korson et al., 1969). Horizontal error bars indicate the upper and lower limits of a_w. Vertical error bars represent 2 standard deviations of log₁₀(viscosity ∕ Pa s).

3.3 Update on the viscosity of erythritol–water particles as a function of a_w and an intercomparison of techniques for measuring the viscosity of particles

In Fig. 9, we have summarized the previous and current measurements of the viscosity of erythritol–water particles as a function of a_w. The black triangles represent measurements by Grayson et al. (2017) using the bead-mobility technique. The blue squares represent the rFRAP results from this work, where experimental data at similar a_w have been binned together so as not to give extra weight to the rFRAP data. The red circles indicate aerosol optical tweezers measurements from Y. C. Song et al. (2016) (open circles) and this study (solid circles). The previous measurements at a_w≤0.1 by Y. C. Song et al. (2016) were excluded from Fig. 9, because the new aerosol optical tweezers measurements reported in this study at a_w≤0.1 are thought to be more accurate. At a_w>0.4, the viscosity measurements from the bead-mobility, rFRAP, and optical tweezers techniques are in reasonable agreement if the experimental uncertainties are considered. At a_w<0.4, the mean viscosity values determined using optical tweezers are higher than those from rFRAP and bead-mobility measurements by 1–2 orders of magnitude. The error bars (2 standard deviations) overlap in some, but not all, cases. Nevertheless, the disagreement in viscosity measured using multiple techniques seen here is smaller than reported previously.

To determine the viscosity of pure erythritol under dry conditions (at a_w=0), a straight line was fit to the data in Fig. 9 based on the orthogonal distance regression-fitting algorithm using IGOR Pro 6 and then extrapolated to a_w=0. This algorithm weighted the fit based on the x and y uncertainties of each data point. The viscosity of pure water (a_w=1) is well constrained (Korson et al., 1969), giving it a larger weighting than data points at a_w<1. The intercept on the y axis was 2.27±0.22 (2 standard deviations), corresponding to a viscosity of pure erythritol of ${\mathrm{184}}_{-\mathrm{73}}^{+\mathrm{122}}$ Pa s.

Figure 8 An example of the captured bright-field images as a function of time after the coalescence of two erythritol particles in optical tweezers at $a_{\mathrm{w}}=\mathrm{0.04}\pm \mathrm{0.02}$. The relaxation to a spherical particle occurred within 56 ms.

3.4 Effect of the addition of OH functional groups to a linear C₄ carbon backbone

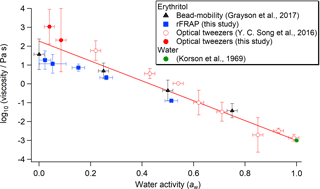
Figure 9 Viscosity of erythritol–water particles as a function of a_w measured by the bead-mobility technique (black triangles) (Grayson et al., 2017), the rFRAP technique (blue squares), and the aerosol optical tweezers technique (open red circles – from Y. C. Song et al., 2016; solid red circles – this study). The viscosity of pure water at 293 K (open green circle) (Korson et al., 1969) is also included for comparison. Horizontal error bars indicate the upper and lower limits of a_w. Vertical error bars represent 2 standard deviations of log₁₀(viscosity ∕ Pa s). The red line is a linear fit to the data points using the orthogonal distance regression-fitting algorithm in IGOR Pro 6, which is weighted based on the x and y uncertainties of each data point. The equation of the linear fit is log₁₀(viscosity ∕ Pa s) = (2.27±0.22) + ($-\mathrm{0.053}\pm \mathrm{0.002}$) ⋅ (100 a_w). Uncertainties in the slope and y-axis intercept correspond to 2 standard deviations.

Grayson et al. (2017) previously estimated the effect of adding OH functional groups on the viscosity of a linear C₄ compound. Here we repeat this analysis (Fig. 10) based on the updated viscosity of pure erythritol (${\mathrm{184}}_{-\mathrm{73}}^{+\mathrm{122}}$ Pa s) determined above. For those compounds with the same number but different positions of OH functional groups, the average of their viscosities was taken from the literature (Grayson et al., 2017; Rothfuss and Petters, 2017; Y. C. Song et al., 2016). Table S4 (in the Supplement) lists the values and sources of literature data used. The data in Fig. 10 were fit to a linear equation, resulting in a slope of 1.43±0.08 (2 standard deviations), which indicates that the viscosity of a linear C₄ molecule increases on average by a factor of ${\mathrm{27}}_{-\mathrm{5}}^{+\mathrm{6}}$ per addition of an OH functional group. The increase in viscosity with the addition of an OH functional group to a linear C₄ backbone is attributed to the increased number of hydrogen bonds (H–O⋯H) formed between adjacent molecules, as discussed previously (Rothfuss and Petters, 2017). Similarly, the addition of carboxyl groups (–COOH) leads to an increase in viscosity due to enhanced formation of intermolecular hydrogen bonds (Rothfuss and Petters, 2017).

The viscosity increase from the addition of OH functional groups to a carbon backbone may depend on the level of prior functionalization. To investigate this aspect further, we calculated the viscosity sensitivity parameter (S_η) for a linear C₄ carbon backbone using the viscosity data presented in Fig. 10 and the following equation (Rothfuss and Petters, 2017):

$$\begin{array}{}\text{(3)}& S_{\mathit{\eta }}=\mathrm{\Delta }{\log }_{\mathrm{10}}(\mathit{\eta }/\mathrm{Pa}\mathrm{s})/\mathrm{\Delta }N,\end{array}$$

where Δlog₁₀(η∕Pa s) is the change in viscosity on a log₁₀ scale and ΔN is the change in the number of OH functional groups. S_η was estimated based on the addition of one OH functional group (ΔN=1), starting from n-butane. The relationship between S_η and N is shown in Fig. 11 for a linear C₄ carbon backbone. S_η is between 0.7 and 1.9 for N=1–3. On the other hand, S_η is between 1.6 and 2.5 for N=4, suggesting S_η likely increases with the addition of the fourth OH functional group to the linear C₄ carbon backbone. However, additional studies are needed in order to reduce the uncertainties of the measurements and make stronger conclusions.

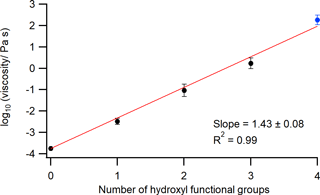
Figure 10 Viscosities of compounds with a linear C₄ carbon backbone at 292–295 K on a log₁₀ scale plotted against the number of OH functional groups. Black circles represent viscosities of the compounds with zero to three OH functional groups (i.e., n-butane, 1-butanol, 2-butanol, 1,2-butanediol, 1,4-butanediol, 2,3-butanediol, 1,2,3-butanetriol, and 1,2,4-butanetriol) taken from the literature (Grayson et al., 2017; Rothfuss and Petters, 2017; Y. C. Song et al., 2016). For the literature data points, the error bars are 2 standard deviations of log₁₀(viscosity ∕ Pa s) of multiple compounds. The blue circle represents the viscosity of pure erythritol, with error bars of 2 standard deviations, based on the linear fit in Fig. 9. The red line is a linear fit to the data, which is weighted based on the uncertainties in viscosity data. The slope and regression coefficient (R²) are shown in the annotation. The uncertainty in the slope corresponds to 2 standard deviations.

4 Summary and conclusion

In this work, viscosities of erythritol–water particles as a function of a_w at 292–295 K were measured using the rFRAP and aerosol optical tweezers techniques. In the rFRAP measurements, a trace amount of RBID (0.2–0.3 wt %) was added to the erythritol–water matrix, and viscosities of erythritol–water particles were estimated based on the measured diffusion coefficients of RBID and the Stokes–Einstein equation. In the new measurements using the aerosol optical tweezers technique, viscosity was measured at a_w<0.1 based solely on bright-field imaging (Y. C. Song et al., 2016).

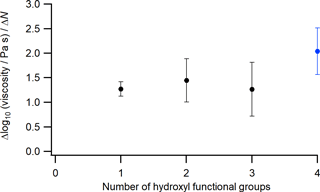
Figure 11 The viscosity sensitivity parameter at 292–295 K plotted against the number of OH functional groups for linear C₄ compounds (alkane, alcohol, and polyols). Black circles represent values estimated using literature data alone (Grayson et al., 2017; Rothfuss and Petters, 2017; Y. C. Song et al., 2016); the blue circle represents the value estimated using experimental results from this work and literature data (Grayson et al., 2017; Y. C. Song et al., 2016). The error bars are propagated from the uncertainties shown in Fig. 10.

In general, at a_w>0.4, the viscosity measurements from the bead-mobility, rFRAP, and optical tweezers techniques are in reasonable agreement if the experimental uncertainties are considered. At a_w<0.4, the mean viscosity values determined using optical tweezers are higher than those using the bead-mobility and rFRAP techniques by 1–2 orders of magnitude. Nevertheless, the disagreement in viscosity measured using multiple techniques seen here is smaller than reported previously. A linear fit was performed for the experimentally determined viscosities of erythritol–water particles against a_w and extrapolated to a_w=0. Based on the extrapolation, the viscosity of pure erythritol at 292–295 K is estimated at ${\mathrm{184}}_{-\mathrm{73}}^{+\mathrm{122}}$ Pa s (2 standard deviations). Based on these results, the addition of an OH functional group to a linear C₄ carbon backbone increases the viscosity by a factor of ${\mathrm{27}}_{-\mathrm{5}}^{+\mathrm{6}}$ (2 standard deviations), on average. In comparison, Grayson et al. (2017) reported a factor of ${\mathrm{41}}_{-\mathrm{16}}^{+\mathrm{27}}$ based on previous measurements.

The viscosity sensitivity parameter was calculated to determine the dependency of viscosity on the degree of prior functionalization for a linear C₄ carbon backbone. Based on the viscosity sensitivity parameter analysis, the increase in viscosity due to the addition of one OH functional group to a linear C₄ carbon backbone is not a strong function of the number of OH groups already present in the molecule, up to the addition of three OH functional groups. On the other hand, the degree of increase in viscosity is likely larger when the linear C₄ carbon backbone already contains three OH groups. These results should help improve the understanding of the viscosity of SOA particles in the atmosphere.