the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Retrieving horizontally resolved wind fields using multi-static meteor radar observations
Jorge L. Chau
Juha Vierinen
Christoph Jacobi
Sven Wilhelm
Recently, the MMARIA (Multi-static, Multi-frequency Agile Radar for Investigations of the Atmosphere) concept of a multi-static VHF meteor radar network to derive horizontally resolved wind fields in the mesosphere–lower thermosphere was introduced. Here we present preliminary results of the MMARIA network above Eastern Germany using two transmitters located at Juliusruh and Collm, and five receiving links: two monostatic and three multi-static. The observations are complemented during a one-week campaign, with a couple of addition continuous-wave coded transmitters, making a total of seven multi-static links. In order to access the kinematic properties of non-homogenous wind fields, we developed a wind retrieval algorithm that applies regularization to determine the non-linear wind field in the altitude range of 82–98 km. The potential of such observations and the new retrieval to investigate gravity waves with horizontal scales between 50–200 km is presented and discussed. In particular, it is demonstrated that horizonal wavelength spectra of gravity waves can be obtained from the new data set.
- Article
(6980 KB) - Full-text XML
-
Supplement
(104131 KB) - BibTeX
- EndNote
The upper mesosphere–lower thermosphere (MLT) is a highly dynamic region dominated by a variety of waves (gravity waves, tides, planetary waves) covering different spatial and temporal scales. To characterize this variability, it is desirable to develop remote sensing techniques to retrieve horizontally resolved structures from continuous observations. A particular challenge is the determination of horizontally resolved wind fields at mesospheric altitudes, needed to access small scale variations associated to gravity waves (GWs). GWs are considered to be a major driver of MLT dynamics as they carry energy and momentum from other (mainly lower) atmospheric layers into the mesosphere (Becker, 2012; Fritts and Alexander, 2003).
Over the past few decades specular meteor radars (SMRs) have become a reliable and widespread tool to investigate mesospheric mean winds (Elford, 1959; Hall et al., 2005; Hocking et al., 2001; Jacobi et al., 2009; McCormack et al., 2017; Nakamura et al., 1991; Roper, 1975; Stober et al., 2017; Wilhelm et al., 2017). These systems are also capable of providing valuable information about gravity waves and tides (Fritts et al., 2010a; Jacobi, 2011) as well as to estimate the gravity wave momentum flux (Fritts et al., 2010b; Hocking, 2005; Placke et al., 2015; de Wit et al., 2014). In particular, Fritts et al. (2012) pointed out that the quality of the gravity wave momentum flux strongly depends on the number of meteor detections per time interval and the diameter of the observation volume.
The spatial and temporal intermittency of GWs are hardly accessible from point measurements. Airglow imagers (Hecht et al., 2000, 2007) or the Advanced Mesospheric Temperature Mapper (Pautet et al., 2014; Taylor et al., 2009) are able to observe small scale GWs as intensity or temperature fluctuations. However, due to the often missing background wind information, the intrinsic GW properties can not be inferred. Smith et al. (2017) combined the 2-D airglow information with MR wind measurements to investigate a bore event across Europe and derived the intrinsic properties of the GW. At present there are only a few attempts to measure horizontally resolved wind structures on comparable scales to airglow imagers by radars (Stober et al., 2013, 2018).
Recently, Stober and Chau (2015) introduced the MMARIA (Multi-static Multi-frequency Agile Radar for Investigation of the Atmosphere) concept to observe horizontally resolved wind fields combining monostatic and multi-static SMR observations. The MMARIA concept allows to increase the number of detected meteors per transmitter, an extended altitude coverage, and more even spatial sampling within the field of view, when compared to traditional monostatic SMRs. They demonstrated the potential to access the kinematic properties of non-homogenous wind fields applying volume velocity processing (VVP) (Waldteufel and Corbin, 1979) to the multi-static SMR observations, i.e., by deriving the horizontal gradients of the horizontal wind components, in addition to their mean values. The multi-static observation geometry allows the observation of almost the same measurement volumes from different angles. Thus, it is possible to access the first order inhomogeneities of the mesoscale wind field, e.g., horizontal divergence, relative vorticity, stretching, and shearing deformation. Here we are going to extent the existing approach to the retrieval of arbitrary wind fields using multi-static observations of meteor radar networks. Figure 1 presents a schematic of such an network.
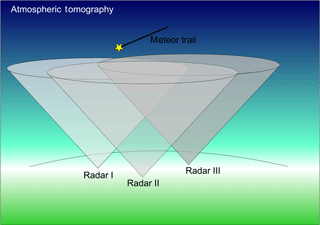
Figure 1Schematic of a multi-static meteor radar network. The grey shaded areas stand for the typical field of views for each systems. Within the network all system should at least overlap to one of the other network members.
The paper is structured as follows. In Sect. 2 we present a summary of the normal meteor radar wind retrieval. This method is going to be expanded in Sect. 3 to horizontally resolved winds in a full Earth geometry. In Sect. 4 we perform an initial validation and consistency check. The potential use of the new horizontally resolved wind retrieval is given in Sect. 5 presenting first horizontal wavelength spectra. Our main conclusions are presented in the last section. The appendix contains all equations required for the WGS84 coordinate transformations.
Meteors entering the Earth's atmosphere form an ambipolar plasma trail, if they are fast and heavy enough. The trail is drifted by the ambient neutral winds at the altitude of its deposition. Combining the radial Doppler measurement with radar interferometry (Jones et al., 1998) permits the measurement of the radial velocity, range, and angle of arrival (here in mathematical convention as ϕ counterclockwise from East, θ off-zenith). Due to the huge number of meteor detections in the course of a day it is possible to determine the prevailing wind speeds by binning the observed meteors in space (vertical) and time applying a so called all-sky fit (Hocking et al., 2001; Holdsworth et al., 2004) over typically 1 h in time and a few kilometers in height.
To increase the robustness of the standard wind fit estimation, e.g., better temporal resolution and altitude coverage, it is possible to use regularization by adding constraints based on a priori information. Recently, we have implemented a routine to derive mesospheric winds using full non-linear error propagation, an additional weighting to account for sampling effects, and a smoothness regularization. The error propagation is straightforward as most of the available systems provide errors for the radial velocity measurements. The angular uncertainties are estimated to be in the order of 2∘ (Jones et al., 1998). Further, the errors of the 3-D wind components are estimated from the covariance matrix and updated with each iteration. The sampling effects are mainly caused by meteors occurring randomly in space and time, but we often analyze the winds on a fixed grid in time and altitude. Therefore, we apply an additional weighting, with a Gaussian kernel, to account for altitude and time differences between the actual occurrence of a meteor and the reference time and altitude. The half width of the Gaussian kernel is given by the width of the altitude (dh) and time bins (dt). The Gaussian weighting due to the randomness of the meteor occurrence is given by
and for the altitude
The temporal and vertical total shear amplitude Atshear and Aashear are estimated from our temporal and vertical regularization gradients from all three wind components. Typical values are 2 h for dtave for a 1 h temporal resolution with over sampling and 1.5 km for dhave for a 2 km vertical altitude resolution. The shear terms σtime and σalt are added to our total statistical error budget during each iteration together with all other statistical uncertainties.
The smoothness regularization scheme consists of the vertical and temporal derivative for each wind component taken as constant within each bin. The initial guess is given by a standard least squares solution without any regularization constraint, but already contains the Gaussian weighting with and . This solution is then used for the next iteration and the new solution is constrained by the previous one. Typically we need 3–5 iterations to achieve convergence. Basically our wind estimates do not change more than the statistical uncertainty, which is in the order of at altitudes between 82–95 km (typically 40–250 meteors). At the edges of the meteor layer (below 82 km or above 95 km) the error can reach up to 15–20 m s−1 as the number of meteors (less than 15) used for each wind estimate drops significantly at these altitudes. More details about the application of this algorithm can be found in Stober et al. (2017). Further, in the manuscript we are referring to this technique as “standard” method or “all-sky” fit.
A bit more sophisticated than the “all-sky” fit is the so called volume velocity processing (VVP) (Waldteufel and Corbin, 1979). This method does no longer assume a homogenous wind field within the observed volume. The wind field is approximated by introducing gradient terms for the wind components.
Here u0, v0, and w0 are the mean zonal, meridional and vertical wind components similar to the “all-sky” fit. The partial derivatives are taken relative to a reference position (x0, y0), which could be the position of a radar or an arbitrarily selected point somewhere between several radar systems. The mean winds as well as the gradient terms are similarly obtained as in the “all-Sky” fit using a regularization including also the gradient terms. Due to the increased number of unknowns at least 10 meteors should be used for the fit. Chau et al. (2017) shows the equations in spherical coordinates.
Such an analysis does not only provide mean winds for each time and altitude bin, but also access higher order kinematic processes as horizontal divergence, relative vorticity as well as stretching and shearing deformation. In order to unambiguously obtain the relative vorticity multi-static measurements are required (Chau et al., 2017; Stober and Chau, 2015). Although the method already allows to access some spatial information it is still not possible to retrieve the phase speed of gravity waves within the volume or to obtain the spatial variability on much smaller scales than the observation volume.
3.1 Implementing the Earth geometry in the wind analysis
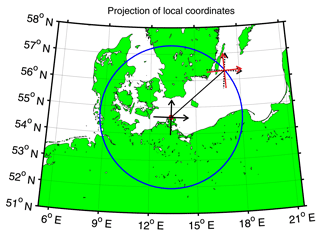
Figure 2Illustration on how local coordinates (zonal, meridional) change with geographic position with respect to a radar location.
A new aspect of the MMARIA concept is the necessity to consider the geometry of the Earth. At present our domain area in Germany has a horizontal extension of approximately 600 km×600 km. These distances are too large to assume a plane geometry, which is very often the case for classical monostatic MRs, where all observations are referred to the location of the radar itself. However, it is straightforward to at least consider that the altitude or height above the surface needs to be corrected for the Earth curvature using a mean Earth radius (RE=6 378 137.0 m). Further, it is possible to obtain a local elevation angle for each meteor, instead of the one observed relative to the receiver location. However, this simple correction turned out to still be insufficient for dealing with large domain areas. Therefore, we outline a more detailed procedure, taking into account the Earth shape with the WGS84 geoid model (National Imagery and Mapping Agency, 2000).
In the following we outline the procedure how to compute new local coordinates (ENU: east–north–up) for each meteor to reduce potential errors in the wind field estimation due to projection issues. Considering that the Earth is not a perfect sphere, we have to deal with two different coordinates, the geodetic coordinates (longitude and latitude) and the Earth-Centered, Earth-Fixed (ECEF) coordinates, also called geocentric coordinates. The geodetic coordinates are determined by the normal to the ellipsoid, whereas the ECEF coordinates are defined by the Earth center using a (X, Y, Z)-coordinate system. Thus, the geodetic and geocentric latitude can be different.
We need to transform the observed meteor positions relative to the radar into a local coordinate frame (ENU) by determining the geodetic longitude, latitude and height of the meteor itself. The corresponding transformations are listed in the appendix. The procedure contains four steps: firstly the geodetic coordinates of the radar (longitude-ϕ,latitude-λ, height-h) are converted into ECEF, which means we receive a vector , with respect to the Earth center. From the interferometric solution we also know the position vector with respect to the receiver location for each meteor. This vector xP is then transformed into ECEF coordinates and we obtain a vector pointing from the Earth center towards the meteor position with coordinates . Further, we convert the vector xM given in ECEF coordinates back into a geodetic position given by the latitude, longitude, and height above the Earth's surface for each meteor. Finally, we use the ECEF vector xM and the geodetic reference to compute a local coordinate set ENU at the position of the meteor itself. A detailed description of all applied coordinate transformations is summarized in the appendix.
In summary we perform the following steps:
-
conversion of the geodetic coordinates of the radar by using the transformation geodetic to ECEF;
-
transformation of meteor coordinates into ECEF by using the transformation of ENU to ECEF;
-
conversion of ECEF frame meteor position into geodetic coordinates ECEF to geodetic;
-
determination of local ENU using the geodetic position of each meteor in ECEF coordinates .
Figure 2 shows an example of the difference between the ENU coordinates (black cross) of the radar location and the ENU coordinates (red cross) of a meteor observed at a horizontal distance of 300 km. The blue circle marks the 300 km range around the radar, which is assumed to be located at Juliusruh. Although the difference appears to be small, it introduces an error of a few meters per second in the derived zonal and meridional and vertical wind speeds. Depending on the range and geographic latitude of the measurements the local azimuth and zenith shows differences up to 4∘ compared to the radar site. As our wind measurements are supposed to be aligned along the zonal and meridional direction it is beneficial and straightforward to remove this bias. In the case of the standard SMR wind analysis technique (Hocking et al., 2001), where a homogenous wind is assumed within the observation volume, the error is almost compensated due to the large number of meteors used for the wind estimate. However, it turns out that the random distribution of meteors within the observation volume is sometimes not favorable to compensate for this bias, thus, it also has an effect on the standard analysis. In particular, altitudes where only a small number of meteors are used for the wind estimation procedure are more prone to this type of error. In particular, it appears to be very critical or in fact almost impossible to obtain a reliable vertical wind velocity or momentum flux, if the full Earth geometry is not taken properly into account.
3.2 Retrieving arbitrary non-homogenous wind fields
The retrieval of arbitrary and non-homogenous wind fields is mathematically more demanding as the number of unknowns exceeds the number of measurements, which does not allow to directly solve the equations applying standard least squares or singular value decomposition algorithms. However, it is possible to constrain the problem by additional assumptions or a priori knowledge. Very often the smoothness is used to regularize the problem so that it can be solved by applying statistical inversion algorithms (Aster et al., 2013).
At first we define a spatial grid and a domain area. In the case of the German MMARIA network we use a 30 km×30 km grid spacing in zonal and meridional direction. The total domain area is about 600 km×600 km. The spatial grid is fixed for each altitude and follows the Earth's surface. A schematic view of the spatial grid is given in Fig. 3. There are many other possibilities to define the spatial grid, e.g., using fixed longitude and latitude bins or arbitrary grids by using each individual meteor position. It turns out that spatial grids with fixed horizontal distance have benefits for the diagnostic of the wind fields as they allow to use discrete Fourier transforms or wavelength based spatial spectral analysis techniques. In this study, we have adopted a regular grid.
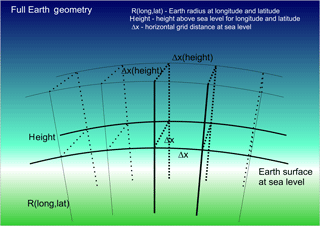
Figure 3Schematic of 3-D gridding to compute horizontally resolved wind fields including the Earth surface.
A first step of the wind field inversion procedure is to assign each observed meteor to a grid cell j centered at time t and position xj. This is equivalent to averaging measurements in time and space. The temporal and vertical weighting due to the random occurrence of the meteors is done similarly to the general case (see above). At present we still use a mean total temporal and vertical shear amplitude for the whole domain area. In order to take into account that each observed meteor does not occur exactly at the position of the grid point xj, which denotes the center of our grid cells, we assign a weight to each observation (Shepard, 1968), i.e.,
The weight wi for meteor i at position xi and at time ti is inversely proportional to its distance to the center of the grid cell j. The exponent p is used to control how fast the weight is reduced as a function of distance. Assuming a value p=0 results in a box car with equal weight for each meteor independent of its distance from the grid cell center. We use the distance in meters and p=0.2. The value of p is selected in such a way that a meteor at 30 km distance from the grid cell center enters the retrieval with a non negligible weight. The term γ is used to control the slope of the space distance, we use γx=1.0. The main reason for the averaging is that a single meteor, which lasts for 20–200 milliseconds, does not necessarily provide a representative mean wind velocity for a 30 min time bin at a grid point or cell. At least two meteors have to occur within one grid cell, otherwise we do not attempt to estimate the wind speed for that grid cell. We will discuss later how this weight is applied in the inversion procedure.
We can relate the measured radial velocity of each meteor to the three dimensional wind velocity by using local ENU coordinates for each measurement i as follows:
where vr,i is radial velocity for meteor i; and wj are the zonal, meridional, and vertical wind components in grid cell j, corresponding to the meteor location. The angles θi and ϕi, corresponding to meteor i, are the local ENU coordinates corresponding to the line of sight velocity along the direction vector from the radar. In the case of a forward scatter geometry the measurement of the radial velocity is more complicated. For multi-static geometries it has to be considered to obtain the effective Bragg wavelength and pointing vector (see Stober and Chau, 2015).
The radial wind equation for arbitrary measurements and grid cells can be expressed as a linear matrix equation. The mapping from the zonal, meridional, and vertical components to observed radial velocities is given by a geometry matrix . All the measurements during an analysis interval are represented as a vector , where n is the number of measurements. The radial velocity vector vr contains all observed radial velocities, either for each individual meteor weighted by its distance from the grid cell, further referred to as “full wind retrieval”, or an averaged value that is already interpolated to the defined grid cells, further referred to as “packed wind retrieval”. The packed retrieval has the advantage that the inversion matrix only scales with the number of grid cells and not with the number of meteors, as is the case for the “full wind retrieval”. The unknown 3-D wind components for each grid cell are also expressed as a vector
where m is the number of grid cells. The mapping in Eq. (7) can be compactly expressed using the following matrix equation:
which relates all measured radial velocities to 3-D velocities within a grid. More explicitly, this is
The geometry matrix G combines all measurements from all possible viewing geometries, but it is not directly invertible. Although we have several different viewing geometries, we do not get always three independent measurements for each grid cell. Hence, the number of unknowns is still larger than the number of measurements (rows in matrix G). This is the case in particular for the edges of our domain area.
Ill-posed problems can be solved by adding additional constrains. Very often the smoothness of the unknown provides a reasonable way to regularize an ill-posed problem (Aster et al., 2013). The smoothness in our case corresponds to the spatial derivative for each wind component and grid cell. This is equivalent to the assumption that the wind field is only slightly changing between neighbored grid cells. Hence, we define a smoothness matrix in such a way that we couple neighbored grid cells for each velocity component separately. For one velocity component, and one grid cell, the elements of matrix L would be
The matrix L contains such differences for all grid cells and all velocity components. The L matrix is constructed that the total difference between a grid cell and its for neighboring grid cells is small and gradients within the x–y plane are not damped. In Fig. 4, a scheme of how the smoothness matrix is constructed is shown. The number of neighbor grid cells defines the number of entries in L for each grid cell.
Finally, we have to deal with grid cells in the domain area where no measurement is available for a given time–altitude bin. This issue is solved by introducing a mesoscale wind field solution to these grid cells. We tested three possible mesoscale solutions and checked how much the final solution depends on this mesoscale boundary condition. The most trivial way is zero padding or simply not using an explicit a priori for these grid cells, the second one is estimating a mean wind using all radial velocity measurements with the “all-sky” fit and the third possibility is to derive a mesoscale wind field solution by computing local mean winds for each multi-static geometry and to estimate a distance weighted background wind field for each grid cell. A similar result is achieved by applying volume velocity processing (VVP) (Browning and Wexler, 1968; Waldteufel and Corbin, 1979), which was already successfully applied using horizontally resolved radial wind measurements (Stober et al., 2013) or multi-static SMR observations (Chau et al., 2017; Stober and Chau, 2015). The mesoscale solution is considered in the retrieval as diagonal matrix prescribing a velocity (zonal, meridional, vertical) for each grid cell. The mesoscale regularization uses a rather low regularization strength αmeso, which is one order of magnitude smaller than the L regularization for the cases presented here.
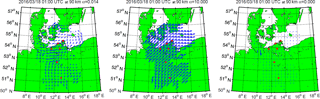
Figure 5Comparison of 2-D wind fields for three different α=0.014, α=10, and α=0.000001. The length of the arrows between the images does not scale.
Combining all the information and the smoothness constraints into a set of equations allows solving the ill-posed problem. We obtain an estimate for the 3-D wind components at all grid cells solving the equation
which is a standard regularized weighted linear least-squares estimator (Aster et al., 2013). The matrix is a diagonal matrix that contains the variance (i.e., measure of uncertainty) given to each measurement . The regularization parameter α provides a weight to the regularization constraint. It describes the coupling strength between neighboring grid cells. It should be noted that a number of alternatives to regularizing the solution also exist.
In the inversion process the weight Σ−1 consists of contributions due to the radial velocity uncertainty, the spatial and temporal weighting functions as outlined above, the angular uncertainties in the measurements of ϕ and θ and the errors in the zonal, meridional vertical wind components after each iteration step. There are grid cells where a sufficient number of measurements is not available (more than 2 meteors are required) and only the mesoscale wind field is used. In this case, the measurement is weighted by a large uncertainty () to ensure that this does not strongly bias the inversion. However, there are areas where ,due to the radial nature of the meteor measurements, the solution can differ rather significantly due to the mesoscale regularization.
In the following we are going to demonstrate the robustness of our algorithm, independent of the choice of regularization parameter α and the mesoscale boundary conditions. For simplicity we will only focus on horizontal winds, and leave the discussion of vertical mesoscale wind velocity for future work. In order to obtain reliable and physically meaningful vertical velocities, additional regularization constraints might be required.
3.3 Robustness of wind field solution
Solving Eq. (12) is straightforward using singular value decomposition or matrix inversion algorithms. As the wind field inversion is still a linear problem, we just need to find a proper solution for the regularization parameter α. A large α means that our solution is dominated by the regularization constraint, a too small α results in a too weak coupling between neighboring grid cells, making the solution unstable as erratic points start to dominate. This is usually expressed in the so-called “L-curve” (Aster et al., 2013).
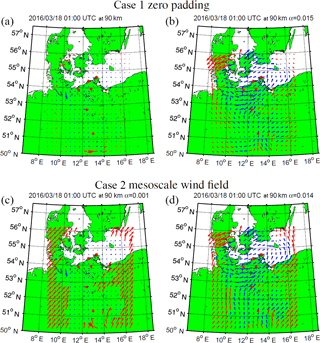
Figure 6Comparison of wind field solution in dependence of the background mesoscale solution. (a, b) Test case with zero padding: first (a) and final iteration (b). (c, d) Test case with mesoscale wind field (obtained from the data): first (c) and final iteration (d).
In Fig. 5, we compare the obtained wind fields for different strengths of the regularization parameters α. The left picture shows what we consider as solution with α=0.014, which seemed to be sufficient in this case. The wind field in the center was computed assuming a much too strong α=10. This obviously leads to a much too smooth wind field, but still keeps some mesoscale wind field structure. A much higher value in the order of 100 or 1000 is going to further reduce the shown variability. The right picture shows an example with a regularization constraint of α=0.000001 that is intentionally much too small. This obviously leads to some erratic structures and outlier solutions begin to dominate the wind field.
We tested different possibilities to define an optimal regularization strength α. At present we optimize our solution with a global estimate that is valid for the whole domain and constant in time, instead of estimating a local regularization strength α for each grid cell. The local approach did not suppress erratic structures or outliers in the same way, but is going to be further considered as it is going to be beneficial for larger domain areas. After comparing thousands of images using different strengths and ways of estimating the optimal α, it turned out that α=0.1 is very often a useful value, which leads to a convergence within eight iterations. However, the choice of α depends on the used statistical weights and uncertainties entering the retrieval.
As already mentioned above, there are grid cells where we have no direct measurements from one of the systems. We suggested using a mesoscale solution for these points. Now there is the question whether our solution depends on this pre-described mesoscale wind field. Therefore, we prepared two test cases. In the first test, all grid cells with no direct measurements are zero padded. For the second test, we use a computed mesoscale wind field estimated from VVP. Figure 6 shows four pictures using the two test cases. Different colors label grid cells with direct radial velocity measurements (blue) and grid cells with the mesoscale solution (red). The left plot displays the first iteration step and the right one shows the finally obtained wind field solution. North of 52∘ N there are almost no differences of the solution if one just compares the blue arrows. The main reason for this good agreement is that almost all points are linked by multiple observing geometries, whereas south of 52∘ N we basically have only monostatic observations. As a result the obtained wind field in the southern part of the domain area is more prone to be affected by the boundary conditions. However, as there is almost no visible difference between the wind fields at latitudes north of 52∘ N, we conclude that there is almost no impact on the determined wind fields by the pre-described mesoscale winds.
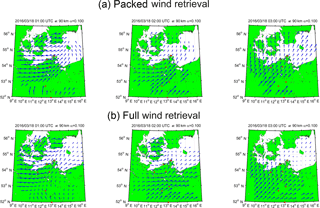
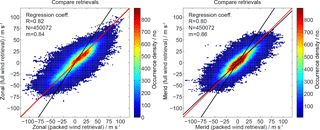
Figure 7Comparison of wind retrievals. Panel (a) shows the solutions of the “packed wind retrieval”. Panel (b) shows the same time and altitudes for the “full wind retrieval”.
Further, we investigated the differences between the full wind retrieval and the packed wind retrieval. Therefore, we kept the regularization strength fixed for both retrievals. The packed retrieval makes use of the total wind variances for each grid cell and a mesoscale regularization, whereas the full wind retrieval uses each individual radial velocity uncertainty and no explicit mesoscale regularization. The other weights and the error treatment is the same. Figure 7 shows a sequence of three successive time steps for both retrievals. The difference in coverage is because we reduced the limit for the full wave retrieval to one meteor per cell, which would be not sufficient for the packed wind retrieval. Further, the packed wind retrieval indicates the impact of the mesoscale solution at the edges of the domain area. However, the general shape of the wind field is reproduced by both approaches with a remarkable agreement. This is further underlined by a correlation density plot shown in Fig. 8. The scattering around the center line is mainly due to the different weights and the mesoscale regularization, which was used in the packed wind retrieval compared to the full wind retrieval.
The above described algorithm is applicable to all types of multi-static observations. In 2014 we started to build the MMARIA network in Germany. At present the network consists of 2 monostatic SMRs (located at Juliusruh 54.6∘ N, 13.4∘ E; and Collm 51.3∘ N, 13.0∘ E; see Table 1). In addition to that we installed three receiver-only stations, namely a dual frequency station in Kuehlungsborn (54.1∘ N, 11.8∘ E) and a single frequency station in Juliusruh, i.e., resulting in 5 different links. Our preliminary results using such observations from two links (i.e., Jruh–Jruh, Kborn–Jruh) are described in detail in Stober and Chau (2015); Vierinen et al. (2016).
In parallel, we also operated a newly developed continuous wave (CW) coded system that complement our pulsed SMR network for one week. The CW-coded prototype was tested from 10–12 June 2015 (Vierinen et al., 2016). The first campaign used the existing infrastructure by transmitting from Juliusruh and recieving at Kuehlungsborn. From 14–20 March 2016 there was a second CW-coded campaign where two temporary transmitters were installed. The transmitters were located in Luebs (53.7∘ N, 13.9∘ E) and Schwerin (53.6∘ N, 11.4∘ E), and operated at the same frequency as the Juliusruh pulsed system, i.e, 32.55 MHz.
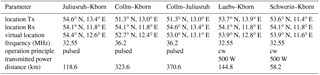
During the March campaign in 2016 the multistatic network consisted of two monostatic and five multi-static links. Some technical specifications of the experiment settings of the SMRs and the locations of the multi-static links are summarized in Tables 1 and 2, respectively. To simplify the discussion about the different viewing geometries, we introduce the virtual radar location of each multi-static link (see Fig. 9). The virtual radar location is defined as the center point of the ellipse created by the transmitter and receiver antennas, which are located in the focal points of this ellipse. The derived Doppler velocities are measured with respect to the virtual radar location, or defined by the middle point of the corresponding transmitter and receiver link, i.e., projected in the unit vector of the meteor position and this middle point. The resulting MR network is shown in Fig. 10. Panel (a) shows the position of all used transmitter and receiver sites. Panel (b) shows the diversity of viewing geometries that results from the combination of the active radars and the multi-static links. The red points label either the position of the MRs or the virtual locations of the multi-static links.
Table 2Technical specification of the multi-static links used in the experiment campaign in March 2016.
Kborn – Kuehlungsborn
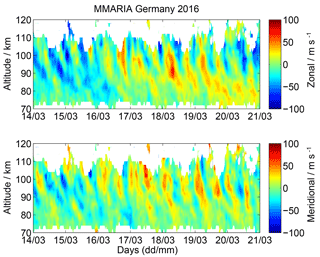
In Fig. 11 we show an overview of the zonal and meridional winds obtained from an all-sky fit as described above. The campaign was conducted during the transition from winter to summer circulation. The first 3 days are characterized by a mean westward zonal wind that becomes weaker in the second half of the campaign, which is typical for this time of the year (Wilhelm et al., 2017). The mean meridional wind is close to zero. Both wind components indicate a moderate tidal activity, which is dominated by the semi-diurnal tide with a tidal amplitude of less than 50 m s−1.
For the same period we generated three movie sequences at 82, 90, 96 km altitude using the full wind retrieval. They show the 2-D wind fields and their temporal evolution with 1 h time steps. The movies can be found in the Supplement. The clockwise rotation of vector field is mainly due to the semi-diurnal tide. However, the movies also show the temporal and spatial variability due to GWs. The appearance and disappearance of the red points indicates whether this viewing geometry was available during the inversion or not. Note that arrows are scaled within each image. As a result more distorted wind fields are often related to weak winds (), whereas very smooth wind fields are often related to higher wind speeds ().
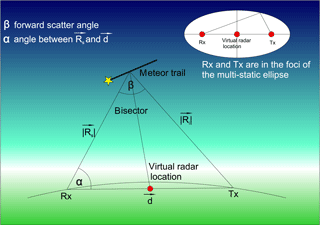
Figure 9Schematic of a typical forward scatter meteor radar. The position of the Tx and Rx are known and all other parts are measured. The Bragg vector kb always points towards the center of the direction vector d.
Figure 12 presents two examples of obtained 2-D wind fields. The domain area was reduced and optimized to cover the Baltic coast where most of multi-static meteor links are concentrated. The wind fields are computed using the full wind retrieval and do not include an explicit mesoscale wind field regularization. The left figure indicates a potential body force of a breaking GW causing an acceleration of the flow (Vadas and Fritts, 2001). The second example indicates a closed small scale vortex above the Baltic coast. The vortex is also rather likely the result of a body force event in the North East corner of the domain area accelerating the flow towards the south west direction.
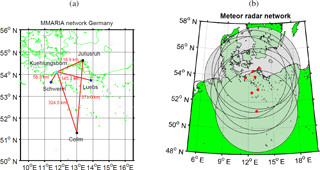
Figure 10(a) Schematic view of multi-static network during the campaign in March 2016. (b) Geographic map of different viewing geometries (red points). The shaded areas label a circle of 300 km in diameter around each center of radial velocity measurements.
We did also perform an initial validation of the derived wind field for the complete campaign period through testing the consistency of the wind observations compared to the “all-sky” fit and the VVP. A comparison of the mean zonal and meridional winds obtained from the all-sky fit and the mean wind velocities of the full wind retrieval over the domain area and for all available altitudes between 82–98 km are shown in Fig. 13. The mean wind velocity was obtained by summation of all grid cells that are constrained by observations. The comparison shows that there is a remarkable agreement between the all-sky fit and the mean 2-D wind velocity (full wind retrieval) within the domain area. The correlation is as high as 0.98 for the zonal mean wind and 0.97 for the mean meridional winds. The slightly weaker agreement of the meridional component is likely related to the in general lower meridional wind speeds compared to the zonal winds.
We also performed an initial comparison between the VVP derived wind estimates for each grid point and the 2-D horizontally resolved wind fields, which were again obtained from the full wind retrieval. We compared all wind velocities at all grid cells between 82–98 km altitude. In Fig. 14 we show the resulting correlation density plot. The correlation of the zonal and meridional winds are lower compared to the agreement of the mean winds. The main reason for the increased scattering is attributed to two effects. Firstly, the VVP uses a linear extrapolation towards the edges of the domain area, which is not necessarily the best approximation. Secondly, the 2-D full wind retrieval reveals much more of the small scale structures in the wind field compared to the VVP.
The presented full and packed wind retrieval algorithms opens new possibilities to investigate atmospheric dynamics. The spatial information seems to be useful to study the horizontal wavelength/wavenumber power spectra of kinetic energy. For the troposphere and lower stratosphere, Nastrom and Gage (1985) analyzed about 6000 commercial aircraft flights. They found a spectral slope of for wavelengths between 2.6 and 400 km, which steepens to k−3 for larger wavelengths. The slope is considered to be representative for mesoscale GWs, whereas the steeper slope is more characteristic for the synoptic scale.
Due to the regular spatial grid horizontal wavelength spectra are easily obtained from the derived horizontally resolved wind fields. The mean spectrum is computed by adding all latitudinal cuts through the domain area at a given altitude during one day. Considering that the coverage of our 2-D wind fields is variable, we included only latitudinal cuts with more than 12 grid points constrained by measurements. The resultant spectra are shown in Fig. 15 and are based on the full retrieval results. The grey points are obtained by plotting each individual spectrum. The black line indicates the mean spectrum. We further added two reference slopes with and k−3. The straight green and black lines are estimated by a linear fit and label two different slopes using a wavelength window 60–140 km (green) and 140–800 km (black). The vertical light blue lines represent the domain boundaries. The spectra are estimated by using Lomb–Scargle periodograms (Lomb, 1976; Scargle, 1982).
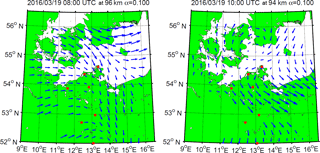
Figure 12Two examples of obtained wind fields showing a small vortical structure above the Baltic coast and a potential body force of a breaking GW.
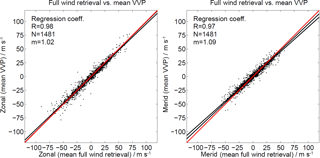
Figure 13Scatter plots of mean zonal and meridional winds obtained from the full wind retrieval and VVP. The mean is computed as average over the domain area.
The spectra shown in Fig. 15 suggests that our domain area has a sufficient large extension to get an idea of the transition between the to k−3 spectral slopes at the mesosphere. However, we have not yet gathered enough statistics to pinpoint a transition scale. Typically, the synoptic scale is associated to a more vortical driven flow, whereas the mesoscale GW flow regime is characterized by divergent modes or GWs. At least for the 5 campaign days there is only a weak day-to-day variability.
Retrieving horizontally resolved wind fields from multi-static SMR networks at the MLT provides new possibilities to investigate the intermittency and spatial characteristics of GWs and vortical modes, which are not yet accessible by other remote sensing techniques for these spatial scales and with that temporal resolution. In particular, the wind and its spatial characteristics are required to understand wave breaking and the associated momentum transfer to the background (Fritts and Alexander, 2003; Fritts et al., 2014).
A crucial part of the presented wind field analysis, independent of the choice of the retrieval method, is the spatio-temporal sampling. Increasing the spatial resolution is only meaningful if we also decrease the temporal sampling window. However, with a decreasing number of detections per grid cell within the domain area the more sparse our wind field is constrained. This brings us to the question on how representative an observed radial velocity of an individual meteor is for our selected time, altitude and spatial resolution. If we want to resolve small scale structures with characteristic life times of minutes and horizontal scales comparable to our grid resolution, e.g., bore events or breaking GW (ripples) (Hecht et al., 2007), a much denser MR network is desirable. However, even with the present stage of the MMARIA Germany network we are able to resolve mesoscale vortical modes as well as GWs. As a result of the spatio-temporal sampling we expect to be more sensitive to vortical modes and to resolve the effects of body forces of breaking GW (Vadas and Fritts, 2001). A duplication of meteor counts within the domain area would allow to decrease the temporal resolution down to 10–15 min compared to the present stage (30–60 min). A significant improvement (15 km×15) of the spatial resolution would require more than 4 times the number of counts if the temporal resolution is kept the same (30 min).
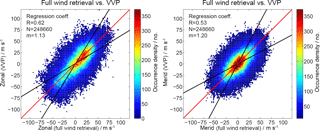
Figure 14Comparison of zonal and meridional winds as derived from the new retrieval algorithm and the estimates for each grid point applying VVP.
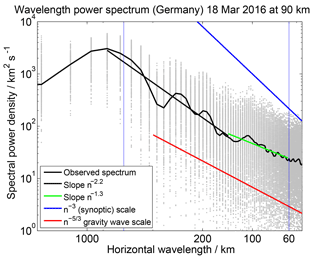
Figure 15Horizontal wavelength spectra and estimated slopes to identify the transition from the mesoscale GW to the synoptic scale.
The obtained 2-D wind fields are also ideal to complement other mesospheric measurements. The combination of the horizontally resolved wind fields with other mesospheric observations like airglow imagers (Hecht et al., 2007) or the Advanced Mesospheric Temperature Mapper (Pautet et al., 2014, 2016; Taylor et al., 2009) is going to provide a more complete picture of the MLT dynamics. The horizontally resolved wind fields allow a better characterization of the mesoscale mean flow. The airglow imagers provide more information to small scale structures (a few kilometers).
During the past few years, there were also several attempts to retrieve horizontally resolved wind fields using Fabry–Perot Interferometer (FPI) in the thermosphere (Harding et al., 2015; Meriwether et al., 2008). In particular, Harding et al. (2015) used a comparable retrieval and constrained the wind field solution by the smoothness and the curvature. They showed data collected above Brazil using up to 7 FPI combined to a FPI network. They obtained rather smooth wind fields similar to those shown in Fig. 5 (α=10). A combination of a FPI and a MR network, in combination with further optimized retrieval algorithms, can enhance our understanding of the vertical coupling between the layers and the propagation of waves, their interaction, and dissipation.
After establishing the MMARIA-concept in Stober and Chau (2015), we extended the SMR network in Germany, which now consists of two monostatic SMRs at Juliusruh and Collm and three multi-static links between Juliusruh–Kborn, Collm–Kborn, and Collm–Juliusruh. Further, we investigated new technological concepts by adding two CW-coded transmitter (Vierinen et al., 2016). Here we present initial results from a 5 day campaign in March 2016 combining pulsed and cw-coded multi-static SMR observations, that resulted in 7 links.
The introduced packed and full wind retrieval algorithms for arbitrary non-homogeneous wind fields show the potential to investigate mesoscale dynamics at the MLT by employing multi-static SMR networks. Horizontally resolved winds open possibilities to study the MLT dynamics. We demonstrate that our preliminary derived wind fields are suitable to obtain horizontal wavelength spectra to access the transition scale between a k−3 to a slope, that has been observed in the troposphere (Nastrom and Gage, 1985).
Horizontally resolved winds at the MLT open new ways to investigate dynamical processes on scales between hundreds down to a few kilometers. Based on these winds it is going to be possible to study the momentum transfer of breaking gravity wave in case studies in much more detail. The resolved winds are further suitable to obtain a spatially resolved momentum flux, or to measure propagation directions of GW directly as well as their intrinsic spatial characteristics. The retrieved winds are also usable to complement other measurements such as airglow observations combining both data sets to estimate the intrinsic wave parameters, which are often not accessible without the knowledge of the background winds. At present there is also no other measurement technique available to observe and study the relative importance of vortical compared to divergent atmospheric modes.
We performed an initial validation of our packed and full wind retrieval algorithms by comparing the mean winds to the standard SMR wind analysis, which shows remarkably good agreement. Further, we compared the wind fields obtained from VVP, using a gradient extrapolation of the winds to our grid points with our full wind retrieval solution. This comparison reveals that both methods provide a good approximation of the mesoscale wind field, but show larger discrepancies at the smaller scales, which is expected as the 2-D full wind retrieval of 3-D wind vectors is designed to infer such small scale features.
The presented algorithms demonstrate the potential of SMRs to be used as networks. These systems are cheap enough and sufficiently automated to be deployed at remote locations and to build rather large networks with several hundred kilometers in diameter. Further, the derived packed and full wind retrieval algorithms are applicable to existing data collected from closely co-located SMRs like in Scandinavia (Chau et al., 2017).
The data can be accessed upon request by the authors. Please contact Christoph Jacobi (jacobi@uni-leipzig.de) for the Collm meteor radar data. The cw-meteor radar data are available from Jorge L. Chau (chau@iap-kborn.org). The meteor radar data from Juliusruh and Kuehlungsborn can be requested from Gunter Stober (stober@iap-kborn.de).
In the following we present a short summary of all the coordinate transformations that we used in the presented analysis scheme. All relevant parameters are listed and the used transformation matrices are shown.
A1 Geodetic to ECEF
The first transformation that we used converts geodetic coordinates into the ECEF. The geodetic coordinates from the radar are given in longitude (λ), latitude (ϕ), and height (z). The height denotes the altitude of the radar above Earth surface with respect to WGS84 (Hofmann-Wellenhof et al., 1994; National Imagery and Mapping Agency, 2000). The WGS84 defines the semi-major axis of the Earth to be a=6 387 137.0 m and a reciprocal of flattening of . The semi-minor axis is defined to be b=6 356 752.3142 m. The first eccentricity squared e2, the second eccentricity squared , and the radius of Earth's curvature N is given by
Based on the WGS84 ellipsoid geometry of the Earth any given geodetic location defined by a longitude, latitude and a height (height above WGS84 surface) is given by the ECEF coordinates ()
A2 ECEF to Geodetic
The backward transformation to transform a given coordinate in ECEF into a geodetic longitude (λ), latitude (ϕ) and height (z) is more difficult. A summary of possible algorithms is provided in Zhu (1993). We apply the closed form presented in Heikkinnen (1982). According to Zhu (1993), the average error is mainly determined by the numerical error introduced in the computer, which is in the order of 1 nm. The algorithm presented in Heikkinnen (1982) is valid from the Earth center () up to height of geostationary orbits.
A3 ENU to ECEF
Typically, MR observe meteors at a given distance and direction relative to its geodetic coordinates. The meteor is given in ENU coordinates with respect to the radar location. The up direction is defined by the tangent plane to the Earth's ellipsoid. The meteor position is defined by ENU coordinates () at a geodetic longitude (λ), latitude (ϕ), and height (z). Hence, we have to rotate the ENU-vector () into the ECEF reference () system by using the following expression:
A4 ECEF to ENU
Finally, we want to express our line of sight vector from the radar towards the meteor in the frame of the ENU coordinates at the geodetic location of the meteor itself, e.g., the line of sight velocity vector is observed at a certain azimuth (az) and zenith (ze) angle relative to the radar, but has a different azimuth (az′) and zenith (ze′) in the frame of the local geodetic coordinates of the meteor. Assuming that we know the ECEF coordinates of the meteor (), and our radar location () it is straightforward to compute the ENU () by using
Hence, we obtain a local azimuth az′ and ze′ with respect to the geodetic position of the meteor, instead of the radar site
The supplement related to this article is available online at: https://doi.org/10.5194/amt-11-4891-2018-supplement.
The manuscript was prepared from GS with contributions from all co-authors. The source codes of the presented wind retrievals are developed by GS. JV and JLC developed the CW-experiments and carried them out. CJ helped with the data interpretation and ensured the operation of the Collm meteor radar. SW contributed to the mean wind analysis for the shown wind comparisons.
The authors declare that they have no conflict of interest.
We acknowledge the technical support of our radar systems by Falk Kaiser,
Dieter Keuer, Jörg Trautner, and Thomas Barth. We are grateful for the
support provided by Sven Geese, Nico Pfeffer, and Matthias Claßen in
developing, deploying, and operating the CW-coded radars. We thank both
reviewers for their help improving our manuscript.
Edited by: Markus Rapp
Reviewed by: two anonymous referees
Aster, R. C., Borchers, B., and Thurber, C. H.: Parameter Estimation and Inverse Problems, 2 Edn., Academic Press, Boston, 2013. a, b, c, d
Becker, E.: Dynamical Control of the Middle Atmosphere, Space Sci. Rev., 168, 283–314, https://doi.org/10.1007/s11214-011-9841-5, 2012. a
Browning, K. and Wexler, R.: The Determination of Kinematic Properties of a Wind field Using Doppler Radar, J. App. Meteorol., 7, 105–113, 1968. a
Chau, J. L., Stober, G., Hall, C. M., Tsutsumi, M., Laskar, F. I., and Hoffmann, P.: Polar mesospheric horizontal divergence and relative vorticity measurements using multiple specular meteor radars, Radio Sci., 52, 811–828, https://doi.org/10.1002/2016RS006225, 2017. a, b, c, d
de Wit, R. J., Hibbins, R. E., Espy, P. J., Orsolini, Y. J., Limpasuvan, V., and Kinnison, D. E.: Observations of gravity wave forcing of the mesopause region during the January 2013 major Sudden Stratospheric Warming, Geophys. Res. Lett., 41, 4745–4752, https://doi.org/10.1002/2014GL060501, 2014. a
Elford, W. G.: A study of winds between 80 and 100 km in medium latitudes, Planetary Space Sci., 1, 94–101, 1959. a
Fritts, D. and Alexander, M. J.: Gravity wave dynamics and effects in the middle atmosphere, Rev. Geophys., 41, 1–64, https://doi.org/10.1029/2001RG000106, 2003. a, b
Fritts, D. C., Janches, D., and Hocking, W. K.: Southern Argentina Agile Meteor Radar: Initial assessment of gravity wave momentum fluxes, J. Geophys. Res.-Atmos., 115, d19123, https://doi.org/10.1029/2010JD013891, 2010a. a
Fritts, D. C., Janches, D., and Hocking, W. K.: Southern Argentina Agile Meteor Radar: Initial assessment of gravity wave momentum fluxes, J. Geophys. Res.-Atmos., 115, d19123, https://doi.org/10.1029/2010JD013891, 2010b. a
Fritts, D. C., Janches, D., Hocking, W. K., Mitchell, N. J., and Taylor, M. J.: Assessment of gravity wave momentum flux measurement capabilities by meteor radars having different transmitter power and antenna configurations, J. Geophys. Res.-Atmos., 117, d10108, https://doi.org/10.1029/2011JD017174, 2012. a
Fritts, D. C., Pautet, P.-D., Bossert, K., Taylor, M. J., Williams, B. P., Iimura, H., Yuan, T., Mitchell, N. J., and Stober, G.: Quantifying gravity wave momentum fluxes with Mesosphere Temperature Mappers and correlative instrumentation, J. Geophys. Res.-Atmos., 119, 13583–13603, https://doi.org/10.1002/2014JD022150, 2014. a
Hall, C. M., Aso, T., Tsutsumi, M., Nozawa, S., Manson, A. H., and Meek, C. E.: A comparison of mesosphere and lower thermosphere neutral winds as determined by meteor and medium-frequency radar at 70∘ N, Radio Sci., 40, rS4001, https://doi.org/10.1029/2004RS003102, 2005. a
Harding, B. J., Makela, J. J., and Meriwether, J. W.: Estimation of mesoscale thermospheric wind structure using a network of interferometers, J. Geophys. Res.-Space, 120, 3928–3940, https://doi.org/10.1002/2015JA021025, 2015. a, b
Hecht, J. H., Fricke-Begemann, C., Walterscheid, R. L., and Höffner, J.: Observations of the breakdown of an atmospheric gravity wave near the cold summer mesopause at 54N, Geophys. Rese. Lett., 27, 879–882, https://doi.org/10.1029/1999GL010792, 2000. a
Hecht, J. H., Liu, A. Z., Walterscheid, R. L., Franke, S. J., Rudy, R. J., Taylor, M. J., and Pautet, P.-D.: Characteristics of short-period wavelike features near 87 km altitude from airglow and lidar observations over Maui, J. Geophys. Res.-Atmos., 112, d16101, https://doi.org/10.1029/2006JD008148, 2007. a, b, c
Heikkinnen, M.: Geschlossene Formeln zur Berechnung räumlicher geodätischer Koordinaten aus rechtwinkligen Koordinaten, Z. Ermess., 107, 207–2011, 1982. a, b
Hocking, W., Fuller, B., and Vandepeer, B.: Real-time determination of meteor-related parameters utilizing modern digital technology, J. Atmos. Sol.-Terr. Phy., 63, 155–169, https://doi.org/10.1016/S1364-6826(00)00138-3, 2001. a, b, c
Hocking, W. K.: A new approach to momentum flux determinations using SKiYMET meteor radars, Ann. Geophys., 23, 2433–2439, https://doi.org/10.5194/angeo-23-2433-2005, 2005. a
Hofmann-Wellenhof, B., Lichtenegger, H., and Collins, J.: Global Positioning System: theory and practice, Springer-Verlag, Vienna, 1994. a
Holdsworth, D. A., Reid, I. M., and Cervera, M. A.: Buckland Park all-sky interferometric meteor radar, Radio Sci., 39, rS5009, https://doi.org/10.1029/2003RS003014, 2004. a
Jacobi, C.: Meteor radar measurements of mean winds and tides over Collm (51.3∘ N, 13∘ E) and comparison with LF drift measurements 2005–2007, Adv. Radio Sci., 9, 335–341, https://doi.org/10.5194/ars-9-335-2011, 2011. a
Jacobi, C., Arras, C., Kürschner, D., Singer, W., Hoffmann, P., and Keuer, D.: Comparison of mesopause region meteor radar winds, medium frequency radar winds and low frequency drifts over Germany, Adv. Space Res., 43, 247–252, https://doi.org/10.1016/j.asr.2008.05.009, 2009. a
Jones, J., Webster, A. R., and Hocking, W. K.: An improved interferometer design for use with meteor radars, Radio Sci., 33, 55–65, https://doi.org/10.1029/97RS03050, 1998. a, b
Lomb, N. R.: Least-squares frequency analysis of unequally spaced data, Astrophys. Space Sci., 39, 447–462, https://doi.org/10.1007/BF00648343, 1976. a
McCormack, J., Hoppel, K., Kuhl, D., de Wit, R., Stober, G., Espy, P., Baker, N., Brown, P., Fritts, D., Jacobi, C., Janches, D., Mitchell, N., Ruston, B., Swadley, S., Viner, K., Whitcomb, T., and Hibbins, R.: Comparison of mesospheric winds from a high-altitude meteorological analysis system and meteor radar observations during the boreal winters of 2009-2010 and 2012–2013, J. Atmos. Sol.-Terr. Phy., 154, 132–166, https://doi.org/10.1016/j.jastp.2016.12.007, 2017. a
Meriwether, J., Faivre, M., Fesen, C., Sherwood, P., and Veliz, O.: New results on equatorial thermospheric winds and the midnight temperature maximum, Ann. Geophys., 26, 447–466, https://doi.org/10.5194/angeo-26-447-2008, 2008. a
Nakamura, T., Tsuda, T., Tsutsumi, M., Kita, K., Uehara, T., Kato, S., and Fukao, S.: Meteor wind observations with the MU radar, Radio Sci., 26, 857–869, https://doi.org/10.1029/91RS01164, 1991. a
Nastrom, G. and Gage, K.: A Climatology of Atmospheric Wavenumber Spectra of Wind and Temperature Observed by Commercial Aircraft, J. Atmos. Sci., 42, 950–960, https://doi.org/10.1175/1520-0469(1985)042<0950:ACOAWS>2.0.CO;2, 1985. a, b
National Imagery and Mapping Agency: Department of Defense World Geodetic System 1984: its definition and relationships with local geodetic systems, Tech. Rep. TR8350.2, National Imagery and Mapping Agency, St. Louis, MO, USA, available at: http://earth-info.nga.mil/GandG/publications/tr8350.2/tr8350_2.html (last access: 21 August 2018), 2000. a, b
Pautet, P., Taylor, M., Pendleton, W., Zhao, Y., Yuan, T., Esplin, R., and McLain, D.: Advanced mesospheric temperature mapper for high-latitude airglow studies, Appl. Opt., 53, 5934–5943, https://doi.org/10.1364/AO.53.005934, 2014. a, b
Pautet, P.-D., Taylor, M. J., Fritts, D. C., Bossert, K., Williams, B. P., Broutman, D., Ma, J., Eckermann, S. D., and Doyle, J. D.: Large-amplitude mesospheric response to an orographic wave generated over the Southern Ocean Auckland Islands (50.7∘ S) during the DEEPWAVE project, J. Geophys. Res.-Atmos., 121, 1431–1441, https://doi.org/10.1002/2015JD024336, 2016. a
Placke, M., Hoffmann, P., Latteck, R., and Rapp, M.: Gravity wave momentum fluxes from MF and meteor radar measurements in the polar MLT region, J. Geophys. Res.-Space, 120, 736–750, https://doi.org/10.1002/2014JA020460, 2015. a
Roper, R. G.: The measurement of meteor winds over Atlanta (34∘ N, 84∘ W), Radio Sci., 10, 363–369, https://doi.org/10.1029/RS010i003p00363, 1975. a
Scargle, J. D.: Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data, Astrophys. J., 263, 835–853, 1982.. a
Shepard, D.: A Two-dimensional Interpolation Function for Irregularly-spaced Data, in: Proceedings of the 1968 23rd ACM National Conference, ACM '68, 517–524, ACM, New York, NY, USA, https://doi.org/10.1145/800186.810616, 1968. a
Smith, S. M., Stober, G., Jacobi, C., Chau, J. L., Gerding, M., Mlynczak, M. G., Russell, J. M., Baumgardner, J. L., Mendillo, M., Lazzarin, M., and Umbriaco, G.: Characterization of a Double Mesospheric Bore Over Europe, J. Geophys. Res.-Space, 122, 9738–9750, https://doi.org/10.1002/2017JA024225, 2017. a
Stober, G. and Chau, J. L.: A multistatic and multifrequency novel approach for specular meteor radars to improve wind measurements in the MLT region, Radio Sci., 50, 431–442, https://doi.org/10.1002/2014RS005591, 2015. a, b, c, d, e, f
Stober, G., Sommer, S., Rapp, M., and Latteck, R.: Investigation of gravity waves using horizontally resolved radial velocity measurements, Atmos. Meas. Tech., 6, 2893–2905, https://doi.org/10.5194/amt-6-2893-2013, 2013. a, b
Stober, G., Matthias, V., Jacobi, C., Wilhelm, S., Höffner, J., and Chau, J. L.: Exceptionally strong summer-like zonal wind reversal in the upper mesosphere during winter 2015/16, Ann. Geophys., 35, 711–720, https://doi.org/10.5194/angeo-35-711-2017, 2017. a, b
Stober, G., Sommer, S., Schult, C., Latteck, R., and Chau, J. L.: Observation of Kelvin-Helmholtz instabilities and gravity waves in the summer mesopause above Andenes in Northern Norway, Atmos. Chem. Phys., 18, 6721–6732, https://doi.org/10.5194/acp-18-6721-2018, 2018. a
Taylor, M., Zhao, Y., Pautet, P.-D., Nicolls, M., Collins, R., Barker-Tvedtnes, J., Burton, C., Thurairajah, B., Reimuller, J., Varney, R., Heinselman, C., and Mizutani, K.: Coordinated optical and radar image measurements of noctilucent clouds and polar mesospheric summer echoes, J. Atmos. Sol.-Terr. Phy., 71, 675–687, https://doi.org/10.1016/j.jastp.2008.12.005, 2009. a, b
Vadas, S. L. and Fritts, D. C.: Gravity Wave Radiation and Mean Responses to Local Body Forces in the Atmosphere, J. Atmos. Sci., 58, 2249–2279, https://doi.org/10.1175/1520-0469(2001)058<2249:GWRAMR>2.0.CO;2, 2001. a, b
Vierinen, J., Chau, J. L., Pfeffer, N., Clahsen, M., and Stober, G.: Coded continuous wave meteor radar, Atmos. Meas. Tech., 9, 829–839, https://doi.org/10.5194/amt-9-829-2016, 2016. a, b, c
Waldteufel, P. and Corbin, H.: On the Analysis of Single-Doppler Radar Data, J. Appl. Meteor., 18, 532–542, 1979. a, b, c
Wilhelm, S., Stober, G., and Chau, J. L.: A comparison of 11-year mesospheric and lower thermospheric winds determined by meteor and MF radar at 69∘ N, Ann. Geophys., 35, 893–906, https://doi.org/10.5194/angeo-35-893-2017, 2017. a, b
Zhu, J.: Exact conversion of earth-centered, earth-fixed coordinates to geodetic coordinates, J. Guid. Control Dynam., 16, 389–391, 1993. a, b
- Abstract
- Introduction
- Wind analysis of mean meteor radar winds
- Wind analysis of arbitrary wind fields
- Horizontally resolved wind fields and initial validation
- Obtaining horizontal wavelength spectra
- Discussion
- Conclusions
- Data availability
- Appendix A: Coordinate transformations
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Wind analysis of mean meteor radar winds
- Wind analysis of arbitrary wind fields
- Horizontally resolved wind fields and initial validation
- Obtaining horizontal wavelength spectra
- Discussion
- Conclusions
- Data availability
- Appendix A: Coordinate transformations
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement