Boundary-layer water vapor profiling using differential absorption radar

Remote sensing of water vapor in the presence of clouds and precipitation constitutes an important observational gap in the global observing system. We present ground-based measurements using a new radar instrument operating near the 183 GHz H₂O line for profiling water vapor inside of planetary-boundary-layer clouds, and develop an error model and inversion algorithm for the profile retrieval. The measurement technique exploits the strong frequency dependence of the radar beam attenuation, or differential absorption, on the low-frequency flank of the water line in conjunction with the radar's ranging capability to acquire range-resolved humidity information. By comparing the measured differential absorption coefficient with a millimeter-wave propagation model, we retrieve humidity profiles with 200 m resolution and typical statistical uncertainty of 0.6 g m⁻³ out to around 2 km. This value for humidity uncertainty corresponds to measurements in the high-SNR (signal-to-noise ratio) limit, and is specific to the frequency band used. The measured spectral variation of the differential absorption coefficient shows good agreement with the model, supporting both the measurement method assumptions and the measurement error model. By performing the retrieval analysis on statistically independent data sets corresponding to the same observed scene, we demonstrate the reproducibility of the measurement. An important trade-off inherent to the measurement method between retrieved humidity precision and profile resolution is discussed.

1 Introduction

In this work, we discuss the implementation of differential absorption radar (DAR) for measuring humidity profiles inside of boundary-layer clouds (Lebsock et al., 2015; Millán et al., 2016). The DAR method, which is the microwave analog of the mature differential absorption lidar (DIAL) method (Browell et al., 1979), combines the range-resolving capabilities of radar with the strong frequency dependence of atmospheric attenuation near a molecular rotational absorption line to retrieve density profiles of the absorbing gas along the line of sight. Recently, there was a demonstration of microwave integrated path differential absorption in airborne measurements of sea surface air pressure without range resolution (Lawrence et al., 2011), utilizing the 60 GHz O₂ line to measure the total oxygen column. More recently, our group demonstrated a ground-based DAR for humidity sounding operating between 183 and 193 GHz (Cooper et al., 2018), with primary sensitivity to upper tropospheric water vapor due to significant attenuation in the lower troposphere at these frequencies. That work included a comparison of differential absorption measurements with a millimeter-wave propagation model showing good agreement, and left the topics of error analysis and profile inversion for future investigation. While the 183 to 193 GHz band is attractive for DAR measurements because of the large differential absorption values achievable, transmission at frequencies between 174.8 and 191.8 GHz is prohibited due to reservation for passive-only remote sensing (NTIA, 2015). On the other hand, the 167 to 174.8 GHz band offers fewer transmission restrictions, and features lower absolute absorption, thus enabling penetration into the boundary layer from an airborne or spaceborne platform. Of course, the smaller absolute absorption is accompanied by decreased differential absorption, making the profiling capabilities of this radar coarser than the 183 to 193 GHz DAR. Furthermore, the surface returns in both cloudy and clear-sky areas make a DAR measurement of the total water column possible.

The DAR approach has two unique aspects that complement existing methods for remotely sensing water vapor. First, because of its ranging capabilities it has precise height registration, unlike passive sounding whereby weighting functions can encompass broad swaths of the atmosphere. Second, in contrast with other methods the DAR signal increases with increasing cloud water content and precipitation, with the obvious caveat that the radar signal-to-noise ratio (SNR) will decrease from attenuation as the beam penetrates into the volume. The DAR therefore nicely complements the infrared and microwave sounding techniques, as well as differential absorption and Raman lidar techniques that are commonly used to remotely sense water vapor from the ground (Spuler et al., 2015; Whiteman et al., 1992; Wulfmeyer and Bösenberg, 1998), with a notable airborne DIAL system being the Lidar Atmospheric Sensing Experiment (LASE) (Browell et al., 1998). Importantly, millimeter-wave transparency in clouds allows for airborne or spaceborne measurements of lower tropospheric humidity in cloudy scenes, while DIAL systems typically cannot measure inside boundary-layer clouds due to high optical thickness.

In addition to primary applications in profiling water vapor within clouds, the instrument architecture discussed here represents an important application of recent advances in solid-state G-band technology to meteorological radar. Indeed, there has been lingering interest within the atmospheric remote sensing community for decades in utilizing G-band radar for cloud and precipitation studies, with earlier attempts hampered by limited sensitivity due to available technology (Battaglia et al., 2014). The addition of G-band reflectivity measurements to multi-frequency radar systems, for example a dual-frequency W- and Ka-band system, could provide significantly more information than additional measurements at a lower frequency because the scattering properties at G band for typical cloud particle sizes are not of Rayleigh character.

Here we present ground-based measurements using a 167 to 174.8 GHz DAR, provide in-depth measurement error analysis with emphasis on the role of background noise power, and develop a retrieval algorithm based on performing least squares fits of a spectroscopic model to the data. The retrieved profiles constitute the first active remote sensing measurements of water vapor profiles inside of clouds, and open up possibilities for a variety of scientific studies, including investigation of in-cloud humidity heterogeneity and the coupled relationship between boundary-layer clouds and thermodynamic profiles.

2 Measurement basis and method

2.1 Differential absorption radar

The DAR technique (Cooper et al., 2018; Lawrence et al., 2011; Millán et al., 2014) utilizes range-resolved radar echoes at multiple carrier frequencies in the vicinity of a gaseous absorption line to probe the frequency-dependent optical depth between two points along the radar line-of-sight. The radar echoes, or returns, may originate from cloud hydrometeors or, in the case of an airborne system, from the Earth's surface as well, enabling total column optical depth measurements. For closely spaced transmission frequencies near the absorption line center, the hydrometeor scattering properties vary little, while the gaseous absorption exhibits strong frequency dependence. By comparing with a known propagation model, these measurements can be employed to retrieve range-resolved density profiles of the absorbing molecule. Furthermore, because of the differential nature of the measurement, one does not require absolute calibration of the radar receiver in order to obtain absolute density values for the absorbing molecule. In the case of a calibrated receiver, both range-resolved density profiles of the absorbing molecule and microphysical properties of the reflecting medium can be retrieved.

Assuming negligible multiple scattering, the radar echo power received from a collection of scatterers filling the beam at a distance r is

$$\begin{array}{}\text{(1)}& {\displaystyle }{P}_{\mathrm{e}}(r,f)=C\left(f\right)Z(r,f)r^{-\mathrm{2}}{e}^{-\mathrm{2}\mathit{\tau }(r,f)},\end{array}$$

where C(f) includes the frequency dependence of the radar hardware (e.g., transmit power and gain), Z(r,f) is the (unattenuated) reflectivity, and τ(r,f) is the one-way optical depth including contributions from gaseous and particulate extinction. Taking the ratio of powers for two different ranges r₁ and $r_{\mathrm{2}}=r_{\mathrm{1}}+R$ and assuming frequency independence of the reflectivity and particulate extinction, we find

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{P_{\mathrm{e}}(r_{\mathrm{2}},f)}{P_{\mathrm{e}}(r_{\mathrm{1}},f)}}={\displaystyle \frac{Z\left(r_{\mathrm{2}}\right)}{Z\left(r_{\mathrm{1}}\right)}}{\left({\displaystyle \frac{r_{\mathrm{1}}}{r_{\mathrm{2}}}}\right)}^{\mathrm{2}}{e}^{-\mathrm{2}\mathit{\beta }(r_{\mathrm{1}},r_{\mathrm{2}},f)R},\end{array}$$

where

$$\begin{array}{ll}{\displaystyle }\mathit{\beta }(r_{\mathrm{1}},r_{\mathrm{2}},f)& {\displaystyle }={\displaystyle \frac{\mathit{\tau }(r_{\mathrm{2}},f)-\mathit{\tau }(r_{\mathrm{1}},f)}{R}}\\ \text{(3)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{R}}\underset{r_{\mathrm{1}}}{\overset{r_{\mathrm{2}}}{\int }}\left[\sum _j{\mathit{\rho }}_j\left(r\right){\mathit{\kappa }}_j(r,f)+{\mathit{\beta }}_{\text{part}}\left(r\right)\right]\mathrm{d}r\end{array}$$

is the average absorption coefficient between r₁ and r₂, ρ_j(r) is the density of the gas component with label j, κ_j(r,f) is the corresponding mass extinction cross section, which varies with r due to pressure and temperature, and β_part(r) is the particulate extinction coefficient integrated over local drop size distributions (DSDs).

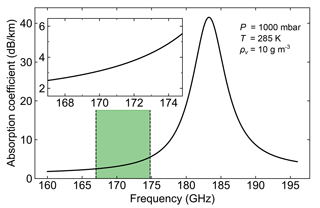
Figure 1 Gaseous absorption coefficient (one-way) calculated using the model from Read et al. (2004) and the parameters listed in the figure. The green shaded region and inset highlight the 167 to 174.8 GHz transmission band for this work.

Restricting our analysis to millimeter-wave propagation near the 183 GHz water vapor absorption line, the sum over gaseous absorption terms can be replaced by ${\mathit{\rho }}_{\mathrm{v}}\left(r\right){\mathit{\kappa }}_{\mathrm{v}}(r,f)+{\mathit{\beta }}_{\text{gas,bg}}\left(r\right)$, where the subscript v corresponds to water vapor and β_gas,bg is the background gas absorption coefficient due to all other components, which is assumed to be frequency-independent. Assuming that pressure and temperature vary slowly compared to the length scale R, we can therefore write Eq. (3) as

$$\begin{array}{ll}{\displaystyle }\mathit{\beta }(r_{\mathrm{1}},r_{\mathrm{2}},f)& {\displaystyle }={\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{v}}(r_{\mathrm{1}},r_{\mathrm{2}}){\mathit{\kappa }}_{\mathrm{v}}\left(f\right)+{\stackrel{\mathrm{‾}}{\mathit{\beta }}}_{\text{gas,bg}}(r_{\mathrm{1}},r_{\mathrm{2}})\\ \text{(4)}& {\displaystyle }& {\displaystyle }+{\stackrel{\mathrm{‾}}{\mathit{\beta }}}_{\text{part}}(r_{\mathrm{1}},r_{\mathrm{2}}),\end{array}$$

where the overbar symbol implies taking the mean value between r₁ and r₂. Thus, we see that measuring the frequency-dependent contribution to the optical depth between r₁ and r₂ reveals the average water vapor density given the known absorption line shape κ_v(f). Figure 1 shows the frequency dependence of the gaseous absorption coefficient ρ_vκ_v(f)+β_gas,bg in the vicinity of the 183 GHz water vapor line for P=1000 mbar, T=285 K, and ρ_v=10 g m⁻³. For this work, we utilize the millimeter-wave propagation model from the EOS Microwave Limb Sounder (Read et al., 2004). The 167 to 174.8 GHz transmission band is highlighted in green, as well as shown in the inset of Fig. 1, revealing a differential absorption coefficient of 3 dB km⁻¹ for 10 g m⁻³ of water vapor.

Important to the validity of this DAR method is the dominance of gaseous differential absorption over particulate differential absorption, since we assume that β_part is frequency-independent. To investigate this for boundary-layer clouds, we perform Mie scattering calculations for liquid spheres and integrate the scattering parameters over DSDs corresponding to clouds and rain for a range of mean diameters. For the DSD, we use a modified gamma distribution of the form

$$\begin{array}{}\text{(5)}& {\displaystyle }N\left(D\right)={\displaystyle \frac{N_{\mathrm{0}}}{\mathrm{\Gamma }\left(\mathit{\nu }\right)}}{\left({\displaystyle \frac{D}{D_n}}\right)}^{\mathit{\nu }-\mathrm{1}}{\displaystyle \frac{\mathrm{1}}{D_n}}{e}^{-D/D_n},\end{array}$$

where N₀ is a normalization factor with units of particle number per volume that fixes the total liquid water content ℒ, ν is the shape parameter, which is set to 4 for clouds and 1 for rain, and D_n is the characteristic diameter. For rain we enforce an additional constraint that $N_{\mathrm{0}}=x_{\mathrm{1}}{D}_n^{\mathrm{1}-x_{\mathrm{2}}}$, where x₁=26.2 m${}^{x_{\mathrm{2}}-\mathrm{4}}$ and x₂=1.57 have been determined in previous studies by comparing to observations (Abel and Boutle, 2012). This allows the entire rain distribution to be determined by the liquid water content. The rain rate is calculated from this distribution by using the terminal velocity relation from Beard (1976).

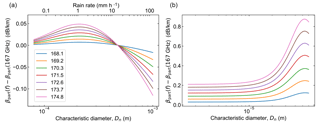
Figure 2 Differential particulate extinction coefficients for (a) rain and (b) cloud. In the case of rain, the DSD characteristic diameter D_n determines the liquid water content and hence the rain rate, while for clouds we fix ℒ=500 mg m⁻³. The legend in (a) gives the corresponding frequencies in GHz.

The results are shown in Fig. 2, where we plot the differential particulate extinction, $\mathrm{\Delta }{\mathit{\beta }}_{\text{part}}\left(f\right)={\mathit{\beta }}_{\text{part}}\left(f\right)-{\mathit{\beta }}_{\text{part}}\left(f_{\mathrm{0}}\right)$, as a function of D_n. Here f₀=167 GHz corresponds to the low-frequency end of the transmission band. In Fig. 2a, the corresponding rain rate is displayed on the upper horizontal axis. For the cloud species, the normalization parameter N₀ is not fixed by any additional constraint, and is therefore determined at each D_n to fix ℒ, which is set here to 500 mg m⁻³. To find the differential particulate extinction for other values of ℒ, one can linearly scale the values in Fig. 2b. Clearly for precipitation scenarios, the differential extinction from rain is more than 2 orders of magnitude smaller than that from water vapor. For clouds in the limit of small diameter, the differential particulate extinction asymptotes to the Rayleigh value of $\mathrm{\Delta }{\mathit{\beta }}_{\text{part}}^{\text{Rayleigh}}=\mathrm{6}\mathit{\pi }\mathcal{L}\text{Im}\left(K_{\mathrm{w}}\right)(f-f_{\mathrm{0}})/\left({\mathit{\rho }}_{\mathrm{w}}c\right)=\mathrm{0.2}$ dB km⁻¹ for f=174.8 GHz, where ρ_w is the density of liquid water, $K_{\mathrm{w}}=(m_{\mathrm{w}}^{\mathrm{2}}-\mathrm{1})/(m_{\mathrm{w}}^{\mathrm{2}}+\mathrm{2})$, m_w is the complex refractive index of water, and c is the speed of light. For larger values of D_n, the differential extinction is enhanced by a resonant feature characteristic of Mie scattering. Thus, for thick clouds with ℒ as large as 500 mg m⁻³, especially those that contain drizzle drops which tend to lie near this resonant size, there are important bias considerations that warrant future study in order to establish the application of DAR in these particular scenarios. Specifically, to mitigate the potential biases stemming from scattering by hydrometeors, the unattenuated reflectivity can be used to distinguish clouds from precipitation, and the frequency-dependent scattering effects can be modeled and incorporated in the retrieval.

2.2 FMCW radar basics and instrument details

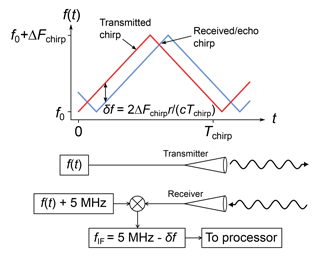
Due to the lower transmit power as compared to conventional radar systems at lower frequencies, the 170 GHz radar is operated in a frequency-modulated continuous-wave (FMCW) mode, which can offer increased sensitivity relative to a pulsed system with the same power because the transmitter is always on. The basic principle of FMCW radar is outlined in Fig. 3. The transmitted signal is frequency-modulated with a linear chirp waveform of bandwidth ΔF_chirp and duration T_chirp. After scattering off of a target at a distance r from the radar, the received chirp is delayed in time by an amount 2r∕c, leading to a fixed frequency offset of $\mathit{\delta }f=\mathrm{2}\mathrm{\Delta }{F}_{\text{chirp}}r/\left(c{T}_{\text{chirp}}\right)$ relative to the transmitted frequency chirp. By downconverting the received signal using the transmitted frequency f(t) shifted by 5 MHz for convenient amplification and detection, the fixed frequency offset between transmitted and received chirps is converted into a constant frequency signal in the intermediate frequency (IF) stage. Signal processing techniques are then used to convert the IF time-domain signal to a range-resolved power spectrum. In the IF power spectrum, the zero-range point is located at 5 MHz and the echo power from a range R is located at f_IF(r)=5 MHz ± δf(r), where the positive(negative) sign applies for decreasing(increasing) frequency chirps.

Figure 3 Basic FMCW radar schematic. See Sect. 2.2 for discussion.

Our system utilizes state-of-the-art millimeter-wave components designed at the Jet Propulsion Laboratory (JPL) and builds on years of FMCW radar development for security and planetary science applications (Cooper et al., 2011, 2017). The architecture is similar to that presented in an earlier work (Cooper et al., 2018) which demonstrated the DAR technique between 183 and 193 GHz, but modified to transmit in the 167 to 174.8 GHz band, in which transmission is not prohibited by international regulations (NTIA, 2015), to perform narrow-bandwidth frequency chirps, and to provide a 5 MHz offset of the zero-range radar signal from zero frequency within the IF band. The IF offset is helpful for future calibrated power measurements because of various effects that inhibit accurate power estimation near zero frequency. The radar has an average transmit power of 140 mW, is outfitted with a 6 cm primary aperture with corresponding gain of 40 dB, and uses a frequency chirp of bandwidth ΔF_chirp=60 MHz and duration T_chirp=1 ms, resulting in a range resolution of $\mathrm{\Delta }r=c/\mathrm{2}\mathrm{\Delta }{F}_{\text{chirp}}=\mathrm{2.5}$ m. In general, the choice of radar range resolution involves a compromise between acquiring more statistically independent samples within a given target volume to reduce uncertainty for bright targets and having a longer integration time to reduce noise power and thus increase the SNR for weak targets. The choice of 2.5 m allows us to downsample the range dimension by a factor of 11 to realize our desired profile resolution of 27.5 m, with decreased uncertainty for the bright clouds measured in this work. A summary of relevant radar hardware parameters is given in Table 1.

Table 1 Hardware and radar signal acquisition parameters used in this work. The noise figure reported is for a complex radar signal detected using a double-sideband front-end mixer.

To process the downconverted radar signal, we first sample it using an analog-to-digital converter (ADC) with a sampling frequency of 20 MHz for the 1 ms duration of the chirp. Then we apply a Hanning window in the time domain before performing a fast Fourier transform (FFT) to obtain the range-resolved power spectrum. Application of the Hanning window reduces side lobes from bright targets as well as the large transmit–receive leakage signal that is always present at zero range. For the radar parameters listed above, the corresponding conversion factor from IF frequency to the target range is $\mathit{\delta }f\left(r\right)/r=\mathrm{400}$ kHz km⁻¹.

2.3 Power measurement uncertainty

The starting point for assessing the achievable precision in humidity using DAR measurements is the statistical uncertainty of the radar power measurements themselves. Until this point, we have ignored the role of background noise power in the radar spectrum, which is an important factor in any realistic receiver. In general, the noise power within a given radar range bin P_n is proportional to the sum of the receiver noise temperature and the antenna temperature, which itself is proportional to the scene brightness temperature. By considering the simultaneous coherent detection of noise (P_n) and radar echo (P_e) power, one can show that the statistical uncertainty of the detected power, $P_{\mathrm{d}}=P_{\mathrm{e}}+P_{\mathrm{n}}$, is given by (see Appendix A)

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{d}}={\displaystyle \frac{\mathrm{1}}{\sqrt{N_{\mathrm{p}}}}}{\left(P_{\mathrm{e}}^{\mathrm{2}}+\mathrm{2}{P}_{\mathrm{e}}{P}_{\mathrm{n}}+P_{\mathrm{n}}^{\mathrm{2}}\right)}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where N_p is the number of radar pulses transmitted.

In order to accurately determine the frequency-dependent optical depth between two range bins, it is critical to obtain a separate measurement of the background noise power in the absence of radar echoes and subtract this off of P_d. To see why this is, consider Eq. (2) with the left-hand side replaced by $P_{\mathrm{d}}(r_{\mathrm{2}},f)/P_{\mathrm{d}}(r_{\mathrm{1}},f)$, which is equivalent to interpreting the detected power as the true echo power, set Z(r₂)=Z(r₁) for simplicity, and consider the limit P_e≪P_n (i.e., P_d→P_n). In this case we would find that $\exp (-\mathrm{2}\mathit{\beta }(r_{\mathrm{1}},r_{\mathrm{2}},f\left)R\right)\to \mathrm{1}$ regardless of the actual value of P_e, and thus would incorrectly estimate a vanishing water vapor density, when in fact it is the echo power which has vanished. Similarly, for modest values of the $\text{SNR}\equiv P_{\mathrm{e}}/P_{\mathrm{n}}$, this would lead to a systematic underestimate of the true humidity. Therefore, after subtracting the separate noise power measurement from P_d we obtain a measurement of P_e with total uncertainty ${\mathit{\sigma }}_{\mathrm{e}}=({\mathit{\sigma }}_{\mathrm{d}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}$, where ${\mathit{\sigma }}_{\mathrm{n}}=P_{\mathrm{n}}/\sqrt{N_{\mathrm{p}}}$ is the noise power measurement uncertainty (see Eq. 6 with P_e=0). The relative uncertainty in the measured echo power is therefore

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{e}}}{P_{\mathrm{e}}}}={\displaystyle \frac{\mathrm{1}}{\sqrt{N_{\mathrm{p}}}}}{\left(\mathrm{1}+{\displaystyle \frac{\mathrm{2}}{\text{SNR}}}+{\displaystyle \frac{\mathrm{2}}{{\text{SNR}}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

As will be discussed in Sect. 3, the range dimension is purposefully oversampled in our measurements, allowing us to decrease the statistical power uncertainty at a given range by averaging N_b adjacent range bins. The resulting relative power uncertainty is given by

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{e}}}{P_{\mathrm{e}}}}={\displaystyle \frac{\mathit{\xi }\left(N_{\mathrm{b}}\right)}{\sqrt{N_{\mathrm{p}}{N}_{\mathrm{b}}}}}{\left(\mathrm{1}+{\displaystyle \frac{\mathrm{2}}{\text{SNR}}}+{\displaystyle \frac{\mathrm{2}}{{\text{SNR}}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where ξ(N_b)≥1 is a factor of order unity accounting for covariances between adjacent range bins that arise due to applying a window function to the time-domain radar signal before transforming to Fourier space. For the Hanning window used in this work, this function is given by $\mathit{\xi }\left(N_{\mathrm{b}}\right)={\left(\mathrm{1}+\frac{N_{\mathrm{b}}-\mathrm{1}}{N_{\mathrm{b}}}\frac{\mathrm{8}}{\mathrm{9}}\right)}^{\mathrm{1}/\mathrm{2}}$.

2.4 Inversion algorithm for profile retrieval

Under the simplifying assumptions introduced in Sect. 2.1, and assuming that pressure and temperature are known as a function of range, the inverse problem to retrieve humidity can be solved directly. The implications of the latter assumption are explored in Appendix C. To invert the radar spectra, we consider a set of measured echo powers P_e(r_i,f_j) for ranges $\mathit{\{}{r}_{\mathrm{1}},r_{\mathrm{2}},\mathrm{\dots },r_m\mathit{\}}$ and transmission frequencies $\mathit{\{}{f}_{\mathrm{1}},f_{\mathrm{2}},\mathrm{\dots },f_{N_f}\mathit{\}}$, where $r_{i+\mathrm{1}}-r_i=\mathrm{\Delta }r$ is the radar range resolution. We note that in most circumstances we employ a retrieval step size R that is larger than Δr, since, as we will show below, the precision in our retrieved humidity scales favorably with total optical depth and hence with increasing R. Then, given a step size such that $R=r_{i+S}-r_i$ for some integer S, we form the frequency-dependent measured quantity

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathit{\gamma }}_i\left(f_j\right)=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}R}}\ln \left[{\left({\displaystyle \frac{r_{i+S}}{r_i}}\right)}^{\mathrm{2}}{\displaystyle \frac{P_{\mathrm{e}}(r_{i+S},f_j)}{P_{\mathrm{e}}(r_i,f_j)}}\right]\end{array}$$

for each starting range r_i. From Eq. (2), we see that we can extract the average humidity between r_i and r_i+S by performing a least squares fit of the function

$$\begin{array}{}\text{(10)}& {\displaystyle }\widehat{\mathit{\gamma }}\left(f\right)=\stackrel{\mathrm{‾}}{\mathit{\rho }}{\mathit{\kappa }}_{\mathrm{v}}\left(f\right)+B\end{array}$$

to the measurements for each i, where B is a frequency-independent offset containing information about dry air gaseous absorption, particulate extinction, and the relative reflectivity of the two ranges in question. We drop the v subscript on the water vapor density in the above equation for simplicity of notation. The resulting humidity estimates $\mathit{\{}{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{1}},{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{2}},\mathrm{\dots },{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{m-S}\mathit{\}}$ have a corresponding range axis $\mathit{\{}{\stackrel{\mathrm{‾}}{r}}_{\mathrm{1}},{\stackrel{\mathrm{‾}}{r}}_{\mathrm{2}},\mathrm{\dots },{\stackrel{\mathrm{‾}}{r}}_{m-S}\mathit{\}}$, where ${\stackrel{\mathrm{‾}}{r}}_i=(r_i+r_{i+S})/\mathrm{2}$, and have associated uncertainties determined from the fitting procedure.

Using standard error propagation, the estimated uncertainty in the measured quantity γ_i(f_j) defined in Eq. (9) is

$$\begin{array}{}\text{(11)}& {\displaystyle }{\mathit{\sigma }}_{{\mathit{\gamma }}_i}\left(f_j\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}R}}{\left[{\left({\left.{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{e}}}{P_{\mathrm{e}}}}\right|}_{r_{i+S},f_j}\right)}^{\mathrm{2}}+{\left({\left.{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{e}}}{P_{\mathrm{e}}}}\right|}_{r_i,f_j}\right)}^{\mathrm{2}}\right]}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

In order to derive a simple analytical expression for the relative uncertainty in the retrieved humidity, we restrict ourselves for the moment to considering two transmission frequencies, f₁ and f₂. In this case, we can combine Eqs. (2), (4), and (9) to obtain the humidity directly,

$$\begin{array}{}\text{(12)}& {\displaystyle }\stackrel{\mathrm{‾}}{\mathit{\rho }}\left({\stackrel{\mathrm{‾}}{r}}_i\right)={\left[{\mathit{\kappa }}_{\mathrm{v}}\left(f_{\mathrm{2}}\right)-{\mathit{\kappa }}_{\mathrm{v}}\left(f_{\mathrm{1}}\right)\right]}^{-\mathrm{1}}\left[{\mathit{\gamma }}_i\left(f_{\mathrm{2}}\right)-{\mathit{\gamma }}_i\left(f_{\mathrm{1}}\right)\right],\end{array}$$

with the associated relative uncertainty

$$\begin{array}{ll}{\displaystyle }{\left.{\displaystyle \frac{{\mathit{\sigma }}_{\stackrel{\mathrm{‾}}{\mathit{\rho }}}}{\stackrel{\mathrm{‾}}{\mathit{\rho }}}}\right|}_{{\stackrel{\mathrm{‾}}{r}}_i}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathrm{\Delta }\mathit{\tau }}}\left[\sum _{j=\mathrm{1},\mathrm{2}}\left({\left({\left.{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{e}}}{P_{\mathrm{e}}}}\right|}_{r_{i+S},f_j}\right)}^{\mathrm{2}}\right.\right.\\ \text{(13)}& {\displaystyle }& {\displaystyle }{\left.\left.+{\left({\left.{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{e}}}{P_{\mathrm{e}}}}\right|}_{r_i,f_j}\right)}^{\mathrm{2}}\right)\right]}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where $\mathrm{\Delta }\mathit{\tau }=\left[{\mathit{\kappa }}_{\mathrm{v}}\left(f_{\mathrm{2}}\right)-{\mathit{\kappa }}_{\mathrm{v}}\left(f_{\mathrm{1}}\right)\right]\stackrel{\mathrm{‾}}{\mathit{\rho }}\left({\stackrel{\mathrm{‾}}{r}}_i\right)R$ is the differential optical depth for f₁ and f₂ between range bins r_i and r_i+S. Equation (13) reveals that there are three linked quantities determining the sensitivity of the system: (1) the magnitude of the DAR signal quantified by Δτ, (2) the statistical uncertainty of the power measurements given by the quadrature sum of relative errors in Eq. (13), and (3) the relative uncertainty in the derived value for the humidity. Thus, given a set of measured echo powers and a specific value for the humidity, there is a trade-off between spatial resolution of the retrieval and relative uncertainty in the humidity estimate.

An important and subtle point regarding the uncertainty in the measured quantity γ_i(f_j) is that Eq. (11) relies on a Taylor expansion in the relative error σ_e∕P_e, and therefore is only valid for measurements with SNR above some critical value that depends on the number of measurements N_p. Because there is no closed-form expression for the probability distribution function (PDF) of γ_i(f_j), we resort to a Monte Carlo analysis, which is described in Appendix B, to generate the relevant PDFs for the parameters used in this work numerically. From this analysis, we find that for N_p=2000 pulses and N_b=11 averaged bins, the Taylor expansion method is accurate for measurements with $\text{SNR}>-\mathrm{10}$ dB.

We note here that it is typical of differential absorption systems to utilize only two frequencies: one online and one offline. However, in this work we are concerned with validating both the spectroscopic model used and the radar hardware itself, which could be subject to unknown frequency-dependent systematic effects. The regression approach discussed above thus provides for a robust comparison of the measured frequency dependence γ_i(f_j) with the model $\widehat{\mathit{\gamma }}\left(f\right)$, while a two-frequency approach would mask inconsistencies between measurements and model, or systematic hardware effects, since the two free parameters $\stackrel{\mathrm{‾}}{\mathit{\rho }}$ and B are fully determined given two frequency points. Furthermore, a distributed set of frequencies allows for the possibility of extending retrievals deeper in range for moist atmospheres, as frequencies closer to the line center will be attenuated more strongly, and can be excluded from the fits described above when the critical SNR value is reached.

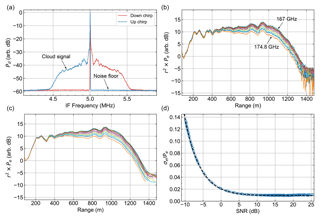
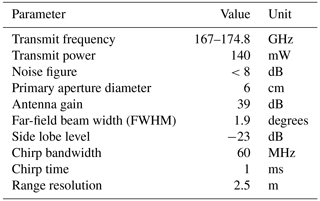
Figure 4 DAR measurement spectra. (a) The bidirectional frequency chirp technique provides for accurate, real-time characterization of the background noise floor within the radar's IF band, with no loss of measurement duty cycle. Here the detected power spectrum for f_j=167 GHz is shown. The IF frequency to range conversion factor is 400 kHz km⁻¹. (b) Echo power spectra normalized to their value at 100 m for the 12 transmission frequencies. The large variability in the signals near 1.4 km indicates the system reaching the noise floor. (c) Echo power spectra after averaging N_b=11 adjacent bins, and filtered for points with $\text{SNR}>-\mathrm{10}$ dB. (d) Measurement relative error (blue circles) for all traces in (c) compared with the statistical model (Eq. 8, dashed black line).

3 Boundary-layer measurements and analysis

3.1 Radar characteristics, spectra, and filtering

In this section we report on measurements performed at JPL on 15 March 2018 using the proof-of-concept differential absorption radar described in Sect. 2.2. For these measurements, we implement a new signal processing technique for real-time noise floor characterization, utilizing a triangle-wave frequency chirp (i.e., bidirectional) instead of a sawtooth-wave chirp (i.e., unidirectional). According to FMCW radar principles, the echo spectrum switches from residing on the low- to the high-frequency side of the zero-range signal (i.e., 5 MHz) for increasing and decreasing linear frequency chirps, respectively. As shown in Fig. 4a, this fast switching of the chirp direction alternately exposes the noise floor on each side of the zero-range point within the IF band, and provides accurate and nearly continuous estimation of the system noise power and the passive signal corresponding to the scene brightness temperature at each frequency bin. This technique is especially advantageous for airborne/spaceborne applications, as the brightness temperature of the observed scene can change on fast timescales due to different surface types (e.g., ocean versus land) and from the presence or absence of clouds.

Figure 4 showcases a few aspects of a single ground-based DAR measurement, for which the conditions were light drizzle and a cloud located a few hundred meters off the ground. For all the field measurements discussed in this work, we acquire N_p=2000 pulses for each of 12 frequencies equally spaced between 167 and 174.8 GHz, with the radar positioned just inside a building, pointing at 30^∘ elevation. The experimental sequence is as follows: first, we perform 40 frequency chirps at a given transmission frequency before switching to another frequency, which takes 1 ms. The received signal is downconverted to baseband, digitized in an ADC, and processed in real time as described in Sect. 2.2. We achieve a system duty cycle of >90 %, resulting in a total measurement/observation time of ≈25 s.

By subtracting the respective noise floors from the increasing and decreasing frequency chirp measurements (Fig. 4a), and subsequently combining the mirrored spectra, we obtain our estimate of the echo power spectra. In Fig. 4b, we plot the echo power spectra scaled by r² for the 12 transmission frequencies before bin averaging, which reveals the range dependence of the quantity $Z\left(r\right)\exp (-\mathrm{2}\mathit{\tau }(r,f\left)\right)$. Each spectrum is normalized to its value at 100 m. Thus, we observe the differential absorption due to water vapor directly from the spreading of the spectra with increasing range, whereby for a particular range, the plotted values increase monotonically with decreasing transmit frequency. After averaging the quantity $r_i^{\mathrm{2}}{P}_{\mathrm{e}}(r_i,f_j)$ within a swath of size N_b=11, we filter the spectra based on the Monte Carlo analysis in Appendix B, keeping only those points with $\text{SNR}>-\mathrm{10}$ dB, and are left with the smoothed profiles shown in Fig. 4c. Figure 4d shows the relative error in the binned (N_b=11) echo power measurement (blue circles) plotted against the measured SNR for all 12 frequencies. The measured values agree very well with those predicted by Eq. (8) (black dashed line), indicating that our statistical model based on speckle noise, which underlies the Monte Carlo simulations implemented in this work, is accurate.

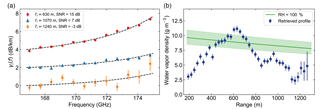
Figure 5 Water vapor profile retrieval for DAR spectra from Fig. 4. (a) Three examples of least-squares fits of the millimeter-wave propagation model to DAR measurements. Artificial offsets are imposed in order to plot all three on the same graph. (b) The retrieved profile exhibits roughly constant absolute humidity error until SNR≈10 dB (1 km). See Sects. 2.4 and 3.2 for retrieval details. The green line shows the saturated water vapor density range dependence using a near-surface temperature of 11 ^∘C and lapse rate of 6 ^∘C km⁻¹. The shaded regions correspond to deviations of ±2 ^∘C.

3.2 Water vapor profile retrieval

Using the averaged, filtered spectra in Fig. 4c, we proceed towards retrieving the water vapor density profile using the procedure outlined in Sect. 2.4. For the profiles presented in this section, we utilize a retrieval step size of R=200 m. Beginning with an initial range of r₁=100 m, we form the 12 quantities γ_i(f_j) for each starting r_i in the set $\mathit{\{}{r}_{\mathrm{1}},r_{\mathrm{2}},\mathrm{\dots },r_{m-S}\mathit{\}}$, and perform a least-squares fit of the function $\widehat{\mathit{\gamma }}\left(f\right)$ to the data at each range point. Note that the retrieved water vapor density ${\stackrel{\mathrm{‾}}{\mathit{\rho }}}_i$ is related only to the difference between the value of the fitted function at 174.8 and 167 GHz, while the offset is related to particulate extinction and hydrometeor reflectivity, and is disregarded in this work. The pressure and temperature dependence of the absorption line shape is included in the fitting model using reported values at the surface from a nearby weather station, and assuming an exponential pressure profile with a scale height of 7.5 km and a temperature lapse rate of 6 ^∘C km⁻¹. We note that for the relatively short vertical extents of the profiles from these ground measurements (e.g., 1.4sin30^∘ km for Figs. 4 and 5), the retrieved $\stackrel{\mathrm{‾}}{\mathit{\rho }}$ values are quite insensitive to the assumed thermodynamic profiles (see Appendix C).

An important element of the DAR technique in general is utilizing an accurate model for the absorption line shape. Examples of line shape fits to the data are shown in Fig. 5a for three different values of SNR, with arbitrary offsets imposed on the three traces to permit simultaneous plotting. To assign SNR values to these points, we compute the mean SNR for the 12 frequencies at r_i and r_i+S, and use the smaller of the two. Clearly the millimeter-wave model accurately captures the frequency dependence of the measurements, which is supported quantitatively by the typical reduced chi-square values of ${\mathit{\chi }}_{\text{red}}^{\mathrm{2}}\approx \mathrm{1}$ for these fits. The retrieved water vapor density profile is shown in Fig. 5b, where the range ${\stackrel{\mathrm{‾}}{r}}_i$ assigned to each fitted value ${\stackrel{\mathrm{‾}}{\mathit{\rho }}}_i$ is the midpoint of r_i and r_i+S. Also plotted here is an estimate of the saturation vapor density given our lapse rate assumption. This profile is consistent with a cloud base between 400 and 600 m and shows qualitatively good agreement with the expectation that the relative humidity is approximately 100 % in liquid cloud layers. Note that because the retrieved values correspond to the mean humidity between r_i and r_i+S, we effectively retrieve the profile convolved with a box of size R (200 m here). For this retrieval, the absolute humidity errors lie between 0.55 and 0.60 g m⁻³ until around 1 km (SNR≈10 dB), where the error steadily increases until the final retrieval point at 1.25 km with ${\mathit{\sigma }}_{\stackrel{\mathrm{‾}}{\mathit{\rho }}}=\mathrm{2.9}$ g m⁻³. The value of ${\mathit{\sigma }}_{\stackrel{\mathrm{‾}}{\mathit{\rho }}}$ in the high-SNR regime (i.e., the first 1 km) remains roughly constant, even though $\stackrel{\mathrm{‾}}{\mathit{\rho }}$ varies by a factor of 3, since the absolute humidity error is independent of the humidity itself, and depends only on the differential mass extinction cross section κ_v(174.8 GHz) − κ_v(167 GHz), the retrieval step size R, and the power measurement uncertainty (see Eq. 13).

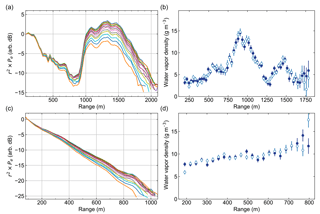
Figure 6 Retrievals for different cloud and precipitation conditions. (a) Averaged DAR power spectra (N_b=11) for light rain near the surface, with a cloud extending from 1 to 2 km. (b) Retrieved humidity profiles for two independent data sets corresponding to the same scene from (a). (c) Averaged DAR power spectra (N_b=11) for heavy precipitation near the surface with strong particulate extinction. (d) Independent retrievals from two data sets for the scene in (c).

Though we do not have independent, coincident water vapor profile measurements with which to validate the accuracy of the retrieval, we can investigate repeatability of this DAR method by performing the retrieval on coincident, independent DAR measurements of the same exact scene. To do so, we acquire N_p=4000 pulses at each frequency with a total measurement time of 50 s, and parse the data into two groups of N_p=2000 pulses both spanning the full 50 s. The results are shown in Fig. 6, where we also present measurements of different cloud and precipitation scenarios than that presented in Figs. 4 and 5. In Fig. 6, panels (a) and (b) correspond to light rain at the surface with a cloud boundary at 1 km range, and panels (c) and (d) to heavy rain at the surface with strong particulate extinction. The retrievals from the two independent sample sets in both cases agree quite well, which showcases the reproducibility of the measurement and indicates that the estimated humidity error accurately captures the sample scatter.

Given a measured range-resolved echo power spectrum, what retrieval range resolution can we achieve for a specified minimum retrieval precision? As discussed briefly in Sect. 2.4, the relative error in the retrieved humidity ${\mathit{\sigma }}_{\stackrel{\mathrm{‾}}{\mathit{\rho }}}/\stackrel{\mathrm{‾}}{\mathit{\rho }}$ (see Eq. 13) for a given power measurement uncertainty varies inversely with the differential optical depth, and thus depends on both the retrieval step size R (i.e., retrieval resolution) used and the absolute value of the humidity $\stackrel{\mathrm{‾}}{\mathit{\rho }}$. Alternatively, one can look at the absolute error and rearrange Eq. (13) to find that, for a given pair of frequencies and power measurements at two ranges, the product of ${\mathit{\sigma }}_{\stackrel{\mathrm{‾}}{\mathit{\rho }}}$ and R is constant. Hence, reducing the retrieval step size by some factor increases the absolute humidity error by the same factor. In future work we will implement a retrieval algorithm that has adaptive range resolution based on both the inherent signal (i.e., humidity) and the measurement noise.

4 Conclusions

A proof-of-concept humidity-profiling DAR operating between 167 and 174.8 GHz has been constructed and tested from the ground. The instrument builds on progress made in an earlier version operating between 183 and 193 GHz (Cooper et al., 2018), and employs a new signal processing technique for performing real-time noise power spectrum characterization and subtraction, providing for higher accuracy measurements of the radar echo power. A new direct inversion algorithm for retrieving humidity based on least squares fits to a spectroscopic model is applied to the measured echo power spectra, showing close agreement between the measurement and model frequency dependence. The humidity profiles retrieved from two statistically independent measurement sets of the exact same scene are in close agreement, highlighting the reproducibility of the method. The uncertainties in the power measurements, which in part determine the retrieved humidity uncertainty, agree very well with a statistical model based on radar speckle noise that incorporates the effects of background noise subtraction and downsampling, or binning, of the measured spectra.

Development of an operational airborne 167–174.8 GHz DAR is currently in progress, which will include an additional 20 dB of antenna gain and a factor of 4 increase in transmit power. Important future steps for this instrument include validation of the measurement accuracy using coincident measurements of humidity, pressure, and temperature (e.g., from radiosondes), and eventually testing from an airborne platform. Specifically, the surface returns while measuring from an airborne platform will be investigated for the retrieval of total column water within the boundary layer. A more significant augmentation of the system could include the addition of passive radiometric channels near the 183 GHz line. This would allow for continuous measurement of vertical humidity profiles when transitioning between clear-sky and cloudy areas, and opens the possibility to study biases in the humidity retrieved from radiometric measurements that are caused by scattering and emission from clouds.

Appendix A: Error in detected power

In this appendix, we derive the expression for the detected power uncertainty within a single radar range bin in the presence of background noise (Eq. 6). To do so, we begin by assuming that all targets within the scattering volume are randomly distributed, leading to the well-known Rayleigh fading model for the received echo signal (Ulaby et al., 1982). In the context of FMCW radar, we then consider the received complex electric field amplitude E_i corresponding to the ith frequency bin in the FFT spectrum, where we only consider the polarization direction that couples into the radar receiver. Within the Rayleigh fading model, it is shown that for $E_i=E_{\mathrm{0},i}{e}^{i{\mathit{\varphi }}_i}$, the modulus of the field amplitude E_0,i is normally distributed with zero mean and standard deviation σ_E, and the phase ϕ_i is uniformly distributed over the interval [0,2π]. Alternatively, we can write the corresponding voltage in the receiver as $V_{e,i}=a_i+i{b}_i$, where a_i and b_i are uncorrelated and are both normally distributed with zero mean. Then, from the expression converting electric field to power, $P_{\mathrm{e},i}=|V_{\mathrm{e},i}{|}^{\mathrm{2}}=\mathit{\alpha }|E_i{|}^{\mathrm{2}}$, we find the probability distribution function for the received echo power

$$\begin{array}{}\text{(A1)}& {\displaystyle }p(P_{\mathrm{e},i}\ge \mathrm{0})={\displaystyle \frac{\mathrm{1}}{\langle P_{\mathrm{e},i}\rangle }}{e}^{-P_{\mathrm{e},i}/\langle P_{\mathrm{e},i}\rangle },\end{array}$$

where the mean equals the variance and is given by $\langle P_{\mathrm{e},i}\rangle =\mathrm{2}\mathit{\alpha }{\mathit{\sigma }}_E^{\mathrm{2}}$, α is a field-to-voltage conversion factor for the radar, and $p(P_{\mathrm{e},i}<\mathrm{0})=\mathrm{0}$. Furthermore, we find that $\langle a_i^{\mathrm{2}}\rangle =\langle b_i^{\mathrm{2}}\rangle =\langle P_{\mathrm{e},i}\rangle /\mathrm{2}$. Though not proven here, the Rayleigh fading model also shows that the expectation value of the received power from N randomly distributed targets is the sum of the expectation values of the individual target echo powers.

Similarly, one can show that Gaussian white noise in the radar signal, which comes from both the scene brightness temperature and the radar electronics, results in a noise voltage within the ith frequency bin of the FFT spectrum with Fourier coefficient $V_{\mathrm{n},i}=c_i+i{d}_i$, where $\langle c_i\rangle =\langle d_i\rangle =\mathrm{0}$ and $\langle c_i^{\mathrm{2}}\rangle =\langle d_i^{\mathrm{2}}\rangle =\langle P_{\mathrm{n},i}\rangle /\mathrm{2}$. We proceed towards deriving Eq. (6) by considering the coherent detection of both the radar echo and noise signals. In this case, the detected voltage signal in the Fourier domain within the ith range bin is $V_{\mathrm{d},i}=V_{\mathrm{e},i}+V_{n,i}$, and the detected power is $P_{\mathrm{d},i}=|V_{\mathrm{d},i}{|}^{\mathrm{2}}$. Using the expectation values listed above, it is easy to show that

$$\begin{array}{}\text{(A2)}& {\displaystyle }\langle P_{\mathrm{d},i}\rangle =\langle P_{\mathrm{e},i}\rangle +\langle P_{\mathrm{n},i}\rangle \end{array}$$

and

$$\begin{array}{}\text{(A3)}& {\displaystyle }\text{Var}\left(P_{\mathrm{d},i}\right)={\left(\langle P_{\mathrm{e},i}\rangle +\langle P_{\mathrm{n},i}\rangle \right)}^{\mathrm{2}}.\end{array}$$

Therefore, we recover Eq. (6) by computing the standard error for N independent measurements, ${\mathit{\sigma }}_{\mathrm{d},i}^{\mathrm{2}}=\text{Var}\left(P_{\mathrm{d},i}\right)/N$.

Appendix B: Monte Carlo Analysis

As discussed in Sect. 2.3, subtracting off the noise power contribution to the detected power P_d is critical for accurate humidity estimation. However, for low values of SNR, we clearly expect the result $\langle P_{\mathrm{e}}\rangle =\langle P_{\mathrm{d}}\rangle -\langle P_{\mathrm{n}}\rangle$ to be negative some of the time due to finite sampling, where “〈⋯〉” denotes the sample average. This is nonphysical. Therefore, in order to account for these finite sampling effects and the potential breakdown of standard error propagation when σ_e∕P_e is not small, we employ a Monte Carlo simulation of the DAR measurement. The PDF for the echo power received from randomly distributed hydrometeor targets within a single range bin is given by Eq. (A1). In order to generate random samples of the radar spectrum for transmission frequency f_j, we begin with an idealized spectrum 〈P_e(r_i,f_j)〉 for which we set $C\left(f\right)=Z(r,f)=\mathrm{1}$ and ρ_v(r)=constant, and sample the distribution (Eq. A1) at each range bin r_i. We then perform a fast Fourier transform (FFT) to obtain the corresponding time-domain radar signal, add the effects of background noise using Gaussian white noise, and apply a Hanning window. Taking the inverse FFT thus supplies a single random realization of a measured P_d spectrum. For the simulated spectra used in this work, we generate N_p=2000 radar pulses with range resolution Δr=2.5 m and average them to realize a single radar measurement. These values for N_p and Δr are the same parameters utilized in the field measurements presented in Sect. 3. We generate 10 000 averaged spectra for both P_d and P_n, giving 10 000 random realizations of the echo power measurement. For these simulations, we use f_j=167 GHz and ρ_v=7.4 g m⁻³.

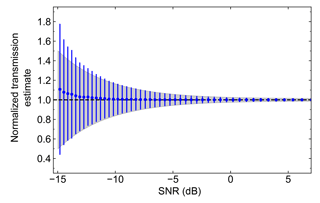
Figure B1 Statistics of low-SNR estimation of two-way transmission. The blue data points represent the means and standard deviations of the Monte Carlo probability distributions, while the gray shaded area represents the error calculated using Eq. (8). For $\text{SNR}<-\mathrm{10}$ dB, the systematic bias of the Monte Carlo mean and the underestimation of the true error by Eq. (8) imply that measurements in this region should be disregarded. In order to access lower values of SNR, one must increase the number of pulses N_p for each measurement.

Our aim is to utilize the Monte Carlo simulations to inform where the Taylor expansion method for error propagation breaks down in our estimation of ${\mathit{\sigma }}_{{\mathit{\gamma }}_i}\left(f_j\right)$, and thus provide a criterion for filtering our measurements. To do so, we fix N_b=11 and the step size S=10 (i.e., 275 m) and compute the mean and standard deviation of the Monte Carlo probability distribution for the two-way transmission between r_i and r_i+S for each r_i. Figure B1 shows the results, where we plot the Monte Carlo mean value divided by the a priori two-way transmission used to generate the Monte Carlo results, as a function of the SNR at r_i+S. The gray shaded area represents the SNR-dependent errors predicted from Eq. (8). There are two notable deviations that arise for SNR values below 0.1: (1) the error estimated using the standard error propagation formalism begins underestimating the true standard deviation calculated using the Monte Carlo ensemble, and (2) the mean of the Monte Carlo-generated distribution systematically overestimates the true two-way transmission. We note here that this point of departure between the naive error propagation estimate and that from the Monte Carlo distributions does not depend on N_b or S, but is determined by the number of independent pulses N_p used to realize a single radar measurement. From these simulations, we conclude that the standard error propagation model is sufficient for $\text{SNR}>-\mathrm{10}$ dB. Therefore, after downsampling the measured spectra with N_b=11, we eliminate all measured values with $\text{SNR}<-\mathrm{10}$ dB, as described in Sect. 3.1.

Appendix C: Retrieval dependence on assumed pressure and temperature values

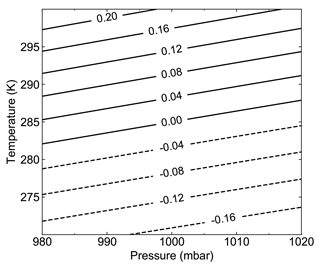
To assess the dependence of the retrieved humidity on temperature and pressure, we will consider again the case of the two-frequency measurement, using transmission frequencies f₁=167 GHz and f₂=174.8 GHz. Then, for a given starting range r_i and step size R, we use the measured quantities γ_i(f₁) and γ_i(f₂) to solve for the mean humidity between the two ranges,

$$\begin{array}{}\text{(C1)}& {\displaystyle }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_i={\displaystyle \frac{{\mathit{\gamma }}_i\left(f_{\mathrm{2}}\right)-{\mathit{\gamma }}_i\left(f_{\mathrm{1}}\right)}{{\mathit{\kappa }}_{\mathrm{v}}(f_{\mathrm{2}},P,T)-{\mathit{\kappa }}_{\mathrm{v}}(f_{\mathrm{1}},P,T)}}={\displaystyle \frac{{\mathit{\gamma }}_i\left(f_{\mathrm{2}}\right)-{\mathit{\gamma }}_i\left(f_{\mathrm{1}}\right)}{\mathrm{\Delta }{\mathit{\kappa }}_{\mathrm{v}}(P,T)}},\end{array}$$

where we now explicitly write κ_v as a function of temperature T and pressure P, and we have defined the differential mass extinction cross section Δκ_v(P,T) for these two frequencies. Given reference values of P₀=1000 mbar and T₀=285 K, and corresponding retrieved humidity ${\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{i,\mathrm{0}}$, we calculate the error in our humidity estimate for different conditions P and T as

$$\begin{array}{}\text{(C2)}& {\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_i-{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{i,\mathrm{0}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{i,\mathrm{0}}}}={\displaystyle \frac{\mathrm{\Delta }{\mathit{\kappa }}_{\mathrm{v}}(P_{\mathrm{0}},T_{\mathrm{0}})}{\mathrm{\Delta }{\mathit{\kappa }}_{\mathrm{v}}(P,T)}}-\mathrm{1}.\end{array}$$

Figure C1 shows the humidity error for pressure deviations of ±20 mbar and temperature deviations of ±15 K. Here we see that the retrieved humidity is very weakly dependent on the assumed pressure, and only accrues an error of 10 % for a temperature deviation of about 8 K.

Figure C1 Humidity error for assumed temperature T₀=285 K and pressure P₀=1000 mbar versus actual values T and P.