Precipitable water vapour content from ESR/SKYNET sun–sky radiometers: validation against GNSS/GPS and AERONET over three different sites in Europe

The estimation of the precipitable water vapour content (W) with high temporal and spatial resolution is of great interest to both meteorological and climatological studies. Several methodologies based on remote sensing techniques have been recently developed in order to obtain accurate and frequent measurements of this atmospheric parameter. Among them, the relative low cost and easy deployment of sun–sky radiometers, or sun photometers, operating in several international networks, allowed the development of automatic estimations of W from these instruments with high temporal resolution. However, the great problem of this methodology is the estimation of the sun-photometric calibration parameters. The objective of this paper is to validate a new methodology based on the hypothesis that the calibration parameters characterizing the atmospheric transmittance at 940 nm are dependent on vertical profiles of temperature, air pressure and moisture typical of each measurement site. To obtain the calibration parameters some simultaneously seasonal measurements of W, from independent sources, taken over a large range of solar zenith angle and covering a wide range of W, are needed. In this work yearly GNSS/GPS datasets were used for obtaining a table of photometric calibration constants and the methodology was applied and validated in three European ESR-SKYNET network sites, characterized by different atmospheric and climatic conditions: Rome, Valencia and Aosta. Results were validated against the GNSS/GPS and AErosol RObotic NETwork (AERONET) W estimations. In both the validations the agreement was very high, with a percentage RMSD of about 6, 13 and 8 % in the case of GPS intercomparison at Rome, Aosta and Valencia, respectively, and of 8 % in the case of AERONET comparison in Valencia.

Analysing the results by W classes, the present methodology was found to clearly improve W estimation at low W content when compared against AERONET in terms of % bias, bringing the agreement with the GPS (considered the reference one) from a % bias of 5.76 to 0.52.

1 Introduction

The precipitable water vapour content, hereafter referred to as W, is the total atmospheric water vapour contained in a vertical column of unit cross-sectional area extending between any two specified levels, commonly expressed in terms of the height to which that water substance would stand if completely condensed and collected in a vessel of the same unit cross section (American Meteorological Society, 2015). The estimation of this quantity is of great interest to meteorological and climatological studies. Near-real-time W measurements can be used for weather diagnoses and forecasting applications (Poli et al., 2007; Hong et al., 2015) and for studying meteorological disturbances occurring in some areas in order to improve the prediction of local heavy rainfall, a difficult task with current mesoscale numerical prediction models (Realini et al., 2014; Bock et al., 2016). Water vapour also plays a key role in the Earth's climate system, leading the hydrological cycle and affecting the global radiation budget as greenhouse gas (Schmidt et al., 2010). Also, microphysical processes leading to the formation of clouds are influenced by W variations, whose effect on the size, shape and chemical composition of aerosols can modify their role in the direct and indirect radiative forcing (Yu et al., 2014; Haywood et al., 2011).

Therefore it is really important to perform measurements of W with high temporal and spatial resolution because of its high variability in both space and time across the Earth. Several methodologies have been recently developed in order to obtain accurate estimations: Global Navigation Satellite System (GNSS), including the Global Positioning System (GPS) (Bevis et al., 1992; Guerova et al., 2016), microwave radiometers (Elgered et al., 1982) and sun photometers (Campanelli et al., 2014; Halthore et al., 1997; Alexandrov et al., 2004) are the automatic remote sensing instruments able to provide precise and frequent measurements of W. All of them have some pros and cons. The GNSS methodology is based on the signal received from positioning satellites by ground-based antennas; W calculated with this technique has a high temporal resolution (typically from 30 s to tens of minutes, depending on the processing strategy), and if the network of ground receivers is very dense then the spatial resolution is high as well. However, the networks of receivers do not provide automatically the final product, that is W, and to get the highest accuracy out of the GPS measurements careful post-processing using available scientific softwares must be performed (Bock and Doerflinger, 2001). Microwave radiometers have a very high temporal resolution (up to 1 s) and good accuracy but, because of the cost of the instrument and maintenance needed, there are not many installed. Finally, the relatively low cost and easy deployment of sun photometers allowed the establishment of several international networks in the last 30 years worldwide. AErosol RObotic NETwork (AERONET) network (Holben et al., 1998; Smirnov et al., 2004), Global Atmospheric Watching Precision Filter Radiometer (GAW-PFR) network (Wehrli, 2000; Nyeki et al., 2005) and European Skynet Radiometers (ESR-SKYNET) network (Campanelli et al., 2012, 2014) provide operationally free estimation of W or develop algorithms and open-source packages for improving the retrieval of this important atmospheric parameter. However, the great problem of this methodology is the estimation of the sun-photometric calibration parameters. The objective of this paper is to validate a new methodology, originally developed and applied at a single site in Japan (Campanelli et al., 2014), at three European ESR-SKYNET sites characterized by different atmospheric and climatic conditions. The methodology is based on the hypothesis that the calibration parameters characterizing the atmospheric transmittance at 940 nm (the wavelength used by sun photometers for retrieving W) are dependent on vertical profiles of temperature, air pressure and moisture typical of each measurement site. To obtain calibration parameters, simultaneous and season-dependent measurements of W are needed, taken over a large range of solar zenith angle and covering a wide range of W. In the present paper yearly GPS datasets are used to obtain a table of photometric calibration constants for each site, covering a range of W from 0 to 40 mm. Results are validated against a co-located AERONET sun photometer and a subset of GPS measurements.

Figure 1 Geographical position of ESR sites in the European region (white dots) and of the stations used in this work (black stars).

2 Measurement sites and equipment

The methodology for the determination of precipitable water vapour content from sun–sky radiometers was applied to measurements taken at three ESR sites (Fig. 1), Rome (Italy; 12.500^∘ E, 41.900^∘ N; 83 m a.s.l.), Burjassot-Valencia (Spain; 0.418^∘ W, 39.508^∘ N; 60 m a.s.l.) and Saint-Christophe, Aosta Valley (Italy; 7.357^∘ E, 45.742^∘ N; 570 m a.s.l.), during three different years, 2010, 2011 and 2014, respectively. The sites under study are different both in location and in atmospheric conditions.

Table 1 Characteristics of the sun–sky radiometers located at the three sites. The exact wavelengths of the CIMEL at Valencia can slightly change depending on particular instrument replacements.

Rome is an urban site, with about 3.0 million of inhabitants, 25 km east from the Mediterranean Sea, in the middle of an undulating plain. The atmosphere is affected by traffic emission as well as by semi-rural particulates and, especially during summer season, by sea breeze and desert dust advection from the Saharan region. The zenith angle for this site varies within the interval [18.46–65.31^∘], and hours of sunlight recorded in 2010 were 2431.8 (provided by the Italian Air Force).

Burjassot is an urban site located in the metropolitan area of Valencia (Spain) with approximately 1.4 million inhabitants, 10 km west from the coast and 5 km northwest from the Valencia city centre. Therefore, it is mainly affected by urban pollution, but also by rural aerosols from non-irrigated inland areas and marine aerosols from the Mediterranean Sea (mainly under the sea breeze dynamics). Occasional events of mineral dust from the Sahara and biomass burning from Mediterranean type forests happen mainly during summer months. In general, its environment is relatively humid, mainly when the site is under the effect of the sea air mass; however, during the Saharan air advections, or when the wind flows mainly from inland Iberian Peninsula, the environment can be very hot and dry. The zenith angle for this site varies within the interval [16.07–62.91^∘] and hours of sunlight recorded in 2011 were 2678.7.

Saint-Christophe is located in the Aosta Valley, 3 km far from the small city of Aosta (about 30 000 inhabitants). The location is in a semi-rural context, partially influenced by anthropogenic activity on both local (emissions from cars, heating systems, steel mill) and regional (advection from the Po Valley) scale. The prevalent wind circulation is forced by mountain–valley and mountain–plain breezes, and foehn episodes are not infrequent. The ground surface is covered with soil, grass and buildings and during wintertime with snow. Zenith angle for this site varies within the interval [22.31–69.14^∘] and hours of sunlight recorded in 2011 were 2396.

The different atmospheric conditions typical of each site, and therefore the seasonal variability of W, make these locations appropriate for a validation of the proposed technique.

2.1 Sun–sky radiometers

A sun–sky radiometer is a narrow band filter photometer able to perform measurements of direct solar and diffuse sky irradiances at some selected wavelengths and at several scattering angles.

The three ESR sites under study are equipped with the standard SKYNET network instrument, that is a sun–sky radiometer model POM-01 or POM-02, produced by PREDE Co., Ltd, Japan. Although mainly used for studying atmospheric aerosol optical and physical properties in clear sky conditions, these instruments also perform irradiance measurements at 940 nm for water vapour studies. The methodology used in this paper has been specifically developed for estimating columnar water content from POM sun–sky radiometers (W_P) but can also be applied to other spectral radiometers.

A CIMEL CE318 sun–sky radiometer, part of the AERONET network (often called simply sun photometer), has operated in Valencia since 2007 and co-located with the ESR-POM since 2008. This instrument, also aimed at characterizing atmospheric aerosols, performs the same kind of measurements as the POM model but has some technical differences that require a further calibration for the diffuse radiance, which is not needed in the POM model (Campanelli et al., 2007). Precipitable water vapour content from this instrument (W_AER) is calculated using the official AERONET inversion algorithm (Smirnov et al., 2004) and successive updates, also providing the aerosol products.

Table 1 shows the most important characteristics of both the POM and CIMEL sun–sky radiometers.

2.2 GNSS/GPS receivers

Three dual-frequency GNSS/GPS receiver stations (hereafter called simply GPS) were used for estimating the precipitable water vapour content, hereafter called W_GPS.

The M0SE system (12.493^∘ E, 41.893^∘ N; ellipsoidal height: 120.6 m; altitude: 72.14 m) is located on the roof of the Faculty of Engineering, University of Rome “La Sapienza”, about 2 km far from the sun–sky radiometer position. This system is part of the EUREF Permanent GNSS Network and the observational files, in Receiver INdependent EXchange (RINEX) format used for the retrieval of W_GPS, were provided by the Geodesy and Geomatics Division, University of Rome “La Sapienza”.

The AOST system (7.345^∘ E, 45.741^∘ N; ellipsoidal height: 624.1 m; altitude: 570.97 m) is located in Valle d'Aosta region, about half a kilometre from the sun–sky radiometer position; it is part of the NetGEO network and the observational files, for the calculation of W_GPS, were provided by the NetGEO network operators. For both the above stations dataset with time interval of 30 s was used to retrieve W_GPS with a temporal resolution of 15 min.

The VALE system (0.3376^∘ W, 39.481^∘ N; ellipsoidal height: 77.7 m; altitude: 26.88 m) is located on the roof of the Escuela de Cartografia y Geodesia of Universidad Politecnica de Valencia, Spain, about 7 km east from the sun–sky radiometer position. This system is part of the EUREF Permanent GNSS Network, and RINEX data are available from the EUREF website (http://www.epncb.oma.be). For this station W_GPS was retrieved with time interval of 1 h.

3 Methodology

3.1 GPS receivers

Dry air and water vapour molecules in the troposphere affect GNSS signals by lowering their propagation velocities with respect to vacuum (Saastamoinen, 1973; Bevis et al., 1992). A diminished speed results in a time delay in the signal propagation along the satellite–receiver path, which multiplied by the vacuum speed of light, adds an extra distance to the satellite–receiver geometrical one. It is worth reminding here that the tropospheric delay (the word delay is usually referred to the extra distance and is expressed in metres) due to the dry air and water vapour molecules is just one out of many other systematic errors affecting GNSS observations that must be accounted for in order to achieve sub-centimetre accuracy positions. During GNSS data processing, the contribution of dry air and water vapour to the total delay is separated and estimated in the zenith direction. This leads to the definition of three delay parameters: ZTD (zenith total delay), ZHD (zenith hydrostatic delay) and ZWD (zenith wet delay), related by the equation ZTD = ZHD + ZWD (Bevis et al., 1992). If from the positioning point of view this delay were just a systematic error to be removed, it suggests GNSS as a tool for the remote sensing of the troposphere water vapour content. For many years, the meteorological community has considered this by-product of high-accuracy positioning as one of the available observations, and time series of GNSS tropospheric water vapour delays are currently assimilated by some number of numerical weather prediction models, in some cases in a routine way (Bennitt and Jupp, 2012; Gerova et al., 2016). The methodology to retrieve columnar water vapour content consists in the following steps:

1. The satellite-related parameters (ephemeris orbits and satellite clocks) provided by the Centre for Orbit Determination in Europe (CODE) are used as input in the Bernese GNSS Software 5.0 for station VALE and 5.2 for stations M0SE and AOST (http://www.bernese.unibe.ch/docs/DOCU52.pdf) in order to estimate the values of the ZTD from the satellite–receiver range observations of a selected receiver. The Bernese software, developed at the Astronomical Institute of the University of Bern (AIUB), is a scientific package meeting highest-quality standards for geodetic and further GNSS applications. In this work, only the GPS signals were processed.

   Concerning the M0SE receiver, a part of the EUREF Permanent GNSS Network, the coordinates provided by CODE in the Solution INdependent EXchange (SINEX) format files are known and the Precise Point Positioning (PPP) absolute positioning and coordinates' constrained methodology were used in the Bernese analysis. Regarding the AOST receiver, the SINEX files are not available and the PPP and free network solution methodology was used, allowing the Bernese GNSS Software to estimate the station coordinates. Station VALE was processed in double-difference mode within a global network as a loosely constrained solution (10 m). The ZTD estimates were quality checked based on inspection of ZTD time series and formal errors following the methodology described in Bock et al. (2016).

2. From the values of ZTD, W_GPS can be calculated using pressure and temperature predicted by a numerical weather prediction model or measured at the surface by weather stations located nearby the GNSS station. These datasets, were provided by the Agenzia Regionale per la Protezione Ambientale (ARPA) Lazio for M0SE station and by Regione Valle d'Aosta for AOST receiver. For station VALE, the surface pressure values from ECMWF reanalysis (ERA-Interim) were used. The height difference between receivers and weather stations has been corrected according to Realini et al. (2014). Latitude and altitude of receivers, read in the RINEX files, are also used to convert ZTD to precipitable water content W_GPS using the procedure by Bevis et al. (1992). This technique allows calculating the ZHD and the ZWD. Finally, according to Askne and Nordius (1987), Eq. (1) returns the amount of IWV (integrated water vapour):

   $$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathrm{IWV}=K\left(\mathrm{Tm}\right)\cdot \mathrm{ZWD},\end{array}$$

   where the coefficient K depends on the vertically integrated mean temperature (Tm) (Davis et al., 1985) and can be obtained either from meteorological models or by the linear relationships proposed by Bevis et al. (1992): Tm ∼ 70.2 + 0.72 Ts, where Ts is the measured temperature. In the analysis of Aosta GPS data, the Bevis equation was used, whereas ECMWF data were used for VALE. Consequently, the values of W are obtained dividing the value of IWV by the water density (1000 kg m⁻³). Many studies have assessed the accuracy of GPS IWV estimates by comparison with measurements from other sensors (e.g. microwave radiometers, radiosondes, lidars). It is well recognized that results are dependent on the IWV itself, and thus on the geographic location (cold–warm climates) and on time (cold–warm or dry–wet season), but also on GPS processing options and of course on the quality of measurements from the reference sensor. Recent measurement campaigns performed at mid-latitudes have demonstrated root mean square differences < 0.1 cm or 4–7 % (Bock et al., 2013; Bonafoni et al., 2013; Pérez-Ramírez et al., 2014), which can be considered as representative for this study.

3.2 Sun–sky radiometers

3.2.1 ESR/PREDE-POM

Precipitable water vapour content from ESR/PREDE-POM sun–sky radiometer (W_P) was calculated using the methodology described in Campanelli et al. (2014). For specific spectral regions in the near infrared, where absorption of dominant trace gases can be considered negligible, we can express the transmittance of the atmosphere (T_atm) as follows: T_atm = $e^{-m_{\mathrm{0}}({\mathit{\tau }}_{\mathrm{R}}+{\mathit{\tau }}_{\mathrm{a}})}$ ⋅ T, where m₀ is the relative optical airmass (Kasten and Young, 1989), τ_a and τ_R are the extinction aerosol optical depth and the molecular Rayleigh scattering at 940 nm respectively, and T is the transmittance of the water vapour (T = $e^{-a(mW{)}^b}$, where m is the water vapour optical airmass, calculated according to Kasten (1966), and W the columnar water vapour content; Bruegge et al., 1992). The main aspect of this technique is the consideration that the atmospheric transmittance in the water vapour band depends on the vertical profile of temperature, pressure and moisture of each site of measurement, as much as its characteristic parameters a and b, whose values depend on the characteristics of the interferential filter but also vary with the columnar water vapour amount. This procedure allows the estimation of a and b parameters directly from the measurements taken by the sun–sky radiometer, potentially containing the information on seasonal changes in vertical profiles of temperature, air pressure and moisture occurring in the site of measurement and not relying on any radiative transfer calculation, therefore reducing simulation errors.

The direct solar irradiance F (mA) measured by the POM sun–sky radiometer at the 940 nm wavelength in clear sky conditions can be expressed by Eq. (2):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }V=V_{\mathrm{0}}{e}^{-m_{\mathrm{0}}({\mathit{\tau }}_{\mathrm{a}}+{\mathit{\tau }}_{\mathrm{R}})}{e}^{-a(mW{)}^b},\end{array}$$

where V₀ is the solar calibration constant, i.e. the extra-terrestrial solar irradiance in current units (mA).

The procedure for the retrieval of a, b and V₀, completely described in Campanelli et al. (2014), is here briefly summarized.

Equation (2) can be also written in the form

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }y=\ln V_{\mathrm{0}}-ax,\end{array}$$

with

$$\begin{array}{}\text{(4)}& {\displaystyle }\left\{\begin{array}{l}y=\ln V+m\cdot \left({\mathit{\tau }}_{\mathrm{a}}+{\mathit{\tau }}_{\mathrm{R}}\right)\\ x=(m\cdot W{)}^b\end{array}\right..\end{array}$$

τ_a is estimated at wavelength λ = 940 nm, according to the well-known Ångström formula in Eq. (5):

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }{\mathit{\tau }}_{\mathrm{a}}\left(\mathit{\lambda }\right)=\mathit{\beta }{\mathit{\lambda }}^{-\mathit{\alpha }},\end{array}$$

where α is the Ångström exponent and β is the atmospheric turbidity parameter. α and β are determined by the regression from Eq. (5), where the spectral series of τ_a are retrieved by the sun–sky radiometer measurements taken at the other visible and near-infrared wavelengths 400, 500, 675, 870 and 1020 nm.

From Eq. (4) x values are calculated for several different values of b and each time the (x, y) squared correlation coefficient is calculated; then the maximization of the (x, y) squared correlation coefficient is used to determine the best exponent b. Once the optimal b is retrieved, the series of x values is computed and used in Eq. (3), where the regression line of y vs. x allows the retrieval of the coefficients a and V₀. The errors affecting a, b and V₀ retrievals are evaluated using a Monte Carlo method as explained in Campanelli et al. (2014).

This regression line is a modified version of a Langley plot where V₀ is retrieved by plotting y vs. the product ax, with x = (m ⋅ W)^b. This approach, as demonstrated in Campanelli et al. (2014), extends the application of the Langley methods to cases where the time patterns of W is not stable.

Once parameters V₀, a and b have been determined, the values of precipitable water content W_P can be calculated according to the Eq. (6):

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{W}_{\mathrm{P}}={\displaystyle \frac{\mathrm{1}}{m}}\cdot {\left[{\displaystyle \frac{\mathrm{1}}{a}}\cdot \left(\ln V_{\mathrm{0}}-y\right)\right]}^{\frac{\mathrm{1}}{b}}.\end{array}$$

In order to calculate x values in Eq. (4), an independent dataset of columnar water vapour W, measured by other instrumentation (such as radiosondes, microwave radiometers or GPS receivers) taken over a large range of solar zenith angle simultaneously with the sun–sky radiometer irradiance measurements, is needed. If seasonal dependent measurements of W are available, it is possible to calculate a table of calibration constants (a, b) as a function of the amount of columnar water vapour typical of the site under consideration. This table can be used for the calculation of W_P until the instrument is moved to another location or its status is deteriorated.

Table 2 For each class and each site are listed the number of data points, the optimal values of calibration constants, their estimated errors, the mean value of W and the estimated uncertainty of W_P.

3.2.2 AERONET/CIMEL

In the AERONET methodology (Pérez-Ramírez et al., 2014), the transmittance T at 940 nm is fitted to those generated from the HITRAN 2000 spectral database (Rothman et al., 2003) using the Spherical Harmonics (SHARM) radiative transfer code (Lyapustin, 2005); then the coefficients a and b are computed by a curve-fitting procedure of T as a function of W. The output of the HITRAN 2000 spectral database is convolved with recently measured filter response functions (Smirnov et al., 2004). Each AERONET instrument has its own unique set of a and b values depending on the filter configuration, and these coefficients are considered fixed until the filter is changed. Since only one pair of a and b parameters is used, the dependence of T on the vertical profile of temperature, pressure and moisture that can seasonally happen at each site is neglected, introducing uncertainties in their retrieval. The use of a different database for the determination of water vapour transmittance could also affect their value.

Once the coefficients a and b are known, the calibration constant V₀ is calculated by another modified Langley method, from observations taken at a high mountain site (Reagan et al., 1986; Bruegge et al., 1992; Halthore et al., 1997). This modified method, different from the one used in the ESR/PREDE-POM procedure, determines V₀ as the intercept of the straight line obtained by fitting y vs. the power term m^b in Eqs. (3) and (4). In this case, as demonstrated in Campanelli et al. (2014), the stability of the W time pattern is required in order to avoid calibration errors. Finally using the retrieved calibration parameters a, b and V₀ the precipitable water vapour content, W_AER, can be calculated from Eq. (6).

4 Estimation of calibration constants

W_GPS obtained by the three GPS receivers in Rome, Aosta and Valencia was used as an independent dataset for calculating the calibration constants of the co-located ESR/PREDE-POM sun–sky radiometers. The cloud screening of radiometers measurements was performed by selecting those measurements whose root mean square deviation (RMSD) between measured and reconstructed diffuse sky irradiance at all the wavelengths, used for aerosol study, and all angles is lower than 20 %. For the Rome site, an additional procedure was applied consisting in intercomparing the selected measurements with those provided by a co-located Multi-Filter Rotating Shadowband Radiometer (MFRSR), whose cloud screening is performed following the methodology by Alexandrov et al. (2004). In order to limit the influence of largest uncertainties at very high solar zenith angles, we selected the data with m < 8.

The closest W_GPS retrievals within 30 min, 15 min before and after the sun–sky radiometer measurements, were selected. Then the simultaneous [W_GPS, V] dataset was divided in two parts by picking every other day among the available days: one part [W_GPS1, V₁] was used for the application of the methodology and then the estimation of the calibration constants, while the other part of GPS estimations (W_GPS2) was used to validate the W_P retrievals. The two GPS datasets were found to be equally populated and with similar frequency distributions, and the statistical independence between the W_GPS2 data used for the validation and W_P was ensured.

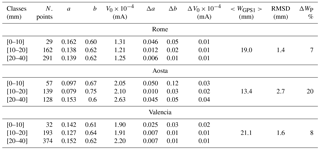
Because a and b parameters are supposed to depend on the total amount of water vapour, the entire yearly independent W_GPS1 dataset was divided in three classes: [0–10] mm, [10–20] mm and [20–40] nm; an insufficient number of points were found with water vapour larger than 40 mm for the three sites. The sun–sky radiometer calibration parameters (a, b and V₀) for each site and class were calculated (Table 2, Fig. 2).

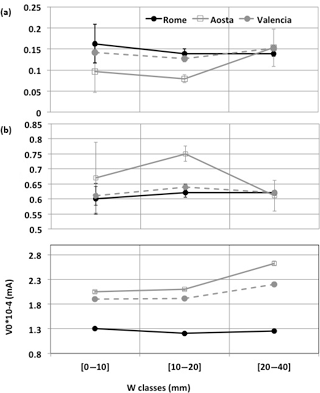
Figure 2 Behaviour of the estimated calibration parameters vs. W classes. The errors bars are the errors affecting the parameters as evaluated using a Monte Carlo method.

In the first application of this methodology (Campanelli et al., 2014), performed to calibrate a sun–sky radiometer at a Japanese site characterized by a wide yearly range of W (from a few millimetres up to about 60 mm), nearly parabolic opposite behaviours of a and b as a function of W were found. The similar behaviour of the boundary W classes (being two maxima of the distribution) was demonstrated to be linked to two different atmospheric regimes, with similar W vertical distribution: trapping of W due to winter inversion and occurrence of convection in summer. Both these regimes have a vertical structure with a well-mixed layer at the bottom and a rapid decrease upward. This behaviour is recognizable in Aosta for the higher W class. In this season, in fact, the well-mixed layer at the bottom is likely due to humid polluted air masses transported from the Po Valley region, starting from late afternoon and staying in the atmosphere up to the morning. This advection was observed by the ceilometer, which measured the increase of suspended particles in the atmosphere, and by hygrometers for the growth of absolute humidity (Díemoz et al., 2016). Unfortunately there are no vertical profile measurements of W at this site to verify this statement. Conversely in Rome and Valencia all the classes seem characterized by similar synoptic situations.

Looking at Fig. 2, a slight fictitious tendency of V₀ on the water vapour class is recognizable. It should be noted that the retrieved V₀ in this methodology should be considered as an effective calibration constant whose variation could not be related to a real instrumental drift. Nevertheless, its total uncertainty (estimated as the standard deviation of the assumed values in each class divided by their average) resulted to be about 4, 8 and 14 % for Rome, Valencia and Aosta, respectively.

Table 3 Parameters of the statistical analysis in the comparison against sun photometer and GPS water vapour estimations: squared correlation coefficient, slope and intercept of the fitting lines, RMSD and bias.

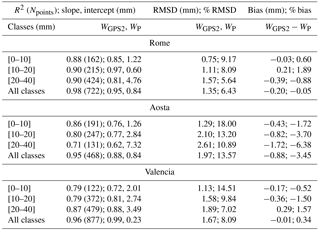
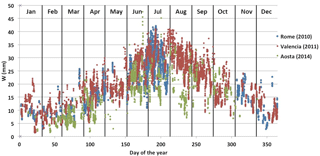
Figure 3 Temporal behaviours of WP retrieved with the presented methodology for the years 2010 (Rome), 2011 (Valencia) and 2014 (Aosta).

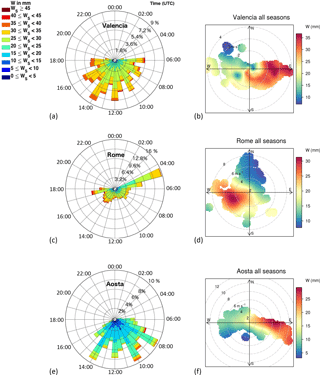
Figure 4 (a, c, e) Polar plot showing the distribution of W values, during summer season, grouped according to their numeric range; the 24 quadrants are hours in UTC; the radius represents the frequency of events normalized to the number of point of the season. The frequency scales are different for the three histograms. (b, d, f) Bivariate polar plot with smoothing, showing the distribution of W content, for the entire year, by wind speed (radius of the circles) and direction.

The uncertainty affecting the retrieval of W_P (ΔW_P %) was estimated (as in Eq. 7) by calculating the percentage RMSD between W_P and the W_GPS1 dataset, used for calibrating the sun–sky radiometer:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{RMSD}=\sqrt{<{\left(W_{\mathrm{P}}-W_{\mathrm{GPS}\mathrm{1}}\right)}^{\mathrm{2}}>}\\ \text{(7)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{W}_{\mathrm{P}}\mathit{\%}={\displaystyle \frac{\mathrm{RMSD}}{<W_{\mathrm{GPS}\mathrm{1}}>}}\cdot \mathrm{100}.\end{array}$$

One must bear in mind that this uncertainty is a statistical measure but not the total uncertainty of W retrieval which should include instrumental uncertainties, errors introduced at different steps of the method and their spread, and any other systematic errors.

The estimated uncertainties (Table 2) values are comparable with that of AERONET retrievals (Pérez-Ramírez et al., 2014), i.e. approximately 10 %, with the exception of Aosta, where a value of 20 %, with a RMSD of 2.7 mm, is obtained. This is due mainly to two reasons: one is that the denominator $<W_{\mathrm{GPS}\mathrm{1}}>$ in Eq. (7) is smaller for Aosta than for the other two sites, resulting in higher ΔW_P % value; the other is related to the performance of GPS measurements in sites with rough orography. In fact, the methodology used for the calculation of ZTD assumes an azimuthal isotropy of the atmosphere above the antenna, within a conical field of view with an angular aperture of about 170^∘ (since the elevation angle cut-off was set to 5^∘) centred in the site where the antenna is located. However, the orography can make the distribution of fluxes at high levels quite complex and not uniform; the rougher the orography, as that surrounding the Aosta site, the greater is the atmospheric anisotropy and therefore, in principle, the error introduced by the failure of the hypothesis assumed by GPS methodology. This degradation of the quality of GPS retrieval, not quantifiable, together with the missing of a large amount of GPS data in Aosta during the summer months, makes the fitting procedures used for the retrieval of calibration constants less stable and therefore increased the uncertainty in their estimation.

5 Intercomparison of methodologies

Once the calibration parameters a, b and V₀, characterizing each sun–sky radiometer, were estimated for all the water vapour classes, water vapour from sun–sky radiometer W_P was directly calculated as in Eq. (6) using the Table 2 parameters and the iterative procedure described in Campanelli et al. (2014). Figure 3 shows the retrieved time pattern of W_P for all the sites. As expected, the winter season is the driest period in the three sites, and in summer Aosta shows a lower W content compared to Rome and Valencia. Seasonal angle histograms of the hourly distribution of W values, grouped according to their numeric range, were performed in order to highlight the main differences among the three sites. Looking at Fig. 4a (summertime), it is worth highlighting that Valencia is the site where high W values (> 30 mm) are more homogenously distributed over time, with a very slight increment in the afternoon due to breeze circulation. This is principally due to the location of this site, very close to the sea, from where humid air masses are transported all over the day. This kind of distribution of greater water vapour content is also visible in the other seasons, showing a sort of homogeneity of W distribution throughout the year. In Fig. 4b a bivariate polar plot with smoothing, obtained from openair package, is shown. W content, for the entire year, in polar coordinates is shown by wind speed (radius of the circles) and direction. Mean contents are calculated for wind speed–direction “bins” (0–1, 1–2 m s⁻¹, etc. and 0–10, 10–20^∘, etc.). It is evident from this plot that the largest amount of W is brought by easterly winds from the seacoast 10 km east from the site.

In Rome W values > 35 mm are mostly recognizable during summer afternoons, from about 14:00 UTC, due to the presence of a breeze circulation that advects air from the sea (Fig. 4c). The importance of wind from the southwest (that is from the sea) in transporting W to the site is highlighted in Fig. 4d, whereas lower W content is mostly recorded when wind comes from the north, having also the highest speed. In all seasons greater water vapour content is retrieved in the early morning and late afternoon showing, also for this site, a generally homogeneous W yearly distribution. A smaller number of measurements is available in Rome during the middle part of the day in all seasons. This is mostly due to the formation of convective clouds at around 12:00 UTC, favoured by the urban heat island phenomenon, that did not allow the photometer to operate.

In Aosta, as shown in Fig. 4f, the greater amount of W comes from the east, that is from the Po Valley, a humid region with higher atmospheric stability and weaker winds, and mostly during summer and autumn seasons; elevated values of W (> 35 mm) during summer were retrieved more frequently in the morning, but this hourly distribution was found also in autumn for W > 25 mm (Fig. 4e). This behaviour could be caused by the atmospheric stability; in the late morning, especially in summer and autumn when the insolation is higher, valley–mountain flows develop, mixing the humid air of the lower levels with the dried air above. Then, winds aloft could remove part of this humidity by advection, decreasing the water content of the air column. The other seasons conversely show more homogeneous W distribution during the day. Low W content associated with winds from W is due to the foehn. When wind comes from this side, air masses passed the Alps and arrived drier over Aosta.

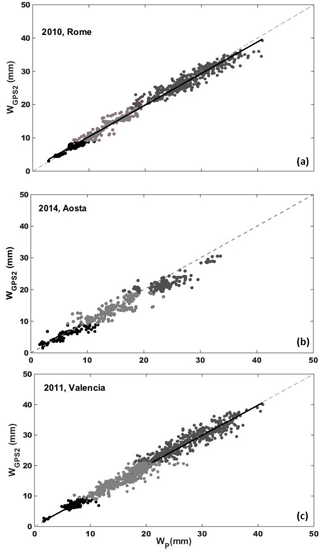
Figure 5 Scatter plot of W_GPS2 vs. W_P. Alternations of black and greys indicate the three water vapour classes.

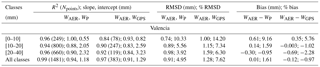
W_P for each site was then validated against W_GPS2 (the part of the GPS dataset not used for the calibration) to compare measurements within 1 min of difference (if more than one measurement of W_GPS2 was found, their average was performed). RMSD and bias, defined in Eq. (8), as well as squared correlation coefficient R², slope and intercept of the fitting straight line, were used for the statistical analysis, whose results are shown in Table 3 and Fig. 5.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{RMSD}=\sqrt{<{\left(W_{\mathrm{GPS}\mathrm{2}}-W_{\mathrm{P}}\right)}^{\mathrm{2}}>}\mathit{\%}\mathrm{RMSD}={\displaystyle \frac{\sqrt{<{\left(W_{\mathrm{GPS}\mathrm{2}}-W_{\mathrm{P}}\right)}^{\mathrm{2}}>}}{<W_{\mathrm{P}}}}>\cdot \mathrm{100}\\ \text{(8)}& {\displaystyle }& {\displaystyle }\mathrm{Bias}=<\left(W_{\mathrm{GPS}\mathrm{2}}-W_{\mathrm{P}}\right)>\mathit{\%}\mathrm{Bias}=<\left({\displaystyle \frac{W_{\mathrm{GPS}\mathrm{2}}-W_{\mathrm{P}}}{W_{\mathrm{P}}}}\cdot \mathrm{100}\right)>\end{array}$$

The comparison between W_P and W_GPS2 for Rome and Valencia (Table 3) when all W classes are analysed shows high R², varying from 0.98 and 0.96; RMSD assumes values from 1.35 mm (6.43 %) and 1.67 mm (8.09 %), and the bias is within −0.01 mm (0.34 %) and −0.20 mm (−0.05 %), which is within the estimated error ΔW_P. Investigating separately the three classes (divided using the thresholds on the W_GPS2 dataset), the greatest difference was found for the first class in terms of % RMSD (9.17–14.51 %) but for the same class it was the smallest in terms of absolute RMSD (0.75–1.13 mm); conversely for the same class the smallest difference was found in terms of bias, both in percentage and absolute values, varying from −0.03 mm (0.60 %) to −0.17 mm (−0.52 %). However, each class remained within the ΔW_P error.

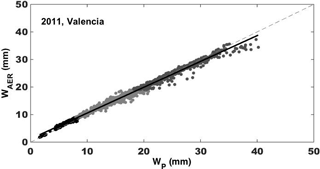
Figure 6 Scatter plot of W_AER vs. W_P for Valencia site; alternations of black and greys indicate the three water vapour classes.

The retrieval of W_P for Aosta was generally less performing than for the other sites. For the entire W classes, RMSD and bias were found to be the highest values, 13.57 % (1.97 mm) and −3.45 % (−0.88 mm) respectively, while R² is the lowest among the three sites (0.95). Also for this site the greatest % RMSD (18.00 %) and the smallest RMSD (1.29 mm) were found for the first class and the bias (both percentage and absolute values) remained for each class within the ΔW_P error. The lower-quality performance of the methodology in this site is discussed in Sect. 4.

Co-located with the ESR-SKYNET/POM by the University of Valencia, there was an AERONET/CIMEL simultaneously operating in 2011. Since the philosophy used by the two networks for the radiometer's calibration is substantially different, it is worthwhile to compare the columnar precipitable water content estimated by the two methodologies and verify whether there are some improvements in assuming the calibration parameters dependent on the vertical distribution of W, and then on its total amount, with respect to the commonly used assumption of fixed values.

Figure 6 shows the scatter plot of AERONET estimation (W_AER) vs. W_P for measurements within 1 min of difference (if more than one measurement of W_AER was found, their average was performed). A very high squared correlation coefficient was found (Table 4) between the two series (0.99), with a total % bias of 1.61 % (0.01 mm). However, analysing the results by classes, a larger discrepancy is evident for the first class in terms of % RMSD (10.33 %) and % bias (9.16 %) within the combined uncertainty of both W_P and W_AER, with an overestimation of AERONET retrieval.

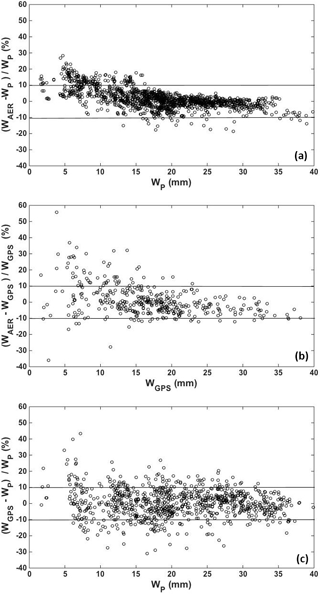
Figure 7 Percentage relative differences between W_AER and W_P (a), W_AER and W_GPS (b), and W_GPS and W_P (c) for Valencia site.

W_AER was then compared against W_GPS, showing a % bias of −0.97 % and % RMSD of 7.62 % if all the classes are considered. The negative bias, consisting in an underestimation of AERONET retrieval, was also documented by Pérez-Ramírez et al. (2014), who found values varying from 2.2 to 7.9 % depending on the site under study when comparing estimations from AERONET vs. GPS. However, the agreement against GPS was not so good for the first class of W_AER, where a higher positive discrepancy was found (% bias of 5.76) with respect to the one shown in the comparison between W_P and W_GPS (0.52 %) in the same class. Looking at Fig. 7, in fact, it is clear that the difference between W_AER and W_P has a decreasing trend with increasing W (Fig. 7a) being greater than 10 % (threshold of AERONET uncertainty) mostly for values below 15 mm, which is about the first class of W. A similar trend (even if less marked) is visible between W_AER and W_GPS (Fig. 7b). Conversely there is no clear tendency in the difference between W_P and W_GPS (Fig. 7c). This confirms that the methodology here proposed takes to a general improvement of W estimation, particularly evident for low W content, in agreement with the findings in Campanelli et al. (2014), where the assumption of variable of a and b parameters increased the agreement with GPS retrievals of about 10 % for the first W class respect to the commonly assumption of fixed a and b.

6 Conclusions

A methodology for retrieving precipitable water content W_P from sun–sky radiometers measurements at 940 nm was applied to three sites of the ESR-SKYNET network with different atmospheric and climatic conditions. In order to provide W_P, the sun–sky radiometer must be calibrated in terms of the solar calibration constant V₀, that is the solar radiation incident at the top of the atmosphere and the calibration parameters characterizing the atmospheric transmittance at this wavelength, a and b. This methodology considers that a and b are dependent on vertical profiles of temperature, air pressure and moisture typical of each measurement site, and therefore allows for the calculation of pairs of (a, b) values for several classes of W. To obtain the calibration parameters, GPS-based yearly independent estimations of W, simultaneously with the sun–sky radiometer measurements, were used and a table of calibration constants, covering a range of W from 0 to 40 mm, was built for each site. In this work the GPS dataset was divided in two parts by picking every other day from the available days: one part was used for the calibration of the sun–sky radiometer and the other part for the validation.

In principle 1 entire year of W independent measurements are required for building the calibration table, but a smaller dataset can also be used, provided that it is taken over a large range of solar zenith angle and it covers a wide range of W.

Table 4 Parameters of the statistical analysis in the comparison against W_AER of W_P and W_GPS estimations for Valencia site: squared correlation coefficient, slope and intercept of the fitting lines, RMSD and bias.

The obtained W_P values were characterized by an uncertainty ΔW_P below 10 % for Rome and Valencia and of 20 % for Aosta. The yearly time pattern of W_P for each site was then validated against the part of the GPS dataset not used for the calibration and against an AERONET sun photometer co-located in Valencia. In the former case for Rome and Valencia the agreement was found to be within the uncertainty ΔW_P when all the classes together are analysed, whereas for Aosta a % RMSD of about 14 % was found. Investigating separately the three classes, the greatest difference was found for the first class in terms of % RMSD: 9.18, 14.51 and 18 %, for Rome, Valencia and Aosta respectively.

When compared against the AERONET retrieval, the agreement was found to be very good and within the uncertainties of both methodologies when all the classes together are considered. However, analysing the results by classes, and after a cross-check among W_P, GPS and AERONET estimates, it was highlighted that the present methodology is able to generally improve W estimation, particularly for low W content in term of % bias, bringing the agreement with the GPS (considered the reference) from a % bias of 5.76 to 0.52. This finding is in agreement with what was already demonstrated by Campanelli et al. (2014), in which the assumption of variable of a and b parameters was compared with the results from the assumption of fixed a and b.

The present methodology can be easily applied to other kind of sun photometers or radiometers measuring the solar direct radiation at 940 nm wavelength, as PFR or MFRSR, provided that Ångström, exponent and aerosol optical depth at 940 nm are available. The calibration table containing a and b values for each W class can be used until the instrument is moved to another location or is submitted to maintenance. In these cases all the calibration parameters must be recalculated.

The problem in the application of this methodology is, however, the availability of an independent, simultaneous W dataset to be used for calibrating the sun–sky radiometer or any other similar sun photometer. In Campanelli et al. (2014) the possibility of using a rough estimation of the needed W dataset was tested, using surface observations of moisture parameters that are much more common than W values estimated by other equipment. The test provided very interesting results but still needs to be improved and validated in different sites and climatic conditions, which will be the next task for this kind of research. Finally, a sensitivity study about the time frequency of the independent external measurements (both daily and monthly but also inside a single day) will be a future prospect of this research in order to build guidelines for the operational use of the methodology and delivering a software.