The use of GNSS zenith total delays in operational AROME/Hungary 3D-Var over a central European domain

The delay of satellite signals broadcasted by Global Navigation Satellite System (GNSS) provides unique atmospheric observations which endorse numerical weather prediction from global to limited-area models. Due to the possibility of its frequent and near-real-time estimation, the zenith total delays (ZTDs) are valuable information for any state-of-the-art data assimilation system. This article introduces the data assimilation of ZTDs in a Hungarian numerical weather prediction system, which was carried out by taking into account observations from central European GNSS analysis and processing centres. The importance of ZTD observations is described and shown by a diagnostic tool in the 3-hourly updated 3D-Var assimilation scheme. Furthermore, observing system experiments are done to evaluate the impact of GNSS ZTDs on mesoscale limited-area forecasts. The results of the use of GNSS ZTDs showed a clear added value to improve screen-level temperature and humidity forecasts when the bias is accurately estimated and corrected in the data assimilation scheme. The importance of variational, i.e. adaptive bias correction, is highlighted by verification scores compared to static bias correction. Moreover, this paper reviews the quality control of GNSS ground-based stations inside the central European domain, the calculation of optimal thinning distance and the preparation of the two above-mentioned bias correction methods. Finally, conclusions are drawn on different settings of the forecast and analysis experiments with a brief future outlook.

1 Introduction

The interaction of satellite signals from Global Navigation Satellite Systems (GNSS) with atmospheric constituents has been recognised as valuable information for meteorological applications and numerical weather predictions (NWPs). The GNSS signals were delayed along the emitted satellite ray's path, which can be formulated as an excess length and are most generally determined in zenithal path above the ground-based receiver station, providing the zenith total delay (ZTD) (Bevis et al., 1992). The total delay includes a wet delay component, which is a function of the water vapour distribution of the troposphere, bringing key humidity-related observations for meteorological users. The high-resolution NWP and data assimilation are demanding more frequent and denser observations (Benjamin et al., 2004, 2010), in particular by applying non-conventional data sources to a larger extent. Consequently, state-of-the-art data assimilation systems rely significantly on remote-sensing measurements like RADAR, satellite products including data from navigation satellites as well. Therefore, the use of GNSS measurements has been widely included in experimental and also operational data assimilation systems since the second half of the 2000s. In a global 4D-Var system, Poli et al. (2007) demonstrated the positive forecast impact of the ZTD observations by correcting synoptic scales up to 4 days. Macpherson et al. (2008) and De Pondeca and Zou (2001) published data assimilation impacts and a case study, respectively, showing that the use of zenith tropospheric delay observations over North America led to forecast improvements and error reductions. At that time, the added value of ZTDs in European limited-area DA (data assimilation) systems has been also justified by a number of authors such as Cucurull et al. (2004), Faccani et al. (2005), Yan et al. (2009b) and Boniface et al. (2009), focusing on local area and data set. After various inter-European studies and projects, e.g. MAGIC (Meteorological Applications of GPS Integrated Column Water Vapour Measurements in the Western Mediterranean), COST Action 716, and TOUGH (Targeting Optimal Use of GPS Humidity Measurements in Meteorology) the European Meteorological Services Network (EUMETNET) organised the GNSS Water Vapour Programme (E-GVAP). This EUMETNET observation programme shares ZTD estimates in near real-time (NRT), primarily for use in operational meteorology. It aims to expand the existing network with inclusion of new regions and helps its members to use ground-based GNSS data in their operations. The programme was set up in April 2005 through establishing timeliness and precision requirements of distributed ZTD data. Given the efforts of the E-GVAP programme, and with a view of increasing such observation usage, new actions and explorations of meteorological applications were initiated during the last decade. Recently a new European COST Action (ES1206), using advanced GNSS products for severe weather events and climate (Guerova et al., 2016), was also launched. In the meantime, more recent studies have been carried out, for instance, by Bennitt and Jupp (2012), De Haan (2013) and Mahfouf et al. (2015), who pursued the objective of improved GNSS ZTD assimilation and took into account one or more E-GVAP networks. All these studies agreed that more accurate description of humidity and precipitation forecast can be gained by the use of GNSS ZTD, although its absolute contribution in terms of observation number is smaller compared to other observation types. However, GNSS ZTD – like most of the observations – include systematic errors which must be taken into account in the assimilation procedure. Better characterisation and assessment of ZTDs were proposed, e.g. by Storto and Randriamampianina (2010) and recently Sánchez-Arriola et al. (2016) and Lindskog et al. (2017), who demonstrated that the variational bias correction approach is successful for eliminating GNSS ZTD bias and is advantageous for controlling bias correction in an adaptive manner. The main objectives of this paper are to assess the added value of GNSS ZTD observations in a central European domain by taking into account all available E-GVAP ZTD networks and summarising the work that has been done in the frame of COST ES1206. In addition, the latest bias correction developments are studied and used in the data assimilation system of AROME/Hungary. The paper is constructed as follows. Section 2 introduces the operational AROME NWP model and data assimilation system used in the current study. Section 3 gives an overview of the applied data, the characteristics of E-GVAP networks and their ZTD observations. In Sect. 4 the passive assimilation experiment, the pre-processing of ZTD observations and the bias correction are described. In Sect. 5 the results of active assimilation runs are discussed and, in the last section, conclusions are drawn with a brief future outlook.

2 Description of operational model and observations

At the Hungarian Meteorological Service (OMSZ), limited-area (LAM) NWP activities were started in the 1990s as part of the ALADIN (Aire Limitée Adaptation Dynamique Développement International) consortium, which led to the implementation of the ALADIN model (Horányi et al., 1996) and later its data assimilation system (Bölöni, 2006). For the purpose of having a high (kilometric) spatial resolution of LAM, the non-hydrostatic dynamical core of ALADIN (Bubnová et al., 1995) and the physical parameterisation package of the French research model, called Meso-NH (Lafore et al., 1997; Lac et al., 2018), have been merged while setting up the AROME (Application of Research to Operations at Mesoscale) model. After the successful operation of AROME at Météo-France (Seity et al., 2011), OMSZ also began to implement an AROME system running over a central European domain. The first Hungarian AROME configuration (AROME/Hungary) has been performed with dynamical adaptation of ALADIN/Hungary forecasts as the initial and boundary conditions. Later, major upgrades brought significant improvements to operational AROME/Hungary forecasts (Mile et al., 2015) by the ECMWF (European Centre for Medium-Range Weather Forecasts) IFS (Integrated Forecasting System) lateral boundary conditions and a local 3D-Var data assimilation system. The recent operational NWP model domain covers the entire Carpathian Basin (highlighted by the black frame in Fig. 1) with a horizontal mesh size of 2.5 km and 60 vertical levels from the surface up to 0.6 hPa. The surface characteristics of the AROME model are described by the surface scheme of Meso-NH called Externalized Surface (SURFEX) and initialised by the optimal interpolation method (Mahfouf, 1991; Masson et al., 2013) before every model integration.

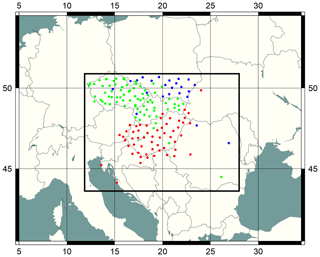
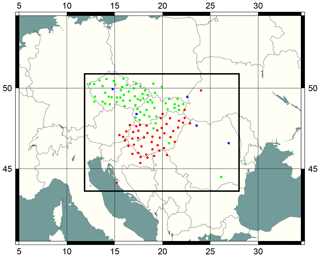
Figure 1 The computational domain of AROME/Hungary (black rectangle) and all available GNSS stations from SGO1 (red), GOP1 (green) and WUEL (blue) E-GVAP networks.

For the time being, the upper-air assimilation system of AROME/Hungary considers only conventional observations, namely surface SYNOP, aircraft (AMDAR, ACARS and Mode-S from Slovenia) and radiosonde reports. To use a larger number of conventional observations, the 3 h assimilation cycle is set to produce eight analyses per a day, which, for example, enable the utilisation of aircraft data measured at asynoptic network times by the ±1.5 h assimilation window in 3D-Var. The timeliness of conventional observations collected from GTS (Global Telecommunication System) plus local sources in a 3-hourly rapid update cycle (RUC) is still met with the time-critical applications of operational AROME/Hungary. For forecasting needs at OMSZ, the short cut-off AROME analysis and related forecast are scheduled to be performed no later than 2 h after the actual time of the analysis, which includes the long cut-off analyses and updated first guesses for the more accurate background information. Regarding future perspectives of AROME/Hungary's upper-air DA, the applied RUC approach favours observations which have a large temporal frequency and small latency. For particular diagnostic purposes the AROME 3D-Var was experimentally run with all available non-conventional observations. That is, the use of satellite radiances from Meteosat-10 SEVIRI (Spinning Enhanced Visible and Infrared Imager), from NOAA-19 AMSU-A (Advanced Microwave Sounding Unit-A) and MHS (Microwave Humidity Sounder), from Metop-A and Metop-B AMSU-A, MHS, and IASI (Infrared Atmospheric Sounding Interferometer) sensors. Additionally, this diagnostic consists of the assimilation of satellite-derived winds MPEF (Meteorological Product Extraction Facility), called Geowind and HRW (high-resolution winds) AMVs (atmospheric motion vectors), from Meteosat-10 satellite, the use of RADAR reflectivity and radial winds from Hungarian RADAR sites, and most importantly the use of GNSS ZTD observations. The non-conventional satellite and RADAR observations were added to AROME experimental analyses solely for a diagnostic study and they were not considered in the GNSS ZTD observing system experiments. This experimental DA system performed 3D-Var analyses with perturbed and unperturbed observation sets on a 10-day period (between 5 and 15 June 2017) in order to compute the degree of freedom for signal (DFS) diagnostic as the following (Girard, 1987; Chapnik et al., 2006):

$$\begin{array}{}\text{(1)}& \mathrm{DFS}\approx Tr\left(\mathbf{HK}\right)\approx (\mathit{y}{}^{\prime }-\mathit{y}{)}^T{\mathbf{R}}^{-\mathrm{1}}(\mathbf{H}\left(\mathit{x}{{}^{\mathbf{\prime }}}_{\mathrm{a}}\right)-\mathbf{H}\left({\mathit{x}}_{\mathrm{a}}\right)),\end{array}$$

where HK is the product of the linearised observation operator by the Kalman gain, and the DFS scores can be approximated by its trace in Eq. (1). The y and y^′ are the unperturbed and perturbed observation sets, R is the observation-error covariance matrix, and H(x_a) and $\mathbf{H}\left(\mathit{x}{{}^{\mathbf{\prime }}}_{\mathrm{a}}\right)$ are the unperturbed and perturbed analyses states in the observation space. DFS provides information on the observation's influence on analyses with respect to the different observation types. Figure 2 shows absolute and relative DFS scores computed on the 10-day period in the AROME/Hungary system. The relative DFS is normalised by the number of observations for each observation subset, providing the diagnostic information, regardless of the actual amount and geographical coverage in the assimilation system. The GNSS ZTD has a limited absolute DFS due to the small number of ZTD observations compared to other observation types. However, it has a considerably high relative contribution, which can significantly affect the AROME/Hungary analysis.

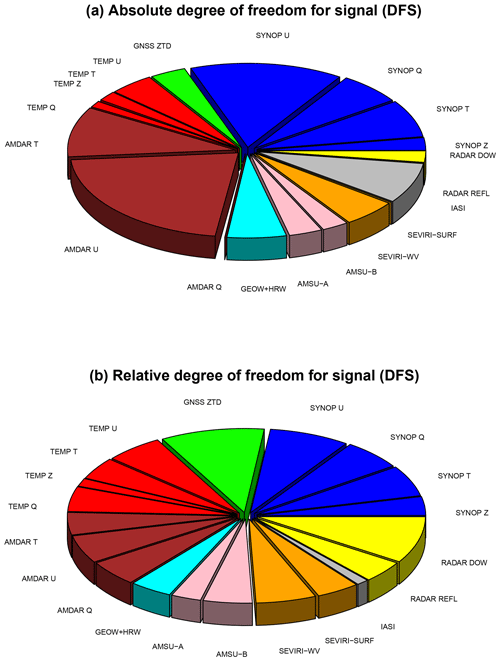
Figure 2 The absolute (a) and relative (b) DFS scores computed in AROME/Hungary 3D-Var experimental analyses for the period 5–15 June 2017. The considered observations in DFS computation are the following: SYNOP (parameter U, Q, T, Z) with blue, TEMP (parameter U, T, Q, Z) with red, AMDAR (parameter U, T, AMDAR Q) with maroon, GEOW+HRW (parameter U) with cyan, RADAR (parameter reflectivity, radial wind) with yellow, AMSU-A and AMSU-B (parameter Tb) with pink, SEVIRI-WV and SEVIRI-SURF (parameter Tb) with orange, IASI (parameter Tb) with grey and GNSS (parameter ZTD) with green.

3 GNSS ZTD observations

The first tests of ZTD retrievals using permanent GNSS stations in Hungary started in 2009 (Rózsa et al., 2009). Due to the positive results of this study, a near-real-time GNSS processing facility was set up by the collaboration of the Satellite Geodetic Observatory Penc and the Budapest University of Technology and Economics (BME). The applied computational strategy can be found in Rózsa et al. (2014). The processing centre (SGOB, later renamed to SGO1) joined the EUMETNET's E-GVAP programme in 2013. Since then, the ZTD estimates at the stations of the Hungarian GNSS Network are available for meteorological applications. Hungary, with its representing institutions, BME, OMSZ and SGO, participated in the COST ES1206. The network processed by the SGO1 processing centre involves more than 80 ground-based stations and provides accurate ZTD estimates using the Bernese software v5.2 (Dach et al., 2015). The estimates are computed from the network solution with a +90 min latency. Due to its coverage, the SGO1 network provides most of the ZTD estimates in the AROME/Hungary's NWP domain. To extend the coverage of GNSS ZTD, other central European E-GVAP networks were included in this study. For a long time the Geodetic Observatory Pecny (GOP) in the Czech Republic has been preparing GNSS-based measurements for various users and also contributing to E-GVAP with a large network (more than 120 stations), called GOP1. Moreover, the GNSS network developed by Wroclaw University of Environmental and Life Science (WUELS) serves additional ZTD estimates inside our area of interest. The WUEL analysis centre provides ZTD estimates for a network of 130 stations. Both of the latter centres use a network solution provided by the Bernese software.

Figure 3 The computational domain (black rectangle) and preselected GNSS stations from SGO1 (red), GOP1 (green) and WUEL (blue) E-GVAP networks.

4 Evaluation of the quality and use of GNSS ZTDs on a training period

4.1 Passive assimilation and preselection procedure set-up

The assimilation of ZTDs with very large observation errors has been conducted in an experimental AROME/Hungary system for a training period. This “passive” assimilation allows monitoring of ZTD observations inside the variational assimilation scheme without influencing the analysis. Although the quality-control procedure of the variational scheme contains the so-called background check (which is dedicated to reject observations far from model background state), one also needs to ensure that only observations with Gaussian, zero mean and uncorrelated errors are selected in the assimilation (i.e. reliable stations). For that purpose, a specific preselection procedure has to be performed that checks passive observation minus first-guess (OMF) departures over a training period. Due to the high analysis cycle frequency, i.e. 8 AROME/Hungary analyses per a day, the training period of 15 and 31 May 2017 is chosen, assuming a sufficient sample for every GNSS station. The preselection of GNSS ZTDs means consecutive tests of time availability, normality, maximum standard deviation and bias, and metadata consistency together with domain and altitude difference examination of GNSS stations. Considering that particular stations can be processed by a several analysis centre (we can call it station multiplication), the station–processing-centre pair is selected which has the smallest standard deviation of OMF. Furthermore, the station thinning is also part of a procedure to avoid observation error correlations. More details about the preselection design are given in Yan et al. (2009b) and Poli et al. (2007).

4.2 Results of the preselection procedure

The actual training period led to the availability of 197 GNSS stations inside the NWP domain (from three different networks). The preselection procedure excluded more than 30 % of them, resulting in 122 trusted GNSS stations for active assimilation experiments. Due to time coverage (e.g. data gaps or outages) and Gaussianity issues, 10 % of the data were rejected. A further 2 %–3 % of the stations were denied, since the detected bias and standard deviation of OMF were higher than the predefined limits. The thresholds of bias, standard deviation and altitude difference limits were set according to Yan et al. (2009b). Due to multiple station–analysis-centre pairs, 12 % of the stations are excluded from one or two networks during the preselection. The selected GNSS stations are written into a specific whitelist, which ensures the active assimilation of ZTDs. The location of all available GNSS stations and trusted stations inside the NWP domain can be seen on Figs. 1 and 3 respectively.

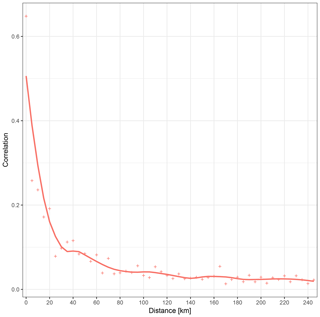
In order to determine the optimal thinning distance which is employed for preselection, horizontal observation error correlations as a function of various separation distances have been computed. The computation of error correlations are based on the method proposed by Desroziers et al. (2005):

$$\begin{array}{}\text{(2)}& E\left[d_{\mathrm{b}}^{\mathrm{o}}{\left(d_{\mathrm{a}}^{\mathrm{o}}\right)}^T\right]=\mathbf{R}\end{array}$$

where observation error covariances are estimated based on the expected value of background $\left(d_{\mathrm{b}}^{\mathrm{o}}\right)$ and analysis $\left(d_{\mathrm{a}}^{\mathrm{o}}\right)$ departures considering various departure pairs for horizontal distances. The Desroziers method has the advantage of providing error correlation structures in observation space, i.e. at observation locations from the collected pairs of background and analysis departures in a computationally efficient approach. For this diagnostic purpose, a revised whitelist is generated with zero thinning in order to execute very first active assimilation and to collect its OMF departures. Liu and Rabier (2003) showed that horizontal thinning distance is optimal, where the observation error correlations are less than 0.2–0.3. By the visualisation of these error correlations, which can be seen in Fig. 4, a 20 km thinning distance is chosen for the final GNSS preselection procedure.

Figure 4 Observation error correlations estimated by Desroziers method as a function of separating distances for GNSS ZTDs inside AROME/Hungary's domain. Local polynomial regression method was used to fit a smooth curve and the diagnostic was computed for the period of 15–31 May 2017.

4.3 Detected bias and static bias correction

During the preselection procedure, OMF departures are used to evaluate the quality of ZTDs and also to identify systematic errors in measurements. The bias might originate from the mapping function of ZTD processing, the conversion of time delay to excess length, the contribution of the atmosphere above the model top or, for instance, the altitude differences between the model orography and the GNSS station elevation. The observation bias of a GNSS station (station) is detected as the time average of the observation (o_i) minus model-background (b_i) differences considering the number of analyses (n) during the time period (Eq. 3).

$$\begin{array}{}\text{(3)}& {\mathrm{BIAS}}_{\mathrm{station}}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{o}_i-b_i\end{array}$$

Although, it assumes that the first-guess is an unbiased reference which is not necessarily true, Poli et al. (2007) showed that this approach can be efficiently applied for the initial bias estimation of GNSS ZTDs. The distribution of OMF values taking into account all GNSS stations is plotted in Fig. 5. Concerning the detected bias of each GNSS station separately, one can see in Figs. 6 and 7 that the observed bias strongly varies by station in SGO1, WUEL and GOP1 networks respectively. Therefore, the bias correction should be done individually for different GNSS stations.

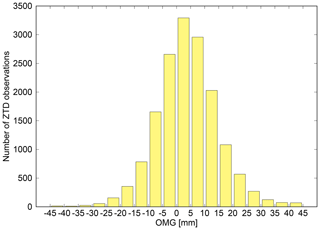
Figure 5 Distribution of OMF values for all GNSS stations inside AROME/Hungary's domain. The period of 15–31 May 2017 was used for the calculation of OMF statistics.

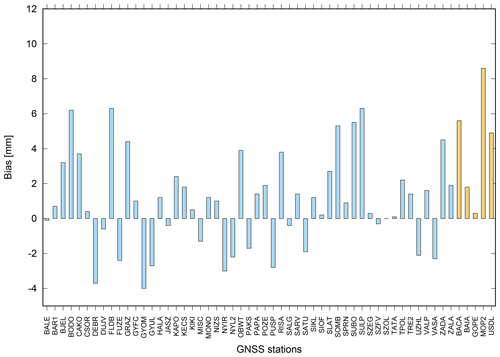
Figure 6 The ZTD bias in millimetres for SGO1 (light blue) and WUEL (light orange) networks calculated for the period of 15–31 May 2017.

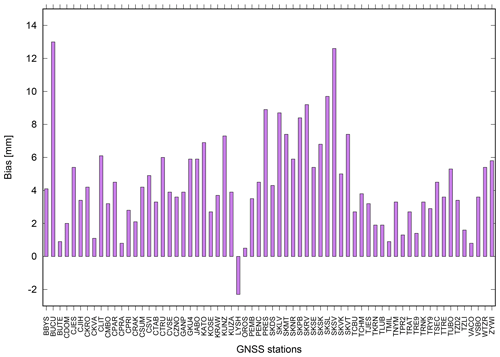
Figure 7 The ZTD bias in millimetres for GOP1 (purple) network calculated for the period of 15–31 May 2017.

After the preselection procedure, the bias and the standard deviation of background departures are added to the whitelist for each station independently. The standard deviation of OMF is assigned as the observation error of trusted GNSS stations, ranging between 6 and 14 mm. The static bias information of the whitelist can be applied before active assimilation by removing the bias during the observation pre-processing. The impact of GNSS ZTDs with the use of static bias correction (called ESGPS2 hereafter) is investigated in observing system experiments presented in Sect. 5.

4.4 Variational bias correction

Besides the choice of static bias correction, the AROME's variational assimilation system offers the possibility of variational bias correction (VARBC) as well. In this scheme, the bias parameters are a part of the minimisation via the extension of control vectors and the cost function (Auligné et al., 2007; Sánchez-Arriola et al., 2016). The GNSS ZTD is considered as a type of surface observation in the data assimilation, therefore, VARBC controls the bias separately for each station using a bias offset predictor, similarly to static correction. This predictor in the current implementation of the linear regression scheme is assumed to remove most of the bias. Moreover, the introduction of additional predictors shown by Lindskog et al. (2017) has a limited impact on the forecasting system. The simplified background bias parameter error covariance matrix contains only diagonal elements $\left({\mathit{\sigma }}_{{\mathit{\beta }}_{\mathrm{b}}}^{\mathrm{2}}\right)$, which are characterised by the proportion of observation error variance (${\mathit{\sigma }}_{\mathrm{o}}^{\mathrm{2}}$) and the so-called stiffness parameter (N_bg) (Dee, 2004) (Eq. 4).

$$\begin{array}{}\text{(4)}& {\mathit{\sigma }}_{{\mathit{\beta }}_{\mathrm{b}}^{\mathrm{2}}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{o}}^{\mathrm{2}}}{{\mathit{N}}_{\mathrm{bg}}}},\end{array}$$

In contrast to the static scheme, the VARBC adjusts bias information at every analysis, making bias correction updates in an adaptive manner. The magnitude of the adaptivity is decided by the stiffness parameter, which is set to 60 by default and takes into consideration that AROME/Hungary has eight analyses in a day, with the bias halving time corresponding to about 5 days (Cameron and Bell, 2016). For the active assimilation trial, instead of cold-start initialisation of the bias, VARBC coefficients were spun up on the preselection training period and stored to prepare a warm-start initialisation. As the observation bias does not significantly vary during a day (not shown), the 3-hourly cycled VARBC strategy was chosen, which supports faster adaptivity compared to a daily cycled bias correction. The use of GNSS ZTDs and variational bias correction are called EVGPS2 hereafter.

5 Active assimilation and the observing system experiment

An observing system experiment (OSE) has been carried out for a summer period, estimating the impact of GNSS ZTDs and the performance of static and variational bias corrections. The first AROME/Hungary configuration using the operational set-up (without ZTD observations) is considered as a reference (EEGPS2 in verification). The one (ESGPS2) with ZTD observations on the top of the operational observation set and a static bias correction is compared to the reference. Furthermore, the second experiment is similar to ESGPS2 but employs a variational bias correction (EVGPS2), which is analysed together with ESGPS2. The experiment and the basic set-up are summarised in Table 1.

Table 1 Summary of the observing system experiment with the data assimilation system of AROME/Hungary and the use of GNSS ZTDs. Dates are in dd/mm/yy format.

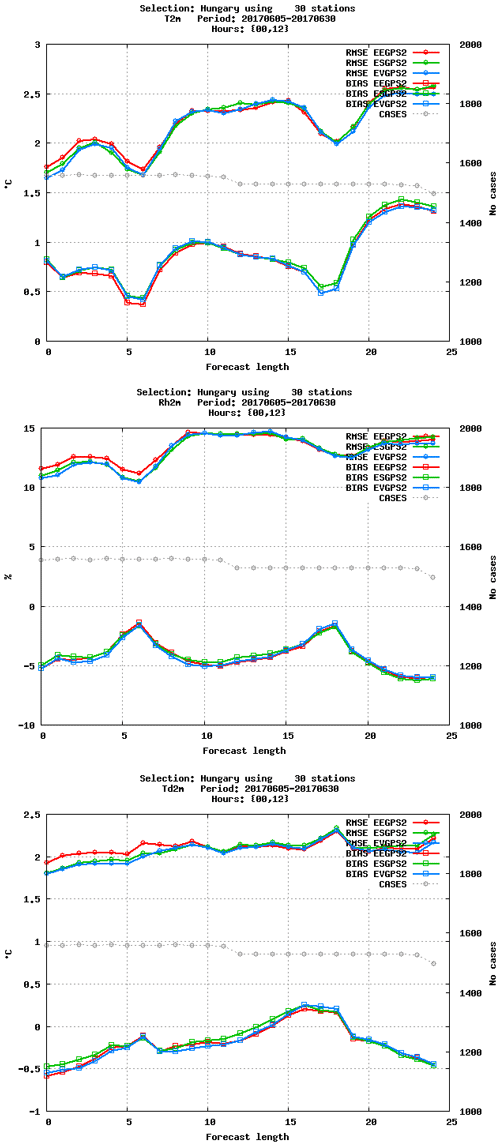
Figure 8 The RMSE and bias of screen-level temperature (^∘C), relative humidity (%), and dew-point temperature (^∘C) as a function of forecast range. Scores are plotted for EEGPS2 (red), ESGPS2 (green) and EVGPS2 (blue). Verification period between 5 and 30 June 2017. Data selection: Hungary, 30 stations.

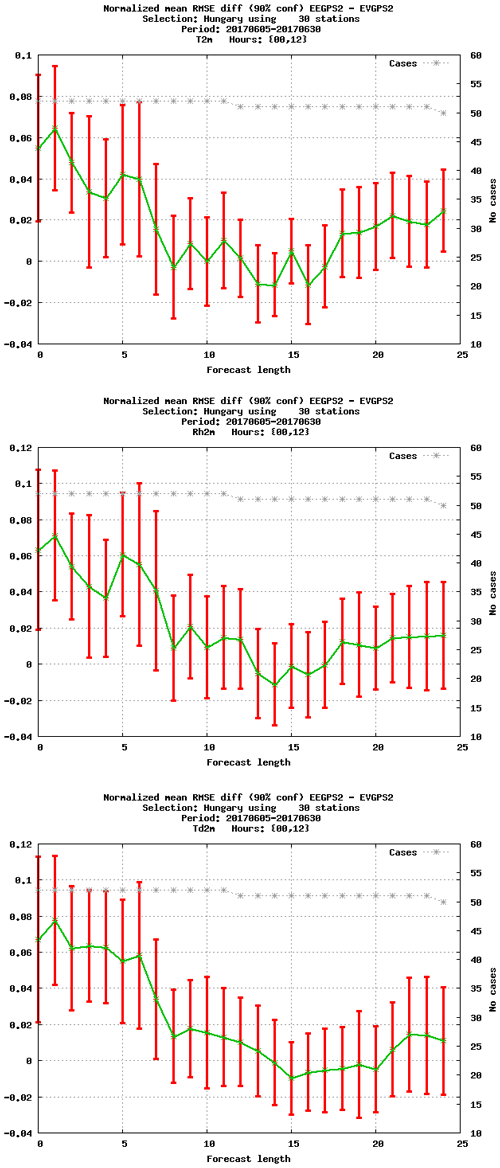
Figure 9 The normalised RMSE difference of screen-level temperature (^∘C), relative humidity (%), and dew-point temperature (^∘C) as a function of forecast range. Scores are comparing EEGPS2 and EVGPS2 experiment. Verification period between 5 and 30 June 2017. Data selection: Hungary, 30 stations.

Verification of AROME/Hungary forecasts

The examined summer period is basically the continuation of the training period excluding 5 days from the verification and covering 25 days until the end of June 2017. This means that statistical verification was computed for 00:00 and 12:00 UTC AROME +24 h forecasts between 5 and 30 June 2017. The verification was performed against quality-controlled conventional observations for the measurement of all scores. For the same reason that GNSS ZTDs are used as surface observations in the variational assimilation method, the added value of ZTD observations is expected to reflect more on near-surface verification scores. More importantly, temperature and humidity parameters are the most influenced because the model equivalent of wet delay is closely related to the temperature and humidity fields of the model via the observation operator. Figure 8 shows RMSE and bias scores for screen-level temperature, relative humidity, and dew-point temperature forecasts, while in Fig. 9, the related normalised RMSE differences of EEGPS2 and EVGPS2 can be seen. For these surface parameters the error reduction with respect to the reference during the first 6 h in the AROME forecast is apparent by the use of ZTD observations, with both static and variational bias corrections. Nevertheless, the temperature bias is slightly overestimated, but dew-point temperature and relative humidity bias remain more or less the same for short forecast ranges. The AROME/Hungary forecasts usually have warm and dry biases at night-time. However, the assimilation of GNSS ZTD cannot mitigate this issue. The most important result is that the error reduction is statistically significant for the short and very short ranges (see Fig. 9), when variational bias correction is used. Furthermore, similar results are obtained with the static bias correction, but they are not statistically significant (not shown).

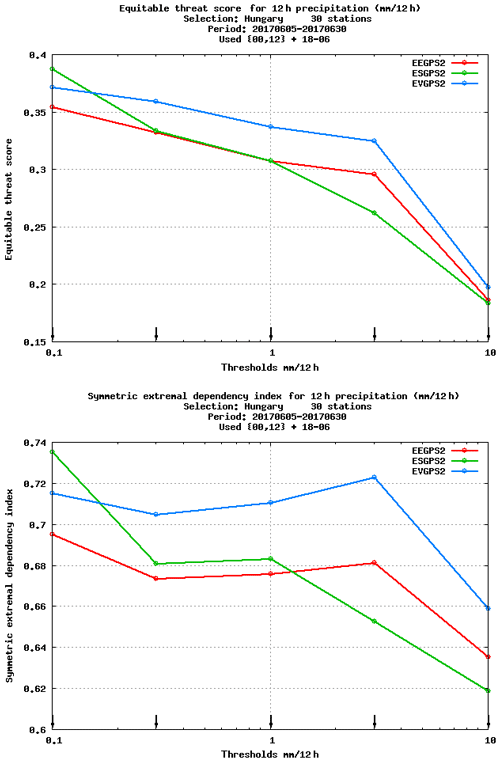
Figure 10 The ETS and SEDI scores of +12 h precipitation (12 h accumulation) as a function of precipitation thresholds. Scores are visualised for experiments EEGPS2 (red), ESGPS2 (green) and EVGPS2 (blue). Verification period between 5 and 30 June 2017. Data selection: Hungary, 30 stations.

The AROME's precipitation forecasts are verified in Fig. 10, in terms of equitable threat score (ETS) and a symmetric external dependency index (SEDI) (Ferro and Stephenson, 2011) for a +12 h forecast range. Overall, for the small (less or equal than 1 mm) precipitation thresholds, both ESGPS2 and EVGPS2 can improve the precipitation forecasts, but for 3 or 10 mm thresholds only the experiment with ZTD and VARBC (EVGPS2) has a positive impact compared to the reference. Due to the limited number of high precipitation cases, the verification of larger precipitation thresholds (above 10 mm) is not taken into account. These results suggest that the update of bias information during the (active) assimilation cycles is important for better precipitation forecasts. Other surface variables and also upper-air scores show a mostly neutral impact, i.e. slightly better or worse scores at various levels without statistically significant differences (not shown). It is also important to note that significant differences can only be seen in surface verification scores against 30 Hungarian SYNOP stations (see the header of verification figures). Taking into account all available SYNOP stations inside the NWP domain would indicate a smaller impact given the relatively small amount of assimilated ZTD observations. Furthermore, another reason might be that AROME/Hungary's background errors are derived from AROME EDA statistics (ensemble data assimilation), which provide more localised increments and sharp background error correlations.

6 Conclusions

The use of GNSS ZTDs from three central European E-GVAP networks in AROME/Hungary was presented and discussed in detail. The potential and the importance of this observation type was shown through DFS diagnostics. This is particularly relevant in data assimilation system with a high frequency analysis cycle. It was also discussed that GNSS products including ZTD can bring extra humidity-related observations for the initial conditions of NWP models and have the potential to improve precipitation forecasts. A preselection of reliable GNSS ground-based stations has been done carefully, this was described in Sect. 4. The studied E-GVAP networks cover sufficiently a wide area of Hungary, although there is still room for further extension and the system is still lacking such observations from the southern and eastern parts of the NWP domain. Furthermore, the optimal thinning distance was determined to maximise the number of ZTDs from neighbouring networks and to avoid observation error correlations. It was also shown that the detected bias varies by station; therefore, a specific correction for each station makes sense during the assimilation of GNSS ZTDs. In addition, using only the bias-offset predictor in the VARBC scheme satisfies its functionality for removing the bias of GNSS ZTD observations in the variational analysis. During the active assimilation experiment, it was demonstrated that GNSS data have a positive impact on short-range screen-level temperature and humidity forecasts. This positive impact on forecast scores during the summer period was held for 6 h, which is considerable given the small number of GNSS observations. Additionally, the precipitation forecasts clearly became better in AROME forecasts when using the variational bias correction, whereas with the static bias correction the impact of ZTDs was rather mixed. It can be concluded that the use of GNSS ZTD, together with VARBC, has a positive impact on AROME/Hungary forecasts, which correspond to other impact studies. In this paper the use of central European E-GVAP networks and their ZTD estimations were highlighted in an operational AROME mesoscale data assimilation system. It became evident that a small amount of GNSS ZTD observations can still provide valuable atmospheric information for a well-characterised and -parameterised NWP system and its data assimilation. For future perspectives and to understand the importance of bias correction, an improved stiffness parameter might be investigated in order to allow more flexibility into the system. Moreover, a better description and use of observation errors should be studied as well.