Investigation of observational error sources in multi-Doppler-radar three-dimensional variational vertical air motion retrievals

Multi-Doppler-radar network observations have been used in different configurations over the last several decades to conduct three-dimensional wind retrievals in mesoscale convective systems. Here, the impacts of the selected radar volume coverage pattern (VCP), the sampling time for the VCP, the number of radars used, and the added value of advection correction on the retrieval of the vertical air motion in the upper part of convective clouds are examined using the Weather Research and Forecasting (WRF) model simulation, the Cloud Resolving Model Radar SIMulator (CR-SIM), and a three-dimensional variational multi-Doppler-radar retrieval technique. Comparisons between the model truth (i.e., WRF kinematic fields) and updraft properties (updraft fraction, updraft magnitude, and mass flux) retrieved from the CR-SIM-generated multi-Doppler-radar field are used to investigate these impacts. The findings are that (1) the VCP elevation strategy and sampling time have a significant effect on the retrieved updraft properties above 6 km in altitude; (2) 2 min or shorter VCPs have small impacts on the retrievals, and the errors are comparable to retrievals using a snapshot cloud field; (3) increasing the density of elevation angles in the VCP appears to be more effective to reduce the uncertainty than an addition of data from one more radar, if the VCP is performed in 2 min; and (4) the use of dense elevation angles combined with an advection correction applied to the 2 min VCPs can effectively improve the updraft retrievals, but for longer VCP sampling periods (5 min) the value of advection correction is challenging. This study highlights several limiting factors in the retrieval of upper-level vertical velocity from multi-Doppler-radar networks and suggests that the use of rapid-scan radars can substantially improve the quality of wind retrievals if conducted in a limited spatial domain.

1 Introduction

Measurements of vertical air motion in deep convective clouds are critical for our understanding of the dynamics and microphysics of convective clouds (e.g., Jorgensen and LeMone, 1989). Convective mass flux is responsible for the transport of energy, mass, and aerosols in the troposphere, which significantly impact large-scale atmospheric circulation and local environment and affect the probability of subsequent formation of clouds (e.g., Hartmann et al., 1984; Su et al., 2014; Sherwood et al., 2014). Consequently, the vertical air motion estimates are widely employed to improve convective parameterizations in global models (e.g., Donner et al., 2001) and also to evaluate the cloud resolving model (CRM) simulations and large eddy simulations (LESs; e.g., Varble et al., 2014; Fan et al., 2017).

Aircraft penetration of convective clouds offers the most direct method to measure the vertical air motions (e.g., Lenschow, 1976); however, practical hazards and operational costs have resulted in a valuable but limited dataset (e.g., Byers and Braham, 1948; LeMone and Zipser, 1980). Current aviation regulation does not permit such penetration anymore. Ground-based and airborne profiling Doppler radars provide a high degree of detail of convective clouds in both time and height and can sample even the most intense convective cores (e.g., Wakasugi et al., 1986; Heymsfield et al., 2010; Williams, 2012; Giangrande et al., 2013; Kumar et al., 2015). One drawback of profiling radar techniques is their limited sampling of individual storms and the lack of information on the temporal evolution of the convective dynamics and structure; the observational limitations thus make the use of the techniques in model evaluation challenging.

Since the pioneering work of Lhermitte and Miller (1970), networks of two or more scanning Doppler radars and the use of multi-Doppler-radar wind retrieval techniques have been widely used to overcome the aforementioned limitations (Junyent et al., 2010; North et al., 2017). In addition to research radars, operational Doppler radar networks can, in certain conditions, accomplish a large coverage of multi-Doppler-radar retrievals (e.g., Bousquet et al., 2007; Dolan and Rutledge, 2007; Park and Lee, 2009). While various Doppler radar wind retrieval techniques have been proposed (Chong and Testud, 1996; Chong and Campos, 1996; Bousquet and Chong, 1998; Gao et al., 1999; Protat and Zawadzki, 1999; Bell et al., 2012), three-dimensional variational (3D-Var) techniques are commonly used because of their robust and reliable solutions by minimizing errors (e.g., Potvin et al., 2012b).

Multi-Doppler-radar analysis has been used to better understand mesoscale dynamics, low-level divergence, and microphysical–dynamical interactions (e.g., Kingsmill and Houze Jr., 1999; Friedrich and Hagen, 2004; Stonitsch and Markowski, 2007; Collis et al., 2013; Oue et al., 2014, and many others). There is also considerable literature discussing different sources of uncertainties in dual- or multi-Doppler-radar wind retrieval. The interpolation and smoothing techniques used (Cressman, 1959; Barnes, 1964; Given and Ray, 1994; Miller and Fredrick, 1998) can have an impact on the quality of Doppler radar wind retrieval (e.g., Collis et al., 2010). Another source of uncertainties is related to the hydrometeor fall speed estimates (e.g., Steiner, 1991; Caya, 2001), especially at shorter wavelengths (e.g., X and C bands) where the signal attenuation can bias the estimates. Clark et al. (1980) estimated errors attributed to cloud evolution in horizontal and vertical wind estimates from multiple Doppler radar measurements. Bousquet et al. (2008) estimated uncertainties in wind fields from their operational multi-Doppler-radar retrieval by simulating radar measurements using numerical model output. They pointed out that missing low-level measurements and poor vertical sampling could produce significant uncertainties in retrieval of low-level wind fields. These investigations have been conducted by formulating suitable Observing System Simulation Experiments (OSSEs). Potvin et al. (2012b) investigated potential sources of errors in multi-Doppler-radar wind retrievals for supercell observations using OSSEs. They suggested that the magnitudes of vorticity and its tendency fields were sensitive to the smoothness constraint in the analysis, and assumptions of spatially constant storm motion and no storm evolution led to significant errors in middle and upper levels.

A common result from the studies above is that the uncertainties increase with height because scanning radar data density inevitably becomes lower at higher altitudes. Meanwhile, deep convective clouds generally show maximum updrafts at middle and upper parts of the clouds (e.g., Giangrande et al., 2013). Here we are concerned with the retrieval uncertainties of vertical air motion especially in the middle and upper levels of deep convective clouds. The motivation for this study is twofold. First, the US Department of Energy (DOE) Atmospheric Radiation Measurement (ARM) program operates an atmospheric observatory at Southern Great Plains (SGP), Oklahoma (Mather and Voyles, 2013), where scanning Doppler radars and profiling instruments provide unique dynamical and microphysical measurements. During the Midlatitude Continental Convective Clouds Experiment (MC3E; Jensen et al., 2016), the ARM precipitation scanning Doppler radars obtained a dense network of Doppler radar measurements of deep convective clouds explicitly designed to retrieve three-dimensional (3-D) wind (North et al., 2017). However, our experience with the data and a series of experiments performed in this study suggest that despite the plethora of radar systems at the ARM SGP observatory, the 3-D wind retrievals are subject to large errors, especially at the upper levels. It is possible that some of the errors are associated with a radar volume coverage pattern strategy that does not satisfy the requirement for high spatiotemporal observations. This issue has been highlighted in recent studies with high-resolution CRM simulations of convective cloud properties (e.g., Morrison et al., 2015; Hernández-Deckers and Sherwood, 2016). Secondly, the paucity of available datasets of vertical air motion limits our ability to quantitatively analyze structures and characteristics of the mesoscale convective systems (MCSs) and evaluate model outputs of the MCSs (e.g., Varble et al., 2014; Liu et al., 2015; Donner et al., 2016; Fan et al., 2017). Thus, we are interested in determining the sampling capabilities required for a multi-Doppler-radar network to address these errors and investigating if radar networks based on different technology (e.g., phased-array radars; Otsuka et al., 2016; Kollias et al., 2018b) can address these errors. To do so, we focus on impacts of the multi-Doppler-radar network setup and not how we quality-control, interpolate, or use the Doppler radar observations in a minimization routine. The latter is the same in all the experiments performed here and is described in North et al. (2017). We investigate the impacts of the selected radar volume coverage pattern (VCP), the sampling time for the VCP, the number of radars used, and the added value of advection correction upon the uncertainties of multi-Doppler-radar wind retrieval.

2 Data and methodology

In this study, the OSSE is conducted for an MCS case on 20 May 2011 observed in Oklahoma during MC3E. This squall-line MCS was oriented in the northeast–southwest direction extending for approximately 1000 km (Fan et al., 2017). The convective region was approximately 50 km wide and trailed a distinct stratiform precipitation area when it passed through the ARM SGP observatory from 09:20 to 11:40 UTC. This case has been analyzed for its dynamical and microphysical structures by several previous studies (e.g., Liu et al., 2015; Wu and McFarquhar, 2016; Fan et al., 2017).

OSSE studies are generally used to assess impacts of operational observing systems on, for example, observation-based value-added products and weather forecasts (Timmermans et al., 2009). The OSSE conducted in this study consists in the following.

1. We produce the set of simulation data with a high-resolution numerical weather model of a convective cloud system and generate the model hydrometeor and dynamical fields at a high temporal resolution to capture the storm evolution at scales unresolved by typical VCPs.

2. We use a sophisticated radar simulator to reproduce the VCP of a multi-Doppler-radar system and produce radar observables at radar coordinates with the realistic radar characteristics (beamwidth, range resolution, and sensitivity).

3. We grid the simulated radar observations to a Cartesian coordinate and conduct a variational 3-D multi-Doppler-radar wind retrieval algorithm to estimate the dynamical field.

4. We evaluate the retrieved wind field against the corresponding field from the numerical model direct output.

The Weather Research Forecasting (WRF) model is used to produce simulation of the MCS case on 20 May 2011 (step 1). The WRF output is used as an input to the Cloud Resolving Model Radar SIMulator (CR-SIM; Tatarevic et al., 2018) to simulate equivalent radar reflectivity factor (Z) and Doppler velocity (V_r) from scanning radars (step 2). The simulated Z and V_r fields are then resampled and converted into radar polar coordinates according to VCPs (step 2). The Z and V_r fields at radar polar coordinates are converted into the Cartesian grid, and then they are used to estimate 3-D wind field using the 3D-Var multi-Doppler-radar wind retrieval algorithm developed by North et al. (2017) (step 3). The obtained vertical velocity fields are compared against the WRF-simulated dynamical field to investigate impacts of the limitations attributed to the radar observations and the retrieval technique on the retrieved vertical wind field (step 4).

2.1 WRF simulation for 20 May 2011 MCS

The WRF simulation horizontal domain is 960 km×720 km with 0.5 km horizontal grid spacing. The vertical resolution varies from approximately 30 m near the surface to 260 m at 2 km in altitude and maintains this resolution approximately constant above 2 km altitude. To include time evolution in the volume scan coverage pattern, the WRF simulation provides output every 20 s. The Morrison double-moment microphysics scheme was used, which predicts mass and number mixing ratios for liquid cloud, rain, ice cloud, snow, and a medium-density lump graupel representing the rimed ice with a switch to modify the settings for graupel to a high-density hail (Morrison et al., 2005). Tao et al. (2016) pointed out that simulations including the hail option better represented the observed MCSs during the MC3E period than those not using hail. In their study for the 20 May MC3E case, Fridlind et al. (2017) used the Morrison double-moment microphysics scheme with the hail option. The present study also applies the hail category to the simulation instead of graupel. The simulated MCS comprised a convective precipitation region at the leading edge of the system and a stratiform precipitation trailed by the convective region, similar to the observation. The MCS passed through the ARM SGP observatory approximately 1 h later than the observation (at around 12:18 UTC), and a stronger convective precipitation region formed slightly (∼20 km) to the north of the ARM SGP observatory. In this study, we treat the WRF-simulated vertical velocity field as “truth” to evaluate the performance of multi-Doppler-radar wind retrieval.

2.2 CR-SIM simulation of the 20 May 2011 MCS case

The CR-SIM is a sophisticated radar forward operator developed to bridge the gap between high-resolution cloud model output and radar observations (Tatarevic et al., 2018). The CR-SIM can be applied to the 3-D model output produced by a variety of CRMs and LESs, such as WRF, Regional Atmospheric Modelling System (RAMS), System for Atmospheric Modeling (SAM), and the Icosahedral Nonhydrostatic (ICON) model. It emulates the interaction between transmitted polarized radar waves and rotationally symmetric hydrometeors and can simulate the power (equivalent radar reflectivity factor), phase (Doppler velocity), and polarimetric (specific differential phase, differential reflectivity, depolarization) variables with a fixed elevation angle or varying elevation angles with respect to a specified radar location.

Several experiments are performed to evaluate the limitations of the sensing techniques employed in the network of three X-band scanning ARM precipitation radars (X-SAPRs, located at the I4, I5, and I6 sites) at the SGP observatory (Fig. 1), which provided high-resolution radar observations of convective systems during MC3E (e.g., North et al., 2017). The ARM SGP network is selected because it is comprised of three identical radar systems that are employed together and can be operated in a coordinated manner. Furthermore, since it is a long-term facility for the study of deep convective clouds, it is important to assess the capability and uncertainties. Using CR-SIM, we simulated measurements of the three X-SAPRs. In order to investigate the impact of an increased number of radars, observations from the C-band Scanning ARM Precipitation Radar (C-SAPR) at the SGP observatory (Fig. 1) are also simulated. Characteristics and settings of the simulated radar measurements are shown in Table 1. To investigate the impact of increasing the number of elevation angles and the maximum elevation angle, a VCP including additional elevation scans for the X-SAPR measurements is introduced. These simulations with X-SAPR aim to examine effects of using faster scanning radars, such as the Doppler on Wheels (DOW; Wurman, 2001), the Atmospheric Imaging Radar (AIR; Isom et al., 2013), the Rapid scanning X-band polarimetric (RaXPol; Pazmany et al., 2013), and low-power X-band phased array radars (LPAR; Kollias et al., 2018b). Locations of radars used in this study and the simulated retrieval domain are shown in Fig. 1. Details about the elevation angle settings are described in Sect. 2.4.

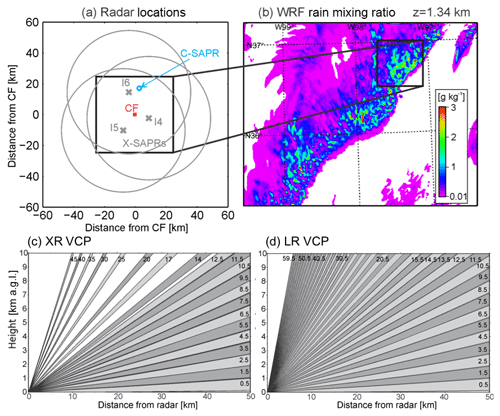
Figure 1 (a) Locations of the simulated X-band scanning ARM precipitation radars (X-SAPRs) and the Department of Energy Atmospheric Radiation Measurements (ARM) Central Facility. Large gray circles represent the maximum range of each X-SAPR. (b) Rainwater mixing ratios at 1.3 km in altitude from the WRF simulation of a mesoscale convective system at 12:18:00 UTC on 20 May 2011. Black boxes represent the domain used for wind retrievals. (c, d) Elevation coverage for X-SAPR general VCP (XR) and high-density elevation VCP (LR).

Table 1 Simulated radar configurations and measurement strategy.

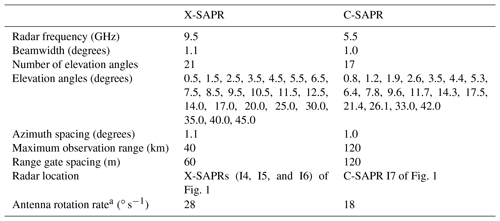
^a Antenna rotation rates used during MC3E are presented and not used in this study.

The retrieval simulation domain size is $\mathrm{50}\mathrm{km}\times \mathrm{50}\mathrm{km}\times \mathrm{10}\mathrm{km}$ above the ground level (a.g.l.) centered around the ARM SGP Central Facility (CF). In the simulations, CF and the domain were virtually located within a vigorous convective region of the MCS to capture the intense vertical velocity (Fig. 1b). We assume that the lowest boundary of the simulation domain is idealized as flat at the ground level of 0.3 km above sea level.

For each radar, the CR-SIM forward-simulated Z and V_r are provided at the WRF grid coordinate by CR-SIM. They are then converted into radar polar coordinates considering all the radar characteristics that control the spatial resolution of radar observations (range weighting function, antenna beamwidth, and VCP strategy). The settings shown in Table 1 are consistent with the settings used during the MC3E period. For each radar the minimum detectable signal (Z_min) curve, which is attributed to the number of samples integrated for each radar sampling volume, is estimated using an equation $Z_{\min }\left(r\right)=C+\mathrm{20}{\log }_{\mathrm{10}}\left(r\right)$. In this equation, Z_min is expressed in logarithmic units (dBZ) with the range r (distance from the radar) in kilometers, and the constant C that depends on the radar system characteristics expressed in decibels relative to Z; $C=-\mathrm{40}$ for X-band radars and $C=-\mathrm{35}$ for C-band radar are used in this study. These values are similar to those for X-SAPRs and C-SAPR at the SGP observatory.

2.3 Wind retrieval

The 3D-Var wind retrieval technique described in North et al. (2017) is used to estimate the 3-D wind field. The wind retrieval algorithm inputs the Cartesian coordinate Z and V_r fields from each radar and uses a 3D-Var technique proposed by Potvin et al. (2012a). In the technique, the optimal wind field solution is obtained at the minimum of a cost function, which consists of the physical constraints of radar radial velocity observations, anelastic mass continuity, surface impermeability, background wind field, and spatial smoothness. The surface impermeability constraint was used to dictate that vertical velocity vanishes at the ground with a relatively large weight. Details of the constraints are described in North et al. (2017).

The simulated Z and V_r with the radar polar coordinates are converted to the Cartesian coordinates for each radar measurement at horizontal and vertical spacings of 0.25 km using a single-pass isotropic Barnes distance-dependent weight (Barnes, 1964), with a constant smoothing parameter κ.

$$\begin{array}{}\text{(1)}& w_{i,q}\left(d\right)=\exp \left({\displaystyle \frac{-d^{\mathrm{2}}}{\mathit{\kappa }}}\right)\forall i=\mathrm{1},\mathrm{\dots },n\text{ and }q=\mathrm{1},\mathrm{\dots },Q\end{array}$$

Here w_i,q is the weight for grid box i and radar gate q separated by distance d. The equation was applied in both horizontal and vertical interpolations. At each grid box, radar moments are estimated using the nearest 200 radar data gates with weights (Eq. 1) using κ=0.13 km² for interpolation. The cutoff distance is determined as the distance where the weight is less than 0.01 (d≈0.8 km). These parameters are chosen so that the statistical error in retrieved vertical velocity is minimal for the present case. Generally, data density at constant altitudes decreases with height and when increasing a distance from radar. Figure 2c–f show distance to the nearest radar data point at each Cartesian grid box at constant altitudes. These settings for gridding are fixed for all radar simulations, and this study does not consider uncertainties attributed to the settings for the gridding process. The gridding technique has been well optimized in North et al. (2017), and the uncertainties in the gridding method and data smoothing processes have been well investigated in previous studies (e.g., Majcen et al., 2008; Potvin et al., 2012a).

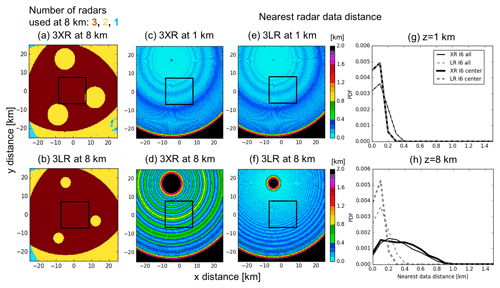
Figure 2 (a, b) The number of radars used for retrievals at each grid box at 8 km above ground level (a.g.l.) for 3XR VCP (a) and 3LR VCP (b), (c–f) distance of the nearest radar data point at each grid box at 1 km (c, e) and 8 km (d, f) a.g.l. for the radar location of I6 with XR VCP (c, d) and LR VCP (e, f), and (g, h) histograms of the distance of the nearest radar data point at 1 km (g) and 8 km (h) a.g.l. normalized by the total number of data samples and the nearest distance bin size (0.1 km). In (g) and (h), black solid lines represent the radar location of I6 with XR VCP, gray dashed lines represent the radar location of I6 with LR VCP, thin lines represent the entire horizontal domain, and thick lines represent the box area shown in (a)–(f).

There are several important sources of errors when considering the retrieval of vertical motion in convective systems other than the radar VCP; the most important among them are unfolding of observed Doppler velocity, estimation of hydrometeor fall velocities, attenuation correction, and assumption of background environments. In all experiments in this study, Doppler velocity folding is disabled as an option; thus, the simulated radial Doppler velocities are correct and do not need to be unfolded. This eliminates the possibility of errors being introduced by incorrect Doppler velocity unfolding.

The difference between the true hydrometeor fall velocity V_f and the assumption based on an empirical formula that relates V_f with the radar reflectivity (e.g., Caya, 2001) can be a possible source of errors in wind retrievals (e.g., Potvin et al., 2012b; North et al., 2017). In the WRF simulations used here, V_f is parameterized depending on the microphysics scheme as a function of particle diameter. The hydrometeor's fall speeds (V_f) are given as a function of the hydrometeor diameter (D) and altitude (h) in the form

$$\begin{array}{}\text{(2)}& V_{\mathrm{f}}\left(h,D\right)=f_{\mathrm{c}}\left(h\right)\cdot a_{\mathrm{v}}\cdot D^{b_{\mathrm{v}}},\end{array}$$

where a_v and b_v are coefficients, and $f_{\mathrm{c}}\left(h\right)={\left({\mathit{\rho }}_{\mathrm{surf}}/\mathit{\rho }\left(h\right)\right)}^k$ is the correction factor for air density (ρ(h): air density at height h; ρ_surf: surface air density) with exponent k (Morrison et al., 2005; Tatarevic et al., 2018). In the CR-SIM, reflectivity-weighted mean velocity is computed at each grid box in the following manner. The hydrometeor fall speeds as a function of the hydrometeor diameter are averaged over the diameter range with weights that are proportional to the CR-SIM estimated reflectivity for each hydrometeor particle size, and then the mean hydrometeor fall speeds are again averaged over all hydrometeor types present in each grid box with weights of reflectivity. In all experiments carried out in this study, the simulated reflectivity-weighted mean V_f are used in the retrieval; thus, no error attributed to the fall velocity estimates is introduced in the wind retrieval technique.

Another source of errors is the impact of signal attenuation by the hydrometeors along the propagation path, especially in C-band and X-band radar measurements. Since the attenuation is unknown, any attenuation-corrected radar reflectivity acts as a possible error source in the wind retrievals, particularly for hydrometeor fall speed estimates. However, as previously specified, the hydrometeor particle size distributions and V_f used in this study are the ones prescribed by the WRF model microphysics; thus, no error is introduced.

Finally, the background horizontal wind vector, temperature, and air density are obtained by averaging WRF output values over the retrieval domain at each altitude and are used in place of sounding measurements over the SGP CF site. Although this study does not consider uncertainties in the background assumption, the change in the background data would have a small impact on the retrieved updraft velocities as discussed in North et al. (2017).

2.4 Settings for wind retrieval experiments

Three factors influencing the updraft velocity estimates are investigated. The first is radar volume coverage pattern (VCP), which determines the set of elevation angles used by the radars to sample the volume of the analysis domain. The second is time interval needed by the radars of the network to complete the specified VCP to emulate both the advection and temporal evolution of the convective cloud system. Third, the added value of the advection correction for the different sets of VCP settings is evaluated. The experiments and their names are listed in Table 2.

Table 2 Overview and short description of the different sensitivity simulations.

2.4.1 Control wind retrieval simulation (3FullGrid)

The control wind retrieval simulation is an ideal instantaneous VCP where all radars of the network sample all the WRF grid points. As a result, three measurements of equivalent radar reflectivity factor and radial Doppler velocity from the three X-SAPRs are available at each grid box of the WRF grid (named 3FullGrid). This experiment does not undergo the conversion process from the WRF grid to radar coordinate or the gridding process from radar coordinate to the Cartesian coordinates. Therefore, this does not include uncertainties from VCP, radar characteristics (beamwidth and range-bin spacing), or gridding process. Thus, the retrieved wind field should be a very good estimate of the true wind field and only the potential uncertainty in the wind retrieval algorithm can affect its quality. In this OSSE, the 3FullGrid is used for an upper bound of the performance of any of the conducted experiments and also serves as a sanity check for the wind retrieval algorithm.

2.4.2 Radar VCP

In a typical radar VCP, the number of elevation angles depends on the antenna scan rate and the desired time period for completing the VCP (typically 5–6 min). The antenna scan rate depends on the pedestal technical specifications and the minimum number of radar samples needed to estimate the radar observables with low uncertainty. The elevation angles are generally tightly selected at low elevations to provide good coverage over long horizontal distances and relatively sparse at higher elevations such as the X-SAPR's VCP shown in Table 1 and Fig. 1c.

In the experiments performed here, the impact of an increased number of elevation angles especially at high elevations is investigated while the antenna beamwidth, range-gate spacing, and maximum unambiguous range are kept unchanged and similar to the radar settings during MC3E. The following VCPs are used: (i) three X-SAPRs with the general VCP, which is the same as during MC3E (named 3XR, Fig. 1c); (ii) three X-SAPRs with denser elevation angles (named 3LR, Fig. 1d; the name “LR” stands for low-power X-band phased array radar, LPAR; Kollias et al., 2018b); and (iii) same as (i) but the C-SAPR measurements are added (named 4SR). Details of the VCPs are shown in Table 1. The settings (i) and (iii) use general VCPs for X-SAPR and C-SAPR, which are the same as those during MC3E. The X-SAPR VCP is composed of 21 elevation angles ranging from 0.5 to 45^∘, and the C-SAPR VCP is 17 elevation angles ranging from 0.75 to 42^∘. Elevation angles for the setting (ii) are equally distributed from 0.5 to 59.5^∘ with a 1^∘ increment; in total there are 60 elevation angles. This elevation setting intends to simulate rapid scanning radar observations.

The selection of the VCP (XR or LR) affects the density (spacing) and availability of observations at each height for gridding. Figure 2a and b show the coverage from the three radars for the retrieval domain for 3XR and 3LR VCPs, respectively. The cone of silence (absence of radar observations) from each radar is represented as a yellow circle, in the middle of which the X-SAPR is located. Within the cone of silence of each radar, we only have two available radar measurements for the wind retrieval. In addition to the availability of radar observations, the spacing of the radar observations affects the quality of the gridding. Regions including few radar data points, particularly higher-elevation angle regions for the XR VCP, may need to interpolate radar data at longer distances from the grid points. Figure 2c–f show the distance of the nearest radar data point at each grid box at heights of 1 and 8 km for X-SAPR I6, and Fig. 2g and h show normalized histograms of the nearest distance. At lower altitudes, the nearest distances in the entire retrieval domain (thin lines in Fig. 2h) are mostly less than 0.3 km for both VCPs. At higher altitudes (thin lines Fig. 2h), the distances of the nearest radar data points from the LR VCP are the same as at lower altitudes, indicating that the LR VCP has similar radar data density at higher and lower altitudes. For the XR VCP, in contrast, many of the grid boxes at 8 km a.g.l. needed to use radar data at distances farther than 0.4 km, resulting in stronger smoothing during the gridding process.

2.4.3 Time duration of the radar VCP

Three time periods are considered here for the completion of the radar network VCP: (i) snapshot (named Snap), where it is effectively assumed that the first WRF model output (at time 0 s, Fig. 3a, b, c) is frozen in time and the radars instantaneously collect data according to their VCP without any cloud evolution; (ii) a 2 min (named 2min) radar network VCP to emulate the performance of rapid scanning radar networks; and (iii) a 5 min (named 5min) radar network VCP to emulate the performance of the ARM SGP network during MC3E and the performance of other mechanically scanning radar networks. The 3FullGrid simulation (Sect. 2.4.1) uses a Snap VCP. The Snap VCP eliminates any concerns regarding advection and temporal evolution of the convective cloud and is used as a benchmark of performance.

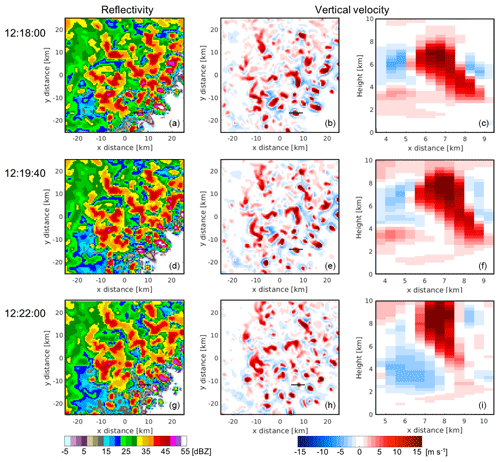
Figure 3 (a, d, g) Horizontal distributions of X-band Z at 7 km a.g.l. from CR-SIM, (b, e, h) horizontal distributions of the WRF-simulated vertical velocity at 7 km a.g.l., and (c, f, i) vertical distributions of WRF-simulated vertical velocity along a line in the horizontal plots. Each row from top to bottom represents a simulation time of 12:18:00, 12:19:40, and 12:22:00 UTC, respectively.

A set of WRF simulations at different times is used to construct the plan position indicator (PPI) scans of the VCP; if a PPI scan takes more than 20 s, the WRF output in the following time step is used for the next PPI scan. An example demonstrating how different WRF model outputs are used in this experiment is shown in Fig. 3. Figure 3 shows horizontal cross sections of the Z and vertical velocity at 7 km and a vertical cross section of the vertical velocity at the area indicated with the solid line in the horizontal cross sections. The snapshot simulations use the WRF model output data at 12:18:00 UTC (Fig. 3a, b, c). The 2 min VCP simulations use the WRF model output data from six consecutive model outputs extracted from 12:18:00 to 12:19:40 UTC every 20 s. Each model output is used to forward simulate three to four PPI scans from the C-SAPR and the X-SAPRs when nominal (MC3E) VCP elevation angles are used (3XR and 4SR) and 10 PPI scans for X-SAPR simulations when the denser elevation angle VCP is simulated (3LR). The corresponding plots for the latest model output (12:19:40 UTC) used to forward simulate the highest elevations of the 2 min VCP are shown in Fig. 3d, e, f. In accordance, the 5 min VCP simulations use the WRF data for 5 min composed of 15 snapshots ranging from 12:18:00 to 12:22:40 UTC every 20 s. Each snapshot data selection was used for one to two PPI scans for C-SAPR and X-SAPR simulations with general VCP elevation angles (3XR and 4SR) and four PPI scans for denser VCP elevation angles (3LR). The corresponding plots for the 13th model output (4 min after the first scan, 12:22:00 UTC) used to forward simulate the 5 min VCP simulations is shown in Fig. 3g, h, i.

2.4.4 Advection correction

The high-temporal-resolution WRF output allows us to evaluate the impact of advection and evolution of the cloud field during the time period needed to complete the radar network VCP. If the cloud field was frozen (no cloud evolution), horizontal advection and wind shear are expected to tilt the cloud and dynamical structures in the vertical direction. Advection schemes have been proposed to address this issue (e.g., Protat and Zawadzki, 1999; Shapiro et al., 2010b; Qiu et al., 2013). The present study used a reflectivity-based spatially variable advection correction scheme described in Shapiro et al. (2010a) that allows trajectory of individual clouds and smooth grid-box-by-grid-box corrections of cloud locations. The advection correction procedure seeks to minimize a cost function that contains the frozen turbulence constraint and terms that confer spatial smoothness on the pattern-translation components and takes into account changes in cloud shape with time by using two different time PPI scans. The advection correction process is similarly implemented in this case.

The advection correction is applied between two similar elevation angle PPIs from consecutive VCPs. Each simulated Z field in PPI is converted and projected onto the two-dimensional (2-D) Cartesian coordinate plane at a spatial resolution of 250 m. A weighting coefficient of the spatial smoothness terms in the cost function depends on the analysis grid spacing and the structure of the field being advected. An appropriate value of the coefficient can be determined by running some sensitivity tests. Based on preliminary tests (not shown), we deemed a coefficient of 300 dBZ² to be acceptable. Using two 2-D Cartesian coordinated PPI data at two different times at the same elevation angle, the advection correction algorithm performs horizontal trajectory analysis of reflectivity and estimates the reflectivity pattern translation components U and V on the 2-D surfaces for each VCP elevation angle. The pattern translation components U and V fields, along with the associated trajectories of virtual particles moving with the reflectivity field, are then used to affect the advection correction of the radial wind field according to a time difference between a PPI scan and the base PPI scan, when creating the 3-D Cartesian coordinated data. Such processed simulated radar measurements in 3-D Cartesian coordinates are then incorporated into the 3D-Var algorithm for the 3-D wind retrieval as described in Sect. 2.3.

However, the cloud and dynamical field evolve while advected. This results in observing different cloud life stages by different PPI scans. Figure 3c, f, i show a vertical cross section of the vertical air motion within a convective cell that is tracked using the WRF model output. The location of the convective cell and vertical distributions of updrafts and downdrafts significantly vary from 12:18:00 to 12:22:00 UTC. Thus, we need to consider that gridded radar observations collected after the completion of the VCP do not represent an actual snapshot of the 3-D convective dynamics. Consequently, the mass continuity constraint will be applied in the column of gridded radar observations that is a mosaic of different stages of the lifetime of a convective element, and this, in turn, will limit the ability for this 3D-Var approach to satisfy the mass continuity equation (e.g., Clark et al., 1980; Gal-Chen, 1982), resulting in large potential uncertainties of the wind retrievals. The experiments presented here are designed to quantify the impact of cloud evolution on the retrieved wind field (Sect. 3.4).

3 Results

The evaluation of velocity retrievals based on multiple Doppler radars using independent observations is challenging to perform (e.g., Collis et al., 2013; North et al., 2017). Profiles of percentiles of updraft magnitudes are often used to evaluate numerical model results against vertical velocity retrievals from scanning Doppler radar networks and/or profiling radars (e.g., Wu et al., 2009; Varble et al., 2014; Fan et al., 2017). Here, we are interested in the estimation of the convective mass flux; thus, profiles of updraft morphology (number and area) and intensity (magnitude) are used to represent the impact of the selected sampling strategy.

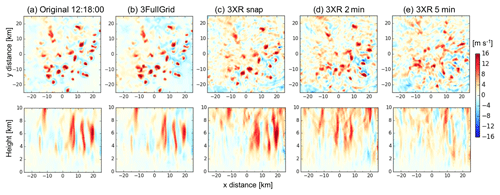
Figure 4 The top row shows horizontal distributions at 7 km a.g.l. and the bottom row shows vertical cross sections at y=0 km of vertical velocity. Each column represents (a) the original WRF vertical velocity field and the retrieved vertical velocity fields from the (b) 3FullGrid, (c) 3XRSnap, (d) 3XR2min, and (e) 3XR5min retrieval simulations.

3.1 Evaluation of multi-Doppler-radar updraft property retrievals

Horizontal cross sections at 7 km a.g.l. and vertical cross sections along y=0 km of the retrieved vertical velocity field from the X-SAPR network, using the original grid (3FullGrid) and using the standard (XR) VCP for three different time periods (Snap, 2min, and 5min), are shown in Fig. 4b, c, d, and e, respectively. The WRF model out at t=0 (12:18:00 UTC) is also shown in Fig. 4a. The selection of the height of 7 km is based on the WRF model output analysis: the chosen height is the one with maximum updraft values. The WRF model output vertical velocity field indicates the presence of several cell-like, horizontally coherent updraft structures with updraft magnitude exceeding 5 m s⁻¹. The 3FullGrid simulation (Fig. 4b) provides results in good agreement with the original WRF vertical velocity field (Fig. 4a), suggesting that the 3D-Var wind retrieval algorithm is performed well.

The snapshot simulation (3XRSnap, Fig. 4c) provides results that are comparable to the original WRF vertical velocity field (Fig. 4a) and 3FullGrid-retrieved vertical velocity field (Fig. 4b) at 7 km a.g.l. but slightly overestimates the updraft velocity above 8 km a.g.l. The 3XRSnap simulation reproduces the location and size of the stronger updraft areas defined with updraft magnitudes above 5 m s⁻¹, which show the cell-like structures, but it tends to have higher uncertainty in the areas around the location of strong convection (vertical velocity <5 m s⁻¹). Updraft fractions for 1–5 m s⁻¹ from the 3XRSnap simulation were overestimated by 0.1–0.17, which accounts for 40 %–88 % of those from the WRF output. The uncertainty is attributed to the selected radar VCP due to gridding of sparse observations, rather than the 3D-Var wind retrieval algorithm. As increasing VCP time periods (2 and 5 min) shown in Fig. 4d and e, respectively, the retrieved velocity features became less sharp, broader, and shifted in space. The retrieved vertical velocity field shows the impact of interpolating the sparse observations (ring structures representing the poor X-SAPR sampling at 7 km), and the vertical velocity features appear elongated and connected.

At any vertical level in the WRF model output and in the retrieved 3-D velocity field, a convective updraft core is defined as an area larger than 0.5 km² and with updraft velocities higher than 5 m s⁻¹. Figure 5a displays the profiles of the number of updraft cores from the 3FullGrid control wind retrieval simulation and from the WRF snapshot data at 12:18:00 UTC, WRF 2 min average (12:18:00–12:19:40), and WRF 5 min average (12:18:00–12:22:40). As expected, the 3FullGrid-retrieved profile of the number of updraft cores captures the profile of the number of updraft cores in the WRF snapshot model output very well. Differences appear small between WRF Snap and 3FullGrid and are attributed to the potential uncertainty in the retrieval algorithm. The 2 and 5 min WRF output averaged profiles suggest that the number of convective updraft cores does not change over a period of 2 to 5 min. Figure 5b–e demonstrate performance of the 3D-Var wind retrieval for several different configurations as described in Table 2. A noticeable departure between the WRF direct model output (number of updraft cores) and the estimated number of updraft cores above 6 km a.g.l. is observed for all the detecting configurations with the exemption of the LR VCP. The use of a fourth radar or the implementation of the advection correction has little to no impact on the findings. The retrieved profiles of the number of coherent updraft structures show little sensitivity to the VCP time. This can be attributed to the fact that the number of updraft coherent structures does not change within the 5 min required to complete all sampling strategies. Another possibility is that any stretching/distortion of the coherent structures due to cloud evolution and advection does not result in changes in the number of coherent structures.

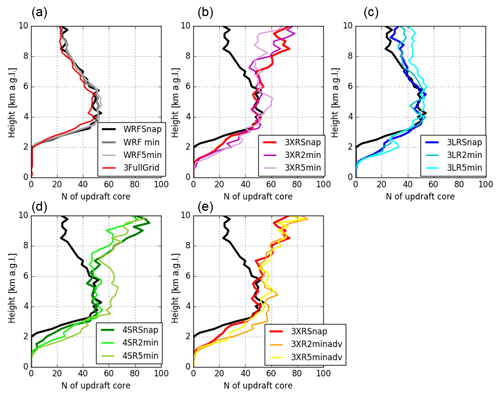
Figure 5 Vertical profiles of the number of coherent updrafts with vertical velocity >5 m s⁻¹. Color represents different retrieval simulations as displayed in each panel. The dark gray line in (a) represents the WRF output averaged over 2 min from 12:18:00 to 12:19:40 UTC, and light gray in (a) represents the WRF output averaged over 5 min from 12:18:00 to 12:22:40 UTC. Each panel displays a profile from the WRF snapshot at 12:18:00 UTC by a black solid line.

In a similar manner, the retrieved updraft fraction (UF), the retrieved convective mass flux (MF), and the mean updraft velocity ($\stackrel{\mathrm{‾}}{w}$) for the different VCPs are investigated and compared to the direct model output. In this study, convective mass flux (MF) is estimated at each height as

$$\begin{array}{}\text{(3)}& \text{MF}=\text{UF}\stackrel{\mathrm{‾}}{w}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{d}}}\left[\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{m}}^{-\mathrm{2}}\right],\end{array}$$

where UF is updraft fraction over the domain, $\stackrel{\mathrm{‾}}{w}$ is mean vertical velocity over the updraft area, and $\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{d}}}$ is dry air density averaged over the domain. The updraft fraction and mean updraft velocity strongly impact the domain-averaged convective mass flux, which can be used to understand mass, energy, and aerosol transport by the convective system.

Table 3 Root-mean-square error (RMSE) of UF₅, UF₁₀, MF₅, MF₁₀, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$, and ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$ profiles above 2 km a.g.l. for all experiments.

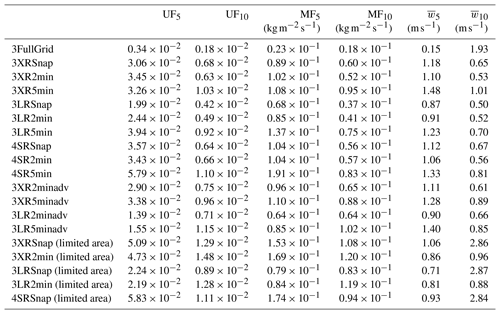
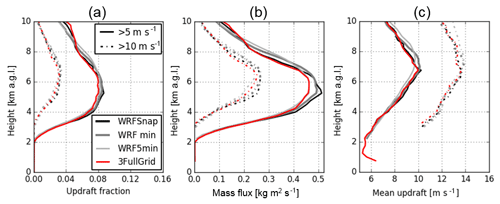
Figure 6 Vertical profiles of (a) updraft fraction, (b) mass flux, and (c) mean updraft velocity, with different thresholds of 5 m s⁻¹ (solid lines) and 10 m s⁻¹ (dashed lines) for the entire retrieval domain. Black lines represent the WRF snapshot at 12:18:00 UTC, dark gray lines represent the WRF output averaged over 2 min from 12:18:00 to 12:19:40 UTC, and light gray lines represent the WRF output averaged over 5 min from 12:18:00 to 12:22:40 UTC. Red lines represent the 3FullGrid retrieval simulation.

The analysis in this study is presented in Figs. 6, 7, and 8 for the two different updraft thresholds: 5 m s⁻¹ (UF₅, MF₅, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$) and 10 m s⁻¹ (UF₁₀, MF₁₀, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$). Furthermore, a comparison limited to a smaller domain where the higher density radar observations are available (squared area in Fig. 2) is added (Fig. 7g–i). Each panel shows their profiles from the WRF snapshot at 12:18:00 by a black solid line (threshold of 5 m s⁻¹) and a black dashed line (threshold of 10 m s⁻¹) for the comparison. Table 3 presents root-mean-square errors (RMSEs) of UF, MF, and $\stackrel{\mathrm{‾}}{w}$ profiles above 2 km a.g.l. for all experiments. In contrast to the number of coherent updraft cores, the profiles of UF, MF, and $\stackrel{\mathrm{‾}}{w}$ exhibit larger sensitivity to the sampling parameters. In subsequent sections, a more detail analysis of the impact of the different options in the observational setup on the UF, MF, and $\stackrel{\mathrm{‾}}{w}$ profiles are discussed.

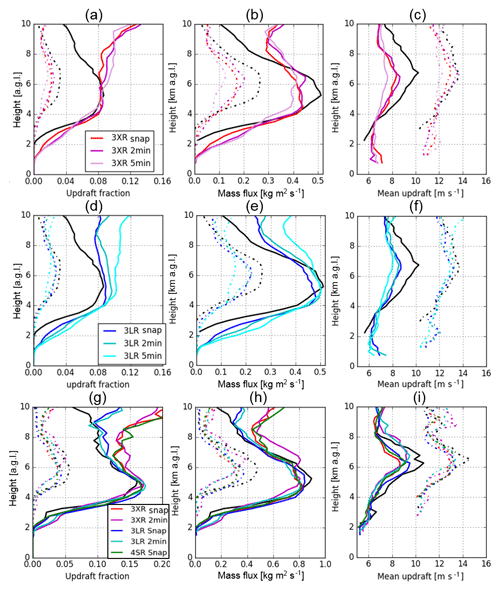
Figure 7 Vertical profiles of (a, d, g) updraft fraction, (b, e, h) mass flux, and (c, f, i) mean updraft velocity, with different thresholds of 5 m s⁻¹ (solid lines) and 10 m s⁻¹ (dashed lines) for the entire retrieval domain (a–f) and a center region shown as a box in Fig. 2 (g–i). Color represents different retrieval simulations as displayed in (a, d, g). Each panel displays profiles from the WRF snapshot at 12:18:00 UTC by black lines.

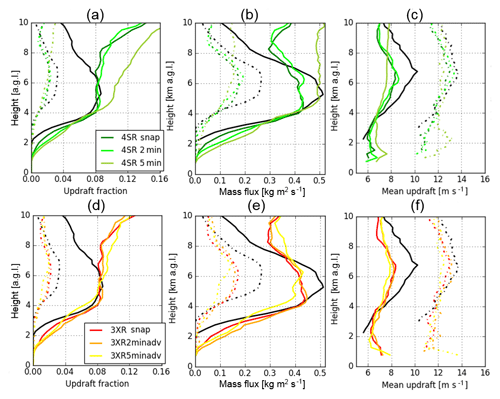
Figure 8 Vertical profiles of (a, d) updraft fraction, (b, e) mass flux, and (c, f) mean updraft velocity, with different thresholds of 5 m s⁻¹ (solid lines) and 10 m s⁻¹ (dashed lines) for the entire retrieval domain. The colors represent different retrieval simulations as displayed in (a, d). Each panel displays profiles from the WRF snapshot at 12:18:00 UTC by black lines.

Figure 6 compares the WRF snapshot at 12:18:00, the WRF 2 min average, and the WRF 5 min average. The UF profiles from both the WRF 2 min average and the WRF 5 min average are in very good agreement with that from the WRF snapshot; this consistency is also shown in MF and $\stackrel{\mathrm{‾}}{w}$ profiles (Fig. 6b and c, respectively), indicating that the updraft properties are statistically similar throughout the 5 min in this case. Figure 6 also compares the profiles from WRF outputs with those from the 3FullGrid simulation. As expected, the UF profiles from 3FullGrid simulation are in very good agreement with the WRF output for all thresholds (Fig. 6a, RMSE <0.004) but show an underestimation by ∼0.01 at 5.3 km a.g.l. For reference, 1 % difference in the updraft fraction corresponds to 25 km² for a 50 km×50 km retrieval domain. All the retrieved profiles of the coherent updraft fraction exhibit considerable differences from the WRF output above 6 km a.g.l. (Figs. 7 and 8). In general, the retrieved updraft fractions increase above 6 km a.g.l., while the WRF output indicates that the updraft fraction decreases.

Figure 6b and c show MF and $\stackrel{\mathrm{‾}}{w}$ profiles, respectively, from simulated wind retrievals for 3FullGrid together with those from the WRF output. The MF and $\stackrel{\mathrm{‾}}{w}$ profiles in Fig. 6b and c are coupled with updraft areas for updraft values larger than 10 m s⁻¹ (MF₁₀, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$) and for velocities larger than 5 m s⁻¹ (MF₅, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$). For the WRF output, the peaks of MF values are found at heights between 5 and 7 km a.g.l., and the MF₁₀ values are generally half of MF₅. The 3FullGrid simulation (Fig. 6b) captures those features well, but the maximum values at 5.25 km a.g.l. are slightly underestimated as MF₅ decreases by up to 0.05 $\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{m}}^{-\mathrm{2}}$ (RMSE of 0.02 $\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{m}}^{-\mathrm{2}}$). Since the $\stackrel{\mathrm{‾}}{w}$ values are well estimated (RMSE of 0.15 m s⁻¹ for ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$), the underestimation is driven by the small underestimation of UF (by 0.01, Fig. 6a).

3.2 Effects of VCP elevation sampling and number of radars

The impact of the maximum elevation angle and density of elevation angles used in the VCP is easily demonstrated when comparing the 3XRSnap and 3LRSnap retrievals for the entire domain (Fig. 7a–f) or within the smaller domain (square area in Figs. 2, 7g–i). For all updraft parameters investigated here (number of updraft cores, UF, MF, and $\stackrel{\mathrm{‾}}{w}$), the 3LRSnap produces improved comparisons to the direct model output, especially when limiting the evaluation area to the center square domain. The comparison for the number of cloud cores (Fig. 5) shows that 3XRSnap overestimated above 6.5 km. Figure 7a shows that UF₅ values from the 3XRSnap are overestimated above 6.5 km a.g.l., while UF₁₀ values above 6.5 km are underestimated. These profiles indicate that updraft areas of 5–10 m s⁻¹ are overestimated for the 3XRSnap retrievals, resulting in the overestimation of the number of updraft cores. This feature is also shown in other snapshots and 2 min VCP retrievals. The impact of a longer time VCP is more pronounced in the UF retrievals than the number of coherent updraft cores. As in the case for the profile of the number of coherent updraft cores, the use of the LR VCP improves the updraft fraction profile retrievals. The errors generally increase with height above 6 km a.g.l. This result is similar to the dual-Doppler-radar wind retrieval OSSE study for supercell storms by Potvin et al. (2012b).

The UF₁₀ values from the 3XRSnap simulation are underestimated by 0.01 at 5–7 km a.g.l. (∼30 % of the true fraction, Fig. 7a) at higher altitudes above 5 km. The mean updraft velocities are also underestimated by 1 m s⁻¹ for UF₁₀ above 5.5 km (Fig. 7c). The underestimations in ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$ and UF₁₀ profiles result in underestimation of MF₁₀, and the maximum underestimation of 0.1 $\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{m}}^{-\mathrm{2}}$ is found at 6 km a.g.l. For the threshold of 5 m s⁻¹, the overestimation of UF₅ above 7 km results in overestimation of MF₅, while the underestimation of the mean updraft velocity by 2 m s⁻¹ above 4.5 km for UF₅ leads to the underestimation of MF₅ at 4.5–7 km a.g.l. (Fig. 7b).

The mean updraft velocities for both UF₁₀ (${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$) and UF₅ (${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$) from 3LRSnap slightly increase above 6 km a.g.l. (Fig. 7d). Consequently, the MF₅ profile is improved as it increases at 4.5–7 km and decreases above 7 km (Fig. 7e, 24 % decrease in RMSE). Similarly, the MF₁₀ profile is also improved as it increases above 4.5 km, but it is still underestimated by 0.05 $\mathrm{kg}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{m}}^{-\mathrm{2}}$ at 5–9 km a.g.l. (38 % decrease in RMSE). Compared to the same VCP periods, the 3LR retrievals also show similar improvements at 2 min VCP and 5 min VCP. These results suggest that the VCP with dense elevation angles can improve the retrieval of strong updrafts with velocities larger than 10 m s⁻¹ and is more effective at higher altitudes (>8 km).

Substantially improved retrievals can be obtained in a region near the CF where data density from each radar is higher (square region shown in Fig. 2). Figure 7g, h, and i show UF, MF, and $\stackrel{\mathrm{‾}}{w}$, respectively, for the square region. The UF, $\stackrel{\mathrm{‾}}{w}$, and hence MF are improved for 3LR simulations in particular, where distances to the nearest data are mostly less than 0.2 km (Fig. 2g and h). Although the profiles from 3XRSnap and 4SRSnap are improved as they capture the peak at middle altitude, the improvements are weaker than 3LR simulations at higher altitudes, where the distances of the nearest radar data points in the square region are similar to those from the entire domain for XR (Fig. 2g and h). It is suggested that the high data density should be considered as an indicator of improved retrievals, as long as the scanning of the VCP is completed in 2 min.

Increasing the number of Doppler radars in retrievals would reduce the uncertainties as analyzed by Bousquet et al. (2008) and North et al. (2017). Here we compare the 4SRSnap simulation with the 3LRSnap and 3XRSnap simulations (Fig. 8a–c, Table 3). The 4SRSnap retrieval cannot significantly improve the UF₅ and UF₁₀ profiles compared to those from 3XRSnap, as well as the number of updraft cores and $\stackrel{\mathrm{‾}}{w}$ profiles, and hence MF. Lower spatial resolutions of the C-SAPR VCP than that of the X-SAPR might induce more artifacts in the weaker updraft retrievals. The lower-frequency radar (C-SAPR) can provide radar reflectivity measurements that may be easier to correct for hydrometeor and radome attenuation (e.g., Kurri and Huuskonen, 2008). In this case, it is perhaps advantageous to use the lower-frequency radar to cover the domain sampled by the X-SAPR network. However, if additional radars of the same or better spatial resolution and VCP are available, the network architecture should be considered in order to maximize the triple-Doppler-radar area by creating another sampling area with triple-Doppler-radar observations.

3.3 Effect of VCP time period

The 2 min and 5 min time period VCP retrievals are compared to the snapshot retrievals to see how the VCP time periods affect the updraft retrievals. For the 3XR retrieval simulations, profiles of the number of updraft cores do not show significant differences among 3XRSnap, 3XR2min, and 3XR5min (Fig. 5b), consistent with small difference among those from WRFSnap, WRF2min, and WRF5min. This feature is also found in the 3LR simulations. However, some differences can be found in Figs. 7a–c, d–f, and 8a–c showing updraft fractions, convective mass flux, and mean updraft for 3XR, 3LR, and 3SR simulations. For updraft threshold of both 10 and 5 m s⁻¹, 3XR2min and 3XRSnap UF, $\stackrel{\mathrm{‾}}{w}$, and hence MF are in close agreement at all altitudes and even with WRF output (WRFSnap and WRF2min) below 4.5 km, as well as with 3LR and 4SR simulations. The small impacts of the 2 min time period are also found for the center square region (Fig. 7g–i). For 3XR5min and 3LR5min simulations, however, UF₁₀ and ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$ are significantly underestimated at 4–9 km a.g.l. (50 %–110 % increase in RMSE for UF₁₀ and 40 %–55 % increase in RMSE for ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{10}}$ from snapshot simulations) when compared to the snapshot retrievals (3XRSnap and 3LRSnap, respectively). The differences from the 3XR5min simulation result in significant underestimation of MF₁₀ at middle altitudes. These differences in UF and MF are also found even when comparing with the WRF UF and MF profiles averaged over 5 min (WRF5min). These features are common in 3XR, 3LR, and 4SR simulations.

The comparison of UF₅, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$, and MF₅ for different time periods from a given VCP show different features compared to those for the larger updraft threshold. As discussed in Sect. 3.2, the UF₅ profiles from the simulations are largely overestimated above 6 km and cannot resolve a peak at middle altitudes. The difference becomes larger for the 5 min VCP retrieval simulations. It is suggested that a longer VCP time period tends to underestimate areas of larger updrafts (>10 m s⁻¹) and overestimate areas of weaker updraft (<10 m s⁻¹). Conversely, ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$ from 3XR5min is underestimated above 5 km. These errors in UF₅ and ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$ from 3XR5min produce large underestimation of MF₅ at middle altitudes and overestimation above 7 km. These features are also shown in 3LR5min and 4SR5min, but the underestimations of MF₅ at middle altitudes are small since underestimation of ${\stackrel{\mathrm{‾}}{w}}_{\mathrm{5}}$ is relatively small for 3LR5min or overestimation of UF₅ is larger for 4SR5min.

Overall, the impacts from the 2 min VCP on the updraft retrieval can be small, whereas the 5 min VCP can significantly intensify uncertainties, especially for stronger updraft regions above 6 km a.g.l. This is likely due to small convective evolution in 2 min, while there is large evolution and advection in 5 min as shown in Fig. 3. Potvin et al. (2012b) also showed a similar result that the data sampling in 3 min produced significant errors compared to a shorter time period (1.5 min) and snapshot for supercell storms. Compared to the 3XR and 4SR retrievals for each VCP time period (2 and 5 min), the 3LR2min and 3LR5min show better agreements.

3.4 Effect of advection correction

As presented in the previous section, the longer time VCPs emphasize the uncertainties at upper levels more. Because profiles of the updraft properties from WRF output do not change among the snapshot, 2 min average, and 5 min average, the differences found when comparing the simulated retrievals for 2 and 5 min VCPs without advection correction and those for the snapshot VCPs are probably associated with (i) imposed advection and (ii) cloud evolution, rather than time change in the updraft properties. Advection will move clouds and cause mismatch of cloud locations between PPI scans from different radars and even from the same radar. Meanwhile, cloud evolution alters vertical and horizontal distributions of hydrometeors and vertical velocity, resulting in observing different cloud life stages by different PPI scans. Both issues result in deformation of cloud structures and may cause uncertainties in the wind retrieval algorithm, especially if the mass continuity assumption is not satisfied adequately. The cloud locations can be corrected using an algorithm proposed by Shapiro et al. (2010a) as described in Sect. 2.4.4. Here, we compare 2 and 5 min VCP experiments to which the advection correction has been applied (2minadv, 5minadv) with those without the advection correction and snapshot experiments to see how the advection correction can improve the retrievals using 2 and 5 min VCPs.

Figure 8d–f show UF, MF, and $\stackrel{\mathrm{‾}}{w}$ profiles, respectively, from the 2 and 5 min VCP 3XR simulations corrected for advection (3XR2minadv and 3XR5minadv, respectively), together with those from the WRF snapshot and 3XRSnap. The advection-corrected retrievals for the 2 min VCP improve these profiles well as they are closer to the WRF2min profiles and even to the snapshot retrieval (e.g., 16 % decrease in RMSE of UF₅ from 3XR2min), while improvements are not significant for the 5 min VCP. Very similar improvements for the 2 and 5 min VCPs by advection corrections are found in 3LR simulations with advection correction (not shown).

Figure 9 shows comparisons of vertical cross sections between wind retrievals obtained before and after applying the advection correction for the updraft core shown in Fig. 3 (right column). Chosen vertical cross sections go through the maximum updraft area at 7 km a.g.l. For the 2 min VCP retrievals, regions of updraft values >5 m s⁻¹ are significantly corrected by the advection correction technique and maintain the top-left to bottom-right tilt of the WRF updraft structure. It is clear (Fig. 3c, f, i) that within 5 min the updraft structure has evolved not only in its tilt but also by the presence of a downdraft near its lower levels. Thus, when using a 5 min VCP, a completely different updraft structure is reconstructed with different tilt and location of the maximum updraft velocity. The difficulty in improving the updraft retrieval using the advection correction, particularly for the 5 min VCP, is likely due to fast evolution of convective clouds. The rapid evolution of the updraft structures simulated by the WRF is consistent with that from other modeling studies where the temporal evolution of the convective thermals can be significant over time periods larger than 2 min (e.g., Morrison et al., 2015; Hernández-Deckers and Sherwood, 2016).

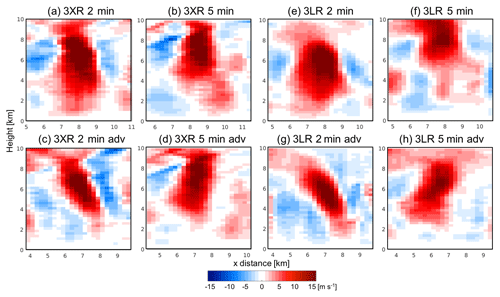
Figure 9 Vertical cross sections of vertical velocity for an updraft core from 3XR (a–d) and 3LR (e–h) wind retrieval simulations with 2 and 5 min VCPs. Top row and bottom row display non-advection-corrected and advection-corrected retrievals, respectively. A selected updraft core is the same as shown in Fig. 3.

4 Summary and conclusions

Convective motions affect microphysical processes and control the transport of moisture, momentum, heat, trace gases, and aerosols from the boundary layer to the upper troposphere. Accurate characterization of the convective transport requires vertical air velocity retrievals in particular in the middle and upper part of convective cloud systems, and multi-Doppler-radar networks have been used to probe convection and provide wind retrievals including vertical air motion estimates. While there is a plethora of studies illustrating the ability of multi-Doppler-radar observations to capture the low-level wind divergence and circulation, there is little to show regarding the capability of this observing system to capture the upper-level convective dynamics. This study addressed potential observational sources of errors in triple-Doppler-radar three-dimensional variational (3D-Var) updraft retrieval using a sophisticated forward radar simulator (CR-SIM) with the WRF simulation output for an MCS on 20 May 2011 during the Midlatitude Continental Convective Clouds Experiment (MC3E) for a domain of $\mathrm{50}\mathrm{km}\times \mathrm{50}\mathrm{km}\times \mathrm{10}\mathrm{km}$. An extensive sensitivity analysis is conducted to investigate impacts of radar volume coverage pattern (VCP), the number of radars used for the multi-Doppler-radar analysis, time periods for VCP (2 and 5 min), and advection correction. An advection correction technique proposed by Shapiro et al. (2010a) was applied to the 2 and 5 min VCP radar data. Updraft properties such as updraft fraction, mass flux, and updraft magnitude profiles with two different thresholds (5 and 10 m s⁻¹), from simulated multi-Doppler-radar wind retrievals using three X-band scanning ARM precipitation radars (X-SAPRs) are examined. The number of updraft cores are also investigated with a threshold of 5 m s⁻¹ at each height. The analysis results presented the following findings.

• As the previous literature has pointed out, the updraft fraction profiles from the simulated wind retrievals suggested that the selected VCP elevation strategy and radar sampling volume resolution affect uncertainties in upper-level (>4.5 km) updraft retrievals, owing to low density and low resolution of radar data attributed to gaps between plan position indicator (PPI) elevation angles and the radar sample volume increasing with distance from the radar. Those uncertainties increase with height above 6 km a.g.l. Overall in experiments using VCPs, stronger updrafts >10 m s⁻¹ tend to be underestimated above 4.5 km, while areas of updrafts of 5–10 m s⁻¹ are overestimated above 6.5 km. This impacts the retrieval of convective mass flux.

• Increasing the maximum elevation angle and the density of the elevation angles of the radar VCP (i.e., 60^∘ over elevation with 1^∘ increments) can effectively improve the updraft retrieval, whereas an addition of data from a Doppler radar cannot significantly improve the updraft retrievals if the added radar VCP has inferior spatial resolutions.

• Shorter-duration (2 min or less) radar VCPs are critical to producing high-quality vertical air motion retrievals. The 2 min VCP has small impacts on the snapshot updraft retrievals, but the 5 min VCP induces an important overestimation of areas of updrafts 5–10 m s⁻¹ above 6.5 km, underestimation of updrafts >10 m s⁻¹ at 4.5–8 km, and overestimation of updrafts >10 m s⁻¹ above 8–9 km.

• The advection correction works to improve the updraft fraction and mean updraft profiles as the profiles become closer to those from the snapshot retrievals and time-averaged updraft fields, but it is still challenging to improve stronger updraft retrievals, especially for 5 min VCP, due to the rapid deformation of the dynamical structures in the simulated mesoscale convective system. The magnitude of improvement by the increase in elevation angles is larger than that by advection correction, even though the VCP needs 2 min. However, for the increasing elevations taking 5 min, the improvement is less than that from the original VCP completed within 2 min.

Gridding technique is also an important factor to determine the uncertainties in the wind retrievals. Sophisticated gridding techniques to cover the three-dimensional analysis domain at high spatial resolution, even for higher altitudes, tend to suppress the uncertainty (e.g., Majcen et al., 2008; Collis et al., 2010; North et al., 2017). Another error source that we did not consider in this study is the hydrometeor fall speed estimate, which is generally estimated from radar reflectivity. The sophisticated attenuation correction techniques in particular for shorter wavelength radars (e.g., Kim et al., 2008; Gu et al., 2011) and best estimates of hydrometeor fall speeds (Giangrande et al., 2013) are required to reduce the wind retrieval uncertainties.

In brief, the retrieval of the high-quality vertical velocities in the upper part of convective clouds is very challenging, while the multi-Doppler-radar vertical velocity retrievals have been conventionally used to evaluate the CRM simulated dynamical fields. Some of the CRM simulations significantly overestimated compared to multi-Doppler-radar vertical velocity retrievals (e.g., Varble et al., 2014; Fan et al., 2017). The present study would suggest that the multi-Doppler-radar retrievals for MCSs tend to underestimate the strong updraft values at middle and upper levels and need to be carefully used considering the limitations of the radar observing system. The assessment of the multi-Doppler-radar retrieval presented in this study could vary for different storm characteristics (e.g., isolated storm and less wind shear).

Although the present study focused on the ARM X-band radar network, the similar dense radar network has been installed in several regions (e.g., Bousquet et al., 2007; Maesaka et al., 2011; Helmert et al., 2014), and field campaigns targeting deep convection (past, ongoing, and future) would be strongly motivated to install multiple Doppler radars to observe vertical air motions in convective clouds. The present analysis can give valuable information to improve the observation strategies and decide optimized scan strategies for the networks. Most of the improvements required in the sampling strategy of the observing system (higher maximum elevation angle, higher density elevation angles, and rapid VCP time period) can be accomplished using rapid scan radar systems such as the Doppler on Wheels mobile radars (DOWs) or even phased array radar systems. However, even when such rapid scan radar networks are available, the multi-Doppler-radar retrieval spatial domain will be fairly small compared to the entire radar network coverage. Despite the limited domain, the observations do cover enough area to track isolated convective updrafts and contain enough samples to derive reliable, low-uncertainty estimates of updraft and downdraft properties in convective clouds. Spaceborne radar systems with Doppler velocity capability such as the Earth Clouds Aerosols and Radiation Explorer (EarthCARE; Illingworth et al., 2015; Kollias et al., 2018a) or future spaceborne radar concepts (Tanelli et al., 2018) are expected to provide additional middle- and upper-level convective velocity observations, especially over the tropical oceans.