Use of polarimetric radar measurements to constrain simulated convective cell evolution: a pilot study with Lagrangian tracking

To probe the potential value of a radar-driven field campaign to constrain simulation of isolated convection subject to a strong aerosol perturbation, convective cells observed by the operational KHGX weather radar in the vicinity of Houston, Texas, are examined individually and statistically. Cells observed in a single case study of onshore flow conditions during July 2013 are first examined and compared with cells in a regional model simulation. Observed and simulated cells are objectively identified and tracked from observed or calculated positive specific differential phase (K_DP) above the melting level, which is related to the presence of supercooled liquid water. Several observed and simulated cells are subjectively selected for further examination. Below the melting level, we compare sequential cross sections of retrieved and simulated raindrop size distribution parameters. Above the melting level, we examine time series of K_DP and radar differential reflectivity (Z_DR) statistics from observations and calculated from simulated supercooled rain properties, alongside simulated vertical wind and supercooled rain mixing ratio statistics. Results indicate that the operational weather radar measurements offer multiple constraints on the properties of simulated convective cells, with substantial value added from derived K_DP and retrieved rain properties. The value of collocated three-dimensional lightning mapping array measurements, which are relatively rare in the continental US, supports the choice of Houston as a suitable location for future field studies to improve the simulation and understanding of convective updraft physics. However, rapid evolution of cells between routine volume scans motivates consideration of adaptive scan strategies or radar imaging technologies to amend operational weather radar capabilities. A 3-year climatology of isolated cell tracks, prepared using a more efficient algorithm, yields additional relevant information. Isolated cells are found within the KHGX domain on roughly 40 % of days year-round, with greatest concentration in the northwest quadrant, but roughly 5-fold more cells occur during June through September. During this enhanced occurrence period, the cells initiate following a strong diurnal cycle that peaks in the early afternoon, typically follow a south-to-north flow, and dissipate within 1 h, consistent with the case study examples. Statistics indicate that ∼ 150 isolated cells initiate and dissipate within 70 km of the KHGX radar during the enhanced occurrence period annually, and roughly 10 times as many within 200 km, suitable for multi-instrument Lagrangian observation strategies. In addition to ancillary meteorological and aerosol measurements, robust vertical wind speed retrievals would add substantial value to a radar-driven field campaign.

1 Introduction

Since the Intergovernmental Panel on Climate Change's first scientific assessment report (IPCC, 1990), the conclusion has been generally strengthened that aerosol pollution from anthropogenic activities is likely to have commonly offset regional and global radiative forcing of the Earth's climate by anthropogenic greenhouse gases to date, but uncertainty, especially in aerosol effects on cloud-related forcing, still remains high (IPCC, 2013). Although such anthropogenic aerosol radiative forcing will be diminutive relative to that from buildup of anthropogenic greenhouse gases on century timescales under most scenarios, the variable degree to which anthropogenic aerosols offset greenhouse gas warming in simulations that reproduce the observational record of surface temperature change since preindustrial times continues to be a leading factor limiting simulation constraints on Earth's climate sensitivity (e.g., Kiehl, 2007). Fundamental understanding of the relationships between global cloud processes and atmospheric circulations and thermodynamics is another leading factor, as demonstrated by studies that find grossly differing predicted climate sensitivities associated with differing parameterization of fundamental processes such as convective mixing, convective aggregation, or cloud glaciation (e.g., Sherwood et al., 2014; Mauritsen and Stevens, 2015; Tan et al., 2016).

Addressing aerosol–cloud–precipitation–climate interactions locally and regionally, Rosenfeld et al. (2014) describe how field campaigns designed to measure closed energy and moisture budgets over relatively large domains, referred to as box flux closure experiments, could help advance understanding of primary microphysical mechanisms and regional-scale dynamical feedbacks. Here we further consider how observations designed for a box flux closure experiment could be amended to aid attribution of primary cloud responses to aerosol variability, specifically in the case of convective cells responding to a boundary layer aerosol perturbation. The observational objective of establishing microphysical and dynamical differences across a population of evolving convective cells is considered an amendment because observing the details of updraft cell evolution within a flux closure campaign box well poses a significant additional challenge beyond constraining fluxes at the box boundaries. However, there may be overlapping utility in the use of polarimetric radar systems to observe convective cell spatial evolution within the box and to provide state-of-the-art retrievals of surface precipitation rate at the lower box boundary, as discussed further below. Especially when coordinated with detailed high-resolution modeling, we argue that measurements optimized to observe convective cell evolution would additionally be uniquely valuable for advancing understanding and accurate simulation of cloud processes such as entrainment and glaciation, thereby further addressing understanding of fundamental cloud processes relevant to climate sensitivity.

As understood for decades, cloud parcels rising in convective updrafts from a warm cloud base height pass through the melting level (0 ^∘C) carrying liquid water that does not instantaneously freeze owing to an energy barrier to ice crystal formation (Pruppacher and Klett, 1997). For individual drops, that barrier would not be spontaneously overcome in commonly occurring dilute solution drops until they are supercooled by at least 30 ^∘C below their melting temperature (e.g., Herbert et al., 2015). However, relatively rare aerosols that commonly exhibit solid surfaces, such as dust, may serve as ice-nucleating particles (INPs) that lower the energy barrier to ice crystal formation (Vali et al., 2015). Such INPs may nucleate individual crystals with varying efficiencies that have been widely measured in the field over activation temperatures of roughly −10 to −35 ^∘C, for instance (DeMott et al., 2010); some biological agents may lead to primary ice formation at temperatures as warm as −3 ^∘C (e.g., Du et al., 2017). Once ice is present in an updraft parcel, whether via primary nucleation by INPs present or via some means of transport (sedimentation or entrainment), so-called secondary ice crystal formation may potentially progress via ice–liquid or ice–ice collisions or some fracturing process related to ice expansion during drop freezing (e.g., Hallett and Mossop, 1974; Vardiman, 1978; Yano and Phillips, 2011; Lawson et al., 2015, and references therein). Based on several recent field campaigns, it has been argued that multiplication is likely a process that may commonly dominate ice size distribution evolution in warm-base convective updrafts and long-lived stratiform outflow (Lawson et al., 2015; Ackerman et al., 2015; Fridlind et al., 2017; Ladino et al., 2017). In general, there is increasing evidence that the processes that determine updraft and outflow ice properties to first order, and by extension their relationship to environmental conditions, are still not yet well understood or well represented in microphysics schemes to date (Lawson et al., 2015; Ackerman et al., 2015; Fridlind et al., 2017; Stanford et al., 2017).

Although the latent heat of fusion is only roughly 15 % of the latent heat of condensation, liquid water freezing does contribute to updraft buoyancy, and has been identified as a factor explaining updraft extent in tropical environments (Zipser, 2003). If rain formation leads to liquid water sedimentation from an updraft before it reaches the melting level or before it freezes at some colder temperature above, clearly no latent heat of fusion is contributed; to the extent that more liquid water reaches freezing temperatures when rain formation is weaker, increasing aerosol loading will lead to stronger updrafts, all else being equal. This is borne out in simulations under some environmental conditions to an extent that may be dependent on the complexity of the microphysics scheme, and has been supported by large-domain statistical studies (e.g., Fan et al., 2013, and references therein). Conversely, it has also been repeatedly demonstrated that differing microphysics schemes predict grossly differing updraft and cloud properties, at least in part owing to a lack of observational constraints on important factors such as liquid water content and ice properties, making it extremely challenging to establish whether any scheme is performing substantially better than any other for the correct reasons (e.g., Fridlind et al., 2012; Varble et al., 2014a, b; Wang et al., 2015).

Polarimetric radar systems such as those operated by the National Weather Service Next-Generation Radar (NEXRAD) program (NOAA, 2017) provide a rich source of information about the size distribution, phase, and shape of hydrometeors (Zrnić and Ryzhkov, 1999), which is especially valuable for the study of convective updraft physics because of the paucity of such data available from aircraft (e.g., Loney et al., 2002; Fridlind et al., 2015; Snyder et al., 2015). Comparison of reflectivity and phase-shift differentials between horizontal and vertical radar polarizations yields differential reflectivity (Z_DR) and specific differential phase (K_DP), which are related to the presence of horizontally aligned oblate or prolate hydrometeors when positive (Bringi and Chandrasekar, 2001). Vertically elongated columns of positive Z_DR and K_DP that extend above the environmental melting level (Z_DR and K_DP columns) have been generally attributed to the presence of supercooled liquid associated with a deep convective updraft that is not otherwise identifiable from reflectivity alone (Bringi et al., 1996; Hubbert et al., 1998; Loney et al., 2002; Kumjian et al., 2014a). Recent studies suggest a strong connection between K_DP and Z_DR columns and other metrics of deep convective activity such as overshooting tops (Homeyer and Kumjian, 2015) and lighting flash rate and updraft mass flux (van Lier-Walqui et al., 2016). Observations also show differences in K_DP versus Z_DR column morphology (Zrnić et al., 2001; Loney et al., 2002; Kumjian and Ryzhkov, 2008), which have been attributed to differing sensitivities to hydrometeor size distribution and phase characteristics (e.g., Kumjian et al., 2014b; Snyder et al., 2017b). However, precise attribution of specific morphological features at various wavelengths remains a challenge due to a paucity of colocated in situ measurements, the complexity of updraft microphysics, and uncertainties in calculating hydrometeor electromagnetic properties, especially for mixed-phase particles (e.g., Loney et al., 2002; Ryzhkov et al., 2011; Snyder et al., 2013, 2017b).

Many past studies have effectively examined deep convective cells using observations from individual radar scans (e.g., Hubbert et al., 1998; Loney et al., 2002). Tracking convective cells or other identified features in time increases the amount of information that can be gleaned from scanning radar because temporal aspects such as cell lifetime can be quantified (e.g., Stein et al., 2015). Feature identification and tracking have wide applications in the atmospheric sciences. Many studies have applied unsupervised feature identification to locating cloud regimes using satellite observations (e.g., Jakob and Tselioudis, 2003; Rossow et al., 2005; Pope et al., 2009). Automatic tracking is perhaps most widely applied in nowcasting using surface radar observations (Dixon and Wiener, 1993; Johnson et al., 1998; Scharenbroich et al., 2010; Limpert et el., 2015). Surface radar observations generally have a frequency on the order of 5–10 min, and the rate of successful tracking can be 60 % to 90 % according to Lakshmanan and Smith (2010). Here we investigate isolated convective cells, which have smaller sizes and shorter life spans than the storm features in most radar weather tracking. The K_DP column identification algorithm used in this pilot study was described by van Lier-Walqui et al. (2016). We also introduce a more efficient tracking algorithm for compilation of long-term statistics using parallel computing.

For the study of updraft microphysics we target conditions where a relatively strong aerosol perturbation exists and updrafts are not being strongly driven by synoptic flow, which are commonly satisfied in the vicinity of Houston when there is onshore flow. Such conditions increase the likelihood of observationally establishing the statistical relationship between aerosol and updraft properties, which can in turn be used as a constraint for evaluating and improving models. The Houston region currently offers the significant advantage of a lightning mapping array (LMA; Orville et al., 2012), which can provide independent three-dimensional information on updraft location and phase (e.g., van Lier-Walqui et al., 2016). The objectives of this pilot study are to establish the lifetime and observable properties of typical isolated convective cells and to demonstrate comparison of isolated cell observations with an example regional model simulation.

Next in Sect. 2, we describe the data sources and methods of analyzing isolated cell features in a selected case study and in long-term statistics. Results are presented in Sect. 3. In Sect. 4, we discuss results in the context of pilot study objectives.

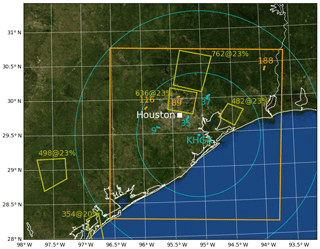
Figure 1 Map of Houston region (white symbol marks city center), NU-WRF inner domain boundaries (orange square), KHGX NEXRAD radar location (cyan symbol with 100 and 200 km range rings), tracks of three example features from KHGX K_DP observations (cyan tracks numbered 9, 35, and 37) and from NU-WRF q_r output (orange tracks numbered 89, 116, and 188), and CCN number concentration and supersaturation retrieved from satellite data (within yellow boxes in number per cubic centimeter and as a percentage, respectively).

2 Methodology

2.1 Data sources

Level II data from the NEXRAD KHGX radar on 8 June 2013 (NOAA, 1991) were mapped to Cartesian coordinates at 1 km resolution and approximately 5 min frequency using the Python ARM Radar Toolkit (Py-ART; Helmus and Collis, 2016). A linear programming (LP) phase processing algorithm based on Giangrande et al. (2013), and included in Py-ART, was used to unfold and process raw differential phase into propagation differential phase. The LP phase processing algorithm imposes a monotonicity constraint on phase, which makes it inappropriate for estimating regions of decreasing propagation phase shift (i.e., regions where differential phase shift, or K_DP, is negative). Conversely, this fact makes the LP algorithm better suited for identifying regions of positive K_DP, such as those associated with oblate particles like rain and liquid-coated hail that are expected in convective updrafts.

From a NASA Unified Weather Research and Forecasting (NU-WRF; Peters-Lidard et al., 2015) model simulation, 5 min frequency outputs were analyzed. The model is configured with a 600 km × 600 km outer domain grid centered around Houston with 3 km horizontal grid spacing and, centered within the outer domain, a nested 300 km × 300 km inner domain with 120 vertical levels and 500 m horizontal grid spacing (Fig. 1). Time steps of 12 and 2 s were used on the outer and inner grids, respectively. The same physics options were used on both grids. The planetary boundary layer parameterization used the Mellor–Yamada–Nakanishi–Niino level 2.5 turbulent kinetic energy scheme (Nakanishi and Niino, 2009). The Morrison et al. (2009) two-moment cloud microphysics scheme was used with a fixed droplet number concentration of 100 cm⁻³, and reflectivity at horizontal polarization (Z_HH) was calculated using the resulting hydrometeor size distributions with temperature-dependent refractive indices following Blahak et al. (2011). The Goddard broadband two-stream radiative transfer scheme was used to calculate radiative fluxes and atmospheric heating rates (Chou and Suarez, 1999, 2001; Matsui et al., 2018a). Model terrain was smoothed from the 30 s and 0.9 km U.S. Geological Survey topography data for both domains, and land cover was mapped from 30 s MODIS land use data. Sea surface temperature and atmospheric initial and lateral boundary conditions are obtained from 6-hourly output of the Modern-Era Retrospective Analysis for Research and Applications Version 2 (MERRA-2; Bosilovich et al., 2015). Land surface initial conditions (soil moisture and temperature) were derived from a 6-month spin-up (Kumar et al., 2007) of the Noah land surface model (LSM) using the MERRA-Land meteorological forcing (Reichle et al., 2011). The LSM spin-up was conducted at the grid configuration identical to that used in the simulation. The simulation was started at 00:00 UTC on 8 June 2013 and integrated for 24 h. At 16:00–17:00 UTC, convective cells begin to appear within 100 km of the KHGX radar location in both the simulation and the observations.

Additional data shown below are cloud condensation nucleus (CCN) number concentrations retrieved from satellite observations, raindrop size distribution parameters retrieved from NEXRAD measurements, and observed lightning flashes. CCN number concentration and associated supersaturation at cloud base were retrieved from National Polar-orbiting Partnership (NPP) Visible Infrared Imaging Radiometer Suite (VIIRS) cloud-top temperature and effective radius with an estimated uncertainty of 30 % (Rosenfeld et al., 2016). Rain mass-weighted mean diameter (D_m; the fourth moment of the drop number size distribution divided by the third moment) and generalized intercept parameter (N_w) (see Testud et al., 2001) were retrieved from KHGX data at elevations below the melting level following Ryzhkov et al. (2014), with an estimated uncertainty of roughly 5 %–10 % in D_m and log (N_w) (Thurai et al., 2012). Collocated rain rate has been retrieved from the specific attenuation A using the R(A) methodology that is most efficient at the S band, with an estimated bias less than 6 % (Ryzhkov et al., 2014; Zhang et al., 2017). Lightning flashes were estimated from raw very-high frequency (VHF) signals detected by the LMA. A simple set of heuristics was used to cluster VHF sources into discrete flashes, similar to MacGorman et al. (2008): the first 10 VHF sources in a flash are required to be within 0.25 s and 3 km of one another, and each flash is not allowed to exceed 3 s in total duration and must be composed of at least 10 VHF sources.

For comparison with the additional observational data, we calculate several further quantities from standard NU-WRF outputs. From rain mixing ratio and number concentration, we use the microphysics scheme assumptions and limitations on rain size distribution properties to calculate rain D_m and N_w. From D_m we further estimate rain Z_DR following Bringi and Chandrasekar (2001, their Eq. 7.14a). From both D_m and N_w, rain K_DP is estimated as described in Appendix A.

2.2 K_DP column tracking

Convective cells can be objectively identified and tracked using observed or forward-calculated radar variables (Z_HH, Z_DR, K_DP) or model variables such as rain water mixing ratio (q_r). From three-dimensional gridded KHGX data for this study, K_DP-based values were first calculated in each model column following

$$\begin{array}{}\text{(1)}& \mathit{\xi }=\underset{z_{\text{m}}}{\overset{z_{\text{f}}}{\int }}\mathit{\varphi }\left(z\right)(z-z_{\text{m}})\mathrm{d}z,\end{array}$$

where z_m and z_f are the melting and homogeneous freezing heights and ϕ(z) is the value of K_DP in each column grid cell, similar to the approach taken in van Lier-Walqui et al. (2016). Such a metric favors both the ϕ(z) value and its height. Since hydrometeor size distribution assumptions made in bulk microphysics schemes such as that used in the NU-WRF simulation are not generally adequate to forward simulate fully realistic K_DP fields (e.g., Ryzhkov et al., 2011), analogous values were calculated from NU-WRF output first using rain water mixing ratio (q_r), and then using rain K_DP estimated as described in Appendix A. In observations, fixed z_m and z_f grid cell bottom and top edge values of 4.5 and 9 km, respectively, were estimated from 00:00 and 12:00 Z soundings at Lake Charles, Louisiana, such that the lowest gridded radar volume was above 0 ^∘C and the highest gridded radar volume below −40 ^∘C. Similar heights were found from soundings at Corpus Christi, Texas. In NU-WRF output, fixed z_m and z_f values of 4.1 and 10 km were taken from the inner domain grid layer mean temperature profile. The conclusions of this pilot study are not sensitive to the precise choice of z_m and z_f values. However, we note that obtaining accurate time- and space-dependent z_m and z_f values from observations could be challenging. It could conceivably be preferable to derive relevant integration limits from observed and forward-simulated radar variables in future work.

Using the two-dimensional fields of ξ values, features were identified and tracked using Trackpy, an open-source Python object tracking toolbox. Whether using observations or model data, regional relative maxima were identified and tracked using Trackpy's predictive tracker with a maximum tracked object velocity of 30 m s⁻¹ and a “memory” of three frames to allow for splitting or merging cells to be followed. Paths with five or fewer time frames were discarded. We note that this procedure serves to objectively identify a “trackable” cell without requiring a definition of cell initiation.

When comparing observed and simulated reflectivity fields from tracked objects, the variables and tracking parameters described above were subjectively deemed adequate for the purposes of this pilot study. A more in-depth future study would motivate additional focus on optimizing such choices for any specific conditions of interest. We also found that tracking performed on ξ values obtained from simulated q_r versus simulated K_DP did not influence study results, likely attributable to the fact that the K_DP estimation approach used here is so closely linked to q_r alone. In the following we focus only on simulated objects tracked from ξ based on K_DP.

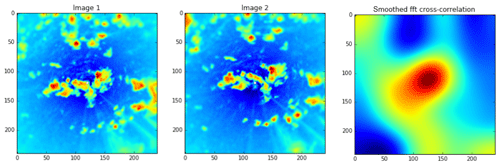
Figure 2 Two reflectivity factor snapshots (gridded to a constant height of 1 km) from subsequent NEXRAD scans of KHGX and their cross-correlation. The peak in the cross-correlation gives a good indication of the image shift between the two time steps and is used as the position start of the search to identify cells in subsequent images.

2.3 Long-term cell tracking, introducing TINT

As the study of individual cell cases proceeded, it became clear that a long-term study of suitable cell existence was needed. The aforementioned column tracking method did not lend itself well to implementation on large data sets and did not scale well on multiprocessor computer clusters. Therefore, motivated by this and several other projects, development commenced on a simple-to-use and open-source tracking code base designed specifically for atmospheric data. The TINT Is Not TITAN (TINT) package works directly with the Py-ART grid object in Python and is based on the Thunderstorm Identification, Tracking, Analysis and Nowcasting package (TITAN; Dixon and Wiener, 1993). While TITAN was designed to be used in operational settings and can be challenging to configure, TINT is designed to simply take a temporal sequence of grids, a function that renders the 3-D grids to a 2-D binary mask (for example, a reflectivity threshold at a single level) denoting cell or no cell and returns a Pandas (McKinney, 2010) data frame containing cell locations and characteristics as a function of time. TINT does not deal with splits or mergers but is thread-safe and pleasantly parallel when radar data are stratified by storm events. TINT uses an N step algorithm to associate cells across time steps, t₀ and t₁:

• Cells are identified based on minimum thresholds for cell area and field value.

• Phase correlation is performed in a neighborhood around each cell c_i to give an estimated translation vector, V_i, between t₀ and t₁; example images (reflectivity) and their cross-correlation are given in Fig. 2.

• Translation vector estimates are corrected based on prior cell movement.

• For each identified cell in t₀ the algorithm searches for cells in t₁ at location ${\mathit{V}}_i\times (t_{\mathrm{1}}-t_{\mathrm{0}})$.

• The Hungarian algorithm is used to compare candidates and find optimal cell pairing; see Dixon and Wiener (1993) for details.

• Cell positions are updated, and statistics are recorded.

• New cells are assigned new unique identifiers.

Figure 3 An example of TINT-generated cell tracks from 7 July 2013 (randomly colored lines). A constant-altitude plot of reflectivity at 1.5 km is shown for reference. Each line showing the path of each cell is given a randomly generated cell identification number. The data are loaded into memory as a Pandas data frame and saved to a comma-separated variable file for later analysis.

The final product can then be analyzed and plotted either spatially (as tracks, as in Fig. 3) or time series. For the work presented in this study the binary mask was constructed by thresholding each level of the grid at 35 dBZ. If any level for a given latitude–longitude is above that threshold, then the 2-D binary mask is marked as being part of a cell. Effectively this constitutes a 2-D projection of a 3-D binary field using a cascading AND operator.

A total of 3 years of KHGX data were processed (2015–2017) using aforementioned techniques, mapped to a Cartesian grid, and saved as CF-complaint NetCDF. Processing was parallelized by event, with events identified based on any radar grid exceeding a minimum reflectivity of 0 dBZ. Job scheduling and management was handled by the Dask library (Dask, 2016). Over the 3 years, 7 TB of NEXRAD data resulted in 20 MB of cell track data in a CSV file, yielding an efficient data reduction.

TINT tracks all convective cells. However, as we are interested in statistics of isolated cells, all TINT analyses presented here include only isolated cells. A cell is considered isolated if it is not connected to any other cell by a contiguous path of grid cells exceeding a field threshold. Isolated cells therefore contain at most one peak field value.

3 Results

3.1 Observed case study cell evolution

Starting with the 8 June 2013 case study, Fig. 1 illustrates the routes of three observed features tracked using radar K_DP data, as well as the routes of three simulated features tracked using NU-WRF K_DP. Most tracks are moving roughly northeastward, consistent with boundary layer onshore flow conditions. Both observed and simulated tracks are roughly 10–20 km in distance. The only requirement for their selection was that they be isolated convective cells over land within 100 km of KHGX, such that cross sections exhibited no near neighbors on a subjective basis (as demonstrated below). Relatively few such cells were found in the observations or the simulation owing to lack of isolated cells developing or lack of developing cells remaining isolated, respectively. Although the somewhat disorganized convection observed versus simulated differed, the tracking algorithm operating on K_DP fields yielded satisfactory results for the purposes of this pilot study.

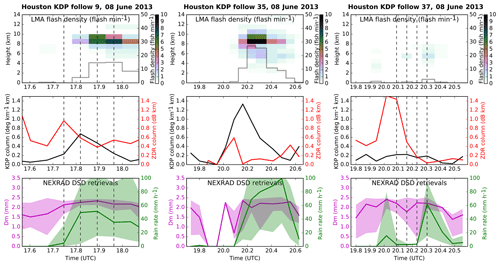
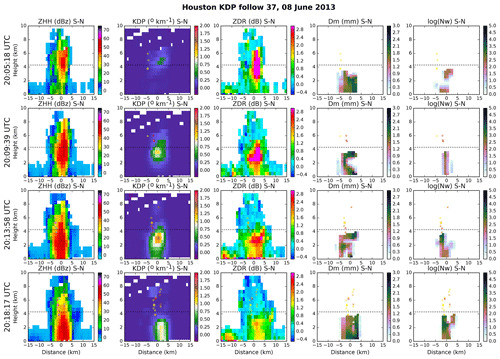
Figure 4 Time series from three K_DP column objects tracked from observations show (top-to-bottom) lightning flashes per KHGX volume time (grey line) and occurrence density as a function of height (see color bar), K_DP and Z_DR column strength (calculated following Eq. 1), and retrieved rain rate and drop D_m. Lightning and rain statistics collected within 2.5 km of the tracked K_DP column center. Vertical dashed lines indicate times of column 9 and 37 cross sections shown in Figs. 5 and 6.

From the three observed tracks numbered 9, 35, and 37 in Fig. 1, Fig. 4 shows the time series of several quantities from track start to track end time, with durations of roughly 30, 55, and 40 min, respectively. The top panels in Fig. 4 show lightning flash rate within 2.5 km of the track, as well as flash occurrences within 2.5 km horizontally as a histogram in the two dimensions of height and time. Here we see that cells 9 and 35 become electrically active roughly halfway through the track, and flashes are most concentrated between 8 and 10 km, just below the homogeneous freezing level (below the −40 ^∘C level). Flash activity in cell 37 remains very weak and is limited to elevations below 8 km. Cells 9 and 37 also show weak flash activity early in their tracks. We note that isolated flashes below the estimated melting level may be artifacts of the processing algorithm used here, which could be refined in future work.

The second row of Fig. 4 shows two quantities calculated following Eq. (1), where ϕ(z) is taken as the average value of K_DP or Z_DR within 2.5 km of the track location. The resulting ξ values, which we refer to as column strengths, allow a more robust measure of the feature K_DP and Z_DR along the track than provided by the two-dimensional grids used by the tracking algorithm (in other words, a value applicable to the whole feature); we defer optimization of the averaging footprint to future work beyond this pilot study. Since we found that the selected tracks follow relatively isolated and coherent reflectivity features in both the observations and the simulation (not shown), we also refer to the tracked features interchangeably as cells and columns, with the understanding that the features tracked contain continuous peaks of ϕ(z) at the resolution observed or simulated (otherwise they would not have been tracked) but they do not necessarily correspond to individual isolated updrafts, however that may be defined. As shown in Fig. 4, K_DP column strength reaches sizable peaks roughly halfway through the track in cells 9 and 35, but cell 37 shows no such peak. By contrast, all cells exhibit a Z_DR column peak during the first half of their track, and that peak is greatest for cell 37. The robustness of the Z_DR column strength appears indicative that all cells loft sufficiently large raindrops sufficiently far above the melting level to generate a strong Z_DR signal (e.g., Kumjian et al., 2012; Snyder et al., 2015).

The third row of Fig. 4 shows the median value and inner half of raindrop D_m values within 2.5 km of the track location at all elevations below the melting level, as well as rain rates retrieved at the lowest elevation angle (0.5^∘). All cells show nearly continuous rain somewhere below z_m from track start to end, as evidenced by the continuity of D_m retrievals, but that rain does not reach the lowest scan elevation until at least 10 min after the start of each track. In cells 9 and 35, the near surface rain reaches peak rates during the second half of the track, beginning around the time that the K_DP column strength reaches its maximum. The considerable spread in surface rain rates indicates localized heavy rain that exceeds 100 mm h⁻¹ in both cells. With the absence of a K_DP column, cell 37 by contrast exhibits weaker and shorter surface rain rate maxima before and after its Z_DR column maximum. The raindrop D_m is quite variable below all three tracked columns, but the behavior seen in cell 9 appears for many tracked cells (not shown), namely, D_m increasing with K_DP column strength and then plateauing at relatively high values along with decreased variance across the analyzed volume.

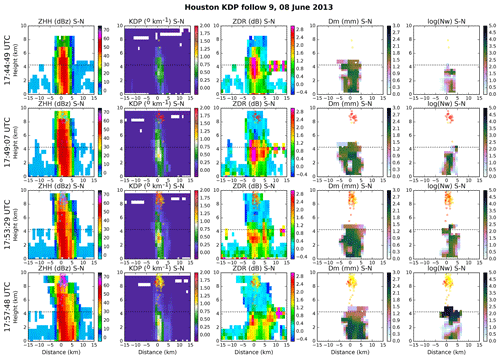
Figure 5 Sequential south–north cross sections from observed K_DP column 9 show (left to right) Z_HH, K_DP, Z_DR, D_m, and N_w. In all panels, the approximate melting level is indicated with a dotted line and each identified lightning flash is overplotted with a dot color indicating time sequence (yellow to red). Full time series shown in Fig. 4.

Figure 6 As in Fig. 5 except for observed K_DP column 37.

Figures 5 and 6 show four sequential north–south cross sections across the tracks of cells 9 and 37, which remain within similar distances from the radar (roughly 60 to 75 km; see Fig. 1), although cell 37 occurs roughly 2 h after cell 9. The cross-section times are indicated with vertical dotted lines in Fig. 4.

In cell 9 (Fig. 5), the first cross section corresponds to the time of peak Z_DR and the last cross section corresponds to the peak in electrical activity. The columns of Fig. 5 show Z_HH, K_DP, Z_DR, D_m, and log(N_w), respectively, with lightning flashes overplotted in colors that indicate age from current to 10 min old. The first time shows the peak in Z_DR column strength, with elevated positive values (>1 dB) visible almost 3 km above the melting level. At this time the K_DP column is already visible, but lightning is absent. Within a rain shaft that is roughly 5–10 km in diameter, D_m is most commonly greater than 1.8 mm and N_w is most commonly less than 300 mm⁻¹ m⁻³. The second time slices capture the peak of the K_DP column strength, concurrent with the beginning of electrical activity. Already at this point the Z_DR column has decreased in height, with some evidence of negative Z_DR values associated with graupel or hail. By the third time, scarcely any Z_DR column remains, but the K_DP column remains visible and the lightning flash rate has intensified. By the fourth and last time, the K_DP has also largely vanished above the melting level. The lightning flash rate has not yet diminished in strength but flashes have lowered a bit in height (see also Fig. 4). The rain shaft has generally widened, with increasingly greater peak values of both D_m and log(N_w) from track start to end.

In cell 37 (Fig 6), a vigorous Z_DR column can be seen initially. The diameters of the cell as measured by radar reflectivity signal (roughly 10 km) and the Z_DR column as indicated by peak values (roughly 4 km) are similar to those of cell 9, but the Z_DR values are larger and the rain shaft appears weaker. However, in contrast to cell 9, K_DP enhancements are weak and almost isolated above the melting level at the first time. Retrieved rain parameters do not extend as high as seen in cell 9, consistent with a lower melting level that could be associated with its later time or more inshore location; owing to the absence of adequate meteorological observations, as discussed in Sect. 4, we assumed fixed z_m and z_f values here. Within the rain shaft initially, occurrences of D_m greater than 2 mm are less common than in cell 9 and N_w values are notably smaller. Enhanced K_DP subsequently descends over the course of the four radar volumes shown (roughly 15 min). At the third time, there is a sharp and localized peak of enhanced K_DP roughly 1 km below the melting level, as in cell 9 at the third time shown, but the diameter of the region where K_DP exceeds 0.5^∘ km⁻¹ (often wider than 5 km) is roughly twice as great as that in cell 9 (roughly 3 km throughout). Perhaps related to the absence of a pronounced K_DP column above the melting level, electrical activity remains weak at all times in cell 37. The evolving rain shaft remains generally weaker than in cell 9, with generally smaller D_m and log(N_w).

A common pattern in observed tracked cells in this particular case study is that first Z_DR column strength peaks, followed by K_DP column strength, and then lightning activity. However, cell 37 and other tracked cells that initiate northeast (downwind) of Houston exhibit the following deviations from that pattern: a greater leading Z_DR peak followed by negligible K_DP peaks above the melting level and much weaker lightning activity. According to satellite retrievals (see Fig. 1), the updraft cells in this latter class appear to exist within a region of generally more elevated aerosol concentration than is found upwind or adjacent to the Houston plume flow. All else being equal, enhanced aerosol could at least initially lead to larger and fewer raindrops (e.g., Storer and van den Heever, 2013), potentially consistent with stronger Z_DR and weaker K_DP rain contributions in cell 37, whereas cleaner conditions could at least initially lead to a more active warm rain process with more numerous and therefore smaller raindrops. Rain shaft retrievals do show generally smaller N_w values below cell 37, consistent with fewer raindrops. There is some hint that D_m at the top of the cell 37 rain shaft at intermediate times shown may be larger than at the top of the cell 9 rain shaft, but D_m values exceeding 2 mm are clearly more common in cell 9, which produces consistently greater rain rates than cell 37 (see Fig. 4). We note that although electrification mechanisms and lightning production are not well understood, increased aerosol concentrations have been more commonly associated with increased rather than decreased electrical activity (Murray, 2016, and references therein). Substantially more complex coupled microphysical and dynamical pathways could also be primary contributors to both Z_DR and K_DP column evolution (e.g., Ryzhkov et al., 2011; Kumjian et al., 2014a; Snyder et al., 2015, and references therein). Owing to the short cell life cycles here, even basic and well observed factors such as height trends below the melting level (e.g., Kumjian and Prat, 2014) could be more indicative of time trends than quasi-steady properties. We defer robust analysis to future work, which would also need to address the role of meteorology, topography, observability (distance from radar), and other factors. Here we make the limited conclusion that such patterns in observed convective cells around Houston can be effectively identified and analyzed in an integrated fashion.

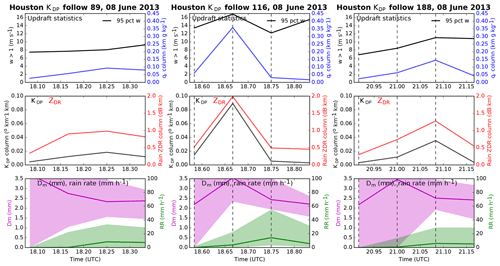
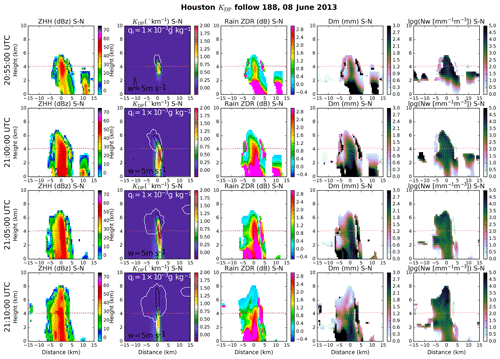
Figure 7 Time series from three K_DP columns tracked from NU-WRF simulation output show (top-to-bottom) updraft strength, q_r, K_DP, and Z_DR column strengths (calculated following Eq. 1), and rain rate and drop D_m and N_w. Updraft and rain statistics collected within 2.5 km of the tracked K_DP column center. Vertical dashed lines indicate times of columns 116 and 188 cross sections shown in Figs. 8 and 9.

3.2 Simulated case study cell evolution

Figure 7 shows time series from three cells tracked from NU-WRF output in the same format as shown in Fig. 4 from observations. The times from track start to end for simulated cells 89, 116, and 188 are each roughly 25–30 min. The isolated cell tracks in the simulation are generally shorter than the isolated cell tracks in observations. Although many longer-lived cells were tracked in the simulation, they tended not to remain isolated. These general differences did not, however, hinder some basic comparisons of observed and simulated isolated cells as follows.

Since we did not attempt forward simulation of lightning flashes here, the first row of panels in Fig. 7 instead shows the 95th percentile of vertical wind speed (w) between the melting and freezing levels within 2.5 km of the track, which could potentially be retrieved from additional radar measurements in a future field campaign (e.g., Collis et al., 2013; North et al., 2017), and the column strength of supercooled q_r. The second row of panels in Fig. 7 shows the time series of column strengths of K_DP and Z_DR estimated from simulated D_m and N_w (see Sect. 2). The third row of panels in Fig. 7 shows the median value and inner half of raindrop D_m values within 2.5 km of the track location at all elevations below the melting level, as well as rain rate at the surface.

All three simulated cells show surface rain beginning shortly after the track start and either declining or continuing after the track end time, as in observed cells, but the peak of median rain rates tends to be at least 5–10 times weaker than retrieved beneath observed cells. Despite weaker precipitation, simulated raindrop D_m values are often near 2.5 mm, greater than observed values often near 2 mm; we note that a fixed droplet number concentration of 100 cm⁻³ was used in the simulation (see Sect. 2) owing to the absence of aerosol size distribution measurements, which are discussed further in Sect. 4. Simulated cells show peaks of q_r, K_DP, and Z_DR column strength roughly collocated in time, consistent with the simplified use of supercooled rain properties to estimate the polarimetric quantities. Simulated Z_DR column strengths are a bit greater than those observed, with variable peak values of 1–2 dB km in each cell that are reached sometime during the inner half of the track duration. Simulated K_DP column strengths are by contrast roughly an order of magnitude weaker than observed, consistent with the rain-based estimate of K_DP, resulting in underestimates aloft (Ryzhkov et al., 2011) that are amplified by height weighting (Eq. 1). Whereas individual well-defined Z_DR peaks tend to consistently lead to K_DP peaks in observations when the latter is present, all column strength peaks in the simulated cells tend to be coincident with one another, as well as with local peaks in the strongest colocated w values to a somewhat lesser degree. Simulated columns tend to show more peakedness than the w statistic, indicating that phase in this particular case study simulation is not as tightly controlled by local updraft strength as might be expected; future work could examine whether a differing w statistic than shown here is more correlated. Simulated surface rain rate peaks with or shortly after the Z_DR column strength, similar to observed cells.

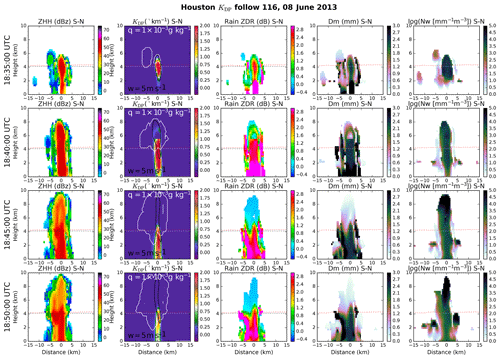
Figure 8 Sequential south–north cross sections from tracked K_DP column 116 show (left to right) calculated Z_HH, K_DP with overplotted contours of updraft strength (w) greater than 5 m s⁻¹ and total ice mixing ratio (Q_i) greater than 0.001 g kg⁻¹, Z_DR, and raindrop D_m and N_w. In all panels the melting level averaged over the inner domain and at a single point (similar to a sounding) are shown by red dotted and black dotted lines, respectively. Full time series shown in Fig. 7.

Figure 9 As in Fig. 8 except for simulated K_DP column 188.

Figures 8 and 9 show north–south cross sections along the tracks of simulated cells 116 and 188 at the times indicated with vertical dotted lines in Fig. 7. In overall structure, both simulated cells are 5–10 km in diameter and their 45 dBZ echoes reach at least 6–8 km, similar to the observed cells shown in Figs. 5 and 6. Simulated K_DP structures appear generally similar to those observed insofar as a single column is found at the center of each cell cross section, but the simulated columns exhibit substantially higher peak values at column center (> 1.75 ^∘ km⁻¹) and do not decrease as rapidly with height. In the case of cell 116, higher peak values abruptly decrease just below 6 km where rain appears to be rapidly frozen. The narrowness of simulated q_r columns is more similar to observed cell 9 than 37.

In contrast to observations, there is a strong increase in simulated rain Z_DR and D_m from the melting level to the surface, an expected signature of raindrop size sorting that can be severely overestimated in two-moment bulk microphysics schemes such as that used here (Kumjian and Ryzhkov, 2010, 2012). The presence of mixed-phase particles complicates interpretation above the melting level. It can nonetheless be noted that simulated rain Z_DR greater than 2 dB reaches 5 km, as in both observed cells shown. Rain size distribution parameters shown from the mixed-phase region of the simulation, where they cannot be retrieved, indicate that weaker Z_DR approaching the homogeneous freezing level in cell 116 is associated with increasing rather than decreasing N_w. Simulated cells commonly exhibit isolated and narrow regions of high Z_DR at supercooled temperatures on their north and south flanks, similar to a less prominent feature on the north flank of observed cell 9.

3.3 Long-term statistics of cell occurrence

Using TINT as described in Sect. 2 enables a long-term statistical analysis of isolated cell occurrence from KHGX observations. From a 3-year climatology, Fig. 10 shows the total number of isolated cells that initiated as a function of month of the year. There is a pronounced period of enhanced occurrence between June and September (approximately the summer months). This raises the question, is the increase in cells over the enhanced period due to an increased density of cells on a given day or more days with convective initiation events? Figure 11 shows the percentage of days in a given month with an initiation event within range of the KHGX radar. There is only a weak seasonal cycle, ranging from a 35 % chance of observing an isolated cell on a given day in December to just over 50 % on a given day in July, indicating that the abrupt increase seen in June in Fig. 10 can be attributed to an increase in cell population density.

Focusing on the enhanced occurrence season, Fig. 12 shows the number of cells that initiate in that season as a function of time of day. The peak at a local time of 13:00 is consistent with a strong diurnal forcing. Furthermore, the lack of any apparent overnight maximum gives us confidence that we are effectively filtering out large-scale systems that have a nocturnal maximum (Nesbitt and Zipser, 2003).

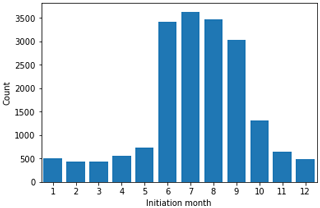
Figure 10 Total number of isolated convective cells that initiated within a 200 km range of the KHGX radar during 2015–2017 by month.

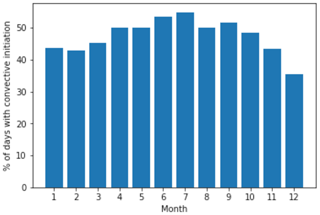
Figure 11 Monthly percentage of days during 2015–2017 with at least one isolated cell initiation within a 200 km range of the KHGX radar.

The 2013 case study investigated above focused on observing the microphysical and dynamical evolution of convective cells in a Lagrangian frame of reference. When investigating the feasibility of deploying an agile radar system to Houston an important question arises: as a function of the radar's unambiguous maximum range, how many cells will the radar see from initiation to dissipation? That is, how many full cell life cycles might the radar system collect? Figure 13 shows the total number of cells as a function of the cell lifetime that would occur within 70, 150, and 200 km of a radar placed at the KHGX site during the enhanced occurrence period. The totals are 441, 2442, and 4834 cells, respectively. If the assumption is made that the 3 years studied are typical, we could therefore expect to see roughly 150, 800, and 1600 full life cycles in a single June through September deployment for a 70 km (e.g., X band), 150 km (C band), and 200 km (S band) radar range, scaling roughly with range area as would be expected if track density were geographically uniform.

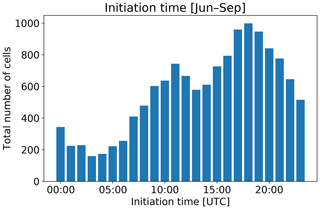
Figure 12 Total number of isolated cells that initiated within a 200 km range of the KHGX radar as a function of time of day during June through September of 2015–2017. The peak at 18:00 UTC corresponds to 13:00 local time.

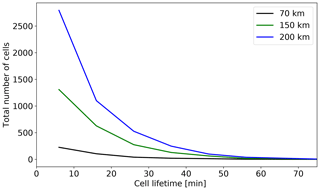
Figure 13 Number of isolated cells that both initiated and dissipated with 70, 150, and 200 km of the KHGX radar as a function of cell lifetime during June through September of 2015–2017. Integrated totals are 441, 2442, and 4843, respectively.

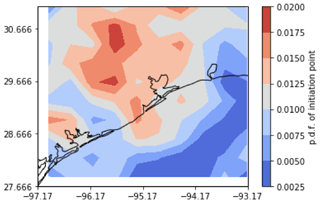
We lastly investigate the initiation location and propagation direction of isolated cells, with relevance for both configuring multi-site deployments and contextualizing measurements. Cells preferentially initiate in the northwest sector of the KHGX range (Fig. 14). For each cell within and outside of the enhanced occurrence period a vector was calculated by linking the location of dissipation to the location of initiation, giving a mean propagation direction. Figure 15 shows the directional cumulative distribution including the enhanced occurrence period versus the remainder of the year. During the enhanced period the cells dominantly propagate slightly east of due southerly, in contrast to south-southwesterly during the rest of the year. This indicates that most convective cells in the enhanced period might be expected to flow from a cleaner Gulf of Mexico air mass into a more polluted Houston air mass. This quirk of climatology suggests that the enhanced period convection lends itself well to studying the impact of aerosols on isolated, precipitating convective cells.

Figure 14 Distribution of isolated cell initiation location during 2015–2017.

4 Conclusions and discussion

The comparison of tracked cells from Houston NEXRAD observations and a NU-WRF simulation demonstrates the potential value of polarimetric weather radar observations for systematically observing and improving the understanding and simulation of convective cell physics. Factors related to the meteorological and aerosol environment, such as the structure of rain size distribution parameters below the melting level, are particularly well suited to analysis using such data. Above the melting level, further investigation of the microphysical properties controlling K_DP and Z_DR signatures is likely to yield additional quantitative constraints on simulation physics; comparing observations with forward-simulated values from well-observed case studies is likely to yield substantial progress, especially using an integrative approach that also considers rain properties below the melting level and overall cell structural evolution. Future simulations could employ bin microphysics or other approaches to avoid errors associated with sedimentation or hydrometeor size distribution shape, as well as mixed-phase particle representation to improve forward simulation of polarimetric signatures (e.g., Ryzhkov et al., 2011; Kumjian et al., 2014a; Snyder et al., 2017a; Matsui et al., 2018b). Forward simulation of lightning flash rates (e.g., Barthe et al., 2010; Basarab et al., 2015) may be simultaneously compared with collocated LMA observations to study the correlations of updraft physics and flash rate signatures such as those shown in Fig. 4.

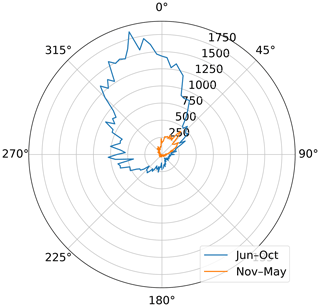
Figure 15 Directional cumulative distribution of propagation direction during June through October versus November through May.

However, cell tracking in both KHGX observations and a simulation also demonstrates the potential value of improved spatiotemporal resolution that could be achieved using mobile research radars. Isolated cell cores are relatively poorly resolved and their evolution is rapid compared with the KHGX operational volume scan rate. K_DP and Z_DR columns associated with updraft cores rise and fall within 10–15 min time spans, as shown in Figs. 4 and 7. Similar conclusions have been reached in past studies (e.g., Loney et al., 2002). Future simulations can obtain arbitrarily higher spatial resolution and output timing, whereas radar measurements are subject to cell distance from the radar and, in this study, the fixed scanning strategies of the operational weather radar. For the purposes of studying isolated convection around Houston, we conclude that substantial value could be added by mobile research radars that could achieve higher resolution and faster scan rates (e.g., Isom et al., 2013; Pazmany et al., 2013; Snyder et al., 2013; Kumjian et al., 2014b). Stein et al. (2015) demonstrate the value of applying a statistical approach to convective cells that are tracked in simulations and in radar observations using an adaptive rapid scan strategy. Sufficient radar resources to perform wind vector retrievals (e.g., Collis et al., 2013; North et al., 2017) could supply observations adequate to statistically study the relationship of cell microphysics and updraft strength.

A statistical analysis of 3 years of Houston KHGX data indicates that there is a period of enhanced isolated convection from June through September, when the number of cells per day dramatically increases, indicating a most favorable season for studying such cells. During this period approximately half the days can be expected to experience cell formation, and isolated cell number follows a strong diurnal cycle with a peak at 13:00 local time. During the June through September period, a hypothetical C-Band radar with a range of 150 km deployed to the site of the KHGX could be expected to observe the full life cycle of roughly 800 cells within range of the radar according to the statistics collected in our 3-year sample. Finally, cells observed would have a dominant propagation vector just west of southerly, indicating that cells forming along the shoreline would likely experience aerosol perturbations corresponding to their proximity to emission sources.

The demanding objectives of a box flux closure experiment (Rosenfeld et al., 2014) would require meteorological measurements at high spatiotemporal resolution at all domain boundaries, but even for the more limited study of updraft physics investigated here as an amendment to such a campaign, we note that routine meteorological data are lacking in the Houston region. The nearest operational soundings are at Lake Charles and Corpus Christi, roughly 200 km to the northeast and 300 km to the southwest, respectively. Obtaining soundings during convective activity, ideally at more than one site within the KHGX domain, would provide a foundation required to establish atmospheric structure, which is of first-order importance to convective cell development. To the extent that improving model physics is an objective, it would be imperative to collect observations that are adequate to demonstrate that simulations reproduce basic properties of atmospheric structure. The capability of state-of-the-art regional models to reproduce basic atmospheric structure should not be assumed a given even when using an assimilation-informed data set for inputs at domain boundaries. Owing to the relatively rapid evolution of the diurnal boundary layer properties with time and distance from the coastline under the target conditions of onshore flow, ground-based in situ and remote-sensing measurements capable of establishing boundary layer height and water vapor mixing ratio would also add great value.

Finally, in situ measurements remain the most robust means of observing cloud-active aerosol properties from the surface to the middle free troposphere. At a minimum, surface measurements of boundary layer CCN spectra and total aerosol number concentration measurements from ideally more than one location in the KHGX domain would allow a means of constraining at least boundary layer fields. To avoid the challenge and expense of a long aircraft campaign, past aircraft measurements from recent field campaigns in the Houston region could provide statistical guidance on expected discontinuities at the boundary layer top (e.g., Lance et al., 2009). Measurement of INPs from at least one surface site would add substantial value; we are aware of no past INP measurements in the Houston region.

Appendix A: Calculation of K_DP

Specific differential phase K_DP for liquid drops at the S band is calculated from the simulated mass-weighted diameter D_m and intercept N_w assuming an exponential drop size distribution

$$\begin{array}{}\text{(A1)}& N\left(D\right)=N_{\text{w}}\exp (-\mathrm{4}D/D_{\text{m}}),\end{array}$$

consistent with model microphysics, and

$$\begin{array}{}\text{(A2)}& K_{\mathrm{DP}}=N_{\text{w}}f\left(D_{\text{m}}\right),\end{array}$$

where

$$\begin{array}{}\text{(A3)}& {\log }_{\mathrm{10}}f\left(D_{\text{m}}\right)=-\mathrm{5.98}+\mathrm{6.64}{\log }_{\mathrm{10}}{D}_{\text{m}}-\mathrm{1.28}({\log }_{\mathrm{10}}{D}_{\text{m}}{)}^{\mathrm{2}},\end{array}$$

with D_m in millimeters, N_w in reciprocal cubic meters per millimeter, and K_DP in degrees per kilometer. Equations (A2)–(A3) are derived for the radar wavelength 11 cm.