Method to measure the size-resolved real part of aerosol refractive index using differential mobility analyzer in tandem with single-particle soot photometer

Knowledge on the refractive index of ambient aerosols can help reduce the uncertainties in estimating aerosol radiative forcing. A new method is proposed to retrieve the size-resolved real part of the refractive index (RRI). The main principle of deriving the RRI is measuring the scattering intensity by a single-particle soot photometer (SP2) of size-selected aerosols. This method is validated by a series of calibration experiments using the components of the known RRI. The retrieved size-resolved RRI covers a wide range, from 200 to 450 nm, with uncertainty of less than 0.02. Measurements of the size-resolved RRI can improve the understanding of the aerosol radiative effects.

1 Introduction

Aerosols exert significant influence on the earth energy budget by scattering and absorbing radiation (Ramanathan and Carmichael, 2008). Great uncertainties still remain when estimating the aerosol-effective radiative forcing (RF; Ghan and Schwartz, 2007), and an accurate estimation of the aerosol optical properties can help reduce the RF variations. The optical properties of the ambient aerosol particles are determined by their particle size and complex refractive index (RI; $m=n+ki$; Bohren and Huffman, 2007; Levoni et al., 1997). Despite the fact that the ambient aerosol particle size distribution can be measured with high accuracy (Wiedensohler et al., 2012), an accurate measurement of the ambient aerosol RI remains challenging. The RI is also widely used in remote sensing (Redemann et al., 2000; Dubovik, 2002; Zhao et al., 2017) and atmospheric modeling (Ghan and Schwartz, 2007; Kuang et al., 2015) because the aerosol single scattering albedo (SSA) and aerosol-scattering-phase function are highly related to the RI. At the same time, a small uncertainty in the real part of the RI (RRI) can lead to great uncertainties when estimating the aerosol RF. Zarzana et al. (2014) found that a variation of 0.003 in the RRI can lead to uncertainties of 1 % in RF for non-absorbing ammonium sulfate particles. Moise et al. (2015) estimated that the RF would increase by 12 % if the RRI varies from 1.4 to 1.5. Valenzuela et al. (2018) reported that the uncertainties in RF are estimated to be 7 % when the aerosol RRI varies by 0.1. Therefore, it is pressing that the uncertainties of the RI be reduced when estimating the RF.

Many methods were proposed to derive the RRI. The RRI can be estimated with the linear volume average of the known aerosol chemical components by

$$\begin{array}{}\text{(1)}& n={\sum }_i{f}_i{n}_i,\end{array}$$

where f_i and n_i are the volume fraction and known partial refractive index of ith component (Wex et al., 2002; Hand and Kreidenweis, 2002; Hänel, 1968; Liu and Daum, 2008). The aerosol RRI can also be calculated by a partial molar refraction approach (Stelson, 1990; Hu et al., 2012) which is essentially consistent with the linear volume method (Liu and Daum, 2008). The ambient aerosol RRI can be derived by synthetically using the radiative transfer calculations and the ground-based solar extinction and scattering measurements (Wendisch and Hoyningen-Huene, 1994, 1992). Sorooshian et al. (2008) developed a method to measure the aerosol RRI based on the differential mobility analyzer (DMA) and optical particle counters (OPCs). The RRI could be retrieved from the known particle size from the DMA and the aerosol-scattering intensity from the OPC for aerosol particles larger than 500 nm. The scanning mobility particle sizer (SMPS) and OPC were used in combination to derive the RRI by aligning the particle size distributions in the instrument-overlap regions (Hand and Kreidenweis, 2002; Vratolis et al., 2018). The aerosol-effective RRI was also retrieved by applying the Mie scattering theory to the aerosol particle number size distribution (PNSD), aerosol bulk scattering coefficient and aerosol absorbing coefficient data (Cai et al., 2011; Liu and Daum, 2000). Spindler et al. (2007) retrieved the aerosol RRI value by using the cavity ring-down spectroscopy for measuring the scattering and absorbing properties of bulk aerosols. Eidhammer et al. (2008) measured the light scattering at different angles and retrieved the RRI. Similarly, the aerosol RRI was retrieved by measuring the aerosol-phase function (Barkey et al., 2007). Recently, a method using single-particle mass spectrometry was proposed to measure the aerosol RRI (Zhang et al., 2015). At the same time, the aerosol time-of-flight mass spectrometer proved to be capable of measuring the aerosol RRI (Moffet et al., 2008). The aerosol RRI can also be retrieved from the Mie spectroscopy by using the optical tweezers in the laboratory (Shepherd et al., 2018).

Many studies show that aerosols of different diameters share different properties, such as shape (Zhang et al., 2016; Peng et al., 2016), density (Qiao et al., 2018), aerosol hygroscopicity (Wang et al., 2017) and, most importantly, the chemical components (Liu et al., 2014; Hu et al., 2012). Thus, there might be significant variations in the aerosol RRI for aerosols of different diameters because the aerosol RRI is highly related to the aerosol density (Liu and Daum, 2008) and chemical components (Stelson, 1990). On the other hand, information on the size-resolved aerosol RRI can help with studying the chemical information and the aging process of aerosols among different diameters. Therefore, measurement of the size-resolved aerosol RRI is necessary.

Up to now, there is little information in the literature on the size-resolved ambient aerosol RRI (Ebert et al., 2002, 2004; Kandler et al., 2007). Traditionally, the size-resolved ambient aerosol RRI is estimated by measuring the molar fraction or volume fraction of the main aerosol chemical compositions. However, the influence of the organic component on the aerosol RRI is ignored. The organic component contributes more than 20 % of the total aerosol component in the North China Plain (Hu et al., 2012; Liu et al., 2014). At the same time, the RRI of the organic aerosol changes significantly between 1.36 and 1.66 (Moise et al., 2015). Ignoring the organic component may lead to significantly uncertainties when estimating the aerosol RRI. There were no techniques, to our knowledge, that directly measure the size-resolved aerosol optical properties and derive the size-resolved aerosol RRI.

In this study, a novel method is proposed to measure the size-resolved ambient aerosol RRI by using a DMA in tandem with a single-particle soot photometer (SP2). The principle of the system is using the SP2 to measure the scattering properties of size-selected aerosols. Knowing the aerosol diameter and corresponding scattering intensity, the size-resolved aerosol RRI can be retrieved based on the Mie scattering theory. This proposed method can measure the ambient aerosol RRI over a wide size range and with high accuracy. The measurement system is employed in a field campaign in the North China Plain, and the corresponding results are discussed further.

The structure of this paper is as follows: Sect. 2 provides the instruments setup and details of the instrument. The method for retrieving the size-resolved aerosol RRI is given in Sect. 3. Section 4 shows the discussions about the uncertainties of the proposed method and field measurements results of the size-resolved aerosol RRI. Conclusions are discussed last.

2 Instrument

2.1 Instrument setup

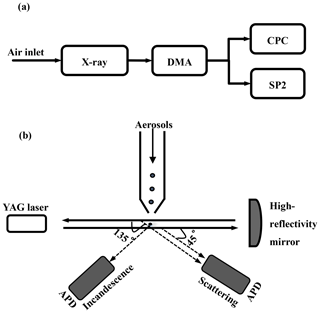
The instrument setup is schematically shown in Fig. 1a. Firstly, the dried sample aerosols are guided to a X-ray soft diffusion charger and then lead to a DMA (Model 3081, TSI, USA). The quasi-monodisperse aerosols that pass though the DMA at a given diameter are then drawn into an SP2 to measure the aerosol-scattering properties with a flow ratio of 0.12 L min⁻¹ and a condensation particle counter (CPC; Model 3776, TSI, USA) to count the aerosol number concentration with a flow ratio of 0.28 L min⁻¹. Thus, the sample flow (Q_a) of the DMA is 0.4 L min⁻¹. Accordingly, the sheath flow (Q_sh) of the DMA is 4 L min⁻¹. The DMA is set to scan the aerosol diameter from 12.3 to 697 nm over a period of 285 s and repeats after a pause of 15 s. The combination of the DMA, CPC and SP2 can provide information on aerosol PNSD and size-resolved RRI.

Figure 1 (a) Schematic of the measurement system. (b) Diagram of SP2 chamber.

On 8 June 2018, the measurement system was employed at the field measurement of the AERONET station of BEIJING_PKU (39^∘59^′ N, 116^∘18^′ E) to test the reliability of retrieving the ambient size-resolved RRI. This measurement site is located in the northwest of the city of Beijing, China, and is about 1.8 km north of the Zhongguancun, Haidian district, which is one of the busiest areas in Beijing. It is surrounded by two main streets: Zhongguancun North Street to the west and Chengfu Road to the south. This site can provide representative information on the urban roadside aerosols (Zhao et al., 2018).

2.2 DMA

When a voltage (V) is applied to the DMA, only a narrow size range of aerosol particles, with the same electrical mobility (Z_p), can pass through the DMA (Knutson and Whitby, 1975). The Z_p is expressed as

$$\begin{array}{}\text{(2)}& Z_{\mathrm{p}}={\displaystyle \frac{Q_{\mathrm{sh}}}{\mathrm{2}\mathit{\pi }VL}}\ln \left({\displaystyle \frac{r_{\mathrm{1}}}{r_{\mathrm{2}}}}\right),\end{array}$$

where Q_sh is the sheath flow rate, L is the length of the DMA, r₁ is the outer radius of annular space and r₂ is the inner radius of the annular space. The transfer function refers to the probability that a particle with a certain electrical mobility can pass through the DMA. For a given V, the transfer function is shaped like a triangle, with the peaking value of 100 % and a half width (HW) of

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }{Z}_{\mathrm{p}}=Z_{\mathrm{p}}{\displaystyle \frac{Q_{\mathrm{a}}}{Q_{\mathrm{sh}}}}.\end{array}$$

The aerosol Z_p, which is highly related to the aerosol diameter (D_p) and the number of elementary charges on the particle (n), is defined as

$$\begin{array}{}\text{(4)}& Z_{\mathrm{p}}={\displaystyle \frac{neC\left(D_{\mathrm{p}}\right)}{\mathrm{3}\mathit{\pi }\mathit{\mu }{D}_{\mathrm{p}}}},\end{array}$$

where e is the elementary charge, μ is the gas viscosity coefficient, and C(D_p) is the Cunningham slip correction that is defined by

$$\begin{array}{}\text{(5)}& C=\mathrm{1}+{\displaystyle \frac{\mathrm{2}\mathit{\tau }}{D_{\mathrm{p}}}}\left(\mathrm{1.142}+\mathrm{0.558}{e}^{-\frac{\mathrm{0.999}{D}_{\mathrm{p}}}{\mathrm{2}\mathit{\tau }}}\right),\end{array}$$

where τ is the gas mean-free path.

Based on the discussion above, the aerosols that pass through the DMA with the same Z_p can have different D_p values and different elementary charges.

2.3 SP2

The SP2 is a widely used instrument that can measure the optical properties of every single particle. The measurement principle and instrumental setup of the SP2 have been discussed in detail previously (Stephens et al., 2003; Schwarz et al., 2006) and will be briefly described here. When the sample aerosol particles pass through the continuous Nd:YAG laser beam at 1064 nm with the circulating power of about 1 mW cm⁻² in the cavity, eight sensors distributed at four directions synchronously detect the emitted or scattered light by using an avalanche photodetector (APD) at different angles (45 and 135^∘). For each direction, the two APDs sample the same signal with different sensitivities to get a wider measurement range. The low-gain channels are less sensitive to the measured signal and can be used to measure the stronger signal of larger particles. Accordingly, the high-gain channels are more sensitive to the measured signal and can be used to measure the weaker signal of smaller particles. The optical head of the SP2 is shown schematically in Fig. 1b.

In this study, we utilize signals from four channels of the SP2: two of them measure the scattering signals, and another two measure the incandescent light between 350 and 800 nm. The peak height (H) of the incandescence signals is used to infer whether the sampled aerosol contains black carbon (BC). If the H of the incandescence signal is larger than 500, the sample aerosol contains BC and the scattering signals should deviate from the signals of pure scattering aerosols. Those sample aerosols are not considered when dealing with the aerosol-scattering signals. This is achieved by just studying the signals when the particles are recognized as pure scattering particles.

Despite some aerosol particles being internally mixed with a small BC core, whose incandescence signal is below the detection threshold of SP2, we demonstrate that these particles have little influence on the retrieved aerosol RRI. At the same time, there are some weakly absorbing organic components that absorb light intensity in the near-infrared range, which were termed as brown carbon (BrC). These BrC components have insignificant influence on the retrieving of the aerosol RRI, which will be discussed in detail in Sect. 4.2. Thus, the imaginary part of complex refractive index is set to zero in the following discussion.

3 Methodology

3.1 Scattering intensity measured by the SP2

From Fig. 1b, the APDs of the SP2 receive signals that were scattered by the sampled aerosols in a certain small range at 45 and 135^∘. Thus, the scattering intensity (S) measured by the APD can be expressed as

$$\begin{array}{}\text{(6)}& S=C_{\mathrm{0}}\cdot I_{\mathrm{0}}\cdot \mathit{\sigma }\cdot ({\mathrm{PF}}_{\mathrm{45}{}^{\circ }}+{\mathrm{PF}}_{\mathrm{135}{}^{\circ }}),\end{array}$$

where I₀ is the laser's intensity, σ is the scattering coefficient of the sampled aerosols, PF₄₅ and PF${}_{\mathrm{135}{}^{\circ }}$ are scattering phase function at 45 and 135^∘ respectively of the sampled aerosols, and C₀ is a constant that is determined by the distance from the aerosol to the APD and the area of the APD. The scattering intensity of the aerosol is recorded as the H of the scattering signals in SP2. The following calibration studies show that the scattering intensity S is highly related to the H measured by SP2. Therefore, the SP2 can be used as a powerful tool to measure the scattering signals of the sampled aerosols, thus determining the corresponding scattering intensity.

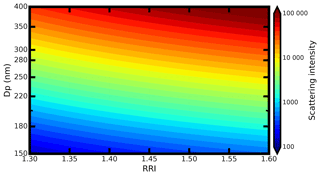
Based on the Mie scattering theory, the scattering coefficient σ can be calculated by integrating the square of scattering intensity function $Q(\mathit{\theta },x,\mathrm{RRI})$ from 0 to 180^∘. Angle θ is defined as the angle between the light incident direction and scattering-light direction. The size parameter x is defined as $x=\frac{\mathit{\pi }{D}_{\mathrm{p}}}{\mathit{\lambda }}$, where λ is the light incident wavelength. The scattering phase function can be directly derived from $S\left(\mathit{\theta },x,m\right)$, too. Therefore, the σ, PF${}_{\mathrm{45}{}^{\circ }}$ and PF ${}_{\mathrm{135}{}^{\circ }}$ in Eq. (6) are determined by the D_p and RRI of the aerosol. The amount of scattering signals from the sample aerosol varies with the aerosol D_p and RRI (Bohren and Huffman, 2007). The scattering intensity at different aerosol diameters and RRI is calculated based on Eq. (6) and shown in Fig. 2. The C₀ is assumed to be 1 here. From Fig. 2, we can see that the aerosol-scattering intensity increases monotonously with the increasing aerosol RRI at a given D_p, which makes it possible to retrieve the aerosol RRI with given D_p and the scattering intensity.

Figure 2 The distribution of the aerosol-scattering intensity at a different D_p and different RRI.

Bridging the scattering H values measured by the SP2 scattering channel and the scattering intensity S defined by Eq. (6) is achieved by calibrating the SP2 with ammonium sulfate. The instrument setup of the calibration procedure is the same as that described in Sect. 2.1. The diameters of the aerosols passing through the DMA are manually changed from 100 to 450 nm with a step of 10 nm. For each diameter, the scattering H value and incandescence signal of every particle are analyzed. When calibrating, there is no aerosol that has an incandescence signal exceeding 1000 (this value depends on the stability of the instrument and working conditions; this can be different for different instruments), which means that the SP2 works stably and the incandescence signal channel can distinguish the BC-containing aerosols well. With the calibration, the relationship between the measured H and theoretically calculated S can be determined.

The procedure of retrieving the RRI is summarized as follows: (1) measuring the scattering H values at a given D_p, (2) transferring the H into to S by the established relationship from calibration, and (3) calculating the refractive index with the given D_p and S by using Eq. (6).

3.2 Multiple charging

Figure S1 in the Supplement gives the aerosol-scattering H probability distribution under different aerosol diameters. For each diameter, the distributions of the scattering H may have more than one mode for both the high-gain and low-gain channels. The following discussions would give an explanation about the multiple mode distributions of H.

For each mode, the number of recorded aerosol particles at a given H is fit by the log-normal distribution function

$$\begin{array}{}\text{(7)}& N\left(H\right)={\displaystyle \frac{N_{\mathrm{0}}}{\sqrt{\mathrm{2}\mathit{\pi }}\log \left({\mathit{\sigma }}_{\mathrm{g}}\right)}}\cdot \exp \left[-{\displaystyle \frac{\log \left(H\right)-\log \left(H_{\mathrm{0}}\right)}{\mathrm{2}{\log }^{\mathrm{2}}\left({\mathit{\sigma }}_{\mathrm{g}}\right)}}\right],\end{array}$$

where σ_g is the geometric standard deviation, H₀ is the geometric mean value of H and N₀ is the number concentrations for a peak mode. The geometric standard deviation is highly related to the half width of the transfer function (Eq. 3). The H₀ is further used for discussion in the following part.

The H₀ values corresponding to different elementary charges are labeled with different markers in Fig. 3. The σ_g is fitted to be a small range at 1.182±0.02 for different modes and different aerosol diameters. In the following discussion, we conclude that the different H₀ values in Fig. 3 represent the aerosols being charged with a different number of elementary charges. Based on the Mie scattering theory (Bohren and Huffman, 2007), the scattering intensity increases with increasing D_p, which implies that the H₀ of the singly charged aerosol should increase with the increment of D_p. Thus, the black square markers in Fig. 3 represent the aerosols that are singly charged. At the same time, the relationships between the H₀ and D_p can be interpolated.

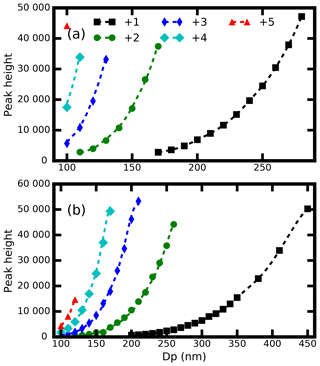
Figure 3 The geometric mean peak height for different diameters of the high-gain channel. The markers gives the measured values, and the dotted line shows the theoretically calculated value. Different colors represent the different number of elementary charges.

Other colored markers represent the aerosols having more than one charge. We calculated the corresponding diameter (${\stackrel{\mathrm{̃}}{D}}_{\mathrm{p}}$) of the aerosols that share the same Z_p but different charges with those particles that have a diameter of D_p with one charge. Next the corresponding $\stackrel{\mathrm{̃}}{H_{\mathrm{0}}}$ at ${\stackrel{\mathrm{̃}}{D}}_{\mathrm{p}}$ ia calculated. Then the relationship between $\stackrel{\mathrm{̃}}{H_{\mathrm{0}}}$ and D_p is shown in the dashed line in Fig. 3a. From Fig. 3a, the calculated H₀ shows good consistency with the measured H₀.

From the discussion above, we conclude that the SP2 can only detect those ammonium sulfate aerosols with the diameter larger than 160 nm. However, the ambient aerosol RRI is always lower than that of ammonium sulfate (Liu and Daum, 2008); thus the lower detecting limit of the ambient scattering aerosols should be larger than 160 nm. The measured H₀ values of the SP2 scattering low-gain channel signals are shown in Fig. 3b. From Fig. 3b, the same results can be deduced as those of the high-gain channel signals.

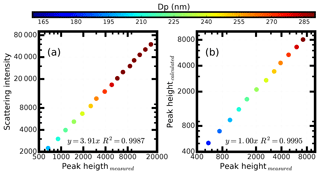
Figure 4 (a) The relationship between the scattering peak height from the SP2 high-gain scattering channel when calibrating by using the ammonia sulfate, and (b) the comparison between the measured scattering peak height from SP2 high-gain scattering channel using the ammonia chloride and the calculated scattering peak height using the Mie scattering theory. Different colors represent the results at different diameters.

Figure 4a gives the relationships between the calculated scattering intensity and the SP2 aerosol-scattering H₀ at different diameters. When calculating the scattering intensity, the RRI value of ammonium sulfate is set to 1.521 (Flores et al., 2009), and the C₀ in Eq. (6) is set to unity. The aerosol-scattering intensity shows good consistency with the peak height (R²=0.9992), which to some extent reflects the high accuracy of our proposed method. When regressing the scattering intensity on the measured peak height, the value 0.36 was obtained for the slope, which means that the scattering intensity can be calculated by multiplying the peak height by a factor of 0.36.

3.3 Validation of the calibration

Ammonium chloride is used to validate the method of deriving the RRI from SP2. The RRI value of ammonium chloride is 1.642 (Lide, 2006). The scattering H of the ammonium chloride under different diameters is measured and analyzed. Figure 4b shows the comparison between the measured scattering high-gain peak heights and the theoretical peak heights at different aerosol diameters. Results show that the measured peak heights and the calculated ones are well correlated with R²=0.9994, which means that the DMA and SP2 can be used to derived the aerosol RRI with high accuracy.

Figure S2 gives the corresponding results of the scattering low-gain channel. In Fig. S2, the relationship between the aerosol-scattering peak height of the low-gain channel and the scattering intensity is determined. At the same time, the comparison between the measured peak height and the calculated peak height shows good consistency, too.

Figure 5 The measured probability of the size-resolved RRI (shaded portion), the measured mean PNSD (the solid line) and the mean scattering size distribution (the dotted line).

4 Results and discussion

4.1 Field measurements

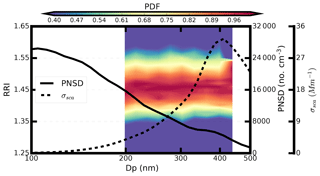
Figure 5 shows the measured average probability distribution of the ambient size-resolved RRI and the measured mean PNSD over 2 h during the measurement. From Fig. 5, we can see that the derived RRI is 1.46±0.02 and does not vary significantly with a diameter between 199 nm and 436 nm. The aerosol chemical component may not vary significantly for different diameters during the measurement. Another field measurement shows that the measured RRI varies significantly from 1.47 at 198 nm to 1.54 at 450 nm, as shown in Fig. S4.

The measured aerosol PNSD during the measurement has a maximum of 26 400 # cm⁻³ at 107 nm. The mass concentration of the BC measured by the SP2 is 6.31 µg m⁻³. Based on the measured PNSD and the measured RRI, the size distribution of the scattering coefficient is calculated based on the Mie scattering theory. The results in Fig. 5 show that the measured RRI diameter range covers most of the aerosols that contribute a fraction of 0.63 to the aerosol-scattering properties, with an integrated scattering coefficient at 385 Mm⁻¹. Thus, the derived size-resolved RRI of this range is representative of the ambient aerosol-scattering properties.

4.2 Uncertainty analysis

4.2.1 Uncertainties from SP2

The factors that influence the accuracy of retrieving RRI include the aerosol scattering H measured by SP2 and the aerosol diameter selected by the DMA.

The uncertainties of the selected diameter by the DMA are well characterized based on Eqs. (2) and (3). The uncertainties from the DMA transfer function can be avoided by fitting the scattering H using the log-normal distribution function. However, the uncertainties of the measured H from the SP2 remain unknown. The half width (ΔZ_p∕Z_p) of the transfer function is 0.1 times the scanning diameter, which means that the geometric standard deviation of the aerosol PNSD selected by the DMA is estimated to be 1.102. At the same time, the measured geometric standard deviation of the measured H mode by SP2 is 1.182. Thus, the additional broadening by the H distribution is 1.073, which implies that the geometric standard deviation of the measured H from the SP2 is estimated to be 1.073; its corresponding uncertainty is 6.8 %.

The uncertainties of the retrieved RRI to the variations in the measured H are analyzed. Firstly, we calculated the theoretical scattering intensity that can be measured by the SP2 for a given aerosol diameter and RRI. The scattering intensity is changed by ±6.8 %, and the corresponding RRI can be derived using the given aerosol diameter and changed scattering intensity. Finally, the derived RRI is compared with the given aerosol RRI. The uncertainties are analyzed for different aerosol diameters and a different RRI. The corresponding results are shown in Fig. 6. The variations in RRI increase with the increment of RRI but decrease with the increment of the D_p. For most ambient aerosols, the RRI ranges from 1.4 to 1.5 and corresponds to a variation in RRI of 0.015.

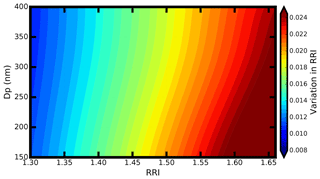
Figure 6 The variation in RRI for different kinds of aerosols that have different diameters and a different RRI.

Table 1 lists the retrieved ammonium chloride RRI under different diameters. The absolute difference between the retrieved RRI and theoretical values is always smaller than 0.02 regardless of the particle diameter, which means that the measured RRI is in line with the theoretical one. Thus, we conclude that the uncertainty of the retrieved RRI is within 0.02 due to the uncertainties of SP2 measurement.

Table 1 The retrieved RRI and the absolute difference between the retrieved RRI and the theoretical RRI for different ammonia chloride diameters.

4.2.2 Uncertainties due to BC exist

There are some particles with a small soot core, and the incandescence signal is below the detection threshold of SP2. The derived aerosol RRI should be influenced by the small soot core. Uncertainties might result when deriving the RRI for these BC-containing aerosols. With the calibration of the SP2 with Aquadag soot particles, we concluded that the SP2 cannot detect the soot particles lower than 80 nm, which is shown in detail in the Supplement in Sect. S3.

We derived the aerosol equivalent refractive index when the aerosols have BC cores lower than 80 nm with two steps. The scattering strength of the BC-containing aerosols are first calculated based on Mie scattering theory. Then the scattering strength is used for deriving the equivalent refractive index with the assumption that the BC-containing aerosols are pure scattering aerosols.

Monte Carlo simulations were applied to investigate the influence of the BC core on the retrieved ambient aerosol RRI. Firstly, the aerosol with a diameter between 200 nm and 500 nm was chosen. Then the core diameter are randomly determined lower than 80 nm. The core diameters flow the log-normal distribution with the mean core diameter of 120 nm (Raatikainen et al., 2017). When calculating the scattering strength, the complex refractive index of the core 1.8+0.54i (Zhao et al., 2018) is used. The complex refractive of the shell adopts the measured mean values (1.46+0i) during the field measurements. The scattering strength can be calculated with the above information. With the calculated scattering strength, the equivalent real part of the refractive index (RRI) can be derived with the assumption that the aerosols are pure scattering aerosols. If the core diameter is 0, then the derived aerosol equivalent aerosol RRI should be 1.46.

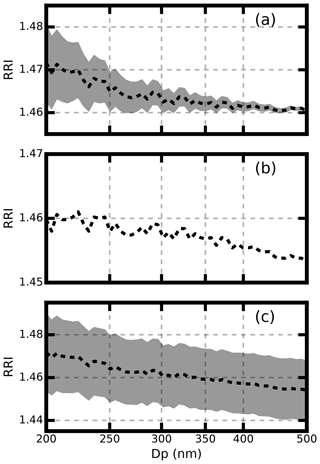
For each aerosol diameter, the Monte Carlo simulations were conducted 10 000 times. Figure 7a gives the retrieved aerosol equivalent RRI at different diameters. Results show that the retrieved aerosol equivalent RRI is larger than 1.46 for all of the given aerosol diameters. When the aerosols have a BC core, the scattering strength is larger than that of pure scattering aerosols with the same aerosol diameter. The derived mean equivalent RRI tends to be closer to 1.46 when the aerosol diameter is larger, where the BC core contributes less and the influence of the BC core is smaller. The derived mean aerosol equivalent to the RRI is 1.47 and 1.462 at 200 and 500 nm respectively. At the same time, the uncertainties associated with the equivalent RRI are larger when the aerosol diameter are smaller. We conclude that the uncertainties associated with BC core are smaller than 0.01 when the aerosol diameter is larger than 250 nm. The maximum of the difference of the derived RRI is 0.02.

Figure 7 The retrieved aerosol RRI at different aerosol diameters. The shaded portion represents the 5th and 95th percentiles.

4.2.3 Uncertainties from BrC

There is some BrC that absorbs the light intensity in the near-infrared range. The imaginary part of the refractive index at a given wavelength λ (k_λ) of the BrC can be calculated as

$$\begin{array}{}\text{(8)}& k_{\mathit{\lambda }\mathrm{1}}=k_{\mathit{\lambda }\mathrm{2}}\times {\left({\displaystyle \frac{\mathit{\lambda }\mathrm{2}}{\mathit{\lambda }\mathrm{1}}}\right)}^w,\end{array}$$

where w is defined by ratio of mass of BC to the organic aerosol (R; Saleh et al., 2015), with

$$\begin{array}{}\text{(9)}& w={\displaystyle \frac{\mathrm{0.21}}{R+\mathrm{0.07}}}.\end{array}$$

Based on the work of Saleh et al. (2015), the k₅₅₀ can be expressed as

$$\begin{array}{}\text{(10)}& k_{\mathrm{550}}=\mathrm{0.016}\times {\log }_{\mathrm{10}}\left(R\right)+\mathrm{0.04}.\end{array}$$

The value R ranges between 0.09 and 0.35 for different types of aerosols (Saleh et al., 2015). Based on Eqs. (8), (9) and (10), the k₁₀₂₄ ranges between 0.01 and 0.024. The maximum value 0.024 is used for further analysis.

The uncertainties of the retrieved RRI when ignoring the effect of BrC are analyzed. Firstly, the scattering-light intensity at a given diameter with a refractive index of 1.46+0.024i is calculated using the Mie model. Then the corresponding RRI is retrieved using the given diameter and the calculated light intensity with the assumption that these are pure scattering aerosols. The retrieved aerosol RRI values for different aerosol diameters are shown in Fig. 7b. For the light-absorbing particles, their scattering-light intensity is smaller than that of the pure scattering particles with the same diameter and RRI. Therefore, the retrieved aerosol RRI is underestimated for most of the conditions. The differences between the given RRI value (1.46) and retrieved RRI value are lower than 0.006 for all of the diameters, as shown in Fig. 7b. The BrC component has little influence on the retrieved aerosol RRI.

4.2.4 Summary of the uncertainties

Monte Carlo simulations were conducted to study the influence of the above three uncertainty sources. Four steps are involved in the Monte Carlo simulations. First, the core diameter of an aerosol particle at a given diameter is randomly given, with the core diameter following the log-normal distribution with the mean core diameter of 120 nm (Raatikainen et al., 2017). The refractive index of the core is set to be the same as that in Sect. 4.2.2. The RRI of the shell uses the measured mean value 1.46. The imaginary part of the shell is determined randomly with a mean value of 0.023. Second, the light-scattering intensity can be calculated using the Mie model and the information in step one. Then the light-scattering intensity was randomly changed with uncertainties of 6.8 %. Finally, the changed light-scattering intensity is used to derive the aerosol RRI with the given diameter and the assumption that the particles are pure scattering particles.

The aerosol diameters were changed from 200 to 500 nm, and the simulations were conducted 10 000 times for each diameter. The overall uncertainties are shown in Fig. 7c. The uncertainties from SP2 instrument measurement do not lead to bias of the retrieved aerosol RRI. When the aerosol diameter is lower than 300 nm, the influence of the BC core is more important than the influence of BrC. The retrieved RRI tends to be overestimated when the aerosol is lower than 300 nm. When the aerosol diameter is larger than 300 nm, the influence of BrC domains and the retrieved aerosol RRI are underestimated. However, the bias caused by BC and BrC is lower than 0.01. For most of the conditions, the retrieved aerosol RRI is within the range of 1.46±0.02. Thus, we conclude that the uncertainty of the retrieved RRI is 0.02 when considering all of the factors.

5 Conclusions

Knowledge on the microphysical properties of ambient aerosols is import for better evaluating their radiative forcing. The aerosol RRI is a key factor that determines the aerosol-scattering properties. In this study, a new method to measure the ambient aerosol RRI is developed by synthetically using a DMA in tandem with an SP2. This method can continuously measure the size-resolved RRI over a wide range between 198 and 426 nm. At the same time, it is free from the influence of the BC-containing aerosols.

The basic principle of measuring the size-resolved RRI is to select the aerosols at a certain diameter by the DMA and measure the corresponding scattering intensity by the SP2. The relationship between the aerosol-scattering intensity and the peak height of the scattering signal channels is determined by calibrating the SP2 using ammonium sulfate (RRI =1.521).

The method is validated by measuring the size-resolved RRI of the ammonium chloride with the RRI value of 1.642 as the sample aerosol, and the corresponding derived value is 1.642±0.02. There are three factors that influence the accuracy of derived aerosol RRI. The measured scattering intensity by SP2 has an uncertainty of 0.68 %, which can lead to the uncertainties of the derived RRI values less than 0.15. There are some particles with a small soot core, and the incandescence signal is below the detection threshold of SP2. The light-scattering intensity of these particles increases compared with that of the pure scattering particles with the same aerosol diameters. The retrieved aerosol RRI values can be overestimated by up to 0.02. Some BrC absorbs the light intensity in the near-infrared range. The corresponding scattering intensity is weaker than that of pure scatter particles for the same diameter, and the retrieved aerosol RRI value can be underestimated by up to 0.006. Based on Monte Carlo simulations, the uncertainty of the retrieved RRI is 0.02 when considering all of the factors.

This instrument is employed at a field measurement at the AERONET PKU station, and the size-resolved RRI of the ambient aerosols is 1.46 and does not show significant variation among the diameter. The corresponding aerosol diameter range, which can be detected by SP2 to derive the RRI, covers most of the aerosol scattering. Thus, the derived size-resolved RRI of this range can be used as a good representative of the ambient aerosol-scattering properties.