Minimizing aerosol effects on the OMI tropospheric NO₂ retrieval – An improved use of the 477 nm O₂ − O₂ band and an estimation of the aerosol correction uncertainty

Global mapping of satellite tropospheric NO₂ vertical column density (VCD), a key gas in air quality monitoring, requires accurate retrievals over complex urban and industrialized areas and under any atmospheric conditions. The high abundance of aerosol particles in regions dominated by anthropogenic fossil fuel combustion, e.g. megacities, and/or biomass-burning episodes, affects the space-borne spectral measurement. Minimizing the tropospheric NO₂ VCD biases caused by aerosol scattering and absorption effects is one of the main retrieval challenges from air quality satellite instruments. In this study, the reference Ozone Monitoring Instrument (OMI) DOMINO-v2 product was reprocessed over cloud-free scenes, by applying new aerosol correction parameters retrieved from the 477 nm O₂−O₂ band, over eastern China and South America for 2 years (2006–2007). These new parameters are based on two different and separate algorithms developed during the last 2 years in view of an improved use of the OMI 477 nm O₂−O₂ band:

1. the updated OMCLDO2 algorithm, which derives improved effective cloud parameters,

2. the aerosol neural network (NN), which retrieves explicit aerosol parameters by assuming a more physical aerosol model.

The OMI aerosol NN is a step ahead of OMCLDO2 because it primarily estimates an explicit aerosol layer height (ALH), and secondly an aerosol optical thickness τ for cloud-free observations. Overall, it was found that all the considered aerosol correction parameters reduce the biases identified in DOMINO-v2 over scenes in China with high aerosol abundance dominated by fine scattering and weakly absorbing particles, e.g. from [$-\mathrm{20}\mathit{\%}:-\mathrm{40}\mathit{\%}$] to [0 %:20 %] in summertime. The use of the retrieved OMI aerosol parameters leads in general to a more explicit aerosol correction and higher tropospheric NO₂ VCD values, in the range of [0 %:40 %], than from the implicit correction with the updated OMCLDO2. This number overall represents an estimation of the aerosol correction strategy uncertainty nowadays for tropospheric NO₂ VCD retrieval from space-borne visible measurements. The explicit aerosol correction theoretically includes a more realistic consideration of aerosol multiple scattering and absorption effects, especially over scenes dominated by strongly absorbing particles, where the correction based on OMCLDO2 seems to remain insufficient. However, the use of ALH and τ from the OMI NN aerosol algorithm is not a straightforward operation and future studies are required to identify the optimal methodology. For that purpose, several elements are recommended in this paper. Overall, we demonstrate the possibility of applying a more explicit aerosol correction by considering aerosol parameters directly derived from the 477 nm O₂−O₂ spectral band, measured by the same satellite instrument. Such an approach can, in theory, easily be transposed to the new-generation of space-borne instruments (e.g. TROPOMI on board Sentinel-5 Precursor), enabling a fast reprocessing of tropospheric NO₂ data over cloud-free scenes (cloudy pixels need to be filtered out), as well as for other trace gas retrievals (e.g. SO₂, HCHO).

1 Introduction

Long-time series of UV–visible (UV–vis) satellite measurements are a great asset for monitoring the distribution and evolution of pollutants such as NO₂, HCHO, or SO₂ and aerosol particles in the troposphere. With the forthcoming new generation of sensors like TROpospheric Ozone Monitoring Instrument (TROPOMI) on board Sentinel-5-Precursor (Veefkind et al., 2012), Sentinel-4-UVN and Sentinel-5-UVNS within the Copernicus programme (Ingmann et al., 2012), they will become an important tool for verifying the effectiveness of implemented technology to protect the environment and population against air pollution (Duncan et al., 2016). While the last generation of space instruments have had a pixel size of 13 × 24 km² for the Ozone Monitoring Instrument (OMI) or 80 × 40 km² for the Global Ozone Monitoring Experiment (GOME-2), the new generation has smaller pixel sizes (about 7 × 3.5 km² for TROPOMI), allowing air quality mapping of complex urban and city areas. This is also expected to reduce the probability of cloud contamination. However, the significant probability of aerosol contamination in areas such as India, China or regions dominated by biomass-burning episodes will likely remain or may even increase.

OMI is the Dutch–Finnish push-broom spectrometer flying on the National Aeronautics and Space Administration (NASA)'s Earth Observation Satellite (EOS) Aura platform since 15 July 2004. Its Sun-synchronous orbit has a local equator crossing time of approximately 13:40 LT. The operational tropospheric NO₂ product derived from the visible backscattered spectral light (405–465 nm), such as the OMI DOMINO-v2 (Boersma et al., 2011) or the very recent Quality Assurance for Essential Climate Variables (QA4ECV), is nowadays used as a reference. The related global mapping of tropospheric NO₂ concentrations has been used by many air quality research studies focusing on NO_x emissions and secondary pollutant formation, as well as tropospheric NO_x chemistry and transport, e.g. Curier et al. (2014), Reuter et al. (2014) and Ding et al. (2015).

A critical element for an accurate tropospheric NO₂ vertical column density (VCD) retrieval is our capability to reproduce the average light path along which the photons travelled before being detected by the satellite sensor at the top of the atmosphere (TOA) in the visible spectral window. In particular, scattering and absorption induced by atmospheric aerosol particles over cloud-free scenes are known to lead to very complex light paths. Because they are emitted by the same sources, high NO₂ and aerosol concentrations are often spatially correlated (Veefkind et al., 2011). Therefore, aerosol contamination needs to be properly addressed in the retrieval algorithms. In the frame of tropospheric NO₂ retrievals from visible spectral measurements based the differential optical absorption spectroscopy (DOAS) approach, the aerosol correction has to be applied to the air mass factor (AMF): a unitless number representative of the length of the average light path.

Over cloud-free scenes, a full explicit aerosol correction ideally requires a comprehensive set of parameters describing aerosols: the single-scattering albedo ω₀, scattering phase function, load through the aerosol optical thickness (AOT) τ, size and vertical distribution (Martin et al., 2003; Leitão et al., 2010; Bousserez, 2014). Among all these variables, many studies emphasized the importance of the aerosol layer height (ALH) knowledge (Leitão et al., 2010; Castellanos et al., 2015; Chimot et al., 2016). Assuming no aerosol correction, i.e. an aerosol-free scene (Richter and Burrows, 2002), would clearly create large biases in the OMI tropospheric NO₂ retrievals (Chimot et al., 2016).

There are basically two strategies for achieving the aerosol correction in the AMF:

1. either by considering external data, or

2. by using the available particle parameters that can be simultaneously derived from the same UV–visible spectral space-borne measurement.

Studies that reprocessed DOMINO-v2 data set using external data usually relied either on atmospheric transport model outputs, e.g. GEOS-Chem in the Peking University OMI NO₂ (POMINO) (Lin et al., 2014, 2015) or observations issued from different satellite platforms, e.g. the Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP) (Castellanos et al., 2015), or even both combined (Liu et al., 2019). Resulting changes mostly occurred in cases of high aerosol pollution (τ(550 nm)>0.8) with increased or decreased tropospheric NO₂ VCDs depending on the geophysical conditions and aerosol properties and distributions. However, the resulting AMF computation becomes dependent on these data sources, their quality and the possibility (or not) to combine them. In general, spatial and temporal co-registration between the different instruments or due to different resolutions between the observation pixel and the model grid cell may become an issue. In the frame of an operational processing, it is generally preferred to maximize the exploitation of the spectral measurement acquired by a same instrument representative of the considered observation pixel. One of the main reasons is the need to have an indication of particle height representative of the average light path associated with every single OMI field of view (FOV). Such information is generally not easily and directly available from an external source. Exploitation of the 477 nm O₂−O₂ absorption for aerosol retrieval is very promising. It is not only measured by OMI, but also by GOME-2, TROPOMI, Sentinel-4-UVN and Sentinel-5-UVNS. Several studies based on ground-based and satellite instruments have demonstrated its relatively high sensitivity to aerosols, in particular to ALH (Wagner et al., 2004; Castellanos et al., 2015; Park et al., 2016; Chimot et al., 2016, 2017).

Because of the difficulty of easily distinguishing clouds from aerosols and identifying the right aerosol model to use, it has always been preferred to retrieve effective clouds assuming a Lambertian and opaque reflector model (Joiner et al., 2004; Acarreta et al., 2004; Stammes et al., 2008; Vasilkov et al., 2018) and consequently to compute the resulting troposphere NO₂ AMF for all the OMI scenes, regardless of the type of particles present in the scene (clouds and/or aerosols). Such a correction is historically named an “implicit aerosol correction” (Boersma et al., 2004, 2011). Chimot et al. (2016) clearly demonstrated that, in spite of its implicit nature, the implicit aerosol correction mitigates biases in the OMI DOMINO NO₂ product over cloud-free scenes compared to an aerosol-free pixel assumption. However, limitations were identified:

1. A numerical artefact is present due to a too-coarse sampling employed in the OMI cloud look-up table (LUT), leading to a strong underestimation in the OMI tropospheric NO₂ VCD over scenes with τ(550 nm) ≥ 0.6 and aerosols located at high altitude.

2. The Lambertian cloud model, in spite of its benefits, somehow remains too simple and likely does not fully reproduce all the multiple scattering effects inherent to aerosol properties. The OMI effective cloud algorithm was then updated in order to remove these numerical artefacts (Veefkind et al., 2016). It also includes many additional relevant improvements related to the OMI 477 nm O₂−O₂ measurement. But its impact on the correction for aerosols has not yet been evaluated.

To move one step further, Chimot et al. (2017) developed a novel machine-learning algorithm, based on the neural network (NN) technique, that allows ALH to be retrieved together with τ from the same OMI 477 nm O₂−O₂ spectral band over cloud-free scenes. These retrievals were performed in various cases both over land and sea and compared with reference CALIOP observations and related climatology (Chimot et al., 2017, 2018). They benefit from a strong synergy with MODIS on board the NASA Aqua platform flying together with Aura in the same NASA A-Train constellation in order to identify the cloud-free scenes and to better constrain the ALH retrieval quality. For such a purpose, the 477 nm O₂−O₂ band represents some advantages compared to the more traditional O₂-A band at 760 nm, which is not measured by OMI:

1. It is spectrally closer to the NO₂, HCHO, or SO₂ absorption features.

2. It has a wider spectral range but weaker signal, leading to high sensitivities in the case of high aerosol loading.

3. It has fewer radiative transfer challenges arising from strong absorption lines like in the near-infrared. Moreover, the NN technique development allows very fast OMI data processing, which is an important requirement within an operational environment. The aerosol retrievals performed with this algorithm are expected to lead to an explicit aerosol correction over cloud-free scenes by using the OMI 477 nm O₂−O₂ measurement simultaneously acquired with the 405-465 nm NO₂ band.

This paper aims to evaluate the benefits of our improved use of the OMI 477 nm O₂−O₂ band for correcting aerosol effects in tropospheric NO₂ VCD retrieval from the same visible observation. We evaluate the potential of directly using the OMI NN aerosol ALH (and τ) in view of an explicit correction. We also assess the expected changes in the implicit aerosol correction based on the improved OMI effective cloud algorithm. To compare the different aerosol correction strategies, we reprocessed 2 years (2006–2007) of the DOMINO-v2 data over different areas and seasons, dominated by different types of pollution episodes, and thus, NO₂ and aerosol sources:

1. the large urban and industrialized eastern China region dominated by a mix of continental polluted fine and weakly absorbing particles, and dust coarse and scattering particles in summertime (June–July–August),

2. the same area essentially dominated by continental polluted fine and weakly absorbing particles in wintertime (December–January–February), and

3. South America during the biomass-burning season associated with heavy load of strongly absorbing aerosol emission (August–September).

Given all the aerosol corrections available from our improved use of the OMI 477 nm O₂−O₂ band, their comparison in this paper gives an estimation of the aerosol correction uncertainty in the OMI tropospheric NO₂ VCD retrieval. Sections 2 and 3 describe the algorithms and the reprocessing methodology. Section 4 evaluates the results of the applied aerosol corrections in the reprocessed tropospheric NO₂ retrievals. To complete the analyses, Sect. 5 includes specific discussions based on reference simulations to better understand the behaviour of the new OMI tropospheric NO₂ VCD. Similarly to Chimot et al. (2016), the advantage of such simulations is to determine, on well controlled cases, the expected new biases of the reprocessed OMI tropospheric NO₂ VCD and to identify the key geophysical factors driving them. At the end, in Sect. 6, we discuss the benefits and challenges of each aerosol correction.

2 The OMI O₂−O₂ algorithms

2.1 O₂−O₂ DOAS spectral fit

In this paper, both effective cloud and aerosol algorithms are based on the same OMI 477 nm O₂−O₂ spectral band. More specifically, they use the continuum reflectance R_c(475 nm) and the O₂−O₂ slant column density (SCD) $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$. These variables are derived from the DOAS spectral fit approach, which is a prerequisite to applying either the OMI cloud LUT (see Sect. 2.2) or the aerosol neural networks (see Sect. 2.3).

The DOAS method is a specific spectral fit approach following basic principle of absorption spectroscopy employed for UV and visible absorbing trace gases. The various DOAS techniques rely on the same key concept: a simultaneous fit of several trace gas slant column densities from the fine spectral features due to their absorption (i.e. the high frequency part) present in passive UV–visible spectral measurements of atmospheric radiation (Platt and Stutz, 2008). The assumed Beer–Lambert (or Bouguer–Lambert) law describes the light attenuation as a function of the travelled distance in the atmosphere, gas concentration and its spectral absorption intensity. It is commonly employed for absorption spectroscopy analyses of NO₂, SO₂, HCHO and O₃ from the OMI, TROPOMI, GOME, GOME-2 and SCIAMACHY sensors, e.g. Boersma et al. (2011) and De Smedt et al. (2018). The spectral fit is achieved within a predefined spectral window and the slant column density N^s is defined as the column density of a trace gas absorber along the average light path travelled by the detected photons from the Sun through the atmosphere, surface and back to the satellite sensor.

Here, the OMI 477 nm O₂−O₂ DOAS fits together the absorption cross-section spectrum of O₂−O₂ with a first-order polynomial over the (460–490 nm) spectral band (Acarreta et al., 2004; Veefkind et al., 2016). Note that the O₃ absorption, also present in this band, is taken into account. The continuum reflectance R_c at the reference wavelength λ₀ = 475 nm is the reflectance which would be measured in the absence of O₂−O₂ in the atmosphere.

In the absence of clouds, both OMCLDO2 and OMI aerosol algorithms rely on how aerosols affect the length of the average light path along which O₂−O₂ absorbs. R_c(475 nm) is known to represent the enhanced scene brightness due to the additional scattering effects induced by the particles. In particular, R_c(475 nm) directly increases with increasing τ. The enhancement magnitude, however, depends on aerosol properties as well as the surface albedo (Boersma et al., 2011; Chimot et al., 2016; Castellanos et al., 2015). $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ is governed by the overall shielding or enhancement effect of the absorption of the photons by the O₂−O₂ complex in the visible spectral range along the average light path. A reduction in the length of the average light path, i.e. the shielding effect, reduces the absorption by O₂−O₂. The aerosol layer height is the primary driver (Castellanos et al., 2015; Chimot et al., 2016, 2017). An aerosol layer located at high altitudes causes a large shielding effect on the O₂−O₂ located in the atmospheric layers below, by reducing the amount of photons coming from the top of the atmosphere and reaching the lowest part of the atmosphere, compared to an aerosol-free scene. As a second-order effect, aerosol properties such as τ and ω₀, and surface reflectance also contribute to $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ (Castellanos et al., 2015; Chimot et al., 2016, 2017).

2.2 OMI cloud algorithm OMCLDO2

The OMI cloud algorithm also named OMCLDO2 (Acarreta et al., 2004) derives the effective cloud fraction c_f and cloud pressure c_p assuming a single cloud layer as an opaque Lambertian reflector with a constant albedo of 0.8 (Stammes et al., 2008) and the independent pixel approximation (IPA) (Martin et al., 2002; Acarreta et al., 2004). The measured reflectance R is formulated as a linear combination of a clear-sky R_Clear and a cloudy reflectance R_Cloud (Martin et al., 2002; Acarreta et al., 2004):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }R\left(\mathit{\lambda }\right)=c_{\mathrm{f}}\cdot R_{\mathrm{Cloud}}+(\mathrm{1}-c_{\mathrm{f}})\cdot R_{\mathrm{Clear}}.\end{array}$$

An LUT enables the conversion of R_c(475 nm) and $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ into c_f and c_p. It requires knowledge of the surface reflectance and surface pressure in addition to the viewing and sun geometry configurations (Acarreta et al., 2004; Veefkind et al., 2016). Because of the low impact of small clouds on the O₂−O₂ band, c_p has large uncertainties in the case of low c_f (Acarreta et al., 2004). The term “effective” here means that these cloud parameters do not represent actual clouds, but our best explanation of the measured radiance is obtained by combining these variables with the assumed approximate model (Sneep et al., 2008; Stammes et al., 2008). Therefore, the retrieved c_f and c_p values of each observed scene match the measurement summarized by (R_c(475 nm)-$N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$), such that the (460–490 nm) radiance budget is comprehensively closed (apart from instrument noise). For example, true optically thin clouds will be retrieved as a an opaque and bright Lambertian reflector covering only a small part of the OMI pixel, mostly because of the large assumed cloud albedo value (Veefkind et al., 2016).

The main motivation of this cloud retrieval scheme has been the correction of cloud effects in trace gas retrievals (Stammes et al., 2008). However, this algorithm is actually applied both to cloudy and cloud-free scenes with aerosols, without any prior distinction. Many studies demonstrated that OMCLDO2 accounts for a large part of aerosol effects in the retrieved c_f and c_p (Boersma et al., 2004, 2011; Castellanos et al., 2015; Chimot et al., 2016; Wang et al., 2015). Under these conditions, the OMI cloud parameters then become more effective as they do not represent cloud any more but aerosol effects on the (460–490 nm) radiance. One could claim that OMCLDO2 then becomes an approximate aerosol model, independent of those considered in Sect. 2.3. Chimot et al. (2016) demonstrated how OMCLDO2 responds to aerosols:

1. c_f is mostly driven by R_c(475 nm) and increases with increasing aerosol load, regardless of its altitude. Its magnitude is weighted by aerosol properties and surface conditions.

2. c_p represents beforehand the degree of shielding effect applied by aerosols, which results from a complex combination of ALH as a first order aerosol load τ and type, surface properties and geometry angles as a second order. A stronger shielding effect leads to a lower c_p. In general, over scenes with high τ values, c_p correlates well with ALH. Furthermore, regardless of true aerosol layer altitude, strongly absorbing particles lead to a decrease in c_p, while the presence of more scattering particles increases c_p values (Castellanos et al., 2015; Chimot et al., 2016).

Veefkind et al. (2016) released a new version of the OMCLDO2 product. The new algorithm, here named OMCLDO2-New, includes several improvements such as a better consistency of gas absorption cross sections with the OMI NO₂ retrieval algorithm, outlier removal from the spectral fitting, etc. However, in the context of the implicit aerosol correction, the expected highest changes come from the higher number of nodes of the OMI cloud LUT. Indeed, the coarse sampling of the OMI cloud LUT associated with the OMCLDO2-Old version created a numerical artefact: c_p was increasing with decreasing c_f (or aerosol τ) without any physical explanation (Chimot et al., 2016; Veefkind et al., 2016). This has strong impacts on the OMI tropospheric NO₂ product, DOMINO v2, in scenes dominated by aerosols (see Sect. 3.3). Furthermore, a temperature correction is implemented in OMCLDO2-New to take into account the density-squared dependence of the O₂−O₂ absorption. Its impact, however, depends on the temperature conditions and latitude area (Veefkind et al., 2016).

2.3 OMI aerosol neural network

The OMI O₂−O₂ aerosol algorithm relies on a NN multilayer perceptron approach to primarily retrieve ALH over cloud-free scenes, but also aerosol τ(550 nm) as a secondary parameter (Chimot et al., 2017, 2018). Since a fine characterization of aerosol vertical profiles cannot be retrieved from OMI UV–visible measurements, they are assumed as one box layer with a constant pressure thickness (100 hPa). ALH is the middle altitude of this layer in kilometres over sea level but can also be expressed in pressure. Here, the strategy differs from the OMI effective clouds of Sect. 2.2. The main motivation is to try to reproduce aerosol scattering and absorption in the visible spectrum via a more explicit aerosol model than the assumed opaque Lambertian reflector. Particle properties in this layer are considered to be homogeneous.

The ALH retrieval requires several input variables, the most critical being τ(550 nm), as both ALH and τ(550 nm) similarly affect $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ and need to be separated (Chimot et al., 2017). In theory, τ information may be available from diverse sources (e.g. atmospheric models, statistical prior guess or observations). In practice, the MODIS τ product has systematically been preferred due to its good spatial and temporal collocation with OMI measurements, and its recognized high quality. Retrieved OMI τ may also be used as they come from a same spectral measurement (same instrument). However, due to its higher uncertainty compared to MODIS, its use impacts the quality of OMI ALH (Chimot et al., 2017). For OMI τ retrieval, R_c(475 nm) is considered instead of τ as prior input. Note that, in the next sections, we define NN_MODIS when prior MODIS τ is considered, NN_OMI based on the retrieved OMI τ, and NN_True when the true τ value is considered for the synthetic cases (see Sect. 3.1).

The training data set was generated by full-physical spectral simulations, assuming explicit aerosol particles without clouds, and with the Determining Instrument Specifications and Analyzing Methods for Atmospheric Retrieval (DISAMAR) software by the KNMI (de Haan, 2011). Aerosol scattering phase function Φ(Θ) was simulated by the Henyey–Greenstein (HG) function parameterized by the asymmetry parameter g and the average of the cosine of the scattering angle (Hovenier and Hage, 1989). Aerosols were specified as standard fine particles with a typical value of the extinction Ångström exponent α=1.5 and g=0.7. They are assumed to fully cover the OMI pixel. To take into account the inaccuracies of the assumed aerosol single-scattering albedo ω₀ properties, two training data sets were generated with a different typical value: one with ω₀=0.95 and one with ω₀=0.9 in the visible spectral domain. Therefore, two separate OMI ALH NN algorithms were developed, one for each aerosol ω₀ value. The rational of these ω₀ values relies on those that are typically identified in the regions dominated by high NO₂ pollution, notably in eastern China (Lin et al., 2014, 2015).

The HG phase function is known to have some limitations compared to more physical aerosol scattering models. Nevertheless, it was consciously chosen in Chimot et al. (2017) as the main motivation has been as exploratory development of an ALH retrieval algorithm, using the OMI 477 nm O₂−O₂ absorption band, in view of correcting aerosol scattering and absorption effects in the visible spectral range for tropospheric NO₂ retrieval. For such a purpose, Chimot et al. (2016) quantitatively demonstrated that τ and ALH are the key needed parameters. Other aerosol parameters, that are more related to their optical properties, shape and size are of a secondary importance. This is supported by a significant number of additional studies (Boersma et al., 2004; Leitão et al., 2010; Castellanos et al., 2015). The main reason is that a comprehensive aerosol correction requires the length of the average light path in the presence of scattering and absorbing particles. This is primarily driven by τ and ALH (in addition to the shape of the NO₂ vertical profile), much less by the detailed properties of particles. Consequently, other details describing the shape of the scattering phase function are of secondary importance, even if they are not negligible. Moreover, geographical areas impacted by heavy NO₂ abundance are generally dominated by fine spherical particles, weakly absorbing (e.g. sulfate, and nitrate) or strongly absorbing (e.g. smoke) particles like in eastern China, South America, and Russia and include urban, industrial and biomass-burning pollution events (Chimot et al., 2017, 2018). Spheroid particles such as dust are sometimes mixed but do not dominate.

The HG function is known to be smooth and reproduce the Mie scattering functions reasonably well with g=0.7 for most aerosol types, especially for spherical particles (Dubovik et al., 2002). The evaluation results obtained in Chimot et al. (2017, 2018) showed that this approximation is not oversimplified for all these cases over eastern China, Russia and South America. A similar approach is considered for the operational ALH retrieval algorithms for the Sentinel-4 Precursor and the Sentinel-5 Precursor (Leitão et al., 2010; Sanders et al., 2015; Colosimo et al., 2016; Nanda et al., 2018) and when applying various explicit aerosol corrections in the tropospheric NO₂ AMF calculation over urban and industrial areas dominated by anthropogenic pollution, for instance in eastern China (Spada et al., 2006; Wagner et al., 2007; Castellanos et al., 2015; Vlemmix et al., 2010).

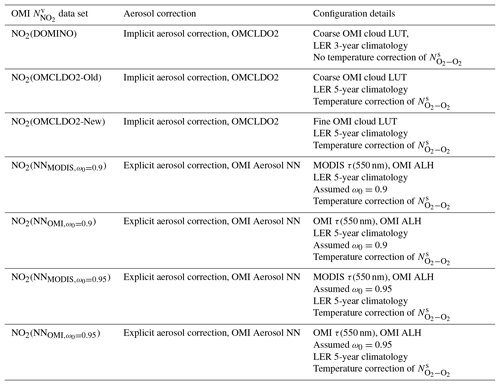
Similarly to the high c_p inaccuracy in the case of low c_f, a high ALH bias is expected below a minimum particle load (i.e. threshold of τ(550 nm)=0.5). This is directly due to the weak O₂−O₂ absorption within the 460–490 nm spectral band. Below this threshold, low aerosol amounts eventually have negligible impacts on $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$. The ALH retrieval performance was assessed over areas in eastern China, South America and Russia with scenes including urban, industrial and biomass-burning pollution events and for different seasons (Chimot et al., 2017, 2018). These scenes are mostly dominated by fine spherical particles, weakly absorbing (e.g. sulfate, and nitrate) or strongly absorbing (e.g. smoke). Dust particles may sometimes be mixed. Over cloud-free scenes, OMI ALH has shown consistent spatial patterns with CALIOP level 2 (L2) ALH over urban and industrial areas in eastern China, with an uncertainty in the range of [500:700] m and for collocated MODIS scenes with τ(550 nm) ≥0.5 (Chimot et al., 2018). Additional analyses showed that differences between the LIdar climatology of vertical Aerosol Structure for space-based lidar simulation (LIVAS) and 3-year OMI ALH with MODIS τ(550 m)≥1.0 were in the range of [180:800] m (Amiridis et al., 2015; Chimot et al., 2017). Finally, Chimot et al. (2018) showed the potential of OMI visible measurements to observe the height of thick and absorbing aerosol layers released by widespread fire episodes such as in South America. The aerosol model assumptions, in particular ω₀, are the most critical as they may affect ALH retrieval uncertainty up to a maximum of 660 m. An accuracy of 0.2 is necessary in prior τ(550 nm) information to limit the ALH bias close to zero over scenes with τ(550 nm) ≥1.0, and below 500 m for τ(550 nm) values smaller than 1.0. A summary of all the OMI NN aerosol algorithms as well as related input and output parameters is given in Table 1.

Table 1 Summary of the different OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ mentioned in this paper, and the configuration of the associated aerosol correction: input OMI Lambertian equivalent reflectivity (LER) climatology, OMI cloud look-up table (LUT) for the effective cloud retrievals, aerosol parameters (see for more details Sects. 2.2, 2.3 and 3).

3 From aerosol impacts to aerosol correction – methodology

3.1 General methodology

Reprocessing of the OMI tropospheric NO₂ product is based on the DOMINO-v2 data set (see Sect. 3.3) in which the AMF (see Sect. 3.2) is recomputed with diverse aerosol correction strategies using the DISAMAR radiative transfer model, over cloud-free scenes contaminated by aerosols. Recomputed AMF values then replace the original ones in DOMINO. They are applied to the available NO₂ SCD to derive consequently the tropospheric NO₂ VCD. The tropospheric NO₂ AMF computation follows the formulation detailed in Sect. 3.2, which relies either on an implicit or an explicit aerosol correction: the implicit correction considers the effective cloud retrievals obtained from OMCLDO2 (see Sect. 2.2); the explicit aerosol correction employs aerosol parameters: either OMI ALH and OMI τ from the OMI aerosol NN (see Sect. 2.3), or OMI ALH and MODIS τ. The complementary aerosol parameters (i.e. ω_o, g, α) follow those specified in the associated training data set.

The surface albedo is based on the OMI Lambertian equivalent reflectivity (LER) climatology (Kleipool et al., 2008). In DOMINO-v2, this climatology is derived from 3-year OMI time series measurements. However, it has evolved since then with an extended 5-year OMI time series (Veefkind et al., 2016). This evolved OMI LER is considered for all the reprocessed tropospheric NO₂ VCD of this study. All the other geophysical parameters associated with DOMINO-v2, such as the NO₂ vertical profile, remain identical.

To identify cloud-free OMI observation pixels with aerosols, a similar strategy to Chimot et al. (2016, 2017) is considered. The DOMINO-v2 NO₂ scenes are collected together with the MODIS-Aqua aerosol τ(550 nm) from the combined Dark Target (DT) and Deep Blue (DB) products of Collection 6 available at a resolution of 10 km (Levy et al., 2013). They are collocated within a distance of 15 km. The probability of cloud-free OMI scene is a priori ensured by the availability of the MODIS aerosol product with the highest quality assurance flag. In this case, MODIS Aqua τ was then exclusively retrieved when a sufficiently high amount of cloud-free subpixels was available (i.e. at the MODIS measurement resolution of 1 km) (Levy et al., 2013). However, it is well recognized this may be not completely representative for the atmospheric situation of the OMI pixel. Therefore, we added two thresholds for each collocated OMI-MODIS pixel: the geometric MODIS cloud fraction to be smaller than 0.1, and OMI c_f lower than 0.1. Past experiences showed that OMI c_f values in the range of [0.1:0.2] may still contain clouds (or both clouds and aerosols) (Boersma et al., 2011; Chimot et al., 2016).

Additional synthetic cases analysed in Sects. 4 and 5 are also based on the DISAMAR model, specified in a similar way to the NN training data set in Sect. 2.3. Either OMCLDO2 or the OMI NN aerosol algorithms are used to determine the expected tropospheric NO₂ VCD biases.

3.2 Air mass factor computations

The computation of tropospheric NO₂ AMF $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ is a key step for converting NO₂ SCD $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{s}}$ into tropospheric NO₂ VCD $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$, which represents the number of NO₂ molecules cm⁻² integrated along the vertical direction from the surface P₀ to the tropopause P_trop pressure. The application of $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ is crucial to correct the average light path variability contained in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{s}}$. The $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ computation has generally been recognized as the principal source of errors in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ determination in areas with a high level of air pollution (Boersma et al., 2007). This was emphasized even more by Lorente et al. (2017), who discussed how AMF structural uncertainty is driven by assumed prior information, and cloud and aerosol correction strategies: up to 42 % over polluted regions and 31 % over unpolluted regions.

In the context of OMI visible spectral measurements, $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ is defined as the ratio of the atmospheric SCD and VCD (Boersma et al., 2011):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{A}_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}(\mathrm{\Psi },\mathit{\lambda })=N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{s}}(\mathrm{\Psi },\mathit{\lambda })/N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}},\end{array}$$

with Ψ the list of input parameters prerequired for the radiative transfer model. Note that before performing this conversion, the stratospheric and tropospheric contributions to $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{s}}$ must be separated. Therefore, $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}(\mathrm{\Psi },\mathit{\lambda })$ is only applied to the tropospheric NO₂ SCD. The OMI $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ formulation follows Palmer et al. (2001), Boersma et al. (2004) and the concept of altitude-resolved AMF a(z) (also named block AMF or BAMF) introduced by Palmer et al. (2001); Eskes and Boersma (2003) and then generalised by Wagner et al. (2007), Rozanov and Rozanov (2010) and Richter and Wagner (2011). The ratio of a to the total air mass factor $A_{{\mathrm{NO}}_{\mathrm{2}}}$ (deduced from the NO₂ shape profile) gives the vertical averaging kernel AK, i.e. the sensitivity of the satellite measurement to each vertical atmospheric layer (Eskes and Boersma, 2003; Richter and Wagner, 2011). Overall, $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ can then be seen as a unitless number representative of the length of the average light path followed by the detected photons in the troposphere. It includes an indication of the sensitivity to the amount of NO₂ in the troposphere, with larger values indicating a higher sensitivity, assuming no change in vertical NO₂ profile. Indeed, in those cases, a change in $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ is directly associated with a change in a at the atmospheric levels where the trace gas is present. The reference wavelength considered in this paper is 439 nm, following the OMI NO₂ product (see Sect. 3.3) (Boersma et al., 2011).

Aerosols may cause either a shielding or an enhancement effect. A shielding effect occurs when the length of the average light path is reduced leading to a decrease in $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. Reciprocally, an enhancement effect results in an increase in $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ (Leitão et al., 2010; Chimot et al., 2016). Following Eq. (2), any bias in the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ calculation leads to a direct bias in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$, with the same value but opposite sign.

Note that, in the case of real OMI tropospheric NO₂ retrievals, a temperature correction is often applied as the temperature of the assumed NO₂ absorption cross section, fixed at 221 K, can differ from the actual temperature when deriving $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{s}}$. The correction term is thus implemented in the computation of $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ such that it represents the ratio of $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{s}}$ derived with a NO₂ cross section at the real temperature T to the column derived at 221 K. European Centre for Medium-Range Weather Forecasts (ECMWF) temperature fields are used for this correction (Boersma et al., 2004, 2011).

The computation of $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ requires accurate knowledge about all the parameters Ψ, affecting the optical properties of the atmosphere and the length of the average light path. For an aerosol and cloud-free scene, Ψ generally includes the satellite and solar geometries, ground pressure and the surface reflectance. In the presence of clouds and/or aerosols, adequate parameters describing their properties must be added. Among all these variables, many studies emphasized that ALH and τ are the most critical aerosol parameters primarily affecting $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ over cloud-free scenes dominated by aerosol particles (Leitão et al., 2010; Castellanos et al., 2015; Chimot et al., 2016). It was clearly demonstrated that other parameters describing aerosol properties, such as size, are generally of second order of magnitude for such a purpose. The main reason is because, to correct aerosol effects, we need the overall length of the average light path in the presence of scattering and absorbing particles. This is primarily driven by τ and ALH (in addition to the shape of the NO₂ vertical profile) and much less by the detailed properties of particles that affect the TOA radiance measurement more (Chimot et al., 2016).

3.3 OMI tropospheric NO₂ data set – DOMINO v2

DOMINO v2 (Boersma et al., 2011) is a reference worldwide tropospheric NO₂ product derived from the OMI visible measurements and can be downloaded from the Tropospheric Emissions Monitoring Internet Service (TEMIS) website (http://www.temis.nl, last access: 12 January 2019). Chimot et al. (2016) demonstrated that the implicit aerosol correction in DOMINO-v2 is better than the clear-sky assumption (Richter and Burrows, 2002), with remaining biases between −20 % and −40 % on tropospheric NO₂ VCD, especially in the presence of absorbing particles and for τ(550 nm) ≥0.5. One of the main identified limitations has been the coarse sampling of the OMI cloud LUT nodes used in OMCLDO2 (see Sect. 2.2). The effect of the OMCLDO2-New version on the implicit aerosol correction has not yet been analysed.

To our knowledge, no reprocessing has yet been done by applying an explicit aerosol correction based on (nearly) explicit aerosol parameters retrieved from the OMI 477 nm O₂−O₂ spectral band. Thus, the use of OMI ALH and τ parameters from Sect. 2.3 is a first attempt to apply a (nearly) explicit aerosol correction in the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ computation by using visible spectral measurements from the same sensor.

DOMINO has recently evolved through the Quality Assurance for Essential Climate Variables (QA4ECV) project (http://www.qa4ecv.eu, last access: 23 January 2019), which aims to address reliable and fully traceable quality information on some of the essential climate variables (ECVs), such as tropospheric NO₂, as defined by the Global Climate Observing System (GCOS) (Lorente et al., 2017). This reprocessing contains numerous changes in the complete chain of retrieval, from the calibrated spectrum, spectral fitting with DOAS, to the AMF computation and all the ancillary data sets. This new generation of product is expected to represent one of the best NO₂ data sets. Since the reprocessing products of QA4ECV are still under thorough validation and were not completely available at the time of this paper (and its technical work), and given our specific objective focused on the aerosol scattering and absorption correction by using information from the O₂−O₂ spectral band, the last version of DOMINO (v2) is preferred.

The OMI cloud algorithm configuration used at the time of DOMINO-v2 and its comparison with the other algorithms are summarized in Table 1.

4 Results of reprocessing OMI NO₂ and O₂−O₂ products

All the reprocessed OMI tropospheric NO₂ results achieved here are based on the OMI cloud and aerosol algorithms discussed in the previous sections and summarized in Table 1. The main differences between the different reprocessings are synthesized in Table 2 for all collocated OMI-MODIS aerosol scenes.

Table 2 Summary of the changes in the diverse reprocessing OMI tropospheric NO₂ VCD $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ depending on the applied aerosol correction strategy (see Table 1) over all collocated MODIS aerosol scenes (MODIS τ(550 nm) ≥0.). See more analyses in Sect. 4.1 and 4.2.

4.1 Implicit aerosol correction – benefits of the updated OMI cloud algorithm

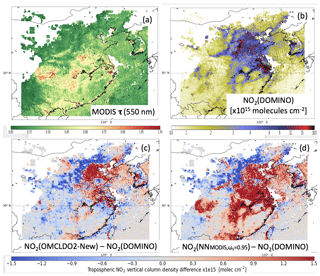
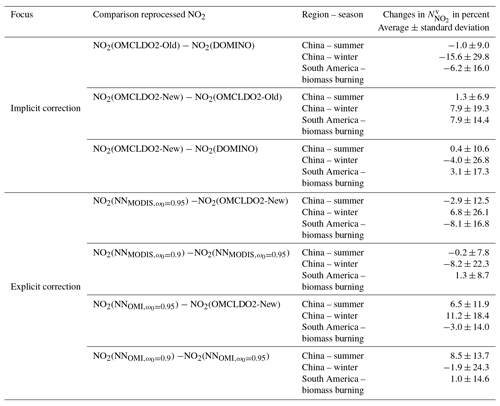
Among all the main changes that are included in the updated version of OMCLDO2, the increased sampling of the OMI cloud LUT is expected to show the most important impacts on the aerosol correction (see Sect. 2.2). Indeed, the coarse sampling of the OMI cloud LUT in the former version was clearly identified by Chimot et al. (2016) as a limitation regarding the behaviour and the magnitude of c_p, and thus, when deriving $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ in the presence of aerosols (see Sect. 3.3). As depicted by Fig. 1, differences in c_p are now quite significant for low τ. On average, c_p from OMCLDO2-New are about 200 hPa lower than from OMCLDO2-Old (with a large standard deviation) over scenes with MODIS τ(550 nm) ≤ 0.5. Indeed, the low aerosol load has a very limited effect on $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ and does not dominate the measured radiance signal. This results in large uncertainties in the retrieved c_p and a large sensitivity of the resolution at which the LUT interpolation is performed for these cases. Over scenes with high aerosol load (MODIS τ(550 nm) ≥1.0), differences are more minor and may even reverse sign. We attribute the small reverse sign to the application of the temperature correction of $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ (see Sect. 2.1), which, depending on the temperature difference compared to the assumed midlatitude summer atmosphere, may apply a positive or negative small modification of c_p in cases of high τ. However, as analysed by Veefkind et al. (2016), the impact of the temperature correction of c_p remains minor in cases of high c_f and thus aerosol load, compared to the updated OMI cloud LUT. Overall, all these changes are consistent with those analysed by Veefkind et al. (2016) over cloudy scenes, with low and high c_f.

Based on synthetic cases, Fig. 2 illustrates the expected improvements of the implicit aerosol correction of $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ due to the higher OMI cloud LUT sampling. While remaining $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases were contained between −20 % and −40 % with OMCLDO2-Old, they should be now limited to the range of [0:20] with the use of OMCLDO2-New over scenes with relatively scattering or weakly absorbing aerosol particles (i.e. ω₀=0.95) and assuming a typical NO₂ summer vertical profile over north-eastern China. Such improvements are particularly good in the case of aerosols located at an elevated altitude (i.e. more than 1 km). However, although they were improved, the biases could be higher in the case of strongly absorbing particles: in the range of [$-\mathrm{10}:\mathrm{20}$] % for ω₀=0.9. Additional geophysical parameters, in particular the NO₂ profile shape, may affect these biases and are therefore of high importance (see further discussions in Sect. 5.2).

Figure 1 Statistics of effective cloud pressure differences between OMCLDO2-new and OMCLDO2-old (see Sect. 2.2 and Table 1) in [hPa] in 2006–2007 as a function of MODIS aerosol optical thickness (AOT) τ(550 nm). An example over China in summertime (June–July–August).

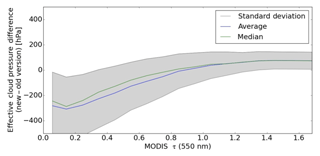
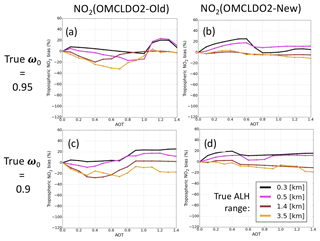
Figure 2 Relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases after application of the implicit aerosol correction as a function of true aerosol optical thickness (AOT) τ(550 nm) and based on synthetic cases including different true ALH, surface albedo =0.05, μ₀ = 25^∘, μ=25^∘ and a typical TM5 NO₂ vertical profile for 1 July 2006 at 12:00 over China (van Noije et al., 2014; Chimot et al., 2016). True aerosol properties are defined by α=1.5, ω₀=0.95 or 0.9 and g=0.7. Implicit aerosol correction is derived from the retrievals given by OMCLDO2-Old or OMCLDO2-New, which, among other elements, includes the new OMI cloud LUT with a higher sampling (see Sect. 2.2 and Table 1). (a) Relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ bias resulting from OMCLDO2-Old, true ω₀=0.95, (b) relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ resulting from OMCLDO2-New, true ω₀=0.95, (c) relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ bias resulting from OMCLDO2-Old, true ω₀=0.9 and (d) relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ resulting from OMCLDO2-New, true ω₀=0.9.

Overall, the future changes when applying the new implicit aerosol corrections from DOMINO will result from a combination of different parameters, mainly the higher sampling of the OMI cloud LUT, the temperature correction of $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ and the updated OMI surface albedo database. To quantify the resulting changes in the reprocessed OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$, the results are separated into two categories. Firstly, Fig. 3a, c and e illustrate the changes in reprocessed $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ from DOMINO to OMCLDO2-Old. As indicated in Table 1, these changes result from two consequences:

1. the temperature correction of $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ and the new OMI surface albedo, which both directly modify the retrieval of the effective cloud parameters, and

2. the direct application of this new albedo when computing $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$.

A higher surface albedo should result in an increased length of the average light path and therefore an enhanced $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. However, this can become more complex when combined with the new effective cloud parameters as they may either enhance, reduce or even counterbalance this effect. On average, $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ is lower (i.e. higher $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$), between $-\mathrm{1}\mathit{\%}\pm \mathrm{9}$ % in China in summertime and $-\mathrm{15.6}\mathit{\%}\pm \mathrm{29.8}$ % in China in wintertime. The quality of these changes, however, depends on the accuracy of the new surface albedo climatology, which is primarily expected to be more robust due to the longer time series considered in the OMI reflectance observations (see Sect. 3.3).

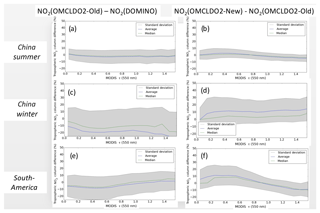
Figure 3 Statistics of relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ differences in percentage as a function of MODIS τ(550 nm) over China and South America in 2006–2007 due to changes in the applied implicit aerosol correction (see Sect. 4.1) from DOMINO to OMCLDO2-Old (with the LER climatology based on a longer time series) and from OMCLDO2-Old to OMCLDO2-New (OMI cloud LUT with a higher sampling): (a) summer in China (June–July–August), (b) winter in China (December–January–February) and (c) South America (August–September).

Secondly, Fig. 3b, d and f depict the impacts of the implicit aerosol correction evolution from OMCLDO2-Old to OMCLDO2-New. They are directly driven by the improved c_p (see Table 1). Over scenes with MODIS τ(550 nm) in the range of [0.0:0.5], a decreased c_p (see Fig. 1) results in a stronger shielding (or reduced enhancement) effect from particles: $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ generally increases. In contrast, larger c_p over scenes with MODIS τ(550 nm) ≥ 1.0 leads to a lower shielding (or stronger enhancement) effect: $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ decreases. Standard deviation of these changes is between 15% and 20% in China in wintertime and South America, and lower than 10% in China in summertime and South America. Averages are in the range of [1.3 %:7.9 %]. Regional and seasonal differences may reflect the implicit dependencies on the aerosol types, the combined effects on c_f−c_p, spatially variable surface albedo and the impacts of seasonal NO₂ vertical profile. All these observed changes are in line with the analyses deduced from the synthetic cases in Fig. 3b, d and f, confirming the improvements thanks to the updated OMI cloud LUT. Interestingly, these overall changes seem to be in line with the average AMF uncertainty of 11 % evaluated by Lorente et al. (2017) due to a different cloud correction scheme in polluted conditions and assuming c_f≤0.2.

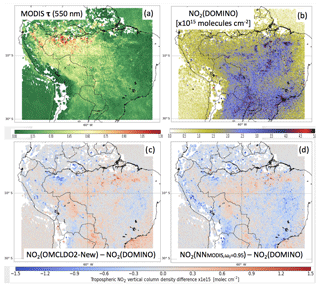
Overall, maps in Figs. 4c–6c show that the total changes in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$, from DOMINO to OMCLDO2-New, mostly occur in the eastern part of China, where the NO₂ pollution is higher. Spatial patterns of these overall changes mostly result from a complex combination with MODIS aerosol horizontal distribution as suggested by Fig. 3, but also aerosol types and vertical distribution: a decrease over Beijing areas in summertime and an increase in the same area in wintertime.

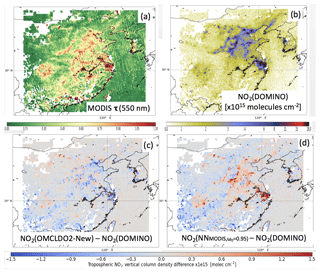
Figure 4 Average maps of MODIS τ(550 nm), OMI DOMINO $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ and differences after applying the implicit (with OMCLDO2-New) or explicit (with NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$) aerosol correction over China in summertime (June–July–August) 2006–2007. (a) MODIS τ(550 nm), (b) OMI DOMINO $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$, (c) OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ differences due to changes between OMCLDO2-New and DOMINO implicit aerosol corrections, (d) $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ differences between explicit aerosol correction based on the NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ aerosol parameters (i.e. aerosol forward model assuming ω₀=0.95, MODIS τ(550 nm) and retrieved ALH) and implicit aerosol correction implemented in DOMINO.

Figure 5 Same as Fig. 4 but over China in wintertime (December–January–February) 2006–2007.

Figure 6 Same as Fig. 4 but over South America during the biomass-burning season (August–September) in 2006–2007.

4.2 Explicit aerosol correction results

In this study, there are four possibilities for applying an explicit aerosol correction from the OMI 477 nm O₂−O₂ band. Each of them differ regarding the assumed aerosol properties (i.e. ω₀), aerosol τ observations (i.e. MODIS or OMI) and the consequent fitted ALH (see Sect. 2.3). All these possibilities were individually applied when reprocessing the OMI DOMINO product to quantify their overall differences.

Similarly to the benefits of the new implicit aerosol correction based on OMCLDO2-New evaluated in Sect. 4.1, Fig. 7 shows the benefits of the applied explicit aerosol corrections. Provided that the aerosol model (e.g. ω₀) is in line with the actual aerosol type present in the observed scene (i.e. ideal scenario), remaining biases in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ are below 20 % and are slightly dependent on aerosol parameters (τ, ω₀ and ALH) when assuming a NO₂ vertical profile representative of a typical summer day over the east of China (van Noije et al., 2014; Chimot et al., 2016). In such a scenario, using either the retrieved OMI τ value or a more accurate one is not expected to make a major difference. However, in practice, these results may vary with respect to the NO₂ profile shape and additional errors in the employed aerosol model (see next subsections).

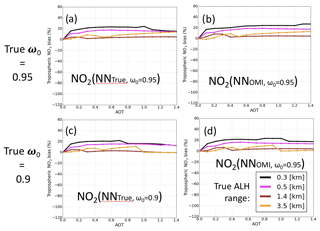
Figure 7 Relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases after application of the explicit aerosol correction as a function of true aerosol optical thickness (AOT) τ(550 nm) and based on synthetic cases of Fig. 2. No bias is included in ω₀; i.e. true and assumed values are identical. (a) True τ and ω₀=0.95, (b) retrieved OMI τ and ω₀=0.95, (c) true τ and ω₀=0.9 and (d) retrieved OMI τ and ω₀=0.9.

Figure 8 shows that all reprocessed $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ with implicit or explicit corrections are larger by [10 %:50 %] than if no correction was performed, especially over scenes with MODIS τ(550 nm) ≥1.0. This suggests that both corrections converge in the same direction (i.e. same sign) in spite of some different magnitudes of the aerosol correction. Since all the considered strategies attenuate the $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases due to aerosols from an aerosol-free scene assumption, it is worth emphasizing that all of them, without distinction, are an aerosol correction, regardless of their implicit or (more) explicit nature.

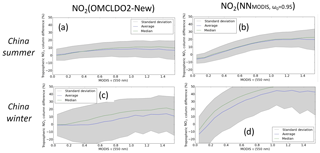
Figure 8 Statistic of relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ differences in percentage over China 2006–2007 in summer (June–July–August) and winter (December–January–February), after implicit or explicit aerosol correction compared to no aerosol correction (i.e. aerosol-free scene assumption): (a) implicit aerosol correction based on OMCLDO2-New, (b) explicit aerosol correction based on NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$.

Overall, over OMI pixels collocated with MODIS τ(550 nm) ≥0.5, Fig. 9 depicts that most of the reprocessed $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ values are generally higher with the explicit aerosol correction than with the implicit aerosol correction from OMCLDO2-New. This suggests a stronger shielding effect leading to lower $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm). The differences increase with increasing MODIS τ as aerosol effects consequently amplify along the average light path.

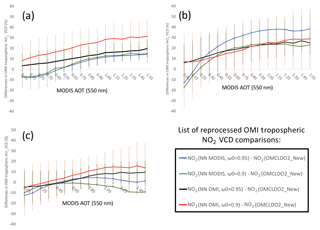
Figure 9 Statistics of relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ changes in percentage in 2006–2007 due to differences between the different explicit aerosol corrections (see Table 1) and the implicit aerosol correction based on OMCLDO2-New (improved effective cloud parameters, up-to-date version): (a) China in summertime (June–July–August), (b) China in wintertime (December–January–February) and (c) South America biomass burning season (August–September).

In eastern China, by using the explicit aerosol correction with NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$, $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ values are higher than with the implicit aerosol correction, with OMCLDO2-New at about 12±12.5 % in summer and 40±26.1 % in winter over scenes with MODIS τ(550 nm) ≥0.5 (see Fig. 9). The larger increase in wintertime is likely due to different NO₂ profile shapes, with NO₂ molecules being closer to the surface (see further discussions in Sect. 5.2). The differences with OMCLDO2-New are somehow reduced when assuming a lower aerosol ω₀. In such a configuration, the main differences are as follows:

1. a lower ALH due to an assumed lower ω₀ value (Chimot et al., 2017), combined with

2. a more absorbing aerosol model used to compute $A_{{\mathrm{NO}}_{\mathrm{2}}}$(439 nm).

In both cases, NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.9}}$ and NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$, prior τ (coming from MODIS) remains unchanged. As illustrated in Figs. 9, resulting $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ using NN_MODIS, ω_0=0.9 over China are smaller (i.e. $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ (439 nm) higher) by about $-\mathrm{0.2}\pm \mathrm{7.8}\mathit{\%}$ in summer, and $-\mathrm{8.2}\pm \mathrm{22.3}\mathit{\%}$ in winter compared to $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ with NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$. These numbers represent a first evaluation of the impact of aerosol model uncertainty, assuming one may use a very accurate prior τ information for both the ALH retrieval and the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) computation.

Over scenes in South America with MODIS τ(550 nm) ≥ 0.5, the difference between $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ from NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ and from OMCLDO2-New is on average close to zero with a standard deviation of 16.8 %. The use of NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.9}}$ reduces $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ by about $-\mathrm{1.3}\pm \mathrm{8.7}\mathit{\%}$. Interestingly, Castellanos et al. (2015) reported an average change of 0.6±8 % on $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ after reprocessing DOMINO $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ over cloud-free scenes during the biomass-burning season in South America and applying an explicit aerosol correction based on the OMI near-UV aerosol algorithm (OMAERUV) and CALIOP aerosol ALH.

When using the retrieved OMI τ as prior input instead of MODIS τ over eastern China, $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ differences with respect to the use of OMCLDO2-New differ by 5–10 % on average over scenes with MODIS τ(550 nm)≥0.6 (higher in summer but lower in winter). This suggests a higher sensitivity to the combination of OMI τ and ALH when used together for the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ computation.

Figures 4–6 show that most of the changes in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ are located on the eastern part and over areas dominated by heavy NO₂ pollution such as the megacities and the Pearl River delta. The horizontal distribution of aerosol load adds some complex patterns. Overall, the quantitative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ differences between the applied explicit aerosol corrections and the improved implicit aerosol correction can be considered an average uncertainty related to the choice of an aerosol correction approach. Similar numbers are reported by Lorente et al. (2017), who indicated an average aerosol correction uncertainty of 45 % over highly polluted scenes and with large aerosol loading (τ(550 nm) ≥0.5). Furthermore, it was found that $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ from the POMINO data set over China (Lin et al., 2015) is 55 % higher ($A_{{\mathrm{NO}}_{\mathrm{2}}}$ smaller) than if no explicit aerosol correction was considered when the aerosol layer is located above the tropospheric NO₂ bulk. The main identified reason was a reduced shielding effect applied by the effective cloud parameters resulting from a higher effective cloud pressure (c_p=350 hPa); i.e. the Lambertian reflector was defined at a lower altitude. The reduction of this shielding effect may of course be attenuated when aerosols are mixed with NO₂, as their multiple scattering effects increase, then the average light path length increases and so does the NO₂ absorption.

Finally, over scenes with a small amount of aerosol (i.e. MODIS τ(550 nm)≤0.2), the difference in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ between the explicit aerosol correction assuming prior MODIS τ and the implicit aerosol correction with OMCLDO2-New is systematically lower and non-null: about an average of −10 % over all the considered regions. This difference may seem strange as small aerosol amounts are expected to have an almost negligible effect on the light path and thus on $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. When OMI τ is instead considered, this difference becomes positive over China, but is reduced everywhere (less than 10 %). Note that NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ and NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.9}}$ algorithms differ from OMCLDO2 by using an external geophysical parameter (i.e. MODIS τ). Although it is more accurate than using the retrieved OMI τ, the combination of an external MODIS aerosol parameter derived from different assumptions about the scattering model and surface reflectance may in the end lead to inconsistencies when combined with the OMI NN model: the 477 nm O₂−O₂ radiance budget is likely not closed. This radiance budget is always closed with OMCLDO2 (apart from the instrument noise), since it simultaneously adjusts both c_f and c_p to match the $R_{\mathrm{c}}\left(\mathrm{475}\mathrm{nm}\right)-N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ combination. The topic of radiance closure budget and its impacts on $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ are further discussed in Sect. 5.5.

4.3 Explicit vs. implicit aerosol correction – main reasons for the differences

As discussed in Sect. 3.2, ALH is the first crucial parameter for the computation of $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm). Therefore, as a first assumption, it is expected that the accuracy of the OMI ALH retrieval, and its difference with c_p, may be one of the first causes (although not unique) of the difference between the applied implicit and explicit aerosol corrections.

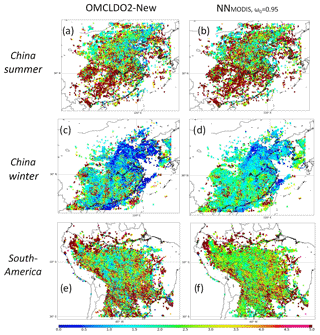
Figure 10 Maps of c_p (converted into cloud height) from OMCLDO2-New and ALH from NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ in kilometres in 2006–2007: (a) c_p, China in summer, (b) ALH, China in summer, (c) c_p, China in winter, (d) ALH, China in winter, (e) c_p, South America and (f) ALH, South America.

Figure 10 compares the average OMI ALH (retrieved with the NN trained with aerosol ω₀=0.95) and c_p from OMCLDO2-New, both converted into metric unit (km) over cloud-free scenes and for collocated MODIS scenes with τ(550 nm) ≥0.5. Overall, both variables are quite well correlated, with similar spatial and seasonal distributions. Values are higher in China in summertime and over South America and lie in the range of [1.5:5.0] km. They are lower in China in wintertime, between 0.4 and 2.0 km. Quantitatively, ALH values from NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ show that the fitted aerosol layers are located higher than the fitted opaque Lambertian clouds; i.e. aerosol pressures are smaller than c_p with average differences in the range of [$-\mathrm{0.49}:-\mathrm{50.3}$] hPa. Standard deviation of the differences are of the order of 120 hPa. The sign of the differences is reversed when employing NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.9}}$ (average differences 12.9–59.3 hPa).

As a first assumption, when ALH values are higher than c_p, the explicit aerosol corrections shall generally apply a stronger shielding effect to $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. Therefore, the resulting $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ should be larger. However, this element alone is likely insufficient to explain the differences observed in Sect. 4.2. The combined impacts of the assumed prior τ value also play a significant role. Furthermore, the assumed Lambertian cloud and the aerosol Henyey–Greenstein models differ for the horizontal coverage of the OMI pixel: the opaque Lambertian cloud model only covers part of the pixel (the fraction coverage is fitted through c_f, optical properties are fixed). The clear pixel fraction ensures the transmission part of the signal and the related multiple scattering not present by definition within the Lambertian cloud layer. In contrast, the aerosol model (and analysed synthetic cases) covers all pixels (optical properties can be changed, fraction coverage is fixed). The transmission and multiple scattering properties are included within the aerosol layer and vary as a function of the optical properties. Therefore, one can assume that, in the case of optically thick layers, the aerosol model generally applies a stronger screening effect by fully covering the scene and thus obstructing the surface transmission signal. By opposition, the surface transmission signal is more or less always ensured with the Lambertian opaque model by the non-covered pixel fraction.

5 Advantages and challenges of an explicit aerosol correction based on the 477 nm O₂−O₂ measurement

This section discusses specific elements in order to evaluate the relevancy of the developed explicit aerosol correction strategy over cloud-free scenes from OMI, but also in general from all UV–vis satellite measurements. In particular, we wish to draw the reader's attention to the advantage of using an explicit aerosol correction based on the exploitation of the 477 nm O₂−O₂ spectral band from a satellite measurement, but also the remaining difficulty of implementing it in practice. The next subsections focus on the significance of the aerosol model error, the importance of the NO₂ vertical profile, the cases with absorbing particles, the NO₂ vertical averaging kernels and the OMI visible radiance closure budget issue.

5.1 Impact of aerosol model error on tropospheric NO₂ air mass factor

When applying an explicit aerosol correction, the accuracy of each variable describing aerosol properties, once combined with the NO₂ vertical profile (see Sect. 5.2) and surface reflectance, drives the overall $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) computation uncertainty. The $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ uncertainty due to this whole set of variables, not only ALH, can be defined as the aerosol model error for OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ retrieval.

To understand the quantitative impact of each aerosol model variable uncertainty, Fig. 11 shows the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) biases resulting from some aerosol model inputs. A single bias in ALH of 100 hPa directly affects $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ within the range of [60 %:70 %] when absorbing aerosols (ω₀=0.9) are located below 0.5 km, assuming a wintertime NO₂ profile and with τ(550 nm)=1.4. The uncertainties are below 50 % for τ(550 nm) ≤0.5 and overall below 10 % when particles are located at elevated altitudes (i.e. true ALH≥1.4 km). This quantitatively emphasizes how essential ALH information quality is when particles are actually mixed with NO₂ molecules due to the complexity of reproducing the enhancement of the average light path caused by scattering effects. A bias of 0.2 in the assumed τ(550 nm) mostly impacts scenes with a small aerosol load: while resulting $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ uncertainties lie in the range of [$-\mathrm{20}\mathit{\%}:\mathrm{20}\mathit{\%}$] for τ(550 nm) ≤0.5, they decrease to the range of [0 %:10 %] for τ(550 nm)=1.4. Finally, an overestimation of aerosol scattering efficiency (i.e. ω₀ bias of 0.05) leads to an underestimation of $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ up to −20 % over scenes with high τ as a consequence of an underestimation of aerosol shielding effect and therefore a $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) that is too large. Overall, ALH uncertainty is the key driver of the AMF computation quality. ALH uncertainty must be better than 50 hPa to limit $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ bias below 40 %. With τ uncertainty, they form the most important set of aerosol parameters prerequired for a high quality of the $A_{{\mathrm{NO}}_{\mathrm{2}}}$(439 nm) computation. Although it is not negligible, the uncertainty of aerosol model parameters that are more related to the particle optical and scattering properties, such as ω₀, g and α, is of secondary importance provided that both the ALH and τ qualities are ensured.

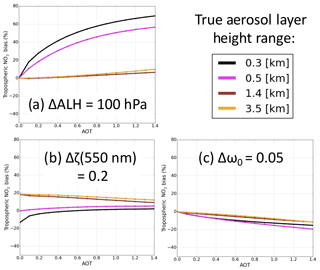
Figure 11 Relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases due to a direct impact of individual aerosol parameter biases on the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) calculation. Synthetic cases are similar to Fig. 2, with true aerosol ω₀=0.9, except a typical midlatitude winter NO₂ profile is considered instead: (a) ALH bias=100 hPa, (b) τ(550 nm) bias=0.2 and (c) ω₀ bias=0.05.

5.2 The importance of the relative layer height

A comprehensive aerosol correction for an accurate $A_{{\mathrm{NO}}_{\mathrm{2}}}$(439 nm) computation also requires the actual NO₂ vertical profile. Figure 12a shows the accuracy of the aerosol corrections in $A_{{\mathrm{NO}}_{\mathrm{2}}}$(439 nm), based on a synthetic case, assuming the presence of absorbing aerosol particles (ω=0.9) but a typical NO₂ vertical profile of wintertime (1 January, 12:00) over China. The main difference with Fig. 2 and Fig. 7 is the presence of a more abundant tropospheric NO₂ bulk closer to the surface and a stronger decrease rate to higher altitudes (Chimot et al., 2016). In such a case, relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases with the implicit aerosol correction are strongly degraded from [$-\mathrm{10}\mathit{\%}:\mathrm{20}\mathit{\%}$] (summertime) to [$-\mathrm{80}\mathit{\%}:\mathrm{40}\mathit{\%}$] (winter). As already identified in Sect. 4.1 with the summertime NO₂ profile, the insufficient shielding effect applied by the effective cloud parameters from OMCLDO2-New in the case of aerosol layers located at elevated altitude is severely degraded here (from −10 % to −80 %). The insufficient enhancement effect when particles are mixed with the tropospheric NO₂ molecules is also amplified here (from 20 % to 40 %).

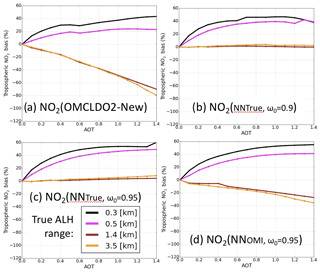
Figure 12 Relative $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases after application of the implicit or explicit aerosol correction (see Table 2) as a function of true aerosol optical thickness (AOT) τ(550 nm). Synthetic cases are similar to Fig. 2, except the summer NO₂ profile was replaced by a typical winter one. Furthermore, only absorbing aerosols with true ω₀=0.9 are considered. Finally, the impact of a bias on the assumed ω₀ through the application of the explicit aerosol correction is illustrated: (a) implicit aerosol correction based on OMCLDO2-New, (b) explicit aerosol correction, true τ and assumed ω₀=0.9, (c) explicit aerosol correction, true τ and assumed ω₀=0.95 and (d) explicit aerosol correction, retrieved OMI τ and assumed ω₀=0.95.

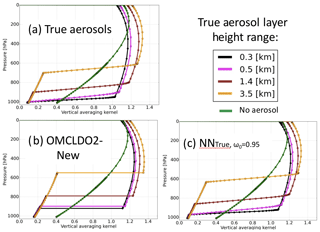
When considering an explicit aerosol correction using NN${}_{\mathrm{True},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.9}}$, the $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ bias is changed to 0 %–40 %. Similarly to summertime, they are lower in the case of particles at high altitude, suggesting strong benefits of such a correction scheme in wintertime and/or in the presence of absorbing particles. The cases of aerosols close to the surface (i.e. lower than 0.5 km) remains an issue due to the difficulty of distinguishing the scattering effects from the surface and the adjacent aerosol layer when retrieving ALH. The retrieval seems, in such a case, to overestimate the aerosol layer altitude.

The observed positive difference of about 40 % between explicit and implicit aerosol corrections is in line with the analyses over China in wintertime (see Sect. 4.2 and Fig. 9). All these elements strongly remind us and emphasize that the quality of the aerosol corrections and their differences for $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ retrieval are actually more dependent on the relative height between the particles and the tropospheric NO₂ bulk than the absolute values of ALH or c_p themselves. The evolutions of operational aerosol correction schemes in present and future air quality UV–visible space-borne sensors, such as TROPOMI on board Sentinel-5 Precursor, then need to consider a proper joint characterization of trace gas vertical profiles together with aerosol vertical distribution and related optical properties.

5.3 Explicit vs. implicit aerosol correction – focus on absorbing particles

In this study, the cases with absorbing particles, i.e. aerosol ω₀=0.9, brings more challenges to the implicit aerosol correction than scenes dominated by more scattering aerosols. Such difficulties were also identified by Castellanos et al. (2015). As a reminder, the presence of absorbing particles leads to a reduced c_p (increasing the shielding effect) but a lower c_f (lower shielding effect) with a higher transmittance coming from the clear part of the pixel. Part of the insufficient shielding effect observed with the implicit correction in Sect. 4.1 and 5.2 may thus be explained by insufficient coverage of the observation scene by the Lambertian opaque cloud layer; i.e. a higher fraction of the cloud-free part of the OMI scene, including the surface, is assumed to lead to a higher transmittance of the associated atmospheric layers. This last element likely overall limits the potential of the effective cloud model to apply an adequate shielding effect to $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. However, these biases still remain lower than if no aerosol correction was achieved (Chimot et al., 2016).

Figures 7 and 12a showed the potential of the explicit aerosol correction but by assuming no bias in the assumed τ and ω₀ parameters. To investigate this further, Fig. 12c–d depict the impacts of a wrong prior aerosol ω₀ (overestimation of 0.05) when applying the explicit aerosol correction through the use of the OMI aerosol NN. When the true prior τ value for both the ALH retrieval and the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ computation is conserved, the increases in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases are limited from 0 %–40 % (see Fig. 12a) to 0 %–60%. This reflects how the quality of prior τ knowledge helps to constrain both ALH retrievals and then limit the perturbation of $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. However, this may be more severely degraded when inaccurate prior τ is considered (see Sect. 5.5). Figure 12d shows the impacts of replacing true τ by the retrieved OMI one. $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases are higher, about [$-\mathrm{40}\mathit{\%}:\mathrm{60}\mathit{\%}$]. This is a direct result of a degradation of ALH retrieval due to an overly biased aerosol τ and the resulting impact on the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$. As discussed in Sect. 5.1, although the ω₀ parameter is of secondary importance for $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) itself compared to the (ALH-τ) combination, its direct impact on τ retrieval consequently affects the ALH determination accuracy and then indirectly affects $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$.

In spite of these drawbacks, $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ biases remain smaller than if the derived effective cloud parameters were employed through the implicit aerosol correction (see Fig. 12a). Thus, even if imperfect, the explicit aerosol correction based on OMI ALH and τ retrievals seem to remain advantageous for an efficient aerosol correction in tropospheric NO₂ VCD retrieval from visible satellite radiance. Nevertheless, true horizontal distributions of aerosols within the observation pixel may actually be quite heterogeneous. Such problems should be further investigated with a focus on areas where absorbing particles are expected, such as in wintertime in China, or during large biomass-burning episodes. Future studies should also determine how often such an effect occurs and its overall impact depending on the NO₂ vertical profile variability.

5.4 Aerosol model and NO₂ vertical averaging kernel

Theoretically, the application of an explicit aerosol model is expected to simulate more realistic scattering and absorption effects due to particles when computing $A_{{\mathrm{NO}}_{\mathrm{2}}}$(439 nm). Figure 13 illustrates the vertical averaging kernel (AK) (see Sect. 3.2) assuming τ(550 nm) = 1.0 and from the application of OMCLDO2-New, NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ and true aerosol conditions, assuming no bias in prior aerosol assumptions. AKs are very important for estimating the surface NO_x emissions by convoluting the NO₂ vertical profiles from the used atmospheric models to match the OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ observations (Eskes and Boersma, 2003; Ding et al., 2015). AKs based on OMCLDO2-New display a sharp distinction between the enhanced atmospheric layers located above aerosols and the shielded layers located below. On the contrary, AKs from NN${}_{\mathrm{MODIS},{\mathit{\omega }}_{\mathrm{0}}=\mathrm{0.95}}$ depict a smoother transition, which is then enhanced at the shielded layers. This transition is more in line with the actual AKs (Fig. 13a) and results from the scattering effects induced by the more or less wide aerosol particle layer. A bright Lambertian reflector is by nature fully opaque and does not induce multiple scattering effects. This is partly compensated by the transmission of the clear fraction of the pixel through the IPA assumption (see Sect. 2.2). This suggests that applying an explicit aerosol correction leads to the consideration of more realistic physical assumptions and AK productions. However, such a suggestion critically depends on an ensemble of other parameters that contribute to the AK generation: the accuracy of the retrieved ALH which triggers the location of the enhancement/shielding transition, the potential aerosol model biases (e.g. ω₀, scattering phase function, etc…) and the difference between actual and assumed aerosol vertical profiles.

Figure 13 Vertical AK (see Sects. 3.2 and 5.4) based on aerosol τ(550 nm)=1.0, NO₂ vertical profile of 1 July 2006 at 12:00 over China. Other conditions are similar to Fig. 2.

5.5 Radiance closure budget issue and potential impacts

The discussions about the model error in the previous subsections implicitly made the assumption that the whole set of parameters such as (c_f, c_p and surface reflectance) on the one hand, or (τ, ALH, ω_o, g, α and surface reflectance) are fully consistent in the sense that they form one unique particle model. However, when external data are used to constrain ALH retrieval accuracy, such as MODIS aerosol τ, one may combine inconsistent model assumptions, leading to complex artefacts such as the issue of the OMI closure radiance budget.

The radiance closure budget is not only important in the 477 nm O₂−O₂ band, but also in the NO₂ absorption band at the wavelength where the AMF is computed. Aerosol τ combined with surface reflectance are expected to drive OMI R_c(475 nm). As discussed in Sect. 2.2, OMCLDO2 simultaneously adjusts both c_f and c_p based on the same prior surface reflectance, such that their combination allows the (R_c(475 nm)-$N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$) budget to be closed and thus the OMI 477 nm O₂−O₂ radiance occurs independently of the accuracy of the selected model. On the contrary, by using MODIS τ, only OMI $N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$ is exploited, not R_c(475 nm). If all the prior parameters are accurate and derived from a unique set of aerosol model and surface reflectance parameters, the (R_c(475 nm)-$N_{{\mathrm{O}}_{\mathrm{2}}-{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{s}}$) budget should be closed. However, any mismatch between the model employed for MODIS τ determination and the one used in the OMI NN training data set, between MODIS and OMI instrument radiance, and/or the surface reflectance hypothesis, may leave this budget open. In particularly, it is worth remembering that the surface reflectance data set behind MODIS τ, OMI c_f and $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) are not identical: for OMI, a multi-spectral surface Lambertian equivalent reflectance (LER) was used (Kleipool et al., 2008), while MODIS aerosol retrieval uses a directional surface spectral reflectance (Levy et al., 2013).

Therefore, the strategies of the implicit vs. explicit aerosol correction analysed in Sect. 4.2 do not only differ in terms of assumed particle optical and scattering property model but also on how much the whole OMI radiance budget is eventually fitted. This last difference likely explains the strange systematic difference (about −10 %) identified over OMI scenes with MODIS τ(550 nm) ≤0.2, where aerosol effects could be assumed to be almost insignificant (see Fig. 9). When. MODIS τ is replaced by the retrieved OMI τ (see Table 1), which is, like c_f, mostly constrained by R_c(475 nm), prior OMI surface albedo and the same aerosol model used for ALH retrieval and $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$(439 nm) calculation, resulting $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ are higher than with the use of MODIS τ (see Table 2). Moreover, as analysed in Sect. 4.2, the differences between the implicit and explicit aerosol corrections are smaller everywhere over scenes with small aerosol load confirming the consistency in the employed models for each set of parameters and an almost complete closure of the OMI visible radiance budget (except instrument noise).

At the end, one might wonder what the best option is for an optimal aerosol correction:

1. using the best aerosol and surface parameters available for the most accurate correction at the cost of not closing the satellite radiance budget, or

2. applying a less accurate correction but with an ensemble of aerosol and surface parameters that eventually comprehensively fit the spectral measurement.

The first option gives more weight to the used auxiliary data, while the second option maximises the weight of the amount of information contained in the satellite measurement.

Due to the differences in the OMI-derived LER and the MODIS surface reflectance, it may be very tempting to select primarily both the OMI τ and ALH variables to avoid inconsistencies when correcting aerosol effects. However, in this study, such a choice is not necessarily obvious for everyone, as the accuracy of the ALH retrieval is strongly dependent on the requested prior τ (Chimot et al., 2017). The most accurate OMI ALH retrievals were obtained with collocated MODIS τ, not with the derived OMI AOT. This would naturally suggest first that the combination of OMI ALH and MODIS τ shall give the most accurate tropospheric NO₂ AMF. However, the apparent inconsistencies due to the different algorithms employed for each physical product are mostly observed in the present study through the discussion on the TOA radiance closure budget issue. They do not necessarily mean that the aerosol correction is less accurate.

The answer to such a problem is, in our opinion, not clear at this stage. But, given the fact that several studies prioritise the application of multiple parameters from very diverse sources (models, ancillary instruments with different techniques, etc.) to satellite spectral measurements, we think that the issue of radiance closure budget should be kept in mind by the scientific community and further investigated in future research studies. At the end, an optimal trade-off must be found between the quality of the $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ product and the weight given to the original satellite measurement.

6 Conclusions

This paper reprocesses the reference OMI tropospheric NO₂ vertical column density $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ for cloud-free scenes over eastern China and South America for 2006 and 2007. These regions are dominated by high aerosol loadings. The goal of this study is to evaluate the benefits of the recently achieved developments during the last years to improve the aerosol correction in the tropospheric NO₂ air mass factor $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$, a crucial parameter when retrieving $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ from visible air quality satellite backscattered measurements. In particular, the tested aerosol correction strategies rely on our recent experiences with the 477 nm O₂−O₂ spectral band: a key spectral band present in current and future air quality UV–vis satellite instruments such as OMI, GOME-2, TROPOMI, Sentinel-4-UVN and Sentinel-5-UVNS. The use of this band is important in view of operational data processing, as it allows parameters to be derived that, in principle, could reproduce the particle scattering and absorption effects on the average light path in the visible spectral window and represent the sensor field of view. Regardless of the type of algorithm employed here, these parameters can all be derived using computationally inexpensive methods, are directly representative of the OMI pixel in terms of spectral measurement, spatial coverage and temporal acquisition, and can directly be used for the $A_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ computation.

The two tested algorithms are the OMI cloud software OMCLDO2 (Veefkind et al., 2016) and the OMI aerosol neural network (NN) approach (Chimot et al., 2017, 2018). The most important difference between these methods is the assumed aerosol model, not only for the retrieval of the aerosol parameters in the O₂−O₂ band, but also how they represent aerosol effects in the tropospheric NO₂ air mass factor. The OMCLDO2 represents the aerosols as effective cloud parameters and thus implicitly correct the aerosol effects, whereas the NN approach explicitly models and corrects for aerosols. The most recent OMCLDO2 update from (Veefkind et al., 2016) includes, among many elements, an increased number of nodes in the LUTs and the necessary temperature correction of the O₂−O₂ slant column density.

For both methods, the reprocessed $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ shows smaller biases over cloud-free scenes dominated by aerosol pollution, compared to the standard DOMINO retrieval and its related aerosol correction. Previous studies showed an underestimation of the OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ between −20 % and −40 % over scenes with MODIS aerosol optical thickness τ(550 nm) ≥ 0.6, assuming scattering aerosol particles with aerosol single-scattering albedo ω₀=0.95 and summertime NO₂ vertical profile. In similar conditions, these biases are expected to be contained in the limit of [0 %:20 %] for both the most recent OMCLDO2 method and the NN method. On average, the applied explicit NN correction leads to higher $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ values compared to the implicit OMCLDO2 correction up to 40% depending on the seasons, regions and aerosol pollution episodes. This represents our best estimate of the aerosol correction uncertainty for the OMI $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ retrieval due to the possible choices of the algorithm correction. They are attributed to the model differences and the associated output variables.

Although both the implicit OMCLDO2 and explicit NN methods are a significant improvement over the current OMI DOMINO retrieval, we also found limitations that need to be further studied:

• If absorbing aerosols (i.e. single-scattering albedo ω₀≤0.9) are present, the implicit aerosol correction still leads to substantial biases in $N_{{\mathrm{NO}}_{\mathrm{2}}}^{\mathrm{v}}$ due to an insufficient applied shielding effect: between −80 % and 20 % assuming a typical NO₂ wintertime profile. This is most severe when particles are located at high altitude (above 1.4 km) and with heavy aerosol load. In similar conditions, the explicit aerosol correction allows us to mitigate the biases to the range of [0 %:40 %] if accurate τ and aerosol model are available, or [$-\mathrm{40}\mathit{\%}:\mathrm{60}\mathit{\%}$] with inaccurate τ (e.g. retrieved OMI τ) and aerosol model.

• Biases remain high when particles are located close to the surface, regardless of the aerosol correction methodology. The distinction between aerosol scattering and surface reflectance is challenging under such conditions. Since particles are close to the tropospheric NO₂ bulk (either mixed or slightly above), small errors in the retrieved aerosol height or effective cloud pressure have a significant impact on the derived NO₂ column.

• All aerosol correction methodologies are sensitive to the NO₂ vertical profile and the employed surface albedo or reflectance. Future improvements need to address both these parameters together with any evolution that can still be done in the aerosol or effective cloud retrievals from the 477 nm O₂−O₂.

• Although the OMI aerosol NN algorithms lead to a promising ALH retrieval, its use for an explicit aerosol correction is not straightforward. Indeed, ALH is only one variable (although a key one) of a set of aerosol parameters that need to be applied for the required explicit aerosol correction. Its combination with other aerosol parameters (size, ω₀, τ) can lead either to model errors and/or to the risk of not closing the OMI radiance budget if any of these parameters were issued from an external source (model or instrument) that is not consistent with the OMI ALH retrieval.

Based on its estimated performances, we recommend an operational processing of OMI data, where no distinction is made between cloudy, cloud-free and aerosol-contaminated scenes, to first use the implicit aerosol correction based on OMCLDO2. It allows both cloud and aerosol particle effects to be adequately corrected on the average light path. If cloud-free scenes can be carefully identified and collected in the same way as has been done here, then the explicit aerosol correction based on the OMI NN aerosol algorithms should be considered. We demonstrated in this study, for the first time, its high performance and the realism of the simulated physical effects. Moreover, the developed NN approach can ensure a fast cloud-free data processing.

Overall, the considered aerosol corrections can in principle be transposed to the future generation of air quality UV–vis satellite sensors, such as TROPOMI, Sentinel-4 and Sentinel-5-UVNS. It can also be considered for other trace gases of interest, e.g. SO₂ or HCHO. However, such an approach has to be adapted to the specificities of this new generation of instruments.