Sulfur dioxide layer height retrieval from Sentinel-5 Precursor/TROPOMI using FP_ILM

The accurate determination of the location, height, and loading of sulfur dioxide (SO₂) plumes emitted by volcanic eruptions is essential for aviation safety. The SO₂ layer height is also one of the most critical parameters with respect to determining the impact on the climate. Retrievals of SO₂ plume height have been carried out using satellite UV backscatter measurements, but, until now, such algorithms are very time-consuming. We have developed an extremely fast yet accurate SO₂ layer height retrieval using the Full-Physics Inverse Learning Machine (FP_ILM) algorithm. This is the first time the algorithm has been applied to measurements from the TROPOMI instrument onboard the Sentinel-5 Precursor platform. In this paper, we demonstrate the ability of the FP_ILM algorithm to retrieve SO₂ plume layer heights in near-real-time applications with an accuracy of better than 2 km for SO₂ total columns larger than 20 DU. We present SO₂ layer height results for the volcanic eruptions of Sinabung in February 2018, Sierra Negra in June 2018, and Raikoke in June 2019, observed by TROPOMI.

1 Introduction

Global satellite observations allow for the timely detection and monitoring of SO₂ emitted from volcanic eruptions, even in remote regions, where no ground-based instruments are installed (see, e.g., Fioletov et al., 2013). Satellite measurements of UV earthshine spectra in the wavelength range between 305 and 335 nm provide the highest sensitivity to SO₂ in the Earth's atmosphere. Volcanic eruptions can inject large amounts of sulfur dioxide (SO₂) into the atmosphere, where it is either subject to wet and dry deposition, as well as oxidization within a few days in the troposphere (see, e.g., Lee et al., 2011 or Myles et al., 2011), or oxidization over a period of several weeks to sulfate aerosols in the stratosphere (see, e.g., Robock, 2000; Forster et al., 2007 and von Glasow et al., 2009). Sulfate aerosols can affect the Earth's radiative forcing and have an impact on clouds (see, e.g., McCormick et al., 1995; Robock, 2000 and Malavelle et al., 2017).

Based on UV earthshine measurements, SO₂ vertical column densities (VCDs) can be retrieved easily using techniques such as differential optical absorption spectroscopy (DOAS; see, e.g., Rix et al., 2012), a principal component analysis (PCA; see, e.g., Li et al., 2017), or the Krueger–Kerr algorithm, which was applied to retrieve SO₂ from NASA TOMS (see, e.g., Krueger et al., 1995). These methods are fast enough for near-real-time (NRT) retrievals. Nevertheless, all algorithms retrieve only the slant column – to calculate the VCD, a conversion factor (called the air mass factor, AMF) has to be applied, which includes explicit or implicit assumptions about the vertical distribution of SO₂ in order to determine the effective light path. Note that AMFs are calculated by means of multiple-scattering radiative transfer models assuming known vertical distributions of SO₂ and O₃, as well as viewing, surface, and cloud properties.

Unfortunately, the vertical distribution (in terms of the plume layer height) of SO₂ is usually unknown at the time of the measurement as it is not easy to extract from the spectral signature (see Yang et al., 2009 and Nowlan et al., 2011): the SO₂ loading (the VCD) has a direct effect on the optical depth, whereas the layer height (LH) has an indirect effect on the optical depth as it influences the number of photons passing through the SO₂ layer, the UV wavelengths interacting with the SO₂ layer, and the layer optical depth due to the temperature dependency of the SO₂ absorption cross sections (Yang et al., 2009).

Even if there are ground-based or aircraft measurements of the SO₂ layer height (LH), the data are generally difficult to use for validation, as, e.g., for strong eruptions (a volcanic explosivity index, VEI, of greater than or equal to 3), volcanic plumes are typically transported over long distances and the number of collocations is small. Thus, for volcanic SO₂ measurements, the vertical distribution of SO₂ is a key parameter limiting the product accuracy. The usual approach for operational SO₂ retrievals is to assume several different a priori SO₂ vertical distributions and provide VCDs for each (see, e.g., Theys et al., 2017) along with an averaging kernel (AK), so that the user can calculate the VCD for an arbitrary SO₂ vertical distribution. However, in the upper troposphere and above, the vertical SO₂ distribution has little impact on the VCD.

To date, SO₂ layer height retrievals have used computationally demanding direct fitting inversion methods, which are not suitable for NRT applications. For the retrievals based on satellite UV measurements, Yang et al. (2009) and Yang et al. (2010) developed an “Extended Iterative Spectral Fitting” (EISF) algorithm for the Ozone Monitoring Instrument (OMI) aboard the NASA Aura satellite, and Nowlan et al. (2011) introduced an optimal estimation (OE) scheme for the GOME-2 instrument (Global Ozone Monitoring Experiment-2) aboard the EUMETSAT/ESA MetOp satellite fleet. For strong volcanic eruptions (VEI ≥ 3), the accuracy of the retrieved SO₂ LHs using this approach is in the 0.5–1 km range, whereas for small SO₂ absorption it is around 2 km (see Nowlan et al., 2011).

Satellite infrared sounders also offer the opportunity to measure both SO₂ VCDs and LHs (see Clarisse et al., 2008, 2014; Carboni et al., 2012, 2016) using optimal estimation algorithms for the Infrared Atmospheric Sounding Interferometer (IASI) aboard the EUMETSAT/ESA MetOp satellite fleet. While infrared sounders have an inferior sensitivity to lower tropospheric SO₂ compared with UV instruments, the layer height retrievals tend to have a better accuracy, and perform well even for low column amounts (up to the single-DU level; see, e.g., Clarisse et al., 2014 or Carboni et al., 2016); however, the horizontal resolution (12 km) is rather coarse.

In contrast, the TROPOMI instrument onboard the Sentinel-5 Precursor satellite (S5P) launched on 13 October 2017 has a much higher spatial resolution of 7×3.5 km², and will operate at an even smaller resolution of 5.5×3.5 km² beginning mid-August 2019. This allows us to observe and study SO₂ plumes at an unprecedented level of detail. Data turnover from TROPOMI is very large, and this consideration will require the development of new retrieval schemes for the fast and accurate retrieval of SO₂ layer heights in an operational environment.

To this end, we have developed an algorithm called “Full-Physics Inverse Learning Machine” (hereafter referred to as FP_ILM) for the retrieval of the SO₂ LH based on satellite UV earthshine spectra. The FP_ILM algorithm has been used for the retrieval of ozone profile shapes (Xu et al., 2017), the retrieval of surface properties accounting for bidirectional reflectance distribution function (BRDF) effects (Loyola et al., 2019), and the retrieval of SO₂ LH from GOME-2 (Efremenko et al., 2017). The algorithm creates a mapping between the spectral radiance and SO₂ LHs using machine learning methods. The time-consuming training phase of the algorithm using radiative transfer model calculations is performed off-line, and only the inversion operator has to be applied to satellite measurements – this makes the algorithm extremely fast; thus, it can be used in near-real-time processing environments. In this second paper on the FP_ILM SO₂ LH, we describe some improvements to the original algorithm from Efremenko et al. (2017), and we apply it to a number of volcanic eruptions observed by TROPOMI during the operational phase of the mission (started April 2018).

The paper is organized as follows. In Sect. 2 we describe the improved FP_ILM SO₂ LH algorithm. The sensitivity of retrieved SO₂ LHs to a number of different parameters is discussed in Sect. 3. In Sect. 4, the FP_ILM is applied to S5P data to retrieve SO₂ LHs for selected volcanic eruptions. Section 5 describes how the algorithm could be integrated in the operational TROPOMI SO₂ VCD retrieval algorithm. We summarize the paper in Sect. 6.

2 FP_ILM algorithm

Conceptually, the FP_ILM consists of a training phase, in which the inversion operator is obtained using synthetic data generated with an appropriate radiative transfer (RT) model, and an operational phase, in which the inversion operator is applied to real satellite measurements. The main advantage of the FP_ILM over classical direct fitting approaches is that the time-consuming training phase involving complex RT modeling is performed off-line; the inverse operator itself is robust and computationally simple and, therefore, extremely fast. In our previous paper (see Efremenko et al., 2017), we first introduced the FP_ILM algorithm and applied it to GOME-2 observations of a number of volcanic eruptions. We used a combination of principal component analysis (PCA) and principal component regression (PCR) methods to train the inversion operator in order to retrieve the SO₂ LH. For the current paper we have improved the FP_ILM algorithm with the use of a neural network (NN) approach, as outlined below.

Table 1 Physical parameters varied for the generation of reflectance spectra. The optimized parameter range for training the final FP_ILM retrieval operator is shown. (SZA: solar zenith angle; VZA: viewing zenith angle; RAA: relative azimuth angle; VCD: vertical column density; LH: layer height.)

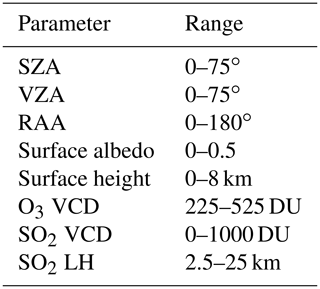
During the training phase, the LInearized Discrete Ordinate Radiative Transfer model (LIDORT) with inelastic rotational Raman scattering (RRS) implementation (Spurr et al., 2008) is deployed to compute simulated reflectance spectra in the 310–335 nm wavelength range. These spectra depend upon the following n=8 input parameters: the SO₂ VCD and LH, the surface albedo, the surface height, the O₃ VCD, the solar zenith angle (SZA), the viewing zenith angle (VZA), and the relative azimuth angle (RAA). Table 1 provides a summary of the final parameter space after optimization (see below) used for the training of the final retrieval operator. Note that O₃ has to be included due to the strong spectral interference between SO₂ and O₃ in the spectral range considered. Ozone profiles are classified according to the total column amount of O₃, and the month and latitude zones as specified in the TOMS Version 8 O₃ profile climatology (Bhartia, 2003). The SO₂ plume profile is taken to have a Gaussian shape, characterized by the total SO₂ VCD loading and centered at a peak-concentration layer height z_p, along with a half-width fixed to 2.5 km. In the following, the retrieval of the SO₂ layer height refers to the retrieval of the peak-concentration height z_p.

Simulations were carried out on a pressure/temperature/height grid from the US standard atmosphere, with a finer-grid vertical height resolution of 0.25 km below 15 km in order to properly resolve the Gaussian SO₂ plume shape. In total, some 131 072 simulated reflectance spectra have been calculated on a selective parameter grid established by means of a smart sampling technique developed by Loyola et al. (2016). Further details on the smart sampling technique applied to the SO₂ LH retrieval can be found in Efremenko et al. (2017).

The use of the LIDORT-RRS RT model is necessary, as it enables us to account for the effect of Raman scattering in the atmosphere: solar irradiances exhibit strong Fraunhofer structures in this part of the UV spectral range, and earthshine spectra are characterized by the “filling-in” of Fraunhofer-solar and telluric-absorber features due to “inelastic” (wavelength-redistributed) rotational-Raman scattering by air molecules. For further details, see Efremenko et al. (2017) and Spurr et al. (2008).

The simulated high-resolution reflectance spectra are convolved with the TROPOMI instrument spectral response function (ISRF) v3.0.0 (released 1 April 2018) (available at: http://www.tropomi.eu/data-products/isrf-dataset/, last access: 14 October 2019). Note that the TROPOMI instrument comprises 450 rows, which are in principle single detectors with their own ISRFs. The signal-to-noise ratio (SNR) is about 1000 in our UV wavelength range. Thus, to account for instrumental noise in the training phase, uncorrelated Gaussian noise with a fixed SNR of 1000 is added to the simulated spectral data.

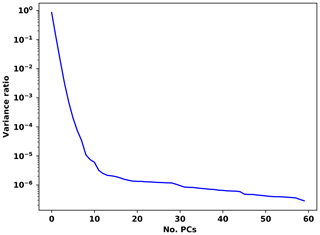
Figure 1 “Explained” variance ratio as a function of the number of principal components. The inclusion of 10 PCs already accounts for 99.994 % of the spectral variance.

To extract the information about the layer height and to reduce the dimensionality of the spectral dataset, a PCA is applied to the simulated spectra. By characterizing the set of simulated measurements with fewer parameters in this fashion, a simpler, more stable, and computationally efficient inversion scheme can be realized. It was found that using 10 principal components (PCs) was sufficient to retrieve information about the SO₂ LH. These 10 PCs accounted for 99.994 % of the spectral variance. The inclusion of additional PCs beyond 10 did not result in any improvements to the LH retrievals, as higher-order PCs are increasingly affected by noise. Figure 1 shows the ratio between the variance of the PCA-derived dataset and the total variance of the complete spectra dataset (the “explained” variance ratio) as a function of the number of PCs included in the PCA.

The 10 PCs, along with the information about the O₃ VCD, the SZA/VZA/RAA angles, the surface pressure, and albedo of each training data point, are then used as input to train a feed-forward artificial neural network (NN) including regression (in our case a “Multilayer Perceptron Regression” – MLPR), with the corresponding SO₂ LH as the output layer. Note here that the SO₂ VCD is not part of the training, as it depends directly on the SO₂ layer height.

In general, NNs can be used for establishing a non-linear mapping between a dataset of numeric inputs and a set of numeric outputs. A NN consists of interconnected neurons (or nodes) that implement a simple, non-linear function (a sigmoid function in our case) of the inputs. Neural networking is a powerful tool for determining non-linear dependencies between datasets in remote sensing, as shown by Loyola (2006). It consists of an input layer (representing the abovementioned input parameters), at least one so-called hidden layer, and an output layer (representing the expected output – in our case the SO₂ LH). Each neuron in the hidden layer(s) transforms the values from the previous layer(s) with a weighted linear summation, followed by a non-linear activation function, which is the sigmoid function in our case. The output layer receives the values from the last hidden layer and transforms them into output values.

The training of the MLPR is an iterative process that tries to minimize the so-called loss function (also known as the cost function), which is a measure of how well a model predicts the expected outcome; at each time step, the partial derivatives of the loss function with respect to the model parameters are computed in order to update the parameters. We note here that MLPR uses the “mean square error” loss function. A regularization term is added to the loss function that shrinks model parameters to prevent over-fitting: By building a complex neural network, it is quite easy to perfectly fit the training dataset. However, when this model is evaluated on new data (here the satellite measurements), it performs very poorly. Thus, the regularization modifies the loss function by adding additional terms that penalize large weight vectors and preferring diffuse weight vectors.

After carrying out a PCA and MLPR parameter optimization using closed-loop retrievals to minimize differences between the retrieved and simulated layer heights, the final configuration for the neural network settled on the use of two hidden layers, with 32 nodes in the first layer and 10 nodes in the second.

In the operational phase, the first step is to use the principal component scores acquired during the training phase to transform a given TROPOMI spectral measurement dataset to one with a lower dimension. Once this is done, the neural network inverse function is then applied to retrieve the SO₂ LH. In order to avoid the training of the NN for each of the 450 TROPOMI detector rows (with their own ISRF), we only trained the network for every 50th detector row and interpolated the retrieved SO₂ LH results to the actual row where it was detected.

We note that the FP_ILM algorithm only needs to be re-trained when large changes in the ISRF or SNR occur (see Sect. 3).

3 Dependencies

In this section, we study the dependency of the layer height retrieval on different parameters. We discriminate between direct dependencies (i.e., those parameters affecting the reflectance spectra) and indirect dependencies (i.e., affecting the training data and inversion algorithm) of the retrieved layer height:

• Direct dependencies are defined as the viewing geometry, surface properties, ISRF, noise level (SNR), instrumental stray light, and O₃ VCD.

• Indirect dependencies are defined as the number of layers in the neural network, number of PCs, and parameter ranges for training.

First, we train the FP_ILM operator using 90 % of the training dataset (see Table 1), and then apply the trained operator to the remaining 10 % training spectra, for which we know the exact SO₂ LH. Figure 2 (red dots) shows the SO₂ LH difference as a function of solar/viewing geometry, SO₂ VCD, O₃ VCD, albedo, and surface pressure, respectively. The figure clearly shows a number of marked dependencies in the retrieved layer height, with notably high differences with respect to the real SO₂ LH for low and high layer heights, for low SO₂ VCD as well as for high SZA.

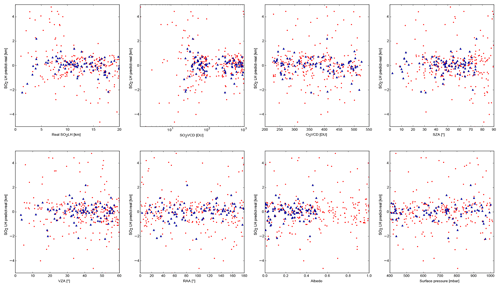
Figure 2 Dependency of the retrieved SO₂ layer height as a function of eight parameters as indicated. Plotted are the layer height differences (in km) between the retrieved layer heights and those simulated using the independent verification dataset (i.e., a 10 % subdivision of the entire training dataset). Red dots show the dependencies using the entire training dataset, whereas blue triangles show the dependencies with an optimized training dataset (i.e., restricted to SO₂ VCD values greater than or equal to 20 DU, SZAs less than or equal to 75^∘, and albedos less than or equal to 0.5).

Regarding the SZA dependency, a cutoff limit of 75^∘ is usually set in operational SO₂ retrievals, because at high SZAs the light path becomes very long and the noise level increases. Accordingly, we limit the SZA of the spectra used in the training to SZA values less than or equal to 75^∘ in the following.

Clearly, for small SO₂ VCDs, the information content on the LH in the spectral signature is very low. It follows that the inclusion of spectra with low SO₂ content in the training will have a negative effect on the entire neural network. In principle, for lower SO₂ VCD loadings, more PCs could be included, but at some point the noise level signature will exceed that of the actual SO₂ absorption.

We performed several tests in which we limited the training dataset by varying the allowed input parameter ranges. We found an optimal parameter range that allows for the retrieval of a broad range of SO₂ LHs, even for low SO₂ VCDs. In the training phase, we only use spectra with SO₂ VCDs greater than or equal to 20 DU, surface albedo values less than or equal to 0.5, and SZAs less than or equal to 75^∘ to train the final inversion operator for TROPOMI. The albedo limit is set to 0.5, as large albedo values will induce large variations in the spectra (multiple reflections from the surface). These additional variations correlate with the variations due to perturbations in the SO₂ VCD and LH. Therefore, to make the algorithm more stable, we restrict the albedo range to the physically relevant cases. We further limited the training values of the SO₂ LH to the range between 0 and 25 km. Although higher LHs from strong volcanic eruptions can occur, the use of a broad training data range also has an influence on the accuracy of the retrieval. To a limited extent, however, the FP_ILM is also able to extrapolate to an untrained parameter range, although with significantly less accuracy.

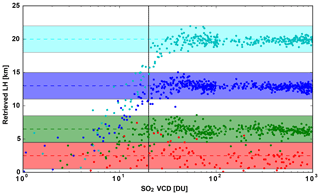
Figure 3 Dependency of the retrieved SO₂ LH as a function of SO₂ total vertical column, using the independent test dataset. The different LHs for which the test spectra have been generated are color-coded. The horizontal color bars indicate a 2 km uncertainty on the retrieved SO₂ LH.

Using the optimized training dataset (see Table 1 for a summary of the parameter space), Fig. 2 (blue triangles) shows that the error on the retrieved SO₂ LH is less than 2 km and the dependency on the SO₂ VCD is reduced. Figure 3 shows the retrieved layer height as a function of the SO₂ VCD. As mentioned above, for low SO₂ VCDs, high-altitude layer heights cannot be retrieved – there is always a bias towards low layer heights. Only for SO₂ loadings in excess of 20 DU, do we retrieve layer heights with an uncertainty of less than 2 km.

To investigate the dependency of the retrieved SO₂ LHs as a function of the SNR, we used two different noise levels (a SNR of 500 and 1500). Figure 4 clearly shows that the SNR only has a minor effect on the accuracy of the retrieved layer height, with only slightly higher accuracy for increased SNR. This is to be expected, as we used the first 10 PC scores and, thus, basically removed all noise features.

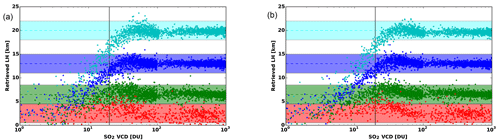
Figure 4 Dependency of the retrieved SO₂ LHs on the SNR. Same as Fig. 3 with different SNR values. Panel (a) shows a SNR of 500, and panel (b) shows a SNR of 1500.

Concerning the dependency on the ISRF, we note that in the operational retrieval of SO₂ LHs from TROPOMI data, each detector row is effectively a single instrument with its own ISRF. The accuracy of the retrieved SO₂ LH can vary across detector rows. Figure 5 shows the SO₂ LH results when applied to the Sinabung eruption (see Sect. 4.1). Black dots show the LHs for each 50th row, whereas the red cross shows the interpolated LH for the measurement row. Clearly, the retrieved LH is slightly different in each row (within 1 km) due to the different ISRF used for training the NN. Note that we determine the LH for a set of fixed detector rows (for which we have trained the FP_ILM separately), and then interpolate the layer height to the actual row. In this way we avoid jumps in the retrieved layer height between adjacent detector rows.

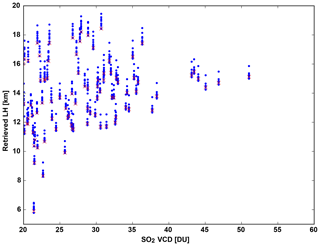
Figure 5 Dependency of the retrieved SO₂ LH on the TROPOMI instrument row. The SO₂ LH as a function of the SO₂ VCD is shown for the Sinabung eruption. Blue dots show the SO₂ LH result for every 50th detector row, whereas red crosses show the LH interpolated to the measurement row.

Instrumental stray light can introduce spectral features that may lead to bias in the retrieved SO₂ LH. However, according to Kleipool et al. (2018) the in-band stray light of TROPOMI after correction is as low as 0.5 % and, thus, can be neglected. Furthermore, no evidence for out-of-band-stray light was found (Quintus Kleipool, personal communication, 2019).

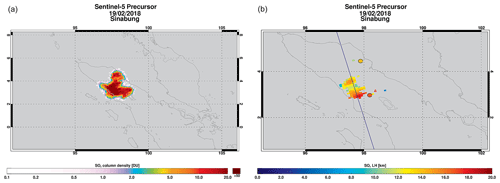
Figure 6 SO₂ VCD (a) and SO₂ LH (b) for the TROPOMI measurements of the Sinabung volcano on 19 February 2018, at an overpass time of around 06:30 UTC. SO₂ LH results are only shown for VCD values greater than or equal to 20 DU. In panel (b)  MLS/Aura results (the two colored circles) and the CALIPSO ground track (cf. Fig. 7) are shown.

During major volcanic eruptions (VEI ≥ 3) with very high SO₂ loadings, the O₃ VCD retrievals may be inaccurate due to SO₂ interference. However, this effect is negligible for weak eruptions. For strong eruptions (exceeding about 50 DU of SO₂) the error on the O₃ VCD may reach a few percent (see Lerot et al., 2014), which means that the error on the SO₂ LH is still negligible.

4 Application to TROPOMI data

Reflectance spectra from TROPOMI are determined from the operational L1 solar irradiance and earthshine radiance data (solar irradiance is measured on a daily basis). To correct for Doppler shifts between earthshine and irradiance spectra, we apply the wavelength calibration information from the operational L2 SO₂ product to first register the solar spectrum and then we use the fitted shift and squeeze parameters from the DOAS retrieval to calibrate the earthshine spectra. From this calibrated L1 data, we then calculate reflectances in the 310–335 nm wavelength range.

In the following subsections, we have applied the FP_ILM operator to three major volcanic eruptions measured by TROPOMI. We chose eruptions with a peak SO₂ VCD exceeding our 20 DU threshold criterion and with an extended SO₂ plume that allows us to compare the FP_ILM results with independent retrievals from other satellite data sources. In addition to L1 reflectances, we use information on SO₂ VCD, O₃ VCD, surface, and viewing conditions from the operational SO₂ L2 product (see Pedergnana et al., 2018).

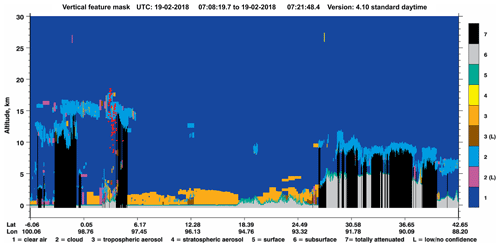
Figure 7 CALIOP/CALIPSO vertical feature mask for the measurement of the Sinabung volcanic eruption on 19 February 2018 at around 07:15 UTC. Red dots show the retrieved LH for pixels with SO₂ VCD values greater than or equal to 20 DU. The ground track of the CALIPSO measurements is shown in Fig. 6. The volcano is located at 3.17^∘ N, 98.39^∘ E. The plume is clearly visible in the left section of the image. Note that the classification scheme sometimes cannot pick up the volcanic ash or sulfate aerosol because of competing clouds. CALIPSO image credit: NASA.

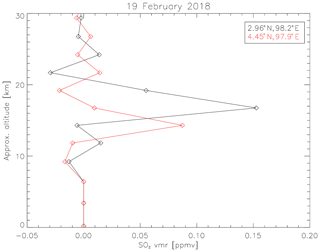
Figure 8 MLS SO₂ profile for two measurements intersecting the volcanic plume of the Sinabung volcanic eruption on 19 February 2018, clearly showing the presence of an SO₂ layer at an altitude of around 16 km close to the volcano (black) and 13 km in the extended plume farther north (red). The position of the measurements is shown in Fig. 6.

For validation of our results, we performed comparisons with independent MetOp/IASI SO₂ LH data (see Clarisse et al., 2014 for details), as well as SO₂ profile data from the Microwave Limb Sounder (MLS) on the NASA/Aura satellite (see Pumphrey et al., 2015). The MetOp platforms have different orbits from that of S5P, with widely different overpass times; thus, direct satellite comparisons with IASI data will only give a qualitative validation on the accuracy of retrieved SO₂ LHs from TROPOMI measurements. The afternoon Aura/MLS overpass is nearly coincident with TROPOMI. The MLS can provide some information on the SO₂ LH, albeit with limited spatial coverage and vertical resolution, as it is only sensitive above an altitude of about 147 hPa (i.e., above around 13 km). We also checked on the availability of an overpass of the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO, Winker et al., 2010) satellite with the Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP) instrument. Note that CALIPSO measures only ash and aerosol absorption profiles. In this regard, we note that SO₂ plumes and ash or aerosols are not necessarily colocated, as gas and ash can separate in volcanic clouds. At the time of writing, IASI and MLS data are unfortunately the only sources for independent SO₂ LH satellite validation.

4.1 Sinabung

The Sinabung stratovolcano (2460 m summit elevation) on the island of Sumatra had been highly active until September 2010 and was then quiet until a new eruptive phase began in September 2013 that lasted until March 2018 (see Venzke, 2018b). On 19 February 2018, Sinabung erupted violently at around 02:55 UTC with its largest explosion to date, emitting a volcanic ash plume that rose to an altitude of at least 16.8 km and an SO₂ plume of up to 50 DU of SO₂ that was observed by several satellite instruments, including TROPOMI (see Fig. 6, overpass time of around 06:30 UTC), OMI, IASI (overpass times of around 03:30 and 15:00 UTC), and MLS (overpass time of around 07:10 UTC). There was also an overpass of CALIPSO/CALIOP at about 07:15 UTC, over the volcanic plume.

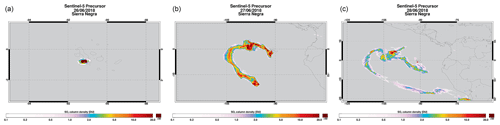
Figure 9 SO₂ VCD for the TROPOMI measurements of the Sierra Negra volcano from 26 (a) to 28 June 2018 (b), with overpass times of around 19:50 UTC.

The FP_ILM algorithm retrieved SO₂ LHs extending up to 17 km (see Fig. 6); these show excellent agreement with the MLS SO₂ profile measurements inside the plume (see colored circles in Fig. 6), with peaks at 16.75 km close to the volcano, and 14.31 km in the northern part of the plume (see Fig. 8). Furthermore, our results are in close agreement with CALIPSO measurements, clearly showing an attenuation by ash or aerosols at altitudes around 15–18 km (color-coded in orange). Fresh volcanic plumes are typically rich in water vapor (especially for tropical eruptions); thus, the volcanic clouds also contain high concentrations of water droplets. Therefore, the classification in the CALIPSO vertical feature mask sometimes fails to pick up the volcanic ash or sulfate aerosol because of competing clouds. Nevertheless the altitudes of the identified features are likely those of the volcanic plumes themselves, given the collocations in time and space. We note that the brightness temperature difference plots (not shown) can help in the identification of an ash layer, as the difference in the brightness temperature between the CALIPSO channels at 10.6 and 12.05 µm becomes negative for ash, whereas for normal clouds it is positive.

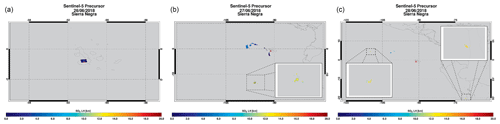
Figure 10 FP_ILM SO₂ LHs for the TROPOMI measurements shown in Fig. 9. Note that only pixels with SO₂ VCD values greater than or equal to 20 DU are shown. The MLS SO₂ measurement of the volcanic plume on 27 June is indicated by a colored circle.

In the figure we have superimposed our FP_ILM SO₂ LH results in red dots. SO₂ LHs retrieved for IASI/MetOp-A and -B measurements (not shown) indicated LH values at about 13 km for the 03:30 UTC overpass and LHs up to 18 km around the overpass time of 15:00 UTC; these results agree well with the TROPOMI results.

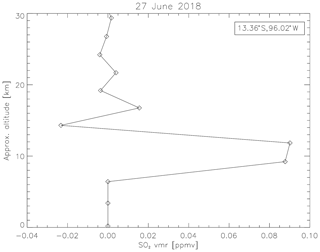
Figure 11 MLS SO₂ profile measured on 27 June 2018 (at a measurement time of 20:16 UTC) in the extended volcanic plume from the Sierra Negra eruption, clearly showing the presence of an SO₂ layer at an altitude range from 9 to 11 km. The position of the measurements is shown in Fig. 10.

Also the Pusat Vulkanologi dan Mitigasi Bencana Geologi (see http://vsi.esdm.go.id/, last access: 14 October 2019) (PVMBG, also known as CVGHM) reported “a dark gray plume with a high volume of ash that rose at least to 16.8 km” at 08:53 UTC. Furthermore, the Darwin Volcanic Ash Advisory Center (see http://www.bom.gov.au/aviation/volcanic-ash/, last access: 14 October 2019) (VAAC) reported that LH values for these Sinabung ash plumes identified in satellite images, recorded by webcams, and reported by PVMBG continued to rise throughout the day to 13.7 km.

4.2 Sierra Negra

On 26 June 2018 a strong eruption occurred at the Sierra Negra shield volcano (1124 m summit elevation), located on Isabela Island (Galapagos). According to Venzke (2018a), this volcano has erupted several times since 1948, with the last eruption reported in 2005. After an increase in seismicity, Sierra Negra erupted at 20:09 UTC, producing a dense ash and SO₂ plume. The eruption was divided into an initial very energetic phase (VEI = 3) characterized by the opening of five fissures that lasted 1 day, and a long phase with lava flows from 27 July to 23 August 2018 that also displayed decreased gas emissions. TROPOMI was able to measure a very strong SO₂ plume (with loading in excess of 500 DU) only a few minutes (overpass at 20:12 UTC) after the start of the first eruption, as well as an extended SO₂ plume for several days after the eruption.

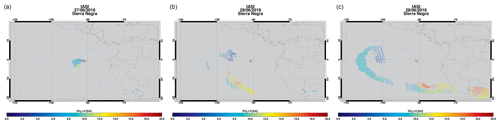
Figure 12 MetOp-A and -B IASI SO₂ LH results for the Sierra Negra SO₂ plume from 27 (a) to 29 June 2018 (b) with overpass times of around 02:00 – about 6 h after the TROPOMI measurement.

Figure 9 shows the SO₂ plume from 26 to 28 June at overpass times of around 20:12 UTC. The corresponding FP_ILM SO₂ LH is shown in Fig. 10. On 26 June, shortly after the eruption began, the retrieved SO₂ LH was around 4–6 km. On the following days, however, a much higher SO₂ LH of around 14 km was retrieved by FP_ILM, with some parts of the plume reaching an altitude of about 18 km. We note here that these high SO₂ LH values are not visible in the figure as they were retrieved for a SO₂ VCD of about 10 DU and, hence, with low accuracy – in the figure only SO₂ LH results for SO₂ VCDs great than or equal to 20 DU are shown.

We found only one closely related MLS SO₂ profile measurement intersecting the SO₂ plume on 27 June, at a measurement time of 20:16 UTC, i.e., shortly after the TROPOMI measurement (see colored circle in Fig. 10b). The MLS data in Fig. 11 show an SO₂ layer in the altitude range from 9 to 12 km, which is in excellent agreement with the FP_ILM SO₂ LH results of around 11 to 13 km at the same coordinates (see zoom-in).

Figure 12 shows the SO₂ LHs retrieved by IASI from 27 to 29 June. Note that the IASI overpass is at around 02:00 UTC – about 6 h after the TROPOMI overpass. Nevertheless the LHs retrieved close to the volcano are in very good agreement with the FP_ILM results, which are also at about 4–6 km. Similarly for the extended plume, for which only a few pixels are shown in Fig. 10, the agreement is very good, with LHs of about 13 km.

4.3 Raikoke

On 22 June 2019 at 04:00 local time, the Raikoke stratovolcano located on the Kuril Islands (Russia, 551 m summit elevation) erupted explosively (VEI ≥ 4) after being dormant since 1924. There were several strong distinct explosions, producing a dense ash and SO₂ plume that rose to an altitude of 13 km the on the first few days and was entrained into the stratosphere (see Sennert, 2019). This was the strongest volcanic eruption since the Merapi eruption in 2011, producing a colossal SO₂ plume with an SO₂ loading of more than 900 DU on 22 June 2019, which was dispersed by strong winds over Russia and North America, and was even detectable 2 weeks after the volcanic eruption. The Raikoke eruption was still ongoing during the writing of this paper. Further results for this eruption are expected to be the subject of a future publication.

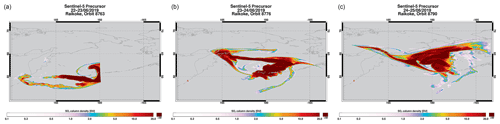
Figure 13 SO₂ VCD for the TROPOMI measurements of the Raikoke volcanic eruption, measured on 22/23 June 2019 (a), 23/24 June 2019 (b), and 24/25 June 2019 (c), with overpass times of around 02:00 UTC (Orbit 8763, a), and 00:00 UTC (orbits 8776 and 8790).

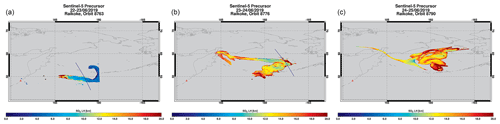
Figure 14 SO₂ LH retrieved for the TROPOMI orbits shown in Fig. 13. Only pixels with SO₂ VCDs greater than or equal to 20 DU are shown. Colored circles indicate the MLS/Aura SO₂ profile peak height for the results shown in Fig. 15. The blue lines indicate the CALIPSO ground track for the results shown in Fig. 16.

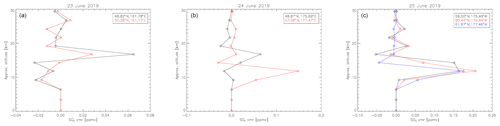
Figure 15 MLS SO₂ profiles measured on 23 June 2019 (a, overpass at around 02:20 UTC), 24 June 2019 (b, overpass at around 01:30 UTC), and 25 June 2019 (c, overpass at around 00:30 UTC), in the extended volcanic plume from the Raikoke eruption, clearly showing the presence of an SO₂ layer at an altitude of around 17 km on 23 June, two distinct layers at 12 and 17 km at different positions of the plume on 24 June 2019, and around 12–14 km on 25 June 2019. The position of the measurements is shown in Fig. 14.

Figure 13 shows SO₂ VCD measured by TROPOMI for the first 3 days after the eruption. Note that the SO₂ plume is close to the date line with several overlapping S5P orbits at different overpass times. Therefore, we have chosen to plot only one single orbit per day in the images. The figure shows the plume at overpass times of around 00:00 and 02:00 UTC.

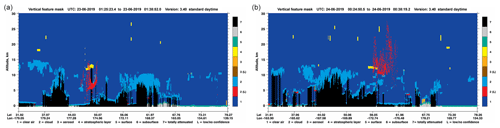
Figure 16 CALIOP/CALIPSO vertical feature mask for the measurements of the Raikoke plume on 23 June 2019 at around 01:30 UTC (a) and on 24 June 2019 at around 00:30 UTC (b). Red dots show the retrieved FP_ILM SO₂ LH for pixels with SO₂ VCDs greater than or equal to 20 DU. The ground track of the CALIPSO measurements is shown in Fig. 14. Note that the classification scheme sometimes cannot pick up the volcanic ash or sulfate aerosol because of competing clouds. CALIPSO image credit: NASA.

Figure 14 shows the corresponding SO₂ LH retrieved by the FP_ILM for SO₂ VCDs greater than or equal to 20 DU. Clearly, the plume shows several layers, with SO₂ LHs ranging from 6–8 km up to 19 km on 23 June and from 11 km up to 20 km on 24 June 2019. This is in very good agreement with MLS data (colored circles in the figure) with overpass times of around 02:20 UTC on 23 June (panel a), around 01:30 UTC on 24 June (panel b) and around 00:30 UTC on 25 June (panel c): the MLS profiles in Fig. 15 show an SO₂ layer at 17 km on 23 June, two distinct layers at 12 and 17 km at different positions of the plume on 24 June, and a layer in the range from 12 to 14 km on 25 June.

In addition, CALIOP/CALIPSO was able to detect the ash plume during the first few days after the eruption, with plume height values in very good agreement with the FP_ILM SO₂ LH results. On 22 June an ash plume at 17 km was detected (not shown here). The CALIPSO data from 23 June (overpass at around 01:30 UTC; shown in Fig. 16a) show an ash layer around 5–8 km in the northern part of the plume (i.e., around 46^∘ N), and a second ash layer around 13 km in the southern part, which is in very good agreement with the FP_ILM SO₂ LH results. On 24 June an ash layer at 13 km is visible which is in agreement with the lowest SO₂ LHs retrieved. Note that the CALIPSO ground tracks are shown in Fig. 14 (blue line).

The latest IASI retrievals indicate that the bulk of the SO₂ mass is contained at an altitude between 9 and 15 km (not shown here). We note that at the time of writing this paper, the IASI LH retrieval algorithm is undergoing improvements to handle cases with very large SO₂ loadings in the center of the plume. As the Raikoke eruption was still ongoing during the writing of this paper, we refer here to an upcoming publication of the IASI results for the Raikoke eruption.

5 Implementation in an operational environment

In this section we describe the manner in which the algorithm could be implemented in the operational S5P/TROPOMI ground segment.

As the same input parameters are used for retrieving operational SO₂ VCD, i.e., O₃ VCD, viewing parameters, and surface conditions as well as radiance and irradiance data, the FP_ILM algorithm can be easily integrated within the operational UPAS processor used for generating the SO₂ products. In the operational TROPOMI environment, cloud properties and the O₃ VCD are retrieved before the SO₂ algorithm is started. Thus, all of the required input parameters are already available when the FP_ILM algorithm is triggered in the case of a volcanic eruption. Only the wavelength calibration and calculation of the reflectance spectrum has to be performed prior to retrieving the SO₂ LH, as this step differs from the operational SO₂ VCD retrieval.

To process a satellite pixel containing volcanic SO₂, the FP_ILM algorithm should be triggered by the operational enhanced SO₂ detection flag (see Theys, 2018 for a reference) and using a threshold (a priori) SO₂ VCD of at least 10 DU. The resulting SO₂ LH for this pixel should be stored in the final L2 SO₂ product and can be also used to calculate an optimized SO₂ VCD for this LH.

The SO₂ LH retrieval only takes about 2 ms per TROPOMI spectrum; hence, even for an extended volcanic plume, the entire LH retrieval can be performed in a matter of seconds. This is important for operational retrieval environments with strong time constraints. Currently, the entire processing of a single TROPOMI pixel (i.e., cloud parameters, O₃ and SO₂ VCD retrieval) in the operational ground segment takes about 90 ms, which translates to about 24 min for an entire S5P orbit. Thus, the additional time required for the retrieval of the SO₂ LH for selected pixels is not significant.

6 Conclusions

We have developed a new algorithm for the fast and accurate retrieval of SO₂ layer heights from UV earthshine observations of volcanic SO₂ eruptions by the TROPOMI sensor onboard the Sentinel-5 Precursor platform. The SO₂ LH retrieval has two phases: (1) a computationally expensive off-line training phase in which the retrieval inverse operator is obtained using the FP_ILM (Full-Physics Learning Machine) algorithm, and (2) a fast operational phase, in which the FP_ILM inverse operator is applied to measured UV reflectance spectra. The FP_ILM combines a principal component analysis with a neural network regression using the UV reflectance, O₃ total column, viewing geometries, and surface properties as input. Based on an optimized training dataset created with smart sampling techniques, the principal component scores calculated for reflectance spectra in the 310–335 nm wavelength range are used along with the other parameters to train a feed-forward artificial neural network. For S5P/TROPOMI measurement data, an initial dimensionality reduction of the reflectance spectra is performed by applying the PCA-derived principal component scores before retrieving SO₂ LH with the trained neural network.

The FP_ILM can be used for NRT applications with strict time constraints. S5P/TROPOMI, with its high spatial and spectral resolution, provides a huge amount of data and the computationally intensive direct fitting approaches to SO₂ LH retrieval developed so far are not applicable. In contrast, the FP_ILM operator performs SO₂ LH retrieval within about 2 ms per TROPOMI spectrum. Hence, even the retrieval on extended volcanic plumes can be performed in a matter of a few seconds, allowing for the determination of the SO₂ layer height with an accuracy better than 2 km for SO₂ total column densities larger than 20 DU.

In this paper, we deployed an independent simulated reflectance spectra dataset to investigate the accuracy of SO₂ LH retrievals and their dependencies on a number of different factors and parameters both direct and indirect. In particular, it was found that the retrieved SO₂ LH is strongly dependent on the SO₂ VCD for low VCDs (VCDs ≤ 20 DU) as well as for high SZAs (SZAs ≥ 75^∘). For high VCDs and low SZA, according to closed-loop tests, the SO₂ LH can be retrieved with an accuracy of better than 2 km. We also investigated the dependencies on ISRF and SNR, both of which turned out to be relatively slight effects.

Broad-band spectral scattering and absorption due to sulfate aerosols or volcanic ash plumes will certainly affect SO₂ LH retrievals. Although not considered in the present work, we will address this important issue in a forthcoming paper in this series; aerosols will be explicitly accounted for in the training of the FP_ILM. Nevertheless, we should note that SO₂ and ash are likely to be colocated only for fresh volcanic plumes. For mature plumes, mass differences will ensure that ash and SO₂ plumes are not located at similar altitudes, and the corresponding plumes are thus subject to different wind-direction dispersal.

We applied the FP_ILM to a number of volcanic eruptions (VEI ≥ 3) observed recently by S5P/TROPOMI. Our SO₂ LH results were compared to SO₂ LHs retrieved from IR measurements from two MetOp/IASI satellites, as well as the NASA Aura/MLS SO₂ profile and CALIOP/CALIPSO ash and aerosol measurements. Unfortunately the orbits of the MetOp satellites and S5P have widely different overpass times, allowing for only qualitative comparisons. Despite this, there is generally very good agreement between the IASI and TROPOMI results. Very good agreement with MLS data was found, which provides SO₂ profiles with limited spatial coverage and vertical resolution, however with overpass times close to the S5P overpass. Nevertheless, further verification work is certainly needed. For the Sinabung eruption in February 2018 and the Raikoke eruption in 2019, our results also showed excellent agreement with CALIOP/CALIPSO LIDAR data measuring the ash plume.