Field comparison of dry deposition samplers for collection of atmospheric mineral dust: results from single-particle characterization

Frequently, passive dry deposition collectors are used to sample atmospheric dust deposition. However, there exists a multitude of different instruments with different, usually not well-characterized sampling efficiencies. As a result, the acquired data might be considerably biased with respect to their size representativity and, as a consequence, also composition. In this study, individual particle analysis by automated scanning electron microscopy coupled with energy-dispersive X-ray analysis was used to characterize different, commonly used passive samplers with respect to their size-resolved deposition rate and concentration. This study focuses on the microphysical properties, i.e., the aerosol concentration and deposition rates as well as the particle size distributions. In addition, computational fluid dynamics modeling was used in parallel to achieve deposition velocities from a theoretical point of view.

Scanning electron microscopy (SEM)-calculated deposition rate measurements made using different passive samplers show a disagreement among the samplers. Modified Wilson and Cooke (MWAC) and Big Spring Number Eight (BSNE) – both horizontal flux samplers – collect considerably more material than the flat plate and Sigma-2 samplers, which are vertical flux samplers. The collection efficiency of MWAC increases for large particles in comparison to Sigma-2 with increasing wind speed, while such an increase is less observed in the case of BSNE. A positive correlation is found between deposition rate and PM₁₀ concentration measurements by an optical particle spectrometer. The results indicate that a BSNE and Sigma-2 can be good options for PM₁₀ measurement, whereas MWAC and flat-plate samplers are not a suitable choice. A negative correlation was observed in between dust deposition rate and wind speed. Deposition velocities calculated from different classical deposition models do not agree with deposition velocities estimated using computational fluid dynamics (CFD) simulations. The deposition velocity estimated from CFD was often higher than the values derived from classical deposition velocity models. Moreover, the modeled deposition velocity ratios between different samplers do not agree with the observations.

1 Introduction

Mineral dust aerosol in the climate system has received considerable scientific attention mainly due to its direct effect on the radiative budget and indirect one on cloud microphysical properties (Arimoto, 2001; Huang et al., 2010). Mineral dust particles also play a key part with respect to gas-phase chemistry by providing a reaction surface, e.g., ozone depletion (Nicolas et al., 2009; Prospero et al., 1995). Moreover, dust aerosol also plays an important role in biogeochemical cycles by supplying important and limiting nutrients to ocean surfaces (Jickells et al., 2005). Mineral dust is emitted mainly from the arid and semi-arid regions of the world and believed to have a global source strength ranging from 1000 to 3000 Tg yr⁻¹ (Andreae, 1995). It forms the single largest component of global atmospheric aerosol mass budget, contributing about one-third of the total natural aerosol mass annually (Penner et al., 2001).

Deposition measurement data of mineral dust are useful to validate numerical simulation models and to improve our understanding of deposition processes. However, the scarcity and the limited representatively of the deposition measurement data for validation pose a major challenge to assess dust deposition at regional and global scales (Schulz et al., 2012; WMO, 2011). This is in part linked to the uncertainties evolving from the use of different and non-standardized measurement techniques.

Commonly, deposition is measured by passive techniques, which provide an acceptor area for the depositing atmospheric particles. The advantage of these passive samplers is that they operate passively, resulting in simple and thus cheaper instruments, so that many locations can be sampled at a reasonable cost (Goossens and Buck, 2012). The usual lack of a power supply allows also for unattended remote setups. However, the most important disadvantage is that collection efficiency and deposition velocity are determined by the environmental conditions not under operator control and in remote setups also frequently also unknown. That implies, in addition, that the sampler shape can have a strong and variable impact on the collection properties.

While there is previous work describing and modeling single samplers (Einstein et al., 2012; Wagner and Leith, 2001a, b; Yamamoto et al., 2006) and a few comparison studies (Goossens and Buck, 2012; Mendez et al., 2016), most previous studies (Goossens and Buck, 2012; López-García et al., 2013) only compare total mass, thereby neglecting size dependence and potential comparison biases. Also, a systematic assessment of the impact of wind conditions is not commonly carried out, but, for example, Mendez et al. (2016) showed that the efficiency of the BSNE and MWAC samplers for collecting PM₁₀ varies with wind speed, and Goossens and Buck (2012) found that PM₁₀ concentrations from BSNE and DustTrak samplers have comparable values for wind speeds from 2 to 7 m s⁻¹.

The purpose of this study is to assess the particle collection properties of different deposition and other passive samplers based on single-particle measurements and to assess their agreement with theory. From the available data, also relations of the collected particle microphysics and composition homogeneity between the samplers will be presented, which can be used as estimators for the comparability of previous literature data based on the different techniques. To the best of our knowledge, this is the first study to analyze dry deposition measurements collected using passive samplers by means of a single-particle scanning electron microscopy – energy-dispersive X-ray analysis (SEM-EDX) analysis approach (particularly in the size fraction larger than 10 µm).

2 Material and methods

2.1 Sampling location and time

The Sahara and Sahel provide large quantities of soil dust, resulting in a westward flow of mineral dust particles over the North Atlantic Ocean accounting for up to 50 % of global dust budget (Goudie and Middleton, 2001). Due to proximity to the African continent, the Canary Islands are influenced by dust particles transported from the Sahara and Sahel regions. Therefore, Tenerife is one of the best locations to study relevant dust aerosol in a natural environment.

For this study, we conducted a 2-month (July to August 2017) aerosol collection and dry deposition sampling campaign at Izaña Global Atmospheric Watch Observatory (Bergamaschi et al., 2000; Rodríguez et al., 2015) (28.3085^∘ N, 16.4995^∘ W). Sampling inlets were placed at a height of 2 m above ground, on top of a measurement installation. The installation was made on a 160 m² flat concrete platform. The trade wind inversion, which is a typical meteorological feature of the station, shields most of the time the observatory from local island emissions (García et al., 2016). Therefore, the Izaña Global Atmospheric Watch Observatory is an ideal choice for in situ measurements under “free-troposphere” conditions (Bergamaschi et al., 2000; García et al., 2016).

2.2 Wind measurements

An ultrasonic anemometer (Young model 81000, R. M. Young Company, Traverse City, MI, USA) was installed at approximately 2 m height above the ground to obtain the 3-D wind velocity and direction. It was operated with a time resolution of 10 Hz to get basic information on turbulence structure.

2.3 Particle sampling

Samples were collected from different, commonly used samplers, namely Big Spring Number Eight (BSNE) (Fryrear, 1986), modified Wilson and Cooke (MWAC) (Wilson and Cook, 1980), Sigma-2 (VDI2119, 2013) and flat plate (UNC derived) (Ott and Peters, 2008). In addition, the free-wing impactor (FWI) (Kandler et al., 2018) was used to collect coarser particles. The BSNE, MWAC, FWI and filter samplers were mounted on wind vanes to align them to the ambient wind direction. Samples were collected continuously, and substrates were exchanged at intervals of 24 h. The sampling duration for FWI (12 mm Al stub) was 30 min only to avoid overloading. The sampling duration for filter sampler was set to be 1 h. It has to be noted that the PM₁₀ from optical measurements for this particular 0.5 or 1 h only deviates by 2 % and 0.2 %, respectively, from the 24 h average.

2.3.1 Dust deposition samplers

Flat-plate sampler

The flat-plate sampler used in this work was taken from the original flat-plate geometry used in Ott and Peters (2008). Briefly, the geometry contains two round brass plates (top-plate diameter of 203 mm, bottom plate 127 mm, thickness 1 mm each) mounted in a distance of 16 mm. Unlike the original design, the geometry of the current work has a cylindrical dip in the lower plate, which recedes the sampling substrate – a SEM stub with a thickness of 3.2 mm – from the airflow, thereby reducing the flow disturbance. A preliminary study with the modified and original setup side by side in a rural environment had shown that this recession approximately doubles the collection efficiency for large particles. In this design, larger droplets (> 1 mm) are prevented by this setup from reaching the SEM stub surface at the local wind speeds (Ott and Peters, 2008). As described in Wagner and Leith (2001a, b), the main triggers for particle deposition on the substrates for this sampler are diffusion, gravity settling and turbulent inertial forces, of which only the latter two are relevant in our study.

Upward–downward deposition rate sampler

It is important to compare the upward and downward rates to understand the turbulent and the gravitational share in aerosol deposition rate measurement. Following an approach by Noll and Fang (1989), it was assumed that turbulent transport is the main mechanism for upward-directed deposition rate, while turbulent transport and sedimentation are the mechanisms for the downward one. Therefore, a sampler with an upward- and a downward-facing substrate in analogy to the flat-plate sampler was designed. Air is flowing between two circular 1 mm thick steel plates with a diameter of 127 mm. In the centers of the plates, two substrates are mounted opposite to each other. The substrate holders are recessed, so that their adhesive collection surface is in plane with the steel surface. The construction is mounted into a frame with a distance of 16 mm between the plates/substrates.

Sigma-2 sampler

The Sigma-2 sampling device is described in Dietze et al. (2006), Schultz (1989) and VDI2119 (2013). Briefly, the geometry consists of a cylindrical sedimentation tube with a height of about 27 cm made of antistatic plastic, which is topped by a protective cap with diameter of 158 mm. At its top, the cap has four rectangular inlet windows (measuring 40 mm × 77 mm, all at the same height) at its side providing a passive entrance of particles to the collection surface. Once they have entered the tube, particles are assumed settle down to the collection surface due to gravitation (Stokes law) (VDI2119, 2013). The sampler is designed in a way that it protects the sample from direct radiation, wind and precipitation.

The modified Wilson and Cooke (MWAC) sampler

The MWAC sampler is based on an original design developed by Wilson and Cook (1980). The sampler consists of a closed polyethylene bottle, serving as settling chamber, to which an inlet tube and an outlet tube have been added. The MWAC sampling bottles are 95 mm long, with a diameter of 48 mm. The two inlet and outlet plastic tubes with inner and outer diameter 8 and 10 mm, respectively, pass air through the cap into the bottle and then out again. The large volume of the bottle relative to the inlet diameter makes the dust particles entering the bottle to be deposited in the bottle due to the flow deceleration in the total bottle area and due to impaction below the exit of the inlet tube. The air then discharges from the bottle via the outlet tube. MWAC is one of the most commonly used samplers (Goossens and Offer, 2000) and has a high sampling efficiency for large particles (Mendez et al., 2016).

The Big Spring Number Eight (BSNE) sampler

The BSNE sampler, originally designed by Fryrear (1986), is intended to collect airborne dust particles from the horizontal flux (Goossens and Offer, 2000). Briefly, the particle-laden air passes through a rectangular inlet (21 mm wide and 11 mm high, with a total area of 231 mm²). Once inside the sampler, air speed is reduced by continuous cross-section increase (angular walls), and the particles settle out on a collection surface. Air discharges through a mesh screen.

2.3.2 Free-wing impactor (FWI)

A free-rotating wing impactor (Jaenicke and Junge, 1967; Kandler et al., 2009, 2018) was used to collect particles larger than approximately 5 µm. A FWI has a sticky impaction surface attached to a rotating arm that moves through air; particles deposit on the moving plate due to their inertia. The rotating arm is moved at constant speed by a stepper motor, which is fixed on a wind vane, aligning the FWI to wind direction. The particle size cutoff is defined by the impaction parameter, i.e., by rotation speed, wind speed and sample substrate geometry. Details of working principle of FWI can be obtained from Kandler et al. (2018).

2.3.3 Filter sampler

A filter sampler with Nuclepore filters (Whatman^® Nuclepore^™ track-etched membranes, diameter of 25 mm, pore size of 0.4 µm, polycarbonate) mounted on a wind vane was used for isoaxial particle collection. An inlet nozzle of 6 mm was used to achieve pseudo-isokinetic conditions. Sample flow (0.75 m⁻³ h⁻¹ volumetric at ambient conditions) was measured by a mass flow meter (MASS-STREAM, M+W instruments, Leonhardsbuch, Germany). The filter sampler was operated at least two times a day.

2.4 Ancillary aerosol data

Additional information regarding the aerosol particle size distributions has been obtained by using an optical particle counter (OPC, GRIMM, Ainring, Germany), which is operationally available at the Izaña Global Atmospheric Watch Observatory (Bergamaschi et al., 2000; Rodríguez et al., 2015).

2.5 SEM analysis

All aerosol samples (except the filter sampler) were collected on pure carbon adhesive substrates (Spectro Tabs, Plano GmbH, Wetzlar, Germany) mounted to standard SEM aluminum stubs. The filter samples were stored in standard “petrislides” (Merck KGaA, Darmstadt, Germany). All adhesive samples were stored in standard SEM storage boxes (Ted Pella Inc., Redding, CA, USA) in dry conditions at room temperature. Individual particle analysis by automated SEM (FEI ESEM Quanta 400 FEG, FEI, Eindhoven, the Netherlands; operated at 12.5 kV, lateral beam extension 3 nm approximately, spatial resolution of 160 nm) was used to characterize particles for size and composition. A total of 316 000 particles from six samplers were analyzed. A total of 26 samples from BSNE (53 000 particles), 23 samples from MWAC (49 000), 23 samples from Sigma-2 (39 000), 18 samples from the flat plate (12 mm) (24 000), 22 samples from the flat plate (25 mm) (21 000), 13 samples from the filter (80 000) and 12 samples from FWI (12 mm) (50 000) were analyzed. Each sample was characterized in areas selected by a random generator, until a total of 3000 particles with projected area diameters greater than 1 µm was reached. For particle identification, the backscattered electron image (BSE image) has been used, as dust particles contain elements with higher atomic number than carbon and therefore appear as detectable bright spots in the BSE image.

Chemistry information was derived by EDX (Oxford X-Max 120, Oxford Instruments, Abingdon, United Kingdom). The internal ZAF correction (Z – atomic number, A – absorption, F – fluorescence, accounting for material-dependent efficiencies) of the detector/software system – based on inter-peak background radiation absorption measurements for correction – was used for obtaining quantitative results.

2.6 Particle size determination

The image analysis integrated into the SEM-EDX software determines the size of particles as a projected area diameter:

$$\begin{array}{}\text{(1)}& d_g=\sqrt{{\displaystyle \frac{\mathrm{4}B}{\mathit{\pi }}}},\end{array}$$

where B and d_g are the area covered by the particle on the sample substrate and the projected area diameter, respectively.

Following Ott et al. (2008), the volumetric shape factor, S_v, is determined from the count data as

$$\begin{array}{}\text{(2)}& S_{\mathrm{v}}={\displaystyle \frac{P^{\mathrm{2}}}{\mathrm{4}\mathit{\pi }A}},\end{array}$$

where P and A are the perimeter and the projected area of the particle, respectively.

The volume-equivalent diameter (sphere with the same volume as the irregular shaped particle) is then calculated from the projected area diameter via the volumetric shape factor (Ott et al., 2008) and is expressed by particle-projected area and perimeter as

$$\begin{array}{}\text{(3)}& d_{\mathrm{v}}={\displaystyle \frac{\mathrm{4}\mathit{\pi }B}{P^{\mathrm{2}}}}dg={\displaystyle \frac{\mathrm{1}}{P^{\mathrm{2}}}}\sqrt{\mathrm{64}\mathit{\pi }{B}^{\mathrm{3}}}.\end{array}$$

The aerodynamic diameter (d_a) is calculated from projected area diameter through the use of a volumetric shape factor and aerodynamic shape factor (Wagner and Leith, 2001b):

$$\begin{array}{}\text{(4)}& d_{\mathrm{a}}=d_{\mathrm{v}}\sqrt{{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{p}}}{S_d{\mathit{\rho }}_{\mathrm{0}}}}},\end{array}$$

with S_d the aerodynamic shape factor; ρ_p and ρ₀ are particle density and unit density, respectively. For this work, a value of S_d=1.41 was used (Davies, 1979). Cunningham's slip correction was neglected in this study, as all particles considered were supermicron size.

2.7 Mass and number deposition rate calculation

The mass deposition rate (MDR) and number deposition rate (NDR) are calculated from deposited particle numbers per area, individual particle size and, in the case of MDR, density. The particle density was assumed to be equal to the bulk material density of the dominating identified compound for each particle (Kandler et al., 2007). A window correction (Kandler et al., 2009) was applied to the particle deposition rate as

$$\begin{array}{}\text{(5)}& C_{\mathrm{w}}={\displaystyle \frac{w_x{w}_y}{(w_x-d_{\mathrm{p}})(w_y-d_{\mathrm{p}})}},\end{array}$$

where w_x and w_y are the dimensions of the analysis rectangle.

The MDR of the samples is then determined as

$$\begin{array}{}\text{(6)}& \mathrm{MDR}={\displaystyle \frac{\mathrm{1}}{\mathrm{Ati}}}{\sum }_k\mathit{\rho }{d}_{\mathrm{p}}^{\mathrm{3}}{C}_{\mathrm{w}}(d_{\mathrm{p}},k).\end{array}$$

Similarly, the NDR of the samples is determined as

$$\begin{array}{}\text{(7)}& \mathrm{NDR}={\displaystyle \frac{\mathrm{1}}{\mathrm{Ati}}}{\sum }_k{C}_{\mathrm{w}}(d_{\mathrm{p}},k),\end{array}$$

with A is the total analyzed area, t is the sample collection time, ρ particle density, and k is the index of the particle.

Size distributions for all properties were calculated for the logarithmic-equidistant intervals of 1–2, 2–4, 4–8, 8–16, 16–32 and 32–64 µm.

2.8 Modeling atmospheric concentrations and size distributions from flux measurements

Concentrations are calculated from the deposition rate using different deposition velocity models for different samples, namely the models of Stokes and Piskunov (Piskunov, 2009). The basic relationship between concentration and deposition rate was already given by Junge (1963) as the ratio of deposition rate to concentration:

$$\begin{array}{}\text{(8)}& V_d=F/C,\end{array}$$

with F is deposition rate and C is concentration. Note that the formulation is independent of the type of concentration; i.e., it can be equally applied to number or mass concentrations.

All different approaches now give different formulations for the deposition velocity based on a set of assumptions and neglections.

2.8.1 Stokes settling

Terminal settling velocity (V_ts) is calculated according to Stokes law:

$$\begin{array}{}\text{(9)}& V_{\mathrm{ts}}={\displaystyle \frac{d_{\mathrm{p}}^{\mathrm{2}}g({\mathit{\rho }}_{\mathrm{p}}-{\mathit{\rho }}_{\mathrm{a}})}{\mathrm{18}\mathit{\mu }}},\end{array}$$

where d_p is the particle size; g is the gravitational acceleration (9.81 m s⁻²); ρ_p the density of particle; ρ_a is the air density; μ is the dynamic viscosity of air ($\mathrm{1.8}\times {\mathrm{10}}^{-\mathrm{5}}$ kg ms⁻¹).

2.8.2 Turbulent deposition and more complex deposition models

To calculate the turbulent impaction velocity, which depends on the wind speed, the friction velocity is needed. Friction velocity (u_∗), which is a measure of wind-generated turbulence, is one most important variables affecting deposition velocity (Arya, 1977). Mainly two different approaches have been used to estimate u_∗. On one hand, the momentum flux or the eddy covariance (EC) approach (Ettling, 1996), which directly estimates u_∗ from the correlations between the measured horizontal and vertical wind velocity fluctuation, and on the other, the law of the wall (LoW) approach (Shao et al., 2011), which estimates u_∗ from the wind profile. The latter can be approximated from free-stream velocity and roughness assumptions (Wood, 1981), where the flow inside the sampler is assumed to be in the hydraulically smooth regime (Schlichting, 1968). Figure 1 shows correlations between u_∗ estimated using Wood (1981) and Ettling (1996) approaches. Obviously, the approaches lead to different results for which no clear explanation is available (Dupont et al., 2018).

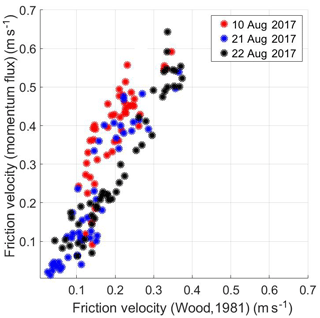
Figure 1 Comparison of the friction velocities obtained from the momentum flux and the Wood (1981) approaches for different days with different wind speeds (average wind speeds of 2.9, 2.1 and 3.1 m s⁻¹ for 10, 21 and 22 August 2017, respectively).

For the current work, the friction velocity is calculation is based on Wood (1981) approach:

$$\begin{array}{}\text{(10)}& u_{\ast }=\left(u/\sqrt{\mathrm{2}}\right)\left[\left(\mathrm{2}\log \mathrm{10}\right(Re)-\mathrm{0.65}{)}^{-\mathrm{1.15}}\right],\end{array}$$

where Re is the flow Reynolds number at the sampling stub location and is given as

$$\begin{array}{}\text{(11)}& Re=uX/V.\end{array}$$

X is the distance from the lower plate edge to the center of the sampling stub (6.3 cm) and V is kinematic viscosity.

The reason why we opted to use the Wood (1981) over the Ettling (1996) approach is (a) its simplicity, as it requires only average wind speeds instead of 3-D high-resolution ones and therefore will be more commonly applicable; and (b) the fact that the momentum approach yields sometimes uninterpretable data, in particular in the case of buoyancy-driven flow. For some case studies, both approaches are compared below.

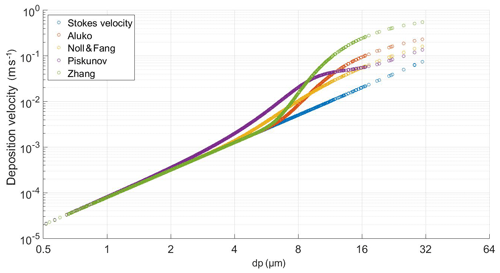
There are a variety of models estimating the particles' deposition speed (Aluko and Noll, 2006; Noll and Fang, 1989; Noll et al., 2001; Piskunov, 2009; Slinn and Slinn, 1980; Wagner and Leith, 2001a) (see Fig. 2) and these different deposition velocity models yield different results, which could be due to negligence of unaccounted forces (Lai and Nazaroff, 2005) or due to how friction velocity is determined, or can be related to suppositions by different models (Kandler et al., 2018). Unless otherwise stated, the particle density used in deposition velocity calculation is 2600 kg m⁻³.

It can be noted that a particular deposition model therefore may not be suitable in different cases for describing the deposition velocity precisely, so as a result concentrations derived from deposition rate measurements are likely to be biased (Giardina and Buffa, 2018; Kandler et al., 2018).

Figure 2 Deposition velocities for single particles to a smooth surface (flat-plate sampler) calculated by using a set of different classical deposition models for the Tenerife samples (9 August 2017; average wind speed of 3.0 m s⁻¹).

2.8.3 Deposition models applied to the samplers

Table 1 shows the different deposition velocity models applied to the various samplers. The Piskunov deposition velocity model is made for flat surfaces, and therefore it is applied to the BSNE and flat-plate samplers, where deposition occurs to such surfaces. For the Sigma-2 sampler, it is assumed that each particle settles with the terminal settling velocity (Tian et al., 2017), and therefore Stokes velocity was used for calculation of concentrations. In the case of MWAC, a different approach was required due to its geometry. It is internally in principle an impactor design with the incoming tube pointing at the substrate but is operating at very low flow speed and therefore low Reynolds numbers. As a result, it cannot be described by the impactor theory only. Therefore, we assumed that the deposition velocity cannot become smaller than the one prescribed by the Piskunov model. As a result, we derived a velocity model based on wind speed (or a reduced wind speed) and calculated the collection efficiency assuming MWAC to act as impactor for particles in the range of the cutoff diameter and larger. For smaller particles, we assumed that flow is like a flow over a smooth surface, so the Piskunov deposition velocity model was applied (e.g., as soon as the deposition velocity from impactor considerations becomes smaller than the Piskunov one, the latter was used).

Table 1 A summary of different deposition velocity models applied to the samplers.

2.9 Determining the size distributions for mass concentration from the free-wing impactor measurements

Considering the window correction and the collection efficiency dependence on the impaction speed and geometry, the overall collection efficiency E is calculated according to Kandler et al. (2018). After calculating the collection efficiency, the atmospheric concentration is calculated from deposition rate and deposition velocity as

$$\begin{array}{}\text{(12)}& C={\displaystyle \frac{M}{V_{\mathrm{d}}}}={\displaystyle \frac{M}{E{V}_{\mathrm{imp}}}},\end{array}$$

with E being the collection efficiency and V_imp the impaction velocity, calculated from ambient wind speed and rotation speed.

2.10 Determining the size distributions for mass concentration from the filter sampler measurements

Apparent number concentrations are determined from the particle deposition rate and the volumetric flow rate calculated from the mass flow for ambient conditions. The inlet efficiency (Eff_in) – accounting for the sampling biased caused by the difference in wind speed and inlet velocity – is calculated (Belyaev and Levin, 1974). The ambient concentration N_out is calculated by dividing the measured number concentration by the inlet efficiency. The effect for the regarded particles size, however, is small in comparison to the differences between the samplers.

2.11 Statistical uncertainty

Due to the discrete nature of the particle size measurement, the uncertainty coming from counting can pose a significant contribution to the uncertainty of mass deposition rate measurement (Kandler et al., 2018). It is, therefore, important to assess the uncertainties in our mass deposition rate measurements, which is done in accordance with the previous work (Kandler et al., 2018). For the mass deposition rate, the statistical uncertainty is assessed by a bootstrap simulation approach using Monte Carlo approximation (Efron, 1979). In this work, the bootstrap simulations and the two-sided 95 % confidence interval calculation were performed by using Matlab's bootstrap function (MATLAB R2016a; MathWorks, Inc.). Here, MATLAB function uses a non-parametric bootstrap algorithm (Neto, 2015) to compute the 95 % bootstrap confidence interval.

3 Computational fluid dynamics (CFD) simulation

Computational fluid dynamics (CFD) simulations were conducted to predict the deposition of particles onto different passive samplers (MWAC, Sigma-2 and flat plate). A discrete phase model without interaction with continuous phase was used to calculate the trajectories of the particles. The CFD software ANSYS-FLUENT 18.2 was used for performing the numerical simulations.

3.1 Evaluating the mean flow field

In a first step, the geometry of samplers was created using ANSYS DesignModeler. In a second step, an enclosure around the geometry was generated. To ensure that there are no large gradients normal to the boundaries at the domain boundary, the domain was created depending on the width, the height and the length of the geometries. The space in front of the geometry is 2 times the height of the sampler, the space behind the sampler is 10 times the height, the spaces left and right of the geometry are 5 times the width of the geometry, and the spaces below and above the sampler are 5 times the height.

Afterwards, a mesh was created using the ANSYS meshing program. For the enhanced wall treatment, the first near-wall node should be placed at the dimensionless wall distance of $y^{+}\wedge \approx$1. The dimensionless wall distance is given by

$$\begin{array}{}\text{(13)}& y^{+}={\displaystyle \frac{u_{\ast }y}{\mathit{\nu }}},\end{array}$$

with y the distance to the wall, ν the kinematic viscosity of the fluid and u_∗ the friction velocity, which is defined for this purpose by

$$\begin{array}{}\text{(14)}& u_{\ast }=\sqrt{{\mathit{\tau }}_{\mathrm{w}}/\mathit{\rho }},\end{array}$$

with τ_w the wall, shear stress and ρ the fluid density at the wall. The wall is then subdivided into a viscosity-affected region and a fully turbulent region depending on the turbulent Reynolds number Re_y:

$$\begin{array}{}\text{(15)}& R{e}_y={\displaystyle \frac{\mathit{\rho }y\sqrt{k}}{\mathit{\mu }}},\end{array}$$

with y the wall-normal distance from the wall to the cell centers, k the turbulence kinetic energy and μ the dynamic viscosity of the fluid. If Re_y>200, the k-ε model is used. For Re_y<200, the equation of Wolfstein is employed (Chmielewski and Gieras, 2013; Fluent, 2015). The flow field was calculated by solving the Reynolds-averaged Navier–Stokes equations with the software ANSYS Fluent. The standard k-ε model was used to calculate the Reynolds stresses. The boundary conditions at the sides of the domain were set to symmetric. The inlet boundary condition was set to 2, 4 or 8 m s⁻¹ with air as fluid (density: 1.225 kg m⁻³, viscosity: $\mathrm{1.7849}\times {\mathrm{10}}^{-\mathrm{5}}$ kg ms⁻¹). The outlet boundary condition was set to pressure outlet.

The turbulence intensity T_i was calculated as

$$\begin{array}{}\text{(16)}& T_{\mathrm{i}}={\displaystyle \frac{{\left(\frac{\mathrm{2}}{\mathrm{3}}k\right)}^{\mathrm{1}/\mathrm{2}}}{v}},\end{array}$$

with k the turbulence intensity and v the velocity at the inlet of the domain.

Details of the sampler construction and geometry are found in the electronic Supplement (see Figs. S24, S25 and S26). Different cases were calculated for the flat-plate sampler (deposition areas of 12 and 25 mm), for Sigma-2 and MWAC (Fig. 3). For the flat plate, a mesh with 3 920 000 cells was generated; for Sigma-2, one with 7 600 000 cells; and for MWAC, one with 4 620 000. After the meshing, the flow fields were calculated. Figure 3 shows, as an example, the velocity magnitude in the middle of the domain for a velocity of 4 m s⁻¹ at the inlet.

In the last step, particles were injected into the velocity field and their trajectories computed. For all samplers, the deposition area boundary condition was set to “trap” and the walls were defined as reflecting boundaries. Different particle sizes (1, 2.5, 5, 10, 20 and 50 µm, Stokes diameter) for three different wind speeds (2, 4, 8 m s⁻¹) were investigated. The particle density was set to a value of 2600 kg m⁻³ to match an approximate dust bulk density. The particle concentration was 4×10⁸ m⁻² in all cases, while the injection area was adjusted to the geometries (Fig. 3).

The number of particles trapped in the deposition area was determined. The deposition velocity V_d was calculated by

$$\begin{array}{}\text{(17)}& V_{\mathrm{d}}={\displaystyle \frac{N_{\mathrm{pt}}v}{A_{\mathrm{d}}{C}_{\mathrm{p}}}},\end{array}$$

with N_pt the number of trapped particle at the deposition area, v the velocity of the air at the inlet boundary of the domain, A_d the deposition area and C_p the particle concentration at the particle injection area (Sajjadi et al., 2016).

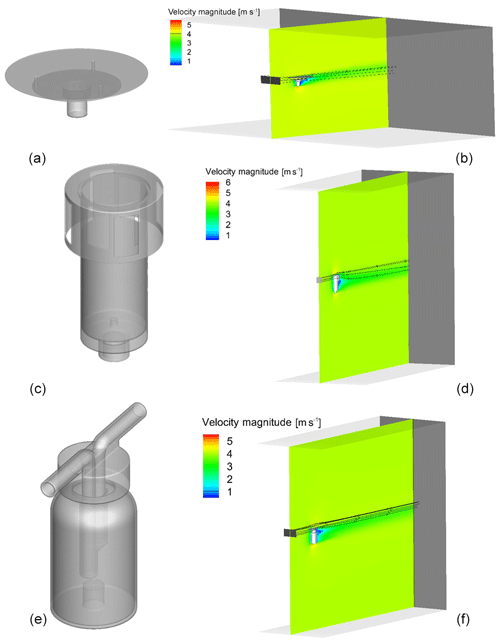
Figure 3 Geometries of the flat-plate sampler (a, b), Sigma-2 sampler (c, d) and MWAC sampler (e, f). CFD modeling domain and velocity magnitude, inlet velocity: 4 m s⁻¹ (b, d, f); in addition, the injection area is shown in black (flat-plate sampler: width 0.2 m, height 0.05 m; Sigma-2 sampler: width 0.2 m, height 0.1 m; bottle sampler: width 0.1 m, height 0.05 m), along with exemplary stream traces.

3.2 Velocity contours and vectors for the samplers

For the flat-plate sampler, stream velocities and turbulence intensities are shown in Fig. 4. The formation of the boundary layer at the wall of the sampler is clearly visible at all velocities. At the central sampling location, the flow between the plates has the same velocity as the free stream, so for the analytical deposition models, the lower plate can be treated as single surface. The highest velocity is found at the sharp edge at the bottom of the sampler. Due to the high velocity gradients, in this part, there is also the highest turbulence intensity in the domain. As expected, the turbulent wake becomes smaller with increasing wind speed.

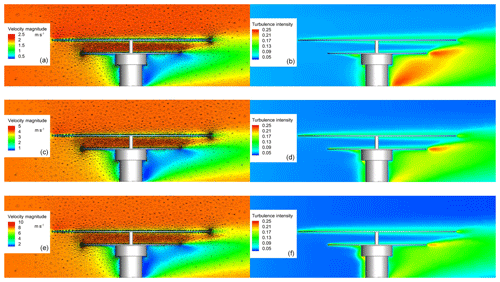
Figure 4 Flat-plate sampler: velocity magnitude and turbulence intensity at wind speed of 2 m s⁻¹ (a, b), flat-plate sampler: velocity magnitude and turbulence intensity at wind speed of 4 m s⁻¹ (c, d), flat-plate sampler: velocity magnitude and turbulence intensity at wind speed of 8 m s⁻¹ (e, f).

Sigma-2 sampler

The cross sections of the velocities for Sigma-2 are shown for the 4 m s⁻¹ case in Fig. S27. Apparently, the velocity magnitude inside the sampler is much smaller than outside. In the vertical settling tube, the turbulence intensity is low, justifying the idea of Stokes settling inside. Due to the open but bulky geometry, there is a flow into the interior at the back. The highest velocities and turbulence intensities are found at the sharp edges at the top and bottom of the sampler.

Figure S28 shows the cross section of the velocities for MWAC in the 4 m s⁻¹ case. Furthermore, the velocity field and the velocity vectors in the cross sections across and along the inlet tube are shown in Fig. S29. In the tubes, the typical pipe flow is formed. In the figures showing the cross sections, along the inlet tube, a symmetrical flow over the pipe cross section is visible. Finally, Fig. S30 shows the mean flow velocity in the MWAC tube as a function of the outside velocity for the three cases. The fitting curve shows that the mean velocity in the pipe increases linearly with the external velocity.

4 Results and discussion

4.1 Methodical aspects (field measurements)

4.1.1 Mass deposition rate comparison

Mineral dust was the dominating particle type during this campaign, consisting of different silicates, quartz, calcite, dolomite and gypsum, similar to previous findings for this location (Kandler et al., 2007). Therefore, hygroscopicity was not taken into account, as due to the mostly non-hygroscopic compounds and the moderate humidities their impact was rated low. Details on the composition will be reported in a companion paper.

The mass and number deposition rates (given per unit time and sample surface area) along with daily average temperature and wind speed are presented as daily values. Details for all days and all samplers can be found in the electronic Supplement (see Tables S1, S2, S3 and S4). All data shown in this section are calculated from SEM measurements. Particle sizes are reported as aerodynamic diameter, if not otherwise stated. It is also worth mentioning the plots shown in the paper are a few examples of a comparison, while the bulk of the data are presented in the Supplement.

Figure 5 shows as example mass deposition rates for different samplers during a dust event and a non-dust event day. For all samplers, the mass deposition rate size distributions peaked in the 8–16 µm diameter interval. This result is in support of the conclusion that atmospheric dry deposition is dominated by coarse particles due to their high deposition velocities (Davidson et al., 1985; Holsen et al., 1991). There is a considerable difference among different samplers affecting mainly the size range with the highest mass deposition rates, whereas the difference is small for smaller particles. MWAC and BSNE – both horizontal flux samplers – collect coarser material than the flat-plate and Sigma-2 samplers, which in contrast measure the vertical flux. In particular, the MWAC sampler exhibits considerably higher coarse particle mass deposition rates, probably due to its impactor-like design.

Table 2 The campaign maximum, minimum and median mass deposition rates measured by the samplers.

As a consequence, the vertical flux instruments collect much less material than the horizontal flux ones (Table 2), which is in accordance with previous findings (Goossens, 2008). In the present study, horizontal-to-vertical flux mass ratio is approximately between 2.8 and 4.4 (with single size intervals ranging between 2 and 50), while Goossens (2008) reported it to be in between 50 and 160. This difference in the ratio might come from the different approaches. Goossens (2008) used water as a deposition surface, while in our study we used a SEM sampling substrate. Furthermore, from Fig. 5, we can clearly see that there is a strong variation in mass deposition rates between dust event days and non-dust event days (full dataset is shown in Fig. 6). Generally, the temporal variation is higher than the difference between the samplers, so a strict comparison between this and the previous study cannot be done.

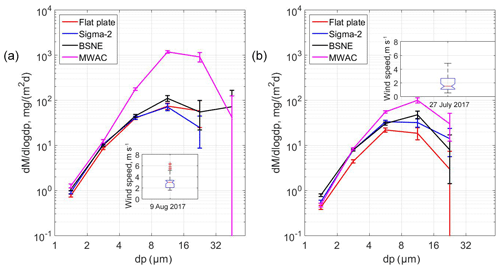
Figure 5 Size-resolved mass deposition rate measured by different passive samplers: (a) dust event day; (b) non-dust event day. Data are derived from SEM measurements. The bars show the central 95 % confidence interval of the daily variation. The inserts show box plots for the wind speed distribution based on 30 min intervals.

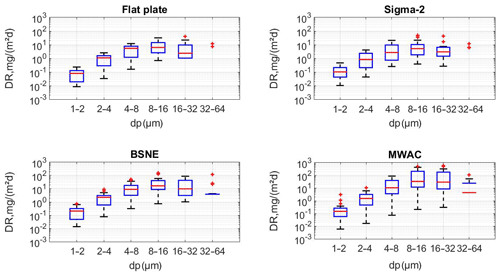
Figure 6 Box plots of size-resolved deposition rate (campaign data; flat-plate, Sigma-2, MWAC and BSNE samplers). On each blue box, the central mark is the median; the edges of the box are the 25th and 75th percentiles. The vertical red lines show the standard deviation. The median, percentiles and standard deviations shown there correspond to the variability of the whole campaign for each instrument and bin. From the structure of the deposition models, a wind speed dependency for the deposition velocity should be expected. The average wind speed during the campaign was about 3.5 m s⁻¹, with the lowest daily median around 1.5 m s⁻¹ and the highest 7 m s⁻¹. A daily box plot of 30 min averaged wind speed at Izaña is shown in Fig. S1.

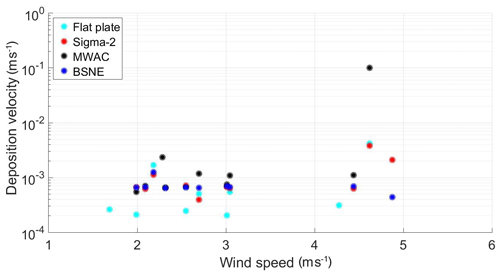
Figure 7 shows the mass deposition rate ratio of MWAC, BSNE and flat plate to Sigma-2 as function of wind speed. The Sigma-2 sampler was chosen for comparison, as due to its settling tube design, it is expected to have the least wind sensitivity. The results show highly scattered values. The collection efficiency of MWAC for large particles has an increasing tendency in comparison to Sigma-2 slightly with increasing wind speed, while there is barely a trend visible for BSNE. Both – being horizontal flux samplers – collect considerably more material than Sigma-2. For the flat plate, the deposition velocity in relation to Sigma-2 has a weak decreasing trend for higher wind speeds, but generally, the deposition speed is similar. Overall, the relation of Sigma-2 to BSNE shows the closest agreement, while the scatter is higher for the other combinations. More information on the relation between the other instruments is shown in Figs. S2, S3, S4, S5, S6, S7, S8, S9 and S10.

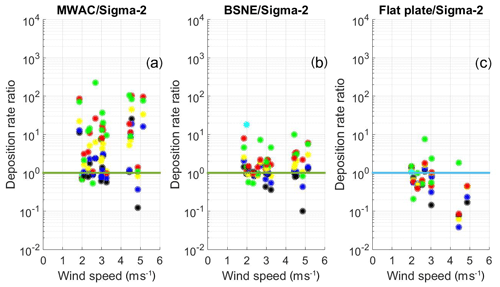
Figure 7 Deposition rate ratio as function of wind speed for different days: MWAC/Sigma-2 (a), BSNE/Sigma-2 (b) and BSNE/Sigma-2 (c). Different colors represent deposition rates measured in different size intervals (black: 1–2 µm; blue: 2–4 µm; yellow: 4–8 µm; red: 8–16 µm; green: 16–32 µm; cyan: 32–64 µm).

While without a true reference technique the absolute deposition velocities cannot be determined, their ratio between different instruments can be compared theoretically and by measurement. The deposition velocity ratios for a pair of different samplers are identical to the deposition rate ratios obtained from the corresponding measurements (Eq. 7), as long as the sampling time and the aerosol concentration are the same; the latter condition is achieved by the close and parallel sampling. Therefore, the experimentally determined ratios can now be compared to the deposition velocity ratios derived from the theoretical considerations. Figure 8 shows the corresponding comparison. Note that this consideration allows for the assessment of relative model performance and sampler efficiency, but lacking a “true” reference, it does not allow for determining the most accurate sampler.

While, for BSNE and Sigma-2, observations and model fit comparatively well, the deposition velocity is misestimated for the flat-plate/Sigma-2 pairing for all particle sizes (overestimate for flat-plate deposition velocity or/and underestimate for Sigma-2). For MWAC/Sigma-2, there is a clear size dependency, indicating that probably the impactor model overestimates the deposition velocity; the latter might be due to unaccounted particle losses (e.g., inlet efficiency). MWAC, BSNE and Sigma-2 agree with respect to deposition velocity better based on the measurement data than predicted by the theory. It may be connected to the non-stationarity of the atmosphere, which is not accounted for by the models, i.e., the permanent wind speed fluctuations smoothing out detail differences of a stationary flow. The flat-plate sampler, however, has a lower-than-predicted deposition velocity.

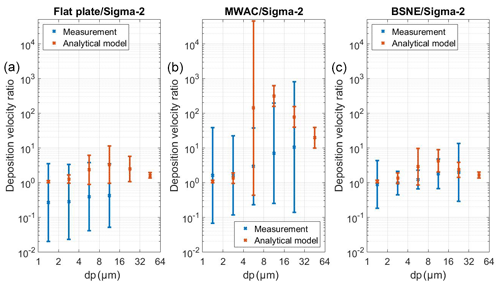
Figure 8 Comparison of geometric mean ratio of deposition velocities for different sampler pairs derived from measured deposition rates (blue) and from corresponding deposition models (orange). (a) Flat plate/Sigma-2; (b) MWAC/Sigma-2; (c) BSNE/Sigma-2. Error bars show geometric standard deviations. The bars show the central 95 % confidence interval of the daily variation. The corresponding deposition models are listed in Table 1.

4.1.2 Dependence of PM₁₀ dust deposition on atmospheric concentration and wind speed

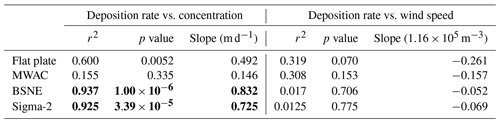
Figure S22 and Table 3 display for the approximate PM₁₀ size range the correlation between number deposition rates, atmospheric particle number concentrations measured by OPC and the wind speed for different samples. For this consideration, only the overlapping size range (1–10 µm aerodynamic diameter) was used. As expected, there is in all cases a positive correlation between concentrations and number deposition rates (see Fig. S22a). In particular, for the BSNE and Sigma-2 samplers, robust correlations with a trend towards underestimation at higher concentrations exist. While the models predict a positive correlation of wind speed and deposition rate, this is not observed in the measurements. For example, the table does not show a linear correlation since the r² values are not close to 1 for the first two samplers (particularly MWAC). Instead, a non-significant anti-correlation can be observed, if at all (e.g., for the flat plate; r²:0.319, p value of 0.070, slope of −0.261; see Fig. S22b), indicating a cross influence of wind speed and concentration. For example, higher concentrations of dust aerosol particles might be meteorologically linked to lower wind speeds due to a different transport situation. Such a general behavior was observed previously, for example, by different techniques for a dust transport region (Kandler et al., 2011). An ambiguous wind dependency has been reported for other places (Xu et al., 2016). In this study, the main driver of the deposition rate is obviously the dust concentration.

Table 3 Summary of the regression analysis for the correlations between the dust deposition rate and the atmospheric concentrations (PM₁₀ size range; measured by the OPC), and for the correlations between the dust deposition rates and the wind speeds. Significant relationships are shown in bold.

In a second step, it was tested whether the application of each sampler's assigned deposition model can increase the correlation between the measurements by the deposition samplers and the OPC observations, i.e., whether the meteorological parameters accounted for in the models can decrease the deviation. Therefore, in analogy to the previous correlation, the concentrations modeled from each sampler's SEM data were correlated with the OPC data for the size range between 1 and 10 µm in particle diameter (see Table S7). However, no increase in correlation quality is observed, indicating that – like already observed from the varying ratio calculations above – the deposition models fail to describe the deposition behavior in detail.

From the correlation relations in Table 3, it can be seen that MWAC is least suitable for estimating PM₁₀, which fully agrees well with previous studies (Mendez et al., 2016). However, the correlation analysis here shows that BSNE is actually a suitable instrument for a PM₁₀ estimation, which is in contrast to the wind-tunnel observation of Mendez et al. (2016). This discrepancy might be due to the different approaches. While in the previous work the loss of concentration from the passing aerosol was measured, in this study, a gain of deposition was investigated. As a result, for lower deposition velocities (discussed below), the former approach will yield high uncertainties. Similar to BSNE, the flat-plate and Sigma-2 samplers appear to be good estimators of PM₁₀, which is in accordance with previous studies (Dietze et al., 2006).

Size-resolved apparent deposition velocity in the PM₁₀ size range

Figure 9 displays the apparent deposition velocity (calculated as the ratio of the number deposition rate to the concentration of the OPC) as function of the wind speed. Obviously, here, there is also no clear trend. The apparent deposition velocities range between $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ and 10⁻¹ m s⁻¹. As can be clearly seen from the plot, the effect of wind speed on deposition velocity is negligible, as indicated already in Table 3. While this is in contradiction to the models, one has to keep in mind that (a) the observed wind speeds are comparatively low here, and (b) the considered size range is not the one most affected by the wind speed. An effect of the wind speed might therefore be much stronger at higher wind speeds and for larger particles.

Figure 9 Apparent deposition velocity: ratio of number deposition rate determined from SEM measurements to the number concentration observed by the OPC as function of wind speed. For the consideration, only the overlapping size range (approximately 1–10 µm) was used.

4.1.3 Atmospheric mass concentrations derived from deposition rates

Consistency between samplers and corresponding models

Figure 10 compares a mass deposition rate size distribution with the corresponding concentrations derived by the modeled deposition velocities. Calculating the mass concentrations from different passive samplers with different models leads in most cases to a better agreement between the measurements, taking into account the statistical uncertainties (see Fig. S11). This indicates that the deposition velocity models selected for the samplers are generally suitable, despite the deviations in single cases.

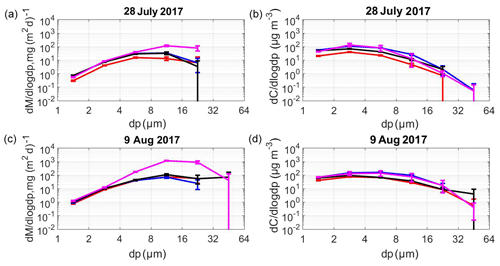
Figure 10 Comparing different samplers with respect to (a, c) dust mass deposition rates and (b, d) dust mass concentrations calculated from application of the corresponding model as function of particle size. Different colors indicate different samplers (red: flat plate; blue: Sigma-2; black: BSNE; magenta: MWAC). The bars show the central 95 % confidence interval of the daily variation. Corresponding deposition models for concentration calculation are given in Table 1.

Size-resolved comparison with active samplers

The calculated number concentrations in the size interval between 1 and 10 µm are compared with the concentrations measured using the OPC. Similarly, the mass concentration size distributions above the PM₁₀ size range are validated using the FWI measurements.

Figure 11 (see also Figs. S14, S15, S16 and S17) shows a comparison of number concentration size distributions calculated from deposition rate measurements of the flat-plate, Sigma-2, BSNE and MWAC samplers with the number size distributions measured by the OPC for different days. Overall, most of the time, the number concentrations obtained from OPC measurements are slightly higher than the ones from the deposition rates for the size range 2–5 µm and for dust days, with the exception of Sigma-2, when considering only Stokes velocity. This reflects the tendency of a relative underestimation of the concentrations by the passive techniques for high concentrations, which was already visible in the correlation analysis above. In general, Fig. 11 shows that the deviation of calculated values from OPC-measured values is significant.

In this context, Fig. 11 shows also the low influence of the two techniques used for u_∗ estimation. While the number concentrations derived using the friction velocity estimated from Wood (1981) formulation are slightly higher and therefore in better agreement with the OPC data, the difference appears to be negligible in general, probably due to the relatively low wind speeds in this study.

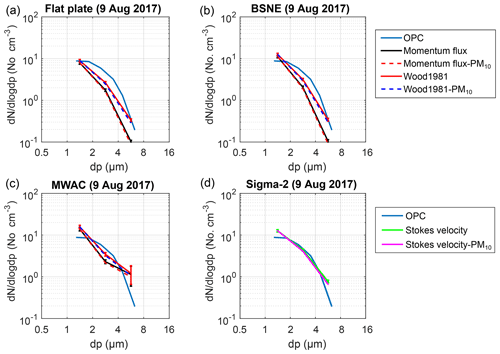
Figure 11 Comparison of the number concentrations calculated from the deposition measurements with the number concentrations measured by the OPC. Number size distributions are obtained by converting the SEM number deposition rates to number concentrations using the different deposition velocity models (Table 1), in analogy to the mass size distributions. For the concentrations obtained from the number deposition rates, two different approaches for the friction velocity are shown. The black curve shows the concentration curve calculated using the momentum flux approach without PM₁₀ inlet correction (i.e., the atmospheric concentration). The red curve shows the concentration curve calculated using the Wood approach without PM₁₀ correction. The dotted blue curve shows the concentration curve calculated using the Wood approach with PM₁₀ inlet correction (simulating the concentration the OPC would supposedly measure). The dotted red curve shows the concentration curve calculated using the momentum flux approach with PM₁₀ inlet correction. In the case of Sigma-2, the green curve shows the concentrations calculated using the Stokes velocity and the magenta curve the ones using Stokes velocity with the PM₁₀ inlet correction. The bars show the central 95 % confidence interval of the daily variation. (a) Flat plate; (b) BSNE; (c) MWAC; (d) Sigma-2. The average wind speed on 9 August 2017 was 3.0 m s⁻¹. Note that panel (d) refers to the second legend.

Figure 12 (see also Fig. S12) shows the comparisons for the larger particles between the deposition-derived number concentrations and the ones from the FWI. Here, a significant inconsistency occurs between the mass size distributions from passive samplers and the ones from FWI. In particular, the size range larger than 10 µm seems to be generally underestimated by the passive samplers. While for particles around 10 µm, this could be partly due to a badly defined collection efficiency curve of the FWI (Kandler et al., 2018; 50 % cutoff at 11 µm) and the corresponding correction, this cannot be the reason for the particles larger than 16 µm, where this efficiency approaches unity. Here, the deposition velocity for the samplers is apparently overestimated. A possible explanation would be inlet losses of the passive sampler, but this needs to be the subject of further research. An overview of the OPC measurements comparing the size distributions between the long-term (deposition) and short-term (FWI) sampling is shown in Fig. S13.

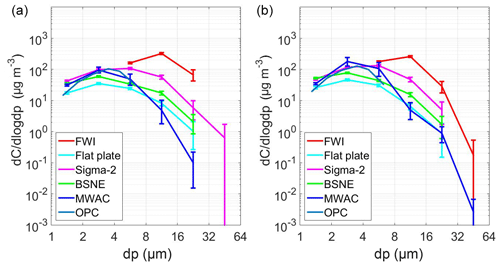
Figure 12 Daily average mass size distributions obtained from the passive sampler techniques in comparison to an active sampler (FWI). Mass concentration size distributions were calculated from the SEM mass flux measurements using the corresponding deposition velocity models. Samples were collected on 26 July (a) and 27 July (b). The mass concentration measurements shown by the FWI are daily averages (three samples per day). The bars show the central 95 % confidence interval of the daily variation.

In a last step, the deposition-derived concentrations are compared to those determined from the isoaxial filter sampler. Figure 13 shows that, while the calculated size distributions are in good agreement with the OPC ones, the filter-derived ones seem to relatively underestimate the concentrations. A correlation analysis (r²: 0.681, p value of 0.0854 and slope of 2.0394) suggests that there is a weak positive correlation between calculated number concentration from filter samples and the OPC-measured concentration. BSNE has been chosen here for comparison, as its agreement with the OPC measurements is generally the closest. The reasons for this weak correlation between the filter sampler and the OPC measurements – in particular compared to the stronger correlation between Sigma-2 and BSNE with the OPC – are not clear. For the sake of completeness, the same comparison for the other samplers is shown in Figs. S18, S19 and S20. While in general here, the disagreement between the filter sampler and the MWAC and Sigma-2 samplers is significant; for the flat-plate sampler, less disagreement occurs. In addition, an overview of the OPC measurements comparing the size distributions between the long-term (deposition) and short-term (filter) sampling is shown in Fig. S21.

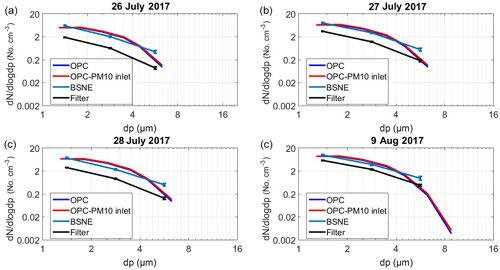
Figure 13 Average size distributions obtained from the SEM analysis of the filter sampler, in comparison to BSNE and OPC for different measurement days: (a) 26 July 2017; (b) 27 July 2017; (c) 28 July 2017; (d) 29 July 2017. Number concentration size distributions from deposition are obtained by converting the SEM-obtained number deposition rates to number concentration using different deposition velocity models. The red curve shows the OPC with PM₁₀ inlet efficiency correction (representing the atmospheric concentration). The number concentration measurements shown for the filter sampler are daily averages. The bars show the central 95 % confidence interval of the daily variation.

4.1.4 Estimating the turbulent vs. gravitational transport fraction

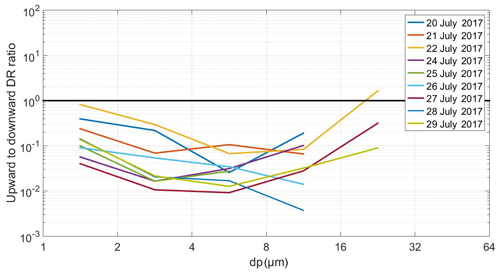
The size-resolved upward and downward deposition rates were derived from the upward-/downward-facing deposition sampler by the same type of SEM analyses. Results of the size-resolved mass and number deposition rate measurements along with daily average temperatures and wind speeds are given in the electronic Supplement (see Tables S5 and S6). The upward deposition rate is always less than the downward deposition rate. This is expected because the upward-facing substrate (i.e., measuring the downward-directed deposition rate) collects particles deposited by gravitational settling and turbulent inertial impaction, while the downward-facing substrate (for the upward-directed deposition rate) collects particles only by means of turbulent impaction. Figure 14 shows the ratio of upward to downward mass deposition rate as function of particle size. The deviation is greatest for the particle size range around 8 µm, which is strongly affected by turbulence (Noll and Fang, 1989). However, nearly no trend of increasing ratio with increasing wind speed can be found here (see Fig. S23). Besides the wind speed magnitude, different properties were calculated from the sonic wind data (e.g., turbulent intensity, Monin–Obukhov length, relative standard deviation of wind speed, average vertical component), but none of them were able to explain the observed variations in the deposition rate ratio.

Figure 14 Ratio of upward- to downward-directed mass deposition rate as function of particle size. The deposition rate is measured using the upward–downward flat-plate sampler (with 25 mm stub).

4.2 CFD simulation

Using CFD, deposition velocities of particles for different passive samplers were predicted and compared to the analytical deposition velocity models used for the different samplers (see Figs. 15 and S31). While for the flat-plate and MWAC samplers, the curves agree qualitatively (i.e., showing deposition speeds higher than Stokes velocity at particle sizes 4–16 µm, which are supposedly most affected by turbulence), for Sigma-2, they are largely contrary except for the lowest wind velocity. The latter might be due to the fact that in a flow model, the non-omnidirectional construction of Sigma-2 might lead to preferred airflows, which are not relevant in a more variable and turbulent atmosphere. However, also for the former ones, the deposition velocity curves are quantitatively largely different. In this context, Fig. S32 shows a comparison of the CFD-derived particle deposition velocities at different wind speed values for different samplers. For the flat-plate and the MWAC samplers, the deposition velocity increases with the wind speed, while for the Sigma-2 sampler, such a relation is not observed. Moreover, it can be seen from the figure that in general for the flat-plate and MWAC samplers, Stokes velocity is considerably lower than the deposition velocities calculated at different wind speeds by the other models. Interestingly, however, this is not true in the case of the Sigma-2 sampler. In general, in terms of the effect of wind speed on the Sigma-2 sampler, it is not yet clear why there is an effect for some sizes and not for others, so further modeling work is needed.

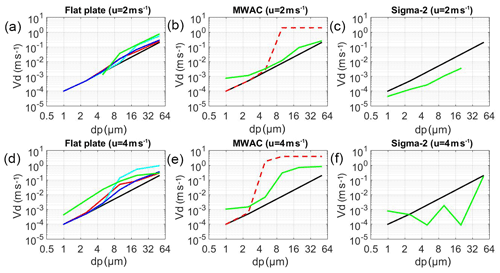
Figure 15 Deposition velocities calculated for different samplers by analytical and CFD approaches. The red curve shows the deposition velocity calculated using the Piskunov model, the dotted red curve shows the combination of the Piskunov and the impaction curve model, the black curve shows the Stokes deposition velocity, the blue curve shows the Noll and Fang model, the cyan curve shows the Zhang model, and the green curve shows the deposition velocity from CFD. Panels (a)–(c) are calculated for 2 m s⁻¹ wind speed and (d)–(f) for 4 m s⁻¹.

4.3 Comparison of measured deposition rate ratios to analytically and CFD modeled ones

As there is no reference instrument for dry deposition sampling, the separate approaches are compared in a relative way. Figure 16a–c show comparisons of the deposition velocity ratios derived from the analytical models with the corresponding measured deposition velocity ratios (equalling the corresponding deposition rate ratios), Fig. 16d–f the respective correlation of the ratios derived from CFD modeling with the measurement. As the CFD models could only be calculated for a limited number of flow velocities, deposition velocity values were interpolated between the calculated cases. Generally, the agreement is very poor. Practically, no variation observed in the measurement data can be explained by model variation, independently of the type of model. While this might be explained to a smaller extent by the propagating measurement uncertainties for the largest particles with low counting statistics, for the smaller ones, this systematic deviation must have other reasons.

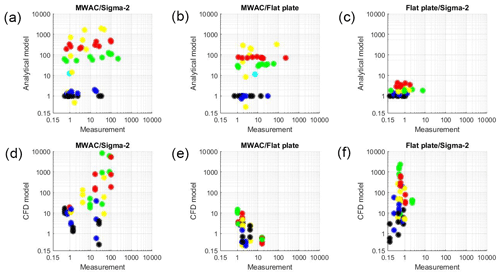
Figure 16 Comparison of the observed deposition velocity ratios with modeled ones by the analytical deposition models (a–c) and by the CFD models (d–f). (a, d) MWAC/Sigma-2; (b, e) MWAC/flat plate; (c, f) flat plate/Sigma-2. Multiple daily measurements are shown in each plot. Different colors represent different size intervals: 1–2 µm: black, 2–4 µm: blue, 4–8 µm: yellow, 8–16 µm: red, 16–32 µm: green, 32–64 µm: cyan.

5 Summary and conclusions

Parallel dust aerosol deposition measurements by means of deposition and other passive samplers were conducted at Izaña Global Atmospheric Watch Observatory continuously from 14 July to 24 August 2017. In addition, active aerosol collection was done with a free-wing impactor and an isoaxial filter sampler. Additional information regarding the aerosol particle size distributions has been obtained by an OPC. Overall, 316 000 single particles from six different samplers were analyzed by SEM-EDX, yielding size-resolved deposition rates.

As known from previous studies, the total deposition rate was dominated by coarse particles (8–16 µm). A high temporal daily variability in total dust deposition rate was observed. The size-resolved deposition rate measurements of different passive samplers varied significantly between the samplers under the same conditions. This was in principle expected from the different sampler construction. Applying suitable deposition velocity models, atmospheric concentrations were calculated from different sampler deposition rates. The resulting concentrations on average are in better agreement between the samplers than the deposition rates. However, discrepancies beyond the measurement uncertainty remain unexplained by the deposition models, in particular with respect to dependency on wind speed, which is predicted by the models but not observed. The estimation of an appropriate deposition velocity from different models for calculating atmospheric concentrations remains obviously a challenge. In particular, when considering the size-resolved deposition velocities and deposition rate ratios, great discrepancies show up. While for an integrated bulk measurement or the PM₁₀ size range at least a qualitative agreement between the samplers can be reached, no model – analytical nor CFD – is able to explain the observed sampler-specific variations in deposition rate. Clearly, a better physical understanding is needed here.

In the PM₁₀ size range, a good agreement is found between the calculated concentrations for samples from different passive samplers and the concentrations measured using an OPC. For particle sizes above PM₁₀, the comparison of the deposition-derived size distributions with impactor and filter measurements shows considerable underestimates of the deposition samplers, which must be interpreted as overestimation of the large-particle deposition velocities.

Deposition velocities from different analytical deposition models are compared to ones calculated using computational fluid dynamics simulations for different samplers. The comparison shows that two methods largely disagree. Moreover, all theory-based deposition velocities (analytical as well as CFD approaches) fail to represent the observed measurement differences between the samplers. This obviously points to the need for better understanding the physics of dry deposition in general.

The correlation analysis between dust deposition rate, dust concentrations and wind speed reveals that the variation in deposition rate is mainly controlled by changes in concentration; variations in wind speed play a minor role for wind speeds lower than 6 m s⁻¹. However, the situation might be different for higher wind speeds (Kandler et al., 2018).

The correlation analysis between deposition rates and OPC measurements demonstrated that BSNE and Sigma-2 can be a good option for PM₁₀ measurement, while MWAC is not a suitable option. Apart from that result with respect to the PM₁₀ size range, no recommendation for a least-biased general purpose deposition sampler can be derived from our study.

Moreover, as the results show that the different samplers cannot deliver consistent results between the sampler types, a recommendation must be that if a certain sampler type is chosen for a study, it should not be modified or replaced by another one for sake of consistency of results, even if it was shown that the results do not agree well, for example, with active sampling. The results show, nevertheless, that passive sampling techniques coupled with an automated single-particle analysis provide insights into the variation of size distribution, deposition rate and concentration of atmospheric particles.