Simultaneous detection of ozone and nitrogen dioxide by oxygen anion chemical ionization mass spectrometry: a fast-time-response sensor suitable for eddy covariance measurements

We report on the development, characterization, and field deployment of a fast-time-response sensor for measuring ozone (O₃) and nitrogen dioxide (NO₂) concentrations utilizing chemical ionization time-of-flight mass spectrometry (CI-ToFMS) with oxygen anion (${\mathrm{O}}_{\mathrm{2}}^{-}$) reagent ion chemistry. We demonstrate that the oxygen anion chemical ionization mass spectrometer (Ox-CIMS) is highly sensitive to both O₃ (180 counts s⁻¹ pptv⁻¹) and NO₂ (97 counts s⁻¹ pptv⁻¹), corresponding to detection limits (3σ, 1 s averages) of 13 and 9.9 pptv, respectively. In both cases, the detection threshold is limited by the magnitude and variability in the background determination. The short-term precision (1 s averages) is better than 0.3 % at 10 ppbv O₃ and 4 % at 10 pptv NO₂. We demonstrate that the sensitivity of the O₃ measurement to fluctuations in ambient water vapor and carbon dioxide is negligible for typical conditions encountered in the troposphere. The application of the Ox-CIMS to the measurement of O₃ vertical fluxes over the coastal ocean, via eddy covariance (EC), was tested during the summer of 2018 at Scripps Pier, La Jolla, CA. The observed mean ozone deposition velocity (v_d(O₃)) was 0.013 cm s⁻¹ with a campaign ensemble limit of detection (LOD) of 0.0027 cm s⁻¹ at the 95 % confidence level, from each 27 min sampling period LOD. The campaign mean and 1 standard deviation range of O₃ mixing ratios was 41.2±10.1 ppbv. Several fast ozone titration events from local NO emissions were sampled where unit conversion of O₃ to NO₂ was observed, highlighting instrument utility as a total odd-oxygen (${\mathrm{O}}_x={\mathrm{O}}_{\mathrm{3}}+{\mathrm{NO}}_{\mathrm{2}}$) sensor. The demonstrated precision, sensitivity, and time resolution of this instrument highlight its potential for direct measurements of O₃ ocean–atmosphere and biosphere–atmosphere exchange from both stationary and mobile sampling platforms.

1 Introduction

The deposition of O₃ to the ocean surface is a significant component of the tropospheric ozone budget. Global chemical transport model studies that explicitly treat O₃ deposition indicate that approximately one-third of total ozone dry deposition is to water surfaces (Ganzeveld et al., 2009). However, the magnitude of total annual global ozone deposition to ocean surfaces is highly sensitive to the deposition velocity parameterization used, with model estimates ranging from 95 to 360 Tg yr⁻¹ (Ganzeveld et al., 2009; Luhar et al., 2017). Several common global chemical transport models including GEOS-Chem (Bey et al., 2001), MOZART-4 (Emmons et al., 2010), and CAM-chem (Lamarque et al., 2012) apply a globally uniform deposition velocity (v_d) that ranges between 0.01 and 0.05 cm s⁻¹ depending on the model. In comparison to terrestrial measurements, where O₃ dry deposition velocities are relatively fast (> 0.1 cm s⁻¹, Zhang et al., 2003), there is a paucity of direct observations of ozone deposition to the ocean surface necessary to constrain atmospheric models. Previous studies of O₃ deposition to water surfaces have been made from coastal towers (Gallagher et al., 2001), aircraft (Faloona et al., 2005; Kawa and Pearson, 1989; Lenschow et al., 1981), underway research vessels (Helmig et al., 2012), and in the laboratory (McKay et al., 1992), with observed v_d(O₃) ranging between 0.01 and 0.15 cm s⁻¹. There is only one reported study of O₃ deposition to freshwater, which showed a v_d(O₃) of 0.01 cm s⁻¹ (Wesely et al., 1981). Measured deposition rates to snow and ice vary widely, with most observations of v_d(O₃) from 0 to 0.2 cm s⁻¹, while models suggest v_d(O₃) from 0 to 0.01 cm s⁻¹ (Helmig et al., 2007). Reactions of O₃ with iodide and dissolved organic compounds (DOCs) in the ocean are known to play a controlling role in setting v_d(O₃) and may explain some of the variability in observations (Chang et al., 2004; Ganzeveld et al., 2009). However, these quantities have not typically been measured during field studies of v_d(O₃). To date there is no consensus on whether measured ocean O₃ deposition velocities show a wind speed dependence (Fairall et al., 2007). The most comprehensive dataset is from Helmig et al. (2012), which reported a deposition velocity range of 0.009–0.034 cm s⁻¹ from 1700 h of observation over five research cruises. This dataset showed variability in v_d(O₃) with wind speed (U₁₀) and sea surface temperature (SST), highlighting the need for further field observations as constraints for model parameterizations.

The small magnitude of O₃ ocean–atmosphere vertical fluxes presents a significant analytical challenge for existing ozone sensors used in eddy covariance (EC) analyses. Driven in part by stringent sensor requirements for EC techniques, significant uncertainties in the magnitude of and variability in ozone deposition to water surfaces remain. In contrast, O₃ vertical fluxes to terrestrial surfaces are 10 to 100 times faster than to water surfaces, significantly loosening sensor precision requirements. Nonetheless, significant variability in v_d(O₃) exists between surface types (e.g., soil vs. leaf; Wesely and Hicks, 2000). Terrestrial deposition velocities also show strong diel and seasonal variability due to factors such as stomatal opening and within-canopy chemistry (Fares et al., 2010; Fowler et al., 2001; Kurpius and Goldstein, 2003). Highly accurate and precise measurements of O₃ are required to correctly model the response of v_d(O₃) to each of these factors. While terrestrial and ocean exchange studies have substantial differences in experimental design, a sensor suitable for ocean–atmosphere ozone deposition measurements via EC is expected to be highly capable of biosphere–atmosphere measurements due to the significantly larger deposition rates and similar accuracy requirements.

Eddy covariance measurements typically require fast (1–10 Hz), high-precision sensors in order to resolve covariance on the timescales of the fastest atmospheric turbulent eddies. Due to this constraint, standard O₃ monitoring instruments which utilize UV-absorption detection do not have a suitable time response or suitable precision for EC measurements, and ozone flux measurements have primarily utilized fast-response chemiluminescence sensors. Chemiluminescence detectors can use either gas-phase, dry, or wet reagents for detection with important differences between them (Muller et al., 2010). Gas-phase chemiluminescence sensors are typically based on the reaction of O₃ with nitric oxide (NO) to form an excited state NO₂^∗ which then relaxes to the ground state, emitting a photon that can be detected. This method has well-understood reaction kinetics and allows for high-sensitivity detection on the order of 2.8 counts s⁻¹ pptv⁻¹ (Bariteau et al., 2010; Pearson, 1990). A practical disadvantage to this technique is the necessity of a compressed cylinder of NO which is highly toxic. Wet chemiluminescence techniques are used less, as they exhibit generally lower sensitivity than dry chemiluminescence sensors and can be limited by issues in the liquid flow (Keronen et al., 2003).

Dry chemiluminescence sensors have the simplest operation and have seen the most regular use for EC studies (Güsten et al., 1992; Tuovinen et al., 2004). However, dry chemiluminescence sensor discs require conditioning with high ozone (up to 400 ppbv for several hours) before operation, are known to degrade over time, and have high variability in sensitivity between sensor discs (Weinheimer, 2007). These factors have led to limitations in long-term stability and to uncertainty in calibration factors for dry chemiluminescence sensors, resulting in uncertainty in the accuracy of the flux measurement (Muller et al., 2010). Muller et al. (2010) also reported a comparison of two identical colocated dry chemiluminescence sensors with half-hourly flux values differing by up to a factor of 2 and a mean hourly flux difference ranging from 0 % to 23 % between sensors. Recently Zahn et al. (2012) reported the development of a commercial dry chemiluminescence ozone detector capable of fast (> 10 Hz) measurements with high sensitivity (∼9 counts s⁻¹ pptv⁻¹) suitable for EC or mobile platform sampling. However, they also report issues of short- and long-term drift and variability between sensor discs. These accuracy and drift concerns have driven an interest in the development of a new, stable, and fast ozone sensor suitable for EC measurements from both stationary and mobile sampling platforms.

In addition to the inherently small magnitude of v_d(O₃), the fast chemical titration of O₃ by NO (Reaction R1) often complicates the interpretation of v_d(O₃) measurements. Surface emissions of NO result in a high bias in the measured deposition velocity when the titration Reaction (R1) is fast relative to the transport time to the height of the sensor.

$$\begin{array}{}\text{(R1)}& \begin{array}{rl}{\mathrm{O}}_{\mathrm{3}}+\mathrm{NO}& \to {\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}k\left({\mathrm{O}}_{\mathrm{3}}+\mathrm{NO}\right)\\ & =\mathrm{1.8}\times {\mathrm{10}}^{-\mathrm{14}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\end{array}\end{array}$$

Surface NO emissions from both biogenic and anthropogenic sources are widespread, with ocean emissions on the order of 1×10⁸ molecules cm⁻² s⁻¹ (Zafiriou and McFarland, 1981) and soil emissions ranging from 5×10⁹ to 2×10¹¹ molecules cm⁻² s⁻¹ (Yienger and Levy, 2004). These emissions correspond to a positive bias in the observed v_d(O₃) dry deposition rate on the order of 5 % in the marine atmosphere (discussed in Sect. 3.7.1) and up to 50 % in a forested site (Dorsey et al., 2004). Simultaneous flux detection of O₃ with one or both of NO or NO₂ is commonly used to address this flux divergence problem (Finco et al., 2018; Stella et al., 2013). However, these studies typically require separate sensors for O₃ and NO_x which can introduce additional sources of uncertainty. Related challenges of fast O₃ titration exist for quantification of O₃ from mobile platforms where there is dynamic sampling of different air masses with potentially differing O₃–NO–NO₂ steady-state conditions.

In what follows, we describe the characterization and first field observations of a novel oxygen anion chemical ionization time-of-flight mass spectrometer (Ox-CIMS) sensor for O₃ and NO₂. Over the past 2 decades, chemical ionization mass spectrometry (CIMS) techniques have emerged as sensitive, selective, and accurate detection methods for a diverse suite of reactive trace gases (Huey, 2007). Successful application of CIMS for EC flux measurements have been demonstrated from many sampling platforms including ground sites (Kim et al., 2014; Nguyen et al., 2015), aircraft (Wolfe et al., 2015), and underway research vessels (Blomquist et al., 2010; Kim et al., 2017; Yang et al., 2013) employing a variety of reagent ion chemistry systems. Here we demonstrate the suitability of the Ox-CIMS for EC flux measurements and provide detailed laboratory characterization of the instrument.

2 Laboratory characterization

2.1 Chemical ionization time-of-flight mass spectrometer

A complete description of the CI-ToFMS instrument (Aerodyne Research Inc., TOFWERK AG) can be found in Bertram et al. (2011). In what follows we highlight significant differences in the operation of the instrument from what is discussed in Bertram et al. (2011). Oxygen anions are generated by passing an 11:1 volumetric blend of ultrahigh-purity (UHP) N₂ and O₂ gas (both Airgas 5.0 grade) through a polonium-210 α-particle source (NRD, P-2021 Ionizer). This N₂:O₂ volume ratio was found empirically to maximize the total reagent ion signal in our instrument while minimizing background signal at the O₃ detection product (${\mathrm{CO}}_{\mathrm{3}}^{-}$, −60 m∕Q). Further discussion of the reagent ion chemistry and precursor concentration can be found in Sect. 2.2 and 2.8. The reagent ion stream then mixes with ambient air in an ion–molecule reaction (IMR) chamber held at 95 mbar where product ions were generated. Further discussion of the dependence of instrument sensitivity on IMR pressure can be found in Sect. 2.6. At this pressure, the residence time in the IMR is estimated to be on the order of 100 ms. Product ions then pass into three differentially pumped chambers before reaching the ToF mass analyzer. Ions first move from the IMR to a collisional dissociation chamber (CDC) held at 2 mbar which houses a short-segmented RF-only quadrupole ion guide. Field strengths in the IMR and CDC were tuned to be as soft as possible to preserve the transmission of weakly bound clusters while still maintaining acceptable total ion signals (ion optic potentials are listed in Table S1 in the Supplement). Ions then sequentially pass into a second RF-only quadrupole chamber held at $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{2}}$ mbar and a final chamber containing focusing optics which prepare the ion beam for entry into the compact ToF mass analyzer (CToF, TOFWERK AG and Aerodyne Research Inc.). The mass resolving power (M∕ΔM) of the instrument as configured for these experiments was greater than 900 at −60 m∕Q. All ion count rates reported here are for unit mass resolution integrated peak areas. In this work extraction frequencies of 75 kHz were used, resulting in mass spectra from 27 to 327 $-m/Q$. All mass spectra were saved at 10 Hz for analysis.

2.2 Oxygen anion chemistry

Oxygen anion (${\mathrm{O}}_{\mathrm{2}}^{-}$) reagent ion chemistry has been investigated previously for its use in the detection of nitric acid and more recently hydrogen peroxide (Huey, 1996; O'Sullivan et al., 2018; Vermeuel et al., 2019). Oxygen anion chemistry has also been used for chemical analysis of aerosol particles in a thermal-desorption instrument, primarily for detection of particle sulfate and nitrate (Voisin et al., 2003). Oxygen anion chemistry has also been used for the detection of SO₂ via a multistep ionization process where ${\mathrm{CO}}_{\mathrm{3}}^{-}$ reagent ions are first generated by the reaction of ${\mathrm{O}}_{\mathrm{2}}^{-}$ with added excess O₃ in the presence of CO₂. The ${\mathrm{CO}}_{\mathrm{3}}^{-}$ reagent ion then ligand switches with SO₂ to form ${\mathrm{SO}}_{\mathrm{3}}^{-}$ which then quickly reacts with ambient O₂ to form the primary detected ${\mathrm{SO}}_{\mathrm{5}}^{-}$ product (Porter et al., 2018; Thornton et al., 2002a). Ionization of analytes by oxygen anion reagent ion chemistry proceeds through both charge transfer (Reaction R2) and adduct formation (Reaction R3).

$$\begin{array}{}\text{(R2)}& {\displaystyle }{\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}+A\to {\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n+A^{-}\text{(R3)}& {\displaystyle }{\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}+B\to B\cdot {\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}\end{array}$$

It is expected that charge transfer from oxygen will occur to any analyte with an electron affinity (EA) greater than O₂ (0.45 eV; Ervin et al., 2003), resulting in a relatively nonspecific reagent ion chemistry (see Rienstra-Kiracofe et al., 2002, for a compilation of molecular EA values) Adduct formation is observed when the binding enthalpy of the adduct is larger than that of the oxygen–water adduct and the adduct is stable enough to be preserved through the ion optics. This adduct formation framework is analogous to what has been shown for iodide reagent ion chemistry (Lee et al., 2014).

The ${\mathrm{O}}_{\mathrm{2}}^{-}$ reagent ions present in the IMR are expected to have a series of attached water molecules at ambient humidity and the IMR pressure (95 mbar) and electric field strengths used in this study (Bork et al., 2011). The reagent ion is therefore reported as O₂(H₂O)${}_n^{-}$ for the remainder of this work. In the recorded mass spectra from our instrument, all the reagent ion signal is observed as n=0–1 (i.e., ${\mathrm{O}}_{\mathrm{2}}^{-}$ and O₂(H₂O)⁻) as seen in Fig. 1. Oxygen anion–water clusters larger than n=1 are likely present in the IMR but H₂O evaporates off the cluster in the CDC before detection due to the lower binding enthalpy of each additional water in O₂(H₂O)${}_n^{-}$ (Bork et al., 2011) and the high field strength at the exit of the CDC (Brophy and Farmer, 2016). Variability in the number of attached water molecules (n) as a function of humidity introduces the possibility of a water dependence on the ion chemistry, which is discussed further in Sect. 2.5.

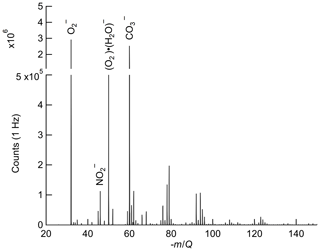
Figure 1 Ox-CIMS mass spectra collected at 1 Hz and mass resolution of 950M∕ΔM (at −60 m∕Q), with major peaks highlighted. ${\mathrm{O}}_{\mathrm{2}}^{-}$ and O₂ (H₂O)⁻ at −32 m∕Q and −50 m∕Q, respectively, are the two observed forms of the reagent ion. The detected ozone product (${\mathrm{CO}}_{\mathrm{3}}^{-}$, −60 m∕Q) is of comparable magnitude to the ${\mathrm{O}}_{\mathrm{2}}^{-}$ reagent ion during ambient sampling. NO₂ is detected as the charge transfer product ${\mathrm{NO}}_{\mathrm{2}}^{-}$ at −46 m∕Q. Masses greater than −150 m∕Q contribute less than 2 % to the total signal and are not plotted.

The detection of ozone (O₃) by oxygen anion reagent ion chemistry proceeds via a two-step reaction leading to the formation of a carbonate anion (${\mathrm{CO}}_{\mathrm{3}}^{-}$), which is the final detected product. First, the oxygen anion (O₂(H₂O )${}_n^{-}$) either transfers an electron to ozone-forming ${\mathrm{O}}_{\mathrm{3}}^{-}$ (Reaction R4a) or forms a stable cluster with ozone (Reaction R4b). The ozone anion (either bare or as a cluster with O₂ (H₂O)_n) then reacts with a neutral CO₂ molecule to form ${\mathrm{CO}}_{\mathrm{3}}^{-}$ (Reaction R5a–5b) which is the primary detected product in the mass spectrometer. The electron affinity of O₃ is 2.1 eV (Arnold et al., 1994).

$$\begin{array}{}\text{(R4a)}& {\displaystyle }{\mathrm{O}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}\to {\mathrm{O}}_{\mathrm{3}}^{-}+{\mathrm{O}}_{\mathrm{2}}+n{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\text{(R4b)}& {\displaystyle }{\mathrm{O}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}\to {\mathrm{O}}_{\mathrm{2}}\left({\mathrm{O}}_{\mathrm{3}}\right){\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}\end{array}$$

$$\begin{array}{}\text{(R5a)}& {\displaystyle }{\mathrm{O}}_{\mathrm{3}}^{-}+{\mathrm{CO}}_{\mathrm{2}}\to {\mathrm{CO}}_{\mathrm{3}}^{-}+{\mathrm{O}}_{\mathrm{2}}\text{(R5b)}& {\displaystyle }{\mathrm{O}}_{\mathrm{2}}\left({\mathrm{O}}_{\mathrm{3}}\right){\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}+{\mathrm{CO}}_{\mathrm{2}}\to {\mathrm{CO}}_{\mathrm{3}}^{-}+\mathrm{2}{\mathrm{O}}_{\mathrm{2}}+n{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

It is not clear whether it is the bare ozone anion (Reactions R4a and R5a) or the cluster (Reactions R4b and R5b) that goes on to react with CO₂ to form the carbonate anion. The O₂(O₃)(H₂O)${}_n^{-}$ product has not been observed in the mass spectrometer, but it may exist in the IMR and dissociate as it transfers into the CDC prior to detection. A small amount of ozone is detected directly as ${\mathrm{O}}_{\mathrm{3}}^{-}$, but the magnitude of this signal is less than 1 % of the signal of ${\mathrm{CO}}_{\mathrm{3}}^{-}$ during ambient sampling. The proposed mechanism of ${\mathrm{CO}}_{\mathrm{3}}^{-}$ formation is supported by a study using isotopically labeled oxygen to form labeled ozone anions (${}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{3}}^{-}$) in a corona discharge source which then reacted with CO₂ to form the detected product ${\mathrm{C}}^{\mathrm{18}}{\mathrm{OO}}_{\mathrm{2}}^{-}$ (Ewing and Waltman, 2010). This product supports a single oxygen being transferred from the ozone anion to carbon dioxide (as in Reaction R5a).

$$\begin{array}{}\text{(R6)}& {\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}\to {\mathrm{NO}}_{\mathrm{2}}^{-}+{\mathrm{O}}_{\mathrm{2}}+n{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

Oxygen anions are expected to be a highly general reagent ion chemistry, showing sensitivity to an array of analytes. While the focus of this work is on detection of O₃ and NO₂, detection of hydrogen peroxide, nitric acid, formic acid, sulfur dioxide, and other species with the Ox-CIMS has demonstrated good performance (Vermeuel et al., 2019). An example ambient mass spectrum recorded at 1 Hz sampling is shown in Fig. 1, with several major peaks highlighted. Also apparent are an abundance of peaks throughout the spectra with high signal intensity. During ambient observations, over one-third of masses from $-m/Q$ 27–327 showed a signal intensity greater than 1×10⁴ counts per second (cps). A larger survey and classification of oxygen anion reagent ion chemistry to utilize this versatility is underway.

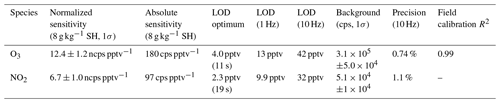
Table 1 Summary of instrument sensitivity, precision, and accuracy for detection of O₃ and NO₂ from laboratory calibrations. Sensitivity is reported at a specific humidity (SH) of 8 g kg⁻¹ which corresponds to 40 % RH at 25 ^∘C. All limits of detection (LODs) are for a signal-to-noise ratio (S / N) of 3. The optimum LOD is reported as the LOD at the optimum averaging time determined by the minimum of the Allan variance spectrum. Optimum averaging times were determined to be 11 s for O₃ and 19 s for NO₂. The reported field comparison (R²) is from a regression of 1 min bin averaged ozone concentration from the Ox-CIMS with an EPA (Environmental Protection Agency) monitor (Thermo Fisher 49i) in Zion, Illinois, during 4 weeks of ambient observation shown in Fig. 7.

2.3 Laboratory calibration

Laboratory calibrations of the Ox-CIMS were performed to determine instrument sensitivity to O₃ and NO₂. Ozone was generated by passing UHP Zero Air (ZA, Airgas 5.0 grade) through a mercury lamp UV source (Jelight Co, Irvine, CA). Outflow from the lamp source was diluted in UHP ZA and split between the Ox-CIMS and a factory-calibrated 2B personal ozone monitor (POM; 2B Technologies) with an accuracy of ±1.5 ppbv, which served as our reference standard. Ozone concentrations were varied over the range 0–80 ppbv and instrument response was determined to generate a calibration curve. NO₂ was delivered from a certified standard cylinder (Scott-Marrin, 4.84±0.1 ppmv). The primary NO₂ standard was diluted in UHP ZA to span the range of 0–10 ppbv. Dilutions of calibration standards were made in UHP ZA which was humidified to the desired amount by splitting a portion of the flow through a bubbler containing 18 MΩ water. CO₂ (Airgas Bone Dry grade) was added to the dilution flow to maintain mixing ratios of 380 ppmv for all calibrations (See Sect. 2.6). A Vaisala HMP110 sensor continuously measured relative humidity (RH) and temperature inline downstream of the Ox-CIMS and POM inlets. All flows were controlled by mass flow controllers (MKS Instruments, 1179C series) with an estimated total uncertainty of 10 %. Example calibration curves for O₃ and NO₂ are shown in Fig. 2. An overview of instrument sensitivity, limits of detection (LODs), and precision for O₃ and NO₂ is given in Table 1.

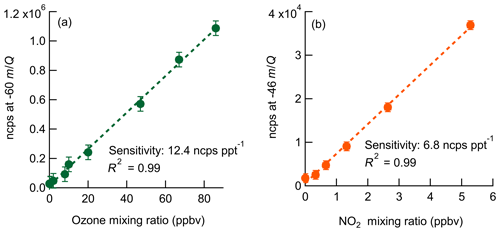
Figure 2 Normalized calibration curves of O₃ (a) and NO₂ (b) at 8 g kg⁻¹ specific humidity (approximately 40 % RH at 25 ^∘C). Ozone is detected as ${\mathrm{CO}}_{\mathrm{3}}^{-}$ at −60 m∕Q. NO₂ is detected as the charge transfer product (${\mathrm{NO}}_{\mathrm{2}}^{-}$) at −46 m∕Q. Error bars are the standard deviation in normalized count rate for each measurement point.

2.4 Absolute sensitivity

The absolute sensitivity of the Ox-CIMS for detection of analytes is controlled by the kinetics and thermodynamics of the reagent ion chemistry and the total ion generation and transmission efficiency of the instrument. Under the operational configuration described in Sect. 2.1, the typical reagent ion signal (${{\mathrm{O}}_{\mathrm{2}}}^{-}+$ ${\mathrm{O}}_{\mathrm{2}}{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}$) ranged from 0.8 to 2.2×10⁷ counts s⁻¹ (Fig. S1 in the Supplement). The mean total reagent ion signal over 6 weeks of ambient sampling (Sect. 3.1) was 1.45×10⁷ cps. The absolute instrument sensitivity at this reagent ion signal to O₃ and NO₂ is 180 and 97 cps pptv⁻¹, respectively, (at 8 g kg⁻¹ SH). Total instrument count rate is a complex function of instrument design, instrument ion optics tuning, Po-210 source decay, microchannel plate (MCP) detector decay, and ToF extraction frequency, all of which either are tunable parameters or vary in time. Conversely, the reagent ion charge transfer or adduct formation chemistry for a given analyte sets a fundamental limit on sensitivity for a given instrument configuration. Sensitivity values can be normalized by scaling all signals to a fixed total reagent ion signal of 1×10⁶ cps to isolate the sensitivity component controlled by reagent ion chemistry, separate from changes in instrument performance due to decay in the ion source or other factors. The total reagent ion signal is taken as the sum of the ${\mathrm{O}}_{\mathrm{2}}^{-}$ and O₂(H₂O)⁻ signals. Sensitivity values through the remainder of the text are reported as either absolute sensitivities in counts per second (cps pptv⁻¹) or normalized sensitivities in normalized counts per second (ncps pptv⁻¹). Absolute sensitivity values control instrument limits of detection (LODs) and precision, while normalized sensitivities are used for comparison of calibration factors.

2.5 Dependence of instrument sensitivity on specific humidity

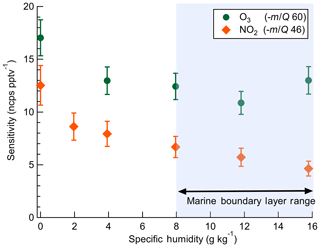
The dependence of instrument sensitivity on ambient water content was assessed for specific humidity (SH) ranging between 0 and 16 g kg⁻¹ (approximately 0 %–80 % RH at 25 ^∘C) by triplicate calibrations as shown in Fig. 3. Sensitivity to O₃ had no significant dependence on specific humidity over the range 4–16 g kg⁻¹. Sensitivity to NO₂ has a specific humidity dependence over the range 4–16 g kg⁻¹, decreasing from 7.9 to 4.6 ncps pptv⁻¹. A 30 % and 45 % decline in sensitivity was observed from 0 to 4 g kg⁻¹ for O₃ and NO₂, respectively. This low-humidity range is rarely sampled in the boundary layer over water surfaces but may be significant in some terrestrial or airborne deployments and would require careful calibration. The SH range from 8 to 16 g kg⁻¹ corresponds to approximately 40 % to 80 % RH at 25 ^∘C which is typical of the humidity range over midlatitude oceans (Liu et al., 1991). Ab initio calculations of ${{\mathrm{O}}_{\mathrm{2}}}^{-}({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_n$ and ${{\mathrm{O}}_{\mathrm{3}}}^{-}({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_n$ clusters performed by Bork et al. (2011) showed that charge transfer from the bare (n=0) ${\mathrm{O}}_{\mathrm{2}}^{-}$ to O₃ was exothermic at ca. −160 kJ mol⁻¹. At larger cluster sizes of n=4–12, charge transfer becomes less favorable and converges to ca. −110 kJ mol⁻¹. An increase in n from 0 to 4 over the SH range 0–4 g kg⁻¹ is a potential explanation for the initial decline in sensitivity observed with SH before leveling off from 4 to 16 g kg⁻¹. It is not known if the enthalpy of charge transfer from ${{\mathrm{O}}_{\mathrm{2}}}^{-}({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_n$ to NO₂ follows a similar trend with n. Ion mobility studies to determine the ${{\mathrm{O}}_{\mathrm{2}}}^{-}({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_n$ cluster size with SH and IMR pressure would provide valuable insight into the observed dependence of sensitivity on water content.

Figure 3 Dependence of O₃ and NO₂ sensitivities on specific humidity. Error bars indicate standard deviation of triplicate calibration curves. The shaded blue region of SH 8–16 g kg⁻¹ is the approximate typical range of specific humidity in the midlatitude marine boundary layer.

2.6 Dependence on CO₂

The ionization pathway for detection of O₃ with ${{\mathrm{O}}_{\mathrm{2}}}^{-}({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_n$ reagent ion chemistry differs from typical chemical ionization schemes in that it involves a two-step reaction of charge transfer to ozone-forming ${\mathrm{O}}_{\mathrm{3}}^{-}$, which then reacts with CO₂ to form the detected ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product (Reactions R4–R5). Therefore, we assessed the impact of the CO₂ mixing ratio in the sample flow on O₃ sensitivity as shown in Fig. 4. Calibration curves were generated by diluting ozone in dry UHP N₂ and mixing in a flow of variable CO₂ (Airgas, Bone Dry grade) mixing ratios before sampling. At nominally 0 ppmv CO₂, the ${\mathrm{O}}_{\mathrm{3}}^{-}$ ionization product (−48 m∕Q) was detected with a sensitivity of 14±2 ncps pptv⁻¹ and the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product (−60 m∕Q) at 5±1 ncps pptv⁻¹. For CO₂ mixing ratios from 60 to 500 ppmv, the ${\mathrm{O}}_{\mathrm{3}}^{-}$ signal is less than 1 % of the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product, and the sensitivity of the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product is independent of CO₂ within the uncertainty range. The presence of a significant fraction (36 %) of the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product with nominally 0 ppmv CO₂ suggests the presence of a slight leak rate of CO₂ via diffusion through the perfluoroalkoxy alkane (PFA) tubing or CO₂ contamination in the UHP N₂ supply. The manufacturer's stated upper limit of CO₂ in the UHP N₂ is 1 ppmv which we take to be the lower limit achievable in our system. A CO₂ mixing ratio of only 1 ppmv is still an order of magnitude excess relative to a high end ambient O₃ mixing ratio of 100 ppbv. An exponential fit of the ${\mathrm{O}}_{\mathrm{3}}^{-}$ product vs. CO₂ indicates that ${\mathrm{O}}_{\mathrm{3}}^{-}$ makes up less than 1 % of the detected ozone at CO₂ mixing ratios greater than 10 ppmv. This suggests ambient samples will always have a substantial excess of CO₂ necessary to drive the reaction completely to the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product. The measured flat response from 60 to 500 ppmv CO₂ indicates that natural variability in ambient CO₂ will have negligible impact on ambient measurements of ozone. No other analytes that we have calibrated for with the Ox-CIMS (HCOOH, HNO₃, H₂O₂) have shown a CO₂ mixing ratio dependence, suggesting that CO₂ may be uniquely involved in the detection of O₃ and is not a general feature of the oxygen anion chemistry. All other reported laboratory calibrations reported here were performed at CO₂ mixing ratios of 380 ppmv, and all reported sensitivities are for the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product. This CO₂ dependence also requires careful consideration during instrument background determinations by UHP N₂ overflow which is discussed in Sect. 2.8.

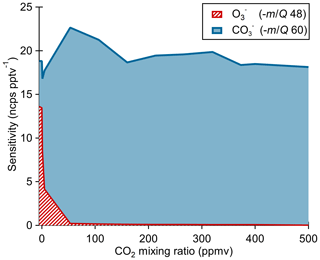
Figure 4 Ox-CIMS cumulative sensitivity to O₃ detected either directly as ${\mathrm{O}}_{\mathrm{3}}^{-}$ or as ${\mathrm{CO}}_{\mathrm{3}}^{-}$ as a function of CO₂ mixing ratio. The sum of sensitivity as ${\mathrm{O}}_{\mathrm{3}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{-}$ shows that total sensitivity to O₃ is conserved as the product distribution shifts with CO₂ mixing ratio. More than 99 % of O₃ is observed as ${\mathrm{CO}}_{\mathrm{3}}^{-}$ at CO₂ mixing ratios greater than 60 ppmv.

2.7 Dependence on IMR pressure

Instrument sensitivity to O₃ increases with increasing IMR pressure as shown in Fig. 5. The normalized signal of O₃ increases by 60 % at an IMR pressure of 95 mbar compared to 70 mbar when sampling a constant O₃ source of 35 ppbv. IMR pressure was increased in approximately 5 mbar steps, with CDC pressure held constant at 2 mbar, and a 3 min dwell time at each step to ensure the signal and pressure were stabilized. Total reagent ion signal did not change significantly over this pressure range. Pressures above 95 mbar were not investigated due to concerns over corresponding increases in CDC pressure with the pinhole and pumping configuration used in this work. There is no evident plateauing in the signal increase over the IMR pressure range investigated here, indicating that further optimization is likely possible by operating at higher IMR pressures. The increase in sensitivity with IMR pressure could be fit well with an exponential least-squares fit, which is plotted in Fig. 5. The physical meaning of the exponential relationship is not clear. The source of the response of sensitivity to pressure is not definitive but can possibly be attributed to the increase in the total number of collisions during the 100 ms residence time in the IMR and the corresponding weakening of those collisions. Higher collisional frequencies also lead to proportionally weaker collisions which could better preserve a weakly bound ${\mathrm{O}}_{\mathrm{2}}\left({\mathrm{O}}_{\mathrm{3}}\right){\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_n^{-}$ cluster and allow for a longer lifetime in which to react with CO₂ before dissociation. The operational IMR pressure of 95 mbar used here was empirically selected to maximize sensitivity to O₃ without increasing CDC pressure beyond the desired range. Investigation of higher IMR pressures, up to the operation of an atmospheric pressure interface, has the potential to further increase the instrument sensitivity to O₃.

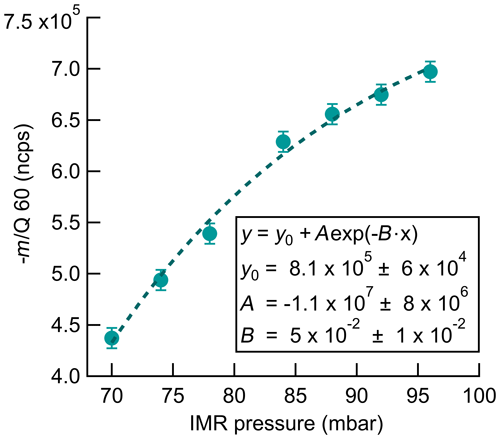
Figure 5 Normalized count rate of ${\mathrm{CO}}_{\mathrm{3}}^{-}$ (−60 m∕Q) ozone detection product as a function of pressure in the IMR during sampling of a constant 35 ppbv O₃ source. The exponential fit of the data is shown by the dashed line. Fit parameters are included to allow for calculation of potential sensitivity improvements with further increases in IMR pressure.

2.8 Instrument background and limits of detection

Instrument backgrounds were assessed by periodically overflowing the inlet with UHP N₂ during field sampling. Details of the inlet and zeroing conditions used are discussed further in Sect. 3.1. During N₂ overflow, O₃ displayed a consistently elevated background on the order of 3.1×10⁵ cps corresponding to 2.1×10⁴ ncps, or approximately 1.3 ppbv O₃, at a typical total reagent ion signal of 1.45×10⁷ cps. A representative background determination is shown in Fig. 6. The magnitude of the O₃ background was observed to vary with the O₂:N₂ ratio in the reagent ion precursor flow when sampling a UHP ZA overflow with 380 ppm CO₂ as shown in Fig. S2. The background O₃ count rate was observed to increase from 3.0×10⁴ to 6.3×10⁴ ncps as the O₂ volume fraction in the reagent ion delivery gas flow ($f_{{\mathrm{O}}_{\mathrm{2}}}$) was increased from 0.05 to 0.4. The dependence of the background O₃ signal on $f_{{\mathrm{O}}_{\mathrm{2}}}$ suggests that the observed background O₃ is formed directly in the alpha ion source and is not from the off-gassing of inlet and instrument surfaces. The magnitude of this background O₃ does not vary when sampling UHP Zero Air or N_2, further confirming that the background O₃ is formed directly in the ion source from the O₂ used to generate the reagent ion. An operational $f_{{\mathrm{O}}_{\mathrm{2}}}$ of 0.08 (actual volumetric flow ratio O₂ : N₂ of 200:2200 sccm) was selected to balance maximizing the total reagent ion signal while minimizing the O₃ ion-source background (3.1×10⁵ cps). The magnitude of this O₃ background was observed to be highly consistent during field sampling at a constant $f_{{\mathrm{O}}_{\mathrm{2}}}$ of 0.08 and well resolved from all ambient observations (Fig. S3). The 1σ deviation of the distribution of normalized adjacent differences of O₃ signal during background periods gives an upper limit of variability of 9 % between adjacent background periods. A variability of 9 % corresponds to a difference of 70 pptv between subsequent O₃ background determinations. The magnitude of this O₃ background is a fundamental limit on the achievable limit of detection.

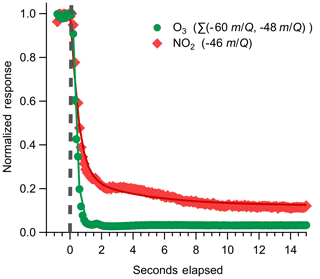
Figure 6 Representative instrument backgrounding determination for O₃ and NO₂, where the inlet was rapidly switched from ambient sampling to an overflow with dry UHP N₂ indicated by the dashed grey line. The O₃ response is fit to an exponential decay, plotted as solid lines, with a mean response time of 0.28 s; NO₂ is fit to a biexponential decay, where the initial rapid decay (τ₁) is attributed to gas evacuation of the inlet line and the second slower decay (τ₂) is attributed to equilibration with the inlet walls. Best-fit estimates for τ₁ of NO₂ are from 0.7 to 1.2 s. τ₂ for NO₂ was determined to be 3.2 s for this decay period.

Because CO₂ was not added to the UHP N₂ overflow during field sampling, the reaction was not driven fully to the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product and some ${\mathrm{O}}_{\mathrm{3}}^{-}$ signal at $-m/Q$ 48 was observed during UHP N₂ overflow periods as shown in Fig. S4. The magnitude of the O₃ signal observed as ${\mathrm{O}}_{\mathrm{3}}^{-}$ was approximately 55 % of the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ product (mean 1.2×10⁴ and 9.6×10³ ncps, respectively) during overflow periods. The total sensitivity to O₃ as the sum of the ${\mathrm{O}}_{\mathrm{3}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{-}$ was observed to be constant as a function of CO₂ as shown in Fig. 4. We therefore assigned equal sensitivity to each O₃ detection product and took the sum of signal at ${\mathrm{O}}_{\mathrm{3}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{-}$ in order to determine the total background O₃ concentration. This issue will be corrected in future deployments by the addition of CO₂ to the N₂ overflow used for backgrounds, which will drive the product fully to ${\mathrm{CO}}_{\mathrm{3}}^{-}$. The mean background of O₃ for the full field sampling period was 1.3±0.3 ppbv. The 10 Hz precision of O₃ during an individual N₂ overflow period was found to be 0.75 %, corresponding to 7.5 pptv as shown in Fig. S5. This suggests that variability in the O₃ signal from this background source is constant over short timescales and has a negligible impact on instrument precision during ambient sampling.

The 10 Hz limit of detection for O₃ is 42 pptv for a S / N of 3 and a mean background O₃ signal of 2.1×10⁴ ncps as calculated using Eq. (1), below, from Bertram et al., 2011, where C_f is the calibration factor, [X] is the analyte mixing ratio, t is averaging time in seconds, and B is the background count rate. The optimum LOD from the minimum of the Allan variance at an 11 s averaging time is 4.0 pptv (Fig. S6a).

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{S}{N}}={\displaystyle \frac{C_{\mathrm{f}}\left[X\right]t}{\sqrt{C_{\mathrm{f}}\left[X\right]t+\mathrm{2}Bt}}}\end{array}$$

The mean background signal during field sampling for NO₂ was 3.5×10³ ncps which corresponds to 0.28 ppbv. At this background level, the 10 Hz LOD for NO₂ is 26 pptv for a S / N of 3. The optimum LOD for NO₂ is 2.3 pptv at an averaging time of 19 s, determined from the minimum of the Allan variance (Fig. S6b). The background signal of NO₂ is notably above zero indicating either off-gassing from inlet walls or a secondary production of NO₂ in the instrument. A possible source of this background is from degradation of other species such as nitric acid or alkyl nitrates on the inlet walls. Additional calibration will be necessary to ensure that observed NO₂ signal is not a secondary product of other species and we can currently quantify their potential interference on measured NO₂.

2.9 Reagent ion saturation and secondary ion chemistry

During ambient sampling the ozone signal (as ${\mathrm{CO}}_{\mathrm{3}}^{-}$ detected at −60 m∕Q) is of comparable magnitude to the ${\mathrm{O}}_{\mathrm{2}}^{-}$ reagent ion signal as shown in Fig. 1. High analyte concentrations (> 5 ppbv) have been shown previously to result in nonlinear calibration curves for unnormalized signals (Bertram et al., 2011; Veres et al., 2008). In our system we do not observe nonlinearity in the normalized O₃ calibration for our highest-concentration calibration point of 80 ppbv despite the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ signal being larger than the ${\mathrm{O}}_{\mathrm{2}}^{-}$ reagent ion (9×10⁶ and 6×10⁶ cps, respectively). The electron affinity (EA) of carbonate is from 3.26 (Hunton et al., 1985) to > 3.34 eV (Snodgrass et al., 1990) and is significantly higher than that of oxygen (EA 0.45 eV), making it unlikely that carbonate is involved in charge transfer reactions when excess ${\mathrm{O}}_{\mathrm{2}}^{-}$ is present. At high O₃ concentrations, the reagent ion signal magnitude is reduced, which necessitates normalizing sensitivities to the 1×10⁶ cps of reagent ion signal before quantification. For NO₂ (EA 2.27 eV), the normalized sensitivity showed no dependence on O₃ concentrations from 0 to 80 ppbv. Carbonate reagent ion chemistry has been utilized for detection of HNO₃ and H₂O₂ via adduct formation, raising an additional concern about potential secondary ion chemistry (Reiner et al., 1998). In laboratory calibrations, shown in Fig. S7, introduction of 0 to 40 ppb H₂O₂ resulted in the titration of the O₃ signal of 0.06 ppbv per parts per billion by volume H₂O₂. H₂O₂ was detected as an adduct with ${\mathrm{O}}_{\mathrm{2}}^{-}$ and not ${\mathrm{CO}}_{\mathrm{3}}^{-}$, indicating that ${\mathrm{O}}_{\mathrm{2}}^{-}$ reagent ion chemistry is more favorable despite high ${\mathrm{CO}}_{\mathrm{3}}^{-}$ signal intensity. The Ox-CIMS O₃ measurement also compared well (R²=0.99) against an EPA Air Quality System (AQS) O₃ monitor over 1 month of ambient sampling where H₂O₂ and HNO₃ concentrations both exceeded 5 ppbv at times (see Sect. 3.1 for further discussion of field intercomparison), further supporting the ${\mathrm{CO}}_{\mathrm{3}}^{-}$ detection product as a robust indicator of O₃ in complex sampling environments.

Ab initio calculations of the binding enthalpies of ${\mathrm{O}}_{\mathrm{2}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{-}$ reagent ions with H₂O, HNO₃, H₂O₂, and CH₃OOH were performed with the MP2/aug-cc-pVDZ-PP theory and basis set in order to assess the relative favorability of adduct formation between ${\mathrm{O}}_{\mathrm{2}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{-}$. Adduct formation with ${\mathrm{O}}_{\mathrm{2}}^{-}$ was favorable relative to ${\mathrm{CO}}_{\mathrm{3}}^{-}$ by 2.5 to 17 kcal mol⁻¹ for all analytes that were calculated. All calculated binding enthalpy values are listed in Table S2.

2.10 Short- and long-term precision

Short-term precision of the instrument was assessed by calculating the normalized difference between adjacent 10 Hz data points over a 27 min sampling period of a constant ambient analyte concentration via Eq. (2).

$$\begin{array}{}\text{(2)}& \mathrm{NAD}={\displaystyle \frac{{\left[mX\right]}_n-{\left[X\right]}_{n-\mathrm{1}}}{\sqrt{{\left[X\right]}_n{\left[X\right]}_{n-\mathrm{1}}}}}\end{array}$$

The standard deviation of the Gaussian fit of the distribution of normalized adjacent differences (NADs) is a direct measure of the short-term instrument precision (Bertram et al., 2011). The 1σ precision from the NAD distribution for 10 Hz sampling of 38 ppbv ozone is 0.74 % (Fig. 7). The 10 Hz precision for sampling of 2.3 ppbv NO₂ is 1.1 % The short-term precision for both analytes was larger than expected if the noise was driven by counting noise alone (10 Hz counting noise limit for O₃ and NO₂ at the concentrations used above are 0.12 % and 0.63 %, respectively), indicating that other potential points of optimization in the instrument configuration are required to further improve short-term precision. Notably, the observed noise source appears to be white noise given the Gaussian distribution of the NAD (Thornton et al., 2002b).

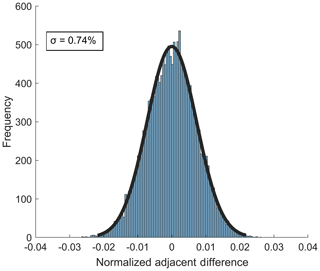
Figure 7 Distribution of normalized adjacent differences measured at 10 Hz during a stable 27 min ambient sampling period of 38 ppbv O₃ from Scripps Pier. The 1σ value of the distribution gives an upper limit of instrument precision of 0.74 %.

Short-term precision was assessed as a function of count rate by calculating the NAD for all masses in the spectrum over a stable 27 min sampling period for both 1 and 10 Hz data averaging. From this assessment, precision was observed to improve approximately linearly with log–log scaling for count rates between 1×10³ and 1×10⁶ cps (Fig. S8) as expected in the case where counting noise drives instrument precision. Above 1×10⁶ cps there is an apparent asymptote where precision no longer improves with count rate. The counting-noise-limited 10 Hz precision for 10⁶ and 10⁷ cps are 0.32 % and 0.1 %, respectively, while the measured values were 0.75 and 2 %. The counting-noise-limited precision is calculated as $\sqrt{N/N}$, where N is the number of counts during the integration time. This precision limit could be driven by an uncharacterized source of white noise in the instrument, including mass flow controller (MFC) drift, IMR turbulence, ion optic voltage drift, and pump drift. Measurement precision of O₃ and NO₂ could be improved by a factor of 5 and 2, respectively, if this noncounting noise source of white noise was eliminated.

In theory, detection limits can be improved by signal averaging to a lower time resolution than the 10 Hz save rate. Signal-to-noise ratios are expected to improve with the square root of the integration time. At longer timescales, factors including instrument drift become significant, creating a limit on the upper end of averaging time which optimizes signal-to-noise ratios. This was assessed quantitatively by calculation of the Allan variance as shown in Fig. S6 (Werle et al., 1993).

3 Field results and discussion

3.1 Ozone field calibration and intercomparison

Performance of the Ox-CIMS was compared against a colocated EPA Air Quality System (AQS) O₃ monitor (Thermo Fisher 49i, AQS ID 17-097-1007) over 1 month of ambient sampling during the Lake Michigan Ozone Study 2017 (LMOS 2017) in Zion, Illinois (Vermeuel et al., 2019). A regression analysis between the two instruments at 1 min averaging showed strong agreement (R²=0.99) as shown in Fig. 8. Ox-CIMS concentrations were averaged to 1 ppbv bins which was the output data resolution of the EPA data logger system for the Thermo Fisher 49i. Error bars are the 1σ standard deviation of each Ox-CIMS bin average. A near one-to-one agreement (slope of 0.99) between instruments lends confidence to the calibration, baselining, and long-term stability of the Ox-CIMS. The Ox-CIMS was located on the roof of a trailer (approx. 5 m above ground) and sampled through a 0.7 m long, 0.925 cm i.d. PFA inlet. The inlet was pumped at a flow rate of 18–20 slpm from which the Ox-CIMS subsampled at 1.5 slpm. Temperature and RH were recorded inline downstream of the subsampling point. The Ox-CIMS sampling point was approximately 10 m horizontally from the Thermo Fisher 49i, and both instruments sampled at approximately equal heights. Instrument backgrounds of the Ox-CIMS were determined every 70 min by overflowing the inlet with dry UHP N₂. Calibration factors were determined by the infield continuous addition of a C-13 isotopically labeled formic acid standard to the tip of the inlet. Laboratory calibrations of the Ox-CIMS to formic acid and O₃ as a function of specific humidity were determined immediately pre- and postcampaign and were used to calculate a humidity-dependent sensitivity of O₃ relative to formic acid. That relative sensitivity was then used to determine the infield sensitivity to O₃ by scaling field sensitivities of formic acid from the continuous additions. Full details of this deployment and the calibration methods are described in Vermeuel et al. (2019). The EPA O₃ monitor shows a persistent high bias at low O₃ concentrations (< 10 ppbv) relative to the Ox-CIMS. This discrepancy could arise from known interferences from water, mercury, and other species in the 254 nm UV absorbance detection of ozone (Kleindienst et al., 1993).

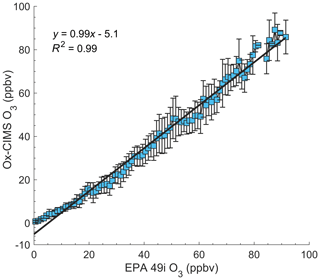
Figure 8 Regression of 1 min average O₃ mixing ratios from the Ox-CIMS against an EPA O₃ monitor (Thermo Fisher 49i) binned to 1 ppbv over 4 weeks of ambient sampling in Zion, Illinois, in May–June 2017. The solid black line is the linear least-squares regression. Error bars represent the standard deviation of each bin. Instrument agreement is strong for O₃, greater than 10 ppbv, with an apparent bias in one or both instruments below 10 ppbv.

3.2 Eddy covariance experiment overview

The Ox-CIMS was deployed to the 330 m long Ellen Browning Scripps Memorial Pier (hereafter referred to as Scripps Pier) at the Scripps Institution of Oceanography (32^∘52.0^′ N, 117^∘15.4^′ W) during July and August 2018 for EC measurements of O₃ vertical fluxes. This site has been used regularly for EC flux observations by our group and others (Ikawa and Oechel, 2015; Kim et al., 2014; Porter et al., 2018). The Ox-CIMS was housed in a temperature-controlled trailer at the end of the pier. The Ox-CIMS sampled from a 20 m long PFA inlet manifold with the intake point colocated with a Gill HS-50 sonic anemometer which recorded three-dimensional winds sampling at 10 Hz. The Ox-CIMS inlet and sonic anemometer were mounted on a 6.1 m long boom that extended beyond the end of the pier to minimize flow distortions. The inlet height was 13 m above the mean lower low-tide level. The Ox-CIMS inlet was located 8 cm below the sonic anemometer with a 0 cm horizontal displacement. The inlet manifold consisted of a 0.64 cm i.d. sampling line, a 0.64 cm i.d. overflow line, and a 0.47 cm i.d. calibration line all made of PFA. The inlet sample line was pumped at 18–23 slpm (Reynolds number 3860–4940) by a dry scroll pump (SH-110, Agilent) to ensure a fast time response and maintain turbulent flow. Flow rates in the inlet sample line were recorded by a mass flow meter but were not actively controlled. The inlet manifold, including calibration and overflow lines, was held at 40 ^∘C via a single resistively coupled circuit along the length of the manifold and controlled by a PID controller (Omega, model CNi16). The Ox-CIMS front block and IMR were held at 35 ^∘C. The Ox-CIMS subsampled 1.5 slpm from this inlet manifold through a critical orifice into the IMR. Ambient humidity and temperature were also recorded inline downstream of the subsampling point.

3.2.1 Calibration

Instrument sensitivity was assessed by the standard addition of a C-13 isotopically labeled formic acid standard for 3 min every 35 min at the ambient end of the inlet manifold. Ozone mixing ratios were determined by scaling the humidity-dependent sensitivity of O₃ from pre- and postcampaign calibrations to the field calibrations of C-13 formic acid. Ambient O₃ was also measured at a 10 s time resolution with a 2B Technologies personal ozone monitor (POM). The POM had a separate 10 m long, 0.47 cm i.d. PFA sampling line located 12 m from the Ox-CIMS inlet manifold and sonic anemometer. The POM was used as an independent verification of the Ox-CIMS measurement and was not used for calibration.

3.2.2 Backgrounds and inlet residence time

Instrument backgrounds were determined every 35 min by overflowing the entire inlet manifold with dry UHP N₂. Background and ambient count rates were first converted to concentrations using the laboratory-determined humidity-dependent sensitivities for O₃ and NO₂ scaled to the C-13 formic acid standard-addition sensitivity. Background concentrations of O₃ and NO₂ from before and after each 30 min ambient sampling period were interpolated over the ambient sampling period which was then subtracted from each 10 Hz concentration data point to obtain a background-corrected time series. Background concentrations of O₃ had a mean 1.5 ppbv and a drift of 1 % between adjacent background periods, determined by the distribution of the NAD of the mean background concentrations.

The signal response of O₃ during dry N₂ overflows were fit to an exponential decay function to characterize inlet gas response times (Ellis et al., 2010). Best-fit estimates for decay time constants for O₃ across overflow periods were from 0.2 to 0.44 s. NO₂ decay responses were fit to a biexponential decay to characterize inlet evacuation time (τ₁) and wall interaction times (τ₂; Ellis et al., 2010). τ₂ for NO₂ was determined to be approximately 3.2 s. This suggests a potential interference at the NO₂ peak, as NO₂ is expected to have minimal wall equilibration, similar to O₃. NO₂ also shows a continually elevated signal during overflow periods suggesting off-gassing from inlet or instrument surfaces. The cause of this slow NO₂ decay and elevated background is not clear but could be from degradation of nitric acid or nitrate containing aerosol on the instrument surfaces.

The instrument response time (τ_r) for O₃ can be calculated during zeroing periods as the time required for the signal to fall to e⁻¹ of its initial value. The response time of the instrument was calculated for each overflow period during field sampling, with a mean value of 0.28 s. The cutoff frequency (f_cut) of the instrument is defined as the frequency where the signal is attenuated by a factor of ${\sqrt{\mathrm{2}}}^{-\mathrm{1}}$ (Bariteau et al., 2010). The cutoff frequency can also be calculated from τ_r according to Eq. (3).

$$\begin{array}{}\text{(3)}& f_{\mathrm{cut}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{\mathit{\tau }}_r}}\end{array}$$

The calculated f_cut from the measured mean response time was 0.57 Hz. This value suggests that minimal attenuation in the flux signal (cospectra) should be apparent at frequencies of less than 0.57 Hz. The instrument response time and thus cutoff frequency are functions of the flow rate and sampling line volume. The flow rate of 18–23 slpm was the maximum achievable with the tubing and pumping configuration used here but could be improved in future to minimize tubing interactions and shift f_cut towards higher frequencies.

Table 2 Overview of flux and concentration measurements of O₃ and NO₂ from Scripps Pier. Concentration ranges are reported for all periods of onshore winds. Flux results are reported only for final quality-controlled flux periods Ozone mean deposition velocity (v_d) was well resolved from the campaign ensemble average LOD of 0.0027 cm s⁻¹. Reported v_d LOD is the ensemble mean of the LOD determined by the root-mean-square error (RMSE) method at long lag times for each 27 min flux period. Of the quality-controlled flux periods, 24 % fell below the campaign ensemble LOD. Deposition velocity of NO₂ across the air–sea interface was expected to be small (< 0.002 cm s⁻¹) and was consistently below the LOD of our instrument so no values are reported here.

3.2.3 Eddy covariance flux method

The transfer of trace gases across the air–sea interface is a complex function of both atmospheric and oceanic processes, where gas exchange is controlled by turbulence in the atmospheric and water boundary layers, molecular diffusion in the interfacial regions surrounding the air–water interface, and the solubility and chemical reactivity of the gas in the molecular sublayer. The flux (F) of trace gas across the interface is described by Eq. (4), as a function of both the gas-phase (C_g) and liquid-phase (C_l) concentrations and the dimensionless gas-over-liquid Henry's law constant (H), where K_t, the total transfer velocity for the gas (with units cm s⁻¹), encompasses all of the chemical and physical processes that govern air–sea gas exchange. Surface chemical reactivity terms of the gas exchange rate are incorporated into the K_t term.

$$\begin{array}{}\text{(4)}& F=-K_{\mathrm{t}}\left(C_{\mathrm{g}}-H{C}_{\mathrm{l}}\right)\end{array}$$

Trace gas flux (F) can be measured with the well-established eddy covariance (EC) technique where flux is defined as the time average of the instantaneous covariances from the mean of vertical wind (w) and the scalar magnitude (here O₃) shown in Eq. (5). Overbars are means, and primes are the instantaneous variance from the mean. Here N is the total number of 10 Hz data points during the 27 min flux averaging period.

$$\begin{array}{}\text{(5)}& {\displaystyle }F={\displaystyle \frac{\mathrm{1}}{N}}{\sum }_{i=\mathrm{1}}^N\left(w_i-\stackrel{\mathrm{‾}}{w}\right)\left({\mathrm{O}}_{\mathrm{3},i}-\stackrel{\mathrm{‾}}{{\mathrm{O}}_{\mathrm{3}}}\right)=\langle w^{\prime }{\mathrm{O}}_{\mathrm{3}}^{\prime }\rangle \text{(6)}& {\displaystyle }{v}_{\mathrm{d}}={\displaystyle \frac{F}{\stackrel{\mathrm{‾}}{C_{\mathrm{g}}}}}\end{array}$$

For purely depositing species where the water-side concentration is negligible, C_l and H can be neglected in Eq. (4) and K_t can be reformulated into a deposition velocity (v_d) calculated according to Eq. (6), where $\stackrel{\mathrm{‾}}{C_{\mathrm{g}}}$ is the mean gas-phase mixing ratio during the flux averaging period. A summary of concentration and flux results for the full deployment period are given in Table 2.

3.3 General data corrections

Several standard eddy covariance data filters and quality control checks were applied before analysis. General filters included

1. wind sector, only periods of mean onshore flow (true wind direction 200–360^∘) were used;

2. friction velocity, a friction velocity (U_∗) threshold was applied to reject periods of low-shear-driven turbulence (Barr et al., 2013) described further below;

3. stationarity, each 27 min flux period was divided into five even nonoverlapping subperiods; flux periods were rejected if any of the subperiods differed by more than 40 % (Foken and Wichura, 1996).

The applied U_∗ filter was determined by comparing the observed U_∗ values to U_∗ calculated with the NOAA COARE bulk flux v3.6 algorithm (Fairall et al., 2011). COARE U_∗ was calculated using measured meteorology including wind speed, sea surface temperature, air temperature, and relative humidity. Flux periods were rejected if the observed U_∗ differed from the calculated U_∗ by more than 50 %. The stress relationship of wind speed to U_∗is well understood over the ocean. Fixed U_∗ filters of ca. 0.2 m s⁻¹ are used frequently as a default in terrestrial flux studies but would reject nearly all observation periods in this study. The observed friction velocities are consistent with other marine flux studies where surface roughness lengths are significantly smaller than over terrestrial surfaces (Porter et al., 2018). Methods of determining site specific U_∗ thresholds typically require long-term data series which were not available here (Papale et al., 2006). Papale et al. (2006) applied a minimum U_∗ threshold of 0.1 m s⁻¹ for forest sites and 0.01 m s⁻¹ for short vegetation sites where typical U_∗ values are lower. The selected U_∗ filter rejects an additional 44 % of the flux periods remaining after the wind direction filter. The stationarity criterion rejected a further 100 flux periods, potentially driven by periods of activity on the pier driving changes in the sampled O₃. Outliers in v_d(O₃) and the flux limit of detection were determined and removed for points that were 3 scaled median absolute deviations from the median. This outlier filter removed an additional 16 data points. After the wind direction filter and all quality control filters were applied, 73 % of flux periods were rejected leaving 246 quality-controlled flux periods. Eddy covariance flux values were calculated using 27 min time windows. The O₃ time series was detrended with a linear function prior to the flux calculation. The O₃ and vertical wind data were despiked using a mean absolute deviation filter before the eddy covariance flux calculation following Mauder et al. (2013).

3.3.1 Planar-fit wind coordinate rotation

Coordinate rotation of the u, v, and w wind components was performed by the planar-fit method to remove unintentional tilts in the sonic mounting and account for local flow distortions (Wilczak et al., 2001). Briefly, the mean u, v, and w wind components and the stress tensor were determined for each 15 min onshore flow period during the full campaign. A linear regression was used to find the best fit of a plane with a coordinate system where the z axis is perpendicular to the mean streamline. Individual 27 min flux periods are then rotated such that the x axis is along the mean wind and $\stackrel{\mathrm{‾}}{v}=\mathrm{0}$. Vertical wind velocity ($\stackrel{\mathrm{‾}}{w}$) in any individual rotation period may be nonzero due to mesoscale motions, but $\stackrel{\mathrm{‾}}{w}$ for the full campaign is zero. The residual mean vertical velocity in any individual rotation period is subtracted out, so it does not impact the Reynolds averaging.

3.3.2 Lag time shift

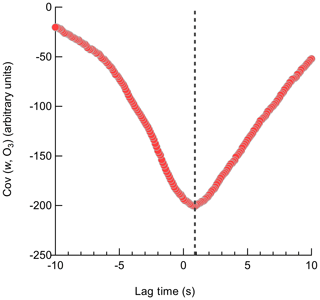
The Ox-CIMS signal is delayed relative to the sonic anemometer due to transit time in the inlet line which must be accounted for before calculating the covariance between the vertical wind and analyte concentration. The cross-covariance of the two time series was first calculated within a ±5 s window to determine the lag time of the Ox-CIMS and synchronize with the anemometer. The volumetric evacuation time of the inlet is 1.65 to 2.1 s for the inlet volume and flow rates of 18 to 23 slpm used in this study. Following the method and terminology outlined in Langford et al. (2015), the position of the maximum (MAX) of the cross-covariance is taken as the lag time needed to align the vertical wind and analyte concentration for that flux period. A representative lag time determination with a larger lag window (±10 s) using the MAX method is shown in Fig. 10. In low signal-to-noise (SNR) data, the use of the MAX leads to high variability in the determined lag time caused by uncertainty in the position of the peak in the cross-covariance. This results in a systematic high bias in the absolute magnitude of the resulting flux. The position of the maximum of a centered running median (AVG) function of the cross-covariance is an alternative method to determine lag time with less expected bias for low SNR data (Langford et al., 2015; Taipale et al., 2010). Lag times for each O₃ flux period determined by the MAX and a 10-point AVG method showed reasonable agreement, with a campaign average lag time from the MAX with a mean of 1.0 s and the AVG at 0.7 s (Fig. S9). This agreement suggests that a clear peak in the cross-covariance was present for most flux periods leading to a convergence of the two methods. This lag time also shows agreement with the inlet response time of 0.9 s determined during dry N₂ overflows. Due to the convergence of the determined lag times around a central value, a prescribed lag time of 0.9 s was used for all reported v_d(O₃) values. A prescribed lag time has the least bias towards extreme values caused by noise, provided that the true lag time is known well (Langford et al., 2015). Deposition velocities were then recalculated with the prescribed lag time of 0.9 s and with the MAX and AVG method over a narrower lag window of ±3 s which is expected to be a physically reasonable range for the flow rate and inlet line volume. The mean v_d(O₃) using the prescribed, MAX, and AVG lag times were 0.013, 0.012, and 0.012 cm s⁻¹, respectively, suggesting the campaign mean value was relatively insensitive to the lag time method.

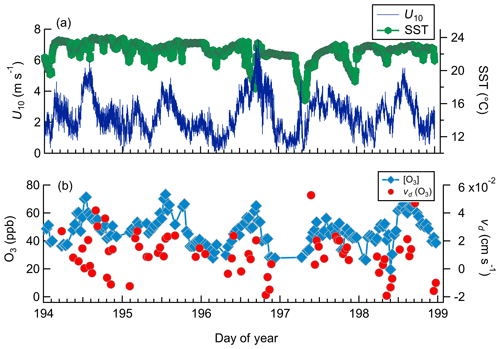
Figure 9 Observed meteorology and O₃ mixing ratio and deposition velocities for day-of-year 194–199 from Scripps Pier. (a) Horizontal wind speed (U₁₀) and sea surface temperature (SST). (b) O₃ mixing ratios and v_d(O₃).

Figure 10 Lag time determination for an individual 27 min O₃ flux averaging period. The lag time for this flux period is determined from the maximum of the covariance to be 0.9 s which compares reasonably with the volumetric evacuation time of the inlet of 1.7 to 2.1 s.

3.4 Cospectra and ogives

The frequency-weighted cospectrum of O₃ with w^′ has a well-characterized form with exhibited dependence on wind speed and measuring height (Kaimal et al., 1972). Comparison of the observed cospectra shape against the idealized Kaimal cospectra is useful for validating that the observed signal was not significantly attenuated at low or high frequencies. Cospectral averaging is performed by binning frequency into 50 evenly log-spaced bins and normalizing the integrated cospectra to 1. The integral of the unnormalized cospectra is the flux for that observation period. The mean wind speed binned cospectra of sensible heat and O₃ appear to match well with the idealized Kaimal cospectra for an unstable boundary layer at sampling height z=13 m (Fig. 11).

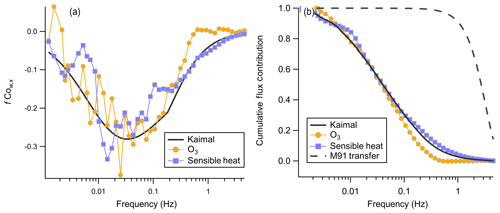
Figure 11 (a) Mean binned frequency-weighted cospectra O₃ and sensible heat flux with vertical wind from the average of two consecutive flux periods from 14:10 to 15:20 local time on 20 July. The Kaimal trace is the idealized cospectra Kaimal et al. (1972) for a mean wind speed of 4.4 m s⁻¹ and an unstable atmosphere. The sensible heat trace is inverted, and the observed net sensible heat flux was positive for this period. (b) Corresponding ogives for cospectra shown in (a). The M91 transfer trace is the calculated transfer function for turbulent attenuation in a tube from Massman (1991).

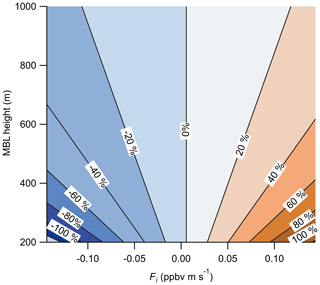
Figure 12 Calculated percent error in the measured O₃ surface flux due to entrainment from the free troposphere as a function of the MBL height and the entrainment flux (F_i). Entrainment flux is the product of the free-troposphere-to-boundary-layer concentration gradient (ΔC) and the entrainment velocity (w_e). Calculation of the percent error used the Scripps Pier measuring height of 13 m and mean surface flux of $-\mathrm{5.6}\times {\mathrm{10}}^{-\mathrm{3}}$ ppbv m s⁻¹.

The ogive is the normalized cumulative distribution of the cospectra, which is used to validate both that no high-frequency attenuation is present and that the flux averaging time is sufficiently long that all frequencies contributing to the flux are captured. Figure 11 shows the averaged cospectra and ogives for O₃ and sensible heat flux from the average of two flux averaging periods 14:10–15:20 local time on 20 July. The asymptote to 1 at low frequencies validates that the 27 min flux averaging time was sufficiently long for this site to capture the largest flux-carrying eddies. High pumping rates in the sampling line ensured that turbulent flow was always maintained in the line (Reynolds number 3860–4940). Higher Reynolds numbers in the turbulent regime lead to smaller high-frequency attenuation (Massman, 1991). The overlap of the idealized Kaimal curve and the observed sensible heat and O₃ ogives suggests that high-frequency attenuation in the sampling line is minimal above approximately 0.4 Hz, consistent with our calculated f_cut of 0.57 Hz. We calculate the high-frequency correction transfer function for turbulent attenuation in a tube from Massman (1991) as a constraint, which is shown in Fig. 11b. This transfer function shows attenuation primarily above 1 Hz and is not sufficient to describe the observed attenuation above 0.4 Hz. This implies that the attenuation observed cannot be explained only as turbulent smearing in the inlet and that other wall interactions are likely present.

Due to the small magnitude of the O₃ EC flux there is a low signal-to-noise ratio in the cospectra at a high frequency for many of the flux averaging periods. This makes application of cospectra-based correction factors challenging and likely to introduce added variance in the signal. We therefore apply an attenuation correction factor following Bariteau et al. (2010). First we calculate the idealized unattenuated Kaimal cospectra (C_{wx_k}) (Eq. 7) for each flux period and then apply frequency attenuation to that cospectra by applying a low-pass filter function (H(f)) characterized by τ_c (Eq. 8). The ratio of the flux of the unattenuated (F_raw) to attenuated (F_att) cospectra is then taken as the correction factor (A_f, Eq. 9) to apply to the observed O₃ flux (Eq. 10). n is the surface layer normalized frequency defined as $n=fz/U$, where z is the measurement height and U is the horizontal wind speed. $F_{{\mathrm{O}}_{\mathrm{3}},\mathrm{corr}}$ is the attenuation-corrected O₃ flux and $F_{{\mathrm{O}}_{\mathrm{3}},\mathrm{obs}}$ is the original measured flux. This approach has the benefit of applying a single correction factor to the total flux rather than frequency-dependent corrections which might serve to amplify noise at high frequencies. The net impact of this correction factor was an increase in the campaign mean v_d(O₃) of 4 %.

$$\begin{array}{}\text{(7)}& {\displaystyle }{C}_{wx\mathit{\_}k}={\displaystyle \frac{\mathrm{11}n}{{\left(\mathrm{1}+\mathrm{11.3}n\right)}^{\mathrm{7}/\mathrm{4}}}}\text{(8)}& {\displaystyle }H\left(f\right)={\left[\mathrm{1}+{\left(\mathrm{2}\mathit{\pi }f{\mathit{\tau }}_c\right)}^{\mathrm{2}}\right]}^{-\mathrm{1}}\text{(9)}& {\displaystyle }{A}_{\mathrm{f}}={\displaystyle \frac{F_{\mathrm{raw}}}{F_{\mathrm{att}}}}{\displaystyle \frac{{\int }_{{\mathrm{0}}_n^f}{C}_{w{x}_k}\left(f\right)\mathrm{d}f}{{\int }_{{\mathrm{0}}_n^f}{C}_{w{x}_k}\left(f\right){\left[H\left(f\right)\right]}^{\mathrm{1}/\mathrm{2}}\mathrm{d}f}}\text{(10)}& {\displaystyle }{F}_{{\mathrm{O}}_{\mathrm{3}},\mathrm{corr}}=A_{\mathrm{f}}{F}_{{\mathrm{O}}_{\mathrm{3}},\mathrm{obs}}\end{array}$$

We also calculate the attenuated flux from the model of Horst (1997), shown in Eq. (11), for a response time (τ_c) of 0.0.28 s and a wind speed of 3 m s⁻¹ to be 6 %. The general agreement of the Horst and Bariteau attenuation correction factors indicates that the applied correction is reasonable.

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{F_{\mathrm{m}}}{F_x}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\left(\mathrm{2}\mathit{\pi }{n}_m{\mathit{\tau }}_{c}U/z\right)}^{\mathit{\alpha }}}},\end{array}$$

where F_m∕F_x is the ratio of the measured flux to the unattenuated flux, U is wind speed, z is measurement height, and n_m and α are scaling factors for an unstable boundary layer taken as 0.085 and seven-eighths, respectively.

3.5 Uncertainty and flux limit of detection

Variance in the atmospheric O₃ signal was estimated by calculating the autocovariance of the signal during a 27 min flux averaging period (Fig. S11). Uncorrelated white noise only contributes to the first point in the autocovariance spectrum, while autocovariance at longer time shifts represents real atmospheric variance or correlated instrument drift (Blomquist et al., 2010; Langford et al., 2015). For the analyzed period, white noise is typically 45 % to 65 % of the total variance and atmospheric variance is 35 % to 55 %. This corresponds to a standard deviation from white noise ${\mathit{\sigma }}_{{\mathrm{O}}_{\mathrm{3}},\mathrm{noise}}$ of 0.4 ppbv.

The error in each flux averaging period (LOD_σ) can be determined by taking the standard deviation of the cross-covariance between the vertical wind speed and mass spectrometer signal at lag times significantly longer than the calculated true lag time (Spirig et al., 2005; Wienhold et al., 1995). The random flux error is determined using lag windows of −150 to −180 and 150 to 180 s, which are significantly larger than the true lag time from sensor separation of 0.9 s as shown in Fig. S12. The selection of the −150 to −180 and 150 to 180 s lag windows is somewhat arbitrary and may still capture organized atmospheric structure that persists over long time periods. We also calculate the root-mean-square deviation (LOD_RMSE) of the cross-covariance over the same lag windows as proposed by Langford et al. (2015), which captures the variance in the cross-covariance in those regions but also accounts for long-term offsets from zero in the cross-covariance. The resulting error from the LOD_σ and LOD_RMSE methods showed good correlation (Fig. S13), with periods where the LOD_RMSE error is larger. We apply the RMSE method to our reported flux error determination. The final deposition velocity limit of detection was determined for each 27 min flux averaging period by multiplying the LOD_RMSE error by 1.96 to give the flux limit of detection at the 95 % confidence level. The flux error was then divided by the mean O₃ concentration for that averaging period to convert from flux to deposition velocity units. The campaign ensemble flux LOD_RMSE was 0.0027 cm s⁻¹, calculated using Eq. (12) following Langford et al. (2015). A total of 59 out of 246 (24 %) flux periods had deposition velocities below the campaign ensemble LOD. These values are still included in the reported mean v_d(O₃).

$$\begin{array}{}\text{(12)}& \stackrel{\mathrm{‾}}{\mathrm{LOD}}={\displaystyle \frac{\mathrm{1}}{N}}{\sum }_{i=\mathrm{1}}^N{\mathrm{LOD}}^{\mathrm{2}}\end{array}$$

3.6 Density fluctuation corrections

The Ox-CIMS measures O₃ as the apparent mixing ratio relative to moist air, as is true of all CIMS-based measurements, which means fluctuations in the density of air due to changes in temperature, pressure, and humidity could introduce a bias into the EC flux measurement (Webb et al., 1980). The temperature and pressure in the Ox-CIMS and sampling lines were both actively controlled during sampling, making density fluctuations from those sources negligible. The long (20 m) inlet sampling line used likely also dampened a substantial portion of the water vapor flux. This has been demonstrated in an EC study utilizing a closed path H₂O sensor for EC flux measurements (through an 18 m long, 0.635 cm i.d. inlet, pumped at 18 slpm, comparable to the inlet used in this study) which showed complete attenuation above 0.1 Hz and overall attenuation of ∼80 % of the H₂O (latent heat) flux (Yang et al., 2016). However, without a direct measure of water vapor fluctuations colocated with the Ox-CIMS, this is difficult to definitively rule out in our measurement. We therefore calculate a conservative estimate of this correction factor from Eq. (45b) in Webb et al. (1980), assuming a latent heat flux of 50 W m⁻² and neglecting the sensible heat term which is removed by active heating of the inlet. For a specific humidity of 12 g kg⁻¹, a temperature of 293 K, a pressure of 1 atm, and an O₃ mixing ratio of 40 ppbv, we calculate a flux correction term of 2.6×10⁹ molecules cm⁻² s⁻¹, which is 20 % of our mean measured flux of $-\mathrm{1.3}\times {\mathrm{10}}^{\mathrm{10}}$ molecules cm⁻² s⁻¹. We expect that the actual density correction for our instrument is much smaller given that water vapor fluctuations were likely dampened in the inlet line and the latent heat flux used in the calculation is high (50 W m⁻²). Due to the uncertainty in this correction term for our instrument, we do not add it to our measured flux values and instead use the calculated value above as a conservative constraint on the magnitude. The addition of a Nafion dryer to the inlet has been successfully implemented in other O₃ flux instruments to fully remove water fluctuations and will be used in future deployments of the Ox-CIMS (Bariteau et al., 2010).

3.7 Flux divergence

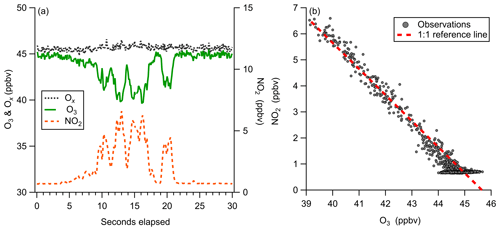
Figure 13 Observations of ozone titration by NO emissions from a boat engine near Scripps Pier. (a) 10 Hz time series of O₃, NO₂, and O_x (O₃+NO₂), demonstrating ability to capture transient titration events. (b) Regression of O₃ and NO₂ plotted with a reference line of slope −1, showing conservation of total O_x at 10 Hz during a NO titration event.

3.7.1 Surface NO emissions

The observed dry deposition velocity of ozone is potentially biased by simultaneous air–sea exchange of nitric oxide (NO). NO is expected to be emitted from the ocean on the order of 1×10⁸ molecules cm⁻² s⁻¹ with a dependence on dissolved surface nitrate and solar irradiance (Zafiriou and McFarland, 1981). This NO source near the surface will cause titration of O₃ to NO₂ resulting in a positive bias for the observed v_d(O₃). Assuming a maximum NO emission flux of 5×10⁸ molecules cm⁻² s⁻¹ and that all NO reacts with O₃ before being advected to the sensor height, the resulting O₃ flux bias would be $-\mathrm{5}\times {\mathrm{10}}^{\mathrm{8}}$ molecules cm⁻² s⁻¹. Our mean case of 40 ppbv O₃ and v_d (O₃) of 0.013 cm s⁻¹ corresponds to a flux of $-\mathrm{1.3}\times {\mathrm{10}}^{\mathrm{10}}$ molecules cm⁻² s⁻¹. Therefore, the resulting bias in observed v_d(O₃) from NO emissions is 3.8 % or $\mathrm{4.9}\times {\mathrm{10}}^{-\mathrm{4}}$ cm s⁻¹. This value is an upper limit for expected ocean NO emissions and is well within the uncertainty of the observed v_d(O₃). There is also potential for short-term anthropogenic emissions of NO (such as from a boat engine passing by the sensor) to create a flux divergence term. We expect that the combination of signal despiking and the flux stationarity criterion described in Sect. 3.3 will minimize the impact of this potential divergence term. Despiking will remove most short-term (< 1 s) emission events, and the stationarity criterion will filter out any period where longer-term titration events cause large changes in the observed flux within a flux measurement period.

3.7.2 Free-troposphere entrainment

The entrainment of O₃-enhanced or O₃-depleted air in the free troposphere to the marine boundary layer (MBL) creates a potential flux gradient that will contribute to the measured flux values at the near-surface measurement height (z_o) of 13 m. Lenschow et al. (1982) presented aircraft observations of O₃ deposition over the Gulf of Mexico at heights of 15, 60, and 325 m which showed a strong flux gradient term driven by entrainment from the free troposphere. The boundary layer height (z_i) during those flights was approximately 1.2 km, suggesting a strong flux gradient was present even within the surface layer (approximated as the lowest 10 % of the boundary layer). The magnitude of this flux gradient depends on the magnitude of the O₃ concentration gradient (ΔC) and the entrainment velocity (w_e) of air from the free troposphere into the MBL. Faloona et al. (2005) reported entrainment velocities from 0.12 to 0.72 cm s⁻¹ and an enhancement in O₃ (ΔC) of 20 ppbv in the free troposphere relative to the boundary layer in the summertime eastern subtropical Pacific. Using those values and Eqs. (13) and (14) below, we calculate the percent fractional error from entrainment on the observed flux for a range of reasonable ΔC and w_e as shown in Fig. 12 (Blomquist et al., 2010).

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\mathrm{\Delta }{F}_{\mathrm{0},\mathrm{est}}}{F_{\mathrm{0}}}}={\displaystyle \frac{z}{z_i}}\left({\displaystyle \frac{F_i}{F_{\mathrm{0}}}}-\mathrm{1}\right),\text{(14)}& {\displaystyle }{F}_i=w_{\mathrm{e}}\mathrm{\Delta }C,\end{array}$$

where z_i is the boundary layer height, z is the measurement height, and F_i and F₀ are the entrainment flux and surface flux, respectively. We use the Scripps Pier measurement height (z)=13 m, mean surface flux ($F_o)=-\mathrm{5.2}\times {\mathrm{10}}^{-\mathrm{3}}$ ppbv m s⁻¹ (from v_d=0.013 cm s⁻¹ and [O₃] =40 ppbv), and an O₃ mixing ratio gradient (ΔC) from −20 to +20 ppbv in the free troposphere relative to the boundary layer. The resulting fractional error in our observed mean surface flux from Scripps Pier using the values from Faloona et al. (2005; ΔC of +20 ppbv, MBL height of 800 m) is 4.4 % for w_e= 0.12 and 33 % for 0.72 cm s⁻¹. This entrainment flux error is clearly significant for marine O₃ flux measurements assuming there is a gradient of O₃ in the free troposphere relative to the boundary layer. This entrainment flux error is independent of the surface flux instrument measurement error and adds a systematic bias into the surface flux measurement. This calculation also makes clear that marine O₃ measurements should be made as close to the surface as possible and that the O₃ concentration gradient and entrainment rate should be explicitly measured if possible. We do not have an explicit measure of ΔC, w_e, or the MBL height, so we tentatively assign an entrainment error of up to 33 % from the maximum values of those parameters reported in Faloona et al. (2005). We emphasize this source of uncertainty is independent of the O₃ sensor and is a systematic bias that should be considered in all O₃ air–sea exchange determinations.

4 Fast NO₂ measurements, eddy covariance, and O₃ titration

Discussion of EC flux results has been limited to O₃ because ocean–atmosphere exchange of NO₂ is expected to be small and below the limit of detection of our instrument. The potential flux divergence from the reaction of O₃ with NO is also below the instrument flux limit of detection as discussed in Sect. 3.6. However, over terrestrial surfaces where NO₂ emissions can be large, we expect this instrument would be well suited for measuring NO₂ flux. From Eqs. (15) and (16), following Bariteau et al. (2010) and Lenschow and Kristensen (1985), we calculate an expected flux LOD for the case where counting noise is the controlling term in the flux error. The calculated flux LOD is 4.3×10⁹ molecules cm s⁻² s⁻¹ (1.6 pptv m s⁻¹) for an NO₂ mixing ratio of 1 ppbv and a friction velocity of 0.2 m s⁻¹.

$$\begin{array}{}\text{(15)}& {\displaystyle }F=C_a\sqrt{{\displaystyle \frac{\mathrm{0.06}{u}_{\ast }^{\mathrm{2}}}{C_a\mathit{\xi }\mathrm{\Gamma }}}},\text{(16)}& {\displaystyle }\mathrm{\Gamma }={\displaystyle \frac{az}{U}},\end{array}$$

where u_∗ is the friction velocity (m s⁻¹), C_a is the gas-phase concentration (ppbv), ξ is the instrument sensitivity (cps ppbv⁻¹), and Γ is the integral timescale (s). Γ can be further expressed following Eq. (12), where a is a constant taken as 0.3 for neutral conditions (Lenschow and Kristensen, 1985), z is the measurement height (here 10 m), and U is the horizontal wind speed at that measurement height (taken as 5 m s⁻¹).

Observations of a short duration NO plume from a boat motor starting near our inlet at Scripps Pier highlight the utility of the simultaneous O₃ and NO₂ detection from this instrument (Fig. 13). Highly localized NO emissions were observed as the titration of O₃ and prompt production of NO₂. Observed total odd oxygen (${\mathrm{O}}_x={\mathrm{O}}_{\mathrm{3}}+{\mathrm{NO}}_{\mathrm{2}}$) was conserved during this titration event, where NO₂ and O₃ concentrations were determined from independent calibration factors and backgrounds. The 1:1 conversion of O_x from O₃ to NO₂, shown in Fig. 13b, validates the laboratory-generated instrument calibration factors for O₃ and NO₂. The temporal agreement of the O₃ and NO₂ signals also demonstrates that both O₃ and NO₂ are transmitted through the inlet and detected with nearly identical instrument response times. This analysis assumes that there were no direct NO₂ emissions during the titration event. A NO₂ to NO_x emission ratio of 0.08 was observed for ship emissions from diesel motors on inland shipping vessels (Kurtenbach et al., 2016). Without additional knowledge about the NO_x emission source during this event, the observed conservation of total O_x could be partially driven by compensating errors within a 10 % margin. This simultaneous detection of both O_x species is likely also well suited for mobile sampling in the presence of dynamic NO emission sources, which challenge other fast ozone measurements. This method would also be well suited for direct measurement of flux divergence in the presence of strong surface NO emission sources.

5 Conclusions and outlook

This study demonstrated the utility of oxygen anion chemical ionization mass spectrometry for the fast and sensitive detection of O₃ and NO₂. Field measurements of O₃ dry deposition to the ocean surface from Scripps Pier, La Jolla CA demonstrate that this method has a suitable time response and suitable precision and stability for successful EC measurements. The mean measured v_d(O₃) with the Ox-CIMS is within the range of prior studies of O₃ ocean–atmosphere exchange. Further optimization and characterization of the Ox-CIMS is ongoing, including efforts to validate the specificity of the NO₂ detection, the addition of a Nafion dryer system, and better background determination methods. While this work has focused primarily on the deposition of O₃ to the ocean surface, the demonstrated instrument performance suggests the Ox-CIMS to be highly capable of O₃ and NO₂ flux measurements in the terrestrial biosphere and urban environments and from mobile platforms.