An intercomparison of CH₃O₂ measurements by fluorescence assay by gas expansion and cavity ring-down spectroscopy within HIRAC (Highly Instrumented Reactor for Atmospheric Chemistry)

Simultaneous measurements of CH₃O₂ radical concentrations have been performed using two different methods in the Leeds HIRAC (Highly Instrumented Reactor for Atmospheric Chemistry) chamber at 295 K and in 80 mbar of a mixture of 3:1 He∕O₂ and 100 or 1000 mbar of synthetic air. The first detection method consisted of the indirect detection of CH₃O₂ using the conversion of CH₃O₂ into CH₃O by excess NO with subsequent detection of CH₃O by fluorescence assay by gas expansion (FAGE). The FAGE instrument was calibrated for CH₃O₂ in two ways. In the first method, a known concentration of CH₃O₂ was generated using the 185 nm photolysis of water vapour in synthetic air at atmospheric pressure followed by the conversion of the generated OH radicals to CH₃O₂ by reaction with CH₄∕O₂. This calibration can be used for experiments performed in HIRAC at 1000 mbar in air. In the second method, calibration was achieved by generating a near steady state of CH₃O₂ and then switching off the photolysis lamps within HIRAC and monitoring the subsequent decay of CH₃O₂, which was controlled via its self-reaction, and analysing the decay using second-order kinetics. This calibration could be used for experiments performed at all pressures. In the second detection method, CH₃O₂ was measured directly using cavity ring-down spectroscopy (CRDS) using the absorption at 7487.98 cm⁻¹ in the A←X (ν₁₂) band with the optical path along the ∼1.4 m chamber diameter. Analysis of the second-order kinetic decays of CH₃O₂ by self-reaction monitored by CRDS has been used for the determination of the CH₃O₂ absorption cross section at 7487.98 cm⁻¹, both at 100 mbar of air and at 80 mbar of a 3:1 He∕O₂ mixture, from which ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{1.49}\pm \mathrm{0.19})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ was determined for both pressures. The absorption spectrum of CH₃O₂ between 7486 and 7491 cm⁻¹ did not change shape when the total pressure was increased to 1000 mbar, from which we determined that ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ is independent of pressure over the pressure range 100–1000 mbar in air. CH₃O₂ was generated in HIRAC using either the photolysis of Cl₂ with UV black lamps in the presence of CH₄ and O₂ or the photolysis of acetone at 254 nm in the presence of O₂. At 1000 mbar of synthetic air the correlation plot of [CH₃O₂]_FAGE against [CH₃O₂]_CRDS gave a gradient of 1.09±0.06. At 100 mbar of synthetic air the FAGE–CRDS correlation plot had a gradient of 0.95±0.024, and at 80 mbar of 3:1 He∕O₂ mixture the correlation plot gradient was 1.03±0.05. These results provide a validation of the FAGE method to determine concentrations of CH₃O₂.

1 Introduction

Methyl peroxy (CH₃O₂) radicals are important intermediates during atmospheric oxidation (Orlando and Tyndall, 2012) and combustion chemistry (Zador et al., 2011), and they are produced mainly by the oxidation of CH₄ and larger hydrocarbons followed by the termolecular reaction between the CH₃ radical, O₂ and a third body M (Reaction R1).

$$\begin{array}{}\text{(R1)}& {\mathrm{CH}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+M\end{array}$$

In environments influenced by anthropogenic NO_x emissions, CH₃O₂ predominantly reacts with NO to produce NO₂ and CH₃O (Reaction R2).

$$\begin{array}{}\text{(R2)}& {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{NO}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{NO}}_{\mathrm{2}}\end{array}$$

CH₃O subsequently reacts with O₂ (Reaction R3) to generate HO₂, which in turn oxidises another NO molecule to NO₂ (Reaction R4). The subsequent photolysis of NO₂ leads to the formation of tropospheric ozone, an important constituent of photochemical smog.

$$\begin{array}{}\text{(R3)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}},\text{(R4)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+\mathrm{NO}\to \mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}.\end{array}$$

In remote, clean environments, i.e. under low-NO_x levels, CH₃O₂ is significantly removed by its self-reaction (Reaction R5) and the cross-reactions with HO₂ and other organic peroxy radicals (RO₂) (Tyndall et al., 2001).

$$\begin{array}{}\text{(R5a)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{OH}+{\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}},\text{(R5b)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Recently the reaction of CH₃O₂ with OH was measured to be fast (Fittschen, 2019; Yan, 2016) and provides an additional loss route for CH₃O₂ under low-NO_x conditions (Fittschen et al., 2014; Assaf et al., 2017). As CH₃O₂ is formed by the oxidation of CH₄, one of the most abundant tropospheric trace gases, as well as by the oxidation of other volatile organic compounds, it is predicted by numerical models to be the most abundant RO₂ species in the atmosphere. Although CH₃O₂ has not (yet) been selectively measured in the atmosphere, its concentration has been estimated using atmospheric models to peak at ∼10⁷–10⁸ molecule cm⁻³ during the daytime (Whalley et al., 2010, 2011, 2018).

At present, CH₃O₂ is not measured selectively in the atmosphere by any direct or indirect method. The sum of HO₂ and all RO₂ species, $\left[{\mathrm{HO}}_{\mathrm{2}}\right]+{\sum }_i\left[{\mathrm{RO}}_{\mathrm{2},i}\right]$, and, separately, the sum of RO₂, ${\sum }_i\left[{\mathrm{RO}}_{\mathrm{2},i}\right]$, have been measured in the atmosphere using a range of indirect methods. Onel et al. (2017a) presents an overview of these methods, such as the peroxy radical chemical amplifier (PERCA) (Cantrell et al., 1984; Hernandez et al., 2001; Green et al., 2006; Miyazaki et al., 2010; Wood et al., 2017), RO_x chemical conversion – CIMS (chemical ionisation mass spectrometry) (RO_xMAS) (Hanke et al., 2002) and RO_x chemical conversion – LIF (laser-induced fluorescence) (RO_xLIF) (Fuchs et al., 2008; Whalley et al., 2013). RO_xLIF uses LIF detection of OH at low pressure, known as fluorescence assay by gas expansion (FAGE) and has been employed for partially speciated RO₂ detection, distinguishing between the sum of alkene, aromatic and long-chain alkane-derived RO₂ radicals and the sum of short-chain alkane-derived RO₂ radicals (Whalley et al., 2013, 2018).

CIMS methods using reagent ions such as H₃O⁺(H₂O)_n, ${\mathrm{NO}}_{\mathrm{3}}^{-}$ and ${\mathrm{NH}}_{\mathrm{4}}^{+}$ have been employed in the simultaneous and selective detection of RO₂ in a number of recent studies (Noziere and Hanson, 2017; Noziere and Vereecken, 2019; Hansel et al., 2018; Jokinen et al., 2014). Volatile small RO₂ radicals such as CH₃O₂ have been selectively measured in CIMS laboratory experiments with detection limits between $\sim \mathrm{1}\times {\mathrm{10}}^{\mathrm{8}}$ and 1×10⁹ molecule cm⁻³ (Noziere and Hanson, 2017). CIMS with ${\mathrm{NO}}_{\mathrm{3}}^{-}$ reagent ion has been employed in field measurements to record diurnal profiles of some highly oxygenated low-vapour-pressure RO₂ radicals produced in the ozonolysis of monoterpenes peaking at a few 10⁷ molecule cm⁻³ (Jokinen et al., 2014).

Many of the early laboratory studies of the CH₃O₂ radical reactions employed UV-absorption spectroscopy to monitor the B←X band centred around 240 nm, which is common to alkyl RO₂ species (Wallington et al., 1992; Tyndall et al., 2001). The similarity of the broad featureless UV-absorption spectra of RO₂ radicals made it challenging to distinguish between the individual RO₂ species, particularly in a mixture (Orlando and Tyndall, 2012). The sensitivity of UV-absorption spectroscopy is quite low; for example, a minimum detectable absorption of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$, corresponding to 4×10¹² molecule cm⁻³ CH₃O₂, was reported (Sander and Watson, 1980). The A←X electronic transition of RO₂ in the near IR (NIR) displays more structured spectra than the UV region, allowing for a selective identification of RO₂ radicals. However, the A←X transition is weaker than the B←X transition, and multipass arrangements have been used to improve the detection sensitivity. A step-scan Fourier transform infrared spectrometer (Huang et al., 2007) operated using a multipass White cell has been used to detect a number of RO₂ species, including CH₃O₂, with a typical minimum detectable absorbance of $\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$, corresponding to a limit of detection (LOD) of $\sim \mathrm{1}\times {\mathrm{10}}^{\mathrm{13}}$ molecule cm⁻³ for most RO₂ species studied. The use of cavity ring-down spectroscopy (CRDS) further improves the sensitivity of the RO₂ detection due to the significantly longer path lengths that can be realised and to the coupling of high-performance NIR lasers, detectors and optical components. For example, an absorbance detection limit of less than $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}$ has been obtained by using cavity mirrors of a maximum reflectivity of 99.995 % (Atkinson and Spillman, 2002).

The CRDS technique has been used under both ambient and jet-cooled conditions to provide insight into the molecular structure of CH₃O₂ and more complex RO₂, as well as to selectively measure [RO₂] in the laboratory (Sharp et al., 2008; Kline and Miller, 2014; Pushkarsky et al., 2000; Farago et al., 2013; Atkinson and Spillman, 2002; Sprague et al., 2013). Good agreement has been found between the experimental spectrum of CH₃O₂ in the range between ∼7200–8600 cm⁻¹ (∼1.18–1.40 µm) measured using pulsed CRDS at typically 200 mbar of ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{1.5}:\mathrm{1.0}$ and theoretical predictions (Chung et al., 2007; Sharp et al., 2008). The origin band of the A←X transition has been located at 7382.8 cm⁻¹ and a value of $\mathrm{2.7}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ has been estimated for the absorption cross section at this wavenumber (Pushkarsky et al., 2000; Chung et al., 2007). A weaker absorption band has been found at 7488 cm⁻¹ and assigned to a transition involving the methyl torsion (ν₁₂) (Pushkarsky et al., 2000; Chung et al., 2007). By using the CH₃O₂ spectrum measured by Pushkarsky et al. (2000) from 7300 to 7700 cm⁻¹, which covers both the origin band and the band involving the methyl torsional mode, a value of ca. $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ is estimated for the maximum cross section for the ν₁₂ transition, σ_max(ν₁₂). A few years later, Atkinson and Spillman (2002) measured ${\mathit{\sigma }}_{\max }\left({\mathit{\nu }}_{\mathrm{12}}\right)=(\mathrm{1.5}\pm \mathrm{0.8})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ at 27 mbar ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{4}:\mathrm{1}$ using continuous-wave (cw) CRDS. Very recent cw-CRDS studies reported ${\mathit{\sigma }}_{\max }\left({\mathit{\nu }}_{\mathrm{12}}\right)=\mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ at 67 mbar of a He+O₂ mixture (Fittschen, 2019) and no dependence of σ_max(ν₁₂) on pressure over the range from 67 to 133 mbar (Farago et al., 2013).

Recently we have developed a new method for the selective and sensitive detection of CH₃O₂ using the conversion of CH₃O₂ to CH₃O with excess NO followed by CH₃O detection by FAGE with laser excitation at ca. 298 nm (Onel et al., 2017b). The LOD for the method whilst sampling from atmospheric pressure is $\sim \mathrm{4.0}\times {\mathrm{10}}^{\mathrm{8}}$ molecule cm⁻³ for a signal-to-noise ratio of 2 and 5 min averaging time; the LOD is reduced to $\sim \mathrm{1.0}\times {\mathrm{10}}^{\mathrm{8}}$ molecule cm⁻³ by averaging over 1 h. Therefore, the method has potential to be used in the measurement of atmospheric levels of CH₃O₂ in clean environments where [CH₃O₂] has been calculated to be of the order of 10⁸ molecule cm⁻³ (Whalley et al., 2010, 2011). As LIF is not an absolute method of detection, FAGE instruments require calibration. Two methods of calibration for CH₃O₂ have been used (Onel et al., 2017b): the 184.9 nm photolysis of water vapour in the presence of excess CH₄ and the kinetics of the second-order decay of CH₃O₂ via its self–reaction observed in the Highly Instrumented Reactor for Atmospheric Chemistry (HIRAC). Good agreement was found; i.e. the calibration factors obtained using the two methods had overlapping error limits at the 1σ level.

However, radicals are difficult to detect accurately and, particularly as FAGE is not an absolute and direct method, may be subject to systematic errors and hence require validation using complementary methods. Recently we intercompared measurements of HO₂ concentrations by the indirect FAGE method and the direct and absolute CRDS method within HIRAC, and we demonstrated good agreement, within 10 % and 16 % at 150 mbar and 1000, respectively (Onel et al., 2017b), which validates the FAGE method for HO₂. In this work, CH₃O₂ measurements by FAGE and CRDS within HIRAC are intercompared at 80 mbar for a mixture of 3:1 He∕O₂ and at 100 and 1000 mbar for air.

2 Experimental

2.1 CH₃O₂ generation in HIRAC

The HIRAC chamber (Glowacki et al., 2007) is constructed from SAE 304 stainless steel and has an internal volume of ∼ 2.25 m³, the contents of which are homogenised by four mixing fans. Eight 50 mm diameter quartz tubes are mounted radially inside the chamber and extend along its ∼2 m length. Each of the eight tubes house a UV lamp that is used to initiate chemical reactions. The lamps can be changed to different wavelength outputs depending on the chemical precursors to be used. The FAGE instrument is connected to the HIRAC chamber through an ISO-K160 flange with an O-ring compression fitting to allow the inlet distance from the wall of the chamber to be varied. The 380 mm long inlet allows the instrument to sample well away from the inner walls of the HIRAC chamber and avoid chemical processes at the metal surface. Because the FAGE system removes gas from the HIRAC chamber, a constant flow of synthetic air is introduced into the chamber to maintain a constant pressure. The CRDS set-up is described in Sect. 2.3.

The experiments were conducted inside the HIRAC chamber at 295 K using three different pressure and gas mixtures. The first used 80 mbar total pressure of helium (BOC, >99.99 %) and oxygen (BOC, >99.999 %) in the ratio of $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$. The second and third mixtures both used synthetic air obtained by mixing oxygen with nitrogen (BOC, >99.998 %) in the ratio ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{4}:\mathrm{1}$ at 100 and 1000 mbar total pressure, respectively. CH₃O₂ was generated in the chamber by photolysing one of two precursor gas mixtures. The first CH₃O₂ precursor system was a mixture of Cl₂ (Sigma Aldrich, ≥99.5 %) and CH₄ (BOC, CP grade, 99.5 %), where the Cl₂ was photolysed at ∼365 nm (Phillips, TL-D36W/BLB, λ=350–400 nm) to generate CH₃O₂ via the following reactions:

$$\begin{array}{}\text{(R6)}& {\displaystyle }{\mathrm{Cl}}_{\mathrm{2}}+hv\left(\text{365\hspace{0.17em}nm}\right)\to \mathrm{Cl}+\mathrm{Cl},\text{(R7)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{4}}+\mathrm{Cl}\to {\mathrm{CH}}_{\mathrm{3}}+\mathrm{HCl},\text{(R1)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+M.\end{array}$$

Typical reagent concentrations were [CH₄]=1.2–2.5×10¹⁶ molecule cm⁻³ and [Cl₂]=1.1–5.5×10¹⁵ molecule cm⁻³. The second method used the photolysis of acetone (Sigma Aldrich, HPLC grade, ≥99.9 %) at 254 nm (GE G55T8/OH 7G lamps) to produce CH₃O₂ via Reactions (R8) and (R9) followed by Reaction (R1):

$$\begin{array}{}\text{(R8)}& {\displaystyle }({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}\mathrm{CO}+hv\left(\text{254\hspace{0.17em}nm}\right)\to \mathrm{2}{\mathrm{CH}}_{\mathrm{3}}+\mathrm{CO}\text{(R9)}& {\displaystyle }({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}\mathrm{CO}+hv\left(\text{254\hspace{0.17em}nm}\right)\to {\mathrm{CH}}_{\mathrm{3}}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{CO}\end{array}$$

Typical initial concentrations were $\left[({\mathrm{CH}}_{\mathrm{3}}{)}_{\mathrm{2}}\mathrm{CO}\right]=\mathrm{8.8}\times {\mathrm{10}}^{\mathrm{14}}$ molecule cm⁻³. In the FAGE calibration experiments using the kinetic decays $[{\mathrm{Cl}}_{\mathrm{2}}{]}_{\mathrm{0}}=\mathrm{1.1}\times {\mathrm{10}}^{\mathrm{14}}$ molecule cm⁻³ with CH₄ at one of two concentrations: 2.5×10¹⁶ and 2.5×10¹⁷ molecule cm⁻³. In the kinetic experiments performed to determine the absorption cross section of CH₃O₂ at 7487.98 cm⁻¹, $[{\mathrm{Cl}}_{\mathrm{2}}{]}_{\mathrm{0}}=\mathrm{1.1}\times {\mathrm{10}}^{\mathrm{14}}$ molecule cm⁻³ and $[{\mathrm{CH}}_{\mathrm{4}}{]}_{\mathrm{0}}=\mathrm{2.5}\times {\mathrm{10}}^{\mathrm{16}}$ molecule cm⁻³ at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and $[{\mathrm{Cl}}_{\mathrm{2}}{]}_{\mathrm{0}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{15}}$ molecule cm⁻³ and $[{\mathrm{CH}}_{\mathrm{4}}{]}_{\mathrm{0}}=\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{16}}$ molecule cm⁻³ at 100 mbar ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{4}:\mathrm{1}$.

2.2 FAGE instrument and calibration for CH₃O₂

The FAGE instrument in HIRAC has been described in detail previously (Winiberg et al., 2015; Onel et al., 2017a, b). The instrument has a ∼1 m long black anodised aluminium sampling tube with an inner diameter of 50 mm. The interior of the tube is held at a low pressure (3.3 mbar for a HIRAC pressure, p_HIRAC of 1000 mbar of synthetic air and 0.9 mbar for p_HIRAC=100 mbar synthetic air and p_HIRAC=80 mbar mixture of $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$) and draws sample gas in through a 1 mm diameter pinhole mounted on one end of the tube at a rate of ∼3 SLPM. Two fluorescence cells are integrated into the tube, the centre of the first cell is ∼300 mm from the pinhole, and the centre of the second cell is a further ∼300 mm downstream, followed by a line of tubing that is connected to a rotary-backed roots blower pump system (Leybold Trivac D40B and Ruvac WAU 251). The first cell is used to detect OH radicals but is not relevant to this work and is not discussed further, whereas the second cell is used for the CH₃O₂ measurements detailed here. The CH₃O₂ radicals sampled through the FAGE pinhole at 1000 mbar in HIRAC reached the detection region in about 85 ms. High-purity NO (BOC, N2.5 nitric oxide) is injected at 2.5 sccm using a mass flow controller (Brooks 5850S) into the centre of the gas flow ∼ 25 mm prior to the second cell to convert CH₃O₂ radicals into CH₃O. Pulsed laser light at 297.79 nm is directed through the cell, propagates perpendicular to the gas flow and is used to excite the $A^{\mathrm{2}}{A}_{\mathrm{1}}({\mathit{\nu }}_{\mathrm{3}}{}^{\prime }=\mathrm{3})\leftarrow X^{\mathrm{2}}E({\mathit{\nu }}_{\mathrm{3}}{}^{\prime \prime }=\mathrm{0})$ transition of CH₃O. The off-resonant red-shifted fluorescence (320–430 nm) from CH₃O (A) is subsequently detected by a microchannel plate photomultiplier (Photek PMT325) using photon counting. Measurements are made at an excitation wavelength of 297.79+2.5 nm in order to determine the laser background, which is subtracted to leave only signal due to CH₃O fluorescence.

The FAGE technique is not absolute and therefore determination of the calibration factor, $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ (counts cm³ molecule⁻¹ s⁻¹ mW⁻¹), is required to convert the measured signal, $S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ (counts s⁻¹ mW⁻¹), to the CH₃O₂ concentration:

$$\begin{array}{}\text{(1)}& {[\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}]={\displaystyle \frac{S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}}{C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}}}.\end{array}$$

2.2.1 Calibration at atmospheric pressure – H₂O vapour photolysis in the presence of excess CH₄

This calibration procedure has been described in detail previously (Winiberg et al., 2015; Onel et al., 2017b), as such only important points are presented here. CH₃O₂ radicals were generated by photolysing water vapour in air (BOC, synthetic BTCA 178) at 184.9 nm to produce OH radicals, which then reacted with methane (BOC, CP grade, 99.5 %) to produce CH₃O₂:

$$\begin{array}{}\text{(R10)}& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+hv\left(\text{185\hspace{0.17em}nm}\right)\to \mathrm{OH}+\mathrm{H},\text{(R11)}& {\displaystyle }\mathrm{OH}+{\mathrm{CH}}_{\mathrm{4}}\to {\mathrm{CH}}_{\mathrm{3}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O},\text{(R1)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+M.\end{array}$$

The subsequent air/radical mixture was then sampled by the FAGE instrument. The concentration of CH₃O₂ generated is given by

$$\begin{array}{}\text{(2)}& \left[{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\right]=\left[\mathrm{OH}\right]=\left[{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right]\cdot \mathit{\sigma }\cdot \mathrm{\Phi }\cdot F\cdot t,\end{array}$$

where σ is the absorption cross section of water vapour at 184.9 nm, $(\mathrm{7.22}\pm \mathrm{0.22})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ (Cantrell et al., 1997; Creasey et al., 2000); Φ is the photodissociation quantum yield of OH at 184.9 nm (unity); t is the residence time of the gas in the photolysis field, which is ∼16.6 and ∼8.3 ms at 20 and 40 SLPM, respectively; and F is the lamp flux at 184.9 nm. The product F⋅t is determined using chemical actinometry (Winiberg et al., 2015). The 184.9 nm photon flux, F, is proportional to the electrical current supplied to the photolysis lamp and is varied to produce a range of CH₃O₂ radical concentrations. A typical calibration plot of the FAGE LIF signal versus generated [CH₃O₂] calculated using Eq. (2) is shown in Fig. S2 in the Supplement. An average of four calibrations gave $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{8.03}\pm \mathrm{1.37})\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹s⁻¹ mW⁻¹ where the error represents the overall uncertainty (17 %) calculated using the statistical error (7 %) and the systematic error (16 %) at the 1σ level (Onel et al., 2017b).

2.2.2 Calibration using kinetics of the CH₃O₂ temporal decay

The calibration described in the previous section is only valid when FAGE is sampling at atmospheric pressure. However, when sampling from lower pressures, as described in Sect. 2.1, the FAGE cell pressure decreases (0.9 mbar sampling from 100 mbar) and the calibration is no longer valid. An alternative calibration procedure using the kinetics of the CH₃O₂ self-reaction inside the HIRAC chamber allowed the FAGE instrument to be calibrated under the same conditions of pressure as the intercomparison experiments, including at lower pressures. Table 1 shows the sensitivity factors, $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$, obtained for each set of chamber conditions. Radicals were generated in the chamber in the same manner as those described in Sect. 2.1. However, instead of measuring steady-state radical concentrations, the lamps were switched off and on at ∼120 s intervals to produce a series of second-order decays, typically four per experiment, in which CH₃O₂ undergoes loss via self-reaction:

$$\begin{array}{}\text{(R5a)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{OH}+{\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}},\text{(R5b)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Assuming no wall loss for CH₃O₂, the kinetic decays can be described by the integrated second-order rate equation:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{1}}{[{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}{]}_t}}={\displaystyle \frac{\mathrm{1}}{[{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}{]}_{\mathrm{0}}}}+\mathrm{2}\cdot k_{\mathrm{obs}}\cdot \mathrm{\Delta }t,\end{array}$$

where [CH₃O₂]_t is the radical concentration at time t of the decay; [CH₃O₂]₀ is the initial concentration at the time t₀, when the lamps are switched off; $\mathrm{\Delta }t=t-t_{\mathrm{0}}$; and k_obs is the observed rate coefficient. The observed rate coefficient is larger than the second-order rate coefficient of just the CH₃O₂ recombination Reaction (R5) as the methoxy radicals generated by Reaction (R5b) react rapidly with oxygen present in large excess to produce HO₂ (Reaction R3), which in turn reacts with CH₃O₂ (Reaction R12).

$$\begin{array}{}\text{(R3)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}},\text{(R12)}& {\displaystyle }\begin{array}{rl}{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}& +{\mathrm{HO}}_{\mathrm{2}}\to \mathrm{0.9}{\mathrm{CH}}_{\mathrm{3}}\mathrm{OOH}\\ & +\mathrm{0.1}{\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+\mathrm{0.1}{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}.\end{array}\end{array}$$

As each HO₂ radical consumes rapidly one CH₃O₂ species on the timescale of Reaction (R5), the CH₃O₂ decay is described by second-order kinetics (Sander and Watson, 1980, 1981; McAdam et al., 1987; Kurylo and Wallington, 1987; Jenkin et al., 1988; Simon et al., 1990), with $k_{\mathrm{obs}}=k_{\mathrm{5}}(\mathrm{1}+r_{\mathrm{5}\mathrm{b}})$, where r_5b is the branching ratio for Reaction (R5b). By using the IUPAC recommendations (Atkinson et al., 2006): $k_{\mathrm{5}}=(\mathrm{3.5}\pm \mathrm{1.0})\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹ and $r_{\mathrm{5}\mathrm{b}}=\mathrm{0.37}\pm \mathrm{0.06}$, a value of $\mathrm{4.8}\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹ is obtained for k_obs.

Modelling of the decay process with a variety of CH₃O₂ and HO₂ concentrations after the lamps were switched off and following the establishment of steady-state conditions showed that Eq. (3) was valid within experimental error. With $k_{\mathrm{5}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹ (Atkinson et al., 2006), a faster observed rate constant (defined by Eq. 3) was obtained from the model with a value, $\mathrm{4.9}\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹, consistent with that recommended by IUPAC, ($\mathrm{4.8}\pm \mathrm{0.6})\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹ (1σ uncertainty; Atkinson et al., 2006). Substituting Eq. (1) into Eq. (3) allows the measured signal over the decay to be related to the instrument sensitivity by

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{1}}{(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_t}}={\displaystyle \frac{\mathrm{1}}{(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_{\mathrm{0}}}}+{\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}}\cdot \mathrm{\Delta }t}{C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}}},\end{array}$$

where $(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_t$ and $(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_{\mathrm{0}}$ are the FAGE signal at time t and t₀, respectively. Taking the reciprocal of Eq. (4) gives

$$\begin{array}{}\text{(5)}& (S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_t={\left({\displaystyle \frac{\mathrm{1}}{(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_{\mathrm{0}}}}+{\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}}\cdot \mathrm{\Delta }t}{C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}}}\right)}^{-\mathrm{1}},\end{array}$$

which is then used to fit to the experimental data with k_obs fixed to the value recommended by IUPAC for 298 K, $\mathrm{4.8}\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹, using the Levenberg–Marquardt algorithm. Figure 1 shows an example CH₃O₂ self-reaction decay trace obtained at 1000 mbar, where the red line shows the result of the fitting process.

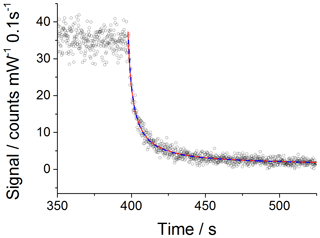
Figure 1 An example of a second-order decay of the FAGE CH₃O₂ signal (normalised for laser power fluctuations) with 0.1 s time resolution (black open circles) recorded at 295 K and a 1000 mbar air mixture. CH₃O₂ was generated using [Cl₂] of $\sim \mathrm{1.1}\times {\mathrm{10}}^{\mathrm{14}}$ molecule cm^− 1 and [CH₄] of $\sim \mathrm{2.5}\times {\mathrm{10}}^{\mathrm{16}}$ molecule cm⁻³. At time zero (∼400 s) the photolysis lamps were turned off to allow the radicals to decay. The data were fitted to Eq. (5) (excluding the wall loss rate, k_loss; red line) and Eq. (6) (including k_loss; blue dashed line) using the Levenberg–Marquardt algorithm. The obtained value for the sensitivity factor was the same for both fits: $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{1.17}\pm \mathrm{0.04})\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹. The $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ errors given above represent statistical uncertainties at the 1σ level.

However, as the HIRAC chamber is constructed from steel, the potential for a loss of CH₃O₂ to the walls was investigated. As circulation fans were used during all the experiments, the “movement” of CH₃O₂ radicals within the chamber is in part molecular diffusion and in part convection. Therefore, the parameter k_loss is controlled by both convection and diffusion processes. By incorporating the wall loss as a first-order process, Eq. (5) becomes

$$\begin{array}{}\text{(6)}& \begin{array}{rl}(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_t& =\left(\left({\displaystyle \frac{\mathrm{1}}{(S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}{)}_{\mathrm{0}}}}+{\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}}}{k_{\mathrm{loss}}\cdot C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}}}\right)\right.\\ & {\left.\times \exp (k_{\mathrm{loss}}\cdot \mathrm{\Delta }t)-\left({\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}}}{k_{\mathrm{loss}}\cdot C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}}}\right)\right)}^{-\mathrm{1}}\end{array}\end{array}$$

Fitting Eqs. (5) and (6) to the experimental data is also shown in Fig. 1. The extracted values for the sensitivity factor are the same for the fit without and with wall loss included: $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{1.17}\pm \mathrm{0.04})\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹ (statistical errors at the 1σ level). The close overlap of the fits without and with wall loss included and the small values extracted for k_loss (upper limit of $\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹) fitting Eq. (6) demonstrates that wall losses are very small and can be neglected. This is evidenced further by the lack of an observable radical gradient across the chamber diameter as shown in Fig. S5. In addition, modelling the CH₃O₂ decays including a wall loss for HO₂ in the range of measured values, 0.03–0.09 s⁻¹ (Onel et al., 2017a), showed a minor impact of the wall loss of HO₂ on k_obs, i.e. k_obs within 98 %–95 % agreement with the IUPAC preferred value of $(\mathrm{4.8}\pm \mathrm{0.6})\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹ (1σ uncertainty; Atkinson et al., 2006).

Table 1 Average sensitivity factors for the FAGE instrument using the CH₃O₂ kinetic decay method under each chamber environment. Examples of these decays can be found in Fig. 1 above and in Figs. S3 and S4, and the reported values are typically from an average of eight decays. All the data were fitted using Eq. (5). The errors given in the table are overall uncertainties (13 %) at the 1σ level.

Table 1 shows the average sensitivity factors obtained by fitting Eq. (5) to a typical number of eight temporal decays of $S_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ under each of the chamber conditions, and example decay traces for the 80 and 100 mbar experiments can be found in Figs. S3 and S4, respectively. These factors are used for their respective experimental conditions. For the 1000 mbar intercomparison experiments with CRDS, an average of the water vapour photolysis sensitivity factor at 1000 mbar ($C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=(\mathrm{8.03}\pm \mathrm{1.37})\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹) and the average sensitivity factor obtained from the kinetic decay ($C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}},\mathrm{kinetic}}$ $=(\mathrm{1.16}\pm \mathrm{0.15})$ $\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹) (Table 1) is used, giving $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}},\text{avg.}}$ $=(\mathrm{9.81}\pm \mathrm{2.03})$ $\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹. We make a brief comment regarding the difference in the sensitivity factors $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}},\mathrm{kinetic}}$, for which the ratio is ∼0.7, showing a ∼30 % difference, although the two calibration methods have overlapping error limits at the 2σ level. The kinetic method relies on the rate coefficient k_obs for the CH₃O₂ self-reaction as recommended by IUPAC (Atkinson et al., 2006), which has a quoted 2σ uncertainty of 23 %. In a separate paper we will present a detailed study of the kinetics of the CH₃O₂ self-reaction, and its temperature dependence, and report a revised rate coefficient for this reaction at 298 K.

As the pressure in the FAGE detection cell was 2–3 orders of magnitude lower than the corresponding pressure in HIRAC (vide supra in Sect. 2.2), the concentrations of the reagents (Cl₂, methane and acetone) were also 2–3 orders of magnitude lower in the fluorescence cells than the reagent concentrations in HIRAC. However, a potential effect of the reagents (Cl₂, methane and acetone) on the FAGE sensitivity factor in the HIRAC experiments was investigated. Two different concentrations of CH₄ were used in the kinetic method for FAGE calibration at 80 mbar of He+O₂ in HIRAC to find practically the same sensitivity factor: $(\mathrm{3.80}\pm \mathrm{0.50})\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹ for 2.5×10¹⁶ molecule cm⁻³ CH₄ (2.8×10¹⁴ molecule cm⁻³ in the fluorescence cell) and $(\mathrm{3.86}\pm \mathrm{0.50})\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹ for 2.5×10¹⁷ molecule cm⁻³ CH₄ (2.8×10¹⁵ molecule cm⁻³ in the fluorescence cell). As shown in Fig. S1 there is a good agreement between the laser excitation scans of CH₃O obtained from the CH₃O₂ generated in HIRAC using the two methods: acetone photolysis in the presence of O₂ and Cl₂ photolysis in the presence of CH₄ and O₂. In addition, a good agreement has been previously found between the laser excitation spectra of CH₃O generated using the reaction of CH₄ with OH (generated by the 184.9 nm photolysis of water) in the presence of O₂ and directly through the 184.9 nm photolysis of CH₃OH (Onel et al., 2017b). Therefore, no effect of the used reagents on the laser excitation spectrum of CH₃O was found.

2.2.3 FAGE measurements of CH₃O₂ concentration gradient across the HIRAC diameter

Measurement of radical gradients across the chamber diameter have been performed previously for HO₂ radicals (Onel et al., 2017a), where no gradient was observed until measuring <10 cm from the chamber wall where the signal began to decrease, ultimately by ∼16 % at the point at which the FAGE sampling pinhole was level with the chamber walls. To investigate any similar gradient effects for CH₃O₂, a steady-state concentration of CH₃O₂ was generated in the chamber at atmospheric pressure by photolysing O₃ in the presence of air and methane:

$$\begin{array}{}\text{(R13)}& {\displaystyle }{\mathrm{O}}_{\mathrm{3}}+hv\left(\mathrm{254}\mathrm{nm}\right)\to {\mathrm{O}}_{\mathrm{2}}+\mathrm{O}{(}^{\mathrm{1}}\mathrm{D}),\text{(R14)}& {\displaystyle }\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{CH}}_{\mathrm{4}}\to {\mathrm{CH}}_{\mathrm{3}}+\mathrm{OH},\text{(R1)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+M.\end{array}$$

Ozone and methane were present in the chamber at $\sim \mathrm{2.5}\times {\mathrm{10}}^{\mathrm{13}}$ and 2.5 ×10¹⁷ molecule cm⁻³, respectively. The FAGE inlet was translated across the width of the chamber and the CH₃O₂ signal was observed to show no decrease within the ∼10 % 1σ statistical error of each measurement up until the point at which the pinhole was level with the chamber walls. Moving the instrument further backwards positioned the pinhole inside the ISO-K160 coupling flange and effectively ∼4 cm behind the chamber walls where there is likely to be little air movement. This position is analogous to that of the CRDS mirrors, which are recessed into the chamber walls as they mount to the outside of the chamber (see Sect. 2.3). In this position a signal drop of ∼14 % was observed, within the statistical error margins of the measurements. A plot of the radical gradient is shown in Fig. S5.

2.3 CRDS set-up

The optical path of the CRDS spectrometer within the HIRAC chamber is shown in Fig. 2 and is the same spectrometer as used to probe HO₂ across the chamber's diameter, which has been described previously (Onel et al., 2017a).

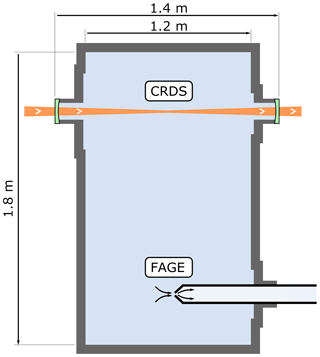
Figure 2 Longitudinal (horizontal) section of the HIRAC chamber. The CRDS spectrometer probes the CH₃O₂ concentration as an average across the chamber's diameter, while the FAGE instrument probes CH₃O₂ in the chamber at a single point close to the centre.

The cavity is formed by two highly reflective 1 in. diameter mirrors (99.999 %, Layertec, curvature radius = 1 m) housed in custom-built mounts that allow the mirrors to be tilted slightly whilst maintaining a gas-tight seal. The position of the mirror on the laser injection side is modulated along the cavity axis by a few micrometres using a piezoelectric transducer at ∼10 Hz, with the overall distance between the two mirrors being ∼1.4 m. Laser light of ∼1.335 µm is generated by a distributed feedback (DFB) fibre pig-tailed diode laser (NTT Electronics, NLK1B5EAAA) held in a butterfly laser diode mount (Thorlabs LM14S2). The electrical current that drives the laser diode and thermoelectric cooler is generated by a Thorlabs ITC502 driver. The DFB is connected to an in-line optical isolator (Thorlabs IO-H-1335APC), an acousto-optic modulator (AOM, Gooch & Housego Fibre-Q M040-0.5C8H-3-F2S) and a fibre collimator (Thorlabs CFC-8X-C). The laser light is then guided into the cavity by two silver mirrors (Thorlabs PF10-03-P01). On the detection side of the cavity, light leaking out of the mirror is directed onto another silver mirror that guides the light through a f=30 mm focusing lens (Thorlabs LA1805-C) onto an InGaAs photodiode (Thorlabs DET10C/M) that is isolated from ambient light by a 1250 nm long-pass filter (Thorlabs FELH1250). The photodiode signal is amplified (FEMTO DLPCA-200) and sent to a data acquisition unit (DAQ, National Instruments USB-6361) and to a custom-built comparator that acts as a trigger unit. The comparator compares the amplified photodiode signal with a manually adjustable threshold voltage, and upon reaching a preset threshold the AOM is switched off, stopping the injection of light into the cavity within tens of nanoseconds and initiating a ring-down event. The DAQ is simultaneously triggered and acquires the signal by a ring-down method. The system resets after a set time (typically 5 ms) and is ready for the next event. The acquired data are processed using a custom-made LabView program that fits the ring-down events with an exponential function to extract the ring-down time, τ. Filters are applied to process the ring-down events to exclude potential outliers caused by dust particles passing through the beam and false positives (when the acquisition is triggered by a transient noise spike), so that only legitimate ring-down events are taken into account. The ring-down time can then be converted into the absorption coefficient, α:

$$\begin{array}{}\text{(7)}& \mathit{\alpha }={\displaystyle \frac{\mathrm{1}}{c}}\times (\mathrm{1}/\mathit{\tau }-\mathrm{1}/{\mathit{\tau }}_{\mathrm{0}}),\end{array}$$

where τ and τ₀ are the ring-down times with and without CH₃O₂ radicals present, respectively, and c is the speed of light. τ₀ would be obtained in a typical experiment by recording ring-down events for ∼1 min before switching on the photolysis lamps in the chamber. As it is not possible to measure τ₀ and τ simultaneously, the background was monitored regularly during each experiment by switching off the photolysis lamps and allowing the signal to return to the baseline.

The molecular chlorine delivery did not result in a change in the measured ring-down time. However, delivery of the methane and acetone reagents led to a decrease in the ring-down time indicating that, in the concentrations delivered to the chamber, methane and acetone absorbed in the wavenumber range used in the present work (∼7486–7491 cm⁻¹). An absorption coefficient of $\sim \mathrm{8}\times {\mathrm{10}}^{-\mathrm{9}}$ cm⁻¹ was measured for [acetone] $\approx \mathrm{9}\times {\mathrm{10}}^{\mathrm{14}}$ molecule cm⁻³ at the typical measurement point of 7487.98 cm⁻¹ (vide infra). An absorption coefficient in the range (0.7–1.4) $\times {\mathrm{10}}^{-\mathrm{8}}$ cm⁻¹ was determined at 7487.98 cm⁻¹ for CH₄ in typical concentrations in the FAGE–CRDS intercomparison experiments in the range (1.2–2.5) ×10¹⁶ molecule cm⁻³. The background ring-down time τ₀ (Eq. 7) contained the contributions of the reagents, methane or acetone, and was monitored regularly during the experiments by turning off the chamber lamps (vide supra).

The CH₃O₂ absorption feature used in these measurements is a band associated with the $A^{\mathrm{2}}A{}^{\prime }\leftarrow X^{\mathrm{2}}{A}^{\prime \prime }$ electronic transition centred around 7488 cm⁻¹, and it has been documented in previous work (Faragó et al., 2013; Atkinson and Spillman, 2002; Pushkarsky et al., 2000). There are interfering methane and water vapour lines in this region, and these together with the change in [CH₃O₂] during longer (10 min) scanning times did not allow us to generate a continuous high-resolution scan across the CH₃O₂ transition. Instead, as shown in Fig. 3, the absorption spectrum was mapped out as a series of point measurements at fixed wavelengths, normalised by the absorption at the optimum measurement point, 7487.98 cm⁻¹, where the absorption feature is sufficiently strong and furthest in wavelength from interfering methane absorption lines and where the CH₃O₂ cross section was determined (Sect. 3.2). The absorption coefficient of CH₄ was about 7 times lower at 7487.98 cm⁻¹ than at 7489.16 cm⁻¹, i.e. at the peak of the CH₃O₂ spectral feature where Fittschen (2019) reported ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$. Therefore, 7487.98 cm⁻¹ (rounded to 7488 cm⁻¹ henceforth) was chosen as the measurement point instead of the value of 7489.16 cm⁻¹ used by Fittschen (2019). Each datum point in Fig. 3 was obtained by measuring the absorption coefficient, ${\mathit{\alpha }}_{\mathrm{7488}{\mathrm{cm}}^{-\mathrm{1}}}$, and the baseline (lamps on, then off) at 7488 cm⁻¹ followed by measuring ${\mathit{\alpha }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ and baseline at another wavelength on the absorption feature and then reverting to measuring at 7488 cm⁻¹ again. This pattern was repeated multiple times for different wavelengths to build up an absorption feature, with all data points normalised to ${\mathit{\alpha }}_{\mathrm{7488}{\mathrm{cm}}^{-\mathrm{1}}}$ and then multiplied by the CH₃O₂ cross section at 7488 cm⁻¹ (Sect. 3.2) to obtain the absorption spectrum shown in Fig. 3. The method was used to measure the CH₃O₂ absorption spectrum under each of the three experimental conditions detailed in Sect. 2.1: 80 mbar (He+O₂) and 100 and 1000 mbar of synthetic air.

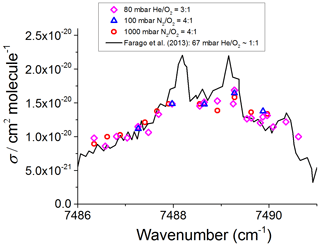
Figure 3 CH₃O₂ absorption spectrum at 295 K. The measured absorption spectrum scaled to the absolute cross section determined at 7488 cm⁻¹ using the kinetics of the CH₃O₂ decay monitored using CRDS (Sect. 3.2 below). The black line represents the CH₃O₂ spectrum measured by Faragó et al. (2013) at 67 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}\sim \mathrm{1}:\mathrm{1}$ but with the absolute cross section scaled to reflect the recent update reported by Fittschen (2019) giving ${\mathit{\sigma }}_{\mathrm{7489}{\mathrm{cm}}^{-\mathrm{1}}}=\mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹.

3 Results

3.1 CH₃O₂ absorption spectrum and comparison with the literature

Figure 3 shows that the relatively broad absorption feature obtained in this work in the range from ∼7486 to 7491 cm⁻¹ is almost the same at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and at 100 and 1000 mbar of synthetic air. As shown in Fig. 3, the spectrum found in this work agrees well with the general shape of the CH₃O₂ spectrum measured by Faragó et al. (2013) at 67 mbar He∕O₂ $\sim \mathrm{1}:\mathrm{1}$ but scaled to reflect the very recent update to the absolute absorption cross section reported by Fittschen (2019), which gave ${\mathit{\sigma }}_{\mathrm{7489}{\mathrm{cm}}^{-\mathrm{1}}}=\mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. The peaks at the top of the spectral feature reported by Faragó et al. (2013) are not reproduced in this work owing to the method of generating the spectrum (Sect. 2.3). Previously Pushkarsky et al. (2000) measured the CH₃O₂ absorption spectrum over a larger wavenumber range (7300–7700 cm⁻¹), where the ν₁₂ transition is located at 7488 cm⁻¹ in agreement with this work. In addition, if the CH₃O₂ spectrum at 27 mbar ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{4}:\mathrm{1}$ reported by Atkinson and Spillman (2002) was shifted by ∼2 cm⁻¹ toward higher wavenumbers compared to this work and the study of Faragó et al. (2013), the shape of the ν₁₂ band from Atkinson and Spillman is in agreement with the results shown in Fig. 3.

The similarity of the results at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and at 100 and 1000 mbar of air reported in this work and their agreement with the previous measurements performed at relatively low pressures (Fittschen, 2019; Faragó et al., 2013; Atkinson and Spillman, 2002; Pushkarsky et al., 2000) can be explained by an overlap of several individual absorption lines resulting in a spectral structure in the range from ∼7486 to 7491 cm⁻¹ with practically no pressure dependence observed between ∼30–1000 mbar. Therefore, it can be assumed that the absorption cross section at 7488 cm⁻¹, σ (7488 cm⁻¹), is the same under the conditions used in this work, i.e. at 80 mbar of He and O₂ and at 100 and 1000 mbar of air.

3.2 Determination of the absorption cross section of CH₃O₂ at 7488 cm⁻¹

The kinetics of the CH₃O₂ temporal decay by its self-reaction (Reaction R5) were used to determine the absorption cross section of CH₃O₂ at 7488 cm⁻¹, i.e. σ (7488 cm⁻¹). Note that the cross section used is not the more standard integrated cross section used by HITRAN and other spectral databases. CH₃O₂ radicals were generated by using CH₄∕Cl₂∕synthetic-air mixtures (Sect. 2.1) with the chamber UV lamps switched on to generate Cl atoms (Reaction R6). By extinguishing the UV lamps, CH₃O₂ radicals were removed by self-reaction and wall loss. Figure 4 shows an example of a kinetic decay obtained at 100 mbar ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{4}:\mathrm{1}$ using CRDS. The experimental data were fitted by using two functions described by Eqs. (8) and (9), which are closely related to Eqs. (5) and (6) used in the analysis of the CH₃O₂ decays measured using FAGE. Equation (8) assumes that the wall loss of CH₃O₂ is negligible, and hence the removal of CH₃O₂ can be described by the integrated second-order rate law equation, leading to

$$\begin{array}{}\text{(8)}& {\mathit{\alpha }}_t={\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\alpha }}_{\mathrm{0}}}}+{\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}.}\mathrm{\Delta }t}{\mathit{\sigma }\left(\mathrm{7488}{\mathrm{cm}}^{-\mathrm{1}}\right)}}\right)}^{-\mathrm{1}},\end{array}$$

where α_t is the CH₃O₂ absorption coefficient at 7488 cm⁻¹ and at time t; α₀ is the absorption coefficient at time zero of the reaction when the lamps are switched off, i.e. t₀; $\mathrm{\Delta }t=t-t_{\mathrm{0}}$; and k_obs is the observed rate coefficient of the self-reaction at 298 K, i.e. $k_{\mathrm{obs}}=(\mathrm{4.8}\pm \mathrm{0.6})\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molecule⁻¹ s⁻¹ (Atkinson et al., 2006).

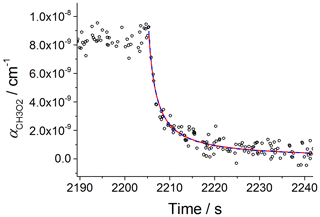
Figure 4 Second-order decay of the CH₃O₂ absorption coefficient at 7488 cm⁻¹ monitored by CRDS. Experiment carried out at 295 K and 100 mbar of synthetic air; [CH₄]${}_{\mathrm{0}}=\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{16}}$ molecule cm⁻³ and [Cl₂]${}_{\mathrm{0}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{15}}$ molecule cm⁻³. At time 2205 s the photolysis lamps were turned off (time t₀). Fitting Eq. (8) to the data (red line) gave σ(7488 cm${}^{-\mathrm{1}})=(\mathrm{1.47}\pm \mathrm{0.07})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. A fit including the wall loss rate, k_loss (Eq. 9), is shown by the blue dashed line and resulted in $\mathit{\sigma }\left(\mathrm{7488}{\mathrm{cm}}^{-\mathrm{1}}\right)=(\mathrm{1.50}\pm \mathrm{0.07})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. The error limits are statistical errors at the 1σ level.

For completeness, Eq. (9) includes the CH₃O₂ wall loss as a first-order process, leading to

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathit{\alpha }}_t& =\left(\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\alpha }}_{\mathrm{0}}}}+{\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}.}}{k_{\mathrm{loss}}\cdot \mathit{\sigma }\left(\mathrm{7488}{\mathrm{cm}}^{-\mathrm{1}}\right)}}\right)\times \exp \left(k_{\mathrm{loss}}\mathrm{\Delta }t\right)\right.\\ & -{\left.\left({\displaystyle \frac{\mathrm{2}\cdot k_{\mathrm{obs}.}}{k_{\mathrm{loss}}\cdot \mathit{\sigma }\left(\mathrm{7488}{\mathrm{cm}}^{-\mathrm{1}}\right)}}\right)\right)}^{-\mathrm{1}},\end{array}\end{array}$$

where k_loss is the rate coefficient describing the CH₃O₂ wall loss (Onel et al., 2017a).

Figure 4 shows that the fits given by Eqs. (8) and (9) to the data overlap over all of the temporal CH₃O₂ decay and the values of σ (7488 cm⁻¹) extracted by the two fits are in a very good agreement: $(\mathrm{1.47}\pm \mathrm{0.07})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ (Eq. 8) and $(\mathrm{1.50}\pm \mathrm{0.07})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ (Eq. 9), where the quoted errors are statistical uncertainties. The values extracted for k_loss by fitting Eq. (9) to the CRDS data were small and similar to the values obtained by fitting Eq. (6) to the kinetic decays monitored by FAGE. An upper limit of $\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ was obtained for k_loss in both FAGE and CRDS measurements, showing that wall losses are negligible. From fitting Eq. (8) to the temporal decays obtained at 100 mbar of synthetic air, an averaged value of $(\mathrm{1.51}\pm \mathrm{0.19})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ was obtained, where the error represents 1σ overall uncertainty (13 %). Fitting Eq. (8) to the data at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ (Fig. S6) gave an average value of σ(7488 cm⁻¹) $=(\mathrm{1.46}\pm \mathrm{0.17})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ (1σ overall uncertainty), in very good agreement with the value at 100 mbar of air. The average of the results at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and 100 mbar of air, $\mathrm{1.49}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹, is in excellent agreement with the determination of Atkinson and Spillman (2002): ${\mathit{\sigma }}_{\max }\left({\mathit{\nu }}_{\mathrm{12}}\right)=(\mathrm{1.5}\pm \mathrm{0.8})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ and consistent with the estimation of $\sim \mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ for σ_max(ν₁₂) obtained using the CH₃O₂ spectrum reported by Pushkarsky et al. (2000). To enable a comparison at 7487.98 cm⁻¹ with the very recent measurement of Fittschen (2019), who found $\mathrm{2.20}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ at 7489.16 cm⁻¹, σ(7487.98 cm⁻¹) $=\mathrm{1.49}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ obtained in this work was multiplied by the σ(7489.16 cm⁻¹) : σ(7487.98 cm⁻¹) ratio obtained by using the high-resolution spectrum reported by Faragó et al. (2013) (Fig. 3). The obtained value, σ(7489.16 cm⁻¹) $=(\mathrm{1.9}\pm \mathrm{0.3})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹, is in reasonable agreement with the result of Fittschen (2019), i.e. σ(7489.16 cm⁻¹) $=\mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹.

3.3 Determination of the CRDS limit of detection

The CRDS limit of detection (LOD) has been computed using plots of the square root of the Allan–Werle variance (Werle et al., 1993; Onel et al., 2017a) obtained by continuously recording single ring-down events for 1–2 h after delivering either acetone or methane in typical concentrations to the chamber filled with the bath gas ($\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ at 80 mbar and synthetic air at 100 and 1000 mbar, respectively). The square root of the Allan–Werle variance, here referred to as the Allan–Werle deviation, σ_A(n), gives an estimate of the error, δα, between successively measured absorption coefficients for a given averaging size n. For a signal-to-noise ratio (S∕N) of 2, the limit of detection for CH₃O₂ was determined as ${\mathrm{LOD}}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=\left(\mathrm{2}\mathit{\delta }{\mathit{\alpha }}_{\min }\right)/{\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$, where ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=\mathrm{1.49}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ is the CH₃O₂ cross section at 7488 cm⁻¹ and is shown in Table 2. The optimum CRDS sensitivity under all conditions is achieved by averaging ∼500 ring-down events, requiring ∼77 s at an acquisition rate of 6.5 Hz on average, with an example shown in Fig. 5.

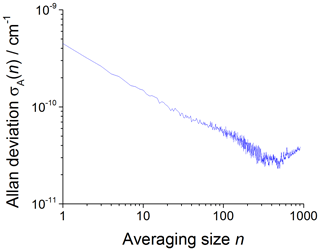
Figure 5 An example of the Allan–Werle deviation plot (the plot of the square root of the Allan–Werle variance) of the absorption coefficient at 7488 cm⁻¹ in the absence of CH₃O₂ and the presence of a typical acetone concentration of 8.8×10¹⁴ molecule cm⁻³ at 1000 mbar against the number of ring-down events averaged, n. For $S/N=\mathrm{2}$, the minimum detectable absorption coefficient for a single ring-down measurement is $\mathrm{4.5}\times {\mathrm{10}}^{-\mathrm{10}}$ cm⁻¹, which decreases to a minimum of $\mathrm{2.89}\times {\mathrm{10}}^{-\mathrm{11}}$ cm⁻¹ after n=500 (requiring 77 s at an acquisition rate of 6.5 Hz).

As the filter (FELH1250 Thorlabs, cut-off wavelength: 1250 nm) used to cut off the laboratory visible light from the background of the CRDS measurements allowed some of the 254 nm light generated by the HIRAC lamps to be transmitted and then detected by the InGaAS photodiode detector, the CRDS sensitivity was worse in the experiments using acetone/O₂ and 254 nm lamps as a source of CH₃O₂ compared to the experiments using Cl₂/CH₄/O₂ and UV black lamps to generate CH₃O₂. Therefore, separate Allan–Werle deviation plots were constructed using measurements of single ring-down events after filling HIRAC with the bath gas and turning the 254 nm lamps on. Then, the composite error, calculated as the sum in quadrature of δα obtained in the presence of acetone and the 254 nm lamps turned off, and δα, determined in the absence of acetone but keeping the 254 nm lamps turned on, were used to determine the LOD of CRDS in the acetone/O₂, and 254 nm light experiments (Table 2). The composite LOD (with acetone/O₂ and 254 nm lamps) was on average ∼55 % greater than the LOD determined with the UV lamps off and in the absence of acetone; on average the LOD with Cl₂/CH₄∕O₂ and UV black lamps was ∼40 % higher than LOD with the bath gas.

Table 2 CRDS detection limits for CH₃O₂ calculated at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and 100 and 1000 mbar of synthetic air for single ring-down measurements (Δt=0.15 s), the optimum averaging time obtained from Allan–Werle deviation plot (Fig. 5 shows an example), Δt_opt. (77 s under all experimental conditions) and Δt=60 s.

^a Using the composite error calculated as the sum in quadrature of δα obtained using a typical concentration of acetone, 8.8×10¹⁴ molecule cm⁻³, and δα determined in the absence of acetone but keeping the 254 nm lamps turned on during all measurements. ^b $\left[{\mathrm{CH}}_{\mathrm{4}}\right]=\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{16}}$ molecule cm⁻³.

As the daytime concentrations of CH₃O₂ have been calculated using an atmospheric box model to peak at ∼10⁷–10⁸ molecule cm⁻³ (Whalley et al., 2010, 2011, 2018), the current CRDS sensitivity is insufficient for the detection of ambient [CH₃O₂]. The typical concentrations of CH₄ and acetone in ambient air are orders of magnitude lower than [CH₄] and [(CH₃)₂CO] used in the HIRAC experiments. However, water vapour, which is present in the atmosphere in much larger concentrations (typically ∼10¹⁷ molecule cm⁻³) than in HIRAC for these experiments (∼10¹³–10¹⁴ molecule cm⁻³) will significantly absorb in this wavelength region and contribute towards the background of the measurements. The limits of detection shown in Table 2 allow for HIRAC measurements of $\left[{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\right]\underset{\mathrm{¯}}{\mathit{\gtrsim }}{\mathrm{10}}^{\mathrm{10}}$ molecule cm⁻³ in steady state (where averaging times of ∼60 s can be used) under all conditions used, and kinetic measurements of $\left[{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\right]\underset{\mathrm{¯}}{\mathit{\gtrsim }}{\mathrm{10}}^{\mathrm{11}}$ molecule cm⁻³ with the present instrument resolution time (0.15 s) at 80 mbar $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and 100 mbar of air.

The relatively long ring-down times achieved here require the lasers to be blocked for several milliseconds during which the full exponential ring-down time is measured. This imposes an upper limit to the ring-down rate. The achieved rate is significantly smaller (6.5 Hz on average) for the following reasons. The width of the resonances of the optical cavity is of the order of 1 kHz, much narrower than the laser linewidth. This makes the injection of light into the cavity inefficient. Reducing the laser linewidth, e.g. with optical feedback techniques, could significantly increase the injection efficiency and the ring-down rate. Moreover, the resonance frequencies jitter and drift due to the unavoidable vibrations associated with the operation of the HIRAC chamber. The cavity length was actively modulated in order to repeatedly force coincidence of laser and resonance frequency. Due to the poor injection efficiency mentioned above, however, not every coincidence resulted in a ring-down event. Furthermore, a significant fraction of the ring-down events have to be discarded because of the passage of dust particles, moved around by the fans within the chamber, through the cavity axis. The use of an additional optical filter to cut off the 254 nm light from the background of the CRDS measurements is expected to improve the CRDS sensitivity if the 254 nm lamps are used in HIRAC. The CRDS sensitivity could be further improved by mounting the cavity mirrors along the HIRAC length, which would result in a cavity of about 2 m length containing CH₃O₂ radicals, and hence above the current 1.4 m length. Although the origin band centred at 7388 cm⁻¹ is about 3 times stronger than the methyl torsional band at 7488 cm⁻¹ (Pushkarsky et al., 2000; Chung et al., 2007), the latter was targeted because absorption due to water vapour is between 1 and 3 orders of magnitude weaker there (assuming 1 % v∕v, atmospheric pressure) (Gordon et al., 2017).

3.4 Intercomparison of CRDS and FAGE CH₃O₂ measurements

All the intercomparison measurements have been performed at 7488 cm⁻¹, where the CH₃O₂ cross section was determined using CRDS (Sect. 3.2). For the measurements at 80 mbar He∕O₂ (3:1) and 100 mbar N₂∕O₂ (4:1), CH₃O₂ was generated either from the photolysis of acetone at 254 nm in the presence of O₂ or from the photolysis of Cl₂ using UV black lamps in the presence of CH₄∕O₂. At 1000 mbar of synthetic air, the overlap of the methane absorption lines due to the pressure broadening resulted in a significant CH₄ absorption over the range from 7486 to 7491 cm⁻¹ in the background of the CH₃O₂ measurements. Therefore, all the measurements at 1000 mbar have been carried out using the photolysis of acetone∕O₂ at 254 nm. The data recorded by CRDS using acetone∕O₂ were more scattered than the CRDS data recorded using ${\mathrm{Cl}}_{\mathrm{2}}/{\mathrm{CH}}_{\mathrm{4}}/{\mathrm{O}}_{\mathrm{2}}$ for the reasons discussed above (see Figs. 6a and 8a in comparison with Fig. 7a) and were the main contributors to the scatter on [CH₃O₂]_CRDS in the correlation plots (Figs. 6b, 7b and 8b below). There was less signal noise present in the FAGE measurements, where the most significant source of noise is the shot noise (Poisson noise), which increases with the number of photons counted by the detector (Figs. 1, S3 and S4) and results in a scatter on the FAGE data growing with [CH₃O₂] in Figs. 6a, 7a and 8a.

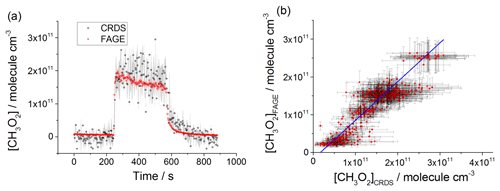
Figure 6 (a) Comparison of CH₃O₂ measurement at 80 mbar He∕O₂ (3:1) where the lamps were turned on at t∼250 s for ∼5 min to generate CH₃O₂ and then turned off again. The measurement by FAGE is shown in red and the measurement by CRDS is plotted in black. CH₃O₂ radicals were generated using the 254 nm photolysis of (CH₃)₂CO (8.8×10¹⁴ molecule cm⁻³). The 1σ statistical errors generated by the data averaging are shown as grey (CRDS) and red (FAGE) shadows. (b) Correlation plot at 80 mbar He∕O₂ (3:1) combining the data obtained using acetone/O₂ and 254 nm lamps with the data generated using Cl₂/CH₄∕O₂ and UV black lamps. [CH₃O₂] measured by FAGE is plotted against [CH₃O₂] measured by CRDS. The linear fit to the data generates a gradient of 1.03±0.05 and an intercept of ($-\mathrm{1.7}\pm \mathrm{0.5})\times {\mathrm{10}}^{\mathrm{10}}$ molecule cm⁻³. The linear fits were generated using the orthogonal distance regression algorithm; fit errors at the 2σ level. In both panels [CH₃O₂]_FAGE was determined using a calibration factor of $\mathrm{3.83}\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹, and [CH₃O₂]_CRDS was calculated using a cross section of $\mathrm{1.49}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. Each point is a value averaged over 3 s.

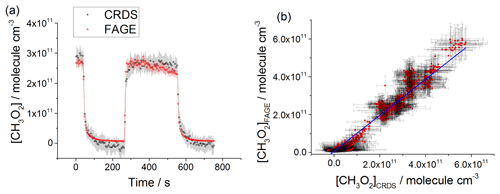
Figure 7 Comparison of CH₃O₂ measurement (a) and the correlation plot at 100 mbar of N₂∕O₂ (4:1) (b). In both figures [CH₃O₂]_FAGE was computed using a calibration factor of $\mathrm{2.80}\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹ and [CH₃O₂]_CRDS was determined using a cross section of $\mathrm{1.49}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. Each point is a value averaged over 5 s. Panel (a) shows the measurement by FAGE (red) and the measurement by CRDS (black) where the CH₃O₂ radicals were generated by the photolysis of Cl₂ (2.5×10¹⁵ molecule cm⁻³) in the presence of CH₄ (2.4×10¹⁶ molecule cm⁻³) and O₂. The UV black lamps were alternately switched on and off: the lamps were turned off at t∼40 s and then turned on at t∼250 s for ∼5 min before being switched off again. The 1σ statistical errors generated by the data averaging are shown as grey (CRDS) and red (FAGE) shadows. Panel (b) combines the data obtained using acetone/O₂ and 254 nm lamps with the data generated using Cl₂/CH₄∕O₂ and UV black lamps. [CH₃O₂] measured by FAGE is plotted versus [CH₃O₂] measured by CRDS. The linear fit to the data is obtained using the orthogonal distance regression algorithm and results in a gradient of 0.95±0.02 and an intercept of $(\mathrm{7.0}\pm \mathrm{0.4})\times {\mathrm{10}}^{\mathrm{9}}$ molecule cm⁻³; fit errors given at the 2σ level.

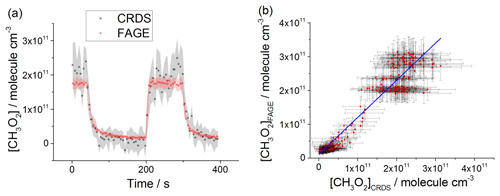
Figure 8 (a) Comparison of CH₃O₂ measurements at 1000 mbar of synthetic air where the lamps were turned off at t∼40 s and then on at t∼200 s for ∼2 min before being switched off again. The measurement by FAGE is shown in red and the measurement by CRDS is plotted in black. CH₃O₂ radicals were generated using the 254 nm photolysis of (CH₃)₂CO (8.8×10¹⁴ molecule cm⁻³). The 1σ statistical errors generated by the data averaging are shown as grey (CRDS) and red (FAGE) shadows. (b) Correlation plot of all the data generated at 1000 mbar of air. [CH₃O₂] measured by FAGE is plotted against [CH₃O₂] measured by CRDS. The linear fit to the data is generated using the orthogonal distance regression algorithm and results in a gradient of 1.09±0.06 and an intercept of ($\mathrm{1.1}\pm \mathrm{0.3})\times {\mathrm{10}}^{\mathrm{10}}$ molecule cm⁻³; fit errors given at the 2σ level. In both panels [CH₃O₂]_FAGE was determined using a calibration factor of $\mathrm{9.81}\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹ and [CH₃O₂]_CRDS was calculated using a cross section of $\mathrm{1.49}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. Each point is a value averaged over 5 s.

As the acquisition rate of CRDS (6.5 Hz in average) differed compared to the FAGE acquisition rate (in the range 1–10 Hz) the comparison data were averaged to enable comparison of [CH₃O₂] by the two instruments at the same moments of time. The averaging interval of time was chosen in the range 3–5 s, depending on the comparison measurement, to average at least 10 ring-down events over each time interval. This was done because the CRDS data were filtered to exclude outliers caused by dust particles passing through the light beam trapped in the optical cavity and the number of encountered “dust events” varied from one experiment to another.

CH₃O₂ was generated over a range of concentrations: 2–26×10¹⁰ molecule cm⁻³ at 80 mbar of He+O₂ mixture, 2–60×10¹⁰ molecule cm⁻³ at 100 mbar of synthetic air and 2–30×10¹⁰ molecule cm⁻³ at 1000 mbar of synthetic air. The comparison involved both periods with lamps on, where the concentration of CH₃O₂ was changing slowly, and where the lamps were turned off and the rapid decay of CH₃O₂ was observed. Figures 6a, 7a and 8a show examples of time-resolved CH₃O₂ concentrations where the lamps were turned on and off. CRDS absorption coefficients were converted into concentrations using the absorption cross section determined by studying the second-order recombination kinetics, σ(7488 cm⁻¹) $=(\mathrm{1.49}\pm \mathrm{0.19})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ (Sect. 3.2). The FAGE signals were converted into [CH₃O₂] using the sensitivity factor derived from the analysis of the temporal decays of CH₃O₂ at 80 mbar of He+O₂ mixture and 100 mbar of air, ($\mathrm{3.83}\pm \mathrm{0.50})\times {\mathrm{10}}^{-\mathrm{9}}$ and ($\mathrm{2.80}\pm \mathrm{0.37})\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹, respectively. The data in the correlation plots of the CH₃O₂ concentrations determined by FAGE (y axis) and CRDS (x axis) (Figs. 6b, 7b and 8b) were fitted using an orthogonal distance linear regression fit (Boggs et al., 1987), which accounts for errors in both the y and x directions. The gradient of the correlation plot of the CH₃O₂ concentrations determined by FAGE (y axis) and CRDS (x axis) at 80 mbar of He+O₂ (Fig. 6b) is 1.03±0.05, showing an overall level of agreement within 3 %. The gradient of the correlation plot of the CH₃O₂ concentrations determined by FAGE (y axis) and CRDS (x axis) at 100 mbar of air (Fig. 7b) is 0.95±0.02, showing an overall level of agreement within 5 %.

At 1000 mbar of air, the FAGE signal observed in HIRAC could be calibrated in one of two ways: either via the photolysis of water vapour to generate OH followed by reaction with CH₄ to form CH₃O₂, or via the kinetic analysis of second-order temporal decays of CH₃O₂. The conversion of the FAGE signals into [CH₃O₂] at 1000 mbar air for the intercomparison with CRDS shown in Fig. 8a and b was based on the average of the results of the water vapour calibration method and the kinetic decay calibration method, which gives ${\stackrel{\mathrm{‾}}{C}}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{9.81}\pm \mathrm{2.03})\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹, Sect. 2.2.2). The gradient of the overall correlation plot (Fig. 8b) using ${\stackrel{\mathrm{‾}}{C}}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ is 1.09±0.06, showing agreement to within 9 %. Figure S7 shows separately the two correlation plots obtained using the sensitivities from the two methods of calibration for FAGE: $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{8.03}\pm \mathrm{1.37})\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹s⁻¹mW⁻¹ (water vapour calibration method) and $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{1.16}\pm \mathrm{0.15})\times {\mathrm{10}}^{-\mathrm{9}}$ counts cm³ molecule⁻¹s⁻¹ mW⁻¹ (second-order kinetic decay method). The gradients of the two linear fits are 1.35±0.07 (water vapour calibration) and 0.92±0.05 (kinetic method of calibration). Therefore, a significantly better agreement (within 8 %) was obtained by using the kinetic method for the calibration of FAGE compared with using the water vapour method for calibration of FAGE (35 % agreement). Better agreement is expected when using the kinetic method to calibrate FAGE, as this is the same method used to determine the absorption cross section and hence calibrate the CRDS method, and the intercomparison is not affected by any error in the rate coefficient, k_obs, for the CH₃O₂ self-reaction. We consider that the main contribution to the discrepancy in $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ values obtained by the two methods of calibration derives from an overestimation of the reported value of the observed rate coefficient for the CH₃O₂ self-reaction, $k_{\mathrm{obs}}=(\mathrm{4.8}\pm \mathrm{0.6})\times {\mathrm{10}}^{-\mathrm{13}}$ molecule⁻¹ cm³ s⁻¹ (1σ error) at 298 K (Atkinson et al., 2006). In a subsequent paper we will report a revised k_obs, which will bring the two methods of calibration into agreement.

4 Conclusions

An intercomparison between the recently developed indirect method for the measurement of the CH₃O₂ radicals using fluorescence assay by gas expansion (FAGE) (Onel et al., 2017b) and the direct cavity ring-down spectroscopy (CRDS) method has been performed within the Leeds Highly Instrumented Reactor for Atmospheric Chemistry (HIRAC). CRDS detected CH₃O₂ by using the A←X (ν₁₂) electronic transition at 7488 cm⁻¹. The CH₃O₂ radical was generated from the photolysis of mixtures of either ${\mathrm{Cl}}_{\mathrm{2}}/{\mathrm{CH}}_{\mathrm{4}}/{\mathrm{O}}_{\mathrm{2}}$ or acetone∕O₂ at room temperature and three total pressures, 80 mbar of $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ and 100 and 1000 mbar of ${\mathrm{N}}_{\mathrm{2}}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{4}:\mathrm{1}$, and CH₃O₂ was measured simultaneously using the two methods.

At all pressures FAGE was calibrated using the kinetics of the CH₃O₂ second-order decay by self-reaction. At 1000 mbar the conventional 185 nm photolysis of water vapour in the presence of excess CH₄ and O₂ was used to calibrate FAGE in addition to the kinetic method. The two calibration methods have overlapping error limits at the 2σ level (34 % for the water vapour photolysis method and 26 % for the kinetic method) as it has been found previously (Onel et al., 2017b). The difference between $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ (water vapour method) and $C_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ (kinetic method) has been discussed in detail previously (Onel et al., 2017b). In the case of HO₂, a very good agreement (difference within 8 %) between $C_{{\mathrm{HO}}_{\mathrm{2}}}$ (water vapour method) and $C_{{\mathrm{HO}}_{\mathrm{2}}}$ (kinetic method) was obtained previously (Onel et al., 2017a; Winiberg et al., 2015), which suggests that the production of OH and HO₂ from the photolysis of water vapour in air can be quantified robustly. We consider it unlikely that there is a significant error in the fraction of OH which is converted to CH₃O₂ upon the addition of methane. We consider instead that the discrepancy between the two calibration methods is due to an overestimation of the reported value of k_obs for the CH₃O₂ self-reaction (Atkinson et al., 2006); the two methods of calibrations agree if k_obs is reduced by 25 %–30 %, which is close to the reported 2σ uncertainty in the rate coefficient (Atkinson et al., 2006). The average value of the sensitivity factor obtained from the two calibration methods, ${\stackrel{\mathrm{‾}}{C}}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{9.81}\pm \mathrm{2.03})\times {\mathrm{10}}^{-\mathrm{10}}$ counts cm³ molecule⁻¹ s⁻¹ mW⁻¹, corresponds to a limit of detection (LOD) for CH₃O₂ of 1.18×10⁸ molecule cm⁻³ for a S∕N of 2 and 60 s averaging period. The FAGE sensitivity factor increased by ∼3 times by decreasing the pressure in the FAGE detection cell (from 3.3 mbar, corresponding to a total HIRAC pressure of 1000, to 0.9 mbar, corresponding to a total chamber pressure of 100 or 80 mbar).

The CH₃O₂ absorption cross section at 7488 cm⁻¹ at 100 mbar of air and 80 mbar of $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$ was determined using the kinetics of the CH₃O₂ second-order decays: ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}=(\mathrm{1.49}\pm \mathrm{0.19})\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹. No change in the shape of the CH₃O₂ spectrum with pressure was found from the reduced pressures (100 mbar of air and 80 mbar of $\mathrm{He}/{\mathrm{O}}_{\mathrm{2}}=\mathrm{3}:\mathrm{1}$) to 1000 mbar of air, showing that ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ is almost independent of pressure. For a time averaging of 60 s, the calculated CRDS LOD using the Allan–Werle deviation plots and ${\mathit{\sigma }}_{{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}}$ is around 8×10⁹ molecule cm⁻³ using acetone/O₂ and 254 nm light at all operating pressures and 6×10⁹ molecule cm⁻³ using CH₄/Cl₂ and black lamps at the reduced pressures.

The FAGE–CRDS intercomparison used measurements of CH₃O₂ under steady-state conditions (photolysis lamps on) as well as rapid decays in [CH₃O₂] (lamps switched off) to cover large concentration ranges: 2–26×10¹⁰ molecule cm⁻³ at 80 mbar of He+O₂ mixture, 2–60×10¹⁰ molecule cm⁻³ at 100 mbar of air and 2–30×10¹⁰ molecule cm⁻³ at 1000 mbar of air. A good agreement between [CH₃O₂]_FAGE and [CH₃O₂]_CRDS was obtained under all conditions as shown by the gradient of the correlation plots: 1.03±0.05 at 80 mbar He∕O₂, 0.95±0.02 at 100 mbar air and 1.09±0.06 at 1000 mbar air (using an average of the sensitivity factors for the two FAGE calibration methods). The study provides a validation for the indirect FAGE method for CH₃O₂ measurements, in agreement with the previous FAGE validation for HO₂ measurements (Onel et al., 2017a).