the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Removing spurious inertial instability signals from gravity wave temperature perturbations using spectral filtering methods
Manfred Ern
Peter Preusse
Martin Riese
Gravity waves are important drivers of dynamic processes in particular in the middle atmosphere. To analyse atmospheric data for gravity wave signals, it is essential to separate gravity wave perturbations from atmospheric variability due to other dynamic processes. Common methods to separate small-scale gravity wave signals from a large-scale background are separation methods depending on filters in either the horizontal or vertical wavelength domain. However, gravity waves are not the only process that could lead to small-scale perturbations in the atmosphere. Recently, concerns have been raised that vertical wavelength filtering can lead to misinterpretation of other wave-like perturbations, such as inertial instability effects, as gravity wave perturbations.
In this paper we assess the ability of different spectral background removal approaches to separate gravity waves and inertial instabilities using artificial inertial instability perturbations, global model data and satellite observations. We investigate a horizontal background removal (which applies a zonal wavenumber filter with additional smoothing of the spectral components in meridional and vertical direction), a sophisticated filter based on 2D time–longitude spectral analysis (see Ern et al., 2011) and a vertical wavelength Butterworth filter.
Critical thresholds for the vertical wavelength and zonal wavenumber are analysed. Vertical filtering has to cut deep into the gravity wave spectrum in order to remove inertial instability remnants from the perturbations (down to 6 km cutoff wavelength). Horizontal filtering, however, removes inertial instability remnants in global model data at wavenumbers far lower than the typical gravity wave scales for the case we investigated. Specifically, a cutoff zonal wavenumber of 6 in the stratosphere is sufficient to eliminate inertial instability structures. Furthermore, we show that for infrared limb-sounding satellite profiles it is possible as well to effectively separate perturbations of inertial instabilities from those of gravity waves using a cutoff zonal wavenumber of 6. We generalize the findings of our case study by examining a 1-year time series of SABER (Sounding of the Atmosphere using Broadband Emission Radiometry) data.
- Article
(6484 KB) - Full-text XML
- BibTeX
- EndNote
In the middle atmosphere, various wave and wave-like processes shape the global structures of temperature and winds. This includes planetary waves (Rossby waves; Salby, 1984), tropical wave modes (e.g. Kelvin waves; Ern et al., 2008; Baldwin et al., 2001), inertial instabilities (Knox and Harvey, 2005) and gravity waves (Fritts and Alexander, 2003; Alexander et al., 2010). These processes usually exhibit very different scales in at least one of the spatial dimensions. For the evaluation of measurement data from ground-based, in situ and satellite instruments, a spatial- or temporal-scale separation of waves and wave-like processes in the atmosphere is key to analysing the effects that one specific process has on the atmosphere. Accordingly, most analysis approaches for gravity wave activity rely on an initial “background removal” using spatial-scale separation to extract only the signal introduced by gravity waves. How efficient different background removals are is highly dependent on the method used and on the kind of other perturbations present.
Recently, Rapp et al. (2018a) derived a global gravity wave temperature perturbation climatology from MetOp GPS radio occultation (GPS-RO) data and found unexpectedly high potential energy densities in the tropics that could not be linked to gravity wave sources. In further investigations, they were able to tie the unexpectedly high gravity wave activity to inertial instability signals remaining in their gravity wave perturbations (Rapp et al., 2018b). They showed the existence of a perturbation structure in their measurements with large horizontal and small vertical extents in the region of interest and demonstrated with a vorticity argument that inertial instability induced those additional perturbations.
Inertial instabilities in a rotating stratified fluid, like the earth's atmosphere, arise from an imbalance between the pressure gradient and the centrifugal forces when the absolute angular momentum decreases with the radius (Dunkerton, 1981). To stabilize the imbalance, horizontal circulation generates transport of angular momentum in the meridional direction. This results in shallow vertical motions accompanying the meridional flow (Rapp et al., 2018b). This flow causes layered temperature perturbations observed around the Equator in the stratosphere (Hitchman et al., 1987; Hayashi et al., 1998; Smith and Riese, 1999). Flow distortion by planetary waves can trigger zonal variations in winter and thereby create local instability that extends into the midlatitudes (Smith and Riese, 1999). Stratospheric inertial instability signals are commonly found at the equatorial stratopause and along channels extending to the winter hemisphere midlatitudes and down into the middle stratosphere (Knox and Harvey, 2005). The analysis of Rapp et al. (2018a) shows the frequent occurrence of midlatitude inertial instability signals around the northern winter solstice.
Gravity waves are small-scale oscillations in the atmosphere that are balanced by buoyancy as restoring force. They are generated mostly in the troposphere by flow over orography, imbalances along jet streams and frontal systems, and convection, e.g. over storm systems (Fritts and Alexander, 2003; Alexander et al., 2010). Breaking and dissipating gravity waves exert drag on the atmospheric circulation. The energy and momentum carried upward by gravity waves contribute to the stratospheric and mesospheric branches of the Brewer–Dobson circulation (Alexander and Rosenlof, 2003; McLandress and Shepherd, 2009; Butchart et al., 2010), the quasi-biennial oscillation in the stratospheric winds (Dunkerton, 1997; Baldwin et al., 2001; Ern et al., 2009, 2014) and the semiannual oscillation at the stratopause (Garcia et al., 1997; Ern et al., 2015). Furthermore, gravity waves contribute to setting the conditions for sudden stratospheric warmings (Wright et al., 2010; Yamashita et al., 2010; Albers and Birner, 2014; Šácha et al., 2016; Ern et al., 2016).
In the last decades, satellite measurements began to allow for insights into global distributions of gravity wave activity (Alexander et al., 2010; Geller et al., 2013). Since the early approaches of Fetzer and Gille (1994), Wu and Waters (1996), and Eckermann and Preusse (1999), many studies have been initiated to collect gravity wave information from space using techniques like limb sounding (Preusse et al., 2002; M. J. Alexander et al., 2008; Wright and Gille, 2011; Ern et al., 2018), microwave sub-limb sounding (McLandress et al., 2000; Jiang et al., 2004b, a; Wu and Eckermann, 2008), infrared (IR) and microwave nadir sounding (Wu, 2004; Eckermann et al., 2006, 2007; Hoffmann and Alexander, 2009; Gong et al., 2012; Hoffmann et al., 2016; Wright et al., 2017; Ern et al., 2017), and GPS-RO (Tsuda et al., 2000; Fröhlich et al., 2007; Schmidt et al., 2008; Wang and Alexander, 2010; Šácha et al., 2014, 2015; Rapp et al., 2018a). All these measurements rely on scale separation to discern gravity wave signals from a background atmosphere.
Historically, different background removal techniques have been applied for different measurement methods because of their specific characteristics (Alexander et al., 2010). For instance, vertical high-pass filters have often been used for GPS-RO measurements, because the observed temperature profiles are quasi-randomly scattered over the globe. For data with very high horizontal sampling, such as from microwave sub-limb and IR nadir observations, local horizontal filters were employed (Wu and Eckermann, 2008; Hoffmann and Alexander, 2010). For data from IR spectrometry sounders, which have both profile information with high vertical resolution and regular coverage of the whole earth, global horizontal low-pass filters have been used. The different background removal techniques also visibly influence the spectrum of waves in the residual data; thus, the background removal is an important part of the observational filter.
Alexander (1998) first discussed the influence of observational filters from different measurement systems, which may largely alter the apparent global distributions (Preusse et al., 2001). This implicitly includes the influence of different background removal techniques. John and Kumar (2012) then compared the influence of using different background removal methods for the same data set. They found that the difference introduced by the application of vertical instead of horizontal filtering exceeds the differences between data sets applying the same method significantly. Schmidt et al. (2016) confirmed that different techniques (in particular vertical spectral filtering versus horizontal S-transform analysis) have a large impact on the global gravity wave activity results, especially comparing gravity wave potential energy densities and gravity wave momentum flux estimates. In addition, they strongly recommend to use horizontal filtering for the detrending. On the one hand, vertical filtering underestimates gravity wave activity in the polar vortex region, where high wind speeds refract waves to larger vertical wavelengths. On the other hand, vertical detrending may overestimate gravity wave activity due to remnant signals from synoptic and planetary waves and their small vertical scale in the tropics. Inertial instabilities have not been considered in these discussions.
Rapp et al. (2018b) further showed in their study that subtracting a large-scale background estimated from ERA-Interim reanalysis temperatures can eliminate spurious inertial instability signals from the gravity wave temperature perturbations and leaves gravity wave activity around the polar vortex. In a comment on this study, Harvey and Knox (2019) pointed out that it is not clear how often inertial instability-induced variations have been misinterpreted as gravity wave signals in the past. They argue that the signals from inertial instabilities, if present, have to be identified consciously by investigating the large-scale meteorologic situation in areas prone to inertial instability.
In this study, we focus on the data with vertical profile information. We investigate the application of both vertical and horizontal gravity wave background removal on different temperature data sets that incorporate inertial instability signals, and we evaluate to what extent the background removals are able to remove these instability signals from the gravity wave perturbations. In particular, we evaluate what cutoff length scales are optimal as a compromise between preserving the full gravity wave spectrum and removing more remnant structures due to inertial instabilities. For a first approach to the topic, we start by analysing artificial inertial instability perturbations. The structure was modelled according to the conditions found for a strong inertial instability event in December 2015, as previously discussed in Rapp et al. (2018b). Then, we focus on a vertical and horizontal filtering approach on ERA5 temperatures. Accordingly, the methodic limitations of vertical- and horizontal-scale separation approaches can be tested by showcasing the challenge of removing a background in a more complex atmospheric data set, where inertial instability signals, gravity wave perturbations and other fluctuations are simultaneously present. Furthermore, we investigate the sensitivity of the methods on the removed characteristic length scales to estimate an optimal cutoff parameter in the particular case. Lastly, we evaluate the performance of a dedicated SABER (Sounding of the Atmosphere using Broadband Emission Radiometry) background removal, as introduced by Ern et al. (2011, 2018), in time and longitude dimensions in comparison to the Butterworth filter applied by Rapp et al. (2018a, b) with respect to spurious inertial instability signals and the reliability of the background removals for the December 2015 case as well as in the course of 1 year of SABER data.
This paper is structured as follows: Sect. 2 describes the different data sets we use in the study. Section 3 introduces the background removal techniques and measures for evaluating the resulting perturbations. In Sect. 4, we apply these techniques to the data and assess their performance, and Sect. 5 summarizes our findings.
For different steps of our analysis, we utilize the characteristics of satellite observations, realistic atmospheric reanalysis data and an idealized data set that only contains inertial instability perturbations. Satellite measurements give unique information by providing global sampling on real observations. The reanalysis data set has the advantage of covering a large range of spatial and spectral scales without being restricted to a specific irregular sampling. The artificial perturbation model gives us the opportunity to see how the background removal techniques are influencing an isolated inertial-instability-like signal. Any residual fluctuations after applying the background removal then indicate remnant inertial instability signals that should not be attributed to other processes. In realistic model data sets or measurement results, possible remnants signals might belong to the gravity wave activity we eventually want to infer. This section describes the various data sets.
2.1 SABER temperatures
The Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) instrument is operated on board the Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) satellite, which was launched in December 2001 and is still operational to this date. The limb-sounding instrument records profiles of the atmospheric radiation by scanning its viewing direction vertically and covers a large altitude range from the tropopause to well above 100 km. For this study, we are mainly interested in the stratosphere and hence consider altitudes ≤60 km. The tangent-point track, i.e. the track of observation points, is roughly 2000 km away from the orbital track. Temperatures are predominantly retrieved from the 15 µm CO2 infrared band. Retrieval results are provided in vertical profiles with about 2 km vertical resolution, 400 m vertical sampling and spaced on average 400 km along the tangent-point track. Detailed information on the retrieval is summarized in Remsberg et al. (2008).
The TIMED satellite covers almost the whole globe with ∼15 orbits d−1. Hence, waves up to a zonal wavenumber of 6 to 7 can be resolved along a latitude circle (Salby, 1982). Furthermore, the satellite performs yaw manoeuvers close to every 60 d. This alternates the SABER viewing geometry between 50∘ S to 82∘ N (northward viewing) and 82∘ S to 50∘ N (southward viewing). While latitudes equatorward of 50∘ are covered continuously, the higher latitudes are only covered 60 d in every 120 d.
According to Remsberg et al. (2008), the precision, i.e. the random instrument error, for the SABER temperature measurements in the V1.07 retrieval results is 0.3 to 0.6 K (mean at 0.45 K) in the stratosphere (between 20 and 50 km altitude). The precision error is predominantly related to pointing jitter. Somewhat stronger pointing jitter than mentioned in Remsberg et al. (2008) was recently reported by Wing et al. (2018). Furthermore, there is a geopotential bias with complex vertical structure. Therefore, precision estimates in Remsberg et al. (2008) may be somewhat too low. In this study we use temperatures obtained with the V2.0 retrieval algorithm. Ern et al. (2018) and the official SABER website (http://saber.gats-inc.com/temp_errors.php, last access: 15 September 2020) report that there are no changes in the retrieval between V1.07 and V2.0 that would impact the precision of the temperature estimates, but the overall accuracy could be altered.
2.2 ERA5 temperatures
ERA5 is the newest reanalysis product based on the 4D-Var data assimilation of ECMWF's Integrated Forecast System (IFS). In the simulation, the grid consists of 137 hybrid model levels with a top at 0.01 hPa. In the stratosphere, the hybrid levels are less than 1 km apart. The IFS is a spectral system. In version cy41r2, the model has a horizontal resolution of ∼0.28∘ or ∼31 km. Power spectral analysis showed that only gravity waves with wavelengths larger than a few grid points (6Δx; in this case ∼1.7∘) may be expected to be well resolved in the model output (Jewtoukoff et al., 2015). Recently, ERA5 has been shown to represent the stratospheric temperature structure with more details than other reanalysis products (Wright and Hindley, 2018).
For our analysis, we use a global interpolated field regularly sampled to km (longitude × latitude × altitude) resolutions. Hence, we expect an effective resolution of ∼180 km at the Equator or ∼90 km at 60∘ latitude. This covers a large range of the gravity wave spectrum as well as inertial instability signals.
2.3 Artificial inertial instability perturbations
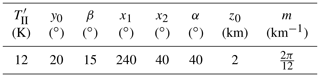
We construct a simple model of artificial inertial instability temperature perturbations () to first evaluate the ability of the background removal on isolated signals. In building the model, we consider both the theoretical knowledge about the spatial structure of stratospheric inertial instability effects (Dunkerton, 1981; Knox and Harvey, 2005) and the situation observed in the particular inertial instability case on 3 December 2015. For each location x (where ), the perturbation value is derived from a constant temperature offset and three independent spatial shape functions w∗ to form the structure.
Following the findings from Dunkerton (1981), we use the first derivative of a Gaussian as meridional component.
The symmetric structure is centred around the latitude y0 and defined by a characteristic width β.
In the vertical, we apply a sinusoid with a given vertical wavenumber m to fit the wave-like “pancake” structure. The lowest level with zero perturbation is defined by z0.
For the zonal dimension, we use a step function with smoothed transition to zero in order to restrict the structure to about a third of a latitude circle, since midlatitude inertial instability signals are often constrained in a so-called “channel” (Knox and Harvey, 2005). To define the step function, we use the edge longitudes x1 and x2, which enclose the longitude range containing the nonzero perturbations, and a width α for the smooth transition from weights 0 to 1. To simplify the notation, we use and as auxiliary parameters.
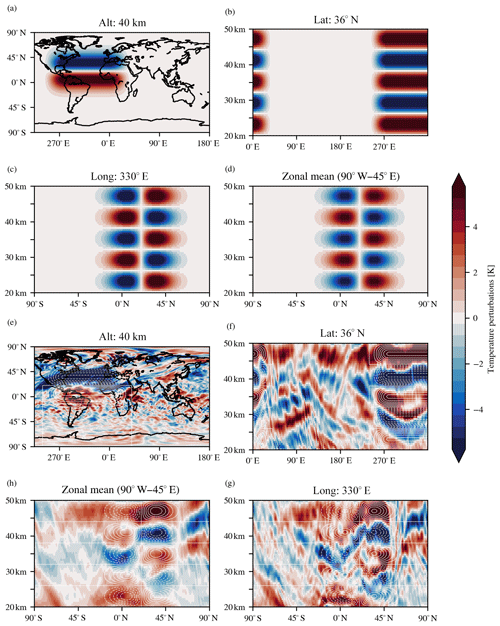
Figure 1Cross sections of temperature perturbations of the artificial inertial instability, we defined in Sect. 2.3, are shown in the upper row: (a) a longitude–latitude cross section at 40 km altitude (black contours mark the coastlines), (b) a longitude–altitude cross section along the 36∘ N latitude circle, (c) a latitude–altitude cross section along the 330∘ E meridian and (d) the zonal mean in the longitude band from 90∘ W to 45∘ E (in the style of Fig. 1b in Rapp et al., 2018b). Panels (e)–(g) show the respective plots as panels (a)–(d) from the ERA5 gravity wave temperature perturbation by applying the fifth-order Butterworth vertical filter with cutoff wavelength of 15 km. For easy comparison, the white contours in the lower row plots show the temperature perturbation levels of the artificial inertial instability in 2 K steps (solid lines indicate positive values, dotted lines negative values).
In order to constrain the free parameters of the three shape functions, we refer to the case of 3 December 2015. Based on a 1-year survey of GPS-RO temperature anomalies and a climatological analysis of ERA-Interim data by Rapp et al. (2018b), this case of 3 December 2015 is a particularly strong one. The vertical and horizontal scales of the inertial instability are representative for typical winter conditions. The same inertial instability signals can also be found in ERA5 and SABER temperatures, as will be discussed in more detail in Sect. 4. Figure 1 shows vertical, longitudinal and latitudinal cross sections as well as the zonal mean structure in a restricted longitude band (similar to Fig. 1b in Rapp et al., 2018b). The upper row depicts the structures of the artificial data set based on Eqs. (1) to (4) and the parameters from Table 1 to generate the structure illustrated. The lower row gives the corresponding plots from ERA5 gravity wave temperature perturbations, calculated using vertical filtering with a fifth-order Butterworth filter with a cutoff vertical wavelength of 15 km. (The definition of gravity wave temperature perturbations and the Butterworth filter will be explained in more detail in Sect. 3.4 and 3.1, respectively.) The lower row also shows the modelled inertial instability signal as white contours for comparison with the ERA5 structures.
In the analysis, we have to distinguish between “regularly sampled” such as outputs from an atmospheric model and “sparsely sampled” such as observations by satellite instruments, though both kinds of data sets are global. This section describes the various methods for background removal applicable to these different data sets.
3.1 Vertical filtering
As a first approach to a background removal, we apply a Butterworth filter defined by a window function H(λz):
with the cutoff wavelength λc. The vertical wavelength is defined as and m represents the vertical wavenumber. The order of the Butterworth window is given by n.
The Butterworth filter was used by Rapp et al. (2018a, b) in their analysis of MetOp GPS temperature profiles and previously introduced in detail by Ehard et al. (2015). Vertical filtering has the advantage that it can be applied profile-wise without assuming any correlation between (adjacent) profiles. It is therefore particularly suited for GPS-RO and ground-based lidar measurements (Rapp et al., 2018a), but it can also be employed easily on model products like ERA5 or the artificial inertial instability signals, which we built in Sect. 2. The Butterworth filter is a high-pass fast Fourier transform (FFT) filter; i.e. we define the gravity wave perturbation as the inverse transform from Fourier space, where scales longer than the critical vertical wavelength λc were smoothly removed by convolving the Butterworth window.
Where we refer to vertical filtering by default in this paper, we use n=5 and λc=15 km as previously applied in Ehard et al. (2015, 2017) and Rapp et al. (2018a, b). This is the case in particular when analysing the satellite data. In Sect. 4.3, we include an analysis of different cutoff vertical wavelengths λc for the artificial inertial instability modelled perturbations and the ERA5 gravity wave temperature perturbations (see Figs. 2, 5 and 6).
3.2 Horizontal filtering for global, regularly sampled data sets
For horizontal filtering in regularly sampled, global snapshots, we apply zonal FFT in the longitude direction to provide a zonal wavenumber spectrum for each altitude and latitude. The background is defined as the low-pass band up to a cutoff wavenumber, kc; i.e. we set the spectral components corresponding to wavenumbers larger than kc to zero. If not stated differently, we apply a cutoff zonal wavenumber kc=6 in the stratosphere. This cutoff has been used in a large number of previous studies on low earth orbiter (LEO, e.g. Fetzer and Gille, 1994; Ern et al., 2018, and references therein). Additionally, we apply a Savitzky–Golay polynomial smoothing on the spectral components in both meridional and vertical direction. We use a fourth-order polynomial on 11 points in the vertical and a third-order polynomial on 25 points in the meridional dimension. Inverse FFT from the spectrum yields a 3D background field containing the large-scale signals. The gravity wave temperature perturbations are then defined by subtracting this background pointwise from the original temperature field.
Zonal spectral filtering is an intuitive solution for a background removal in regularly sampled, global data sets such as general circulation model outputs of free-running models as well as assimilation products like reanalyses. The temperature and wind fields along the latitude circle are naturally periodic, and with a regular (ideally high-resolution) sampling, an FFT analysis is directly applicable.
3.3 Time–horizontal filtering for limb-sounder data
The background removal from Ern et al. (2011) is especially tailored to the sampling pattern of limb sounders on LEO satellites and was applied to SABER and HIRDLS (High Resolution Dynamics Limb Sounder) in the GRACILE climatology (Ern et al., 2018).
SABER provides a global coverage over the course of 1 d. Applying a similar background removal, as for a global model data set, is a reasonable approach. However, data at a given latitude from the ascending or descending orbits are collected at the same local time rather than at the same universal time considering periods as short as a few days. This is the case because the orbit of the TIMED satellite is only slowly precessing. The period of 1 d, which SABER requires to collect the data for one global coverage, is close to the shortest period of planetary waves such as the quasi 2 d waves in the mesosphere (e.g. Ern et al., 2013) or fast modes in the southern polar vortex. Accordingly, the phase shifts in this observation period and the observed structures are not longer cyclical in the longitude direction. In addition, there are gaps between the measurement tracks. Satellite data hence require a more complex background removal including the temporal development.
The observation geometry of a LEO satellite limits the range of zonal wavenumbers and frequencies in which space-time spectra can be uniquely obtained (Salby, 1982). These limits allow us to capture the periods of all Rossby wave modes (Salby, 1984) and equatorial wave modes (Kim et al., 2019). Furthermore, space-time spectra within the geometry limits have been proven to be mathematically correct for all permitted wavenumbers and frequencies (Salby, 1984).
The use of time–longitude spectra also prevents influences of day-to-day variations in the atmospheric background due to short-period travelling planetary waves (Ern et al., 2016, 2018). Due to the characteristic scales of inertial instabilities (long horizontal, short vertical and long temporal with respect to the gravity wave spectrum), they should be easily separable from gravity waves by considering the zonal and time dimensions rather than the vertical dimension.
Ern et al. (2011, 2013) have developed such a dedicated background removal for limb-sounding satellite temperatures by taking both the zonal and temporal dimensions into consideration for the spectral analysis. With the relatively low resolution of the satellite temperatures in longitude and time, gravity wave signatures appear as a uniform white-noise background level in longitude–time spectra. This white-noise spectrum has to be retained after the background removal. Global-scale waves, on the other hand, exceed this white-noise level and should be removed. Ern et al. (2011) used a factor of 5 above the average squared spectral amplitude of the white-noise spectral floor to define a threshold for separating between gravity wave signal and global-scale waves. The method uses overlapping 31 d time windows shifted by 15 d in each step. Spectra include zonal wavenumbers 0–6 and frequencies up to 0.7 cycles per day. In order to compute the spectra, the SABER profiles are interpolated in the vertical and along the observation tracks onto a fixed altitude–latitude grid.
In order to determine the residual temperature fluctuations, the background is reconstructed for the precise location and time of each observation. First, spectra are interpolated in altitude and latitude. The background for the observation longitude and time is then evaluated as the superposition of the single, global-scale waves with significant spectral amplitudes using their spectral amplitudes and phases. In addition, the mean background temperature defined as the 31 d average plus a linear trend is taken into account. Eventually, the method defines the gravity wave temperature perturbation at a particular location and altitude by subtracting the average local background temperature (averaged from the mostly two background temperature estimates) from the overlapping time windows. In addition, in a second step the most relevant tidal modes in stratosphere and mesosphere are explicitly removed (Ern et al., 2013). Lastly, an additional broad correction is applied that helps to calculate follow-up parameters such as gravity wave momentum flux: a dominant vertical oscillation with vertical wavelength λz≥40 km is removed to correct for remnants of quasi-stationary planetary waves and to limit the gravity wave spectrum to vertical wavelength short enough to be covered by the momentum flux estimation procedure.
We apply this method as a horizontal background removal to SABER profiles in the rest of this study.
3.4 Diagnostic quantities
Linear gravity wave theory is based on the assumption that the total state of any atmospheric variable, e.g. temperature T, can be defined as a sum of a background state, , and gravity wave perturbations, T′, i.e.
The background state is the superposition of a mean temperature profile and the large-scale influences like planetary wave and synoptic inertial instability conditions at each instance in space x (long, lat, alt) and time t.
The variance var(T′) of the zonal mean gravity wave temperature perturbation T′, also referred to as gravity wave variance, has been used as a diagnostic quantity for gravity wave activity in measured and modelled atmospheres early on (e.g. Fetzer and Gille, 1994) and is also the basis for our analysis.
In Eq. (7), triangular brackets “〈.〉” represent a zonal mean at a specific snapshot or time range and N stands for the number of averaged values. This quantity shows “true” gravity wave structures in the data if the background removal can be considered a good estimate for the large-scale fluctuations.
In addition, the zonal mean gravity wave temperature perturbation 〈T′〉 is defined as
In the previous subsections, we have introduced two different general methods to separate temperature perturbations from a background that we want to apply in this study – horizontal and vertical spectral filtering. Resulting gravity wave temperature perturbations, T′, are used to calculate more complex diagnostics like gravity wave potential energy densities and gravity wave momentum fluxes to create climatologies of gravity wave activity.
In the case of horizontal filtering, in particular zonal wavenumber filtering, 〈T′〉 is expected to contribute only negligibly to the gravity wave variance, since the zonal average of the temperature state was already subtracted in the definition of the gravity wave temperature perturbations. After vertical filtering, 〈T′〉 is not necessarily small, since the perturbations were estimated in a way that is independent of the zonal structure of the background state. In this situation, gives a good measure for background state remnants in the derived gravity wave perturbations, as shown by Rapp et al. (2018b).
In the ideal case, however, 〈T′〉 is zero or at least very small in comparison to the gravity wave perturbations that are analysed. Then, the zonal mean squared gravity wave temperature perturbation is representative for the gravity wave variance.
The advantage of using rather than var(T′) is that it is consistent with local averages such as used in global maps or spectra and which cannot rely on a zonal mean average.
4.1 A remnant signal threshold for a “successful” background removal
For evaluating gravity waves in real or realistic data, it would suffice to check if the spurious inertial instability remnants in the estimated gravity wave perturbations are smaller than the targeted gravity wave signals. However, the quantification of the gravity wave signal is the purpose of the analysis itself and, hence by definition, not known a priori. It therefore cannot be used as a reference for successful background removal.
For the removal of the background from real observations, it is necessary to define a success criterion. In our approach, the background with respect to gravity waves contains global-scale variations caused by, for example, planetary waves and signals from inertial instabilities. We consider a background removal as successful if the background remnants are smaller than the errors introduced by the measurement method and the retrieval. The error budget of an instrument is usually described by precision and accuracy, where accuracy describes “systematic” errors which are present in a similar magnitude on the entire data set and precision refers to the noise-like errors that affect a measured parameter randomly. In the observation of fluctuations, like gravity waves, the uncertainty is closer linked to the precision than to the accuracy of the instrument, since errors characterized by accuracy are removed together with the background. The magnitude of both accuracy and precision usually vary with altitude. Based on this approach, we use the minimal precision value of the SABER instrument reported for the stratosphere of 0.3K (Ern et al., 2018, and references therein) as a threshold for a successful background removal. For most of the stratosphere and for the mesosphere, this threshold is more conservative than the targeted detection limit for gravity waves.
4.2 Removing artificial inertial instability signals: minimum appropriate filter cutoff for vertical and horizontal background removals
A spectral background removal will usually remove global-scale variations gradually (i.e. each global-scale process is described by several spectral components), and the more wavenumbers are removed the more the background signal is removed as well. The success criterion defined above then allows us to identify threshold characteristic vertical wavelengths or zonal wavenumbers for horizontal or vertical background removals, respectively. In particular, this can be directly applied on the synthetic data. In our artificial inertial instability data set, we can test the different approaches and find the criterion for a successful background removal matched when the mean squared gravity wave temperature perturbation (cf. Eq. 9) falls below 0.09 K2.
Figures 2 and 3 show altitude–latitude cross sections of the zonal temperature variance (cf. Eq. 7) for the artificial inertial instability data (see Sect. 2). In Fig. 2, vertical filtering is applied with decreasing cutoff vertical wavelengths, and in Fig. 3 horizontal filtering is applied with increasing cutoff zonal wavenumbers. The layered pancake structures are a persistent feature, but eventually both methods vertical filtering at cutoff wavelength 6 km (see Fig. 2f) and horizontal filtering at cutoff wavenumber 7 (see Fig. 3f) remove the signal with remaining remnants of less than 0.05 K2 magnitude. This value is even smaller than the threshold of the success criterion we defined in Sect. 4.1.
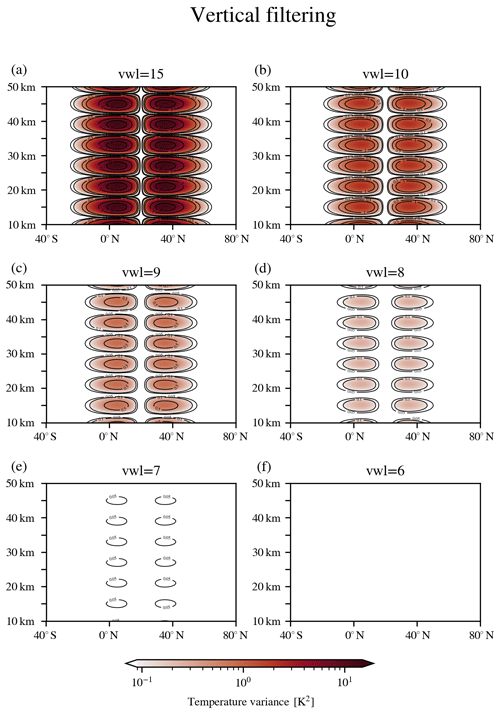
Figure 2Zonal temperature variance of artificial inertial instability temperature perturbations after vertical filtering (fifth-order Butterworth) with a cutoff wavelength of (a) 15 km, (b) 10 km, (c) 9 km, (d) 8 km, (e) 7 km or (f) 6 km.
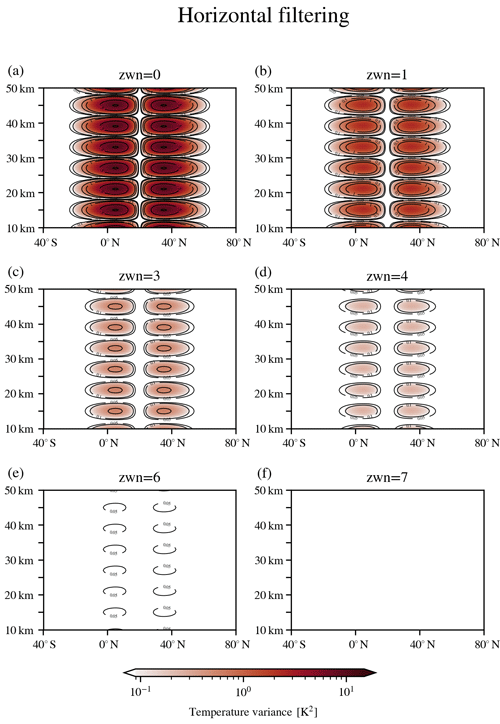
Figure 3Zonal temperature variance of artificial inertial instability temperature perturbations after horizontal filtering (zonal mean with additional smoothing in meridional and vertical components) with cutoff zonal wavenumber (a) 0, (b) 1, (c) 3, (d) 4, (e) 6 or (f) 7.
We chose most of the cutoff limits to match values used in previous satellite studies. Figure 2a shows the structure after removing vertical wavelengths down to 15 km, as used by Rapp et al. (2018b). A similar level of removal is reached by applying cutoff zonal wavenumber 0 in the horizontal filtering case (see Fig. 3a). A cutoff wavelength of 10 km as used in Fig. 2b was used before by Tsuda et al. (2000) and Alexander and Barnet (2007) for vertical filtering. However, it has been shown that this cutoff removes a significant part of the gravity wave spectrum important for the middle atmosphere (Preusse, 2001; Preusse et al., 2008; Alexander et al., 2010). In our case, horizontal filtering with cutoff zonal wavenumber 1 (see Fig. 3b) gives a similar temperature variance result. On the other hand, M. J. Alexander et al. (2008) applied horizontal filtering with cutoff zonal wavenumber 3 using an S-transform approach. Figure 3c shows the temperature variance structure after removing zonal wavenumber 3. On the vertical filtering side, a similar result is achieved with a cutoff wavelength of 9 km (see Fig. 2c). The values of cutoff vertical wavelength 8 km or cutoff zonal wavenumber 4 were not used in previous studies, but the results show an intermediate value for the remnants (see Figs. 2d and 3d). The horizontal filtering with cutoff wavenumber 6 (see Fig. 3e) is the first to fall below the precision threshold of 0.09 K2. A number of studies used this cutoff previously (e.g. Fetzer and Gille, 1994; Preusse et al., 2002; Ern et al., 2018), since zonal wavenumber 6 is close to the sampling limit for infrared sounders on LEO. The vertical filtering variance magnitude counterpart here is found at a cutoff wavelength of 7 km (see Fig. 2e). Finally, with vertical cutoff at 6 km and horizontal cutoff at 7, the zonal variance decreases even to <0.05 K2 (see Figs. 2f and 3f).
4.3 Compromise between removing inertial instability remnants and preserving gravity wave signals in ERA5 temperatures
The upper row of Fig. 4 shows zonal mean structures of gravity wave temperature perturbations (cf. Eq. 8) from ERA5 data on 3 December 2015, 00:00 UTC, after applying different filtering methods. As an indication for significance, we also show the standard deviation of the zonal means, calculated as (cf. Eq. 7), in the lower row. The zonal mean gravity wave temperature perturbation for vertical filtering with cutoff wavelength 15 km (cf. Fig. 4a) displays strong layered bands of vertically alternating positive and negative peaks at the Equator, i.e. spanning from 20∘ S to 20∘ N, as well as in the midlatitudes approximately between 30 and 45∘ N. This shows the presence of the inertial instability also in the ERA5 data. Equatorial values are phase-shifted by 180∘ with respect to values at the midlatitudes, as expected from theory (Dunkerton, 1981) and found in previous inertial instability observations (Hayashi et al., 1998; Smith and Riese, 1999; Rapp et al., 2018b). The midlatitude stack widens in meridional extent with altitudes between 20 and 45 km, while the tropical feature narrows. The main pancake structures are significant, i.e. larger than the corresponding standard deviations.
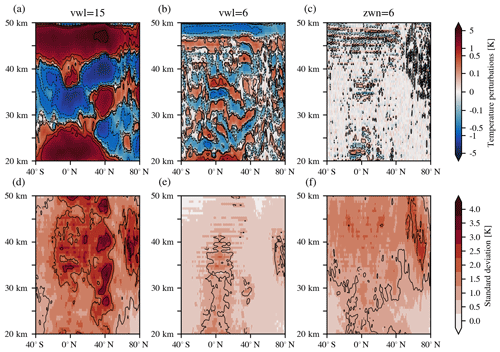
Figure 4Zonal mean gravity wave temperature perturbations inferred from ERA5 temperatures for 3 December 2015, 00:00 UTC, after (a) vertical Butterworth filtering with 15 km cutoff wavelength, (b) vertical Butterworth filtering with 6 km cutoff wavelength and (c) horizontal FFT filtering with cutoff zonal wavenumber 6 and additional vertical and meridional smoothing in panels (a)–(c). In panels (d), (e) and (f), we show the respective standard deviations of panels (a), (b) and (c). Contours show indicated temperature perturbation levels to highlight the structure.
The other two panels in Fig. 4 show the zonal mean gravity wave temperature perturbations for the cutoffs, which provide the best removal of our artificial inertial instability signals (see Sect. 4.2). In the middle panels (Fig. 4b and e), we applied vertical filtering with a cutoff wavelength of 6 km. The mean gravity wave perturbations still show layered structures, in particular in the latitude bands where the pancake structures were found for a cutoff at 15 km. The magnitudes, however, are less than 1 K and overall insignificant. In the tropics (approximately from 20∘ S to 20∘ N), higher values in the standard deviation point to signals that have smaller vertical scales than the removed inertial instability. The symmetric structure around the Equator with a smooth Gaussian-like peak and a half-width of approx. 10∘ indicates that this maximum may be attributed to Kelvin waves (Smith et al., 2002). On the right (Fig. 4c and f), we applied horizontal filtering with a cutoff at wavenumber 6. Except for a few spots above the tropical tropopause (around 5∘ S and below 25 km), at high latitudes (north of 60∘ N) and high altitudes (above 35 km), the zonal mean does not show structures exceeding 0.01 K. The standard deviation, however, shows enhancement at higher altitudes and in particular in a wide range of latitudes associated with the polar jet. Though there may be some structures caused by horizontal gradients at the vortex edge, this enhancement spans approx. 30∘ of latitude and hence indicates real gravity wave activity. This feature is also present in the two other standard deviation plots and will be discussed in more detail later on.
We have seen already that the quality of a spectral filtering is highly dependent on the cutoff length scale used. Ideally, a transition between mesoscale and synoptic-scale fluctuations (previously referred to as “spectral gap”) can be identified, where the temperature variance will be insensitive to the cutoff length separating gravity wave activity at small scales and mesoscales from global-scale inertial instability signals. However, such a transition is not necessarily present in the stratospheric temperature variance (and very unlikely to be found in the troposphere).
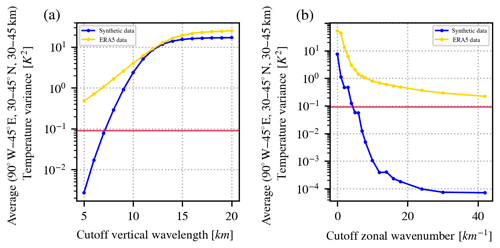
Figure 5Dependence of mean temperature variance in a box of 90∘ W to 45∘ E longitude, 30 to 45∘ N latitude and 20 to 50 km altitude on the characteristic cutoff length scale for different filtering methods: (a) vertical fifth-order Butterworth filter with cutoff in the vertical wavelength and (b) horizontal FFT filter with additional smoothing in vertical and meridional direction and cutoff in zonal wavenumber. In each plot, the blue line represents results from filtering the artificial inertial instability perturbations and the yellow line shows the corresponding results from ERA5 temperatures. The red horizontal line marks 0.09 K2 as precision threshold of the SABER instrument.
With its dense regular sampling, the realistic global ERA5 temperature data allow for a sensitivity study with respect to temperature variances on the cutoff length scales for a wide range of cutoffs of both vertical and horizontal filtering. Figure 5 shows the dependence of temperature variances on the background removal. The variances are calculated using Eq. (9), but here the average is defined over a domain from 90∘ W to 45∘ E longitude, 30 to 45∘ N latitude and 20 to 50 km altitude instead of one latitude circle. This region is chosen, as Fig. 1 shows, to contain the largest inertial instability signal. The two panels of Fig. 5 show the scaling behaviour for (a) vertical filtering with cutoff vertical wavelength in the range 5 to 20 km and (b) horizontal filtering from cutoff zonal wavenumber 0 to 42. The yellow curve shows results for ERA5 data at 3 December 2015 at 00:00 UTC and the blue curve for the artificial inertial instability constructed as described in Sect. 2.3. We use the blue curve as a reference for how a pure inertial instability signal is affected by the background removals.
Different sensitivities of the mean temperature variance for more rigorous filtering are evident. For vertical cutoff wavelengths larger than 15 km, the averaged variance of ERA5 temperatures increases slowly with a linear gradient. In the same cutoff wavelength range, the variance stays mostly constant in the artificial inertial instability perturbations data. The gradient becomes gradually steeper in both data sets between 15 and 10 km. In this range, where both data sets show similar behaviour, the averaged temperature variance is likely dominated by the inertial instability signal. The gradient for the ERA5 data remains similar also for cutoff vertical wavelengths shorter than 10 km, while for the artificial inertial instability data the decrease continues to steepen. This different behaviour indicates a switch to gravity waves as the dominant dynamics process, which is missing in the artificial inertial instability perturbation data.
The sensitivity of temperature variance to increasing cutoff zonal wavenumbers shows a range of cutoffs where both the realistic ERA5 data as well as the artificial inertial instability perturbation data behave in a comparable way. From cutoff zonal wavenumber 1 to 6, both curves of averaged temperature variances are decreasing fast, indicating the dominance of the inertial instability signal. At wavenumber 6 there is an abrupt change in the variance decrease in ERA5 data, and the slope continues to change between wavenumbers 6 and 12. At wavenumbers above cutoff zonal wavenumber 12, the gradient is about constant. In comparison, the decrease of the temperature variances for the artificial perturbation data continues up to wavenumber 12 and then directly switches to stagnation at extremely small averaged temperature variances. The fact that the averaged temperature variance for the synthetic inertial instability stays constant at wavenumbers 2 and 3, wavenumbers 5 and 6, and wavenumbers 10 and 12 in the artificial data is likely connected to the regular structure of the modelled inertial instability, which spans over approximately a third of the latitude circle.
Similar to the vertical filtering case, we interpret similarities and differences in the variances of the two data sets. The variance is likely dominated by the inertial instability influence up to wavenumber 6. For wavenumbers larger than 7, gravity waves are taking over as the most dominant process, though up to wavenumber 12 there may be remnants of the inertial instability. The slow decrease at high wavenumbers shows that eventually energy is taken out of the gravity wave scales as well.
4.4 Situation in a climatology
The diagnostics shown for gravity wave climatologies from measurement or model data are usually energy quantities like gravity wave potential energy densities (Tsuda et al., 2000; de la Torre et al., 2006; Rapp et al., 2018b) or gravity wave momentum fluxes (Ern et al., 2004, 2018; Wang and Alexander, 2010; Alexander, 2015). These quantities are not calculated from gravity wave variances (Eq. 7) but using a spatial average of the squared gravity wave temperature perturbation (Eq. 9). Figures 6 and 7 show the zonal mean structure of ERA5 squared gravity wave temperature perturbations for vertical and horizontal filtering employed with different scales of the background removal. Similar to Figs. 2 and 3, the different cutoff length scales are mostly chosen according to levels that have been used in previous studies. For the vertical filtering, we limit the presented results to cutoff vertical wavelengths of 15 km (Fig. 6a), 10 km (Fig. 6b) and 6 km (Fig. 6c). The first two were used in studies by other groups before, while the 6 km cutoff marks the transition point in our sensitivity curve (Fig. 5) where the gravity wave signal dominated the temperature variance in the stratosphere. For the horizontal filtering, we used cutoff zonal wavenumbers at 0, 1, 3, 4, 6 and 7 as used before for the artificial data. Furthermore, we add the higher-order cutoffs at wavenumber 12, 18 and 42 to the figure to evaluate how the structures are changing if more wave components are removed then necessary to eliminate the inertial instability structures.
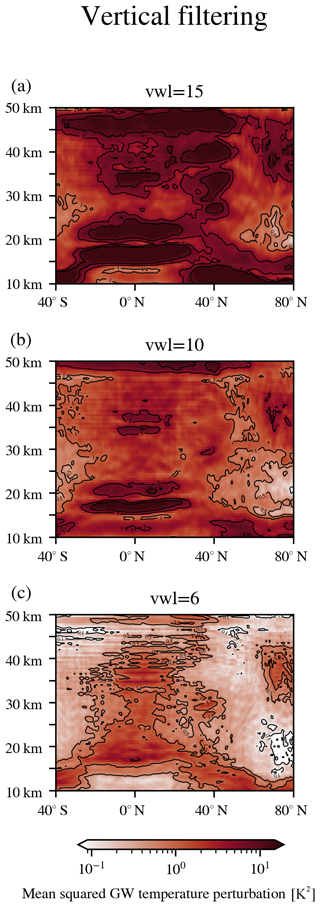
Figure 6Vertically filtered (fifth-order Butterworth) zonal mean squared gravity wave temperature perturbations (cf. Eq. 9) with a cutoff wavelength of (a) 15 km, (b) 10 km and (c) 6 km of ERA5 temperatures on 3 December 2015, 00:00 UTC.
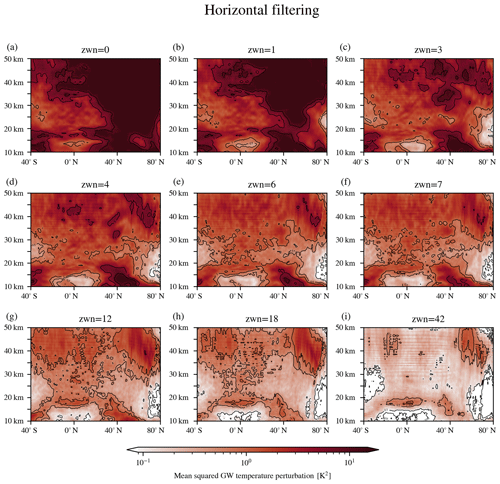
Figure 7Horizontally filtered (with additional smoothing in meridional and vertical components) zonal temperature variance of ERA5 temperatures on 3 December 2015, 00:00 UTC, with cutoff zonal wavenumber (a) 0, (b) 1, (c) 3, (d) 4, (e) 6, (f) 7, (g) 12, (h) 18 or (i) 42.
In the following, we concentrate on four structural features and their evolution under different cutoffs in the two background removals. First, Fig. 6a shows a typical pancake structure in the midlatitude stratosphere (approximately between 30 and 45∘ N and above 25 km altitude) associated with the inertial instability (Rapp et al., 2018b). A corresponding but isolated stack is present above the Equator between 30 and 40 km altitude.
The isolated structures merge into one broad sheet of perturbation at altitudes a few kilometres below the stratopause. Decreasing the cutoff wavelength in the vertical filtering reduces the pancake structure at midlatitudes in a way that it is not further recognizable in the results from 6 km vertical filtering. The tropical band of the structure is more persistent while being reduced in magnitude but remaining especially strong at 35 to 40 km altitude. In addition, a more rigorous vertical filtering seems to narrow the vertical distance between the mean squared gravity wave temperature perturbation peaks. As discussed in Sect. 4.3, the remaining structures may be caused by tropical wave modes and, in particular, by Kelvin waves.
In comparison, the horizontal filtering results show less evidence for the typical pancake structure (both at midlatitudes and in the tropics). In the tropics, above 30 km altitude some layered structures emerge for low cutoff wavenumbers (cf. Fig. 7a and b). The midlatitudes, however, are dominated by a strong (>10 K2) large-scale squared gravity wave perturbation structure that does not show the stacked pancake features and is likely connected to remaining Rossby wave signals. At cutoff zonal wavenumbers 3 and 4 (cf. Fig. 7c and d, respectively), the Rossby wave feature is mostly removed and some pancake-like structures are found in the midlatitudes, which are already reduced compared to the vertical filtering with cutoff wavelength 15 km. In the tropics, no clear pancake structure remains increasing the cutoff zonal wavenumber further, but a small local maximum in Fig. 7e at 40∘ N and 30 km altitude could still be associated with the pancake structures.
At altitudes above 20 km, the general structure continues to decrease in magnitude, but it remains very similar in structure for wavenumbers 6 and larger. This is consistent with gravity waves at a wide range of different scales causing these features. Particularly pronounced is a second structure between 60 and 80∘ N and from 30 to 50 km altitude, which shows still enhanced mean squared gravity wave temperature perturbations at wavenumber 42 (cf. Fig. 7i). This is likely associated with gravity waves in the winter polar vortex, and Rapp et al. (2018b) attribute a major part of the feature to gravity wave sources at Greenland. The structure is also found in the vertical filtering results, but it extends less into higher altitudes as well as less wide equatorwards. In general, the mean squared gravity wave temperature perturbation structures after vertical filtering show a gap that is a few degrees of latitude wide of comparably small values around 60∘ N. This anomaly is located approximately in the centre of the polar night jet where we expect a predominance of long vertical wavelength of gravity waves. The feature is not present in the horizontal filtering results. In fact, at this location, horizontal filtering indicates a maximum of squared temperature perturbation.
For very low cutoff zonal wavenumbers, the high-latitude maximum is concealed by a larger structure due to Rossby waves in middle and high latitudes. From cutoff wavenumber 6, it is not distorted by pancake-like overlaid structures anymore. Then, the overall shape of the enhanced mean squared gravity wave temperature perturbation distribution is not changed up to a cutoff wavenumber 18 and also keeps roughly the same magnitude. This indicates that the horizontal wavelengths of the waves amount to at most ∼1000 km as Coriolis force arguments for gravity waves at these latitudes would suggest (Alexander et al., 2002; Preusse et al., 2006). The very strong horizontal filtering with cutoff zonal wavenumber 42 still shows the feature but with decreased magnitude, which indicates that part of the gravity wave spectrum is also removed by the background removal.
Below 20km, the tropical tropopause and the tropopause inversion layer show up distinctively in the vertically filtered data, which are depicted by an elongated, strong mean squared gravity wave temperature perturbation signal spanning all the way from 30∘ S to 30∘ N between 15 and 25 km (cf. Fig. 6a). Rapp et al. (2018a) explain this third structure with shortcomings of the vertical filtering to identify background temperature structures like the tropical tropopause with the short vertical length scale.
Even a rigorous vertical filtering with a cutoff wavelength of 6 km retains the signal. This problem is similar to the misinterpretation of inertial instability perturbations due to their small vertical wavelength. In comparison, the horizontal filter is removing a large part of the tropopause signal from the perturbations already with cutoff wavenumber 0, i.e. only removing the zonal mean. This could be explained by the tropical tropopause and the tropopause inversion layer being rather stable in altitude over all longitudes. However, even at zonal wavenumber 42, the remnant structure is still larger than the gravity wave fluctuations above and below, indicating that the remnants of the tropopause still mask the gravity wave signal.
Finally, all of the results show enhanced mean squared gravity wave temperature perturbations in the troposphere below 15 km around 40∘ N. With cutting more rigorously, both filtering methods reduce the zonal mean magnitude of this feature, but it is never fully removed, even with high horizontal wavenumber cutoffs of 18 or 42. The dynamically active region of the troposphere is very difficult for all gravity wave background removals due to the large and possibly abrupt variation of the temperature over short distances. In the troposphere a wide spectrum of Rossby waves up to high zonal wavenumbers exists, which is filtered around the tropopause according to the Charney–Drazin criterion (Charney and Drazin, 1961). Accordingly, the stratospheric background atmosphere is dominated by planetary waves with zonal wavenumbers smaller than 4 (e.g. Domeisen et al., 2018; Barnett and Labitzke, 1990; Pawson and Kubitz, 1996), which is consistent with the findings in this paper. In order to investigate altitudes below 20 km from LEO infrared sounders, higher wavenumbers than wavenumber 6 have to be taken into account. Even at high zonal wavenumbers, the results will need further validation, which, however, is beyond the scope of this study.
4.5 Case study and 1-year time series of SABER
So far we have considered a case study for a particular, strong inertial instability event. In order to evaluate whether the results are representative, we investigate 1 year of SABER data.
As already addressed in Sects. 2 and 3, SABER data are much sparser than ERA5, and we have to rely on a more complex horizontal filtering approach. The method is tailored to the regular global sampling pattern of orbiting limb sounders with measurement tracks quasi-parallel to the satellite orbit track. Satellite observations with different sampling methods may need slightly different approaches. For instance, longitude–time spectra can be calculated from GPS-RO profiles; this has been done by S. P. Alexander et al. (2008) for the analysis of Kelvin waves using COSMIC data. Such spectra could be used for background removal, but more care would have to be taken because the number of data points available for a given latitude will vary strongly.
Like Fig. 4 for ERA5, Fig. 8 shows the zonal mean gravity wave temperature perturbations and corresponding standard deviations now from SABER data. On the left (Fig. 8a and c), we applied vertical filtering with a cutoff wavelength of 15 km. Again, we find the pancake structure in the tropics and midlatitudes characteristic of the inertial instability. Since SABER looked southward on 3 December 2015, we do not have data coverage at high latitudes for this case. The standard deviation shows layered structures as well, which are especially strong in the midlatitudes. On the right (Fig. 8b and d), we show the results from the time–horizontal filtering for the SABER data using cutoff zonal wavenumber 6. Over the course of 1 d, SABER data only contain 32 measurement points along one latitude circle and thus provide much weaker statistics than the ERA5 data. This presumably explains remnant values of mean gravity wave temperature perturbations in the SABER data, which, however, do not show the characteristic pancake structure typical for inertial instabilities and are mostly below 0.5 K. In the standard deviation, we see more activity in the winter hemisphere than in the summer hemisphere. This is consistent with the general understanding of source activation and global distributions of gravity waves (Fritts and Alexander, 2003; Geller et al., 2013). Overall, magnitudes are lower than in Fig. 8a and c. In vertical filtering, most of this distribution was distorted by the large, layered features of the inertial instability.
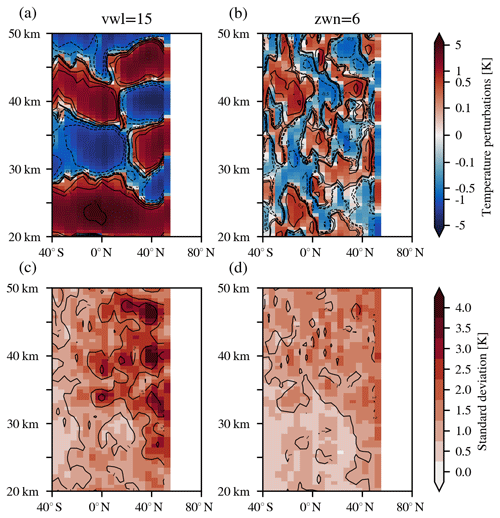
Figure 8Zonal mean gravity wave temperature perturbations and corresponding standard deviations of SABER data. The upper row shows the mean perturbation from (a) vertical filtering (fifth-order Butterworth) with cutoff vertical wavelength of 15 km and (b) horizontal filtering with the method from Ern et al. (2011) with cutoff zonal wavenumber 6 and period ≈1.4 d. The lower row shows in panels (c) and (d) the corresponding standard distributions of panels (a) and (b).
Figure 9 shows daily averages of mean zonal squared gravity wave temperature perturbations (cf. Eq. 9) in a midlatitude box from 90∘ W to 45∘ E and from 30 to 45∘ N for 1 year of SABER data (July 2015 to June 2016). The upper panel shows results from a vertical Butterworth filter with 15 km cutoff wavelength, and the lower panel presents results form horizontal background removal with a cutoff zonal wavenumber 6.
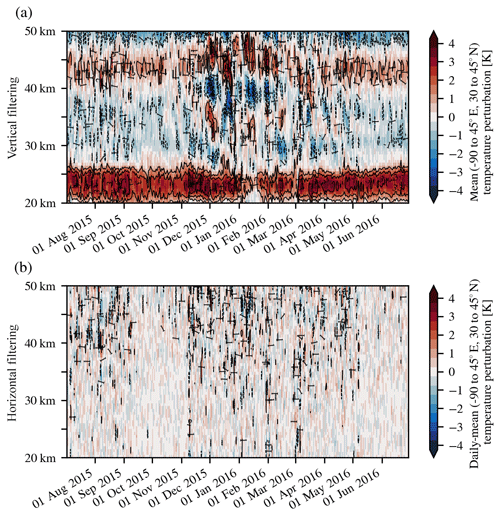
Figure 9Time series of daily-mean gravity wave temperature perturbation profiles from SABER in the midlatitude box (90∘ W to 45∘ E longitude, 30 to 45∘ N latitude) for 1 year (1 July 2015 to 30 June 2016) after (a) vertical Butterworth filtering with 15 km cutoff wavelength and (b) horizontal filtering (zonal mean with additional smoothing in meridional and vertical components) with cutoff wavenumber 6. Contours show the indicated value of daily-mean box mean gravity wave temperature perturbations.
Throughout the entire year, the vertically filtered data show a pronounced signal above the tropopause, i.e. between 20 and 25 km, and around the stratopause, i.e. between 40 and 50 km altitude. Furthermore, this data set exhibits remnant pancake structures persisting for several days through the Northern Hemisphere winter (December to mid February). This is consistent with favourable conditions for inertial instability particularly around the winter solstice (Rapp et al., 2018b).
After horizontal filtering, some wave-like structures are remaining but smaller in magnitude and of shorter duration. These structures indicate very active gravity wave events dominating the average in the domain. Also, the horizontal background removal does not show the very strong signals associated with the tropopause and stratopause.
The analysis of satellite data for gravity waves relies on a scale separation between the targeted gravity waves and larger-scale structures. Recently, concern was raised that inertial instabilities might not be properly removed in generating gravity wave climatologies and thus cause spurious signals in the derived distributions (Rapp et al., 2018b; Harvey and Knox, 2019). Therefore, the subject of this study is to assess the capability of horizontal and vertical spectral background removals to isolate gravity waves from inertial instability effects. In addition, we aim at determining optimal cutoff length scales for the background removal.
We approached this by considering a particularly strong inertial instability event on 3 December 2015, which was discussed in the study of Rapp et al. (2018b). As test data, we use ERA5 reanalysis temperatures, SABER temperature observations and a synthetic data set containing only an idealized inertial instability signal. For the assessment, we also need a criterion for a successful background removal. The background removal is considered successful if the gravity wave variances dominate over the remnants of the removed inertial instability. For practical purposes, we also introduced as a second criterion that the background removal is considered successful if the remnants of the removed inertial instability are smaller than the precision of the instrument from which we determine the climatology. The advantage of this criterion is that the gravity wave distribution does not need to be known a priori.
First, we compared the vertical and horizontal filtering results for the idealized inertial instability signal. Zonal mean gravity wave temperature perturbations and zonal mean variances show that both methods are in principle capable of removing an inertial-instability-like perturbation to a limit that it falls to a level below the SABER precision threshold. However, in vertical filtering we had to eliminate all fluctuations larger than 7 km in the vertical to achieve a sufficient signal reduction. This would lead also to the removal of a major part of the gravity wave spectrum. A comparable level of removal after horizontal filtering was achieved with a cutoff zonal wavenumber of 6, which does not limit the gravity wave analysis, in particular, if momentum flux is considered.
The investigation of ERA5 data shows that for the midlatitude stratosphere, gravity waves dominate over inertial instability signals for vertical cutoff wavelengths shorter than about 10 km and for horizontal cutoff wavenumbers larger than 6. After vertical background removal, remnants of the stratopause remain. In addition, the tropical stratosphere showed perturbations over all altitudes from 20 to 45 km that indicate Kelvin wave activity. Horizontal filtering, in contrast, removes both effects. Horizontal filtering is also more capable of dealing with the tropical tropopause, but remnants larger than the average gravity wave variance remain. In the subtropical troposphere and lowermost stratosphere, zonal wavenumbers larger than 18 are required to reduce the signal of Rossby waves. Further consideration will be needed in future if data sets should be evaluated for such lower altitudes, as well. A zonal wavenumber filter applying wavenumbers higher than 18 removes already part of the gravity wave spectrum.
A 1-year analysis of SABER data reveals inertial instability signals for the vertical filtering but no evidence for inertial instabilities after horizontal filtering. Hence, the case study of one inertial instability event is representative.
Considering existing satellite climatologies, such data sets which are based on time–longitude spectra including zonal wavenumber 6 are likely free of the influence of large-scale inertial instabilities. This includes, for instance, the GRACILE climatology (Ern et al., 2018) and studies based on this or similar data sets. Some influence is expected on data sets generated by vertical filtering with a 10 km cutoff wavelength, such as GPS investigations by Tsuda et al. (2000) and de la Torre et al. (2006). In addition, an influence of Kelvin waves is expected for low latitudes. The relatively short cutoff wavelength applied in these studies, however, is also cutting deep into the gravity wave spectrum, in particular for high-latitude winter conditions. Gravity wave temperature perturbations calculated using vertical filtering with a 15 km cutoff wavelength, on the other hand, are dominated by inertial instability depending on season and geographical region, as was already shown by Rapp et al. (2018b).
In conclusion, for the removal of a background containing inertial instabilities and gravity waves, horizontal spectral filtering with a zonal wavenumber of 6 or higher provides the best results. It is, therefore, recommended to use such an approach where the data allow for it. For altitudes around the tropopause, larger zonal wavenumbers are required, but zonal wavenumbers larger than 18 reduce the fraction of retrievable gravity waves in the stratosphere greatly.
The ERA-5 data used for this study are freely available from CDS (2017). SABER data are freely available from GATS Inc. at http://saber.gats-inc.com (last access: 15 September 2020). Precision estimates for SABER temperatures are given on the SABER website at http://saber.gats-inc.com/temp_errors.php (SABER, 2020) and in Remsberg et al. (2008).
CS generated the artificial inertial instability data set, performed the processing of background removals on the former and the ERA5 data, wrote the paper text and generated the figures. ME processed the background removal on the satellite data set. PP supervised the research and helped with the paper. ME and MR helped with discussions and revision on the paper text and the figures.
The authors declare that they have no conflict of interest.
This research has been supported by the Deutsche Forschungsgemeinschaft (DFG; Source Variability, grant nos. PR 919/4-2 and ER 474/4-2).
The article processing charges for this open-access
publication were covered by a Research
Centre of the Helmholtz Association.
This paper was edited by Robert Sica and reviewed by two anonymous referees.
Albers, J. R. and Birner, T.: Vortex Preconditioning due to Planetary and Gravity Waves prior to Sudden Stratospheric Warmings, J. Atmos. Sci., 71, 4028–4054, https://doi.org/10.1175/JAS-D-14-0026.1, 2014. a
Alexander, M. J.: Interpretations of observed climatological patterns in stratospheric gravity wave variance, Geophys. Res. Lett., 103, 8627–8640, https://doi.org/10.1029/97JD03325, 1998. a
Alexander, M. J.: Global and seasonal variations in three-dimensional gravity wave momentum flux from satellite limb-sounding temperatures, Geophys. Res. Lett., 42, 6860–6867, https://doi.org/10.1002/2015GL065234, 2015. a
Alexander, M. J. and Barnet, C. D.: Using satellite observations to constrain gravity wave parameterizations for global models, J. Atmos. Sci., 64, 1652–1665, 2007. a
Alexander, M. J. and Rosenlof, K. H.: Gravity-wave forcing in the stratosphere: Observational constraints from the Upper Atmosphere Research Satellite and implications for parameterization in global models, J. Geophys. Res., 108, 4597, https://doi.org/10.1029/2003JD003373, 2003. a
Alexander, M. J., Tsuda, T., and Vincent, R. A.: On the latitudinal variations observed in gravity waves with short vertical wavelengths, J. Atmos. Sci., 59, 1394–1404, 2002. a
Alexander, M. J., Gille, J., Cavanaugh, C., Coffey, M., Craig, C., Dean, V., Eden, T., Francis, G., Halvorson, C., Hannigan, J., Khosravi, R., Kinnison, D., Lee, H., Massie, S., and Nardi, B.: Global estimates of gravity wave momentum flux from High Resolution Dynamics Limb Sounder (HIRDLS) observations, J. Geophys. Res., 113, D15S18, https://doi.org/10.1029/2007JD008807, 2008. a, b
Alexander, M. J., Geller, M., McLandress, C., Polavarapu, S., Preusse, P., Sassi, F., Sato, K., Eckermann, S., Ern, M., Hertzog, A., Kawatani, Y., Pulido, M., Shaw, T. A., Sigmond, M., Vincent, R., and Watanabe, S.: Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models, Q. J. Roy. Meteor. Soc., 136, 1103–1124, https://doi.org/10.1002/qj.637, 2010. a, b, c, d, e
Alexander, S. P., Tsuda, T., Kawatani, Y., and Takahashi, M.: Global distribution of atmospheric waves in the equatorial upper troposphere and lower stratosphere: COSMIC observations of wave mean flow interactions, J. Geophys. Res., 113, D24115, https://doi.org/10.1029/2008JD010039, 2008. a
Baldwin, M. P., Gray, L. J., Dunkerton, T. J., Hamilton, K., Haynes, P. H., Randel, W. J., Holton, J. R., Alexander, M. J., Hirota, I., Horinouchi, T., Jones, D. B. A., Kinnersley, J. S., Marquardt, C., Sato, K., and Takahashi, M.: The Quasi-Biennial Oscillation, Rev. Geophys., 39, 179–229, https://doi.org/10.1029/1999RG000073, 2001. a, b
Barnett, J. and Labitzke, K.: Climatological distribution of planetary waves in the middle atmosphere, Adv. Space Res., 10, 1263–1291, 1990. a
Butchart, N., Cionni, I., Eyring, V., Shepherd, T. G., Waugh, D. W., Akiyoshi, H., Austin, J., Brühl, C., Chipperfield, M. P., Cordero, E., Dameris, M., Deckert, R., Dhomse, S., Frith, S. M., Garcia, R. R., Gettelman, A., Giorgetta, M. A., Kinnison, D. E., Li, F., Mancini, E., McLandress, C., Pawson, S., Pitari, G., Plummer, D. A., Rozanov, E., Sassi, F., Scinocca, J. F., Shibata, K., Steil, B., and Tian, W.: Chemistry-climate model simulations of twenty-first century stratospheric climate and circulation changes, J. Climate, 23, 5349–5374, 2010. a
Climate Data Store (CDS): ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate, available at: https://cds.climate.copernicus.eu/cdsapp#!/home (last access: 15 September 2020), 2017. a
Charney, J. G. and Drazin, P. G.: Propagation of planetary-scale disturbances from the lower into the upper atmosphere, J. Geophys. Res., 66, 83–109, https://doi.org/10.1029/JZ066i001p00083, 1961. a
de la Torre, A., Schmidt, T., and Wickert, J.: A global analysis of wave potential energy in the lower and middle atmosphere from CHAMP and SAC-C GPS-RO long term data, Geophys. Res. Lett., 33, L24809, https://doi.org/10.1029/2006GL027696, 2006. a, b
Domeisen, D. I. V., Martius, O., and Jiménez-Esteve, B.: Rossby Wave Propagation into the Northern Hemisphere Stratosphere: The Role of Zonal Phase Speed, Geophys. Res. Lett., 45, 2064–2071, https://doi.org/10.1002/2017GL076886, 2018. a
Dunkerton, T. J.: On the Inertial Stability of the Equatorial Middle Atmosphere, J. Atmos. Sci., 38, 2354–2364, https://doi.org/10.1175/1520-0469(1981)038<2354:OTISFT>2.0.CO;2, 1981. a, b, c, d
Dunkerton, T. J.: Shear Instability of Internal Inertia-Gravity Waves, J. Atmos. Sci., 54, 1628–1641, 1997. a
Eckermann, S. D. and Preusse, P.: Global measurements of stratospheric mountain waves from space, Science, 286, 1534–1537, https://doi.org/10.1126/science.286.5444.1534, 1999. a
Eckermann, S. D., Wu, D. L., Doyle, J. D., Burris, J. F., McGee, T. J., Hostetler, C. A., Coy, L., Lawrence, B. N., Stephens, A., McCormack, J. P., and Hogan, T. F.: Imaging gravity waves in lower stratospheric AMSU-A radiances, Part 2: Validation case study, Atmos. Chem. Phys., 6, 3343–3362, https://doi.org/10.5194/acp-6-3343-2006, 2006. a
Eckermann, S. D., Ma, J., Wu, D. L., and Broutman, D.: A three-dimensional mountain wave imaged in satellite radiance throughout the stratosphere: Evidence of the effects of directional wind shear, Q. J. Roy. Meteor. Soc., 133, 1959–1975, https://doi.org/10.1002/qj.187, 2007. a
Ehard, B., Kaifler, B., Kaifler, N., and Rapp, M.: Evaluation of methods for gravity wave extraction from middle-atmospheric lidar temperature measurements, Atmos. Meas. Tech., 8, 4645–4655, https://doi.org/10.5194/amt-8-4645-2015, 2015. a, b
Ehard, B., Kaifler, B., Dörnbrack, A., Preusse, P., Eckermann, S., Bramberger, M., Gisinger, S., Kaifler, N., Liley, B., Wagner, J., and Rapp, M.: Horizontal propagation of large amplitude mountain waves in the vicinity of the polar night jet, J. Geophys. Res.-Atmos., 122, 1423–1436, https://doi.org/10.1002/2016JD025621, 2017. a
Ern, M., Preusse, P., Alexander, M. J., and Warner, C. D.: Absolute values of gravity wave momentum flux derived from satellite data, J. Geophys. Res. Atmos., 109, D20103, https://doi.org/10.1029/2004JD004752, 2004. a
Ern, M., Preusse, P., Krebsbach, M., Mlynczak, M. G., and Russell III, J. M.: Equatorial wave analysis from SABER and ECMWF temperatures, Atmos. Chem. Phys., 8, 845–869, https://doi.org/10.5194/acp-8-845-2008, 2008. a
Ern, M., Lehmann, C., Kaufmann, M., and Riese, M.: Spectral wave analysis at the mesopause from SCIAMACHY airglow data compared to SABER temperature spectra, Ann. Geophys., 27, 407–416, https://doi.org/10.5194/angeo-27-407-2009, 2009. a
Ern, M., Preusse, P., Gille, J. C., Hepplewhite, C. L., Mlynczak, M. G., Russell III, J. M., and Riese, M.: Implications for atmospheric dynamics derived from global observations of gravity wave momentum flux in stratosphere and mesosphere, J. Geophys. Res., 116, D19107, https://doi.org/10.1029/2011JD015821, 2011. a, b, c, d, e, f
Ern, M., Preusse, P., Kalisch, S., Kaufmann, M., and Riese, M.: Role of gravity waves in the forcing of quasi two-day waves in the mesosphere: An observational study, J. Geophys. Res.-Atmos., 118, 3467–3485, https://doi.org/10.1029/2012JD018208, 2013. a, b, c
Ern, M., Ploeger, F., Preusse, P., Gille, J. C., Gray, L. J., Kalisch, S., Mlynczak, M. G., Russell III, J. M., and Riese, M.: Interaction of gravity waves with the QBO: A satellite perspective, J. Geophys. Res.-Atmos., 119, 2329–2355, https://doi.org/10.1002/2013JD020731, 2014. a
Ern, M., Preusse, P., and Riese, M.: Driving of the SAO by gravity waves as observed from satellite, Ann. Geophys., 33, 483–504, https://doi.org/10.5194/angeo-33-483-2015, 2015. a
Ern, M., Trinh, Q. T., Kaufmann, M., Krisch, I., Preusse, P., Ungermann, J., Zhu, Y., Gille, J. C., Mlynczak, M. G., Russell III, J. M., Schwartz, M. J., and Riese, M.: Satellite observations of middle atmosphere gravity wave absolute momentum flux and of its vertical gradient during recent stratospheric warmings, Atmos. Chem. Phys., 16, 9983–10019, https://doi.org/10.5194/acp-16-9983-2016, 2016. a, b
Ern, M., Hoffmann, L., and Preusse, P.: Directional gravity wave momentum fluxes in the stratosphere derived from high-resolution AIRS temperature data, Geophys. Res. Lett., 44, 475–485, https://doi.org/10.1002/2016GL072007, 2017. a
Ern, M., Trinh, Q. T., Preusse, P., Gille, J. C., Mlynczak, M. G., Russell III, J. M., and Riese, M.: GRACILE: a comprehensive climatology of atmospheric gravity wave parameters based on satellite limb soundings, Earth Syst. Sci. Data, 10, 857–892, https://doi.org/10.5194/essd-10-857-2018, 2018. a, b, c, d, e, f, g, h, i
Fetzer, E. J. and Gille, J. C.: Gravity wave variance in LIMS temperatures. Part I: Variability and comparison with background winds, J. Atmos. Sci., 51, 2461–2483, https://doi.org/10.1175/1520-0469(1994)051<2461:GWVILT>2.0.CO;2, 1994. a, b, c, d
Fritts, D. and Alexander, M.: Gravity wave dynamics and effects in the middle atmosphere, Rev. Geophys., 41, 1003, https://doi.org/10.1029/2001RG000106, 2003. a, b, c
Fröhlich, K., Schmidt, T., Ern, M., Preusse, P., de la Torre, A., Wickert, J., and Jacobi, C.: The global distribution of gravity wave energy in the lower stratosphere derived from GPS data and gravity wave modelling: Attempt and challenges, J. Atm. Sol.-Terr. Phys., 69, 2238–2248, https://doi.org/10.1016/j.jastp.2007.07.005, 2007. a
Garcia, R. R., Dunkerton, T. J., Lieberman, R. S., and Vincent, R. A.: Climatology of the semiannual oscillation of the tropical middle atmosphere, J. Geophys. Res., 102, 26019–26032, 1997. a
Geller, M. A., Alexander, M. J., Love, P. T., Bacmeister, J., Ern, M., Hertzog, A., Manzini, E., Preusse, P., Sato, K., Scaife, A. A., and Zhou, T.: A comparison between gravity wave momentum fluxes in observations and climate models, J. Climate, 26, 6383–6405, https://doi.org/10.1175/JCLI-D-12-00545.1, 2013. a, b
Gong, J., Wu, D. L., and Eckermann, S. D.: Gravity wave variances and propagation derived from AIRS radiances, Atmos. Chem. Phys., 12, 1701–1720, https://doi.org/10.5194/acp-12-1701-2012, 2012. a
Harvey, V. L. and Knox, J. A.: Beware of Inertial Instability Masquerading as Gravity Waves in Stratospheric Temperature Perturbations, Geophys. Res. Lett., 46, 1740–1745, https://doi.org/10.1029/2018GL081142, 2019. a, b
Hayashi, H., Shiotani, M., and Gille, J. C.: Vertically stacked temperature disturbances near the equatorial stratopause as seen in cryogenic limb array etalon spectrometer data, J. Geophys. Res., 103, 19469–19483, https://doi.org/10.1029/98JD01730, 1998. a, b
Hitchman, M. H., Leovy, C. B., Gille, J. C., and Bailey, P. L.: Quasi-Stationary Zonally Asymmetric Circulations in the Equatorial Lower Mesosphere, J. Atmos. Sci., 44, 2219–2236, https://doi.org/10.1175/1520-0469(1987)044<2219:QSZACI>2.0.CO;2, 1987. a
Hoffmann, L. and Alexander, M. J.: Retrieval of stratospheric temperatures from Atmospheric Infrared Sounder radiance measurements for gravity wave studies, J. Geophys. Res., 114, D07105, https://doi.org/10.1029/2008JD011241, 2009. a
Hoffmann, L. and Alexander, M. J.: Occurrence frequency of convective gravity waves during the North American thunderstorm season, J. Geophys. Res., 115, D20111, https://doi.org/10.1029/2010JD014401, 2010. a
Hoffmann, L., Grimsdell, A. W., and Alexander, M. J.: Stratospheric gravity waves at Southern Hemisphere orographic hotspots: 2003–2014 AIRS/Aqua observations, Atmos. Chem. Phys., 16, 9381–9397, https://doi.org/10.5194/acp-16-9381-2016, 2016. a
Jewtoukoff, V., Hertzog, A., Plougonven, R., de la Camara, A., and Lott, F.: Comparison of Gravity Waves in the Southern Hemisphere Derived from Balloon Observations and the ECMWF Analyses, J. Atmos. Sci., 72, 3449–3468, https://doi.org/10.1175/JAS-D-14-0324.1, 2015. a
Jiang, J., Eckermann, S., Wu, D., and Ma, J.: A search for mountain waves in MLS stratospheric limb radiances from the winter Northern Hemisphere: Data analysis and global mountain wave modeling, J. Geophys. Res.-Atmos., 109, D03107, https://doi.org/10.1029/2003JD003974, 2004a. a
Jiang, J., Wang, B., Goya, K., Hocke, K., Eckermann, S., Ma, J., Wu, D., and Read, W.: Geographical distribution and interseasonal variability of tropical deep convection: UARS MLS observations and analyses, J. Geophys. Res. Atmos., 109, D03111, https://doi.org/10.1029/2003JD003756, 2004b. a
John, S. R. and Kumar, K. K.: TIMED/SABER observations of global gravity wave climatology and their interannual variability from stratosphere to mesosphere lower thermosphere, Clim. Dynam., 39, 1489–1505, https://doi.org/10.1007/s00382-012-1329-9, 2012. a
Kim, Y.-H., Kiladis, G. N., Albers, J. R., Dias, J., Fujiwara, M., Anstey, J. A., Song, I.-S., Wright, C. J., Kawatani, Y., Lott, F., and Yoo, C.: Comparison of equatorial wave activity in the tropical tropopause layer and stratosphere represented in reanalyses, Atmos. Chem. Phys., 19, 10027–10050, https://doi.org/10.5194/acp-19-10027-2019, 2019. a
Knox, J. A. and Harvey, V. L.: Global climatology of inertial instability and Rossby wave breaking in the stratosphere, J. Geophys. Res.-Atmos., 110, D06108, https://doi.org/10.1029/2004JD005068, 2005. a, b, c, d
McLandress, C. and Shepherd, T. G.: Simulated anthropogenic changes in the Brewer-Dobson circulation, including its extension to high latitudes, J. Climate, 22, 1516–1540, https://doi.org/10.1175/2008JCLI2679.1, 2009. a
McLandress, C., Alexander, M. J., and Wu, D. L.: Microwave Limb Sounder observations of gravity waves in the stratosphere: A climatology and interpretation, J. Geophys. Res., 105, 11947–11967, 2000. a
Pawson, S. and Kubitz, T.: Climatology of planetary waves in the northern stratosphere, J. Geophys. Res.-Atmos., 101, 16987–16996, https://doi.org/10.1029/96JD01226, 1996. a
Preusse, P.: Satellitenmessungen von Schwerewellen in der mittleren Atmosphäre mit CRISTA, PhD thesis, Wuppertal University, available at: http://elpub.bib.uni-wuppertal.de/servlets/DerivateServlet/Derivate-412/d080111.pdf (last access: 15 September 2020), 2001. a
Preusse, P., Eckermann, S., Oberheide, J., Hagan, M., and Offermann, D.: Modulation of gravity waves by tides as seen in CRISTA temperatures, in: Middle atmosphere temporal and spatial structures, edited by: Riese, M., Spang, R., Swenson, G. R., and Espy, P. J., Elsevier Science BV, Adv. Space Res., 27, 1773–1778, https://doi.org/10.1016/S0273-1177(01)00336-2, 2001. a
Preusse, P., Dörnbrack, A., Eckermann, S. D., Riese, M., Schaeler, B., Bacmeister, J. T., Broutman, D., and Grossmann, K. U.: Space-based measurements of stratospheric mountain waves by CRISTA, 1. Sensitivity, analysis method, and a case study, J. Geophys. Res., 107, 8178, https://doi.org/10.1029/2001JD000699, 2002. a, b
Preusse, P., Ern, M., Eckermann, S. D., Warner, C. D., Picard, R. H., Knieling, P., Krebsbach, M., Russell III, J. M., Mlynczak, M. G., Mertens, C. J., and Riese, M.: Tropopause to mesopause gravity waves in August: measurement and modeling, J. Atmos. Sol.-Terr. Phy., 68, 1730–1751, 2006. a
Preusse, P., Eckermann, S. D., and Ern, M.: Transparency of the atmosphere to short horizontal wavelength gravity waves, J. Geophys. Res., 113, D24104, https://doi.org/10.1029/2007JD009682, 2008. a
Rapp, M., Dörnbrack, A., and Kaifler, B.: An intercomparison of stratospheric gravity wave potential energy densities from METOP GPS radio occultation measurements and ECMWF model data, Atmos. Meas. Tech., 11, 1031–1048, https://doi.org/10.5194/amt-11-1031-2018, 2018a. a, b, c, d, e, f, g, h
Rapp, M., Dörnbrack, A., and Preusse, P.: Large Midlatitude Stratospheric Temperature Variability Caused by Inertial Instability: A Potential Source of Bias for Gravity Wave Climatologies, Geophys. Res. Lett., 45, 10682–10690, 2018b. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t
Remsberg, E. E., Marshall, B. T., Garcia-Comas, M., Krueger, D., Lingenfelser, G. S., Martin-Torres, J., Mlynczak, M. G., Russell III, J. M., Smith, A. K., Zhao, Y., Brown, C., Gordley, L. L., Lopez-Gonzalez, M. J., Lopez-Puertas, M., She, C. Y., Taylor, M. J., and Thompson, R. E.: Assessment of the quality of the Version 1.07 temperature-versus-pressure profiles of the middle atmosphere from TIMED/SABER, J. Geophys. Res., 113, D17101, https://doi.org/10.1029/2008JD010013, 2008. a, b, c, d, e
SABER: SABER Temperature and CO2 Retrieval Accuracies, GATS inc., available at: http://saber.gats-inc.com/temp_errors.php, last access: 15 September 2020. a
Šácha, P., Foelsche, U., and Pišoft, P.: Analysis of internal gravity waves with GPS RO density profiles, Atmos. Meas. Tech., 7, 4123–4132, https://doi.org/10.5194/amt-7-4123-2014, 2014. a
Šácha, P., Kuchař, A., Jacobi, C., and Pišoft, P.: Enhanced internal gravity wave activity and breaking over the northeastern Pacific–eastern Asian region, Atmos. Chem. Phys., 15, 13097–13112, https://doi.org/10.5194/acp-15-13097-2015, 2015. a
Šácha, P., Lilienthal, F., Jacobi, C., and Pišoft, P.: Influence of the spatial distribution of gravity wave activity on the middle atmospheric dynamics, Atmos. Chem. Phys., 16, 15755–15775, https://doi.org/10.5194/acp-16-15755-2016, 2016. a
Salby, M. L.: Sampling theory for asynoptic satellite observatioons. Part I: Space-time spectra, resolution, and aliasing, J. Atmos. Sci., 39, 2577–2600, 1982. a, b
Salby, M. L.: Survey of planetary-scale traveling waves – the state of theory and observations, Rev. Geophys., 22, 209–236, https://doi.org/10.1029/RG022i002p00209, 1984. a, b, c
Schmidt, T., Wickert, J., Heise, S., Flechtner, F., Fagiolini, E., Schwarz, G., Zenner, L., and Gruber, T.: Comparison of ECMWF analyses with GPS radio occultations from CHAMP, Ann. Geophys., 26, 3225–3234, https://doi.org/10.5194/angeo-26-3225-2008, 2008. a
Schmidt, T., Alexander, P., and de la Torre, A.: Stratospheric gravity wave momentum flux from radio occultations, J. Geophys. Res.-Atmos., 121, 4443–4467, https://doi.org/10.1002/2015JD024135, 2016. a
Smith, A. K. and Riese, M.: Cryogenic Infrared Spectrometers and Telescopes for the Atmosphere (CRISTA) observations of tracer transport by inertially unstable circulations, J. Geophys. Res., 104, 19171–19182, 1999. a, b, c
Smith, A. K., Preusse, P., and Oberheide, J.: Middle atmosphere Kelvin waves observed in CRISTA 1 and 2 temperature and trace species, J. Geophys. Res., 107, 8177, https://doi.org/10.1029/2001JD000577, 2002. a
Tsuda, T., Nishida, M., Rocken, C., and Ware, R. H.: A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET), J. Geophys. Res., 105, 7257–7274, 2000. a, b, c, d
Wang, L. and Alexander, M. J.: Global estimates of gravity wave parameters from GPS radio occultation temperature data, J. Geophys. Res.-Atmos., 115, D21122, https://doi.org/10.1029/2010JD013860, 2010. a, b
Wing, R., Hauchecorne, A., Keckhut, P., Godin-Beekmann, S., Khaykin, S., McCullough, E. M., Mariscal, J.-F., and d'Almeida, É.: Lidar temperature series in the middle atmosphere as a reference data set – Part 1: Improved retrievals and a 20-year cross-validation of two co-located French lidars, Atmos. Meas. Tech., 11, 5531–5547, https://doi.org/10.5194/amt-11-5531-2018, 2018. a
Wright, C. J. and Gille, J. C.: HIRDLS observations of gravity wave momentum fluxes over the monsoon regions, J. Geophys. Res.-Atmos., 116, D12103, https://doi.org/10.1029/2011JD015725, 2011. a
Wright, C. J. and Hindley, N. P.: How well do stratospheric reanalyses reproduce high-resolution satellite temperature measurements?, Atmos. Chem. Phys., 18, 13703–13731, https://doi.org/10.5194/acp-18-13703-2018, 2018. a
Wright, C. J., Osprey, S. M., Barnett, J. J., Gray, L. J., and Gille, J. C.: High Resolution Dynamics Limb Sounder measurements of gravity wave activity in the 2006 Arctic stratosphere, J. Geophys. Res.-Atmos., 115, D02105, https://doi.org/10.1029/2009JD011858, 2010. a
Wright, C. J., Hindley, N. P., Hoffmann, L., Alexander, M. J., and Mitchell, N. J.: Exploring gravity wave characteristics in 3-D using a novel S-transform technique: AIRS/Aqua measurements over the Southern Andes and Drake Passage, Atmos. Chem. Phys., 17, 8553–8575, https://doi.org/10.5194/acp-17-8553-2017, 2017. a
Wu, D. L.: Mesoscale gravity wave variances from AMSU-A radiances, Geophys. Res. Lett., 31, L12114, https://doi.org/10.1029/2004GL019562, 2004. a
Wu, D. L. and Eckermann, S. D.: Global Gravity Wave Variances from Aura MLS: Characteristics and Interpretation, J. Atmos. Sci., 65, 3695–3718, https://doi.org/10.1175/2008JAS2489.1, 2008. a, b
Wu, D. L. and Waters, J. W.: Gravity-wave-scale temperature fluctuations seen by the UARS MLS, Geophys. Res. Lett., 23, 3289–3292, 1996. a
Yamashita, C., Liu, H.-L., and Chu, X.: Gravity wave variations during the 2009 stratospheric sudden warming as revealed by ECMWF-T799 and observations, Geophys. Res. Lett., 37, L22806, https://doi.org/10.1029/2010GL045437, 2010. a