the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Solar tracker with optical feedback and continuous rotation
John Robinson
Dan Smale
David Pollard
Hisako Shiona
Solar trackers are often used by spectrometers to measure atmospheric trace gas concentrations using direct sun spectroscopy. The ideal solar tracker should be sufficiently accurate, highly reliable, and with a longevity that exceeds the lifetime of the spectrometer that it serves. It should also be affordable, easy to use, and not too complex should maintenance be required. In this paper we present a design that fulfils these requirements using some simple innovations. Our altitude–azimuth design features a custom coaxial power transformer, enabling continuous 360∘ azimuth rotation. This increases reliability and avoids the need to reverse the tracker each day. In polar regions, measurements can continue uninterrupted through the summer polar day. Tracking accuracy is enhanced using a simple optical feedback technique that adjusts error offset variables while monitoring the edges of a focused solar image with four photodiodes. Control electronics are modular, and our software is written in Python, running as a web server on a recycled laptop with a Linux operating system. Over a period of 11 years we have assembled four such trackers. These are in use at Lauder (45∘ S), New Zealand, and Arrival Heights (78∘ S), Antarctica, achieving a history of good reliability even in polar conditions. Tracker accuracy is analysed regularly and can routinely produce a pointing accuracy of 0.02∘.
- Article
(4570 KB) - Full-text XML
- BibTeX
- EndNote
Altitude–azimuth (ALT-AZ) solar trackers are in widespread use within the atmospheric research community. A solar tracker is often roof-mounted, directing a vertical beam to a spectrometer in the laboratory below. Fourier Transform InfraRed spectrometers (FTIRs) are commonly used to analyse the absorptions of trace gases in the slant column of the atmosphere from the laboratory to the edge of the terrestrial atmosphere (Mahieu et al., 2014; Wunch et al., 2011). In a well-performing system, trace gas vertical column abundances can be accurately determined and to some extent partitioned into altitude layers. These data are vital for studying the dynamics and chemistry of the atmosphere, for example, to study ozone depletion (e.g. Steinbrecht et al., 2017) and greenhouse gases (e.g. Chevallier et al., 2011) and for the validation of similar measurements made by satellites (e.g. Dammers et al., 2017; Hedelius et al., 2019).
Inaccuracies in tracker pointing can lead to errors in calculated gas columns (Wunch et al., 2011). For example, at low solar elevations, the error in assumed absorption path length, or air mass, is significant if the tracker is pointing too high or too low with respect to the solar centre (Reichert et al., 2015). Another type of error occurs if the tracker pointing is unstable in any direction, causing the signal intensity at the spectrometer entrance optics to vary during the observation period, resulting in analysis inaccuracy for an FTIR measurement (Keppel-Aleks et al., 2007).
FTIR measurements often run continuously throughout the day in an automated fashion. Reliability of the tracker is important, especially at remote sites without regular on-site staff present. Common failures include mechanical switches or any wires that move, for example, cables from the lower stationary portion of the tracker to the upper elevation stage, which rotates daily in azimuth. A robust mechanical design is needed to prevent loss of alignment over time.
While modern control electronics have a long lifetime, finding critical replacement components in the future may be difficult. Specialised or proprietary circuit cards may be impossible to obtain after just a few years of service. Computer operating systems (OSs) can update regularly, making control software potentially unsupported or proprietary drivers obsolete.
In considering the issues listed above, we present an example tracker that is sufficiently accurate and highly reliable with potential to replace or update modules in the future, ensuring a long lifetime of service.
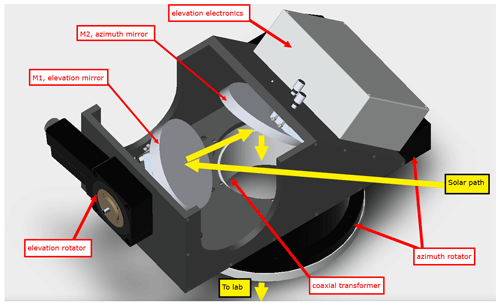
Figure 1Our ALT-AZ solar tracker computer-aided design (CAD) model, with major components identified.
Figure 1 shows our tracker, a standard ALT-AZ configuration, designed to be roof-mounted and used with our Bruker 125HR spectrometers (Pollard et al., 2017). The first flat mirror closest to the sun (M1) is mounted on the elevation optical rotator. M1 tracks the solar altitude (hereafter referred to as elevation). The second flat mirror, M2, is set at a fixed 45∘, accepts the now horizontal beam from M1, and directs it vertically downwards through the laboratory roof. M1, M2, and associated elevation electronics are all mounted upon the larger azimuth optical rotator, which constantly tracks the horizontal (azimuth) movement of the sun. A third mirror within the laboratory, below the tracker, is mounted at 45∘, directing the beam horizontally to the spectrometer input optics. Cables connect the azimuth rotator and elevation power coaxial transformer to the main electronics in the laboratory below. A laptop computer is connected to the main electronics.
Figure 2 shows the completed tracker mounted on the laboratory roof. The main tracker structure is made from 10 mm thick anodised aluminium plate, bolted together with stainless steel screws. The two main mirrors are elliptical aluminium-surfaced 12 mm thick glass mirrors with a protective silicon oxide (SiO) coating. Their reflectivity matches the typical wavelengths used for our spectrometers and the protective surface is hard-wearing, allowing for some limited cleaning. Our design accepts a mirror size of up to 128 mm minor axis. With minimal dimension changes to the supports, it would be possible to use up to 150 mm sized mirrors, fully utilising the central aperture of the tracker. The total weight of the tracker is approximately 25 kg.

Figure 2The completed tracker (Lauder, New Zealand) installed at roof level on a tower mounted to the concrete laboratory floor.
The paper will now discuss a range of solar tracker requirements and the solutions chosen when building our final design. In Sect. 2 we discuss accuracy requirements and the factors that cause mispointing in passive solar trackers. Section 3 describes how optical feedback is used to improve tracker accuracy. In Sect. 4 reliability is discussed, along with the use of a coaxial transformer to remove a major source of tracker failure. Section 5 describes the software and electronics in greater detail. Section 6 shows the performance of our solar tracker in terms of accuracy, reliability, and longevity.
Spending vast resources on improving pointing accuracy is beyond the budget of many institutions. However, the tracker should be fit for purpose, with an accuracy that suits the intended application.
Our trackers play a role in acquiring measurement data for the Network for the Detection of Atmospheric Composition Change (NDACC) (De Mazière et al., 2018) and Total Carbon Column Observing Network (TCCON) (Wunch et al., 2011) databases. Measurements of solar absorption of stratospheric trace gases for the NDACC, made in the mid-infrared wavelengths (MIR), benefit from good tracker accuracy at low solar elevations, preventing errors resulting from air mass uncertainty. The NDACC has no specifications for site tracker accuracy. We aim to take the highest quality measurements practicable. In the past, our main trackers used for MIR would require occasional manual adjustments to correct errors of more than about 0.1∘. This level of accuracy was adequate considering the uncertainties and dynamics of the species being measured.
Our current tracker was designed to meet the site requirements set by TCCON of 0.05∘ accuracy, while recognising that 0.01∘ would be more ideal in achieving an air mass error of 0.1 % at the lower elevation of 80∘ SZA (solar zenith angle) (Gisi et al., 2011). Without this level of pointing accuracy, it would be difficult to measure the small changes in the abundances of the well-mixed greenhouse gases being targeted. For example, to improve our understanding of the carbon cycle we require a measurement precision of about 0.25 % (e.g. Rayner and O'Brien, 2001).
2.1 Factors affecting pointing accuracy of a passive solar tracker
When no optical feedback system is used, the solar tracker is operating in dead-reckoning or passive mode. In this mode, the sun's position is continuously calculated, and the tracker mirrors are adjusted to direct a stable image of the sun into the laboratory below. Total pointing accuracy in this mode is an accumulation of the many sources of error of the complete design. These include the following errors, listed in approximate increasing order of significance.
2.1.1 Timing errors
The sun moves its full diameter (∼ 0.5∘) every 2 min. As a rough guide, each second of timing error is nearly 1 % of the solar diameter (or 0.0042∘). Some computer clocks may drift several seconds over a 24 h period unless a time server or other means of time update is used. Keeping system time accurate to 1 or 2 s is easily achievable, eliminating time as a major source of tracker inaccuracy. Our design features a GPS in the top (elevation) stage of the tracker. This is polled daily and upon startup to update the computer time clock to the nearest second. The geographical coordinates are also updated and the whole process is logged.
2.1.2 Movement speed, resolution, and error for the mechanical rotator stages
Good-quality rotators form the heart of any solar tracker. Gear backlash and wobble are generally much smaller than the movement resolution of the rotator. Rotational movement speed will largely be a function of the control algorithms and electronics and must be adequate for general tracking. If stepper motors are used, care should be taken to avoid resonance and the resulting missed steps when moving fast. The use of acceleration and deceleration algorithms is recommended for a large mass such as the tracker mechanics, especially when parking.
An ALT-AZ tracker can have the limitation of needing very fast movement (in azimuth) at low-latitude sites that see noontime sun directly overhead. In this case, a brief tracking error is to be expected during the period when the rotator cannot move fast enough. Our design could allow for an alternative solution to the overhead sun issue – simply look out the other side of the tracker by rotating the elevation mirror past noon position. We have allowed for this “flip” position in the support hardware but chose not to implement it in software as it required a more complex weatherproof cover.
We selected Newport rotators (Newport Corporation, USA) for our design. For azimuth we use model RV240, with a full step resolution of 0.01∘. The smaller model URS75, with full step resolution of 0.02∘ is used for elevation. It is usual to micro-step the motor, in our case by a factor of 16, yielding a resolution of 0.000625∘ for azimuth and 0.00125∘ for elevation. Both values are more than adequate for our requirements.
2.1.3 Other mechanical errors
Poor mechanical rigidity of the tracker structure, movement in the mirror mounts and temperature coefficients of materials used all contribute to the passive tracking error. With conservative design these problems can be minimised.
2.1.4 Algorithm errors
These are unlikely to be present in a mature design but remain a possibility. For example, refraction at low solar elevation is significant, and is required within the algorithm (Meeus, 1991). For astronomical ephemeris calculations we used the Python PyEphem library (Downey, 2011; Rhodes, 2011).
2.1.5 Errors during mechanical initialisation (park or zero reference position)
The single sensor (or coarse flag) used on some rotators to determine mechanical park position can result in significant uncertainty of this important initial reference. For example, we see a parking uncertainty in our design of approximately 0.05∘ (based upon observation of error offsets resulting from multiple consecutive parking cycles). It may be possible to reduce this uncertainty using a second (fine) flag on the stepper motor shaft that is then logically ANDed with the coarse flag, resulting in a finer resolution for this position. We have not implemented this solution at present, although we allow for this option in our electronics design.
2.1.6 Levelling
Precise levelling using an accurate level is an important requirement for the installation and for the initial alignment procedure. In some installations the tracker must be mounted directly to a roof, which itself is often quite unstable. A well-designed tower, mounted to a stable laboratory floor, will produce the best results.
In our example, we use a level with 1 min of arc sensitivity (Moore & Wright, UK, model ELS). While this specification is nearly 0.02∘, we discovered that in practice it was difficult to find a suitable flat surface that produced repeatable results while at the same time attempting to adjust the baseplate levelling screws in an outdoor environment. Only two of our trackers are mounted to towers on solid concrete floors. When using the precision bubble level, while adjusting the somewhat coarse level-adjustment screws, it is difficult to achieve better than 0.1∘ uncertainty in mounting the tracker in a truly horizontal manner. This is a significant source of error.
2.1.7 Poor initial optical alignment
Without access to specialist tools, such as a large optical alignment bench and a well-collimated precision laser level, it may be difficult to accurately align mirrors in a solar tracker. For example, during our alignment process we use the bubble level, with an accuracy of about 0.02∘, to initially level the tracker. We then use a self-levelling laser of similar accuracy to set a reference mirror vertical. Only then do we begin to adjust the tracker's mirrors, again using the same laser. The resulting alignment accuracy is an accumulation of the laser and bubble level uncertainties at each step in the process, plus other uncertainties involved using an oil bath for beam reflection and the stability of ancillary optics used in the process.
In-use movement and diurnal thermal cycling may degrade alignment further. Based on our experience, we estimate that overall alignment accuracy better than 0.1∘ is difficult to achieve or maintain.
From the above list it becomes clear that the dominant source of error in a passive solar tracker is likely to be from poor levelling and sub-optimal optical alignment. A simple passive tracker will struggle to achieve even 0.1∘ accuracy, far from the 0.01∘ required. Fortunately, acceptable accuracy is possible if a form of optical feedback is used.
When the solar tracker is operating in the dead-reckoning or passive mode, the sun's position is continuously calculated, and the tracker mirrors are adjusted to direct a stable image of the sun into the laboratory below. The process of optical feedback adds an additional loop of control by electronically monitoring a focused image of the sun at the reference position or plane. By using control algorithms, the feedback system makes fine corrections to the rotating optical stages to precisely maintain the position of the image at the plane. The corrections made by the feedback are in the form of small error offsets, which are added to the passive control reference positions for each of the two rotators. Thus, the basic passive tracking process is still occurring in the background, with fine control being contributed by the optical feedback (also known as active mode).
With optical feedback, a sample from the tracker beam is picked off by a small mirror prior to entering the spectrometer. Traditionally, this sample is focused onto a quadrant detector (a four-element photo diode device) located on the reference plane. The four signals are analysed by the algorithm, and any imbalance detected between quadrants is used to correct the pointing. The optics for this method can be quite small, perhaps even mounted within the tracker itself. Signal levels are quite high because of the large surface area of the brightly illuminated quadrant detector. This method can be used for fast (sub-second) control, so it is useful in mobile measurement systems such as balloons, aircraft, or vehicles.
More recently, excellent results have been achieved using a miniature digital camera to analyse the solar image at or near the spectrometer entrance aperture (Franklin, 2015; Gisi et al., 2011). This has the additional advantage of coupling the tracker optical axis directly to the spectrometer, mitigating any error caused by movement of the spectrometer relative to the tracker. The camera can be installed within the spectrometer but only if there is adequate space available.
3.1 A solution using solar edge detection
We chose to use a different solution for our optical feedback design: edge detection using four silicon diodes spaced evenly around the perimeter of a focused solar image of approximately 60 mm in diameter. This method was chosen primarily because the major sources of pointing errors are uncertainty in alignment and poor levelling. By their very nature, these errors appear as a slow-changing function, often sinusoidal, with a wavelength measured in hours. We do not want information from the bright solar image itself because there is a possibility that this could make the system too sensitive to rapid intensity changes caused by passing clouds. The real information instead comes from the high contrast of the intensity gradient found at the perimeter of the solar image.
The size of our focused image is large compared to that used with a typical quadrant detector. The larger image requires longer optics (for the same focal length lens). Each of our installations is different. We have used a variety of solar image sizes ranging from 20 to 60 mm, depending upon the lenses available at the time and the size and location of the free space available to mount the optics. The edge detection diodes are nominally named left, right, up, and down (L, R, U, and D), with an active surface area chosen to suit the solar image size. In our examples we used diodes with about 7 mm2. The diodes are positioned to be partially illuminated by the edge of the image, thus ensuring a high response to any movement of the image across their surface. The diode signals are lower in level and exhibit more noise compared to those from a quadrant detector. This is partially due to the low intensity of the solar image. They are also sensitive to image “jitter” caused by atmospheric turbulence and by constant movement of the mirrors by the tracker itself. If necessary, diode signals can be improved by increasing the size of the sample mirror – but at the expense of using some of the light available for the spectrometer. Diode signals are further improved with an adjustable gain operational amplifier circuit near the diodes, and the jitter is somewhat smoothed in software using a running average of 10 samples.
Despite the differences in solar image size, intensity, and sample pick-off size, each installation appears to perform similarly. This indicates that the edge detection concept is robust in response to the various trade-offs in design parameters.

Figure 3The optical feedback components identified. The main view is from the laboratory and looks upwards towards the roof-mounted solar tracker.
Figure 3 shows an example of our feedback optics. Firstly, a small (∼ 2 mm2) front-surface mirror (Fig. 3a) samples the main solar beam from the tracker above. This is aimed at a distant wall as a useful visual reference for the operator to quickly assess tracker performance or look for the presence of cloud (Fig. 3b). A slightly larger non-vignetted portion of the main beam is directed into the feedback optics using a small mirror with dimensions of about 10 mm × 10 mm (Fig. 3c), with adjustment performed by the alignment mirror (Fig. 3d). This sample is focused with a small spotting telescope, half a set of binoculars (Fig. 3e), or a custom objective lens and eyepiece combination. The image is focused onto the diodes and amplifier printed circuit board (PCB); see Fig. 3g.
Focus and positioning can be checked by placing white paper in front of the diodes. The image should be centred, circular, and sharp. On the larger images, major sunspots may be seen. Electronic gain is adjusted to equal signal levels from the four channels, with emphasis on getting the levels in each pair equal (i.e. L = R, U = D). Physical protection and shielding from stray light are achieved using a sheet of inexpensive plastic IR filter (Optolite™ Industrial Plastics, UK) just in front of the diodes (Fig. 3g). The photodiode chosen needs a wavelength response in the near IR that matches any external filter used, e.g. PIN diode type BPW41N or BPW34F (Vishay). The signals are then routed to the tracker electronics box and sampled at 1 to 2 Hz using four channels of the 10-bit analogue to digital convertor (ADC) within our motor control PCB. The algorithms that translates these values into motor movements are described below in Sect. 3.2 and 3.3.
3.2 Feedback decision algorithm
Two parameters, set in a configuration file, are used to control decision making within the optical feedback system. The “threshold” parameter is used to set the solar intensity level needed to initiate the use of optical feedback. During initial tracker installation, this threshold parameter is set to be somewhat below the minimum expected clear-sky diode signal level. This makes some allowance for taking measurements through haze or thin cloud (if required), and for the effect of mirrors becoming dirty over time. Each (averaged) diode signal level is compared to the threshold parameter value. If no diode signals exceed this value, then the sky is deemed too cloudy and optical feedback is not engaged. The tracker continues following the sun using passive mode. If one or more diodes exceed the threshold value, then optical feedback is activated.
When optical feedback is active, averaged L–R and U–D pairs are analysed individually using a “hysteresis” parameter. The signal difference within each pair must be greater than this value before a control action is taken. The hysteresis parameter helps prevent unnecessary control actions (or “hunting”). If the signal difference within a pair exceeds the hysteresis parameter value, the algorithms act to steer the mirrors to minimise this difference by incrementing or decrementing a combination of azimuth and elevation error offset variables by 0.001∘ about every second. These error offsets are then used as a reference for the azimuth or elevation rotator positioning. The hysteresis parameter works well if set at about 10 %–30 % of the threshold value and seems to have little effect on accuracy if the image perimeter and diode positions are well matched. Movement priority is given to correct the diode pair with the greatest difference in intensities. If all four signals satisfy hysteresis and threshold requirements the tracker can be called “locked”, and no further corrective feedback is necessary. On a well-tuned system with clear sky, the tracker can be locked for longer than a minute. Fast passing clouds have little effect on tracker pointing due to the long time constant of the feedback loop. Any significant cloudiness is recorded in a logged file for post-processing of measurements and can also be used to halt automated observations until the sky is clear again. When the sky is too cloudy, the tracker reverts to passive mode, and continues tracking the calculated position of the sun.
At this stage it is important to note that there is no simple relationship between the required movement to equalise signals in a diode pair (e.g. U and D) and a single error offset variable (e.g. elevation). In other words, we will not necessarily move up and down at the reference plane by solely moving the elevation mirror. This is because the image at the diode reference plane rotates as the day progresses and is additionally modified by translation of the image through the feedback optics. This process is further explained below in Sect. 3.3.
3.3 Image translation and rotation algorithm
An algorithm is needed to map the required image movement directions, relative to the feedback plane (i.e. up, down, left, right), into the correct combination of movement directions for the elevation and azimuth rotators. There are two traditional approaches to finding this solution. One method involves absolute calculation using the knowledge of the illumination source coordinates, tracker baseplate Euler angles, and the tracker and feedback system optical components to calculate the required tracker movement (e.g. Merlaud et al., 2012; Reichert et al., 2015). The second method deduces the required tracker movement empirically, by taking a small subset of deliberate mispointing measurements to calculate the required tracker angular movements (e.g. Gisi et al., 2011). We used the first approach to generate the basic algorithm, and then only once, when the tracker is first installed, manually perform deliberate mispointing to characterise the optical geometry of the installation in terms of two parameters.
The “translation” parameter accounts for the overall effect of the many reflection and projection translations that occur through the tracker and the optical feedback optics. For example, a single lens might invert an image, and a mirror may perform another translation. The translation parameter is easily determined by intentionally commanding the tracker to shift the image in a certain direction. This can be done using the application's buttons on screen (see Sect. 5.1, which discusses the web server, and also Fig. 6). The parameter string is chosen to encode the required translation so that movements commanded to left, right, up, and down work in the correct relationship to each other. The options for this parameter are “LR”, “UD”, “LRUD”, or simply “N” for none. Once this parameter is set, the “rotation” parameter is chosen to map the resulting image movements to the correct direction on the feedback plane at the diodes. To do this, the observed angular offset is estimated in degrees (e.g. 60) and forms the rotation parameter. The rotation parameter need not be very accurate, within 10∘ is adequate. This is because any small trigonometric errors that accumulate are eventually corrected as if they were from a mechanical source. To reduce a mispointing signal imbalance at the diodes, the algorithm may move a combination of the azimuth and elevation rotators. This is achieved by incrementing or decrementing the error offset variable relating to each rotator. These error offsets effectively become the long-term integrator function, and mainly correspond to the systematic error in levelling and alignment. Error plots of consecutive clear days show similar behaviour, as do plots of similar day length even 6 months apart (Fig. 12), opening up the possibility of using recorded error offset values to identify alignment errors or indeed pre-correct errors during passive mode operation.
Figure 4 identifies the optical components and their pointing vectors. The algorithm was developed to reduce the pointing error by using the mispointing vector from the edge detection diodes. Coordinate matrix transformations T, due to tracker mirror reflections and rotations of the incoming radiation, are required to translate the mispointing vector (Ex,Ey), in the optical feedback plane to the tracker azimuth and elevation axis angular movement reference frame (Eaz,Eel). (Eaz,Eel) = T(Ex,Ey). Unlike Merlaud et al. (2012); the tracker offset Euler angles are not considered in the pointing vector coordinate transformations. With adequate tracker levelling and optical alignment, the tracker baseplate Euler angles are minor and can be compensated for by active tracking. The devised algorithm is mathematically equivalent to that described in detail by Reichert et al. (2015). The readers are directed to this reference for a detailed explanation of the coordinate transformations.
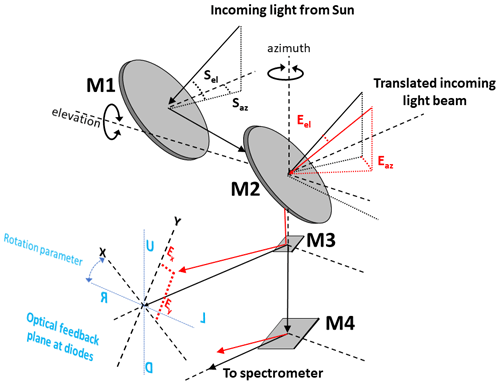
Figure 4Geometry of the Lauder solar tracker optics for the simplest configuration. Focus optics are not shown. M1 and M2 are the tracker ALT-AZ mirrors. M3 is a small flat mirror to direct a portion of the incoming beam to the optical feedback system. M4 is a large flat mirror directing the solar beam into the spectrometer. (Sel,Saz) is the calculated (solar-pointing) incoming beam vector. X–Y is the planar coordinate system of the optical feedback system, shown here prior to correction with the installation-specific rotation parameter. (Ex,Ey) is the mispointing vector. (Eel,Eaz) is the mispointing vector transformed into the tracker vector reference frame.
3.4 Initial adjustment of the optical feedback system during installation
A new solar tracker must be correctly aligned and levelled prior to initial adjustment of the feedback optics. The optical feedback system should be disabled during this process. The solar beam from the tracker must be made vertical (checking by back-reflecting off an oil bath) and the 45∘ mirror (M4 in Fig. 4) under the tracker adjusted to direct the beam horizontally to centre the solar image on the spectrometer input aperture. The tracker and spectrometer optical axes are now co-aligned. The next step is to centre the solar image on the feedback diodes using the adjustment mirror (Fig. 3d). The sky should be clear and cloud-free so that amplifier gains can be adjusted make the four diode values equal. The threshold and hysteresis parameters can now be set as described above (Sect. 3.2). The optical axes of the tracker, spectrometer, and optical feedback are now co-aligned. When the feedback system is enabled it will maintain the solar image centred on the spectrometer entrance aperture regardless of small errors in the solar tracker alignment or levelling.
4.1 Factors affecting reliability
Software crashes, power failures, mechanical fatigue and exposure to extreme weather are common causes of tracker failure. Choosing a stable and mature OS is a good route to reliability. The OS and computer platform could even be of an embedded nature, removing the need for regular software updates which are an ever-present source of interruption. An uninterruptible AC power supply should be used. The tracker needs protection from weather. This is achieved using good design practices such as waterproofing any electronics. The use of a custom-designed automated cover is recommended. (e.g. Heinle and Chen, 2018).
This leaves us with the main source of tracker failure: the eventual fatigue of wiring and switches that experience daily movement. Our design eliminates this point of failure by having no moving wires and or switches.
4.2 A solution using a coaxial transformer
The upper rotating stage is comprised of the elevation rotator, mirror, and electronics and needs less than 10 W of power. Traditionally, this has been supplied via a flexible cable or slip rings and carbon bushes – all potential sources of failure. In 2007 we experimented with power transfer using a coaxial transformer consisting of a stationary primary winding with the secondary nested within and able to rotate freely. The primary can then be fixed to the tracker base, and the secondary is fixed to and rotates with the upper elevation stage.
Figure 5 shows this prototype. Early versions used a dual primary with outer (Fig. 5a) and inner (Fig. 5b) coils, with the secondary (Fig. 5c) able to rotate within. This arrangement made the transformer more efficient and capable of transferring more power than was needed, although at the expense of reducing the available optical aperture. The final version of this transformer uses just the outer primary and has an unobstructed aperture of 150 mm. Power transfer efficiency is approximately 20 %. The external diameter of the transformer is 175 mm, designed to fit within the chosen model of azimuth rotator. The primary former (Fig. 5d) also acts as the tracker's base.
The air-cored transformer is inefficient at the low frequencies of normal AC mains (50–60 Hz) but transfers adequate power at frequencies towards the limit of human hearing. A frequency of 15 kHz was chosen as a compromise between efficiency, acoustic noise, potential for radio frequency emission, and physical size of electronic smoothing components. The primary coil is driven with an oscillator feeding a power audio amplifier integrated circuit (IC) type LM3886. Power transfer efficiency is improved by resonating the secondary winding with a suitable series capacitance prior to rectification at the elevation power supply. In 11 years of operation, this method of electrical power transfer has never failed.
The complete tracker was tested for emissions that cause electromagnetic interference (EMI). Between 10 Hz and 75 MHz, the maximum emission seen was −119 dBm Hz−1. No interference was detected from the coaxial transformer.
In addition to greater reliability than other methods of power transfer, the coaxial transformer has the advantage of allowing continuous 360∘ rotation in azimuth. This avoids the need to reverse and re-initialise the rotator daily. In polar regions, measurements can continue uninterrupted through the summer polar day. The elevation rotator and mirror can also rotate freely through 360∘ with no mechanical obstructions. After sunset, the mirror continues to track the solar position (even below the horizon) so that it is ready for sunrise the next day. Except for power-on initialisation, neither rotator needs parking again.
Except for the AC power switch, no mechanical switches are used on the complete tracker. The ever-reliable stepper motors are used for moving the rotators. Park or zero position detection within the rotators is via contactless sensors. No electronic failures have been experienced over 11 years in our four trackers.
4.3 Data transmission to the rotating stage
Bidirectional wireless communication is needed for the elevation stepper motor controller. We investigated transmission by optical transducers and by modulating the power circuit through the coaxial transformer. Neither method proved easy. Instead we use a generic Bluetooth serial link (e.g. Roving Networks, USA, model RN240F).
We define longevity as the ability to keep the tracker running viably for many decades to come. Factors to consider include the likely ongoing support for the OS and application software language, communication protocols, and of course the electronic components used. Except for specialised items, such as the rotators, the design should attempt to use generic components and to be built in a modular fashion. The ultimate test would be attempting to build a duplicate in the distant future. Although it would be unlikely to achieve an exact copy, with careful design each critical module should be able to be replaced easily with a modern version without the necessity of redesigning the complete tracker.
5.1 Operating system and application software
Our tracker hardware is OS agnostic. The early version of the application was written in Visual Basic and ran on Windows. However, the short lifespan of Windows versions, along with in-house security rules, soon caused our application software to be obsolete. The application was rewritten in Python 2.7, with the user interface (Fig. 6) in the form of a web server using the Python web framework Tornado (https://www.tornadoweb.org/en/stable/, last access: 2 November 2020). All of our trackers now run on recycled laptops running Ubuntu Linux OS. The tracker can be monitored and controlled from the laptop by browsing to the internal web server. The laptop can also be connected via a second network ethernet card to the spectrometer's PC. Thus, the tracker can be monitored and controlled from that PC too.
To some extent, the tracker, Linux OS, and Python application can be thought of as a stand-alone hardware device with an embedded OS. These should never need upgrading until hardware (the laptop) fails. When this occurs, the OS can be reinstalled or a later version can be used. The tracker laptop and hardware do not have to connect to any other device. Because no internet connection is required for operation, the complete system is largely isolated from the outside world, and thus it should prove very safe from common security threats. Our tracker hardware and software has also run successfully on the popular Raspberry Pi platform. We have not attempted to run the current Python application on a Windows OS. We have not attempted to run our Bruker spectrometers on a Linux OS. At present, our preference is to keep the tracker and the spectrometer on separate PCs.
5.2 Main electronics
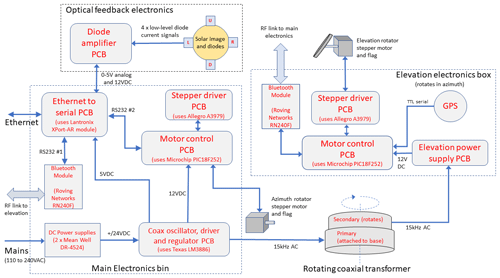
Figure 7 shows a schematic of the overall tracker and the connections between the major modules. Figure 8 shows the inside the main electronics box within the laboratory. The ethernet to serial convertor (Fig. 8a) sends one channel (elevation) direct to the Bluetooth module (Fig. 8b) and the other channel to the azimuth motor control PCB (Fig. 8e) with the stepper driver daughter PCB (Fig. 8d) plugged in on top. The coaxial amplifier and oscillator, along with associated voltage regulators, are included on one PCB (Fig. 8f). This PCB supplies the regulated direct current (DC) voltages needed for the ethernet-to-serial convertor and motor controller. Analogue signals from the optical feedback system (diode signals) connect to ADC channels on the motor control PCB.
The most likely sources of failure in the electronics bin would be the fan used to help cool the amplifier IC and heat sink (Fig. 8g), and the AC to DC power supplies. In the case of fan failure, risk is mitigated using an extra-large heat sink, which in ambient lab temperatures would suffice on its own. The fan used is a high-quality unit with magnetic levitation bearings (Fig. 8h). Generic DIN-standard AC-to-DC power supply modules are used (Fig. 8c), enabling easy replacement in the future. The total power consumption of the tracker is 55 W.
5.3 Elevation electronics
Figure 9 shows the inside of the elevation electronics box. The coaxial secondary winding feeds a custom rectifier PCB (Fig. 9g). This circuit needs to cope with the voltage extremes and high frequency present in the low-efficiency, high-impedance transformer waveform. A switch mode regulator (type LM2592HV, Texas Instruments, USA) handles the high voltage and keeps power usage to a minimum. The series resonance capacitor is seen at Fig. 9h.
The motor controller PCB (Fig. 9c) is identical to the unit used for the main electronics, good practice for keeping spare parts in common. The Bluetooth module (Fig. 9a) is also identical to the one used in the main electronics. A GPS module (Fig. 9d) and temperature sensor (Fig. 9b) connect to spare inputs on the motor controller PCB. Figure 9 also shows how in this version tracker the elevation mirror adjuster micro-thread screws (Fig. 9e) are placed inside the box. This helps prevent accidental adjustment.
5.4 The motor controller in more detail
This is the most complex of the modules used in our tracker. The design uses the very popular PIC18F252 microcontroller IC (Microchip Technology, USA). Although our circuit design dates back to 2006, this IC is still readily available (2020). Firmware is written in C using the freely available development environment MPLAB® X IDE (Microchip, USA). The firmware code runs in a loop, awaiting a command to be received on the serial port. Commands include requests to read the GPS data, temperature sensor, and other analogue and digital voltages on auxiliary pins. Another group of commands deals with the stepper motor control. These commands range from simple step commands to more complex routines such as parking. All commands are acknowledged.
The job of moving the stepper motor is performed by the plug-in daughter PCB – the stepper driver (e.g. Fig. 8f). We made a separate PCB for two reasons. Firstly, this type of driver IC seemed a likely candidate to become obsolete, and secondly this type of IC can be destroyed if abused, for example a short circuit on the cable or unplugging when in use. The IC chosen, type A3979 (Allegro Microsystems, USA), is still readily available as of 2020. Allegro make numerous similar stepper driver ICs and hobby-electronics suppliers use these (and other manufacturers' drivers) in easy-to-use modules for robotics and 3D printers, etc. There is little doubt that suitable stepper motors and drivers are going to be available for decades to come.
5.5 Data communication methods and protocols
5.5.1 RS232
Serial communication to motor controllers is via RS232. This protocol retains strong support throughout the instrumentation industry. RS232 enables easy low-level testing and development of the tracker without the additional complexity of, for example, USB. RS232 ports are still present on most new desktops, and additional plug-in cards are readily available.
5.5.2 Bluetooth
Bluetooth modules are used to link data to the elevation stage. Bluetooth appears to be supported well into the future as it continues to be present in modern consumer devices. Our data speed is low (9600 baud). Many other forms of low-power radio link could be easily be used instead.
5.5.3 Ethernet
In its more basic form, our tracker will run directly from two RS232 ports on a desktop PC and not need to use ethernet at all. However, using an ethernet to serial convertor is a good solution if a laptop (which generally lack RS232 ports) is to be used. In our installations, the ethernet-to-serial convertor, laptop, and spectrometer all share the same subnet and connect to the spectrometer's Windows PC via a second ethernet card. This makes for a very tidy and useable system. Ethernet continues to be well supported. In the future it might be necessary to upgrade to a different model ethernet to serial convertor, but due to the modular design philosophy this is a small task.
Over a period of 11 years we have assembled four solar trackers. These are in use at Lauder (45∘ S), New Zealand, and Arrival Heights (78∘ S), Antarctica, achieving a history of good reliability even in polar conditions. Tracker accuracy has been analysed on our trackers capable of TCCON measurements and can routinely produce a pointing accuracy of 0.02∘ from solar centre.
6.1 Accuracy achieved
We have two methods for monitoring accuracy of our trackers. The first is simply by observation. For this we project a sample of the tracker's vertical beam with a very small (∼ 2 mm2) chip of front-surface mirror (Fig. 3a). Aimed at a distant wall, this acts like a pin-hole camera producing a reasonably well-defined solar image if projected onto a white surface. The circular image can be outlined in ink and any deviations can be assessed in terms of relative movement of the solar diameter. An error of more than 5 % (0.025∘) is very apparent, yet in practice this is never seen. In a similar manner, the focused solar image at the FTIR entrance aperture can be viewed if the instrument source compartment has a transparent cover. Our four FTIRs have these covers.
The second method for assessing accuracy involves post-processing of our routine TCCON FTIR measurements to assess solar-telluric wavelength shift (S-G shift). S-G shift is obtained from analysis of solar absorption features (so-called Fraunhofer lines) in the oxygen column retrieval in the 7882 cm−1 band (Wunch et al., 2011). This analysis uses Doppler wavelength shift of sunlight caused by the relative rotational velocities of the sun and Earth. Absorptions within the solar atmosphere show greatest shift along the equatorial edges of the solar image where the apparent velocity is highest. The main limitation with this method is that sensitivity exists only in the direction normal to the solar polar axis (Reichert et al., 2015). However, the cause of any tracker error is unlikely to fall exactly (and only) along the polar axis for long periods and the solar image also rotates at the spectrometer as the day progresses. This analysis remains very useful. The method does require the use of a spectrometer capable of acquiring suitable high-resolution solar spectra and the user must have the skills to perform the analysis involved. The results are not in real time. Correct analysis relies on the solar image beginning centred on the spectrometer aperture. If this is not done, then the analysis may show a high pointing error even when the tracker is performing well.
We perform S-G shift analysis as part of routine TCCON data processing soon after the day's data are uploaded to our server, and the results are displayed as a web plot for easy viewing.
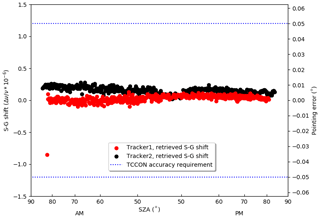
Figure 10Indicative accuracy of two solar trackers, inferred using S-G shift analysis under clear sky conditions during spectrometer intercomparison, 29 March 2019. “Tracker1” and “Tracker2” are local tracker identifier names. The dotted blue line indicates TCCON accuracy specification.
Figure 10 displays S-G shift on a clear-sky day during an intercomparison between our two Bruker IFS125HR spectrometers (with solar tracker names “Tracker1” and “Tracker2”, based at Lauder, New Zealand). With perfect sky, clean mirrors and both spectrometers well-aligned, this plot shows tracker pointing accuracy (for both trackers) better than 0.02∘. A lone red dot represents the first measurement performed at sunrise, before the Tracker1 feedback was locked. The TCCON pointing accuracy requirement of 0.05∘ is easily met.
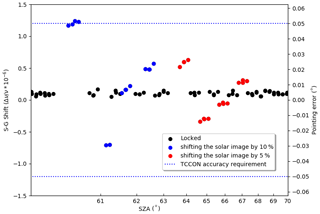
Figure 11Intentional mispointing tests in four quadrants (L, R, U, D) by 10 % (blue) and 5 % (red) of the solar image diameter. Tests performed on 1 May 2020 using Lauder Tracker1.
This sensitivity of using S-G shift as a pointing diagnostic can be tested by intentionally mispointing the tracker by a small amount. Figure 11 shows the results of shifting the solar image by (approximately) 10 % of the diameter (0.05∘) and 5 % (0.025∘). The orientation of the solar polar axis was not known at the time, so mispointing was performed in two orthogonal axes so that a range of positive and negative spectral shift errors would be captured. Figure 11 shows that the sensitivity of this method is adequate to detect such errors.
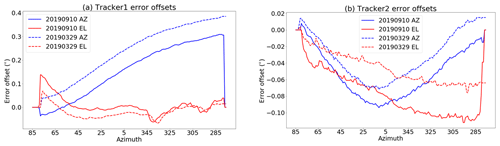
Figure 12Error offsets of Tracker1 (a) and Tracker2 (b) 6 months apart. Blue lines plot azimuth (AZ) offsets, and red lines show elevation (EL) offset.
It is also useful to see the magnitude of error correction performed by the optical feedback system. The error offset variables represent the corrections the feedback system needs to add (or subtract) from the calculated ephemeris for positioning the azimuth and elevation rotators in order to keep the solar image centred within the four photodiodes. The error offsets change slowly over the day and are logged to file. They provide a good indication of the state of mechanical alignment and/or levelling error. Figure 12 plots these offsets for two different trackers during a spectrometer intercomparison. The test was done again 6 months later. Figure 12a plots these offsets for Tracker1. Some change is seen over the period, although part of the shift between date pairs is caused by the operator performing an offset save within the application. This action adds any instantaneous offsets to the setup offset parameters, and re-zeros the instantaneous offsets. The overall pattern, especially evident in the azimuth (AZ) offset, shows the slow-changing nature of the error sources involved. Figure 12b shows a similar plot for Tracker2, with relatively small offsets that indicate good alignment and/or levelling. Because both trackers indicated a similar (and good) level of accuracy at the same time (e.g. Fig. 10), we can infer that Tracker1 is not well aligned or is no longer mounted level (or the beam was not vertical when the feedback optics were last zeroed). This reinforces how effective our simple optical feedback system can be – even large errors are compensated for by the feedback system. However, it is worth mentioning that if the errors get much larger than the solar diameter (0.5∘) then this feedback system may not automatically achieve lock (because in some situations, the solar image could miss all diodes). Tracker1 is close to this situation and probably needs re-levelling or alignment soon.
A solar tracker long-term accuracy and stability assessment was performed by identifying periods of clear sky (using all-sky camera images) and plotting the analysed S-G shift daily averages from measurements made on these days. Since FTIR measurements are taken automatically, they may still include some observations affected by cloud (or other weather conditions such as haze or wind). However, our current TCCON spectra acquisition and processing procedures have further quality assessment and quality control (QAQC) measures to eliminate the majority of weather affected observations.
S-G shift analysis is also affected by events not related to the tracker. For example, any adjustments (planned or accidental) to the spectrometer perturb the instrument. Because the spectrometer is supported by numerous coil springs, even simply leaning on the instrument or bumping it results in moving the optical axis away from its previous location. The effect of this makes the solar image no longer centred on the entrance aperture. In such cases, the solar image can be manually re-steered back onto the centre of the entrance aperture using the 45∘ mirror underneath the tracker tower. A laboratory logbook records these events.
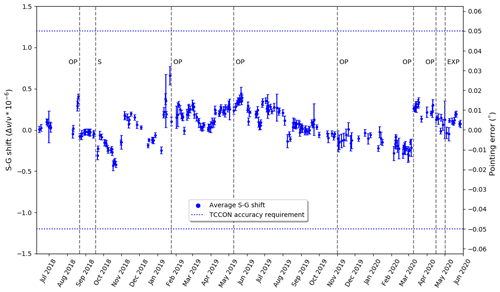
Figure 13Retrieved S-G shift for measurement days over a 24-month period using Tracker1. Each point is a value for TCCON spectral measurements taken during days that experienced at least 1 h of continuous clear sky. Vertical lines mark dates when specific maintenance events were performed on the equipment. Cleaning or adjusting the 45∘ mirror optics in front of the spectrometer was performed on events marked as “OP”, and a major alignment was performed on the spectrometer (“S”). Days with high standard deviation are generally the result of cloud-affected measurements, and this is confirmed when looking at the day in detail. On 1 May 2020 (“EXP”), we performed the intentional mispointing experiments, and this day also shows high standard deviation, which was to be expected.
Figure 13 displays the S-G shift over a 24-month period when Tracker1 was in use. Days with high standard deviation are the result of cloud either affecting a measurement directly or delaying the initial feedback lock of the tracker (and thus are a true pointing error for these few observations). High standard deviation occurring on 1 May 2020 is the result of the intentional mispointing experiments previously discussed. Often logbook entries correlate to a step in S-G shift, especially when the 45∘ mirror underneath the tracker is adjusted. Other large steps in S-G shift, for example in November 2018 and in early January 2019 have no logged cause but are likely the result of human presence in the laboratory resulting in the instruments being bumped. Thus, these steps appear to show the tracker exhibiting poor performance when in fact it is the adjustment of the 45∘ mirror under the tracker or movement of the spectrometer at fault. We have since moved our optical feedback system to be bolted directly to the front of the spectrometer. It appears to compensate for movement of the spectrometer very well but will need to acquire a further time series of measurements to determine the true extent of a system-wide improvement.
6.2 Reliability achieved
We have experienced few interruptions due to failure of our solar trackers. Typically, the trackers run continuously for many months with no operator intervention. The only failure seen appears as a stalled application. To date we have been unable to locate a common cause for this, but suspect it arises from code used in our application or data loss in either the ethernet or Bluetooth links. To put this in context, the spectrometer and PC require restarting much more often than our tracker. The Newport rotators are of excellent quality and are running at such low duty (one rotation per day) that we do not expect them to wear out for a long while.
6.3 Longevity achieved?
Development started in 2006, with the first tracker in constant use since 2009. Our most recent unit was built in 2016–2017. The basic design has remained constant, with the only significant change being recoding of the software from Visual Basic to Python. A range of spare parts has been kept: for example, a complete spare electronics bin has been made and is kept at our remote Antarctic laboratory, along with a spare laptop. The electronics bin is completely interchangeable with any other tracker. The motor controller PCB is compatible with azimuth and elevation electronics, and a range of other PCBs are kept as spares. A spare pair of Bluetooth links is also kept on-site at Lauder. We believe our design demonstrates longevity.
6.4 Other benefits
Raw feedback diode values are logged approximately each second. These data files are downloaded and used in the spectra quality control process to automatically cull measurements made during periods of cloudiness. In addition, the automated scheduling software used to take FTIR measurements (Geddes et al., 2018) can inspect this file in real time and will only initiate observations when the sky is not flagged as “cloudy”. Using these methods, we have increased our measurement density and quality while at the same time reducing the manual effort required in pre-processing quality control. The web server user interface has proven easy to use. When networked, the tracker is easily controlled from a remote location.
The Python application and electronics can be adapted to drive other types of ALT-AZ trackers: for example, we successfully reused an existing tracker dating from the 1980s. A configuration file allows for alternative resolution rotators to be used.
The design of this solar tracker has proven successful for its intended use. We make the following conclusions.
-
The use of a coaxial transformer to transfer power to the upper (moving) stage has proven to be very reliable, with the added advantage of 360∘ continuous rotation.
-
A form of optical feedback is needed to meet today's tracker accuracy requirements.
-
The simple edge-detection method of optical feedback is effective.
-
Analysing the solar spectra for S-G wavelength shift is a useful method of assessing tracker pointing accuracy.
-
The Newport optical rotators used in this design have proven to be long-lasting and reliable, with adequate mechanical resolution when motors are micro-stepped.
Due to the modular design philosophy, the use of basic communication protocols and commonly used software and OS achieves a long-lasting and easily maintainable system. The design detailed in this paper was made for FTIR solar spectral measurements for NDACC/TCCON purposes, but in principle it could be easily adapted for other uses. Mirrors, rotators, and even the coaxial transformer could be scaled to suit larger or smaller applications.
7.1 Potential development and improvements
Our current tracker accuracy is limited by the stability and optical resolution of the feedback system. Although the current feedback optics meet our accuracy requirements, they are far from perfect. Further experimentation using improved mechanical stability and better optics could well be beneficial, especially for when the tracker must be operated in dead-reckoning mode (e.g. using moonlight as a source).
Tracker levelling accuracy could be improved using fine-pitched adjustment screws on the tracker tower baseplate. The use of a permanently attached digital accelerometer may enable easier levelling and ongoing monitoring.
Mirror stepping movements can be perceived in the reference solar image projected to the distant wall, although at times it is no worse than atmospheric turbulence. This movement is the result of the approximate 1 s loop cycle, meaning multiple steps are often needed to track the sun, resulting in a larger (accumulated) single movement than if done several times per second. The present generation of motor controller has rather verbose commands and is quite slow in stepping. The Python application and the firmware of the motor controller have good potential for improvement in this area, especially if greater movement resolution was thought necessary.
There is great potential to add more intelligence to the decision algorithm. Incorporating some Proportional Integral Derivative (PID) control code would make lock occur quicker and remain stable for longer (e.g. Merlaud et al., 2012). Because of the long integration time and “nudge and wait” approach of our feedback method, it takes 1 or 2 min to achieve initial “lock” once clear sun appears. This could also be sped up by saving and reusing offsets from a recent clear day or dynamically changing step size depending on the magnitude of the diode pair difference. The current code is simple, yet few observations are lost with this deficiency because the sky can remain unsuitable for optimum measurements for long periods, and as the sky gradually clears, the tracker is continuously decreasing the pointing error. Once the sun is finally clear, lock is quickly achieved. The algorithm that averages the diode values and uses the threshold and hysteresis parameters could be improved. For example, signal strength history could be used to auto-set the threshold and hysteresis parameters. This would automatically compensate for the reduction in signal level under uniform hazy sky or as mirrors slowly accumulate dust between routine cleaning.
There are clearly potential benefits for switching to a camera-based feedback system, for example it should be easier to perform solar limb measurements (intentionally pointing off solar centre to separate solar and terrestrial absorptions). The tracker has been successfully used for measurements using moonlight, but this was done in passive (non-feedback) mode, requiring careful setup and manual adjustments every hour to account for inherent misalignment and levelling of the tracker. Lunar measurements with optical feedback would be much easier using the extra gain of a camera-based system. If a camera was used, we could retain the philosophy of correcting for a slow-changing error function (“nudging” the error offset variables). An inherent weakness with the edge detection method is the response to a partially obscured solar disc. Under this situation the pointing is affected to some degree but less so than would occur with a quadrant detector. A camera should be able to behave better in this situation.
A camera system, if imaging the spectrometer aperture, provides the important direct coupling of the tracker and spectrometer optical axes that our current system lacks. Alternatively, for critical applications, the current optical feedback system should be moved to attach directly to the spectrometer, effectively tying the optical axes of the tracker and spectrometer together.
Our main code is written in Python 2. A move to Python 3 would be another worthwhile investment.
7.2 Autonomous weatherproof cover
With the tracker design working well, the next step was to design a matching automated cover (Fig. 14). This needed the ability to rotate continuously in azimuth and to protect the tracker from extreme weather. The cover was completed in 2013 and its use has resulted in a significant increase in our number of measurements. The authors would like to present the design of this cover in a future publication.
7.3 3D printed?
It would now be practical to produce much of this solar tracker using modern 3D printing processes. The mechanical structure, including the coaxial transformer components and elevation electronics, should print easily, enabling the design to be easily replicated or scaled to suit, especially for less demanding or cost-sensitive applications. It would be interesting to print semi-adjustable mirror mounts and rely even further on optical feedback to maintain accuracy. The elevation rotator might be a direct-drive stepper motor with a higher micro-stepping value (256 is now possible).
The public processed data sets are available from the following DOIs: https://doi.org/10.14291/tccon.ggg2014.lauder02.R0/1149298 (Sherlock et al., 2014) for spectrometer ll and https://doi.org/10.14291/tccon.ggg2014.lauder03.R0 (Pollard et al., 2019) for spectrometer lr. Raw engineering data, including the SGShifts are available from the authors on request.
JR designed and built the solar tracker, along with the electronic PCBs and optical feedback system. JR programmed the embedded devices and computer software. DS developed the active feedback algorithm. DP provided S-G shift spectral analysis. Plots of S-G shift were produced by HS. JR wrote the paper with contributions from DS.
The authors declare that they have no conflict of interest.
We wish to acknowledge colleagues from NIWA who have contributed to the successful outcome for our solar tracker. Alan Thomas and Paul Johnston contributed their extensive knowledge of optics to the initial design of our prototype. Brian Connor identified the need for a more accurate solar tracker and gained the seed funding and support needed to start the project. Alex Geddes and Bruno Kinoshita contributed important Python coding skills to the final application.
We also thank Antarctica New Zealand for providing logistical support for the FTIR measurements at Arrival Heights, which included testing tracker performance in polar conditions. We were also well supported by our TCCON research colleagues at CalTech. Dougal Hiscock (Engen Engineering, New Zealand) greatly assisted with design and manufacture of our custom mirror mounts.
Tracker development was core-funded by NIWA (programme CAAC_2101) through New Zealand's Ministry of Business, Innovation and Employment Strategic Science Investment Fund.
This paper was edited by Frank Hase and reviewed by two anonymous referees.
Chevallier, F., Deutscher, N. M., Conway, T., Ciais, P., Ciattaglia, L., Dohe, S., Fröhlich, M., Gomez-Pelaez, A., Griffith, D., and Hase, F.: Global CO2 fluxes inferred from surface air-sample measurements and from TCCON retrievals of the CO2 total column, Geophys. Res. Lett., 38, L24810, https://doi.org/10.1029/2011gl049899, 2011.
Dammers, E., Shephard, M. W., Palm, M., Cady-Pereira, K., Capps, S., Lutsch, E., Strong, K., Hannigan, J. W., Ortega, I., Toon, G. C., Stremme, W., Grutter, M., Jones, N., Smale, D., Siemons, J., Hrpcek, K., Tremblay, D., Schaap, M., Notholt, J., and Erisman, J. W.: Validation of the CrIS fast physical NH3 retrieval with ground-based FTIR, Atmos. Meas. Tech., 10, 2645–2667, https://doi.org/10.5194/amt-10-2645-2017, 2017.
De Mazière, M., Thompson, A. M., Kurylo, M. J., Wild, J. D., Bernhard, G., Blumenstock, T., Braathen, G. O., Hannigan, J. W., Lambert, J.-C., Leblanc, T., McGee, T. J., Nedoluha, G., Petropavlovskikh, I., Seckmeyer, G., Simon, P. C., Steinbrecht, W., and Strahan, S. E.: The Network for the Detection of Atmospheric Composition Change (NDACC): history, status and perspectives, Atmos. Chem. Phys., 18, 4935–4964, https://doi.org/10.5194/acp-18-4935-2018, 2018.
Downey, E. C.: XEphem: Interactive Astronomical Ephemeris, Astrophysics Source Code Library, ascl:1112.013, available at: http://ascl.net (last access: 4 November 2020), 2011.
Franklin, J. E.: Solar absorption spectroscopy at the Dalhousie Atmospheric Observatory, PhD Thesis, Dalhousie University, Halifax, Nova Scotia, Canada, 2015.
Geddes, A., Robinson, J., and Smale, D.: Python-based dynamic scheduling assistant for atmospheric measurements by Bruker instruments using OPUS, Appl. Optics, 57, 689–691, https://doi.org/10.1364/ao.57.000689, 2018.
Gisi, M., Hase, F., Dohe, S., and Blumenstock, T.: Camtracker: a new camera controlled high precision solar tracker system for FTIR-spectrometers, Atmos. Meas. Tech., 4, 47–54, https://doi.org/10.5194/amt-4-47-2011, 2011.
Hedelius, J. K., He, T.-L., Jones, D. B. A., Baier, B. C., Buchholz, R. R., De Mazière, M., Deutscher, N. M., Dubey, M. K., Feist, D. G., Griffith, D. W. T., Hase, F., Iraci, L. T., Jeseck, P., Kiel, M., Kivi, R., Liu, C., Morino, I., Notholt, J., Oh, Y.-S., Ohyama, H., Pollard, D. F., Rettinger, M., Roche, S., Roehl, C. M., Schneider, M., Shiomi, K., Strong, K., Sussmann, R., Sweeney, C., Té, Y., Uchino, O., Velazco, V. A., Wang, W., Warneke, T., Wennberg, P. O., Worden, H. M., and Wunch, D.: Evaluation of MOPITT Version 7 joint TIR–NIR XCO retrievals with TCCON, Atmos. Meas. Tech., 12, 5547–5572, https://doi.org/10.5194/amt-12-5547-2019, 2019.
Heinle, L. and Chen, J.: Automated enclosure and protection system for compact solar-tracking spectrometers, Atmos. Meas. Tech., 11, 2173–2185, https://doi.org/10.5194/amt-11-2173-2018, 2018.
Keppel-Aleks, G., Toon, G. C., Wennberg, P. O., and Deutscher, N. M.: Reducing the impact of source brightness fluctuations on spectra obtained by Fourier-transform spectrometry, Appl. Optics, 46, 4774–4779, 2007.
Mahieu, E., Chipperfield, M. P., Notholt, J., Reddmann, T., Anderson, J., Bernath, P. F., Blumenstock, T., Coffey, M. T., Dhomse, S. S., Feng, W., Franco, B., Froidevaux, L., Griffith, D. W. T., Hannigan, J. W., Hase, F., Hossaini, R., Jones, N. B., Morino, I., Murata, I., Nakajima, H., Palm, M., Paton-Walsh, C., Russell, J. M., Schneider, M., Servais, C., Smale, D., and Walker, K. A.: Recent Northern Hemisphere stratospheric HCl increase due to atmospheric circulation changes, Nature, 515, 104–107, https://doi.org/10.1038/nature13857, 2014.
Meeus, J. H.: Astronomical algorithms, Willmann-Bell, Inc., Richmond, Virginia, USA, 1991.
Merlaud, A., De Maziere, M., Hermans, C., and Cornet, A.: Equations for solar tracking, Sensors, 12, 4074–4090, 2012.
Pollard, D. F., Sherlock, V., Robinson, J., Deutscher, N. M., Connor, B., and Shiona, H.: The Total Carbon Column Observing Network site description for Lauder, New Zealand, Earth Syst. Sci. Data, 9, 977–992, https://doi.org/10.5194/essd-9-977-2017, 2017.
Pollard, D. F., Robinson, J., and Shiona, H.: TCCON data from Lauder (NZ), Release GGG2014.R0 [Data set], CaltechDATA, https://doi.org/10.14291/tccon.ggg2014.lauder03.r0, 2019.
Rayner, P. J. and O'Brien, D. M.: The utility of remotely sensed CO2 concentration data in surface source inversions, Geophys. Res. Lett., 28, 175–178, 2001.
Reichert, A., Hausmann, P., and Sussmann, R.: Pointing errors in solar absorption spectrometry – correction scheme and its validation, Atmos. Meas. Tech., 8, 3715–3728, https://doi.org/10.5194/amt-8-3715-2015, 2015.
Rhodes, B. C.: PyEphem: astronomical ephemeris for Python, Astrophysics Source Code Library, ascl:1112.014, available at: http://ascl.net (last access: 4 November 2020), 2011.
Sherlock, V., Connor, B., Robinson, J., Shiona, H., Smale, D., and Pollard, D. F.: TCCON data from Lauder (NZ), 125HR, Release GGG2014.R0 [Data set], CaltechDATA, https://doi.org/10.14291/tccon.ggg2014.lauder02.r0/1149298, 2014.
Steinbrecht, W., Froidevaux, L., Fuller, R., Wang, R., Anderson, J., Roth, C., Bourassa, A., Degenstein, D., Damadeo, R., Zawodny, J., Frith, S., McPeters, R., Bhartia, P., Wild, J., Long, C., Davis, S., Rosenlof, K., Sofieva, V., Walker, K., Rahpoe, N., Rozanov, A., Weber, M., Laeng, A., von Clarmann, T., Stiller, G., Kramarova, N., Godin-Beekmann, S., Leblanc, T., Querel, R., Swart, D., Boyd, I., Hocke, K., Kämpfer, N., Maillard Barras, E., Moreira, L., Nedoluha, G., Vigouroux, C., Blumenstock, T., Schneider, M., García, O., Jones, N., Mahieu, E., Smale, D., Kotkamp, M., Robinson, J., Petropavlovskikh, I., Harris, N., Hassler, B., Hubert, D., and Tummon, F.: An update on ozone profile trends for the period 2000 to 2016, Atmos. Chem. Phys., 17, 10675–10690, https://doi.org/10.5194/acp-17-10675-2017, 2017.
Wunch, D., Toon, G. C., Blavier, J.-F. L., Washenfelder, R. A., Notholt, J., Connor, B. J., Griffith, D. W., Sherlock, V., and Wennberg, P. O.: The total carbon column observing network, Philos. T. Roy. Soc. A, 369, 2087–2112, 2011.