Effects of multi-charge on aerosol hygroscopicity measurement by a HTDMA

The humidified tandem differential mobility analyzer (HTDMA) is widely used to measure the hygroscopic properties of submicron particles. The size-resolved aerosol hygroscopicity κ measured by a HTDMA will be influenced by the contribution of multiply charged aerosols, but this effect on field measurements has seldom been discussed for previous field measurements. Our calculations demonstrate that the number ratio of multiply charged particles is quite considerable for some specific sizes between 100 and 300 nm, especially during a pollution episode. The presence of multiple charges will lead to a compression effect on the aerosol hygroscopicity in HTDMA measurements. Therefore, we propose a new algorithm that performs multi-charge correction of the size-resolved hygroscopicity κ, taking both the compression effect and the multi-charge number contribution into consideration. Application of the algorithm to field measurements showed that the relatively high hygroscopicity in the accumulation size range leads to the overestimation of the hygroscopicity of particles smaller than 200 nm. The low hygroscopicity of coarse-mode particles leads to the underestimation of the hygroscopicity of accumulation particles between 200 and 500 nm in size. The difference between the corrected and measured κ values can be as large as 0.05, highlighting that special attention must be paid to the multi-charge effect when a HTDMA is used for aerosol hygroscopicity measurements.

1 Introduction

Atmospheric particles can scatter solar radiation and absorb longwave radiation, which directly affects the Earth's radiation balance (Haywood and Boucher, 2000; Bond et al., 2013). They can also indirectly affect the climate by acting as cloud nuclei and modifying the optical properties and life cycle of clouds (Albrecht, 1989; Twomey, 1974; Charlson et al., 1992). Both of these effects are closely related to aerosol particle hygroscopicity, which describes the ability of a particle to absorb water under sub- or supersaturated conditions (e.g., McFiggans et al., 2006). Aerosol hygroscopicity also plays a vital role in aspects of environmental science. It is reported to be an important influence on environmental visibility because it can greatly enhance particle light scattering efficiency and degrade visibility when the relative humidity is high (Chen et al., 2012; Xu et al., 2020). It can increase the liquid water content of aerosol particles, affect multiphase chemistry and local photochemistry, and facilitate particle formation and aging processes (Wu et al., 2018; Herrmann et al., 2015; Ervens et al., 2011). In human health, the deposition pattern of inhaled particles in the human respiratory tract depends on the size of the particles, which is influenced by their hygroscopicity (Heyder et al., 1986; Löndahl et al., 2007). In general, the hygroscopicity of an aerosol particle is one of the most important properties to consider when quantifying its climatic and environmental effects. It is also useful to characterize the chemical properties of the particle in detail. Therefore, correct and detailed measurements of aerosol hygroscopicity are required.

While many instruments are currently used to characterize the hygroscopicity of aerosol particles, the humidified tandem differential mobility analyzer (HTDMA) is one of the most widely used (Swietlicki et al., 2008; Tang et al., 2019). As it can directly provide the particle size distribution after water uptake, a HTDMA can be employed to obtain both the mixing state and the bulk mean hygroscopic properties of ambient aerosol particles. Two differential mobility analyzers (DMAs; Swietlicki et al., 2008) are used in this technique to quantify the changes in particle size upon exposure to different relative humidities (RHs). The measured distribution function (MDF) is skewed from the actual particle growth factor probability density function (GF-PDF) and smoothed. Several inversion algorithms have therefore been developed to retrieve the true GF-PDF (Cubison et al., 2005; Gysel et al., 2009; Stolzenburg and McMurry, 2008; Voutilainen et al., 2000), including the TDMAfit algorithm, the optimal estimation method (OEM), and the TDMAinv algorithm. However, these algorithms are based on the assumption that the sampled particles are predominantly singly charged particles. Under this condition, the forward function can be simplified and data analysis can be limited to the particle size of interest (it will not be influenced by other particle sizes). If the number fraction of multiply charged particles with the selected dry diameter becomes significant, the measured results will be affected by contributions from other dry particle sizes. In this case, appropriate data inversion is quite complicated.

However, in some special cases, accurate data inversion for multiply charged particles can be achieved when the sampled particles are exclusively doubly or triply charged. Gysel et al. (2009) obtained the kernel functions for multiply charged particles, and Duplissy et al. (2008) applied them in the data inversion to retrieve the correct growth factors (GFs). The dry sizes he selected are dominated by doubly or triply charged particles. However, in most field measurements, this assumption is invalid. As far as we are aware, no previous studies have performed multi-charge correction of HTDMA measurements of atmospheric aerosol particles. Also, the effect of multi-charge correction on the size-resolved hygroscopicity has not been fully evaluated for atmospheric aerosols.

In this paper, we first analyze the number contributions from particles carrying different charges. Then we present the compression effect of multiply charged particle hygroscopicity on HTDMA measurements. These two effects were included in an algorithm that can perform multi-charge correction of the size-resolved particle hygroscopicity. After that, the effects of multi-charge correction using the algorithm on the particle hygroscopicity are discussed.

2 Multi-charge effects

2.1 Number contribution from multiply charged particles

In the DMA sizing process, only particles within a narrow electrical mobility (Z_p) range can pass through the classifier exit slit and reach the humidification and size distribution measurement system downstream. The electrical mobility is defined as

$$\begin{array}{}\text{(1)}& Z_{\text{p}}={\displaystyle \frac{v\text{e}C\left(D_{\text{p}}\right)}{\mathrm{3}\mathit{\pi }\mathit{\mu }{D}_{\text{p}}}},\end{array}$$

where C(D_p) is the Cunningham slip correction, e is the elementary charge, v is the number of elementary charges on the particle, μ is the gas viscosity, and D_p is the physical diameter of the particle. From Eq. (1), we can see that the same electrical mobility can be achieved using different combinations of particle diameter and charge, and this is where multi-charge effects come from.

The range that can pass through the DMA is termed the mobility bandwidth ΔZ_p, defined as

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{Z}_{\text{p}}={\displaystyle \frac{q_{\text{a}}}{q_{\text{sh}}}}{Z}_{\text{p}}^{\ast },\end{array}$$

where $Z_{\text{p}}^{\ast }$ is the set mobility and q_a and q_sh are the aerosol flow rate and sheath air flow rate, respectively. This equation does not account for diffusion broadening.

We can calculate the particle charge distribution at each size using a theoretical model developed by Wiedensohler et al. (1986). The probability that a particle will pass through a DMA classifier can then be determined using the kernel function

$$\begin{array}{}\text{(3)}& G\left(D_{\text{p}}^{\ast },x\right)={\sum }_{v=\mathrm{1}}^{\mathrm{\infty }}F(x,v)\mathrm{\Omega }(x,v,D_{\text{p}}^{\ast }),\end{array}$$

where $D_{\text{p}}^{\ast }$ is the diameter set in the DMA, x is the scale parameter, and F(xv) is the charge distribution of the particles that exit from a neutralizer with v elementary charges at the scale parameter x. $\mathrm{\Omega }(x,v,D_{\text{p}}^{\ast }$) is the probability that particles will pass through the DMA when the set diameter is $D_{\text{p}}^{\ast }$. In this study, the maximum value of v was set to 10.

Therefore, given a particle number size distribution (PNSD) n(x), the number of particles that can pass through a DMA with a set diameter $D_{\text{p}}^{\ast }$ is

$$\begin{array}{}\text{(4)}& N\left(D_{\text{p}}^{\ast }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}G\left(D_{\text{p}}^{\ast },x\right)n\left(x\right)\mathrm{d}x.\end{array}$$

If the number of particles that are carrying a specific charge is needed, the kernel function in Eq. (4) should be replaced with

$$\begin{array}{}\text{(5)}& G_v\left(D_{\text{p}}^{\ast },x\right)=F(x,v)\mathrm{\Omega }(x,v,D_{\text{p}}^{\ast }),\end{array}$$

and the corresponding number concentration of particles that can pass through the DMA is

$$\begin{array}{}\text{(6)}& N_v\left(D_{\text{p}}^{\ast }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{G}_v\left(D_{\text{p}}^{\ast },x\right)n\left(x\right)\mathrm{d}x.\end{array}$$

The number ratio of particles carrying different charges can be calculated from $N_v\left(D_{\text{p}}^{\ast }\right)/N(D_{\text{p}}^{\ast }$).

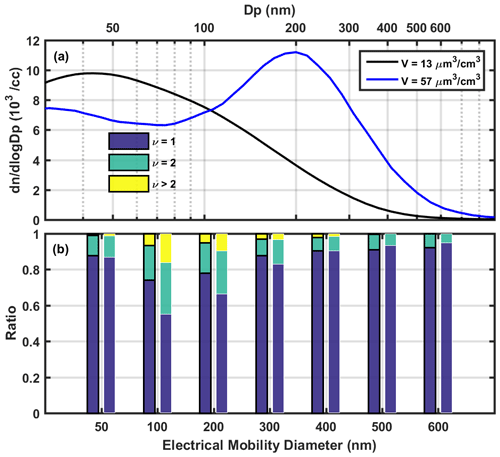
Figure 1 (a) Two particle number size distributions (PNSDs) observed during field measurements. The black line is the distribution during a period of relatively clean air, and the blue line is the distribution during a period of heavy air pollution. (b) The number ratio of particles carrying different charges for each PNSD. For each diameter, the left bar corresponds to the PNSD shown in black in (a), while the right bar corresponds to the PNSD shown in blue.

Two aerosol size distributions discerned from our field measurements during a period of relatively clean air and a period with air pollution (refer to Sect. 4) are shown in Fig. 1. In each case, the ratio of particles carrying different charges was calculated from the PNSD using the abovementioned DMA electrical mobility and charging theory. The detailed calculation procedures are described in Sect. S1 of the Supplement. During the polluted period, when the total particle volume concentration is large, an obvious feature of the PNSD is that the accumulation mode > 100 nm grows very large. The growth of this mode leads to an increase in the proportion of multi-charge particles, especially in the electrical mobility diameter range 100–300 nm. For example, when we set the diameter to 100 nm in the first DMA, more than 40 % of the selected particles are multiply charged. This ratio is about 30 % and 20 % for electrical mobility diameters of 200 and 300 nm, respectively. Thus, the HTDMA-measured size-resolved hygroscopicity will also be influenced by those multiply charged large particles.

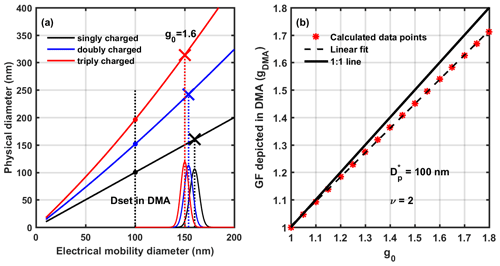
Figure 2 (a) Effects of multiply charged particles on the growth factor. The black, blue, and red lines represent singly, doubly, and triply charged particles, respectively. The circles represent particles selected by the DMA when the electrical mobility diameter is set to 100 nm. When the true growth factor is 1.6, these particles grow to the diameters represented by the corresponding crosses. The mode of the MDF of multiply charged particles peaks at a smaller GF than the true value. (b) The compression effect on the growth factor for doubly charged particles with an electrical mobility diameter of 100 nm.

2.2 Compression effect on hygroscopicity

Gysel et al. (2009) reported that the center of the kernel function is systematically offset toward smaller GFs with increasing charge. Figure 2 explains the cause of this compression effect. For an electrical mobility diameter of 100 nm, doubly and triply charged particles have physical diameters of about 151 and 196 nm, respectively. When these singly, doubly, and triply charged particles have a true growth factor of 1.6, they will grow in size to 160, 242, and 314 nm, respectively. Since the charge each particle carries remains unchanged, their peak sizes in the second DMA are approximately 160, 154, and 150 nm. Therefore, the growth factors they display in the HTDMA measurements are 1.6, 1.54 and 1.5, respectively. Thus, it is clear that the growth factor is decreased or compressed with increasing charge. We call this phenomenon the compression effect on the growth factor or hygroscopicity caused by multi-charge.

When we set a diameter $D_{\text{p}}^{\ast }$ in the DMA, the electrical mobility Z_p can be calculated via electrical mobility theory as

$$\begin{array}{}\text{(7)}& Z_{\text{p}}={\displaystyle \frac{\text{e}C\left(D_{\text{p}}^{\ast }\right)}{\mathrm{3}\mathit{\pi }\mathit{\mu }{D}_{\text{p}}^{\ast }}}.\end{array}$$

The physical diameter ($D_{\text{p}}^{\mathit{\nu }}$) of particles with the same electrical mobility and a charge number of ν is then

$$\begin{array}{}\text{(8)}& D_{\text{p}}^{\mathit{\nu }}={\displaystyle \frac{v\text{e}C\left(D_{\text{p}}^{\ast }\right)}{\mathrm{3}\mathit{\pi }\mathit{\mu }{Z}_{\text{p}}}}={\displaystyle \frac{C\left(D_{\text{p}}^{\mathit{\nu }}\right)}{C\left(D_{\text{p}}^{\ast }\right)}}\mathit{\nu }{D}_{\text{p}}^{\ast }.\end{array}$$

We also define the f function such that

$$\begin{array}{}\text{(9)}& D_{\text{p}}^{\mathit{\nu }}=f\left(D_{\text{p}}^{\ast },\mathit{\nu }\right).\end{array}$$

The f function describes the physical diameters of multiply charged particles given an electrical mobility diameter. The properties of and detailed calculation procedures for this function can be found in Sect. S2 of the Supplement.

For a particle of size $D_{\text{p}}^{\mathit{\nu }}$ with a charge number of ν, if we assume a true growth factor of g₀, the particle will grow in size to $g_{\mathrm{0}}{D}_{\text{p}}^{\mathit{\nu }}$. The virtual growth factor depicted in the DMA is expressed as g_DMA, such that

$$\begin{array}{}\text{(10)}& g_{\mathrm{0}}{D}_{\text{p}}^{\mathit{\nu }}=f\left(g_{\text{DMA}}{D}_{\text{p}}^{\ast },\mathit{\nu }\right)=g_{\mathrm{0}}f\left(D_{\text{p}}^{\ast },\mathit{\nu }\right).\end{array}$$

Given f, $D_{\text{p}}^{\ast }$, and ν, any g₀ can be substituted into Eq. (10) to get a corresponding g_DMA. If ν=1, i.e., the particles carry only one elementary charge, then g_DMA is equal to g₀. If ν>1, i.e., the particles are multiply charged, then g_DMA will be lower than g₀. Figure 2b presents an example with $D_{\text{p}}^{\ast }=\mathrm{100}$ nm and ν=2. The x axis is the assumed true growth factor g₀, and the y axis is the calculated virtual growth factor depicted in the DMA (g_DMA). Generally, the larger the value of g₀, the greater the difference between g_DMA and g₀.

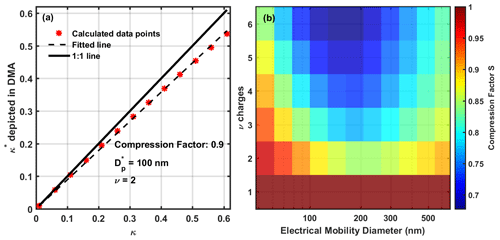
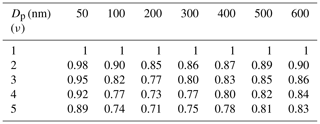
Figure 3 (a) The compression effect on the hygroscopicity (at 85 % RH) for doubly charged particles with an electrical mobility diameter of 100 nm. The fitted slope or compression factor is 0.8953. (b) A summary of the compression factors for different electrical mobility diameters and different charge numbers at 85 % RH.

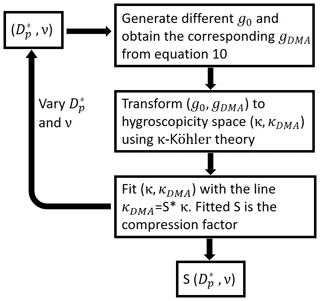
According to Petters and Kreidenweis (2007), the hygroscopic parameter κ for an aerosol particle can be calculated from the growth factor at a specific RH using κ-Köhler theory. As illustrated in Fig. 3a, all the data points shown in Fig. 2b generate corresponding data points in hygroscopicity space. It is clear that a decrease in the growth factor will results in a decrease in the hygroscopicity, and the compression effect increases almost linearly with the hygroscopicity of the particle. If we fit these data points with a straight line that passes through the origin, the slope of the line can be considered the compression factor. Figure 3a provides an example of this for $D_{\text{p}}^{\ast }=\mathrm{100}$ nm and ν=2. For each combination of electrical mobility diameter $D_{\text{p}}^{\ast }$ and charge number ν, we can repeat this calculation and linear fitting process to obtain the hygroscopicity compression factor $S(D_{\text{p}}^{\ast }v$). The algorithm used to calculate the compression factor is depicted in Fig. 4, and the results obtained with it are summarized in Fig. 3b and Table 1.

Table 1 Values of the hygroscopicity compression factor for aerosol particles with different electrical mobility diameters at 85 % RH.

Figure 4 The algorithm for calculating the compression factor.

3 Multi-charge correction method

3.1 Multi-charge correction of size-resolved hygroscopicity

Multi-charge correction is commonly performed when a DMA is used to scan aerosol particle sizes, especially in PNSD measurements. The shape of the PNSD after multi-charge correction can be significantly different from that of the raw measured PNSD. Therefore, it is necessary to evaluate the effect of multi-charge correction on the size-resolved hygroscopicity obtained by HTDMA. In this study, we developed an algorithm to perform the multi-charge correction of measured values, based on the work of Deng et al. (2011) and Zhao et al. (2019).

Our correction is based on the assumption that, for each electrical mobility diameter set at DMA1, all particles that pass through DMA1 contribute to the measured mean hygroscopicity. Each of the contributing particles has the mean hygroscopicity for its physical size. In reality, when a particle with a large dry diameter $D_{\text{p}}^{\mathit{\nu }}$ and a charge number passes through the DMA1 and contributes to the MDF, it is hard to elucidate its actual hygroscopicity because there is a probability distribution function for hygroscopicity. However, in our algorithm, this particle is assumed to have the mean hygroscopicity for the particle size $D_{\text{p}}^{\mathit{\nu }}$. This assumption is statistically correct and feasible, but may not hold at the single-particle scale.

When the scan diameter in the first DMA is set to $D_{\text{p}}^{\ast }$, the mean hygroscopicity K^∗ observed by the HTDMA can be expressed as

$$\begin{array}{}\text{(11)}& K^{\ast }\left(D_{\text{p}}^{\ast }\right)={\displaystyle \frac{\mathrm{1}}{N\left(D_{\text{p}}^{\ast }\right)}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{G}_{\text{s}}\left(D_{\text{p}}^{\ast },x\right)K\left(x\right)n\left(x\right)\mathrm{d}x,\end{array}$$

where K(x) is the true mean κ for the scale parameter x, n(x) is the true aerosol number size distribution, and $N(D_{\text{p}}^{\ast }$) is the total number concentration of particles that pass through the first DMA. $G_{\text{s}}\left(D_{\text{p}}^{\ast },x\right)$ is the transformed kernel function $G\left(D_{\text{p}}^{\ast },x\right)$ of DMA1, which includes the compression effect $S(D_{\text{p}}^{\ast },v$):

$$\begin{array}{}\text{(12)}& {\displaystyle }{G}_{\text{s}}\left(D_{\text{p}}^{\ast },x\right)={\sum }_{v=\mathrm{1}}^{\mathrm{\infty }}F(x,v)\mathrm{\Omega }(x,v,D_{\text{p}}^{\ast })S(D_{\text{p}}^{\ast },v)\text{(13)}& {\displaystyle }N\left(D_{\text{p}}^{\ast }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}G\left(D_{\text{p}}^{\ast },x\right)n\left(x\right)\mathrm{d}x.\end{array}$$

Equation (5) can then be simplified to the following:

$$\begin{array}{}\text{(14)}& K^{\ast }\left(D_{\text{p}}^{\ast }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathbf{H}\left(D_{\text{p}}^{\ast },x\right)\mathrm{K}\left(x\right)\end{array}$$

or

$$\begin{array}{}\text{(15)}& {\mathit{K}}^{\ast }=\mathbf{H}\mathit{K},\end{array}$$

where K(x) or K is the true distribution of κ we want to obtain, $K^{\ast }(D_{\text{p}}^{\ast }$) or K^∗ is the measured κ distribution, and

$$\begin{array}{}\text{(16)}& \mathbf{H}\left(D_{\text{p}}^{\ast },x\right)={\displaystyle \frac{\mathrm{1}}{N\left(D_{\text{p}}^{\ast }\right)}}n\left(x\right)G^{\ast }\left(D_{\text{p}}^{\ast },x\right)\mathrm{d}x.\end{array}$$

$\mathbf{H}\left(D_{\text{p}}^{\ast },x\right)$ (the H matrix) is the forward function and can be calculated from the information available. Given a true κ distribution, we should be able to calculate the measured κ distribution influenced by the multi-charge effect. The H matrix accounts for the DMA transfer function, the particle charge distribution, compression factors, and the number concentration of particles over each size parameter. The detailed steps performed to solve this matrix inverse problem can be found in Zhao et al. (2019).

A hypothetical uncorrected κ distribution $K^{\ast }(D_{\text{p}}^{\ast }$) is shown along with two examples of a corresponding multi-charge-corrected K(x) distribution in Fig. 5a. This κ distribution represents a common case in the ambient environment: relatively low hygroscopicity for ultrafine particles, high hygroscopicity at accumulation-mode sizes, and coarse-mode particles that are nearly hydrophobic. Multi-charge correction was performed using two different PNSDs representing clean and polluted conditions, leading to two corrected K(x) distributions. It can be seen that when κ varies greatly with size, especially among singly, doubly, and triply charged particle sizes, large differences will arise between the pre- and postcorrected κ distributions. For example, the difference between the measured and corrected κ values is largest for sizes of 150 and 350 nm. For a singly charged particle with an electrical mobility size of 150 nm, the corresponding doubly and triply charged particle sizes are around 235 and 314 nm. These three sizes are located in the area of the distribution where κ increases steeply. Similarly, for an electrical mobility size of 350 nm, the corresponding doubly and triply charged particle sizes are about 605 and 852 nm. These three sizes are located in the area where κ drops greatly. Figure 5a also shows that for regions of the curve where κ is increasing, the measured κ will be an overestimate, and for regions of the curve where κ is decreasing, the measured κ will be an underestimate.

3.2 Multi-charge correction of the mixing state

Aside from the size-resolved mean hygroscopicity, other key information that can be obtained from a HTDMA includes the mixing state and the detailed shape of GF-PDF or κ-PDF. The correction of GF-PDF or κ-PDF involves the inversion of two-dimensional vectors, which is too complicated for this study. However, the mixing state can be simply represented by the particle number fraction in different GF ranges. Below, we use the number fraction of less hygroscopic particles as an example.

The correction of the mixing state is similar in general to the correction of the mean hygroscopicity, but it differs in some minor aspects. When the scan diameter in the DMA is set to $D_{\text{p}}^{\ast }$, the number fraction of less hygroscopic (LH) particles observed by the HTDMA can be expressed as

$$\begin{array}{}\text{(17)}& M^{\ast }\left(D_{\text{p}}^{\ast }\right)={\displaystyle \frac{\mathrm{1}}{N\left(D_{\text{p}}^{\ast }\right)}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{G}_{\text{s}}\left(D_{\text{p}}^{\ast },x\right)M\left(x\right)n\left(x\right)\mathrm{d}x,\end{array}$$

where $M^{\ast }(D_{\text{p}}^{\ast }$) is the measured number fraction of LH particles at the selected diameter $D_{\text{p}}^{\ast }$ in the DMA, and M(x) represents the true number fraction at scale parameter x. Also,

$$\begin{array}{}\text{(18)}& {\displaystyle }{G}_{\text{s}}\left(D_{\text{p}}^{\ast },x\right)={\sum }_{v=\mathrm{1}}^{\mathrm{\infty }}F(x,v)\mathrm{\Omega }(x,v,D_{\text{p}}^{\ast })S_M(D_{\text{p}}^{\ast },v)\text{(19)}& {\displaystyle }N\left(D_{\text{p}}^{\ast }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}G\left(D_{\text{p}}^{\ast },x\right)n\left(x\right)\mathrm{d}x,\end{array}$$

where $S_M(D_{\text{p}}^{\ast }v$) represents the correction factor caused by the compression effect. This factor varies with the GF probability distribution function (GF-PDF) and cannot be simplified to a constant. If we assume that the compression effect on the LH number ratio can be neglected, then this parameter is 1, and the equation can be simplified to

$$\begin{array}{}\text{(20)}& M^{\ast }\left(D_{\text{p}}^{\ast }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathbf{H}\left(D_{\text{p}}^{\ast },x\right)M\left(x\right)\end{array}$$

or

$$\begin{array}{}\text{(21)}& {\mathit{M}}^{\ast }=\mathbf{H}\mathit{M},\end{array}$$

where

$$\begin{array}{}\text{(22)}& \mathbf{H}\left(D_{\text{p}}^{\ast },x\right)={\displaystyle \frac{\mathrm{1}}{N\left(D_{\text{p}}^{\ast }\right)}}n\left(x\right)G(D_{\text{p}}^{\ast },x)\mathrm{d}x.\end{array}$$

$\mathbf{H}\left(D_{\text{p}}^{\ast },x\right)$ (the H matrix) can also be calculated from the available information. A hypothetical measured distribution $M^{\ast }\left(D_{\text{p}}^{\ast }\right)$ is shown along with two examples of a corresponding multi-charge-corrected distribution M(x) in Fig. 5b.

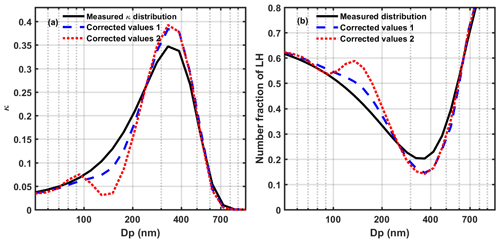
Figure 5 (a) Multi-charge correction of a hypothetical measured κ distribution. The black line is the measured size-resolved κ, and the dashed lines are multi-charge-corrected κ distributions based on different number size distributions. The PNSDs used are shown in Fig. 1. (b) Multi-charge correction for a mixing state distribution. The black line represents the measured size-resolved number fraction of LH particles, and the dashed lines are the multi-charge-corrected values based on different number size distributions.

4 Application in field measurements

During the winter of 2019, a comprehensive set of aerosol measurements focusing on the hygroscopic properties of particles in the size range 50–600 nm were conducted at an urban site in Beijing. The measurements were conducted on the rooftop of a six-story building on the campus of Peking University, which is also the location of the AERONET station of BEIJING_PKU (39^∘59^′ N, 116^∘18^′ E). The sampling site was in the northwest of Beijing, surrounded by schools, residential buildings, and shopping centers.

During the measurements, a HTDMA instrument was employed to measure the hygroscopic growth factors of particles with dry diameters of 50, 100, 200, 300, 400, 500, and 600 nm at 85 % RH. Before the aerosol sampling, a PM₁₀ impactor was used to remove aerosol particles with aerodynamic diameters larger than 10 µm. Then a dryer was used to decrease the RH to less than 30 %. Next, the dried polydisperse particles were guided into a splitter with various instruments located downstream, including the HTDMA and a BMI scanning electrical mobility sizer (BMI SEMS, model 2100). In both of these measurement systems, aerosol particles were first charged by a soft X-ray neutralizer (TSI, model 3088) and then those negatively charged particles were selected by the DMA. For the HTDMA, the sample to sheath ratio in the first DMA was $\mathrm{0.75}/\mathrm{4}$. To calibrate the measurement system, ammonium sulfate particles were tested and the results were compared with the corresponding theoretical values. The calibration included both a dry test and a RH test. To achieve the best working performance, the room was air-conditioned at 25 ^∘C and the air was circulated all the time. Particle number size distributions (PNSDs) for the size range 10–1000 nm were given by the SEMS.

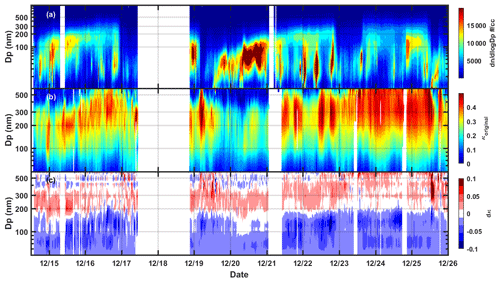
Figure 6 Field measurements of the PNSD and size-resolved hygroscopicity during a winter in Beijing. (a) The fill color indicates the particle number concentration for a particular diameter D_p. (b) The fill color represents the size-resolved hygroscopicity parameter κ. (c) The fill color indicates the difference d_κ between the measured and multi-charge-corrected κ values, i.e., $d_{\mathit{\kappa }}={\mathit{\kappa }}_{\text{corrected}}-{\mathit{\kappa }}_{\text{measured}}$.

To evaluate the effects of multiply charged particles on the size-resolved hygroscopicity, we applied multi-charge correction to two weeks of measurement data. The particle number size distribution and measured size-resolved hygroscopicity κ are shown in Fig. 6. To facilitate comparison, we also present the size-resolved difference between the measured and corrected hygroscopicity values. Note that, since the upper size limit for the hygroscopicity measurements was 600 nm, the hygroscopicity in the higher size range was assumed to decrease linearly to 0 at 1 µm. Also, the hygroscopicity of coarse-mode particles was assumed to be 0. In addition, for particles larger than 1 µm, the number concentration was assumed to decrease linearly to 0 at 1.2 µm in the multi-charge correction.

Generally, the hygroscopicity of particles smaller than 200 nm will be overestimated, while the hygroscopicity of particles larger than 200 nm in size will be underestimated. From Fig. 6b, we can see that, in the urban environment, the hygroscopicity often peaks in the size range 200–400 nm. Because particles in this size range can carry multiple charges and be mistakenly treated as smaller sizes in the HTDMA measurement, their relatively high hygroscopicity will also be assigned to the smaller sizes, leading to a false increase in the measured κ. Similarly, most large ambient particles have relatively low hygroscopicity. When these particles carry multiple charges and sneak into the lower accumulation size set by the DMA, the hygroscopicity for the target size region will be lowered.

The difference between the corrected and the measured size-resolved κ values is generally within 0.05. For the electrical mobility size that was most affected by multi-charge particles (100 nm), doubly or triply charged particles have physical sizes of 151 and 196 nm, respectively. Particles of these three sizes normally have similar hygroscopicities, resulting in only a small effect on the measured κ. However, when particles of these three sizes have significantly different hygroscopicities, multi-charge correction is necessary. For particles between 200 and 400 nm, the multi-charge effect is mostly contributed by particles larger than 400 nm. Field observations of the hygroscopicity of particles in this size range are rare, resulting in large uncertainty in the multi-charge correction for this size range. According to our measurements, the variation in hygroscopicity in this size range is relatively large and depends on the pollution conditions (Shen et al., 2020). On average, the hygroscopicity of particles above 500 nm is lower than it is for other accumulation sizes. Because of the assumption that there are few particles above 1 µm, the multi-charge effect on particle sizes above 400 nm is fairly small. In practice, the multi-charge effect can be removed for these particles by installing an impactor before the inlet of the first DMA.

5 Conclusions

HTDMAs have been extensively used in numerous field measurements to obtain the hygroscopic properties of submicron particles. Aerosol particles sampled by a DMA are quasi-monodisperse; they have different charges and different diameters. Thus, the size-resolved hygroscopicity measured by a DMA will be influenced by the contribution from multiply charged aerosols. This effect has seldom been discussed for field measurements of hygroscopicity using a HTDMA.

In this study, we first demonstrated that multi-charge influences the measurement of hygroscopicity through both its number contribution and a compression effect. On the one hand, the number fraction of multiply charged particles is quite considerable, especially in polluted conditions. Results show that 30–40 % of the particles selected by a HTDMA during a pollution episode can be multiply charged. On the other hand, the growth factor or hygroscopicity measured by a HTDMA can be smaller than its true value for multiply charged particles, which is called the multi-charge compression effect. The resulting compression factor can be quantified using electrical mobility theory and is found to reach its peak at a size of around 200 nm and to increase with the charge number of the particle.

We have also proposed an algorithm that can perform multi-charge correction of the size-resolved hygroscopicity κ and mixing state. This algorithm is based on the principle of SMPS multi-charge correction, and a knowledge of the aerosol PNSD is required. The key stages in this algorithm are obtaining the forward function and solving the inverse problem.

The proposed multi-charge correction was applied to field measurements to evaluate multi-charge effects. Relatively high hygroscopicity in the accumulation size range was found to lead to overestimation of the hygroscopicity for particles smaller than 200 nm, whereas the low hygroscopicity of coarse-mode particles causes the hygroscopicity to be underestimated for accumulation particles. The difference between the measured and corrected κ values can be as large as 0.05.

For particle sizes between 200 and 400 nm, the measured hygroscopicity is influenced by multiply charged particles larger than 400 nm, indicating that hygroscopicity measurements of these large particles are necessary to obtain the correct hygroscopic properties for accumulation-mode particles. For particles larger than 400 nm, the multi-charge effect can be removed by installing an impactor with a cut size of around 700 nm or lower. Our studies highlight that, in future, special attention should be paid to multi-charge effects on hygroscopicity measurements, and multi-charge correction should be done if accurate size-resolved hygroscopicity data are needed.