the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Resolving the ambiguous direction of arrival of weak meteor radar trail echoes
Johan Kero
Alexander Kozlovsky
Mark Lester
Meteor phenomena cause ionized plasmas that can be roughly divided into two distinctly different regimes: a dense and transient plasma region co-moving with the ablating meteoroid and a trail of diffusing plasma left in the atmosphere and moving with the neutral wind. Interferometric radar systems are used to observe the meteor trails and determine their positions and drift velocities. Depending on the spatial configuration of the receiving antennas and their individual gain patterns, the voltage response can be the same for several different plane wave directions of arrival (DOAs), thereby making it impossible to determine the correct direction. A low signal-to-noise ratio (SNR) can create the same effect probabilistically even if the system contains no theoretical ambiguities. Such is the case for the standard meteor trail echo data products of the Sodankylä Geophysical Observatory SKiYMET all-sky interferometric meteor radar. Meteor trails drift slowly enough in the atmosphere and allow for temporal integration, while meteor head echo targets move too fast. Temporal integration is a common method to increase the SNR of radar signals. For meteor head echoes, we instead propose to use direct Monte Carlo (DMC) simulations to validate DOA measurements. We have implemented two separate temporal integration methods and applied them to 2222 events measured by the Sodankylä meteor radar to simultaneously test the usefulness of such DMC simulations on cases where temporal integration is possible, validate the temporal integration methods, and resolve the ambiguous SKiYMET data products. The two methods are the temporal integration of the signal spatial correlations and matched-filter integration of the individual radar channel signals. The results are compared to Bayesian inference using the DMC simulations and the standard SkiYMET data products. In the examined data set, ∼ 13 % of the events were indicated as ambiguous. Out of these, ∼ 13 % contained anomalous signals. In ∼ 95 % of all ambiguous cases with a nominal signal, the three methods found one and the same output DOA, which was also listed as one of the ambiguous possibilities in the SkiYMET analysis. In all unambiguous cases, the results from all methods concurred.
- Article
(2841 KB) - Full-text XML
- BibTeX
- EndNote
Every day the Earth's atmosphere is bombarded by billions of dust-sized particles and larger pieces of material from space. In doing so these objects, called meteoroids, ablate and produce phenomena called meteors (Ceplecha et al., 1998). These phenomena are commonly seen as visible streaks of light in the night sky.
Meteor phenomena cause ionized plasmas that can be roughly divided into two distinctly different regimes: a dense and transient plasma region co-moving with the ablating meteoroid and a trail of diffusing plasma left in the atmosphere and moving with the neutral wind. Both of these plasmas reflect radio waves (Lovell et al., 1947). When measured with a radar, they cause so-called meteor head and meteor trail echoes (McKinley, 1961). To determine the position of these radar targets, interferometric or multi-static radar systems must be used.
Observing this incoming material is important for several reasons. To mention a few, it gives us a unique opportunity to examine the motion and population of small bodies in the solar system (Vaubaillon et al., 2005a, b; Kastinen and Kero, 2017), it provides information about the extraterrestrial input of material into our atmosphere (Plane, 2012; Brown et al., 2002), and it provides a possibility to assess the neutral wind at an altitude otherwise difficult to probe (Holdsworth et al., 2004; Hocking, 2005). The typical ablation altitude where meteor phenomena occur lies between 70 and 130 km (Kero et al., 2019, and references therein). This region is characterized by variability driven by atmospheric tides as well as planetary and smaller-scale gravity waves. As this region is difficult to observe with other methods due to the low atmospheric density and high altitude, specular meteor trail radars have become widespread scientific instruments to study atmospheric dynamics. The extraterrestrial input of matter also affects various physical and chemical processes important for a wide range of phenomena, such as the formation of clouds at 15–25 km altitude responsible for ozone destruction in the polar regions, midlatitude ice clouds at 75–85 km, which are possible tracers of global climate change, and metallic ion layers in the atmosphere (Plane, 2003).
The diffusing meteor trail is an elongated plasma and not a point target. Therefore, specular reflection dominates. This makes interferometric all-sky radar systems efficient at observing the meteor trail phenomena with relatively inexpensive hardware. This has made such systems widespread and there are currently systems deployed at locations covering latitudes from Antarctica to the Arctic (Kero et al., 2019). When determining the position of an object by interferometry, there may be an ambiguity problem (Schmidt, 1986). The position is determined by finding the direction of arrival (DOA) of the incoming echo onto the radar. Depending on the spatial configuration of the receiving antennas and their individual gain patterns, the voltage responses can be the same for several different plane wave DOAs, thereby making it impossible to determine which one is correct. Noise can create the same effect even if the system contains no theoretical ambiguities. These ambiguities then appear with a probability that is a function of the signal-to-noise ratio (SNR) (Kastinen and Kero, 2020; Jones et al., 1998). This problem is general to all DOA determinations made by interferometric radar systems.
Due to its simplicity and theoretically unambiguous meteor trail position determination capability, the so-called Jones 2.5λ radar design has become the standard for specular meteor trail radars (Jones et al., 1998). Holdsworth (2005) investigated the Jones antenna configuration and found that the use of 2.5, 3, and 5.5λ spacings could produce a more accurate echo DOA. Younger and Reid (2017) developed the concept further and presented a solution which utilizes all possible antenna pairs of a meteor radar antenna configuration. However, it has been noted by several authors that if the SNR is low enough, the position determination is still ambiguous (Jones et al., 1998; Hocking, 2005; Kastinen and Kero, 2020). For this reason, the widespread SKiYMET system has implemented a variable in their database referred to as “ambig” which gives several possible position solutions for the same event. A relatively small part of the total number of detected echoes have these angular ambiguities, generally around 10 %–20 % (Fig. 3a Hocking et al., 2001). Practically, these events cannot be used for wind determination as the correct location is needed in order to determine the line-of-sight direction for the wind component estimation. Resolving the ambiguity issue is important also to, e.g., facilitate detailed analysis of meteor head echoes and long-lasting trails.
As the SNR is the deciding factor for whether a detection is ambiguous or not, standard temporal integration methods can be applied to increase the SNR of the signal. The amount of time that can be integrated depends on the coherence time of the phenomena. A meteor trail drifts with the local wind speed, and the echo phase change over time can be reliably modelled during its entire existence. The range rates and Doppler frequencies of head echoes change fast. In practice, unpredictable effects from, e.g., fragmentation limits the usable coherence time to single radar pulse sequence transmissions.
Kastinen and Kero (2020) used direct Monte Carlo (DMC) simulations to theoretically characterize the ambiguities of several radar systems commonly used for both head and trail echo meteor measurements, the Jones 2.5λ radar being one of them. However, the study did not explore to what degree such simulations are practically useful in validating analysis of real measurement data. The simulation results were not applied in the context of comparisons with measurement data or to remove measurement ambiguities.
The standard SKiYMET data products contain ambiguities that can theoretically be resolved by temporal integration but also validated and resolved by DMC simulations. Here, we test the methods presented in the previous study (Kastinen and Kero, 2020) by implementing two different temporal integration methods to compare with the DMC results and resolve angular ambiguities.
Chau and Clahsen (2019) examined the morphology of ambiguities for the Jones 2.5λ design and other radar systems using the beam-forming point spread function (PSF). In the case of radars with identical antenna elements, each having a separate signal channel, the PSF is identical for all input DOAs. The identification done in Chau and Clahsen (2019) thereby applies for all input DOA. The PSF reported in Chau and Clahsen (2019, Fig. 1) matches with the morphology of the Monte Carlo simulations of DOA determination performed here and in Kastinen and Kero (2020). Given a Bayesian method to assign probability distributions to the ambiguities, many of the previously unusable data may again be usable. Events with high certainty in inference of the true DOA provide a validation for methods to resolve the ambiguity in the analysis itself without simulations.
Holdsworth et al. (2004) implemented a coherent detection algorithm where linear regression was applied to the measured cross correlation angles. In essence, the sample zero-lag cross correlation described there is the same as the temporal integration of sample cross correlations we have implemented here. Henceforth we drop the word “sample” in the expression “sample spatial cross correlations” for brevity. When we temporally integrate spatial cross correlations of a virtually stationary plane wave, the integration is coherent. However, a more effective coherent integration is to apply a matched filter to each channel and coherently integrate prior to calculating the cross correlation. Vierinen et al. (2016) implemented a coherent deconvolution on a coded continuous-wave meteor radar. This is practically the same as the matched-filter temporal integration implemented here. A simple derivation of the effectiveness and coherence of these two temporal integration techniques is given in Appendix A.
2.1 System
We use data from the meteor radar at Sodankylä Geophysical Observatory (SGO; 67∘22′ N, 26∘38′ E; Finland). The radar is an all-sky interferometric meteor radar SKiYMET operating at a frequency of 36.9 MHz. The peak power of the radar transmission is 15 kW (upgraded from 7.5 kW in September 2009). The pulse repetition frequency (PRF) is 2144 Hz. The width of each pulse is 13 µs, which gives a range resolution (size of the range bins) of 2 km. The five-antenna receiving array is arranged as a Jones 2.5λ interferometer, and phase differences in the signals arriving at each of the antennas of the interferometer are used to determine a theoretically unambiguous angle of arrival. This allows the determination of meteor echo azimuth and elevation angles to an accuracy of about 1∘ (Jones et al., 1998). Also, the receiving system determines the Doppler velocity of the selected targets. Details of the SKiYMET radar system and algorithms of the radar signal processing are described in Hocking et al. (2001).
2.2 Database
An important task of the standard SKiYMET real-time signal processing is selecting meteor echoes and rejecting other signals, such as echoes from satellites and aircraft, lightning, and sporadic ionospheric layers. The characteristic features used to distinguish meteor echoes from other signals include their rapid onset, relatively short duration (typically less than 0.3 s), and quasi-exponential decay. Only echoes with SNR>2 dB are accepted by the system.
In the routine meteor radar operations, short 4 s records of the signals (real and imaginary components) received at each of the five antennas are analysed and archived as confirmed event (CEV) data files for each echo accepted as a meteor (i.e. “event”). Because of the coherent integration over four subsequent counts, the sampling rate of CEV data is 536 Hz. Examples of such records are presented in Sect. 4.
For the targets selected by the system as meteors, their position (azimuth, elevation, range, and height), Doppler velocity of the scatter from these targets, and the decay time of the scatter from the targets are determined. These parameters are stored in the meteor position data (MPD) files.
Each MPD file corresponds to a 24 h time span starting at 00:00 UTC and ending at 2359.59 UTC the same day. For unambiguous targets, one line per meteor detection is recorded. If a meteor cannot be unambiguously located, all various possible locations are reported in the MPD file with one line per ambiguous location. This is noted in the “ambig” field of the data. If the “ambig” field is 3, for example, then there will be three consecutive entries in the MPD file for this one meteor. There may be ambiguities in both range and/or DOA. The PRF of subsequent transmissions is 2144 Hz, which means that the range is determined with a ∼70 km ambiguity. To reduce the range ambiguity, the SKiYMET data analysis algorithm assumes that meteor trails are located at heights between 70 and 110 km.
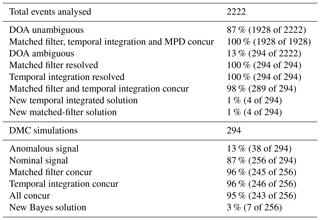
In the present study we used 2222 events collected on 13 December 2018. Of these events, 294 cases (∼ 13 %) contained angular ambiguities indicated in the MPD file.
We have applied two separate methods for inferring the true location of an ambiguous DOA measurement. The first method is based on DOA determination direct Monte Carlo simulation and Bayesian inference and has been presented in Kastinen and Kero (2020). This method is complex and costly in terms of computation resources but yields a probability distribution over the ambiguities. The second method is temporal integration of the spatial correlation matrix, described in detail in Sect. 3.2. This second method is easily implemented in data analysis pipelines as it can rely on previous DOA determination implementations and is only analysing a single integrated pulse rather then all pulses individually.
The DOA determination performance investigation of the Jones 2.5λ radar presented by Kastinen and Kero (2020) successfully made use of the multiple signal classification (MUSIC) algorithm developed by Schmidt (1986). We have applied the same implementation of MUSIC as described by Kastinen and Kero (2020) to analyse the SKiYMET data in this study.
3.1 Sensor response model
The standard Jones type interferometer has five antennas, ideally identical and electrically independent, i.e. no coupling. All antennas are connected to individual channels for recording complex voltage data. A model for this type of radar receiving a plane wave of amplitude A is described by
Here the complex vector Φ(k) is the modelled set of complex voltages output by the radar system given that the incoming wave DOA is k. The ri vectors represent spatial antenna locations and g(k) the combined gain pattern of the transmitting and receiving antennas.
3.2 Spatial correlation matrix
We define a measured sensor response as the complex vector x∈ℂN. The SKiYMET radar uses a single-pulse transmission, i.e. no coded transmission sequences, without oversampling on reception. There is only a single temporal sample of the echo for each pulse. Therefore, the sensor response model in Eq. (1) directly models a received echo. The measurement vector x consists of the ideal response Φ(k) and additive white noise ξ (e.g. Bianchi and Meloni, 2007; Polisensky, 2007):
However, if the noise is spatially correlated, the cross correlations between antennas can exhibit noise spikes at zeroth temporal lag (Holdsworth et al., 2004). Considering the setup of the system, any spatially correlated noise from galactic sources should be small enough not to impact the main purpose of this study, as is discussed further in Appendix A. Instrumental effects (e.g. transmitter and receiver phase noise) and other users on the same frequency are other potential sources of correlated noise. Other users on the same frequency would essentially be taken care of by the MUSIC algorithm: as the signal subspaces are determined (all of them) and the noise subspace is defined as the complement space of only the strongest signal, any such other signal will automatically be filtered away as long as its signal is weaker than the trail echo. Also, the system used in the study is located in a rather underpopulated region of northern Finland where interference in the radio frequency band used does not seem to be a concern (except the transient ionosonde interference, which is easily filtered out; see Sect. 4).
Another possible effect on the sensor response is mutual coupling. It is known that mutual coupling introduces phase errors on the signals from individual antennas, resulting in zenith angle errors of up to 0.5∘ for the Jones configuration (Younger and Reid, 2017). We are not applying corrections specifically for mutual coupling phase errors, but we do apply the system phase calibration data given in the MPD file. Regardless, phase errors that are stationary as a function of time for a fixed-beam pointing direction and pulse transmission sequence will not decorrelate the temporal integration of the spatial correlation matrix between inter-pulse periods (IPPs). They will also not affect the ambiguity dynamics, as the gain pattern of all channels are identical.
As such, we can assume that the white noise ξ is a complex circularly symmetric normal distribution for each dimension; i.e. , which is uncorrelated both in space and time. The spatial correlation matrix R of our measurements is calculated as
The spatial correlation matrix contains the information of all possible phase differences between antennas as measured by the radar, as well as the signal power in the diagonal.
3.3 MUSIC
A detailed description of the MUSIC implementation we have used is given in Kastinen and Kero (2020). Here, we notate the entire process by a function G that takes as input the spatial correlation matrix R and the sensor response model Φ(k). The function G outputs an estimated DOA and the level at which the sensor response model matched the measured signal, F:
The quantity F describes the level to which the MUSIC implementation was able to match the used model Φ with the measured signal x, which we call the MUSIC response. If there is a perfect match F↦∞, while a total mismatch is represented by F=1. We have here adopted the convention that azimuth measures the angle clockwise from north.
3.4 Temporal integration
The key to resolving angular ambiguities is to increase the SNR of the signals used in the DOA determination by temporal integration. There are many ways to implement temporal integration. As the local wind speeds at meteor altitudes are small compared to the distance from the radar, the possible angular change over the typical dynamical lifetime of a meteor trail event is small. This fact allows us to implement a method based on the assumption that the individual spatial correlation matrices for each measured radar pulse are practically statistical sample points of the same quantity. Consequently, this quantity can be temporally integrated to increase the SNR of each element of the matrix. The temporally integrated spatial correlation matrix is defined as
where there are Ns measured pulses from the trail in question. Equation (5) is essentially the same as the zero lag cross covariances described in Holdsworth et al. (2004). The theoretical relation between coherent integrations Ns and SNR is SNR∝Ns. Below, we sometimes refer to a set of Ns measured radar pulses as a number of IPPs. Each IPP corresponds to ∼466 µs of time, i.e. the inverse of the PRF.
The small angular change allows us to implement a second kind of temporal integration given that the radar system transmitted phase is predictable. The method assumes that the target has drifted less than a radar wavelength between subsequent pulses, which is a valid assumption in the case of trail echoes. If no other effects that change the phase of the signal differs between pulses, the drift of the target can be found by the pulse-to-pulse phase difference. More specifically, applying a filter matched to the phase change on the signal allows coherent integration of each channel over the entire lifetime of the trail. A matched filter enables more efficient coherent integration (further discussed in Appendix A).
We have implemented a matched-filter η(ω), where ω is the phase velocity. We search for the parameter ωm that maximizes the coherently integrated filter output, i.e. maxωη(ω)=ωm. This is essentially a simple version of the coherent deconvolution described in Vierinen et al. (2016). Specifically, the filter output is
where xj(tl) are signals at time sample tl from channel j. The optimal matched filter found is then used to coherently integrate the channel signals as
Finally, the MUSIC algorithm is applied to the spatial correlation matrix of this signal, i.e. on R(xm).
The MUSIC response F is equivalent to SNR for DOA determination (Schmidt, 1986). Thus, as the MUSIC response depends on the temporally integrated spatial correlation matrix , we expect . An example is illustrated in Fig. 1, where echoes originating from 0∘ azimuth and 45∘ elevation were simulated at an SNR of 10 dB for the SKiYMET radar. These echoes were analysed with the MUSIC algorithm, G. Then, up to 200 of the spatial correlation matrices were temporally integrated and used as input to the MUSIC algorithm. The results are illustrated in the right column of the figure. Here, as expected, sample points temporally integrated at 1 order of magnitude correspond to a 10 dB MUSIC response increase. Additionally, in the upper right panel on the right vertical axis, we illustrate the probability of ambiguous output. In this example, the probability drops significantly already with 2–3 integrated matrices and the ambiguous output DOA behaviour disappears completely after 10 integrated matrices.
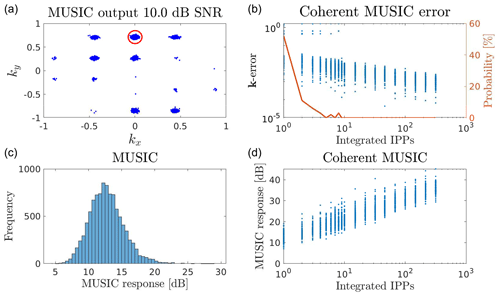
Figure 1DMC simulation example showing the effects on DOA determination using MUSIC when temporally integrating the spatial correlation matrix. Approximately 1×104 echoes originating from 0∘ azimuth and 45∘ elevation, as marked by the red circle in (a), were simulated at an SNR of 10 dB for the SKiYMET radar system. These echoes were analysed with the MUSIC algorithm individually; moreover, up to 200 of the spatial correlation matrices were temporally integrated and analysed. In (a) the MUSIC DOA output for the individual simulations is illustrated in the wave vector ground projection plane, i.e. kx,ky. In (c) the distribution of MUSIC responses are gathered as a histogram. Panels (b) and (d) display the results as a function of the number of temporally integrated matrices. The MUSIC response is given in the panel (d) and the wave vector error in panel (b). Additionally, in the panel (b) on the right vertical axis, we illustrate the probability of ambiguous output. In this example, the probability drops significantly already with two to three integrated matrices and the ambiguous output DOA behaviour disappears completely after 10 integrated matrices.
Even though this shows that SNR and the MUSIC response is perfectly correlated, one must not mistake the MUSIC response for a proxy for absolute precision of the angular determination. The MUSIC response function is the inverse of a scalar vector projection onto the noise subspace (Schmidt, 1986). The basis set of the noise subspace will vary depending on the noise in the signal. The implementation we have used of MUSIC sweeps all parameters of a sensor response model to find the sensor response with the smallest noise subspace component. This means that even though the noise subspace component of the output point would be small, the signal space could simply have been displaced to this point by the noise. Thus, the MUSIC response is not a direct indication of error but simply an indication of how well the sensor response model was able to match the measured signal subspace. Hence, the mean of the distribution of MUSIC responses increases with SNR but is uncorrelated with the true angular error.
3.5 Direct Monte Carlo (DMC)
As outlined in Kastinen and Kero (2020), DMC simulations of DOA determinations can resolve the ambiguity dynamics of a radar system. Such DMC DOA determination simulations are shown in Fig. 1. Using these simulations, one can match the measured ambiguity pattern with a simulated theoretical one to infer the true DOA of an ambiguous measurement.
3.6 Bayesian inference
The matching process of comparing a simulated DOA output distribution with a measured one can be done by hand. Ideally, a quantitative and algorithmic approach should be used. Kastinen and Kero (2020) showed that a Bayesian approach is a suitable way to perform systematic and quantitative matching of simulations to observations. We have implemented a modified version of the method outlined there.
Given a model with parameters y which has generated observations D, Bayesian inference can be used to find the probability distribution of possible model parameters. This distribution is called the posterior 𝒫(y). The posterior is connected to a prior probability θ(y), i.e. what we think the distribution is before any observations. The observed data are used to update the prior distribution by the use of a likelihood function L. This likelihood function determines how probable the observed data D are, given the model parameters y. The relationship between the prior θ, likelihood L, and posterior 𝒫 is given by Bayes' theorem:
Here | indicates conditional probability. In our application, the model parameters y are the ambiguous DOA locations labelled by an index y=j.
The Bayesian approach in Kastinen and Kero (2020) used individual DOA measurements and multinomial sequence generation probabilities to infer the true location. Their approach was designed considering low number statistics, i.e. on the order of 10 independent measurements. The SKiYMET system has a high PRF compared to the typical experimental setups at several of the radar systems that were examined in Kastinen and Kero (2020). Usually, hundreds of received pulses are available from each meteor event. Practically, this makes the discrete sequence Bayesian approach unstable if the simulations do not exactly model the probability of algorithm failure. Modelling this probability is very costly in terms of computational resources. However, as there are generally hundreds of measured sample points one can instead calculate the multinomial distribution itself with high accuracy. The measured multinomial distribution can then be directly compared with the simulated multinomial distribution. A detailed account of how to discretize the DOA distribution into a multinomial distribution was given in Kastinen and Kero (2020). The description includes information both on how multinomial probabilities are generated from the direct Monte Carlo (DMC) simulations, here denoted , and probabilities calculated from measurements, denoted . The index i denotes a possible, ambiguous DOA location, while the index j denotes the true location. As an example, the notation would mean that there is a 25 % probability that ambiguity location 1 is the output from a measurement generated by a target at the location labelled 2 (given the specific SNR in the simulation).
In the current modified Bayesian inference approach we redefine the likelihood function in terms of simulated and measured multinomial parameters. We regard the simulated multinomial parameters as exact and true. The measured multinomial parameters are found by calculating the following probabilities:
where Ai is the region for an ambiguous DOA. This is identical to computing the expected value of 1 over the measured sample points or calculating the multinomial maximum likelihood estimator. Given enough sample points, the central limit theorem applies and the multinomial probability estimator can be regarded as normal. It is therefore equivalent to the Bernoulli mean estimator distribution. The estimator variance can be approximated by substituting the distribution variance with the measured Bernoulli variance (Papoulis and Pillai, 2002):
For the special case of (corresponding to no measurements in an inclusion region Ai) we have implemented an estimator variance similar to the considerations in Hanley and Lippman-Hand (1983) and defined . Then, the modified likelihood function can be written in log form as
where No is the number of ambiguous regions.
To avoid contamination of the probabilities by faulty IPP selection, i.e. selecting IPPs that do not contain a valid echo from the trail, we only use the ambiguous locations as parameters in the multinomial distribution and do not include an algorithm failure probability.
As we have no prior information on the location of the target, Bayes' theorem from Eq. (8) reduces to
3.7 Automation
To facilitate testing on a wide range of events we have created an automated routine to read in an MPD file, iterate through each event, and reanalyse the events using the CEV files. For each event we apply MUSIC to each pulse individually, as well as on the temporally integrated spatial correlation matrix, and perform a matched-filter search that maximizes the coherently integrated filter output, i.e. maxωη(ω)=ωm. Using the phase velocity found, ωm, we apply phase correction to each individual channel and calculate MUSIC using the resulting spatial correlation matrix.
If the event was flagged with angular ambiguities in the MPD file, an ambiguity search is run and a series of DMC DOA determination simulations, again using MUSIC, are executed. Using these DMC simulations and the ambiguity analysis we discretize the measurements and the DMC simulations into input and output locations. The probability distribution over these locations is used in the Bayesian inference to calculate an input DOA probability. All the results, simulations and auxiliary data are then cached to disk. These data are available in the associated open-data repository.
We have four independent methods of determining the DOA: the SKiYMET standard data product, temporal integration of the spatial correlation matrix (), the spatial correlation matrix of matched-filter integrated channel signals (R(xm)), and Bayesian inference based on DMC simulations of DOA determinations (𝒫(j)). We have compared all four methods in order to test and validate them.
In total 2222 events were automatically analysed. To select authentic specular trail echoes we used the time for which the amplitude of the backscattered signal falls to one half of its maximum value τ. We did not include events with undetermined τ (these may be ground echoes or long-lived non-specular echoes (Kozlovsky et al., 2019, 2020; Bronshten, 1983, pp. 356)), τ less than 0.001 s (these may be ionosonde interference), or radial velocities exceeding 100 m/s (these may be due to Farley–Buneman instabilities (Kelley, 2009)) as such events are unlikely to be genuine specular trail echoes. Some of the events still appear likely to have been range-spread non-specular trail echoes (e.g. the “straight line” of black dots in Fig. 5 around all occurred within 1.5 s of each other), but as this does not impact the DOA evaluation, we did not attempt to remove such events from the analysis. By contrast, the methods presented here can be used to successfully analyse such events. A summary of the analysis results is given in Table 1.
Out of the total of 2222 events 294 were listed as having angular ambiguities. These were analysed with both the DMC-simulation-based Bayesian inference and the temporal integration versions of MUSIC. An example of such an event is illustrated in Fig. 2. The upper middle panel illustrates SNR versus radar pulse, and the two vertical black lines denote the region within which the trail event was identified by the SKiYMET analysis. These are the pulses that were also reanalysed using the MUSIC algorithm. The DOA output from these IPPs is illustrated as blue dots in the left and right column of panels. The upper left panel shows azimuth as a function of IPP and the lower one elevation. Here, the transparent grey lines denote the azimuth and elevation given in the MPD file. In this case, the standard SKiYMET analysis produced two angular ambiguities. The orange transparent line denotes the DOA output from the -based MUSIC and the cyan transparent line denotes the DOA output from the R(xm)-based MUSIC. The same information is given in wave vector ground-projected space, kx,ky in the lower right panel with a zoomed-in version in the upper right panel. Here the MPD-file results are marked by grey crosses, the -based MUSIC by an orange circle, the R(xm)-based MUSIC by a cyan circle, and the regular MUSIC output for each IPP is marked by the blue dots. Finally, the distribution of the MUSIC response F is illustrated in the lower middle panel as a function of IPP. Here, the solid lines denotes the MUSIC response for the temporally integrated versions.
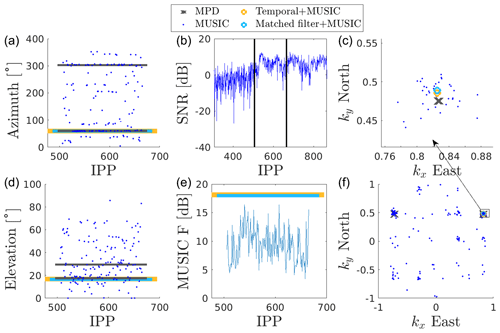
Figure 2Meteor recorded on 13 December 2018 00:03:27.302 UTC. Panel (b) illustrates SNR versus IPP and the two vertical black lines denotes when the event occurred. This particular example was randomly picked from a list of ambiguous events. It is likely an overdense echo, but this does not affect the DOA determination. This event had three range ambiguities (187.9, 257.9, and 327.9 km) and two angular ambiguities. The peak SNR was 8.7 dB. The two angular ambiguities are marked by grey horizontal lines in (a) (azimuth) and (d) (elevation). The MUSIC DOA output from individual IPPs are illustrated as blue dots, while the light blue and orange transparent lines denote the DOA output after temporal integration with and without matched-filter optimization, respectively. The lines are of different widths only to enhance visibility. The same information is given in wave vector ground-projected space, kx,ky, in (c, f). Finally, the distribution of MUSIC responses F as a function of IPP is illustrated in (e). Here, the horizontal lines denote the MUSIC response for the temporally integrated spatial correlation matrices.
For each of the 294 events with angular ambiguities we also performed a series of DMC DOA determination simulations. The noise in the simulations was set to sample from the distribution of SNRs measured for the events themselves so as to reproduce the multinomial probabilities. In Fig. 3, the simulations and the Bayesian inference results are illustrated alongside the measurement data for the event, also illustrated in Fig. 2. The upper left panel shows the MUSIC DOA output in wave vector ground-projected space, i.e. kx and ky. The black circles denote the possible ambiguities and their inclusion regions, i.e. the Ai sets from Eq. (9). The upper middle panel shows the measured distribution of the SNR versus MUSIC response compared to the simulated distribution. The remaining panels show DMC DOA determination simulations with different true inputs. In each of these panels, the input DOA is marked by the large red circle. For reference, the MPD-file results are also marked by transparent grey crosses in each panel. The title of these figures give the Bayesian inference results 𝒫(j) in percent rounded to one decimal. The Bayesian inference can also be evaluated manually by comparing the simulated distribution of DOA outputs with the measurements given in the upper left panel. In this case, the Bayesian inference and the temporally integrated MUSIC, as well as a manual inspection, all agree and identify the same DOA as the true location.
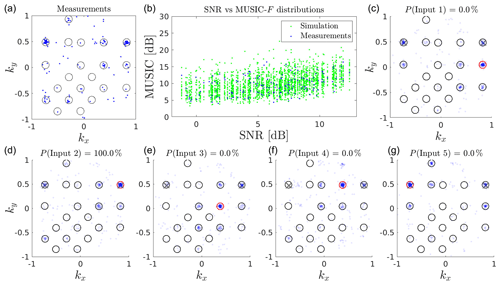
Figure 3Summary of the DOA determination simulations and the Bayesian inference results for the meteor in Fig. 2. Five different possible true DOAs were identified and their individual DMC simulations are illustrated in (c–g). The Bayesian probability of an input DOA being the true location of the trail is given in the title. In each of these panels, the input DOA is marked by a large red circle and the MPD-file results are marked by grey crosses. The measured DOA output distribution is given in (a). The black circles denote the possible ambiguities and their inclusion regions. The temporal integration and matched-filter results illustrated in Fig. 2 coincide with the largest probability location here. Panel (b) shows the measured and simulated distributions of MUSIC response F versus SNR.
Of the 294 analysed events, 256 (87 %) were identified as containing a nominal echo, ideally scattered from a single meteor trail. The remaining 38 events (13 %) contained anomalous signals in the sense that the target model does not match with the real target(s). The SNR of individual pulses in each event typically span several orders of magnitude. The mismatch of model and reality was detected automatically by using the fact that the MUSIC F value did not increase with increasing SNR as a criterion. This indicates that regardless of the measured signal strength, the sensor response model could not be matched to the detected signal. Further examination to identify the sources or causes of these anomalous events was considered outside the scope of this study. The events were marked as anomalous signals in Table 1 and were not processed further.
In 95 % of the nominal ambiguous echoes, all three non-SKiYMET methods found one and the same output DOA, and this DOA was listed as one of the possible ambiguous DOAs in the original SKiYMET analysis. Similarly, in all unambiguous cases with a nominal signal, the results from all three methods also concurred. For the unambiguous cases a comparison between the temporally integrated MUSIC algorithms and the SKiYMET standard data product is illustrated in Fig. 4. This further validates the robustness of the implementation as their difference is typically less (root mean square differences are 0.68∘ for the temporal integration results and 0.79∘ for the matched-filter results) than the reported expected angular measurement accuracy of the system (, Jones et al., 1998).
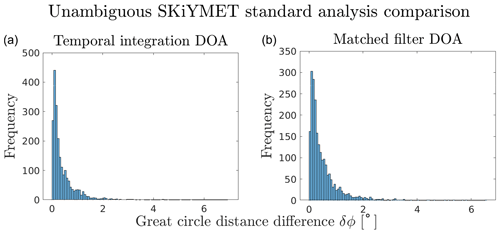
Figure 4Comparison between the nominal signal SKiYMET standard data products and the temporal integration -based MUSIC DOA solutions (a) as well as the matched-filter R(xm)-based MUSIC DOA solutions (b). The difference between the solutions is measured as great-circle angular distance between the DOAs. In total 1928 unambiguous trail events were included in the histograms. The root mean square differences are 0.68∘ for the temporal integration results and 0.79∘ for the matched-filter results.
Upon manual examination of the remaining 5 % where all three methods did not find one and the same DOA, the following observations were made:
-
In five of the cases where the Bayesian inference indicated a solution not listed in the MPD file, the event had too few IPPs to be well determined by any method. In the other two events, both the and the R(xm) solutions concurred with 𝒫(j) and manual inspection indicated they were correct.
-
There were a few cases where the R(xm) yielded a good match while decorrelated. We attribute this to simultaneous targets in the same range gate but with different drift speeds. This would explain why the matched filter was able to yield a good match (optimization towards a single target) while would not. A thorough MUSIC eigenvalue and matched-filter local maximum analysis could confirm this interpretation. If multiple coherent signals are present, there is more than one large MUSIC eigenvalue (Schmidt, 1986).
-
For the remaining events that did not concur, upon manual inspection no events could be identified in these cases and the signal appeared to be only background noise. Hence they were not examined further.
The DOA distribution for all analysed events is illustrated in Fig. 5. The black dots are the 1928 unambiguous meteor trail events, the blue stars are the original ambiguous nominal signal locations that could be discarded, and the red crosses are the 249 resolved ambiguities for which the Bayes solution matched with one of the listed ambiguous locations in the original SKiYMET analysis. There are multiple blue stars per resolved ambiguous event, i.e. per red cross.
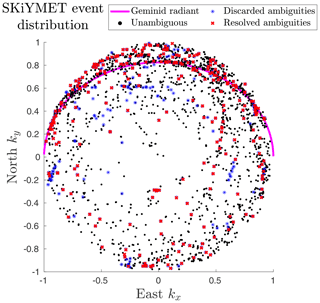
Figure 5Illustration of the DOA distribution of 2222 events in Sodankylä SKiYMET meteor radar data before and after applying temporal integration. The black dots are the unambiguous meteor trail events, the blue stars are the original ambiguous locations that could be discarded, and the red crosses are the resolved ambiguities after temporal integration. There are multiple blue stars per event and red cross. The data were recorded during the Geminid meteor shower. The solid line illustrates directions that fulfil the specular condition for meteors arriving from the Geminid radiant.
The DOA distribution is concentrated towards low elevation in the north. These data were recorded during the Geminid meteor shower. The solid line shows the locations where specular reflection could occur assuming that the meteor originated from the centre of the Geminid meteor shower radiant region (right ascension 112∘, declination 33∘) at the time of the measurement.
At around 00:00 UTC, the Geminid radiant as well as most sporadic meteor source regions were located towards the south (Wiegert et al., 2009) since Sodankylä is located at a high northern latitude. Therefore, most meteors with trajectories fulfilling a specular condition with respect to the radar appeared towards the north. This explains the concentration of DOAs towards the north at low elevation in Fig. 5.
When the remaining resolved direction only has one ambiguous range possibility within the meteor zone, the resolved angular ambiguity also solves the range ambiguity problem, but this is not always the case. The problem with range ambiguities is independent from the angular ambiguity problem and outside of the scope of this study. However, the range ambiguity would be easily avoided with an update of the system to use coded transmission sequences. An advanced example is give by Vierinen et al. (2016), who used coded transmission sequences with a multiple-input–multiple-output bi-static and continuous-wave setup. In the case of the mono-static Sodankylä SKiYMET system, it would be enough to use a small set of binary-phase shift key codes on the pulsed transmitter to enable distinguishing between the pulse trains that come from subsequent echoes within the meteor zone.
The reason why range ambiguities appear in the standardized SKiYMET analysis is the combination of uncoded radar pulses and high PRF. At low-elevation angles from the radar, this means that two or more consecutively transmitted pulses may simultaneously give rise to echoes of meteors in the standardized acceptable altitude range 70–110 km (Hocking et al., 2001). The commonly used PRF 2144 Hz of the SKiYMET radar systems corresponds to a range aliasing of ≃70 km.
We have shown that DMC simulations can characterize the DOA determination behaviour of a system and validate the performance of other analysis methods. Together with a Bayesian inference approach, these simulations can systematically be used to determine the true location of weak meteor radar trail echoes with ambiguous DOA. To perform the Bayesian inference, many simultaneous DMC simulations are required, and this method is as such computationally expensive. However, as the results can be used to validate other methods and characterize the behaviour of a radar system, they are a valuable tool for development work.
We have implemented two versions of standard temporal integration techniques used to increase the SNR of the spatial correlation matrix and subsequent application of the MUSIC algorithm. This is computationally inexpensive and implementation-wise a very simple method able to resolve ambiguous DOAs for SKiYMET meteor radar systems. However, even though the concept itself is not new (cf. Holdsworth, 2005; Vierinen et al., 2016), it does not seem to have been implemented in the SKiYMET standard data analysis. Both the temporally integrated spatial correlation matrix version of MUSIC and the matched-filter version provided the correct output DOA according to the Bayesian inference in ∼ 96 % of the ambiguous cases containing a nominal signal. In the cases when they did not agree, there were either not enough sample points to temporally integrate for the method to be effective or we could not manually conform a specular meteor trail echo in the raw data. For all unambiguous cases both methods coincide with the SKiYMET standard data product.
Standard meteor trail radar systems, such as SKiYMET (Hocking et al., 2001) generally produce enough sample points from each registered meteor for the temporally integrated MUSIC to work. The results indicate that this method will solve the angular ambiguity problem in almost all cases. The problem with range ambiguities is independent from the angular ambiguity problem and outside the scope of this study, but we note that it could be avoided with an update of the system to use coded transmission sequences.
The presented methods do not depend on the MUSIC algorithm per se: for example, the complex signal amplitudes that are used in the DOA determination algorithm by Jones et al. (1998) to calculate the ϕ angles can be temporally integrated in the same way as the spatial correlation matrix R was temporally integrated here.
Finally, one can pose the question whether and at what point the temporally integrated MUSIC becomes ambiguous. This question as well as the validation of a pipeline implementing temporal integration techniques can be addressed by the same type of DMC simulations.
Extending the definition used in Eqs. (1) and (2) to include temporal variations we define
where n denotes the temporal component and the noise is , i.e. a complex circularly symmetric normal random variable. Here kn is the incident wave vector, An is the wave amplitude, is the inner product, rj is the physical location of antenna j, and gj is its gain pattern. We will assume that the noise is uncorrelated between samples of j and between samples of n. In reality, if there is a particularly strong point source of noise compared to the overall background noise, the total noise picked up by an antenna may become spatially correlated. There are galactic sources that produce such noise (Gaensler, 2004). However, given the low directivities of the SKiYMET antennas and the fact that it is a single-pulse system, assuming completely uncorrelated noise is acceptable for this derivation.
For simplicity, we will make the following further assumptions for Eq. (A2): individual antenna gain is unity gj=1; signal amplitude is constant over antennas and time An=A; the wave vector change due to the local wind drift velocity over the meteor trail event time is negligible kn=k. The expected value and variance of the signal is
When stochastic variables are uncorrelated, the expected value operator is linear and multiplicative, i.e. E[XY]=E[X]E[Y], while the variance operator is linear and follows . This applies also to complex random variables (O'Donoughue and Moura, 2012). As such, the moments of a spatial cross correlation of Eq. (A2) integrated over time are
The expected noise power is given by the noisy signal variance when A=0, i.e. PNoise=Ntσ4. Therefore, the “SNR” for a cross-correlated signal would be defined as
There is no standardized definition of coherent integration other than that such an integration should integrate the quadrature components of the signal envelope by taking phase into account (e.g. Miller and Bernstein, 1957). As the phases of the cross correlation signal are preserved by the temporal integration of cross correlations, it is essentially the cross correlation envelope that is integrated; i.e., as the component does not change, a simple summation can be referred to as coherent integration. However, a more efficient coherent integration would be to apply a matched-filter integration prior to cross correlation.
Assuming a matched filter has perfectly modelled the temporal component of the signal ϕn, the statistical moments of the cross correlation of the matched-filter integration would be
Here we have used the fact that complex rotations of ξ do not affect the distribution as it is circularly symmetrical. This shows that a perfect matched-filter integration prior to cross correlation would produce a more effective coherent integration. The SNR for the latter cross-correlated signal is
The data described in Sect. 2.2 that were analysed, i.e. the confirmed event (CEV) files and the meteor position data (MPD) file, are available at https://doi.org/10.5878/vnhd-na43 (Kastinen et al., 2020) together with a short description of their structure.
DK developed the analysis and model code and performed the simulations and data analysis. AK and ML provided the data set analysed. DK prepared the paper with contributions from JK and AK. All the authors contributed to proofreading the paper.
The authors declare that they have no conflict of interest.
The authors would like to thank David Holdsworth and Joel Younger for valuable comments and suggestions that improved the first version of the paper.
This paper was edited by Jorge Luis Chau and reviewed by Joel Younger and David Holdsworth.
Bianchi, C. and Meloni, A.: Natural and man-made terrestrial electromagnetic noise: an outlook, Ann. Geophys.-Italy, 50, 435–445, 2007. a
Bronshten, V. A.: Physics of Meteoric Phenomena, Kluwer, Dordrecht, The Netherlands, 1983. a
Brown, P., Spalding, R. E., ReVelle, D. O., Tagliaferri, E., and Worden, S. P.: The flux of small near-Earth objects colliding with the Earth, Nature, 420, 294–296, https://doi.org/10.1038/nature01238, 2002. a
Ceplecha, Z., Borovička, J., Elford, W. G., Revelle, D. O., Hawkes, R. L., Porubčan, V., and Šimek, M.: Meteor Phenomena and Bodies, Space Sci. Rev., 84, 327–471, https://doi.org/10.1023/A:1005069928850, 1998. a
Chau, J. L. and Clahsen, M.: Empirical Phase Calibration for Multistatic Specular Meteor Radars Using a Beamforming Approach, Radio Sci., 54, 60–71, https://doi.org/10.1029/2018RS006741, 2019. a, b, c
Gaensler, B. M.: Radio Emission from the Milky Way, in: Milky Way Surveys: The Structure and Evolution of our Galaxy, edited by: Clemens, D., Shah, R., and Brainerd, T., Astronomical Society of the Pacific (ASP), ASP Conference Series, Utah Valley University, 217, 2004. a
Hanley, J. A. and Lippman-Hand, A.: If nothing goes wrong, is everything all right?: interpreting zero numerators, Jama, 249, 1743–1745, 1983. a
Hocking, W. K.: A new approach to momentum flux determinations using SKiYMET meteor radars, Ann. Geophys., 23, 2433–2439, https://doi.org/10.5194/angeo-23-2433-2005, 2005. a, b
Hocking, W. K., Fuller, B., and Vandepeer, B.: Real-time determination of meteor-related parameters utilizing modern digital technology, J. Atmos. Sol.-Terr. Phy., 63, 155–169, https://doi.org/10.1016/S1364-6826(00)00138-3, 2001. a, b, c, d
Holdsworth, D. A.: Angle of arrival estimation for all-sky interferometric meteor radar systems, Radio Sci., 40, RS6010, https://doi.org/10.1029/2005RS003245, 2005. a, b
Holdsworth, D. A., Reid, I. M., and Cervera, M. A.: Buckland Park all-sky interferometric meteor radar, Radio Sci., 39, RS5009, https://doi.org/10.1029/2003RS003014, 2004. a, b, c, d
Jones, J., Webster, A. R., and Hocking, W. K.: An improved interferometer design for use with meteor radars, Radio Sci., 33, 55–65, https://doi.org/10.1029/97RS03050, 1998. a, b, c, d, e, f
Kastinen, D. and Kero, J.: A Monte Carlo-type simulation toolbox for Solar System small body dynamics: Application to the October Draconids, Planet. Space Sci., 143, 53–66, https://doi.org/10.1016/j.pss.2017.03.007, 2017. a
Kastinen, D. and Kero, J.: Probabilistic analysis of ambiguities in radar echo direction of arrival from meteors, Atmos. Meas. Tech., 13, 6813–6835, https://doi.org/10.5194/amt-13-6813-2020, 2020. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Kastinen, D., Kozlovsky, A., Lester, M., and Kero, J.: Resolving ambiguous direction of arrival of weak meteor radar trail echoes, Swedish Institute of Space Physics, https://doi.org/10.5878/vnhd-na43, 2020. a
Kelley, M. C.: The Earth's ionosphere: plasma physics and electrodynamics, Academic Press, Cambridge, Massachusetts, United States, https://doi.org/10.1016/B978-0-12-404013-7.X5001-1, 2009. a
Kero, J., Campbell-Brown, M. D., Stober, G., Chau, J. L., Mathews, J. D., and Pellinen-Wannberg, A.: Radar Observations of Meteors, in: Meteoroids: Sources of Meteors on Earth and Beyond, edited by: Ryabova, G. O. and, Asher, D. J., and Campbell-Brown, M. J., Cambridge University Press, 65–89, https://doi.org/10.1017/9781108606462, 2019. a, b
Kozlovsky, A., Shalimov, S., Oyama, S., Hosokawa, K., Lester, M., Ogawa, Y., and Hall, C.: Ground Echoes Observed by the Meteor Radar and High-Speed Auroral Observations in the Substorm Growth Phase, J. Geophys. Res.-Space, 124, 9278–9292, https://doi.org/10.1029/2019JA026829, 2019. a
Kozlovsky, A., Lukianova, R., and Lester, M.: Occurrence and Altitude of the Long-Lived Nonspecular Meteor Trails During Meteor Showers at High Latitudes, J. Geophys. Res.-Space, 125, e27746, https://doi.org/10.1029/2019JA027746, 2020. a
Lovell, A. C. B., Prentice, J. P. M., Porter, J. G., Pearse, R. W. B., and Herlofson, N.: Meteors, comets and meteoric ionization, Rep. Prog. Phys., 11, 389–454, https://doi.org/10.1088/0034-4885/11/1/313, 1947. a
McKinley, D. W. R.: Meteor Science and Engineering, McGraw-Hill Series in Engineering Sciences, McGraw-Hill Book Company, Inc., USA, 309 pp., 1961. a
Miller, K. and Bernstein, R.: An analysis of coherent integration and its application to signal detection, IRE T. Inform. Theor., 3, 237–248, https://doi.org/10.1109/TIT.1957.1057425, 1957. a
O'Donoughue, N. and Moura, J. M. F.: On the Product of Independent Complex Gaussians, IEEE T. Signal Proces., 60, 1050–1063, 2012. a
Papoulis, A. and Pillai, S. U.: Probability, random variables, and stochastic processes, Tata McGraw-Hill Education, McGraw Hill Europe, UK, 852 pp., ISBN-10 0071226613, ISBN-13 978-0071226615, 2002. a
Plane, J. M.: Atmospheric chemistry of meteoric metals, Chem. Rev., 103, 4963–4984, 2003. a
Plane, J. M.: Cosmic dust in the Earth's atmosphere, Chem. Soc. Rev., 41, 6507–6518, 2012. a
Polisensky, E.: LFmap: A low frequency sky map generating program, Long Wavelength Array Memo Series, Bradley Department of Electrical and Computer Engineering at Virginia Polytechnic, Institute and State University, USA, 111 pp., 2007. a
Schmidt, R. O.: Multiple emitter location and signal parameter estimation, IEEE T. Antenn. Propag., 34, 276–280, https://doi.org/10.1109/TAP.1986.1143830, 1986. a, b, c, d, e
Vaubaillon, J., Colas, F., and Jorda, L.: A new method to predict meteor showers – I. Description of the model, Astron. Astrophys., 439, 751–760, https://doi.org/10.1051/0004-6361:20041544, 2005a. a
Vaubaillon, J., Colas, F., and Jorda, L.: A new method to predict meteor showers – II. Application to the Leonids, Astron. Astrophys., 439, 761–770, https://doi.org/10.1051/0004-6361:20042626, 2005b. a
Vierinen, J., Chau, J. L., Pfeffer, N., Clahsen, M., and Stober, G.: Coded continuous wave meteor radar, Atmos. Meas. Tech., 9, 829–839, https://doi.org/10.5194/amt-9-829-2016, 2016. a, b, c, d
Wiegert, P., Vaubaillon, J., and Campbell-Brown, M.: A dynamical model of the sporadic meteoroid complex, Icarus, 201, 295–310, https://doi.org/10.1016/j.icarus.2008.12.030, 2009. a
Younger, J. P. and Reid, I. M.: Interferometer angle-of-arrival determination using precalculated phases, Radio Sci., 52, 1058–1066, https://doi.org/10.1002/2017RS006284, 2017. a, b