Diurnal variability of stratospheric column NO₂ measured using direct solar and lunar spectra over Table Mountain, California (34.38° N)

A full diurnal measurement of stratospheric column NO₂ has been made over the Jet Propulsion Laboratory's Table Mountain Facility (TMF) located in the mountains above Los Angeles, California, USA (2.286 km above mean sea level, 34.38^∘ N, 117.68^∘ W). During a representative week in October 2018, a grating spectrometer measured the telluric NO₂ absorptions in direct solar and lunar spectra. The stratospheric column NO₂ is retrieved using a modified minimum-amount Langley extrapolation, which enables us to accurately treat the non-constant NO₂ diurnal cycle abundance and the effects of tropospheric pollution near the measurement site. The measured 24 h cycle of stratospheric column NO₂ on clean days agrees with a 1-D photochemical model calculation, including the monotonic changes during daytime and nighttime due to the exchange with the N₂O₅ reservoir and the abrupt changes at sunrise and sunset due to the activation or deactivation of the NO₂ photodissociation. The observed daytime NO₂ increasing rate is $(\mathrm{1.34}\pm \mathrm{0.24})\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻² h⁻¹. The observed NO₂ in one of the afternoons during the measurement period was much higher than the model simulation, implying the influence of urban pollution from nearby counties. A 24 h back-trajectory analysis shows that the wind first came from inland in the northeast and reached southern Los Angeles before it turned northeast and finally arrived at TMF, allowing it to pick up pollutants from Riverside County, Orange County, and downtown Los Angeles.

1 Introduction

Nitrogen dioxide (NO₂) plays a dominant role in the ozone (O₃)-destroying catalytic cycle (Crutzen, 1970). NO₂ column abundance has been measured using ground-based instruments since the mid-1970s (Network for the Detection of Atmospheric Composition Change (NDACC), http://www.ndacc.org, last access: 1 December 2021) (e.g., Hofmann et al., 1995; Piters et al., 2012; Roscoe et al., 1999, 2010; Vandaele et al., 2005; Kreher et al., 2020), which serve as the standards for validating satellite measurements. Noxon (1975) and Noxon et al. (1979) retrieved the stratospheric NO₂ column by differential optical absorption spectroscopy (DOAS) in the visible spectral range using ratios of scattered sunlight from the sky and direct sun and moonlight at low (noon and midnight) and high (twilight) air mass factors over Fritz Peak, Colorado (39.9^∘ N). Since the optical path of sun/moonlight at dawn or dusk (solar/lunar zenith angle ≈90^∘) is much longer than the optical path of the direct sunlight at noon–midnight, the NO₂ absorption in the noon–midnight spectrum can be assumed to be small, and the NO₂ absorption in the twilight slant column could therefore be isolated effectively by ratioing the scattered twilight spectrum to the scattered noon spectrum. This DOAS principle also applies to ratios of direct moonlight or sunlight at low and high air mass factors. The measurements of Noxon et al. (1979) revealed sharp changes of the stratospheric NO₂ column before and after sunsets and sunrises at mid-latitudes. Similar DOAS measurements at high latitudes in the 1980s focused on the role of NO_x in controlling O₃ and active halogen species in the polar stratosphere (Fiedler et al., 1993; Flaud et al., 1988; Keys and Johnston, 1986; Solomon, 1999). Johnston and McKenzie (1989) and Johnston et al. (1992) reported a reduction in the southern hemispheric NO₂ over Lauder, New Zealand (45.0^∘ S), following the eruptions of El Chichón (in 1982) and Mount Pinatubo (in 1991), respectively.

NO₂ column abundance has also been measured using direct solar spectra acquired by Fourier-transform infrared (FTIR) spectrometers. Advantages of direct solar measurements are the lack of Raman scattering in the spectra, air mass factors determined geometrically rather than through a radiative transfer code, and provision of NO₂ column abundances at most times during the day. Sussmann et al. (2005) retrieved the stratospheric NO₂ column abundance over Zugspitze, Germany (47^∘ N), using the infrared absorption in the solar spectrum near 3.43 µm. The stratospheric NO₂ column abundance was then subtracted from the total column estimated from satellite measurements to obtain the tropospheric column. Wang et al. (2010) demonstrated how high-spectral-resolution measurements using a Fourier transform spectrometer could perform absolute NO₂ column abundance retrievals without the need for a solar reference spectrum. Because of the solar rotation, the Fraunhofer features in the UV spectra acquired simultaneously from the east and west limbs of the solar disk are Doppler shifted while the telluric NO₂ absorptions are not shifted (Iwagami et al., 1995). Thus, the telluric NO₂ absorptions can be identified by correcting the Doppler shift without the need of an a priori solar spectrum. Other techniques include as balloon-based in situ measurements (May and Webster, 1990; Moreau et al., 2005), balloon-based solar occultations (Camy-Peyret, 1995), and ground-based differential optical absorption spectroscopy – MAX-DOAS (Hönninger et al., 2004; Sanders et al., 1993) and direct-sun DOAS (Herman et al., 2009; Spinei et al., 2014; Herman et al., 2019) – and have been actively applied in NDACC and the Pandonia Global Network. The DOAS techniques have also been employed to further characterize the vertical distributions of NO₂ (Kreher et al., 2020).

Here we retrieve the stratospheric column NO₂ over Table Mountain Facility (TMF) in Wrightwood, California, USA (2.286 km above mean sea level, 34.38^∘ N, 117.68^∘ W), using Langley extrapolation to determine the reference spectrum and considering both daytime and nighttime chemistry. Daytime NO₂ concentration remains significant, albeit small relative to the nighttime concentration, and varies from morning to afternoon. This daytime variation has been a source of error in determination of the DOAS reference spectrum using Langley extrapolation. Comprehensive assessment of NO₂ must include both daytime and nighttime values. We therefore also retrieve daytime column NO₂ by acquiring direct sun spectra throughout the day. We will compare the daytime and nighttime stratospheric column NO₂ with those simulated in a one-dimensional (1-D) photochemical model. The effect of urban pollution on the measured NO₂ can be deduced from this comparison.

2 Data and method

2.1 Instrumentation and measurement technique

The grating spectrometer used for the NO₂ spectral measurement is similar to the one used by Chen et al. (2011) and is installed in the same observatory. A heliostat and a telescope are used to direct and launch light into a fiber optic bundle placed at the focal plane of the telescope (Fig. 1). The bundle consists of 19 silica fibers, is 200 µm in diameter, and is arranged in a circular configuration (in SMA 905 connectors) on the source end and in a linear pattern on the spectrograph end. Before entering the spectrograph, light is passed through an order sorting filter (Schott GG-400 glass) and a shutter. The imaging spectrograph is a Princeton Instruments SP-2-300i with a 0.3 m focal length used with a 1200 g mm⁻¹ grating blazed at 500 nm. A CCD detector (Princeton Instruments PIXIS 400B) is placed at the focal plane of the spectrograph. The 1340×400 imaging array of 20×20 µm² pixels is vacuum sealed and thermoelectrically cooled to −80 ^∘C.

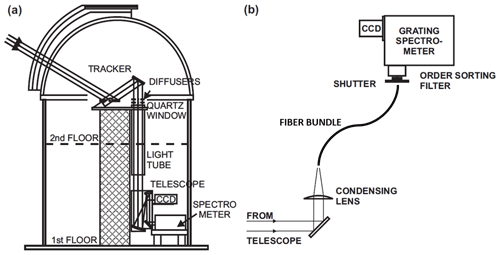
Figure 1 Schematic of the instrument light path over the Table Mountain Facility (TMF, 2.286 km above mean sea level, 34.38^∘ N, 117.68^∘ W, Wrightwood, California, USA). (a) Light is collected by the primary of the heliostat (tracker), reflected down to the telescope on the first floor, which conditions it to a 7 cm diameter beam. (b) The light is then reflected to a condensing lens into a fiber optic bundle, past a shutter and order-sorting filter, and then into the spectrometer. The fiber bundle contains 19 fibers in a round pattern at the entrance, and at the exit fibers are arranged in a line pattern that is set parallel to the spectrometer slit.

Our assessment showed that 2 d away from the full moon would decrease the measured lunar intensity by ∼20 %. Therefore, in the following analysis, we only focus on acquired direct-moon and direct-sun spectra that are within 5 to 7 d of the full moon in order to maximize the signal-to-noise ratio (SNR). In addition, to minimize the terminator effects near sunrise and sunset, we use measurements with lunar and solar zenith angles less than 80^∘. The stray light is typically of the order of 10⁻⁴$-{\mathrm{10}}^{-\mathrm{3}}$.

When direct sunlight is measured, two ground glass diffuser plates are inserted into the beam prior to the telescope primary to integrate over the entire solar disk and to attenuate light. Additional attenuation of light to avoid detector saturation is accomplished by placing a 23 % open area screen in the beam just after the diffuser plates. Overall, the solar throughput is reduced by a factor of $\sim \mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{5}}$. The resulting spectrum has a spectral grid spacing on the detector of 0.048 nm from 411 to 475 nm with a measured line shape of 0.34 nm FWHM sampled at ∼7 pixels. Spectral calibration and line shape measurements are accomplished using a diffuse reflection of an argon lamp near the fiber end, which gives a nearly linear result between pixel and wavelength with a small second-order correction; the second-order correction is considered in the calibration and the QDOAS fitting (see next section).

When direct moonlight is measured, the diffuser plates are removed. Since the sun is ∼400 000 times the intensity of the full moon, the ratio between the light hitting our detector for solar noon (after inserting the diffuser plates) and lunar noon during the full moon is ∼5. To maintain an approximately constant solar and lunar signal-to-noise ratio and fitting residuals, we vary the exposure time during specific times of solar and lunar noon, typically around ∼3 s for lunar noon and ∼0.6 s for solar noon, giving a ratio of ∼5 to homogenize the solar and lunar photon counts mentioned above. At higher zenith angles, longer exposures were taken to keep the detector counts in the same range. The data were dark-corrected and averaged to obtain the desired signal levels; for the sun, this was consistently ∼4 min; for the moon, the averaging time varied from ∼8 min during the night of the full moon to 24 min on the night 3 d from full moon.

We estimate the SNR by assuming that the standard deviation of the difference of two consecutive spectra is close to the noise and that the average intensity of the two consecutive spectra is the signal. As a result, the SNR at full moon and solar transits is ∼2900 and ∼4900, respectively. During the low sun and moon observations, the SNR is more difficult to measure directly. However, the fitting residuals are consistent with these estimates.

2.2 The DOAS retrieval

The DOAS technique is used to retrieve the NO₂ slant column (Noxon, 1975; Noxon et al., 1979; Platt et al., 1979; Stutz and Platt, 1996). A spectrum measured by the grating spectrometer at any time of the day is ratioed to a pre-selected reference spectrum. From the ratioed spectrum, we retrieve the differential slant column NO₂ relative to the column that is represented by the reference spectrum. The total slant column is then the sum of the differential slant column and the reference column.

Our reference spectrum is a solar spectrum measured at the TMF ground level at local noon (Chen et al., 2011). This solar reference spectrum is used to ratio all other spectra collected, including those during the solar and lunar measurement cycles. In principle, one can retrieve the reference NO₂ column from the reference spectrum. However, this requires precise knowledge of the solar spectrum at the top of the atmosphere in order to isolate the NO₂ absorption. We will use a variant of the Langley extrapolation to circumvent the need of the retrieval of the reference column (Lee et al., 1994; Herman et al., 2009); see following section for details.

The differential slant column NO₂ is retrieved by fitting the ratioed spectrum in a smaller window between 430 and 468 nm. This window has stronger NO₂ absorptions relative to other wavelengths in the instrument range (411–475 nm); see Fig. 4 of Spinei et al. (2014). In addition, this window also has less interfering absorption from species other than O₃, O₄ (O₂ dimer), and H₂O (see below).

The spectral fitting is accomplished through the Marquardt–Levenberg minimization using QDOAS 3.2 (Danckaert et al., 2017; released in September 2017) retrieval software (http://uv-vis.aeronomie.be/software/QDOAS/, last access: 1 December 2021). The high-resolution NO₂ absorption cross sections at T=215, 229, 249, 273, 298, and 299 K based on Nizkorodov et al. (2004) are convolved to the instrument resolution using the instrument line shape function and the Voigt line shape prior to its use in QDOAS. The yearly average from the TMF temperature lidar measurements are used to derive a reference for each altitude level by linear interpolation between each adjacent cross section, which is also adjusted for pressure broadening using the results of Nizkorodov et al. (2004). We use third-order polynomials for broadband and offset. Some studies, such as Herman et al. (2009), use fourth- or higher-order polynomials for wider spectral windows. Since the NO₂ absorption features are much narrower than our spectral window (430–468 nm), the broad shape of the third-order polynomial does not affect the NO₂ retrievals. In addition, for our spectral window, we tested our retrieval algorithm using a linear baseline, and we concluded that a third-order polynomial reduces the residuals more effectively than a linear baseline. All five cross sections were used to create a single NO₂ reference. Our NO₂ cross section reference assumes the yearly average temperature profile at TMF and a low level of free tropospheric NO₂. The effective temperature of the NO₂ absorption cross section used in the work is 231 K. To test the sensitivity of these assumptions, we considered two extreme cases: (i) a cooler atmosphere with a lower partition of NO₂ in the free troposphere and (ii) a warmer atmosphere with a higher partition of NO₂ in the free troposphere. The effective temperatures of these two cases are estimated by 229 and 249 K, respectively. The difference between retrievals using these extreme cases is ∼5 %; the regular variation in temperature and tropospheric NO₂ at TMF is well within estimates. Each level's reference is then multiplied by a weight which is proportional to the standard atmosphere and then summed to obtain a single reference used in the fitting. In addition to NO₂, other absorptions by O₃, O₄ (O₂ dimer), and H₂O in the same spectral window are simultaneously retrieved. The O₃ cross section is from Serdyuchenko et al. (2014) for 11 temperature references ranging from 193 to 293 K. Like NO₂, all 11 cross sections are used in the spectral fitting for O₃. In contrast, for O₄ and H₂O, only a single temperature reference is used. The O₄ cross sections are from Thalman and Volkamer (2013) at 273 K. The H₂O cross sections at 296 K are from HITRAN 2016 (Gordon et al., 2017). Figure 2 shows an example of a fitted spectrum on 24 October 2018. The NO₂ abundance retrieved from QDOAS is the desired differential slant column NO₂ relative to our chosen reference spectrum.

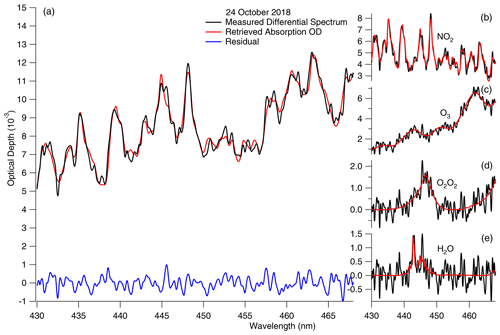
Figure 2 A sample QDOAS spectral fit of a lunar spectrum at an air mass factor of 2.21 on 24 October 2018 at 19:25 PST. The measured spectrum is shown by the black curve in (a). The fitted spectrum (red) is overlaid, and the residual spectrum (blue) is shown at the bottom. Four species are considered in the spectral fit: NO₂, O₃, O₄, and H₂O. The spectral fits are performed simultaneously in QDOAS. The red lines on the right column are the fitted spectra of the corresponding species. To visualize the signal-to-noise ratios, we add the residual spectrum (blue in a) to individual fitted spectra, which are shown as the black spectra in (b)–(e).

The 2σ uncertainty due to the spectral fitting residual lies between 0.1×10¹⁵ and 0.6×10¹⁵ molecules cm⁻², with a mean of $\sim \mathrm{0.4}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻², which is equivalent to a mean of 10 % uncertainty. The distribution of the retrieval uncertainty is shown in Fig. 3 (inset).

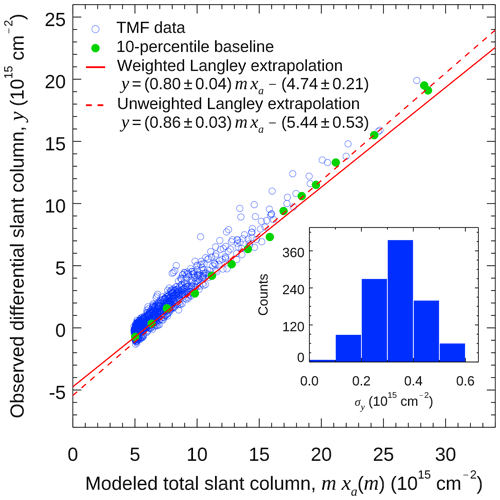
Figure 3 The modified minimum-amount Langley extrapolation (MMLE). The blue circles are the observed differential slant columns during our campaign over TMF from 23 to 28 October 2018. Each observational value is plotted against the total slant column modeled at the same time of the day (e.g., 11:05 PST). The green dots are the 10th percentile of 20 uniform bins on the x axis. The red line is a linear regression of the green dots, which is taken as the background diurnal cycle in a clean atmosphere. The linear fit weighted by the number of data points in the bins is $y=\mathrm{0.80}m{x}_{\mathrm{a}}\left(m\right)-\mathrm{4.74}\times {\mathrm{10}}^{\mathrm{15}}$. The 2σ uncertainties of the slope and the intercept are 0.04 and 0.21×10¹⁵, respectively. The y intercept thus gives a reference column, $y_{\mathrm{0}}=\mathrm{4.74}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻². The unweighted linear fit overestimates the reference column (544×10¹⁵ molecules cm⁻²) because of the sparse data points at air mass factors greater than ∼2. Thus, the weighted linear fit is used as the Langley extrapolation in this work. The inset shows the distribution of the 2σ uncertainty of the observed differential slant columns.

The air mass factor is calculated using secant of the solar or lunar zenith angle. Herman et al. (2009) considered an altitude correction of the air mass factor. The altitude correction is generally negligible except for zenith angles ≥80^∘, but we do not make measurements at those zenith angles (see Sect. 2.1).

2.3 The modified minimum-amount Langley extrapolation (MMLE)

Let y be the differential slant column NO₂ along the line of sight, y₀ the reference column NO₂, m the stratospheric air mass factor (which is proportional to the geometric secant of the solar zenith angle in the stratosphere for these direct solar and lunar observations), and x the total vertical column NO₂; x is our target quantity. The differential slant column can be approximated as the total vertical column multiplied by the stratospheric air mass factor after the subtraction of the reference column:

$$\begin{array}{}\text{(1)}& y=mx-y_{\mathrm{0}}.\end{array}$$

If y₀ were known, then x would simply be $m^{-\mathrm{1}}(y+y_{\mathrm{0}})$. The Langley extrapolation technique for determination of the extra-terrestrial reference obtains x and −y₀ as the slope and the intercept of the linear regression of y against m, respectively, assuming x is temporally constant (i.e., the vertical column does not change during the course of the day). In this formulism, the reference column y₀ is an extrapolated value corresponding to hypothetical zero air mass (m=0).

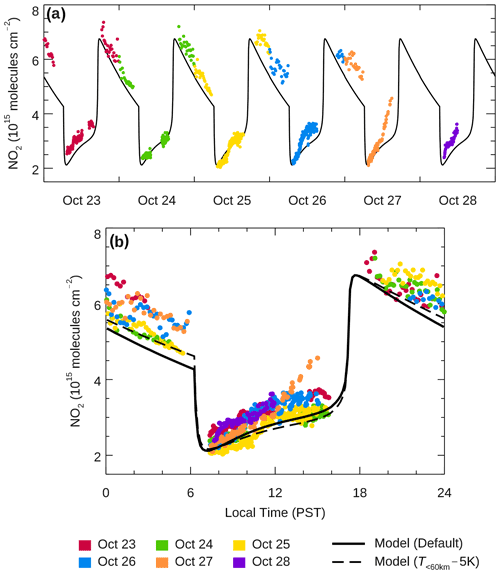
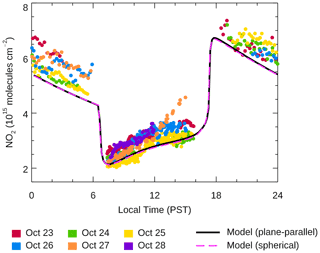
Figure 4 The column NO₂ abundance measured over TMF on 23–28 October 2018, represented by the color dots. The 1-D model simulation, with default input temperature and surface N₂O being 330 ppb, representing 26 October is shown as the solid black line. (a) The column NO₂ measurements on individual dates. (b) The aggregated column NO₂ measurements as a function of local time. An additional 1-D model simulation with temperature below 60 km reduced by 5 K, is shown as the dashed line.

The Langley extrapolation was first used to measure the solar spectrum at the top of the atmosphere (Langley, 1903) and has also been used to measure atmospheric constituents (e.g., Jeong et al., 2018; Toledano et al., 2018; Barreto et al., 2017; Huber et al., 1995; Bhartia et al., 1995). However, the assumption of a constant x is often violated due to diurnal variabilities in the atmospheric constituents driven by, e.g., the incident solar radiation, transmittance, dynamics, and human activities. In our case, the afternoon stratospheric column NO₂ is greater than the morning stratospheric column NO₂ (see our Fig. 4). Several modifications have been proposed to relax the assumption of a constant x (e.g., Ångström, 1970; Shaw, 1976; Long and Ackerman, 2000; Cachorro et al., 2008; Kreuter et al., 2013; Marenco, 2007). In this work, we combine the modifications used in Lee et al. (1994) and Herman et al. (2009) to account for the effects due to the stratospheric NO₂ diurnal variability and urban pollution.

Lee et al. (1994) replaced the constant x with an a priori function of m, denoted by x_a(m):

$$\begin{array}{}\text{(2)}& y=\mathit{\alpha }m{x}_{\mathrm{a}}\left(m\right)-y_{\mathrm{0}}.\end{array}$$

Equation (2) is analogous to Eq. (1) except that now y is regressed against the product m x_a(m). α is the slope of the regression line and it serves as an effective scaling factor that adjusts the chemical rates in the a priori knowledge. Equation (2) presents a modified Langley extrapolation. The y intercept, y₀, obtained from the modified Langley extrapolation, is then used to derived the observed total vertical column through the transformation $m^{-\mathrm{1}}(y+y_{\mathrm{0}})$. Note that α is not used in this transformation.

As in Lee et al. (1994), assuming the chemical processes of NO₂ are much faster than the dynamical processes so that the NO₂ diurnal cycle is at photochemical equilibrium, we obtain x_a(m) from a 1-D photochemical model (to be described in the next section). The x_a(m) we use corresponds to a clean atmosphere only. To perform the regression, we plot y against the product m x_a(m) (Fig. 3, blue open circles). If all NO₂ columns are measured on clean days, then they would ideally fall on a straight line (which, apart from the natural variability in the background, holds true for the Lee et al. (1994) measurements over Antarctica). However, if there is a pollution source near a measurement site, like the TMF, then some of the measured NO₂ columns may be significantly higher than x_a(m), leading to a large vertical spread in the scattered plot. The pollution-induced deviation from x_a(m) may be highly variable, depending on the source types and the meteorology. When a large number of measured NO₂ columns on clean and polluted days are plotted together against x_a(m), the baseline of the scattered data may be considered the background NO₂ diurnal cycle in a clean atmosphere (Herman et al., 2009). Herman et al. (2009) called their method the minimum-amount Langley extrapolation (MLE). Expanding on their terminology, we call our method, which combines the MLE with the modification of Lee et al. (1994), the modified MLE, or MMLE. Note, however, that the MMLE differs from the optimal estimation that is commonly used in satellite retrieval, where the statistics of priori knowledge is used to constrain the retrieved value; no prior constraint is used in the MMLE.

Our measurements made during October (a non-summer season) were mostly under unpolluted conditions (see Sect. 3.5). Thus, we applied the MMLE to derive a baseline for an estimation of the background NO₂ diurnal cycle, which is then used in the regression with the modeled diurnal cycle. On the Langley plot (Fig. 3), we divide the range of m x_a(m) (from 4.5×10¹⁵ to 3×10¹⁶ molecules cm⁻² during our campaign) into 20 equal bins. To be consistent with the 2σ spectral-fit uncertainty, we use the 10th percentile of the y distribution in each bin to define a baseline (Fig. 3, green dots).

Note that the data points are sparsely distributed at high air mass factors in Fig. 3. This is because while the measurements were made at relatively uniform time intervals, the air mass factor m=secθ effectively stretches the time intervals at high air mass factors. The number of data points in the bins drops progressively by a factor of ∼2: the counts drop exponentially from 431 in the first bin, (4.5–6)×10¹⁵ molecules cm⁻², to only 12 in the bin (1.5–1.65)×10¹⁶ molecules cm⁻². The determination of the 10th percentile for bins with centers greater than 1.5×10¹⁶ molecules cm⁻² is then subject to large uncertainties. Since mathematically the 10th percentiles at high air mass factors (i.e., at the edge of the data distribution) have higher effects on a linear fit, the resultant Langley extrapolation would be strongly biased by the uncertainties of the 10th percentiles at high mass factors. Thus, to obtain a linear fit for the Langley extrapolation, we apply more weights to bins with more data counts. This definition of the weights should mimic the reduction of the variance of a sample mean by the factor of $\frac{\mathrm{1}}{N}$ (or $\frac{\mathrm{1}}{\sqrt{N}}$ for the standard deviation of a sample mean). Therefore, we define the weight as unity for the first bin, (4.5–6)×10¹⁵ molecules cm⁻². The weight for the second bin, (6–7.5)×10¹⁵ molecules cm⁻², is the ratio of the data counts of this bin over the first bin. The weight for the third bin is the ratio of the data counts of this bin over the second bin and so on. The weighted linear fit obtained using these weights is used for the Langley extrapolation. Figure 3 compares the Langley extrapolations using the weighted (solid red line) and unweighted linear fits (dashed red line). Since the 10th percentiles at high air mass ($\ge \mathrm{1.5}\times {\mathrm{10}}^{\mathrm{16}}$ molecules cm⁻²) are generally overestimated due to insufficient data counts, the unweighted linear fit tends to have a steeper slope, leading to a ∼15 % higher reference column (5.44×10¹⁵ molecules cm⁻²) relative to the weighted linear fit. This overestimation of the reference column may create an artifact in the diurnal cycle due to the normalization factor $m^{-\mathrm{1}}(y+y_{\mathrm{0}})$.

The weighted Langley extrapolation (Fig. 3, solid red line) provides the values of α and y₀ for our stratospheric column NO₂ estimation. The weighted fit gives $\mathit{\alpha }=\mathrm{0.80}\pm \mathrm{0.04}$ and $y_{\mathrm{0}}=(\mathrm{4.74}\pm \mathrm{0.21})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² (at 2σ levels). This value of y₀ is our reference column used for both daytime and nighttime measurements. We estimate the total retrieval uncertainty to be the root mean square of the spectral fitting uncertainty and the uncertainty in y₀, which is $\sim \mathrm{0.5}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² (2σ).

3 The photochemical model

Our x_a(m) is based on the Caltech/JPL 1-D photochemical model (Allen et al., 1984, 1981; Wang et al., 2020), shown as the black solid line in Fig. 4. This photochemical model includes the stratospheric species that are important for O₃, odd-nitrogen (NO_x = N + NO + NO₂ + NO₃ + 2N₂O₅), and odd-hydrogen (HO_x = H + OH + HO₂) chemistry, including the reactions discussed in Sect. 3.1. Nitrous oxide (N₂O) is the main parent molecule of NO₂ in the lower stratosphere. The concentration of N₂O at the ground level of the model is fixed at 330 ppb (https://www.esrl.noaa.gov/gmd/hats/combined/N2O.html, last access: 1 December 2021). The kinetic rate constants are obtained from the 2019 JPL Evaluation (Burkholder et al., 2019).

The sunrise and sunset times and the solar noontime in the model are calculated using the ephemeris time. We use Newcomb parameterizations of the perturbations due to the Sun, Mercury, Venus, Mars, Jupiter, and Saturn (Newcomb, 1989). We also use Woolard parameterizations for the nutation angle and rate (Woolard, 1953). A more modern calculation of the ephemeris time may be used (e.g., Folkner et al., 2014), but the difference in the resulting ephemeris time is small (less than 0.1 s) and does not significantly impact our model simulation.

We progress the model in time until the diurnal cycle of the stratospheric NO₂ becomes stationary. Throughout the progression, the pressure and temperature profiles are fixed and do not vary with time. The model latitude is set at 34.38^∘ N, and the model day is set as 26 October. The column NO₂ is the vertical integral of the NO₂ concentration. The simulation represents the stratospheric NO₂ abundance in a clean atmosphere without tropospheric sources.

4 Results and discussions

4.1 Diurnal variation in stratospheric column NO₂

Figure 4 presents our preliminary observational data (color dots) obtained from 23–28 October 2018. During the measurements, the skies were mostly clear or only partly cloudy, so we were able to make continuous solar spectral measurements throughout the whole period. During October, the local sunrise and sunset times were around 07:00 and 18:00 PST, respectively. At sunrise and sunset, the ambient twilight in the background of the moonlight occultation should be accounted for in the NO₂ retrieval, which is beyond the scope of this work. For this work, we exclude lunar NO₂ data when the ambient scattered twilight, including that from civil sources, is significant, which typically occurs when the lunar elevation angle is less than 6^∘ above the horizon. Figure 4a shows the daily diurnal cycles during the week of measurements, and Fig. 4b shows the aggregated diurnal cycle as a function of local time. The solid black line in both panels is the simulated 24 h cycle of the stratospheric column NO₂ variability in the 1-D model. The dashed line in Fig. 4b is a second simulation with a slightly lower temperature (see Sect. 3.4). Overall, the baseline simulation captures the observed trends during the daytime and the nighttime. The observations reveal day-to-day variability, but our back-trajectory analysis shows that the day-to-day variations on 23–26 and 28 October are likely due to natural variability of the background in the north while that on 27 October is likely due to urban sources from the Los Angeles Basin in the south (see Sect. 3.5)

On most days, the stratospheric column NO₂ over TMF increased from $\sim \mathrm{2}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² in the morning to $\sim \mathrm{3.5}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² in the evening. There are three main sources of NO_x contributing to the daytime increase. The ultimate source is the reaction of N₂O with excited oxygen O(¹D) resulting from the photolysis of O₃ in the stratosphere between 20–60 km, which produces nitric oxide (NO) molecules and eventually NO₂ through the NO_x cycle aided by O₃:

$$\begin{array}{}\text{(R1)}& {\displaystyle }{\mathrm{N}}_{\mathrm{2}}\mathrm{O}+\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})\to \mathrm{NO}+\mathrm{NO},\text{(R2)}& {\displaystyle }\mathrm{NO}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Another major source is the photolysis of the reservoir species, nitric acid (HNO₃) and dinitrogen pentoxide (N₂O₅):

$$\begin{array}{}\text{(R3)}& {\displaystyle }{\mathrm{HNO}}_{\mathrm{3}}+hv\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{OH},\text{(R4)}& {\displaystyle }{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}+hv\to {\mathrm{NO}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{3}}.\end{array}$$

There is also a small source due to the photolysis of NO₃:

$$\begin{array}{}\text{(R5)}& {\mathrm{NO}}_{\mathrm{3}}+hv\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{O},\end{array}$$

but this source is not significant due to the low NO₃ abundance during daytime. NO₂ is converted back into NO through the reaction with oxygen atoms (O) in the upper stratosphere (above 40 km):

$$\begin{array}{}\text{(R6)}& {\mathrm{NO}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{NO}+{\mathrm{O}}_{\mathrm{2}}\end{array}$$

or via photolysis below 40 km:

$$\begin{array}{}\text{(R7)}& {\mathrm{NO}}_{\mathrm{2}}+hv\to \mathrm{NO}+\mathrm{O}.\end{array}$$

But since NO and NO₂ are quickly interconverted within the NO_x family, Reactions (R6) and (R7) do not contribute to a net loss of NO₂. The ultimate daytime loss of NO₂ is the reaction with the hydroxyl radicals (OH) that forms HNO₃, which may be transported to the troposphere, followed by rainout:

$$\begin{array}{}\text{(R8)}& {\mathrm{NO}}_{\mathrm{2}}+\mathrm{OH}+\mathrm{M}\to {\mathrm{HNO}}_{\mathrm{3}}+\mathrm{M}.\end{array}$$

The significant deviation of daytime NO₂ from the model simulation on 27 October was likely due to urban pollution (see Sect. 3.5).

At sunset, the photolytic destruction (Reaction R7) in the upper stratosphere terminates while the conversion of NO (Reaction R2) continues in the lower stratosphere. Meanwhile, the production of O is significantly reduced, which also reduces the loss of NO₂ via Reaction (R6). As a result, the stratospheric column NO₂ increases by a factor of ∼3 at sunset.

Next, the stratospheric column NO₂ decreases from $\sim \mathrm{6.5}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² after sunset to $\sim \mathrm{4.5}\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² before sunrise. During nighttime, NO₂ is converted to N₂O₅ via the reaction with O₃ and NO₃:

$$\begin{array}{}\text{(R9)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{NO}}_{\mathrm{3}}+{\mathrm{O}}_{\mathrm{2}},\text{(R10)}& {\displaystyle }{\mathrm{NO}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{3}}+\mathrm{M}\to {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}+\mathrm{M}.\end{array}$$

Most N₂O₅ stays throughout the night, although there is a small portion that thermally dissociates back to NO₂ and NO₃. Thus, the net effect is a secular decrease in nighttime NO₂.

Finally, at sunrise, photolytic reactions resume, resulting in an abrupt decrease in the total NO₂ column by a factor of ∼2 due to Reactions (R6) and (R7).

4.2 Vertical profile of NO₂ production and loss

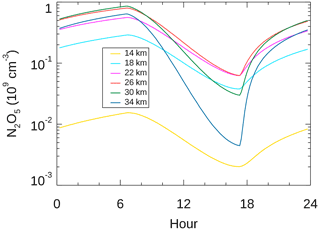
To better understand the contributing factors of the variability of stratospheric column NO₂, we show the simulated vertical NO₂ profile in Fig. 5. The NO₂ concentration is dominant between 20 and 40 km (Fig. 5a). At noontime, the model NO₂ profile has a peak of $\sim \mathrm{1.7}\times {\mathrm{10}}^{\mathrm{9}}$ molecules cm⁻³ at 30 km (Fig. 5a, orange line). At midnight, the NO₂ concentration is much higher throughout the stratosphere. The corresponding peak has a larger value of $\sim \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{9}}$ molecules cm⁻³ and is shifted slightly upward to 32 km (Fig. 5a, green line). Therefore, the stratospheric column NO₂ is dominated by the variability near 30 km.

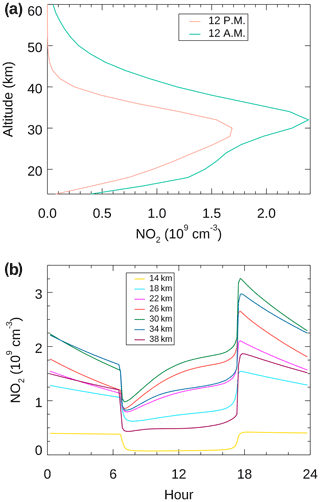
Figure 5 Simulated vertical NO₂ concentration. (a) The simulated NO₂ vertical concentration between 14–38 km at 00:00 PST (green) and 12:00 PST (orange) corresponding to 27 October in the 1-D photochemical model. (b) Same as (a) except the simulated NO₂ variation over the 24 h at selected altitudes.

The diurnal cycles of the NO₂ concentration at altitudes between 14 and 38 km are shown in Fig. 5b. These cycles show that the daytime increase and the nighttime decrease occur only in the lower stratosphere between 18 and 34 km. At other altitudes, the daytime and nighttime NO₂ concentrations are relatively constant. The NO₂ cycles closely resemble those of N₂O₅. Figure 6 shows the N₂O₅ concentrations between 14 and 34 km. During daytime, N₂O₅ is photolyzed into NO₂ and NO₃ through Reaction (R4), leading to an increase in the daytime NO₂; during nighttime, NO₂ is thermally converted into N₂O₅ through Reactions (R9) and (R10), leading to a decrease in the nighttime NO₂. Figure 6 shows that the conversion between the reservoir and NO₂ dominates between 18 and 34 km, consistent with the NO₂ diurnal cycles. In particular, the quadratic decreasing trend of the daytime N₂O₅ is consistent with the quadratic increasing trend of the daytime NO₂. Therefore, the secular NO₂ changes during daytime and nighttime are dominated by N₂O₅ conversions.

Figure 6 Same as Fig. 5b except for N₂O₅.

4.3 Daytime NO₂ increasing rate

Reactions (R1)–(R5) contribute the daytime increase in NO₂. Sussmann et al. (2005) first obtained a daytime NO₂ increasing rate from ground-based measurements. They reported an annually averaged value of $(\mathrm{1.02}\pm \mathrm{0.06})\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻² h⁻¹ over Zugspitze, Germany (2.96 km, 47^∘ N). For October alone, they obtained a value of $(\mathrm{1.20}\pm \mathrm{0.57})\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻² h⁻¹. For comparison, we calculate the daytime increasing rate using our data between 07:00 and 16:00 PST. To obtain a rate corresponding to a clean atmosphere, we define a baseline of the diurnal cycle using the 10th percentile in the 30 min bins from 07:00 to 16:00 (Fig. 7). This results in a total of 19 bins, which is about half of the number of points in October shown in Fig. 4a of Sussmann et al. (2005). We then apply the linear regression to the baseline and obtain an increasing rate of $(\mathrm{1.34}\pm \mathrm{0.24})\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻² h⁻¹ in October over TMF (34.4^∘ N). Thus our value is consistent with the value of Sussmann et al. (2005).

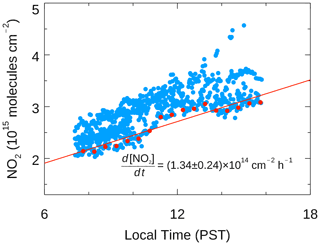
Figure 7 The daytime NO₂ increase obtained from the baseline of the observed diurnal variability. The blue points are the same as the daytime data shown in Fig. 4. The red points are the 10th percentile of the daytime data in 30 min intervals between 07:00 and 16:00 PST, which form a baseline of the daytime variability. The daytime NO₂ increase rate, obtained from the linear regression of the red points, is $(\mathrm{1.34}\pm \mathrm{0.24})\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻² h⁻¹.

4.4 Temperature sensitivity

While the 1-D model simulation captures most of the observed diurnal variability, the rate of decrease in NO₂ during nighttime is slightly overestimated in the model. Here we explore a possible uncertainty due to the prescribed temperature profile.

The chemical kinetic rates in the model are dependent on temperature. The temperature profile that has been used to obtain the baseline diurnal cycle corresponds to a zonal mean temperature profile at the equinox and 30^∘ latitude (Fig. 8, solid line). To test the sensitivity of the simulated 24 h cycle of NO₂, we reduce the input temperature below 60 km by 5 K (Fig. 8, dashed line). Note that the 5 K reduction is much larger than the observed tidal variation in stratospheric temperature below 50^∘ latitude, which is  0.1 K in the lower stratosphere and 1 K in the middle stratosphere (Sakazaki et al., 2012). We choose this exaggerated reduction in order to clearly show the temperature effect on the NO₂ chemistry.

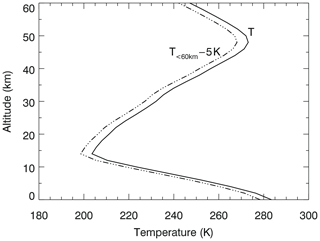
Figure 8 The temperature profiles used in the 1-D Caltech/JPL photochemical model: the baseline profile (solid line) based on the equinox zonal average at 30^∘ latitude and the modified profile where the temperature below 60 km is reduced by 5 K (dashed–dotted line).

Figure 4b (dashed–dotted line) shows the simulated stratospheric NO₂ column using the reduced temperature profile. Because of the reduction in temperature, the nighttime loss due to the reactions with O₃ and NO₃ through Reactions (R9) and (R10) is slower. As a result, the simulated nighttime NO₂ is higher than the baseline simulation, but the rate of decrease agrees better with the observations. On the other hand, due to the less efficient reaction NO+O₃, the simulated daytime NO₂ is slightly lower than the baseline simulation, but it still agrees with the daytime observation. Thus, while the equinox temperature profile used in the baseline run is sufficient for the simulation of the NO₂ diurnal cycle, we do not exclude possible effects of temperature uncertainties on the nighttime simulation.

4.5 Back-trajectories

Since the TMF is located at the top of a mountain in a remote area, high values of NO₂ measured on 27 October 2018 were likely due to atmospheric transport of urban pollutants from nearby cities, especially the Los Angeles megacity. While chemical processes would quantitatively alter the amount of NO₂ to be observed over TMF, a back-trajectory study suffices to provide evidence on how the urban pollutants may be transported to TMF.

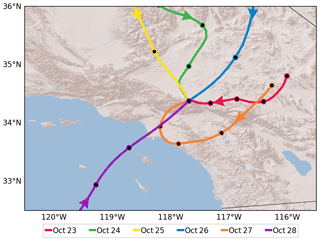
Figure 9 The 24 h back-trajectories of ambient air flow that reached TMF at 15:00 PST on each day from 23 to 28 October 2018. The color codes are the same as those used in Fig. 4. The black dots represent the 6 h intervals on the trajectories.

Figure 9 shows the 24 h back-trajectories that eventually reached TMF (2.286 km above sea level) at 15:00 PST during the observational period. These back-trajectories are calculated using the National Oceanic and Atmospheric Administration (NOAA) Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) model (Stein et al., 2015). We use wind fields from the National Centers for Environmental Prediction (NCEP) North American Mesoscale (NAM) assimilation at a horizontal resolution of 12 km. To illustrate the wind speed, we plot the 6 h intervals using the black dots on the trajectories.

The trajectories on 4 of the 6 d (23–26 October) during the observational period converged towards TMF from inland in the north and the east. These inland areas are behind the San Gabriel and San Bernardino mountain ranges and are shielded from the urbanized Los Angeles Basin. Therefore, the stratospheric column NO₂ measured over TMF on these days closely follows the clean atmosphere simulated by the 1-D model. The trajectories on the other 2 d (27–28 October) converged towards TMF from the Los Angeles Basin in the southwest. But these two trajectories were very different. The back-trajectory of 27 October (Fig. 9, orange) started going southwestward from the Mojave Desert north of the San Bernardino Mountains at the 24 h point and passed across the Riverside Basin between the Santa Ana Mountains and San Jacinto Mountains at 18 h point. The Riverside Basin is one of the most polluted areas in the United States. Then the trajectory continued southwest to pass across Orange County at the 12 h point before it turned northwestward towards downtown Los Angeles at the 6 h point. Finally, the trajectory turned northeastward and reached TMF. The wind speed over the Los Angeles Basin on 27 October was slower than that on other days, favoring more accumulation of pollutants over the basin. Thus, the 24 h back-trajectory on 27 October transported the pollutants in the Riverside Basin and the Los Angeles Basin, resulting in a significant surplus of NO₂ in the TMF observation as seen in Fig. 4. In contrast, the trajectory on 28 October (Fig. 9, purple) came directly from the Pacific Ocean at a relatively high speed, spending only ∼4 h in the Los Angeles Basin before reaching TMF. However, our measurement on 28 October stopped at noon due to a change in instruments, and we are unable to verify whether the urban source would elevate the total column NO₂ in that evening.

5 Summary

We have presented the diurnal measurements of stratospheric column NO₂ that have been made over the TMF located in Wrightwood, California (2.286 km, 34.38^∘ N, 117.68^∘ W), from 23 to 28 October 2018. The instrument measures the differential slant column NO₂ relative to a reference spectrum at noontime. To retrieve stratospheric column NO₂ in the reference spectrum, we applied a variant of the Langley extrapolation. The conventional Langley extrapolation assumes a constant column throughout the day, which does not hold for NO₂. To properly consider the time dependence of NO₂, we combine two methods independently developed by Lee et al. (1994) and Herman et al. (2009). The combined method, called the modified minimum-amount Langley extrapolation (MMLE), first obtains a baseline of the observed diurnal cycle, which is assumed to be the diurnal cycle in a clean atmosphere. Then the baseline is fitted against the modeled diurnal cycle in a 1-D photochemical model so that the stratospheric column NO₂ in the reference spectrum is given by the y intercept of the fitted line.

The measured 24 h cycle of the TMF stratospheric column NO₂ on clean days agrees well with a 1-D photochemical model calculation. Our model simulation suggests that the observed monotonic increase in daytime NO₂ is primarily due to the photodissociation of N₂O₅ in the reservoir. From our measurements, we obtained a daytime NO₂ increasing rate of $(\mathrm{1.31}\pm \mathrm{0.41})\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻² h⁻¹, which is consistent with the value observed by Sussmann et al. (2005), who reported a daytime NO₂ increasing rate of $(\mathrm{1.20}\pm \mathrm{0.57})\times {\mathrm{10}}^{\mathrm{14}}$ over Zugspitze, Germany (2.96 km, 47^∘ N). Our model also suggests that during nighttime, the monotonic decrease in NO₂ is primarily due to the production of N₂O₅. Furthermore, the abrupt NO₂ decrease and increase at sunrise and subset, respectively, are due to the activation and deactivation of the NO₂ photodissociation.

The observed NO₂ in the afternoon on 27 October 2018 was much higher than the model simulation. We conducted a 24 h HYSPLIT back-trajectory analysis to study how urban pollutants were transported from the Los Angeles Basin. The back-trajectories on 4 of the 6 d during the measurement period went directly from inland desert areas to the TMF. The back-trajectory on another day came from the southwest coastline, spending less than 6 h over the Los Angeles Basin before reaching the TMF. Lastly, the 24 h back-trajectory on 27 October 2018 was characterized by a unique slow wind that came from inland in the northeast and spent more than 18 h in the Los Angeles Basin, picking up pollutants from Riverside, Orange County, and finally downtown Los Angeles before reaching TMF.

Appendix A: Comparison of the modified MLE (MMLE) with the standard MLE

The MMLE is used to account for the diurnal asymmetry of the stratospheric NO₂ column before the Langley extrapolation is applied. To illustrate the necessity of the removal of the diurnal asymmetry, consider a single day of observed stratospheric column NO₂. Figure A1a plots the observations on 25 October 2018 against the air mass factor (AMF=secθ) as in a standard MLE. Based on our back-trajectory analysis, the atmosphere above TMF on 25 October 2018 should have little urban NO₂ contamination. Both solar (pale orange dots) and lunar (pale blue dots) data exhibit U shapes, which is due to the secular increase and decrease during the daytime and the nighttime, respectively. For the solar data, the AM data lie on the lower arm of the U shape, and the PM data lie on the upper arm. For the lunar data, the reverse is true: data before sunrise lie on the upper arm of the U shape and data after sunset lie on the lower arm.

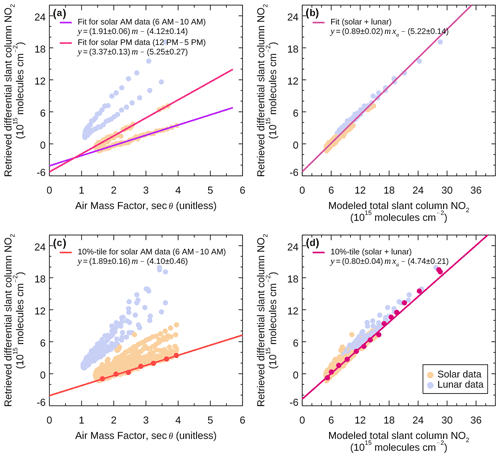
Figure A1 Comparison of the standard MLE (a, c) and the modified MLE (MMLE) (b, d) introduced in this work for single-day (a, b) and multiple-day data (c, d). Panel (d) is the same as Fig. 3 except for the separation of the daytime and nighttime data.

To perform a Langley extrapolation for the data shown in Fig. A1a, one needs to decide which of the four arms to be used for the linear regression model $y=a\mathrm{AMF}+b$. The principle of minimum amount suggests that we should start with the lowest arm, i.e., the daytime AM data. Note that in order to obtain the straight line passing through the 10th percentile baseline, we have ignored the points before noon (around 10:00 to 11:30 PST), i.e., points located around the bottom of the U shape. If we use the observations between 06:00 and 10:00 PST, we obtain the purple line in Fig. A1a, which gives a y intercept of $(-\mathrm{4.12}\pm \mathrm{0.14})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻².

The above Langley extrapolation, however, does not take any of the daytime PM and all lunar data into account. In particular, the daytime PM data should also be used to define a minimum-amount profile, given the fact that the atmosphere was mostly clean on that day. Suppose we perform another Langley extrapolation using the daytime PM data between 12:00 and 17:00 PST (rose line). The resultant y intercept is $(-\mathrm{5.25}\pm \mathrm{0.27})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻² (2σ), which is statistically different from the value obtained using the daytime AM data. A reasonable estimate of the y intercept is then the average of the two values, which is $(-\mathrm{4.69}\pm \mathrm{0.21})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻².

Finally, since the wind on the TMF is mostly downhill during autumn, the lunar data also correspond to a clean atmosphere and should also be used to derive the y intercept. If we use all four arms in Fig. A1a, then the average value of the y intercept is $(-\mathrm{4.36}\pm \mathrm{0.25})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻², where the uncertainty is the root mean square of the uncertainties of the four values.

In the above calculation, the ignorance of the data points near the bottom of the U shape has excluded a large number of observations near local solar and lunar noon, and thus the resultant y intercept is biased by high zenith angles. It is not clear how the data near the solar and lunar noon may be kept in the standard MLE due to the assumption of the linearity in AMF. As a result, a zenith angle-dependent Langley extrapolation model needs to be developed.

The above example shows that the determination of the y intercept of the standard MLE is not straightforward when (i) the background NO₂ has secular trends in daytime and nighttime and (ii) the daytime and nighttime abundances are different before and after the terminator. In contrast, the MMLE approach we have developed in this work minimizes the background diurnal asymmetry, so that the “regularized” data points almost form a straight line (Fig. A1b) when they are plotted against the modeled diurnal cycle. The linear regression model $y=am{x}_{\mathrm{a}}+b$, where m x_a is the modeled slant column NO₂, can be applied to all data points, regardless of the time of the day or whether the data point is a solar or lunar measurement. With this modified MLE, the regressed y intercept is $(-\mathrm{5.22}\pm \mathrm{0.14})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻², which is statistically different from the average of the values derived from the four arms in the standard MLE approach.

The issue with the standard MLE is exacerbated when observations on multiple days are plotted against the AMF. The U shape may be smeared vertically into a continuum (Fig. A1c). The smearing, in our case, is primarily due to natural variability of the background, except for 27 October when the observed NO₂ appears above the continuum of the daytime data due to the urban pollution. As a result, while we are still able to define the minimum-amount profile (10th percentile) for the daytime AM data, the determination of the minimum-amount profiles of the daytime PM and the lunar data is difficult. This leaves us the daytime AM data alone for the Langley extrapolation (red line), but, as shown above, the resultant y intercept ($(-\mathrm{4.10}\pm \mathrm{0.46})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻²) may be biased.

In contrast, the observed data points still almost form a straight line in the MMLE approach when they are plotted against the modeled diurnal cycle (Fig. A1d). This allows the determination of the minimum-amount profile using all solar and lunar measurements (raspberry line). With the weighted Langley extrapolation described in Sect. 2.3, the resultant y intercept, $(-\mathrm{4.74}\pm \mathrm{0.21})\times {\mathrm{10}}^{\mathrm{15}}$ molecules cm⁻², is again statistically different from the one obtained using the standard MLE approach.

Appendix B: Effects of spherical geometry in the 1-D model

The diurnal cycle simulated in the 1-D model (Fig. 3) is calculated assuming a plane-parallel atmosphere, where the times of the sunrise and the sunset do not depend on altitude. For a more realistic simulation, we have conducted another calculation using the spherical geometry, so that the terminator chemistry is dependent on altitude. Figure B1 compares the simulated diurnal cycles in a plane-parallel atmosphere and in a spherical atmosphere. The difference between the two diurnal cycles is the largest in the evening, but it is much smaller than the spread of the observations due to the natural variability. Therefore, the simulation with a plane-parallel atmosphere is adequate to provide a theoretical diurnal cycle for the modified Langley extrapolation.

Figure B1 Comparison of the simulated diurnal cycles of the stratospheric column NO₂ in a plane-parallel atmosphere and a spherical atmosphere. The data points are the same as in Fig. 4b.