Wind speed and direction estimation from wave spectra using deep learning

High-frequency parts of ocean wave spectra are strongly coupled to the local wind. Measurements of ocean wave spectra can be used to estimate sea surface winds. In this study, two deep neural networks (DNNs) were used to estimate the wind speed and direction from the first five Fourier coefficients from buoys. The DNNs were trained by wind and wave measurements from more than 100 meteorological buoys during 2014–2018. It is found that the wave measurements can best represent the wind information about 40 min previously because the high-frequency portion of the wave spectrum integrates preceding wind conditions. The overall root-mean-square error (RMSE) of estimated wind speed is ∼1.1 m s⁻¹, and the RMSE of the wind direction is ∼ 14^∘ when wind speed is 7–25 m s⁻¹. This model can be used not only for the wind estimation for compact wave buoys but also for the quality control of wind and wave measurements from meteorological buoys.

1 Introduction

Sea surface wind and waves are important parameters for the marine environment and ocean dynamics. High-quality simultaneous measurements of sea surface wind and wave information are helpful for the study of many oceanic and coastal phenomena. Such simultaneous measurements can be obtained from meteorological buoys and remote sensing satellites. Many meteorological buoys can provide comprehensive wind and wave information, such as surface wind speeds, wind directions, and wave spectra, with high accuracy. However, the deployment and maintenance of these buoys and platforms usually have relatively high costs. Therefore, meteorological buoys are very sparsely distributed and are mostly only available along the coastlines of developed countries.

The Earth observation satellite network, such as scatterometers, altimeters, and synthetic aperture radars, can serve as effective complements for the buoy network. Meanwhile, these remote sensors also have some limitations. Scatterometers can retrieve both wind speed and wind direction with a wide swath and the best overall accuracy, but wave information is not available from them. Besides, their temporal resolutions (usually one or two revisits per day except for polar regions) are still much lower than those of in situ measurements. Altimeters can simultaneously measure wind speed and significant wave height (SWH), but wind directions and other wave parameters are not available from them. Besides, the cross-track spatial coverage and temporal resolution of an altimeter are low because they can only measure the nadir. Synthetic aperture radars' wave mode can provide wind speed, wind direction, SWH, and low-frequency wave spectra (high frequency is not available due to nonlinear imaging), but the accuracy of wind speed, wind direction, and SWH is usually not as good as that from scatterometers and altimeters, and they are also limited by the sparse sampling. Moreover, spaceborne remote sensors often perform worse in nearshore regions than in the open ocean due to the land contamination of backscatter.

Another important data source for collocated winds and waves is compact wave buoys. These types of buoys are usually low-cost and are suited for deployment in large numbers, and they perform better in measuring waves compared to large meteorological buoys because their small sizes have a more sensitive response to short waves (Voermans et al., 2020). Although wave buoys are not designed for wind observation, Voermans et al. (2020) have shown that both wind speed and wind direction can be estimated from the wave spectra using an f−4 spectral dependence in the equilibrium range. Their model can estimate wind speed with a root-mean-square error (RMSE) of 2 m s⁻¹ and wind directions with an RMSE of ∼20^∘ when wind speed is higher than 10 m s⁻¹. Although this model has good theoretical support, its accuracy is lower than typical remote sensing retrievals. For example, altimeter-retrieved wind speed has a typical overall RMSE of 1.2–1.5 m s⁻¹ (e.g., Jiang et al., 2020) and scatterometer-retrieved wind speed and wind directions have a typical overall RMSE of ∼1 m s⁻¹ and 15^∘ (e.g., Wang et al., 2021) when using buoys' anemometer data as the reference.

Compact wave buoys are increasingly widely used in global wave observations. For example, more than 2000 Spotter buoys have been deployed in global oceans by Sofar Ocean Technologies (the location of these buoys can be viewed at https://weather.sofarocean.com/, last access: 22 December 2021) to improve the performance of their wave modeling (Smit et al., 2021). Although the data are not open to the public, more accurate wind estimation from wave spectra can definitely benefit users of such buoys. Voermans et al. (2020) have shown the possibility of estimating wind speed and wind direction with wave measurements alone. This study aims to improve the accuracy of such estimation as much as possible. A model based on a deep neural network (DNN) is presented to achieve this goal. The rest of this paper is organized as follows: the simultaneous observations of wind and waves to train the DNN model are introduced in Sect. 2, along with the structure and training method of the DNN. The main results are presented in Sect. 3. A brief discussion about the selection of the DNN input terms is given in Sect. 4, followed by the concluding remarks in Sect. 5.

2 Data and methods

2.1 Collocated wind and wave data

Many buoys from the National Data Buoy Center (NDBC) coastal marine automated network can provide quality-controlled in situ wave and wind measurements. The data used in this study are the NDBC buoy data archived in National Centers for Environmental Information where the data are available in NetCDF form. After removing the data records with bad-quality flags, more than 1.6 million records from 101 buoys in coastal and oceanic regions during 2014–2018 were used in this study (Fig. 1). Most buoys' anemometers are 4–5 m from the sea surface, and winds are measured every 10 min with a sampling time of 8 min and accuracy within 1 m s⁻¹ and 10^∘ for wind speed and direction, respectively, in a moderate sea state (in extreme sea states, the swing and tilting of the buoy can introduce larger errors). The wind speed was converted to the standard height of 10 m (U₁₀) using the power law (Hsu et al., 1994) that was also used in Voermans et al. (2020). This conversion was also tried using the log profile (Young et al., 1995), which has almost no impact on the results. The waves are measured every 1 h with a sampling time of 20 min. The buoy wave data include five Fourier coefficients of waves for different frequencies in the range of 0.02–0.485 Hz (47 frequency bins) derived from the translational or pitch–roll information from the accelerometers and inclinometers on board buoys (Steele et al., 1998). The five Fourier coefficients are wave variance spectral densities (E) which describe the wave energy for each frequency, mean and principal wave directions for each frequency (α₁ and α₂), and first and second normalized polar coordinates of Fourier coefficients (r₁ and r₂) which describe the directional spreading about the main direction for each frequency. The five Fourier coefficients of different frequencies are the minimum requirement to reconstruct the directional wave spectrum. These NDBC data, especially the offshore data, are widely used in the validation of wind and wave remote sensing and numerical weather and wave models (e.g., Jiang et al., 2016; Jiang, 2020; Wang et al., 2021). The wave data and the wind data were collocated if their ends of sampling time were within 10 min (the sampling duration is ∼20 min for wave measurements and ∼10 min for wind measurement).

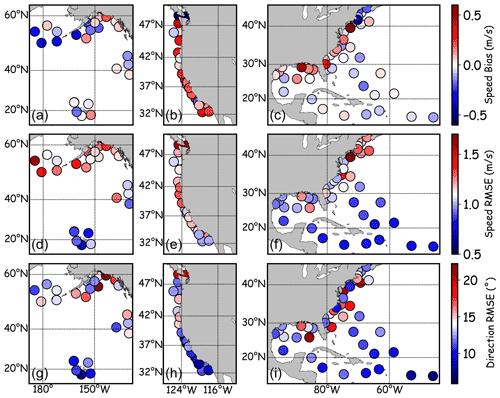
Figure 1 The bias (a, b, c) and RMSE (d, e, f) of DNN-estimated wind speed and RMSE of DNN-estimated wind direction (when wind speed is higher than 7 m s⁻¹, g, h, i) for the individual NDBC buoys in the North Pacific (a, d, g), the west coast of the United States (b, e, h), and the Atlantic region (c, f, i). The overall RMSEs of wind speed and wind direction (when wind speed is higher than 7 m s⁻¹) are ∼ 1.1 m s⁻¹ and ∼ 14^∘, respectively, for the complete validation data set. Therefore, blue and red colors in RMSE maps indicate below and above the overall RMSE, respectively.

2.2 DNN models for estimating wind speed and direction

As a nonparametric model, a DNN can theoretically be used to fit any form of function with any number of input parameters provided the network is wide and deep enough. The DNN has been proved to be effective for regression problems with more than two input parameters and is widely used in the training of retrieval models and correction models in studies of ocean remote sensing (e.g., Wang et al., 2020; Jiang et al., 2020). A DNN is a useful tool for the problem that there are causal relationships between inputs and outputs (in this study, wave spectra and winds, respectively), but the explicit form of the relationship is not known. In this study, two DNNs were established with the same structure, one for estimating wind speed and one for wind directions. In the beginning, the input layer of the DNN, which simply contains 235 (vectorization of 5 Fourier coefficients × 47 frequency bins) neurons, was set up in a “violent” way. However, we will show in Sect. 4 that the input layer of the DNNs can be refined after obtaining the basic knowledge of how these models work. Each of the 235 inputs was normalized to have zero mean and unit variance. The DNNs have two hidden layers with 64 neurons followed by an output layer with one term (wind speed or direction). The activation function is the rectified linear unit (ReLU). It was tested that adding hidden layers and hidden neurons does not improve the performance of these models. The 1.7 million buoy records were randomly divided into training (50 %) and validation (50 %) sets. The DNN for U₁₀ was trained to minimize the RMSE between the target (buoy-measured) and output U₁₀:

$$\begin{array}{}\text{(1)}& {\text{Loss}}_{U_{\mathrm{10}}}=\text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{\left(y_i-x_i\right)}^{\mathrm{2}}},\end{array}$$

where y and x denote the output and target/reference parameters, respectively. The DNN for wind directions was trained to minimize the distance between target and output unit vector corresponding to the wind direction:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& {\mathrm{Loss}}_{\mathrm{Dir}}=\\ & \sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n\left[{\left(\sin \left(y_i\right)-\sin \left(x_i\right)\right)}^{\mathrm{2}}+{\left(\cos \left(y_i\right)-\cos \left(x_i\right)\right)}^{\mathrm{2}}\right]}.\end{array}\end{array}$$

For both DNNs, the training used the Adam optimizer with a batch size of 2048. The learning rate (initially set to 0.004) was decreased by 50 % if the loss of the training set did not decrease for two epochs, and the training process stopped when the RMSE of the validation set did not decrease for six epochs. The DNN was realized by PyTorch. Besides RMSE, the bias, standard deviation (SD), and correlation coefficient (CC) were also selected as the error metrics to evaluate the model performance:

$$\begin{array}{ll}\text{(3)}& {\displaystyle }& {\displaystyle }\text{Bias}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n(y_i-x_i),\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{SD}=\sqrt{{\mathrm{RMSE}}^{\mathrm{2}}-{\mathrm{Bias}}^{\mathrm{2}}},{\displaystyle }& {\displaystyle }\mathrm{CC}=\sum _{i=\mathrm{1}}^n(y_i-\overline{y})(x_i-\overline{x})/\\ \text{(5)}& {\displaystyle }& {\displaystyle }\left[\sqrt{\sum _{i=\mathrm{1}}^n(y_i-\overline{y}{)}^{\mathrm{2}}}\sqrt{\sum _{i=\mathrm{1}}^n(x_i-\overline{x}{)}^{\mathrm{2}}}\right].\end{array}$$

3 Results

The comparison between the collocated DNN-estimated and directly measured U₁₀ for the validation data set is shown as a scatterplot in Fig. 2a, and the corresponding comparison for wind directions is shown in Fig. 2d. These results suggest that estimating wind speed and direction from wave spectra using such a simple DNN works reasonably well. For wind speed, the DNN can give an estimation with an overall RMSE of ∼ 1.3 m s⁻¹ and a small overall bias. For wind direction, the RMSE is ∼ 16^∘ for U₁₀ > 7 m s⁻¹. These results show significant improvement compared to the error metrics of Voermans et al. (2020).

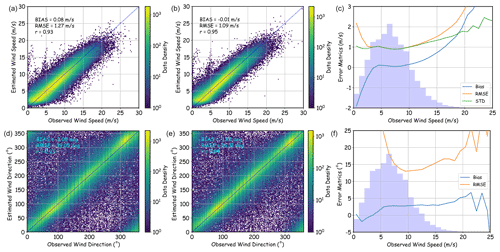
Figure 2 (a–c) Comparison between wind speeds measured by buoys and those estimated by wave spectra. (a) Scatterplot of collocated DNN-estimated wind speed and directly measured wind speed. (b) The same as (a), but the spectra were used to estimate the wind speed 40 min previously. (c) The bias, SD, and RMSE of the DNN-estimated wind speed 1 h previously as a function of directly measured wind speed. The blue shading indicates the empirical distribution function of directly measured wind speed. (d–f) The same as (a–c) but for wind directions.

It is noted that the sampling duration is ∼ 20 min for wave measurements and ∼ 10 min for wind measurement. Differently from the capillary waves with very high frequencies always in instant equilibrium with the local wind, the growth of gravity waves is time-dependent. Besides the current wind information, the wave spectrum measured by a buoy at a given location and time also contains remote and past wind information (Jiang and Mu 2019) because the wave spectrum is, to some degree, integrated winds. Therefore, it is possible that the buoy wave spectrum can better represent the local wind information some time ago. Based on this idea, the wave spectra were also collocated with past wind measurements using different time lags. For the collocations of each time lag, DNNs were re-trained to estimate the corresponding wind speed and directions and the error metrics were re-computed. The error metrics as a function of time lag are shown in Fig. 3. The results indicate that the DNN performs significantly better in estimating wind information from a short period ago than the current wind information. The best error metrics for wind speed and wind direction were found at 40–50 and 40–60 min before the end of wave sampling time, respectively. Voermans et al. (2020) found that the wind acceleration is related to model error residuals, which is consistent with the results here.

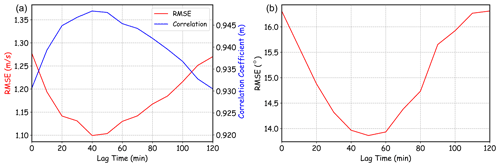
Figure 3 (a) The RMSE and CC of the DNN-estimated wind speed as a function of lag time between wave and wind measurements (waves' end sampling time minus winds' end sampling time). (b) The RMSE of DNN-estimated wind direction as a function of lag time between wave and wind measurements for wind speed higher than 7 m s⁻¹.

Obtaining wind information with only a 40 min delay (near real time) is acceptable for most scientific and operational applications. Therefore, the DNNs for wind of a 40 min delay were used in the following analysis. The results of wind speed and direction in the validation data set are shown in Fig. 2b and e, respectively. The corresponding error metrics as a function of directly measured U₁₀ are shown in Fig. 2c and 2f. The overall RMSE for U₁₀ is ∼ 1.1 m s⁻¹ and is only ∼ 1 m s⁻¹ for U₁₀ between 2 and 10 m s⁻¹, where the sample size is relatively large. The DNN model tends to overestimate the U₁₀ when it is lower than 2 m s⁻¹, and the DNN model seldom gives an output of U₁₀ of less than 1 m s⁻¹. These are probably because the NDBC buoys do not respond well to the small waves generated by very low wind while the geophysical noises such as ocean currents have a large impact on the wind estimation during low wind speed. Meanwhile, it is noted that other indirect methods for wind speed estimation, such as remote sensing, also always overestimate low wind speed (e.g., Stopa et al., 2017; Jiang et al., 2020). Both the bias and SD increase with the U₁₀ when U₁₀ > 10 m s⁻¹. This is partly because the distribution of wind speed is not uniform and the error in DNN is often larger for the less sampled conditions. Although the DNN model tends to underestimate high wind speed, the relative RMSE remains less than 14 % for U₁₀ < 20 m s⁻¹ and the accuracy is also improved for high U₁₀ compared to Voermans et al. (2020). For U₁₀ > 20 m s⁻¹, the bias becomes higher than the SD, which means the systematic error becomes the main contributor to the RMSE. This is not surprising because the air–sea interaction becomes much more complicated during extreme wind, and it is also noted that the U₁₀ extrapolated from the wind speed measured at 4–5 m might be overestimated to some extent in extreme sea states because the anemometers might be within the wave boundary layer (Babanin et al., 2018). The overall RMSEs of U₁₀ retrieved from spaceborne altimeters and scatterometers using corresponding state-of-the-art combinations of sensors and algorithms are ∼ 1.2 and ∼ 1.0 m s⁻¹, respectively, compared to buoy measurements (Jiang et al., 2020; Wang et al., 2021). According to the RMSE, the accuracy of the DNN-estimated U₁₀ is higher than altimeter U₁₀ retrievals, and it is similar to scatterometer U₁₀ retrievals if the data of U₁₀ < 2 m s⁻¹ are excluded.

For wind directions, the RMSE is larger than 25^∘ when U₁₀ < 5 m s⁻¹ but decreases fast with the increase in U₁₀. The RMSE becomes less than 20, 15, and 13^∘ for U₁₀ values of 6, 8, 10 m s⁻¹, respectively. Beyond U₁₀ = 10 m s⁻¹, the RMSE of DNN-estimated wind directions slightly increases with the increase in U₁₀ but remains < 20^∘ until U₁₀ > 21 m s⁻¹. It is noted that there were less than 100 samples for U₁₀ > 21 m s⁻¹, and most of them correspond to some strong cyclones where the directions of the wind vary rapidly. Following Voermans et al. (2020), if only the condition of U₁₀ > 7 m s⁻¹ was considered, the overall RMSE of the DNN-estimated wind directions was only ∼ 14^∘. To test the robustness of the DNN framework, we tried the random division, training, and validation processes more than 20 times, and the resulting error metrics in the validation data set stayed stable, meaning that there was no change in the first two significant digits of RMSEs of both U₁₀ (1.1 m s⁻¹) and wind directions (14^∘). Wind direction information is also available from spaceborne scatterometers, and the RMSE of wind directions between scatterometers (e.g., ASCAT-B and ASCAT-C, OSCAT2, HSCAT-B) and buoys is 15–18^∘ according to Wang et al. (2021). Therefore, the performance of the DNN model is also as good as state-of-the-art scatterometers with respect to wind directions for U₁₀ > 7 m s⁻¹.

The error metrics of the DNN-estimated wind information (with a time lag of 40 min) for different buoy locations are shown in Fig. 1. The error metrics vary with buoy locations. The distribution of U₁₀ RMSE for individual buoys is similar to that of Voermans et al. (2020), but the RMSE values are much lower here. For most buoys in the open oceans to the south of 40^∘ N, the RMSEs of DNN-estimated U₁₀ and wind directions (for U₁₀ > 7 m s⁻¹) are less than 1.0 m s⁻¹ and 10^∘, respectively. Two buoys are found to have a U₁₀ RMSE larger than 2 m s⁻¹: Station 44066 (2.1 m s⁻¹) at ∼ 40^∘ N on the US East Coast and Station 46070 (2.2 m s⁻¹) in the southwest Bering Sea. It is noted that the biases of U₁₀ for the two buoys (44066 and 46070) are also large. After a further check of the time series of measured and estimated U₁₀, it is found that there seems to be an anemometer problem at Station 44066 from 22 January to 13 February 2014 (Fig. 4a). The measured and estimated U₁₀ values have a good agreement before 22 January 2014, but the measured U₁₀ values become significantly lower than the estimated ones after 22 January 2014. After a sudden drop on 26 January 2014, the measured U₁₀ remains lower than 5 m s⁻¹ for more than 15 d, which is unrealistic. A similar condition happened at Station 46070 from 3 March to 20 April 2016 (Fig. 4b), when the estimated U₁₀ suddenly becomes significantly lower than the measured U₁₀. Because the DNN model is unbiased and time-independent, such a systematic underestimation or overestimation of U₁₀ for a long period has to be attributed to the problem of either wind or wave sensor. Therefore, such a DNN-based U₁₀ estimation model can also serve as an additional quality control/monitoring method for wind and wave sensors on meteorological buoys. If the bias between estimated and measured U₁₀ remains significant for a short period (e.g., 3–5 d), the wind and wave data then need to be further checked or discarded. Because the buoy data have been quality controlled by NDBC, such conditions were only identified in the two cases in Fig. 4. If we remove the bad-quality data in Fig. 4, the U₁₀ RMSEs for Station 44066 and 46070 will drop to only 1.10 and 1.25 m s⁻¹, respectively.

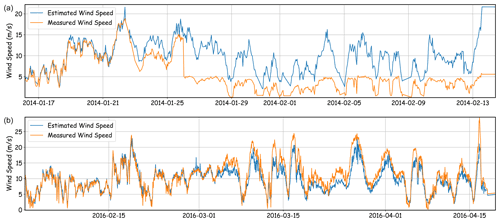
Figure 4 Time-series comparison of directly measured (orange) and DNN-estimate (blue) wind speed for (a) Station 44066 from 16 January to 15 February 2014 and (b) Station 46070 from 1 February to 20 April 2016. For 44066, the measured wind speed values became significantly lower than the DNN-estimated ones after 22 January 2014. For 46070, the DNN-estimated wind speed values became significantly lower than the directly measured ones after 3 March 2016. The date is given in the format year–month–day.

The other two buoys with relatively high U₁₀ RMSEs (> 1.5 m s⁻¹), Station 46087 and 46088, are both at the Strait of Juan de Fuca where tidal currents are strong. First of all, the wind estimated from wave measurements is the wind relative to currents because waves are forced by relative wind. A strong current will make the estimated relative wind deviate from the absolute wind from the anemometer, introducing errors into the DNN model. Secondly, the phase velocity of the high-frequency waves and the current velocity are at the same order of magnitude during strong currents. In this case, the dispersion relation of high-frequency waves is strongly distorted by the currents via Doppler shift. This will lead to different frequency spectra for the same wavenumber spectra, introducing another error source for DNN-estimated wind speed. The surface currents are generally larger in coastal regions (tides) and westerlies (wind drifts) than in low-latitude open oceans, which can explain the spatial distributions of the U₁₀ RMSE and can also partly explain why this model tends to underestimate large winds. Strong drifts along the wind direction will shift the wind-wave energy to lower frequencies.

If the aforementioned problematic data are excluded from the training and validation data set (they are included in the results in Figs. 1–4), the overall performance of the model will not be significantly improved (the overall RMSE will be reduced by only 0.02 m s⁻¹) because the number of samples for these corrupt data is very small compared to the overall sample size. However, the U₁₀ RMSEs will be less than 1.5 m s⁻¹ for all buoys at different locations. This indicates that the geographic dependence of the DNN model's error is weak. To further test the robustness of the DNN model in different locations, the training set, and validation set were divided according to the buoys' locations. The data from buoys 45001–51101 (53 buoys) were selected as the training set and the buoys 41002–44066 (48 buoys) were selected as the validation set. The locations, wind-wave climate, and other environmental properties are significantly different for the two sets because none of the buoys in the validation set is in the same basin as the buoys in the training set. In this case, the established DNN model still has a good performance in the validation set with an RMSE of ∼ 1.15 m s⁻¹ (the result can be seen in the reply to the reviewer in the online discussion).

For wind directions (U₁₀ > 7 m s⁻¹), the lowest RMSE is 7^∘ and $\mathrm{68}/\mathrm{94}/\mathrm{100}$ out of the 101 buoys have RMSEs of less than $\mathrm{14}{}^{\circ }/\mathrm{20}{}^{\circ }/\mathrm{22}{}^{\circ }$, showing the robustness of the DNN model. The spatial distribution of RMSE is similar to that of U₁₀ RMSE (the CC between the RMSEs of U₁₀ and wind directions is 0.51, significant at 99.9 % level) with the lowest value in the open ocean at low latitudes. The only buoy with an RMSE larger than 22^∘ is at Station 46082 (59.68^∘ N, 143.37^∘ W). However, after a further check of the data, a bias of ∼ 25^∘ was found after 22 September 2018 (not shown), indicating there might be something wrong with the data themselves like with the condition shown in Fig. 4. Similar conditions occur at some other buoys with RMSEs > 20^∘ (46001 and 44009). Two aforementioned buoys, 46087 and 46088, that are impacted by currents also have RMSEs > 20^∘. The reason for RMSE > 20^∘ is unknown for the other two buoys, but errors of ∼ 180^∘ sometimes occur at the two buoys, significantly increasing the overall RMSE.

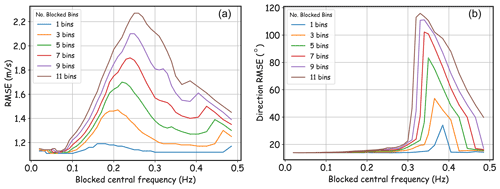
Figure 5 (a) The RMSE between DNN-estimated and directly measured U₁₀ as a function of the blocked central frequency. Different colors indicate the results of blocking different numbers of bins. For example, the orange line indicates that the RMSE of the DNN model is ∼ 1.45 m s⁻¹ (the peak) when the input at 0.2 Hz and its two neighboring bins, 0.19 and 0.21 Hz, are blocked (set to zero after normalization). (b) is the same as (a) but for the RMSE of wind direction.

4 Discussions

The wind information estimated from wave spectra achieves good accuracy, but the DNN model uses all available wave spectral information as the input. Usually, not all input terms are important for the model. Therefore, we tried to refine the DNN model using a sensitivity test. By blocking some of the inputs (setting the values of normalized input to zeros), one can know which input is more important for the DNN model.

Low-frequency waves are usually not coupled to the local wind; thus, the importance of different frequency bins was analyzed. The RMSEs after blocking some frequencies are shown in Fig. 5. For U₁₀, it can be seen that inputs under 0.1 Hz are not important for the model, and blocking only one frequency bin has little impact on the result. However, blocking more bins at high frequencies, especially the bins near 0.2 Hz, has large impacts. For wind directions, it seems the inputs under 0.25 Hz are not important and the inputs near 0.38 Hz play the most important role in the model. Therefore, what the DNN learns from the data is a weighting average of the information from different frequencies. Voermans et al. (2020) also only considered the wave spectra higher than some frequencies in a spectrum, which is consistent with the model here.

The importance of each of the Fourier coefficients was also analyzed. For the U₁₀ (wind direction) DNN, the RMSEs after blocking E, α₁, α₂, r₁, and r₂ are 3.75, 1.17, 1.14, 1.47, and 1.20 m s⁻¹ (17.3, 111.9, 16.2, 14.3, and 14.4^∘, for U₁₀ > 7 m s⁻¹), respectively. This indicates that E and α₁ are the most important parameters for estimating U₁₀ and wind directions, respectively. This is in line with Voermans et al. (2020), where E and α₁ are the only parameters for the estimation of U₁₀ and wind directions, respectively. Meanwhile, r₁ (E and α₂) seems to also play some roles in the estimation of U₁₀ (wind directions). If we re-train the model with only E (α₁), the RMSE in the validation set can only reach 1.26 m s⁻¹ (15.5^∘), slightly worse than the original model. This is probably because r₁ contains the wave-spreading information and the wave spreading at high frequencies is also correlated to the wind speed, which can be used to slightly reduce the random error in the U₁₀ from E only. Similarly, α₂ information can also partially reveal the wave direction at high frequencies, and E is helpful to give the energy weights for each frequency, which in turn are helpful to reduce the random error in estimated wind directions. The above sensitivity test indicates that E and r₁ above 0.1 Hz (α₁, α₂, and E above 0.25 Hz) are the most important inputs for the estimation of U₁₀ (wind directions), which is also in line with Voermans et al. (2020). Previous studies of wind remote sensing showed that the modulation of swells on capillary waves has some impacts on the wind speed retrievals (e.g., Stopa et al., 2017; Li et al., 2018; Jiang et al., 2020). Long swells also modulate short wind seas (waves with relatively high frequencies measured by buoys; they are gravity waves instead of capillary waves). If this modulation process significantly impacts the buoy wind-estimation model, removing the long-swell information will negatively impact the model accuracy. However, according to the results in Fig. 5, the swell's modulation on wind seas has little impact on wind estimation using buoy wave spectra. If we re-train a DNN using only these inputs (33 × 2=66 inputs for U₁₀, and 17 × 3=51 inputs for wind directions) without changing other settings, the performance of the models is nearly the same as the original ones. The RMSEs remain less than 1.15 m s⁻¹ and 14.5^∘ for U₁₀ and wind directions, respectively, in 20 independent experiments.

5 Concluding remarks

Ocean wave spectra can be used to estimate sea surface winds. Here, we trained two DNNs that can estimate U₁₀ and wind directions ∼ 40 min previously from high-frequency wave spectra. The overall accuracy of the wind-estimation DNN models is comparable with the state-of-the-art scatterometers under moderate U₁₀. The two models can also be used as a quality control tool for wind and wave measurements from meteorological buoys.

The DNNs were trained using a large number of data from only NDBC buoys and not compact wave buoys. However, applying the two models directly to compact wave buoy data (after interpolating the spectra from compact buoys into the frequency bins of NDBC buoys) will not result in significantly lower accuracy. This is because the DNN will automatically select the NDBC wave spectra in the frequency with relatively high accuracy, and the accuracy of measured spectra from compact wave buoys is usually higher.

For the wave data from NDBC buoys, the performance of the U₁₀ DNN is significantly biased when U₁₀ is too high or too low, and the performance of the wind direction DNN becomes worse with the decrease in U₁₀. Also, the accuracy of both models decreases when the surface currents are strong. We believe these shortcomings can be partly solved by compact wave drifters, resulting in better accuracy in estimating near-real-time wind properties. First, a smaller buoy size can resolve high-frequency wave spectra more accurately, which is helpful for wind estimation. Second, in the condition of strong wind or currents, the moving velocity of the wave drifter is usually similar to that of the surface current, making the wavenumber and frequency spectra follow a dispersion relation again in the buoy reference system. This can compensate for some of the errors induced by strong surface currents or wind-induced drifts. Therefore, significantly better accuracy can be achieved by training new DNN models with the spectral data (maybe also the drifting velocity data) from compact buoys using collocated wind and wave measurements. Such measurements can be obtained by placing some compact buoys near meteorological buoys or simply using the scatterometer or re-analysis wind as the training target.

Finally, we hope to point out that such DNN models need not be trained from the beginning using a large number of data. The DNN models presented in this paper can serve as pre-trained models which will significantly reduce the complexity of training the new models. With the compact wave buoys becoming increasingly widely used in observing wave parameters, their global network can be a new good-quality data source for both waves and wind after applying these models.