Improved retrieval of SO₂ plume height from TROPOMI using an iterative Covariance-Based Retrieval Algorithm

Knowledge of sulfur dioxide layer height (SO₂ LH) is important to understand volcanic eruption processes, the climate impact of SO₂ emissions and to mitigate volcanic risk for civil aviation. However, the estimation of SO₂ LH from ground-based instruments is challenging in particular for rapidly evolving and sustained eruptions. Satellite wide-swath nadir observations have the advantage to cover large-scale plumes and the potential to provide key information on SO₂ LH. In the ultraviolet, SO₂ LH retrievals leverage the fact that, for large SO₂ columns, the light path and its associated air mass factor (AMF) depends on the SO₂ absorption (and therefore on the vertical distribution of SO₂), and SO₂ LH information can be obtained from the analysis of measured back-scattered radiances coupled with radiative transfer simulations. However, existing algorithms are mainly sensitive to SO₂ LH for SO₂ vertical columns of at least 20 DU. Here we develop a new SO₂ LH algorithm and apply it to observations from the high-spatial-resolution TROPOspheric Monitoring Instrument (TROPOMI). It is based on an SO₂ optical depth look-up table and an iterative approach. The strength of this scheme lies in the fact that it is a Covariance-Based Retrieval Algorithm (COBRA; Theys et al., 2021). This means that the SO₂-free contribution of the measured optical depth is treated in an optimal way, resulting in an improvement of the SO₂ LH sensitivity to SO₂ columns as low as 5 DU, with a precision better than 2 km. We demonstrate the value of this new data through a number of examples and comparison with satellite plume height estimates (from IASI and CALIOP), and back-trajectory analyses. The comparisons indicate an SO₂ LH accuracy of 1–2 km, except for some difficult observation conditions, in particular for optically thick ash plumes or partially SO₂-filled scenes.

1 Introduction

Volcanic eruptions can emit large quantities of rock fragments and fine particles (ash) into the atmosphere as well as several trace gases, such as carbon dioxide (CO₂), sulfur species (SO₂, H₂S), halogens (HCl, HBr, HF), and water vapor. These volcanic ejecta can have a tremendous impact on human health, society, and nature, and on air traffic safety. In particular, injection of sulfur dioxide (SO₂) receives considerable attention due to its subsequent conversion into aerosols and potentially strong effect on global climate (Robock, 2000). Among the emitted constituents, SO₂ is also the easiest to detect from ultraviolet (UV) and thermal infrared (TIR) remote-sensing techniques and has been used for many decades to monitor volcanoes worldwide. In order to understand volcanic processes and assess the impact of eruptions, it is crucial to measure not only the total abundance of SO₂ but also the height of the SO₂ plume. This information is important for (1) aviation actors such as Volcanic Ash Advisory Centres (VAACs) in case ash and SO₂ clouds are collocated (sulfur alone is also becoming increasingly recognized as causing long-term damage to aircraft engines, mainly because of sulfuric acid); (2) volcanology as it informs on eruption rate, eruption type, and underlying volcanic processes (e.g., Mastin et al., 2009); (3) atmospheric chemistry and climate research, e.g., to model the impact of volcanic eruptions on air quality (Schmidt et al., 2015) or to study the partly understood role of modest volcanic eruptions on climate forcing (Solomon et al., 2011; Vernier et al., 2011; Santer et al., 2014); and (4) the estimation of SO₂ emissions, as the measured SO₂ abundances are often directly dependent on the knowledge of the SO₂ vertical distribution.

Ground-based cameras can be used to routinely monitor plume heights (e.g., Scollo et al., 2014), but these measurements are performed in the very near field. For large and sustained volcanic eruptions, estimation of plume heights is very difficult in practice – not to say impossible – and the available measurements generally suffer from poor or infrequent sampling of the volcanic plumes. Moreover, many volcanoes on the globe are not monitored. Consequently, satellite nadir sensors with large swaths and frequent revisiting time offer the best solution to cover completely the injected volcanic cloud.

Space nadir sensors have provided global measurements of SO₂ vertical columns and masses for more than 40 years (Carn et al., 2016, and references therein). However, the retrieval of SO₂ plume height (also referred to SO₂ layer height, SO₂ LH) from satellite hyperspectral measurements is a relatively recent development. In the TIR, global SO₂ LH retrievals from the Infrared Atmospheric Sounding Interferometer (IASI) by Carboni et al. (2012) and Clarisse et al. (2014) and from the Cross-track Infrared Sounder (CrIS) by Hyman and Pavolonis (2020) proved to have an excellent sensitivity to the SO₂ height above ∼ 5 km, even for SO₂ columns at 1 DU level (Dobson unit – 1 DU: 2.69×10¹⁶ molecules cm⁻²). In the UV spectral range, the sensitivity to SO₂ is better at lower altitudes, and the first studies using full radiative transfer calculation schemes were from Yang et al. (2010) and Nowlan et al. (2011), based on the Ozone Monitoring Instrument (OMI; Levelt et al., 2006) and the Global Ozone Monitoring Experiment-2 (GOME-2; Munro et al., 2006). More recently, new approaches based on inverse learning machine schemes have become available for GOME-2 (Efremenko et al., 2017), TROPOspheric Monitoring Instrument-TROPOMI (Hedelt et al., 2019), and OMI (Fedkin et al., 2021). These algorithms greatly improve the computational performance of the previously published techniques. However, all the UV schemes referenced above have demonstrated sensitivity to SO₂ LH only for SO₂ vertical columns of more than ∼ 20 DU, which limits their use to relatively large volcanic events. In this paper, we present a new UV spectral fitting algorithm allowing SO₂ LH to be retrieved for SO₂ columns as low as 5 DU, and for SO₂ layer heights as low as 1 km. This scheme is an extension of our recently published SO₂ Covariance-Based Retrieval Algorithm (COBRA; Theys et al., 2021) that enables drastic reduction in spectral interferences and retrieval noise. Here we combine COBRA with an iterative look-up-table (LUT) approach to treat the non-linear SO₂ contribution to the measured signal. This allows joint retrieval of the SO₂ vertical column density (VCD) and SO₂ layer height with improved sensitivity while avoiding time-consuming on-line radiative transfer simulations. We apply this technique to measurements from TROPOMI (Veefkind et al., 2012) aboard the Sentinel-5 Precursor (S-5P) satellite. The motivation is its high spatial resolution of 3.5×5.5 km². TROPOMI resolves locally enhanced SO₂ columns much better than predecessor instruments like OMI (Theys et al., 2019). The retrieval of SO₂ LH is therefore expected to be possible for several degassing volcanoes. This has the potential to enhance our capability of monitoring height-resolved volcanic plumes globally in the troposphere. In addition, for strong eruptions, retrieved SO₂ LH (and SO₂ vertical columns) at high spatial resolution can also provide unique insights into volcanic processes, atmosphere–plume interactions and transport (Pardini et al., 2018, references).

The paper is structured as follows. Sect. 2 describes the algorithm in detail and demonstrates the performance of the SO₂ LH retrieval. In Sect. 3, the results are evaluated against other satellite datasets and dispersion model results. Conclusions and perspectives are given in Sect. 4.

2 Algorithm description

The theoretical basis for a joint retrieval of SO₂ column amount and layer altitude from satellite nadir back-scattered UV measurements is described by Yang et al. (2010) and Nowlan et al. (2011). The TROPOMI SO₂ layer height algorithm, outlined in this section, is an iterative retrieval scheme. It is conceptually close to these pioneering algorithm studies in the way the SO₂ absorption is handled but differs in the treatment of the other contributions to the measured signal.

We first define the measured top-of-atmosphere total optical depth (OD) by

$$\begin{array}{}\text{(1)}& y_{\mathrm{meas}}=y_{{\mathrm{SO}}_{\mathrm{2}}}+y_{\mathrm{bckg}}+\mathit{\epsilon }.\end{array}$$

All terms of the equation depend on wavelength (not labeled here, for simplicity). $y_{\mathrm{meas}}=-\log (I/I_o)$ is the logarithmic ratio of the wavelength calibrated measured radiance (I) and irradiance (I_o) over a given wavelength range, $y_{{\mathrm{SO}}_{\mathrm{2}}}$ is the unknown SO₂ optical depth, y_bckg is the “background” optical depth (accounting for all contributions to the total OD except that of SO₂), and ε is the measurement error.

In case of strong SO₂ absorption, the optical depth $y_{{\mathrm{SO}}_{\mathrm{2}}}$ is fundamentally a non-linear function of the VCD and LH of SO₂, and solving Eq. (1) is non-trivial. However, we assume here that the expression can be linearized using a Taylor expansion:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{y}_{\mathrm{meas}}& -y_{{\mathrm{SO}}_{\mathrm{2}},i}\approx \mathrm{\Delta }\mathrm{VCD}{\displaystyle \frac{\partial y_{{\mathrm{SO}}_{\mathrm{2}},i}}{\partial \mathrm{VCD}}}+\mathrm{\Delta }\mathrm{LH}{\displaystyle \frac{\partial y_{{\mathrm{SO}}_{\mathrm{2}},i}}{\partial \mathrm{LH}}}\\ & +y_{\mathrm{bckg}}+\mathit{\epsilon }.\end{array}\end{array}$$

$y_{{\mathrm{SO}}_{\mathrm{2}},i}$ is the SO₂ OD at the linearization point $y_{{\mathrm{SO}}_{\mathrm{2}},i}=y_{{\mathrm{SO}}_{\mathrm{2}}}({\mathrm{VCD}}_i,{\mathrm{LH}}_i$), $\partial y_{{\mathrm{SO}}_{\mathrm{2}},i}/\partial$VCD and $\partial y_{{\mathrm{SO}}_{\mathrm{2}},i}/\partial$LH are the corresponding partial derivatives with respect to the SO₂ VCD and LH (Jacobians), and ΔVCD and ΔLH are the VCD and LH increments. Index i stands for the ith iteration.

To solve Eq. (2), we developed a hybrid method. To model the SO₂ signal, the algorithm makes use of a large LUT of SO₂ OD. At each iteration, improved estimations of VCD and LH become available. These results are used to update the SO₂ OD and Jacobians for the next calculation, until convergence is reached. This part of the algorithm will be detailed in Sect. 2.1. To treat the background and error terms of Eq. (2), we propose a COBRA method. In brief, instead of fitting the background optical depth, the algorithm considers a representative set of measured spectra uncontaminated by SO₂ and characterized by a mean optical depth $\stackrel{\mathrm{‾}}{y}$ and a covariance matrix S, to represent statistically y_bckg+ε. The idea of the method, initially presented by Walker et al. (2011) and further developed in other studies (e.g., Carboni et al., 2012; Clarisse et al., 2014; Theys et al., 2021), is to consider y_bckg+ε as an error term, and to interpret S as a generalized error covariance matrix. Thus, the solution of the inverse problem can be expressed as follows (Rodgers, 2000):

$$\begin{array}{}\text{(3)}& {\widehat{x}}_{i+\mathrm{1}}={\widehat{x}}_i+{\left(k_i^T{S}^{-\mathrm{1}}{k}_i\right)}^{-\mathrm{1}}{k}_i^T{S}^{-\mathrm{1}}(y_{\mathrm{meas}}-y_{{\mathrm{SO}}_{\mathrm{2}},i}-\stackrel{\mathrm{‾}}{y}),\end{array}$$

where $\widehat{x_i}$ is the retrieved state vector (${\left[{\mathrm{LH}}_i,{\mathrm{VCD}}_i\right]}^T$) and k_i is the SO₂ forward model ([$\partial y_{{\mathrm{SO}}_{\mathrm{2}},i}/\partial \mathrm{LH}\partial y_{{\mathrm{SO}}_{\mathrm{2}},i}/\partial \mathrm{VCD}$]).

It should be emphasized that the matrix S accounts (if well-constructed) for most atmospheric background and instrumental-related variability of the spectra, including cross-correlations. The strength of the algorithm lies in the fact that only two parameters are retrieved (SO₂ LH and VCD). As will be shown in Sect. 2.3 and 3.1, this constitutes a significant advance in terms of retrieval sensitivity compared to a classical fitting approach such as the differential optical absorption spectroscopy (DOAS; Platt and Stutz, 2008), where multiple parameters are fitted in addition to SO₂ LH and VCD.

The following two sections describe in more detail the SO₂ LUT approach and the specific algorithm settings.

2.1 SO₂ optical depth look-up table: description

Forward modeled SO₂ spectra are based on the LInearized Discrete Ordinate Radiative Transfer (LIDORT) model version RRS 2.2 (Spurr et al., 2008). The input data used to set the atmosphere and spectroscopy are detailed in Table A1. Simulations were carried out to cover a large range of possible measurement conditions, using different combinations of LUT entries for the observation geometry, total ozone column, surface non-directional Lambertian equivalent reflectivity (LER), and SO₂ vertical profiles (Table 1). More details on LUT entries are given below. The simulation results are the SO₂ slant optical depth spectra over a wavelength range from 309 to 329 nm and at a spectral sampling of 0.05 nm. Note that the spectroscopic input data (absorption cross sections and solar spectrum) were not pre-convolved with the Instrumental Spectral Response Function (ISRF) of TROPOMI but rather with a box-car function of 0.05 nm width. Therefore, the simulations are not instrument-specific. For application to TROPOMI, the SO₂ slant OD spectra were convolved with the ISRF, and a specific correction for the so-called solar-I_o effect (Aliwell et al., 2002) was applied, as it turned out to be important for large SO₂ VCDs (100–1000 DU). The solar-I_o correction accounts for the fact that on the one hand, the laboratory cross sections are measured with a spectrally flat light source, and on the other hand, the space-based atmospheric absorption is measured at a lower spectral resolution and with a highly structured solar light source. The convolved I_o-corrected SO₂ OD is written as follows:

$$\begin{array}{}\text{(4)}& {\mathrm{OD}}_{\mathrm{conv}}=-\log [\mathrm{ISRF}*(I_o\cdot \exp (-\mathrm{OD}))/\mathrm{ISRF}*I_o],\end{array}$$

where I_o and OD are the “high-resolution” solar and SO₂ optical depth spectra, respectively.

It should be noted that the TROPOMI ISRF parameters vary smoothly with the position across-track (450 positions in total). For practical ease of use, we assumed that the across-track dependence is well encapsulated by the viewing zenith angle (VZA) entry. To represent the full swath, we used the sign convention of negative and positive VZA for west and east, respectively. For each of the viewing zenith angle grid point (Table 1), a slit function of the TROPOMI detector column was associated with the closest mean VZA. This appears to be a good approximation for TROPOMI and avoids having 450 different LUTs.

From the LUT of SO₂ slant OD spectra, the algorithm extracts a sub-LUT for a given TROPOMI measurement by linear interpolation. To do so, the observation angles at the ground pixel location are used. Input on total ozone is obtained from the TROPOMI off-line total ozone column product (Garane et al., 2019). The latter is well suited for the present application, as it is weakly affected by spectral interferences with SO₂ (bias of only few percentage points in case of strong eruptions; see discussion in Lerot et al., 2014). In addition to the observation geometry and total ozone absorption, the measurement sensitivity to SO₂ is also strongly dependent on the surface reflectance and the presence of clouds or aerosol layers. Here we assume that the radiative transfer in the atmosphere can be sufficiently represented through a lower-bound Lambertian equivalent reflector whose parameters are constrained by the radiance measurements. Treating clouds or aerosols as LERs works very well when the SO₂ plume is above a cloud or aerosol layer. However, it has limited applicability for cases where SO₂ and aerosols are mixed, especially for highly absorbing aerosols such as volcanic ash. This aspect will be further discussed in Sect. 3. The LER is characterized by effective parameters, height, and albedo, which are determined for each pixel. The LER height is computed as the cloud-fraction weighted mean of the cloud and ground altitudes. Cloud parameters are from the operational cloud product OCRA/ROCINN (Optical Cloud Recognition Algorithm/Retrieval of Cloud Information using Neural Networks) using the Cloud as Reflecting Boundaries (CRB) model of Loyola et al. (2018). For the LER albedo, it is constrained by TROPOMI measured radiance averaged over 339.5–340.5 nm, a range mostly unaffected by trace gas absorption (O₃ and SO₂). The LER albedo is retrieved by matching the measured mean radiance to a look-up table of radiances (generated in parallel to the SO₂ OD LUT), and which depends on the angles, surface height, and albedo, with the same grid definition as in Table 1. The simulated radiances are convolved and averaged over the same wavelength range as TROPOMI.

Table 1 Physical parameters that define the SO₂ slant optical depth look-up table. The total number of spectra is about 38.5×10⁶. In practice, note that the look-up table interpolation is performed along the cosine of SZA and VZA.

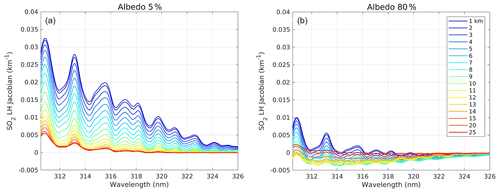
From the interpolation step, a sub-LUT of SO₂ OD spectra is obtained, which depends only on SO₂ VCD and LH. From this table, the SO₂ VCD and LH Jacobians are derived by simple discrete derivatives. These functions are essential for the retrieval (Eq. 3). Example SO₂ LH Jacobians are presented in Fig. 1, for a fixed SO₂ VCD of 25 DU and representative LER albedos of 5 % (panel a) and 80 % (panel b), representative of typical clear-sky and fully cloudy conditions, respectively. For this example, we observe the largest sensitivity to SO₂ LH for low albedo and low SO₂ peak height. This behavior is expected as most of the altitude information comes from the way SO₂ alters the availability of photons to be scattered by air molecules below the SO₂ layer (Yang et al., 2010). Conversely, for high SO₂ height or high albedo (e.g., for an underlying cloud), the scattering weighting functions are weakly dependent on the altitude, and the information on SO₂ LH appears to be less accessible. The performance of the algorithm under various conditions will be discussed further in Sect. 2.3.

Figure 1 Examples of SO₂ optical depth Jacobians with respect to LH for different SO₂ peak heights (1–25 km), and LER albedos of 5 % (a) and 80 % (b). The spectra correspond to SZA: 30^∘, VZA: 0^∘, RAA: 0^∘, SO₂ column: 25 DU, ozone column: 295 DU, surface height: 0 km.

2.2 LUT-COBRA settings

The retrieval of SO₂ vertical column and height is performed from the analysis of measured radiances in the spectral range from 310.5 to 326 nm (TROPOMI band 3). The algorithm starts from an a priori pair (x_o) of SO₂ VCD and LH. The initial value VCD_o is taken as the output of the operational TROPOMI SO₂ column product for a plume height of 7 km (Theys et al., 2017). The height z_o is 7 km, except if the LER height is greater than 5 km. In that case, z_o is equal to the LER height + 2 km. First, the SO₂ optical depth and Jacobian spectra for x_o are derived from the LUT (as described in Sect. 2.1) and interpolated on the wavelength grid of the measurement. Then the results of the fit (Eq. 3) are used to calculate new SO₂ spectra for the next calculation, and the retrieval is repeated until the inverted LH and VCD do not change from one iteration to the next by more than 500 m and 10 %, respectively, or if the number of iterations exceeds a limit value (fixed to 10). In practice, a solution is found typically after four iterations. We conducted a number of sensitivity tests and conclude that the retrieved SO₂ LH and VCD are nearly independent of the prior x_o. Moreover, using forward simulations, we have also estimated the interpolation errors due to the relatively coarse grids of the LUT and found that these are acceptably small in comparison to the noise level. Note that for some iterations, the algorithm gives SO₂ LH occasionally outside the SO₂ height grid. For those cases, the SO₂ height is forced to the surface height +1 km or the grid maximum height −1 km (i.e., 24 km), depending on whether the height is below or above the surface or maximum height, respectively. More rarely, the same can happen for the retrieved SO₂ VCD and then the SO₂ VCD is set to VCD_o for the next iteration.

A key information in the retrieval process is the covariance matrix S (and mean optical depth $\stackrel{\mathrm{‾}}{y}$), as it directly influences the sensitivity of the retrieval (Eq. 3). For the construction of S and $\stackrel{\mathrm{‾}}{y}$ we used a set of measured SO₂-free spectra, following an approach analogous to our previous study (Theys et al., 2021). In brief, for each TROPOMI observation for which the SO₂ LH algorithm is applied (see next section), we consider the spectral data of the corresponding orbit and TROPOMI row. To represent best the zonal dependence, we select the radiance spectra of 300 pixels along the flight direction (i.e., ±150 indices along track). This corresponds to a region of ∼ 1600 km. It permits us to sample a wide range of cloudiness so that the cloud condition of the pixel of interest is likely represented by the covariance (at least to some degree). Note that for the construction of S the pixels with observable SO₂ amounts (with VCD > 2.5 × VCD retrieval error) are filtered out. To keep a viable number of spectra for the covariance calculation (at least 100), we also allow the number of pixels along the flight direction to increase, if necessary. Note that an upper limit on the SZA is fixed to 65^∘ in order to exclude difficult conditions with high ozone absorption. This SZA limit applies both to the measurements to be analyzed for the SO₂ height and for the construction of the covariance matrix S

It should be noted that the quality of the LUT-COBRA results depends strongly on the signal of SO₂. This aspect is addressed in the next section.

2.3 Performance of the retrievals

Following Rodgers (2000), the estimated error covariance of the solution (Eq. 3) is given by the following:

$$\begin{array}{}\text{(5)}& {\widehat{S}}_i={\left(k_i^T{S}^{-\mathrm{1}}{k}_i\right)}^{-\mathrm{1}}.\end{array}$$

This matrix can be calculated for each TROPOMI pixel and the square root of the diagonal elements of ${\widehat{S}}_i$ provide error estimates on the retrieved SO₂ LH and VCD.

To demonstrate the sensitivity of the algorithm for different SO₂ altitudes and vertical columns, the SO₂ LH error was computed for predefined pairs of Jacobians, and a fixed covariance matrix S. The results are summarized in Fig. 2a for typical observation conditions in the tropics, over a land surface, free of snow and clouds. From this example, it is clear the SO₂ LH retrieval uncertainty decreases for high SO₂ columns. This is obvious as the SO₂ signal dominates all variability contributions. The results also suggest that the algorithm performs better for SO₂ at low heights. This behavior is logical and is in line with the dependence of the SO₂ LH Jacobians with the SO₂ height (see Fig. 1a, and related discussion). It is interesting to note that the observed retrieval performance dependence with SO₂ height is complementary to the one found for thermal infrared nadir sounders, like IASI or CrIS. Indeed, Carboni et al. (2012) and Clarisse et al. (2014) demonstrated (using IASI) that the best SO₂ height retrieval is achieved for SO₂ plumes in the upper troposphere and lower stratosphere (UTLS), while in the lower troposphere (below 3–5 km), the sensitivity to the SO₂ height is strongly reduced, as a result of water vapor absorption. This complementarity is further addressed in Sect. 3.

To compare the performance of the LUT-COBRA with more classical fitting approaches, we have also developed a modified DOAS algorithm, referred to as LUT-DOAS in the following. In short, the forward model matrix was expanded to include not only the LH and VCD Jacobians (grouped as k_i) but also other spectra, used to fit the measured OD. Essentially, we implemented a linearized version of the DOAS scheme used in the operational TROPOMI SO₂ algorithm (Theys et al., 2017). More precisely, 13 spectral functions are used to model the ozone absorption, Ring effect, broadband component (in the form of a third-order polynomial), spectral shift and squeeze (Beirle et al., 2013), and linear intensity offset. Based on this DOAS-type forward model matrix, the SO₂ layer height error for the LUT-DOAS scheme was calculated using Eq. (5), by replacing the covariance matrix S with an identity matrix, divided by the square of the signal-to-noise ratio (SNR). The latter was fixed to 800, a typical SNR of TROPOMI radiances over the fitting window considered. The results are presented in Fig. 2b.

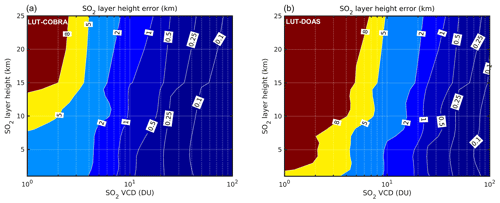
Figure 2 SO₂ layer height theoretical uncertainty for (a) LUT-COBRA and (b) LUT-DOAS schemes. The results correspond to SZA: 30^∘, VZA: 0^∘, RAA: 0^∘, ozone column: 295 DU, surface height: 0 km, surface albedo: 5 %.

This example indicates that, in theory, the LUT-DOAS scheme yields reasonable height retrievals with uncertainty of 1–2 km for SO₂ columns greater than 10–40 DU, depending on the SO₂ height. This finding is mostly consistent with previous studies on UV retrievals of SO₂ plume height (e.g., Nowlan et al., 2011; Hedelt et al., 2019).

However, compared to the LUT-DOAS algorithm, Fig. 2 suggests that our LUT-COBRA scheme significantly improves the SO₂ layer height error by a factor of 2–3. This is an appealing aspect of the LUT-COBRA approach, as it enables the application of the SO₂ LH retrievals to SO₂ columns as low as 5 DU.

The performance results of Fig. 2 were repeated for other observation conditions. In particular, a high reflectance scenario (80 %) was tested to represent the situation of an SO₂ plume lying above a cloud deck. The results show no significant change in the performance of the retrievals indicating that underlying clouds have little impact on the sensitivity to SO₂ LH. In a way, this is counter-intuitive when looking at Fig. 1, but one should keep in mind that the algorithm retrieves both LH and VCD of SO₂. Clearly, high reflectance conditions help better constrain the SO₂ vertical column (especially for low SO₂ heights) which in turn is beneficial to access the spectral information on SO₂ LH. Another interesting result is to test the sensitivity of the retrieval as a function of the observation angles. For instance, increasing the solar zenith angle first leads to improved results, because the SO₂ signal increases as the optical path through the SO₂ layer gets longer, but then the performance quickly deteriorates for high angles due to large absorption by ozone. Those conditions are, however, discarded by the algorithm SZA cutoff of 65^∘ (Sect. 2.2).

It should be emphasized that the SO₂ layer height error presented here does not account for systematic uncertainties. It is clear that in many circumstances, forward model errors can actually dominate the total error in SO₂ LH. These errors are generally difficult to evaluate and depend on the prevailing conditions. In Sect. 3, examples of TROPOMI results will be presented with specific attention to possible sources of error. We also refer to Yang et al. (2010) and Nowlan et al. (2011) for a presentation of the various sources of systematic uncertainties.

In practice, the SO₂ layer height error (Eq. 5) can be computed for each TROPOMI pixel. This is useful as it helps diagnose the retrieval quality. In what follows, the retrievals are considered only for a SO₂ layer height error lower than 2.5 km and retrieved VCD of at least 5 DU. In order to preselect the spectra that potentially fulfill these criteria (and limit the computational effort), the TROPOMI operational SO₂ product was examined. Only measurements with slant column densities (a quantity independent of SO₂ plume height) larger than 2.5 DU were selected and processed by the SO₂ LH algorithm.

3 Results

In this section, we present TROPOMI SO₂ LH data and evaluate the results against independent plume height estimates from satellites and back-trajectory modeling.

3.1 Comparison with satellite plume height estimates

For a selection of eruption events, we performed comparisons with the IASI SO₂ height data of Clarisse et al. (2014), readily available in near-real time in the Support to Aviation Control Service (SACS; Brenot et al., 2014, 2021). Another useful dataset to validate the TROPOMI SO₂ height is from the Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP) instrument on board the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO). Here we used the 532 nm total backscatter coefficient profiles from the standard CALIOP level-2 v4 product (CAL_LID_L2_05kmAPro-Standard-V4), available from NASA (https://www-calipso.larc.nasa.gov, last access: 30 March 2022). Although those datasets are very useful, we note that these can only be used to validate TROPOMI SO₂ LH in a rather qualitative way because (1) IASI has a different overpass time than TROPOMI and (2) CALIOP has a narrow swath (resulting in limited sampling of what S-5P observes) and measures aerosols rather than SO₂. Moreover, CALIOP is generally more representative of the top layer of the plume than TROPOMI-retrieved SO₂ heights. More validation results are shown in Sect. 3.2 and 3.3.

The first example is for the Sierra Negra volcano (0.83^∘ S, 91.17^∘ W, Ecuador) that erupted on 26 June 2018 at ∼ 20:00 UTC, according to the Global Volcanism Program (https://volcano.si.edu/, last access: 30 March 2022). Coincidently, TROPOMI passed over the region shortly after the start of the eruption at ∼ 20:12 UTC and detected a freshly emitted and nearly undispersed SO₂ plume with heights of 3–5 km, in good agreement with the S-5P Full-Physics Inverse Learning Machine (FP_ILM) results of Hedelt et al. (2019). On 27 June, the TROPOMI overpass (orbit 03652, approximate time 19:50 UTC) revealed an SO₂ plume distributed at multiple heights. Figure 3a shows the results of the LUT-COBRA. The retrieved SO₂ heights are as low as 1–2 km near the vent and up to 18 km further downwind. The characteristic pattern of SO₂ height levels observed for the different parts of the plume is consistent with the retrievals of CrIS (Hyman and Pavolonis, 2020). Figure 3 also presents results from IASI on 28 June at ∼ 15:15 UTC (SO₂ height images for other dates and acquisition times are accessible on the SACS web page; http://sacs.aeronomie.be, last access: 30 March 2022). As can be seen, the TROPOMI LUT-COBRA and IASI SO₂ LH results agree qualitatively well considering the relatively large time difference of nearly 20 h between the two measurements. A notable difference though is for the SO₂ plume located below 3 km, which is barely seen in the IASI data. For this particular example, this is partly because the volcano lies between two orbits, but inspection of other SO₂ images does not reveal significant SO₂ detections below 3 km by IASI. The reason is likely the limited sensitivity of IASI in the lowermost troposphere, particularly in the tropics.

In addition to the LUT-COBRA results, Fig. 3b also presents the corresponding retrievals from the LUT-DOAS implementation (introduced in Sect. 2.3). Here we show the results for retrieved SO₂ VCDs greater than 20 DU in order to keep the SO₂ height data with retrieval errors better than 1–2 km (Fig. 2b). This threshold is the same as in Hedelt et al. (2019). Overall, the SO₂ LHs from LUT-DOAS are in close agreement with the LUT-COBRA results, for the pixels in common. The LUT-DOAS values also match very well the results of S-5P FP_ILM (Fig. 10b of Hedelt et al., 2019). However, this example of Fig. 3 clearly demonstrates that the LUT-COBRA is able to retrieve SO₂ LH for many more pixels with greater sensitivity than the LUT-DOAS approach. In the following, only the LUT-COBRA results will be presented and discussed.

A second illustration of the LUT-COBRA SO₂ LH results is for the Raikoke volcano (48.29^∘ N, 153.25^∘ E, Kuril Islands, Russia) that erupted on 21 June 2019 with multiple explosions that started at ∼ 18:00 UTC and lasted several hours. The eruption injected enormous amounts of SO₂ in the atmosphere, around 1.5 Tg (e.g., de Leeuw et al., 2021), as well as volcanic ash. Raikoke is therefore a good case to test the SO₂ LH algorithm under extreme conditions. Note that the eruption of Raikoke is also well documented and is the subject of a special issue from Atmospheric Chemistry and Physics, Atmospheric Measurement Techniques, and Geoscientific Model Development.

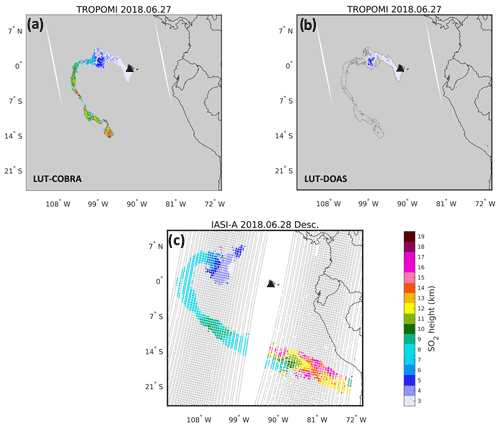
Figure 3 SO₂ layer height results for the eruption of Sierra Negra from (a) TROPOMI LUT-COBRA, (b) TROPOMI LUT-DOAS on 27 June 2018, and (c) IASI/MetOp-A on 28 June 2018 (descending orbit). The Sierra Negra volcano is marked by a black triangle. The gray pixels indicate the measurements with no SO₂ height retrieval. For panel (b), the thin black line shows the 5 DU contour of SO₂ VCD used as threshold for the LUT-COBRA results (a).

Figure 4a and c present two examples of SO₂ LH results for Raikoke on the 23 June 2019. Most of the SO₂ is found between 5 and 15 km, in agreement with Cai et al. (2022). The SO₂ distribution as a function of height seen in this example is also observed by other satellite datasets. The core of the plume is located in the 8–14 km altitude range, similar to Hyman and Pavolonis (2020) and Hedelt et al. (2019), and is consistent with SO₂ profiles from the Microwave Limb Sounder (MLS).

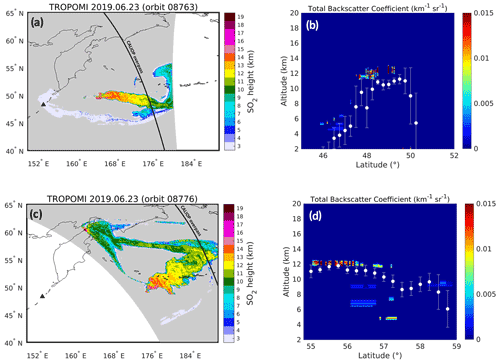
Figure 4 SO₂ layer height results from TROPOMI observations of the Raikoke plume on 23 June 2019, for orbits (a) 08763 and (c) 08776. The retrieved maximum SO₂ VCD is 613 and 274 DU, respectively. The Raikoke volcano is marked by a black triangle. The gray pixels indicate the measurements with no SO₂ height retrieval. The black lines indicate the CALIOP overpasses within 1 h. (b, d) Comparison between CALIOP plume detection from measured 532 nm total backscatter coefficient and TROPOMI SO₂ LH results, for (a, c), respectively. The TROPOMI values (in white) are the mean and standard deviation of the SO₂ LH results within 0.25^∘ × 0.25^∘ boxes, coincident with CALIOP.

Figure 4a and c also feature a plume at much lower altitude, which is consistently observed in other studies (e.g., Hyman and Pavolonis, 2020; de Leeuw et al., 2021; Muser et al., 2020). The TROPOMI results of Fig. 4 also agree reasonably well with IASI SO₂ heights. However, the comparison is left out of this study, as it will be covered in a future publication (Vernier et al., 2022). Instead, we compare the TROPOMI SO₂ LH with nearly coincident CALIOP observations of the Raikoke plume. Figure 4b and d show the comparison between the measured total backscattered coefficient of CALIOP and collocated TROPOMI SO₂ LH, for the two orbits of Fig. 4a and c. Qualitatively, the TROPOMI SO₂ LH is in agreement with the aerosol features detected by CALIOP. For instance, the plume at lower altitudes (∼ 46–48^∘ N in Fig. 4b) is well captured by TROPOMI. However, it is clear that overall the retrieved SO₂ heights are systematically lower than CALIOP by 1–3 km. This finding is in line with the results of Koukouli et al. (2022), who found similar low bias of the S-5P FP_ILM SO₂ height product compared to CALIOP. Note also that the first TROPOMI observations of the Raikoke plume were made on 22 June 2019 (orbit 08749). For that plume, the algorithm retrieves SO₂ heights of ∼ 8 km (not shown). Unfortunately, there was no CALIOP measurement available on that day, but it appears that these heights are much too low when compared to other data. This is not a problem specific to our algorithm, and it highlights the difficulty to retrieve the SO₂ height in the UV range for a scene with a mixture of SO₂ and ash (e.g., Yang et al., 2010; Hedelt et al., 2019). Under these conditions, the LUT and Lambertian equivalent reflector approximation fail to reproduce adequately the complex radiative transfer in the volcanic plume, leading to a low bias on the SO₂ height, which can be as large as 5 km for fresh and thick ash plumes. In addition, the reference set of spectra used for the construction of the covariance matrix is likely not covering well these conditions of low UV intensities.

A last test case is for the Ulawun volcano (5.05^∘ S, 151.33^∘ E, Papua New Guinea) that erupted explosively on 26 June 2019 at around 04:30 UTC and injected SO₂ at the tropical tropopause level in the form of a well-defined umbrella cloud. On 27 June, TROPOMI (orbit 08821, approximate time 04:00 UTC) observed an SO₂ plume over the region of Ulawun (Fig. 5a, b) with SO₂ LH distributed mainly between 15 and 21 km (Fig. 5d), with a center-of-mass height of 17.7 km. Conversely, the IASI/MetOp-A overpass at ∼ 11:20 UTC on the same day revealed a plume of SO₂ injected in a narrower vertical layer, with center-of-mass height of 16.6 km, hence slightly lower than the TROPOMI estimate. It is interesting to note that the total SO₂ mass inferred from TROPOMI is in rather good agreement with the IASI estimate, within 10 %. We argue that the difference in the SO₂ mass distributions could actually relate to the limited sensitivity of the TROPOMI retrievals for that plume. Indeed, the SO₂ columns from TROPOMI (Fig. 5b) are modest, smaller than 20 DU for most pixels, and 9 DU on average. At this VCD level, the retrieval error on TROPOMI SO₂ LH (Fig. 2a) is significant for a SO₂ plume in the UTLS, around 1.5 km. This is compatible with the observed spread of the TROPOMI SO₂ mass distribution (Fig. 5d). Regarding the apparent ∼ 1 km difference between TROPOMI and IASI SO₂ center-of-mass heights, we can of course not completely rule out a systematic error on the IASI retrievals, but it is unlikely to explain fully the observed offset. Importantly, for these conditions (low to medium VCD, high LH), the TROPOMI SO₂ height retrieval is exposed to forward model errors that could easily explain a 1 km bias. For example, the look-up table uses a simplified representation of the atmosphere in terms of temperature and ozone profiles that can ultimately lead to systematic errors in the Jacobians used for the retrievals.

Overall, the examples presented in this section show that there is a general good agreement between TROPOMI SO₂ LH and other satellite heights estimates. Nevertheless, the results also highlight limitations of the retrievals in some (difficult) conditions, in particular for optically thick ash clouds or lower stratospheric SO₂ plumes. More work would be needed to improve these results.

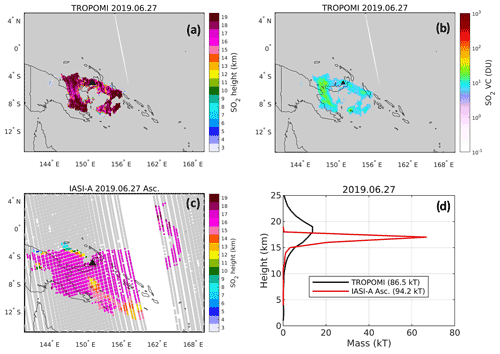
Figure 5 SO₂ plume on 27 June 2019 after the eruption of Ulawun. (a, b) TROPOMI retrievals of SO₂ LH and VCD, respectively; (c) SO₂ LH from IASI/MetOp-A (ascending orbit); (d) comparison of SO₂ mass histograms between TROPOMI and IASI. Total masses are indicated in the legend. The Ulawun volcano is marked by a black triangle. The gray pixels indicate the measurements with no SO₂ height retrieval.

3.2 Comparison with back-trajectory analysis from PlumeTraj: the Etna case

An independent validation of the SO₂ height retrievals of TROPOMI can be obtained from back-trajectory analysis. Recently, a general algorithm has been developed called PlumeTraj (Pardini et al., 2017, 2018; Queißer et al., 2019), which allows the height and age of volcanic SO₂ emissions to be quantified for each TROPOMI pixel in a SO₂ image, using HYSPLIT back trajectories (Stein et al., 2015). PlumeTraj leverages the fact that, because of the wind shear in the atmosphere, only a limited range of back-trajectory altitudes connects a SO₂ pixel location with a given volcanic vent. Importantly, when all pixels containing a volcanic plume are considered together, the height and age parameters inferred by this method can be used in combination with the SO₂ column data to reconstruct height- and time-resolved SO₂ emissions. This approach proves to be very powerful, as it provides unique insights into the volcanic processes driving eruptions (Burton et al., 2021). A similar technique was also applied by Wu et al. (2017) to derive emission time series from SO₂ observations of the Atmospheric Infrared Sounder (AIRS).

Here we have analyzed and compared the height results of TROPOMI SO₂ LH and PlumeTraj for 17 paroxysmal events of Mount Etna, Italy (37.75^∘ N, 15^∘ E), occurring in 2021.

Figure 6 presents an example of comparison, for a plume on 19 February 2021. It should be stressed that the SO₂ plume heights, as shown in Fig. 6, are retrieved independently from each other, as PlumeTraj only needs as input the observation time and pixel coordinates. For this event, PlumeTraj derives SO₂ heights typically between 5 and 9 km with the highest values for the eastern part of the plume and lower heights on the western part, and near the vent. Overall, this pattern is well reproduced by our TROPOMI SO₂ LH retrievals – despite a few outliers. For the core of the plume, the agreement between TROPOMI SO₂ LH and PlumeTraj is generally very good, with differences mainly within ±2 km. However, much larger differences are found for the edges of the plume, where the TROPOMI SO₂ LH algorithm often retrieves SO₂ plume heights much lower than PlumeTraj. We attribute this feature to an effect of the strong SO₂ horizontal inhomogeneity within a TROPOMI pixel, which ultimately causes an underestimation of the retrieved SO₂ height (consistent with Yang et al., 2010). This effect is also visible in Fig. 4.

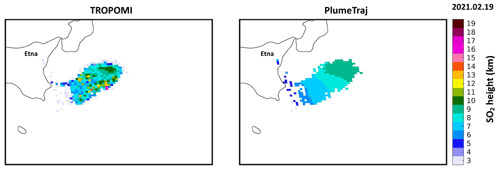
Figure 6 Example of SO₂ height results derived from TROPOMI and PlumeTraj for an Etna plume on 19 February 2021.

Figure 7a summarizes the TROPOMI and PlumeTraj SO₂ height results, for all selected Etna events. For each SO₂ plume, the center of mass height was calculated by averaging the SO₂ height weighted by the SO₂ column amount in each pixel. For TROPOMI SO₂ LH, this is performed using the retrieved SO₂ column data, while for PlumeTraj the SO₂ column is estimated using linear interpolation of the TROPOMI operational SO₂ column product (given at 1, 7, and 15 km; Theys et al., 2017) to the altitude returned from the trajectory analysis. Note that all pixels with retrieved SO₂ heights < 1 km were excluded from the analysis, in an effort to reduce the impact of the pixels near the plume edges affected by pixel under-filling. As can be seen from Fig. 7a, TROPOMI and PlumeTraj capture comparable SO₂ heights (in the range of ∼ 4–11 km) and similar variability (correlation coefficient of 0.85). The estimated total SO₂ masses are also very consistent (not shown) and are in the range between 3.5 to 18.5 kt.

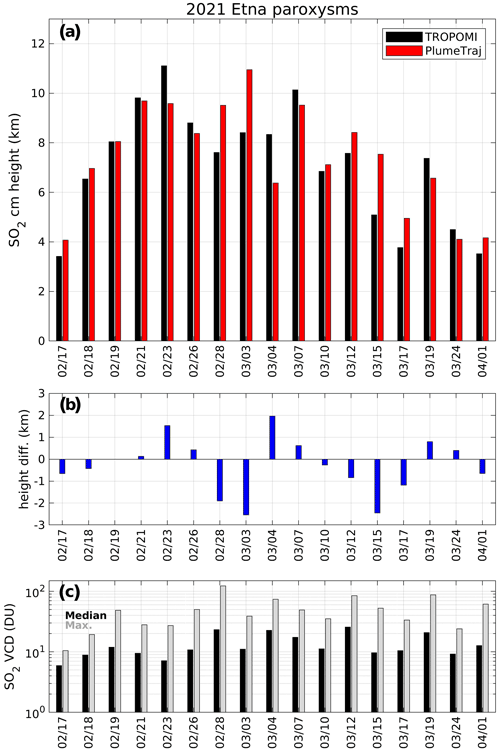
Figure 7 (a) Comparison of SO₂ center of mass height (km) from TROPOMI and PlumeTraj for 17 Etna paroxysmal events in 2021. (b) Differences of TROPOMI minus PlumeTraj SO₂ height (root mean square error: 1.25 km). (c) Median and maximum SO₂ columns retrieved by TROPOMI LUT-COBRA.

Figure 7b shows the differences in height between TROPOMI and PlumeTraj for all paroxysmal events, and Fig. 7c summarizes the corresponding median and maximum SO₂ column values as retrieved by TROPOMI SO₂ LUT-COBRA

For about two third of the cases, the height estimates agree within ±1 km. There are only a few instances for which the height difference is higher than 1.5 km (in absolute value). However, further investigation reveals that these cases correspond to particularly difficult conditions either for the satellite retrievals (e.g., due to the presence of volcanic ash or because the plume was narrow) or for PlumeTraj (unfavorable wind shear settings or because the plume was old (plume age ∼ 1 d)). Importantly, from Fig. 7b and c, we cannot find a relation between the height discrepancy and the SO₂ loadings. The median SO₂ VCD lies in the range between 6 and 25.6 DU, and Fig. 7 confirms that the TROPOMI SO₂ LH algorithm is able to derive reasonable SO₂ heights, even for modest SO₂ vertical columns.

3.3 Temporal analysis over degassing volcanoes

Apart from eruptive events, TROPOMI is able to detect SO₂ emissions from degassing volcanoes worldwide (Queißer et al, 2019; Theys et al., 2019, 2021; Fioletov et al., 2020), and it is therefore important to test our SO₂ LH algorithm on some of these volcanic emitters. Previous studies have shown that IASI is sensitive to weaker volcanic emissions as well (Clarisse et al., 2012; Taylor et al., 2018), and thus it is interesting to compare the TROPOMI and IASI height retrievals. For this, we have considered two complete years of data (2020 and 2021) and analyzed time series of daily height estimates from TROPOMI and IASI/MetOp-B over many different volcanic regions. Because of the limited sensitivity of the satellites, it is clear that not all comparisons were meaningful. However, for some volcanoes, the height of SO₂ was regularly retrieved by both instruments over the studied period. Examples of results are shown in Fig. 8 for five active volcanoes, namely Sabancaya, Peru (15.78^∘ S, 71.85^∘ W, summit elevation: 5967 m), Popocatepetl, Mexico (19.02^∘ N, 98.62^∘ W, 5426 m), Tungurahua, Ecuador (1.47^∘ S, 78.44^∘ W, 5023 m), Nyiragongo, DR Congo (1.52^∘ S, 29.25^∘ E, 3470 m), and Fagradalsfjall, Iceland (63.90^∘ N, 22.27^∘ E, 385 m). Note that the IASI height retrievals are the same as already introduced in Sect. 3.1, except that additional criteria were applied to select the data with sufficient SO₂ signal and to make the results comparable to TROPOMI. In particular, the same lower threshold of 5 DU for the vertical column is applied.

As can be seen from Fig. 8, a remarkable agreement is found between TROPOMI and IASI SO₂ heights. For Sabancaya, it is noticeable that successful SO₂ LH retrievals are frequent for both instruments. The reason is likely due to the relatively high SO₂ columns there but also because Sabancaya is an elevated site characterized by a dry atmosphere. To some extent, this is also true for Popocatepetl and Tungurahua. On the contrary, a site such as Nyiragongo has a summit at lower altitude and a wet atmosphere, resulting in fewer IASI retrievals. Finally, for Fagradalsfjall, SO₂ was emitted much lower in the atmosphere (mainly below 2 km height) than for the other cases. However, the match between TROPOMI and IASI is very good. In this case, IASI seems to be able to retrieve SO₂ LH below 2 km. This is the result of dry conditions over Iceland for the studied period. Note that the time series for Fagradalsfjall covers only a few months, after its 2021 fissure eruption.

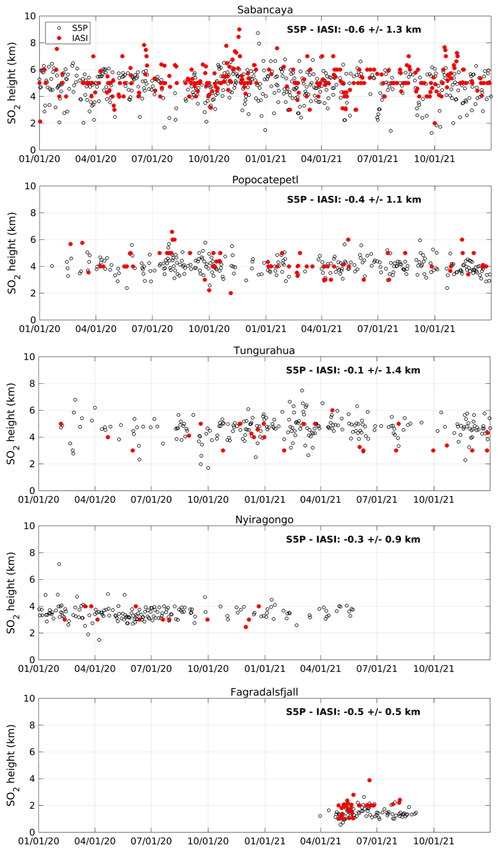
Figure 8 Time series of SO₂ height over five volcanic regions from TROPOMI and IASI/MetOp-B (daytime observations) for January 2020 to December 2021. Daily estimates of SO₂ center of mass height were calculated from quality-filtered data using fixed latitude–longitude boxes (from top to bottom) for Sabancaya (12–20^∘ S, 70–78^∘ W), Popocatepetl (15–22^∘ N, 96.5–102^∘ W), Tungurahua (5^∘ S–1^∘ N, 77–83^∘ W), Nyiragongo (5^∘ S–3^∘ N, 25–32^∘ E), and Fagradalsfjall (60–70^∘ N, 10–32^∘ W). For IASI, the same VCD lower threshold of 5 DU as TROPOMI is applied to select the data. The calculated SO₂ heights are shown only for days with at least 2 pixels. The mean and standard deviation of the differences between TROPOMI and IASI SO₂ daily heights for the complete period are given as an inset for each plot.

Figure 8 indicates that TROPOMI tends to retrieve slightly lower SO₂ heights than IASI by ∼ 0.5 km, although there is significant scatter in the height differences (standard deviation of about 1 km). The nature of this small systematic difference is unknown. However, this result nicely demonstrates the value of the LUT-COBRA approach to infer the height of SO₂ for degassing volcanoes or modest eruptions. For plumes in the lower troposphere, more frequent SO₂ heights are retrieved with TROPOMI than IASI, which is an appealing aspect of the algorithm.

4 Conclusions

We have presented a new algorithm to retrieve the SO₂ layer height and vertical column from TROPOMI UV observations. The retrieval scheme combines a large look-up table to model the SO₂ signal and an error-covariance-based approach, to represent the SO₂-free contribution of the spectrum. The method minimizes atmospheric or instrument-related spectral interferences and reduces the SO₂ layer height error by a factor of 2 to 3 compared to a DOAS-fashioned implementation of the algorithm. This enables derivation of the SO₂ layer height with a precision better than 2 km for SO₂ columns as low as 5 DU and for a wide range of conditions. This is a significant improvement compared to other existing UV retrievals, which are limited to scenes of at least 20 DU of SO₂ columns.

We have demonstrated this approach on a number of eruptive events. Comparison with satellite IASI and CALIOP measurements and back-trajectory analyses indicate an agreement within 1–2 km, except for specific observation conditions. The presence of ash, in large amounts and at the same altitude as SO₂, causes the retrieval to underestimate the SO₂ height by several kilometers, in line with previous studies. Moreover, partially SO₂-filled scenes underestimate the SO₂ layer height, and this is mostly seen at plume edges. Despite these limitations, the performance of the algorithm is particularly good, especially for plumes below 10–12 km. We investigated the results against back-trajectory analysis from the PlumeTraj toolkit, for relatively modest eruptions of Mount Etna in 2021. Using column-weighted average heights of SO₂, we found a very good agreement with PlumeTraj, even for total SO₂ masses of a few kilotons. Capitalizing on this, the temporal evolution of TROPOMI SO₂ plume height was studied over some of the largest degassing volcanoes, for a period of 2 years. An excellent correspondence is found between TROPOMI and IASI with a mean difference of −0.5 km. This highlights the high sensitivity of the proposed technique for the determination of plume height.

The algorithm is fast and could be adapted for near-real-time implementation and used, for example, in the Support to Aviation Control Service, or other volcanic monitoring applications. The SO₂ height results could also be helpful as a constraint for atmospheric dispersion modeling.

Future developments will focus on possibly enhancing the algorithm sensitivity, improving the retrievals in the presence of aerosols, expanding the algorithm to stratospheric injection heights (e.g., the 2022 eruption of Hunga Tonga–Hunga Ha'apai), and producing a proper quality assurance flag.

Appendix A

Table A1 Input settings used to generate radiative transfer simulation.