Synergistic retrieval and complete data fusion methods applied to simulated FORUM and IASI-NG measurements

In the frame of Earth observation remote-sensing data analysis, synergistic retrieval (SR) and complete data fusion (CDF) are techniques used to exploit the complementarity of the information carried by different measurements sounding the same air mass and/or ground pixel. While more difficult to implement due to the required simultaneous access to measurements originating from different instruments, the SR method is sometimes preferred over the CDF method as the latter relies on a linear approximation of the retrieved states as functions of the true atmospheric and/or surface state.

In this work, we study the performance of the SR and CDF techniques when applied to simulated measurements of the Far-infrared Outgoing Radiation Understanding and Monitoring (FORUM) and the Infrared Atmospheric Sounding Interferometer – New Generation (IASI-NG) missions that will be operational in a few years, from two polar-orbiting satellites. The study is based on synthetic measurements generated for the two missions in clear-sky atmospheres. The target parameters of the inversion are the vertical profiles of temperature, water vapor and ozone mixing ratios, surface temperature, and spectral emissivity.

We find that for exact matching of the measurements, the results of the SR and CDF techniques differ by less than $\mathrm{1}/\mathrm{10}$ of their errors estimated through the propagation of measurement noise. For measurements with a realistic mismatch in space and time, the two methods provide more different results. Still in this case, however, the differences between the results are within the error bars due to measurement noise. We conclude that, when applied to FORUM and IASI-NG missions, the two methods are equivalent from an accuracy point of view.

1 Introduction

Synergistic retrieval (SR) and complete data fusion (CDF) are two methods used to combine remote-sensing measurements acquired by independent instruments, simultaneously probing the same air mass and/or surface area. Measurements in different parts of the electromagnetic spectrum (e.g., ultraviolet, visible, infrared), adopting different acquisition geometries (e.g., nadir and limb sounding), have different sensitivities to the vertical distribution of atmospheric and surface variables. For this reason, combining complementary information from different spectral regions and different sensors can significantly improve the performance of the determined vertical profiles and surface parameters, in terms of both enhanced spatial resolution and error reduction.

In the last few decades, the need to advance the knowledge of tropospheric and stratospheric chemical/physical processes stimulated the development of new techniques to fully exploit the synergy of the great number of existing satellite measurements. Recent studies demonstrated the benefits of combining measurements from different sensors operating in different spectral ranges and/or with different observation geometries, by using simulated (Landgraf and Hasekamp, 2007; Worden et al., 2007; Natraj et al., 2011; Costantino et al., 2017; Tirelli et al., 2020; Zoppetti et al., 2021) and real data (Ceccherini et al., 2010b; Cortesi et al., 2016; Kuai et al., 2013; Fu et al., 2013, 2016; Cuesta et al., 2013, 2018; Worden et al., 2015).

The approaches for the combined use of two or more observations of the same portion of atmosphere and/or surface to determine the atmospheric and/or surface state could be divided into two main classes (Aires et al., 2012): the SR and the a posteriori combination of the parameters derived from the inversion of the individual measurements.

The SR is commonly used, as it rigorously combines complementary information of the measurements (see, e.g., Landgraf and Hasekamp, 2007; Natraj et al., 2011; Cuesta et al., 2013, 2018; Fu et al., 2013, 2016; Kuai et al., 2013). The SR, however, requires to integrate into a single inversion system the radiative transfer models capable of simulating the measurements of all the sensors involved in the synergistic inversion. Furthermore, the SR requires the simultaneous access to all the (Level 1) measurements used in the inversion, thus implying the need to handle relevant data volumes. These characteristics complicate the SR implementation and increase the computational resources needed.

The a posteriori techniques, such as data fusion (Ceccherini et al., 2010a) or the Kalman filter (Warner et al., 2014), overcome the main complications implied by the SR method by combining the Level 2 products supplied by the individual retrieval processors of the independent measurements. The CDF method (Ceccherini et al., 2015) can be considered a weighted average of parameters, generalized to the case of averaging kernel matrices (AKMs) that are different from the identity matrix. The CDF takes advantage of its simple implementation and of its capability to reduce the quantity of data involved in the synergistic analysis, and it is able to improve the quality of the operational products of individual instruments in terms of both a reduced total error and an increased number of degrees of freedom (DOFs). Ceccherini et al. (2015) show that CDF and SR provide the same solution with the same error and number of DOFs, under (a) linear approximation of the forward model of each measurement in the range of variability between the solutions of the single retrievals and of the synergistic retrieval and (b) assumption of perfectly matching measurements. In this paper, we characterize the differences between SR and CDF results for realistic conditions that may be encountered in the attempt to combine the complementary measurements of two forthcoming satellite missions: Far-infrared Outgoing Radiation Understanding and Monitoring (FORUM) and Infrared Atmospheric Sounding Interferometer – New Generation (IASI-NG).

FORUM will be the ninth Earth Explorer mission of the European Space Agency (Oetjen, 2019; Palchetti et al., 2020; Carnicero et al., 2020; Pachot et al., 2020; Di Natale et al., 2020; Ben-Yami et al., 2022; Di Natale and Palchetti, 2022; Sgheri et al., 2022; Agócs et al., 2022); its launch is scheduled in 2027 on a polar-orbiting satellite. FORUM will fly in loose formation with the MetOp-SG-1A satellite, which will host IASI-NG (Clerbaux and Crevoisier, 2013; Bermudo et al., 2014; Crevoisier et al., 2014; Andrey-Andrés et al., 2018). The key instrument of the FORUM mission is a Fourier transform (FT) spectrometer. It will measure both the far-infrared (FIR) and the mid-infrared (MIR) portion of Earth's upwelling spectral radiance (from 100 to 1600 cm⁻¹). Conversely, IASI-NG will measure only the MIR spectral range, from 645 to 2760 cm⁻¹. The simultaneous exploitation of matching FORUM and IASI-NG spectra will generate products (namely temperature and H₂O profiles, cloud parameters, surface temperature, and spectral emissivity) that will benefit from the information contained in the whole thermal spectrum (from 100 to 2760 cm⁻¹; see Ridolfi et al., 2020; Tirelli et al., 2021).

When FORUM- and IASI-NG-simulated measurements are combined, usually, the differences between the SR and the CDF solutions are not larger than the retrieval error due to measurement noise. For this reason, to accurately characterize these differences, we base the results of our study on statistically significant sets of test retrievals from simulated observations. A first set of test retrievals uses perfectly matching FORUM and IASI-NG measurements, while a second set uses realistically mismatching measurements. All the synthetic measurements used in this paper refer to a clear-sky Antarctic winter scenario, with Earth's surface covered by snow. A dry atmosphere is in fact a prerequisite to retrieve surface spectral emissivity in the FIR region, a key target for the FORUM mission (Ridolfi et al., 2020). Although less interesting due to the large retrieval errors in FIR surface emissivity, to strengthen the conclusions of the present work, the results of two analogous test experiments carried out at mid-latitudes and tropical latitudes are attached to this paper as a Supplement.

The statistics of the differences between the SR/CDF products and the true state parameters allow us to quantify the possible biases and the random errors of the two solutions. For verification purposes, these ex post statistical error estimates can also be compared to the related ex ante predictions provided by the error covariance matrices (CMs) of the two solutions. Finally, the statistics of the differences between the SR and CDF solutions quantify the discrepancies between the two methods for realistic forward model linearity and mismatch between the measurements.

The structure of the paper is as follows. In Sect. 2, we recall the mathematical background of the SR and the CDF approaches. In Sect. 3, we describe the characteristics of the FORUM- and IASI-NG-simulated measurements. In Sect. 4, we introduce the test scenarios and the retrieval setup. In Sect. 5, we discuss the results of the simulated experiments, and, finally, in Sect. 6, we draw the conclusions.

2 Methods

We first recall the equations of the SR and CDF approaches. The formalism adopted is based on that of Rodgers (2000). We indicate with y_i the vectors including the spectral radiances acquired by FORUM for i=1 and by IASI-NG for i=2, respectively, and with x_i, the state vectors identifying the atmospheres probed by the two measurements. Initially, we assume identical atmospheric states, that is x₁=x₂; later we allow for a mismatch between the measurements, both in space and in time, leading to x₁≠x₂. The vectors x_i and y_i are linked by

$$\begin{array}{}\text{(1)}& {\mathit{y}}_i={\mathit{F}}_i\left({\mathit{x}}_i\right)+{\mathit{ϵ}}_{i}i=\mathrm{1},\mathrm{2},\end{array}$$

where F_i(x_i) are the forward models and ϵ_i are the measurement noise errors characterized by the CMs S_yi. For the inversion of the two measurements, we use the optimal estimation (OE) method (Rodgers, 2000), which obtains the solutions as the minimizers of the following cost functions:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathit{\xi }}_i^{\mathrm{2}}\left(\mathit{x}\right)& ={\left({\mathit{y}}_i-{\mathit{F}}_i\left(\mathit{x}\right)\right)}^t{\mathbf{S}}_{yi}^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathit{F}}_i\left(\mathit{x}\right)\right)\\ & +{\left({\mathit{x}}_{\mathrm{a}i}-\mathit{x}\right)}^t{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\left({\mathit{x}}_{\mathrm{a}i}-\mathit{x}\right)\\ & i=\mathrm{1},\mathrm{2},\end{array}\end{array}$$

where S_ai are the CMs of the a priori state vectors x_ai used to constrain the retrievals.

The minima of these cost functions are found using the Gauss–Newton iterative formula:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\mathit{x}}_{i,k}& ={\mathit{x}}_{i,k-\mathrm{1}}+{\left[{\mathbf{K}}_{i,k-\mathrm{1}}^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_{i,k-\mathrm{1}}+{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\right]}^{-\mathrm{1}}\\ & \cdot \left[{\mathbf{K}}_{i,k-\mathrm{1}}^t{\mathbf{S}}_{yi}^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathit{F}}_i\left({\mathit{x}}_{i,k-\mathrm{1}}\right)\right)\right.\\ & +\left.{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\left({\mathit{x}}_{\mathrm{a}i}-{\mathit{x}}_{i,k-\mathrm{1}}\right)\right]i=\mathrm{1},\mathrm{2},\end{array}\end{array}$$

where k indicates the iteration index and ${\mathbf{K}}_{i,k-\mathrm{1}}$ are the Jacobians of the forward models calculated in ${\mathit{x}}_{i,k-\mathrm{1}}$. Iterations are stopped when the following convergence criterion is fulfilled:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{{\mathit{\xi }}_i^{\mathrm{2}}\left({\mathit{x}}_{i,k}\right)-{\mathit{\xi }}_i^{\mathrm{2}}\left({\mathit{x}}_{i,k-\mathrm{1}}\right)}{{\mathit{\xi }}_i^{\mathrm{2}}\left({\mathit{x}}_{i,k-\mathrm{1}}\right)}}<\mathit{\zeta },i=\mathrm{1},\mathrm{2},\end{array}$$

where ζ is a threshold value that in this work taken to equal $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$. In order to cope with forward model non-linearities, the iterative formula of Eq. (3) is modified with the Levenberg–Marquardt (LM) method (Levenberg, 1944; Marquardt, 1963). Specifically, the diagonal elements of the matrix in the leftmost square brackets of Eq. (3) are multiplied by (1+λ_k), where λ_k is a positive coefficient, damping the correction applied to the state ${\mathit{x}}_{i,k-\mathrm{1}}$. At each iteration k, λ_k is increased or decreased depending on whether the cost function (2) is, respectively, larger or smaller as compared to its value at the previous iteration. To make sure that the LM method does not influence the final solution of the retrieval, we actually check the convergence condition only if ${\mathit{\lambda }}_k\le {\mathrm{10}}^{-\mathrm{3}}$.

We indicate with ${\widehat{\mathit{x}}}_i$ the solutions of the two retrievals. They are characterized by error CMs S_i and AKMs A_i given by

$$\begin{array}{}\text{(5)}& {\displaystyle }{\mathbf{S}}_i={\left[{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\right]}^{-\mathrm{1}}i=\mathrm{1},\mathrm{2},\text{(6)}& {\displaystyle }{\mathbf{A}}_i={\left[{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\right]}^{-\mathrm{1}}{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_{i}i=\mathrm{1},\mathrm{2},\end{array}$$

where K_i are the Jacobians of the forward models calculated at the convergence state ${\widehat{\mathit{x}}}_i$. The noise contributions S_n,i to the CMs of Eq. (5) are given by

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\mathbf{S}}_{\mathrm{n},i}& ={\left[{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\right]}^{-\mathrm{1}}\\ & \cdot {\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i{\left[{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{a}i}^{-\mathrm{1}}\right]}^{-\mathrm{1}}i=\mathrm{1},\mathrm{2},\end{array}\end{array}$$

which are obtained by propagating the measurement noise errors ϵ_i onto the solutions ${\widehat{\mathit{x}}}_i$.

2.1 Synergistic retrieval

The SR is obtained by simultaneously fitting the radiances acquired by the two instruments with the forward model simulations, i.e., by minimizing the cost function:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\mathit{\xi }}^{\mathrm{2}}\left(\mathit{x}\right)& =\sum _{i=\mathrm{1}}^{\mathrm{2}}{\left({\mathit{y}}_i-{\mathit{F}}_i\left(\mathit{x}\right)\right)}^t{\mathbf{S}}_{yi}^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathit{F}}_i\left(\mathit{x}\right)\right)\\ & +{\left({\mathit{x}}_{\mathrm{a}}-\mathit{x}\right)}^t{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\left({\mathit{x}}_{\mathrm{a}}-\mathit{x}\right),\end{array}\end{array}$$

where S_a is the error CM of the a priori state x_a assumed for the SR.

As in the case of the inversion of a single measurement, the minimum of this cost function is found using the Gauss–Newton iterative formula that, in the case of the SR, takes the following form:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathit{x}}_k& ={\mathit{x}}_{k-\mathrm{1}}+{\left[\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{K}}_{i,k-\mathrm{1}}^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_{i,k-\mathrm{1}}+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}\\ & \cdot \left[\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{K}}_{i,k-\mathrm{1}}^t{\mathbf{S}}_{yi}^{-\mathrm{1}}\left({\mathit{y}}_i-{\mathit{F}}_i\left({\mathit{x}}_{k-\mathrm{1}}\right)\right)+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\left({\mathit{x}}_{\mathrm{a}}-{\mathit{x}}_{k-\mathrm{1}}\right)\right].\end{array}\end{array}$$

Also in this case, the used formula is modified with the LM method and we take care of ending the iterations with a sufficiently small LM damping parameter. We indicate with $\widehat{\mathit{x}}$ the SR solution. It is characterized by error CM S and AKM A given by

$$\begin{array}{}\text{(10)}& {\displaystyle }\mathbf{S}={\left[\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right]}^{-\mathrm{1}},\text{(11)}& {\displaystyle }\mathbf{A}={\left[\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{K}}_i^t{\mathbf{S}}_{yi}^{-\mathrm{1}}{\mathbf{K}}_i.\end{array}$$

If the two measurements do not refer to the same atmosphere because of temporal and/or spatial mismatches, then the two state vectors x₁ and x₂ are different. In this case we can write

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{\mathit{y}}_{\mathbf{2}}& ={\mathit{F}}_{\mathrm{2}}({\mathit{x}}_{\mathrm{2}}-{\mathit{x}}_{\mathrm{1}}+{\mathit{x}}_{\mathrm{1}})+{\mathit{ϵ}}_{\mathrm{2}}\approx {\mathit{F}}_{\mathrm{2}}\left({\mathit{x}}_{\mathrm{1}}\right)\\ & +{\mathbf{K}}_{\mathrm{2}}({\mathit{x}}_{\mathrm{2}}-{\mathit{x}}_{\mathrm{1}})+{\mathit{ϵ}}_{\mathrm{2}}={\mathit{F}}_{\mathrm{2}}\left({\mathit{x}}_{\mathrm{1}}\right)+{{\mathit{ϵ}}_{\mathrm{2}}}^{\prime },\end{array}\end{array}$$

where we have assumed the difference x₂−x₁ to be sufficiently small so that an expansion to the first order is sufficiently accurate and have introduced the quantity ${{\mathit{ϵ}}_{\mathrm{2}}}^{\prime }$, given by

$$\begin{array}{}\text{(13)}& {{\mathit{ϵ}}_{\mathrm{2}}}^{\prime }={\mathbf{K}}_{\mathrm{2}}({\mathit{x}}_{\mathrm{2}}-{\mathit{x}}_{\mathrm{1}})+{\mathit{ϵ}}_{\mathrm{2}}.\end{array}$$

From Eq. (12), we see that y₂ (the radiances acquired by IASI-NG) can be seen as a measurement of x₁ (the atmospheric state sounded by FORUM) with an error ${{\mathit{ϵ}}_{\mathrm{2}}}^{\prime }$ greater than ϵ₂. If we introduce the mismatch CM S_M of x₂−x₁, characterizing the statistical distribution of the differences between the atmospheric states sounded by the two instruments, then the CM ${\mathbf{S}}_{y\mathrm{2}}^{\prime }$ of ${{\mathit{ϵ}}_{\mathrm{2}}}^{\prime }$ is given by

$$\begin{array}{}\text{(14)}& {\mathbf{S}}_{y\mathrm{2}}^{\prime }={\mathbf{S}}_{y\mathrm{2}}+{\mathbf{K}}_{\mathrm{2}}{\mathbf{S}}_{\mathrm{M}}{\mathbf{K}}_{\mathrm{2}}^t.\end{array}$$

Therefore, in the presence of a mismatch between the two measurements, we still assume that both instruments are sounding the same atmospheric state x₁; however, in the SR we assign to y₂ the error CM ${\mathbf{S}}_{y\mathrm{2}}^{\prime }$, i.e., a larger error as compared to the original one described by S_y2.

2.2 Complete data fusion

The CDF uses the results of the individual retrievals, and its solution is obtained by minimizing the following cost function (Ceccherini et al., 2015):

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{\mathit{\xi }}_{\mathrm{CDF}}^{\mathrm{2}}\left(\mathit{x}\right)& =\sum _{i=\mathrm{1}}^{\mathrm{2}}{\left({\mathit{\alpha }}_i-{\mathbf{A}}_i\mathit{x}\right)}^t{\mathbf{S}}_{\mathrm{n},i}^{-\mathrm{1}}\left({\mathit{\alpha }}_i-{\mathbf{A}}_i\mathit{x}\right)\\ & +{\left({\mathit{x}}_{\mathrm{a}}-\mathit{x}\right)}^t{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\left({\mathit{x}}_{\mathrm{a}}-\mathit{x}\right),\end{array}\end{array}$$

where

$$\begin{array}{}\text{(16)}& {\mathit{\alpha }}_i={\widehat{\mathit{x}}}_i-(\mathbf{I}-{\mathbf{A}}_i){\mathit{x}}_{\mathrm{a}i},\end{array}$$

where I is the identity matrix and S_a is the error CM of the a priori state x_a that constrains the CDF solution.

From Eq. (15) we see that, differently from the SR cost function of Eq. (8), the cost function of the CDF is a quadratic form of x; therefore, its minimum can be found analytically without the need of an iterative procedure. Imposing the gradient of the cost function ${\mathit{\xi }}_{\mathrm{CDF}}^{\mathrm{2}}\left(\mathit{x}\right)$ to zero, we obtain the CDF solution x_f as

$$\begin{array}{}\text{(17)}& {\mathit{x}}_{\mathrm{f}}={\left(\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{A}}_i^t{\mathbf{S}}_{\mathrm{n},i}^{-\mathrm{1}}{\mathbf{A}}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}\left(\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{A}}_i^t{\mathbf{S}}_{\mathrm{n},i}^{-\mathrm{1}}{\mathit{\alpha }}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}{\mathit{x}}_{\mathrm{a}}\right),\end{array}$$

which is characterized by error CM S_f and AKM A_f given by

$$\begin{array}{}\text{(18)}& {\displaystyle }{\mathbf{S}}_{\mathrm{f}}={\left(\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{A}}_i^t{\mathbf{S}}_{\mathrm{n},i}^{-\mathrm{1}}{\mathbf{A}}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right)}^{-\mathrm{1}},\text{(19)}& {\displaystyle }{\mathbf{A}}_{\mathrm{f}}={\left(\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{A}}_i^t{\mathbf{S}}_{\mathrm{n},i}^{-\mathrm{1}}{\mathbf{A}}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}\sum _{i=\mathrm{1}}^{\mathrm{2}}{\mathbf{A}}_i^t{\mathbf{S}}_{\mathrm{n},i}^{-\mathrm{1}}{\mathbf{A}}_i.\end{array}$$

If the two measurements do not exactly coincide both in space and time, we allow for this mismatch by introducing a coincidence error according to the approach described in Ceccherini et al. (2018). Coherently with what is done in the SR, we consider the measurement of IASI-NG as a measurement of the atmospheric state x₁ sounded by FORUM and add the coincidence error to the IASI-NG measurement error. Specifically, in the presence of a mismatch between the measurements, we still use the abovementioned equations for the CDF, with S_n,2 replaced by ${\mathbf{S}}_{\mathrm{n},\mathrm{2}}^{\prime }$, given by

$$\begin{array}{}\text{(20)}& {\mathbf{S}}_{\mathrm{n},\mathrm{2}}^{\prime }={\mathbf{S}}_{\mathrm{n},\mathrm{2}}+{\mathbf{A}}_{\mathrm{2}}{\mathbf{S}}_{\mathrm{M}}{\mathbf{A}}_{\mathrm{2}}^t.\end{array}$$

2.3 Differences between SR and CDF approaches

First, let us consider the case of perfectly matching measurements. If, on the one hand, in the range of variability of the solutions of the individual retrievals and of the SR, the linear approximation can be applied to the forward model of both measurements, then the two methods are equivalent, as demonstrated in the appendix of Ceccherini et al. (2015). On the other hand, when the forward models of the measurements exhibit significant non-linearities in the range of variability of the solutions of the individual retrievals and of the SR, a difference is expected between SR and CDF results. In this case, the SR should provide a more accurate result as the iterative procedure of Eq. (9) takes correctly into account the non-linearities and models the interactions between the information flows arising from the two contributing measurements (Aires et al., 2012).

Now, let us consider the case of measurements not perfectly matching. In the SR, the CM S_y2 of the radiances of IASI-NG is increased as described by Eq. (14). Then, neglecting the non-linearities, the SR should be equivalent to the CDF of the result of the FORUM retrieval and the result of the retrieval of IASI-NG with CM ${\mathbf{S}}_{y\mathrm{2}}^{\prime }$. The IASI-NG retrieval obtained with ${\mathbf{S}}_{y\mathrm{2}}^{\prime }$ produces a different state vector, CM and AKM with respect to those obtained with S_y2. To deal with the mismatch, in the CDF approach only the CM of the IASI-NG retrieval is changed according to Eq. (20), leaving the state vector and the AKM equal to those obtained in the absence of a mismatch. The two approaches, therefore, are slightly different, and we expect a difference in the results.

3 Simulated measurements

As mentioned in Sect. 1, our tests are based on simulated measurements from two forthcoming satellite missions: FORUM and IASI-NG. The two experiments will be installed on two different satellite platforms operating in loose formation. FORUM will fly on a Sun-synchronous polar-orbiting satellite. The orbit inclination is planned to be of 98.7^∘, with a mean local solar time of 09:30 at descending node and satellite altitude of about 830 km. The orbit repeat cycle will be 29 d. These orbit features coincide with those of the MetOp-SG-1A which will host IASI-NG.

The key instrument of the FORUM mission will be an FT spectrometer measuring the spectrum of the upwelling Earth's outgoing longwave radiation (OLR) by looking at nadir (Oetjen, 2019; Palchetti et al., 2020). The ground pixel will be a circle, with a diameter of approximately 15 km. During the acquisition time (≈ 8 s), the ground pixel will be kept fixed with a continuous adjustment of the pointing angle to compensate for the satellite motion (the so-called step and stare technique). No across-track scanning is foreseen. The resulting distance between neighboring ground pixels will be approximately 100 km. FORUM-measured interferograms will be processed to get geolocated and calibrated spectral radiances in the interval from 100 to 1600 cm⁻¹, with (unapodized) spectral resolution of 0.5 cm⁻¹ (full width at half maximum (FWHM) of the response function). The sampling step of the spectrum will be ≈ 0.36 cm⁻¹. As for noise-equivalent spectral radiance (NESR) of the unapodized spectrum, we assume the goal instrument requirement of 40 nW (cm² sr cm⁻¹)⁻¹ in the range between 200 and 800 cm⁻¹ and 100 nW (cm² sr cm⁻¹)⁻¹ elsewhere. The absolute radiometric accuracy (ARA) of the measured spectral radiance is required to be much smaller than the NESR (see Oetjen, 2019; Ridolfi et al., 2020, and Fig. 1 introduced later).

Like FORUM, IASI-NG will also measure the upwelling spectral radiance; however, its focus will be on the MIR region, with a coverage from 645 to 2760 cm⁻¹. The IASI-NG instrument will exploit a detector array to measure, simultaneously, the spectra upwelling from sets of 4×4 ground pixels with a diameter of 12 km. Each set of 16 pixels constitutes the field of regard (FOR) of IASI-NG. The instrument pointing will be scanned across track to get a global coverage of the measurements by acquiring up to seven FORs on both sides of the orbit track. According to Crevoisier et al. (2014), IASI-NG will provide an apodized spectrum with response given by a Gaussian function with FWHM equal to 0.25 cm⁻¹ (the spectral resolution). The sampling step of the spectrum will be 0.125 cm⁻¹, and its NESR will be half of the NESR typical of the current IASI instrument on board MetOp (Crevoisier et al., 2014). The ARA of IASI-NG is specified to be less than 0.25 K (2σ) at a blackbody temperature of 280 K.

Figure 1 is a summary of the NESR and ARA errors expected for FORUM and IASI-NG measurements as a function of wavenumber. As we can see, while not extended to the FIR region and affected by a non-negligible systematic error (ARA), IASI-NG is far less noisy than FORUM in the atmospheric window region (780–980 cm⁻¹). Since this is the spectral interval that carries most of the information on surface temperature, this feature of IASI-NG is of utmost importance to disentangle the retrieved surface emissivity and temperature.

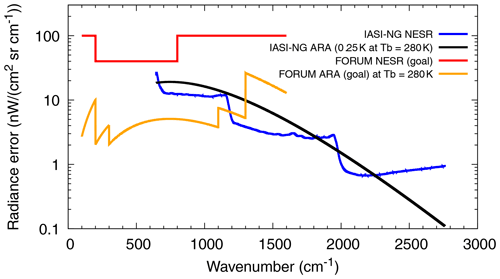
Figure 1 FORUM and IASI-NG NESR and ARA requirements. The ARA errors, originally given in brightness temperature, are converted to radiance units assuming a scene temperature of 280 K. The plotted curves refer to 1σ error bounds.

To generate a synthetic measurement, we proceed as follows. The atmospheric state is first defined by setting the vertical profiles of temperature and constituent's volume mixing ratio (VMR) at a set of fixed pressure levels. The surface is then defined by setting the values of surface pressure, temperature, height above sea level and spectral emissivity (on a 5 cm⁻¹ grid). These inputs are then passed to σ-IASI, a fast monochromatic, parameterized forward model developed at the University of Basilicata, Italy (Amato et al., 2002; Liuzzi et al., 2017; Masiello et al., 2022). From these inputs, σ-IASI computes the outgoing spectral radiance in the interval from 80 to 2780 cm⁻¹, with a wavenumber step as fine as 0.01 cm⁻¹. The instrumental effects are then simulated by convolving this radiance with the apodized instrument spectral response function (AISRF) and adding apodized measurement noise. For FORUM, we assume an AISRF given by a Norton–Beer strong apodizing function (Norton and Beer, 1976, 1977; Naylor and Tahic, 2007) with a maximum optical path difference (MOPD) such that $\mathrm{1}/$(2 MOPD) = 0.413 cm⁻¹, as expected for an unapodized spectral response given by a sinc function with FWHM = 0.5 cm⁻¹ $=\mathrm{1.21}/$(2 MOPD). For IASI-NG, we assume a Gaussian AISRF with an FWHM of 0.25 cm⁻¹.

The measurement error covariance matrices S_y1 and S_y2 of FORUM and IASI-NG measurements are then built considering the NESR figures specified above and the correlations implied by the apodization process. The ARA systematic errors are not considered in the test cases presented in this work. On the one hand, being smaller or of the same order of the NESR, the ARA error has a negligible impact on the convergence of the individual retrievals and on their eventual ill conditioning; thus, discarding this error component does not change the performance of the individual inversions. On the other hand, the ARA error may introduce biases on the retrieved parameters that may show up in the averages. These biases would sum up to the other possible retrieval systematic effects (like convergence error) that we want to keep negligibly small when focusing on the study of the differences between SR and CDF approaches.

Pseudorandom noise extracted from a multi-variate Gaussian distribution consistent with the measurement error CM is finally added to the simulated apodized spectral radiances.

3.1 Mismatches between the FORUM and the IASI-NG measurements

The FORUM orbit will be adjusted to match the MetOp-SG-1A orbit; however, the matching between the two orbits will not be perfect. Necessarily, there will be a time lag between the two satellites. Currently, this lag is specified to be smaller than 1 min. Secondly, the ground tracks of the two satellites will not coincide exactly. The maximum distance between the FORUM and MetOp-SG-1A ground tracks is however required to be smaller than 300 km. These conditions are usually referred to as the requirements for the two satellites to fly in loose formation.

Since FORUM will measure only a single ground pixel in the nadir-looking geometry, its measurements will match only the IASI-NG pixels closest to satellite ground track. The distance between the centers of IASI-NG pixels ranges from ≈ 32 km in the area close to the sub-satellite track to ≈ 87 km for the FORs at the ends of the across-track scan. Simulations actually show that, assuming a distance of 300 km between the ground tracks of the two orbits, the maximum distance between two matching FORUM and IASI-NG pixels will be 26 km, occurring in the unlucky case in which the FORUM pixel falls between two contiguous IASI-NG FORs. On average, the distance between matching pixel centers will be around 10 km, the actual value depending on latitude.

When dealing with mismatching measurements, we always assume the worst case of 1 min time lag and 26 km distance between the closest FORUM and IASI-NG soundings. At these temporal and spatial scales, the inconsistency between the spectra measured by the two instruments may be assumed to arise mainly from the different temperature and H₂O VMR profiles and the different surface temperatures and emissivities. The two measurements may also be inconsistent due to a different cloud coverage; however, as shown in Ridolfi et al. (2020), this occurrence degrades quite significantly the advantages of the synergy. Most likely, in operational conditions, the occurrence of different cloud coverage in the two measurements will be detected from the analysis of co-located imager measurements (available for both FORUM and IASI-NG), and, in this case, neither the SR nor the CDF will be performed. Keeping in mind this possible strategy and considering the additional complications connected with the retrieval of cloud parameters, we decided to limit the present study to clear-sky atmospheres.

The objective of both SR and CDF is to get the best estimate of the atmospheric and surface state corresponding to the air mass and the ground pixel sounded by FORUM, with the help of the IASI-NG measurement. If IASI-NG is not probing the same air mass or ground pixel as FORUM, a mismatch error should be attributed both to the IASI-NG spectrum when used in the SR and to the state vector retrieved from the IASI-NG-only measurement when this is used in the CDF. The mismatch error assigned to the IASI-NG state vector is represented by a block-diagonal CM S_M:

$$\begin{array}{}\text{(21)}& {\mathbf{S}}_{\mathrm{M}}=\left(\begin{array}{ccccc}{\mathbf{S}}_{\mathrm{T}}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& {\mathbf{S}}_{{\mathrm{T}}_{\mathrm{s}}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& {\mathbf{S}}_{\mathrm{H}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& {\mathbf{S}}_{{\mathrm{O}}_{\mathrm{3}}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& {\mathbf{S}}_{\mathrm{e}}\end{array}\right).\end{array}$$

Each block of this matrix is associated with a specific section of the state vector; the various sections describe, respectively: the temperature profile (S_T), surface temperature (${\mathbf{S}}_{{\mathrm{T}}_{\mathrm{s}}}$), H₂O profile (S_H), O₃ profile (${\mathbf{S}}_{{\mathrm{O}}_{\mathrm{3}}}$) and spectral emissivity (S_e).

We estimate the error covariance matrices, S_T, ${\mathbf{S}}_{{\mathrm{T}}_{\mathrm{s}}}$ and S_H, on the basis of the atmospheric and surface fields extracted from the ERA5 reanalysis (Hersbach et al., 2020) for the days from 19 to 21 June 2007. The data refer to a circular area with a radius of 140 km over the Antarctic Plateau. The area is centered around the geographical location (82.861^∘ S, 71.667^∘ E) and the time corresponding to the reference scenario used in the test experiments presented later (see Sect. 4). The data are provided hourly on a regular latitude–longitude grid of $\mathrm{0.25}{}^{\circ }\times \mathrm{0.25}{}^{\circ }$. Profiles are given on 37 pressure levels in the range from 1000 to 1 hPa. Within the selected 140 km radius area, we consider 25 different circular sub-areas with a radius of 26 km (the mismatch threshold). For each of these sub-areas and for each pressure level, we compute the squared deviations of the profile values from the sub-area average. We finally average all the obtained squared deviations to get the space variances used later to build S_M. The time variability is estimated in a similar way. First, we compute the root mean square (rms) of the hourly variations of profiles relating to selected grid points within the 140 km radius area. This hourly rms is then linearly downscaled to estimate the variability corresponding to a 1 min time lag between the FORUM and IASI-NG measurements and then squared to get the covariance of the time variability. The total mismatch variances are obtained by summing up the variances owing to space and time variabilities. Finally, the total error covariance matrices, S_T, ${\mathbf{S}}_{{\mathrm{T}}_{\mathrm{s}}}$ and S_H, are built assuming these total mismatch variances and correlations between profile levels that decrease exponentially with a vertical correlation length of 5 km.

In S_M, we set ${\mathbf{S}}_{{\mathrm{O}}_{\mathrm{3}}}=\mathrm{0}$ for two reasons: first, as compared to the other parameters, ozone shows only a very limited variability within the mismatch margins considered. Second, we retrieve the ozone profile as an auxiliary parameter to limit its interference error on the other target parameters; ozone on its own is not considered a key target parameter for FORUM. Finally, we estimate S_e by applying the statistical estimator of the covariance to a set of 19 surface emissivity models from Huang et al. (2016), preliminarily interpolated to the actual retrieval grid. In the SR, we use Eq. (14) to map the error S_M onto the IASI-NG spectrum.

4 Test scenario and retrieval setup

We illustrate the results of two main sets of tests. The first set is based on the assumption of perfectly matching FORUM and IASI-NG measurements. In the second set, this assumption is dropped and the matching errors described in Sect. 3.1 are considered. In both cases, the objective is to characterize the differences between the results obtained from the SR and CDF approaches. Since these differences are usually smaller or on the order of the retrieval error due to measurement noise, we perform a statistical analysis of a relatively large set of trials obtained by changing the seeds used to initialize the pseudorandom number generator that produces the measurement noise and the perturbed atmospheres. Some features are common to all the test cases presented. For example, the retrieval state vector

$$\begin{array}{}\text{(22)}& \mathit{x}=\left(\begin{array}{c}{\left({\mathit{x}}_{\mathrm{T}}\left(p_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{\mathrm{T}}\left(p_{\mathrm{61}}\right)\right)}^t\\ {\mathit{x}}_{{\mathrm{T}}_{\mathrm{s}}}\\ {\left({\mathit{x}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(p_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(p_{\mathrm{61}}\right)\right)}^t\\ {\left({\mathit{x}}_{{\mathrm{O}}_{\mathrm{3}}}\left(p_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{{\mathrm{O}}_{\mathrm{3}}}\left(p_{\mathrm{61}}\right)\right)}^t\\ {\left({\mathit{x}}_{\mathrm{e}}\left({\mathit{\nu }}_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{\mathrm{e}}\left({\mathit{\nu }}_{\mathrm{63}}\right)\right)}^t\end{array}\right)\end{array}$$

always has the same set of elements, describing the state of the atmosphere and of the surface sounded. It includes the profiles of temperature (${\left({\mathit{x}}_{\mathrm{T}}\left(p_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{\mathrm{T}}\left(p_{\mathrm{61}}\right)\right)}^t$) and H₂O and O₃ VMRs (${\left({\mathit{x}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(p_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(p_{\mathrm{61}}\right)\right)}^t$ and ${\left({\mathit{x}}_{{\mathrm{O}}_{\mathrm{3}}}\left(p_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{{\mathrm{O}}_{\mathrm{3}}}\left(p_{\mathrm{61}}\right)\right)}^t$, respectively), which are represented on a fixed pressure grid of 61 levels in the range from 1013 to 0.005 hPa (p_k with $k=\mathrm{1},\mathrm{\dots },\mathrm{61}$). Surface temperature ${\mathit{x}}_{{\mathrm{T}}_{\mathrm{s}}}$ and spectral emissivity ${\left({\mathit{x}}_{\mathrm{e}}\left({\mathit{\nu }}_{\mathrm{1}}\right),\mathrm{\dots },{\mathit{x}}_{\mathrm{e}}\left({\mathit{\nu }}_{\mathrm{63}}\right)\right)}^t$ are also included in the state vector. Surface spectral emissivity modulates the surface emission (blackbody at temperature ${\mathit{x}}_{{\mathrm{T}}_{\mathrm{s}}}$) and the surface reflectivity (surface is assumed specular in our model); therefore, we expect poor sensitivity to this parameter in spectral intervals where the atmosphere is a strong absorber. For this reason, we retrieve emissivity in the range from 100 to 2200 cm⁻¹ on a fixed, irregular wavenumber grid ${\mathit{\nu }}_{\mathrm{1}},\mathrm{\dots },{\mathit{\nu }}_{\mathrm{63}}$, tuned on the basis of the sensitivity of the measured spectral radiance to this target parameter. Specifically, the retrieval grid step is 20 cm⁻¹ from 300 to 1200 cm⁻¹ and 50 cm⁻¹ in the intervals from 100 to 300 cm⁻¹ and from 1600 to 2200 cm⁻¹. Moreover, emissivity is not retrieved within the interval from 620 to 720 cm⁻¹, where the strong CO₂ absorption band makes the atmosphere fully opaque, and, thus, the measured spectral radiance is not sensitive to the surface parameters. In the radiative transfer computations, surface emissivity is assumed to change linearly between the retrieved grid points. It should be noted that, while the H₂O VMR profile and the FIR surface spectral emissivity of polar regions are key targets for the FORUM mission, the other parameters of the state vector are retrieved only as auxiliary information to preserve the accuracy of the key targets.

Another feature common to all the presented test retrievals is the method used to build the error CMs of the a priori estimates of the state vector. The a priori errors of vertical distribution profiles and of surface temperature coincide with the background errors assumed at the UK Met Office when the current IASI measurements are assimilated in their numerical weather prediction (NWP) system. The specific values of a priori errors are shown in the figures presented later. Regarding the a priori error of surface emissivity, this is set equal to 0.1 in the spectral range covered by the measurements included in the inversion and equal to an arbitrarily small value (10⁻⁴) in the range not covered by the measurements (e.g., from 1600 to 2200 cm⁻¹ in FORUM-only inversions). The large a priori error of 0.1 in the spectral region covered by the measurement permits avoiding any significant bias that may be introduced by the OE approach in the regions where the measurements are sensitive to emissivity. Conversely, the small a priori error in the regions not covered by the measurements ties the retrieved emissivity to its a priori value (equal to 0.99 in all the presented cases), thus avoiding retrieval instabilities. This trick of using an a priori emissivity error dependent on the set of measurements included in the inversion allows us to use the same emissivity retrieval grid in FORUM-only, IASI-NG-only and synergistic FORUM + IASI-NG retrievals, thus making the implementation the CDF technique and its comparison to the SR easier. In all the retrievals, the a priori estimate of the state vector is also used as an initial guess to start the iterations.

As shown in Ridolfi et al. (2020), due to the presence of strong H₂O absorption bands, the FIR emissivity will be retrievable with sufficiently small error only in the presence of dry atmospheres. For this reason, the tests presented in this paper are based on a reference clear-sky atmospheric scenario corresponding to winter conditions over the Antarctic Plateau (82.861^∘ S, 71.667^∘ E, 3600 m a.m.s.l., 20 June 2007) covered by coarse-snow (Huang et al., 2016). This scenario (no. 16) was selected out of a set of 5000 diverse profiles sampled from the outputs of the NWP model of the European Center for Medium-range Weather Forecasts (ECMWF) available from the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT) NWP Satellite Application Facilities (for data and related documentation, see http://www.nwpsaf.eu/site/software/atmospheric-profile-data/, last access: 15 November 2022). These profiles are considered representative of the full range of the atmospheric variability, spanning different seasons, latitudes and surface types. The dataset includes vertical distributions of temperature and VMR of H₂O, CO₂, O₃, N₂O, CO and CH₄ as a function of pressure. For each profile, the database also includes information on geolocation and time of the year, the surface pressure, temperature, and land/sea classification. Profiles of gases not included in the above list, but needed for accurate simulation of atmospheric spectra, were extracted from the Initial Guess for Level 2 (IG2) climatology developed for Michelson Interferometer for Passive Atmospheric Sounding (MIPAS) retrievals (Remedios et al., 2007). In the following we refer to this reference atmospheric and surface state to as x₀.

To reinforce the conclusions of our analysis, additional test experiments were also carried out at mid-latitudes and tropical latitudes. Although at these latitudes the retrieval of FIR surface emissivity is more challenging due to the increased opacity of the atmosphere, the behavior of the SR and CDF methods is actually very similar to that observed with the polar atmospheres considered here. Thus, the results of those experiments are supplied only as a Supplement.

5 Results

5.1 Results in the case of perfectly matching measurements

In the first part of the study, we carried out a set of test retrievals emulating an idealized situation in which both FORUM and IASI-NG measure, with perfect matching, for 900 times, the same area over the Antarctic Plateau, covered by snow with coarse grains. In each occasion of the measurements, surface temperature and the atmospheric state change stochastically with respect to the reference x₀. The stochastic changes comply with the local seasonal variability CM S_S, derived from a 3-month record of ERA5 profiles relating to the grid point closest to the reference location of x₀. The synthetic noise applied to the measurements also changes from measurement to measurement. Since we consider the a priori atmospheric and surface states as extracted from timely updated ECMWF analyses, the a priori estimates for the retrieval also change from measurement to measurement.

More in detail, we repeat for $j=\mathrm{1},\mathrm{\dots },\mathrm{900}$ times the following procedure. We generate FORUM and IASI-NG synthetic observations assuming for both measurements the same true surface temperature and atmospheric state x_t1,j obtained by applying to x₀ a random perturbation (${\mathit{\delta }}_{{\mathbf{S}}_{\mathrm{s}}}\left(j\right)$) belonging to a multi-variate distribution with CM S_S. The surface spectral emissivity used to generate both observations is the reference coarse-snow emissivity spectrum published in Huang et al. (2016). The noise added to FORUM and IASI-NG synthetic observations is consistent with the respective noise error CMs S_y1 and S_y2. As a priori estimates for surface temperature and for the profiles of temperature, H₂O and O₃ VMRs in x_a,j, we use values obtained by applying to the true values in x_t1,j a stochastic perturbation compliant with the a priori error CM. The a priori emissivity estimate is constant versus wavenumber and equal to 0.99. For the generation of each stochastic vector, the routine producing pseudorandom numbers is always reinitialized using the current date and time expressed in nanoseconds. Finally, we carry out the retrievals from FORUM-only, IASI-NG-only and FORUM+IASI-NG (${\widehat{\mathit{x}}}_j$, synergistic) measurements and compute the CDF result x_f,j starting from FORUM-only and IASI-NG-only retrieved state vectors.

After these 900 runs, we evaluate both the average and the standard deviation of the differences between the synergistic/fused results and the true values used for the generation of synthetic observations. The average differences quantify the product's bias, while the standard deviation of the differences is an (ex post) estimate of the product error which, in principle, should equal the product error estimated (ex ante) with the error CMs (see Eqs. 10 and 18). The standard error of the average, i.e., the standard deviation of the differences divided by the square root of the number of trials ($\sqrt{\mathrm{900}}=\mathrm{30}$, in this case), is useful to evaluate whether the determined bias is statistically significant.

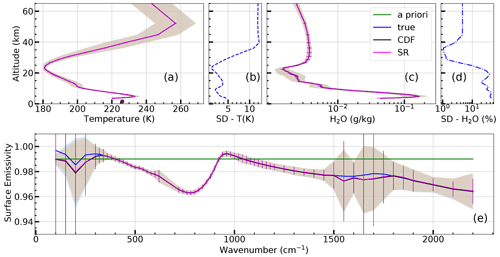
Figure 2 Case of perfectly matching measurements. Average on the 900 trials of a priori (green), true (blue), CDF (black) and SR (magenta) profiles. Panel (a) refers to the temperature profile and to surface temperature (bottom symbol in the plot). Panels (c) and (e) refer to the H₂O VMR and to the surface spectral emissivity profiles, respectively. Error bars represent the average profile errors as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the SR and CDF profiles' standard deviation. The standard deviations of the true profiles of temperature and of the H₂O VMR profiles are plotted in panels (b) and (d), respectively.

Figure 2 shows the 900 trials average of a priori (green), true (blue), CDF (black) and SR (magenta) profiles. Error bars represent the average profile errors as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviation of SR and CDF profiles. Panel (a) refers to the temperature profile and to surface temperature (bottom symbols in the plot). Panels (c) and (e) refer to the H₂O VMR and surface spectral emissivity profiles, respectively. The true profiles used to generate the synthetic observations vary within the local seasonal variability represented by the CM S_S; the resulting standard deviations of temperature and of the H₂O VMR profiles are plotted in panels (b) and (d). This figure is useful for a first visual inspection of the profiles used and of their variability; however, the differences between the various profiles are so small that they cannot be appreciated. With the aim to quantify the agreement of CDF and SR results with the true profiles, Fig. 3 shows the average differences between CDF and true profiles (black) and between SR and true profiles (magenta). Dashed lines represent the average error of CDF (black) and of SR (magenta) solutions, as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviations of the profile differences. From this figure we see that the biases of both the CDF and SR solutions (solid black and magenta lines) are much smaller than the average profile errors (dashed lines). In turn, these latter errors, almost identical for the CDF and the SR solutions, generally agree very well with the ex post error estimation provided by the standard deviation of the differences (shadowed areas). An expected exception occurs for surface emissivity in the spectral regions below 300 cm⁻¹ and between 1550 and 1700 cm⁻¹, where the sensitivity of the measurements to the surface state is very limited. In these regions, the error evaluated from the standard deviation of the differences is smaller than the error predicted by the CMs because here, both the CDF and the SR solutions are strongly tied to the a priori value that, only for emissivity, is constantly equal to 0.99 in all the 900 test runs. For surface temperature we obtain performances analogous to those of the temperature profile at the lowest atmospheric layers. For this reason, for simplicity, surface temperature differences and errors are not shown starting from Fig. 3.

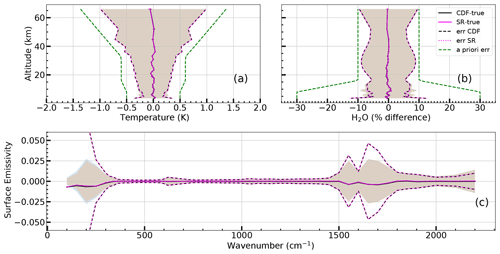
Figure 3 Case of perfectly matching measurements. Average differences between CDF and true profiles (black), and between SR and true (magenta) profiles. Dashed lines represent the average error of CDF (black) and of SR (magenta) as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviations of the differences and error bars are the standard errors of the average differences. Panel (a) refers to the temperature profile. Panels (b) and (c) refer to the H₂O VMR and surface spectral emissivity profiles, respectively.

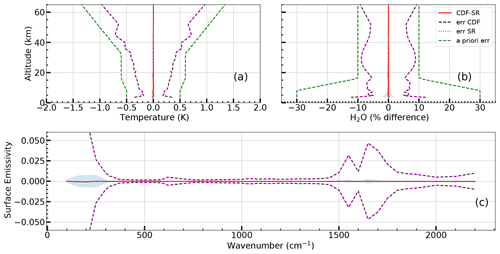
Figure 4 Case of perfectly matching measurements. Average differences between CDF and SR profiles (red). Dashed lines represent the average error of CDF (black) and of SR (magenta) as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviations of the CDF minus SR differences. Panel (a) refers to the temperature profile. Panels (b) and (c) refer to the H₂O VMR and surface spectral emissivity profiles, respectively.

Figure 4 shows the average differences between CDF and SR profiles (solid red lines). Dashed lines represent the average error of CDF (black) and SR (magenta) as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviations of the CDF minus SR differences. Panel (a) refers to the temperature profile, while panels (b) and (c) refer to the H₂O VMR and surface spectral emissivity profiles, respectively. In this case of perfect matching of the measurements, we see that, on average, the differences between CDF and SR solutions are far smaller than the error estimated by the CMs. The standard deviation of the differences (shadowed area) is also much smaller than the error; thus we come to the important conclusion that the differences between the CDF and the SR solutions are much smaller than their associated error also in the individual test runs (not only on average). The very small size of the differences between the CDF and SR solutions implies that the forward model linear approximation used in the CDF is actually very accurate, at least for the FORUM and IASI-NG measurements that we examined.

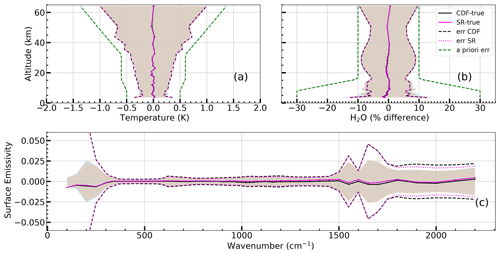
Figure 5 Case of not perfectly matching measurements. Average differences between CDF and true profiles (black), and between SR and true profiles (magenta). Dashed lines represent the average error of CDF (black) and SR (magenta) as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviations of the differences and error bars are the standard errors of the average differences. Panel (a) refers to the temperature profile. Panels (b) and (c) refer to the H₂O VMR and surface spectral emissivity profiles, respectively.

5.2 Results in the case of measurement mismatch

In the second part of the study, we proceed with the same approach adopted for the first set of tests; however, we also introduce a space and time mismatch between the measurements of FORUM and IASI-NG. In this case, we reproduce an idealized scenario in which both instruments measure, for 900 times, a limited area of the Antarctic Plateau surface. The matching of the measurements is not perfect: according to the requirements mentioned earlier, FORUM and IASI-NG measurements are acquired within 1 min from each other and sound, randomly, air masses and surface areas located within a horizontal distance of 26 km from each other. In each of the measurements, the sounded atmosphere and the surface temperature change stochastically with respect to the reference x₀, according to the local seasonal variability represented by the CM S_S. The spectral emissivity of the surface spot sounded by FORUM is always that of the coarse-snow model of Huang et al. (2016), while, to emulate the measurement mismatch, for IASI-NG the emissivity model is that of the medium-snow model from the same authors. As usual, the synthetic noise applied to the measurements also changes from measurement to measurement. As in the first set of tests, the a priori atmospheric and surface states are thought to be extracted from a source like the ECMWF analyses; thus they still change from a pair of FORUM and IASI-NG measurements to another. However, the same a priori data are used to process a given pair of measurements.

Note that, even if the atmospheres and the surface pixels sounded by the two measurements are different, we still assume as homogeneous the individual fields of view (FOVs) of the two instruments. This assumption is motivated by the fact that so far, at least for the FORUM sensor, the response to a non-uniformly illuminated FOV is not known. Moreover, the simulation of FOV inhomogeneities would require an atmospheric model with a spatial resolution on the order of ≈ 2 km; thus, the generation of a statistically significant set of synthetic observations would be extremely demanding from a computational point of view.

In detail, for $j=\mathrm{1},\mathrm{\dots },\mathrm{900}$ times, we repeat the following procedure. We generate the surface temperature and the atmospheric state of the FORUM true state x_t1,j by applying a random perturbation to the reference x₀. The applied perturbation is taken from a multi-variate statistical distribution with zero average and CM S_S, representing the local seasonal variability. The true state x_t2,j sounded by IASI-NG and the a priori state x_a,j are then obtained by applying to x_t1,j two different perturbations consistent, respectively, with the mismatch CM S_M and with the a priori CM S_a,j. Regarding the true surface spectral emissivity, in all the test runs, for FORUM we assume the coarse-snow model of Huang et al. (2016) and for IASI-NG the medium-snow model. The a priori emissivity estimate is constant versus wavenumber and equal to 0.99. Assuming x_t1,j and x_t2,j, we then generate FORUM and IASI-NG synthetic observations, respectively. Finally, we carry out the retrievals from FORUM-only, IASI-NG-only and FORUM+IASI-NG (${\widehat{\mathit{x}}}_j$, synergistic) measurements and compute the CDF result x_f,j starting from FORUM-only and IASI-NG-only retrieved state vectors. In this case the SR uses ${\mathbf{S}}_{\mathrm{y}\mathrm{2},j}^{\prime }$ given by Eq. (14), and, in the CDF, we attribute to ${\widehat{\mathit{x}}}_{\mathrm{2},j}$ the error ${\mathbf{S}}_{\mathrm{n},\mathrm{2},j}^{\prime }$ obtained from Eq. (20). After these 900 runs, we compute the statistics of the differences between the synergistic/fused results and their true values used for the generation of synthetic observations.

Figure 5 is analogous to Fig. 3 for the case of not perfectly matching measurements. We see that the bias of both CDF and SR solutions is still much smaller than the estimated error. As expected, the latter (dashed lines) is slightly increased as compared to the case of perfectly matching measurements; this effect is especially visible for spectral emissivity. We note that, for wavenumbers above 1700 cm⁻¹, the emissivity error of the CDF solution is slightly larger than that of the SR. This difference can be attributed to the different handling of the mismatch error in the CDF and SR approaches, as outlined in Sect. 2.3.

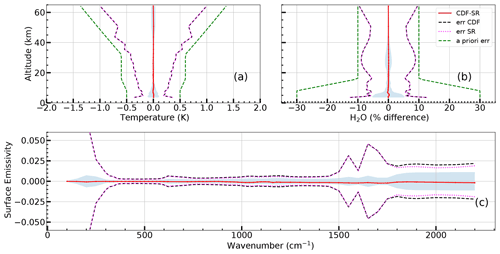
Figure 6 Case of not perfectly matching measurements. Average differences between CDF and SR profiles (solid red lines). Dashed lines represent the average error of CDF (black) and SR (magenta) as evaluated from the error CMs of Eqs. (10) and (18). Shadowed areas represent the standard deviations of the CDF minus SR differences. Panel (a) refers to the temperature profile. Panels (b) and (c) refer to the H₂O VMR and surface spectral emissivity profiles, respectively.

Figure 6 characterizes the differences between CDF and SR solutions in the presence of a mismatch between the measurements. This figure is to be compared to Fig. 4 that refers to perfectly coinciding measurements. We see that, even in the presence of a mismatch, the average differences between the CDF and SR solutions are much smaller than their estimated error. Note, however, that in this case the standard deviation of the spectral emissivity differences between CDF and SR may approach the estimated error. This means that in each individual test run, the difference between the CDF and SR solutions may be of the same order of the error estimated from CMs (10) and (18). Again, since these differences do not exist in the case of perfectly matching measurements, they are to be attributed to the different treatment of the mismatch error in the CDF and SR approaches.

6 Conclusions

In this work, we characterize the differences between synergistic retrieval (SR) and complete data fusion (CDF) techniques that may be used to generate synergistic products from independent remote-sensing measurements of the same air mass and/or ground pixel.

Our assessment is based on synthetic upwelling spectral radiance measurements of the Far-infrared Outgoing Radiation Understanding and Monitoring (FORUM) and the Infrared Atmospheric Sounding Interferometer – New Generation (IASI-NG) missions that will be operational in a few years from two different polar-orbiting satellites. The analysis is limited to clear-sky conditions that are expected to be the most favorable to exploit the complementarity of the measurements considered.

The presented results rely on solid statistics of 900 simulated observations (and related test retrievals) with perfect matching and of 900 simulated observations with a realistic time and space mismatch. The simulated spectral radiances are based on a winter atmospheric scenario over the Antarctic Plateau. The extremely dry atmosphere makes the far-infrared (FIR) region (100–620 cm⁻¹) relatively transparent so that surface spectral emissivity can be retrieved from FORUM measurements with errors smaller than 0.01 in the range from 300 to 600 cm⁻¹. Less favorable conditions that may be encountered at mid-latitudes and tropical latitudes were also investigated, confirming the conclusions of the intercomparison presented here. Therefore, for brevity, the figures relating to the test experiments at mid-latitudes and tropical latitudes are provided only in the Supplement.

For perfectly matching measurements, we find that the differences between the SR and CDF solutions are as small as $\mathrm{1}/\mathrm{10}$ of their error due to the propagation of measurement noise. In the presence of a realistic “worst case” mismatch between the soundings of the two instruments, the two techniques supply more different solutions. In this case, while the average differences are still much smaller than the error due to measurement noise, the SR and CDF solutions from individual pairs of measurements may show differences approaching the errors due to noise. In our simulated experiment, the largest differences are observed in the spectral emissivity and for water vapor at the lowermost altitudes. Since these differences do not exist in the case of perfectly matching measurements, they cannot be ascribed to the forward model linear approximation made in the CDF. The difference is rather due to the different approaches of the two methods in handling the mismatch error.

As a conclusion, we confirm that SR and CDF provide equivalent results when applied to FORUM and IASI-NG complementary measurements. The final choice of which of the two approaches should be preferred for routine operations will depend on the actual architecture of the ground processors of the two missions. The SR approach requires the FORUM ground processor to also access the calibrated spectral radiances measured by IASI-NG with their error CMs; thus it implies a quite relevant throughput of data to be exchanged between the ground processors of the two missions. Conversely, the CDF technique is easily applied a posteriori using state vectors and diagnostic data derived from independent inversions of the individual measurements of the two missions. Despite its simplicity, a drawback of the latter technique originates from the fact that the two combined state vectors, being retrieved by two different mission processors (likely using different forward models), will be affected by different model error components. Some of these components may be correlated; thus specific studies may be required to establish a reliable total error estimate of the fused state vector.