Deep-learning-based post-process correction of the aerosol parameters in the high-resolution Sentinel-3 Level-2 Synergy product

Satellite-based aerosol retrievals provide global spatially distributed estimates of atmospheric aerosol parameters that are commonly needed in applications such as estimation of atmospherically corrected satellite data products, climate modelling and air quality monitoring. However, a common feature of the conventional satellite aerosol retrievals is that they have reasonably low spatial resolution and poor accuracy caused by uncertainty in auxiliary model parameters, such as fixed aerosol model parameters, and the approximate forward radiative transfer models utilized to keep the computational complexity feasible. As a result, the improvement and reprocessing of the operational satellite data retrieval algorithms would become a tedious and computationally excessive problem. To overcome these problems, we have developed a machine-learning-based post-process correction approach to correct the existing operational satellite aerosol data products. Our approach combines the existing satellite retrieval data and a post-processing step where a machine learning algorithm is utilized to predict the approximation error in the conventional retrieval. With approximation error, we refer to the discrepancy between the true aerosol parameters and the ones retrieved using the satellite data. Our hypothesis is that the prediction of the approximation error with a finite training dataset is a less complex and easier task than the direct, fully learned machine-learning-based prediction in which the aerosol parameters are directly predicted given the satellite observations and measurement geometry. Our approach does not require reprocessing of the satellite retrieval products; it requires only a computationally fast machine-learning-based post-processing step of the existing retrieval product. Our approach is based on neural networks trained based on collocated satellite data and accurate ground-based Aerosol Robotic Network (AERONET) aerosol data. Based on our post-processing approach, we propose a post-process-corrected high-resolution Sentinel-3 Synergy aerosol product, which gives a spectral estimate of the aerosol optical depth at five different wavelengths with a high spatial resolution equivalent to the native resolution of the Sentinel-3 Level-1 data (300 m at nadir). With aerosol data from Sentinel-3A and 3B satellites, we demonstrate that our approach produces high-resolution aerosol data with clearly better accuracy than the operational Sentinel-3 Level-2 Synergy aerosol product, and it also results in slightly better accuracy than the conventional fully learned machine learning approach. We also demonstrate better generalization capabilities of the post-process correction approach over the fully learned approach.

1 Introduction

Climate change is one of the biggest challenges our society is facing today (IPCC, 2022). Despite the rapidly progressing climate research, projections of the future climate still contain large uncertainties, with anthropogenic aerosol forcing being among the largest sources of these uncertainties (Pachauri et al., 2014). If more accurate global information about the atmospheric aerosol parameters such as the aerosol optical depth (AOD) and Ångström exponent (AE), and consequently of their product aerosol index (AI), was available, it would enable more accurate modelling of anthropogenic aerosol forcing and could lead to a significant reduction of the uncertainties in future climate projections. Another major challenge for our societies is air quality. In 2017, 2 %–25 % of all deaths worldwide were attributable to ambient particulate matter pollution (GBD 2017 Risk Factor Collaborators, 2018). To monitor air quality and pollution sources more accurately, near-real-time spatially high-resolution estimates of aerosols are needed (van Donkelaar et al., 2015).

Ground-based aerosol observations can be obtained from the Aerosol Robotic Network (AERONET) which utilizes ground-based direct Sun photometers (Giles et al., 2019; Holben et al., 1998). AERONET stations produce accurate information on aerosols because they directly observe the attenuation of solar radiation without interference from land surface reflections. However, AERONET has the limitation that the network consists of a few hundred irregularly spaced measurement stations, leading to a very limited and sparse spatial coverage of aerosol information. The only way to get wide spatial coverage information on aerosols is to use satellite retrievals.

Aerosol satellite retrieval algorithms produce estimates of the aerosol optical properties such as AOD given the satellite observation data such as the top-of-atmosphere (TOA) reflectances or radiances and the information on the observation geometry. Satellite retrieval algorithms have been developed for multiple satellite instruments and the available satellite aerosol data records already span time series that are over 40 years long (Sogacheva et al., 2020). Examples of satellite aerosol data products include the Moderate Imaging Spectroradiometer (MODIS) aerosol products (Salomonson et al., 1989; Levy et al., 2013) and Sentinel-3 Synergy aerosol products.

A satellite aerosol retrieval requires solution of a non-linear inverse problem, where the task is to find aerosol parameters that minimize a misfit (such as the least squares residual) between the satellite observation data and a forward model, which models the causal relationship from the unknown aerosol parameters to the satellite observation data. Atmospheric monitoring satellites cover the globe almost daily with spatial high-resolution observation data, resulting in a huge amount of daily data to be processed by the retrieval algorithms. Due to the excessive amount of data, the operational aerosol retrieval algorithms employ physically and computationally reduced approximations of radiative transfer models as the forward models (e.g. lookup tables) and relatively simple inverse problem approaches, which often ignore some of the observation data to reach fast computation times (Dubovik et al., 2011). Further, the retrieval algorithms typically produce spatially averaged aerosol products that have lower spatial resolution compared to the native satellite Level-1 observation data. Because of these approximations and reductions, the aerosol retrievals have limited accuracy and suboptimal spatial resolution.

Machine-learning-based solutions have been recently proposed for satellite aerosol retrievals in many studies. Compared to conventional inverse problems approaches, machine-learning-based solutions lead to much faster computation time (once the model has been trained) and they also offer a flexible framework for utilization of learning-data-based prior information in the retrieval. Most of the machine learning approaches to aerosol retrieval employ a fully learned approach where the machine learning model is trained to emulate the retrieval directly, that is, to predict the values of the unknown aerosol parameters given the satellite observation data (top-of-atmosphere radiances or reflectances) and observation geometry as the inputs. In Randles et al. (2017), neural-network-based fully learned aerosol retrievals are assimilated into NASA's Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2) reanalysis model. In Di Noia et al. (2017), a fully learned neural network model is used to retrieve the initial AOD for an iterative retrieval algorithm. In Lary et al. (2009), a fully learned approach with MODIS-retrieved AOD and the surface type as additional inputs was used for the AOD retrieval from MODIS data. The results of Lary et al. (2009) were validated using the AERONET data (Holben et al., 1998; Giles et al., 2019). The authors were able to reduce the bias of the MODIS AOD data from 0.03 to 0.01 with neural networks, while with support vector machines even better improvement was reported – AOD bias was less than 0.001 and the correlation coefficient with AERONET was larger than 0.99. However, they performed validation using all the available AERONET network stations both for training and validation. The split between the training and validation datasets was carried out using random sets of the MODIS pixel values. With the random split of all pixels, the data samples from the same AERONET station were present both in training and evaluation datasets, leading potentially to overfitting as the model learns, for example, the surface properties at the locations of the AERONET stations and can thus predict the aerosol properties very accurately at these locations but may not generalize well to data from other regions. In Albayrak et al. (2013), a neural-network-based fully learned model was trained and evaluated for MODIS AOD retrieval. In their model, MODIS reflectances, measurement geometry information, MODIS AOD and its quality flag were used as the input to predict the AOD. They found their model to produce more accurate AOD retrievals than the operational MODIS Dark Target (DT) algorithm. In Lanzaco et al. (2017), a slightly different type of machine-learning-based approach was used to improve satellite AOD retrievals. The authors used MODIS AOD retrievals and local meteorology information as inputs to predict the AOD in South America. This approach, which combines the conventional AOD retrievals and local meteorology information, was found to improve the AOD accuracy over the operational MODIS AOD. A problem in fully learned approaches is that they rely only on the training data and do not employ physics-based models in the retrievals. This may cause problems for the model to generalize to cases in which the inputs are outside the input space spanned by the training dataset.

In Lipponen et al. (2021), we proposed a model-enforced machine learning model for post-process correction of satellite aerosol retrievals. The key idea in the model-enforced approach is to exploit also the model and information of the conventional retrieval algorithm and train a machine learning algorithm for correction of the approximation error in the result of the conventional satellite retrieval algorithm. Previously, the post-process correction approach has been found to produce more stable and accurate results than a fully learned approach in generation of surrogate simulation models (Lipponen et al., 2013, 2018) and in medical imaging; see, for example, Hamilton et al. (2019). The advantages of the model-enforced post-process correction approach are improved accuracy over the existing data products and the possibility to correct the existing products by a simple post-processing step without need for any reprocessing of the existing retrieval algorithms, which are usually managed and operated by the algorithm development teams. In Lipponen et al. (2021), the model-enforced approach was combined with a random forest regression algorithm for post-process correction of MODIS AOD and AE products using collocated MODIS and AERONET aerosol data for training the correction model for the approximation error in AOD and AE in the MODIS DT over land product. The post-process correction was found to yield significantly improved accuracy over the MODIS AOD and AE retrievals, and the correction approach resulted in better accuracy retrievals than the fully learned machine learning approach.

In this paper, we propose a post-process-corrected high-resolution Sentinel-3 Synergy aerosol product. The product is based on the high-resolution Sentinel-3 Level-2 Synergy land product aerosol parameters with 300 m spatial resolution and the model-enforced machine learning approach, where a feed-forward neural network is trained for post-process correction of the approximation error in the Sentinel-3 Level-2 Synergy aerosol product. The training of the neural network is based on collocated Sentinel-3 Synergy and AERONET data from five selected regions of interest. Given the Sentinel-3 observation data and high-resolution aerosol products as input, our model produces an estimate of the AOD at five wavelengths utilizing the native 300 m resolution of the Sentinel-3 observation data.

The rest of this paper is organized as follows. In Sect. 2, we describe the approximation error model for post-process correction of the satellite aerosol retrieval. Section 3 explains the preprocessing of the Sentinel-3 and AERONET data for machine learning and the neural network model used for the regression task. Section 4 gives the results, and Sect. 5 gives the conclusions.

2 Post-process correction model of satellite aerosol retrievals

Let y∈ℝ^m denote an accurate satellite aerosol retrieval:

$$\begin{array}{}\text{(1)}& \mathit{y}=f\left(\mathit{x}\right),\end{array}$$

where vector y contains the output of the satellite retrieval algorithm, $f:{\mathbb{R}}^n\mapsto {\mathbb{R}}^m$ is an accurate retrieval algorithm, and x∈ℝⁿ contains all the algorithm inputs including the observation geometry and Level-1 satellite observation data such as the top-of-atmosphere reflectances. Typically, the retrieval is carried out one image pixel at a time, and the aerosol retrieval y can consist, for example, of AOD and AE for a single image pixel, or as in the present study, AOD in a single image pixel at five wavelengths.

In practice, due to uncertainties in the auxiliary parameters, such as land surface reflectance, of the underlying forward model utilized in the retrieval, extensive computational dimension of the problem and processing time limitations, it is not possible to construct an accurate retrieval algorithm f but an approximate retrieval algorithm,

$$\begin{array}{}\text{(2)}& \stackrel{\mathrm{̃}}{\mathit{y}}\approx \stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right),\end{array}$$

has to be employed instead. The approximate retrieval $\stackrel{\mathrm{̃}}{f}$ is typically based on physically simplified and computationally reduced approximate forward models that are used due to the huge amount of data and the need for computational efficiency. The utilization of the approximate retrieval algorithm leads to an approximation error,

$$\begin{array}{}\text{(3)}& e\left(\mathit{x}\right)=f\left(\mathit{x}\right)-\stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right),\end{array}$$

in the retrieval parameters.

The core idea in the model-enforced post-process correction model is to improve the accuracy of the approximate retrieval (Eq. 2) by machine learning techniques (Lipponen et al., 2021). With Eqs. (1)–(3), the accurate retrieval can be written as

$$\begin{array}{}\text{(4)}& \begin{array}{rl}\mathit{y}& =f\left(\mathit{x}\right)\\ & =\stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right)+\left[f\left(\mathit{x}\right)-\stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right)\right]\\ & =\stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right)+e\left(\mathit{x}\right).\end{array}\end{array}$$

To obtain the corrected retrieval, Eq. (4) is used to combine the conventional (physics-based) retrieval algorithm $\stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right)$ and a machine-learning-based model $\widehat{e}\left(\mathit{x}\right)$ to predict the realization of the approximation error e(x) to obtain a corrected retrieval:

$$\begin{array}{}\text{(5)}& \mathit{y}\approx \stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right)+\widehat{e}\left(\mathit{x}\right).\end{array}$$

Note that this approach is different from a conventional fully learned machine learning model in which the aim is to emulate the accurate retrieval algorithm f(x) with a machine learning model,

$$\begin{array}{}\text{(6)}& \mathit{y}\approx \widehat{f}\left(\mathit{x}\right),\end{array}$$

that is trained to predict the retrieval y directly from the satellite observation and geometry data x; see Fig. 1 for a flowchart of fully learned and model-enforced regression models.

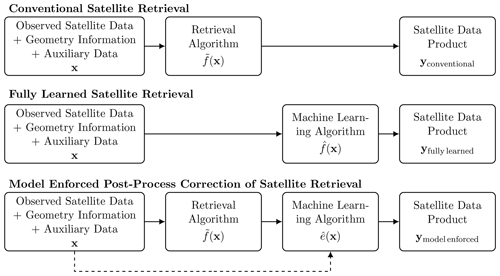
Figure 1 Top: conventional satellite retrieval. Middle: fully learned machine-learning-based satellite retrieval approach. Bottom: model-enforced post-process correction of satellite retrieval approach.

The reason why the model-enforced approach (Eq. 5) can be expected to perform better than the fully learned model (Eq. 6) is that the approximation error e(x) is a simpler function for machine learning regression than the full physics-based retrieval f(x), thus resulting in more accurate results than with a fully learned approach (Lipponen et al., 2013, 2018). Also, while the fully learned approach utilizes an ensemble of satellite observation data as learning data, the model-enforced approach utilizes also the additional information in the approximate retrievals. Also, as the training of the post-process correction is based on existing satellite data and retrievals, the implementation can be done in a straightforward manner, for example, using black-box machine learning code packages and used for correction of past satellite retrievals without recomputing the approximate retrieval products $\stackrel{\mathrm{̃}}{f}\left(\mathit{x}\right)$. In addition, the post-process correction model is also flexible with respect the choice of the statistical regression model, and the choice of the regression model can be tailored to different retrieval problems separately.

3 Methods

This section describes the construction of the learning and test data for the machine learning retrieval of Sentinel-3 aerosol product with the post-process correction model (Eq. 5) and the fully learned model (Eq. 6). The selection of the neural network models and training of the networks is also described. For training and validation of the post-process correction, we use the high-resolution Sentinel-3 Level-2 Synergy and AERONET aerosol data.

3.1 Sentinel-3 satellite datasets

Sentinel-3 is a European ocean and land mission. Currently, two satellites related to this mission (Sentinel-3A and 3B) are flying and collecting data. In this study, we use the Sentinel-3 Ocean and Land Color Instrument (OLCI) and Sea and Land Surface Temperature Radiometer (SLSTR) data. OLCI is a medium-resolution imaging spectroradiometer (spatial resolution about 300 m at nadir) with 21 spectral bands from 400 to 1020 nm. SLSTR is an imaging radiometer with dual-view capabilities. The pixel size of SLSTR is from 500 m to 1 km and spectral coverage is from visible to thermal infrared in nine standard bands (S1–S9). The swaths of these two instruments overlap, allowing combined products to exploit data from both instruments. The high-resolution Sentinel-3 Level-2 Synergy land aerosol product (North and Heckel, 2010) is this type of combined product, which we will post-process correct by the model (Eq. 5).

We use both Level-1b and Level-2 data of the Sentinel-3 satellite mission data products from both Sentinel-3A and Sentinel-3B satellites. The Level-1b data include the information about the measurement geometry and the satellite observed reflectances. The Level-2 data include the Synergy retrieval data and the corresponding quality information. We use the SLSTR Level-1b data from the product SL_1_RBT, OLCI Level-1b data from the OL_1_ERR data product and Sentinel-3 Level-2 data from the SY_2_SYN data product. We use year 2019 data in our study. For more information on the Sentinel-3 mission datasets, see https://sentinel.esa.int/web/sentinel/missions/sentinel-3/data-products (last access: 27 August 2021). 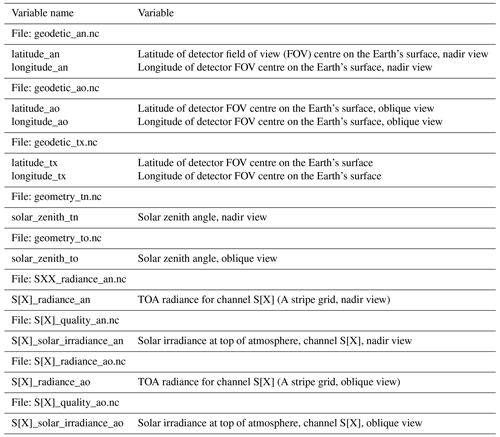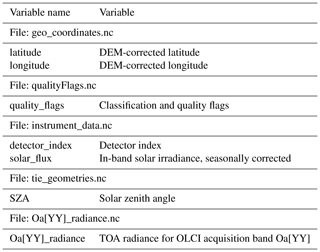The Sentinel-3 data used in the models are listed in Appendix A.

3.2 AERONET

AERONET is a global network of Sun photometers (Holben et al., 1998). AERONET has a direct Sun data product that has both the AOD and AE data that we will use for training and testing of the machine learning models. AERONET is commonly used as an independent data source, and all the data are publicly available at the AERONET website (https://aeronet.gsfc.nasa.gov/, last access: 27 August 2021). An extensive description of the AERONET sites, procedures and data provided is available from this website. Ground-based Sun photometers provide accurate measurements of AOD, because they directly observe the attenuation of solar radiation without interference from land surface reflections. The AOD-estimated uncertainty varies spectrally from ±0.01 to ±0.02, with the highest error in the ultraviolet wavelengths (Giles et al., 2019; Eck et al., 1999). In this study, we use AERONET, version 3, Level-2, direct Sun algorithm data. The AERONET variables used in our studies are listed in Appendix C.

3.3 Regions of interest

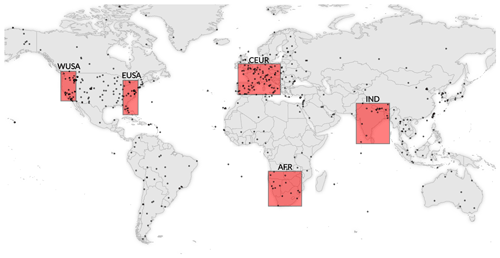
The training and testing of the post-process correction model is based on Sentinel-3 and AERONET data for the year 2019 from five regions of interest shown in Fig. 2. The regions of interest were selected so that different types of aerosol regions based on aerosol source and type, AOD values and different types of surface reflectances are included and also that the areas have good enough coverage of AERONET stations.

Figure 2 Regions of interest. Black dots indicate locations of AERONET stations.

The data for the machine learning procedures consist of collocations of Sentinel-3 pixels with aerosol information and AERONET data. We use the same ±30 min temporal thresholds for the collocation procedure as in Petrenko et al. (2012) and a spatial collocation radius of 5 km. We also require that the aerosol data in the pixels we use are not flagged as filled, climatology data, too-low values, high error, partly cloudy or ambiguous clouds. Furthermore, we require that the pixels we use do not contain any cosmetic Level-1 data. Our selections lead to a total number of 5526 collocated Sentinel-3–AERONET overpasses for the machine learning procedures.

The AERONET stations were divided to separate training, validation and testing sets for good generalization of the machine learning procedures. More specifically, the stations were randomly split into two sets for 2-fold cross validation. To ensure as equal spatial distribution of AERONET stations as possible in both sets, we carried out the random split separately for each region of interest. To study the effect of randomness on the splits of AERONET stations, we tested our approach with multiple random splits. We did not observe significant differences in the results between different random splits of the AERONET stations.

3.4 Input and output data for the machine learning models

The aerosol retrieval y∈ℝ⁵ in both the post-process correction approach (Eq. 5) and the fully learned approach (Eq. 6) consist of AODs for a single 300×300 m² (at nadir) image pixel at wavelengths of 440, 500, 550, 675 and 870 nm. These wavelengths are native wavelengths in the AERONET and Sentinel-3 Level-2 Synergy aerosol products in the sense that the AERONET produces AOD at 440, 500, 675 and 870 nm and the Synergy product at 550 nm.

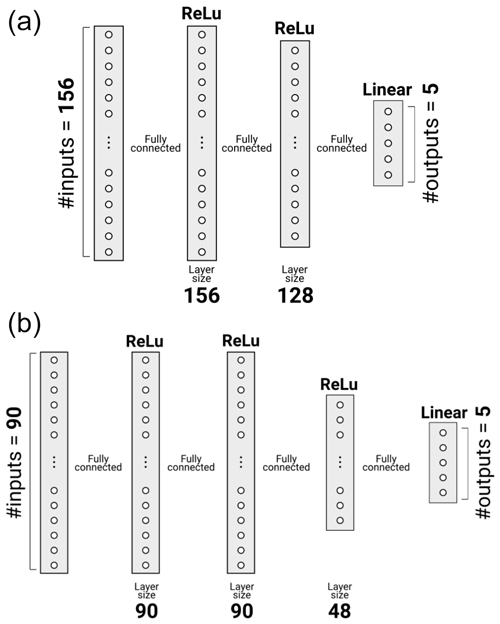
In the fully learned model (Eq. 6), the regression target y∈ℝ⁵ consist of the AERONET AODs at the selected five wavelengths. The AERONET AOD at the Synergy 550 nm channel was estimated as the mean of AOD 550 nm obtained from Ångström law based on AERONET AOD at 500nm and AE 440–870 nm. The input data for the fully learned model contain Sentinel-3 satellite geometry and observation variables for a single image pixel. All the input and output variables were standardized by subtracting the training dataset mean and dividing by the standard deviation. To retain the spectral dependency of the AOD values at different wavelengths, all the AOD variables were standardized together using the mean and standard deviation of all AOD wavelengths. In case some of the inputs contain a missing value, it is filled with the average value of the training dataset. We also add a binary $(\mathrm{0}/\mathrm{1})$ inputs for each input variable to indicate if the data were filled. These selections and processing leads to an input vector x∈ℝ⁹⁰. On average, the input data of the fully learned and post-process correction models contained about 8 % and 6 % of missing values, respectively. See the Appendix B for the Sentinel-3 data file variable names of the inputs and outputs.

In the post-process correction approach, the regression target e∈ℝ⁵ consist of the approximation error between AERONET and Synergy spectral AOD. The Synergy aerosol product contains AOD and AE at 550 nm, which are transformed by the Ångström law to obtain the Synergy AOD product at the wavelengths of 440, 500, 675 and 870 nm. The input data of the post-correction model contain the same geometry and Level-1 data variables that are used in the fully learned model plus the Sentinel-3 Level-2 Synergy aerosol data. Furthermore, the inputs and outputs are standardized and the missing values filled similarly to those for the fully learned model. These selections lead to an input x∈ℝ¹⁵⁶.

3.5 Deep-learning-based regression models

A fully connected feed-forward neural network was selected as the model for the supervised learning tasks of estimating the regressors $\widehat{f}\left(\mathit{x}\right)$ in Eq. (6) and $\widehat{e}\left(\mathit{x}\right)$ in Eq. (5). In the neural network, the rectified linear unit (ReLu) was used as the activation function for all the hidden layers and no activation function was employed for the output layer. The weight coefficients of the neural net were estimated by minimization of the mean squared error (MSE) loss functional with the ADAM optimizer. In the network training, batch size was 512, initial learning rate $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$, and the termination criterion for the learning was set to maximum 10 000 epochs or until validation loss started to increase with patience tolerance set to 10 epochs. For further information on deep learning and neural networks, see, e.g. Goodfellow et al. (2016).

The architecture of the feed-forward neural networks was optimized by utilizing the asynchronous successive halving algorithm (ASHA) (Li et al., 2020). In the ASHA optimization, the maximum number of trial network architectures was set to 2500 and the algorithm was allowed to use up to 500 epochs in a single trial. The space of feasible states for the number of hidden layers in the ASHA optimization was set to $(\mathrm{2},\mathrm{3},\mathrm{4})$ and the number of nodes in the hidden layers was allowed to be up to the number of elements in the input vector x. The optimization of the network architectures by ASHA led to the network structures shown in Fig. 3 for the fully learned approach $\widehat{f}\left(\mathit{x}\right)$ and the post-process correction approach $\widehat{e}\left(\mathit{x}\right)$. These network architectures were utilized in the final training of the models.

Figure 3 Schematic figure of neural network architectures used. (a) Correction network $\widehat{e}\left(\mathit{x}\right)$. (b) Regression network $\widehat{f}\left(\mathit{x}\right)$.

3.6 Implementation

The neural network computations were implemented in Python utilizing Pytorch and the ASHA optimization utilizing the Ray-tune package. The codes for the fully learned model and post-process correction model will be made available. See the code and data availability section for information on how to obtain the code to run the post-process correction and load a sample dataset.

4 Results

The accuracy of the post-process correction is tested using AERONET data as the ground truth for the aerosol retrievals and the results are compared to the high-resolution Sentinel-3 Level-2 Synergy aerosol product and to the fully learned retrieval model (Eq. 6).

Figure 4 shows scatter plots of the AOD retrievals with the Sentinel-3 Level-2 Synergy product (left column), fully learned machine learning (middle column) and post-process correction model (right column) against the AERONET data at all the test data stations at the four visible-to-near-infrared wavelengths of 440, 500, 675 and 870 nm measured by the AERONET. Each figure shows the coefficient of determination based correlation coefficient R², root mean squared error (RMSE) and median bias as the metrics to compare the retrievals. The figures show also the ratio of samples that are inside the Dark Target over land expected error (EE) envelope of $\pm (\mathrm{0.05}\mathit{\%}+\mathrm{15}\mathit{\%})$. As can be seen, the machine learning approaches clearly improve the accuracy of the AODs compared to the high-resolution Sentinel-3 Level-2 Synergy product. Between the two machine learning approaches, the post-process correction model has otherwise better R², RMSE and median bias error metrics than the fully learned model with the exceptions of the bias being the same as with the fully learned model at 500 and 675 nm. The ratio of samples inside the Dark Target EE envelope is very similar to that of the post-process correction and fully learned models. A notable feature in the figures is that there are significantly less samples and relatively more “outliers” for large AOD values than for small AOD values. The accuracy of the machine learning estimates also improves for the higher wavelengths, which do contain fewer high AOD values. These findings can be attributed to the fact that the learning data contain relatively few samples for large AOD (the number of samples with AOD >0.5 is less than 5 %). This indicates that more high-AOD-value learning data would be needed to improve the prediction of the high AOD values.

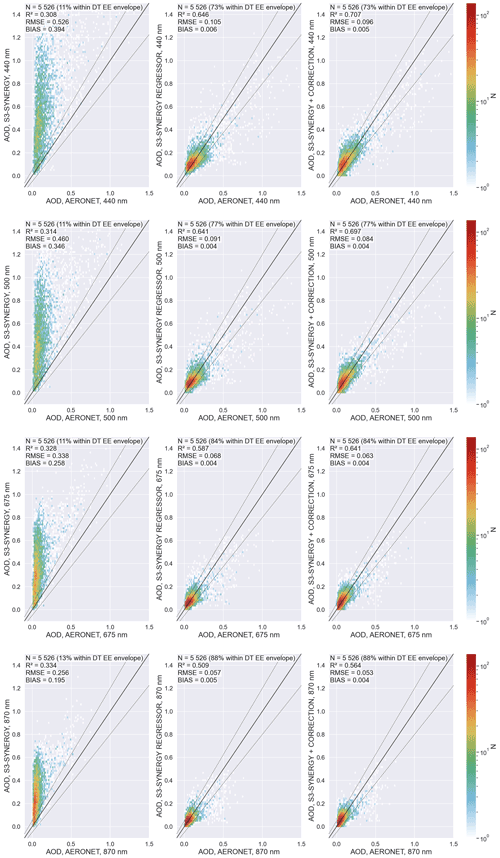
Figure 4 Estimated AODs at the wavelengths employed in the AERONET. Top to bottom: 440, 500, 675 and 870 nm. Left: Sentinel-3 Level-2 Synergy AOD product. Middle: fully learned regressor model. Right: post-process correction.

Figure 5 shows a comparison of AOD at the native Sentinel-3 Level-2 Synergy wavelength of 550 nm, AE and AI. Given the estimated AODs at the five wavelengths, the AE was estimated as a separate post-processing step by utilizing the standard approach (e.g. in AERONET) where AE is estimated by a least squares fit to the linearization of the Ångström law. In AERONET, the AE estimation is carried out using an ordinary least squares type of method that rejects clear outliers from the data to improve the outlier tolerance of the AE estimation. The difference to AERONET AE obtained using ordinary least squares fitting with no outlier treatment, however, is small. The AI is computed then as product of the AOD and AE. AI has been considered as a better proxy for cloud condensation nuclei (CCN) than AOD (Gryspeerdt et al., 2017), since AI is more sensitive than AOD to the accumulation mode aerosol concentration. Figure 5 shows that the machine learning approaches lead to clearly improved estimates of AOD 550 nm, AE and AI compared to the Sentinel-3 Level-2 Synergy product. The post-process correction approach produces the best RMSE, R² and EE metrics for the AOD estimates. From the AE estimates, we observe that the high-resolution Sentinel-3 Level-2 Synergy AE product is uninformative as it produces the same constant value (approximately 1.1) for all of the test data points with a wide range of AERONET AEs. For the AE, the post-process correction approach has a smaller bias and visibly better correlation (with a nearly 2 times larger R² metric) but worse RMSE than the fully learned model. For the AI, the post-process correction has better RMSE, bias and R² metrics compared to the fully learned model.

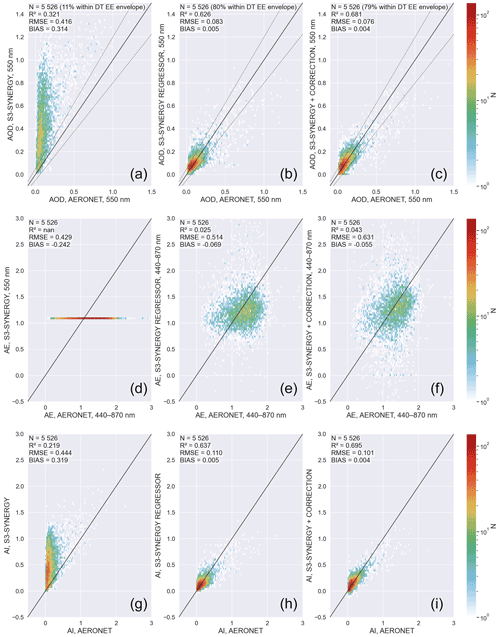
Figure 5 Rows from top to bottom: AOD (550 nm), AE, and AI. (a, d, g) Sentinel-3 Level-2 Synergy product. (b, e, h) Fully learned regressor model. (c, f, i) Post-process correction model.

Figure 6 shows AERONET and Sentinel-3-based time series of AOD at 550 nm over three AERONET stations, Madrid, Paris and Rome_Tor_Vergata, for the year 2019. In all stations, the overestimation of AOD by the Sentinel-3 Level-2 Synergy product is evident. The Sentinel-3 Level-2 Synergy AOD has also a clear seasonal cycle with higher AODs occurring in summer and lower AOD in winter. Both the fully learned model and post-process-corrected Sentinel-3 Synergy AOD are in very good agreement with the AERONET AOD. Furthermore, the regressor and post-process correction model AOD capture very well the events of elevated AOD with a duration of several days.

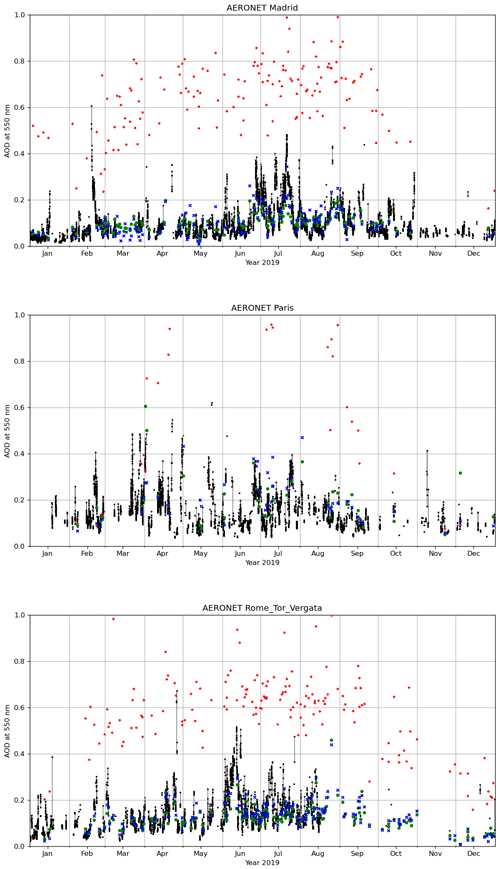
Figure 6 AOD at 550 nm time series for three AERONET stations. The black lines and dots indicate AERONET measurements, red diamonds indicate Sentinel-3 Level-2 Synergy, green circles indicate the fully learned regression model, and blue crosses indicate the corrected Sentinel-3 Synergy retrievals.

In Fig. 7, monthly averages of AOD at 550 nm in western Europe for January, April, July and October 2019 are shown for the Sentinel-3 Level-2 Synergy, fully learned model and post-process correction-model-based data. Again, the significantly higher AOD of Sentinel-3 Level-2 Synergy compared to the other two models is evident. The figure also clearly shows that the amount of data varies quite significantly throughout the year mainly due to clouds and snow, and more data are available for April and July than for January and October. All datasets show some spatial variations of AOD over Europe, and some cities and regions, such as Paris, France and the Po Valley, Italy, clearly show up in AOD maps.

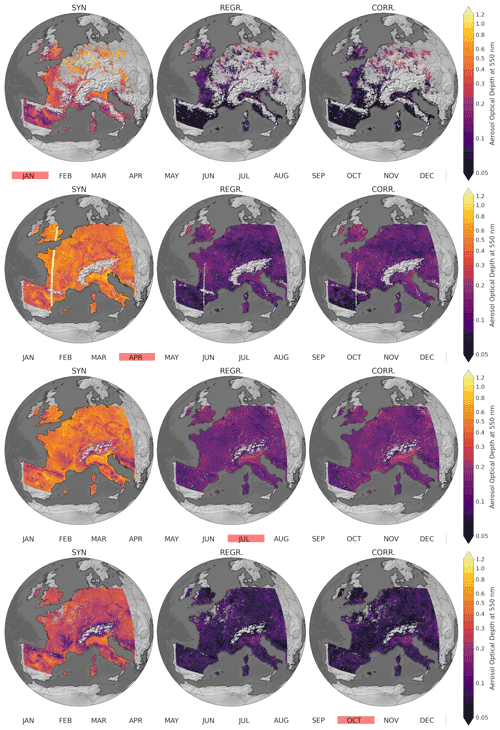
Figure 7 Monthly averages of AOD at 550 nm for January (first row), April (second row), July (third row) and October (fourth row) 2019. Left column: Sentinel-3 Level-2 Synergy. Middle column: fully learned regressor model. Right column: corrected Sentinel-3 Synergy.

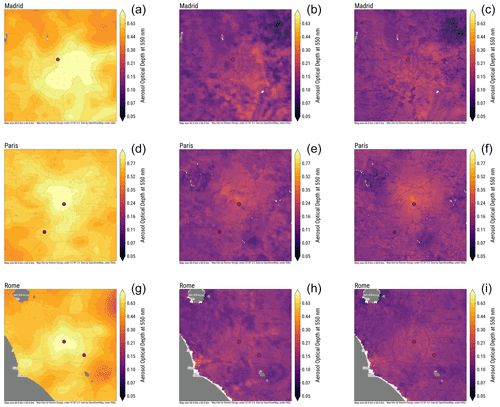
Figure 8 July 2019 monthly averages of AOD at 550 nm for Madrid (a, b, c), Paris (d, e, f) and Rome (g, h, i). (a, d, g) Sentinel-3 Level-2 Synergy. (b, e, h) fully learned regressor model. (c, f, i) Corrected Sentinel-3 Synergy. Circles represent the monthly averages of AERONET stations.

Figure 8 shows monthly averages of AOD at 550 nm for Madrid, Paris and Rome in July 2019. The filled circles in the images indicate the monthly averages of the AERONET stations present in the regions. The Sentinel-3 Level-2 Synergy data product clearly produces a much higher AOD values then the fully learned and post-process correction models, and the overestimation with respect to AERONET is also evident. The Sentinel-3 Level-2 Synergy AOD is also, due to spatial median filtering of the data, much smoother than that of the two other models. For the fully learned and post-process correction models, the AOD values are very close to the AERONET AODs at the AERONET sites, and some high-resolution features are also clearly visible in the data. For all three cities, both the fully learned and post-process correction model show some neighbourhoods with elevated AOD. The correction model AOD shows even more details and less artefacts than the fully learned model AOD. For example, in Rome, the road from the city centre to the airport is clearly visible from the AOD data, while the regression model does not show this road. The fully learned model also has some more box-shaped spatial anomalies than the other models.

To study the generalization capabilities of the models, we carried out a test in which we evaluated the fully learned and post-process correction models' accuracy in the central European region. The machine learning models were trained using data from regions of interest outside central Europe (eastern US, western US, southern Africa, India). The test aimed to evaluate how the models generalize to data far from the training data regions, possibly with different dominant aerosol types and surface reflectances. Figure 9 shows the results for this test for the AOD at 550 nm in the central European region. The post-process correction results in clearly more accurate AOD estimates than the fully learned model. The result indicates that using the training data from nearby regions improves the model performance, and the post-process correction model performs better than the fully learned model also in regions far from the training data regions.

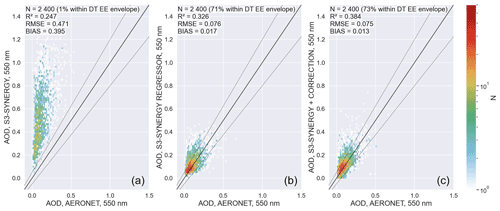
Figure 9 AOD (550 nm) for central Europe and the year 2019. Machine learning models are trained using data outside the central European region. (a) Sentinel-3 Level-2 Synergy product. (b) Fully learned regressor model. (c) Post-process correction.

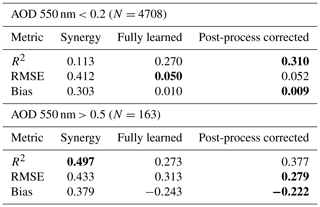
To evaluate the models' performance in low and high AOD conditions, we evaluated the results corresponding to AERONET AOD at 550 nm smaller than 0.2 and larger than 0.5. The results are shown in Table 1. The post-process-corrected model results in the best bias metric in both low and high AOD conditions. In addition, the post-process-corrected model results in the best R² in low AOD and the best RMSE in high AOD conditions. The fully learned model results in about 4 % lower RMSE than the post-process-corrected model in low AOD. The Synergy R² is the best for the high AOD cases but there are only 163 samples in the high AOD cases so more data would be needed for a more reliable evaluation of the models in high AOD conditions.

Table 1 Error metrics for the satellite data product AOD at 550 nm corresponding to small (<0.2) and large (>0.5) AERONET AOD. The bold font indicates the best performing model.

5 Conclusions

We have developed a deep-learning-based post-process correction of the aerosol parameters in the high-resolution Sentinel-3 Level-2 Synergy land product. Sentinel-3 Synergy also has an aerosol data product specifically designed to retrieve the aerosol parameters. The aerosol data product, however, has a spatial resolution of 4.5 km, whereas the land product provides data with the Sentinel-3 instrument's full spatial imaging resolution of 300 m. The drawback in the Synergy land product aerosol parameters is their relatively poor accuracy. The aim of the post-process correction is to significantly improve the accuracy of the Sentinel-3 Level-2 Synergy land product aerosol parameters. The correction is carried out as a computationally lightweight post-processing step, and therefore there is no need for rerunning the actual Synergy retrieval algorithm to obtain the corrected aerosol data. This is a major benefit of the post-process correction approach as rerunning of the original retrieval algorithm is a time-consuming process and often cannot even be carried out by the individual researchers. As a reference for the machine-learning-based post-process correction of the Sentinel-3 Level-2 Synergy data product, we also trained a fully learned machine-learning-based regression model that carries out the full aerosol retrieval using Sentinel-3 Level-1 data.

The results show that the fully learned and post-process correction machine learning approaches produces a clear improvement in the aerosol parameter accuracy over the official Synergy data product. The post-process correction approach leads generally to a more accurate aerosol parameters than the fully learned approach. While the improvement of the post-process correction over the fully learned approach is not very large in the absolute scale, relatively the post-process-corrected product provides the best statistical comparison. For example, in AOD at 550 nm, R² improves by about 9 %, RMSE is 8 % smaller, and bias decreases by 20 % in the post-process-corrected model when compared to the fully learned model. In some applications, such as data assimilation, these relative improvements may be relevant for the accuracy of the data assimilation model. The post-process correction approach combines information both from the physics-based conventional retrieval algorithm and machine learning correction, whereas the fully learned model does not include any physics-based model information. The inclusion of the physics-based model information may make the post-process correction approach more tolerant against samples outside the range of the training dataset when compared to the fully learned approach. The results show that the fully learned model results more often in high errors than the post-process correction.

We also studied the generalization capabilities of the machine learning models. The results show that the post-process correction model performs better than the fully learned model also when trained using data from distant regions. Ideally, in an operational setting, the machine learning models would be trained using global data, but, for example, in AOD retrievals, regardless of the high number of AERONET stations, there are always some regions with relatively poor AERONET coverage. Therefore, based on our results, we expect the post-process correction method to perform better than the fully learned models in these regions.

The high spatial resolution, about 300 m at nadir, and the high accuracy of the post-process-corrected Sentinel-3 Synergy aerosol parameters over the official Sentinel-3 Level-2 Synergy data product may possibly enable usage of the data for new applications. For example, for air quality applications, the high-resolution accurate aerosol data could be a step towards street-level monitoring instead of the typical city or neighbourhood levels in conventional aerosol data products. Improved accuracy high-spatial-resolution aerosol parameter information may also significantly benefit atmospheric correction in many land surface satellite applications. The most impacted land surface applications are especially those that retrieve information from very low signal-to-noise ratio data such as the retrieval of vegetation solar-induced fluorescence.

We acknowledge the difficulty in validating the high-spatial-resolution satellite aerosol data products as accurate high-resolution spatial coverage aerosol validation data do not exist. There are, however, some ground-based and aircraft measurement campaigns, such as the Distributed Regional Aerosol Gridded Observations Network (DRAGON) (e.g. Garay et al., 2017; Virtanen et al., 2018), KORea–United States Air Quality (KORUS-AQ) (e.g. Choi et al., 2021), the Atmospheric Radiation Measurement (ARM) programme (e.g. Javadnia et al., 2017) and ObseRvations of Aerosols above CLouds and their intEractionS (ORACLES) (e.g. Redemann et al., 2021), that could provide helpful insight on high-resolution aerosol features. Using the campaign data from these campaigns to validate the high-resolution satellite aerosol retrievals is a potential topic for future studies. Also, evaluation of the relative differences between the post-process-corrected Synergy data and 1 km MODIS Multi-Angle Implementation of Atmospheric Correction (MAIAC) (Lyapustin et al., 2018) data could reveal useful insight on the spatially varying AOD features.

Appendix A: Sentinel-3 data used

This section describes the Sentinel-3 data used in the study. We use both Level-1b and Level-2 data of the Sentinel-3 satellite mission data products, and we use data from both Sentinel-3A and Sentinel-3B satellites. For more information on the Sentinel-3 mission datasets, please see https://sentinel.esa.int/web/sentinel/missions/sentinel-3 (last access: 27 August 2021).

A1 Level-1b

A1.1 SLSTR

We use SLSTR Level-1b data from the SL_1_RBT data product. The variable names and the corresponding file names in the data products are listed in Table A1.

Table A1 Sentinel-3 SL_1_RBT files and variables used. Here, [X] denotes SLSTR band numbers 1–6.

A1.2 OLCI

We use OLCI Level-1b data from the OL_1_ERR data product. The variable names and the corresponding file names in the data products are listed in Table A2.

Table A2 Sentinel-3 OL_1_ERR files and variables used. Here, [YY] denotes OLCI band numbers 1–21.

A2 Level-2

Synergy

We use Sentinel-3 Level-2 data from the SY_2_SYN data product. The variable names and the corresponding file names in the data products are listed in Table A3.

Table A3 Sentinel-3 SY_2_SYN files and variables used.

Appendix B: Input and output variables of the models

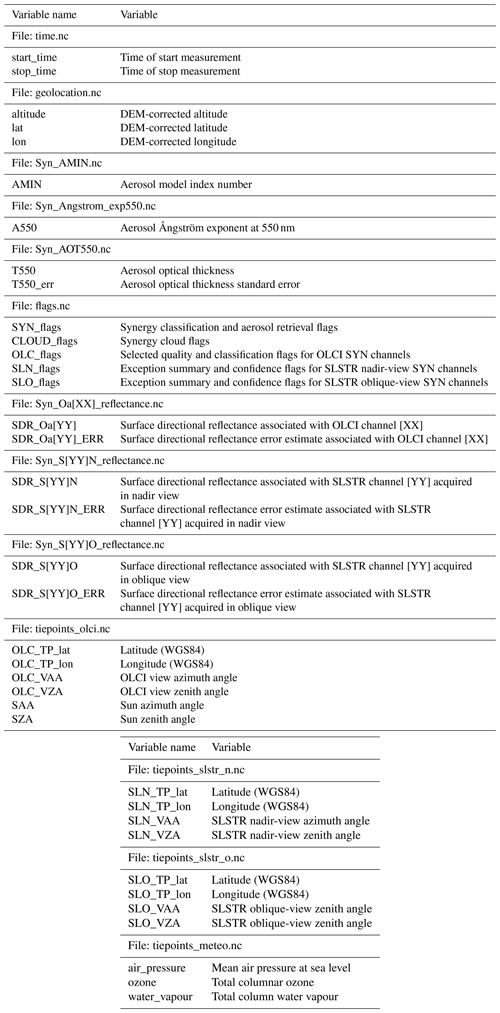
We divide the input and output variables into following five groups.

• Geometry variables

  • SYN_altitude

  • SYN_O_VAA

  • SYN_O_VZA

  • SYN_O_SAA

  • SYN_O_SZA

  • SYN_SN_VAA

  • SYN_SN_VZA

  • SYN_SO_VAA

  • SYN_SO_VZA

  • SYN_O_scattering_angle

  • SYN_SO_scattering_angle

  • SYN_SN_scattering_angle

  Here, all variables are based on the Sentinel-3 Synergy data product. SYN_O, SYN_SN and SYN_SO correspond to OLCI, SLSTR nadir view and SLSTR oblique view, respectively.

• Satellite observation variables

  • SL1_S1_reflectance_nadir

  • SL1_S1_reflectance_oblique

  • SL1_S2_reflectance_nadir

  • SL1_S2_reflectance_oblique

  • SL1_S3_reflectance_nadir

  • SL1_S3_reflectance_oblique

  • SL1_S4_reflectance_nadir

  • SL1_S4_reflectance_oblique

  • SL1_S5_reflectance_nadir

  • SL1_S5_reflectance_oblique

  • SL1_S6_reflectance_nadir

  • SL1_S6_reflectance_oblique

  • OL1_Oa01_reflectance

  • OL1_Oa02_reflectance

  • OL1_Oa03_reflectance

  • OL1_Oa04_reflectance

  • OL1_Oa05_reflectance

  • OL1_Oa06_reflectance

  • OL1_Oa07_reflectance

  • OL1_Oa08_reflectance

  • OL1_Oa09_reflectance

  • OL1_Oa10_reflectance

  • OL1_Oa11_reflectance

  • OL1_Oa12_reflectance

  • OL1_Oa13_reflectance

  • OL1_Oa14_reflectance

  • OL1_Oa15_reflectance

  • OL1_Oa16_reflectance

  • OL1_Oa17_reflectance

  • OL1_Oa18_reflectance

  • OL1_Oa19_reflectance

  • OL1_Oa20_reflectance

  • OL1_Oa21_reflectance

• SYN L2 variables

  • SYN_AOD550

  • SYN_AOD550err

  • SYN_AE550

  • SYN_AMIN

  • SYN_SYN_no_slo

  • SYN_SYN_no_sln

  • SYN_SYN_no_olc

  • SYN_SDR_Oa01

  • SYN_SDR_Oa02

  • SYN_SDR_Oa03

  • SYN_SDR_Oa04

  • SYN_SDR_Oa05

  • SYN_SDR_Oa06

  • SYN_SDR_Oa07

  • SYN_SDR_Oa08

  • SYN_SDR_Oa09

  • SYN_SDR_Oa10

  • SYN_SDR_Oa11

  • SYN_SDR_Oa12

  • SYN_SDR_Oa16

  • SYN_SDR_Oa17

  • SYN_SDR_Oa18

  • SYN_SDR_Oa21

  • SYN_SDR_S1N

  • SYN_SDR_S1O

  • SYN_SDR_S2N

  • SYN_SDR_S2O

  • SYN_SDR_S3N

  • SYN_SDR_S3O

  • SYN_SDR_S5N

  • SYN_SDR_S5O

  • SYN_SDR_S6N

  • SYN_SDR_S6O

• Regression output variables

  • AERONET_AOD_550 nm_mean

  • AERONET_AOD_440nm_mean

  • AERONET_AOD_500nm_mean

  • AERONET_AOD_675nm_mean

  • AERONET_AOD_870nm_mean

• Correction output variables

  • AOD550_approximationerror

  • AOD440_approximationerror

  • AOD500_approximationerror

  • AOD675_approximationerror

  • AOD870_approximationerror

Approximation error variables (ϵ) are computed using Eq. (3).

Inputs and outputs

As the inputs for the regression model, we use the variables from the following variable sets:

• geometry variables;

• satellite observation variables.

As the outputs for the regression model we use the variables from the following variable sets:

• regression output variables.

As the inputs for the correction model we use the variables from the following variable sets:

• geometry variables;

• satellite observation variables;

• SYN L2 variables.

As the outputs for the correction model we use the variables from the following variable sets:

• correction output variables.

Appendix C: AERONET data used

The following variables of the AERONET data were used:

• AOD_440nm;

• AOD_500nm;

• AOD_675nm;

• AOD_870nm;

• 440-870_Angstrom_Exponent.