the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Detection of small drizzle droplets in a large cloud chamber using ultrahigh-resolution radar
Pavlos Kollias
Raymond A. Shaw
Alex B. Kostinski
Steve Krueger
Katia Lamer
Nithin Allwayin
Mariko Oue
A large convection–cloud chamber has the potential to produce drizzle-sized droplets, thus offering a new opportunity to investigate aerosol–cloud–drizzle interactions at a fundamental level under controlled environmental conditions. One key measurement requirement is the development of methods to detect the low-concentration drizzle drops in such a large cloud chamber. In particular, remote sensing methods may overcome some limitations of in situ methods.
Here, the potential of an ultrahigh-resolution radar to detect the radar return signal of a small drizzle droplet against the cloud droplet background signal is investigated. It is found that using a small sampling volume is critical to drizzle detection in a cloud chamber to allow a drizzle drop in the radar sampling volume to dominate over the background cloud droplet signal. For instance, a radar volume of 1 cubic centimeter (cm3) would enable the detection of drizzle embryos with diameter larger than 40 µm. However, the probability of drizzle sampling also decreases as the sample volume reduces, leading to a longer observation time. Thus, the selection of radar volume should consider both the signal power and the drizzle occurrence probability. Finally, observations from the Pi Convection–Cloud Chamber are used to demonstrate the single-drizzle-particle detection concept using small radar volume. The results presented in this study also suggest new applications of ultrahigh-resolution cloud radar for atmospheric sensing.
- Article
(6102 KB) - Full-text XML
- BibTeX
- EndNote
Drizzle formation is one of the most important microphysical processes in warm clouds. Yet the processes controlling drizzle formation remain poorly understood (Wood, 2012). The most challenging aspect is the initial formation of drizzle embryos with diameter around 30–50 µm. The formation of small drizzle particles in this range can be adequately explained neither by the traditionally defined condensation growth process nor by the traditionally defined collision–coalescence (C–C) process owing to their low efficiency (Rogers and Yau, 1996; Pruppacher and Klett, 2010; Falkovich et al., 2006; Beard and Ochs III, 1993). Several mechanisms have been hypothesized to explain the efficiency of these processes including (i) fine-scale turbulence in cloud (Pinsky and Khain, 1997; Shaw, 2003), (ii) giant cloud condensation nuclei (GCCN) (Johnson, 1982; Feingold et al., 1999), and (iii) longwave cooling (Roach, 1976; Harrington et al., 2000). Nevertheless, it remains unclear to what extent these proposed mechanisms can adequately explain the origin of drizzle embryos.
One main barrier that hinders our ability to investigate the drizzle initiation process is the lack of observations with sufficient sensitivity and spatiotemporal resolution to detect the early growth of drizzle particles. As such an instrumented large convection–cloud chamber with well-controlled initial and boundary conditions might help to improve our understanding of the drizzle initiation mechanism (Shaw et al., 2020). Unlike other types of chambers, a convection–cloud chamber can generate a steady-state cloud system for hours in a turbulent environment by maintaining a warm saturated bottom surface, a cold saturated top surface, and a constant aerosol injection rate (Chang et al., 2016). The Michigan Tech Pi Convection–Cloud Chamber with dimensions of 2 m × 2 m × 1 m (width × depth × height) has been used to explore aerosol–cloud–turbulence interactions; however, the Pi Chamber is too small to initiate drizzle embryos, mainly due to the relatively short lifetime of cloud droplets therein. Results from large eddy simulations indicate that drizzle can be initiated in a large convection–cloud chamber with a height on the order of 10 m (Thomas et al., 2023). However, the drizzle drops are sparse in a large chamber, so the detection of single drizzle embryos in a large cloud chamber is challenging for in situ probes that generally have a sampling volume of only a few cubic centimeters. On the other hand, active remote sensors have the ability to rapidly sample large volumes and thus offer an attractive option for the detection of small drizzle droplets in a cloud chamber.
Here, we will demonstrate that the detection of an individual drizzle droplet in the presence of numerous cloud droplets is possible with a radar that can achieve a very small sampling volume. The detection of individual drizzle droplets is possible because the radar signal-to-noise ratio (SNR) of a point target (drizzle droplet) is not affected by the radar observational volume, while the SNR of a distributed target (cloud droplets) scales with the radar volume. In the following sections, the detection limits of an individual drizzle particle are investigated using idealized particle size distributions and real particle size distributions from the Michigan Tech Pi Chamber. In the end, the potential of THz radars offering unprecedented sub-centimeter range resolution will be discussed for developing the single drizzle detection radar (Cooper and Chattopadhyay, 2014).
The detection of early drizzle particles in clouds has been the topic of extensive research. First, the radar needs to have sufficient sensitivity to detect cloud and drizzle droplets. This is typically accomplished using millimeter-wavelength radar (Kollias et al., 2007). Early methodologies for the detection of drizzle drop in clouds employ the use of reflectivity thresholds, ranging from −15 to −20 dBZ, to identify drizzle existence (Frisch et al., 1995; Liu et al., 2008; Comstock et al., 2004). Kollias et al. (2011) introduced the use of the radar Doppler spectra skewness as a more sensitive method for detecting the presence of small drizzle droplets (Acquistapace et al., 2017; Zhu et al., 2022). The radar Doppler spectra technique improved the detection of drizzle droplets that can produce as low as −30 dBZ (Zhu et al., 2022).
However, the use of the radar Doppler spectra technique in a cloud chamber is challenging. First, this will require that the radar point vertically to take advantage of the differential velocity between cloud and drizzle droplets. If we assume a monodisperse droplet size distribution (DSD) and Rayleigh scattering conditions, a drizzle detection limit of −30 dBZ is equivalent to a concentration of 10−3 cm−3 of drizzle droplets with diameter equal to 100 µm or a concentration of cm−3 of drizzle droplets with 50 µm diameter. In the former case, the drizzle particle size is quite large and not quite an early drizzle droplet detection. In the latter case, the concentration of drizzle droplets is much higher than the concentration observed in nature ( cm−3) (Zhu et al., 2022).
Furthermore, the conventional cloud radar has a range resolution of tens of meters, which is not applicable in a chamber facility that may be on the order of several meters (approaching the collision mean free path).
As a result, we consider alternative methods to increase the probability of early drizzle droplet detection against the cloud droplet signal. As the number concentration of a drizzle particle is low, by applying a small radar sampling volume VRadar, it is possible that only one drizzle droplet is present in VRadar. In this case, the drizzle particle can be considered a point target with backscattering cross-section σ(m2), and the received radar echo power Pr (mW) is commonly expressed as (Battan, 1973)
where Pt is the transmit peak power (mW), G is the antenna gain, r (m) is the range of the target relative to the radar receiver, and λ (m) is the radar wavelength. It is noteworthy that Pr for a point target does not depend on the radar sampling volume VRadar. For distributed targets such as a cloud droplet population described by a droplet size distribution (DSD) that represents the number concentration of cloud droplets as a function of diameter, the received radar echo power is given by
where n is the number of cloud droplets in the radar volume and Nc(D) is the DSD with units of m−4. In this case, the received radar echo power depends on the radar sampling volume, which is given by the following expression:
where θ3dB is the antenna radiation pattern 3 dB beamwidth in radians and ΔR is the range resolution. Assuming Rayleigh scattering, the backscatter cross-section of the drizzle and cloud droplets is proportional to the sixth power of the particle diameter and inversely proportional to the fourth power of the wavelength . Combing Eqs. (1) and (2), the ratio of received radar echo power from drizzle and cloud is given by the following expression:
Equation (4) indicates that the probability of detecting a single drizzle droplet in the radar sampling volume increases inversely to the radar sampling volume (point vs. distributed target).
Here, we will evaluate how small the radar sampling volume needs to be to detect drizzle drops with different diameters against three background (cloud) conditions: (i) monodisperse cloud DSD, (ii) cloud DSD from a theoretical model, and (iii) observed cloud DSD from the Michigan Tech Pi Chamber. For simplicity, we will assume that a drizzle drop is detectable if its radar return power is equal to that of the background echo contributed from cloud droplets.
3.1 Monodisperse cloud DSD
We first construct an idealized scenario by considering two categories of droplets, i.e., cloud droplet with a diameter of Dc and a single drizzle drop with a diameter of Dd; the number concentration of cloud droplets in the radar sampling volume is Nc (m−3).
In this case, Eq. (4) is simplified as
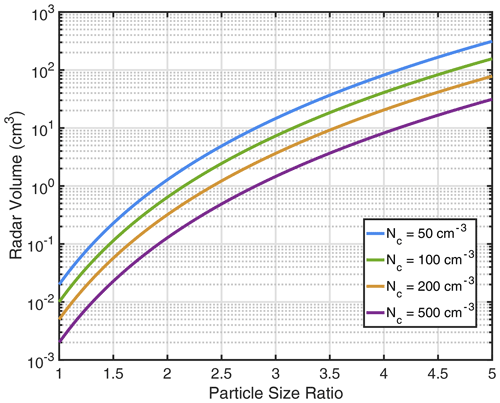
When the signal power equals the background, the radar sampling volume enabling single-drizzle-particle detection is estimated as a function of the size ratio shown in Fig. 1. The results are shown for various cloud droplet concentrations. It is noted that the required radar volume for detection depends on the drizzle drop size and the cloud number concentration. Larger radar volume would be required for drizzle detection as the particle size ratio increases; for a given particle size ratio, decreasing cloud number concentration can enhance the required radar volume. For example, if the cloud number concentration is 50 cm−3 and the mean cloud diameter (Dc) is 20 µm, then the detection of a drizzle particle with diameter of 40 µm (x=2) requires radar volume around 1 cm3. Such sampling volumes are not achievable with traditional radar systems that employ sampling volumes of the order of 1000 m3 or more (Kollias et al., 2016).
3.2 Drizzle detection against an idealized cloud droplet background
In a realistic cloud chamber environment, we expect a population of cloud droplets with various sizes that can be represented by a DSD. Particularly, when condensation and fallout are the main sources and sinks for the evolution equation for the DSD, the DSD in the cloud chamber can be approximately described by theoretically derived distributions (Saito et al., 2019; Chandrakar et al., 2020; Krueger, 2020). Here we adapt the theoretical DSD formula derived by Krueger (2020) to investigate the ability of a radar to detect a drizzle embryo present in a small sample volume under different chamber environment conditions. To better represent the cloud DSD under different environments, the analytical DSD is rearranged to be expressed as a function of liquid water content (LWCc; g m−3) and number concentration (Nc; m−3) as
where ρl is liquid water density (g m−3), and Dc is cloud droplet diameter (m). N(Dc) represents the number concentration of a cloud droplet for the given diameter (cm−3 µm−1).
Here we define the minimal drizzle drop (Dd,min) as the size of a particle with radar return power equal to the total return power from cloud droplets in a given radar volume (V). Given the cloud DSD described by Eq. (6), Dd,min can be estimated as
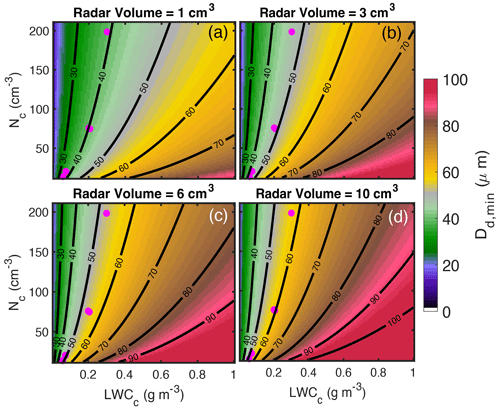
Figure 2The minimal detectable drizzle particle (Dd,min) under different LWCc and Nc conditions with radar sampling volume of (a) 1 cm3, (b) 3 cm3, (c) 6 cm3 and (d) 10 cm3. The black lines are the Dd,min contour of 30, 40, 50, 60, 70 µm. The magenta dots indicate the LWCc and Nc observed in the Pi-cloud chamber.
Figure 2 illustrates Dd,min under different LWCc and Nc combinations for various radar volumes. For a given steady-state cloud in a convection chamber (i.e., fixed LWCc and Nc), Dd,min generally increases as the radar volume increases. This is because larger radar volumes contain more cloud droplets that produce stronger background power; thus, only a larger drizzle particle with a higher backscattering signal would be detectable. On the other hand, for a given radar observational volume, Dd,min is jointly determined by LWCc and Nc, which are inversely proportional. As such, Dd,min increases rapidly with increasing LWCc but slightly decreases with increasing Nc. This contrasting relationship is caused by a larger sensitivity of radar reflectivity to particle size than to number concentration. Thus, increasing LWCc can increase mean cloud particle size and greatly enhance the background power, leading to a larger detectable Dd,min. On the other hand, when LWCc is fixed, increasing cloud total number concentration tends to decrease particle size. The reduced cloud particle size would reduce the backscattering power and more than compensate for the power enhancement contributed from the increased number concentration.
It should be noted that LWCc and Nc in a convection–cloud chamber have a stronger correlation compared with those in atmospheric clouds (Shaw et al., 2023). Instead, the LWCc and Nc often exhibit a positive covariance relationship. To understand the typical value of these two quantities in the chamber environment, we refer to typical measurement data from the Pi Chamber (magenta dots in Fig. 2). The data are from experiments conducted by Chandrakar et al. (2018). We can notice that for this specific experiment setup, drizzle embryos with diameter ranging from 40 to 60 µm can be detected using radar observational volume from 1 to 10 cm3.
The aforementioned estimation is conducted under the assumption that signal (drizzle) power is equal to the background (cloud) power. In practice, to reduce the detection false alarms, the drizzle signal should be larger than the backgrounds. Here we define the signal-to-noise ratio (SNR) to investigate the drizzle detectability in the chamber environment:
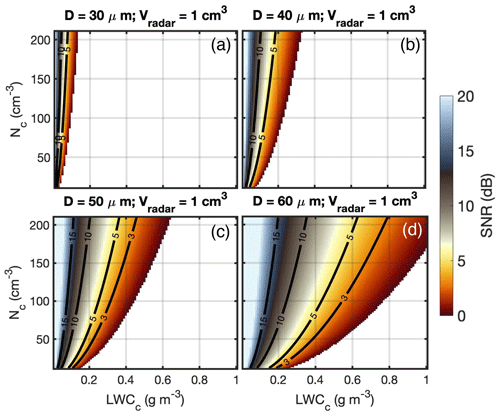
Figure 3 shows the estimated SNR for four drizzle particles under varying LWCc and Nc conditions with a radar volume of 1 cm3. Generally, a smaller LWCc and a larger Nc correspond to a large SNR, which is preferable for drizzle detection. If we arbitrarily choose SNR > 3 as the detection threshold, to detect a drizzle drop with diameter of 50 µm in a radar volume of 1 cm3 (Fig. 3c), LWCc in the cloud chamber should be lower than 0.3 g m−3 and Nc should be higher than 90 cm−3. The required LWCc and Nc would be different for different drizzle particle targets: to detect drops with diameter of 60 µm, LWCc should be lower than 0.5 g m−3 and Nc should be higher than 90 cm−3. It should be noted that although a drizzle drop is more likely to be detected by the radar at a lower LWCc, drizzle initiation is generally more likely to occur at a higher LWCc because the collision–coalescence rate is thought to be proportional to the square of LWC (Kostinski and Shaw, 2005). This suggests that appropriate LWCc and Nc combinations should be achieved such that drizzle can form by the C–C process in a convection–cloud chamber and it can also be detected by radar in a small sampling volume. It is also noted that the results shown in Fig. 3 are based on a radar volume of 1 cm3, and the estimated SNR would change if a different radar volume size was applied. For instance, increasing the radar volume will enhance the background power, thus decreasing the SNR for the given cloud chamber environment.
In the previous section, it was demonstrated that a radar with very small sampling volume (∼cm3) can plausibly achieve the detection of single drizzle droplets against a cloud background signal. On the other hand, the smaller the radar volume, the lower the probability of a drizzle particle encountering the volume. To illustrate this trade-off scenario, we define the probability of drizzle occurrence in the radar volume (p(Dd)) as
Specifically, the product of V and N(Dd) represents the expected number of drizzle drops in the radar volume. If the product is smaller than 1, it indicates the probability of the occurrence of a drizzle particle in a given volume, while if the product is larger than 1, it means that, statistically, at least one drizzle drop with a diameter of Dd exists in the radar volume, and thus we set p(Dd)=1.
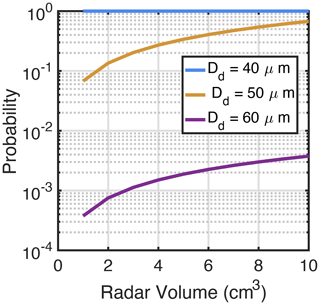
Figure 4The probability of drizzle occurrence as a function of radar observational volume. The blue, yellow, and purple lines indicate the drizzle particle with diameters of 40, 50, and 60 µm.
The probability of occurrence for three selected drizzle particles as a function of radar volume is shown in Fig. 4. The N(D) in Eq. (9) is adapted from the size distribution described by Eq. (6), with LWCc and Nc set as 0.5 g m−3 and 50 cm−3, respectively. For these conditions, drizzle droplets with a diameter of 40 µm have a sufficiently high concentration to be on average always present in volumes larger than 1 cm3. For drizzle droplets with a diameter of 50 or 60 µm, their concentration is low enough that their probability of being found in a 10 cm3 volume is on average below 1. It is also noticed that the occurrence probability is strongly sensitive to the particle size: the probability of drizzle with 60 µm diameter occurring in the volume is almost 2 orders of magnitude smaller than that for a particle with 50 µm diameter. A smaller drizzle occurrence in the volume indicates that a larger number of radar samples would be required to find one particle, leading to a longer observational time.
The probability of a drizzle drop to be in the radar sampling volume or passing through the radar volume within a finite time period should be an important consideration for a practical measurement system. Figure 5 shows the probability of the occurrence of a drizzle particle under different chamber environments that are the same as in Fig. 3. The blank region in Fig. 5 indicates that the corresponding SNR shown in Fig. 3 is lower than 0 (i.e., cannot be detected by the radar even they exist in the sampling volume). Generally, it is noticed that the probability of occurrence differs in various chamber environments for different droplet sizes: large droplets have a lower occurrence probability under small-LWC and high-N conditions.
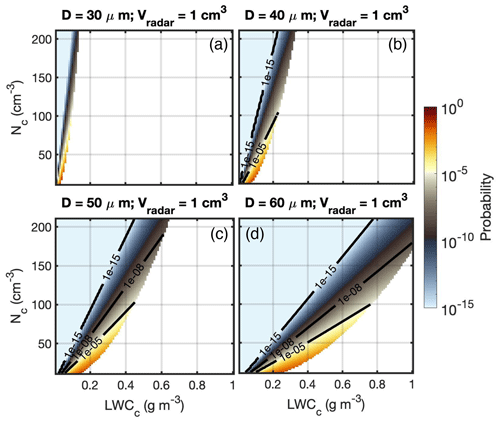
Figure 5Drizzle occurrence probability under different LWC and N conditions for a 1 cm3 radar volume with particle diameter of (a) 30 µm, (b) 40 µm, (c) 50 µm, and (d) 60 µm. The black lines are probability contours of 10−15, 10−8, and 10−5. The blank region indicates that the associated SNR is smaller than 0 (Fig. 3).
Comparison of Figs. 3 and 5 reveals that conditions that favor high radar SNR (i.e., larger drops or smaller radar sampling volume) are associated with a lower probability of occurrence of the drizzle droplet in the radar volume and subsequently increase the radar sampling time. For example, to detect a drizzle particle of 50 µm diameter under the condition of LWCc and Nc of 0.3 g m−3 and 90 cm−3, the particle occurrence probability is of the order of 10−8 (Fig. 5c) for SNR equal to 3 (Fig. 3c). A 1 dB enhancement of the SNR threshold would decrease the occurrence probability to 10−11. This implies that, on average, a volume of air equal to 1011 times the size of the radar sampling volume needs to be sampled before a drizzle droplet will be detected. Assuming an air mean flow within the cloud chamber of 1 m s−1, this implies that a radar sampling volume with a typical dimension of 1 cm will be updated (through advection) 100 times per second. If the radar is sampling along 1000 range gates (i.e., assuming a chamber with a height of 10 m), this suggests that the radar can sample a volume equal to 105 times its radar sampling volume each second. To reach the average required sampling volume (1011), it will take 106 s or 11.5 d. This is an unrealistically long observational time. For practical application, we want to work with sampling configurations that will not require sampling more than 109 times the radar sampling volume (approximately tens of minutes).
Another factor to consider in estimating the probability of drizzle occurrence with a certain diameter in a specific volume is the realism of using Eq. (6) for describing the N(D) in a cloud chamber. Equation (6) describes the cloud droplet distribution controlled by the condensation process alone, and thus the results may underestimate the actual drizzle occurrence as condensation is inefficient to produce large drizzle particle. In nature or in a large convection–cloud chamber, the C–C mechanism is expected to be a more efficient process to increase the size and concentration of drizzle droplets.
Here we apply the ClusColl model to demonstrate that Figs. 4 and 5 may underestimate the drizzle occurrence probability with the collision–coalescence process being activated. ClusColl is a simulation method for describing droplet motions and collisions in turbulent flows (Krueger and Kerstein, 2018). ClusColl simulates the movement of individual droplets in a vertical column due to turbulence and gravitational sedimentation. The unique capability of the ClusColl model is its capability to efficiently simulate the droplet collision and coalescence process. Figure 6 shows the simulated DSD with and without the collision–coalescence process for a 10 m height cloud chamber and with a cloud number concentration of 100 cm−3. The temperature difference between top and bottom walls is 40 ∘C. Noticeable differences can be identified at the right tail of the distribution, particularly for a droplet diameter larger than 40 µm: more larger droplets are generated if the collision–coalescence process is active. The higher concentration of large drops results in a significantly shorter waiting time for detection compared to what was calculated for the condensation-only examples given in the earlier part. For instance, for the generated particle with a diameter of 50 µm, the C–C process can generate a number concentration more than 100 times higher than the one without the C–C process included. Reviewing the earlier estimation, to detect a drizzle particle with a diameter of 50 µm and SNR higher than 4, the required 106 s becomes 104 s. This is approximately 3 h, which is much more achievable for laboratory experiments. Thus, the estimation based on the condensation-only distribution (Eq. 6) is the most conservative scenario. The actual radar measurement time would likely be much shorter when the C–C process is activated.
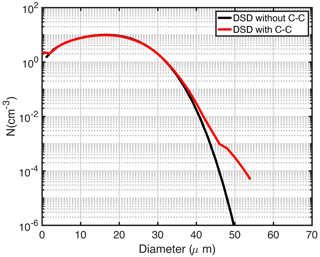
Figure 6DSD simulated from the ClusColl model with (red line) and without (black line) droplet growth by collision–coalescence. In both cases, growth by condensation in a uniform supersaturation field and removal by size-dependent droplet sedimentation are calculated. Therefore, the black line is described by the distribution given by Eq. (6).
In a cloud chamber and in the real atmosphere, the DSD in the radar sampling volume is expected to be time-dependent due to turbulent fluctuations. To better quantify the particle backscattering power and its fluctuation in a small volume, observations made in the Pi Chamber using a holographic system (Holo-Pi) are used. Holo-Pi uses the principle of in-line digital holography to measure the spatial distribution and sizes of cloud particles (Fugal and Shaw, 2009; Beals et al., 2015) and is specifically designed for the Pi Chamber environment (Desai et al., 2018). In contrast to the typical measurement strategy of single-particle detections requiring time averaging, Holo-Pi captures instantaneous snapshots of all cloud droplets in the sample volume of 3.6 cm3 (0.6 cm × 0.6 cm × 10 cm) and is well suited to measure the temporal variations of cloud droplet populations within a sample volume similar to plausible radar sample volumes. The inability to resolve the smallest cloud droplets in the size distribution is not expected to be a significant limitation as the backscattering radar power is more sensitive to larger particle diameters. For the results presented here, cloud droplets are formed in the Pi Chamber by activation of size-selected sodium chloride aerosol particles (dry particle diameter ≈ 130 nm) injected into a supersaturated turbulent flow sustained by an unstable temperature difference of 20 K. An illustration of the 3D view of the cloud droplets measured by Holo-Pi at different time instants in the Pi Chamber is shown in Fig. 7. The sample volume used for our calculations is limited to a vertical extent of 5 cm as particle detectability falls off beyond this point; this results in a total sample volume of 1.8 cm3. The Holo-Pi system is set up to capture a hologram every 10 s during a 720 s period. For the optical configuration used here, the Holo-Pi has a lower size resolution of 12 µm throughout its sample volume.
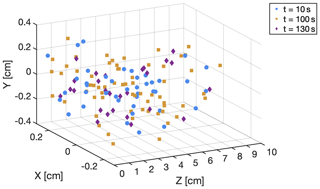
Figure 7A 3D view of the particle locations observed by Holo-Pi in the Pi Chamber. Different colors and symbols represent observations taken at different time steps.
The Holo-Pi observational volume is divided into five sub-volumes with the cross-section of 0.36 cm2 and the depth increasing from 1 to 5 cm with an increment of 1 cm, thus corresponding to a volume of 0.36, 0.72, 1.08, 1.44, and 1.8 cm3. Within each sub-volume at each time step, the total backscattering cross-section for the detected droplets is estimated using a THz radar with a wavelength of 0.44 mm. The calculated radar backscattering cross-section as a function of volume size is shown in Fig. 8. Similar to the previous estimation, we see that the background power increases with volume size due to the increment of cloud droplets. Importantly, the uncertainty bars shown in Fig. 8 represent the standard deviation of the backscattering cross-section during the observational time, which indicates that the background power fluctuations. We notice that the cloud distribution in a small radar sampling volume is highly heterogeneous in time, and the magnitude of the background fluctuation varies by approximately a factor of 10. In order to detect drizzle drops, the backscattering power of the drizzle drop should be larger than the range of background fluctuations. For example, a radar volume smaller than 0.36 cm3 should be utilized to detect a droplet with a diameter larger than 22 µm, and a radar sampling volume smaller than 1 cm3 is needed to detect a droplet with a diameter larger than 30 µm for this particular Pi Chamber experiment setup.
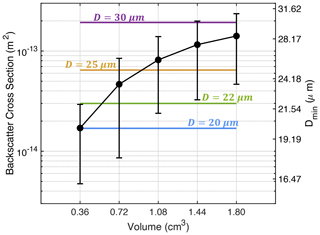
Figure 8Dots and uncertainty bars indicate the mean and standard deviation of the total backscattering cross-section (with units of m2) of droplets measured in different volumes by Holo-Pi during the observational period. The right axis and the horizontal lines represent the diameter of a single drizzle drop with backscattering power equivalent to the background.
To further demonstrate the single drizzle detection concept using a small radar volume, a pseudo-radar observation experiment is conducted based on the Holo-Pi measurements. The Holo-Pi observational volume is divided into four sub-volumes indicated as different lines shown in Fig. 9. In each volume, we consider the mean radar backscattering power from all cloud particles sampled during the observational period to be the background noise and the power estimated at each time step to be the signal such that the SNR as a function of observation time is estimated. To simulate the drizzle occurring events, artificial drizzle droplets with diameter of 30, 40, and 50 µm are added to the volume at 200, 400, and 600 s, respectively, and the associated SNR is estimated. Figure 9 shows a clear SNR enhancement when the drizzle droplets are added. The signal enhancement is more significant when using a small sampling volume and for larger drizzle drop diameter, which is consistent with the theoretical estimation in Sect. 3. For instance, a drizzle drop with a diameter of 50 µm can have an SNR of 23 dB with a volume of 0.36 cm3, while it has an SNR of 15 dB with a volume of 1.44 cm3. For a drizzle drop of 30 µm, the SNR with a volume of 0.36 cm3 can reach 10 dB, which is an adequate SNR value for radar detection, while with a volume of 1.44 cm3, the drizzle drop SNR is overwhelmed by background fluctuation and it is unable to be detected.
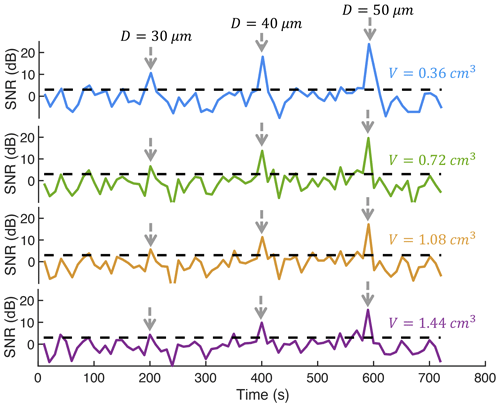
Figure 9Simulated SNR of radar measurements during the Holo-Pi observational period using four sampling volumes: 0.36 cm3 (blue line), 0.72 cm3 (green line), 1.08 cm3 (yellow line), and 1.44 cm3 (purple line). The grey arrows indicate that an artificial drizzle particle is added at the indicated time step. The dashed black line indicates an SNR of 3, which is used as a threshold to distinguish the signal (drizzle) from the background (clouds) in Fig. 3.
Recent simulation results suggest that drizzle initiation could occur in a large convection–cloud chamber. Such a facility would provide measurements in a controlled environment that can advance our understanding of warm rain formation in clouds. One of the critical measurements in a large convection–cloud chamber is the detection of low-concentration drizzle droplets in the presence of numerous cloud droplets. Early in the drizzle initiation, those drizzle drops are rare and inhomogeneously distributed in the chamber, presenting a significant detection challenge for conventional in situ probes. Here, the potential of a radar with ultrafine sampling volume for drizzle detection is investigated. It was demonstrated that if the radar sampling volume becomes orders of magnitude smaller (e.g., several cm3) compared to those typically available in research radars (∼ 103–106 m3), isolated drizzle particles can be detected against the cloud background signal. This concept is based on the notion that the SNR of point targets (i.e., drizzle droplet) is independent of the radar sampling volume, while the SNR of background (i.e., high-concentration cloud droplets) scales with the sampling volume.
A theoretical DSD was adapted to represent the distribution of cloud droplets in a convection–cloud chamber and to estimate properties of a detectable drizzle particle. It was shown that the minimum size of an isolated drizzle droplet that can be detected with such a radar depended on the radar sampling volume and the strength of the background signal (i.e., cloud droplet radar return), which in turn depends on LWC and Nc. To minimize the false alarm drizzle detection, we require the backscattering power from a drizzle particle to be larger than the backscattered power contributed from the cloud particles (SNR > 1). It is demonstrated that the application of a small radar volume can significantly enhance SNR under a given chamber environment. On the other hand, the smaller the radar sampling volume the lower the probability that an isolated drizzle droplet will be sampled. Thus, the determination of the radar volume for drizzle detection should account for the size of the drizzle particle of interest, the environment conditions that favor drizzle initiation, and the required observational time.
In addition to analytical estimates, real observations from the MTU Pi Convection–Cloud Chamber are used to demonstrate the single-drizzle-particle detection framework. The Holo-Pi system (Desai et al., 2018) is applied to provide detailed 3D imaging of the cloud particles in the cloud chamber, from which the fluctuations of the backscattering power in a small volume can be well estimated. Generally, the observational results are consistent with the theoretical estimation showing that the background power is decreased and the ability to detect drizzle particles is enhanced as radar sample volume is decreased. It is also noticed that the magnitude of the background fluctuation is comparable to the mean power, which indicates that the distribution of cloud droplets is highly inhomogeneous in the small volume. Thus, the power from a drizzle particle should at least dominate the background power fluctuation in order to be detected. With the cloud chamber environment from the experiment, drizzle particles with a diameter larger than 30 µm can be confidently detected using a radar sampling volume of 1 cm3 or lower.
The key remaining question is the technological feasibility of building a radar that can operate within a box (large convection–cloud chamber) and achieve the required ultrafine range resolution. In fact, the effort of using “small” radar volumes for single-particle detection has already been achieved in previous studies. For example, Schmidt et al. (2012) utilized a C-band radar with a 14 m3 observational volume and successfully detected the trajectories of rain droplets with diameters down to 0.5 mm. In our case, the required radar sampling volume for drizzle detection is much smaller (with several cm3). Such ultrafine range resolution can be achieved using a THz radar operating at 340 or 680 GHz that can support wide-bandwidth waveforms and thus enable sub-centimeter range resolution (Cooper and Chattopadhyay, 2014). If the radar operates at a very high carrier frequency (THz) it can afford a very wide bandwidth for pulse modulation. In this case, the range resolution is not dictated by the pulse length but by the radar bandwidth (Cooper and Chattopadhyay, 2014). The ultrafine range resolution along with a reflector that minimizes the angular spread of the radar beam can result in radar sampling volumes of a few cm3. Such radar imaging capabilities have been extensively used for security screening at airports, for example. In our context, additional complexity is introduced by the fact that this radar needs to operate in a chamber with typical dimensions of ∼ 10 m. These technical design issues will be the focus of a follow-up paper study that will include real observations of drizzle droplets from a THz radar system.
To conclude, we outline three issues that will need to be properly addressed before a radar can be applied to the drizzle detection problem in a cloud chamber.
-
Does the radar have enough sensitivity to detect a single drizzle particle? With the development of THz technology, radars with centimeter resolution are achievable; however, the currently developed THz radars are mainly used to detect relatively hard targets that do not require ultrahigh sensitivity. For the purpose of drizzle detection, however, the backscattering cross-section is on the order of 10−13 m2; such lower receiving power would require the radar to have a much higher transmitting power or a larger antenna size. Fortunately, an advantage for the drizzle detection in a cloud chamber is that the radar detection range is only several meters depending on the size of the chamber. According to Eq. (1), radar receiving power is inversely proportional to the fourth power of the target distance. Thus, the small detection range may greatly relieve the demand for high sensitivity in the radar design. In addition, recent advancements in THz transmitters allow us to utilize higher-power output transmitter (∼ 50 to 200 mW) at THz frequencies such as 340 GHz.
-
What are the appropriate radar sampling strategies for drizzle detection in a cloud chamber facility? Most of the cloud radars applied in the atmosphere are vertically pointing and can provide continuous observation at a given location along the radar beam. However, as discussed in the paper, drizzle occurrence in the chamber is extremely rare and inhomogeneous in space and time. If the radar is vertically pointing, with a radar beam several centimeters in width, it may take significant time for the radar to detect one drizzle drop. Adding a scanning capability to the radar may provide a more efficient way to observe and detect drizzle in the cloud chamber.
-
How can we eliminate or reduce the degradation effect of the chamber environment on a radar signal? In particular, the cloud chamber is a humid environment with liquid particles continually falling towards the bottom. Accumulation of water on the radar antenna can also severally attenuate the transmitting power and degrade the radar detectability. Furthermore, the chamber walls and the in situ instruments mounted inside would produce strong backscattering signals and pollute the backscattering signal from hydrometeors. Thus, the design of the radar should also account for radar instrument design and sampling strategies that minimize these noise sources so that the best possible detection capability can be achieved.
In short, this paper demonstrates the conceptual feasibility of THz radars for rare drizzle detection in a laboratory context. Undoubtedly, the development of a high-resolution radar for drizzle detection in a cloud chamber needs close collaborations between cloud physics scientists and radar engineers moving forward.
The codes and observations used to conduct all the analyses in this study are available upon request.
ZZ conceptualized and implemented the method, performed the analysis, produced the figures, and wrote the initial draft of the paper. PK and FY contributed to the conceptualization and provided guidance on the analysis. RAS and ABK contributed to the simplified model described in Sect. 3.1. SK provided the ClusColl model. NA provided the Holo-Pi measurements from the Pi Chamber. All authors read the paper draft and contributed to comments and paper editing.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Measurement Techniques. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors thank Ken Cooper for the constructive discussions and for providing feedback on the paper.
Authors from Brookhaven National Laboratory were supported by the Office of Biological and Environmental Research in the Department of Energy, Office of Science, through the United States Department of Energy (contract no. DE-SC0012704). Authors from Michigan Technological University and from Stony Brook University (subaward sub-award 2105003Z8) acknowledge support from National Science Foundation (award AGS-2133229). Alex B. Kostinski, Steve Krueger, Raymond A. Shaw, and Fan Yang accomplished some of this work during a visit at the Kavli Institute for Theoretical Physics as part of the Multiphase Flows in Geophysics and the Environment program. KITP is supported in part by the National Science Foundation (grant no. PHY-1748958).
This paper was edited by Maximilian Maahn and reviewed by two anonymous referees.
Acquistapace, C., Kneifel, S., Löhnert, U., Kollias, P., Maahn, M., and Bauer-Pfundstein, M.: Optimizing observations of drizzle onset with millimeter-wavelength radars, Atmos. Meas. Tech., 10, 1783–1802, https://doi.org/10.5194/amt-10-1783-2017, 2017.
Battan, L. J.: Radar Observation of the Atmosphere. The University of Chicago Press, 324 pp., 1973.
Beals, M. A., Fugal, J. P., Shaw, R. A., Lu, J., Spuler, S. M., and Stith, J. L.: Holographic measurements of inhomogeneous cloud mixing at the centimeter scale, Science, 350, 87–90, 2015.
Beard, K. V. and Ochs III, H. T.: Warm-rain initiation: An overview of microphysical mechanisms, J. Appl. Meteorol. Climatol., 32, 608–625, 1993.
Chandrakar, K. K., Cantrell, W., Kostinski, A. B., and Shaw, R. A.: Dispersion aerosol indirect effect in turbulent clouds: laboratory measurements of effective radius, Geophys. Res. Lett., 45, 10738–10745, https://doi.org/10.1029/2018GL079194, 2018.
Chandrakar, K. K., Saito, I., Yang, F., Cantrell, W., Gotoh, T., and Shaw, R. A.: Droplet size distributions in turbulent clouds: Experimental evaluation of theoretical distributions, Q. J. Roy. Meteorol. Soc., 146, 483–504, 2020.
Chang, K., Bench, J., Brege, M., Cantrell, W., Chandrakar, K., Ciochetto, D., Mazzoleni, C., Mazzoleni, L., Niedermeier, D., and Shaw, R.: A laboratory facility to study gas–aerosol–cloud interactions in a turbulent environment: The Ð chamber, B. Am. Meteorol. Soc., 97, 2343–2358, 2016.
Comstock, K. K., Wood, R., Yuter, S. E., and Bretherton, C. S.: Reflectivity and rain rate in and below drizzling stratocumulus, Q. J. Roy. Meteorol. Soc. A, 130, 2891–2918, 2004.
Cooper, K. B. and Chattopadhyay, G.: Submillimeter-wave radar: Solid-state system design and applications, IEEE Microw. Mag., 15, 51–67, 2014.
Desai, N., Chandrakar, K. K., Chang, K., Cantrell, W., and Shaw, R.: Influence of microphysical variability on stochastic condensation in a turbulent laboratory cloud, J. Atmos. Sci., 75, 189-201, 2018.
Falkovich, G., Stepanov, M. G., and Vucelja, M.: Rain initiation time in turbulent warm clouds, J. Appl. Meteorol. Climatol.y, 45, 591-599, 2006.
Feingold, G., Cotton, W. R., Kreidenweis, S. M., and Davis, J. T.: The impact of giant cloud condensation nuclei on drizzle formation in stratocumulus: Implications for cloud radiative properties, J. Atmos. Sci., 56, 4100–4117, 1999.
Frisch, A., Fairall, C., and Snider, J.: Measurement of stratus cloud and drizzle parameters in ASTEX with a Ká-band Doppler radar and a microwave radiometer, J. Atmos. Sci., 52, 2788–2799, 1995.
Fugal, J. P. and Shaw, R. A.: Cloud particle size distributions measured with an airborne digital in-line holographic instrument, Atmos. Meas. Tech., 2, 259–271, https://doi.org/10.5194/amt-2-259-2009, 2009.
Harrington, J. Y., Feingold, G., and Cotton, W. R.: Radiative impacts on the growth of a population of drops within simulated summertime arctic stratus, J. Atmos. Sci., 57, 766–785, 2000.
Johnson, D. B.: The role of giant and ultragiant aerosol particles in warm rain initiation, J. Atmos. Sci., 39, 448–460, 1982.
Kollias, P., Clothiaux, E., Miller, M., Albrecht, B., Stephens, G., and Ackerman, T.: Millimeter-wavelength radars: New frontier in atmospheric cloud and precipitation research, B. Am. Meteorol. Soc., 88, 1608–1624, 2007.
Kollias, P., Szyrmer, W., Rémillard, J., and Luke, E.: Cloud radar Doppler spectra in drizzling stratiform clouds: 1. Forward modeling and remote sensing applications, J. Geophys. Res.-Atmos., 116, D13201, https://doi.org/10.1029/2010jd015237, 2011.
Kollias, P., Clothiaux, E. E., Ackerman, T. P., Albrecht, B. A., Widener, K. B., Moran, K. P., Luke, E. P., Johnson, K. L., Bharadwaj, N., and Mead, J. B.: Development and applications of ARM millimeter-wavelength cloud radars, Meteor. Mon., 57, 17.11–17.19, 2016.
Kostinski, A. B. and Shaw, R. A.: Fluctuations and luck in droplet growth by coalescence, B. Am. Meteorol. Soc., 86, 235–244, 2005.
Krueger, S. K.: Technical note: Equilibrium droplet size distributions in a turbulent cloud chamber with uniform supersaturation, Atmos. Chem. Phys., 20, 7895–7909, https://doi.org/10.5194/acp-20-7895-2020, 2020.
Krueger, S. K. and Kerstein, A. R.: An economical model for simulating turbulence enhancement of droplet collisions and coalescence, Journal of Adv. Model. Earth Syst., 10, 1858–1881, 2018.
Liu, Y., Geerts, B., Miller, M., Daum, P., and McGraw, R.: Threshold radar reflectivity for drizzling clouds, Geophys. Res. Lett., 35, L03807, https://doi.org/10.1029/2007GL031201, 2008.
Pinsky, M. and Khain, A.: Turbulence effects on droplet growth and size distribution in clouds – A review, J. Aerosol Sci., 28, 1177–1214, 1997.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Atmos. Oceanogr. Sci. Libr., Vol. 18, 2nd Edn., Springer Netherlands, 954 pp., https://doi.org/10.1007/978-0-306-48100-0, 2010.
Roach, W. T.: On the effect of radiative exchange on the growth by condensation of a cloud or fog droplet, Q. J. Roy. Meteorol. Soc., 102, 361–372, 1976.
Saito, I., Gotoh, T., and Watanabe, T.: Broadening of cloud droplet size distributions by condensation in turbulence, J. Meteorol. Soc. JPN II, 97, 867–891, https://doi.org/10.2151/jmsj.2019-049, 2019.
Schmidt, J. M., Flatau, P. J., Harasti, P. R., Yates, R. D., Littleton, R., Pritchard, M. S., Fischer, J. M., Fischer, E. J., Kohri, W. J., and Vetter, J. R.: Radar observations of individual rain drops in the free atmosphere, P. Natl. Acad. Sci. USA, 109, 9293–9298, 2012.
Shaw, R. A.: Particle-turbulence interactions in atmospheric clouds, Annu. Rev. Fluid Mech., 35, 183–227, 2003.
Shaw, R. A., Cantrell, W., Chen, S., Chuang, P., Donahue, N., Feingold, G., Kollias, P., Korolev, A., Kreidenweis, S., and Krueger, S.: Cloud–aerosol–turbulence interactions: Science priorities and concepts for a large-scale laboratory facility, B. Am. Meteorol. Soc., 101, E1026–E1035, 2020.
Shaw, R. A., Thomas, S., Prabhakaran, P., Cantrell, W., Ovchinnikov, M., and Yang, F.: Fast and slow microphysics regimes in a minimalist model of cloudy Rayleigh-B\'enard convection, Phys. Rev. Res., 5, 043018, https://doi.org/10.1103/PhysRevResearch.5.043018, 2023.
Thomas, S., Yang, F., Ovchinnikov, M., Cantrell, W., and Shaw, R. A.: Scaling of turbulence and microphysics in a convection–cloud chamber of varying height, J. Adv. Model. Earth Syst., 15, e2022MS003304, https://doi.org/10.1029/2022MS003304, 2023.
Wood: Stratocumulus Clouds, Mon. Weather Rev., 140, 2373–2423, https://doi.org/10.1175/mwr-d-11-00121.1, 2012.
Rogers, R. R. and Yau, M. K.: A short course in cloud physics, Butterworth-Heinemann, Woburn, MA, USA, 143 pp., ISBN 9780080570945, 1996
Zhu, Z., Kollias, P., Luke, E., and Yang, F.: New insights on the prevalence of drizzle in marine stratocumulus clouds based on a machine learning algorithm applied to radar Doppler spectra, Atmos. Chem. Phys., 22, 7405–7416, https://doi.org/10.5194/acp-22-7405-2022, 2022.
- Abstract
- Introduction
- Drizzle detection using radar
- Detection requirement
- Probability of detection due to drizzle concentration
- Evaluation from cloud chamber observations
- Summary
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Drizzle detection using radar
- Detection requirement
- Probability of detection due to drizzle concentration
- Evaluation from cloud chamber observations
- Summary
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References