Intercomparison of aerosol optical depth retrievals from GAW-PFR and SKYNET sun photometer networks and the effect of calibration

In this study, we assess the homogeneity of aerosol optical depth (AOD) between two sun photometer networks, the Global Atmosphere Watch-Precision Filter Radiometer (GAW-PFR) and the European SKYNET radiometers network (ESR), at the common wavelengths of their main instruments (500 and 870 nm). The main focus of this work is to evaluate the effect of the improved Langley plot calibration method (ILP) used by SKYNET and to investigate the factors affecting its performance. We used data from three intercomparison campaigns that took place during 2017–2021. Each campaign was organized at two locations (mountainous rural – Davos, Switzerland; urban – Rome, Italy). Our analysis shows that differences in AOD due to post-processing and instrument differences are minor. The main factor leading to AOD differences is the calibration method. We found a systematic underestimation of AOD in ESR compared to in GAW-PFR due to underestimation of the calibration constant calculated with the ILP method compared to the calibration transfers using the PFR as a reference. The calibration and AOD differences are smaller in Davos, where the traceability criteria are satisfied at 870 nm and where the median differences are below 0.01 at 500 nm. In Rome, the AOD median differences at 500 nm were in the 0.015–0.034 range. We conducted a sensitivity study, which shows that part of the difference can potentially be explained by errors in the assumed surface albedo and instrument solid-view angle provided as inputs to the ILP code (based on Skyrad pack 4.2). Our findings suggest that the ILP method is mainly sensitive to the measured sky radiance. The underestimation in calibration is probably caused by an error in the retrieved scattering AOD (sc-AOD) through the sky radiance inversion. Using an alternative retrieval method (Skyrad MRI pack version 2) to derive sc-AOD and to recalibrate the instruments with the ILP method, we found no significant differences between the retrieved sc-AOD and no systematic increase in the ILP-derived calibration constant when using the MRI pack for sc-AOD inversion instead of the Skyrad 4.2. The potential error may be a result of the model assumptions used for the sky radiance simulations. In conclusion, the on-site calibration of sun photometers has several advantages, including the fact that instrument shipments and data gaps can be avoided. However, it has also the disadvantages of a larger uncertainty and significant systematic differences compared to the traditional Langley calibration performed under low- and constant-AOD conditions at high-altitude sites. The larger uncertainty of the ILP method can be attributed to the required modelling and input parameters.

1 Introduction

Atmospheric particulate matter (aerosols) is a component of high importance in atmospheric sciences and modern environmental problems. It scatters and absorbs solar radiation, significantly affecting the Earth's energy budget. It also greatly assists water and ice nucleation in the atmosphere, leading to the formation of clouds (Winkler and Wagner, 2022; Maloney et al., 2022). Aerosols have been the main driver of variations in surface solar radiation for several decades (Wild, 2012; Correa et al., 2024). Their influence on surface solar radiation can alter the exposure of organisms to biologically active radiation (Barnes et al., 2019; Bais et al., 2018) and also the efficiency of solar-energy production systems (Papachristopoulou et al., 2024; Hou et al., 2022). Both the direct and indirect effects of aerosols on surface solar radiation can lead to a significant forcing of the climate. Aerosols therefore represent a source of large uncertainty in the attribution of radiative forcing (IPCC, 2023).

According to the World Meteorological Organization (WMO), the most important parameter related to aerosols for Earth energy budget studies is the aerosol optical depth (AOD) (WMO, 2003). AOD describes the overall effect of the total aerosol column on the attenuation of solar radiation and is correlated with the total aerosol load in the atmosphere and its spectral dependence with the size of aerosols. AOD is calculated from direct solar irradiance (DSI) measurements by subtracting the effect of gas absorption and scattering in the absence of clouds covering the solar disc. The main instruments used for this purpose are sun photometers, which measure DSI at selected wavelengths where gas absorption is minimal and the AOD calculation is more accurate.

Different types of sun photometers are used in several worldwide networks. The main sun photometer networks are the Aerosol Robotic Network (AERONET), the Global Atmosphere Watch-Precision Filter Radiometer (GAW-PFR) and SKYNET. AERONET is the largest network with more than 400 stations worldwide and uses the CIMEL sun and sky photometer (hereafter CIMEL) as the standard instrument (Holben et al., 1998). GAW-PFR includes 15 stations, mainly in remote worldwide locations. Its standard instrument is the Precision Filter Radiometer (PFR) and includes the WMO AOD reference instruments (PFR-Triad) (Kazadzis et al., 2018b). SKYNET is a multi-instrument research network divided into sub-networks and includes around 100 stations, mainly in East Asia and western Mediterranean regions. Its standard instrument for AOD observation is the PREDE POM sun and sky radiometer (hereafter POM) (Nakajima et al., 2020). Each sub-network has developed its own calibration protocols and post-processing algorithms independently. Procedures developed by two sub-networks, led by ESR and the Center for Environmental Remote Sensing (CEReS) at Chiba University, are recognized as the standard in the International SKYNET Committee (Nakajima et al., 2020). Due to the differences among the main networks (i.e. AERONET, GAW-PFR, SKYNET) described above, it is important to evaluate the homogeneity between them to ensure that AOD observations are comparable and have a similar accuracy. For this purpose, the Filter Radiometer Comparison (FRC) campaign takes place in Davos (Switzerland) every 5 years, which includes all types of sun photometers (Kazadzis et al., 2023). There have been several other intercomparison campaigns (Doppler et al., 2023; Mitchell and Forgan, 2003; Cachorro et al., 2009; Mazzola et al., 2012; Nyeki et al., 2013; Kazadzis et al., 2018a; Gröbner et al., 2023), as well as long-term comparisons between different networks (Cuevas et al., 2019; Karanikolas et al., 2022).

A necessary parameter for the calculation of AOD is the DSI that the instrument would measure at the top of the atmosphere (extraterrestrial or calibration constant). There are different ways to calibrate a sun photometer. Conventionally, they are calibrated by the standard Langley plot method (SLP) (Shaw et al., 1973) and the calibration transfer from a reference co-located instrument. An alternative method is the laboratory calibration to the International System of Units (SI). Using this alternative approach, we can use satellite measurements for the top-of-the-atmosphere irradiance that are also in SI units. Recent developments show that laboratory calibration can also be accurate (Gröbner and Kouremeti, 2019; Kouremeti et al., 2022; Gröbner et al., 2023). Another method is the improved Langley plot method (ILP) (Tanaka et al., 1986; Campanelli et al., 2004). This is a modification of the SLP method that accounts for AOD variations during the day in contrast to SLP, which assumes a constant AOD. The assumption of constant AOD results in larger errors in more polluted areas, and SLP is therefore only used at high-altitude locations. The aim of ILP is to calibrate instruments at the station where they are normally operated, regardless of the station's location, instead of being transported to a calibration site. This method therefore has several advantages: (i) instrument damage during transportation can be avoided, (ii) there will be a minimal amount of missing data during the calibration period, (iii) maintenance is less costly, and (iv) the variation of the calibration constant can be more frequently monitored. AERONET and GAW-PFR calibrate instruments either by means of SLP at Mauna Loa (Hawaii) and Izaña (Tenerife) or by means of calibration transfer from reference instruments, while SKYNET uses the ILP method.

Other than the calibration procedures, each network also uses different post-processing and cloud-screening algorithms. One of the main differences between GAW-PFR as used by AERONET and SKYNET is a correction for absorption due to nitrogen dioxide (NO₂) and water vapour (H₂O) (Kazadzis et al., 2018a; Estellés et al., 2012; Drosoglou et al., 2023; Sinyuk et al., 2020). However, there are also differences in the way the optical depths of ozone absorption and Rayleigh scattering are calculated (Cuevas et al., 2019). In addition, the cloud-screening algorithms exhibit some differences, with the SKYNET algorithm being particularly strict (Kazadzis et al., 2018a).

Table 1 Reference and comparison instruments used at each location, including the time periods of the common datasets. ^∗ Modified version of POMCNR suitable for lunar observations.

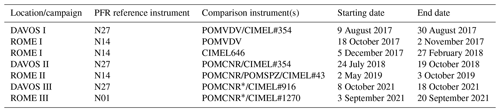
In order to evaluate the ILP method, GAW-PFR and ESR have signed a memorandum of understanding (MoU) for scientific collaboration, including several intercomparison campaigns (Quality and Traceability of Atmospheric Aerosol Measurements or QUATRAM I, II and III). During the 2017–2021 period, a PFR was transported to Sapienza University (Rome, Italy) to measure AOD in parallel with one or more POM and CIMEL (Table 1, Sect. 2.1) instruments. In addition, at least one POM was transported to Davos during three different periods (Table 1, Sect. 2.1), where the WMO AOD reference (PFR-Triad) and a CIMEL are operated. The POMs were calibrated using both the ILP method and calibration transfer with a PFR as a reference (Campanelli et al., 2024).

This study aims to assess the AOD differences between GAW-PFR and ESR and the effect of the different calibration approaches. In addition, we investigate the extent to which different factors such as atmospheric conditions and input parameters required to perform the ILP method contribute to the calibration differences. In intercomparisons (e.g. Kazadzis et al., 2023), the study of AOD differences was limited to the differences in terms of the AODs provided by each network. In the present study, we also separate the effect of the calibration approaches and the effect of the post-processing and instrument differences. We also include one campaign at each location with a duration of several months, which provided a significantly larger amount of data compared to the shorter campaigns that are more frequently organized. Finally, we include a detailed analysis of the ILP calibration method in relation to the aerosol properties and its sensitivity to all required input parameters.

2 Instruments, calibration methods and AOD datasets

2.1 Instrumentation and locations

In order to evaluate the ILP performance under different conditions, we used the sun photometer measurements from the 2017–2021 period at two locations: Davos (Switzerland) and Rome (Italy). The station at PMOD/WRC (1590 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$) is close to Davos, which lies in the eastern Alps mountain region of Switzerland. The area has no significant local pollution. Aerosols can reach the area from other parts of Europe due to its proximity to several European countries and during strong Sahara dust transport episodes. The other station at Sapienza University (83 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$) is close to the centre of Rome.

For this study, we used the sun photometer PFRN27 (part of the PFR reference triad) as a reference in Davos, while in Rome we used PFRN14 (2017–2019) and PFRN01 (2021). We also used a co-located CIMEL in each campaign for AOD cross-validation. In total, we compared three POM instruments with the PFRs: two ESR network reference (master) instruments (one of the POM masters in two different versions due to modifications between QUATRAM II and III to make it suitable for lunar measurements) and one travelling standard. A summary of all instruments and datasets is shown in Table 1.

2.1.1 PFR

The PFR (Wehrli, 2000) is a sun photometer that measures DSI at four wavelengths nominally centred at 368, 412, 501 and 862 nm; it is mounted on an independent tracking system to follow the motion of the Sun. The entrance window of the instrument is protected by a quartz window, and the internal parts are fully protected from outside conditions. It is filled with dry nitrogen at approximately 2 bar, and the internal temperature is kept constant by an active Peltier system at approximately 20 °C, with an accuracy of 0.1 °C. Radiation passes through the quartz window and interference filters to allow solar radiation from only a narrow spectral region to reach the silicon photodiode detector. The full-width-at-half-maximum (FWHM) bandwidth of the filters varies from 3 to 5 nm, and its field-of-view (FOV) angle is approximately 2° at FWHM. Measurements occur every minute when a shutter opens for 10 s to perform the 10 sequential measurements at each wavelength. This minimizes the exposure time of the filters to solar radiation and hence minimizes their degradation. The stability of the travelling-standard PFRs is validated by calibration before and after each campaign.

2.1.2 PREDE POM

The PREDE POM (Estelles et al., 2012; Prede Co. Ltd., Japan: https://prede.com/english/skyradio.html, last access: 10 April 2024) is a sun and sky radiometer with a two-axis stepping motor as a tracking system to perform observations of both direct sun and diffuse sky irradiance. The step is 0.0036° per pulse. There are two major versions of the instrument with different wavelengths. POM-01 measures direct solar irradiance and diffuse sky irradiance at seven wavelengths centred at 315, 400, 500, 675, 870, 940 and 1020 nm. POM-02 is an extended version measuring at 315, 340, 380, 400, 500, 675, 870, 940, 1020, 1627 and 2200 nm. In both cases, the FWHM bandwidth is 2–10 nm depending on the channel. The wavelengths are isolated using filters mounted on a filter wheel, and the detector is a silicon photodiode, except for the case of wavelengths above 1600 nm in the POM-02, which are measured by an InGaAs photodiode. The FOV of the instrument is approximately 1° and includes a temperature control system to maintain an internal temperature of 30 °C, a four-element silicon Sun sensor and a rain sensor. In this study, we used a standard POM-01 instrument, while the rest of the instruments used were modified POM-01 versions to measure at 340 nm instead of 315 nm.

2.1.3 CIMEL

The CIMEL sun and sky photometer (Giles et al., 2019) is an instrument including a two-axis robotic tracking system. This tracking system allows it to perform direct sun and sky scans in order to measure either DSI or diffuse sky radiance. There are different versions measuring at different wavelengths. The smallest wavelength is 340 nm, and the largest wavelength is 1640 nm, although for some versions it is 1020 nm. The number of wavelengths is up to 10. In this study, we used CIMELs with at least eight interference filters centred at 340, 380, 440, 500, 675, 870, 940 and 1020 nm. The FWHM is 10 nm, except for 340, 380 and 1640 nm (2, 4 and 25 nm, respectively). A silicon detector is used to measure the radiation. Filters are mounted on a filter wheel that moves every second to switch to a different wavelength until all channels are measured in a measurement sequence. The sequence is then repeated three times within 30 s to provide triplet observations. The instrument has an FOV of 1.2°. It also has a four-quadrant detector, which detects the point of maximum solar-radiation intensity, enabling it to correctly point to the Sun before the measurement sequence starts. AERONET AOD data are publicly available at three levels (1.0, 1.5 and 2.0). In this study, we only used level 2.0, which included cloud screening, the final calibration and quality assurance.

2.2 Calibration methods

We used two different calibration methods to calculate the extraterrestrial constant of the POMs: the ILP method and a calibration transfer using a PFR as reference.

2.2.1 Improved Langley plot

The ILP method (Campanelli et al., 2004; Nakajima et al., 2020; Campanelli et al., 2024) is a modification of the conventionally used SLP. The basic principle in both methods is to use the solar radiation measured at the ground during at least a half-day, as well as the Beer–Lambert–Bouguer law:

$$\begin{array}{}\text{(1)}& I=I_{\mathrm{0}}{e}^{-m\mathit{\tau }},\end{array}$$

where I is the DSI measured at the ground, I₀ is the calibration constant (solar irradiance at the top of the atmosphere in the units of the instrument), m is the air mass coefficient, and τ is the total optical depth of the atmosphere. The solar irradiance is measured in the instrument's units as the SLP and ILP methods do not require conversion to units of W m⁻². The total optical depth is the sum of the scattering and absorption optical depths of the atmospheric constituents.

For the case of no clouds, in front of the solar disc,

$$\begin{array}{}\text{(2)}& \mathit{\tau }={\mathit{\tau }}_{\mathrm{R}}+{\mathit{\tau }}_{\mathrm{g}}+{\mathit{\tau }}_{\mathrm{a}},\end{array}$$

where τ_R is the Rayleigh scattering optical depth, τ_g is the gas absorption optical depth, and τ_a is the extinction aerosol optical depth.

Equation (1) can be written as follows:

$$\begin{array}{}\text{(3a)}& \ln I=\ln I_{\mathrm{0}}+m\mathit{\tau }\end{array}$$

or

$$\begin{array}{}\text{(3b)}& \ln I=\ln I_{\mathrm{0}}-m{\mathit{\tau }}_{\mathrm{R}}-m_{\mathrm{g}}{\mathit{\tau }}_{\mathrm{g}}-m_{\mathrm{a}}{\mathit{\tau }}_{\mathrm{a}}.\end{array}$$

The value of τ_R is calculated using the atmospheric pressure. The value of τ_g is calculated from the total column of gases absorbing at a certain wavelength. The values of m_g and m_a are the air masses corresponding to gases and aerosols, respectively.

The SLP method uses Eq. (3a), and by measuring DSI during the day at several known air masses, we can perform a linear fitting procedure assuming that the total optical depth of the atmosphere is constant for at least several hours (slope of the linear fit). However, the optical depth can vary under real atmospheric conditions. At wavelengths where gas absorption is minor or where the gases that absorb radiation show no rapid variability, AOD dominates the total optical depth. The SLP method (sun photometers use carefully selected wavelengths to avoid strong absorption) is applicable with high accuracy at high-altitude locations where the AOD is usually very low and where its fluctuations do not have a significant effect on the total optical depth over timescales of a few hours. On the other hand, the SLP method cannot be used at sites with aerosol pollution (Shaw et al., 1983; Toledano et al., 2018). In order to avoid the shipment of instruments to such locations, to increase the frequency of calibration and to monitor their status, we require a method that is usable at any type of station. The ILP method was developed for this purpose. Instead of using Eq. (3a), a modified version of Eq. (3b) is used, which is now described.

The Rayleigh scattering and gas absorption optical depths can be calculated, and so AOD is the only parameter to be retrieved before deriving the calibration constant. In the ILP method, instead of AOD, the scattering aerosol optical depth (sc-AOD) is used as a parameter. If ω is the single scattering albedo (SSA), τ_a is​​​​​​​ the AOD and τ_sc is the sc-AOD then τ_sc=ωτ_a, and Eq. (3b) takes the following form:

$$\begin{array}{}\text{(4)}& \ln I+m{\mathit{\tau }}_{\mathrm{R}}+m{\mathit{\tau }}_{\mathrm{g}}=\ln I_{\mathrm{0}}-m{\displaystyle \frac{{\mathit{\tau }}_{\text{sc}}}{\mathit{\omega }}}.\end{array}$$

Assuming $y=\ln I+m{\mathit{\tau }}_{\mathrm{R}}+m{\mathit{\tau }}_{\mathrm{g}}$ and x=mτ_sc, we obtain a straight line $y=ax+b$, where the slope is $a=-\frac{\mathrm{1}}{\mathit{\omega }}$ and b=ln I₀.

Therefore, calculating τ_sc for several times during the day, we can apply a linear fit to all pairs of x and y values and calculate the calibration constant. This method takes into account the variability of the AOD but assumes constant SSA during the measurement period instead. Therefore, large variability of SSA can affect the accuracy of the method.

The estimation of τ_sc is possible through inversion modelling (Skyrad pack code version 4.2 in our case) applied to the angular distribution of normalized sky radiance (NSR) (Eq. 5) observed in almucantar geometry at scattering angles up to 30°. The NSR is defined in Eq. (5):

$$\begin{array}{}\text{(5)}& R\left(\mathit{\theta }\right)={\displaystyle \frac{E\left(\mathit{\theta }\right)}{m\mathrm{\Omega }I}},\end{array}$$

where E is the measured diffuse sky irradiance, θ is the scattering angle, m is the air mass, Ω is the solid-view angle (SVA) of the instrument, and I is the direct solar irradiance.

The model estimates sc-AOD and the aerosol phase function by retrieving the size distribution with an a priori refractive index. To model the radiative transfer and to retrieve sc-AOD, the surface albedo (SA), the total ozone column (TOC) and the surface pressure (P) are also required as inputs.

The Skyrad code also derives SSA and therefore AOD, but it is not used in the ILP calibration. However, it is used for a screening criterion as all values corresponding to AOD ≥ 0.4 are rejected before the final calibration.

2.2.2 Calibration transfer and AOD calculation

To evaluate ILP, we calibrated the POMs using a PFR as a reference for the campaign. We begin by assuming that two co-located instruments (a PFR and a POM) measure DSI at the same wavelength. If I₁ is the DSI at the ground measured with a PFR, I₂ is the DSI measured with a POM at the same time, I₀₁ is the PFR calibration constant and I₀₂ is the POM calibration constant then the irradiances satisfy the following equation:

$$\begin{array}{}\text{(6a)}& {\displaystyle \frac{I_{\mathrm{1}}(\mathit{\lambda },t)}{I_{\mathrm{2}(\mathit{\lambda },t)}}}={\displaystyle \frac{I_{\mathrm{01}\left(\mathit{\lambda }\right)}}{I_{\mathrm{02}\left(\mathit{\lambda }\right)}}}.\end{array}$$

The POM calibration constant is

$$\begin{array}{}\text{(6b)}& I_{\mathrm{02}}=I_{\mathrm{01}}{\displaystyle \frac{I_{\mathrm{2}}}{I_{\mathrm{1}}}}.\end{array}$$

Therefore, we used the raw signal ratio of the instruments for measurements with a maximum of 30 s time difference and the known calibration of the PFR to calculate the calibration for the POM. The calibration constants and raw signals are in the instrument units (different for each instrument) and were corrected for an Earth–Sun distance of 1 au.

The signal ratios were cloud-screened with the PFR AOD cloud-screening algorithm (Kazadzis et al., 2018a) and were visually filtered for outliers and days with erroneous measurements. Due to diurnal variation of the signal ratios, we only used data from 09:00–13:00 UTC. We also excluded all days with fewer than 20 measurements in this time interval and calculated a point-to-point calibration for the remaining data. We checked whether the 2 standard deviations (σ) of all points during each day fell below or were equivalent to 0.5 % of the daily median calibration. If the 2σ values were above 0.5 % of the daily calibration, we repeatedly removed all points outside the 2σ range until the day satisfied this criterion. If the remaining points of that day fell below 20 during this procedure, the day was rejected. Finally, we further examined the point calibrations and their corresponding AODs to reject any remaining days with erroneous calibrations. From the quality-assured datasets, we calculated the POM daily median calibrations and their monthly average (since ESR calculates the calibration with ILP on a monthly basis).

To calculate the AOD, we used the following procedure (used by ESR): for the first month of each campaign, we used the monthly calibration constant for all measurements of the month. For the rest of the months, we assumed that the monthly calibrations correspond to the last day of each month at 12:00 UTC. For measurements between two monthly calibrations, we used linear interpolation to calculate the calibration at the time of the measurement. The interpolation is only based on these two consecutive monthly calibrations. We only used two wavelengths, 500 and 870 nm, as they are directly comparable between the instruments. For the second channel, the nominal wavelength of the PFR is 862 nm, while for the POM, it is 870 nm. Despite the difference of 8 nm in wavelength, Rayleigh and Mie scattering are weaker at longer wavelengths so the effect of the difference is less significant in this spectral region.

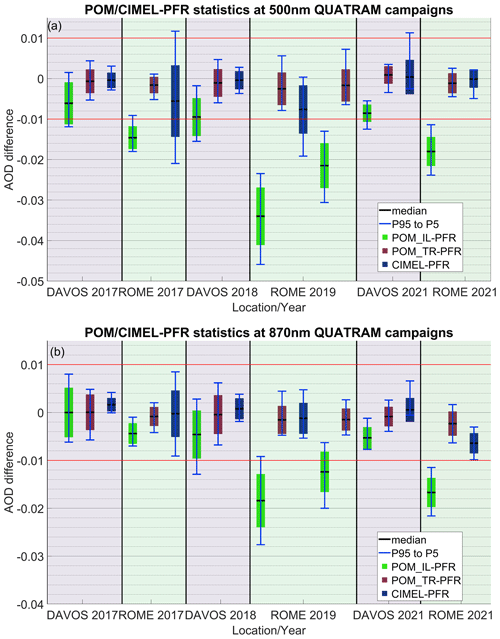
Figure 1 Boxplot of the statistics of AOD differences for all instrument comparisons for both locations of the three QUATRAM campaigns. Panel (a) is for 500 nm. Panel (b) is for 870 nm. The black line is the median difference, the size of the boxes denotes the distance between the median and the standard deviation, while the error bars show the 5th and the 95th percentiles of the AOD differences. In all cases, the PFR AOD is the reference instrument. The green boxes correspond to the differences between the original AOD from POMs and the reference. The red boxes correspond to the POM AOD calculated with the calibration retrieved with transfer from the PFR. The blue boxes correspond to the differences between CIMEL and PFR. For the Rome 2019 campaign, we compare two different POMs with the same PFR (left POMCNR and right POMSPZ).

3 Intercomparison

3.1 Methodology

In order to assess the effect of calibration differences on AOD, we compare the AODs of POMs retrieved from different calibrations at 500 and 870 nm. There are two AOD datasets for each POM: the original AOD provided by ESR and the AOD calculated from the calibration transfer. Both sets of monthly calibrations used and their differences are shown in Table S1 in the Supplement. These two AOD datasets also differ as the algorithms to calculate AOD were different (Kazadzis et al., 2018a). The ESR algorithm calculates AOD, at a given moment, based on the average of three consecutive measurements in 1 min. In the calibration-transfer-based dataset, we use the AOD from the raw signals corresponding to individual measurements. In addition, the second dataset has no correction for nitrogen dioxide (NO₂), while SKYNET takes NO₂ into account. Finally, there are differences regarding the pressure and ozone column values. We screened the data for clouds according to the GAW-PFR algorithm. The reference AOD in all cases is the PFR AOD.

We added the co-located CIMEL instruments into the comparison as a third independent instrument, taking advantage of the long-term experience of measurements between AERONET and GAW-PFR (Kazadzis et al., 2018a; Cuevas et al., 2019; Karanikolas et al., 2022). The CIMEL data were cloud-screened by the AERONET algorithm (Smirnov et al., 2000; Giles et al., 2019) and then further screened according to the GAW-PFR algorithm (Kazadzis et al., 2018b).

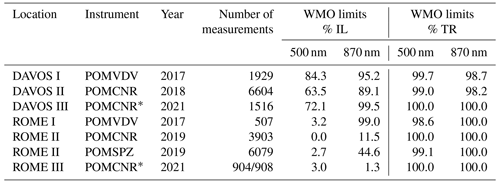
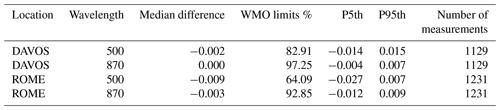
Table 2 The percentage of AOD differences within WMO limits for the comparison between PFRs and POMs. IL refers to the original POM AOD retrieved using the ILP calibration method, and TR refers to the calibration-transfer-based AOD.

^∗ Modified version of POMCNR suitable for lunar observations.

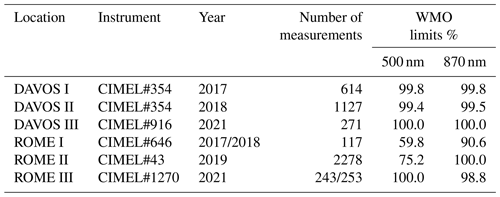
Table 3 The percentage of AOD differences within WMO limits for the comparison between PFRs and CIMELs.

As indicators of the AOD differences, we use the median difference, the standard deviation of the differences, and their 5th and 95th percentiles. According to the World Meteorological Organization (WMO), instruments are considered to be traceable when at least 95 % of the AOD differences are within specific limits (Kazadzis et al., 2018a) given by Eq. (7):

$$\begin{array}{}\text{(7)}& \text{lim}=\pm (\mathrm{0.005}\pm \mathrm{0.01}/m),\end{array}$$

where m is the air mass coefficient. Therefore, the percentage of data within the WMO limits is another indicator we used for the comparison.

3.2 Results

In this section, we present the main findings of the study. First, we show the AOD differences between the CIMEL or POM using different calibrations and the reference PFR. Then we present the stability and uncertainties of the used calibrations.

3.2.1 AOD intercomparison

There were three campaigns per location, and we present the AOD differences between the PFR and POMs or CIMEL. In Fig. 1, we show the median AOD differences and standard deviations (box size), as well as the 5th and 95th percentiles of the differences (error bars). A noticeable feature is that the ESR AOD calculated with the ILP method is systematically lower than the PFR AOD. In Davos, the median differences are between −0.006 and −0.01 at 500 nm and 0.000 to −0.005 at 870 nm. In Rome, the median differences range from approximately −0.014 to −0.034 at 500 nm, with the vast majority of differences being < −0.01. At 870 nm, QUATRAM I in Rome shows a median difference of −0.005, and the other campaigns show a median difference of < −0.01. For QUATRAM II in Rome, which was the longest campaign and the one with the largest differences in terms of the POM master (POMCNR), we included a second POM (POMSPZ). This shows a performance similar to the POM master (POMCNR^∗) during QUATRAM III in Rome.

When using a PFR calibration transfer to recalculate the AOD for POMs, the absolute median differences are < 0.005 for all cases. The CIMEL–PFR comparison shows similar results with all median AOD differences below 0.01. In addition, the majority of the 5th–95th percentiles for either CIMEL–PFR or POM–PFR using the calibration transfer are within 0.01.

Regarding the WMO traceability criteria, the data within the WMO limits for POM AOD with an ILP calibration are below 95 % for all cases at 500 nm, as well as for QUATRAM II and III in Rome at 870 nm (Table 2). However, there is a large deviation between both locations: while at 500 nm, the percentage in Davos is above 60 %, and it is below 4 % in Rome. Using the calibration transfer to calculate POM AOD, > 98 % of data are within the WMO limits (Table 2). The CIMEL–PFR comparison (Table 3) also shows percentages mainly above 98 %. Exceptions are QUATRAM I and II in Rome at 500 nm and QUATRAM I in Rome at 870 nm. All CIMEL–PFR comparisons show at least ∼ 60 % differences within the WMO limits.

Recalculating the AOD with the same post-processing algorithm and for the same instrument (once for each POM) for both POM calibrations (ILP and calibration transfer), we can more clearly observe the effect of just the calibration on AOD. In this case, the median AOD difference is similar to the difference between the original POM and PFR datasets shown by the green boxes in Fig. 1. The results of the comparison, showing the calibration effect along with the “original” differences, are in Fig. S1 in the Supplement (Sect. S1). The median AOD differences attributed to the calibration deviate from the “original” AOD differences by < 0.003, except for three cases. It is approximately 0.005 for QUATRAM III in Rome at 500 nm and in Davos at 870 nm. A larger value of 0.01 was observed for QUATRAM II in Rome at 500 nm for only one of the POMs (POM_CNR). These deviations are not systematically larger or smaller than the “original” at 870 nm, but they are smaller for most campaigns at 500 nm.

The variability of AOD differences for the comparison between both recalculated POM AOD datasets (which just show the calibration effect) is a result of the dependence of the calibration effect on the air mass. Therefore, it depends on the magnitude of the calibration difference, its month-to-month variability and the air mass distribution present in the data.

These results suggest that the overall contributions of the post-processing algorithm and instrument differences between the networks result in AOD differences that are within the PFR AOD retrieval uncertainty. For ESR, the calibration method dominates the overall AOD difference.

3.2.2 Calibration stability and uncertainties

In the previous section, we showed that the major source of AOD differences was due to differences in the PFR and POM calibration methods. The calibration differences between the ILP method and the PFR-based transfer can be found in Table S1 (Sect. S1). The values in the Supplement show some minor differences compared to Campanelli et al. (2024) for some months, mainly due to differences in the selected days. The difference is larger for August 2018 in Davos. During this month, we observed an abrupt shift of daily calibrations early in the month. Hence, we removed the days before the shift as the monthly calibration is attributed to the end of the month when retrieving the AOD. In this section, we discuss the stability and the uncertainties of the different calibrations.

The ILP calibrations show either positive or negative fluctuations for consecutive months at the same location, lying in the 0.17 %–2.3 % range with a median absolute value of 0.55 % and a standard deviation of 0.87 %. These calibration fluctuations can be attributed either to changes in the instruments' response or to the random component of the ILP method uncertainty. The coefficient of variation (CV%) of the daily ILP calibrations per month (Campanelli et al., 2024, Table 2a) is an estimate of the ILP monthly calibration uncertainties. CV% is the percentage of the standard deviation of daily calibration constants during the month divided by the monthly calibration constant. The CV% for the ILP calibrations used in this study lies in the 0.18 %–2.87 % range at 500 and 870 nm.

The PFR calibration differences between consecutive calibrations are in the 0.00 %–0.45 % range at 500 and 870 nm (Table S3), with all calibrations having an uncertainty below 0.4 % (Table S2).

The PFR-based calibration transfers of POMs show fluctuations for consecutive months at the same locations in the 0.00 %–1.72 % range, with a median absolute value of 0.19 % and a standard deviation of 0.56 %. The uncertainties of the calibration transfers calculated as the combination of the PFR calibration uncertainty σ_PFR and the standard deviation of the daily calibrations σ_d are calculated as follows:

$$\begin{array}{}\text{(8)}& {\mathit{\sigma }}_{\text{TR}}=\sqrt{{\mathit{\sigma }}_{\text{PFR}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{d}}^{\mathrm{2}}}.\end{array}$$

Applying Eq. (8) shows that the calibration transfer uncertainties are in the 0.27 %–0.8 % range (Table S2).

The month-to-month variabilities of the ILP method and the transfer-based calibrations do not coincide. This is reflected in the month-to-month variability of the calibration differences between both methods, which is in the 0.01 %–1.93 % range. Their median absolute value is 0.55 %, and their standard deviation is 0.96.

However, not all calibration fluctuations can be explained by the uncertainties in the present section. A particularly interesting case is the calibration change from July to August 2019 in Rome for POMCNR at 870 nm. The CV% of the ILP calibrations of these 2 months is below 0.5 % (Campanelli et al., 2024), while their calibration difference is 1.3 %. The calibration transfers from the PFR for the same months differ by only 0.2 %, providing no evidence of changes in the instrument response. The same months show an ILP calibration change above 2 % for POMSPZ, with the calibration transfers differing by 0.3 %. At 500 nm for the same months, the ILP differences are above 1 %, while the calibration transfer differences are 0 %. Therefore, the ILP differences between these 2 months are attributable to the overall uncertainty of the ILP calibration.

4 Investigation of potential ILP error sources

As the findings presented in Campanelli et al. (2024) showed systematically negative differences between the ILP calibration and PFR-based calibration transfers that are always larger in Rome compared to in Davos, we investigate several potential causes. Initially, we explore whether the aerosol properties between both locations show any systematic difference in terms of value and variability. We also assess the sensitivity of the ILP method to the pre-assigned values of six input parameters: SVA, P, TOC, SA, and the real and the imaginary part of the aerosol refractive index (RRI and IRI). Finally, we investigate whether the AOD, sc-AOD and SSA retrieved from the inversion modelling can provide evidence that may lead to an explanation of the observed differences.

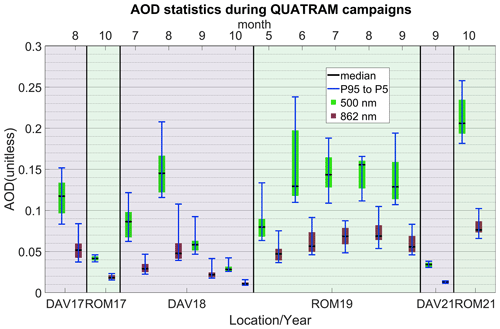
Figure 2 PFR AOD statistics for all months for all campaigns. The green boxes correspond to 500 nm, and the red boxes correspond to 862 nm, with each pair being 1 month. Each box represents 1 month of the campaign.

4.1 Aerosol properties

4.1.1 Methodology

Three parameters are discussed in this section, namely AOD, SSA and the Angström exponent (AE). According to Nakajima et al. (2020), the level of AOD affects the ILP performance. Also, the ILP method uses a pre-assigned refractive index value and assumes a stable SSA (which is connected with IRI) during the half-day in which the ILP is performed (Eq. 4). Therefore, the SSA value and variability may affect the calibration. Due to the above, we assess whether there is an association of the levels or the variability of AOD and SSA with the differences between the ILP method and the calibration-transfer-based calibrations. For the AOD, we used the PFR dataset. For the SSA, we used the AERONET level-1.5 retrievals due to lack of data availability in terms of the quality-assured level 2.0. Because of the limited SSA dataset and the larger uncertainty (compared to level 2.0), we also used the AE from the PFR in the investigation. AE is related to the size of aerosols, and a change in AE reflects a change in aerosol composition that may affect IRI and SSA. For the AOD and AE, we used only data corresponding to the half-days used for ILP calibrations. In addition, we removed all points corresponding to AOD ≥ 0.4 at 500 nm and air masses ≥ 3 according to the screening criteria of the ILP method. For the SSA, we used all data during the campaign months except values < 0.1 corresponding to AOD at 440 nm and a very small number of outliers. Since ESR provides monthly calibrations, we used the monthly median values as indicators of the AOD, SSA and AE average levels. Each monthly median is the median of the daily medians. As indicators of the variability during the ILP method, we use the discrepancies between the monthly medians of the daily 5th, 20th, 80th and 95th percentiles.

4.1.2 Results

Here, we investigate whether there is any systematic difference between Davos and Rome with respect to AOD, SSA and AE values or variabilities that could potentially be associated with the larger calibration differences in Rome for all months. We use AOD and AE from the PFR data during the half-days and full days of the ILP calibrations. SSA is from the AERONET data obtained during the QUATRAM campaigns. We used monthly median statistics as the average level and monthly medians of the daily percentiles (5th, 20th, 80th and 95th) as a variability indicator, as described in Sect. 4.1.1.

Aerosol optical depth

Figure 2 shows the PFR AOD values for all months of the campaigns at both locations. For most months, it is evident that the AOD is higher and more variable in Rome, but there are exceptions, such as for the QUATRAM I (DAV17/ROM17) campaign. Also, we can see that the highest AOD corresponds to QUATRAM III in Rome (ROM21) (Fig. 2), while the largest calibration and AOD differences between PFR and POM were in QUATRAM II (ROM19) (Fig. 1, Table S1). Both AOD values and AOD variability vary at the same location and between both locations from month to month, showing no consistency between AOD (Fig. 1) and calibration differences (Table S1).

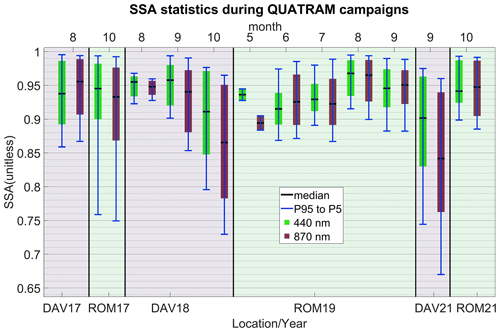
Figure 3 The AERONET SSA statistics for all months and for all campaigns. The green boxes correspond to 440 nm, and the red boxes correspond to 870 nm, with each pair being 1 month. Each box represents 1 month of the campaign. In QUATRAM II (DAV18), the first month of the campaign (July) is missing due to lack of data.

Single scattering albedo

The ILP method assumes a constant SSA as the inverse slope of the linear fit (Sect. 2.2.1) and uses an a priori refractive index (selected by the operator). These assumptions potentially reduce the accuracy of the method. Here, we present the SSA values provided by AERONET, along with their variability during the campaign months (Fig. 3), at 440 nm (green) and 870 nm (red). For the Davos 2018 campaign, there are 3 months instead of 4 as there was a lack of data during the first month, July 2018, due to the fact that the campaign started towards the end of the month. In general, there is no evidence of either any systematic difference between both locations or an association between the calibration and AOD differences, even for the same location. In Rome, the largest SSA variability corresponds to QUATRAM I (ROM17) (Fig. 3), where we observed the smallest calibration and AOD differences during the Rome campaigns (Fig. 1, Table S1). Similarly, the largest variability is during QUATRAM III (DAV21) in Davos, which also exceeds the Rome SSA variability. However, we did not observe larger differences between ILP and the calibration transfer in Davos during QUATRAM III (DAV21) compared to during QUATRAM II (DAV18). In terms of median SSA, depending on the month, either Rome or Davos may have larger SSA. The fluctuations of SSA do not seem to significantly affect the calibration differences. However, we acknowledge that the limitations of the SSA dataset (Sect. 4.1.1) limit the confidence in the conclusions.

Angström exponent

Due to the limitations of the SSA dataset (Sect. 4.1.1), we included a comparison of the AE medians and variabilities during the campaigns as an additional indicator of aerosol composition. During QUATRAM I (DAV17/ROM17), both locations have similar median AE values, but Davos shows the largest variability. During QUATRAM II (DAV18/ROM19), the AE in Davos is the largest, while the variability varies significantly between the months. Similarly, during QUATRAM II in Rome, AE is lower, and each variability largely depends on the month. Finally, during QUATRAM III (DAV21/ROM21), Rome shows the largest AE and variability. Again, there is neither a systematic difference between both locations nor an association of calibration differences and AE at the same location.

4.2 Sensitivity of the ILP method with respect to input parameters

As the ILP calibration requires the instrument SVA, P, TOC, SA, the real and the imaginary part of aerosol refractive index (RRI and IRI) as inputs, we examine to what extent they affect the ILP calibration.

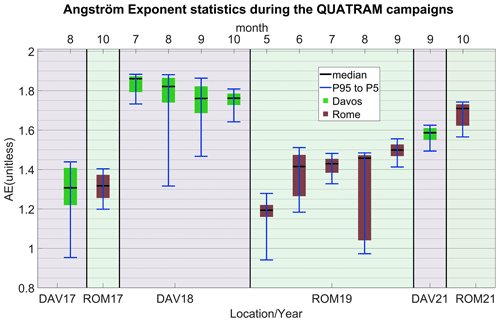
Figure 4 The PFR AE statistics for all months and for all campaigns. The green boxes correspond to Davos, and the red boxes correspond to Rome. Each box represents 1 month of the campaign.

Pre-selected user values for each of the last five parameters (P, TOC, SA, RRI and IRI) can be entered into the Skyrad 4.2 code. Surface pressure depends on the altitude of the station and is calculated using Eq. (9):

$$\begin{array}{}\text{(9)}& P=P_{\mathrm{0}}{e}^{-\mathrm{0.0001184}h},\end{array}$$

where P is the pressure (in atm, P₀ = 1 atm), and h is the altitude in metres. TOC is fixed to 300 DU for both Davos and Rome. SA is fixed to 0.1 (for non-polar regions such as those in the present study), RRI is set to 1.5, and IRI is set to 0.005 for all wavelengths (340, 400, 500, 675, 870 and 1020 nm).

SVA is derived with the disc scan method, an on-site calibration procedure (Nakajima et al., 2020; Campanelli et al., 2024).

To investigate the effect of the aforementioned input parameters, we performed a set of ILP calibrations under different conditions in three sub-studies. For these sub-studies, we only used data from QUATRAM II as it was the longest campaign.

4.2.1 Sub-study 1: ILP test based on local observations – one variable parameter per case

Sub-study 1: methodology

In the first sub-study, we focus separately on each a priori parameter of the ILP calibration. All other parameters are left at their original values except for one that is variable. The goal is to recalculate the ILP calibrations for the local station conditions. Therefore, for each parameter under study, we select a value based on observations at the measurement site. Specifically, TOC and P are present in the PFR data. The TOC used in the PFR algorithm corresponds to the OMI satellite product (aura_omi_l2ovp_omto3_v8.5, https://acd-ext.gsfc.nasa.gov/anonftp/toms/omi/data/overpass/, last access: 25 January 2024), and P was measured with a Setra barometer (uncertainty of less than 10 mbar). The refractive index values (RRI and IRI) are available from datasets of the AERONET almucantar scans (only at 440, 675, 870 and 1020 nm). SA is also taken from the AERONET datasets at the same wavelengths. Over land, this originates from a Ross-Li bidirectional reflectance distribution function (BRDF) model (Lucht and Roujean, 2000) based on MODIS (or Moderate Resolution Imaging Spectroradiometer) satellite observations (Sun et al., 2017). For the rest of the wavelengths (340, 400 and 500 nm), we had to select values based on the existing wavelengths. For RRI and IRI, we used linear interpolation and extrapolation to estimate their values at those three missing wavelengths. The SA selection at 340, 400 and 500 nm is based on its observed values and its spectral dependence in the IGBP library from the libRadtran package (Emde et al., 2016). SVA is provided by ESR.

For each parameter, we used three different values to calculate three different ILP calibration constants. We calculated one ILP calibration using the median (RRI, IRI) or the mean (TOC, P and SA) value during all the months of the three QUATRAM campaigns. The other two calibrations correspond to values equivalent to 1 standard deviation above and below each average. For SVA, we used the values provided by ESR for the first ILP calibration. The other two values are based on the maximum difference observed between ESR SVA and other SVA calibration methods for POMs presented in Campanelli et al. (2024). In the Supplement (Sect. S3–S5 and Tables S4–S6), we present all the values used for the six input parameters.

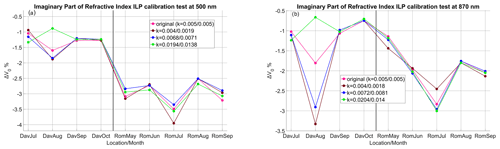
Figure 5 The percentage differences between the IL calibration and calibration transfer for POMCNR during the QUATRAM II months using different values of the imaginary refractive index (original calibration, median k and median ± SD). Panel (a) shows 500 nm. Panel (b) shows 870 nm. The left of the vertical black line corresponds to the Davos calibrations, and the right corresponds to Rome.

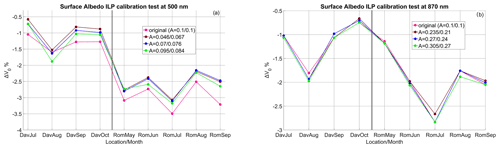
Figure 6 The percentage difference between the IL calibration and calibration transfer for POMCNR during the QUATRAM II months using different values of surface albedo (original calibration, median A and median ± SD). Panel (a) shows 500 nm. Panel (b) shows 870 nm. The left side of the vertical black line corresponds to the Davos calibrations, and the right corresponds to Rome.

Sub-study 1: results

Here, we present the results of the ILP calibration using different values for the input parameters of Skyrad 4.2. The selection is described in the subsection of Sect. 4.2.1 referring to the methodology.

The RRI average observations from AERONET were similar to the pre-assigned input of Skyrad pack 4.2 (1.5 for all wavelengths), while the standard deviation was small. Hence, we used the original, minimum and maximum values (1.33, 1.5 and 1.6). The calibration difference due to this change in RRI was in the 0.00 %–0.21 % range.

For P, we used the values 0.8, 0.83 and 0.85 atm for Davos and 0.97, 1 and 1.02 atm for Rome (the original values for ILP were 0.83 and 1). Most differences were below 0.05 %. In 1 month at 870 nm, we obtained a maximum difference of 0.2 %.

For TOC, we used 260, 300 and 400 DU for both locations, which resulted in differences of up to 0.43 %. The comparisons for RRI, P and TOC are available in more detail in Tables S8–S10.

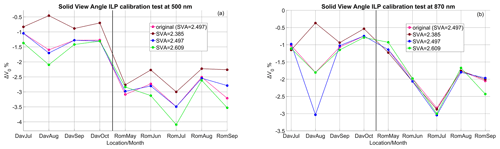
Figure 7 The percentage difference between ILP calibration and transferred calibration for POMCNR during the QUATRAM II months using different values of SVA (original calibration and runs with the provided SVA and SVA ± fixed deviation). Panel (a) shows 500 nm. Panel (b) shows 870 nm. The left of the vertical black line corresponds to the Davos calibrations, and the right corresponds to Rome.

For IRI, SA and SVA, we show the ILP calibration differences in Figs. 5–7. For the majority of the cases, the calibration differences due to IRI are smaller than 0.5 % (Fig. 5). For specific months (August 2018 for Davos and July 2019 for Rome), they are 1 % or higher.

Using SA from AERONET noticeably reduces the calibration difference (Fig. 6) at 500 nm for most months at both locations, but the effect can explain a calibration difference of up to 0.75 %, approximately (September 2019, Rome), while the calibration differences in Rome are in the 2.5 %–3.5 % range (Table S1).

For SVA, there are also noticeable differences of 0.5 %–1 % from the central value (Fig. 7). SVA, like IRI, also shows a particularly high sensitivity during the second month (August 2018, Davos). The central SVA value corresponds to identical input parameters with respect to the original calibration; therefore, we expect the magenta line (original) in Fig. 7 and the blue line (central SVA) to be identical. Some differences below 0.1 % are probably present in most months due to the use of different compilers and versions of the Skyrad pack 4.2. However, for September 2019 in Rome at 500 nm, they differ by up to 0.5 %, and for August 2018 in Davos at 870 nm, they differ by > 1 %. This may be a result of computational instability. For the other months, such differences are below 0.1 %.

4.2.2 Sub-study 2: ILP test based on local observations – all parameters as variables

Sub-study 2: methodology

In the second sub-study, we alter the values of all parameters simultaneously except SVA (we used the value provided by ESR). Again, the goal is to adapt the input parameters to the site conditions. We calculated the ILP calibration for two separate cases:

• a.

  Average case. This included one calibration per month using the monthly average values used in the first sub-study for all five parameters being tested (RRI, IRI, P, TOC and SA).

• b.

  “Selected” case. This included one calibration per month. Here, we selected one of the three values used in the first sub-study for the same five parameters. The selected values are those three that lead to a larger calibration constant. We picked only 1 month per location for this case. The values of the input parameters used for this second sub-study are shown in Sect. S6.

Sub-study 2: results

In this section, we present the results of the second sub-study is described in the subsection of Sect. 4.2.2 referring to the methodology. There are two calibration cases that we tested in the whole QUATRAM II campaign.

The results in Table 4 show changes of < 0.5 % for the average case with the exception of August 2018 in Davos. Due to the large sensitivity in the IRI, the calibration changed by > 1 %.

Table 4 The percentage difference between the original ILP and calibration transfers minus the percentage difference between the ILP method for selected conditions and the calibration transfer. Positive values indicate a smaller difference between the ILP calibration and calibration transfers compared to the differences of the original calibrations.

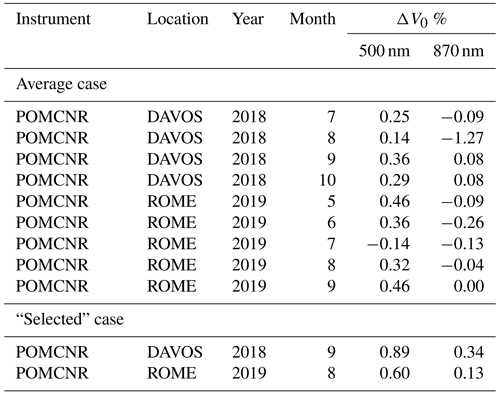
Under the “selected” case (selected conditions for all parameters that increase the ILP calibration), there is a larger increase in the calibration in Davos compared to in Rome at both wavelengths (Table 4), but all differences are below 1 %.

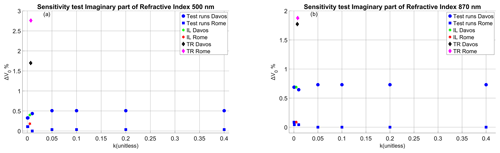
Figure 8 Sensitivity test of the IL calibration with respect to the imaginary refractive index at 500 nm (a) and 870 nm (b). The vertical axis shows the percentage difference of each calibration from the selected zero value. For the latter, we selected the lowest calibration constant of the sensitivity tests present in each graph. The blue squares correspond to sensitivity runs in Rome, the blue circles correspond to sensitivity runs in Davos, the stars correspond to the original ILP calibration transfer, and the diamonds correspond to the calibration constants with a PFR as the reference.

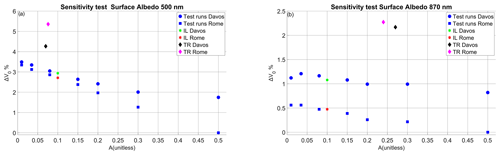
Figure 9 Sensitivity test of the IL calibration with respect to the imaginary refractive index at 500 nm (a) and 870 nm(b). The vertical axis shows the percentage difference of each calibration from the selected zero value. For the latter, we selected the lowest calibration constant of the sensitivity tests present in each graph. The blue squares correspond to sensitivity runs in Rome, the blue circles correspond to sensitivity runs in Davos, the stars correspond to the original ILP calibration, and the diamonds correspond to the calibration transfer constants with a PFR as reference.

4.2.3 Sub-study 3: ILP sensitivity tests

Sub-study 3: methodology

In the third sub-study, we tested the IRI, SA and SVA for a more extensive number of values (seven fixed values regardless of the location) to assess the behaviour of the calibration. For IRI and SA, the selection is based on the three values of the first sub-study, the 5th–95th percentiles of the observations, and the minimum and maximum values. We also added semi-arbitrary values between the observed and two extreme values (one very small and one very large) to test the performance of the method over a wider range of inputs. For SVA, we use values based on the differences between the different SVA calibration procedures appearing in Campanelli et al. (2024). The actual values for each parameter are in Sect. S10; see Table S11.

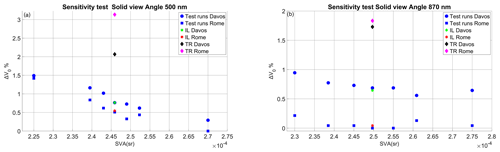
Figure 10 Sensitivity test of the IL calibration with respect to the imaginary refractive index at 500 nm (a) and 870 nm (b). The vertical axis shows the percentage difference of each calibration from the selected zero value. For the latter, we selected the lowest calibration constant of the sensitivity tests present in each graph. The blue squares correspond to sensitivity runs in Rome, the blue circles correspond to the sensitivity runs in Davos, the stars correspond to the original ILP calibration, and the diamonds correspond to the calibration transfer constants with a PFR as reference.

Sub-study 3: results

In this section, we present the results of the third sub-study described in the subsection of Sect. 4.2.3 referring to methodology, where we only test IRI, SA and SVA for seven values over a larger range. We only selected 1 month per location, avoiding August 2018 and July 2019 due to the behaviour presented in the subsections of Sect. 4.2.1 and 4.2.2 referring to the results. Figures 8–10 show the results for each parameter.

Changing only IRI (while it is < 0.05) shows that ILP changes by < 0.25 % for both wavelengths and locations (Fig. 8). Increasing IRI > 0.05 or to other rare and unrealistic values has no effect on the calibration. Therefore, IRI appears to either have a significant or a small effect on the ILP calibration, depending on the month.

Changing only SA (Fig. 9) shows a monotonic but nonlinear dependence of the ILP calibration, where larger SA leads to a smaller calibration constant. At 870 nm, there is a maximum calibration constant at SA = 0.04, with approximately 0.07–0.08 being the average values from AERONET and 0.1 being the value used by ESR. At 500 nm, the difference between the ILP calibrations in Davos and Rome is also smaller at lower SA, showing that ILP in Rome is affected to a larger extent by the SA value at 500 nm. However, even when using an SA value as low as 0.02, the remaining calibration difference between the calibration transfer and ILP at 500 nm is approximately 2 % in Rome and 0.7 % in Davos. At 870 nm, the difference is at least 0.95 % for Davos and 1.7 % for Rome for all SA values used as input.

Finally, for SVA (Fig. 10), there is a monotonic decreasing dependency in terms of the calibration constant and SVA at 500 nm, while some fluctuations occur at 870 nm. The minimum calibration difference at 500 nm is approximately 0.58 % for Davos and 1.7 % for Rome, while at 870 nm, the results are 0.78 % for Davos and 1.6 % for Rome.

4.3 Investigation of the AOD retrievals from sky radiance

4.3.1 Methodology

Since the ILP method is performed using a linear fit of the logarithm of DSI with respect to the product of the air mass coefficient and sc-AOD (Eq. 4), errors from the retrieval of sc-AOD will transfer errors to the calibration. Since there is no reference dataset available for sc-AOD, we tried to indirectly investigate potential errors using available data.

The Skyrad code retrieves both sc-AOD and SSA through inversion modelling and calculates the corresponding AOD as additional information. Therefore, we initially compare the AOD dataset with the PFR AOD for potential differences. However, systematic underestimation or overestimation of both the sc-AOD and SSA retrievals can result in opposing errors to the corresponding AOD that cancel each other. Due to the limitations of the AERONET SSA dataset (lack of level-2.0 data and limited number of retrievals per day), we cannot evaluate the SSA retrieved by Skyrad 4.2 with confidence. Also, part of the SSA difference between the AERONET product and the output of the Skyrad code for the ILP calibration may be attributed to the fixed refractive index and the different scattering angles in the almucantar geometry used for the sky radiance measurements (ILP uses only forward scattering, having a maximum angle of 30°).

Another indirect method to investigate the effect of the sc-AOD retrievals on the calibration performance is to use a different inversion model to retrieve sc-AOD and to re-calibrate the instrument with the ILP method. We therefore used the inversion model Skyrad pack MRI version 2 (Kudo et al., 2021). MRI allows the modelling of non-spherical particles in contrast to Skyrad pack 4.2 retrievals. It also introduces stability constraints on the edges of the size distribution, as well as other smoothness constraints (see Kudo et al., 2021, for a detailed description). As mentioned in Kudo et al. (2021), the MRI method is more accurate at high AOD. Under low-AOD conditions in Davos, a noticeable portion of data showed large retrieval errors and unrealistic sc-AOD and/or AOD values. However, there were sufficient data at both locations to recalculate the ILP calibration, and, hence, it was applied to the QUATRAM II data.

We also investigated whether the variability of the SSA corresponding to the Skyrad 4.2 and MRI retrieval shows any association with the calibration differences. All retrieved AOD, sc-AOD and SSA data retrieved by MRI are screened according to the ILP criteria: keeping only data corresponding to AOD at 500 nm < 0.4 and air masses at < 3.

Table 5 The percentage of daily ILP calibration constants below the corresponding monthly calibration transfer (column 4) and below calibration transfer values of %ΔV₀ ≦ −0.5 % (column 5) and %ΔV₀ ≦ −1 % (column 6). The rows correspond to the days used for the final ILP monthly calibrations for each location and for all campaigns at a single wavelength.

4.3.2 Results

As discussed in Sect. 3.2.2, the ILP method can have significant random uncertainty as individual ILPs for half-days can lead to different average monthly values. However, the vast majority of daily calibration constants are lower than the calibration transfers from PFR, most of them by > 0.5 %–1 % (Table 5), for both locations and wavelengths. One way to obtain such biased results is a systematic underestimation in sc-AOD by the inversion of NSR or an underestimation of sc-AOD in the small air masses and overestimation in large air masses.

In this section, we investigate the effect of the sc-AOD retrieval through inversion of the ILP calibration. As there were two inversion algorithms available, we compare the calibration and the sc-AOD calculated by Skyrad pack 4.2 with the calibration and sc-AOD from Skyrad MRI.

The AOD from Skyrad 4.2 is retrieved through the inverted sc-AOD and may show similar errors. Since we do not have an sc-AOD reference dataset, we compared the Skyrad AOD with PFR AOD.

Table 6 The statistics of the differences between AOD from Skyrad pack 4.2 using POM almucantar scans and AOD from PFR. The results correspond to all QUATRAM campaigns at each location. The time difference threshold is 30 s.

The differences between the AOD retrieved from the Skyrad pack 4.2 using almucantar scans of POM and the PFRs show a systematic underestimation as expected, except for the comparison at 870 nm for Davos (Table 6). The differences are also higher in Rome than in Davos. However, the median differences are significantly smaller than those corresponding to the ESR direct-sun AOD product compared to the same PFRs, and the percentage of differences within the WMO limits is higher. The AOD differences also increase with smaller air masses in Rome but not in Davos. For air masses below 1.5, the median AOD difference is $-\mathrm{0.012}/-\mathrm{0.004}$ at $\mathrm{500}/\mathrm{870}$ nm in Rome and $\mathrm{0.000}/\mathrm{0.001}$ at $\mathrm{500}/\mathrm{870}$ nm in Davos. For air masses above 2, the median AOD difference is $-\mathrm{0.005}/-\mathrm{0.000}$ at $\mathrm{500}/\mathrm{870}$ nm in Rome and $-\mathrm{0.003}/\mathrm{0.000}$ at $\mathrm{500}/\mathrm{870}$ nm in Davos. More details including linear fitting of the air mass dependencies are available in Sect. S12 and Table S15.

Table 7 The percentage differences between the original ILP calibrations and the ILP calibrations using sc-AOD inverted by Skyrad MRI (columns 3 and 4) and the median differences of the corresponding sc-AOD (columns 6 and 7).

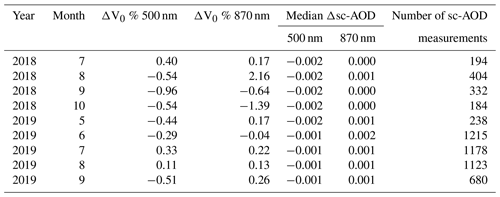
Using the sc-AOD from MRI as an input to the ILP method instead of Skyrad 4.2 in Davos 2018 and Rome 2019, we obtained different calibration constants for each month, but there is no consistent improvement (Table 7). At 500 nm, 6 out of 9 months show a calibration closer to the calibration transfers by between 0.29 % to 0.96 % (negative differences in Table 7), while at 870 nm, the calibration constant is larger for only 3 months (0.04 %–1.39 %). However, the AOD median differences are very small (up to 0.002), and there is no consistency between sc-AOD and calibration differences (Table 6). Due to the fact that the datasets are different, there is also a different selection of individual sc-AOD inversions and days that pass the criteria for the final ILP calibration. The combination of using randomly different sc-AOD points and half-day selections results in the observed calibration differences that are mainly < 1 %. Such random differences are similar to the magnitude of ILP CV% values (defined in Sect. 3.2.2) in Campanelli et al. (2024).

The ratio of the provided sc-AOD and AOD in the ILP output allows us to calculate the corresponding SSA. The number of available QUATRAM II common measurements between Skyrad 4.2 and MRI is 1114 for Davos and 4434 for Rome. For ILP-retrieved SSA from both Skyrad 4.2 and MRI, we mainly observe a larger median in Davos ($\mathrm{0.952}/\mathrm{0.926}$ for $\mathrm{500}/\mathrm{870}$ nm from Skyrad 4.2 and $\mathrm{0.959}/\mathrm{0.939}$ from MRI) compared to Rome ($\mathrm{0.934}/\mathrm{0.917}$ from Skyrad 4.2 and $\mathrm{0.942}/\mathrm{0.927}$ from MRI). The monthly values are in Table S12. The difference between the 80th and 20th percentiles in terms of the SSA is, overall, larger in Rome at 500 nm ($\mathrm{0.03}/\mathrm{0.02}$ from Skyrad 4.2 at 500/870 nm and $\mathrm{0.025}/\mathrm{0.015}$ from MRI) and larger in Davos at 870 nm ($\mathrm{0.021}/\mathrm{0.029}$ from Skyrad 4.2 nm and $\mathrm{0.014}/\mathrm{0.02}$ from MRI). However, there are month-to-month variations. In Table S13, we show the monthly medians of the daily differences between the 80th and 20th percentiles. Depending on the month, either Rome or Davos shows a larger variability.

5 Discussion

In Sect. 3.2.1, we compared the AODs between several PFRs and POMs at two locations with different characteristics (Davos and Rome) using different POM calibration methods. Using the original POM AOD (calculated after ILP calibration of the POMs), we found that the POMs systematically gave lower AOD values than the PFRs up to the 0.034 range at 500 nm and up to 0.018 at 870 nm (median difference). This systematic difference is larger in Rome. Using calibration transfers with the PFR as a reference to re-calibrate the POMs, we achieved excellent agreement, showing that the differences between the post-processing algorithms of the networks and the technical characteristics only have a minor effect on AOD differences. The major cause of AOD differences was the calibration method. The calibration differences per campaign were approximately 0.7 %–1.6 % in Davos and 1.6 %–3.5 % in Rome at 500 nm and 0.2 %–1.8 % in Davos and 1 %–3.4 % in Rome at 870 nm (Table S1). The AOD differences per campaign were approximately 0.006–0.01 in Davos and 0.015–0.034 in Rome at 500 nm and 0–0.005 in Davos and 0.005–0.017 in Rome at 870 nm (Sect. 3.2.1).

We also compared the AOD between the reference PFR and the co-located CIMEL for each case for cross-validation. All median AOD differences between CIMEL and PFR were < 0.01, and the traceability criteria were satisfied, with the exception of the QUATRAM I campaign in Rome and at 500 nm for the QUATRAM II campaign, also in Rome. The generally good agreement between PFR and CIMEL is consistent with the small differences in terms of the CIMEL- and PFR-based calibration transfers in Campanelli et al. (2024).

Regarding the PFR calibrations, the uncertainty is lower, as shown in Sect. 3.2.2. The PFRN01 and PFRN14 sun photometers used in Rome showed good calibration stability before and after their shipment (Sect. 3.2.2). PFRN27, used in Davos as a reference, was present in Davos as part of the PFR reference triad for the whole of the 2017–2021 period. In addition, it is used in a long-term comparison study with AERONET (Karanikolas et al., 2022) and has shown very good agreement with a co-located CIMEL during the 2007–2019 period.

In an attempt to explain the observed calibration differences, we investigated whether both stations show some systematic difference during the campaigns in terms of the values or variability in aerosol properties that could explain the different calibration performance. The available datasets of AOD, SSA and AE showed no such association. However, the AERONET SSA dataset has important limitations with regard to data availability and accuracy, as explained in Sect. 4.1.1. One explanation could be that the values or the variability of SSA and AE affect the calibration proportionally to the AOD values. However, we cannot identify such an association from our results (details in Figs. 2–4 and Table S1). For example, in Davos, the last 2 months of QUATRAM II (September–October 2018) show similar calibration differences between the ILP method and calibration transfers under different conditions for all three parameters (AOD, SSA and AE). Similarly, in Rome, the third month (July 2019) shows the largest calibration difference under similar AOD and SSA conditions but lower AE variability compared to June and August 2019.

We also conducted a sensitivity analysis of the ILP method under different conditions with respect to its six input parameters: RRI, IRI, SA, TOC, P and SVA. SVA and SA errors can explain part of the underestimation in the ILP calibration. Regarding IRI, the ILP calibration showed very little sensitivity during most months (which is consistent with Campanelli et al., 2004) but was very large for specific months. This showed some evidence of model instabilities under certain conditions and combinations of NSR and IRI values. RRI, TOC and P showed no evidence of a significant effect. To conclude, the largest part of the calibration differences remained unexplained.

By comparing the retrieved AOD from the Skyrad code (using NSR) with PFR AOD, we can identify an underestimation, mainly in Rome, although this is smaller than the AOD retrieved from direct-sun scans and the ILP calibration. However, the ILP calibration uses sc-AOD instead of AOD. A stronger underestimation of sc-AOD compared to AOD or the dependence of the sc-AOD error in relation to the air mass can explain the calibration difference. Such underestimation may not be fully visible in the AOD dataset due to a systematic error in the ILP-inverted SSA that reduces the AOD error.

Using an alternative inversion model (Skyrad MRI) to retrieve sc-AOD, we found no significant systematic differences in terms of sc-AOD compared to Skyrad 4.2. The ILP calibration using MRI had positive and negative differences compared to the original one, mainly by less than 1 %. Such differences can be attributed to the different selections of data and random differences in terms of sc-AOD between both models. Under both models, we found no consistency between the SSA variability corresponding to the provided sc-AOD or AOD. The AERONET median SSA is higher in Davos (0.02); however, the difference is within the uncertainty of the inversions and corresponds to different scattering angles. Also, the high SSA uncertainties and the mainly low sensitivity of the ILP calibration with respect to IRI further limit the significance of this finding.

Another issue related to the ILP calibration is its random uncertainty. Despite the clear systematic bias we observed compared to the calibration transfers, the random-uncertainty component remains significant. In Sect. 3.2.2, we showed that there can be both a month-to-month variability in terms of the calibration constant and estimated random-uncertainty components in terms of the ILP calibration above 1 %. The lack of coincidence between the month-to-month variability of ILP and transfer-based calibrations suggests that we cannot indeed attribute the month-to-month variability of ILP calibrations to instabilities of the instruments. The calibration transfers showed smaller uncertainty and larger stability, apart from large shifts during specific months. The PFR calibrations are more stable and have smaller uncertainties than the calibration transfers, and so we cannot attribute the calibration transfer fluctuations to changes in the PFR response. However, as described in Sect. 3.2.2, we cannot attribute all fluctuations in ILP calibrations to their CV% value. A potential source of uncertainty (or bias) is the linearity of the fit during the ILP calibration. The currently used standard error threshold of the linear fit may allow a discrepancy with regard to linear behaviour that is large enough to cause uncertainties at the observed level. More research is needed to further clarify the matter.

The calibration underestimation observed by the ILP calibration compared to the calibration transfers is probably a result of errors in the sc-AOD retrievals. As the ILP method shows sensitivity, mainly to the provided NSR, the retrieval errors are probably a result of assumptions in the forward model that simulates the NSR. The effect is amplified in Rome compared to in Davos. A known constant difference between both locations is the altitude. As Davos is higher by about 1500 m, the atmospheric pressure is constantly lower, leading to a reduced Rayleigh scattering optical depth, which contributes to a reduced DSI and decreased multiple radiation scattering. Therefore, the NSR dependence with the scattering angle can be systematically different between both locations for any given solar zenith angle (SZA). In that case, the forward ILP model may simulate less accurately the effect of multiple scattering in Rome, or the increased multiple scattering there may amplify the errors of the simulations. More research is required to investigate whether the source of the larger calibration differences in Rome is indeed due to the lower altitude of the station in Rome and to what extent this can be generalized to other sites.

Significant improvement may be possible using the cross-improved Langley plot (XILP) (Nakajima et al., 2020; Campanelli et al., 2024), which seems to lead to smaller biases. XILP performs ILP with the axes reversed but also includes different criteria for the selection of data used for the final linear fit and the days considered to be valid. However, XILP also showed a few cases with large differences (even larger than ILP) compared to the calibration transfer. Therefore, more research is required to assess the XILP sensitivity in terms of the sc-AOD and the input parameters and whether it can lead to long-term traceability of AOD regardless of the location and conditions.

6 Conclusions

In this study, we assess AOD differences between GAW-PFR and ESR instruments and investigate their causes. We used data from three intercomparison campaigns, each with two locations: Davos, a mountainous area, and Rome, a low-altitude urban area. A comparison of different pairs of PFR and POM instruments showed that the traceability criteria are satisfied at 870 nm in Davos in all campaigns and in Rome in one campaign. Criteria are not satisfied at 500 nm, but the differences in Davos are smaller and below the AOD standard uncertainty (median AOD difference below 0.01). Our analysis shows that the contribution of the instrument and post-processing differences to the AOD differences is minor. The major cause is the different calibration methods. We concluded that the ILP calibration method used by ESR results in a systematic underestimation of the calibration constant and, as a result, an underestimation in AOD as well compared to GAW-PFR and AERONET measurements. Our investigation of the causes showed that part of the difference (mainly at 500 nm) can be explained by potential errors in SA and the instrument SVA used as input for the ILP calibration. However, the largest part of the difference cannot be attributed to errors in the input parameters but can be explained by errors in the sc-AOD retrieval, which is required to perform the ILP method. The error is probably a result of the forward-model assumptions. A potential explanation could be related to the way the model handles multiple scattering, which probably amplifies the error at lower-altitude sites. This work is a demonstration of the limitations and challenges of the ILP “on-site” calibration procedure for sun photometers. The present study and that of Campanelli et al. (2024) offer a starting point for future research aimed at a better understanding, with more general conclusions and potential improvements.