High-precision oxygen isotope (δ¹⁸O) measurements of atmospheric dioxygen using optical-feedback cavity-enhanced absorption spectroscopy (OF-CEAS)

Atmospheric dioxygen (O₂) concentration and isotopic composition are closely linked to the carbon cycle through anthropic carbon dioxide (CO₂) emissions and biological processes such as photosynthesis and respiration. The measurement of the isotopic ratio of O₂, trapped in ice core bubbles, brings information about past variation in the hydrological cycle at low latitudes, as well as past productivity. Currently, the interpretation of those variations could be drastically improved with a better (i.e., quantitative) knowledge of the oxygen isotopic fractionation that occurs during photosynthesis and respiration processes. This could be achieved, for example, during experiments using closed biological chambers. In order to estimate the isotopic fractionation coefficient with good precision, one of the principal limitations is the need for high-frequency online measurements of isotopic composition of O₂, expressed as δ¹⁸O of O₂ (δ¹⁸O(O₂)) and O₂ concentration. To address this issue, we developed a new instrument, based on the optical-feedback cavity-enhanced absorption spectroscopy (OF-CEAS) technique, enabling high-temporal-resolution and continuous measurements of O₂ concentration as well as δ¹⁸O(O₂), both simultaneously. The minimum Allan deviation occurred between 10 and 20 min, while precision reached 0.002 % for the O₂ concentration and 0.06 ‰ for δ¹⁸O(O₂), which correspond to the optimal integration time and analytical precision before instrumental drift started degrading the measurements. Instrument accuracy was in good agreement with dual-inlet isotope ratio mass spectrometry (IRMS). Measured values were slightly affected by humidity, and we decided to measure δ¹⁸O(O₂) and O₂ concentration after drying the gas. On the other hand, a 1 % increase in O₂ concentration increased the δ¹⁸O(O₂) by 0.53 ‰. To ensure the good quality of O₂ concentration and δ¹⁸O(O₂) measurements we eventually proposed to measure the calibration standard every 20 min.

1 Introduction

Dioxygen (O₂) is the second most important constituent of the atmosphere, and the evolution of its atmospheric concentration is closely related to the evolution of the carbon cycle through fossil fuel combustion and biosphere processes (respiration and photosynthesis). The O₂ concentration has been shown to have decreased by 0.7 % over the last 800 kyr probably because of changes in organic carbon burial and oxidation rates with a stabilizing effect of silicate weathering (Stolper et al., 2016). On shorter timescales, the O₂ concentration shows clear seasonal variations anticorrelated with atmospheric carbon dioxide (CO₂) concentration, the combination of both O₂ and CO₂ concentrations enabling the variability in the marine and terrestrial biosphere productivity to be documented through the calculation of the atmospheric potential oxygen (e.g., Goto et al., 2017; Keeling and Manning, 2014; Keeling and Shertz, 1992; Stephens et al., 1998).

The isotopic composition of O₂, expressed as δ¹⁸O of O₂ (δ¹⁸O(O₂)), exhibits variations at the orbital (10 000 years) and millennial scale (Landais et al., 2010; Severinghaus et al., 2009), but no appreciable variation at the seasonal scale has been evidenced. Past δ¹⁸O(O₂) variability has been linked to variations in the low-latitude water cycle and possibly to the variability in the relative proportions of terrestrial and marine productivity (Bender et al., 1994; Extier et al., 2018; Luz and Barkan, 2011). Still, evaluating the relative importance of these two contributions remains difficult since it relies on fractionation factors associated with the biological processes consuming and producing oxygen. These fractionation factors have only been determined for a small number of species and often at the micro-organism scale.

Combining measurements of δ¹⁷O of O₂ (δ¹⁷O(O₂)) and δ¹⁸O(O₂) permits access to gross primary production and is largely used for this purpose in the ocean in combination with the elemental ratio between O₂ and argon (Ar), i.e., ${\mathrm{O}}_{\mathrm{2}}/\mathrm{Ar}$ ratio (Jurikova et al., 2022; Luz and Barkan, 2000; Stanley et al., 2010). In addition, when measuring both δ¹⁷O(O₂) and δ¹⁸O(O₂) in old air trapped in ice cores, we have access to the past variability in the global biosphere productivity, although with large uncertainties (Blunier et al., 2002; Brandon et al., 2020; Luz et al., 1999; Yang et al., 2022). Part of this limitation is again linked to our poor knowledge of the isotopic fractionation factors during the biological processes.

In order to make progress on the quantitative determination of the oxygen fractionation factors in the biosphere, a good approach is to work on closed biological chambers where plants grow in controlled conditions. This approach was already applied in previous studies, mostly at the micro-organism scale with regular sampling of air from the biological setup (Guy et al., 1993; Helman et al., 2005; Stolper et al., 2018). At a larger scale such as for a macroscopic study on a terrarium, the duration of the experiment needs to be larger to have a quantified signal (Luz et al., 1999).

One of the main limitations when working on the experimental determination of the fractionation factors is that we need numerous measurements of δ¹⁸O(O₂) and O₂ concentration to make a precise determination (Paul et al., 2023). However, sampling air from the chamber at high resolution is not convenient since it implies reducing the quantity of atmospheric air in the biological chamber.

The development of continuous measurements of O₂ concentration has permitted the monitoring of O₂ concentration to be improved in parallel with greenhouse gases. These methods use different techniques such as fuel cell analysis (Goto et al., 2013) or gas chromatography coupled with a thermal conductivity detector (Tohjima, 2000). More recently, Berhanu et al. (2019) developed an analyzer based on the cavity ring-down spectroscopy (CRDS) technique which is able to measure the concentration of O₂ with high precision (standard error of 0.0001 % over 1 min measurement) on one mode as well as the δ¹⁸O(O₂) with a 0.01 ‰ standard error on a second mode. However, δ¹⁸O(O₂) and O₂ concentrations are not measured on the same mode and so not at the same time (an instrument software restart is required for switching between modes).

We present here a new instrument based on the optical-feedback cavity-enhanced absorption spectroscopy (OF-CEAS) technique (see Morville et al., 2005), primarily designed and optimized to measure δ¹⁸O(O₂) but also able to measure the atmospheric O₂ concentration in parallel. After a presentation of the instrumental design, we discuss the performance of the instrument as well as the influences of humidity on the determination of O₂ concentration and isotopic composition and O₂ concentration on δ¹⁸O(O₂). Based on our tests, we propose a sequence for the calibration of the instrument during a series of measurements. This sequence is then used to compare the performance of this instrument to a dual-inlet isotope ratio mass spectrometry (IRMS) instrument for measurements of δ¹⁸O(O₂) and O₂ concentration.

2 Material and methods

2.1 Instrument description

We present here a new analyzer for O₂ exploiting the high-sensitivity absorption spectroscopy technique OF-CEAS. This technique is based on a high-finesse optical cavity and is analogous to the well-known cavity ring-down spectroscopy. It was first described in Morville et al. (2005) (see also Morville et al., 2014), and since then, it has been successfully exploited in different laboratories and field applications such as multispecies breath analysis (Ventrillard-Courtillot et al., 2009), analyses of geothermal gases (Kassi et al., 2006), water isotopes measurements in atmospheric air (Lauwers et al., 2024) and analyses of fossil air extracted from ice cores (Faïn et al., 2014). In addition, the simple and compact optical layout of OF-CEAS led to the development of robust devices now commercialized by the AP2E company (https://www.ap2e.com, last access: 14 November 2024). The instrument used in this study is based on an AP2E analyzer customized to satisfy some specific demands, in our case the possibility to measure simultaneously δ¹⁸O(O₂) and O₂ concentration because no such analyzer has been commercialized by the company before. To our knowledge this is the first OF-CEAS implementation using a distributed feedback (DFB) diode laser in the visible range. For the rest, this instrument represents a standard implementation of the OF-CEAS technique as described in the above-cited publications; therefore we address the interested reader to those references for an OF-CEAS schematic and details of its working principle and operation (in particular Morville et al., 2014, and in addition Lechevallier et al., 2019). In short, the OF-CEAS technique uses a V-shaped high-finesse optical cavity which sends back to the laser a fraction of the resonating light. This optical feedback (OF) allows a self-locking of the laser to the successive cavity resonance frequencies during a frequency scan. This enables a less noisy output signal and increased stability compared to what is typically observed with conventional cavity-enhanced absorption spectroscopy (CEAS). A simplified schematic of an OF-CEAS V-shaped optical cavity is presented in Fig. 2b. Variations relative to those publications are the proprietary AP2E electronics and software for system and laser control and the acquisition, digitization and analysis of signals. In addition, the AP2E instrument opto-mechanical layout is a revisited version of previous OF-CEAS layouts, of which different versions can be found in the cited works. In any case, the AP2E proprietary implementation follows the previously described OF-CEAS principles of operation, signal analysis, etc., all the way to obtaining absorption spectra like those in Fig. 1, which are then fitted by a multi-line spectrum model with polynomial baseline, also previously discussed (Gorrotxategi-Carbajo et al., 2013).

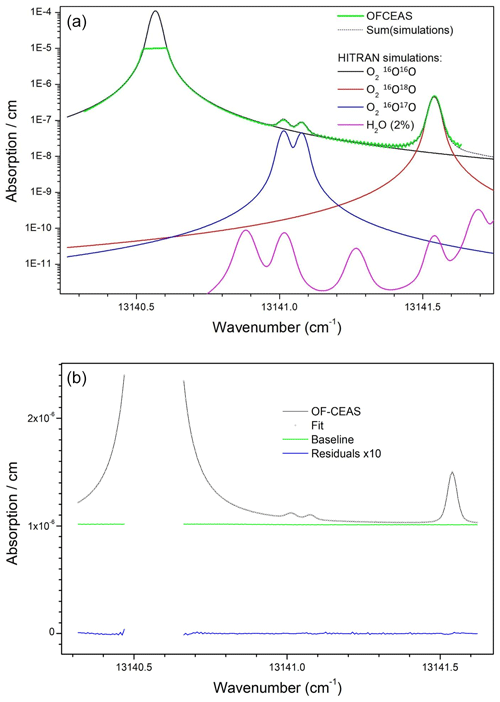
Figure 1 (a) Air absorption spectrum from the instrument (green) superposed with the HITRAN2021 simulation (dotted black) which results as the sum of absorption from the main O₂ isotopologues and the ¹⁸O and ¹⁷O varieties (respectively in red and blue). Simulated water vapor absorption for a 2 % molar fraction (corresponding to a high level of ambient relative humidity) is plotted to show that it can be neglected in the spectral analysis. Vertical scale is logarithmic in order to allow the clearer display of weaker absorption features. (b) OF-CEAS absorption spectrum (black) superposed with spectral fit (dotted black), together with baseline polynomial from fit (green) and fit residuals (data fit) multiplied by 10 (blue).

Concerning the most relevant difference relative to previous OF-CEAS implementations, the selected operating wavelength of the DFB diode laser targets a specific region of the O₂ absorption band around 760 nm. This so-called oxygen “A” band is the strongest absorption band of this molecule in the visible and infrared spectral range, even though it is still a relatively weak “forbidden” magnetic-dipole transition. In this spectral region, several weak lines of the same transition for the ¹⁸O–¹⁶O and ¹⁷O–¹⁶O isotopologues are present near strong lines of the main ¹⁶O–¹⁶O isotopologue. The specific spectral window chosen for our analyzer, which can be covered by a single current-driven laser frequency scan, is displayed in Fig. 1a. A second novelty of this instrument, discussed further below, is the presence of a saturated absorption line in the measured absorption spectrum, as visible in Fig. 1b.

The analyzer is a modified prototype of a new series of AP2E devices under development at the time of this work, featuring enhanced thermal insulation and stabilization (in particular, sample cell temperature is 37 °C with millikelvin fluctuations). As is the case for most instruments, improved temperature stabilization allows stable measurements on longer timescales, as necessary in this case for averaging isotopic ratios and detecting their small variations when switching among samples and in particular for isotopic ratio measurements relative to a reference sample. Since gas sample switching typically implies dead times of about 2 min due to limited flow rates and memory effects, and since at least 5 min averaging is additionally required to attain sufficient precision, the shortest time for the measurement of one sample is in the range of 5 to 10 min. We then need to consider the instrumental drift (assessed by the Allan deviation presented below) which should remain below the desired precision level over the measurement time for two samples (∼ 20 min) of which one would be a reference. Smaller drift would afford duty cycle gains by flushing several samples through the analyzer before the injection of one calibration sample. The chosen measurement strategy will be discussed later.

The most recent description of an OF-CEAS instrument close to the present one is described in Lechevallier et al. (2019). The main difference is the visible DFB diode laser emitting at 760 nm (TOPTICA LD-0760-0040-DFB) in place of the mid-infrared DFB intraband cascade laser (ICL) of that work. Obviously, optical elements are replaced with ones adapted to 760 nm, including a simple room temperature Si PIN photodiode to monitor cavity transmission. However, no reference photodiode is installed, with a simulated ramp proficiently replacing the laser power ramp for normalization of cavity transmission signals.

For this setup we obtained from LAYERTEC cavity mirrors (1 m radius of curvature) with a reflection coefficient as good as 0.999956, allowing for ring-down times of up to 30 µs (with room air at the working pressure of 150 mbar from a 40 cm cavity as in Lechevallier et al., 2019). The sample cell has a small volume (less than 20 mL) which, combined with a low sample pressure (150 mbar), results in a transit time of about 10 s with a sample flow of only ∼ 15 mL min⁻¹. Another improvement is a more accurate, stable and fast control of the sample pressure inside the measurement cell, which is also important for low drift. In particular, the fast response allows the minimization of flow and pressure perturbations when switching between samples, which contributes to obtaining short commutation times. Figure 2 shows a picture of the instrument (Fig. 2a) and a simplified schematic of the optical and airflow systems (Fig. 2b).

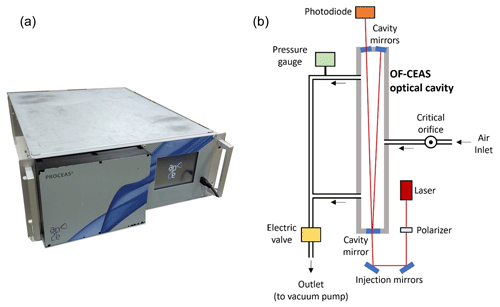
Figure 2 (a) External view of the O₂ analyzer: dimensions (without the pump) are 675 × 485 × 180 mm. (b) Schematic principle of the analyzer: black arrows are showing the direction of the airstream and red lines the laser path in the optical system.

As previously described by Kerstel and Gianfrani (2008) isotopic ratios can be measured by optical absorption spectroscopy by obtaining spectra containing at the same time the absorption line profiles of an isotopologue and its main variety. In our case, we are considering the dioxygen isotopologues mentioned above, in particular the ¹⁸O–¹⁶O variety. A simulated absorption spectrum showing in detail absorption lines for the working spectral region of the instrument is plotted in Fig. 1 (based on the HITRAN spectral database: https://hitran.iao.ru/, last access: 14 November 2024, Gordon et al., 2022) together with a real spectrum obtained from the instrument. As visible in Fig. 1b, the strong ¹⁶O–¹⁶O line is truncated at the top due to saturation of the absorption scale of the instrument (this point will be addressed below). The isotopic ratio is then obtained as the ratio of the line areas for the considered isotopologue normalized to that of the main isotopologue. It is straightforward to demonstrate that, under conditions of constant gas sample temperature and pressure, this ratio is indeed linearly proportional to the ratio of the mole fractions of these species in the sample. The isotopic ratio variation (delta value – δ – in per mil units – ‰) is then calculated after measuring the ratio of areas of the same absorption lines for a reference gas sample relative to which the delta will be defined by using Eq. (1) (written here for the ¹⁸O–¹⁶O case):

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=\left({\displaystyle \frac{{\left(\frac{A_{\mathrm{18}}}{A_{\mathrm{16}}}\right)}_{\mathrm{sample}}}{{\left(\frac{A_{\mathrm{18}}}{A_{\mathrm{16}}}\right)}_{\mathrm{reference}}}}-\mathrm{1}\right)\times \mathrm{1000},\end{array}$$

where A₁₈ and A₁₆ are the area of the absorption line for ¹⁸O–¹⁶O and ¹⁶O–¹⁶O respectively.

Given the low abundances of ¹⁸O–¹⁶O (0.2 %) and ¹⁷O–¹⁶O (0.04 %) relative to the main isotopologue ¹⁶O–¹⁶O, the corresponding absorption lines appear much less intense, by about the abundance ratio (Fig. 1). This requires that the instrument sensitivity be high in order to obtain the absorption lines of these minor isotopologues with a sufficient signal-to-noise ratio. On the other hand, the absorption signal of the main variety will be so strong as to actually exceed the dynamic range of the instrument. Indeed, the high-finesse optical cavity containing the sample becomes opaque (no light transmitted) when the laser diode is tuned across the center of any of the ¹⁶O–¹⁶O lines available near the strongest ¹⁸O–¹⁶O and ¹⁷O–¹⁶O lines in this absorption band. This problem could be avoided by choosing weaker absorption bands at other wavelengths, but no instrument would currently be capable of providing a sufficiently good signal for the lines of the minor isotopologues. One way to avoid this would be to use a second diode laser to address a sufficiently weak main isotopologue line lying rather far away in the same absorption band or even in another absorption band (each diode laser covers a small spectral region). However, this would double the size and complexity of the experimental setup. Therefore, we decided to rely on the measured wings of the main isotopologue line in order to obtain an estimate of the absorption line area. This proved to be a good strategy given the excellent performance, comparable to those obtained by the OF-CEAS technique with non-saturated absorption lines (see, for example, isotopic measurements on H₂O; Landsberg et al., 2014). Even if this estimate may be affected by a multiplicative form factor, this same factor will affect measurements of the reference sample and cancel out in the above equation. The situation is particularly favorable for the measurement of samples presenting small concentration variations from the target species, as is the case here for dioxygen varying from about 18 % to 23 % in biological experiments.

In order to obtain the area of the saturated line of the main isotopologue, we exploit the fact that the data analysis software is able to “count” the cavity modes, each corresponding to a data point in the spectrum (Morville et al., 2014). This works perfectly even in the presence of a large region in the laser spectral scan where points are missing. This is possible thanks to the fact that cavity modes appear uniformly spaced over the laser scan. In addition, we had to take care of the fact that, due to temperature drift, the cavity length slowly changes. As a consequence, the absolute frequency positions of the cavity modes change, and thus the position of the data points over the absorption line profiles changes too. In particular there are two modes which correspond to the first exploitable data points in the spectrum on the two sides of the strong line, which may go above/below the threshold applied in the analysis software for using them in the spectral fit. Such a change in the number of data points in the fit causes a discontinuity in the retrieved line areas used to establish the concentration of the corresponding molecule. In order to fix this problem, we used the position of the data points relative to the absorption lines to continuously adjust (at the millikelvin level) the cavity temperature set point and keep the cavity modes at absolute fixed-frequency positions (with rms time fluctuations of 1 % of the cavity mode spacings or about 200 kHz in absolute frequency units). This additionally provides a more stable retrieval of all line areas from the spectral fit, as the spectral data points keep fixed positions relative to the absorption profiles which are fitted by Rautian profiles. Even if the Rautian model is much better than the more widely used Voigt profile, it still does not perfectly describe real line profiles. Thus, a displacement of the data points induces small changes in the fit results (even in the absence of noise).

Over the time span of presented results (18 months), we could test two different instrument configurations, but we obtained a similar performance. The main difference between the two configurations is the high-reflectivity mirrors installed on the V-shaped optical cavity. For the initial configuration and its corresponding set of mirrors (R = 0.999979), the cavity finesse (∼ 74 800) was higher by about a factor of 2. The cavity throughput was also higher, which induced a higher level of scattered light and stronger interference fringes on the recorded spectra. The set of mirrors (R = 0.999956) corresponding to the second configuration with lower cavity finesse (F∼ 35 700) actually also had a lower transmission (thus relatively higher absorption losses in the coatings). This produced less signal on the photodetector at cavity output but with fractionally less parasitic fringes, partially compensating for the lower finesse. In both cases the setup was carefully optimized; in particular light traps were placed at all positions, possibly causing light scatter by secondary reflected beams. In the following, we will specify which setup was used for which results, accounting for somewhat varying performance. It should be noted that for both configurations, the laser scan time over the monitored spectral window displayed in Fig. 1 was the same at about 300 ms, while the photodiode response and digital acquisition times were around 3 µs in order to resolve the profiles of the transmitted cavity modes in the presence of optical feedback and also the ring-down decay obtained at the end of each laser scan, as detailed in the cited OF-CEAS references.

2.2 Airstream selection

The airstream allowed to enter the instrument inlet was selected using a Valco multiposition valve (EUTF-SD8MWE, VICI AG, Switzerland) and $\mathrm{1}/\mathrm{8}$ PFA (perfluoroalkoxy alkanes) tubing (PFA-T2-030-100, Swagelok), and it was filtered using a Swagelok 7 µm filter (SS-2F-7). Three gas streams, at ambient pressure, could be selected by the Valco valve: (1) synthetic mixture of O₂ and dinitrogen (N₂) with an O₂ concentration similar to ambient (synthetic dry air, ALPHAGAZ 2, Air Liquide France), (2) ambient atmospheric air (sampled at the inlet of the room ventilation duct) dried with a 40 mL magnesium perchlorate filter, and (3) a natural dry atmospheric air cylinder enriched in oxygen (natural air enriched at 22.9 % O₂, Air Liquide Spain) subsequently diluted with N₂ (ALPHAGAZ 2, Air Liquide France) using two mass flow controllers (F200CV and F201CV, Bronkhorst, the Netherlands). All the measurements took place in a temperature-controlled room, with temperature fluctuations within ±2 °C around set point.

When measuring atmospheric air, humid air was dried using a 20 cm long home-made humidity trap made with 6 mm PFA tubing (Swagelok PFA-T6M-1M-30M) and filled with magnesium perchlorate. This trap was replaced daily. For water vapor dependency measurements, the humidity trap was removed, and a stream of synthetic air (air product, < 3 ppm of water), with constant O₂ concentration and δ¹⁸O(O₂), was humidified at a constant set point using a vapor generator (see Leroy-Dos Santos et al., 2021, for more details) up to 9000 ppm.

2.3 Isotope ratio mass spectrometry (IRMS) measurements

IRMS analyses were used as a reference method to validate measurements achieved with the OF-CEAS technique. Samples of air were punctually collected in 5 mL glass flasks to be analyzed through IRMS. Operation of the automated sampling system is detailed in Paul et al. (2024). Briefly, air from a closed-chamber system was circulated through the instrument and the flask for 30 min. Then the flask was automatically isolated thanks to two valves and collected to be analyzed. Results from the flask and the 30 min data acquisition were, in the end, compared.

Flasks were analyzed for δ¹⁸O(O₂) and δO₂ $/$ Ar. δO₂ $/$ Ar can be converted into O₂ concentration (or vice versa) following Eq. (2):

$$\begin{array}{}\text{(2)}& {\mathit{\delta }}_{\frac{{\mathrm{O}}_{\mathrm{2}}}{\mathrm{Ar}}}=\left({\displaystyle \frac{{\left(\frac{\left[{\mathrm{O}}_{\mathrm{2}}\right]}{\left[\mathrm{Ar}\right]}\right)}_{\mathrm{sample}}}{{\left(\frac{\left[{\mathrm{O}}_{\mathrm{2}}\right]}{\left[\mathrm{Ar}\right]}\right)}_{\mathrm{reference}}}}-\mathrm{1}\right)\times \mathrm{1000},\end{array}$$

where [O₂] and [Ar] are the concentrations of O₂ and Ar respectively and the reference is the present-day atmospheric air.

Before analysis, samples are purified to isolate O₂ and Ar from total air using a gas chromatography column as in Barkan and Luz (2003). Measurements are then performed using a Thermo MAT 253 mass spectrometer (Thermo Scientific) equipped with a dual inlet as described in Paul et al. (2023). For each sample, 2 sequences of 16 measurements are performed for measurements of δ¹⁸O(O₂) with a final uncertainty of 0.03 ‰ (1σ). These sequences are followed by two peak jumping sequences to determine δO₂ $/$ Ar, which is associated with a final uncertainty of 0.5 ‰ (1σ).

3 Results and discussion

3.1 Precision and drift

The first characterization of the instrument was done through the measurement of the Allan–Werle deviation (Fig. 3), which we will call Allan deviation for simplicity. Over 24 h we introduced in the instrument atmospheric air (dried with a 30 mL magnesium perchlorate trap), which had a constant elemental and isotopic O₂ composition. Allan deviation plots were obtained repeatedly for each different configuration, and the result shown is a typical reproducible result. The minimum of the Allan deviation was reached between 10 and 20 min of measurements for both O₂ concentration and δ¹⁸O(O₂) and with both configurations (Fig. 3). The precision achieved for the O₂ concentration measurement was better using the initial configuration (0.002 % at 10 min averaging; Fig. 3 dark green data) than the second configuration (0.005 % at 3 min; Fig. 3 light green data). In contrast, the δ¹⁸O(O₂) minimal Allan deviation was lower with the second configuration than the initial one (0.05 ‰ at 6 min vs. 0.08 ‰ at 20 min respectively; Fig. 3 gray and dark data).

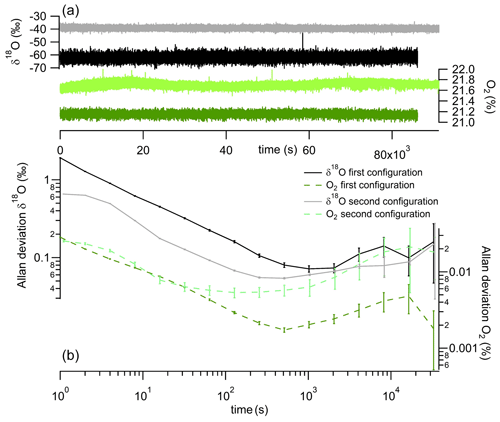
Figure 3 Panel (a) shows continuous measurement of δ¹⁸O(O₂) (gray and black) and O₂ concentration (light and dark green). Panel (b) shows Allan deviation plots based on continuous measurement of both δ¹⁸O(O₂) (gray and black) and O₂ concentration (dotted light and dark green). Black and dark green are used for the initial configuration and gray and light green for the second configuration.

After 2 h, the values of the Allan deviations stayed below 0.2 ‰ for δ¹⁸O(O₂) and 0.03 % for the O₂ concentration. Considering this drift, in order to maintain measurement repeatability below 0.1 ‰ for δ¹⁸O(O₂), we see that calibrations with a measurement of a standard sample are needed over time intervals of at most 2000 s (30 min), in particular for the first configuration (for the second, the Allan deviation for δ¹⁸O(O₂) appears to reach the 0.1 ‰ limit over longer times).

To assess the stability of the instrument on periods longer than 2 h, we ran measurements of two standards during 8 consecutive days. The two standards were dry atmospheric air and a mixing of O₂ and N₂ in atmospheric proportions (synthetic air from Air Liquide). The evolution of the Allan deviation in Fig. 4 was calculated from successive injections of the two standards every 4 min. This calibration frequency, higher than required by the Allan deviation discussed above, was chosen as a compromise towards obtaining measurements with high time resolution. Averages of δ¹⁸O(O₂) and O₂ concentration were calculated considering the last 2 min (the first 2 min after injection were removed from the calculation to take into account the memory effect). With this approach, we obtained an Allan deviation for calibrated measurements of δ¹⁸O(O₂) below 0.03 ‰ after 6 h of measurements. The evolution of the O₂ concentration was marked by a diurnal variability which may have been linked with room temperature changes. The Allan deviation however reached values lower than $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{3}}$ % after 15 h of measurements.

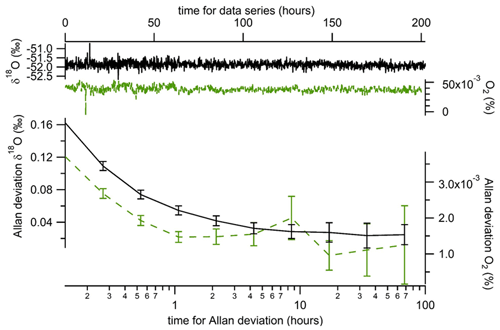
Figure 4 Evolution of difference in mean δ¹⁸O(O₂) (black line) and O₂ concentration (dotted green line) when running successive measurements of two samples (dry atmospheric air and synthetic air) at a periodicity of 8 min (4 min of atmospheric air followed by 4 min of synthetic air). The data used for calculation are the mean values obtained over the last 2 min of measurements of each gas. For this series of measurements, the initial configuration has been used, but a similar result was obtained with the second configuration.

3.2 Influence of water vapor concentration

We measured the dependence of δ¹⁸O(O₂) on humidity and found a significant relationship between both (Fig. 5). Within our range of water vapor mixing ratio (0 to 9 mmol mol⁻¹), a variability of about 1.4 ‰ was found for δ¹⁸O(O₂). The relationship between δ¹⁸O(O₂) and humidity showed a decreasing trend but was highly variable, making any correction unreliable. This dependence of δ¹⁸O(O₂) on humidity could be expected for two reasons. The first reason is linked to the possible existence of weak water vapor absorption lines. However, there is no water line with sufficient intensity to be significant even at high humidity levels within the wavelength range analyzed by the instrument. Second, water vapor could affect the linewidth of the oxygen lines by collisional broadening. Indeed, for a 1 % mixing ratio corresponding to high atmospheric humidity, water vapor induces a slightly enhanced pressure broadening compared to major atmospheric components like N₂ or O₂. Because it was not easy to propose a correction for the humidity influence, we decided that the most reliable choice for high-precision measurements was to measure δ¹⁸O(O₂) after drying the gas flow.

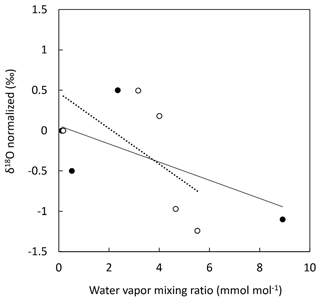
Figure 5 Evolution of δ¹⁸O(O₂) of atmospheric air with increasing water vapor mixing ratio. δ¹⁸O(O₂) was normalized for dry conditions. Two experiments were conducted. Experiment 1: dry atmospheric air was progressively humidified using a vapor generator (filled black dots). Experiment 2: humid atmospheric air was progressively dried using a Nafion dryer (hollow dots). Each data point is the result of 10 min signal integration. Solid line: linear regression for experiment 1 (y = −0.1126x + 0.0597, R² = 0.45); dotted line: linear regression for experiment 2 (y = −0.2205x + 0.4661, R² = 0.36).

3.3 Influence of oxygen concentration

An influence of O₂ concentration in the sample on the measured δ¹⁸O(O₂) was expected as is usual in all spectroscopic measurements. Indeed, the parameters in the models used for spectral simulations are associated with uncertainties which do not enable us to reproduce sufficiently well the changes in the shape of the experimental spectrum, in particular the strong saturated ¹⁶O line as a function of oxygen concentration. In fact, we use a simple Voigt profile which allows us to fit down to the experimental noise level the wings of this strong line which are captured by the measurements. However, rather than trying to figure out the variation in the model parameters as a function of O₂ concentration, we found it simpler (and equivalent as a first-order treatment of the problem) to take this effect into account through the study of the influence of O₂ concentration directly on the measured δ¹⁸O(O₂) while using constant line shape parameters. Figure 6 shows the linearity effect, i.e., the evolution of δ¹⁸O(O₂) with increasing O₂ concentration. Standard dry atmospheric air enriched with O₂ was diluted with nitrogen to measure six different O₂ mixing ratios (Fig. 6, x axis). The difference in δ¹⁸O(O₂) between the diluted standard and atmospheric air was then used to correct for any instrument drift (Fig. 6, y axis). The influence of O₂ concentration on δ¹⁸O(O₂) was clearly significant. δ¹⁸O(O₂) increased by 0.53 ‰ with a 1 % increase in O₂ concentration (Fig. 6).

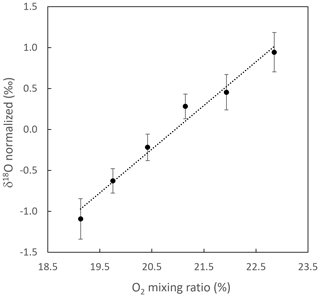
Figure 6 Evolution of the difference in δ¹⁸O(O₂) between a standard (atmospheric air enriched with O₂) diluted with N₂ and the atmospheric air vs. the O₂ concentration of the diluted standard. δ¹⁸O(O₂) is normalized for the ambient O₂ mixing ratio, and error bars are the standard deviation of individual measurements (n = 27). The typical standard deviation for the O₂ mixing ratio was 0.01 %. Dotted line: linear regression (y = 0.5336x − 11.178, R² = 0.9782). This result was obtained with the initial configuration (see end of Sect. 2.1).

Finally, note that absorption line profiles are influenced by sample parameters such as temperature and pressure. Because of possible long-term drift in pressure and temperature sensors, it is good practice to regularly check the evolution of this influence of O₂ on the measured δ¹⁸O(O₂) (which we did as a precaution once every 15 d).

3.4 Memory effect and response time

The response time of the analyzer and associated inlet system, when switching between different gas streams, was dependent on the total volume of the system (valve, filter, dryer, tubing and the instrument internal volume) and the flow rate at the inlet. It was determined that a 2 min purge time between samples (with a constant flow rate) was necessary to reach a new steady state for both O₂ concentration and δ¹⁸O(O₂) (Fig. 7).

Figure 7 Raw data of δ¹⁸O(O₂) (3 Hz, gray line) and moving average (over 5 s, black line) measured with two gas streams with contrasted O₂ concentration (green line). The response time is outlined in yellow. These results were exactly the same for the two configurations.

3.5 Calibration strategy

Based on the detailed results above, we used the following strategy to ensure good-quality measurements of the isotopic and elemental composition of O₂ in atmospheric air using an OF-CEAS instrument.

First, we always place a magnesium perchlorate trap at the entrance of the instrument to work with dry air, hence easily working with standards made of dry air and avoiding the dilution effect observed on the O₂ concentration. Then, for calibration of the signal we need to follow different steps. The dependency of the δ¹⁸O(O₂) on O₂ concentration is rather stable, and it can be checked regularly by running successive dilutions of a standard with N₂ (as a precaution it was done every 15 d). On top of it, a two-point calibration is needed with different values of δ¹⁸O(O₂) and O₂ concentration. In our case, we used dry atmospheric air and a standard made of dry atmospheric air enriched with 2 % O₂ (hence O₂ concentration of 23 % instead of 21 % in dry atmospheric air). Our tests have shown that the measured difference in δ¹⁸O(O₂) and in O₂ concentration between the two standards is stable over a 24 h period. As a consequence, it is enough to run the two standards only once or twice a day and then to measure only one standard with the measurements in the daily routine. If the two-point calibration is rather stable over the course of 1 d, the drift of the instrument occurs on a much shorter timescale. The evolution of the Allan deviation suggested that, to avoid any drift, a one-point calibration should be done at least every 20 min. Moreover, to obtain a small 1σ value (< 0.1 ‰ as mentioned in Sect. 3.1), averages over 5–10 min should be done for each sample injection.

Finally, in order to account for the instrument response time, it is important to remove the first 2 min from the measurement series (purge time) when we switch from one standard to a sample or from one standard to another standard.

Gathering the recommendations listed above, we suggest using the following measurement sequence:

• every 15 d – calibration of the influence of O₂ concentration on δ¹⁸O(O₂);

• every morning – 6 min measurements of atmospheric air enriched with O₂ and 6 min measurements of atmospheric air (only the last 4 min of each plateau was kept for the calculation of the average values);

• during the day – 6 min measurements of dry atmospheric air, 6 min measurements of sample 1, 6 min measurements of sample 2, 6 min measurements of sample 3 and back to 6 min measurements of dry atmospheric air (only the last 4 min of each plateau was kept for the calculation of the average values).

3.6 Accuracy of measurements: comparison with IRMS measurements

In order to validate the performance of this new analyzer with the calibration sequence proposed in the previous section, we measured the same samples with our analyzer and with an IRMS. We sampled air in 5 mL flasks from a closed biological chamber while the analyzer was measuring the elemental and isotopic composition of O₂ following the sequence described above. We measured the δ¹⁸O(O₂) from the flasks by IRMS (see Sect. 2.3). These values were compared to the values obtained by the analyzer after corrections of the different influences (see previous section) during the same period.

The results of this comparison are displayed in Fig. 8 for the initial instrument configuration (same result was obtained for the final configuration). The values obtained for the three biological samples by the two techniques align well on a line of slope 1 with zero y intercept within the uncertainty range for measurements of δ¹⁸O(O₂) and with only a slight discrepancy for the O₂ concentration. This validates the use of the spectroscopy analyzer for ambient air and biological chamber measurements when the values for the concentration of O₂ do not deviate more than a few percent from the current concentration of O₂. If the composition of the analyzed air is too different from the current atmospheric air, nonlinear effects on both the concentration of O₂ and δ¹⁸O(O₂) are expected through the modification of the shape of the absorption lines.

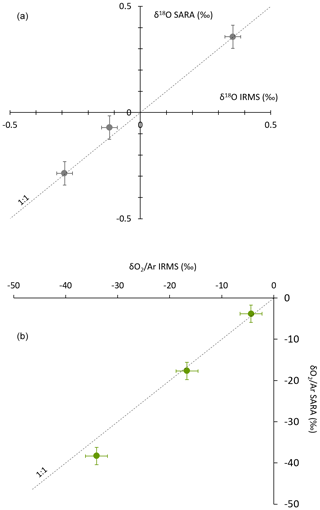
Figure 8 Comparison of the concentration (a) and isotopic composition (b) of O₂ obtained by IRMS and by our spectroscopic analyzer (SARA) for different biological samples. The dashed line shows the 1:1 relationship between δ¹⁸O(O₂) measured by IRMS and δ¹⁸O(O₂) measured by the spectroscopic analyzer.

4 Conclusion

We developed a new instrument based on the OF-CEAS technique enabling continuous measurements of the elemental and isotopic composition of O₂ in the atmosphere. We targeted the region of the O₂ absorption band around 760 nm to capture a signal for ¹⁶O–¹⁷O, ¹⁶O–¹⁶O and ¹⁸O–¹⁸O and developed a special fitting for the ¹⁶O–¹⁶O peak which is saturated.

The instrument has been characterized, and we could reach a precision of 0.002 % on O₂ concentration and 0.05 ‰ on δ¹⁸O(O₂) for an integration time of 10 min. The drift of the instrument deteriorates the signal, but the values for Allan deviation stay below 0.2 ‰ for δ¹⁸O(O₂) and 0.03 % for the O₂ concentration after 2 h of continuous measurement. δ¹⁸O(O₂) measurements were slightly affected by humidity, and we chose to dry the airflow at the inlet of the instrument. O₂ concentration had an influence on δ¹⁸O(O₂), which should hence be regularly quantified.

Based on the performance of the instrument, we proposed a procedure for running O₂ measurements for samples or in a continuous way based on a frequent (every 20 min) injection of calibration standard. This procedure permitted us to obtain performance in good agreement with dual-inlet IRMS measurements in a shorter time. It was particularly adapted for monitoring biological processes in a continuous way.

In the future, this instrument may be used in several setups where a continuous measurement of O₂ concentration and δ¹⁸O(O₂) is needed, such as measurements during biological experiments to follow respiration and photosynthesis evolution, medical setups following the evolution of respiration, or continuous measurements of the elemental and isotopic composition of fossil air in ice cores. The instrument was also able to measure the δ¹⁷O(O₂), but the current precision was not yet sufficient to compete with IRMS measurements.