Fast and sensitive measurements of sub-3 nm particles using Condensation Particle Counters For Atmospheric Rapid Measurements (CPC FARM)

New particle formation (NPF) is the atmospheric process whereby gas molecules react and nucleate to form detectable particles. NPF has a strong impact on Earth's radiative balance as it produces roughly half of global cloud condensation nuclei. However, the time resolution and sensitivity of current instrumentation are inadequate in measuring the size distribution of sub-3 nm particles, the particles critical for understanding NPF. Here we present the Condensation Particle Counters For Atmospheric Rapid Measurements (CPC FARM), a method to measure the concentrations of freshly nucleated particles. The CPC FARM consists of five CPCs operating in parallel, each configured to operate at different detectable particle sizes between 1–3 nm. This study explores two methods to calculate the size distribution from the differential measurements across the CPC channels. The performance of both inversion methods was tested against the size distribution measured by a pair of stepping particle mobility sizers (SMPSs) during an ambient air sampling study in Pittsburgh, PA. Observational results indicate that the CPC FARM is more accurate with higher time resolution and sensitivity in the sub-3 nm range compared to the SMPS.

1 Introduction

Atmospheric new particle formation (NPF) is a process where gas molecules cluster and react to form stable particles around 1 nm in diameter that then grow to larger sizes (Kerminen et al., 2018; Lee et al., 2019). NPF is an important source of particles as it produces approximately 50 % of the global cloud condensation nuclei (Gordon et al., 2017; Spracklen et al., 2008). Consequently, understanding the frequency and intensity of NPF is crucial for modeling cloud properties and ultimately Earth's climate. An atmospheric NPF event is traditionally identified by the appearance of the smallest detectable particle (typically between 1–3 nm diameter) and the growth of these particles to larger sizes over several hours. However, these identifying characteristics of NPF are based on the capabilities of commonly used particle instruments. This implies that the NPF event must have a high enough particle concentration and occur over a large enough area or within a slow enough air volume to be detectable with traditional instrumentation. NPF events that occur rapidly and at diameters and concentrations below the detection limits of the instruments are obviously not observed but could still contribute significantly to atmospheric particle number concentrations and produce clusters that can help grow existing particles. In addition, studying these rapid and/or more subtle events is critical in obtaining information on the needed conditions that result in NPF events or lack thereof. Thus, improving the instruments used to observe newly formed particles will help improve the understanding of NPF and reduce the uncertainty in the associated radiative forcing.

Currently, instruments used to measure the 1–3 nm size distribution include the stepping or scanning particle mobility sizer (SMPS) (Chen et al., 2018; Jiang et al., 2011a; Kangasluoma et al., 2020) and the scanning particle size magnifier (PSM) (Chan et al., 2020; Kontkanen et al., 2017; Sebastian et al., 2021; Sulo et al., 2021). These instruments require relatively long scan times to measure the size distribution and exhibit high measurement uncertainty in the 1–3 nm particle range (Kangasluoma et al., 2020). Only a short time is spent at a given size bin, which introduces uncertainty due to potential fluctuations in the sampled air mass and/or reduced counting statistics. Also, poor time resolution (typically between 1–10 min per scan through a wide size distribution such as 2–30 nm) limits the identification of key processes that result in the rapid production of 1–3 nm particles. For example, many NPF events occur with the sudden appearance of 1 nm particles which have been observed in the field to grow at rates up to 50 nm h⁻¹ (Iida et al., 2008; Svenningsson et al., 2008). In laboratory experiments, growth rates of up to 700 nm h⁻¹ have been observed at conditions similar to transient conditions in winter urban environments (Wang et al., 2020). In addition, the lifetime of 1–3 nm particles can be short due to scavenging by pre-existing particles and range in timescale from a few hours in clean environments (Weber et al., 1997) to the order of seconds to minutes in polluted urban environments (Deng et al., 2021; Kangasluoma et al., 2020). Faster scans at ∼ 1 Hz resolution are necessary to fully capture the formation and growth dynamics during NPF events.

Beyond time resolution limitations, traditional particle instruments also experience high measurement uncertainty in the 1–3 nm size range due to functional constraints. The most commonly used instrument, the SMPS, operates by first charging particles with a bipolar charge conditioner and then size-selecting charged particles by their electrical mobility using a differential mobility analyzer (DMA). Size-selected particles are then counted with a condensation particle counter (CPC). Significant uncertainty can arise from charger ions which are able to pass through the mobility analyzer and be counted by the CPC (Hering et al., 2017); this would interfere with the signal from real sub-3 nm particles produced during NPF events. Most of the uncertainty and poor sensitivity of SMPS measurements stem from the low and poorly understood charging efficiency of small particles classified by the DMA. For example, bipolar charging efficiency of 1–3 nm particles at charge equilibrium is below 1 % (Wiedensohler, 1988). Additionally, the process of charge transfer from charger ions to clusters or particles is highly dependent on the compositions of the ion and particle in this size range. This dependency has been observed but not corrected for between atmospheric samples as it is not well quantified (Kangasluoma et al., 2020; Kangasluoma and Kontkanen, 2017). Poor SMPS sensitivity is also compounded by diffusion wall losses within the DMA. For commonly used DMAs such as the TSI 3085 NanoDMA, losses can exceed 90 % of the selected particle size (Jiang et al., 2011b).

Fast-scanning (i.e., high-time-resolution) SMPS methods have been developed, but these methods require high concentrations (> 2×10⁵ cm⁻³) of 1–3 nm particles to overcome the low counting statistics associated with the short sampling intervals at a given size (Kangasluoma et al., 2020; Tröstl et al., 2015). Another type of instrument, the DMA train, utilizes multiple SMPSs sampling in parallel but with each mobility analyzer set at a specific voltage in order to take high-time-resolution measurements of the size distribution (Stolzenburg et al., 2017). The DMA train enables measurements of size distributions down to 1.6 nm and can have a time resolution on the order of seconds. However, the DMA train is still susceptible to poor sensitivity due to the challenges of ionizing sub-3 nm particles and diffusional losses. For example, during a chamber experiment that resembled atmospheric conditions, the DMA train detected only a few counts per minute at sizes below 2.5 nm. As a result, size bins < 2.0 nm required 5 min time averaging (Stolzenburg et al., 2017). The nano-scanning electrical mobility spectrometer (nSEMS), a scanning instrument similar to the SMPS, uses a radial opposed migration ion and aerosol classifier, in contrast to a DMA. The nSEMS can take 1 min scans from 1.5–25 nm with minimal degradation to the transfer function. However, due to the nSEMS's reliance on charged particles, it encounters similar sensitivity issues as SMPS-based techniques (Kong et al., 2021).

Pure CPC-based methods have also been developed to measure size distributions. The particle size magnifier (PSM) mixes air saturated with diethylene glycol (DEG) with sample air to activate particles to a size large enough to be counted by a CPC (Vanhanen et al., 2011). By altering the flow rate of the DEG-saturated air between 0.1–1 L min⁻¹, the d₅₀ cut point (i.e., particle diameter with 50 % detection efficiency) of the original PSM can be varied between 1.2 and 3.5 nm. A new version of the PSM uses different flow rates to produce variable cut points between 1 and 12 nm (Sulo et al., 2024). The size distribution between the cut points can be measured by “scanning” through the d₅₀ cut points. The PSM is typically operated with 2 min scans to ensure flow stability (Lehtipalo et al., 2014). Although the PSM has higher time resolution than some SMPSs, the minutes-long scans can still lead to similar data quality issues as seen with the SMPS due to air mass fluctuations and low counts (Chan et al., 2020).

Another CPC-based method used to measure size distributions is known as the CPC battery (CPCB) (Kulmala et al., 2007). Multiple CPCs are set at different cut points, and the particle size distribution is determined from the difference in counts between each CPC. The CPCB has been previously implemented for sizing in the 2–9 nm size range. However, in this configuration, the CPCB had poor size resolution for studying NPF as the CPC cut points were spaced far apart at 2 and 9 nm (Riipinen et al., 2009). Another CPCB was the nucleation-mode aerosol size spectrometer (NMASS) for fast sampling of the size distribution from 3–60 nm on a flight campaign (Brock et al., 2019; Williamson et al., 2018). The NMASS consisted of 10 CPCs, operated at low absolute pressure, with channels spaced evenly throughout the size range. The particle counts from each channel were then used to solve a non-negative matrix minimization problem to arrive at the size distribution. However, one limitation common to all CPC-based methods is that the activation efficiency is dependent on composition and charging state (Kangasluoma and Attoui, 2019). Previous studies have shown that the d₅₀ of the TSI 3789 (Wlasits et al., 2020), a water CPC, ranges from 2.3 nm for sodium chloride and ammonium sulfate to 3.4 nm for oxidized β-caryophyllene. Similarly, the TSI 3777, a diethylene glycol growth tube coupled with a butanol TSI 3772 CPC, has a d₅₀ of 1.6 nm for sodium chloride and ammonium sulfate and 2.7 nm for oxidized β-caryophyllene (Wlasits et al., 2020).

Here we present the Condensation Particle Counters For Atmospheric Rapid Measurements (CPC FARM), an instrument similar to the NMASS but with five water CPCs with cut points spanning the range of 1–3 nm. The CPC FARM provides 1 s time resolution measurements of the 1–3 nm size distribution. The cut points of the five CPC channels were set to 1.6, 1.8, 2.1, 2.5, and 3.0 nm. The concentration difference between channels was used to invert the size distribution. Two inversion techniques are provided with sources of systematic measurement uncertainty in observed particle counts and sizing discussed. The inversions were then used to compare Pittsburgh, PA, ambient measurements of the CPC FARM with a traditional SMPS.

2 Methods

2.1 CPC FARM description

The CPC FARM consists of five laminar-flow water condensation particle counters that are similar in design to the Aerosol Dynamics Inc. MAGIC 250 (Hering et al., 2014) and the TSI 3789 (Hering et al., 2017). These instruments utilize wet-walled tubes with three temperature regions as shown in the Supplement (Sect. S1). The first section (conditioner) cools the incoming flow and brings it to near saturation. In the second hot section (initiator), particle activation and condensational growth occur because the diffusion of water vapor from the walls is faster than the diffusion of sensible heat. In the third cold stage (moderator), supersaturation is maintained, continuing particle growth while reducing the flow's dew point to avoid water condensation in the optics and further downstream. Each channel of the CPC FARM (i.e., growth tube) is based on the MAGIC 250 but shares the water injection, transport flow, and water removal features of the TSI 3789. The internal diameter of a CPC FARM growth tube is the same as the MAGIC 250 (4.7 mm vs. 5.6 mm for the TSI 3789), while the combined length of the three temperature-controlled sections has been increased because of the large temperature differences needed (17.3 cm compared with 19 cm for the TSI 3789 and 13 cm for the MAGIC 250). The cooling and heating power is higher than either of the other instruments, which allows for a conditioner and moderator temperature of 1 °C and for the initiator to be as hot as 99 °C. The optics head is held at 35 °C to ensure water vapor does not condense in the optics. The flows are set by using critical orifices and an external pump. The design flow rate through each growth tube is 0.30 L min⁻¹. The transport flow may be adjusted depending on the measurement application. A 3.0 L min⁻¹ transport flow rate per channel was used in this study. Aerosol Dynamics MAGIC 250 electronics and optics were used for each channel, with slight modifications to the firmware. The firmware reports the particle concentration, instrument temperatures, and other operating parameters at a rate of up to 64 Hz.

2.2 CPC FARM experimental characterization

Each channel of the CPC FARM was calibrated separately in a similar manner as described in previous CPC calibration studies, with pertinent details given here and in Sect. S2 (Hering et al., 2017; Kangasluoma and Attoui, 2019; McMurry, 2000). 1–7 nm clusters of ammonium sulfate were generated by first atomizing a 1 mM aqueous solution of ammonium sulfate in purified N₂, which then flowed through a tube furnace with a 20 mm inner diameter quartz tube at 275 °C. The hot flow was then quenched with humidified, filtered, compressed air. This created ammonium sulfate particles with sizes between 1–20 nm. Note that the exact composition of these particles is not known, but they are predominately composed of ammonium sulfate with potential trace contamination. Ammonium sulfate particles were chosen for calibration as these have similar hygroscopic properties as newly formed atmospheric particles (Riipinen et al., 2009). In addition, ammonium sulfate particles are the most commonly used calibration particles for sub-10 nm CPCs including the PSM and TSI 3789 (Hering et al., 2017; Lehtipalo et al., 2014). Furnace-generated particles were then passed through two 500 µCi Po-210 neutralizers. A high-resolution Half-Mini (p) mobility analyzer was then used to size-select the positively charged particles (Fernandez de la Mora, 2017). The Half-Mini was operated in recirculating sheath flow mode using an Ametek blower and a HEPA-filter cartridge. The size-selected ions from the Half-Mini were homogeneously split between a SEADM Lynx E12 electrometer and a channel of the CPC FARM. The flow rates of the electrometer and a single channel of the CPC FARM were both set to 3.30 L min⁻¹.

2.3 Particle sizing devices

Two stepping mobility particle sizer (SMPS) systems were operated to measure the size distribution of particles between 1.4 and 300 nm. The combination of these two systems will be referred to as the particle sizing devices (PSDs). In both SMPSs, the aerosol flow first passes through a bipolar charge conditioner containing two 500 µCi Po-210 strips (NRD). Both systems then use different DMAs and CPCs to size-select and measure the concentration of size-selected particles. One system uses a TSI 3085A NanoDMA and a TSI 3025 CPC to measure the size distribution of 1.5–30 nm particles (Chen et al., 1998; Stolzenburg and McMurry, 1991). The TSI NanoDMA was set up with a 2.0 L min⁻¹ aerosol flow, 20.0 L min⁻¹ sheath flow, and 5.0 L min⁻¹ bypass flow. The TSI 3025 CPC was modified to detect ∼ 1 nm particles with a d₅₀ of 2.2 nm by increasing the total flow rate to 2.0 L min⁻¹ and increasing the saturator and optics temperature to 44 and 46 °C, respectively, while the condenser remains at 10 °C (Kuang et al., 2012). The detection efficiency of the modified TSI 3025 was measured using the same calibration setup as the CPC FARM. A LabJack T7 was used to count the TSI 3025 digital pulses.

The second system used a custom-built long-column DMA similar to the TSI 3081 and a TSI 3772 CPC to measure the size distribution of 10–300 nm particles (Reineking and Porstendörfer, 1986). The d₅₀ of the TSI 3772 has previously been measured at 9.4 nm (Mordas et al., 2008). The long-column DMA was operated at 1.0 L min⁻¹ aerosol and 10.0 L min⁻¹ sheath flow rates (Reineking and Porstendörfer, 1986). A separate LabJack T7 was used to count the TSI 3772 digital pulses.

Both PSD instruments were operated in “stepping-voltage” mode. Scans consisted of 30 discrete, log-spaced voltage steps, with an average time of 10 s per step, resulting in a total scan duration of 5 min. Data inversion was done similar to previous methods (Jiang et al., 2011a; Stolzenburg and McMurry, 2008). We accounted for the diffusion losses, charging efficiency, DMA transmission efficiency, and CPC activation efficiency. Effective lengths for diffusion loss calculations used for the TSI NanoDMA and the custom long-column DMA are 1.58 and 13 m, respectively (Jiang et al., 2011b; Reineking and Porstendörfer, 1986). Multiply charged particles were not accounted for, as the main focus of this study is on sub-10 nm particles where doubly charged particles at charge equilibrium contribute negligibly to the detected concentration (Wiedensohler, 1988).

2.4 Pittsburgh campaign setup

Comparison of the PSD with the CPC FARM was done by sampling Pittsburgh, PA, air in October 2023 as this location has previously been observed to experience frequent NPF events (Saha et al., 2018; Stanier et al., 2004). The instruments were collocated in Doherty Hall on Carnegie Mellon University's campus. Doherty Hall is located ∼ 5 km east of downtown Pittsburgh. Air was sampled from a third-floor window (∼ 15 m above surface) facing south and less than 200 m from the northern edge of Schenley Park, a 1.8×10⁶ m² wooded park. Pittsburgh air was sampled through a 100 mm diameter galvanized-steel duct by a brushless Domel blower, as depicted in Fig. 1. All instruments sampled directly from the center of the duct through a 4.57 mm inner diameter stainless-steel tube. The sampling end of the tube was bent at a 90° angle toward the flow to sample incoming particles. The TSI NanoDMA and the custom long-column systems of the PSD were connected directly to the common duct through 290 and 315 mm long sampling lines, respectively. Each channel of the CPC FARM was connected directly to the community inlet and sampled at a 3.3 L min⁻¹ flow rate through a 150 mm long sample line.

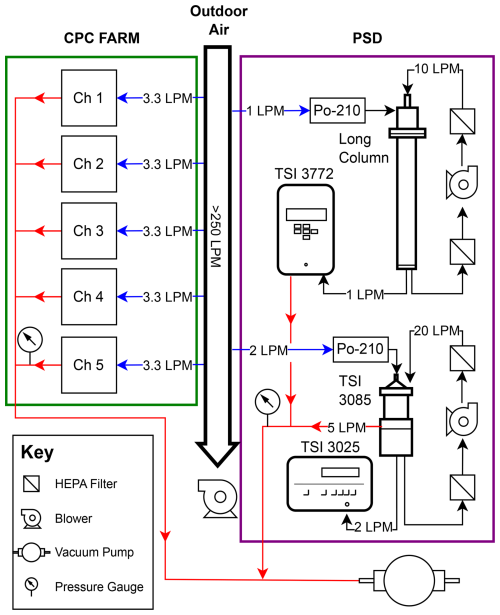
Figure 1 Schematic displaying the PSD and CPC FARM sampling setup during the Pittsburgh measurement campaign. The PSD is enclosed by the purple box. The CPC FARM is enclosed by the green box. Blue arrows indicate instrument sample flows. Red arrows indicate instrument exhaust flows.

The d₅₀ values of the CPC FARM were adjusted by controlling the operating temperature difference between the initiator and conditioner stage of each channel. To obtain uniform log spacing in the size bins, desired d₅₀ values were selected based on the experimental characterization results via interpolation of operating temperatures, namely the initiator since the conditioner was always operated at 1 °C. The resulting initiator temperatures used in the field testing were 98, 77, 68, 49, and 42 °C. The detection efficiency fit parameters used in the data analysis were then interpolated to the calculated initiator temperatures. During the measurement campaign, efforts were made to ensure data quality of the CPC FARM. Once a week, all channels were set to the highest and lowest cut points to verify that the measured particle concentration agreed within ±200 cm⁻³ between channels, regardless of total concentration. In addition, the Durapore wicks were replaced once a month to ensure any particles or gases deposited on the walls of the growth tube did not affect the particle activation characteristics.

2.5 Data inversion

2.5.1 Instrument response

When set to different d₅₀ cut points, each channel of the CPC FARM detects a slightly different fraction of the size distribution and therefore generates a different response (i.e., measurement signal). For a given input size distribution, the number concentration measured by each channel, i, is given by

$$\begin{array}{}\text{(1)}& N_i=\int f_n\left(D_{\mathrm{p}}\right){\mathit{\eta }}_i\left(D_{\mathrm{p}}\right)\mathrm{d}{D}_{\mathrm{p}}+e_i,\end{array}$$

where f_n is the number-weighted particle size distribution, η_i is the experimentally determined size-dependent detection efficiency, D_p is the particle diameter, and e_i is potential measurement error in channel i. N_i represents the number concentration of detectable particles at the growth tube outlet (i.e., activated particles grown larger than the minimum detectable droplet size). The raw signal measured by each channel, S_i, is particle counts over a sampling interval, t_s, and is associated with N_i according to

$$\begin{array}{}\text{(2)}& S_i=N_i{q}_{\mathrm{a}}{t}_{\mathrm{s}}{f}_{\mathrm{L},i},\end{array}$$

where q_a is the aerosol sample flow rate, and f_L,i is the “live-time” fraction of the sample interval (i.e., the fraction of time where the optical detection is active). As particle concentration increases, the live-time fraction is reduced due to particle coincidence in the optical detector. The live-time fraction is calculated in each sample interval from the measurement of the “dead-time” fraction, the time period where the optical detection is inactive.

2.5.2 Approximate inversion

The simplest data inversion approach is to approximate the CPC FARM detection efficiency curves as ideal step functions. This allows the differential particle number (ΔN) between consecutive channels to be calculated according to

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }{N}_i={\displaystyle \frac{N_i}{{\mathit{\eta }}_{\max ,i}}}-{\displaystyle \frac{N_{i+\mathrm{1}}}{{\mathit{\eta }}_{\max ,i+\mathrm{1}}}},\end{array}$$

where η_max is the maximum detection efficiency (plateau value) of the respective channel, effectively acting as a calibration correction factor to the corrected measured concentration (N_i). The resulting ΔN_i value corresponds to a size bin with [d_50,i, $d_{\mathrm{50},i+\mathrm{1}}$] edges and a midpoint diameter of

$$\begin{array}{}\text{(4)}& \stackrel{\mathrm{‾}}{D_{\mathrm{p},i}}=\mathrm{0.5}\left(d_{\mathrm{50},i}+d_{\mathrm{50},i+\mathrm{1}}\right).\end{array}$$

2.5.3 Numerical inversion

The accuracy of the “approximate” inversion method is limited by the fact that the actual detection efficiency curves of the instrument are not ideal step functions (see Fig. S2 in the Supplement). An alternative approach is to employ numerical data inversion that incorporates the nonideal detection efficiency curves of the instrument. Equation (1), which describes the instrument response functions, can be represented in matrix notation as

$$\begin{array}{}\text{(5)}& \mathit{b}=\mathbf{A}x+\mathit{e},\end{array}$$

where b is a vector of the observations (instrument signals), A is a kernel matrix that contains the instrument detection efficiency curves, x is the (unknown) size distribution, and e is a vector of potential measurement errors. Solving for x is an inverse problem that can be approximated with numerical methods. As is typical for CPCs, the detection efficiency of each channel in the CPC FARM resembles a sigmoid, with efficiency reaching a plateau value for particles slightly larger than the d₅₀ size. This characteristic presents a challenge since the measured signal includes contributions from particles larger than the cutoff size; however, these larger particles provide no information in the < 5 nm size range of interest. Therefore, the numerical data inversion needs to be evaluated over a wider range of particle sizes than where sizing information can be resolved from the instrument response functions.

Following the above, the presented data inversion approach discretizes the kernel over a size vector that includes the d₅₀ size range (1–5 nm) of the CPC FARM, as well as larger particles up to 400 nm. The particle size vector is log-spaced with n=20 elements. This implies that the inversion is an underdetermined problem given that the number of observations (measured signals) is m=5. The best results were attained with a size vector that includes four evaluation points within the steep region of the activation efficiency size range (∼1–4 nm). The resulting 5×20 system of linear equations is then solved by least-squares minimization using zeroth-order Tikhonov regularization to suppress the effects of measurement noise in the data inversion. The optimal regularization parameter, λ, is calculated using the L-curve method according to Cultrera and Callegaro (2020). In the search algorithm for the optimal λ, the range of initial λ values is initialized between 0.001σ₁ and 0.1σ₁, where σ₁ is the largest singular value of the inversion kernel A, calculated via singular value decomposition. The inversion result is then interpolated within the meaningful range of the CPC FARM particle sizing kernel, namely within 1–4 nm, to generate a final output vector of m−1 elements (i.e., m=4 in this configuration).

3 Results and discussion

3.1 Experimental characterization of detection efficiency curves

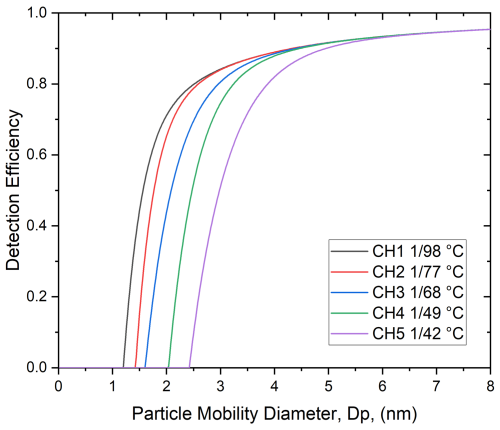
The detection efficiency of each CPC FARM channel was determined experimentally over a wide range of temperature differences (ΔT=30 °C to ΔT=97 °C) between the initiator and conditioner stages. The moderator stage was held at 1 °C. An analytical function, consisting of a particle activation term combined with a diffusion loss term in Eq. (S1) (Stolzenburg and McMurry, 1991), was fitted to the experimentally measured detection efficiencies as shown in Fig. S2. The d₅₀ of each channel, defined as the diameter at which the detection efficiency corrected for diffusion loss reaches 50 % of the plateau value, was calculated based on the fitted curve. The lowest d₅₀ was approximately 1.5 nm mobility diameter at the maximum ΔT=97 °C. The cut points of the five channels were very similar at a given temperature setting except for the smallest at ΔT=30 °C, which had d₅₀ ranging between 5 and 7 nm. This temperature setting was not used in the field study or inversion.

The operating temperatures of the CPC FARM were selected based on the experimentally determined relationship between d₅₀ and ΔT for each channel such that the resulting d₅₀ values were spaced evenly in log scale over the 1.5–3.0 nm range. Figure 2 shows the resulting modeled detection efficiencies of the CPC FARM channels. The curve fit parameters were calculated by interpolation of the corresponding parameters at measured ΔT settings. Note that all curves shown in Fig. 2 are normalized to a common plateau efficiency of 1 for visual clarity. Actual plateau efficiencies of the modeled curves varied between 0.93–0.98.

Figure 2 Interpolated and normalized detection efficiencies as a function of mobility diameter for each channel of the CPC FARM. Each color represents a CPC FARM channel set at the indicated conditioner and initiator temperatures to achieve the targeted d₅₀.

3.2 Measurement uncertainty

3.2.1 Particle number – random error

The CPC FARM's raw signals, S_i, are measurements of particle counts over a sampling interval. The uncertainty in S_i can be described by Poisson statistics, where the variance (σ²) in a measurement sample is expected to be equal to its mean value (μ). Therefore, S_i detected over the sampling interval, t_s, corresponds to both the mean and variance of this sample, i.e., ${\mathit{\mu }}_i={\mathit{\sigma }}_i^{\mathrm{2}}=S_i$. Combining this relationship with Eq. (2), the relative error (ε_i) for each channel is given by

$$\begin{array}{}\text{(6)}& {\mathit{\epsilon }}_i={\displaystyle \frac{{\mathit{\sigma }}_i}{{\mathit{\mu }}_i}}={\displaystyle \frac{\sqrt{S_i}}{S_i}}={\displaystyle \frac{\mathrm{1}}{\sqrt{S_i}}}={\displaystyle \frac{\mathrm{1}}{\sqrt{N_i{q}_{\mathrm{a}}{t}_{\mathrm{s}}{f}_{\mathrm{L},i}}}}.\end{array}$$

The above equation indicates that the counting error is generally reduced with a higher flow rate or longer sampling interval. Higher number concentrations also reduce the error, but this is an uncontrollable parameter during measurement. Further, as concentration continues to increase, the live-time fraction is progressively reduced, thereby offsetting the net effect of increasing number concentration on the random error.

Since the CPC FARM uses the difference between the signals of consecutive channels to estimate the particle distribution, both channels contribute to the uncertainty in the differential number measurement. The resulting standard deviation is ${\mathit{\sigma }}_{\mathrm{\Delta }N}=\sqrt{{\mathit{\sigma }}_i^{\mathrm{2}}+{\mathit{\sigma }}_{i+\mathrm{1}}^{\mathrm{2}}}$ , while the mean value is the difference in particle counts, ${\mathit{\mu }}_{\mathrm{\Delta }N}=S_i-S_{i+\mathrm{1}}$. Therefore, the relative error for two channels with the same flow rate and sampling interval is

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\mathit{\epsilon }}_{\mathrm{\Delta }N,i}& ={\displaystyle \frac{\sqrt{{\mathit{\sigma }}_i^{\mathrm{2}}+{\mathit{\sigma }}_{i+\mathrm{1}}^{\mathrm{2}}}}{S_i-S_{i+\mathrm{1}}}}={\displaystyle \frac{\sqrt{S_i+S_{i+\mathrm{1}}}}{S_i-S_{i+\mathrm{1}}}}\\ & ={\displaystyle \frac{\sqrt{N_i{f}_{\mathrm{L},i}+N_{i+\mathrm{1}}{f}_{\mathrm{L},i+\mathrm{1}}}}{\left(N_i{f}_{\mathrm{L},i}-N_{i+\mathrm{1}}{f}_{\mathrm{L},i+\mathrm{1}}\right)\sqrt{q_{\mathrm{a}}{t}_{\mathrm{s}}}}}.\end{array}\end{array}$$

The error in Eq. (7) consists of three parameter groups: (1) the square root of the sum of the number concentration detected by each channel, (2) the number concentration difference, and (3) the square root of the aerosol flow rate and sampling interval. Of these, the number concentration difference is the parameter with the strongest effect on the error. For the other parameter groups, the error scales with the square root of these parameters. Moreover, the differential raw signal, $\mathrm{\Delta }S=S_i-S_{i+\mathrm{1}}$, presents some fraction of S_i measured by the single channel. Introducing the relative differential raw signal, ${\mathit{\delta }}_{S,i}=\frac{S_i-S_{i+\mathrm{1}}}{S_i}=\frac{\mathrm{\Delta }S}{S_i}$, Eq. (7) can be rewritten as

$$\begin{array}{}\text{(8)}& {\mathit{\epsilon }}_{\mathrm{\Delta }N,i}={\displaystyle \frac{\mathrm{1}}{{\mathit{\delta }}_{S,i}}}\sqrt{{\displaystyle \frac{\mathrm{2}-{\mathit{\delta }}_{S,i}}{N_i{q}_{\mathrm{a}}{t}_{\mathrm{s}}{f}_{\mathrm{L},i}}}}.\end{array}$$

To demonstrate the effect of counting uncertainty on the differential raw signal measured by the CPC FARM, Fig. 3a shows a contour plot of the error according to Eq. (8) over a wide range of single-channel number concentrations (N_i) and over the range of 0 %-25 % relative differential signal ($\mathrm{\Delta }S/S_i$). The calculations correspond to a sample flow rate of 0.3 L min⁻¹ and a sampling interval of 5.0 s. Since the live-time fraction decreases with increasing N_i, an analytical function was fitted to CPC FARM experimental data to describe the relationship between f_L and N_i. As shown in Fig. S3, this relationship is described reasonably well by a two-phase exponential decay of f_L with increasing N_i. Figure S3 also suggests that the live-time fraction is relatively constant over small changes N_i. This implies that Eq. (8) can be rewritten in terms of relative differential concentrations ${\mathit{\delta }}_{S,i}\approx {\mathit{\delta }}_{N,i}=\frac{N_i-N_{i+\mathrm{1}}}{N_i}=\frac{\mathrm{\Delta }N}{N_i}$. The range of N_i and δ_N,i values this assumption holds likely varies between different CPCs; thus Fig. 3a serves as an approximate estimate of random error if ${\mathit{\delta }}_{S,i}={\mathit{\delta }}_{N,i}$ is assumed and the live-time fraction is not known.

Each line in Fig. 3a represents a relative error level in the differential measurement (ε_ΔN) where the lowest error occurs at the top right region of the plot (i.e., high N_i and $\mathrm{\Delta }S/S_i$). For example, achieving an error of 10 % when N_i=1000 cm⁻³ requires a relative differential signal of ∼ 9 % between two CPC channels. Following a single contour line where the error remains constant, $\mathrm{\Delta }S/S_i$ generally needs to increase when N_i is reduced. This effect becomes stronger at low concentrations. At $N_i>\mathrm{6}\times {\mathrm{10}}^{\mathrm{4}}$ cm⁻³, the $\mathrm{\Delta }S/S_i$ needed to maintain a constant error value increases due to the rapid decrease in live-time fraction at these high concentrations. Figure 3b shows an analogous plot of the minimum sampling time required for a maximum error of 10 %. According to this analysis, 10 and 30 s sampling times should be adequate at N_i higher than ∼ 12 500 and ∼ 3500 cm⁻³, respectively, even at a relatively small $\mathrm{\Delta }S/S_i$ value of 0.02. Faster time resolution, on the order of 1 s, is possible when $\mathrm{\Delta }S/S_i$ is at least 0.19 at N_i∼1000 cm⁻³ or 0.07 at N_i∼10 000 cm⁻³.

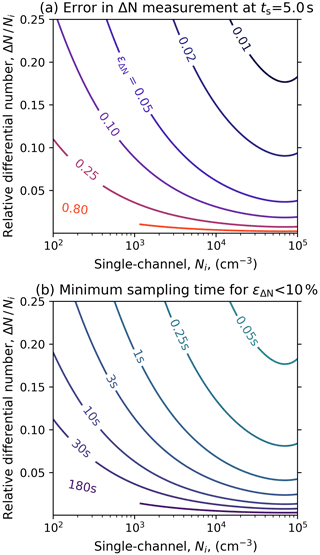
Figure 3 (a) Relative error in differential number measurement (ε_ΔN), shown as different lines, as a function of the single-channel number concentration (N_i) and the relative differential raw signal ($\mathrm{\Delta }S/S_i$) at a sample flow rate of 0.3 L min⁻¹ and a sampling interval of 5.0 s. (b) Analogous plot of the minimum sampling time required for < 10 % error.

3.2.2 Particle number – systematic error

In addition to counting uncertainty, the reported number concentration of each CPC FARM channel may be affected by systematic errors in the measurement. These errors can be due to signal drift with time, as well as due to potential temporal variation in the instrument calibration or operating parameters (e.g., sample flow rate). One of the calibration parameters used to generate the detection efficiency curve of each channel is η_max, the plateau value of the curve that is reached at particle diameters larger than d₅₀. η_max is effectively implemented in the data inversion as a correction factor to the signal (i.e., number concentration) measured by each channel, and hence any bias will propagate to the differential number concentration calculation between the channels. Experiments were conducted to examine how much the signal drifts with time by using the CPC FARM to measure > 10 nm particle distribution over several days. Figure S4 shows η_max, calculated daily over 2 weeks. The η_max was found by taking the ratio of the N_i measured by each channel to the average of all N_i values during a 10 min span. The 10 min span was chosen when both the difference in measured concentrations between channels and the change in the sum of those differences are the lowest. During the 2 weeks shown in Fig. S4, η_max varies less than ±2 % from the starting value and does not drift over time.

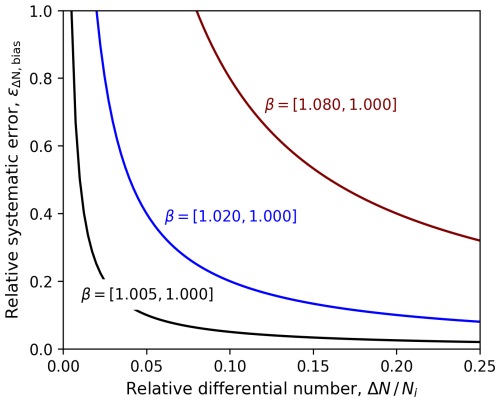
The combined relative systematic error in the differential measurement, ε_ΔNbias, from variations in η_max and other operating parameters can be expressed as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathit{\epsilon }}_{\mathrm{\Delta }N\mathrm{bias},i}& ={\displaystyle \frac{\mathrm{\Delta }{N}_{i,\mathrm{biased}}-\mathrm{\Delta }{N}_{i,\mathrm{true}}}{\mathrm{\Delta }{N}_{i,\mathrm{true}}}}\\ & ={\displaystyle \frac{{\mathit{\beta }}_i{N}_i-{\mathit{\beta }}_{i+\mathrm{1}}{N}_{i+\mathrm{1}}}{N_i-N_{i+\mathrm{1}}}}-\mathrm{1},\end{array}\end{array}$$

where β_i and β_i+1 are bias multipliers to the true number concentrations N_i and N_i+1. Figure 4 shows an example of the resulting systematic error for 0.5 %, 2 %, and 8 % bias applied to one channel and no bias in the second channel. These values are representative of the “best-case”, “typical”, and “worst-case” bias expected during the instrument operation. Similar to Fig. 3, the error is determined from the relative differential number, $\mathrm{\Delta }N/N_i$. As expected, the error decreases with increasing $\mathrm{\Delta }N/N_i$ and with lower bias, but the error also rapidly increases as $\mathrm{\Delta }N/N_i$ is reduced below a certain level. At 2 % bias, the error is 20 % at $\mathrm{\Delta }N/N_i\sim \mathrm{0.10}$, while at $\mathrm{\Delta }N/N_i\sim \mathrm{0.05}$ the error doubles to 40 %. These calculations highlight the importance of keeping systematic biases as low as possible to minimize errors in the reported differential particle number concentrations.

Figure 4 Relative error in the differential number measurement due to systematic bias, β, as a function of the relative differential number ($\mathrm{\Delta }N/N$) for 0.5 %, 2 %, and 8 % bias in the first channel and no bias in the second.

3.2.3 Particle size – sizing error

Another key source of error in the reported size distribution of the CPC FARM is the uncertainty in the composition of the measured particles and their respective detection efficiencies. The detection efficiency of water-based CPCs is dependent on particle composition, charge state, and solubility (Hering et al., 2017; Kangasluoma et al., 2014; Kangasluoma and Attoui, 2019; Wlasits et al., 2020). If the detection efficiency at a given set point is higher or lower than the positively charged ammonium sulfate calibration ion, the measured concentration will be reported in a smaller or larger size bin, respectively. Particles with extremely low detection efficiencies on water CPCs may not be detected at all. However, it is expected that all channels respond similarly to particles of a given composition as the CPC geometries and working fluids are identical, resulting in an overall shift in the size distribution diameter range.

Errors in the reported sizing can also be caused by changes in the physical instrument parameters, such as growth tube temperatures, that control the supersaturation ratio achieved in the growth tube. A change in the supersaturation ratio achieved by a CPC alters the detection efficiency curve. An incorrect detection efficiency curve impacts the numerical and approximate inversion methods because of incorrect diameter spacing between channels. Inaccurate diameter spacing would shift the midpoint of the inverted diameter bin and result in overestimation or underestimation of the number concentration. In this analysis, we assumed that the small changes in temperature have little effect on the supersaturation. Each channel maintains the temperature difference (ΔT) between the initiator and conditioner stages within 5 %. The calibration experiments (Fig. S2) show that the d₅₀ shifts by 4.7 % when the ΔT varies 5 % from 60 to 57 °C.

3.3 Data inversion

Figure 5 shows an inversion example with a synthetic particle size distribution. The input distribution, shown in Fig. 5a, is the sum of three lognormal distributions with mean and standard deviation parameters of [N₁=5000 cm⁻³, d_g1=2 nm, σ_g1=1.5], [N₂=3500 cm⁻³, d_g2=10 nm, σ_g2=1.8], and [N₃=1500 cm⁻³, d_g1=80 nm, σ_g1=2.0]. The simulated instrument response is calculated numerically using the known input size distribution and instrument detection efficiency kernel matrix by solving the “forward” problem in Eq. (5). To increase accuracy in the forward problem, a high-resolution size vector (1000 elements) was used over the 0.5–600 nm size range. A 0.3 L min⁻¹ sample flow rate and a 5 s sampling time interval were used in this example. The resulting five synthetic signals are then perturbed with random Poisson noise to simulate counting uncertainty. Figure 5b shows the mean differential number between the channels and the resulting spread due to Poisson noise for 100 random samples. The relative differential number, $\mathrm{\Delta }N/N_i$, varied between about 0.05–0.10 across the instrument bins. Because of the close channel spacing and relatively low number concentration, the live-time corrections between consecutive channels are nearly identical, and hence $\mathrm{\Delta }N/N_i\cong \mathrm{\Delta }S/S_i$. Predicted noise, according to Eq. (7), and potential systematic error, according to Eq. (9), are also included in the plot. A ±1 % bias in the number concentration between consecutive channels is shown in this example. The predicted noise is in good agreement with the standard deviation observed in the simulated data. Moreover, the error due to potential systematic bias is higher than that due to counting uncertainty.

Figure 5a shows the size distribution calculated by inverting the noisy signals using the numerical and approximate data inversion methods as described in Sect. 2.5. The resulting numerical distribution output, shown as a histogram, is in good agreement with the true input distribution but only within the steep detection efficiency size range of the inversion kernel; the evaluation points calculated at larger sizes only represent the averaged number concentration of the remaining size distribution. Figure 5a also includes error bars (±1σ) that show the effect of measurement noise on the numerical inversion output. In contrast, the resulting approximate inversion shows poor agreement with the true input. While the shape of the distribution is represented well, the approximate inversion outputs lower concentrations compared to the input distribution in all except the largest size bin. The lower calculated concentrations reflect the inability of the approximate inversion to account for both the sigmoid shape of the detection efficiency curve and overlap in the steep section of the detection efficiency curve for neighboring channels. A simulated distribution with lower concentrations is shown in Fig. S5 with similar input-to-output agreement for both inversion methods to those at higher concentrations.

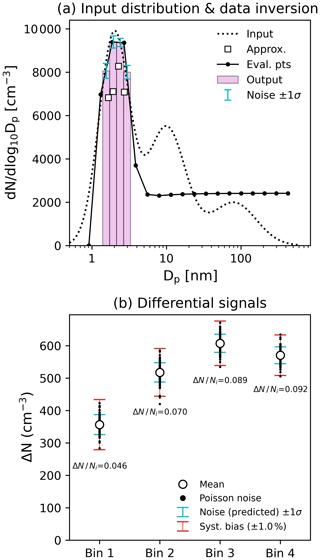
Figure 5 Simulated data inversion example with a three-mode lognormal distribution. (a) Output (numerical data inversion, pink bars) and approximate (approximate data inversion, square points) vs. input size distribution (dots) for noisy CPC FARM signals. Blue error bars represent 1σ of instrument noise. Black circles are the 20 evaluation points used in the particle size vector used in the kernel matrix (Eq. 5). (b) The resulting differential number across the instrument channels (mean values and noise due to random Poisson counting error), as well as systematic error due to ±1 % bias in the signal of the first channel of each bin. $\mathrm{\Delta }N/N_i$ values indicate the relative differential number concentration in each bin. A sample flow rate of 0.3 L min⁻¹ and a sampling time interval of 5 s were used in this example.

The numerical inversion used here is a regularized linear least-squares method and differs from the nonlinear, iterative Twomey–Markowski inversion used with the NMASS (Brock et al., 2019; Williamson et al., 2018). The Twomey–Markowski algorithm (Markowski, 1987) requires an initial guess that is a good estimate of the final solution to begin the iteration. The initial guess is then further refined and smoothed in each iteration loop. Smoothing is important as it dampens any oscillations in the solution during the nonlinear inversion process. While the Twomey–Markowski method is likely applicable to the CPC FARM data, it was not explored here because of the smoothness and initial guess requirements. None of these are required in the linear least-squares method, which was also found to be robust and reasonably accurate when evaluated with synthetic instrument data. Therefore, the proposed numerical inversion method is used for the CPC FARM, but further studies are needed to determine the best inversion method.

3.4 Field evaluation

Figure 6 presents the particle size distribution measured in Pittsburgh on 12 October 2023 by the PSD and CPC FARM. From the discussion above, the numerical inversion method with 10 s averaging was used to calculate the CPC FARM size distribution. The CPC FARM size distribution calculated using the approximate inversion is shown in Fig. S6. An NPF event is observed in the PSD size distribution at 11:20 EDT as evident by a sudden increase in concentrations of sub-3 nm particles in Fig. 6a. As shown in Fig. 6b, the CPC FARM also detected this event at the same start time as the PSD. Another increase in 2–3 nm particle concentration occurs between 12:00 and 13:00 EDT, with both instruments detecting the increase at the same time. Additionally, the ratio of PSD to CPC FARM concentrations as a function of particle diameter (Fig. 6c) is approximately 1, which indicates that the PSD and the CPC FARM agree well for particles larger than 2 nm during the NPF event. However, the PSD reports significantly fewer particles at sub-2 nm sizes. The lack of agreement in this size range can also be seen in Fig. 7b, which displays a vertical slice in the size distribution at 11:20 EDT. At the smallest sizes, the PSD undercounts the CPC FARM by an order of magnitude.

Outside of the NPF event, the CPC FARM measures particles that the PSD misses. Between 00:00 and the start of the NPF event at 11:20 EDT, the CPC FARM detects 1000 cm⁻³ or fewer particles between 2 and 3 nm except during a few plumes. During this time period, Fig. 6c shows that the concentrations measured by the PSD in this size range are mostly noise. In the sub-2 nm size range, the CPC FARM measures a continuous concentration of 10⁴ cm⁻³ particles. The PSD appears to intermittently measure 2-nm particles; however, these sporadic measurements are indistinguishable from noise and are often much higher than the CPC FARM measurements. Figure 7a illustrates a size distribution of the PSD and CPC FARM between 05:05 and 05:10 EDT. During this scan, the PSD measures a concentration of sub-2 nm particles an order of magnitude higher than the CPC FARM, which signifies that this PSD measurement is primarily noise. The large magnitude of the noise is not surprising as correction factors for charging efficiency, diffusion wall loss, and CPC transmission increase as particle diameter decreases. When combined, the correction factor to convert the measured concentration of 1.9 nm to dN/dlogD_p is roughly 1.8×10⁴. While newer CPCs may have a lower d₅₀ than the TSI 3025, potentially reducing the overall correction factor, the effect would be minimal as the charging efficiency is still 1 order of magnitude lower than the current CPC transmission efficiency of 25 % at 1.5 nm.

A brief particle formation event was also observed between 05:25–05:30 EDT in the morning (Fig. 6), where the PSD detected 2–3 nm particles during a plume event. This short event is captured by both the PSD and the CPC FARM, where the CPC FARM measures a particle concentration of roughly 10⁴ cm⁻³, whereas the PSD reports half this concentration. It is currently somewhat unclear why this plume is well-defined on the PSD while the longer-lasting plumes detected by the CPC FARM at 06:30, 07:15, and 08:30 EDT were missed by the PSD. These plumes appear to be real events as there is a corresponding increase in the smallest size bins observed on the CPC FARM over the same periods. One potential explanation is that the concentration of particles in the plume is around the PSD detection limit of around 3×10⁴ cm⁻³ at 2.4 nm (Fig. S7c). Another explanation is that different plumes could contain particles of different compositions. The water CPCs used in the CPC FARM and the butanol CPCs used in the PSD have been shown to exhibit different composition-based detection efficiencies in the sub-10 nm size range (Kulmala et al., 2007).

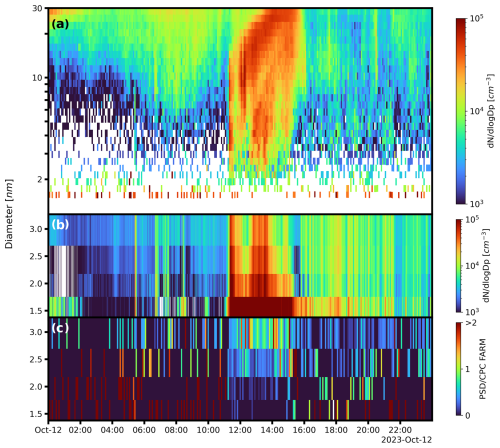
Figure 6 Plot data taken on 12 October 2023. (a) Contour plot showing the inverted PSD size distribution from 1.4–30 nm. (b) Contour plot showing the numerically inverted CPC FARM data recorded at 1 Hz with a 10 s average applied. The midpoints of the four size bins are 1.6, 1.9, 2.3, and 2.9 nm. (c) Contour plots showing the ratio of the concentration measured by the PSD to the CPC FARM. The CPC FARM data were averaged over the same time intervals as the PSD scans. The PSD size bins with midpoints closest to the CPC FARM midpoints were used for the comparison.

After the NPF event ends at 15:00 EDT, the CPC FARM detects a near-constant concentration of 10⁴ cm⁻³ particles between 2 and 3 nm. Note that the constant particle concentration observed by the CPC FARM is not an artifact of the instrument but likely continuous nucleation or primary emissions of sub-3 nm particles, as other days exhibited no particles in the 1–3 nm range. While the PSD detects a higher concentration of particles between 2 and 10 nm in the afternoon and evening compared to the morning, Fig. 6c shows that the PSD measurements are still sporadic and comparatively lower than the CPC FARM. Similar to the plumes in the morning, the PSD likely measures these particles irregularly because the concentration is at the lower detection limit of the instrument. As in the morning, the PSD reports significantly lower concentrations of sub-2 nm particles, apart from the measurement noise. The concentrations between the two instruments momentarily agree but only when the noise of the PSD matches the measured CPC FARM concentration. Figure 7c shows a vertical slice of the size distribution between 20:00 and 20:05 EDT where the noise of the PSD is similar to the measured CPC FARM concentration.

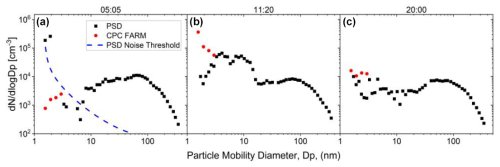
Figure 7 Size distribution of a single 5 min PSD scan and 5 min CPC FARM averaged from (a) 05:05–05:10 EDT, (b) 11:20–11:25 EDT, and (c) 20:00–20:05 EDT.

The uncertainty in the CPC FARM measurement due to random error can be estimated using Eq. (7). The uncertainty from random error is < 10 % on all channels during the two sub-3 nm growth events during the midday NPF event. However, at times between the two growth events around 12:15 EDT, there are few particles between 2–3 nm. Hence, the systematic error in the larger two channels is high, occasionally exceeding 100 %. The random error analysis can also be used to increase confidence in the measurement of plumes. For example, during the plume observed from 05:25–05:30 EDT the random error across the channels suddenly decreased from over 20 % to under 10 %.

Similarly, the uncertainty from systematic error can be estimated using Eq. (9). From Fig. S6, 2 % is an appropriate bias error to use with the CPC FARM. The resulting potential systematic error exceeds 75 % for most of the day apart from the NPF event where the first and second CPC FARM channels have potential systematic errors of around 20 % and 40 %, respectively. In future testing, systematic error can be reduced by further spacing out the d₅₀ cut points for the five channels to increase the $\mathrm{\Delta }N/N_i$. A sheath flow could also be added to the growth tube of each CPC to increase the steepness of the detection efficiency curve. Increasing the number of channels would increase the size range of the CPC FARM and would improve data inversion accuracy if the size distribution varies dramatically over a small diameter range. Also, the systematic measurement uncertainty caused by any changes in transmission efficiency could be reduced by running a daily test where < 10 nm particles are filtered out, or the CPC FARM could be switched to sample lab-generated aerosol particles with controlled properties for several minutes.

4 Conclusions

In summary, we demonstrated the operation of a five-channel, 1 nm water-based CPC battery, referred to as the CPC FARM, to measure the sub-3 nm size distribution at a 1 s time resolution. Random and systematic measurement uncertainties were evaluated to determine the best methods to operate the instrument and to analyze the observations. In addition, a numerical data inversion process was developed and was found to be more accurate than an approximate inversion method. Simulations of the CPC FARM response to various size distributions show that the numerical inversion method can recover the original size distribution, albeit with some error due to measurement uncertainty inherent to the CPC as well as uncertainty in the stability of operational parameters. Field testing in Pittsburgh, PA, verified that the CPC FARM observes NPF at significantly higher time resolution and sensitivity in the sub-3 nm size range compared to traditional SMPS systems. However, high concentrations of sub-3 nm particles in Pittsburgh made it difficult to determine potential changes to the maximum transmission efficiency of each CPC. Furthermore, the random and systematic errors are likely lower in polluted cities like Pittsburgh, PA, as the sub-3 nm and total particle concentrations are high. This allows for short sampling intervals of 1 s. For cleaner regions, longer sampling times and further spaced cut points are likely required to obtain accurate size distribution measurements. Ultimately, the CPC FARM is a very sensitive and fast instrument for detecting rapid processes that produce sub-3 nm particles.