Cancellation of cloud shadow effects in the absorbing aerosol index retrieval algorithm of TROPOMI

Cloud shadows can be detected in the radiance measurements of the TROPOspheric Monitoring Instrument (TROPOMI) on board the Sentinel-5P satellite due to its high spatial resolution and could possibly affect its air quality products. The cloud-shadow-induced signatures are, however, not always apparent and may depend on various cloud and scene parameters. Hence, the quantification of the cloud shadow impact requires the analysis of large data sets. Here we use the cloud shadow detection algorithm DARCLOS to detect cloud shadow pixels in the TROPOMI absorbing aerosol index (AAI) product over Europe during 8 months. For every shadow pixel, we automatically select cloud- and shadow-free neighbour pixels in order to estimate the cloud-shadow-induced signature. In addition, we simulate the measured cloud shadow impact on the AAI with our newly developed three-dimensional (3D) radiative transfer algorithm MONKI. Both the measurements and simulations show that the average cloud shadow impact on the AAI is close to zero (0.06 and 0.16, respectively). However, the top-of-atmosphere reflectance ratio between 340 and 380 nm, which is used to compute the AAI, is significantly increased in 95 % of the shadow pixels. So, cloud shadows are bluer than surrounding non-shadow pixels. Our simulations explain that the traditional AAI formula intrinsically already corrects for this cloud shadow effect via the lower retrieved scene albedo. This cancellation of cloud shadow signatures is not always perfect, sometimes yielding second-order low and high biases in the AAI which we also successfully reproduce with our simulations. We show that the magnitude of those second-order cloud shadow effects depends on various cloud parameters which are difficult to determine for the shadows measured with TROPOMI. We conclude that a potential cloud shadow correction strategy for the TROPOMI AAI would therefore be complicated if not unnecessary.

1 Introduction

The TROPOspheric Monitoring Instrument (TROPOMI) is a spectrometer on board the Sentinel-5 Precursor (S5P) satellite in low Earth orbit, launched on 13 October 2017 (Veefkind et al., 2012). TROPOMI provides daily global maps of trace gases, aerosols and clouds, derived from the spectrum of sunlight reflected by the Earth. The spatial resolution of TROPOMI of 5.6 × 3.6 km² in the nadir-viewing direction is very high compared to its predecessors, such as OMI with 24 × 13 km² (Levelt et al., 2006), GOME-2 with 80 × 40 km² (Munro et al., 2016) and SCIAMACHY with 60 × 30 km² (Bovensmann et al., 1999). Because of this unprecedented spatial resolution and its high data quality, TROPOMI is able to observe local NO₂ emission sources such as power plants (Beirle et al., 2019), gas compressor stations (van der A et al., 2020), and cities (Lorente et al., 2019); CH₄ leakage from oil and/or gas fields (Pandey et al., 2019; Varon et al., 2019; Schneising et al., 2020); volcanic SO₂ plumes (Theys et al., 2019); and NO₂ trails along ship tracks (Georgoulias et al., 2020).

TROPOMI also effectively tracks aerosols that absorb light in the UV part of the spectrum, such as desert dust, volcanic ash, and smoke from biomass burning, by providing the absorbing aerosol index (AAI) in every pixel of each orbit (Stein Zweers et al., 2018; de Graaf et al., 2005). Unlike most other aerosol retrieval products, the AAI can also successfully be derived above clouds and bright surfaces. In addition, the AAI is an important input for the retrieval algorithms of other TROPOMI products. For example, the pixel selection for the aerosol layer height (ALH) (Sanders et al., 2015; Nanda et al., 2019) and aerosol optical thickness (AOT) (de Graaf, 2022) retrievals of TROPOMI is based on the AAI. Hence, AAI features that are not related to absorbing aerosols, for example caused by the ocean glint, absorbing constituents in the ocean water, and clouds at specific scattering geometries (Kooreman et al., 2020), may be undesired for those retrievals.

The effect of clouds on the AAI in cloudy pixels has been studied before using data from SCIAMACHY (Penning de Vries et al., 2009; Penning de Vries and Wagner, 2011), OMI (Torres et al., 2018; Jethva et al., 2018) and TROPOMI (Kooreman et al., 2020). Besides cloud signatures in cloudy pixels, clouds can also leave signatures in adjacent cloud-free pixels, for example in the form of cloud shadows. Contrary to the large pixel sizes of its predecessors, the small pixel size of TROPOMI sometimes causes one or several pixels to be fully covered by a single cloud shadow, particularly for high clouds at large viewing and/or solar zenith angles (Trees et al., 2022). Those three-dimensional (3D) radiative transfer effects are not yet taken into account in the current AAI retrieval algorithm, and their influence on the AAI has not yet been investigated. The natural horizontal variation in the AAI complicates the quantification of the cloud-shadow-induced AAI signatures. Recently, we developed an accurate and fast cloud shadow detection algorithm for TROPOMI, called DARCLOS (Trees et al., 2022), which allows for a statistical analysis of the cloud shadow effect on the AAI in large data sets.

In this paper, we present a statistical analysis of the cloud shadow effect on the measured TROPOMI AAI for all pixels above Europe during 8 months. We use the cloud shadow detection algorithm DARCLOS to detect the cloud shadow pixels, and we select cloud- and shadow-free neighbour pixels for comparison with the non-shadow state. In addition, we simulate the measured cloud shadow effect on the AAI for various scenes using our 3D radiative transfer code MONKI, recently developed by us at the Royal Netherlands Meteorological Institute (KNMI). Using our simulations, we explain the measured cloud shadow effects on the AAI. Finally, we discuss the implications of our findings for the TROPOMI AAI product.

This paper is structured as follows. In Sect. 2, we describe the methods we used to measure and to simulate cloud shadow effects on the absorbing aerosol index product of TROPOMI. In Sect. 3, we show the results of those measured and simulated cloud shadow effects. In Sect. 4, we discuss the implications of our results and state the most important conclusions of this paper.

2 Method

In this section, we first give a brief description of TROPOMI (Sect. 2.1), the absorbing aerosol index product (Sect. 2.2), and the data set we selected (Sect. 2.3). Then, we explain the employed methods to detect cloud shadow pixels (Sect. 2.4) and their shadow-free neighbour pixels (Sect. 2.5). Finally, we describe our model to simulate cloud shadow effects (Sect. 2.6).

2.1 Description of TROPOMI

The TROPOspheric Monitoring Instrument (TROPOMI) was launched on 13 October 2017 as the only instrument on board the Sentinel-5 Precursor (S5P) satellite (Veefkind et al., 2012). Operating in a near-polar, Sun-synchronous orbit at an average altitude of 824 km above the Earth's surface, TROPOMI completes an orbit approximately every 101 min. TROPOMI is a nadir-looking instrument. During its ascending node, it collects measurements every 1.08 s in a 2600 km swath width, providing a daily global coverage. The local Equator crossing time of TROPOMI is 13:30 LT. TROPOMI initially featured a footprint size of 7.2 × 3.6 km² in the nadir-viewing direction, which was later adjusted to 5.6 × 3.6 km² on 6 August 2018 (Ludewig et al., 2020).

TROPOMI is a spectrometer continuously measuring the Earth radiance I_λ at wavelengths λ and in units of W m⁻² nm⁻¹ sr⁻¹ and the solar irradiance E_0λ in units of W m⁻² nm⁻¹ daily to derive the measured local top-of-atmosphere (TOA) reflectance $R_{\mathit{\lambda }}^{\mathrm{meas}}$:

$$\begin{array}{}\text{(1)}& R_{\mathit{\lambda }}^{\mathrm{meas}}\left(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}},\mathit{\varphi },{\mathit{\varphi }}_{\mathrm{0}}\right)={\displaystyle \frac{\mathit{\pi }{I}_{\mathit{\lambda }}\left(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}},\mathit{\varphi },{\mathit{\varphi }}_{\mathrm{0}}\right)}{{\mathit{\mu }}_{\mathrm{0}}{E}_{\mathrm{0}\mathit{\lambda }}}},\end{array}$$

where μ = cos θ and μ₀ = cos θ₀ and with θ, θ₀, φ, and φ₀ the viewing zenith, solar zenith, viewing azimuth, and solar azimuth angles, respectively. From $R_{\mathit{\lambda }}^{\mathrm{meas}}$, properties of the local Earth's atmosphere and surface can be retrieved. Covering wavelengths in the ultraviolet–visible (UV-VIS, 267–499 nm), near-infrared (NIR, 661–786 nm), and shortwave infrared (SWIR, 2300–2389 nm) with high spectral resolution, TROPOMI globally and daily retrieves the concentrations of trace gases (NO₂, O₃, CH₄, CO, and SO₂) and properties of aerosols and clouds with unprecedented accuracy.

2.2 Absorbing aerosol index (AAI)

The air quality product that we analyse is the TROPOMI level 2 absorbing aerosol index (AAI). The AAI is retrieved from the measured and calculated TOA reflectances at 340 and 380 nm as follows (see Torres et al., 1998; de Graaf et al., 2005; Stein Zweers et al., 2018):

$$\begin{array}{}\text{(2)}& \mathrm{\text{AAI}}=-\mathrm{100}\cdot \left[{\log }_{\mathrm{10}}{\left({\displaystyle \frac{R_{\mathrm{340}}}{R_{\mathrm{380}}}}\right)}^{\mathrm{meas}}-{\log }_{\mathrm{10}}{\left({\displaystyle \frac{R_{\mathrm{340}}}{R_{\mathrm{380}}}}\right)}^{\mathrm{calc}}\right],\end{array}$$

where “meas” and “calc” indicate the measured (Eq. 1) and calculated TOA reflectances, respectively. The calculated TOA reflectances are for a clear-sky atmosphere above a Lambertian (i.e. isotropically reflecting and fully depolarizing) surface and were obtained using the formula of Chandrasekhar (1960):

$$\begin{array}{}\text{(3)}& R_{\mathit{\lambda }}^{\mathrm{calc}}\left(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}},\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}\right)=R_{\mathit{\lambda }}^{\mathrm{0}}\left(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}},\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}\right)+{\displaystyle \frac{A_{\mathrm{s}}{T}_{\mathit{\lambda }}(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}})}{\mathrm{1}-A_{\mathrm{s}}{s}_{\mathit{\lambda }}^{*}}}.\end{array}$$

In Eq. (3), R⁰ is the path reflectance, which represents the contribution to the TOA reflectance of the clear-sky atmosphere bounded below by a black surface. The second term in Eq. (3) represents the effect of the surface on the TOA reflectance. It contains the Lambertian surface albedo A_s, the total two-way transmittance of the atmosphere T, and the spherical albedo s^* of the atmosphere for illumination from below. Quantities R⁰, T, and s^* are computed with the “Doubling Adding KNMI” (DAK) radiative transfer code (de Haan et al., 1987; Stammes, 2001). This computation accounts for the effects of single and multiple Rayleigh scattering and the absorption of sunlight by molecules within a pseudo-spherical atmosphere, fully taking into account the polarization of light.

The Lambertian surface albedo A_s in Eq. (3) is retrieved at λ = 380 nm assuming that $R_{\mathrm{380}}^{\mathrm{calc}}\left(A_{\mathrm{s}}\right)=R_{\mathrm{380}}^{\mathrm{meas}}$. The value of A_s which satisfies this assumption is known as the “scene albedo” or the “scene Lambertian-equivalent reflectance” (scene LER), denoted in this paper as A_scene. From Eq. (3) it then follows that

$$\begin{array}{}\text{(4)}& A_{\mathrm{scene}}={\displaystyle \frac{R_{\mathrm{380}}^{\mathrm{meas}}-R_{\mathrm{380}}^{\mathrm{0}}}{T_{\mathrm{380}}(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}})+s_{\mathrm{380}}^{*}\left(R_{\mathrm{380}}^{\mathrm{meas}}-R_{\mathrm{380}}^{\mathrm{0}}\right)}}.\end{array}$$

A_scene is assumed to be wavelength-independent, allowing for the computation of $R_{\mathrm{340}}^{\text{calc}}$ using Eq. (3) but with λ = 340 nm. Finally, the AAI is computed using Eq. (2).

In a scene without aerosols and clouds, above a spectrally neutral Lambertian surface, the AAI is, in theory, equal to zero. The AAI of TROPOMI has an offset of ∼ −2. The offset in the AAI collection 1 data used for this paper is due to radiometric calibration offsets and degradation in the TROPOMI radiance and irradiance data (Tilstra et al., 2020; Ludewig et al., 2020). The degradation in the radiance and irradiance results in an increase in the derived reflectances at 340 and 380 nm, decreasing the average AAI values over time. The AAI tends to increase in the presence of absorbing aerosols and can also identify aerosols that are located above clouds (see, for example, Torres et al., 2012). We refer to Herman et al. (1997), Torres et al. (1998), de Graaf et al. (2005), Penning de Vries et al. (2009), and Kooreman et al. (2020) for more details about the sensitivity of the AAI to aerosols, surfaces, and clouds. For this research about cloud shadow effects, it should be noted that dark pixels (low $R_{\mathrm{380}}^{\mathrm{meas}}$) give low A_scene (Eq. 4) resulting in relatively small contributions of the surface to $R_{\mathrm{340}}^{\mathrm{calc}}$ and $R_{\mathrm{380}}^{\mathrm{calc}}$ (Eq. 3).

2.3 Selected data set

We analysed 8 months of TROPOMI AAI collection 1 data (processor version 1.3.0) from 1 November 2020 to 30 June 2021 (https://doi.org/10.5270/S5P-3dgz66p, Copernicus Sentinel-5P, 2018). For each day in the data set, we use all pixels that fall in the selected area, on average resulting in 511 616 px d⁻¹ available for our analysis. The selected area ranges from 34° S to 61° N latitude and from 11° W to 40° E longitude, as shown in the left panel of Fig. 1. This area covers all capitals of Europe (except for Reykjavik), Ankara, Moscow, and some northern African cities such as Tangier, Algiers, and Tunis. The area of interest in Europe was covered by TROPOMI during three successive, partially overlapping overpasses on 11 November 2020, as shown in Fig. 1. Days with missing data (23 May, 20 May, and 29 June 2021), inconsistent ground pixel grids of the AAI and NO₂ products (24 June 2021), and a solar eclipse (10 June 2021) were removed from the data set.

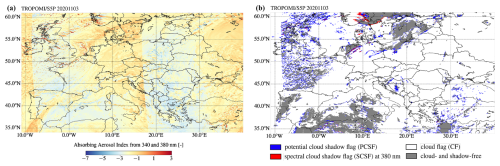
Figure 1 Example of the AAI (a) and cloud shadow flags (b) in three partly overlapping TROPOMI orbit swaths covering the selected area for this research on 3 November 2020. In panel (b), the blue pixels contain a potential cloud shadow flag (PCSF), the red pixels contain (in addition) a spectral cloud shadow flag (SCSF), the white pixels contain a cloud flag (CF), and the grey pixels are cloud- and shadow-free.

2.4 Cloud shadow detection

The flagging of pixels affected by cloud shadows was performed with the cloud shadow detection algorithm DARCLOS, recently developed for TROPOMI at KNMI (see Trees et al., 2022).

In DARCLOS, first, cloud pixels are identified using a threshold on the already available effective cloud fraction in the TROPOMI NO₂ product (van Geffen et al., 2021), after which cloud flags (CFs) are raised. Then, potential cloud shadow flags (PCSFs) are raised, indicating TROPOMI ground pixels that are potentially affected by cloud shadows. The PCSFs are determined using a geometrical calculation of the shadow location based on the cloud height from the TROPOMI cloud product FRESCO (Koelemeijer et al., 2001; Wang et al., 2008) and illumination and viewing geometries. The PCSFs generally overestimate the true visible cloud shadow area but minimize the omission of pixels affected by cloud shadows.

After the PCSFs are raised, DARCLOS raises spectral cloud shadow flags (SCSFs). The SCSFs are a subset of the PCSFs, based on a threshold on the contrast Γ between the retrieved scene albedo, A_scene (see Eq. 4), and the expected surface albedo from a climatology, A_DLER. An SCSF is raised for a pixel if (see Eqs. 11 and 17 of Trees et al., 2022)

$$\begin{array}{}\text{(5)}& \mathrm{\Gamma }\left(\mathit{\lambda }\right)<-\mathrm{15}\mathit{\%},\end{array}$$

where

$$\begin{array}{}\text{(6)}& \mathrm{\Gamma }\left(\mathit{\lambda }\right)={\displaystyle \frac{A_{\mathrm{scene}}\left(\mathit{\lambda }\right)-A_{\mathrm{DLER}}\left(\mathit{\lambda }\right)}{A_{\mathrm{DLER}}\left(\mathit{\lambda }\right)}}\times \mathrm{100}\mathit{\%}.\end{array}$$

The variable A_DLER is also known as the directionally dependent Lambertian-equivalent reflectivity or DLER (see Tilstra et al., 2024). For this research about cloud shadow effects on the AAI retrieved at 340 and 380 nm, we employ λ = 380 nm. The SCSFs are a better estimate of the cloud shadows than the PCSFs. As an example, Fig. 1b shows the SCSFs indicated in red, the PCSFs indicated in blue, and the CFs indicated in white in three TROPOMI orbits covering the area of our case study on 3 November 2020, which is one of the days in our data set. Figure 2b shows the SCSFs and PCSFs zoomed in on north-west Germany. From a visual comparison of Fig. 2b to the map of the scene albedo A_scene (Fig. 2a), it may be observed that the SCSFs are indeed located at pixels where A_scene is lower than at surrounding pixels along cloud edges, which may be interpreted as cloud shadows. For more details about the cloud shadow flagging with DARCLOS, refer to Trees et al. (2022).

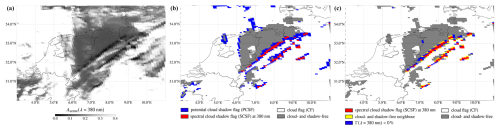
Figure 2 The scene albedo at 380 nm, A_scene(λ = 380 nm), derived by TROPOMI on 3 November 2020 above the Netherlands, Belgium, and north-west Germany (a); the potential cloud shadow flags (PCSFs) in blue, spectral cloud shadow flags (SCSFs) in red, and cloud flags (CFs) in white (b); and the first cloud- and shadow-free neighbour pixels in yellow and possibly shadow-affected pixels according to Eq. (7) in blue (c).

2.5 Selecting cloud- and shadow-free neighbours

In order to be able to quantify the cloud shadow effect on the AAI in a shadow pixel (i.e. for which a SCSF was raised), we identify cloud- and shadow-free reference pixels in the proximity of the shadow pixel and assume that they represent the hypothetical non-shadow state of the shadow pixel, i.e. as if the shadow pixel would not be affected by cloud shadow. In what follows, we call those reference pixels the neighbour pixels. We distinguish between first and second neighbour pixels for the closest and second-closest neighbour pixels, respectively. The second neighbour pixels are used for comparison with the first neighbour pixels as a control case, since both the first and second neighbour pixels should not be affected by cloud shadow.

First, for each shadow pixel, we define a search area with potential neighbour pixels within a 2 px radius around the shadow pixel; i.e. a neighbour pixel cannot be located more than two scan lines, or more than two pixel rows, away from the shadow pixel. The cloud pixels and shadow pixels are removed from the search area. Some pixels that are darker than expected are possibly (partly) affected by cloud shadows but not severely enough to raise a SCSF by DARCLOS (see Eqs. 5 and 6). Because we do not trust them as shadow-free pixels, they are removed from the search area when

$$\begin{array}{}\text{(7)}& \mathrm{\Gamma }(\mathit{\lambda }=\mathrm{380}\mathrm{nm})<\mathrm{0}\mathit{\%}.\end{array}$$

For each leftover potential neighbour pixel in the search area, we compute the distance in latitude–longitude space from the centre of the potential neighbour to the centre of the shadow pixel. The leftover potential neighbour pixel with the closest distance to the shadow pixel is selected as the first neighbour pixel for this shadow pixel. Similarly, we define the second neighbour pixel as the leftover potential neighbour pixel with the second-closest distance to the shadow pixel. The shadow pixel is considered in our analysis only if both a first and second neighbour pixel can be determined.

Figure 2c shows an example of the SCSFs at λ = 380 nm indicated in red and the first neighbour pixels indicated in yellow for 3 November 2020 above north-west Germany. In this scene, cloud shadows are found northward of the clouds between 6.0 and 10° E longitude. The pixels that could not be selected as a neighbour because Γ < 0 % (see Eq. 7) are indicated in blue. Note that there are fewer neighbour pixels than raised SCSFs because (1) some shadow pixels do not have at least two cloud- and shadow-free pixels with Γ ≥ 0 % in their search area and (2) neighbours can be recycled for multiple shadow pixels. In Fig. 2, the first neighbour pixels are indeed not located where there are clouds (i.e. pixels for which A_scene ≳ 0.3 in Fig. 2a) or possibly where cloud shadow darkening occurs.

2.6 Simulating the cloud shadow effect

Three-dimensional radiative transfer simulations are required for the explanation of cloud shadow effects on the AAI as found in the observations. In this research, we use the 3D radiative transfer code MONKI (Monte Carlo KNMI) that we recently developed at KNMI. MONKI computes the TOA reflectance of an atmosphere–surface system defined in a 3D Cartesian grid in a horizontally cyclic domain, using a forward Monte Carlo technique (see, for example, Marshak and Davis, 2005), and fully takes into account linear and circular polarization of light for all orders of scattering. The simulated photon packets travelling through the grid cells of the atmosphere–surface system are scattered by the atmospheric gas through (anisotropic) Rayleigh scattering (Hansen and Travis, 1974) and by cloud droplets through Mie scattering (de Rooij and van der Stap, 1984) if the grid cell is cloudy. Absorption of the light by the gas and by cloud droplets is taken into account. The surface reflection is Lambertian (i.e. isotropic and fully depolarizing), with a specified surface albedo. Instead of collecting the reflected photon packets at TOA in the very small solid angle subtended by the satellite, MONKI uses the more efficient “local estimation method” (Marchuk et al., 1980; Marshak and Davis, 2005), commonly used in Monte Carlo radiative transfer algorithms (see, for example, Spada et al., 2006; Mayer, 2009; Deutschmann et al., 2011), in which at each scattering event the contribution to the reflectance is computed as the probability that the photon is being scattered towards the satellite. The TOA reflectance of MONKI has been compared to the DAK (Doubling Adding KNMI) polarized radiative transfer code (de Haan et al., 1987; Stammes, 2001) for plane-parallel and horizontally homogeneous cloudy and cloud-free scenes, and it shows an excellent agreement.

For this research, we use 50 × 50 grid cells in the horizontal directions of the 200 × 200 km² cyclic domain and 33 grid cells in the vertical direction ranging from 0 to 100 km. Ozone is the only absorbing gas in our model, with absorption cross-sections taken from Bass and Paur (1985). The pressure, temperature, and ozone volume mixing ratios solely depend on altitude according to the standard mid-latitude summer profile (Anderson, 1986). We assume that the pressure$/$temperature ratio decreases exponentially with height within each grid cell (see Stam et al., 2000, for the calculation of the gaseous absorption and scattering optical thicknesses). For our analysis, we vary the cloud optical thickness, cloud height, cloud horizontal dimensions, solar and viewing zenith and azimuth angles, and surface albedo, resulting in various sizes and shades of cloud shadows in the atmosphere and cast on the surface.

Figure 3 Daily cloud fraction (grey curve) and cloud shadow fraction (black curve) in the selected area over Europe from 1 November 2020 until 30 June 2021.

3 Results

In this section, we present the results of the determined cloud shadow fraction in our selected data set (Sect. 3.1) and of the measured (Sect. 3.2) and simulated (Sect. 3.3) cloud shadow effect on the TROPOMI AAI.

3.1 Cloud shadow fraction

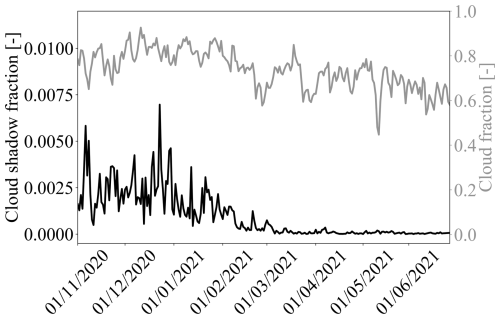
Figure 3 shows the cloud fraction and cloud shadow fraction in the selected area over Europe from 1 November 2020 to 30 June 2021. The cloud fraction and cloud shadow fraction were defined as the fraction of pixels with a raised CF and SCSF, respectively. The cloud shadow fraction was relatively large from 1 November to 31 January with an average daily mean value of 0.002, which corresponds to 1124 cloud shadow pixels on average per day. After January, the cloud shadow fraction decreases. From 1 March to 30 June, the average daily mean cloud shadow fraction was $\mathrm{7.4}\times {\mathrm{10}}^{-\mathrm{5}}$, corresponding to 38 cloud shadow pixels on average per day. We note that changes in the trend of the daily mean cloud fraction are much less apparent. The higher cloud shadow fraction in the winter months than in the spring and summer months can be explained by the larger solar zenith angles resulting in longer shadow extents.

3.2 Measured cloud shadow effects on the AAI

Here we present the results of the measured cloud shadow effect on the TROPOMI AAI; i.e. we compare the AAI in the shadow pixels of our data set with the AAI in their first cloud- and shadow-free neighbour pixels. To show the natural variation irrespective of cloud shadows, we also compare the AAI in the first and second neighbour pixels. In addition, we analyse the results for the measured TOA reflectance ratio ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ and calculated TOA reflectance ratio ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$, which determine the AAI (Eq. 2), and the retrieved scene albedo A_scene, which determines ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ via $R_{\mathrm{340}}^{\mathrm{calc}}$ (Eq. 3).

3.2.1 First-order cloud shadow effect

Figure 4 shows the AAI (top row) in the first neighbour pixels compared in a scatter plot to the second neighbour pixels (first column) and to the shadow pixels (second column). In both cases, the scatter plots show a high positive correlation (r = 0.82 and 0.81, respectively). The AAI in the shadow pixels is not consistently larger or smaller than the AAI in the first neighbour pixels: 55 % of the shadow pixels show a larger AAI compared to their first neighbour pixels. This inconsistency is observed throughout the complete time span of the data set, which is clear from the daily mean AAI time series in the third column of Fig. 4: the daily mean AAI in the shadow pixels is higher on some days and lower on other days compared to their first neighbour pixels. Note that the number of shadow pixels is significantly smaller in the spring months in the second half of the data set, as seen in Fig. 3, which increases the uncertainty of the daily mean AAI. The fourth column of Fig. 4 shows that the histograms of the AAI difference between the shadow pixels and first neighbour pixels are approximately centred around 0 (the mean AAI difference is 0.055 ± 0.002) and are about an order of magnitude smaller than the standard deviation of the data set (σ = 0.316).

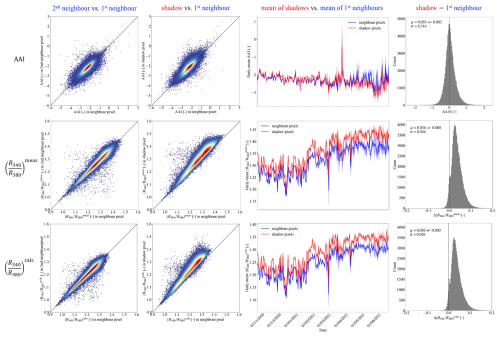
Figure 4 Comparison of the values in the second and first neighbour pixels (first column), the cloud shadow pixels and the first neighbour pixels (second column), the daily mean values of the cloud shadow pixels and the first neighbour pixels (third column), and the histograms of their differences (shadow minus first neighbour, fourth column) for the TROPOMI AAI (first row), the measured TOA reflectance ratio between 340 and 380 nm (second row), and the calculated TOA reflectance ratio between 340 and 380 nm in the AAI retrieval algorithm (third row).

The second row of Fig. 4 shows the measured TOA reflectance ratio ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$. Interestingly, although in the previous paragraph we reported no consistent cloud shadow effect on the AAI, the value of ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ in the AAI formula (Eq. 2) is consistently higher in the shadow pixels than in their first neighbour pixels: 95 % of the shadow pixels show a larger ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ compared to their first neighbour pixels. This higher reflectance ratio in the shadow pixels is observed on all days (panel in the third column and second row of Fig. 4) and clearly alters its distribution (panel in the fourth column and second row of Fig. 4). The difference of the mean ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ in the shadow pixels with respect to their neighbours is 0.036, which is larger than the standard deviation σ = 0.026. Those results imply that the measured TROPOMI UV TOA reflectances were consistently “more blue” in the shadow pixels than in the neighbour pixels.

The missing cloud shadow effect on the AAI, while TROPOMI consistently measured higher values for ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ in the cloud shadows, can be explained by the behaviour of the calculated reflectance ratio ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$. Indeed, as shown in the third row of Fig. 4, ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ is also elevated in the shadow pixels, which happens to be similar to the increase in ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$. This increase in ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ is caused by the lower retrieved scene albedo A_scene in the shadow pixels as a result of the lower measured reflectance $R_{\mathrm{380}}^{\mathrm{meas}}$ in the cloud shadows (see Eq. 4). With lower A_scene, the contribution of the (spectrally flat) Lambertian surface in the DAK model decreases, which increases the “blueness” of the calculated TOA reflectances (Eq. 3) and thus increases ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$. A similar effect on ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ can be found during solar eclipses (Trees et al., 2021). However, in contrast to cloud shadows, the lunar shadow is imposed from outside the Earth system such that the light paths in principle do not change and ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ is not altered, resulting in a strong increase in the AAI during solar eclipses. In cloud shadows, simultaneous increases in ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ and ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ lead, to the first order, to cancellations of cloud shadow effects in the AAI through Eq. (2). The explanation of the missing first-order cloud shadow effect is explained in more detail using our simulation results in Sect. 3.3.1.

The cancellation of the cloud shadow effect on the AAI is also apparent in the AAI map of a single-cloud-shadow case. Figure 5 shows maps of the AAI (first column), ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ (second column), and ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ (third column) over the Netherlands, Belgium, and north-west Germany on 3 November 2020. From Fig. 2, it was known that cloud shadows were present in this scene northward of the clouds between 6.0 and 10° E longitude. Indeed, those cloud shadows appear to have increased ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ and ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$, which is clear from the darker-blue shade compared to their cloud- and shadow-free surroundings. In the AAI map, the cloud shadows can hardly be distinguished from their surroundings.

Figure 5 Examples of the TROPOMI AAI (a), the measured TOA reflectance ratio between 340 and 380 nm (b), and the calculated TOA reflectance ratio between 340 and 380 nm in the TROPOMI AAI retrieval (c) for 3 November 2020 over the Netherlands and Germany.

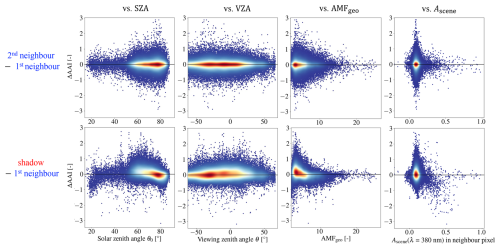
Figure 6 Similar AAI data to those in Fig. 4 but now plotted as the differences between the second and first neighbour pixels (first row) and between the cloud shadow pixels and first neighbour pixels (second row), as functions of solar zenith angle (first column), viewing zenith angle (second column), geometric air mass factor (third column), and retrieved scene albedo at 380 nm in the first neighbour pixel (fourth column).

3.2.2 Second-order cloud shadow effects

Although ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{meas}}$ and ${\left(R_{\mathrm{340}}/R_{\mathrm{380}}\right)}^{\mathrm{calc}}$ are more blue in the shadow than their surroundings in almost all cases, we found that the cancellation of cloud shadow effects in the measured AAI as discussed in the previous section is not always perfect. We investigated the dependency of the second-order cloud shadow effect on the AAI to physical parameters and found a slight dependency on the illumination and viewing geometries, as well as the surface albedo. We call those the second-order cloud shadow effects.

Figure 6 shows the AAI difference between the shadow and first neighbour pixels (bottom row) versus the solar zenith angle θ₀ (first column), viewing zenith angle θ (second column), geometric air mass factor AMF${}_{\mathrm{geo}}=\mathrm{1}/\mathit{\mu }+\mathrm{1}/{\mathit{\mu }}_{\mathrm{0}}$ (third column), and scene albedo A_scene of the first neighbour pixel (fourth column). Also, we present the differences between the second and first neighbour pixels (top row), which represent the natural AAI variation irrespective of cloud shadows. From the results in the bottom row, it can be concluded that cloud shadows tend to increase the AAI slightly for decreasing θ₀ from 80 to ∼ 50° (the mean ΔAAI is 0.18 in the shadow case between θ₀ = 50 and 70°) and for small θ (the mean ΔAAI is 0.09 in the shadow case for $\left|\mathit{\theta }\right|$ < 30°). This dependency, however, seems to be more apparent when combining θ and θ₀ in the geometric air mass factor: smaller AMF_geo gives slightly increased AAI (the mean ΔAAI is 0.14 in the shadow case for AMF_geo < 5). We count an increase of 377 px for which ΔAAI > 1 when cloud shadow pixels instead of second neighbour pixels are compared with first neighbour pixels, provided that AMF_geo < 5. This number corresponds to 0.47 % of the total number of shadow pixels. Another dependency can be measured in A_scene: bright surfaces (A_scene ≳ 0.2) tend to decrease the AAI. However, for most pixels in our data set A_scene equals approximately 0.1, for which this dependency does not seem apparent. We count an increase of 70 px for which ΔAAI < −1 when cloud shadow pixels instead of second neighbour pixels are compared with first neighbour pixels, provided that A_scene > 0.2. This number corresponds to 0.09 % of the total number of shadow pixels.

3.3 Simulated cloud shadow effects on the AAI

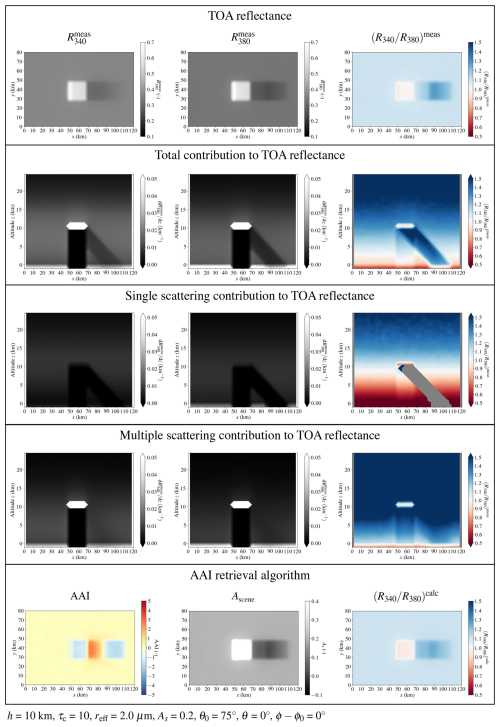
Here we present the results of the simulated cloud shadow effect on the TROPOMI AAI using our 3D radiative transfer code MONKI. We considered a box-shaped cloud with dimensions of 10 × 10 × 1 km³ consisting of spherical droplets with an effective radius r_eff of 2.0 µm and placed it at three altitudes: at 2, 5, and 10 km cloud base height h_c. Furthermore, we varied the cloud optical thickness (τ_c = 1, 5, or 10), the surface albedo (A_s = 0, 0.1, or 0.2), the viewing zenith angle (θ = 0, 30, 45, 60, or 75°), the solar zenith angle (θ₀ = 0, 30, 45, 60, or 75°), and the azimuth difference (ϕ−ϕ₀ = 0 or 180°), resulting in 1350 simulated scenes.

3.3.1 First-order cloud shadow effect

The first row of Fig. 7 shows an example of the simulated TOA reflectances that would be measured with TROPOMI at 340 and 380 nm, $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$, respectively, together with their ratio $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$, for a scene with h_c = 5 km, τ_c = 10, θ₀ = 75°, θ = 0°, and ϕ−ϕ₀ = 0° (i.e. the instrument is nadir-viewing and the Sun is located on the left side of the scene). Here, we assume a black surface (A_s = 0.0). The cloud, located at x = 48–68 km and y = 28–48 km, gives the strongest signal in both $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$ due to light multiply scattered by the rather thick cloud towards the satellite instrument, which is approximately wavelength-independent, resulting in a white appearance of the cloud ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ ≈ 1). Outside the cloudy region, the signal is more “blue” ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ > 1) due to the λ⁻⁴ dependence of the Rayleigh scattering optical thickness of the gas. In the cloud shadow, located along the right edge of the cloud, the signal of $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$ is smallest. Indeed, the “blueness” of the cloud shadow is even larger than that of the cloud- and shadow-free region ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ ≫ 1), which was also found in the observations by TROPOMI (see Sect. 3.2.1).

In order to explain the “blue” appearance of cloud shadows as seen from space, we analyse the vertical profiles of the contributions to $R_{\mathrm{340}}^{\mathrm{meas}}$, $R_{\mathrm{380}}^{\mathrm{meas}}$, and $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ in the second row of Fig. 7. In the cloud- and shadow-free region, most of the signal originates from below ∼ 15 km where the gaseous atmosphere is most dense. This signal of the background gas is larger at 340 nm than at 380 nm due to the λ⁻⁴ dependence of the Rayleigh scattering optical thickness of the gas. We note that the “colour” of the background contribution changes from “blue” ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ > 1) through “white” ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}=\mathrm{1}$) to “red” ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ < 1) with decreasing altitude, as the blue light has been scattered out of the direct beam that is incident on the lowest atmospheric layers. The contribution from the surface is equal to 0 because all the light reaching the surface is absorbed as A_s = 0.0 in this example.

Directly below the cloud, from 5 km to the surface, the contribution to both $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$ is approximately 0, as the nadir-looking instrument cannot look through the rather thick cloud. Inside the cloud shadow volume, located on the lower right side of the cloud, the contributions are indeed smaller than in the cloud- and shadow-free region but still larger than 0 (see second row of Fig. 7). Contrary to the cloud- and shadow-free contribution at those altitudes, the colour of the cloud shadow contribution is blue ($R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ > 1). Comparing the vertical profiles in the cloud- and shadow-free region (e.g. at x = 26 km) and through the cloud shadow (e.g. at x = 74 km), it can readily be concluded that a vertical integration of the contribution indeed leads to a relatively blue cloud shadow signal at TOA, thus a higher $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ in the cloud shadow than in the cloud- and shadow-free surroundings (see upper right panel in Fig. 7).

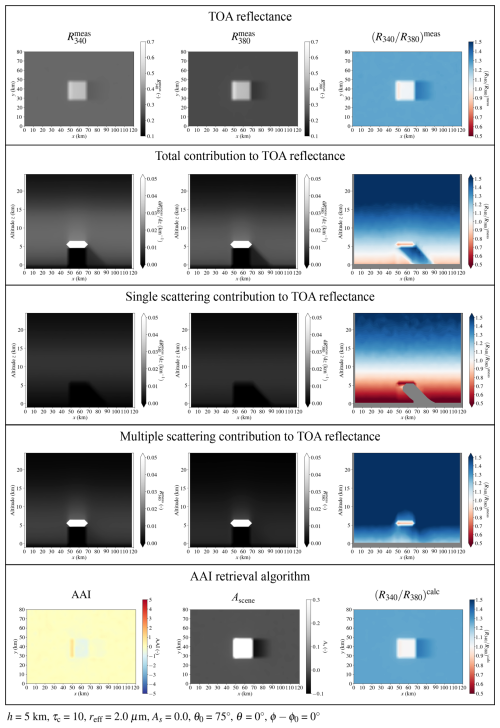
Figure 7 Simulations by MONKI of the measured TOA reflectance (top row) and the vertical profiles (in km⁻¹) of the contribution to the TOA reflectance for all photons (second row) for single scattering only (third row) and for multiple scattering only (fourth row) at 340 nm (first column), at 380 nm (second column), and for their ratio (third column). The bottom row shows the corresponding AAI (first column), the scene albedo at 380 nm (second column), and the calculated TOA reflectance ratio between 340 and 380 nm using the TROPOMI AAI retrieval algorithm (third column). The vertical profiles were made using the mean values from y = 30 km to y = 46 km. The data point below 0 km altitude represents the contribution of the surface.

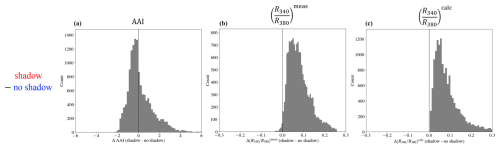
Figure 8 Histograms of the differences in the simulated values by MONKI between cloud shadow pixels and cloud- and shadow-free pixels for the AAI (a), the measured TOA reflectance ratio between 340 and 380 nm (b), and the calculated TOA reflectance ratio between 340 and 380 nm using the TROPOMI AAI retrieval algorithm (c) for all 1350 simulated scenes. The total count is higher than the number of scenes because a scene can have multiple cloud shadow pixels.

We investigated the cause of the non-zero and blue contribution of the cloud shadow volume by separating the vertical profiles of the contributions from single scattering only (third row of Fig. 7) and of multiple scattering only (fourth row of Fig. 7). Note that the sum of those contributions is again the total contribution as shown in the second row of Fig. 7. In the cloud shadow, there is no contribution from single scattering in our simulation, as shown by the black shades in the contributions to $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$, as well as the undefined values in the contribution to $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$. Apparently, all photons were scattered away from the direct beam passing through the cloud before reaching the cloud base. In multiply scattered light, however, photons can reach the cloud shadow volume after being scattered by the gas in the cloud- and shadow-free region, as illustrated by the non-zero values in the cloud shadow in the fourth row of Fig. 7. Also, it should be noted that, regardless of cloud shadows, the signal from multiple scattering is more blue than that of single scattering (see third and fourth rows of Fig. 7). Thus, because in cloud shadows the singly scattered light is intercepted and the multiply scattered light is left and because the multiply scattered light is more blue than singly scattered light, the appearance of cloud shadows is relatively blue (second row).

Finally, we computed the AAI that would be retrieved from our simulated TOA reflectances; i.e. we used the simulated $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$ as input for the TROPOMI AAI retrieval algorithm (see Sect. 2.2). The last row of Fig. 7 shows the retrieved AAI, A_scene(380 nm), and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$. In the cloud- and shadow-free region the simulated AAI equals 0, since $R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{calc}}$ are virtually identical due to the excellent agreement between MONKI and DAK for clear-sky scenes. In the cloud shadow, the AAI is also approximately 0, but A_scene(380 nm) appears dark as a direct result of the lower $R_{\mathrm{380}}^{\mathrm{meas}}$ (see Eq. 4). Note that for this scene with a black surface, the retrieved A_scene(380 nm) is even negative in the cloud shadow (it should be noted that a negative albedo is non-physical and a result of the AAI algorithm, as explained in Sect. 2.2). Consequently, the calculated (spectrally flat) surface contribution to $R_{\mathrm{340}}^{\mathrm{calc}}$ is relatively small in the cloud shadow and is negative, resulting in a relatively large and blue contribution from the path reflectance R⁰ (see Eq. 3). Indeed, $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ is enhanced in the cloud shadow, as shown in the last row of Fig. 7. Because cloud shadows are more blue in both R^calc and R^meas (note that the panels of $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ and $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ look approximately identical in Fig. 7), there is no visible cloud shadow signature in the AAI (lower left panel in Fig. 7). In conclusion, the AAI retrieval already automatically corrects for cloud shadows via the lower retrieved scene albedo, which is in agreement with the first-order cloud shadow effect that we found in the TROPOMI observations (Sect. 3.2.1).

We note that at the opposite side of the cloud, the AAI is slightly increased in our simulations (AAI ∼ 1). This increase is found on the cloud itself at x = 50 km, where the cloud is directly illuminated by the Sun from the side. We speculate that this result demonstrates the positive TROPOMI AAI signatures at the bright side of vertical cloud structures at high latitudes that were found by Kooreman et al. (2020) (see their Figs. 1 and 2). Numerical experiments indeed showed that an increase in the cloud vertical extent from 1 to 5 km further increased this positive AAI signature. Because the scope of our article is the analysis of shadows, we leave the analysis of the bright side of clouds for future research.

In the previous paragraphs of this section, we discussed the results of one simulated scene. As mentioned in the beginning of this section, we did those simulations for 1350 scenes. Figure 8 shows the difference between the AAI in the simulated shadow pixels and the AAI in the cloud- and shadow-free regions of all simulated scenes. In addition, we show those differences for $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$. For almost all cases (99 % and 100 % for the measured and calculated values, respectively), indeed the cloud shadow pixels are more blue than their cloud- and shadow-free surroundings, and $\mathrm{\Delta }{R}_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}=\mathrm{0.079}$ and $\mathrm{\Delta }{R}_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}=\mathrm{0.086}$. The consistent enhanced blueness in both R^calc and R^meas resulted in a mean AAI difference close to zero (ΔAAI = 0.16, while σ = 1.2), showing that, on average, cloud shadow effects are approximately cancelled out in our simulated data set. In Fig. 9 we summarize the cancellation of cloud shadow effects in the AAI with a conceptual model.

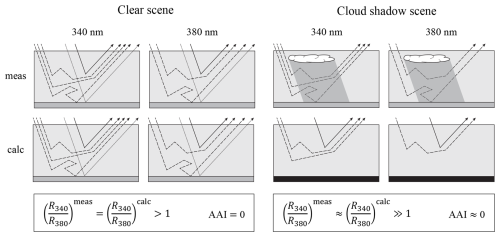
Figure 9 Sketches explaining the first-order cloud shadow effect on the absorbing aerosol index (AAI). The top and bottom sketches are for the measured (meas) and the calculated (calc) top-of-atmosphere (TOA) reflectances, respectively. The left four sketches are for the clear case (i.e. without clouds and shadows), and the right four sketches are for the cloud shadow case, where the first row is for 340 nm and the second row for 380 nm. Solid arrows indicate singly scattered light, dashed arrows indicate multiply scattered light, and dotted arrows indicate light reflected once by the surface. The number of arrows leaving TOA illustrate the magnitude of the respective TOA reflectance. The AAI retrieval algorithm automatically assumes a dark surface when the measured reflectance is low due to the shadow (Eq. 4), as illustrated by the black shaded surface area. Because cloud shadows increase the ratio of the TOA reflectance at 340 nm with respect to 380 nm in both the measurements and the retrieval algorithm calculations by approximately the same amount, the AAI is more or less unaffected (Eq. 2).

3.3.2 Second-order cloud shadow effects

Although the simulated average AAI difference between pixels inside and outside the cloud shadow is close to 0, in some cases the cloud shadows leave signatures in the simulated AAI. This can be concluded from the negative and positive tails of the ΔAAI histogram in Fig. 8, indicating that the cancellation was not always perfect and could have values of several AAI points. Those imperfect cancellations, while both R^calc and R^meas are both more blue in the cloud shadow, were also found in the observations (Sect. 3.2.2). They are the second-order cloud shadow effects.

In the TROPOMI observations (Sect. 3.2.2) we found a slight dependency of the second-order cloud shadow effects on geometric air mass factor and surface albedo (through the scene albedo of the first cloud- and shadow-free neighbour). We did not analyse the dependency on cloud parameters in the observations because our cloud shadow detection algorithm DARCLOS does not allow for a precise determination of the clouds responsible for certain cloud shadows. Figure 10 shows $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ for all shadow pixels in our simulated scenes, grouped per cloud height (upper left), cloud optical thickness (upper right), geometric air mass factor (lower left), and surface albedo (lower right). Data points on the symmetry line $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}=R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ are related to an AAI of 0 (see Eq. 2), just as in the cloud- and shadow-free region in our simulations, and to a perfect cancellation of cloud shadow effects. Data points in the regions for which $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}>R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ and $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}<R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ result in cloud shadow signatures with negative and positive AAIs, respectively. Regardless of the grouping of the data points, Fig. 10 demonstrates that the strongest positive AAI cloud shadow signatures are caused by the bluest shadows: when $R_{\mathrm{340}}/R_{\mathrm{380}}$ ≳ 1.4, the data points deviate towards the right from the symmetry line. The negative AAI signatures seem to be caused by cloud shadows with $R_{\mathrm{340}}/R_{\mathrm{380}}$ ≲ 1.4.

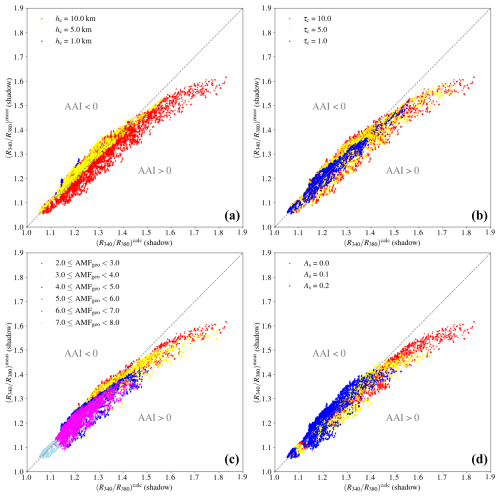
Figure 10 Analysis of the simulated measured and calculated TOA reflectance ratios between 340 and 380 nm for the 1350 simulated scenes with MONKI. The results are grouped per cloud height (a), cloud optical thickness (b), geometric air mass factor (c), and surface albedo (d).

Figure 10 (upper left) shows that the strong positive AAI cloud shadow signatures are primarily caused by high clouds (h_c = 10 km). Note that the low-cloud group (h_c = 1 km) only contains a few data points because for viewing and/or illumination geometries that are too small, the size of the cloud shadow is too small to be visible from space. Figure 10 (upper right) shows that the thick clouds (τ_c = 10) give stronger (negative and positive) AAI cloud shadow signatures than thin clouds (τ_c = 1). Figure 10 (lower left) shows that the AAI cloud shadow signatures tend to become more positive with decreasing geometric air mass factor, which was also found in the TROPOMI observations (see Fig. 6). Figure 10 (lower right) shows that the AAI cloud shadow signatures tend to become more negative with increasing surface albedo, which is also consistent with the TROPOMI observations.

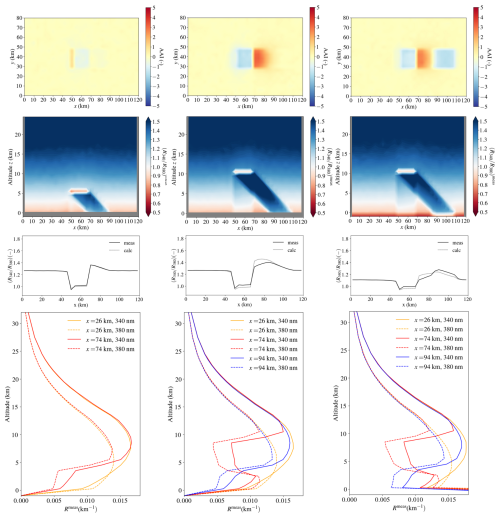
Figure 11 Simulations by MONKI of the AAI (first row), vertical profiles of the simulated altitude-dependent $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ TOA contribution (second row), cross-sections of $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ at TOA (third row), and the vertical profiles of the TOA contributions of $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$ (fourth row) at x = 26 km (unshadowed region), x = 74 km (atmosphere shadow), and x = 94 km (surface shadow). The scene parameters in the first column are similar to those in Fig. 7: h = 5 km, τ_c = 10, r_eff = 2.0 µm, A_s = 0.0, θ₀ = 75°, θ = 0°, φ−φ₀ = 0°. In the second row, h was modified to 10 km. In the third row, in addition A_s was modified to 0.2. The vertical profiles were made using the mean values from y = 30 km to y = 46 km. The data point below 0 km altitude represents the contribution of the surface.

The explanation of the positive second-order cloud shadow AAI signature can be found by analysing the differences in the shadow simulation results between a low and high cloud. Figure 11 shows a top view of the AAI (first row), vertical profiles of the simulated altitude-dependent $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ contribution (second row), cross-sections of $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ at TOA (third row), and the vertical profiles of the contributions of $R_{\mathrm{340}}^{\mathrm{meas}}$ and $R_{\mathrm{380}}^{\mathrm{meas}}$ at several locations for x (fourth row). The left column shows the results again for a cloud at 5 km altitude (similar to those in Fig. 7), while in the middle column the cloud is raised to an altitude of 10 km. For this higher cloud, the AAI is increased by up to ∼ 3 points in the shadow but only close to the cloud (x = 74 km) where the shadow is located in the atmosphere above ∼3 km altitude. Here, more light is being intercepted than at lower altitudes, since the contribution to the TOA signal in the shadow-free background (x = 26 km) at these higher altitudes is larger than close to the surface (see orange lines in the bottom panels in Fig. 11). Hence, A_scene is much darker than for the low cloud at x = 74 km, which strongly increases $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ (see Sect. 2.2). Also, $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ is larger for this shadow at higher altitudes, as multiple-scattering contributions at those higher altitudes are more blue (see fourth row in Fig. 7) and the shadow only contains multiply scattered light (see Sect. 3.3.1). However, the latter effect on the vertically integrated signal is relatively weak because the single-scattering background contribution that is being intercepted is also more blue at higher altitudes than at lower altitudes (see third row in Fig. 7), which suppresses the increase in measured blueness of the high shadow as seen from space. The suppression of the increase in measured shadow blueness is most effective at small geometric AMF, for which the vertical profiles of the single-scattering background contribution are more blue due to the relatively short path lengths (not shown) and because the contribution peaks at lower altitudes (i.e. the lower atmosphere, where the shadows usually occur, are better visible from space). Consequently, the positive second-order cloud shadow signature increases with decreasing geometric AMF. In summary, both $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ at TOA are larger for shadows located higher in the atmosphere, but $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ increases more strongly with altitude than $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$, causing the AAI to become positive according to Eq. (2).

The explanation of the negative second-order cloud shadow AAI signature can be found by increasing the surface albedo A_s from 0 to 0.2 (see third column in Fig. 11 and Fig. A1 in the Appendix for more detailed simulation results). Without shadows, wavelength-independent Lambertian surface reflection makes the signal at TOA stronger but more “white”, resulting in both smaller $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ (see upper and lower right panels, respectively, in Fig. A1) and a neutral effect on the AAI (see de Graaf et al., 2005) (see lower right panel in Fig. A1). In our simulations, at a relatively large distance from the cloud where the shadow is cast on the surface (at x = 94 km), the AAI is decreased by ∼ 1.5 points. Here, incident light on the surface is being reflected, resulting in a larger TOA reflectance compared to that in the black-surface case. Consequently, A_scene in the AAI retrieval is higher (see bottom middle panel in Fig. A1) such that the Lambertian surface in the DAK model reflects more direct and scattered light, which relatively decreases $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$. However, in reality in the cloud shadow on the surface at x = 94 km, the surface only reflects light that has been scattered before at least once (see third row in Fig. A1). Because the multiply scattered light contribution is more blue (see fourth row in Fig. A1) than that of singly reflected light by the surface in the background, the measured surface shadow is relatively blue, which increases $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$. In summary, the Lambertian surface reflection decreases both $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ in the cloud shadow cast on the surface, but because the decrease in $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ is stronger, the AAI becomes negative.

4 Discussion and conclusion

The cancellation of cloud shadow effects on both the measured and simulated TROPOMI AAI (Sect. 3.2 and 3.3, respectively) shows that the traditional AAI retrieval by itself already (partly) corrects for cloud shadows via the retrieved scene albedo. Simultaneously, through measurements and simulations we found that cloud shadows are almost always more blue than cloud- and shadow-free regions. If the traditional AAI retrieval would not correct for this enhanced blueness, strong cloud shadow signatures could have been expected in the AAI. But, due to the automatic cancellation, the average AAI difference between shadow and non-shadow cases is close to zero. We note that other TROPOMI products that depend on the pixel blueness, such as the aerosol optical thickness (AOT) (de Graaf, 2022), may be affected by cloud shadows, but that was not studied in this paper.

We have shown that, for individual cases in the measurements and in the simulations, the blueness of the cloud shadows is not always perfectly compensated for by the lower scene albedo in the AAI retrieval. This results in second-order cloud shadow effects which sometimes yield lower, and sometimes higher, AAI than in the cloud- and shadow-free regions. In the observations, we found weak positive and negative relations of those second-order cloud shadow effects to the geometric air mass factor and surface albedo, respectively. Our simulations indeed demonstrated that positive AAI cloud shadow signatures can mostly be related to high, thick clouds with a small geometric air mass factor above dark surfaces, while negative AAI cloud shadow signatures should be most prominent near thick clouds above bright surfaces. In the observations, 0.47 % and 0.09 % of the shadow pixels show an absolute AAI difference larger than 1 with respect to their cloud- and shadow-free neighbours that can be attributed to the cloud shadow when selecting data with AMF_geo < 5 and A_scene > 0.2, respectively. We did not specifically select scenes that also include absorbing aerosol for this paper. We note that only 0.01 % of the shadow pixels may also contain absorbing aerosols (based on an AAI > 0.8 threshold for the cloud- and shadow-free neighbour pixels; see de Graaf, 2022).

Our simulations thus suggest that a potential correction of the second-order cloud shadow effects on the AAI should depend on cloud height, optical thickness, surface albedo, and geometric air mass factor. However, the height and thickness of the clouds responsible for the measured cloud shadows are uncertain. That is because, although the cloud height is a TROPOMI product (e.g. FRESCO; see Koelemeijer et al., 2001; Wang et al., 2008), the cloud height product has a limited accuracy (the cloud height obtained with FRESCO is in fact the cloud centroid height) and the optical thickness and vertical extent of the clouds are not retrieved. Moreover, the clouds responsible for certain cloud shadows are difficult to determine in the observations. The responsible clouds are not an output of DARCLOS, as DARCLOS uses spectral tests to determine the cloud shadow flags in the final step of its algorithm. Additionally, the accuracy of a “reverse calculation” of the responsible cloud (height) would never be better than the ∼ 4 km spatial resolution of TROPOMI in the nadir-viewing direction, and again the cloud optical thickness and vertical extent would be unknown. Hence, we conclude that a reliable correction method for the second-order cloud shadow effects on the TROPOMI AAI would be complicated. Moreover, because of the automatic cancellation of the cloud shadow effects to the first order, such a correction method may not be needed.

For this study, we have developed the 3D radiative transfer code MONKI which successfully simulated the effect of cloud shadows on the TROPOMI AAI. MONKI fully takes into account the polarization of light for all orders of scattering and can store the vertical profiles of the altitude-dependent reflected light contribution at TOA for the total, singly, and multiply scattered light. In future research, MONKI can be used to find explanations of more cloud effects on sensitive retrieval algorithms, such as the AAI algorithm, in which polarization and geometry play an important role. For example, the positive AAI increases at the bright side of clouds that are found in both our simulations and previous observations, can be further analysed using the MONKI model.

Appendix A: MONKI simulations of a shadow cast on a reflecting surface produced by a high cloud

Figure A1 shows the MONKI output results as in Fig. 7 but also for a high cloud (h = 10 km) above a reflecting Lambertian surface (A_s = 0.2). Although cloud shadows in the atmosphere and on the surface are more blue than their shadow-free surroundings in both $R_{\mathrm{340}}^{\mathrm{meas}}/R_{\mathrm{380}}^{\mathrm{meas}}$ and $R_{\mathrm{340}}^{\mathrm{calc}}/R_{\mathrm{380}}^{\mathrm{calc}}$ (first-order effect), the blueness is not increased equally, resulting in a positive AAI signature of ∼ 2.5 in the atmosphere close to the cloud at x = 74 km and a negative AAI signature of ∼ −1.5 in the shadow cast on the surface at x = 94 km (second-order effects).

Figure A1 Similar to Fig. 7 but for h = 10 km and A_s = 0.2.