On the distortions in calculated GW parameters during slanted atmospheric soundings

The significant distortions introduced in the measured atmospheric gravity wavelengths by soundings other than those in vertical and horizontal directions, are discussed as a function of the elevation angle of the sounding path and the gravity wave aspect ratio. Under- or overestimation of real vertical wavelengths during the measurement process depends on the value of these two parameters. The consequences of these distortions on the calculation of the energy and the vertical flux of horizontal momentum are analyzed and discussed in the context of two experimental limb satellite setups: GPS-LEO radio occultations and TIMED/SABER ((Atmosphere using Broadband Emission Radiometry/Thermosphere–Ionosphere–Mesosphere–Energetics and Dynamics)) measurements. Possible discrepancies previously found between the momentum flux calculated from satellite temperature profiles, on site and from model simulations, may to a certain degree be attributed to these distortions. A recalculation of previous momentum flux climatologies based on these considerations seems to be a difficult goal.

1 Introduction

In the last few years, we have observed the ongoing development of several techniques to sound the lower, middle and upper atmosphere (e.g. Wu and Waters, 1996; Tsuda et al., 2000; Preusse et al., 2002; Alexander et al., 2011; Hertzog et al., 2012; John and Kumar, 2013; Lieberman et al., 2013; Oliver et al., 2013; Alexander, 2015; de Wit et al., 2017). The advantages and disadvantages of each choice are clearly distinguishable among the available rocket-, balloon- and satellite-borne instruments, as well as radar and lidar ground-based devices. Regarding the retrieval of information on atmospheric dynamics from satellite measurements, we know that both satellite limb and nadir observing techniques are needed to resolve different parts of the gravity wave (GW) spectrum (Wu et al., 2006) and that a better understanding of GW complexities requires joint analyses of these data and high-resolution model simulations. The global observation of the atmosphere and the ionosphere using limb or nadir sounding paths, makes it possible to obtain vertical profiles of refractivity, density, temperature (T), pressure, water vapor content and electron density, which is a remarkable achievement considering the available experimental resources.

One of the main objectives pursued by current observations is the permanent improvement required for the understanding of GW sources of generation (such as flow over topography, convection, and jet imbalance), as well as their propagation, breaking and dissipation around and above the tropopause, forcing atmospheric circulation. This knowledge is needed in the sub-grid parameterizations in global models for climate and weather forecasting applications, in order to simulate the influence of orographic and non-orographic GWs and produce realistic wind and temperature (e.g. Fritts and Alexander, 2003; McLandress and Scinocca, 2005; Kawatani et al., 2009; Alexander et al., 2010; Shutts and Vosper, 2011; Geller et al., 2013). In these parameterizations, some parameters describe the global distributions of GW vertical flux of horizontal momentum (MF), as well as their wavelengths and frequencies. Until recently, the necessary parameters could not be determined through global observations, because the waves are small in scale and intermittent in occurrence. The parameterizations compute a momentum forcing term by making assumptions about the unresolved wave properties that have not been properly constrained by observations. The assumptions are formulated as a set of tuning parameters that are used to adjust the circulation and temperature structure in the upper troposphere and middle atmosphere (Alexander et al., 2010).

Among recently developed sounding devices, global positioning system (GPS) radio occultation (RO) is a well-established technique for obtaining global GW activity information. RO uses GPS signals received by low Earth-orbiting (LEO) satellites for atmospheric limb sounding. T profiles are derived with high vertical resolution and provide global coverage under any weather condition, offering the possibility to carry out the global monitoring of the vertical T structure and atmospheric wave parameters. Several authors have contributed to global analyses of horizontal and vertical GW wavelengths, specifically potential energy and MF distribution (Tsuda et al., 2000; de la Torre et al., 2006; Wang and Alexander, 2010; Faber et al., 2013; Schmidt et al., 2016; Alexander et al., 2015). In particular, Alexander et al. (2008) (A08) stated that it is not possible to fully resolve GW from RO measurements because there are different kinds of distortions. In each occultation, the outcome depends on wave characteristics (essentially wavelengths and amplitude), the line of sight (LOS) and the line of tangent points (LTP), both with respect to the phase fronts to be detected. Ideal conditions for accurate wave amplitude extraction in occultation retrievals are given by quasi-horizontal wave phase surfaces or when the LOS and LTP are nearly contained and out of those planes. Short horizontal scale waves are weakened or even filtered out with high probability. Another result from A08 is that the detected vertical wavelengths will always differ from the original ones, but only the presence of inertio-GWs, which have nearly horizontal constant phase surfaces, will ensure small discrepancies. They concluded that extreme caution is needed when addressing the issues of amplitude, wavelength and phase of gravity waves in occultation data. Some years before A08, de la Torre and Alexander (1995) (TA95) already observed and established analytically the discrepancies to be expected between measured and real horizontal and vertical wavelengths during balloon soundings, taking into account the motion of the gondola with respect to the constant GW phase surfaces. This analysis was performed both from the intrinsic and the ground frame of reference.

In Sect. 2, we analyze the distortion to be expected in the detection of real vertical and horizontal wavelengths from almost instantaneous soundings. These are different from vertical and horizontal, specifically for satellite measurements. In Sect. 3, the consequences of this distortion in the calculation of GW energy and MF are discussed. In Sect. 4, the implications of using two different satellite setups are considered in some detail. In Sect. 5, some conclusions are outlined for future applications and a possible careful reconsideration of some results and conclusions obtained in previous climatologies is suggested.

2 GW wavelengths distortion

From TA95 and A08, it is clear that when an on-site or remote sensing instrument sounds the atmosphere along a given direction, which is different from the vertical or the horizontal plane, the measured vertical and horizontal wavelengths are expected to considerably differ from “real” (or “actual”) values. In the Appendix from TA95, (1) a stationary GW observed from (2) a ground-fixed frame of reference (Fig. A1 and Eqs. A1–A5) was specifically considered. Now, it may be accepted that both these conditions are emulated by GPS-LEO RO (e.g. Kursinski et al., 1997), as well as by TIMED–SABER (atmosphere using broadband emission radiometry and thermosphere–ionosphere–mesosphere energetics and dynamics) (Russell et al., 1999) measurements (see below Sect. 4). In relation to the first condition, we may assume that satellite-based soundings yield T profiles almost instantaneously. Following this reasoning, the vertical “real” and “apparent” (or measured) wavelengths (λ_z and ${\mathit{\lambda }}_z^{\text{ap}}$, respectively) are related by the following expression (TA95, Eqs. A3–A5):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }{\mathit{\lambda }}_Z^{\text{ap}}={\displaystyle \frac{{\mathit{\lambda }}_Z}{\text{abs}\left(\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)\right)}},\end{array}$$

where α is the elevation angle defined by a straight sounding path direction and the horizontal plane. In turn, cot (ψ) is the ratio between the horizontal wavenumber vector (k_H) projected on the vertical α-plane and the vertical wavenumber k_Z (Fig. 1). The ratio (k_H∕k_Z) is also known as the GW aspect ratio. Figure 1, with two arbitrary successive GW phase surfaces, φ₁ and φ₂, cutting α plane defined, show a clear difference between real and apparent vertical (and horizontal) wavelengths. This distortion, frequently present in radiosoundings or satellite-based GW studies, is in general non-negligible and affects the calculation of all magnitudes requiring previous identification of wave parameters.

Here we recall that cot (α) is equal to the ratio between ${\mathit{\lambda }}_H^{\text{ap}}$ and ${\mathit{\lambda }}_Z^{\text{ap}}$, and this result will be used below. A similar relation to Eq. (1) may be derived between horizontal real and apparent wavelengths, from Eqs. (A3) to (A6) in TA95. The resulting relation is as follows (not shown in TA95):

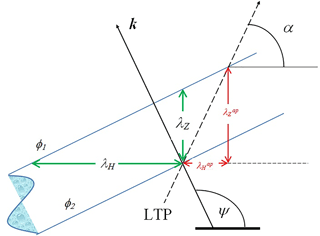
Figure 1 Vertical α-plane defined by the elevation angle between the sounding path direction and its projection on the horizontal plane. Real and apparent, vertical and horizontal wavelengths are indicated. φ₁ and φ₂ represent two arbitrary successive constant phase surfaces belonging to a monochromatic GW (see text). The expected distortion from real to apparent wavelengths, is seen.

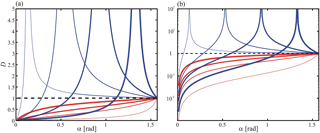
Figure 2 (a) Examples of the distortion in $D={\mathit{\lambda }}_Z^{\text{ap}}/{\mathit{\lambda }}_Z$, as a function of α, leaving a parametric dependence with ψ (see text). Arbitrary constant and progressive ψ values within the interval [0,π] rad are shown. Underestimation of λ_Z occurs when $(D<\mathrm{1})\mathit{\psi }=\mathrm{0.1}$, 0.5, 0.9, 1.3 rad (curves with increasing thickness, from thin red to thickest red). Overestimation of λ_Z occurs when D>1 and ψ=1.7, 2.1, 2.5 and 2.9 rad (thin blue to thickest blue curves). Note that the upper blue branches for $\mathit{\psi }>\mathit{\pi }/\mathrm{2}$ diverge at singular values. This is better appreciated in (b). The horizontal dashed line corresponds to the “non distortion” case. Considerable general departures from this non distortion limit (D=1) are seen. (b) The same content as in (a), here in linear-log axes.

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{\mathit{\lambda }}_H^{\text{ap}}={\displaystyle \frac{{\mathit{\lambda }}_H}{\text{abs}\left(\mathrm{1}+\tan \left(\mathit{\alpha }\right)\tan \left(\mathit{\psi }\right)\right)}}.\end{array}$$

We should mention that λ_H is real but may not be the true horizontal wavelength, as information must be sampled along two different horizontal directions in order to be able to calculate it (e.g. Faber et al., 2013; Schmidt et al., 2016). We will now focus on the consequences derived from the expected distortion in k_Z or in λ_Z. As is known, in global atmospheric models the subgrid parameterization of GW energy and MF is based on a successful identification of GW parameters, after proper processing of T profiles. The effects of GW on large-scale circulation have been treated via parameterizations in both climate and weather forecasting applications. In these parameterizations, key parameters describe a global distribution of MF, GW wavelengths and frequencies (e.g. Alexander et al., 2010).

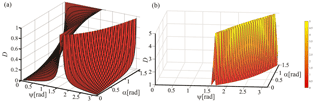
Figure 3 (a) 3-D perspective of the distortion D shown in Fig. 2, as a function of ψ and α, for underestimations of λ_Z. (b) The same as in (a), for overestimations of λ_Z. Black lines in this figure are only intended to make easier a visual appreciation of the curved nature of the surfaces. The color bar illustrates D values in both plots for intervals [0,1] and [1,5] respectively.

Equation (1) provides the magnitude of the expected departure in ${\mathit{\lambda }}_Z^{\text{ap}}$ from λ_Z, for each monochromatic GW component, within a given wave ensemble at any atmospheric region. In order to better understand this distortion, we will consider this equation as parametric in α or ψ. As stated above, both independent parameters are simple trigonometric functions of the apparent and real (and horizontal or vertical) wavenumber components ratio, respectively. The angle α only depends on the sounding path direction during the observation process through progressive atmospheric layers, and ψ, on the GW direction of propagation, k∕k. Here, k and k are the wavenumber vector and its absolute value, respectively. We note here that Eq. (1) is symmetric with respect to α and ψ, which are in turn, totally unrelated. For example, in the case of GPS-LEO RO measurements (to be considered below in Sect. 4), α represents the angle defined by the line of tangent points (LTP) and the horizontal plane. In Fig. 1, an arbitrary segment of LTP is roughly represented by a straight line. In this figure we observe, for example, that a vertical sounding of the atmosphere in the nadir direction (i.e. lidar measurements or balloon measurements under zero wind conditions) will produce no distortion at all in k_Z or in λ_Z. The same can be said for horizontal soundings producing no distortions in k_H or in λ_H belonging to the α-plane.

In Fig. 2, we define the distortion as the ratio:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }D={\displaystyle \frac{{\mathit{\lambda }}_Z^{\text{ap}}}{{\mathit{\lambda }}_Z}}.\end{array}$$

Following Eq. (1), D may be equivalently represented as a function of α leaving ψ as a parameter, or vice versa, making use of the symmetric dependence on both of them. We first describe this function in terms of α in Fig. 2a and b. For illustration, we show the variation of D for increasing selected values of ψ between 0 and π rad. Note that the underestimation of λ_Z occurs when (D<1) ψ=0.1, 0.5, 0.9, 1.3 rad and the overestimation of λ_Z occurs when $(D>\mathrm{1})\mathit{\psi }=\mathrm{1.7}$, 2.1, 2.5 and 2.9 rad. For each ψ value, a singular α value associated to two upper diverging branches is seen. This is better appreciated in Fig. 2b. The horizontal dashed line corresponds to the “non-distortion” D=1 case. Considerable departures from this non-distortion limit are seen. Note that the functional behavior of D is non-symmetric for ψ greater than and less than π∕2 rad. Also, notice that all possible sounding and wave orientations are covered by defining one of the angles between 0 and π∕2 rad and the other one between 0 and π rad.

From the above arguments, we can conclude that for a given GW ensemble, a net significant distortion of the measured spectra should be expected. This net distortion will become more or less significant, depending on (i) the composition of the ensemble and (ii) the specific measuring device. In the next section we will illustrate this argument for the case of satellite-borne measurements. A 3-D plot presents better the functional dependence of D with ψ and α already shown in Fig. 2a and b, now separately for under- and overestimations of λ_Z, below and above the plane D=1 (Fig. 3a and b respectively).

The 3-D plot shows the complete variability of D for a between 0 and π∕2 and ψ between 0 and π. For any fixed ψ value, starting at α=0, each D curve increases from zero, crosses the D=1 boundary diverging at a given α value, located (after/before) π∕2 depending on ψ is (less/greater) than π∕2 and decreases again to zero, as α approaches the π limit. Due to the symmetric dependence of D with both parameters, to avoid a possible confusion and redundancy, in Fig. 2 it seems enough to show the D variability for α between 0 and π∕2.

3 GW energy, spectra and momentum flux

The computation of the specific potential energy per unit mass, Ep, for a GW ensemble, is given by the following equation:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }\mathrm{Ep}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{g}{N}}\right)}^{\mathrm{2}}\stackrel{\mathrm{‾}}{{\left({\displaystyle \frac{\widehat{T}}{T_{\mathrm{0}}}}\right)}^{\mathrm{2}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{g}{N}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{z_{\mathrm{2}}-z_{\mathrm{1}}}}\underset{Z_{\mathrm{1}}}{\overset{Z_{\mathrm{2}}}{\int }}{\left({\displaystyle \frac{\widehat{T}}{T_{\mathrm{0}}}}\right)}^{\mathrm{2}}\mathrm{d}z,\end{array}$$

where z₁ and z₂ are the minimum and maximum altitudes for integration, g is the acceleration due to gravity, N is the buoyancy frequency, $\widehat{T}$ and T₀ are the perturbation amplitude and background temperature, respectively, and the overbar indicates a space averaging process. This average must be performed for the GW ensemble considered, over at least one wavelength corresponding to the GW mode with the largest amplitude in any direction (i.e. horizontal, slanted or, as usually, vertical). Consistently, different choices of this direction involving the same ensemble should ideally yield identical results. Alternatively, the average may be also performed over a time interval at a fixed point, considering a general non-stationary ensemble of GW. In this case, the net contribution of stationary waves would be obviously underestimated. In addition, we recall that the computation of instantaneous Ep at fixed points is sometimes reported without the corresponding averaging process, but we consider that this procedure lacks a clear, physical sense.

In Eq. (4) we must have previously removed the noise and long scale structures from the T profiles. The remaining GWs should include amplitudes expected to significantly contribute to Ep. The vertical interval for integration is usually about 10 km. But, depending on α, ψ_i and the azimuth of each one of the dominant modes in the GW ensemble, some waves may not be contained for at least one complete cycle within the integration interval. Then, the integral in Eq. (4) may not include at least one full wavelength from all of these dominant modes. As a result, the individual contribution of each mode to the net Ep will be under- or overestimated to a significant extent.

To extend these considerations to a quite realistic scenario, let us consider a particular modeled distribution of GW vertical wavelengths, selected among the numerous theories developed and based on diverse experimental setups, after the seminal paper by Dewan and Good (1986) (e.g. Smith et al., 1987; Hines, 1991; Fritts and Alexander, 2003; Yiğit et al., 2017, and references therein). It has been observed and broadly assumed that part of a GW spectrum (the larger vertical wavenumbers) is saturated beyond a given characteristic $k_Z^C$ value that decreases with increasing altitude. Smaller wavenumbers than $k_Z^c$ are not expected to be saturated and their amplitudes increase with increasing altitude. One example of the spectral models proposed to describe energy density, E, assumes its separability as the product of three functions A, B and C, depending respectively on the vertical wave number, the intrinsic frequency, ω, and the azimuthal direction of propagation, Φ (Fritts and VanZandt, 1993) as follows:

$$\begin{array}{ll}{\displaystyle }\mathrm{Ep}\left(k_Z,\mathit{\omega },\mathrm{\Phi }\right)& {\displaystyle }=A\left(k_Z\right)B\left(\mathit{\omega }\right)C\left(\mathrm{\Phi }\right)\\ \text{(5)}& {\displaystyle }& {\displaystyle }=A_{\mathrm{0}}{\displaystyle \frac{\mathrm{1}}{\frac{k_Z^c}{k_Z}+{\left(\frac{k_Z}{k_Z^c}\right)}^{\mathrm{3}}}}B\left(\mathit{\omega }\right)C\left(\mathrm{\Phi }\right).\end{array}$$

In the above form, A(k_Z) takes into account the requirement of a positive slope (to get a finite vertical energy flux) at small wavenumbers and the proposed $k_Z^{-\mathrm{3}}$ dependence at large wavenumber values. This “universal model” has been the subject of several objections and variations in the last three decades (see e.g. Fritts and Alexander, 2003). Note that a given Ep distribution like Eq. (5) is obtained based on an experimental setup (for example, the parameters may be derived after an analysis of COSMIC GPS RO T data). Consistently, k_Z as well as $k_Z^C$ should then be considered apparent values, estimated after a spectral analysis (e.g. Tsuda et al., 2011). For vertical (i.e. lidar) soundings, apparent and real parameters are indistinguishable. Following this argument, expressed as follows:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{k_Z^{\text{ap}}}_{(\mathrm{1},\mathrm{2})}=k_{Z(\mathrm{1},\mathrm{2})}{\left[\text{abs}\left(\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)\right)\right]}^{-\mathrm{1}},\end{array}$$

we consider Eq. (5) with $k_Z^{\text{ap}}$ instead of k_Z and $k_Z^{C\text{, ap}}$ instead of $k_Z^C$ to quantitatively illustrate the distortion in Ep and (below) in MF, derived from the misinterpretation between real and apparent parameters. In doing so, the GW energy contained in a given vertical wavenumber interval $\mathrm{\Delta }{k}_z^{\text{ap}}$ is as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{Ep}}_{\mathrm{\Delta }{k}_Z}^{\text{ap}}=A_{\mathrm{0}}B\left(\mathit{\omega }\right)C\left(\mathrm{\Phi }\right)\underset{k_{Z\mathrm{1}}^{\text{ap}}}{\overset{k_{Z\mathrm{2}}^{\text{ap}}}{\int }}{\displaystyle \frac{\mathrm{1}}{\frac{k_Z^{c,\text{ap}}}{k_Z^{\text{ap}}}+{\left(\frac{k_Z^{\text{ap}}}{k_Z^{c,\text{ap}}}\right)}^{\mathrm{3}}}}\mathrm{d}{k}_Z^{\text{ap}}\\ \text{(7)}& {\displaystyle }& {\displaystyle }=A_{\mathrm{0}}B\left(\mathit{\omega }\right)C\left(\mathrm{\Phi }\right)\left[{\displaystyle \frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{2}}^{{\text{ap}}^{\mathrm{2}}}}{k_Z^{c,{\text{ap}}^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c,{\text{ap}}^{-\mathrm{1}}}}}-{\displaystyle \frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{1}}^{{\text{ap}}^{\mathrm{2}}}}{k_Z^{c,{\text{ap}}^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c,{\text{ap}}^{-\mathrm{1}}}}}\right].\end{array}$$

Let us assume that from a given slanted sounding, after extracting the GW perturbations with a wavelet or bandpass filtering analysis, a clearly dominant quasi-monochromatic wave packet, encompassed by two apparent wavenumber bounds, $k_{Z\mathrm{1}}^{\text{ap}}$ and $k_{Z\mathrm{2}}^{\text{ap}}$, is identified. We may calculate the wave energy associated to this wave packet, directly from Eq. (6). The relative error in Ep may be estimated after replacing apparent by real wavenumbers in Eq. (6). To simplify the argument, we assume in Eq. (5) that $k_{Z\mathrm{1}}^{\text{C,ap}}$ and $k_{Z\mathrm{2}}^{\text{C,ap}}$ are close enough to assume a parametric dependence with constant α and ψ values. The relative error in Ep takes the following form:

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{\Delta }\mathrm{Ep}}{\mathrm{Ep}}}& {\displaystyle }={\displaystyle \frac{\left[\begin{array}{c}⌈\frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{2}}^{{\text{ap}}^{\mathrm{2}}}}{k_Z^{c,{\text{ap}}^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c,{\text{ap}}^{-\mathrm{1}}}}-\frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{1}}^{{\text{ap}}^{\mathrm{2}}}}{k_Z^{c,{\text{ap}}^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c,{\text{ap}}^{-\mathrm{1}}}}⌉\\ -\left[\frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{2}}^{\mathrm{2}}}{k_Z^{c^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c^{-\mathrm{1}}}}-\frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{1}}^{\mathrm{2}}}{k_Z^{c^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c^{-\mathrm{1}}}}\right]\end{array}\right]}{\left[\frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{2}}^{\mathrm{2}}}{k_Z^{c^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c^{-\mathrm{1}}}}-\frac{{\tan }^{-\mathrm{1}}\left(\frac{k_{Z\mathrm{1}}^{\mathrm{2}}}{k_Z^{c^{\mathrm{2}}}}\right)}{\mathrm{2}{k}_Z^{c^{-\mathrm{1}}}}\right]}}\\ \text{(8)}& {\displaystyle }& {\displaystyle }={\left[\text{abs}\left(\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)\right)\right]}^{-\mathrm{1}}.\end{array}$$

That is to say, under the above assumptions the relative error in Ep does not depend on vertical wavenumbers or parameters other than simply α and ψ.

The MF for internal GWs may be calculated under certain hypotheses based on the existence of a dominant mode, characterized by λ_Z and λ_H within a given intrinsic frequency range, applying the following equation (for its detailed derivation and discussion refer to Appendix A of Ern et al., 2004):

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathrm{MF}={\displaystyle \frac{\mathit{\rho }}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}}{\left({\displaystyle \frac{g}{N}}\right)}^{\mathrm{2}}\stackrel{\mathrm{‾}}{{\left({\displaystyle \frac{\widehat{T}}{T_{\mathrm{0}}}}\right)}^{\mathrm{2}}}=\mathit{\rho }{\displaystyle \frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}}\mathrm{Ep},\end{array}$$

where ρ is the background density. Note that in this derivation, the dominant mode with λ_Z and λ_H dominates within the narrow wavenumber interval mentioned above in the discussion of the spectral distribution of Ep. A first order estimation of the MF relative error may be derived, by propagating up to the first order the relative errors in Ep and (λ_Z∕λ_H). The relative error in MF will simply result in the sum of those relative errors:

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{\Delta }\left(\mathrm{MF}\right)}{\mathrm{MF}}}& {\displaystyle }=\left|{\displaystyle \frac{\mathrm{\Delta }\left(\frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}\right)}{\frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}}}\right|+\left|{\displaystyle \frac{\mathrm{\Delta }{E}_p}{E_p}}\right|\\ {\displaystyle }& {\displaystyle }=\left|{\displaystyle \frac{{\left(\frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}\right)}^{\text{ap}}-\left(\frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}\right)}{\left(\frac{{\mathit{\lambda }}_Z}{{\mathit{\lambda }}_H}\right)}}\right|+\left|{\displaystyle \frac{\mathrm{\Delta }{E}_p}{E_p}}\right|\\ {\displaystyle }& {\displaystyle }=\left|{\displaystyle \frac{\tan \left(\mathit{\alpha }\right)-\cot \left(\mathit{\psi }\right)}{\cot \left(\mathit{\psi }\right)}}\right|\\ \text{(10)}& {\displaystyle }& {\displaystyle }+{\left[\text{abs}\left(\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)\right)\right]}^{-\mathrm{1}},\end{array}$$

remembering that ${\mathit{\lambda }}_Z^{\text{ap}}/{\mathit{\lambda }}_H^{\text{ap}}=\tan \left(\mathit{\alpha }\right)$ and ${\mathit{\lambda }}_Z/{\mathit{\lambda }}_H=\cot \left(\mathit{\psi }\right)$. Note that, under the above assumptions, the MF relative error does not depend on the wavenumber bounds nor on the wavenumber width of the GW packet considered. Note that an erroneous replacement in Eq. (9) of apparent instead of real wavelengths, would lead to the conclusion that the MF would depend on the geometry of the sounding path.

To provide a measure of the distortion in MF from data retrieved during a specific slanted case study, let us consider a GPS RO slanted sounding close to Andes mountains analyzed in detail by Hierro et al. (2017, H17). In that case study, from a collocation database between RO and cloud data and from weather research and forecasting (WRF) mesoscale model simulations, real and apparent vertical wavelengths during COSMIC RO soundings were identified. From the model, coherent bi-dimensional GW structures with constant phase surfaces oriented from SW to NE were noted. From the orographic quasi-monochromatic structures detected below the cloud tops, averages of λ_Z≈22.5 km and λ_H=20 km were estimated, yielding the ratio ${\mathit{\lambda }}_Z/{\mathit{\lambda }}_H=\mathrm{1.12}$ with a wave propagation angle $\mathit{\psi }={\tan }^{-\mathrm{1}}({\mathit{\lambda }}_H/{\mathit{\lambda }}_Z)\approx \mathrm{0.73}\mathrm{rad}$. In this case study, the LOS stands at each TP almost aligned to the GW phase surfaces observed, it is to say, at 190^∘ from north direction (dotted lines in Fig. 7 from H17). This particular geometry between LOS and constant phase surfaces should allow to observe vertical oscillations in the RO profile corresponding to short λ_H structures, as described in A08. In Sect. 2 we mentioned that α may be calculated from a rectilinear approximation of the LTP and cot (α) is also equal to the ratio between ${\mathit{\lambda }}_H^{\text{ap}}$ and ${\mathit{\lambda }}_Z^{\text{ap}}$ in the region and altitude interval considered in H17. From the average inclination of LTP, cot $\left(\mathit{\alpha }\right)={\mathit{\lambda }}_H^{\text{ap}}/{\mathit{\lambda }}_Z^{\text{ap}}\approx \mathrm{0.68}\mathrm{rad}$, which considerably differs from the ratio between the corresponding real wavelengths, ${\mathit{\lambda }}_H/{\mathit{\lambda }}_Z=\mathrm{0.89}$. From Eq. (9) the proportionality of MF to the real wavelengths ratio indicates that when this ratio is erroneously replaced by the apparent wavelengths ratio, a significant error is in the general case, introduced.

As stated above, the estimation of the MF relative error for this particular Andes case study gives the following results:

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{\Delta }\left(\mathrm{MF}\right)}{\mathrm{MF}}}& {\displaystyle }=\left|{\displaystyle \frac{\tan \left(\mathit{\alpha }\right)-\cot \left(\mathit{\psi }\right)}{\cot \left(\mathit{\psi }\right)}}\right|\\ {\displaystyle }& {\displaystyle }+{\left[\text{abs}\left(\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)\right)\right]}^{-\mathrm{1}}\\ \text{(11)}& {\displaystyle }& {\displaystyle }=\mathrm{0.31}+\mathrm{0.57}=\mathrm{0.88}.\end{array}$$

The error result should be observed as indicative, as the uncertainty affecting the determination of the parameters α and ψ also affects this result.

Now we may wonder about the logically expected following point: would the distortion previously described and clearly affecting a single case study be able to affect the results and conclusions from any specific existing GW global or local climatology? At first glance, given the slanted nature of soundings upon which a given climatology is obtained and the anisotropic nature of the dependence on α and ψ, we have no reason to assume that the distortion expected on each sounding should be averaged out in the climatology, notwithstanding the available density of soundings. To try to answer this question, the option to accurately calculate each of the distortions introduced respectively in each sounding is clearly not possible, due to the unknown ψ parameter. Nevertheless, in an effort to address this point, we resort to one of the idealized modeled distributions of GW available in the literature (Alexander and Vincent, 2000). This is a linear model describing one-dimensional GW propagation through a vertically varying background atmosphere. It was used to clarify the relationship between GW properties at stratospheric heights and the GW sources at the troposphere. The authors aimed to test whether all of the observational results retrieved from radiosonde profiles could be synthesized into a consistent physical model of a spectrum of vertically propagating GW. In doing so, modeled energy densities and MF were computed before they were compared with the radiosonde results. The model uses the general dispersion relation for the intrinsic and ground-based frequency, $\widehat{\mathit{\omega }}$ and ω respectively, including a background zonal wind u and Coriolis acceleration f, derived i.e. in Gill (1982) as follows:

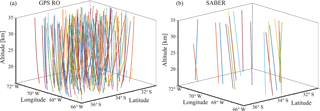
Figure 4 (a) LTPs corresponding to available profiles during the period January–February 2009, retrieved from tropo-stratospheric GPS-RO events (see text). (b) The same as (a), for SABER measurements. Arbitrary colors were included to make easier the visual inspection.

$$\begin{array}{}\text{(12)}& {\displaystyle }{\widehat{\mathit{\omega }}}^{\mathrm{2}}={\left(\mathit{\omega }-k_{H}u\right)}^{\mathrm{2}}={\displaystyle \frac{N^{\mathrm{2}}{k}_H^{\mathrm{2}}+f^{\mathrm{2}}\left(k_Z^{\mathrm{2}}+{\mathit{\mu }}^{\mathrm{2}}\right)}{k_H^{\mathrm{2}}+k_Z^{\mathrm{2}}+{\mathit{\mu }}^{\mathrm{2}}}},\end{array}$$

where N is the buoyancy frequency, $\mathit{\mu }=(\mathrm{2}H{)}^{-\mathrm{1}}$ and H is the density scale height. The GW source is specified as a distribution of MF vs. horizontal phase speed, $c=\mathit{\omega }/k_H$, for fixed k_H values. In this model, the intrinsic frequency and vertical wavenumber vary with u and stability, while k_H remains constant. The changes in $\widehat{\mathit{\omega }}$ with u(z) refer to Doppler shifting and the changes in k_Z with u(z) are referred to as refraction (see Alexander and Vincent, 2000 for details). From the different GW sources proposed by these authors as spectra of MF vs. phase speed located at fixed tropospheric heights, we illustratively consider the following source function that is perfectly antisymmetric and isotropic:

$$\begin{array}{}\text{(13)}& {\displaystyle }{B}_{\mathrm{0}}\left(c\right)=B_m\left({\displaystyle \frac{c-u_{\mathrm{0}}}{c_w}}\right)\exp \left(\mathrm{1}-\left|{\displaystyle \frac{c-u_{\mathrm{0}}}{c_w}}\right|\right),\end{array}$$

where B_m represents a spectral amplitude and c_w a source spectrum width. Note that in the high-middle frequency approximation and when neglecting μ, we may write the argument in Eq. (13) as follows:

$$\begin{array}{ll}{\displaystyle \frac{c-u_{\mathrm{0}}}{c_w}}& {\displaystyle }={\displaystyle \frac{{\widehat{\mathit{\omega }}}_i}{k_H{c}_w}}={\left[{\displaystyle \frac{N^{\mathrm{2}}{k}_H^{\mathrm{2}}}{k_H^{\mathrm{2}}+k_Z^{\mathrm{2}}}}\right]}^{\mathrm{0.5}}{\displaystyle \frac{\mathrm{1}}{k_H{c}_w}}\\ \text{(14)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{N\mathrm{|}\cos \left(\mathit{\psi }\right)\mathrm{|}}{k_H{c}_w}}.\end{array}$$

We now analyze the explicit inclusion of the previous distortion D parameter in the scope of this model. As stated, we assume only GW within the high or middle intrinsic frequency regime, neglecting f and μ. The fitting of MF from modeled results (MF^mod) to measured radiosonde data (MF^mea) at a fixed location and for constant k_H, involves a comparison between MF profiles which are, in essence, functions of real and apparent data, respectively. Then it looks reasonable to fit modeled to measured data after applying the corresponding transform to the modeled source spectrum. In doing so, we replace cos ψ in Eq. (14) following Eq. (5):

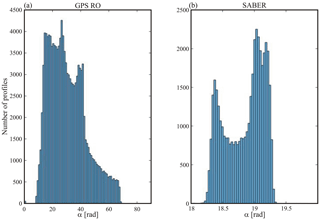
Figure 5 Distribution of available profiles with elevation angle between the sounding path direction and the horizontal plane, globally retrieved, during the period January–February 2009 from (a) GPS-LEO RO and (b) TIMED/SABER measurements (see text). The total number of profiles are 127 617 and 83 712 respectively.

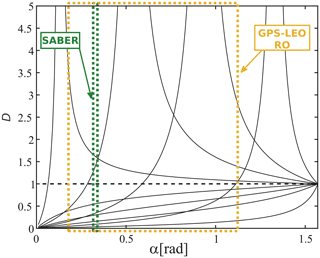
Figure 6 The α ranges corresponding to both experimental setups, are defined within dash-dotted colored boxes. These ranges are [0.17–1.22] rad and [0.32–0.34] rad, respectively in yellow and green, for GPS-RO and SABER, according to Fig. 5. The curves already selected in Fig. 2a and b for successive and constant ψ values (Δψ step =0.4) between 0.1 and 2.9, are included in black for reference purposes.

$$\begin{array}{ll}{\displaystyle }D=& {\displaystyle \frac{k_Z}{k_Z^{\text{ap}}}}=\text{abs}\left(\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)\right)\\ \text{(15)}& {\displaystyle }& {\displaystyle }=\left\{\begin{array}{ll}\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right),& \text{ if }\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)>\mathrm{0}\\ -\mathrm{1}-\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right),& \text{ if }\mathrm{1}+\cot \left(\mathit{\alpha }\right)\cot \left(\mathit{\psi }\right)<\mathrm{0}\end{array}\right.,\end{array}$$

and in the first case,

$$\begin{array}{}\text{(16)}& {\displaystyle }& {\displaystyle }\mathit{\psi }={\cot }^{-\mathrm{1}}{\displaystyle \frac{D-\mathrm{1}}{\cot \mathit{\alpha }}}\text{(17)}& {\displaystyle }& {\displaystyle }\cos \mathit{\psi }=\cos {\cot }^{-\mathrm{1}}\left({\displaystyle \frac{D-\mathrm{1}}{\cot \mathit{\alpha }}}\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+{\left(\frac{\cot \mathit{\alpha }}{D-\mathrm{1}}\right)}^{\mathrm{2}}}}},\end{array}$$

after applying a trigonometric identity and for over- or under estimation of k_Z, when D is different from one. Eq. (13) as a function of D, for constant B_m, N, k_H, c_w and viewing path α is as follows (i.e. α is expectedly constant during any radiosounding with uniform and constant background wind):

$$\begin{array}{ll}{\displaystyle }{B}_{\mathrm{0}}\left(D\right)=& {\displaystyle }{B}_m\left({\displaystyle \frac{N}{k_H{c}_w}}{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+{\left(\frac{\cot \mathit{\alpha }}{D-\mathrm{1}}\right)}^{\mathrm{2}}}}}\right)\\ \text{(18)}& {\displaystyle }& {\displaystyle }\times \exp \left(\mathrm{1}-{\displaystyle \frac{N}{k_H{c}_w}}{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+{\left(\frac{\cot \mathit{\alpha }}{D-\mathrm{1}}\right)}^{\mathrm{2}}}}}\right).\end{array}$$

Finally, under the second case of Eq. (15), D−1 is to be replaced by $-D-\mathrm{1}$. Following this reasoning, we may expect that this or any other source function, expressed from the onset in terms of measured data that undergo distortions due to the slanted nature of the soundings, will provide for the optimum value of D≠1, the best fit to a given experimental MF^mea profile. This may provide a quantitative estimation of the distortion to be expected in a climatology at a fixed geographic point. To resume the idea, what really matters in any quantitative estimation of the distortion introduced by the slanting nature of atmospheric soundings (radiosoundings, radio occultation profiles, etc) is to consistently compare real (apparent) modeled data with real (apparent) measured data.

4 Distortion of vertical wavelengths for specific setups

To illustrate the considerations from Sects. 2 and 3, let us consider the T retrievals obtained from (1) RO events detected from different LEO-GPS satellites and from (2) SABER/TIMED measurements. A GPS-LEO RO occurs whenever a transmitting satellite from the global navigation network at an altitude about 20 000 km rises or sets from the standpoint of a LEO receiving satellite at a height of about 800 km and the signal goes across the atmospheric limb. The doppler frequency alteration produced through refraction of the ray by the Earth's atmosphere in the trajectory between the transmitter and the receiver is detected, and then may be converted into slant profiles of diverse variables in the neutral atmosphere and the ionosphere. GPS-LEO RO observations, available since 2001, have been broadly used to study global distributions of GW energy and momentum, mainly in the troposphere and the stratosphere (e.g. de la Torre et al., 2006; Alexander et al., 2010; Geller et al., 2013; Schmidt et al., 2016). The RO technique is a global limb sounding technique, sensitive under all weather conditions to GW with small ratios of vertical to horizontal wavelengths (Wu et al., 2006; Alexander et al., 2016). The SABER–TIMED limb measurements provide continuous global T data for the latitude range 50^∘ N–50^∘ S, from the lower stratosphere to the lower thermosphere and represent an unprecedented opportunity for studying in detail the atmospheric waves, in particular GW, as well as their role in lower and upper atmosphere coupling (e.g. Pancheva and Mukhtarov, 2011). The TIMED satellite provides observations beginning in January 2002. It measures CO₂ infrared limb radiance from approximately 20 to 120 km altitude. Kinetic temperature profiles are retrieved over these heights using local thermodynamic equilibrium (LTE) radiative transfer in the stratosphere and lowest part of the mesosphere (up to 60 km) and a full non-LTE inversion in the mesosphere and lower thermosphere (i.e. Mertens et al., 2004; Pancheva and Mukhtarov, 2011).

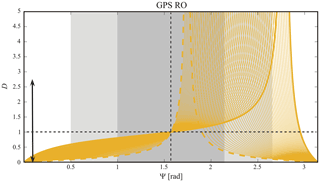
Figure 7 The yellow curves represent progressive and constant selected α values (step Δα=0.02 rad). They are selected within the allowed bounds [0.17–1.22] rad in the D–ψ GPS RO region, according to Fig. 5. These lower and higher bounds are indicated by thick dotted and full lines, respectively. White, light grey and grey sectors roughly indicate the non-hydrostatic, hydrostatic non-rotating and hydrostatic rotating GW regimes. Both quadrants are separated by the vertical dashed curve. The black double arrow indicates an hypothetical dominant non-hydrostatic GW that may be observed at different α directions, from different GPS-LEO satellite pairs. The “forbidden GPS-LEO RO sectors” are any sectors excepting those covered by yellow lines.

In Fig. 4a and b, LTPs corresponding to both setups are illustratively shown, for the higher tropospheric and lower stratospheric regions bounded by 31–37^∘ S and 66–72^∘ W, close to central southern Andes mountains, observed during January–February 2009.

Keeping in mind that the observed difference between horizontal and vertical scales in these figures is that there is a typical distribution of the sounding path direction (α) among GPS-RO occultation events and among SABER measurements. The large number of available RO as compared to SABER profiles is evident but no significant variation with latitude was detected. The approximation of the sounding paths by straight segments seems, at least for our purpose here, quite reasonable. Let us now consider the global data retrieved from both setups during January–February 2009 (RO from LEOs: SAC-C, CHAMP, MetOp-A, and COSMIC), of which Fig. 4 only represents a regional subset. In Fig. 5a and b the α distribution is shown. Here a linear interpolation was applied to the weakly variable α angle in each RO event, between the lowest and upper available LTP values. Note the considerably narrower variability α-range among SABER profiles. We did not observe remarkable differences in the general latitudinal or geographical distribution. The possible ranges observed from both experimental setups allow some preliminary consequences to be drawn regarding the expected wavelength distortions. For example, for the subset in Fig. 4, we know that very close to the Andes mountains region dominant large-amplitude, stationary and non hydrostatic GWs are usually observed (de la Torre et al., 1996, 2005, 2015).

Accordingly, large GW aspect ratios may be expected there (Gill, 1982). On the other hand, at tropical latitudes, where convective GWs dominate the scenario, or even close to polar jet regions where hydrostatic rotating or non rotating GWs are usually found, considerably lower characteristic aspect ratios should be dominant. In Fig. 6, we reproduce the D–α curves selected in Fig. 2a and b, for successive ψ values (Δψ step =0.2), now adding in dash-dotted green and yellow squares, the D–α ranges affected for both experimental setups. These ranges are, respectively, [0.17–1.22] rad for GPS-RO and [0.32–0.34] rad for SABER. For each setup, the relevant difference mainly depends on whether α and ψ belong to the same or different $[\mathrm{0},\mathit{\pi }/\mathrm{2}]$ and $[\mathit{\pi }/\mathrm{2},\mathit{\pi }]$ intervals.

Here, we may here observe that depending on GW aspect ratio and sounding direction, general under- and overestimations of λ_Z are both possible throughout both experimental setups. Within a given ensemble, the behavior of D is different for ψ lower and greater than π∕2. This suggests that different modes in the ensemble may show individual distortions less than or greater than 1. Then, some compensations contributing to Ep and MF are expected from different modes in the ensemble, but the net distortion should still be considerable. In Fig. 7, the D–ψ constraint imposed to GPS-RO observations, now for constant and progressive α values, is shown. Δα steps of 0.02 rad and within the corresponding bounds [0.17–1.22] rad indicated in Fig. 5, are shown. The white, light grey and grey sectors approximately indicate the non-hydrostatic, hydrostatic non-rotating and hydrostatic rotating GW regimes, respectively. We observe general underestimations for ψ less than π∕2 and in the vicinity of π rad. Between these sectors, under and overestimations are possible. To illustrate the consequences on a realistic and simple scenario, let us consider again the region situated to the east of the central Andes, mentioned in Figs. 4a and b. Let us suppose that, consistently with observations and numerical simulations (i.e. de la Torre et al., 2012; Jiang et al., 2013; Fritts et al., 2016), constant and stationary GW phase surfaces exhibit a systematic inclination with respect to the ground and a high aspect ratio, following the almost omnipresent forcing by mean westerlies at the mountain tops. This feature is represented in Fig. 7 by the black arrow.

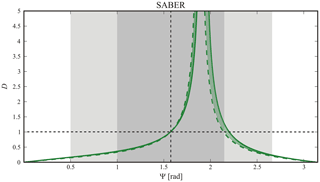
Figure 8 The same as Fig. 7, but for SABER measurements, within the considerably narrower α bounds [0.32–0.34] rad than for the GPS-RO setup, according to Fig. 5. These lower and higher bounds are indicated by thick dotted and full green lines, respectively. The “forbidden SABER sectors” are any sectors excepting those covered by green lines.

This arrow spans over all possible α directions within the bounds imposed by the geometry of every GPS-LEO satellites combination during each occultation event. This assumed scenario would reveal a net underestimation of λ_Z, regardless of the inclination of LTPs during the sounding of the region and the considered period. In general the analysis is expected to be more complex, given distinct LTP contributions that may under- or overestimate λ_Z. Finally, Fig. 8 indicates the corresponding D–ψ features for SABER measurements, similarly as in Fig. 7.

Here we observe general underestimations for ψ, along the 3 GW regimes, for values less than π∕2 and greater than around 2.3 rad. For intermediate values, only overestimations are expected. Note that for SABER measurements, the forbidden D−ψ region is considerably more extended than for GPS-LEO RO measurements.

5 Discussion and conclusions

The expected distortions observed in the measured vertical wavelengths during any near instantaneous slanted atmospheric sounding, as may be the case for satellite instruments, is discussed. For the particular case of vertical or horizontal soundings, we know that no distortion is expected in λ_Z and λ_H, respectively. The features observed are described as a function of GW aspect ratio and the inclination of the sounding path.

To gain a better understanding of this distortion, and making use of the symmetric D dependence with α and ψ, we consider the expression for D as a parametric equation in both independent variables. To illustrate the constraints imposed to both parameters by applying different instrumental setups and GW scenarios, we show the results conveniently in D–α and D–ψ plots. Above and below the non-distortion limit (D=1), general under and overestimations occur depending on the relative parametric values. The main difference is produced by two possible situations: α and ψ belonging to the same or different quadrants, taken from $[\mathrm{0},\mathit{\pi }/\mathrm{2}]$ and $[\mathit{\pi }/\mathrm{2},\mathit{\pi }]$. Given a GW ensemble and a number of measurements within arbitrary bounds of space and time intervals, distinct wavelength under- and overestimations should be expected.

When Ep is calculated over a GW ensemble in any individual T profile, an integral must be performed over the largest wavelength along any chosen direction. The selection of the upper and lower vertical wavelength bounds, should include those prevailing GW amplitudes expected to mostly contribute to Ep. Depending on α and the respective ψ values for each one of the dominant GW modes, some dominant real wavelengths may not be fully contained within the integration interval. The integral in Ep then will not include at least one wavelength of every dominant mode. The Ep calculation could be under- or overestimated up to a significant extent.

We illustrate these arguments in a realistic scenario considering a modeled distribution of GW. This is based on the usual saturation of large vertical wavenumbers and in the separability of the spectral function in the vertical wave number, the intrinsic frequency and the azimuthal direction of propagation. To calculate the wave energy associated to a given GW packet within an ensemble, we use a simple analytical result derived from the spectral model to get an idea of the distortion expected by wrongly replacing the integration limits by apparent instead of real wavenumber values. This (or any) distortion in Ep will in turn be translated to the MF, by applying a previous result obtained by Ern et al. (2004). In addition, through a multiplying factor, the MF would be then illogically dependent on the inclination angle of the sounding path.

The results are considered for two specific experimental setups: GPS-RO and SABER measurements. For our analysis we approximate the sounding paths in both cases by using straight segments. The relevance of this assumption was assessed. A clearly larger number of available T profiles is seen from RO events. The α ranges in both techniques allow the definition of forbidden regions in D–α as well as in D–ψ diagrams, relative to the different GW aspect ratios (the non-hydrostatic, hydrostatic non-rotating and hydrostatic rotating regimes). Within a given GW ensemble, even expecting some compensation when D is less than and greater than 1, the net distortion effect, as well as its contribution to Ep and MF, should be considerable. With the exception of GWs with prevailing high aspect ratio, as for example near the Andes mountains where a net underestimation of λ_Z should be observed, under- and overestimations are in general expected, from both setups respectively. This occurs for T profiles where α and ψ belong to the same or different quadrants $[\mathrm{0},\mathit{\pi }/\mathrm{2}]$ and $[\mathit{\pi }/\mathrm{2},\mathit{\pi }]$. For SABER measurements, the forbidden D–ψ region is considerably more extended than the one corresponding to the GPS-RO measurements.

In the global study of Geller et al. (2013), which compares models with diverse parameterizations with satellite and balloon data, the faster fall off in relation to the height of the gravity wave MF derived from satellite measurements than in the models considered in that study was the most significant discrepancy between measured and model fluxes. These authors concluded that the reasons for those differences remain unknown, although various explanations for the differences were proposed. As we know from model simulations, the MF is not computed from Eq. (8), but from its formal definition based on the average of the products of the three perturbed components of the air velocity. Based on the above considerations and regarding the dramatic distortions on vertical and horizontal wavelengths during slanted soundings, we may infer that if MF is computed from Eq. (8), the wavelength distortion will unavoidably be translated to the calculation of MF. Obviously, this situation must be considered together with the additional constraints imposed to any satellite-borne observational window, discussed by several authors, including A08. Finally, we must admit that the global calculation of MF from slanted T profiles, including all necessary corrections, even assuming quasi-monochromatic GW packets, appears to be a very complex task. The distortions described above are only avoided in the calculation of MF if the atmosphere is sounded in vertical or horizontal directions, as provided (but only locally) by lidar or radar and balloon setups, respectively. Up to now, from the satellite data at disposal, an attempt to quantitatively illustrate the implications and possible misrepresentation (or distortion) of our general understanding of GW parameters values from slanted soundings, as their global distribution and variability, seems unrealistic. After some research to improve this simulation, we are now working on previous GW parameter solution-schemes which were modified for the use of close sounding-groups of RO profiles. The method is currently being applied to calculate GW propagation direction, net MF and real vertical and horizontal wavelength for some case studies. The unavoidable constraint imposed to extend preliminary results to a future GW climatological useful description is strictly conditioned by the still largely insufficient density of satellite-based soundings.