Retrieval of snowflake microphysical properties from multifrequency radar observations

We have developed an algorithm that retrieves the size, number concentration and density of falling snow from multifrequency radar observations. This work builds on previous studies that have indicated that three-frequency radars can provide information on snow density, potentially improving the accuracy of snow parameter estimates. The algorithm is based on a Bayesian framework, using lookup tables mapping the measurement space to the state space, which allows fast and robust retrieval. In the forward model, we calculate the radar reflectivities using recently published snow scattering databases. We demonstrate the algorithm using multifrequency airborne radar observations from the OLYMPEX–RADEX field campaign, comparing the retrieval results to hydrometeor identification using ground-based polarimetric radar and also to collocated in situ observations made using another aircraft. Using these data, we examine how the availability of multiple frequencies affects the retrieval accuracy, and we test the sensitivity of the algorithm to the prior assumptions. The results suggest that multifrequency radars are substantially better than single-frequency radars at retrieving snow microphysical properties. Meanwhile, triple-frequency radars can retrieve wider ranges of snow density than dual-frequency radars and better locate regions of high-density snow such as graupel, although these benefits are relatively modest compared to the difference in retrieval performance between dual- and single-frequency radars. We also examine the sensitivity of the retrieval results to the fixed a priori assumptions in the algorithm, showing that the multifrequency method can reliably retrieve snowflake size, while the retrieved number concentration and density are affected significantly by the assumptions.

1 Introduction

Atmospheric ice formation and growth processes have a major impact on the Earth's radiative balance and on the hydrological cycle. Ice clouds and snowfall occur nearly everywhere, as ice processes occur at high altitudes even in areas where freezing temperatures at the surface are rare (Field and Heymsfield, 2015; Mülmenstädt et al., 2015). Ice clouds have also long been a challenge for weather and climate models (Waliser et al., 2009). Improving the microphysics schemes, which describe nucleation of small ice crystals and their transformation into precipitation-sized particles, is also currently an active area of model development in which conceptually new schemes have been recently introduced (Harrington et al., 2013; Morrison and Milbrandt, 2015).

Observational data are needed to evaluate the representation of ice and snow in models. While direct measurements of ice particle properties can be made in situ, such measurements only produce limited samples and are difficult and expensive to make, especially when surface observations are not possible and aircraft-based measurements are needed. Remote-sensing instruments are able to sample far larger volumes. Radars, in particular, can make range-resolved measurements and thus map the vertical structure of the ice cloud–precipitation column. However, the interpretation of radar signatures of ice particles is subject to uncertainties because the microwave scattering properties of icy hydrometeors depend on their size, shape and structure. These are extremely variable, as deposition growth alone results in diverse and often complicated shapes, and further growth through aggregation and riming adds to the complexity (Lamb and Verlinde, 2011; Pruppacher and Klett, 1997).

Multifrequency radars have emerged as a potential tool for ice microphysics investigations. It has been recognized for a while that snowflake size can be constrained with collocated measurements at two different frequencies (Hogan et al., 2000; Liao et al., 2005; Matrosov, 1993, 1998). More recently, several studies have shown, using detailed numerical scattering simulations and empirical evidence, that triple-frequency measurements provide information on both the size and density of icy hydrometeors (Gergely et al., 2017; Kneifel et al., 2011, 2015; Kulie et al., 2014; Leinonen and Moisseev, 2015; Leinonen and Szyrmer, 2015; Leinonen et al., 2012a; Stein et al., 2015; Yin et al., 2017). The availability of this information has been expected to enable more accurate quantitative estimation of ice water content (IWC) and snowfall rate and to provide a method to remotely distinguish and characterize icy hydrometeor growth processes.

Studies on the triple-frequency signatures of snow have, so far, been mostly limited to numerical and theoretical investigations, as well as empirical studies that demonstrated the plausibility of the concept. Only very recently have databases of snow scattering properties covering a wide range of snow growth processes (Kuo et al., 2016; Leinonen and Szyrmer, 2015; Lu et al., 2016) become available, enabling the development of a versatile radar forward model that can produce the radar signatures of many types of snowflakes. This, together with the expanded availability of collocated triple-frequency measurement datasets from field campaigns, has provided the prerequisites for the development of a practical snowfall retrieval algorithm for triple-frequency radars.

In this paper, we introduce a method for retrieving certain microphysical properties of snow – namely, the number concentration, size and density – from multifrequency radar observations. The algorithm is based on a Bayesian framework and uses radar cross sections from detailed snowflake models that cover a wide range of sizes and densities. In Sect. 2, we describe the algorithm formulation. Section 3 describes the datasets used for demonstrating and evaluating the algorithm, and Sect. 4 describes how the a priori distributions used in the retrieval were derived. In Sect. 5, we investigate case studies of airborne radar data from the Olympic Mountain Experiment–ACE Radar Definition Experiment 2015 (OLYMPEX–RADEX'15) coordinated by NASA and compare the retrieval results to ground-based polarimetric radar observations. Section 6 describes comparisons to collocated in situ measurements. Section 7 presents statistical analyses of the sensitivity of the algorithm to the number of frequencies available and to the a priori assumptions. Finally, we discuss the implications of the results and summarize the study in Sect. 8.

2 Algorithm

2.1 Physical basis

The objective of a radar retrieval algorithm for snowfall is to provide the best estimate of the microphysical properties of the snowflakes based on the received radar signals. The unattenuated equivalent radar reflectivity factor Z_e for a given wavelength λ is

$$\begin{array}{}\text{(1)}& Z_{\mathrm{e}}={\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{4}}}{{\mathit{\pi }}^{\mathrm{5}}|K_w{|}^{\mathrm{2}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\mathit{\sigma }}_{\mathrm{bsc}}\left(D\right)N\left(D\right)\mathrm{d}D,\end{array}$$

where σ_bsc(D) is the backscattering cross section as a function of the maximum diameter D, N(D) is the particle size distribution and K_w is the dielectric factor defined as $K_w=(n_{\mathrm{w}}^{\mathrm{2}}-\mathrm{1})/(n_{\mathrm{w}}^{\mathrm{2}}+\mathrm{2})$, where n_w is the complex refractive index of liquid water assumed at a reference temperature and frequency.

The attenuation of the radar signal must be accounted for in radar-only retrieval algorithms. The attenuated reflectivity at distance r from the radar is given by

$$\begin{array}{}\text{(2)}& Z_{\mathrm{e}}^{\prime }\left(r\right)=Z_{\mathrm{e}}\left(r\right)\exp \left(-\mathrm{2}\underset{\mathrm{0}}{\overset{r}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\mathit{\sigma }}_{\mathrm{ext}}(D,r^{\prime })N(D,r^{\prime })\mathrm{d}D\mathrm{d}{r}^{\prime }\right),\end{array}$$

where σ_ext is the extinction cross section. The resulting reflectivity is usually expressed in logarithmic units of decibels relative to Z (dBZ), defined by

$$\begin{array}{}\text{(3)}& Z_{\mathrm{dB}}^{\prime }=\mathrm{10}{\log }_{\mathrm{10}}{\displaystyle \frac{Z_{\mathrm{e}}^{\prime }}{Z_{\mathrm{0}}}},\end{array}$$

where $Z_{\mathrm{0}}=\mathrm{1}{\mathrm{mm}}^{\mathrm{6}}{\mathrm{m}}^{-\mathrm{3}}$. The attenuated reflectivity can be written as

$$\begin{array}{}\text{(4)}& Z_{\mathrm{dB}}^{\prime }\left(r\right)=\mathrm{10}{\log }_{\mathrm{10}}{\displaystyle \frac{Z_{\mathrm{e}}\left(r\right)}{Z_{\mathrm{0}}}}-\underset{\mathrm{0}}{\overset{r}{\int }}{A}_{\mathrm{dB}}\left(r^{\prime }\right)\mathrm{d}{r}^{\prime },\end{array}$$

where A_dB is the two-way specific attenuation, that is, the attenuation in decibels per unit length.

It was shown as early as Hitschfeld and Bordan (1954) that weather radar attenuation correction is subject to mathematical instabilities that can lead to small errors multiplying in a positive feedback loop. Namely, overestimation of attenuation in one radar range bin leads to overcompensation in all subsequent bins away from the radar, causing overestimation of the precipitation signal, which in turn leads to further overestimation of the attenuation. In multifrequency radars, the lower-frequency signals are generally attenuated less. In the case of snowfall, the W-band signal can be significantly attenuated, the Ka band much less so, and the Ku band is practically unattenuated by the snowflakes. Thus, the Ku-band radar reflectivity can be used to correct the Ka- and W-band signals in a stable manner.

We use a technique similar to Kulie et al. (2014) for attenuation correction: we draw samples from the a priori distribution (described in Sect. 4), calculate both the Ku-band reflectivity and the specific attenuation at the Ka or W band for each sample, and fit a function between the reflectivity and the attenuation. We found that a linear function between Z_dB and ln A_dB fits the relationship well. We validated this approach by computing attenuation afterwards from the retrieved microphysical values; the root-mean-square (RMS) difference in the total attenuation, calculated over all bins in the case shown in Sect. 5.2, is only 0.27 dB, so this approximate approach to attenuation correction seems to work adequately.

Attenuation also results from atmospheric gases and from supercooled liquid water. The gaseous attenuation was calculated and corrected for with the ITU-R P.676-11 model (ITU, 2016), using radio sounding data for the temperature, pressure and humidity required by the model. The gaseous attenuation varies spatially since it is dependent on water vapor, but the error introduced by this is likely small given that the maximum two-way gaseous attenuation in the cases analyzed in this study is only 1.1 dB at 94 GHz (W band), and much less at the lower frequencies. However, supercooled liquid water found in mixed-phase clouds can cause significant radar attenuation. However, the radar echo of the supercooled water is very weak because of the small size of the drops, making it practically impossible, using radar signals alone, to detect supercooled water coexisting with ice. Thus, we do not correct for attenuation caused by supercooled water, while acknowledging its role as a potential error source.

In order to manage the dimensionality of the problem, the microphysical properties of the snowflakes must be parameterized. We utilize two common assumptions for this. First, we assume that the particle size distribution (PSD) follows the exponential distribution

$$\begin{array}{}\text{(5)}& N\left(D\right)=N_{\mathrm{0}}\exp (-\mathrm{\Lambda }D),\end{array}$$

where N₀ and Λ are the intercept and slope parameters, respectively. Although gamma distributions, and other forms that introduce additional parameters, are sometimes used, the exponential distribution has been found to describe snowflake size distributions well (Heymsfield et al., 2008; Sekhon and Srivastava, 1970). We also found it to be a good match to the in situ airborne size distribution measurements used in this study (see Sect. 6). Therefore, we find it preferable over more complicated alternatives. Second, we assume that the mass of snowflakes is given as a function of the diameter as

$$\begin{array}{}\text{(6)}& m\left(D\right)=\mathit{\alpha }{D}^{\mathit{\beta }}\end{array}$$

as has been commonly done in microphysics literature (Pruppacher and Klett, 1997). In the following section, we explain how these assumptions are used to compute the radar reflectivities.

2.2 Forward model

The forward model in an inversion algorithm is responsible for calculating the measurements that correspond to a given state vector – in our case, the radar reflectivity at each wavelength given the microphysical parameters. The simulation of radar reflectivity from snowflakes whose diameters are comparable to or larger than the wavelength is known to require calculations that account for the internal structure of the snowflake (Botta et al., 2011; Petty and Huang, 2010; Tyynelä et al., 2011). Recently, such calculations have been used for a wide variety of model snowflakes in order to establish databases of scattering properties. We chose a combination of two such datasets as the basis of our forward model: the rimed snowflakes of Leinonen and Szyrmer (2015) and the OpenSSP database of Kuo et al. (2016). The dataset of Leinonen and Szyrmer (2015) covers a wide range of snowflake densities, but due to the relatively coarse resolution of the volume elements, it mostly contains moderate- and large-sized snowflakes. The Kuo et al. (2016) dataset was used to augment the set of snowflakes used by the forward model at small sizes, D<1 mm.

While there have been considerable recent advances on the problem of modeling snowflakes produced by different ice processes and calculating their scattering properties, the abundance of available snowflake models leads to another question: which set of snowflakes should be used by the forward model in a particular situation? We use an approach that does not force us to select any one dataset. Instead, the scattering properties are given as a function of mass and size: σ(D,m), where σ can be one of σ_bsc, σ_sca or σ_abs, the last two being the scattering and absorption cross sections, respectively, with ${\mathit{\sigma }}_{\mathrm{ext}}={\mathit{\sigma }}_{\mathrm{sca}}+{\mathit{\sigma }}_{\mathrm{abs}}$. The function σ(D,m) is constructed by organizing all model snowflakes from the combined scattering database into bins by D and m; we use 128×128 logarithmically spaced bins to cover the range of diameters and masses found in the dataset. For each bin, we compute the average of ${\mathit{\sigma }}_{\mathrm{norm}}\equiv \mathit{\sigma }/m^{\mathit{\gamma }}$, where γ=2 for the backscattering and scattering cross sections, and γ=1 for the absorption cross section. The reason for the normalization by m² or m is that in the Rayleigh scattering regime (D≪λ) σ_bsc and σ_sca are proportional to m², and σ_abs is proportional to m (Bohren and Huffman, 1983). It follows that the normalized cross sections are roughly constant at the small-particle limit. To smoothen the binned values, the samples used in the averaging are weighted using a Gaussian function of the distance from the bin center, with a standard deviation of 0.15 for both lnD and lnm. A continuous function of the form

$$\begin{array}{}\text{(7)}& \ln {\mathit{\sigma }}_{\mathrm{norm}}(\ln D,\ln m)\end{array}$$

is then formed by interpolation among the bin centers. Not all bins have snowflakes in them; for those we are unable to do the averaging and instead assign the scattering properties to zero. This means that the limits of the coverage of the snowflake database in the (D,m) space are effectively assumed to be the limits of the natural variability in snowflakes. While this is not exactly true, the combined database does cover a wide range of microphysical processes. The assumption that the cross section goes to zero (as opposed to, for instance, extrapolating it) outside the coverage area also effectively truncates the integrals in Eqs. (1) and (2).

With a method to calculate the cross sections as a function of D and m, it is relatively straightforward to compute radar reflectivities from the microphysical inputs. As can be seen from the previous section, the input parameters for the forward model are N₀, Λ, α and β. We start with a fixed set of 1024 logarithmically spaced integration points that span the interval [D_min,D_max]. The parameters α and β are used to find the corresponding masses using Eq. (6). The cross section for each integration point is then found from the lookup table using interpolation. The cross sections are multiplied with the size distribution determined by N₀ and Λ, which allows us to compute the integral in Eq. (1) with fixed-point numerical integration.

2.3 Retrieval

A radar retrieval algorithm needs to invert Eqs. (1) and (2) such that an input of $Z_{\mathrm{e}}^{\prime }$ at one or more wavelengths yields the properties of N(D) and m(D). The inversion is unavoidably inexact, as the wide variety of snowflake number concentrations, size distributions and densities leads to a variability too large to constrain with a few radar reflectivities. The retrieval must be performed in a probabilistic sense, deriving the most likely solution from the possible alternatives, using the prior information about snowflake properties as a constraint.

The retrieval problem is commonly stated as finding a state vector x that explains a given measurement vector y. The formulation of the state vector depends on which variables are chosen for retrieval and which ones are simply assumed. In our experimentation with different combinations, we found that the most stable solution was to retrieve N₀, Λ and α. The β parameter was fixed at 2.1. While β varies in nature, many experimental and modeling studies (Delanoë et al., 2014; Erfani and Mitchell, 2017; Leinonen and Moisseev, 2015; Mascio and Mace, 2017; Mascio et al., 2017; Mitchell et al., 1990; Moisseev et al., 2017; Pruppacher and Klett, 1997; Westbrook et al., 2004) have found exponents near this value for various types of snowflakes; we will examine the sensitivity of the results to this assumption in Sect. 7.3. We retrieve the logarithm of each microphysical parameter because the dynamic ranges of the retrieved values are large and because using the logarithmic values makes the forward model more linear; this was examined analytically for the simpler case of cloud water retrieval by Leinonen et al. (2016). The state vector then becomes

$$\begin{array}{}\text{(8)}& \mathit{x}={\left[\ln N_{\mathrm{0}}\ln \mathrm{\Lambda }\ln \mathit{\alpha }\right]}^T.\end{array}$$

In our multifrequency radar retrieval algorithm, the most straightforward way to formulate the measurement vector would be to use each of the three radar reflectivities. However, earlier studies (Kneifel et al., 2011; Leinonen and Szyrmer, 2015) have shown that combinations of dual-wavelength ratios (DWRs), such as simultaneous measurements of Ka–W-band and Ku–Ka-band DWRs, contain information about the size and density of the snowflakes. Following this concept, we form the measurement vector with the Ku-band reflectivity and the Ka–W-band and Ku–Ka-band DWRs. The measurement vector is then

$$\begin{array}{}\text{(9)}& \mathit{y}={\left[Z_{\mathrm{dB},\mathrm{Ku}}{\mathrm{DWR}}_{\mathrm{Ka}/\mathrm{W}}{\mathrm{DWR}}_{\mathrm{Ku}/\mathrm{Ka}}\right]}^T.\end{array}$$

The choice of the Ku-band reflectivity is somewhat arbitrary, as any of the three bands could be used, but the Ku band does benefit from that band being the least attenuated of the three. In studies in which we omit one of the radar bands, instead operating with a dual-frequency radar, y consists of the reflectivity from the lowest-frequency radar and the DWR. For single-frequency retrievals, y simply contains Z_dB at the single band.

The measurement vector must be accompanied by an error estimate, which should include not only the radar instrument error but also the error due to the forward model assumptions. In our case, the latter includes the errors due to the assumptions of an exponential size distribution, a fixed mass–dimensional exponent β and the orientation distributions assumed in the scattering databases. The extent of these errors is difficult to quantify, but their effect should be similar on each collocated radar frequency: for example, the radar cross section will increase with increasing particle size for all frequencies, and thus the errors in radar reflectivity at different frequencies will partially cancel out when computing the DWRs. This suggests that the DWRs can be assumed to have smaller errors than the absolute value of the reflectivity. Accordingly, we assign 3 dB of error standard deviation for the absolute value of the radar reflectivity and 1 dB for each of the DWRs.

In atmospheric remote sensing, the inversion problem is often solved using optimal estimation (Rodgers, 2000). This is a Bayesian method that assumes that x and y are jointly distributed according to the multivariate normal distribution and which is solved using optimization methods. We found this technique to be problematic for our retrieval, partly due to the limited and discrete nature of the snowflake scattering database used in the forward model. The optimization in OE often converged to local minima, especially near the extreme values supported by the snowflake database, introducing sudden changes to the retrieved values.

Despite the shortcomings of OE, a Bayesian approach was still desirable in order to constrain the retrieved microphysical parameters. We found that the retrieval can be performed in a robust way through a global calculation of the expected value of the state x given a measurement y. This is given by

$$\begin{array}{}\text{(10)}& \mathbf{E}\left[\mathit{x}\right|\mathit{y}]=\int \mathit{x}p(\mathit{x}\left|\mathit{y}\right)\mathrm{d}\mathit{x}={\displaystyle \frac{\mathrm{1}}{p\left(\mathit{y}\right)}}\int \mathit{x}p\left(\mathit{y}\right|\mathit{x}\left)p\right(\mathit{x})\mathrm{d}\mathit{x},\end{array}$$

where p(y) is the marginal probability of y, p(y|x) is the conditional probability of a measurement y given a state x and p(x) is the a priori probability of x, described in detail in Sect. 4. This approach is slightly different from the common strategy of finding the most likely solution given the prior and the measurement: That method aims to find the mode of the conditional distribution; ours determines the mean.

Using Eq. (10), we can construct a lookup table that maps discrete values of y to the corresponding expected values E[x|y]. Multilinear interpolation is used to estimate E[x|y] for values of y that fall between the discrete values used in the table. The errors associated with the discretization can be reduced to be arbitrarily small by making the intervals between the values finer. In the studies presented here, the lookup table for E[x|y] ranged between 0 and 35 dBZ for Z_dB,Ku, between −2 and 14 dB for DWR_Ka∕W, and between −2 and 9 dB for DWR_Ku∕Ka, with 0.25 dB discretization for each dimension. The integral in Eq. (10) was computed by evaluating the integrand at approximately 10 000 discrete points, which were distributed uniformly across a finite search space spanning (${\stackrel{\mathrm{‾}}{x}}_i-\mathrm{3}{\mathit{\sigma }}_i$,${\stackrel{\mathrm{‾}}{x}}_i+\mathrm{3}{\mathit{\sigma }}_i$) along each variable, where ${\stackrel{\mathrm{‾}}{x}}_i$ is the prior mean of the ith variable in x, and σ_i is its prior standard deviation. Making the discretization finer than this did not seem to change the retrieval results significantly in our case, although we encourage those using this approach for other problems to establish the appropriate discretization for their problem.

Error estimates for the retrieved values can be computed using the same technique. The error covariance matrix of the state given an observation, S_x|y, can be computed as

$$\begin{array}{}\text{(11)}& {\mathbf{S}}_{\mathbf{x}|\mathbf{y}}=\mathbf{E}[\mathit{x}\otimes \mathit{x}|\mathit{y}]-\mathbf{E}[\mathit{x}\left|\mathit{y}\right]\otimes \mathbf{E}\left[\mathit{x}\right|\mathit{y}],\end{array}$$

where “⊗” is the outer product. $\mathbf{E}[\mathit{x}\otimes \mathit{x}|\mathit{y}]$ can be evaluated using a lookup table and interpolation in the same manner as explained for E[x|y] above.

The method described above allows the state and its covariance to be retrieved robustly and very quickly, with only a table lookup and an interpolation needed for each measurement. This comes at the cost of a relatively expensive initialization of the tables before the retrieval is started. However, with our parameters for the discretization, this only took about 1 min on a modern laptop computer with no parallelization, so it does not present a major computational burden.

2.4 Derived variables

The results of the retrieval are the parameters of Eq. (8), but for further analysis of the results, it is useful to derive other variables that are important for microphysics or more intuitively understood by end users. Perhaps most importantly, the IWC (denoted by W_ice), which expresses the ice mass in a unit volume of air, is given by

$$\begin{array}{}\text{(12)}& W_{\mathrm{ice}}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}m\left(D\right)N\left(D\right)\mathrm{d}D.\end{array}$$

Consistently with the calculation of the scattering properties, we set m(D)=0 in the integral (and other integrals in this section) where no snowflake samples are available for the (D,m) combination. If this truncation is not used, the assumptions of Eqs. (5) and (6) give W_ice in the simple form

$$\begin{array}{}\text{(13)}& W_{\mathrm{ice}}=N_{\mathrm{0}}\mathit{\alpha }{\mathrm{\Lambda }}^{-\mathit{\beta }-\mathrm{1}}\mathrm{\Gamma }(\mathit{\beta }+\mathrm{1}),\end{array}$$

where Γ is the gamma function.

When discussing the snowflake size, Λ⁻¹ gives the average diameter for the untruncated exponential size distribution, but it is often clearer and more convenient to state the diameter that contributes most to the IWC. This is the mass-weighted mean diameter

$$\begin{array}{}\text{(14)}& D_{\mathrm{m}}={\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}Dm\left(D\right)N\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}m\left(D\right)N\left(D\right)\mathrm{d}D}}.\end{array}$$

Similarly, the total number concentration of snowflakes may be a more meaningful quantity than N₀. This is given simply by

$$\begin{array}{}\text{(15)}& N_T=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}N\left(D\right)\mathrm{d}D.\end{array}$$

Also, the density of the snowflakes depends on the diameter, but a bulk density for the snowflake ensemble can be computed by dividing the IWC by the volume spanned by the enclosing spheres of the snowflakes in a unit volume:

$$\begin{array}{}\text{(16)}& {\mathit{\rho }}_{\mathrm{bulk}}={\displaystyle \frac{W_{\mathrm{ice}}}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}\frac{\mathit{\pi }}{\mathrm{6}}{D}^{\mathrm{3}}N\left(D\right)\mathrm{d}D}}.\end{array}$$

We use this definition for simplicity; a somewhat higher density would be obtained by using the volume of the enclosing spheroid or ellipsoid in the integral in the denominator, but the shape of this ellipsoid is in general dependent on D and m, which would complicate the calculation.

The quantities in Eqs. (12)–(16) are nonlinear functions of the state x, and consequently estimating their errors is not completely straightforward. Since our algorithm returns a probability distribution function (PDF) for x, we can obtain statistically valid error estimates by computing the standard deviation of a quantity over the PDF. This can be estimated quickly with Gauss–Hermite quadratures; see Appendix A.

3 Data

The main source of data that we use to demonstrate the triple-frequency retrieval is from the Airborne Third Generation Precipitation Radar (Sadowy et al., 2003) flown onboard the NASA DC-8 aircraft during the OLYMPEX–RADEX experiment, which took place around the Olympic Mountains of Washington State, USA, in late 2015 (Houze et al., 2017). The RADEX involvement in this field campaign was intended specifically to assess the the capabilities of multifrequency radar observations for satellite remote sensing of precipitation processes. APR-3 acquired simultaneous measurements at three frequencies: 13.4 GHz (Ku band), 35.6 GHz (Ka band) and 94.9 GHz (W band). APR-3 is a scanning polarimetric cloud-profiling radar with Doppler capability. With a vertical resolution of 30 m, it provides high-resolution 3-D measurements of clouds and precipitation. OLYMPEX was the first time it was deployed in its triple-frequency configuration.

We investigated the ability of the triple-frequency algorithm to identify snowfall processes qualitatively by comparing the results to collocated ground-based dual-polarization radar observations. These observations were made by the NASA S-Band Dual-Polarimetric Radar (NPOL), which was deployed 2 km from the coast at 47.277^∘ N, 124.211^∘ W, 157 m above mean sea level (m.s.l.). The NPOL scanning strategy interleaved planned position indicator scans (PPIs) with a series of high-resolution range-height indicator (RHI) sector scans to the west over the ocean and to the east over the Quinault River valley (Houze et al., 2017). During OLYMPEX, the NASA DC-8 aircraft frequently flew directly along NPOL RHI azimuths, making it relatively straightforward to collocate with the nadir-pointing scans from APR-3. We collocated NPOL data to the APR-3 radar coordinates using the Python ARM Radar Toolkit (Helmus and Collis, 2016) by first identifying RHI scans whose time and direction coincided with the APR-3 overpass, then copying data from the nearest NPOL bin to each APR-3 bin. We used two variables from NPOL: the radar reflectivity and the hydrometeor identification (HID) product (Dolan and Rutledge, 2009). The latter uses fuzzy logic to assign the most likely hydrometeor class to each radar bin based on temperature and the radar reflectivity and polarimetric parameters. We use this product to provide independent estimates of the type of icy hydrometeors and compare them to the microphysical properties retrieved by our algorithm.

During the OLYMPEX campaign, the University of North Dakota Citation aircraft often flew in the same area as the NASA DC-8. Typically, the Citation flew at lower altitudes than the DC-8, and consequently there are many data points where the Citation measurements are collocated with the APR-3. A total of 16 cases from OLYMPEX were analyzed. The APR-3 gate closest to the Citation is found using a k-dimensional-tree search algorithm. The Citation measured the PSD using the 2D-S (Stereo) Probe (Lawson et al., 2006) in the range of $\mathrm{225}\mathrm{\mu }\mathrm{m}\le D<\mathrm{1}\mathrm{mm}$ and the High-Volume Particle Spectrometer ($\mathrm{1}\mathrm{mm}\le D\le \mathrm{3.25}\mathrm{cm}$). To eliminate shattered artifacts created from ice crystals colliding with the probe housing, anti-shattering tips are used in conjunction with the University of Illinois Oklahoma Optical Array Probe Processing Software (Jackson et al., 2014). In addition to the optical array probes, the Citation also carried a Nevzorov probe (Korolev et al., 1998) to measure bulk total water content.

The ground-based observations of snowfall microphysics used to derive the a priori distribution were gathered at the Hyytiälä Forestry Field Station (61.845^∘ N, 24.287^∘ E, 150 m above mean sea level) of the University of Helsinki, Finland, during the Biogenic Aerosols – Effects on Clouds and Climate (BAECC) campaign (Petäjä et al., 2016) and the following winter of 2014–2015. The weather conditions during BAECC and the following winter were mostly mild, and most of the snowfall observations were collected at temperatures above $-\mathrm{4}{}^{\circ }\mathrm{C}$. Both aggregation and riming occurred frequently during the measurement period (Moisseev et al., 2017). The PSDs were measured with a video disdrometer, the Snowflake Video Imager (Newman et al., 2009), as a function of the disk-equivalent diameter (the diameter of a disk with the projected area of the particle image). The mean PSD was calculated for every 5 min period. The resolution of the SVI is 0.1 mm, although in practice, the smallest disk-equivalent diameter used in the computations was approximately 0.2 mm. The PSD was divided into 120 bins with a bin size of 0.2 mm; the highest bin is for diameters larger than 26.0 mm. A linear scaling factor between the disk-equivalent diameter and the maximum diameter was determined by analyzing SVI images of snowflakes from each case and utilized to give the PSD as a function of maximum diameter. The mass retrievals were obtained by combining SVI observations with a collocated precipitation gauge. Based on the particle fall velocity and shape measurements provided by the SVI, the masses of individual falling snow particles were estimated with hydrodynamic theory (Mitchell and Heymsfield, 2005; von Lerber et al., 2017). The mass–dimensional relation in the form of Eq. (6) was determined for every 5 min with mass as a function of maximum diameter and with a linear regression fit in the log scale.

We also used balloon sounding data to support the analysis of the case studies. These data were derived from publicly available operational soundings launched daily at 00:00 and 12:00 UTC from Quillayute, Washington, near the area where the radar measurements took place.

4 A priori assumptions

Bayesian retrievals depend on the availability of a priori data. We based our a priori values on two sources of in situ data: the Citation dataset from OLYMPEX and the ground-based measurements from BAECC. Both of these datasets can be used to derive the N₀, Λ and α parameters. For both datasets, N₀ and Λ can be derived from the binned PSDs. The α parameter can be derived by fitting a curve defined by Eq. (6) to the mass as a function of diameter; this is included in the BAECC data, in which the mass was derived from the snowflake fall velocity (von Lerber et al., 2017). In calculating α from the BAECC dataset, we fixed β to 2.1, consistent with the assumptions in the retrieval algorithm. For the Citation data, mass is not directly available as a function of diameter, but W_ice is estimated with the Nevzorov probe and thus α can be roughly estimated using Eq. (13).

For the purposes of demonstrating the algorithm, we based the a priori distribution used in this study on a combination of the two datasets, taking an equal number of samples from each for a total N≈6000. We recognize that this is an imperfect solution, and a further analysis using these and other datasets should be conducted to establish a priori distributions suitable for remote-sensing retrievals of snowfall under various atmospheric conditions. Doing this rigorously will likely require an entire study of its own.

The analysis resulted in means of $\stackrel{\mathrm{‾}}{\ln N_{\mathrm{0}}}=\mathrm{15.4}$, $\stackrel{\mathrm{‾}}{\ln \mathrm{\Lambda }}=\mathrm{7.50}$, and $\stackrel{\mathrm{‾}}{\ln \mathit{\alpha }}=-\mathrm{2.30}$ and standard deviations of Std[ln N₀]=1.67, Std[ln Λ]=0.52 and Std[ln α]=0.69. Because the two datasets cannot be expected to cover the entire natural distribution of these parameters, basing the a priori distribution on them would likely result in an overly restrictive prior. To compensate for this, we increase the standard deviations given above by a factor of 1.5, acknowledging that this choice is somewhat arbitrary. The correlation matrix of x derived from the datasets is

$$\begin{array}{}\text{(17)}& {\mathbf{C}}_{\mathrm{a}}=\left[\begin{array}{ccc}\mathrm{1}& \mathrm{0.46}& -\mathrm{0.07}\\ \mathrm{0.46}& \mathrm{1}& \mathrm{0.54}\\ -\mathrm{0.07}& \mathrm{0.54}& \mathrm{1}\end{array}\right],\end{array}$$

from which the a priori covariance matrix can be computed as

$$\begin{array}{}\text{(18)}& {\mathbf{S}}_{\mathbf{a}}={\mathbf{DC}}_{\mathrm{a}}\mathbf{D},\end{array}$$

where D is a diagonal matrix with the standard deviations of x on the diagonal. The resulting distribution, used as the prior in all retrievals in this study, is then given by the mean x_a and covariance S_a:

$$\begin{array}{}\text{(19)}& {\displaystyle }& {\displaystyle }{\mathit{x}}_{\mathrm{a}}={\left[\begin{array}{ccc}\mathrm{15.4}& \mathrm{7.50}& -\mathrm{2.30}\end{array}\right]}^T,\text{(20)}& {\displaystyle }& {\displaystyle }{\mathbf{S}}_{\mathrm{a}}=\left[\begin{array}{ccc}\mathrm{6.28}& \mathrm{0.90}& -\mathrm{0.18}\\ \mathrm{0.90}& \mathrm{0.61}& \mathrm{0.44}\\ -\mathrm{0.18}& \mathrm{0.44}& \mathrm{1.07}\end{array}\right].\end{array}$$

In Sect. 7.2 we examine the sensitivity of the results to the choice of prior.

We assume that the a priori distribution is multivariate normal. Given the limited scope of the datasets used to derive the prior distribution in this study, we cannot rigorously test this assumption, but the choice is motivated by probabilistic arguments that the normal distribution is the most natural choice for an unknown distribution (Jaynes, 2003). Global distributions for microphysical quantities have also often been found to be lognormal (Kedem and Chiu, 1987; Leinonen et al., 2012b), meaning that the distributions of their logarithms (we use the logarithmic values in the state vector) are normal. Thus a multivariate normal distribution is a reasonable assumption for this study, although larger datasets should be analyzed in this manner in order to derive appropriate global priors.

5 Case studies and comparison to NPOL

5.1 3 December 2015

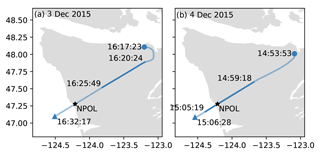
Figure 1 The paths of the flights used in Sect. 5.1 (a) and 5.2 (b). The darker sections of the paths show the flight data used in this study (the rest of the measurements were discarded for the lack of useful data). The time stamps (UTC) denote the beginning and end of each flight and the beginning and end of the data that were used. The gray background shows the outline of the Olympic Peninsula, with Vancouver Island to the north.

The first of the two cases that we examined together with NPOL data took place on 3 December 2015. The APR-3 flight leg started at 16:17:23 UTC over the Olympic Mountains, from where the DC-8 flew towards the coast, passing directly over the NPOL site. A map of the flight path is shown in Fig. 1a. The case consisted primarily of prefrontal stratiform precipitation; see Houze et al. (2015a) for details. We only used data from regions above the melting layer, which we identified just below 3 km in altitude based on the the radar bright band; this also agrees with the 0 ^∘C isotherm of 2.85 km in the 12:00 UTC balloon sounding from nearby Quillayute, Washington.

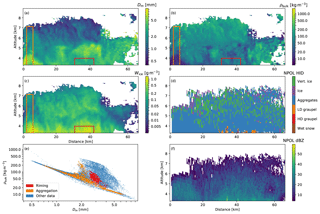
Figure 2 Data from the 3 December 2015 case described in Sect. 5.1. (a) The mass-weighted mean diameter D_m (Eq. 14). (b) The bulk density ρ_bulk (Eq. 16). (c) The ice water content (Eq. 12). (d) The NPOL hydrometeor identification. (e) A scatter plot of D_m and ρ_bulk from (a) and (b), with the red and orange points identifying the data inside the boxes of corresponding colors shown in those panels. (f) The radar reflectivity observed by NPOL.

The retrievals from the case are shown in Fig. 2a–e. On the left side of Fig. 2a–c, an orange box delineates a column in which D_m increases significantly with decreasing altitude, accompanied by a rapid decrease in ρ_bulk. Together, these changes point to the onset of aggregation, which results in rapid growth of snowflakes accompanied by a decrease in density as single ice crystals stick together to form aggregates, whose density decreases as a function of size. The transition can also be seen in Fig. 2e, in which orange dots denote the data points from the orange box in Fig. 2a–c.

The transition from ice crystals to aggregates is also detected at around 5 km in altitude, 20–45 km on the distance scale, by both the triple-frequency retrieval, which shows a sudden increase in D_m (Fig. 2a), and by NPOL, which identifies a change in the hydrometeor type at roughly the same altitude. According to NPOL HID, the hydrometeors above this altitude consist mostly of a mixture of ice crystals and aggregates, while the hydrometeors below it are identified as aggregates. While the altitude at which aggregation initiates appears to be similar between NPOL and our retrieval, small discrepancies are to be expected because the APR-3 observations are not perfectly simultaneous with the NPOL scan. The time difference ranges from 4 min at the beginning of the observations shown in Fig. 2 to 14 min at the end. Further evidence for aggregation is provided by sounding data, which indicate a temperature between −15 and $-\mathrm{12}{}^{\circ }\mathrm{C}$ in the layer at 5.0–5.5 km in altitude, a common temperature range for the onset of aggregation driven by dendritic growth of ice crystals at these temperatures (Bailey and Hallett, 2009; Lamb and Verlinde, 2011).

Another interesting feature found in this case is denoted by the red boxes in Fig. 2a–c. In this region, the retrieved microphysical variables indicate moderately sized snowflakes with relatively high ρ, which suggests that rimed snowflakes occur in the area. The data points located within this box are shown in red in the scatter plot of Fig. 2e, which confirms these attributes. It is interesting to note that the red region and the bottom of the orange region have similar IWCs, but the sizes and densities are very different. NPOL also detects some graupel in this region, which suggests that the three-frequency retrieval detects snowflake riming and graupel formation. In the following case, we further explore this capability.

5.2 4 December 2015

On 4 December 2015, precipitation originated mostly from postfrontal convection following the passage of the front on the previous day (Houze et al., 2015b). The DC-8 followed a flight path similar to in the previous case (Fig. 1b); APR-3 data collection for the dataset shown here started at 14:53:21 UTC. We collocated two NPOL RHIs to APR-3 coordinates, one pointing toward land and the other toward the ocean. For the ocean-pointing scan, we selected an RHI that is offset by 4^∘ from the optimal collocation with APR-3 in order to better capture a convective plume that was observed by APR-3 but had moved before being scanned by NPOL 2 min later. This shifted the location of the scan by only 500 m at the distance of the plume. The sounding data and the radar bright band both placed the melting level at around 1.3 km, lower than on the previous day. We again only used data points located above the melting layer.

Figure 3 As Fig. 2, except for the 4 December 2015 case described in Sect. 5.2. The location of NPOL on the flight track is marked by the arrow in panels (a)–(d) and (f).

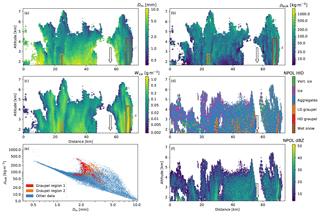
The large convective plume found by APR-3 in this case is marked with a red box in Fig. 3a–c. As with Fig. 2, the data points from this box are denoted with red dots in Fig. 3e. In this case, the data points from the plume are particularly distinct from the rest of the joint distribution of D_m and ρ_bulk, indicating moderately large particles with high density, characteristic of graupel. NPOL also indicates a similarly sized plume of graupel in this region. The time separation of the scans in the region to the right of NPOL in Fig. 3 is only 2 min, so it seems likely that the same plume was captured by both radars. The spatial shift between the plumes observed by APR-3 and NPOL appears to be 1–2 km; this is consistent with the 13 m s⁻¹ wind speed measured by the sounding at 3 km in altitude, which translates to a 1.5 km distance over 2 min.

On the left side of NPOL, another graupel-containing region is denoted by an orange box. This region is also accompanied by an NPOL detection of graupel in the vicinity. The time separation in this region was longer, between 4 and 8 min, so the plume had more time to move away from the vertical cross section before being observed by APR-3. Regardless, the two radars agree on location of the plume to within 2 km and on its height to within 0.5 km.

Our retrieval and the NPOL HID also seem to be in reasonably good agreement regarding the transition from ice crystals to aggregates. Both indicate the presence of ice crystals (i.e., small, relatively dense hydrometeors) at higher altitudes and aggregates at lower altitudes (below approximately 4 km), with the transition point varying considerably within this case. Both products also identify the presence of smaller particles at 2–3 km in altitude in the region, around 20 km on the horizontal scale.

6 Comparison to in situ data

As described in Sect. 3, the UND Citation aircraft gathered particle probe measurements simultaneously with the NASA DC-8 radar observations during OLYMPEX. This resulted in a set of collocated radar and in situ data. The retrieval algorithm was run using the collocated and attenuation-corrected radar reflectivity values. The retrieved microphysical quantities were then compared to those measured in situ. The availability of variables from the in situ dataset is somewhat limited: while the number and projected sizes of the ice particles can be measured quite accurately using the imaging probes, the two-dimensional nature of the imager limits the accuracy of the maximum dimension as this must be estimated from a projection of the particle. The snowflake masses are also difficult to determine. The bulk IWC can be estimated with the Nevzorov probe, but its inlet is only 8 mm in diameter, which causes it to underestimate IWC when the maximum particle size exceeds approximately 4 mm (Korolev et al., 2013). Unfortunately, the cases with large snowflakes are where one would expect the largest benefits from multifrequency methods because of the stronger resonance effects involved in scattering. Thus, this limitation of the Nevzorov probe somewhat diminishes its value in validating the retrievals. While the Citation measurements do not give the masses of individual particles, α can be estimated from Eq. (13) if the IWC given by the Nevzorov probe is assumed to be correct.

To filter out outliers and poor collocations, we applied two filters. First, to ensure an acceptably accurate collocation between the two measurements, the time separation between them was required to be less than 2 min. Second, for adequate sampling, the total number concentration N_T was required to be more than 10³ m⁻³. These criteria successfully removed most outliers that we found in the unfiltered comparisons.

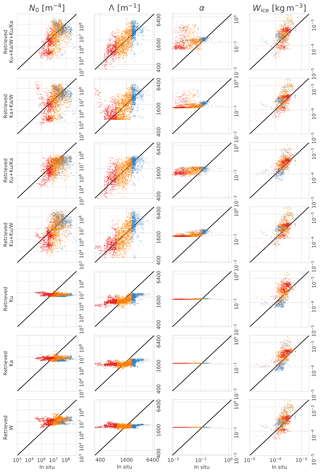
Figure 4 Scatter plots of in situ measured (horizontal axis) and retrieved (vertical axis) microphysical values from the collocated Citation–APR-3 dataset. The columns correspond to different microphysical parameters: from left to right, the intercept parameter N₀, the slope parameter Λ, the mass–dimensional prefactor α and the ice water content W_ice. The rows correspond to different combinations of radar frequencies and DWRs used to run the retrieval, as shown to the left of each row. The color denotes the size of the snowflakes: blue dots correspond to small particles (largest 25 % of Λ), orange to medium-sized particles and red to large particles (smallest 25 % of Λ). In each plot, the black line is the 1:1 line. Note the logarithmic scales on the axes.

The comparisons of the retrievals against the in situ values are shown on the top row of Fig. 4 (the same analysis run with reduced frequencies, shown on the other rows of Fig. 4, is discussed in Sect. 7.1). The figures show that retrievals of the slope parameter Λ compare considerably better to the in situ values than do the retrievals of the intercept parameter N₀, which in turn are better than those of the mass–dimensional factor α. The Λ parameters agree well throughout the range of values (for ln Λ, root-mean-square error is RMSE[ln Λ]=0.41, bias is bias[ln Λ]=0.023 and correlation is Cor[ln Λ]=0.70), showing that particle sizing can be carried out reliably using the multifrequency retrieval. N₀ is also quite well matched (Cor[ln N₀]=0.56), but the relative errors are much larger than for Λ (RMSE[ln N₀]=3.01, $\mathrm{bias}\left[\ln N_{\mathrm{0}}\right]=-\mathrm{0.73}$). The α parameters are poorly matched between the two datasets, although the retrieval produces some variation in this parameter. In any case, one should be skeptical of the α comparison as the in situ values have been derived from the Nevzorov probe data, which suffers from the abovementioned problems, and using Eq. (13), which is an approximation. Furthermore, fixing the β parameter may further exacerbate the problem with estimating α.

The retrieved IWCs W_ice correspond quite well to the in situ values (RMSE[ln W_ice]=0.72, bias[ln W_ice]=0.30, Cor[ln W_ice]=0.67). Interestingly, the IWC, which is a function of N₀ and α, appears to be better retrieved than either of those parameters. Opposite errors in N₀ and α, seen in their respective scatter plots, suggest that their retrieval errors compensate for each other in a way that allows W_ice to be constrained better than either N₀ or α alone. This is also supported by the correlation matrix of the retrieval errors, for which the error correlation between ln N₀ and ln α is −0.30 on average. The red dots in Fig. 4 correspond to larger ice particles, where the Nevzorov probe might be prone to underestimation. However, there does not appear to be a significant difference in W_ice between the small and large particles. However, the large particles stand out in the α scatter plot, where they are clearly the worst match between the in situ and retrieved values.

7 Sensitivity analysis

7.1 Sensitivity to the number of frequencies

In the assessment of a multifrequency algorithm, one interesting question is what are the benefits of introducing additional frequencies? To evaluate this, we reran the analysis of Sect. 6 with subsets of the frequencies used in the full analysis. We examined all the possible combinations of available bands, always using the lowest frequency for the absolute reflectivity, combined with the DWRs that were available (one DWR for dual-frequency retrievals and two DWRs for the triple-frequency retrieval).

The scatter plots of the in situ and retrieved microphysical parameters are shown in Fig. 4. These plots suggest that the results of the triple-frequency retrieval are similar to those of the dual-frequency retrievals. However, the multifrequency retrievals clearly outperform single-frequency retrievals. The triple- and dual-frequency scatter plots are visually similar for all two- and three-frequency combinations for Λ, and to a lesser extent N₀. The dual-frequency retrieval using the Ka–W bands seems to be limited in its ability to determine the size of large particles (small Λ), presumably because the dual-frequency ratio saturates at large sizes, while the Ku–Ka-band retrieval suffers from a similar problem with small particles. The Ku–W-band retrieval and the triple-frequency retrieval do not suffer from this problem. Meanwhile, the single-frequency retrievals all have poor sensitivity to N₀. Ku- and Ka-band single-frequency retrievals have some sensitivity to Λ for small particles, while the W-band retrieval also cannot discern this parameter particularly well. None of the retrievals perform adequately with α, although the multifrequency retrievals, especially the triple-frequency retrieval, permit considerably more variation in the values of that parameter: α is almost constant with the single-frequency retrievals, while its relative standard deviation is about 60 % in the triple-frequency results, indicating that the retrieval algorithm is confident enough in the signal to estimate α as something other than the a priori mean. The results for α should be interpreted skeptically because of the issues with the derivation of α, as explained in Sect. 6. The single-frequency retrievals appear to constrain W_ice much better than they constrain any of the individual microphysical parameters.

Another way to evaluate the sensitivity to the number of frequencies is to examine the a posteriori errors reported by the algorithm itself. These errors, derived from the 4 December 2015 case, are shown in Fig. 5 for the different frequency combinations. According to the error estimate from the algorithm, the three-frequency retrieval seems to yield a modest but fairly consistent improvement over the dual-frequency results. These, like with the in situ data comparison, are clearly better than the single-frequency results for all parameters, although the differences for α, W_ice and ρ_bulk are less pronounced.

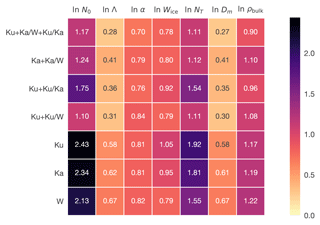
Figure 5 The average posterior retrieval errors of the logarithms of microphysical variables with different combinations of radar frequencies. The data from the 4 December 2015 case (Sect. 5.2) are used in this figure.

The errors in the single-frequency retrievals are all similar; the W band seems to have somewhat smaller errors for W_ice and N₀ while the Ku band is slightly better with the particle size. Notably, the a posteriori errors for the single-frequency retrievals are not much smaller than the a priori errors of Std_a[ln N₀]=2.45, Std_a[ln Λ]=0.83 and Std_a[ln α]=1.13, which emphasizes the poor information content in the single-frequency retrievals. Regardless, with W_ice the single-frequency retrievals perform nearly as well as the multifrequency ones, consistent with what was shown in the comparison to in situ values. None of the dual-frequency options are significantly better than the others, either, although the Ku–Ka-band configuration underperforms the Ka–W-band and Ku–W-band configurations in retrievals of N₀ and N_T, and to a lesser extent W_ice. The Ka–W- and Ku–W-band configurations are nearly equally good.

We have additionally created plots of the microphysical parameters shown in Fig. 3 using each of the frequency combinations found in Fig. 5. Due to the large number of plots resulting from this analysis, these plots are not shown here, but can be found in Figs. S1–S21 of the Supplement accompanying this article. A notable feature of these plots is the higher level of detail and wider range of variation found in the triple-frequency plots of D_m and especially ρ_bulk compared to the dual-frequency plots. The Ka–W band dual-frequency retrieval appears to capture the plume found by the triple-frequency approach, albeit with a more subdued signal; the other two dual-frequency configurations miss the plume altogether. Consistent with the results of other comparisons shown in this section, the dual-frequency plots capture more detail than the single-frequency plots. This is especially striking for the plots of ρ_bulk, in which the single-frequency retrievals appear to always give nearly the same density. In contrast to D_m and ρ_bulk, W_ice has only small differences, and similar levels of detail between the single-frequency and multifrequency retrievals. This is again similar to the findings in Fig. 4.

7.2 Sensitivity to prior assumptions

In order to examine the sensitivity of the results of the retrieval algorithm to the prior assumptions, we ran the case of 4 December 2015 with shifted prior means. We changed the mean of each variable in the state vector x, one at a time, by ±1 standard deviation of that variable. The results are shown in Fig. 6. The results are consistent with the retrievals in the sense that a shift in the prior of a variable causes a smaller shift of the same sign in the a posteriori value of that variable.

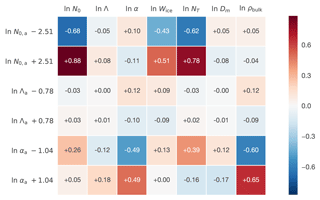
Figure 6 The root-mean-square changes in the microphysical parameters in response to changes in the prior. The change in the prior is indicated on the left side of each row. The data are from the 4 December 2015 case (Sect. 5.2).

The effects on other variables from adjusting the prior of one variable are not straightforward to interpret. These are connected in a complicated way due to the significant a priori correlations among the different variables, as well as the necessity of explaining the observed reflectivities with other parameters when one of them is shifted. The dependencies are clearly not linear. The shifts in the prior also interact with the limits of the scattering database, which further complicates the interpretation. The IWC is the most sensitive to the prior of ln N₀. The results are the least sensitive to the prior assumption of ln Λ, indicating that ln Λ is very well constrained by the observations. Changes to the priors of either ln N₀ or lnα induce considerably larger changes in the results. Thus, the triple-frequency algorithm is clearly still somewhat dependent on the a priori assumptions, although the changes in the posterior values are much smaller than the corresponding changes in the prior, showing that the radar signal constrains them quite effectively.

In Figs. S22–S28, we repeat this analysis with the reduced frequencies. These clearly show the increasing dependence on the prior assumptions with fewer available frequencies. Again, the difference between triple and dual frequency is fairly modest, while the single-frequency retrievals shift much more in response to changes in the prior.

7.3 Sensitivity to mass–dimensional exponent

The most significant fixed parameter in the retrieval is the exponent β of the mass–dimensional relationship (Eq. 6). Similar to Sect. 7.2, we carried out an analysis of the sensitivity of the retrieval results to the choice of β. We used the value usually adopted in this paper, β=2.1, as the reference and compared the results obtained with β=1.9, β=2.3 and β=2.5 to the reference retrieval. The values were chosen based on exponents found in the literature for single crystals, aggregate snowflakes and rimed particles (Mitchell et al., 1990); higher exponents such as those close to 3.0 often found for graupel (Heymsfield and Kajikawa, 1987; Locatelli and Hobbs, 1974) were not tested because the distribution of particles in the scattering databases does not support such high exponents well. The results are shown in Fig. 7. This figure is similar to Fig. 6, but we have omitted the changes in the mass–dimensional prefactor α because this parameter does not have a physical meaning independent of β.

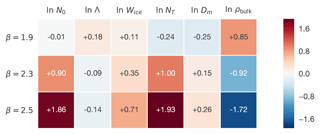
Figure 7 The root-mean-square changes in the microphysical parameters in response to changes in the mass–dimensional exponent β. The standard assumption of this paper, β=2.1, is used as the baseline. The value of β is indicated on the left side of each row. The analysis is based on the 4 December 2015 case (Sect. 5.2).

The changes in the retrieval results for different values of β exhibit patterns similar to those resulting from the change in prior values: The parameters corresponding to number concentration (N₀ and N_T) and density (ρ_bulk) are the most sensitive to the assumptions. Meanwhile, parameters related to particle size (Λ and D_m) and, to a lesser extent, the IWC W_ice are less affected by changes in β. The changes in retrieved parameters with changing β can be substantial, suggesting that a good estimate of β is important for quantitatively correct retrievals. However, the changes are predictable and reasonable, which suggests that the algorithm is robust and can function with different values of β without major problems. A notable exception to the predictable behavior is that of W_ice, whose retrieved value increases in response to both increase and decrease in β from 2.1.

8 Conclusions

In this study, we described and evaluated an algorithm for snow microphysical retrievals using multifrequency radar measurements. The probabilistic method is based on direct application of Bayes' theorem using lookup tables. We examined the capabilities and limitations of the retrieval algorithm using data from the OLYMPEX–RADEX measurement campaign, comparing the results to ground-based radar measurements from the NASA NPOL radar and to in situ measurements from the UND Citation aircraft, both of which were collocated with the APR-3 measurements. We also examined the sensitivity of the algorithm to various assumptions used in its formulation.

The results indicate that, at least for the retrieval approach presented here, triple-frequency radar retrievals provide modest benefits over dual-frequency retrievals of snowfall properties. The probabilistic error estimates from the triple-frequency retrievals are generally only slightly smaller than those from dual-frequency retrievals, but closer examination of the retrieved values shows that the triple-frequency approach produces more detailed retrievals with higher degrees of variability than the dual-frequency retrievals. The triple-frequency method can also determine particle size throughout the range of snowflake sizes studied here, avoiding problems with some of the dual-frequency methods with sizing either small or large particles. Multifrequency retrievals significantly outperform those using only one frequency, and none of the three dual-frequency configurations studied (Ka–W-, Ku–Ka- and Ku–W-bands) appear to be decisively better than the others, although the Ka–W band combination was found to have more sensitivity to the snowflake density than the Ku–Ka- or Ku–W-band combinations. Similarly, we found the relative performances of Ku-, Ka- and W-band single-frequency retrievals to be approximately equal. Thus, information content analysis appears to suggest that multifrequency radars are preferable to single-frequency radars in snowfall retrievals, but it does not provide much insight into the exact choice of frequencies; this choice should probably be more dependent on other factors such as achievable sensitivity and resolution, the importance of attenuation, and cost.

The triple-frequency technique appears to be useful at identifying graupel, that is, ice particles that are heavily rimed and thus considerably denser than most aggregate snowflakes, providing a sufficient signal for the triple-frequency retrieval to detect. This was confirmed in this study with the comparison to polarimetric observations with the NPOL ground-based radar. Globally, graupel occurs in relatively rare events that represent only a small fraction of snow cases, and consequently graupel events do not impact the statistics much. However, graupel (and hail, which is even denser) can have a substantial societal impact where it occurs, and thus detecting it can be valuable even though it only occurs in a small percentage of icy precipitation. Detecting graupel plumes, together with accurate snowflake size determination elsewhere in a precipitating region, can also shed light on the processes involved in the formation of graupel. These plumes are usually small in their horizontal extent, of the order of 1 km, requiring a fairly high spatial resolution in the radars used to detect them, which can be challenging to achieve if multifrequency radars are considered for satellite applications.

Despite the improvements in retrieval precision in multifrequency retrievals, the retrieved results are still dependent on the assumptions regarding the a priori distribution of the retrieved microphysical parameters, as well as the mass–dimensional exponent β. Different retrieved parameters have widely different sensitivities to the assumptions: the retrieved snow particle size changes only modestly in response to changes to the prior and to β, indicating that the size can be retrieved robustly with the multifrequency method. In contrast, the retrieved number concentration and density are much more sensitive to the assumptions and therefore potentially susceptible to retrieval errors caused by inaccurate prior data. Therefore, it is still vital to constrain the algorithm using in situ measurements that provide not only the size and number concentration of snowflakes but also their mass–dimensional scaling parameters α and β. Later versions of the algorithm should include β as a retrievable parameter and incorporate it in the multivariate prior so that the retrieval errors originating from the uncertainty of β can be properly quantified.

The findings of this study concern the retrieval accuracy of multifrequency radars and do not address their other potential benefits. For instance, multifrequency radars can utilize lower-frequency channels (e.g., Ku band) to penetrate deeper into precipitation, particularly heavy rain that can attenuate higher frequencies (e.g., W band) heavily enough to block detection altogether. Conversely, higher-frequency radars can generally be made more sensitive, allowing detection in regions below the sensitivity thresholds of low-frequency bands. These benefits should be considered together with the retrieval performance when decisions about instrument specifications are made; see, e.g., Leinonen et al. (2015) for a quantitative assessment of retrieval capabilities of a potential spaceborne triple-frequency radar.

This work builds on earlier experimental and modeling results that suggested that triple-frequency radars can be used to constrain snowflake habits and examines this capability in practice with a prototype retrieval algorithm. Based on the experience gained in this study, we can identify two requirements for future research that need to be fulfilled in order to use such an algorithm in an operational setting. First, the snowflake scattering database, while more extensive than those previously available, is still limited in its scope, and its coverage of snowflake sizes, densities and habits should be expanded in order to support the forward model in all scenarios. Second, the a priori distributions used in the retrievals in this study are based on relatively few data points. An abundance of in situ data from ice clouds and snowfall currently exists as a result of many ground- and aircraft-based field campaigns; analyses of the data from these are needed to support retrieval algorithm development by providing representative a priori distributions of snowfall properties. The substantial cross correlations found in this study among the snow microphysical properties (Eq. 17) emphasize the need for a multivariate analysis of these datasets.

Appendix A: Fast derivation of error estimates for retrieved quantities

Consider a scalar Q(x) that is a function (not necessarily a linear function) of the vector x of normally distributed random variables, whose probability distribution p(x) is given by the mean 〈x〉 and the covariance S. For example, Q can be ln W_ice or the logarithm of any variable introduced in Sect. 2.4. Then, a probabilistic error estimate is given by the standard deviation

$$\begin{array}{}\text{(A1)}& \mathrm{\Delta }Q=\mathrm{Std}\left[Q\right]=\sqrt{\langle Q^{\mathrm{2}}\rangle -\langle Q{\rangle }^{\mathrm{2}}},\end{array}$$

where the expectation, denoted by 〈⋅〉, is taken over the PDF of x. The expectation can be estimated efficiently using a Gauss–Hermite quadrature. For a three-variable x (generalization to other numbers of variables is straightforward), the expectation 〈Q〉 is obtained as follows:

$$\begin{array}{}\text{(A2)}& {\displaystyle }\langle Q\rangle & {\displaystyle }=\underset{\mathit{x}}{\int }Q\left(\mathit{x}\right)p\left(\mathit{x}\right)\mathrm{d}\mathit{x}\approx \sum _{i,j,k}{w}_i{w}_j{w}_{k}Q\left({\mathit{x}}_{ijk}\right),\text{(A3)}& {\displaystyle }{w}_i& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathit{\pi }}}}{w}_{\mathrm{GH},i},\text{(A4)}& {\displaystyle }{\mathit{x}}_{ijk}& {\displaystyle }=\langle \mathit{x}\rangle +\sqrt{\mathrm{2}}\mathbf{V}{\mathbf{\Lambda }}^{\mathrm{1}/\mathrm{2}}{\left[x_{\mathrm{GH},i}{x}_{\mathrm{GH},j}{x}_{\mathrm{GH},k}\right]}^T,\end{array}$$

where

• V is a matrix whose columns contain the normalized eigenvectors of S,

• Λ is a diagonal matrix containing the corresponding eigenvalues of S,

• x_GH and w_GH are the points and weights of a Gauss–Hermite quadrature that gives the approximation

  $$\begin{array}{}\text{(A5)}& \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\exp (-x^{\mathrm{2}})f\left(x\right)\mathrm{d}x\approx \sum _{i=\mathrm{1}}^N{w}_{\mathrm{GH},i}f\left(x_{\mathrm{GH},i}\right),\end{array}$$

  where the approximation is exact if f is a polynomial of at most degree 2N−1; x_GH and w_GH can be found in many tables (Beyer, 1987) and in scientific software packages (Oliphant, 2007).

〈Q²〉 can also be estimated using the above method, thus giving the error estimate when substituted into Eq. (A1). This is derived by computing the Gauss–Hermite quadrature for the standard multivariate normal distribution with zero mean and identity covariance, then mapping the quadrature points to the corresponding points in the distribution of x.