Evaluation of atmospheric profiles derived from single- and zero-difference excess phase processing of BeiDou radio occultation data from the FY-3C GNOS mission

The Global Navigation Satellite System (GNSS) Occultation Sounder (GNOS) is one of the new-generation payloads onboard the Chinese FengYun 3 (FY-3) series of operational meteorological satellites for sounding the Earth's neutral atmosphere and ionosphere. The GNOS was designed for acquiring setting and rising radio occultation (RO) data by using GNSS signals from both the Chinese BeiDou System (BDS) and the US Global Positioning System (GPS). An ultra-stable oscillator with 1 s stability (Allan deviation) at the level of 10⁻¹² was installed on the FY-3C GNOS, and thus both zero-difference and single-difference excess phase processing methods should be feasible for FY-3C GNOS observations. In this study we focus on evaluating zero-difference processing of BDS RO data vs. single-difference processing, in order to investigate the zero-difference feasibility for this new instrument, which after its launch in September 2013 started to use BDS signals from five geostationary orbit (GEO) satellites, five inclined geosynchronous orbit (IGSO) satellites and four medium Earth orbit (MEO) satellites. We used a 3-month set of GNOS BDS RO data (October to December 2013) for the evaluation and compared atmospheric bending angle and refractivity profiles, derived from single- and zero-difference excess phase data, against co-located profiles from European Centre for Medium-Range Weather Forecasts (ECMWF) analyses. We also compared against co-located refractivity profiles from radiosondes. The statistical evaluation against these reference data shows that the results from single- and zero-difference processing are reasonably consistent in both bias and standard deviation, clearly demonstrating the feasibility of zero differencing for GNOS BDS RO observations. The average bias (and standard deviation) of the bending angle and refractivity profiles were found to be about 0.05 to 0.2 % (and 0.7 to 1.6 %) over the upper troposphere and lower stratosphere. Zero differencing was found to perform slightly better, as may be expected from its lower vulnerability to noise. The validation results indicate that GNOS can provide, on top of GPS RO profiles, accurate and precise BDS RO profiles both from single- and zero-difference processing. The GNOS observations by the series of FY-3 satellites are thus expected to provide important contributions to numerical weather prediction and global climate change analysis.

1 Introduction

The radio occultation (RO) technique (Melbourne et al., 1994; Ware et al., 1996) using signals from global navigation satellite systems (GNSSs), in particular from GPS, has been widely used to observe the Earth's atmospheric parameters (e.g., bending angle, refractivity, temperature, pressure, and water vapor) for applications such as numerical weather prediction (NWP; e.g., Healy and Eyre, 2000; Kuo et al., 2000; Healy and Thepaut, 2006; Aparicio and Deblonde, 2008; Cucurull and Derber, 2008; Poli et al., 2008; Huang et al., 2010; Le Marshall et al., 2010; Harnisch et al., 2013) and global climate monitoring (GCM; e.g., Steiner et al., 2001, 2009, 2011, 2013; Schmidt et al., 2005, 2008, 2010; Loescher and Kirchengast, 2008; Ho et al., 2009, 2012; Foelsche et al., 2011a; Lackner et al., 2011).

The RO concept was experimentally tested by the first experimental Global Positioning System/Meteorology (GPS/MET) mission launched in 1995 right after full operational capacity of GPS was achieved (Ware et al., 1996; Kursinski et al., 1996; Kuo et al., 1998). GPS/MET has demonstrated the unique properties of the GPS RO technique, such as high vertical resolution, high accuracy, all-weather capability and global coverage (Ware et al., 1996; Gorbunov et al., 1996; Rocken et al., 1997; Leroy, 1997; Steiner et al., 1999).

The subsequent low Earth Orbit (LEO) satellite missions such as the CHAllenging Minisatellite Payload (CHAMP; Wickert et al., 2001, 2002), the Constellation Observing System for Meteorology, Ionosphere and Climate (COSMIC; Anthes et al., 2000, 2008; Schreiner et al., 2007), the Gravity Recovery And Climate Experiment (GRACE; Beyerle et al., 2005; Wickert et al., 2005), and the Meteorological Operational (MetOp; Edwards and Pawlak, 2000; Luntama et al., 2008) satellites have further affirmed the long-term stability and remarkable consistency (e.g., < 0.2–0.5 K in temperature) of RO observations from different RO missions (Foelsche et al., 2009, 2011a).

The development of GNSS such as China's BeiDou Navigation Satellite System (BDS), Russia's GLObal NAvigation Satellite System (GLONASS), and the European Galileo system, has significantly enhanced the availability and capacity of the GPS-like satellites which will make RO even more attractive in the future. These new GNSS navigation satellites together with planned LEO missions will offer many more RO observations. One of these LEO missions is the FengYun 3 series C satellite (FY-3C), carrying China's first GNSS, Occultation Sounder (GNOS). FY-3C was successfully launched on 23 September 2013 (Bai et al., 2014; Liao et al., 2016).

FY-3C GNOS, developed by National Space Science Center/Chinese Academy of Sciences (NSSC/CAS), is the first BDS/GPS compatible sounder and combines a state-of-the-art RO receiver with an ultra-stable oscillator. The future satellites of the Chinese FY-3 series of operational meteorological satellites, the next being FY-3D, scheduled for launch in 2017, will also carry GNOS instruments, similar to the MetOp series of European satellites with its GNSS Receiver for Atmospheric Sounding (GRAS) instruments (Loiselet et al., 2000).

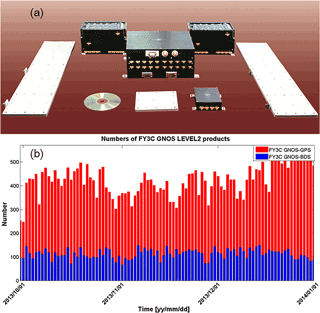
Figure 1 Components of the GNOS instrument (setting/rising occultation antenna and RF unit, left/right; navigation antenna and RF unit, middle in front; tracking and data processing unit, middle in back) (a), and illustration of the daily number of high-quality FY-3C GNOS GPS and BDS RO events for October–December 2013 as used in this study (b).

The GNOS instrument consists of three antennas, three radio frequency (RF) units and a data processor (Fig. 1a), which uses high-dynamic, high-sensitivity signal acquisition and tracking techniques, in which the navigation antenna has a stable phase. Additionally, the different features of BDS and GPS signals have been taken into account in the GNOS design. The GNOS can observe the atmosphere and ionosphere, and its detection height range is from Earth's surface to around 800 km altitude. So far, a 4-year data set of FY-3 GNOS RO observations has been obtained. Figure 1b illustrates the number of both the GPS RO and BDS RO events processed over the 3 months from October to December 2013, which are used for the single- and zero-difference excess phase analysis in this paper.

Regarding the excess phase processing, a single-difference method removes the LEO satellite clock offset by the difference between the GNSS occultation satellite and its GNSS reference satellite (Wickert et al., 2002). Comparing with the original double-difference method (Ware et al., 1996; Rocken et al., 1997), the single-difference method uses the solved GNSS satellite clock offset estimates instead of further differencing between the GNSS satellites and a GNSS ground station; hence, the single-difference method can minimize the effects of ground data error sources (Hajj et al., 2002; Schreiner et al., 2010). Because single differencing (SD) needs no ground station data, the processing is simpler and easier to realize. Therefore the single-difference approach has become widely used in RO data processing after the switch-off of the GPS “selective availability” (SA) mode as of May 2000 (Hajj et al., 2002), which made GPS clock offset estimation sufficiently reliable.

Even more recently, zero-difference processing was started to be used (Beyerle et al., 2005; Wickert et al., 2005), which can compute excess phase data by applying prior estimated LEO and GNSS clock offsets without need of a reference satellite or ground station. However, it requires that the LEO receiver is equipped with an ultra-stable oscillator that, so far, was only available for the GRACE and MetOp missions (Beyerle et al., 2005; Luntama et al., 2008). The FY-3 GNOS instrument is equipped with such an ultra-stable oscillator as well.

BDS is China's global navigation satellite system designed to provide global coverage starting around 2020, with positioning, navigation, timing, and short-message communication service capabilities (Li, 2016). So far, BDS can provide good regional coverage in the Asia-Pacific area with an incomplete constellation, by using two L band frequencies, B1I = 1561.098 MHz (B1) and B2I = 1207.140 MHz (B2). For the time period of this study in fall 2013, the FY-3C GNOS received signals from five geostationary orbit (GEO) satellites (inclination 0^∘, mean altitude 35 786 km), five inclined geosynchronous orbit (IGSO) satellites (inclination 55^∘, mean altitude 35 786 km) and four medium Earth orbit (MEO) satellites (inclination 55^∘, mean altitude 21 528 km) to conduct the radio occultation measurements.

This still growing constellation also provides a practical motivation for zero differencing (ZD) because not all of the FY-3C GNOS BDS RO events can be processed by single differencing, since the incomplete BDS system cannot provide reference satellites for all RO events. On the other hand, the ultra-stable oscillator driving the GNOS receiver makes zero differencing attractive to be potentially used as the method of choice for all BDS RO events. To investigate the feasibility of the zero-difference algorithm for BDS RO data processing, and to evaluate the quality of the retrieved RO data products, we therefore perform in this study a comparative analysis of zero- and single-difference processing for GNOS.

The paper is structured as follows. Section 2 provides a description of our single- and zero-difference excess phase processing. Section 3 presents the FY-3C GNOS data sets and the methods for the inter-comparison analysis. Section 4 presents the statistical analysis results for the various reference data sets. Finally, conclusions are drawn in Sect. 5.

2 Calculation of the FY-3C GNOS excess phase profiles

Excess phase is a key variable during the radio occultation data processing, and GNSS satellite and LEO satellite clock errors are main factors affecting the excess phase accuracy. As summarized above, these two clock error components can either be eliminated by double differencing or (for GPS after the SA mode has been deactivated) the GNSS clock errors can be estimated and subtracted, and so single differencing can be applied, or (given an ultra-stable oscillator at the LEO) both clock errors can be estimated and subtracted, and so zero differencing is possible. Recently, because of its higher complexity and degraded accuracy, double differencing has rarely been used. In this section we describe the single- and zero-difference procedures which we used for the FY-3C GNOS excess phase processing.

2.1 Basic algorithm of the excess phase processing

The GNOS RO excess phase processing determines the total excess phase, which is caused by both the atmosphere and ionosphere, of the GPS L1, L2 and BDS B1, B2 signals as a function of coordinate (GPS) time in the Earth-centered inertial (ECI) true-of-date (TOD) reference frame. The inputs to the processing are GPS, BDS and LEO satellite positions, velocities and clock offsets as a function of coordinate time, LEO satellite attitude information, carrier-phase measurements, antenna-phase center information and Earth orientation information.

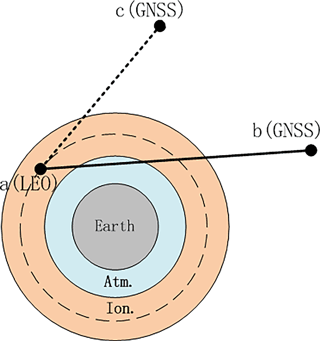
Figure 2 Schematic geometry of GNSS radio occultation for single differencing (using link a-c in addition to link a-b) and zero differencing (using link a-b only).

The outputs of this process include GPS time of the RO event observations, where we adopt the LEO's signal reception time, GPS L1, L2 and BDS B1, B2 total excess phases, position and velocity of the LEO satellite at signal reception time and position and velocity of the GNSS satellite at signal transmission time. Hereafter, we will use the term GNSS to refer to GPS and BDS satellites, as well as L to denote the excess phases for GPS signals as well as for BDS signals. Specifically, in this study, we use the BDS satellite data as orbital data at transmitter side, while time-wise using the GPS time also for the processing of the BDS data. Figure 2 illustrates the geometrical basis of the differencing procedures as part of the excess phase processing.

The observed carrier-phase $L_{a,i}^b$ (in units of length) at carrier signal i between the LEO receiver satellite a and the occulting GNSS transmitter satellite b, as shown in Fig. 2, is the essential raw observable which is modeled as (Schreiner et al., 2010)

$$\begin{array}{ll}{\displaystyle }{L}_{a,i}^b\left(t_{\mathrm{r}}\right)=& {\displaystyle }{\mathit{\rho }}_a^b\left(t_{\mathrm{r}}\right)+c\left(\mathit{\delta }{t}_a-\mathit{\delta }{t}_{a,\text{rel}}\right)-c\left(\mathit{\delta }{t}^b-\mathit{\delta }{t}_{\text{rel}}^b\right)\\ {\displaystyle }& {\displaystyle }+\mathit{\delta }{\mathit{\rho }}_{a,\text{rel}}^b\left(t_{\mathrm{r}}\right)+\mathrm{\Delta }{\mathit{\phi }}_{a,i}^b\left(t_{\mathrm{r}}\right)+\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^b\left(t_{\mathrm{r}}\right)\\ \text{(1)}& {\displaystyle }& {\displaystyle }+\mathit{\delta }{\mathit{\rho }}_{a,\text{trop},i}^b\left(t_{\mathrm{r}}\right),\end{array}$$

where t_r is receive time; c speed of light in vacuum; ${\mathit{\rho }}_a^b$ geometric range between a and b at receive time; δt_a, δt^b offsets between receive time and proper time and transmit time and proper time, respectively; δt_a,rel, $\mathit{\delta }{t}_{\text{rel}}^b$ offsets between proper time and coordinate time due to special and general relativity for the receiver clock and the GNSS satellite clock, respectively; ${\mathit{\tau }}_a^b$ light travel time between receiver and transmitter in vacuum; $\mathit{\delta }{\mathit{\rho }}_{a,\text{rel}}^b$ gravitational delay between receiver and transmitter; $\mathrm{\Delta }{\mathit{\phi }}_{a,i}^b$-phase wind-up correction at receive time; $\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^b$ ionospheric excess phase between receiver and transmitter satellite; $\mathit{\delta }{\mathit{\rho }}_{a,\text{atm},i}^b$ neutral atmospheric excess phase between receiver and transmitter satellite. The ionospheric and neutral atmospheric components $\mathit{\delta }{\mathit{\rho }}_{a,\text{atm},i}^b$ and $\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^b$ jointly are the desired total excess phase to be determined based on Eq. (1).

As it is needed for single-difference processing only, the carrier phase observable $L_{a,i}^c$ at carrier signal i between LEO receiver a and reference GNSS satellite c is formally very similar to the one of the occultation link a-b and modeled as

$$\begin{array}{ll}{\displaystyle }{L}_{a,i}^c\left(t_{\mathrm{r}}\right)=& {\displaystyle }{\mathit{\rho }}_a^c\left(t_{\mathrm{r}}\right)+c(\mathit{\delta }{t}_a-\mathit{\delta }{t}_{a,\text{rel}})-c\left(\mathit{\delta }{t}^c-\mathit{\delta }{t}_{\text{rel}}^c\right)\\ \text{(2)}& {\displaystyle }& {\displaystyle }+\mathit{\delta }{\mathit{\rho }}_{a,\text{rel}}^c\left(t_{\mathrm{r}}\right)+\mathrm{\Delta }{\mathit{\phi }}_{a,i}^c\left(t_{\mathrm{r}}\right)+\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^c\left(t_{\mathrm{r}}\right),\end{array}$$

where the superscript c denotes the reference GNSS satellite and the meaning of the terms is otherwise as for Eq. (1). Since the reference link a-c only crosses (a part of) the ionosphere, the atmospheric excess phase term does not appear in Eq. (1).

The geometric range ${\mathit{\rho }}_a^{b,c}$, of the occultation link a-b or the reference link a-c, can be computed by

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{\mathit{\rho }}_a^{b,c}=\sqrt{{\left(X^{b,c}-X_a\right)}^{\mathrm{2}}+{\left(Y^{b,c}-Y_a\right)}^{\mathrm{2}}+{\left(Z^{b,c}-Z_a\right)}^{\mathrm{2}}},\end{array}$$

where ($X_a,Y_a,Z_a$) denotes the coordinates of the LEO satellite (a) at receive time and ($X^{b,c},Y^{b,c},Z^{b,c}$) denotes the coordinates of the GNSS satellite b or c at transmit time.

The GNSS satellite orbits (positions and velocities) and the GNSS clock offset estimates δt^b,c are provided by the International GNSS Service (IGS) and applied as needed (a transformation from the International Terrestrial Reference Frame of IGS to our true-of-date reference frame is performed). Using the orbit information, the periodic relativistic effect of the GNSS satellite clock $\mathit{\delta }{t}_{\text{rel}}^{b,c}$ can be modeled by (Schreiner et al., 2010)

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }\mathit{\delta }{t}_{\text{rel}}^{b,c}=-\mathrm{2}{\displaystyle \frac{{\mathit{r}}^{b,c}\cdot {\mathit{v}}^{b,c}}{c^{\mathrm{2}}}},\end{array}$$

where r^b,c and v^b,c are the GNSS satellite position and velocity vectors at signal transmit time. Similar to the GPS, BDS clocks include an intrinsic frequency adjustment (to effectively beat at the rate of clocks at the Earth's mean sea-level surface) in order to reduce the relativistic effect on the observations (Ashby, 2003). Regarding the values of the frequency adjustment, they depend on the orbit altitudes; i.e., the adjustment for BDS MEO satellites (∼ 21 500 km altitude) is similar to GPS satellites (∼ 20 200 km) while the BDS IGSO and GEO satellites (∼ 35 800 km) receive slightly different values. In our processing we do not (yet) account for the small relativistic effects on the LEO (GNOS) clocks but investigate potentially including these effects in the future.

The gravitational delay $\mathit{\delta }{\mathit{\rho }}_{a,\text{rel}}^{b,c}$ is modeled by (Schreiner et al., 2010)

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }\mathit{\delta }{\mathit{\rho }}_{a,\text{rel}}^{b,c}={\displaystyle \frac{\mathrm{2}G{M}_{\mathrm{E}}}{c^{\mathrm{2}}}}\ln \left({\displaystyle \frac{r^{b,c}+r_a+{\mathit{\rho }}_a^{b,c}}{r^{b,c}+r_a-{\mathit{\rho }}_a^{b,c}}}\right),\end{array}$$

where G is Newton's gravitational constant, M_E is the Earth's mass and r^b,c and r_a are the transmitter and receiver radial positions at signal transmit and receive times, respectively.

The phase wind-up correction term $\mathrm{\Delta }{\mathit{\phi }}_{a,i}^{b,c}$ can be modeled in the form

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }{\mathit{\phi }}_{a,i}^{b,c}={\mathit{\lambda }}_i\cdot \text{sign}\left(\mathit{k}\cdot \left(\mathit{D}\times D\right)\right)\cdot {\cos }^{-\mathrm{1}}\\ \text{(6)}& {\displaystyle }& {\displaystyle }\left(D\cdot \mathit{D}/\left(\left|D\right|\cdot \left|\mathit{D}\right|\right)\right),\end{array}$$

where λ_i is the wavelength of carrier signal i, k is the unit vector from transmitter to receiver and D and D are so-called effective dipole vectors; for details on this modeling see Kouba (2015).

2.2 Single-difference processing

In the single-difference processing, we use Eq. (1) as the basic equation and Eq. (1) as the auxiliary equation. GNSS clock offsets are subtracted, and Eqs. (1) to (4) are applied to model and also subtract the GNSS-related geometric and relativistic terms from the occultation and reference link so that only the excess phases and LEO clock offsets remain.

Next, the excess phase of the reference link (which is only an ionospheric excess phase $\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^c$) can be effectively eliminated by the classical dual-frequency ionospheric correction of L1 and L2 phases (e.g., Ware et al., 1996). That is, an ionosphere-corrected-phase $L_{a,\mathrm{3}}^c$ can be calculated for the reference link by

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{L}_{a,\mathrm{3}}^c=L_{a,\mathrm{1}}^c\left(t_{\mathrm{r}}\right)+c_{\mathrm{2}}〈L_{a,\mathrm{1}}^c\left(t_{\mathrm{r}}\right)-L_{a,\mathrm{2}}^c\left(t_{\mathrm{r}}\right)〉\end{array}$$

or

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }{L}_{a,\mathrm{3}}^c=L_{a,\mathrm{2}}^c\left(t_{\mathrm{r}}\right)+c_{\mathrm{1}}〈L_{a,\mathrm{1}}^c\left(t_{\mathrm{r}}\right)-L_{a,\mathrm{2}}^c\left(t_{\mathrm{r}}\right)〉,\end{array}$$

where 〈⋅〉 denotes moving-average smoothing (over 2 s) and where $c_{\mathrm{1}}=f_{\mathrm{1}}^{\mathrm{2}}/\left(f_{\mathrm{1}}^{\mathrm{2}}-f_{\mathrm{2}}^{\mathrm{2}}\right)$ and $c_{\mathrm{2}}=f_{\mathrm{2}}^{\mathrm{2}}/\left(f_{\mathrm{1}}^{\mathrm{2}}-f_{\mathrm{2}}^{\mathrm{2}}\right)$ are just constants in which f₁ and f₂ are the frequencies of the L1 and L2 signals, respectively. In our processing we chose to employ Eq. (4) for the $L_{a,\mathrm{3}}^c$ calculation.

Finally, the effects of the receiver clock, $c(\mathit{\delta }{t}_a-\mathit{\delta }{t}_{a,\text{rel}})$, are eliminated by single differencing (SD), that is, by the subtraction of the reference-link-phase $L_{a,\mathrm{3}}^c$ from the occultation-link-phase $L_{a,i}^b$, so that we obtain the desired SD-based total excess phase $\mathrm{\Delta }{L}_{a,i}^{\text{SD}}$,

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathrm{\Delta }{L}_{a,i}^{\text{SD}}\left(t_{\mathrm{r}}\right)=L_{a,i}^b\left(t_{\mathrm{r}}\right)-L_{a,\mathrm{3}}^c\left(t_{\mathrm{r}}\right)=\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^b\left(t_{\mathrm{r}}\right)+\mathit{\delta }{\mathit{\rho }}_{a,\text{atm},i}^b\left(t_{\mathrm{r}}\right).\end{array}$$

2.3 Zero-difference processing

The single-difference approach has some advantages over the double-difference approach, as noted in the introduction, and has therefore been widely used in GPS RO data processing. However, it is difficult to find a suitable reference satellite for each RO event to calculate the excess phase using single-difference when the GNSS space segment is still an incomplete constellation, as with the current BDS.

Zero differencing also will likely produce lower-noise excess phase data than single differencing, from applying the estimated LEO clock offsets and avoiding the use of a reference link (being an additional error source). It can be employed if the LEO receiver is equipped with an ultra-stable oscillator such as in the case of the GNOS instrument.

In the zero differencing (ZD) approach we employ Eq. (1) directly and model and subtract all relevant terms as summarized in Sect. 2.1 above, including the GNSS and LEO clock offsets, so that we obtain the desired ZD-based total excess phase $\mathrm{\Delta }{L}_{a,i}^{\text{ZD}}$,

$$\begin{array}{ll}{\displaystyle }\mathrm{\Delta }{L}_{a,i}^{\text{ZD}}\left(t_{\mathrm{r}}\right)& {\displaystyle }=\mathit{\delta }{\mathit{\rho }}_{a,\text{ion},i}^b\left(t_{\mathrm{r}}\right)+\mathit{\delta }{\mathit{\rho }}_{a,\text{trop},i}^b\left(t_{\mathrm{r}}\right)\\ {\displaystyle }& {\displaystyle }=L_{a,i}^b\left(t_{\mathrm{r}}\right)-\left({\mathit{\rho }}_a^b\left(t_{\mathrm{r}}\right)+c(\mathit{\delta }{t}_a-\mathit{\delta }{t}_{a,\text{rel}})\right.\\ \text{(10)}& {\displaystyle }& {\displaystyle }\left.-c\left(\mathit{\delta }{t}^b-\mathit{\delta }{t}_{\text{rel}}^b\right)+\mathit{\delta }{\mathit{\rho }}_{a,\text{rel}}^b\left(t_{\mathrm{r}}\right)+\mathrm{\Delta }{\mathit{\phi }}_{a,i}^b\left(t_{\mathrm{r}}\right)\right).\end{array}$$

3 Differencing and analysis methods for the GNOS BDS RO data

3.1 Necessity of zero differencing for GNOS BDS RO data

As mentioned, the single-difference approach involves a GNSS reference satellite, which normally has high signal-to-noise ratio (SNR) and high-phase measurement accuracy. In order to use the specific reference satellite most likely to have the best signal quality and lowest ionospheric influence, our FY-3C GNOS receiver software chooses the GNSS satellite with highest elevation angle seen by the navigation (zenith) antenna. For reasons of robustness and for ensuring best consistency, here we only use BDS reference satellites for BDS occultations (likewise GPS reference satellites only for GPS occultations).

The largest gain and half-power beam width of GNOS's POD antenna is 5 dB and 40^∘, respectively, and the normal vector of the antenna plane points to the zenith; hence, the antenna gain increases with increasing elevation angle. Therefore, ignoring the multi-path effect, the positioning channel carrier-phase error increases with decreasing elevation and, ultimately, the satellite tracking will lose the lock when the elevation angle becomes very small.

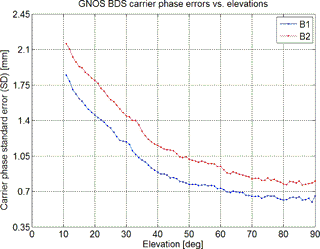
Figure 3 Statistics of FY-3C GNOS BDS carrier-phase SDs (blue for B1 signal carrier phase; red for B2 signal carrier phase) as a function of elevation angle, calculated by using positioning channel measurements.

Figure 3 illustrates the GNOS in-orbit testing results of the BDS B1 and B2 carrier-phase observation error SD, as a function of elevation angle. As can be clearly seen, both the B1 and B2 carrier-phase measurement errors decrease with increasing elevation angle. At elevation angles larger than 10^∘, the B1 and B2 carrier-phase errors are less than 2.2 mm. Therefore, currently we select the reference satellite for the single-difference method from those satellites whose elevation angle is at least larger than 10^∘.

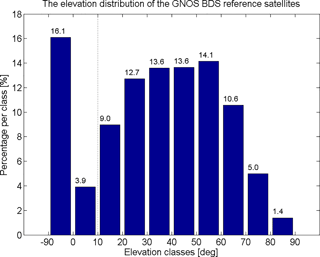
Figure 4 Histogram of the maximum elevation angle of the BDS reference satellites, with the statistics based on the 13 564 BDS RO events that occurred over October–December 2013.

Applying this 10^∘ elevation threshold criterion, we counted the number of GNOS BDS RO events with and without reference satellites. In this statistical analysis all the GNOS BDS RO events that occurred from 1 October to 31 December 2013 were included. Figure 4 shows that during these 3 months there were 13 564 GNOS BDS RO events in total, of which about 16 % had a maximum elevation angle of possible reference satellites below 0^∘, and a total of 20 % had their reference satellites below 10^∘. In practice, less than 10^∘ means that the reference satellites' tracking accuracy is considered not sufficient for single differencing. Therefore, these 20 % of BDS RO events can only be meaningfully processed by the zero-difference approach, since the still-regional BDS system coverage cannot satisfy the 10^∘ elevation threshold criterion for these events.

3.2 GNOS BDS RO data and statistical analysis method

To evaluate the performance of the zero- and single-difference methods, we have conducted a comparison analysis of the retrieved FY-3C GNOS BDS RO bending angle and refractivity data for the selected 92 days from 1 October to 31 December 2013, retrieved by either including the single-difference or zero-difference method in the excess phase processing.

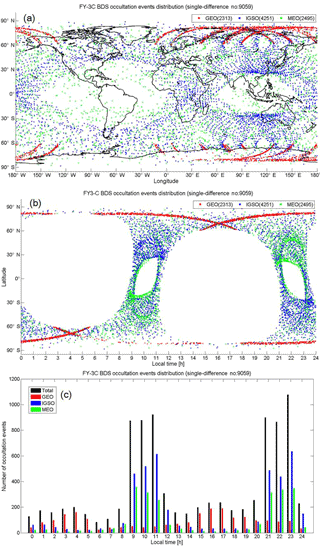
Figure 5 Geographical and local time distribution of the GNOS BDS RO events that have proper BDS reference satellites for single-difference processing (red from the BDS-GEO satellites; blue from BDS-IGSO; green from BDS-MEO; numbers in parentheses denote the associated number of events during October–December 2013). Distributions are shown as a function of latitude and longitude (a), as a function of local time and latitude (b), and in histogram style as a function of local time (black denotes from all BDS satellites) (c).

In our data processing of bending angle and refractivity, a quality control algorithm has been used (which for single differencing reduced the profile data set by about 2 % and for zero differencing by less than 1 %). The processing statistics we obtain show that, after quality control, the number of RO events obtained by zero differencing is higher by about 13 % than the one obtained by single differencing, which we find is due to some ineffective reference BDS satellite links during the single-difference processing. The geographic and local time distribution of the RO events that also have proper BDS reference satellites for single-difference processing is shown in Fig. 5.

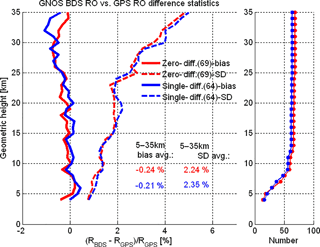
Figure 6 Mean difference (bias) and standard deviation (SD) statistics of GNOS-derived refractivity (R) profiles retrieved based on the zero differencing (red) and single differencing (blue) methods, from an ensemble of BDS RO profiles collocated with GPS RO profiles (±200 km/±1 h collocation criterion; outlier quality control with maximum of 8 % deviation to ECMWF within 5–35 km, leading to slightly more collocations for the zero differencing data). Bias (solid) and SD (dashed) profiles as well as the number-of-event profiles (small panel on the right) are shown. The legend indicates the average bias and SD values within 5–35 km.

Figure 5a shows that the geographic distribution of events well reflects the different BDS orbit types. BDS-GEO RO events mainly distribute in the Southern and Northern Hemisphere high-latitude zones along the longitude sector of the Chinese region. The number of BDS-IGSO RO events is highest, almost equal to the number of GEO and MEO RO events together. The BDS-IGSO RO event coverage forms a quasi-global “8” shape, with the larger oval over the South American, Pacific, and Atlantic Ocean areas, and the somewhat smaller oval over Southeast Asia, Northwest Australia, Pacific, and Indian Ocean areas. Similar to the typical distribution of GPS RO events (e.g., Pirscher et al., 2007; Anthes et al., 2008), the BDS-MEO RO events show essentially global coverage, with more RO events in the mid- and high-latitude zones and less at low latitudes.

Figure 5b and c show the distribution of the RO events in a complementary way with focus on local time, again reflecting well the different BDS orbit types and their impact on RO event locations in space and time. It can be seen that the BDS-GEO RO events occur during all 24 h of the day, while the BDS-IGSO and BDS-MEO RO events distribute mainly in the 09:00–11:00 and 21:00–23:00 LT ranges (best seen in Fig. 5c). In particular, at low and middle latitudes, equatorward of about 50 to 60^∘, not one BDS RO event occurs within about 00:00–08:00 and 12:00–20:00 LT (see Fig. 5b). This is due to the near-polar sun-synchronous orbit of the FY-3C meteorological satellite, similar to the European MetOp satellites as analyzed by Pirscher et al. (2007).

The distribution of the GNOS BDS RO events processed by using zero differencing (not separately shown) is very similar to Fig. 5, though with slightly more RO events (2623 BDS-GEO, 4820 BDS-IGSO and 2863 BDS-MEO) passing the quality control.

Before the validation against the GNOS-independent reference data from the European Centre for Medium-Range Weather Forecasting (ECMWF) and radiosondes, we did a cross-check of the quality of the BDS RO events based on a limited ensemble of co-located profiles undertaken between GNOS BDS and GPS RO events.

Figure 6 shows the results of our inter-comparison of retrieved refractivity profiles from zero differencing and single differencing for BDS against the single-differencing results for GPS (zero-differencing GPS data were not available). A reasonably high consistency of the BDS- and GPS-derived RO profiles is found: the BDS refractivities both from zero and single differencing appear essentially unbiased against the GPS refractivities within 5 to 25 km. Also, the SD is found to be within about 2 % in this core height range. Future more refined GNOS data processing and analysis will clearly allow further improvement of this consistency, including higher up into the stratosphere, from improvements to both BDS RO and GPS RO processing; work towards this goal is ongoing.

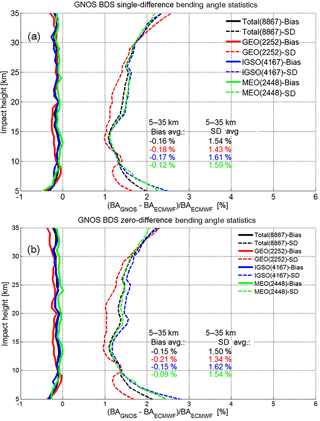
Figure 7 Mean difference (bias) and standard deviation (SD) statistics of the GNOS bending-angle profiles retrieved by using excess phases from the single-difference processing (a) and the zero-difference processing (b), respectively, with the co-located ECMWF bending-angle profiles used as reference. Bias (solid) and SD (dashed) profiles are shown for the set of all BDS RO events (black), and the subsets of BDS-GEO (red), BDS-IGSO (blue), and BDS-MEO (green). Legends also indicate the number of events involved (the joint set of RO events from both the single- and zero-difference processing) and the average bias and SD values over the 5–35 km range.

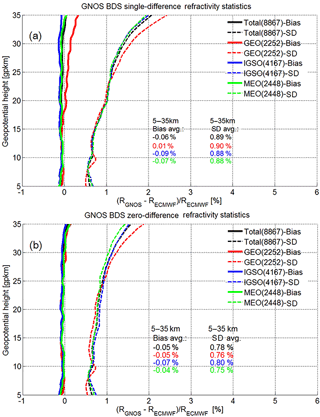
Figure 8 Mean difference (bias) and standard deviation (SD) statistics of the GNOS refractivity profiles retrieved by using excess phases from the single-difference processing (a) and the zero-difference processing (b), respectively, with the co-located ECMWF refractivity profiles used as reference. Same layout as Fig. 6; see caption there for further details.

For producing the statistical validation analysis results compared to the independent reference data, we calculated the fractional error of the retrieved bending-angle (α) and refractivity (R) profiles in the form,

$$\begin{array}{}\text{(11)}& {\displaystyle }& {\displaystyle }{E}_{\mathit{\alpha }}=\mathrm{100}\times {\displaystyle \frac{\mathit{\alpha }-{\mathit{\alpha }}_{\text{ref}}}{{\mathit{\alpha }}_{\text{ref}}}}\left[\mathrm{\%}\right],\text{(12)}& {\displaystyle }& {\displaystyle }{E}_R=\mathrm{100}\times {\displaystyle \frac{R-R_{\text{ref}}}{R_{\text{ref}}}}\left[\mathrm{\%}\right],\end{array}$$

where E denotes the estimated fractional error profiles (against the reference data) for which ensemble estimates of biases (bias) and standard deviations (SD) are illustrated in the result figures. For retrieving bending-angle and refractivity profiles from our excess phase data we employed the radio occultation processing package ROPP from the European ROM SAF consortium (Offiler, 2008).

As reference data we used analysis data from the European Centre for Medium-Range Weather Forecasts (ECMWF) as well as radiosonde data obtained from the global radiosonde archive of the National Oceanic and Atmospheric Administration–National Centers for Environmental Information (NOAA-NCEI).

The ECMWF analysis data were used as 6-hourly fields (00:00, 06:00, 12:00, 18:00 UTC time layers every day) at a horizontal resolution of about 300 km and with 137 vertical model levels (yielding about 0.5 to 1.5 km resolution over the upper troposphere/lower stratosphere domain of interest). Vertical profiles co-located with the GNOS RO profiles were extracted from these fields by bilinear interpolation in latitude and longitude to the mean RO event location, using the nearest-neighbor time layer of the RO event time. Since the GNOS data were not assimilated into the ECMWF system the data are clearly independent.

The radiosonde profiles had about 0.5 to 3 km vertical resolution over the domain of interest, and were used with a ±1^∘ lat–long/±1 h collocation criterion to the RO event. This criterion pairs the data sufficiently horizontally close in order to ensure reasonably low representativeness error (e.g., Hajj et al., 2004; Anthes et al., 2008).

4 GNOS BDS RO single-difference and zero-difference result analysis

The target domain for the comparative statistical analysis is from 5 to 35 km height (upper troposphere and lower stratosphere, UTLS), since the data quality above 35 km and below 5 km is usually poorer, due to the ionospheric effects and tropospheric multipath effects, respectively (e.g., Scherllin-Pirscher et al., 2011a, b; Steiner et al., 2013). We first inspect difference statistics to ECMWF and subsequently to radiosondes.

4.1 Comparison analysis of bending angle with ECMWF data

Figure 7 shows the statistics of the GNOS BDS RO bending-angle results for the different BDS subsystems (GEO, IGSO, MEO) and the full BDS (total), for both single differencing (Fig. 7a) and zero differencing (Fig. 7b). The bias and SD profiles have been calculated from the large ensembles of these event data sets, based on the fractional difference profiles according to Eq. (3).

In line with expectations, the biases and SDs are slightly smaller for the zero differencing than for the single differencing (though even smaller SDs might be expected from avoiding the reference link computation; e.g., Schreiner et al., 2010), but in general they are very similar. Both cases show a small negative bias of around −0.15 % against ECMWF, and a SD of around 1.5 %. At least part of the bias is likely from slight differences in vertical geolocation of GNOS and reference profiles, for which ensuring rigorous consistency is a subtle process (Scherllin-Pirscher et al., 2017). Likewise, part of the SD is from representativeness errors between the GNOS and ECMWF profiles since, despite being co-located in the mean location, they have different detailed locations and resolutions (Foelsche et al., 2011b; Scherllin-Pirscher et al., 2011b).

Several aspects of small visible differences (e.g., specific difference of GEO results from the other results, increasing SD differences below 10 km) will be clarified by detailed excess phase processing and retrieval error analyses as part of follow-up work. Regarding the larger deviation of the GEO results in general, these may be related to the fact that the GEO orbit determination is more challenging as well as to the limited geographical coverage of these RO events, with event locations only at latitudes beyond 60^∘ (see Fig. 5).

Overall the results confirm the high quality of the GNOS retrievals, in line with recent results by Liao et al. (2016), and a robust zero-difference processing being a viable alternative to the single-difference processing. The results also indicate that the BDS retrievals can achieve quality comparable to what is well established for GPS retrievals. Thanks to the diversity of BDS orbits, we can also demonstrate RO retrievals from occultations with GNSS transmitters not in medium Earth orbit (MEO). The results clearly indicate that the GNSS transmitters in GEO and IGSO can also provide quality comparable to that of MEO.

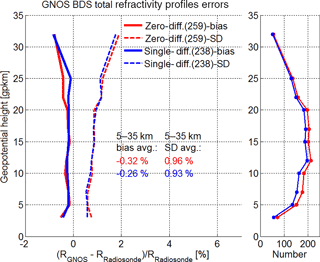
Figure 9 Mean difference (bias) and standard deviation (SD) statistics of the GNOS refractivity profiles retrieved by using either zero differencing (red) or single differencing (blue), with collocated radiosonde refractivity profiles used as reference (±1 lat–long$/\pm$1 h collocation criterion). Bias (solid) and SD (dashed) profiles as well as the number-of-event profiles (small panel on the right) are shown for the total set of BDS RO events. The legends also indicate the number of events involved and the average bias and SD values within 5–35 km.

4.2 Comparison analysis of refractivity with ECMWF data

Figure 8 shows the statistics of the GNOS BDS RO refractivity results, again for the different BDS subsystems (GEO, IGSO, MEO) and the full BDS (total), for both single differencing (Fig. 8a) and zero differencing (Fig. 8b). The bias and SD profiles have been calculated from these large BDS event ensembles based on the fractional refractivity difference profiles according to Eq. (7).

Similar to the bending-angle results (Fig. 4), the biases and SDs for the refractivity results are a bit smaller for the zero differencing than for the single differencing but are otherwise quite similar. Both cases show a small negative bias of around −0.05 % against ECMWF, and a SD of near 0.8 % (single differencing closer to 0.9 %). This reduction of bias and SD magnitudes compared to the bending angle (by about a factor of 2) is due to the filtering properties of the Abelian integral that transforms the bending angle to refractivity profiles (Rieder and Kirchengast, 2001; Scherllin-Pirscher et al., 2011a; Schwarz et al., 2017).

As for the bending angles, aspects of small visible differences of refractivity, such as more deviation of the GEO results, will also be explored by detailed excess phase processing and retrieval error analyses as part of follow-up work.

Overall the refractivity results confirm the messages summarized in Sect. 4.1 based on the bending-angle results. That is, they underline the high quality of the GNOS BDS retrievals as being (nearly) comparable to GPS retrievals, the robustness of both the zero- and single-difference processing and the reliable retrieval quality of RO events with GNSS transmitters on MEO satellites as well as on GEO and IGSO satellites.

4.3 Comparison analysis of refractivity with radiosonde data

Figure 9 shows the single- and zero-difference results for refractivity statistics, bias and SD profiles, against collocated radiosonde profiles and only for the whole set of BDS RO events, since the number of collocations is more limited. The number of RO events entering into the statistics is also strongly height-dependent in this case and is therefore shown as (maximum) number in the legend in addition to as height profiles in the side panel (Fig. 9, right).

Given the smaller ensemble size of about 50 to 200 events (depending on height), and the less strict collocation and thus somewhat higher representativeness error than for the ECMWF data extracted at the mean RO event location, these refractivity results are expected to exhibit somewhat more deviations than those in Fig. 8. As Fig. 9 shows, the bias is nevertheless still fairly small, near −0.3 %, and the SD is near 0.95 %, i.e., still below 1 %.

In summary, the comparison to this entirely independent radiosonde data set underpins the finding that both zero and single differencing are robust and that the GNOS BDS retrievals can perform similarly to GPS retrievals. The latter were established to compare well to quality radiosondes (Anthes, 2011; Ladstaedter et al., 2015).

5 Conclusions

In this study we have introduced our single- and zero-difference excess phase processing of BeiDou System (BDS) RO data of the FY-3C GNOS mission and evaluated the quality of atmospheric profiles derived from this single- and zero-difference processing.

The single differencing can correct the receiver clock offset, and thus it has lower requirements on the receiver clock stability. However, it requires a proper reference GNSS satellite and will induce some of this reference satellite's positioning and carrier-phase measurement errors into the RO processing. The advantage of the zero-difference algorithm is its independence from reference satellites, but it requires a receiver clock of very high quality (ultra-stable oscillator such as available for GNOS) to obtain a highly accurate receiver clock offset estimate, which nevertheless can leave some residual errors after the clock offset correction.

Because BDS is still a regional navigation system, we found that about 20 % of the GNOS BDS RO events do not have proper reference satellites for single differencing, providing another argument for a zero-difference alternative. We performed a comparative analysis of the zero-difference and single-difference excess phase processing chains for the FY-3C GNOS BDS RO observations, in which independent reanalysis data from ECMWF and collocated high-quality data from radiosondes have been used as reference for evaluating the retrieved bending-angle and refractivity profiles over the upper troposphere and lower stratosphere (UTLS, 5 to 35 km).

The results showed that the GNOS BDS RO profiles derived by using both the zero-difference and single-difference algorithms exhibit very good consistency with the ECMWF and radiosonde data. The zero-difference method appeared to perform slightly better than the single-difference method, especially visible at stratospheric altitudes (above 15 km).

Compared to ECMWF data, the average UTLS bending-angle bias was found to be near −0.15 % and the associated average SD near 1.5 %; the average refractivity bias was accordingly found to be as small as around −0.05 % and the associated SD at about 0.8 %. Compared to radiosonde data, the GNOS BDS RO refractivity profiles both from zero- and single-difference processing also showed high consistency, with the average refractivity bias in the UTLS found to be near −0.3 % and the associated SD near 0.95 %, i.e., also below 1 %, despite increased representativeness error in this latter comparison.

Overall these results indicate the high quality of the GNOS BDS retrievals, and that robust zero-difference processing is a viable alternative to single-difference processing. The results also indicate that the BDS retrievals can achieve quality comparable to the established GPS retrievals. Based on the diversity of BDS orbits, we also demonstrated for the first time RO retrievals from occultations with GNSS transmitters not in MEO. We also found that the GNSS transmitters in GEO and in IGSO provide quality comparable to the ones on MEO satellites.

Currently, the GRAS onboard the European meteorological satellite series MetOp and the GNOS occultation receiver onboard the Chinese meteorological satellite series FY-3 are the only two RO instruments for long-term operational observations that include an ultra-stable crystal oscillator featuring a very high-quality Allan deviation at the 10⁻¹² s accuracy level. In the future, additional RO missions such as COSMIC-2, MetOp-SG and advanced-GNOS instruments will improve the quality even further. For these operational backbone missions, leading the field with their data quality, the zero-difference method will generally perform better and will thus likely replace the single-difference method in the future.