Development of time-varying global gridded T_s–T_m model for precise GPS–PWV retrieval

Water-vapor-weighted mean temperature, T_m, is the key variable for estimating the mapping factor between GPS zenith wet delay (ZWD) and precipitable water vapor (PWV). For the near-real-time GPS–PWV retrieval, estimating T_m from surface air temperature T_s is a widely used method because of its high temporal resolution and fair degree of accuracy. Based on the estimations of T_m and T_s at each reanalysis grid node of the ERA-Interim data, we analyzed the relationship between T_m and T_s without data smoothing. The analyses demonstrate that the T_s–T_m relationship has significant spatial and temporal variations. Static and time-varying global gridded T_s–T_m models were established and evaluated by comparisons with the radiosonde data at 723 radiosonde stations in the Integrated Global Radiosonde Archive (IGRA). Results show that our global gridded T_s–T_m equations have prominent advantages over the other globally applied models. At over 17 % of the stations, errors larger than 5 K exist in the Bevis equation (Bevis et al., 1992) and in the latitude-related linear model (Y. B. Yao et al., 2014), while these large errors are removed in our time-varying T_s–T_m models. Multiple statistical tests at the 5 % significance level show that the time-varying global gridded model is superior to the other models at 60.03 % of the radiosonde sites. The second-best model is the 1^∘ × 1^∘ GPT2w model, which is superior at only 12.86 % of the sites. More accurate T_m can reduce the contribution of the uncertainty associated with T_m to the total uncertainty in GPS–PWV, and the reduction augments with the growth of GPS–PWV. Our theoretical analyses with high PWV and small uncertainty in surface pressure indicate that the uncertainty associated with T_m can contribute more than 50 % of the total GPS–PWV uncertainty when using the Bevis equation, and it can decline to less than 25 % when using our time-varying T_s–T_m model. However, the uncertainty associated with surface pressure dominates the error budget of PWV (more than 75 %) when the surface pressure has an error larger than 5 hPa. GPS–PWV retrievals using different T_m estimates were compared at 74 International GNSS Service (IGS) stations. At 74.32 % of the IGS sites, the relative differences of GPS–PWV are within 1 % by applying the static or the time-varying global gridded T_s–T_m equations, while the Bevis model, the latitude-related model and the GPT2w model perform the same at 37.84 %, 41.89 % and 29.73 % of the sites. Compared with the radiosonde PWV, the error reduction in the GPS–PWV retrieval can be around 1–2 mm when using a more accurate T_m parameterization, which accounts for around 30 % of the total GPS–PWV error.

1 Introduction

Water vapor is an important trace gas and one of the most variable components in the troposphere. The transport, concentration and phase transition of water vapor are directly involved in the atmospheric radiation and hydrological cycle. It plays a key role in many climate changes and weather processes (Adler et al., 2016; Mahoney et al., 2016; Song et al., 2016). However, water vapor has high spatial–temporal variability, and its content is often small within the atmosphere. It is a challenge to measure water vapor content accurately and timely. For decades, several methods have been studied, such as radiosondes and water vapor radiometers, sun photometers and GPS (Campmany et al., 2010; Ciesielski et al., 2010; Liu et al., 2013; Perez-Ramirez et al., 2014; Li et al., 2016). Compared with the traditional water vapor observations, ground-based GPS water vapor measurement has the advantages of high accuracy, high spatial–temporal resolution, all-weather availability and low-cost (Haase et al., 2003; Pacione and Vespe, 2008; Lee et al., 2010; Means, 2013; Lu et al., 2015). Ground-based GPS water vapor products, mainly including precipitable water vapor (PWV), are widely used in many fields such as real-time vapor monitoring, weather and climate research, and numerical weather prediction (NWP) (Van Baelen and Penide, 2009; Karabatic et al., 2011; Rohm et al., 2014; Adams et al., 2017).

GPS observations require some kind of meteorological element to estimate PWV. Zenith hydrostatic delay (ZHD) can be calculated using surface pressure P_s with the equation (Ning et al., 2013):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathrm{ZHD}=(\mathrm{2.2767}\pm \mathrm{0.0015}){\displaystyle \frac{P_{\mathrm{s}}}{f(\mathit{\phi },H)}},\end{array}$$

where φ is the latitude, H is the geoid height in meters, and

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }f(\mathit{\lambda },H)=\left(\mathrm{1}-\mathrm{2.66}\times {\mathrm{10}}^{-\mathrm{3}}\cos \mathit{\phi }-\mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{7}}H\right).\end{array}$$

Then, zenith wet delay (ZWD) is generated by subtracting ZHD from zenith total delay (ZTD). ZTD can be directly estimated from precise GPS data processing. Finally, a conversion factor Q, which is used to map ZWD onto PWV, is determined by the water-vapor-weighted mean temperature T_m over a GPS station. The mapping function from ZWD to PWV is expressed as follows (Bevis et al., 1992):

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }\mathrm{PWV}={\displaystyle \frac{\mathrm{ZWD}}{Q}}={\displaystyle \frac{\mathrm{ZTD}-\mathrm{ZHD}}{Q}},\end{array}$$

and Q is computed using following formula:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }Q={\mathrm{10}}^{-\mathrm{6}}{\mathit{\rho }}_{\mathrm{w}}{R}_{\mathrm{v}}\left[\left(k_{\mathrm{3}}/T_{\mathrm{m}}\right)+k_{\mathrm{2}}^{\prime }\right],\end{array}$$

where ρ_w is the density of liquid water, R_v is the specific gas constant for water vapor, $k_{\mathrm{2}}^{\prime }=(\mathrm{22.1}\pm \mathrm{2.2})$ K mbar⁻¹ and $k_{\mathrm{3}}=(\mathrm{3.739}\pm \mathrm{0.012})\times {\mathrm{10}}^{\mathrm{5}}$ K² mbar⁻¹ are physical constants (Ning et al., 2016). T_m is the weighted mean temperature which is defined as a function related to the temperature and water vapor pressure. It can be approximated as the following formula (Bevis et al., 1992):

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }{T}_{\mathrm{m}}={\displaystyle \frac{\int \frac{e}{T}\mathrm{d}z}{\int \frac{e}{T^{\mathrm{2}}}\mathrm{d}z}}\approx {\displaystyle \frac{\sum _{i=\mathrm{1}}^n\frac{e_i}{T_i}\mathrm{\Delta }{z}_i}{\sum _{i=\mathrm{1}}^n\frac{e_i}{T_i^{\mathrm{2}}}\mathrm{\Delta }{z}_i}},\end{array}$$

where e and T represent vapor pressure in hPa and temperature in Kelvin, i denotes the ith level and Δz_i is the height difference of ith level. Vapor pressure e is calculated using equation e=e_s × RH; RH is the relative humidity, and the saturation vapor pressure e_s can be estimated from the temperature observations using a Goff–Gratch formula (Sheng et al., 2013).

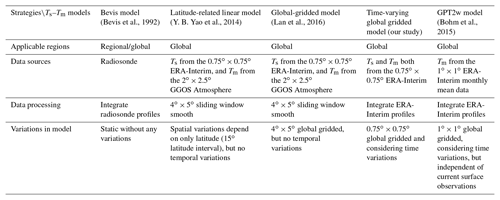
Table 1 Main differences between T_s and T_m models developed in this study and other global used T_m estimation models.

There are the three main approaches that are used to estimate T_m. They have respective advantages and disadvantages when they are applied for different purposes:

1. The integration of vertical temperature and humidity profiles is believed to be the most accurate method. The profile data can be extracted from radio soundings or NWP data sets (Wang et al., 2016). However, some inconveniences have to be endured. It usually takes a considerable amount of time to acquire the NWP data, which are normally released in a large volume every 6 h. This limits the use of NWP data in the near-real-time GPS–PWV retrieval. Radiosonde data are another profile data source, but it has low spatial and temporal resolution. At most of the radiosonde sites, sounding balloons are cast daily at 00:00 and 12:00 UTC. Furthermore, a large number of GPS stations are not located close enough to the radio sounding sites. Therefore, such methods are appropriate for climate research or the study of long-term PWV trends, but do not meet the real-time requirements.

2. Several global empirical models of T_m are established based on the analyses of T_m time series from NWP data sets or other sources (Yao et al., 2012; Chen et al., 2014; Bohm et al., 2015). T_m at any time and any location can be estimated from these models. They are often independent of the current meteorological observations, which are required to be observed together with the GPS data. However, some important real variations, which may be dramatic during some extreme weather events, can be lost without the constraints of current real data (Jiang et al., 2016). Therefore, these modeled estimates are not accurate enough for high-precision meteorological applications, such as providing GPS–PWV estimates for weather prediction.

3. Many studies indicated that the T_m parameter has a relationship with some surface meteorological elements, such as surface air temperature or surface air humidity (Bevis et al., 1992; Y. Yao et al., 2014). These surface meteorological parameters can be measured accurately and rapidly. T_m is then estimated using these surface measurements. However, these studies also revealed that the relationships are often weak, except the T_s–T_m relationship. For example, Bevis et al. (1992) introduced the equation T_m=0.72 T_s+70.2 [K] after analyzing 8712 radiosonde profiles collected at 13 sites in the US over 2 years. This equation has been widely used in many other studies.

According to Rohm et al. (2014), GPS–ZTD can be estimated very precisely by real-time GPS data processing. This means that T_m is one of the key parameters in the near-real-time GPS–PWV estimation. On the other hand, method (3) is the most suitable method for estimating T_m in near real-time because of its balance between timeliness and accuracy. The T_s–T_m relationship has spatial–temporal variations. Several regional T_s–T_m equations were established using the profile data over corresponding fields (Wang et al., 2012). However, a T_s–T_m model without spatial variation is not good enough for a vast field, e.g., the Indian region (Singh et al., 2014). Aside from this, some vast areas have no specific high-precision T_s–T_m model, for example over the oceans. In general, significant differences exist between oceanic and terrestrial atmospheric properties, especially near the surface layer and within the boundary layer. The change in T_s from land to ocean may be very different from that of T_m. Therefore it is necessary to model the T_s–T_m relationship over oceanic regions, since several ocean-based GPS meteorology experiments demonstrated the potential of this technique to retrieve PWV over the broad ocean (Rocken et al., 2005; Kealy et al., 2012). A global gridded T_s–T_m model has been established by Lan et al. (2016). In this model, the 2.0^∘ × 2.5^∘ T_m data from GGOS Atmosphere and the 0.75^∘ × 0.75^∘ T_s data from the European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis data are both smoothed to the resolution of 4^∘ × 5^∘. However, the T_s–T_m relationship is varying in time (Y. Yao et al., 2014), while the Lan et al. (2016) model is static.

The objective of this study is mainly to (1) develop global gridded T_s–T_m models without any smoothing of the data, then assess their precision, and (2) study the performances of GPS–PWV retrievals using our T_s–T_m models. Table 1 lists the main differences between the T_s and T_m models developed in this study and the other global used T_m models. In Sect. 2, the data sources and determining methods of T_m are introduced in detail. Then, in section 3 we analyze the T_s–T_m relationships and their variations on a global scale. Global-gridded T_s–T_m estimating models in different forms are established and evaluated in Sect. 4. Section 5 assesses the accuracies of different PWV retrievals and Sect. 6 presents conclusions based on our experiments.

2 Data sources and methodology

As the definition of T_m in Eq. (5), the e_i parameter in the middle of ith level is calculated by vertical exponential interpolation of the water vapor pressure of its two neighbor measurement points. The temperature is estimated by linear interpolation of the two neighbor temperatures. The integral intervals are from the Earth's surface to the top level of the profile data. The height of the top level depends on the data sources we employed. The essential profile data, including the temperature, height and relative humidity values through the entire atmospheric column, can be obtained from the radiosondes or NWP data sets.

We employed radiosonde data from the Integrated Global Radiosonde Archive (IGRA, ftp://ftp.ncdc.noaa.gov/pub/data/igra, last access: 25 February 2019) to calculate T_m. Version 2.0 of the IGRA-derived sounding parameters provides pressure, geopotential height, temperature, saturation vapor pressure and relative humidity observations at the observed levels. A bias may be introduced if the integrals were terminated at lower levels (Wang et al., 2005); thus the integrations were performed up to the topmost valid radiosonde data. According to our quality control processes, some radiosonde profile data were rejected. In each profile, the surface observations must be available and the top profile level should not be lower than the standard 300 hPa level. Furthermore, the level number between the surface and the top level should be greater than 10 to avoid vertical profiles that are too sparse. At most of the radio sounding stations, sounding balloons are launched every 12 h, and their ascending paths are assumed to be vertical.

Profile data are usually provided by NWP products at certain vertical levels. The ERA-Interim product from ECMWF provides data on a regular 512 longitude by 256 latitude N128 Gaussian grid after the grid transformation performed by the NCAR Data Support Section (DSS). On each grid node of ERA-Interim, temperature, relative humidity and geopotential at 37 isobaric levels from 1000 to 1 hPa can be obtained. By dividing the geopotential by constant gravitational acceleration value (g≈9.80655 m s⁻²), we can determine the geopotential heights of the surface and levels. Data sets are available at 00:00, 06:00, 12:00 and 18:00 UTC every day and have been covering a period from 1979.01 to the present.

In theory, the computation of Eq. (5) should be integrated through the entire atmospheric column, and the geopotential height should be converted to the geometric height. However, water vapor is solely concentrated in the troposphere, and most of it is specifically located within the first 3 km a.s.l. (above sea-level). Moreover, in the two selected data sets, the geopotential heights of top pressure levels are approximately 30–40 km. Geopotential height is very close to geometric height in such height ranges. According to our computation, the relative difference between them is only between 0.1 % and 0.9 %. In fact, the height difference Δz can be replaced by the geopotential height difference Δh in Eq. (5), since the division can almost eliminate the difference between the two different height types. The T_m value nearly has no change after such height replacement. For the convenience of the calculation, we directly employed the geopotential height variable. In this paper, we denoted the T_m derived from ERA-Interim as T_{m_ERAI}.

At each reanalysis grid node, the computation of Eq. (5) always starts from the surface height to the top pressure level. The pressure levels below surface height were rejected. T_s is defined as the variable of “temperature at 2 m above ground”, and surface water vapor pressure can be derived from the “2 m dew-point temperature” variable in ERA-Interim. These T_s were also used in the regression analyses between T_s and T_m.

3 Correlation between T_s and T_m

Many studies have indicated the close relationship between T_s and T_m. However, T_mis also found to not be closely related to T_s in some regions, e.g., in the Indian zone (Suresh Raju et al., 2007). Using the T_m and T_s generated from the global gridded reanalysis data, we are able to study the T_s–T_m relationship in detail.

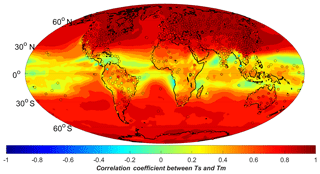
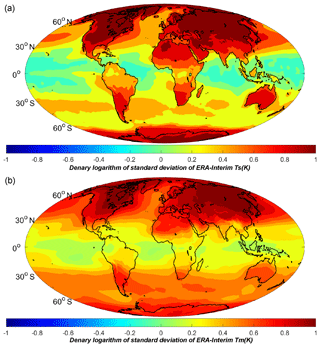
Figure 1 Correlation coefficients between T_s and T_m generated from radiosonde data (dots) and ERA-Interim reanalysis data sets (color-filled contours) over a period of 4 years from 2009 to 2012.

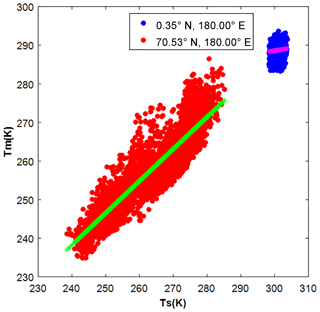
We first carried out a linear regression analysis on 4 years of T_s and T_m data generated from the radiosonde data and the global gridded ERA-Interim data sets, with data covering the period January 2009 to December 2012. The analysis results are shown in Fig. 1. Although the two data sets have different temporal resolutions (12 h for the radiosonde data and 6 h for the ERA-Interim data) and spatial resolutions, both analyses agree well with each other. This is expected because the radiosonde data have been assimilated into the ERA-Interim products. Our analyses also indicate that the T_s-=T_m correlation coefficient is generally related to the latitude. The same conclusion has been drawn in other studies (Y. B. Yao et al., 2014). Significant positive correlation coefficients can be found at middle and high latitudes and reach a maximum in the polar regions. The correlation coefficients drop dramatically at low latitudes. This is because T_m is stable there, showing independency of the other parameters. To study the variations of T_s and T_m, we illustrated the denary logarithm values of their standard deviations in Fig. 2. It is evident that T_m varies to a lesser degree than T_s at low latitudes. Aside from the latitude-related features, there are obvious differences of the T_s–T_m correlation coefficients between land and ocean. We even found that negative correlation coefficients over certain oceans, e.g., low-latitude western Pacific, Bay of Bengal or Arabian Sea (see Fig. 1). Unreliable regression analysis results may be derived when the T_s and T_mdata both have small variations. In Fig. 3, scatter plots of T_s and T_m from ERA-Interim at two locations 0.35^∘ N 180.00^∘ E and 70.53^∘ N 180.00^∘ E are given. As the blue dots show, the T_s–T_m relationship is weak in the areas near the equator, because the entire variation ranges of T_s and T_m are both within 10 K. This results in a meaningless linear regression (see the magenta line). The T_s–T_m correlation coefficient is only −0.0893 there. Other than the large spatial variations, studies have revealed that the T_s–T_m relationship also has temporal variations (Wang et al., 2005). Therefore, a good T_s–T_m model should take both the spatial and temporal variations into consideration, and this is the main aim in the following sections.

Figure 2 Denary logarithm of the standard deviation of (a) T_s and (b) T_m generated from the ERA-Interim data covering the years 2009 to 2012. Temperature unit is Kelvin.

4 Development of global-gridded T_s–T_m models

Since the T_s–T_m relationship has large spatial variations, a global gridded T_s–T_m model is preferred for precise GPS–PWV estimations. In this section, a static global gridded model and a time-varying global gridded model are established and assessed.

4.1 Static global-gridded T_s–T_m model

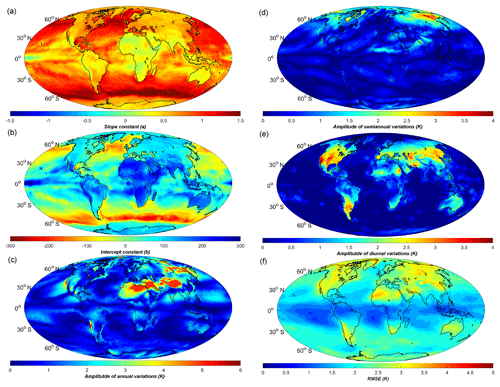
A linear formula $T_{\mathrm{m}}=a{T}_{\mathrm{s}}+b$ for the relation between T_m and T_s has been adopted in many studies. Based on the T_s and T_m products from the ERA-Interim data covering the years 2009 to 2012, we performed linear fittings of T_m versus T_s on each grid point. Then, the slope constant (a), the intercept constant (b) and the fitting root mean square error (RMSE) of each linear expression were calculated and contoured in Fig. 4. The a and b values are related to the latitude as well as the underlying surface (e.g., land, ocean). In the middle–high latitudes over the Northern Hemisphere, constant a value varies from 0.6 to 0.8, and constant b is approximately 100–50 over most of the continents. The constants in the Bevis equation are within these value ranges. Constant a is smaller (approximately 0.5–0.7) over land at the middle–high latitudes over the Southern Hemisphere. In particular, there are abrupt changes in the values of constants a and b from land to ocean at the middle–high latitudes due to the different feature variations of T_s and T_m (see Fig. 2). At low latitudes, the a value is smaller than over the other regions, because of the low variations of T_s and T_m. The fitting RMSEs are within 2–4 K over the middle–high latitude lands, and lower values are obtained over the oceans or at low latitudes. The reason for the low RMSE around the equator is the smaller fluctuation of T_m. Meanwhile, there is no RMSE larger than 4.5 K in the results of our model. As we did not perform any spatial or temporal smoothing of the data during the data processing, both the precision and resolution of our static model are better than other models (e.g., Lan et al., 2016).

Figure 3 T_s–T_m scatter plots at two locations: (blue dots) 0.35^∘ N 180.00^∘ E and (red dots) 70.53^∘ N 180.00^∘ E. The magenta and green lines are their linear fitting curves. Temperature unit is Kelvin.

4.2 Time-varying global-gridded T_s–T_m model

The time variation in the T_s–T_m relationship should also be considered in a precise T_s–T_m model. Therefore, a time-varying equation is applied for T_s–T_m regression at each grid node:

$$\begin{array}{ll}{\displaystyle }{T}_{\mathrm{m}}& {\displaystyle }=a{T}_{\mathrm{s}}+b+m_{\mathrm{1}}\cos \left({\displaystyle \frac{\mathrm{doy}}{\mathrm{365.25}}}\mathrm{2}\mathit{\pi }\right)+m_{\mathrm{2}}\sin \left({\displaystyle \frac{\mathrm{doy}}{\mathrm{365.25}}}\mathrm{2}\mathit{\pi }\right)\\ {\displaystyle }& {\displaystyle }+n_{\mathrm{1}}\cos \left({\displaystyle \frac{\mathrm{doy}}{\mathrm{365.25}}}\mathrm{4}\mathit{\pi }\right)+n_{\mathrm{2}}\sin \left({\displaystyle \frac{\mathrm{doy}}{\mathrm{365.25}}}\mathrm{4}\mathit{\pi }\right)\\ \text{(6)}& {\displaystyle }& {\displaystyle }+p_{\mathrm{1}}\cos \left({\displaystyle \frac{\mathrm{h}}{\mathrm{12}}}\mathit{\pi }\right)+p_{\mathrm{2}}\sin \left({\displaystyle \frac{\mathrm{h}}{\mathrm{12}}}\mathit{\pi }\right),\end{array}$$

where “doy” represents the observed day of year and “h” is the observed hour in UTC time; (m₁, m₂), (n₁, n₂) and (p₁, p₂) are fitting coefficients. These equations can reflect the amplitudes of annual, semiannual and diurnal variations in our T_s–T_m models.

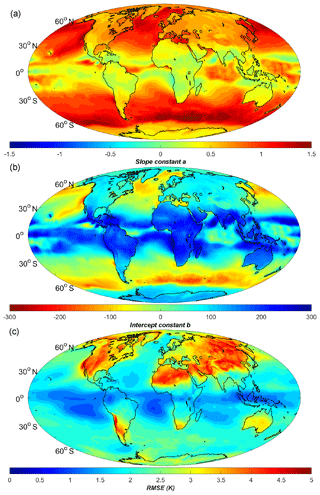
Figure 4 Distributions of the (a) slope constant a, (b) intercept constant b and (c) RMSE of static linear T_s–T_m equations at ERA-Interim grid nodes. Temperature unit is Kelvin.

Our new regression model found similar values for the coefficients a and b (of its static term) as for the static model in Sect. 4.1, except for some differences over the oceans. In Fig. 5, besides these constants a and b, we illustrate the amplitudes of annual, semiannual and diurnal terms. We can see that there are large annual variations (amplitude > 5 K) in the vast regions from Tibet to northern Africa, and in some places of the Siberia and Chile. Large diurnal variations (amplitude > 3 K) mainly occur over the midlatitude lands such as northeastern Asia or North America. Semiannual variations, however, are small in most areas except some high-latitude areas (amplitude > 3 K). All variations are smaller over the oceans due to the slower temperature changes over water than over land. The estimated T_m RMSE is also contoured in Fig. 5, and we can see that the RMSE dropped significantly in the regions with large annual or diurnal variations.

Figure 5 (a) The slope constant a, (b) intercept constant b, amplitudes of T_m (c) annual, (d) semiannual and (e) diurnal terms in our time-varying global gridded T_s–T_m model, and (f) the model-estimated T_m RMSE distribution. Temperature unit is Kelvin.

4.3 Assessments of T_s–T_m models

To further assess the precision of the T_s–T_m models using other independent data sources, we generated T_m and T_s from the radiosonde data at 723 radiosonde stations in the year 2016. These data are not assimilated into the 2009–2012 ERA-Interim data sets. As a result, we can regard them to be independent of our model. At each radiosonde site, different T_s–T_m models were employed to calculate T_m. In addition, we also estimated T_m using the 1^∘ × 1^∘ GPT2w model (Bohm et al., 2015), which is a global gridded T_m empirical model independent of the surface meteorological observation data. Then, these calculated T_m will be evaluated by being compared with the integrated T_m of radiosondes (denoted as T_{m_RS}) twice a day.

The model estimations of T_m are denoted by T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w} for the Bevis equation, the latitude-related model, our static global gridded model, time-varying global gridded model and the GPT2w model. When the global gridded models are employed, the radiosonde station may not be located at a grid node. Therefore, we interpolated the coefficients in the T_s–T_m equations from the neighboring grids to the radiosonde sites. The interpolation formula is expressed as follows (Jade and Vijayan, 2008):

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{C}_{\mathrm{site}}=\sum _{i=\mathrm{1}}^{\mathrm{4}}{w}^i{C}_{\mathrm{grid}}^i.\end{array}$$

C_site and $C_{\mathrm{site}}^i$ represent the coefficients in T_s–T_m equations at the radiosonde site location and its neighboring grids, respectively. wⁱ are the interpolation coefficients, which are determined using the equation

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }{w}^i={\displaystyle \frac{{\left(R{\mathit{\psi }}^i\right)}^{-\mathit{\lambda }}}{\sum _{j=\mathrm{1}}^{\mathrm{4}}{\left(R{\mathit{\psi }}^j\right)}^{-\mathit{\lambda }}}},\end{array}$$

where R=6378.17 km is the mean radius of the earth, λ is the scale factor which equals one in our study, and ψⁱ is the angular distance between the ith grid node and the station's position. ψⁱ are computed using following formula (with latitude φ and longitude θ):

$$\begin{array}{}\text{(9)}& {\displaystyle }{\displaystyle }\cos {\mathit{\psi }}^i=\sin {\mathit{\phi }}^i\sin \mathit{\phi }+\cos {\mathit{\phi }}^i\cos \left({\mathit{\theta }}^i-\mathit{\theta }\right)\cos \mathit{\phi }.\end{array}$$

Considering the fact that the reanalysis grids are definite and every radiosonde site is in situ, we can compute the interpolation coefficients in Eq. (7) for all of the radiosonde stations. Then, these coefficients are stored as constants to avoid reduplicating the calculation.

Taking T_{m_RS} as the reference values, we calculated the biases and RMSEs of T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w} at each radiosonde site. The results are illustrated in Fig. 6. Obviously, in many regions, the Bevis equation has bad precision with the absolute bias and RMSE both larger than 5 K. T_{m_LatR} can reduce the estimated biases in many areas, but the RMSEs remain large. Large biases still exist at quite a few radiosonde stations, e.g., in Africa or western Asia. T_{m_static} and T_{m_GPT2w} remove the large T_m biases at most of the radiosonde stations. T_{m_varying} performs significantly better over the world, especially in the Middle East, North America, Siberia, etc.

Detailed statistics of the distributions of the bias and RMSE using different models are shown in Fig. 7 and Table 2. At over 97.37 % of the radiosonde stations, the biases of T_{m_varying} are within −3–3 K. Large positive biases (>3 K) nearly disappear in T_{m_varying}. In contrast, there are significant large biases in T_{m_Bevis} and T_{m_LatR}. Improvements in RMSE are more evident. The RMSEs of T_{m_varying} are smaller than 4 K at over 91 % of the radiosonde sites, while few sites (<1 %) have RMSEs larger than 5 K. This is clearly better than the other models. In T_{m_Bevis} and T_{m_LatR}, there are more than 17 % of the radiosonde sites with RMSEs larger than 5 K. The overall performance of T_{m_GPT2w} is very close to T_{m_Bevis}, except that its absolute bias is smaller than the other T_s–T_m models.

Table 2 Statistics of T_m estimates from different models. Reference data are the radiosonde T_m derivations.

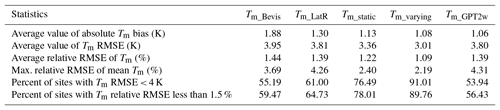
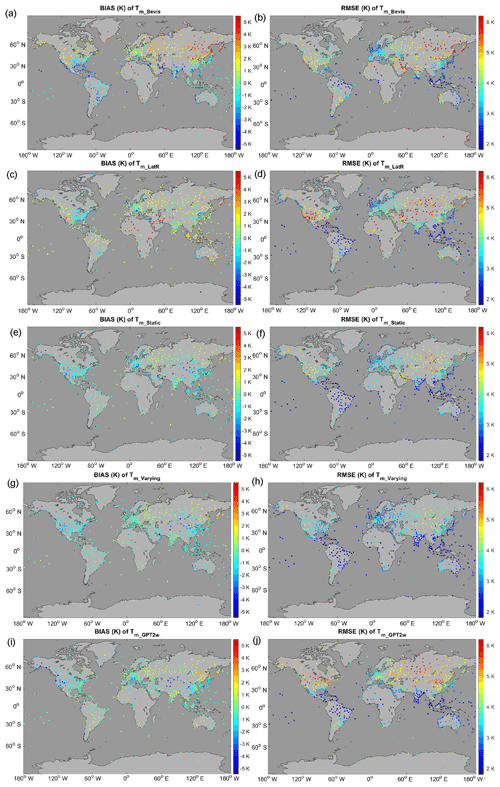
Figure 6 (a, c, e, g, i) The biases and (b, d, f, h, j) the RMSEs of the estimated T_m from (a, b) the Bevis equation, (c, d) the latitude-related model, (e, f) our static global gridded model, (g, h) our time-varying global gridded model and (i, j) the GPT2w model at each radiosonde station. Reference data are the radiosonde data of the year 2016. Temperature unit is Kelvin.

Figure 7 The distributions of (1) the biases and (2) the RMSEs of T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w} compared with the radiosonde data at 723 stations in the year 2016. Temperature unit is Kelvin.

Table 3 Number of radiosonde sites at which the five global applied T_m estimation models had superior performance.

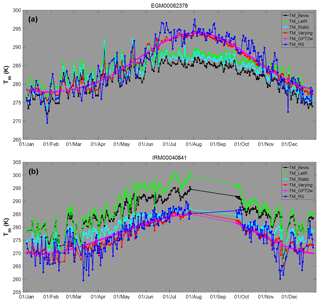
Figure 8 T_m series of T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying}, T_{m_GPT2w} and T_{m_RS} at the IGRA station (a) no. 62378 and (b) no. 40841. Temperature unit is Kelvin.

To identify the superior T_m estimation model at each radiosonde site, we employed the following statistical tests under the assumption of a normal distribution of the estimated T_m error:

1. First, Brown–Forsythe tests (Brown and Forsythe, 1974) of the equality of variances were carried out at each site for estimating the T_m errors from two different models, e.g., model A and B. The purpose of this step is to determine whether there are significant differences in the variances of the T_m results. If the test rejects the null hypothesis at a 5 % significance level and the errors of model A and B have the same variance, the model with the smaller sample variance is regarded as the better one. However, if the test does not reject the homogeneity of variances, analysis of variance (ANOVA) is performed in the next step.

2. ANOVA is a technique used to analyze the differences among group means (Hogg and Ledolter, 1987). It evaluates the null hypothesis that the samples all have the same mean against the alternative that the means are not the same. If the null hypothesis is rejected at a 5 % significance level, the T_m sample with smaller absolute mean value is believed to be better. Otherwise, we think that the two models perform almost as well at this radiosonde site.

3. After multiple tests and comparisons, the best model at each radiosonde station may be identified. However, at some sites no superior model can be confirmed. All the models are believed to have equivalent performance.

Finally, we counted the number of sites at which each T_m model performed the best. The results are given in Table 3. The time-varying global gridded model is superior to the others at 434 radiosonde stations (60.03 % of all sites), while the second-best estimation, T_{m_GPT2w}, is superior at only 12.86 % of the sites.

In Fig. 8 the T_m series at the IGRA station no. 62378 (29.86^∘ N 31.34^∘ E in Egypt) are given. We can see that large negative biases ($<-\mathrm{5}$ K) between T_{m_Bevis} (or T_{m_LatR}) and T_{m_RS} exist. T_{m_static} performs only slightly better from July to October. However, T_{m_varying} and T_{m_GPT2w} can eliminate most of the seasonal errors. Different properties of T_m series appear at another IGRA station no. 40841 (30.25^∘ N 56.97^∘ E in Iran). Some observation data are missing, but we can still see that there are large positive differences (>5 K) between T_{m_Bevis} (or T_{m_LatR}) and T_{m_RS} throughout the year. The biases of T_{m_static} are much smaller, but some large errors still appear in many months. The T_{m_varying}, however, performs as well as the T_m calculated from the radiosonde data, with small biases, and captures the variations well. The time series ofT_{m_GPT2w} are smoother and cannot capture the fluctuations of the T_m time series, causing an accuracy worse than T_{m_varying}.

On the other hand, even T_{m_varying} have large differences from T_{m_RS} at a few IGRA stations. This can be explained by the fact that our fitting analyses are based on the T_m values derived from ERA-Interim profiles. The quality of ERA-Interim data can be very poor in the regions with sparse observation data (Itterly et al., 2018).

Figure 9 Variation in the uncertainty in Q with the value of T_m and the uncertainty in T_m.

5 GPS–PWV retrieval experiments

GPS–PWV has different error sources with different properties. It is complicated to evaluate the GPS–PWV uncertainty here due to the lack of collaborated additional independent techniques that monitor water vapor at the GPS site.

5.1 Theoretical analysis of the GPS–PWV uncertainty

Comprehensive research on the uncertainty in GPS–PWV has been carried out by Ning et al. (2016). The uncertainties in ZTD, ZHD and conversion factor Q have been studied in detail. The total uncertainty in GPS–PWV is as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\sigma }}_{\mathrm{PWV}}={\displaystyle \frac{\mathrm{1}}{Q}}\\ \text{(10)}& {\displaystyle }& {\displaystyle }\sqrt{{\mathit{\sigma }}_{\mathrm{ZTD}}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{2.2767}{\mathit{\sigma }}_{P_{\mathrm{s}}}}{f(\mathit{\phi },H)}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{P_{\mathrm{s}}{\mathit{\sigma }}_{\mathrm{c}}}{f(\mathit{\phi },H)}}\right)}^{\mathrm{2}}+{\left(\mathrm{PWV}\cdot {\mathit{\sigma }}_Q\right)}^{\mathrm{2}}},\end{array}$$

where σ_PWV, σ_ZTD, ${\mathit{\sigma }}_{P_{\mathrm{s}}}$ and σ_Q are, respectively, the uncertainties of GPS–PWV, the ZTD estimation, the P_s observations and the conversion factor Q. σ_c=0.0015 denotes the uncertainty in constant C=2.2767 in Eq. (1), PWV is the value of GPS–PWV, and

$$\begin{array}{}\text{(11)}& {\displaystyle }{\displaystyle }{\mathit{\sigma }}_Q={\mathrm{10}}^{-\mathrm{6}}{\mathit{\rho }}_{\mathrm{w}}{R}_{\mathrm{v}}\sqrt{{\left({\displaystyle \frac{{\mathit{\sigma }}_{k_{\mathrm{3}}}}{T_{\mathrm{m}}}}\right)}^{\mathrm{2}}+{\mathit{\sigma }}_{k_{\mathrm{2}}^{\prime }}^{\mathrm{2}}+{\left(k_{\mathrm{3}}{\displaystyle \frac{{\mathit{\sigma }}_{T_{\mathrm{m}}}}{T_{\mathrm{m}}^{\mathrm{2}}}}\right)}^{\mathrm{2}}},\end{array}$$

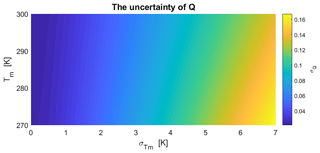
where ${\mathit{\sigma }}_{k_{\mathrm{3}}}=\mathrm{0.012}\times {\mathrm{10}}^{\mathrm{5}}$ K² hPa⁻¹, ${\mathit{\sigma }}_{k_{\mathrm{2}}^{\prime }}=\mathrm{2.2}$ K hPa⁻¹ and ${\mathit{\sigma }}_{T_{\mathrm{m}}}$, respectively, denote the uncertainties of k₃, $k_{\mathrm{2}}^{\prime }$ and T_m in Eq. (4). The variation in σ_Q with the values of T_m and ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ is depicted in Fig. 9. Assuming that T_m is 280 K, we find that the σ_Q increases by over 60 % (from 0.069 to 0.112) as the ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ rises from 3.0 to 5.0 K. However, the σ_Q is less sensitive to the value of T_m. The σ_Q rises only by 17.96 % (about from 0.061 to 0.075) as the value of T_m drops from 300 to 270 K with ${\mathit{\sigma }}_{T_{\mathrm{m}}}=\mathrm{3.0}$ K.

Ning et al. (2016) assumed the T_m were obtained from NWP models so the uncertainty in T_m was set to be small (${\mathit{\sigma }}_{T_{\mathrm{m}}}=\mathrm{1.1}$ K). However, as shown in Sect. 4.3, the uncertainties of T_m from different T_m models are significantly larger at the radiosonde stations. For each radiosonde station, we calculated the mean value of T_m and assigned the ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ with the RMSEs of T_m given in Fig. 6. Then we obtained the σ_Q in Eq. (11). Our statistics indicate that the σ_Q using our varying T_s–T_m model decreases on average by 19.26 %, 17.77 %, 7.79 % and 18.67 % with respect to the σ_Q, respectively, using T_{m_Bevis}, T_{m_LatR}, T_{m_static} and T_{m_GPT2w}. For example, at the IGRA station no. 42724 (22.88^∘ N 91.25^∘ E in India), σ_Q drops by 53 % from 0.141 of the T_{m_Bevis} to 0.066 of the T_{m_varying}.

The uncertainty in Q will be propagated to the total uncertainty in GPS–PWV according to Eq. (10). We obtained the contributions of the different terms in Eq. (10) to the total GPS–PWV uncertainty. The contribution of one term is measured by the percentage it accounts for the total σ_PWV. The percentages are computed using the formulas

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{p}_{\mathrm{ZTD}}={\displaystyle \frac{{\left({\mathit{\sigma }}_{\mathrm{ZTD}}/Q\right)}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{PWV}}^{\mathrm{2}}}},p_{P_{\mathrm{s}}}={\displaystyle \frac{{\left[\mathrm{2.2767}{\mathit{\sigma }}_{P_{\mathrm{s}}}/\left(f\right(\mathit{\phi },H\left)Q\right)\right]}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{PWV}}^{\mathrm{2}}}},\\ \text{(12)}& {\displaystyle }& {\displaystyle }{p}_{\mathrm{C}}={\displaystyle \frac{{\left[P_{\mathrm{s}}{\mathit{\sigma }}_{\mathrm{c}}/\left(f\right(\mathit{\phi },H\left)Q\right)\right]}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{PWV}}^{\mathrm{2}}}},p_Q={\displaystyle \frac{{\left(\mathrm{PWV}\cdot {\mathit{\sigma }}_Q/Q\right)}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{PWV}}^{\mathrm{2}}}}\end{array}$$

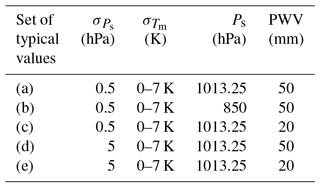
where p_ZTD, $p_{P_{\mathrm{s}}}$, p_C and p_Q, respectively, indicate the contributions of the uncertainties associated with ZTD, P_s, constant C and factor Q to the total σ_PWV. Following the summaries of Ning et al. (2016), we assumed that σ_ZTD=4 mm and σ_C=0.0015. T_m identically equals 280 K since the σ_Q is less sensitive to the value of T_m with respect to the ${\mathit{\sigma }}_{T_{\mathrm{m}}}$. Table 4 gives five sets of typical values which are assigned to the ${\mathit{\sigma }}_{P_{\mathrm{s}}}$, ${\mathit{\sigma }}_{T_{\mathrm{m}}}$, P_s and PWV in Eqs. (10)–(12).

Table 4 Different typical values for ${\mathit{\sigma }}_{P_{\mathrm{s}}}$, ${\mathit{\sigma }}_{T_{\mathrm{m}}}$, P_s and PWV.

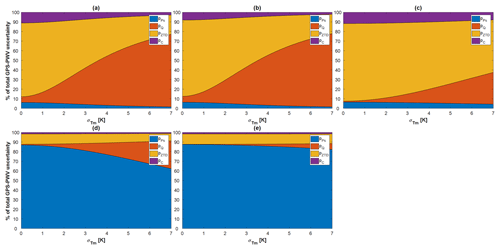
Figure 10 Contributions of different terms to the total uncertainty in GPS–PWV with the typical values shown in Table 4.

The ${\mathit{\sigma }}_{P_{\mathrm{s}}}$ equals 0.2 hPa in Ning et al. (2016); however we enlarged its typical value to 0.5 hPa in consideration of the possible worse performance of the surface barometers. In Fig. 10, we illustrated the contributions of the terms in Eq. (12) based on the assumptions (a)–(e) in Table 4. Some feature variations of the contributions of different terms can be found from the comparisons between different subplots:

1. No significant difference exists between Fig. 10a and b. Because of the small value of σ_c in Eq. (10), the σ_PWV is not sensitive to the value of P_s. Meanwhile, the uncertainty associated with σ_c contributes less than 10 % of the σ_PWV.

2. With the typical values in Table 4 (values a and b), a reduction of ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ can reduce the p_Q significantly. For example, in Fig. 10a, the p_Q accounts for 69.54 % with ${\mathit{\sigma }}_{T_{\mathrm{m}}}=\mathrm{6}$ K, and it declines to 38.19 % with ${\mathit{\sigma }}_{T_{\mathrm{m}}}=\mathrm{3}$ K.

3. As Fig. 10c shows, the uncertainty associated with σ_ZTD accounts for the main part of σ_PWV when the values of PWV and ${\mathit{\sigma }}_{P_{\mathrm{s}}}$ are not high. With the typical values in Table 4 (value c), the p_ZTD can be up to 74.21 % with ${\mathit{\sigma }}_{T_{\mathrm{m}}}=\mathrm{3}$ K. The p_Q, however, can drop from 26.76 % to 9.00 % as the ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ decreases from 6 to 3 K. Although the p_Q is not large under this situation, a smaller ${\mathit{\sigma }}_{T_{\mathrm{m}}}$can still reduce the contribution of σ_Q to the σ_PWV.

4. The uncertainty associated with ${\mathit{\sigma }}_{P_{\mathrm{s}}}$ dominates the error budget of PWV when the ${\mathit{\sigma }}_{P_{\mathrm{s}}}$ is large. In Fig. 10d and e, the $p_{P_{\mathrm{s}}}$ is over 80 % with ${\mathit{\sigma }}_{T_{\mathrm{m}}}<\mathrm{3}$ K and ${\mathit{\sigma }}_{P_{\mathrm{s}}}=\mathrm{5}$ hPa. In Fig. 10d, the p_Q increases from 7.55 % to 23.19 % as the ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ rises from 3 to 6 K. However, in Fig. 10e, the p_Q only grows from 1.29 % to 4.61 % with the same variation in ${\mathit{\sigma }}_{T_{\mathrm{m}}}$.

Theoretical analyses of σ_PWV were also carried out at two representative stations. At the IGRA station no. 42971 (20.25^∘ N 85.83^∘ E, in India), the mean value of PWV is 53.88 mm. The RMSEs of T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w} are 4.30, 3.15, 2.41, 1.93 and 1.97 K. The ${\mathit{\sigma }}_{T_{\mathrm{m}}}$ in Eq. (11) was replaced by the calculated RMSEs, and the p_ZTD, $p_{P_{\mathrm{s}}}$, p_C and p_Q were generated with two typical values, 0.5 and 5 hPa, assigned to the ${\mathit{\sigma }}_{P_{\mathrm{s}}}$. With ${\mathit{\sigma }}_{P_{\mathrm{s}}}=\mathrm{0.5}$ hPa, the p_C accounts for around 7 %, while the $p_{P_{\mathrm{s}}}$ accounts for around 4 % of the total σ_PWV. By using different T_m estimations, the variations of p_C and $p_{P_{\mathrm{s}}}$ are both within 4 %. However, the p_Q varies more evidently. It accounts for averages of 55.69 %, 40.77 %, 30.70 %, 23.53 % and 24.11 % of the σ_PWV with the estimations of T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w}, respectively. The p_ZTD rises with the reduction of p_Q, e.g., from 36.23 % of T_{m_Bevis} to 62.53 % of T_{m_varying}. On the other hand, with ${\mathit{\sigma }}_{P_{\mathrm{s}}}=\mathrm{5}$ hPa, the $p_{P_{\mathrm{s}}}$ accounts for more than 75 % of the σ_PWV, while the p_Q decreases from 14.21 % of T_{m_Bevis} to 3.9 % of T_{m_varying}.

At another representative station, the IGRA station no. 50557 (49.17^∘ N 125.22^∘ E, in northeastern China), the mean PWV is only 12.17 mm. The RMSEs of T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w} are 5.16, 3.94, 3.54, 2.99 and 5.10 K. We can see that the accuracy of T_m has been improved significantly. However, because of the low average value of PWV, the p_ZTD averagely contributes over 73.5 % of the σ_PWV, while the p_Q averagely contributes less than 10.5 % assuming ${\mathit{\sigma }}_{P_{\mathrm{s}}}=\mathrm{0.5}$ hPa and less than 1.5 % assuming ${\mathit{\sigma }}_{P_{\mathrm{s}}}=\mathrm{5}$ hPa. But such a discussion only concerns the average values. In fact, even at this station there are still some high values of PWV, for example at 12:00 UTC 22 July 2016, the PWV reached 48 mm. For the observations with high PWV, the improvement in the accuracy of T_m can still exert a significant positive impact on the reduction of p_Q.

Table 5 Statistics on the relative errors of different PWV retrievals.

It is worth mentioning that the uncertainty in ZHD may be underestimated in some situations. There are two reasons for this. Firstly, the calculation of ZHD assumes that the water vapor does not contribute to the mass of the atmosphere. The ZHD error introduced by this assumption is often negligible. But in some very wet regions, the mass of water vapor could produce significant errors in the ZHD calculation. Secondly, and more importantly, the error of P_s in Eq. (1) can sometimes be very large. Small ${\mathit{\sigma }}_{P_{\mathrm{s}}}$ is reasonable when the surface barometer is calibrated routinely and equipped together with the GPS antenna. However, if there were significant height difference between the GPS antenna and the barometer, the error for ZHD would increase significantly. Snajdrova et al. (2006) found that 10 m of height difference approximately causes a difference of 3 mm in the ZHD. On the other hand, P_s can be generated from NWP data if there are no nearby barometers at GPS site. The error of P_s could be very large using this method (Means and Cayan, 2013; Jiang et al., 2016). In these cases, the GPS–PWV error reduction will be very limited due to the more precise T_m estimation.

5.2 Impact of real T_m estimation

To study the impact of T_m on the real GPS–PWV retrieval, we first downloaded GPS ZTD products (Byun and Bar-Sever, 2009) at 74 IGS sites in the year 2016 from the NASA Crustal Dynamics Data Information System (CDDIS) ftp address (ftp://cddis.gsfc.nasa.gov/pub/gps/products/troposphere/zpd, last access: 25 February 2019). These selected GPS sites were equipped with meteorological sensors so that the surface pressure and temperature measurements could also be obtained. ZHD was calculated using Eq. (1). It is subtracted from ZTD to obtain ZWD. Then, T_m was generated with six approaches: the first five T_m series were T_{m_Bevis}, T_{m_LatR}, T_{m_static}, T_{m_varying} and T_{m_GPT2w}. The sixth T_m was integrated from the ERA-Interim profiles and interpolated to each GPS site (Jiang et al., 2016; Wang et al., 2016). Finally, the GPS–PWV was generated from the ZWD and the six different T_m estimates leading to over 100 compared points for each GPS–PWV series. We denoted these GPS–PWV sets as PWV_BTm, PWV_LTm, PWV_STm, PWV_VTm, PWV_GTm and PWV_ETm. The only difference between these GPS and PWV estimations is the T_m estimation model; therefore, the impact of other errors is excluded.

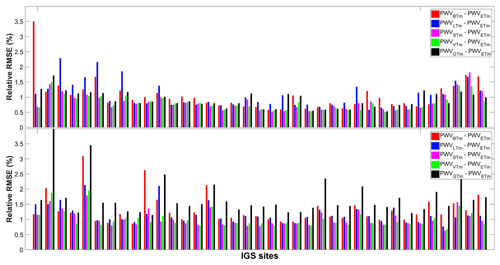
Figure 11 Relative RMSEs of PWV_BTm, PWV_STm, PWV_VTm and PWV_GTm compared with PWV_ETm at 74 IGS stations in the year 2016.

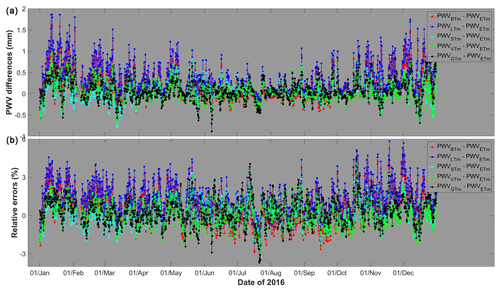
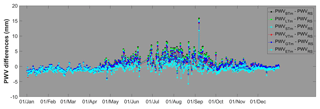
Figure 12 (a) PWV differences and (b) relative differences of PWV_BTm, PWV_LTm, PWV_STm, PWV_VTM and PWV_GTm compared with PWV_ETm at the ALIC station in the year 2016. PWV unit is millimeters.

The T_m from ERA-Interim is believed to be the most accurate among our T_m estimates at the selected GPS sites. We therefore took the PWV_ETm as reference values to assess the other PWV. The relative RMSEs of PWV_BTm, PWV_LTm, PWV_STm, PWV_VTm and PWV_GTm at these selected stations were calculated and are illustrated in Fig. 11. Detailed statistics are given in Table 5. The mean relative error of all sites drops from 1.18 % of the PWV_BTm to 0.91 % of the PWV_VTm. PWV_VTm has the minimum mean relative errors at 51.35 % of the sites, while PWV_STm is superior at 27.03 % of the sites. PWV_STm and PWV_VTm obtain relative RMSEs smaller than 1.0 % at 55 sites, while only 28 sites of PWV_BTm, 31 sites of PWV_LTm and 22 sites of PWV_GTm perform similarly. For example, at the ALIC site (23.67^∘ S 133.89^∘ E, in Australia), with a mean PWV of approximately 23 mm, the relative RMSE dropped from 1.97 % of PWV_BTm to 1.10 % of PWV_VTm. The time series of the relative differences of PWV_BTm, PWV_LTm, PWV_STm, PWV_VTm and PWV_GTm are given in Fig. 12. We found that some relative RMSEs could be reduced by more than 2 % from PWV_BTm to PWV_VTm. Obviously, PWV_BTm and PWV_LTm have larger relative errors throughout the year, while the PWV differences are significantly larger only in the summer season (when the PWV values are highest). Apparently, the T_m variations in summer are not modeled well by either the Bevis model and the latitude-related model. PWV_STm eliminate those large differences but still retain some residual errors, which are removed by more than 0.5 mm in PWV_VTm. PWV_GTm has some large errors during the period from May to July. All of these results demonstrate that our time-varying model has a precision advantage.

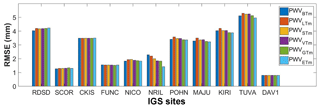
Figure 13 RMSEs of the PWV_BTm, PWV_STm, PWV_VTm, PWV_GTm and PWV_ETm compared with the PWV_RS at 11 IGS stations in 2016. PWV unit is millimeters.

Figure 14 PWV differences of the PWV_BTm, PWV_LTm, PWV_STm, PWV_VTm, PWV_GTm and PWV_ETm compared with the PWV_RS at the NIRL station in the year 2016. PWV unit is millimeters.

5.3 Comparisons between GPS–PWV and radiosonde PWV

Among our selected 74 IGS sites, there are only 11 sites located within 5 km to a nearby IGRA radiosonde station. At these common stations, we generated PWV from the radiosonde data (PWV_RS) by adjusting the sounding profiles to the heights of IGS sites. It is worth noting that a geoid undulation correction should be carried out on each IGS site geoid height (Jiang et al., 2016). Then, we compared PWV_BTm, PWV_LTm, PWV_STm, PWV_VTm, PWV_GTm and PWV_ETm with PWV_RS. Figure 13 shows the statistics. The RMSEs of GPS–PWV are approximately 1–5 mm. Comparisons indicate that the RMSEs of different GPS–PWV retrievals are very close (differences < 0.2 mm) regardless of the applied T_m sources at most of the selected sites. This means that other errors (e.g., ZTD estimation errors or sounding sensors errors) instead of the T_m make up the bulk of the differences between the GPS–PWV and the radiosonde PWV. Actually, each sounding does not represent the vertical sounding centered at the radiosonde site because of the complex path of the balloon. And GPS–PWV represents the averaged value of the water vapor zenithal projection from all the slant signal paths during the observation period. Such differences can introduce significant uncertainty into our comparisons. However, we still found obvious gaps between PWV at the NRIL station (88.36^∘ N 69.36^∘ E, 4.1 km away from the IGRA station no. 23078 in Russia). The RMSE decreases from 2.29 mm of PWV_BTm to 1.84 mm of PWV_VTm and 1.42 mm of PWV_ETm. As shown in Fig. 14, the large PWV differences appear mainly from May to September. During those five months, the mean GPS–PWV difference to PWV_RS decreases by over 30 % from 2.52 mm of PWV_BTm to 1.67 mm of PWV_VTm, and the reductions of GPS–PWV error are mainly around 1–2 mm. This is attributed to the wetter atmosphere in these months. As indicated by the uncertainty analysis in Sect. 5.1, the improvement in the accuracy of T_m can be translated into more error reduction in the GPS–PWV retrieval with higher values of PWV.

6 Summary and conclusion

We developed two global gridded T_s–T_m models, which are, respectively, static and time-varying with a spatial resolution of 0.75^∘ × 0.75^∘. The models are established by analyzing the ERA-Interim reanalysis data sets covering the years 2009–2012, which indicated the significant spatial–temporal variations in T_s–T_m relationship as well as the radiosondes covering the same period. The annual, semiannual and diurnal variations in T_s–T_m relationship are considered in the time-varying model. The time-varying global gridded T_s–T_m model has a significant global precision advantage over the other globally applied models, including the Bevis equation, the latitude-related model and the GPT2w model. The average RMSE of T_m reduces by approximately 1 K. At over 90 % of the radiosonde sites, our time-varying model has RMSE smaller than 4 K, while the RMSEs larger than 5 K nearly disappear. On the other hand, in the Bevis model or in the latitude-related model, there are more than 17 % of the radiosonde sites with RMSEs larger than 5 K. Multiple statistical tests at the 5 % significance level identified the significant superiority of our varying model at more than 60 % of the radiosonde sites. Analyses at the specific stations demonstrate that the errors larger than 5 K in the estimated T_m series can be eliminated by our varying T_s–T_m model.

More precise T_m estimations can decrease by around 20 % of the uncertainty in the conversion factor Q, which maps GPS–ZWD to GPS–PWV, and the reduction can be even more than 50 % at some stations. The contribution of the uncertainty associated with Q to the total GPS–PWV uncertainty also declines when using a more precise T_m model. The reduction is related to the value of PWV and the uncertainty in the surface pressure. With GPS–PWV higher than 50 mm, the uncertainty associated with Q contributes more than 55 % of the uncertainty in GPS–PWV when using the Bevis equation and less than 25 % when using our varying T_s–T_m model, assuming the ZTD and the surface pressure are measured accurately with the uncertainties of 4 mm and 0.5 hPa, respectively. However, the uncertainty in ZTD or in surface pressure would dominate the error budget of GPS–PWV (>70 %) if the value of GPS–PWV were small or the uncertainty in surface pressure were large. In these cases, the uncertainty associated with Q only contributes around 10 % of the GPS–PWV uncertainty or even smaller. Taking the GPS–PWV, using ERA-Interim T_m estimates at 74 IGS sites as the references, we found that the GPS–PWV using our time-varying T_s–T_m model obtained the minimum mean relative error at 51.35 % of the sites, while the GPS–PWV using the static gridded T_s–T_m model is superior at only 27.03 % of the sites. The differences between GPS–PWV and radiosonde PWV are approximately 1–5 mm. And our varying T_s–T_m model can reduce the error in the GPS–PWV retrieval by 30 % (around 1–2 mm) with respect to the Bevis equation.

According to our experiments, we are confident that the time-varying global gridded T_s–T_m models presented here will help us to retrieve GPS PWV more precisely and to study the precise PWV variations in high temporal resolution. The Matlab array file consisting of the global gridded coefficients in our model, as well as codes for interpolating coefficients at any given location, is provided in the supplement of this study.