Improvement of airborne retrievals of cloud droplet number concentration of trade wind cumulus using a synergetic approach

In situ measurements of cloud droplet number concentration N are limited by the sampled cloud volume. Satellite retrievals of N suffer from inherent uncertainties, spatial averaging, and retrieval problems arising from the commonly assumed strictly adiabatic vertical profiles of cloud properties. To improve retrievals of N it is suggested in this paper to use a synergetic combination of passive and active airborne remote sensing measurement, to reduce the uncertainty of N retrievals, and to bridge the gap between in situ cloud sampling and global averaging. For this purpose, spectral solar radiation measurements above shallow trade wind cumulus were combined with passive microwave and active radar and lidar observations carried out during the second Next Generation Remote Sensing for Validation Studies (NARVAL-II) campaign with the High Altitude and Long Range Research Aircraft (HALO) in August 2016. The common technique to retrieve N is refined by including combined measurements and retrievals of cloud optical thickness τ, liquid water path (LWP), cloud droplet effective radius r_eff, and cloud base and top altitude. Three approaches are tested and applied to synthetic measurements and two cloud scenarios observed during NARVAL-II. Using the new combined retrieval technique, errors in N due to the adiabatic assumption have been reduced significantly.

1 Introduction

Clouds influence the Earth's radiative energy budget by reflecting, absorbing, and emitting solar and terrestrial radiation. These effects are typically quantified by the cloud radiative forcing (CRF), which is defined by the difference between the net radiation (downward minus upward irradiance) in cloudy and cloud-free conditions. Depending on the cloud type, the cloud optical and microphysical properties, and their spatial and temporal occurrence, the CRF can vary significantly (Rosenfeld, 2006). In the tropics, clouds can either cool or warm the atmosphere and surface below the cloud. While for cirrus a warming effect dominates (Wendisch et al., 2007), boundary layer trade wind cumuli typically cool the subjacent atmosphere and surface by efficiently reflecting solar radiation (Warren et al., 1988). Therefore, a realistic representation of clouds in numerical weather prediction (NWP) and global climate models (GCMs) is essential. Due to their sub-grid scale, internal variability, and boundary layer interactions, trade wind cumulus clouds are not well represented in NWP and GCMs (Kollias and Albrecht, 2010). An important source of uncertainty of these models is caused by an insufficient representation of the first aerosol effect (Bony and Dufresne, 2005), which describes the correlation of the cloud droplet number concentration N and the cloud optical thickness τ or cloud-top reflectivity ℛ, commonly known as the Twomey effect (Twomey, 1977). It is most prominent for optically thin, low-level clouds such as trade wind cumulus (Platnick and Twomey, 1994; Werner et al., 2014), which are a ubiquitous cloud type in the tropics (Warren et al., 1988; Eastman et al., 2011). Despite their small vertical and horizontal extent, trade wind cumuli can have fractional cloudiness of more than 25 % (Albrecht, 1991) and therefore may influence the Earth radiative energy budget significantly (Chertock et al., 1993). In addition, trade wind cumuli play an important role in maintaining the thermodynamic energy budget in the atmospheric boundary layer. They couple the surface and free atmosphere by transporting latent heat and developing deep convection (Lamer et al., 2015). Another important factor determining the CRF is the number concentration of aerosol particles, in particular the amount of particles that can act as cloud condensation nuclei (CCN) (Werner et al., 2013). Depending on the CCN number concentration, precipitation formation can be promoted or inhibited (Lee and Feingold, 2013). The CCN concentration influences the cloud life cycle and lifetime (Albrecht, 1989). The magnitude of both effects depends on the individual cloud regime.

Operational NWP models usually do not have the computational capability to consider size-resolved microphysical schemes, and therefore the usage of simplified parameterizations is inevitable. The most important parameter, which links microphysical and radiative properties of clouds, is the cloud droplet effective radius r_eff, which represents the radiative effective size of a cloud droplet population (Pontikis and Hicks, 1992). In NWP and GCMs, r_eff is calculated from N and the liquid water content (LWC). In simple models, assumptions of constant N are applied for different situations, e.g., the classification of polluted and clean air masses. As r_eff is derived from LWC and N, the cloud droplet number concentration is a key parameter for models to calculate reasonable values of r_eff and to represent the Twomey effect. Also for NWP with two-moment schemes, which use N in addition to the mass mixing ratio, a validation of N as a prognostic variable emerges.

To measure N and LWC, airborne in situ measurements are applied by utilizing different physical methods and instruments (Baumgardner et al., 2011; Wendisch and Brenguier, 2013). These are based on optical measurement principles such as forward scattering, phase Doppler interferometry, and holographic imaging. Beside the uncertainties of the individual measurement techniques, the total sample volume of the instruments is rather limited in comparison to the typical horizontal and vertical extent of clouds. Due to the limited flight time and range, airborne in situ observations cannot cover the natural variability of N, r_eff, and LWC completely. To directly quantify the Twomey effect, colocated measurements of cloud microphysical and radiative properties are required, which was realized only on a few occasions (Ackerman et al., 2000; Siebert et al., 2013; Werner et al., 2014).

To improve global statistics of estimates of the Twomey effect, several approaches to derive N from satellite observations have been developed (Grosvenor et al., 2018b; Quaas et al., 2009; Minnis et al., 2011; Mace et al., 2016; Bennartz and Rausch, 2017). These techniques provide useful global data sets with large spatial and temporal coverage. Based on passive remote sensing in the solar and terrestrial wavelength range, N is estimated by combining the results of bi-spectral retrievals of τ and r_eff with cloud-top temperature T_CT by Brenguier et al. (2000), Quaas et al. (2006), and Zeng et al. (2014). They assumed a vertically constant LWC and N throughout the cloud profile, which is at least for LWC not a realistic scenario. Slightly deviating, Bennartz and Rausch (2017) assumed a sub-adiabatic vertical profile in which the LWC increases linearly with height with values corresponding to about 80 % of the respective adiabatic value. More complex vertical profile types of LWC and N are applied by Boers et al. (2006), in which a heterogeneous mixing model assumes that entrainment dilutes the air parcel with a constant mean-volume radius of the droplets r_vol (the radius of cloud droplets with a volume corresponding to the average of the volume size distribution of the cloud population), while r_eff follows an adiabatic profile. The retrieved values of N using the homogeneous or the heterogeneous model differ by several percent. Further studies show that the heterogeneous model represents nature more realistically compared to the homogeneous assumption (Boers et al., 1998; Brenguier et al., 2000). These methods often use the dependence of τ on N to connect cloud microphysical and radiative properties. However, so far no operational satellite products of N are available. Retrievals of N, in general, can have uncertainties of up to 80 % (Grosvenor et al., 2018b).

Assuming an adiabatic cloud, the LWC increases linearly with height and the LWP is determined by integrating LWC from cloud base (CB) to cloud top (CT):

$$\begin{array}{}\text{(1)}& \mathrm{LWP}=\underset{\mathrm{CB}}{\overset{\mathrm{CT}}{\int }}\mathrm{LWC}\left(z\right)\mathrm{d}z={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\cdot \mathit{\pi }\cdot {\mathit{\rho }}_{\mathrm{w}}\cdot \underset{\mathrm{CB}}{\overset{\mathrm{CT}}{\int }}N\left(z\right)\cdot r_{\mathrm{vol}}^{\mathrm{3}}\left(z\right)\mathrm{d}z,\end{array}$$

with the density of liquid water ρ_w, the geometric height z, and the mean-volume radius r_vol. Following Hansen and Travis (1974) and Stephens (1978), the cloud optical thickness τ is related to the LWP by

$$\begin{array}{ll}{\displaystyle }\mathit{\tau }& {\displaystyle }=\underset{\mathrm{CB}}{\overset{\mathrm{CT}}{\int }}{\mathit{\sigma }}_{\mathrm{ext}}\mathrm{d}z=\underset{\mathrm{CB}}{\overset{\mathrm{CT}}{\int }}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{Q}_{\mathrm{ext}}\left(x\right)\cdot N(r,z)\cdot r^{\mathrm{2}}\mathrm{d}r\mathrm{d}z\\ \text{(2)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{CB}}{\overset{\mathrm{CT}}{\int }}\mathit{\pi }\cdot Q_{\mathrm{ext}}\left(\stackrel{\mathrm{‾}}{x}\right)\cdot N\left(z\right)\cdot r_{\mathrm{srf}}^{\mathrm{2}}\mathrm{d}z,\end{array}$$

with the extinction coefficient σ_ext, the extinction efficiency factor Q_ext, which is approximately 2 for cloud droplets in the solar wavelength range, the size parameter $x=(\mathrm{2}\cdot \mathit{\pi }\cdot r)/\mathit{\lambda }$, and the mean radius r_srf (the radius of cloud droplets with a surface area corresponding to the average of the surface area size distribution of the cloud population). According to Martin et al. (1994), r_eff correlates with the mean-surface radius r_srf and the mean-volume radius r_vol of the droplet size distribution given by

$$\begin{array}{}\text{(3)}& k={\left({\displaystyle \frac{r_{\mathrm{vol}}}{r_{\mathrm{eff}}}}\right)}^{\mathrm{3}}={\left({\displaystyle \frac{r_{\mathrm{srf}}^{\mathrm{3}}}{r_{\mathrm{vol}}^{\mathrm{2}}}}\right)}^{\mathrm{6}}.\end{array}$$

This relation depends on the shape of the droplet size distribution and is referred to as the k parameter (Martin et al., 1994). Using k as the distribution shape factor, r_srf and r_vol in Eqs. (1) and (2) are replaced by r_eff, leading to

$$\begin{array}{}\text{(4)}& \mathit{\tau }={\displaystyle \frac{\mathrm{3}\cdot {\int }_{h_{\mathrm{CB}}}^{h_{\mathrm{CT}}}\mathrm{LWC}\left(z\right)\cdot \mathrm{d}z}{\mathrm{2}\cdot {\mathit{\rho }}_{\mathrm{w}}\cdot r_{\mathrm{eff}}}}.\end{array}$$

A typical value for the k parameter in the case of maritime clouds is k=0.8 (Martin et al., 1994). Equation (4) assumes a homogeneous, adiabatic cloud characterized by a linear increase in LWC with height, which is not confirmed with most cloud observations that show that a majority of clouds are sub-adiabatic (Brenguier et al., 2000; Painemal and Zuidema, 2011; Min et al., 2012).

Instead of using τ in the retrieval of N, LWP from passive microwave sensors can be exploited (Minnis et al., 2011). This approach has the advantage that LWP is determined at wavelengths not influenced by aerosol particles, sun glint, or three-dimensional (3-D) radiative effects. Further, active remote sensing techniques have been applied to derive N, e.g., by Austin and Stephens (2001) and Mace et al. (2016), who combined r_eff vertical profiles derived from cloud radar observations and τ obtained from passive solar remote sensing. Nevertheless, a disadvantage of the radar is that the radar reflectivity Z is mainly determined by large cloud droplets, which biases the results.

The dependence of τ on N is investigated by Quaas et al. (2009) using satellite measurements. The correlations of τ and N obtained by satellite are weaker compared to aircraft remote sensing results or in situ measurements, which is primarily due to the large-scale averaging of the satellite measurement (McComiskey and Feingold, 2008). Analyzing satellite measurements of large-scale averaged N and τ in different thermodynamic conditions, and therefore varying LWP, updraft velocity, and aerosol particle concentrations, masks the effect of N on τ. As a result, parameterizations derived from satellite observations are not well suited for trade wind cumuli with their highly variable and small extent.

Airborne remote sensing techniques are able to bridge the scale gap between in situ and satellite measurements, as they allow for the sampling of individual clouds under specific conditions and to cover a sufficiently large area to quantify the natural variability of N, r_eff, and LWC.

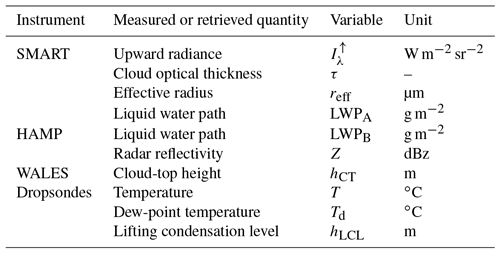
Here, a method is proposed to combine passive and active airborne remote sensing measurements of cloud vertical profiles of microphysical parameters and cloud radiative properties. Measurements of upward radiance $I_{\mathit{\lambda }}^{\uparrow }$ collected by the Spectral Modular Airborne Radiation measurement sysTem (SMART) are used to determine τ, r_eff, and the thermodynamic phase of cloud water close to the cloud top. Observations by the High Altitude and LOng range research aircraft Microwave Package (HAMP), which is comprised of a multichannel microwave radiometer and a cloud radar, provide LWP and radar reflectivity profiles that are used to determine cloud boundaries and allow for a discrimination between precipitating and nonprecipitating clouds. Furthermore, an alternative retrieval to determine r_eff from the spectrometer–microwave combination of SMART and HAMP is developed and tested. Lidar measurements by the Water Vapour Lidar Experiment in Space (WALES) are additionally implemented to determine the cloud-top height h_CT, while HAMP and dropsondes provide estimates of the cloud base height h_CB.

This paper is structured as follows. In Sect. 2 the sensitivity of the cloud-top reflectivity ℛ (ratio of the upward radiance and downward irradiance) and cloud-top albedo α (ratio of the upward and downward irradiance) of typical trade wind cumuli with respect to changes in N is quantified to access the required accuracy of N retrievals and the cloud regime most sensitive to N. The remote sensing instruments utilized in this study are introduced briefly in Sect. 3. In Sect. 4 the retrieval of the optical properties and the cloud filtering is described. Subsequently, three different methods to determine N are presented in Sect. 5 and applied to synthetic measurements and two exemplary cases of trade wind cumulus. Resulting values of N are correlated with measured ℛ and separated for different thermodynamic conditions (binned LWP) to demonstrate the possibility to obtain parameterizations for the Twomey effect.

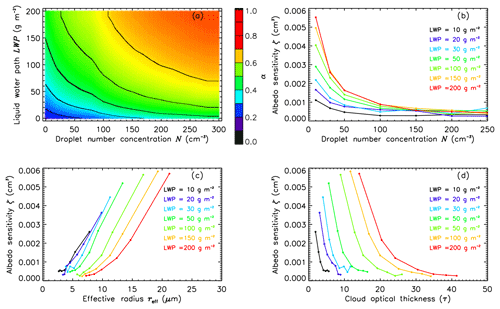
Figure 1 Simulations for a liquid water cloud between 1000 and 1500 m with LWP from 10 to 200 g m⁻² and for a solar zenith angle ϑ of 5^∘. The simulations are integrated over a wavelength range from 250 to 2500 nm. Panel (a) shows cloud-top albedo α for combinations of cloud droplet number concentration N and LWP. Panel (b) shows cloud-top albedo sensitivity ζ as a function of N for different LWPs. Panels (c) and (d) display ζ as a function of effective radius r_eff and cloud optical thickness τ, respectively.

2 Sensitivity of the Twomey effect for different cloud regimes

To quantify the Twomey effect for trade wind cumulus with different LWPs, radiative transfer simulations (RTSs) with the radiative transfer package libRadtran 2.0.2 (Emde et al., 2016) are performed. The solar cloud-top albedo was calculated for a homogeneous liquid water cloud located between 1000 and 1500 m with a solar zenith angle ϑ of 5^∘. Liquid water path is varied in a range between 10 and 200 g m⁻², typical for shallow trade wind cumulus (Siebert et al., 2013).

Figure 1a shows simulated α as a function of N and LWP. For constant LWP and increasing N (decreasing r_eff), α increases, which is described by the Twomey effect. However, this sensitivity is not equal for the different LWPs. For constant N and increasing LWP (increasing r_eff), α increases with different rates for N. This illustrates the fact that different cloud regimes exhibit various sensitivities in terms of the Twomey effect. Therefore, LWP, N, and r_eff have to be considered to parameterize the radiative properties of trade wind cumuli.

To quantify the Twomey effect for different cloud regimes, the cloud albedo sensitivity ζ is defined as

$$\begin{array}{}\text{(5)}& \mathit{\zeta }(\mathrm{LWP},r_{\mathrm{eff}},N)={\displaystyle \frac{\mathrm{d}\mathit{\alpha }(\mathrm{LWP},r_{\mathrm{eff}},N)}{\mathrm{d}N}},\end{array}$$

which represents the change in α with respect to an increase in N and is given in units of cm³.

Figure 1b displays ζ as a function of N for different LWPs. In general, ζ decreases with increasing N. Clouds with low LWP (black) and low N have a lower ζ compared to clouds with higher LWP (red) but the same N. The highest ζ is obtained for clouds with the highest LWP of 200 g m⁻², while thicker clouds with the lowest LWP of 10 g m⁻² have the lowest ζ. Because of $r_{\mathrm{vol}}\propto \sqrt[\mathrm{3}]{\mathrm{LWP}/N}$ the change in N for constant LWP is larger for large LWP (e.g., 200 g m⁻²) compared to lower values of LWP=10 g m⁻² and resulting absolute differences in simulated α and ζ. The simulations further revealed that due to low τ and LWP or LWC, the calculated α and ζ are easily affected by variations in r_eff resulting from the dependence of α on the phase function (describing the angular dependence of the scattering of a liquid water droplet or ice crystal), which changes with r_eff. Therefore, calculations of ζ in this cloud regime have to be performed with high precision and for small steps of N (e.g., ΔN=10 cm⁻³) to minimize numerical noise and to sufficiently resolve small variations in ζ. The presented simulations focus on low numbers of N, and therefore steps of 50 cm⁻³ for N>200 cm⁻³ are used. As a result, the lines for constant LWP cross for higher values of N.

In Fig. 1c the cloud albedo sensitivity ζ is shown as a function of r_eff for clouds of different LWPs. With cloud geometric thickness H and assuming a constant LWP, the effective radius determines N or vice versa following

$$\begin{array}{}\text{(6)}& r_{\mathrm{eff}}=\sqrt[\mathrm{3}]{{\displaystyle \frac{\mathrm{3}\cdot \mathrm{LWP}}{\mathrm{4}\cdot {\mathit{\rho }}_{\mathrm{w}}\cdot \mathit{\pi }\cdot H\cdot N}}}\cdot k^{-\mathrm{3}}.\end{array}$$

For all LWP cases the sensitivity increases with increasing r_eff (decreasing N). This agrees with Fig. 1b in which low N values have the highest ζ. Clouds with lower LWP show higher ζ and are therefore more sensitive to changes in r_eff compared to clouds with higher LWP.

In Fig. 1d ζ is plotted as a function of τ, which is calculated using Eq. (4) from LWP, N, and r_eff used in the simulations. For all clouds with different values of LWP, ζ decreases with increasing τ. This implies that changes in N have larger effects on α for clouds with low τ. As a result, optically thin clouds with low N and large r_eff, which is typical of shallow trade wind cumulus, are subject to the strongest Twomey effect. Therefore, the Twomey effect of trade wind cumulus is highly relevant for NWP and GCMs.

The simulations further illustrate the challenge of estimating α of shallow trade wind cumuli by satellite remote sensing. Typically, satellite retrievals of N can have uncertainties of up to 80 % (Grosvenor et al., 2018b). For clouds with low N, e.g., 30 cm⁻³, and LWC=0.1 g m⁻³, the concentration of N might be biased by up to ±23 cm⁻³. This would result in a bias of α of ± 0.08 (80 W m⁻² increased cloud forcing for 1000 W m⁻² insolation). For clouds with higher N of 200 cm⁻³ the retrieval uncertainties of N increase in absolute terms ($\mathrm{\Delta }N=\pm \mathrm{156}$ cm⁻³) and lead to a similar uncertainty of $\mathit{\alpha }=\pm \mathrm{0.07}$ even though ζ is reduced for clouds with higher N. This shows that retrievals of N need to be improved in order to reduce the uncertainties of global estimates of N and α calculations in NWP and GCMs.

3 Observations and instrumentation

Convective low-level cumuli were observed by airborne remote sensing during the second Next Generation Remote Sensing for Validation Studies (NARVAL-II) campaign between 8 and 31 August 2016 (Stevens et al., 2018). The High Altitude and Long Range Research Aircraft (HALO) based on Barbados was mostly flying eastward into an area dominated by shallow trade wind cumulus unaffected by anthropogenic influences. HALO was equipped with a set of passive and active remote sensing instruments. Reflected solar radiation was measured by the passive instruments SMART (Wendisch et al., 2001, 2016) and specMACS (Ewald et al., 2016), while radiation emitted in the microwave spectral range was measured by the HAMP. For active remote sensing, HAMP included a cloud radar (Mech et al., 2014). Lidar observations by the WALES completed the cloud remote sensing instrumentation. WALES measures the backscatter coefficient and depolarization at 532 and 1064 nm wavelength and contains a high-spectral-resolution lidar channel at 532 nm wavelength (Wirth et al., 2009). Additionally, numerous dropsondes were released from HALO.

All instruments were pointed in the nadir direction and synchronized in time. However, the different fields of view (FOVs) of the instruments cause a systematic difference in the observed time series. All measured and retrieved quantities from SMART, HAMP, WALES, and the dropsondes are summarized in Table 1.

Table 1 Measured and retrieved quantities from SMART, HAMP, WALES, and the dropsondes.

3.1 Spectral Modular Airborne Radiation measurement sysTem

During NARVAL-II, SMART measured the spectral upward $F_{\mathit{\lambda }}^{\uparrow }$ and downward irradiance $F_{\mathit{\lambda }}^{\downarrow }$, as well as spectral upward radiance $I_{\mathit{\lambda }}^{\uparrow }$. Each quantity was recorded with two separate Zeiss grating spectrometers, one for the visible (Vis) range from 300 to 1000 nm wavelength and a second one for sampling the near-infrared (NIR) range from 900 to 2200 nm. By merging the spectra, about 97 % of the solar spectrum is covered (Bierwirth et al., 2009). The spectral resolution defined by the full width at half maximum is 2–3 nm for the Vis spectrometer and 8–10 nm for the NIR spectrometer.

The radiance optical inlet of SMART has an opening angle of 2^∘. The sampling time t_int was set to 0.5 s. For an average aircraft ground speed of about 220 m s⁻¹ and a distance of 10 km between cloud top and the aircraft, this results in a FOV of about 100 m × 120 m for an individual pixel.

The optical inlets for $F_{\mathit{\lambda }}^{\uparrow }$ and $F_{\mathit{\lambda }}^{\downarrow }$ mainly consist of integrating spheres, which collect, direct, and scatter solar radiation from the upper or lower hemisphere. During NARVAL-II, the upward-looking inlet was equipped with an active stabilization platform to ensure horizontal alignment of the sensor, which is crucial as $F_{\mathit{\lambda }}^{\downarrow }$ refers to a horizontal plane (Wendisch et al., 2001).

Prior to and after NARVAL-II, SMART was radiometrically calibrated in the laboratory using certified calibration standards traceable to the National Institute of Standards and Technology (NIST). A secondary calibration by a mobile standard was applied during the campaigns to track potential changes in the instrument sensitivity. The total measurement uncertainty of downward irradiance $F_{\mathit{\lambda }}^{\downarrow }$ and upward radiance $I_{\mathit{\lambda }}^{\uparrow }$ for typical conditions and observations of shallow cumulus is about 5.4 % for the Vis and 8.4 % for the NIR range, which are composed of individual errors due to spectral calibration, spectrometer noise and dark current, and primary radiometric calibration (Brückner et al., 2014).

3.2 HALO Microwave Package

HAMP is a combination of a passive microwave radiometer and an active cloud radar specifically designed for operation on HALO (Mech et al., 2014). The microwave radiometer includes 26 frequency channels between 22.24 and 183.31 GHz ± 12.5 GHz. The brightness temperature (BT) measured along the 22.24 and 183.31 GHz rotational water vapor lines provide the total column water vapor (Schnitt et al., 2017) and information on its vertical distribution. Liquid water emission increases roughly with the frequency squared. By combining BT in window channels, i.e., 31.4 and 90 GHz, mostly affected by liquid water with channels sensitive to water vapor, the LWP can be retrieved. This principle is also employed by satellite instruments that provide global climatologies of LWP, but suffer from the coarse footprint of a few tens of kilometers (Elsaesser et al., 2017).

The statistical LWP retrieval is based on a large variety of atmospheric profiles with differently structured warm clouds as training data composed from the dropsondes (Schnitt et al., 2017). Synthetic BTs are simulated from these profiles and subsequently used to fit a multiparameter linear regression model employing higher-order terms (Mech et al., 2007). Testing the retrieval algorithm on an independent subsample provides an accuracy of about 20 g m⁻² for LWP values below 100 g m⁻² and an accuracy of 20 % for LWP above (Jacob et al., 2019).

The cloud radar MIRA-36 operates at a frequency of 36 GHz and has a similar horizontal resolution as the LWP of about 1000 m and a temporal resolution of 1 s. Vertical profiles are divided into 30 m bins (Mech et al., 2014). The radar provides different parameters linked to the cloud microphysical properties, including the radar reflectivity Z, the linear depolarization, and the Doppler velocity, and the spectral width of the droplet size distribution. Note that the latter two are affected by the relative motion of the aircraft to the wind and the antenna width (Mech et al., 2014).

Radar reflectivity represents the sixth moment of the cloud droplet size distribution and is therefore strongly influenced by large droplets. In order to calculate the LWC, which is proportional to the third moment of the droplet size distribution (DSD), from Z, so-called Z–LWC relations are used, which are typically derived from in situ measurements. According to Khain et al. (2008), there is quite a lot of variability involved and as soon as the transition to drizzle sets in the relation can be off by orders of magnitude. Here the Z–LWC relation

$$\begin{array}{}\text{(7)}& {\mathrm{LWC}}_{\mathrm{p}}=\mathrm{LWP}\cdot {\displaystyle \frac{\sqrt{Z_{\mathrm{p}}}}{\sum _{j=\mathrm{1}}^{j=M}\sqrt{Z_j}\cdot \mathrm{\Delta }h}},\end{array}$$

following Frisch et al. (2000), is used to derive vertical profiles of LWC. With the binned LWC_p at height gate p resulting from the vertical resolution of the radar, the LWP of the cloud is distributed by the weighting of Z_p (Z at height gate p) and ${\sum }_{j=\mathrm{1}}^{j=M}\sqrt{Z_j}\mathrm{\Delta }h$ is the sum of the Z over all height gates at which a cloud was present. The techniques to derive brightness temperatures and radar reflectivity profiles are described in more detail by Konow et al. (2018a).

3.3 Water Vapour Lidar Experiment in Space (WALES)

The differential absorption lidar (DIAL) called WALES operates at four wavelengths near 935 nm to measure atmospheric water vapor. Mixing ratio profiles cover the whole atmosphere below the aircraft. WALES also contains channels for aerosol measurements at 532 and 1064 nm wavelengths with depolarization detection. At 532 nm, WALES uses the high-spectral-resolution technique, which distinguishes molecular from particle backscatter, to enable direct extinction measurements. Within this study only the aerosol channels are used to provide information on the cloud-top height. The ranging resolution of the instrument is 15 m. Together with the flight altitude inferred from the HALO onboard positioning system and an appropriate attitude correction, the accuracy of the cloud-top height detection is about 20 m.

The laser has a beam divergence of 1 mrad, which leads to an illuminated spot 10 m in diameter on the ground at a flight altitude of 10 km. Laser pulses are emitted with a repetition rate of 100 Hz; 20 signals are averaged to improve the signal-to-noise ratio, resulting in an along-flight-track resolution of 44 m at 200 m s⁻¹ aircraft speed. Thus, the horizontal resolution is reduced compared to SMART and HAMP. Along track, this can be taken into account by further signal averaging.

4 Measurement analysis

Trade wind cumuli mostly appear randomly distributed with a tendency to form self-organizing structures (Bony et al., 2015). Typically, the vertical cloud extent is larger than the horizontal one within an individual cell. This is in contrast to stratiform cloud fields if common retrieval techniques to derive N are applied. Clouds smaller than the pixel size covered by the FOV bias the retrieval of microphysical properties (Oreopoulos and Davies, 1998a, b). The dominance of small-scale cumulus during NARVAL-II, ranging in the horizontal size of a few hundred meters, results in heterogeneous cloud scenes. This induces challenges with respect to cloud masking and RTS.

4.1 Cloud mask and precipitation flag

4.1.1 Cloud mask

To distinguish between cloud and cloud-free measurements over ocean surfaces, the difference in the spectral reflectivity is analyzed. The ratio χ of $I_{\mathit{\lambda }}^{\uparrow }$ between 858 and 648 nm wavelengths is calculated in analogy to the MODIS cloud mask (Platnick et al., 2013) by

$$\begin{array}{}\text{(8)}& \mathit{\chi }={\displaystyle \frac{I_{\mathrm{858}}^{\uparrow }}{I_{\mathrm{648}}^{\uparrow }}}.\end{array}$$

The cloud mask is based on the relative intensity of $I_{\mathit{\lambda }}^{\uparrow }$ and χ. Therefore, a single measurement can be identified as cloudy when only a part of the SMART FOV with 100 m × 120 m is cloud covered. Masking each measurement point as cloudy or cloud free, the cloud length l_cld is determined by counting the number n of consecutive cloud-masked measurements. Multiplied with the flight speed v_ac and the constant integration time of SMART of t_int=0.5 s, the cloud length is calculated by

$$\begin{array}{}\text{(9)}& l_{\mathrm{cld}}=n\cdot t_{\mathrm{int}}\cdot v_{\mathrm{ac}}.\end{array}$$

For v_ac≈220 m s⁻¹ the smallest resolvable cloud size is in the range of 120 m along the flight track.

The length of trade wind cumulus can be shorter than the SMART FOV. To identify such cases, an additional homogeneity cloud flag (HCF) is introduced. The cloud is considered homogeneous (HCF is true) when a single observation is enclosed by five cloud-masked measurements. For clouds not surrounded by at least two cloudy pixels, the HCF is set to false. Therefore, the HCF identifies clouds that are large enough to fill the FOVs of SMART, HAMP, and WALES at the same time.

4.1.2 Precipitation flag

Precipitation is identified using the radar reflectivity Z. Measurements are considered to be affected by precipitation when Z exceeds a threshold of $Z<-\mathrm{20}$ dBz within 50 to 200 m above sea level (Schnitt et al., 2017). This allows for the discrimination of precipitation events, which affect the LWP measured by the microwave radiometer and retrieved by SMART. The simple thresholding of radar reflectivity close to the sea surface might not capture all precipitating clouds as drizzle particles might evaporate before reaching the lower 200 m close to the sea surface.

4.2 Retrieval of cloud optical thickness and droplet effective radius

Based on the reflected solar radiance $I_{\mathit{\lambda }}^{\uparrow }$ measured by SMART, a retrieval of τ and r_eff is performed by applying the radiance ratio method proposed by Werner et al. (2013). The use of radiance ratios at two different wavelengths reduces the uncertainties by the radiometric calibration of SMART. For the wavelength ratio applied here, an uncertainty of 6 % is assumed. Additionally, the use of ratios increases the retrieval sensitivity with respect to r_eff by clearly separating the dependence of $I_{\mathit{\lambda }}^{\uparrow }$ on τ and r_eff and therefore the retrieval accuracy. Forward simulations of reflected spectral radiance $I_{\mathit{\lambda }}^{\uparrow }$ were carried out with the libRadtran 2.0.2 package (Emde et al., 2016). The Fortran 77 discrete ordinate radiative transfer solver version 2.0 (FDISORT 2) after Stamnes et al. (2000) is used. The extraterrestrial $F_{\mathit{\lambda }}^{\downarrow }$ is given by Gueymard (2004) and a marine aerosol profile after Shettle (1989) is selected. Vertical profiles of air temperature, pressure, and humidity are obtained from radiosondes released at the Bridgetown International Airport. For the optical properties of liquid water droplets, Mie calculations are performed.

The cloud optical thicknesses τ and r_eff are determined by a modified lookup table (LUT) method after Nakajima and King (1990). While τ is derived at 870 nm wavelength, r_eff is retrieved with the radiance ratio method using a ratio of measurements at 1050 and 1645 nm wavelengths. Compared to retrievals using larger wavelengths, e.g., 2.1 or 3.7 µm, r_eff retrieved by the SMART measurements represents not only the cloud particles at cloud top. The vertical weighting function for 1.6 µm also covers a significant amount of information from lower cloud layers (Platnick, 2000). Therefore, retrieved r_eff values are smaller than the actual cloud droplet size at CT, which are considered in Eq. (12) to calculate N. This leads to a systematic overestimation of N calculated from SMART measurements. Results from the SMART retrieval are denoted with the subscript “A”.

Clouds that do not cover the entire FOV of SMART bias the retrieved optical properties because they violate the assumption of plane-parallel clouds used in the RTS (Oreopoulos and Davies, 1998a, b). Lower values of $I_{\mathit{\lambda }}^{\uparrow }$ bias τ towards lower values, whereas r_eff is shifted to larger droplet sizes (Cahalan et al., 1995). Further, the heterogeneous structure of trade wind cumulus is likely to cause 3-D radiative effects, like shadowing cloud areas by nearby cloud towers or enhanced reflectivity due to additional reflection into the FOV. These effects may also bias the retrieval of τ and r_eff and the calculation of N. Therefore, the HCF filter is applied to exclude measurements that are influenced by these processes. However, due to the low vertical extent of shallow trade wind cumuli that are analyzed here, these 3-D radiative effects are assumed to be negligible.

Liquid water path is obtained directly from libRadtran on the basis of τ and r_eff similar to Eq. (4). Liquid water path derived from SMART is again denoted with the subscript “A”. In the case of cloud heterogeneity, sun glint, or 3-D radiative effects, the retrieval of τ is very likely biased. Following Eq. (4), a bias of τ also influences the retrieval of r_eff and therefore LWP. To mitigate these effects, measurements of LWP from HAMP (denoted with the subscript “B”) are applied in the libRadtran radiation simulations of the cloud retrieval. Liquid water path data from microwave radiometers are obtained from wavelengths not influenced by sun glint or 3-D radiative effects. Using LWP from HAMP as a precondition, the LUTs reduce to one absorbing wavelength sensitive to r_eff. Therefore, the nonlinear dependence between τ and r_eff is removed and the retrieval becomes more reliable. Retrieved r_eff values from combined passive solar radiance and microwave measurements are denoted with the subscript “B”.

5 Retrieval of cloud droplet number concentration

The retrieval of N from remote sensing observations is based on the relation proposed by Brenguier et al. (2000), which links N of a stratiform cloud to τ and r_eff by

$$\begin{array}{}\text{(10)}& N_{\mathrm{A}}={\displaystyle \frac{\sqrt{\mathrm{10}}}{\mathrm{4}\cdot \mathit{\pi }\cdot \sqrt{{\mathit{\rho }}_{\mathrm{w}}}}}\cdot \sqrt{f_{\mathrm{ad}}\cdot {\mathrm{\Gamma }}_{\mathrm{ad}}}\cdot {\displaystyle \frac{\sqrt{\mathit{\tau }}}{\sqrt{r_{\mathrm{eff},\mathrm{A}}^{\mathrm{5}}}}}.\end{array}$$

The technique assumes an adiabatic vertical cloud profile, in which temperature linearly decreases and LWC linearly increases with height. An adiabatic profile implies that the total water mass mixing ratio of the cloud is conserved. This is true when (i) no water is removed from the cloud (no precipitation or fallout), (ii) no entrainment of drier air at the cloud edges occurs, and (iii) no evaporation from precipitation happens. As a result, the proposed method should be applied to nonprecipitating clouds only, which do not undergo strong vertical convection and mixing. A vertically constant N throughout the cloud layer is assumed. This assumption is verified for stratiform clouds and shallow trade wind cumulus by in situ measurements; e.g., Reid et al. (1999) and Wendisch and Keil (1999). The vertically constant N is mainly determined by the amount of available CCN at cloud base and their potential to form cloud droplets depending on the degree of supersaturation, which is controlled by temperature, entrainment of dry air, and updraft velocity.

The k parameter, relating the effective radius r_eff and the volumetric radius r_vol, is set to k=0.8 for marine clouds following the suggestion by Martin et al. (1994) and Pontikis (1996). Depending on the cloud type the k parameter can vary by ±0.1 (Martin et al., 1994).

With the help of cloud properties retrieved by airborne remote sensing, Eq. (10) can be applied in different complexity to derive N. In the following three methods are proposed. Method A uses only SMART data, while method B additionally includes HAMP observations of LWP, and method C also involves measurements by WALES. The obtained parameters and applied assumptions are summarized in Table 2.

Table 2 Overview of the cloud droplet number concentration retrievals and applied measurements, retrieval parameters, and assumptions.

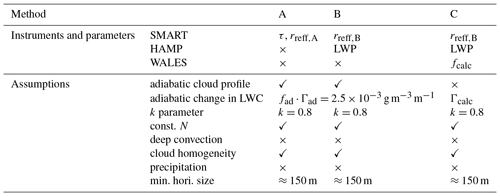
5.1 Method A: based on cloud optical thickness and droplet effective radius

Method A follows the traditional satellite approach to feed Eq. (10) with τ and r_eff obtained by a single passive remote sensing instrument. Here, τ_A and r_reff,A retrieved by SMART are applied. Using the radiance ratio retrieval of SMART to derive τ and r_eff,A from two infrared wavelengths, absolute calibration errors are reduced and the sensitivity on r_eff is increased. The degree of adiabacity is assumed to be 1. This implies that for trade wind cumuli, which are typically sub-adiabatic, the estimated N is potentially biased. However, similar retrieval assumptions are frequently applied to observations from satellites such as MODIS (Grosvenor et al., 2018b).

5.2 Method B: based on liquid water path and droplet effective radius

For adiabatic clouds, Eq. (4) can be solved analytically, which results in a relation that directly links LWP to τ and r_eff:

$$\begin{array}{}\text{(11)}& \mathrm{LWP}={\displaystyle \frac{\mathrm{5}}{\mathrm{9}}}\cdot {\mathit{\rho }}_{\mathrm{w}}\cdot \mathit{\tau }\cdot r_{\mathrm{eff}},\end{array}$$

following (Brenguier et al., 2000). Equation (11) allows for the application of Eq. (10) with an independent measure of LWP instead of τ to calculate N. Combining Eqs. (10) and (11) leads to

$$\begin{array}{}\text{(12)}& N_{\mathrm{B}}={\displaystyle \frac{\mathrm{3}\cdot \sqrt{\mathrm{2}}}{\mathrm{4}\cdot \mathit{\pi }\cdot {\mathit{\rho }}_{\mathrm{w}}}}\cdot \sqrt{f_{\mathrm{ad}}\cdot {\mathrm{\Gamma }}_{\mathrm{ad}}}\cdot {\displaystyle \frac{\sqrt{{\mathrm{LWP}}_{\mathrm{B}}}}{r_{\mathrm{eff},\mathrm{B}}^{\mathrm{3}}}}.\end{array}$$

In method B, LWP measurements by HAMP and derived r_eff,B from the combined SMART microwave–radiometer retrieval are applied. The results are denoted with N_B. Exchanging r_eff,A by r_eff,B takes into account the fact that LWP is determined from HAMP only. This makes the retrieval independent of τ derived by SMART and therefore less sensitive to effects by sun glint. Further, LWP determination from HAMP applies wavelengths between 20 and 100 GHz, which are not influenced by aerosol particles. An additional advantage of the determination of LWP from HAMP is the separation of clouds for different LWPs and untangling the effects of varying LWP on α (McComiskey and Feingold, 2008).

5.3 Method C: based on liquid water path, droplet effective radius, and cloud geometric thickness

Equations (10) and (12) assume constant values of f_ad and Γ_ad. Therefore, in method A and B the adiabatic profile of LWC follows the maximum theoretically possible profile under which liquid water is released due to condensation from upward motion in the atmosphere.

In situ measurements of stratocumulus and trade wind cumulus indicate that a majority of cloud profiles do not follow this adiabatic assumption (Wendisch and Keil, 1999; Merk et al., 2016). In most cases the profiles are sub-adiabatic, meaning a reduced increase in LWC with height, mostly due to entrainment and mixing from dry air at the cloud edges. When convection and mixing are moderate, an equilibrium between the droplets and the surrounding air can be assumed. Entrainment and mixing reduce f_ad but not necessarily N. Further, it might reduce the (super)saturation at the cloud edges, causing a shrinking of the droplets but not their complete vanishing. To account for a sub-adiabatic increase in LWC with height in method C, f_ad⋅Γ_ad is replaced by observations. Observed Γ_calc is determined by

$$\begin{array}{}\text{(13)}& {\mathrm{\Gamma }}_{\mathrm{calc}}={\displaystyle \frac{\mathrm{2}\cdot {\mathrm{LWP}}_{\mathrm{B}}}{H^{\mathrm{2}}}},\end{array}$$

with LWP_B obtained by the microwave radiometer. The cloud geometric thickness $H=h_{\mathrm{CT}}-h_{\mathrm{LCL}}$ is estimated from a combination of the WALES cloud-top height h_CT observations and the lifting condensation level h_LCL from dropsondes.

WALES can only derive h_CT when the laser is attenuated by clouds with high τ. As a result, the lidar signal is attenuated soon and the cloud base height is not detectable. Therefore, h_CB=h_LCL is determined separately from dropsondes, which represent the large-scale thermodynamic structure of the atmosphere. Using the temperature T and dew-point temperature T_d at the two lowermost points of the sounding, the lifting condensation level with $h_{\mathrm{LCL}}\approx \mathrm{125}\cdot (T-T_{\mathrm{d}})$ is approximated (Espy, 1836). Nevertheless, uncertainties of estimated h_LCL from dropsondes are in the range of ±35 m not considering additional uncertainties caused by the assumptions in the equation (Romps, 2017). Alternatively, cloud boundary determination by combinations of lidar, radar, and dropsonde are applied where (i) the cloud droplets are large enough to produce a detectable radar echo and (ii) no precipitation is present, but are complicated for heterogeneous cloud fields. Selection of the appropriate instrument synergy depends on the observed cloud scene. Utilization of radar observations is preferred, giving the best vertical resolution for well-defined cloud edges. Using the estimated Γ_calc, Eq. (12) changes to

$$\begin{array}{}\text{(14)}& N_{\mathrm{C}}={\displaystyle \frac{\mathrm{3}\cdot \sqrt{\mathrm{2}}}{\mathrm{4}\cdot \mathit{\pi }\cdot {\mathit{\rho }}_{\mathrm{w}}}}\cdot {\displaystyle \frac{{\mathrm{LWP}}_{\mathrm{B}}}{H\cdot r_{\mathrm{eff},\mathrm{B}}^{\mathrm{3}}}}.\end{array}$$

5.4 Simulated synthetic measurements

To systematically test the potential of the proposed synergistic retrieval methods, synthetic measurements of spectral upward radiance $I_{\mathit{\lambda },\mathrm{syn}}^{\uparrow }$ are created. In that way, the three different methods are compared, omitting the influence by measurement errors. Further, varying environmental conditions, like sea surface albedo, heterogeneous cloud conditions, and 3-D cloud radiative effects, do not influence the systematic comparison of the retrieval methods. The comparison is based on retrieved cloud droplet number concentration N with methods A, B, and C and N_cld calculated from the model clouds serving as the true value.

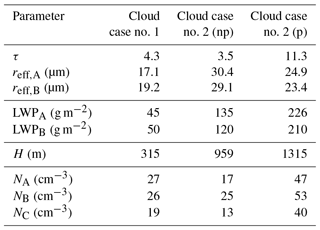
Six synthetic clouds are simulated. Their respective parameters are listed in Table 3. Cloud droplet number concentrations N_cld of 50, 100, and 200 cm⁻³ represent the typical range of pristine shallow trade wind cumulus (Siebert et al., 2013). For each N_cld an adiabatic and a sub-adiabatic cloud profile was set up. Cloud base height is 500 m and cloud-top height is 1000 m. For all cloud cases a linear increase in LWC and a constant N_cld with height are assumed. In the adiabatic cases (I, III, V) an LWP of 362 g m⁻² and an adiabatic increase in LWC with height Γ_ad of $\mathrm{2.9}\times {\mathrm{10}}^{-\mathrm{6}}$ kg m⁻³ m⁻¹, for a surface temperature of ≈30 ^∘C, are used. For the sub-adiabatic cases (II, IV, VI) Γ is set to ${\mathrm{\Gamma }}_{\mathrm{ad}}\cdot \mathrm{0.6}=\mathrm{1.7}\times {\mathrm{10}}^{-\mathrm{6}}$ kg m⁻³ m⁻¹, representing a cloud, which follows Γ_ad by 60 % and leads to an LWP of 217 g m⁻². To calculate the volumetric radius r_vol(z), the cloud profiles are divided into 20 layers of equal thickness of 25 m. For each layer the parameterization of Martin et al. (1994) is applied:

$$\begin{array}{}\text{(15)}& r_{\mathrm{vol}}\left(z\right)=\sqrt[\mathrm{3}]{{\displaystyle \frac{\mathrm{3}\cdot \mathrm{LWC}\left(z\right)}{\mathrm{4}\cdot {\mathit{\rho }}_{\mathrm{w}}\cdot \mathit{\pi }\cdot N_{\mathrm{cld}}}}}.\end{array}$$

In the radiative transfer model, the effective radius r_eff is used to determine the optical properties of the cloud particles instead of the volumetric radius r_vol. To convert r_vol(z) into r_eff(z) a k of 1.0 is applied, which considers the monodisperse droplet size distribution used in the model clouds. The synthetic measurements of $I_{\mathit{\lambda },\mathrm{syn}}^{\uparrow }$ are calculated with the same simulation setup as for the cloud retrieval described in Sect. 4.2.

Table 3 Overview of all six synthetic cloud cases. The predefined cloud LWP and droplet number concentration N are denoted with the subscript “cld”. Cloud properties are calculated from the given cloud profile (subscript “lib”) and retrieved from synthetic spectral cloud reflectivities (subscript “R”). Calculated N is listed for all three methods: A, B, and C using the predefined cloud properties “lib” and the retrieval results from “R”.

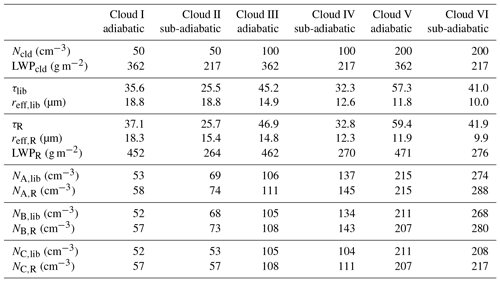
Simulated synthetic measurements of $I_{\mathit{\lambda },\mathrm{syn}}^{\uparrow }$ are applied to the retrieval method of τ, r_eff, and N of Sect. 5. All three methods (A, B, and C) are applied and results are denoted with the additional subscript “R”. The true values of τ from the RTS (subscript “lib”) are calculated directly from the given r_eff,lib, which represents the cloud-top r_eff of the model cloud. Total cloud optical thickness τ_lib and r_eff,lib from the libRadtran radiative transfer simulations are considered to be the reference values used to compare the retrieval results and the calculated N. For consistency the labeling of N for the three methods follows Sect. 5. An overview of all retrieved and calculated parameters is given in Table 3.

The retrieved cloud optical thickness τ_R is higher compared to the true value τ_lib for all cloud cases. The largest difference of 26 % is observed for cloud I. With increasing N_cld the absolute and relative differences become smaller. Systematically larger errors are found for the adiabatic clouds. A similar pattern is obtained for r_eff,R, which is always up to 2 % smaller than r_eff,lib. The sub-adiabatic clouds show the largest differences. The relative error decreases for higher N_cld. The systematic underestimation of r_eff,R, especially for the sub-adiabatic cases, with respect to r_eff,lib results from the penetration depth of the incident solar radiation into the cloud. For constant LWP, clouds with lower N have a lower τ, which reduces scattering. Therefore, the incident radiation can penetrate deeper into the cloud compared to clouds with higher N and τ (Platnick, 2000). As a result, $I_{\mathit{\lambda }}^{\uparrow }$ is more influenced by lower cloud layers and the retrieved r_eff,R is systematically smaller than r_eff,lib. In this case, r_eff,R does not represent r_eff,lib at CT. The bias of r_eff,R from the r_eff,lib at CT feeds back into the retrieval of τ_R because of the dependence of τ and r_eff and the non-rectangular shape of the lookup table. The overall underestimation of retrieved r_eff,R, which appears for all passive remote sensing measurements based on reflected solar radiation, generally leads to an overestimation of N, which is intensively discussed, e.g., by Brenguier et al. (2000) and Grosvenor et al. (2018a, b), and therefore not repeated here.

Liquid water path LWP_R is calculated with Eq. (11) from the retrieved τ_R and r_eff,R by assuming an adiabatic cloud profile. In all cases, the retrieval overestimates LWP_R by 18 % for low N_cld up to 27 %. The deviation becomes larger for high N_cld.

The cloud droplet number concentration N_A,lib is calculated with method A by using τ_lib, r_eff,lib and assuming an adiabatic vertical profile with Γ_ad. This provides a reference for N_A,R, which applies τ_R and r_eff,R. By comparing N_A,lib and N_A,R the influence of the remote sensing retrieval method (forward simulations and error due to penetration depth) on N for different N_cld becomes obvious. In general, N_A,lib and N_A,R of all clouds are larger compared to N_cld. Differences among N_A,lib, N_A,R, and N_cld result from smaller retrieved r_eff,R and higher τ_lib compared to τ_R. Another reason is the difference between Γ_ad used in the model cloud and the assumed LWP parameterization in Eq. (11), which is applied in Eq. (10) to correlate LWP and τ. For all clouds, N_A,R is larger than N_A,lib and N_cld because in Eq. (10) N is dominated by $r_{\mathrm{eff}}^{-\mathrm{5}/\mathrm{2}}$ and less sensitive to τ^1∕2. Differences between N_A,lib and N_A,R vary between 0 % and 17 %, being largest for cloud I for which the deviation in r_eff,lib and r_eff,R is largest. The simulations also show that N_A,lib and N_A,R are largest for the sub-adiabatic cloud cases.

For method B, N_B,lib and N_B,R are larger than N_cld with smaller differences for the reference values of N_B,lib and larger differences of N_B,R compared to N_cld. For method B the deviations of N_B,lib and N_B,R compared to N_cld are largest for the sub-adiabatic cloud cases. The systematic overestimation of N_B,R for all clouds is due to the lower r_eff,R. The differences are reduced for increasing N_cld because the differences between r_eff,R and r_eff,lib decrease. This clearly shows that a wrong estimation of r_eff influences the calculation of N most significantly, while τ contributes to a minor part only, independently of which method is used. These results allow for the conclusion that r_eff must be retrieved close to cloud top. This is possible if the retrieval applies an appropriate wavelength in the infrared, whereby radiation is effectively absorbed within the uppermost part of the cloud. Otherwise, systematic overestimation of N occurs.

By applying method C the sub-adiabatic nature of the cloud profiles (II, IV, VI) is considered in the estimation of N. The calculated Γ_calc is assumed to be correct and identical to the profile of the constructed clouds, with f_ad=0.6 and ${\mathrm{\Gamma }}_{\mathrm{calc}}={\mathrm{\Gamma }}_{\mathrm{ad}}\cdot \mathrm{0.6}$. Therefore, it is obvious that N values calculated from method B and C are also identical for adiabatic clouds. In general, N_C,R derived from method C is closer to N_cld than N_B,R. However, for the sub-adiabatic clouds (II, IV, VI) the results for methods B and C differ. Cloud droplet number concentration N_C,lib is closest to N for all cloud cases and methods. The same pattern is present for N_C,R with the best agreement to N_cld compared to method A and B. Deviations in N_C,lib and N_C,R to N_cld are reduced with increasing N. This shows that a correct assumption of Γ_calc, as possible with method C, is crucial for a reliable calculation of N and can compensate for biases in N that result from the sub-adiabatic cloud profile.

5.5 Calculation of retrieval uncertainty of cloud droplet number concentration

Cloud droplet number concentrations calculated with Eqs. (10), (12), and (14) are mainly affected by uncertainties from τ, LWP, and especially r_eff, but also depend on the accuracy of k, f_ad, and Γ_ad. To estimate the uncertainties of retrieved N, it is assumed that the errors are normally distributed and independent from each other. In this case the uncertainty of N_A from Eq. (10) is calculated by

$$\begin{array}{ll}{\displaystyle }\mathrm{\Delta }N& {\displaystyle }=\sqrt{{\left({\displaystyle \frac{\partial N}{\partial k}}\right)}^{\mathrm{2}}{\left(\mathrm{\Delta }k\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial N}{\partial f_{\mathrm{ad}}}}\right)}^{\mathrm{2}}{\left(\mathrm{\Delta }{f}_{\mathrm{ad}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial N}{\partial {\mathrm{\Gamma }}_{\mathrm{add}}}}\right)}^{\mathrm{2}}{\left(\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathrm{add}}\right)}^{\mathrm{2}}}\\ \text{(16)}& {\displaystyle }& {\displaystyle }\stackrel{\mathrm{‾}}{+{\left({\displaystyle \frac{\partial N}{\partial \mathit{\tau }}}\right)}^{\mathrm{2}}{\left(\mathrm{\Delta }\mathit{\tau }\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial N}{\partial r_{\mathrm{eff}}}}\right)}^{\mathrm{2}}{\left(\mathrm{\Delta }{r}_{\mathrm{eff}}\right)}^{\mathrm{2}}}\end{array}$$

and analogous for Eqs. (12) and (14). All uncertainties of N presented in the following sections are based on calculations with this approach. The uncertainties of the single parameters assumed in the calculations are summarized below.

For method A, B, and C, the uncertainty of k, representing the shape of the droplet size distribution, is set to $k=\mathrm{0.8}\pm \mathrm{0.1}$ according to the range of values suggested by Martin et al. (1994) and Pontikis and Hicks (1992).

For methods A and B the degree of adiabacity f_ad is fixed to 1. In that case, no uncertainty in a measurement scene is attributed to f_ad. For method C, the uncertainty of f_calc is determined by the uncertainty of h_CT, h_CB, and retrieved LWP following Eq. (13). Cloud-top height from WALES is determined with an accuracy of $\mathrm{\Delta }{h}_{\mathrm{CT}}=\pm \mathrm{20}$ m. The cloud base height is derived from single dropsondes and therefore prone to horizontal variability in T, p, and T_d. Based on an analysis of different dropsondes in close vicinity, a cloud base height h_LCL=660 m ± 35 m is assumed. The evaluation of all dropsondes shows that the thermodynamic conditions in the selected area stayed constant (ΔT<2 K and Δp<4 hPa) during the flight time with h_CT≈1800 m, T_CT=20.2 ^∘C, and p_CT=820 hPa. The accuracy of the deployed Vaisala dropsondes RD94 is reported to be within $\mathrm{\Delta }T=\pm \mathrm{0.2}$ K and $\mathrm{\Delta }p=\pm \mathrm{0.4}$ hPa. Uncertainties of N_C caused by errors in Γ_ad are therefore negligible compared to the influence of τ and r_eff.

The adiabatic increase in LWC with height calculated from the Clausius–Clapeyron equation depends mostly on cloud-top temperature T_CT and to a lesser degree on cloud-top pressure p_CT. Therefore, Γ_ad depends on T_CT and p_CT, too. The cloud droplet number concentration is mostly affected by the assumed T_CT, whereby p_CT makes only a minor contribution. Despite that, the cloud-top pressure more strongly affects warm than cold clouds (Grosvenor et al., 2018b). For the uncertainty calculation, a temperature difference of 2 K is considered, which changes Γ_ad by $\pm \mathrm{0.1}\times {\mathrm{10}}^{-\mathrm{3}}$ g m⁻³ m⁻¹ for the reference value of $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{3}}$ g m⁻³ m⁻¹.

The uncertainty of the retrieval of τ and r_eff,A results from the measurement uncertainties of SMART, which are described in Sect. 3.1. For typical trade wind cumulus, uncertainties of ±0.1 for τ and ±1.1 µm for r_eff,A are assumed.

Small clouds not covering the entire FOV bias the retrieval of the optical properties towards low τ, large r_eff, and resulting low N. Additionally, the uncertainties in r_eff increase for low τ. Correlation of τ and Δr_eff reveals that this effect is pounced for τ≤5. This mostly results from the increasing influence of the ocean surface with low albedo in broken cloud regions.

From the error estimation of the N retrieval it can be concluded that uncertainties in r_eff, LWP, and H have to be minimized as they influence the retrieval the most. Determination of h_CB, either from the dropsondes or the radar, and resulting H have to be accurate within at least ±60 m.

In addition to the measurement uncertainties, the sensitivities of the individual retrievals on τ, r_eff, LWP, h_CT, and h_CB have to be considered. The retrieval of LWP by SMART is sensitive for thin clouds (LWP<100 g m⁻²) with an increasing uncertainty for optically thicker clouds caused by a reduced response of reflected I^↑ in the case of high optical thickness. The usage of LWP from SMART for optical thin clouds is further supported by the retrieval uncertainty in LWP by HAMP for LWP values below 100 g m⁻². For clouds with LWP around 100 g m⁻², both methods A and B (assuming an uncertainty of LWP derived by HAMP of about 20 %) lead to an uncertainty of N in the range of 10 cm⁻³. In the case of thicker clouds (LWP>100 g m⁻²), method B with LWP from HAMP is used, achieving N accuracy of ±14 cm⁻³ from SMART. For clouds with LWP>100 g m⁻² and considerable geometric thickness (H>1500 m), HAMP-retrieved LWP becomes more representative as the retrieval represents the entire cloud and not only the CT properties observed by SMART. Common satellite-based microwave radiometer retrievals of LWP above 180 g m⁻² are error-prone because of their large footprint. With the smaller footprint of HAMP these uncertainties in LWP are reduced, resulting in a lower uncertainty in retrieved N_B and N_C.

The retrievals of r_eff,B from combined measurements of SMART and HAMP are slightly more prone to uncertainty of the LWP_B measurements and lead to uncertainties of r_eff,B of up to ±1.5 µm, being sightly higher than r_eff estimated for method A. However, the uncertainty of N with respect to r_eff is lower, as the sensitivity of N_B with respect to r_eff,B is lower in Eq. (12) compared to Eq. (10). The sensitivity study leads to the conclusion that an appropriate retrieval of r_eff is the most important factor for the calculation of N.

For the exemplary ideal adiabatic case study discussed above, the total uncertainties of the three methods are $\mathrm{\Delta }{N}_{\mathrm{A}}=\pm \mathrm{7.1}$ cm⁻³, $\mathrm{\Delta }{N}_{\mathrm{B}}=\pm \mathrm{14.1}$ cm⁻³, and $\mathrm{\Delta }{N}_{\mathrm{C}}=\pm \mathrm{15.1}$ cm⁻³. For sub-adiabatic clouds, the uncertainties of method A and B increase due to the assumption of adiabaticity. The additional error in N results from the increased variability in f_ad.

Figure 2 Flight track of HALO (white) from RF 06 (19 August 2016) plotted on a MODIS Terra satellite image from 19:30 UTC. The section for which the remote sensing measurements are analyzed (19:24 to 19:39 UTC) crosses a region with aggregated trade wind cumulus and is plotted in gray.

6 Results

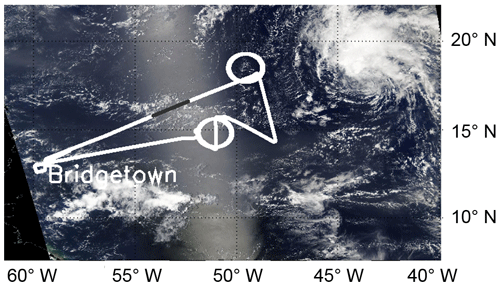
The retrieval of N is applied to two measurement cases observed during NARVAL-II. Figure 2 shows the flight track (white) of Research Flight 06 (RF 06) from 19 August 2016 and the flight section (19:24 to 19:39 UTC) of the track for which the remote sensing measurements are analyzed. The satellite image represents the cloud situation at 19:30 UTC. The presence of intense sun glint is visible, which enhances the reflected radiance $I_{\mathit{\lambda }}^{\uparrow }$ and influences the cloud detection (low contrast) and the retrieval of τ and r_eff,A. The analyzed time period is divided into two parts, cloud case no. 1 and cloud case no. 2. The northeastern part of the flight track (19:29–19:32 UTC) was dominated by aggregated trade wind cumuli, whereas in the southwestern part (19:32–19:36 UTC) shallow cumuli were present. The general weather situation was characterized by moderate convection with low cloud-top altitudes. Locally, more dense cloud fields formed at about 10 and 16^∘ N at 55^∘ W.

Time series of measured and retrieved parameters of both cloud cases are shown in Figs. 3 and 4. The three methods to calculate N assume that there is no precipitation present. Because measured Z is most sensitive to large cloud droplets, it cannot be guaranteed that drizzle is excluded completely. Estimation of the drizzle rate on the basis of H and N as proposed by Pawlowska and Brenguier (2003) and vanZanten et al. (2005) is not possible as retrieved N is biased by the process of drizzle formation and therefore not applicable with the presented instrument setup of HALO. Flight sections flagged for precipitation are highlighted by gray boxes. At the top of Figs. 3 and 4 the cloud mask (blue) and the homogeneity cloud flag HCF (yellow) are indicated. Images of RGB composites by specMACS are given in the lower part of the plots to illustrate the visual cloud characteristics. Data gaps are due to cloud-free pixels.

6.1 Cloud case no. 1

Case no. 1 represents a stratiform single-layer cloud without any convective areas, which is an ideal test case for the N retrieval. The cloud optical thickness τ shown in Fig. 3a is generally low and ranges between 0 and 2 at the beginning of the section, while τ increases to up to 6 with time. The uncertainty of τ is estimated to be ±0.1. The effective radius r_eff,A (panel b, black line) ranges between 9.6 and 26.3 µm with an uncertainty of ±1.0 µm, while r_eff,B is between 8.3 and 30 µm retrieved with a slightly higher uncertainty of ±1.5 µm. For the first cloud part, the SMART liquid water path LWP_A (panel c) is calculated with Eq. (4) using retrieved τ and r_eff,A. For the first part of the cloud LWP_A is slightly lower than the LWP_B measured by the microwave profiler, while with increasing τ the agreement between the two LWPs improves. Vertical profiles of LWC shown in Fig. 3g are below the detection threshold except for four cloud patches. This indicates that no precipitation was detected, but slight drizzle cannot be excluded. Cloud base height is estimated from dropsondes to be around 1500 m, while h_CT is determined by WALES. The resulting cloud geometric thickness H (Fig. 3d) varies between 100 and 420 m. Cloud adiabaticity f_calc (Fig. 3e) is mostly below 0.5, indicating a considerable sub-adiabatic cloud. Calculated N_A and N_B are shown in Fig. 3f and range between 5 and 40 cm⁻³, which results from the low τ and LWP_B and the large r_eff,A and r_eff,B. The cloud droplet number concentration N_A shows a peak around 19:34:30 UTC and N_A at 19:35:00 UTC. Cloud droplet number concentration N_C derived by method C is lower than N_A and N_B and does show a reduced variability compared to N_A and N_B. However, the uncertainty of all N is about ±15 cm⁻¹. While in the first part of cloud case no. 1 the differences in N are large, there is a good agreement among all three methods in the second part, for which all results are inside the uncertainty range of each method. Mean values of measured and retrieved parameters for cloud case no. 1 are listed in Table 4.

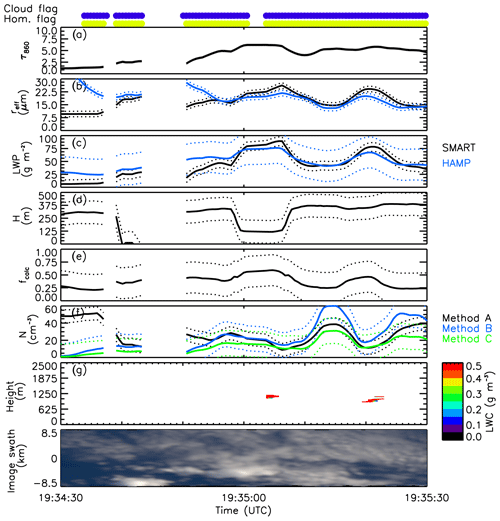
Figure 3 Time series of measured and retrieved cloud properties for cloud case no. 1 from 19:34:30 to 19:35:30 UTC of RF 06. Cloud droplet number concentration N is shown for all three methods (A, B, and C). Uncertainty ranges of the individual parameters are indicated by dotted lines. At the top, the cloud mask (blue) and the homogeneity cloud flag (HCF) (yellow) derived by SMART are indicated.

6.2 Cloud case no. 2

The second case represents a more heterogeneous single-layer cloud observed between 19:29 and 19:32 UTC, shown in Fig. 4. This cloud is in a later state of development and shows moderate convection with slight precipitation. In these areas (highlighted in gray), the criteria for cloud homogeneity are not fulfilled. Despite that and the slight precipitation, calculation of N is performed, knowing that the retrieval of N using method A and B is prone to errors under these circumstances. These results are used to evaluate the improvement of retrieved N by method C, which accounts for cloud geometry and sub-adiabacity. By comparing convective and non-convective areas of cloud case no. 2, the limitations and advantages of the three methods are investigated. Mean values of the measured and retrieved parameters from the three different methods, separated for nonprecipitation and precipitation, are summarized in Table 4.

For the nonprecipitating and homogeneous part of cloud case no. 2, τ does not exceed a value of 30 and r_eff,A and r_eff,B range between 18 and 40 µm (Fig. 4a, b). The uncertainty of all measured and retrieved parameters is in a similar range as calculated for cloud case no. 1. Retrieved LWP from SMART and HAMP (Fig. 4c) agrees within the uncertainty range of HAMP for most parts of the homogeneous cloud sections. Larger differences appear around 19:29:30 UTC when LWP_A is larger than LWP_B. For method C, cloud geometrical thickness H is calculated from a combination of HAMP and WALES. Radar reflectivity Z is above the precipitation detection threshold of −20 dBZ and allows for the determination of vertical profiles of the LWC and h_CB with an average value of h_CB≈900 m when no precipitation is present. Cloud-top height h_CT from WALES ranges between 200 and 1000 m for the nonprecipitating regions. This results in a highly variable f_calc, which varies strongly between 0.05 and 1.0.

Cloud droplet number concentrations from method A and B calculated for cloud case no. 2 are generally low (see also Table 4), mostly ranging between 20 and 40 cm⁻³. Together with large r_eff,A and r_eff,B these values indicate typical pristine maritime clouds. An exception is observed around 19:29:30 UTC when N peaks up to 120 cm⁻³ for all three methods mostly resulting from a decrease in r_eff,A and an increase in τ. The decrease in r_eff might result from 3-D radiative effects at the cloud edge overestimating the cloud particle size and could have biased the retrieval of N.

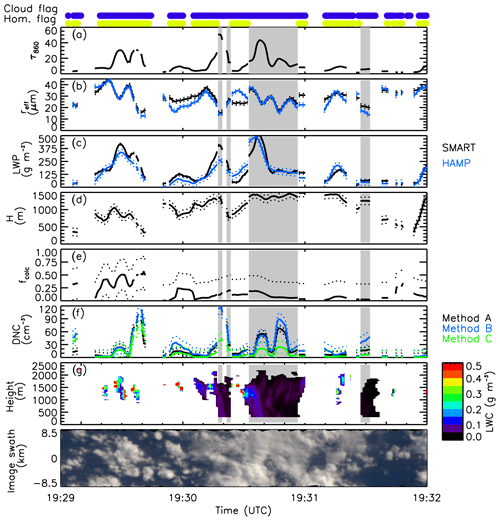
Figure 4 Time series of measured and retrieved cloud properties for cloud case no. 1 from 19:29 to 19:32 UTC of RF 06. Cloud droplet number concentration N is shown for all three methods (A, B, and C). Uncertainty ranges of the individual parameters are indicated by dotted lines. At the top, the cloud mask (blue) and the homogeneity cloud flag (HCF) (yellow) derived by SMART are indicated.

In the areas marked with precipitation, retrieved τ, LWP_A, and LWP_B are higher compared to the precipitation-free regions, while r_eff,A and r_eff,B are in the same range as for the nonprecipitating areas. In contrast to the homogeneous parts of the cloud, the convective regions show stronger horizontal heterogeneity in all parameters. The optical thickness reaches up to 40 and r_reff,A ranges from 20 to 38 µm. In these areas the LWP_B from HAMP exceeds 270 g m⁻² and shows a maximum value up to 500 g m⁻². Liquid water path from SMART is in the same range of LWP_B except for the first precipitation section (19:30:30 UTC) in which LWP_B is lower than LWP_A. For the precipitating regions h_CB is assumed to be at the same level as determined for the nonprecipitating regions, as precipitation makes the cloud base invisible for the radar. The cloud geometric thickness H is slightly higher for the connective regions and ranges between 800 and 1300 m. The calculated adiabaticity f_calc is lower than 0.5 for the majority of the measurement and shows that most parts of the cloud are sub-adiabatic. For the precipitation regions calculated N values are between 10 and 90 cm⁻³, with the highest concentrations for method B, followed by method A and the lowest N for method C. In the areas with precipitation, N shows a systematically higher variability observed by all three methods and likely caused by the variability of r_eff retrieved from SMART. One reason for this variability is the relation of r_vol to r_reff, which is assumed to be (i) constant in the retrieval of r_eff,A and r_eff,B and (ii) significantly influenced by the formation of precipitation. Therefore, calculated N values by all three methods are highly prone to errors for precipitating clouds. The variability of N might also be caused by intense turbulent mixing processes within the cloud. Concluding from that, it is suggested to filter areas with stronger convection, precipitation, and heterogeneous scenes and analyze the retrieved N with special care.

Table 4 Mean values of cloud properties for cloud cases no. 1 and no. 2.

6.3 Statistical analysis of liquid water path, droplet effective radius, and number concentration

Statistics of retrieved cloud properties are analyzed for measurements between 19:24:00 and 19:39:00 UTC only, when the HCF indicates homogeneous clouds and uncertainties of the retrieved cloud parameters are low. An extension of the analysis to other flights is not possible yet because the reliable application of the retrieval of N requires careful data selection and good quality data from all individual instruments. However, in total 700 individual measurements are included, which represents a cloud field 77 km in length. The clouds were separated into precipitating (p) and nonprecipitating (np) pixels. Mean values of the parameters for each measurement are summarized in Table 4.

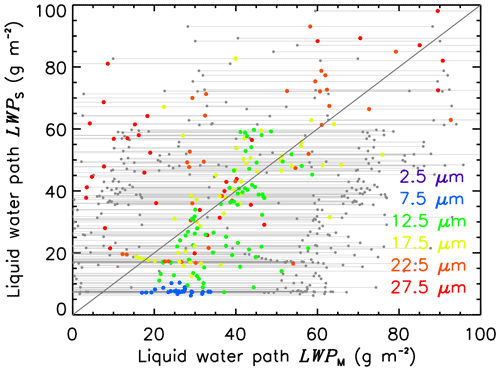
Figure 5 Comparison of liquid water path LWP_B from HAMP microwave radiometer and LWP_A calculated from τ and r_eff,A retrieved by SMART. The color code indicates different ranges of r_eff,A. HAMP uncertainties of LWP (±30 g m⁻²) are indicated by gray errors bars.

Figure 5 compares measurements of LWP_A and LWP_B. The data are separated for different r_eff,A split into bins of 5 µm size. For the selected time period, LWP_A agrees with LWP_B within the uncertainty range of HAMP of ±30 g m⁻² indicated by the gray error bars. The differences of LWP_A and LWP_B show a larger variability for clouds with large r_eff,A than for clouds with small r_eff,A. For larger cloud droplets, the retrieval uncertainty of τ and r_eff,A increases, as does LWP_A derived from SMART. Additionally, SMART has a higher sensitivity to droplets at cloud top and the FOV of HAMP is slightly larger compared to SMART, which can explain some of the observed variability. Slightly different viewing directions have to be considered, too. While for SMART the LWP_A is calculated assuming an adiabatic profile with the retrieved r_eff,A representing cloud top, HAMP obtains an integrated measure of LWP, whereby all cloud layers are more homogeneously weighted and no assumption on the cloud profiles is required. Therefore, a difference between LWP_A and LWP_B indicates that the observed clouds are nonadiabatic. For LWP_A>LWP_B less liquid water is at CB than predicted by adiabatic theory and clouds are sub-adiabatic. For LWP_A<LWP_B liquid water at CT is reduced, likely by precipitation as supported by the preferred r_eff in these LWP regimes (Fig. 5).

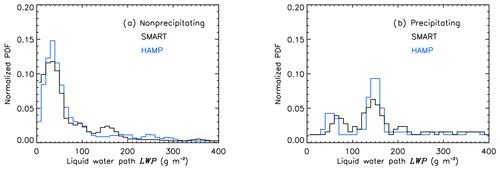
Figure 6 Normalized probability density function (PDF) of measured and calculated LWP from HAMP (blue) and SMART (black). Distributions are filtered for nonprecipitating (a) and precipitating (b) clouds.

Figure 6a and b show the normalized probability density function (PDF) of LWP retrieved by HAMP and SMART separated for precipitating and nonprecipitating clouds. For the nonprecipitating clouds, the distributions of LWP retrieved by SMART and HAMP are dominated by clouds below 100 g m⁻². Higher LWPs are obtained for regions with precipitation, for which the distribution is shifted towards larger values of LWP. The PDFs of LWP_A and LWP_B show a dominant mode at around 150 g m⁻². A second smaller mode is present for LWP_A at 80 g m⁻² and LWP_B at 50 g m⁻² for both instruments. The agreement of the LWP retrievals, utilizing reflected solar radiation from CT (method A) and passive microwave measurements (method B), indicate that the cloud microphysical properties are sufficiently determined by the SMART retrieval, despite the assumption of an adiabatic cloud profile in method A.

Table 5 Measured and retrieved properties in the entire period for both cloud cases, separated for precipitating (p) and nonprecipitating (np) clouds.

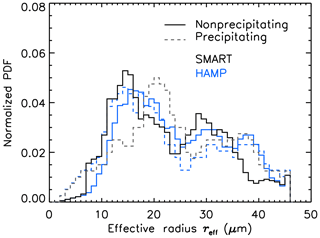
Figure 7 Normalized PDF of the effective radius r_eff,A retrieved by using the ratio of 1645 to 1050 nm in black and r_eff,B from the combined spectrometer–microwave retrieval in blue. Distributions are filtered for nonprecipitating (solid line) and precipitating (dashed line) clouds.

In Fig. 7 the normalized PDFs of r_eff,A retrieved from SMART only (method A) and r_eff,B retrieved synergistically from SMART and HAMP (method B) separated for precipitating and nonprecipitating clouds are presented. The mean value for nonprecipitating clouds is around ${\stackrel{\mathrm{‾}}{r}}_{\mathrm{eff},\mathrm{A},\mathrm{np}}=\mathrm{23.2}$ µm and the median is at $r_{\mathrm{eff},\mathrm{A},\mathrm{np},\mathrm{med}}=\mathrm{21.1}$ µm. This droplet size range agrees with in situ measurements of pristine trade wind cumulus by Siebert et al. (2013) and remote sensing measurements by Werner et al. (2014) in the same geographic region. The distribution shows a bimodal structure with a first mode around 15 µm and a second mode around 32 µm. The PDF of r_eff,A for precipitation situations shows a similar structure being shifted towards larger r_eff,A with values of ${\stackrel{\mathrm{‾}}{r}}_{\mathrm{eff},\mathrm{A},\mathrm{p}}=\mathrm{25.1}$ µm and $r_{\mathrm{eff},\mathrm{A},\mathrm{p},\mathrm{med}}=\mathrm{24.5}$ µm. The first mode is at 21 µm and the second mode is at 36 µm. The PDFs of r_eff,B for the np clouds are shifted to larger values by approximately 3 µm, additionally showing a third mode around 38 µm. In contrast, the PDF for the p clouds is shifted to lower values by up to 8 µm and showing only the bimodal structure with peaks around 15 and 33 µm.

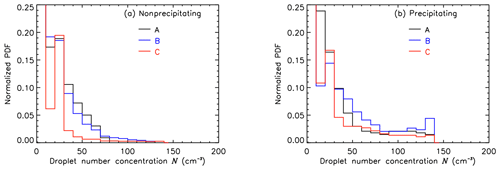
Figure 8 Normalized probability density function of the cloud droplet number concentration N for the selected flight path using method A, B, and C. Distributions are filtered for nonprecipitating (a) and precipitating (b) clouds.

Figure 8a and b show normalized PDFs of the calculated N for nonprecipitating (panel a) and precipitating regions (panel b) of the selected flight leg from all three methods (A, B, and C). For nonprecipitating clouds (Fig. 8a) the distribution of N_A peaks at N_A≈30 cm⁻³ with a steep decrease towards a concentration of ≈100 cm⁻³. The first local maximum of the N_B distribution is at N_B≈30 cm⁻³, slowly decreasing for larger N. Only a slight difference between N_A and N_B is present for higher N_A. This can be explained by the slightly higher values of SMART LWP_A compared to HAMP LWP_B. The PDFs of N_A and N_B show reasonable results for pristine, maritime clouds with relatively large r_eff,A and accordingly low N from method A and B. Cloud droplet number concentrations from method C are significantly lower as a result of the considered adiabaticity of the individual clouds.

Measurements affected by precipitation compared to Fig. 8a show almost the same distribution with a shift to larger N for all three calculation methods, especially for method C. Filtering for precipitating clouds, the statistics might be biased by only considering further developed clouds in which precipitation formation changes and broadens the droplet size distribution. This leads to differences in the means of r_vol and r_eff, influencing the k parameter, which is assumed to be 0.8 in the N calculation.

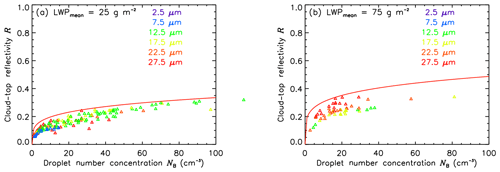
Figure 9 Cloud-top reflectivity ℛ₅₃₂ as a function of cloud droplet number concentration N_B for homogeneous, nonprecipitating clouds of different liquid water paths LWP_B (a: 0–50 g m⁻², b: 50–100 g m⁻²). The droplet effective radius r_eff of each measurement is indicated by the color code. The red line represents simulated reflectivity ℛ₅₃₂ from radiative transfer calculations for clouds with the same LWP.

Figure 9 shows the cloud-top reflectivity ℛ₅₃₂ measured by SMART at 532 nm as a function of N_B retrieved from combined SMART and HAMP measurements. Only measurements of the flight leg during which no precipitation was observed are presented. The data are binned for two different LWPs. Figure 9a shows clouds with LWP between 0 and 50 g m⁻², and Fig. 9b shows clouds in the range between 50 and 100 g m⁻². Colors represent r_eff,B binned from 5 to 30 µm in 5 µm steps (label in Fig. 9 refers to the mean bin value). Using ℛ₅₃₂ as a measure for the reflectivity of the cloud, the sensitivity of ℛ₅₃₂ to changes in N is comparable to the model-based sensitivity study in Sect. 2. Therefore, in Fig. 9 radiative transfer simulations of theoretical ℛ_532,sim for clouds of the same LWP are added by the red line. For the thin clouds in Fig. 9a the measured ℛ₅₃₂ shows a clear increase for higher N_B over the entire measurement range. This correlation is less pronounced for the thicker clouds in Fig. 9b due to a reduced range of ℛ₅₃₂ and N, and the observations may not cover the entire natural variability. However, for both cloud subsamples, the measurements follow the theoretical line given by the simulations and the measured ℛ₅₃₂ values are too low or retrieved N too high. Both might be attributed to measurement biases: either the radiometric calibration of SMART or the retrieved LWP_B and r_eff,B, which feed the calculation of N_B. Additionally, the homogeneous assumption of cloud properties applied in the RTS can lead to an overestimation of ℛ_532,sim compared to the measurements. The subdivision of data for different r_eff,B shows that clouds in an early developing state with low LWP_B (Fig. 9a) are dominated by smaller cloud droplets up to $r_{\mathrm{eff},\mathrm{B}}=\mathrm{17.5}$ µm, whereas clouds in a later development state with higher LWP_B (Fig. 9b) are dominated by cloud droplets larger than $r_{\mathrm{eff},\mathrm{B}}=\mathrm{17.5}$ µm.

7 Conclusions

Trade wind cumuli are a ubiquitous cloud type in the tropics influencing the Earth radiative energy budget significantly. In spite of their importance, they are not appropriately represented in numerical weather prediction (NWP) and global climate models (GCMs), causing considerable uncertainties in the radiation schemes of the models. Platnick and Twomey (1994) showed that the cloud-top albedo α of clouds with low cloud droplet number concentration N and low liquid water path (LWP), such as trade wind cumuli, respond sensitively to changes in N. In order to obtain improved parameterizations and global distributions of N, several methods, including active and passive remote sensing from the ground and satellites, are developed, but no operational products are available yet. Only a limited number of field campaigns with in situ measurements of selected cloud cases exist. As a result, the natural variability of trade wind cumulus is poorly covered by appropriate measurements.

Sensitivity simulations in this paper show that shallow trade wind cumuli with LWP below 200 g m⁻² and N below 100 cm⁻³ are very sensitive to changes in N. In the case of an LWP of 75 g m⁻², an increase in N from 50 to 100 cm⁻³ leads to an increase in α by 0.1. Therefore, the influence of trade wind cumuli on the Earth radiation energy budget is variable and significantly depends on the interaction among α, N, cloud optical thickness τ, cloud droplet effective radius r_eff, and different thermodynamic conditions (e.g., varying LWP), which has to be investigated systematically.

Applying the common satellite retrieval techniques of N to measurements conducted with a high-flying aircraft, such as HALO, shows the potential of combined airborne passive and active remote sensing instruments. Using aircraft instead of satellite platforms allows for the investigation of specific cloud types under selected atmospheric conditions, e.g., cloud-top temperature T_CT, cloud-top pressure p_CT, and LWP.

This was done during the second campaign of NARVAL-II, for which HALO was equipped with a set of passive and active remote sensing instruments. The SMART measured upward and downward spectral irradiance $F_{\mathit{\lambda }}^{\uparrow \downarrow }$ and upward radiance $I_{\mathit{\lambda }}^{\uparrow }$, which enables the calculation of α and retrieval of τ and r_eff,A at cloud top. The HAMP enables the performance retrievals of LWP and radar reflectivity Z used to separate for bins of LWP and to discriminate between nonprecipitating and precipitating cloud sections. Combining measured values of $I_{\mathit{\lambda }}^{\uparrow }$ by SMART and LWP by HAMP, alternative values of r_eff are retrieved, which are less influenced by 3-D cloud radiative effects. Cloud-top height h_CT is determined by the WALES, while the cloud base height h_CB is estimated from dropsondes or radar data.

The heterogeneity of shallow trade wind cumulus fields during NARVAL-II has to be considered in the analysis. This is especially important in the retrieval of τ, r_eff, and N at the average flight speed of HALO (v_ac≈220 m s⁻¹) and different instrument FOVs, being in the size range of individual clouds. The heterogeneity is indicated by the high occurrence (63 %) of clouds with a horizontal size smaller than 300 m. In this context, careful cloud masking and filtering for homogeneous cloud regions is crucial. Using cloud flagging and masking, the calculation of N can be applied to approximately 55 % of all observed clouds.

Three different methods to retrieve N based on Eq. (10) are presented and the application is shown for synthetic measurements of six different clouds with N_cld of 50, 100, and 200 cm⁻³, each following an adiabatic and sub-adiabatic cloud profile. From the synthetic measurements it can be concluded that the calculation of N on the basis of τ and r_eff,A from SMART method A is suggested for optically thin clouds (LWP<100 g m⁻²), while for optically thicker clouds method B is preferred, whereby τ is replaced by LWP retrieved by HAMP. For homogeneous clouds when the cloud boundaries can be determined precisely from active radar, lidar, and dropsonde measurements, the resulting calculated adiabaticity factor Γ_calc can be determined and used as a correction factor in the calculation of N as the optimal case (method C). The synthetic measurements further showed that the differences between modeled N_cld and retrieved N_C,lib or N_C,R with method C are significantly reduced compared to method A or B for all three cloud cases. This indicates that a correction with Γ_calc is vital and necessary for the calculation of N of shallow trade wind cumuli using remote sensing techniques. Otherwise, a systematic overestimation of retrieved N is present and measurements are not feasible.

Subsequently, the three methods are applied to a homogeneous and a heterogeneous cloud section. Both cloud cases are statistically analyzed. Determination of the cloud geometric thickness H was relatively uncertain in both cases and method C was excluded from the statistical analysis. Probability density functions of LWP, r_eff, and N for the two cloud scenes are presented. Correlations of cloud-top reflectivity ℛ₅₃₂ at 532 nm to N_B for two binned LWP_B cases are shown. These are used to validate modeled ℛ₅₃₂, to describe the sensitivity of ℛ₅₃₂ with respect to N, and allow for the parameterization of the Twomey effect. Comparison of simulated and measured ℛ₅₃₂ showed systematically lower values of observed ℛ₅₃₂. Further testing of the proposed method on longer flight sections is necessary to cover the natural variability of trade wind cumuli and thermodynamic conditions. Despite remaining uncertainties and assumptions, the application of Γ_calc, the separation for different LWPs, and the smaller FOV of all instruments allow for the better investigation of cloud–radiation interactions compared to large-scale averaged satellite measurements.

Appendix A

Table A1 List of symbols, long names, and related units.