A new method of inferring the size, number density, and charge of mesospheric dust from its in situ collection by the DUSTY probe

We present a new method of analyzing measurements of mesospheric dust made with DUSTY rocket-borne Faraday cup probes. It can yield the variation in fundamental dust parameters through a mesospheric cloud with an altitude resolution down to 10 cm or less if plasma probes give the plasma density variations with similar height resolution. A DUSTY probe was the first probe that unambiguously detected charged dust and aerosol particles in the Earth's mesosphere. DUSTY excluded the ambient plasma by various biased grids, which however allowed dust particles with radii above a few nanometers to enter, and it measured the flux of charged dust particles. The flux measurements directly yielded the total ambient dust charge density.

We extend the analysis of DUSTY data by using the impact currents on its main grid and the bottom plate as before, together with a dust charging model and a secondary charge production model, to allow the determination of fundamental parameters, such as dust radius, charge number, and total dust density. We demonstrate the utility of the new analysis technique by considering observations made with the DUSTY probes during the MAXIDUSTY rocket campaign in June–July 2016 and comparing the results with those of other instruments (lidar and photometer) also used in the campaign. In the present version we have used monodisperse dust size distributions.

1 Introduction

The Earth's mesosphere has for a long time been the least known part of the Earth's atmosphere, and it probably still is. One reason for this is its inaccessibility to direct in situ observations – it being too high for balloons and planes and too low for satellites. Its main cloud phenomena, the noctilucent clouds (NLCs), which occur in its polar regions, were first observed in 1885 (Jesse, 1885; Backhouse, 1885; Symons, 1888; Gadsden and Schröder, 1989). They are the highest-altitude clouds in the Earth's atmosphere. It now appears that the NLC occurrence frequency is increasing with time and that the NLCs spread further away from the poles with time (DeLand et al., 2007; Lübken et al., 2018), possibly due to changes in the composition of trace elements, like water vapor, in the mesosphere region. As such, one reason for the interest to understand the mesosphere is that it may be an indicator of climatic changes in the troposphere and stratosphere (Thomas, 1996). Another reason is that the mesosphere is the transition zone between outer space and the lower part of the atmosphere, where energetic particle precipitation, meteors, and UV radiation normally deposit most of their energy. Disturbed magnetosphere conditions, with high energy particle precipitation, can create large numbers of reactive NO_x molecules, which, when transported downwards, react with and reduce the ozone content (Reddman et al., 2013). Also, there is an influx of meteorites into the Earth's atmosphere, the total mass of which has been claimed to be from 4 to 300 t day⁻¹ (Plane, 2012; Asmus et al., 2015; Carrillo-Sánchez et al., 2016). Many of the meteorites evaporate as they are heated due to air friction when they enter the atmosphere, and the evaporated material recondenses and creates nanometer-sized particles, the meteoric smoke particles (MSPs) (Rosinski and Snow, 1961; Hunten et al., 1980; Hervig et al., 2017). The MSPs are thought to be crucial in creating NLCs, where they probably act as condensation sites for water vapor to form the larger icy NLC particles, but homogeneous condensation may also be part of the cause of this (Turco et al., 1982; Rapp and Thomas, 2006). In the growth process the icy NLC particles, growing by water vapor condensing on them, also capture MSPs, so that NLC particles will have MSPs embedded in them (Havnes and Naesheim, 2007; Havnes et al., 2009; Hervig et al., 2012, 2017). It also appears that the MSPs, when transported downwards, can influence the cloud formation in the stratosphere and possibly also the troposphere (Ogurtsov and Raspopov, 2011).

In order to understand the mesosphere it is crucial to understand the evolution and role of various types of dust particles in it, such as the icy NLCs and polar mesospheric summer echo (PMSE) particles, and MSPs that are probably also present in the winter mesosphere to create the weak radar PMWE (polar mesospheric winter echo) clouds (Czechovsky et al., 1979; Zeller et al., 2006; Latteck and Strelnikova, 2015). The progress in ground-based instrumentation and observing techniques during the last few decades has been impressive. For example, lidars now routinely observe in full daylight to determine NLC particle sizes and densities (Baumgarten et al., 2007), and they also measure the metallic content in the mesosphere (Huang et al., 2015) and mesospheric temperatures (Höffner and Lautenbach, 2009). The powerful new mesosphere–stratosphere–troposphere (MST) radar MAARSY with its large increase in sensitivity has profoundly changed our knowledge of PMSE occurrence rates and the altitude ranges in which they can be found (Latteck and Strelnikova, 2015). Satellites have identified MSP cloud layers by observing along them (Hervig et al., 2009) and have also confirmed earlier predictions (Havnes and Næsheim, 2007; Havnes et al., 2009; Kassa et al., 2012) that MSPs are embedded in the icy NLC and PMSE particles with 0.01 to 3 % by volume (Hervig et al., 2012).

One of the obvious advantages of the ground-based instrumentation and satellites is that they can observe the mesospheric clouds continuously. However, they have a limited space resolution (ca. 100 m and upwards) and time resolution (seconds and upwards). Rocket instrumentation, however, hand, although presenting only a snapshot of the conditions along its trajectory, observes with a time resolution typically of $\sim {\mathrm{10}}^{-\mathrm{3}}$ to 10⁻⁴ s, corresponding to a spatial resolution of ∼0.1 to 1 m. Various rocket probes are developed to observe the plasma conditions (Friedrich and Rapp, 2009), the dust charge density (Havnes et al., 1996a), and the total density of small dust (MSP) using a flashing technique (Rapp and Strelnikova, 2009) while MASS is a coarse dust mass spectrometer (Knappmiller et al., 2008; Amyx et al., 2008; Robertson et al., 2009, 2014). The MUDD (Multiple Dust Detector) finds the mass distribution of the collision fragments of the icy NLC particles and relates this to the mass distribution of embedded MSP (Havnes et al., 2014; Antonsen and Havnes, 2015; Antonsen et al., 2017).

In spite of the progress made with rocket instrumentation, there is a lack of high-time-resolution and high-space-resolution instruments to measure parameters such as dust size, number density, and charge. In the present paper we consider the principles of the much used DUSTY impact probe (Havnes et al., 1996a) and how its performance can be improved. The DUSTY probe, the principle of which is shown in Fig. 1, is equipped with three grids, G0, G1, and G2. The grid G1 prevents ambient plasma from reaching G2 and the bottom plate BP but allows dust particles to enter and collide with the grids and the BP. The potentials of the grids are given in Fig. 1. The observed currents to the probe were originally used to find only the dust charge density of the ambient dust cloud, but in the present paper we will show how to extend the analysis of the DUSTY probe currents to allow it to also determine other dust parameters. The extension of the original method of analysis is based on earlier works, which have demonstrated the importance of secondary charge and secondary current production in glancing dust impacts on rocket probes and payload bodies (Havnes and Næsheim, 2007; Havnes et al., 2009; Kassa et al., 2012).

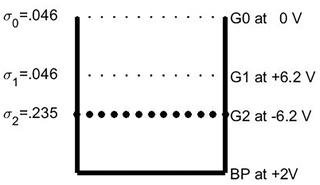
Figure 1 The design of the DUSTY probe used in the MAXIDUSTY campaign. The fractional coverage of the different grids, relative to the total probe cross section, are ${\mathit{\sigma }}_{\mathrm{0}}={\mathit{\sigma }}_{\mathrm{1}}=\mathrm{0.046}$ and σ₂=0.235. The electric potentials of all the grids and the bottom plate are relative to the payload potential Φ_P. The currents are measured on G1, G2, and BP but not on G0.

In Sect. 2 we extend the earlier analysis method for the DUSTY impact probe and now use the currents to G2 and BP to find not only the dust charge density as before but also the total dust density, the dust radius, and the mean dust charge. In Sect. 3 we show the values for dust density and dust radius from this new method, used for the observations by the DUSTY probe on the payload MXD-1, which was launched on 30 June 2016 at 09:43:18 UT in the MAXIDUSTY rocket campaign (Havnes et al., 2019). In Sect. 4 we compare the DUSTY results with those from the RMR lidar at Andøya (von Cossart et al., 1999; von Zahn et al., 2000; Baumgarten et al., 2007) and the onboard MISU photometer (Gumbel et al., 2001; Hedin et al., 2008; Megner et al., 2009) and conclude the paper in Sect. 5.

2 The extended analysis of dust observations made with DUSTY type Faraday cup probes

The DUSTY probe (Havnes et al., 1996a; Havnes and Næsheim, 2007), the design of which is shown in Fig. 1, has grids G0, G1, and G2 and a solid bottom impact plate BP. The probe must point forward along the payload axis. The dust impact currents to G1, G2, and BP are all registered but not the current to G0, which is at the payload potential Φ_P. The registered currents are I_G1,I_G2, and I_BP. The current I_G1 will not be used in the analysis. It is the grid that is most influenced by effects like payload charging and the plasma environment and as such not directly connected to the measurements of dust. G0 and G1 are made of thin cylindrical wires and they each cover only 4.6 % of the opening cross section of DUSTY. G2 is made of thicker wires to increase the secondary charging effect. It covers 23.5 % of the DUSTY cross section.

The dust current into the probe in front of G2 is designated I_D and is part of the expressions for the total current I_G2 measured on G2,

$$\begin{array}{}\text{(1)}& I_{\mathrm{G}\mathrm{2}}={\mathit{\sigma }}_{\mathrm{2}}{I}_{\mathrm{D}}+I_{\mathrm{S}},\end{array}$$

and for I_BP measured on the BP.

$$\begin{array}{}\text{(2)}& I_{\mathrm{BP}}=\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{2}}\right)I_{\mathrm{D}}-I_{\mathrm{S}}\end{array}$$

The current to G2 is made up of σ₂I_D, which is the part of I_D that hits G2 and deposits its charge, plus the secondary current I_S, which is produced by glancing dust impacts on G2, which rubs off electrons from it. If this last process is effective it can lead to the total current I_G2 becoming positive even if the impacting dust particles are charged negatively. The current I_BP to the bottom plate is made up of the direct hits on to BP by the dust that was not hitting G2 and minus the secondary current I_S. The electrons that are rubbed off from G2, producing a positive current I_S to G2, will be deposited on BP and create a negative current -I_S there. We can eliminate I_S to find I_D by

$$\begin{array}{}\text{(3)}& I_{\mathrm{D}}=I_{\mathrm{G}\mathrm{2}}+I_{\mathrm{BP}}.\end{array}$$

The two upper grids G0 and G1 are made of thin wires and each cover only 4.6 % of the DUSTY cross section (Fig. 1). Many of the small negatively charged fragments produced on them by impacts will be stopped by air friction and probe internal electric fields (Antonsen et al., 2017). We therefore neglected a possible contribution of their secondary production to the currents to G2 and BP. However, they will together stop ∼9.2  % of the incoming dust current from passing G0 and G1. The current I_Total into the probe just above G0 can be expressed as $I_{\mathrm{Total}}=I_{\mathrm{D}}(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{0}}{)}^{-\mathrm{2}}=\mathrm{1.1}\times I_{\mathrm{D}}$, which directly gives us the observed ambient dust charge density Σ(N_ZZ_D) from the relationship

$$\begin{array}{}\text{(4)}& I_{\mathrm{Total}}=\mathit{\pi }{R}_{\mathrm{p}}^{\mathrm{2}}{V}_{\mathrm{R}}e\sum \left(N_Z{Z}_{\mathrm{D}}\right).\end{array}$$

Here R_p is the probe radius, and $e=\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{19}}$ C. The number density of dust particles with charge number Z_D is N_Z and the rocket velocity is V_R. We should note that the dust charge density ∑(N_ZZ_D), which can be extracted from Eq. (4) is independent of the model for secondary production of charge since this cancels in Eq. (3).

Some information on the expected size of the dust particles, and the role of secondary charge production, can be found from examining the ratio

$$\begin{array}{}\text{(5)}& R={\displaystyle \frac{I_{\mathrm{G}\mathrm{2}}}{I_{\mathrm{BP}}}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{G}\mathrm{2}}{I}_{\mathrm{D}}+I_{\mathrm{S}}}{\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{G}\mathrm{2}}\right)I_{\mathrm{D}}-I_{\mathrm{S}}}}.\end{array}$$

This ratio R should have values between $R=\frac{{\mathit{\sigma }}_{\mathrm{G}\mathrm{2}}}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{G}\mathrm{2}}}=\mathrm{0.31}$ when the secondary charging current I_S→0 and $R=-\mathrm{1}$ for I_S≫I_D. In Fig. 2 we show R and I_D as functions of altitude. It is reassuring that R, even though it varies significantly with altitude, stays so well within the above limits. This has been shown to also be the case in several earlier launches of the DUSTY probe (Havnes and Næsheim, 2007; Havnes et al., 2009).

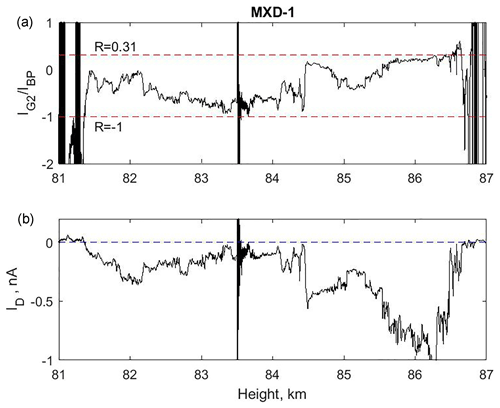
Figure 2 The ratio of the currents to G2 and BP in panel (a) compared to the current I_D in panel (b). The large disturbance at ∼83.5 km in altitude is caused by a squib being fired to open for another experiment on the payload. The values of R, at and outside the borders of the cloud, at 81.36 and 86.85 km in height, are to be neglected since the dust density there is low or zero and R is therefore dominated by noise and uncertainties in their background level.

We see from Fig. 2a that the ratio R is dominated by secondary charging effects in the middle of the NLC cloud system at ∼82.5 to ∼84.4 km, while at the upper edge around 86 km secondary charging is not very significant. This is in accordance with a scenario in which small cloud particles normally can be expected to be found in the upper parts of the clouds (Robertson et al., 2009), from where they sink and grow, to reach maximum sizes in the middle regions of the clouds. In the lower parts, melting should lead to a reduction of the icy dust particle sizes and a release of embedded MSPs. Laboratory studies of impacts of small ice particles below a diameter of ∼14 nm, at impact velocities of ∼1400 m s⁻¹, indicate that the secondary production is proportional to the cross section of the impacting ice particle (Tomsic, 2001). Since the charge on a dust particle at given plasma conditions is roughly proportional to its radius, and since the cross section is proportional to the square of the radius, a significant secondary current (R < 0) indicates large particles, while small secondary production (R > 0) indicates small dust particles. We will later show that this is what we get for the dust size from the extended method.

The secondary charging, or the rubbing-off effect by impacting dust on surfaces, is strongly dependent on the impact angle θ_i, the angle between the surface normal and the direction to the impacting particle. The impact angle θ_i will be zero for impacts at the top of a grid wire and 90^∘ for a glancing impact at the extreme side of a wire. In experiments with ice particles (Tomsic, 2001) the maximum of the secondary production probably was at an impact angle θ_i of ∼80^∘, the highest impact angle used in the experiments, or slightly above. It should be reduced to 0 at 90^∘. Little secondary charge production took place below θ_i∼65 to 70^∘. This means that of the dust particles impacting on the cylindrical grid wires, only a fraction will rub off electrons from the grid. Havnes and Næsheim (2007) analyzed, in detail, the rotational effect on the currents to the grids of a DUSTY probe, launched in the summer of 1994 (Havnes et al., 1996a). They found that a substantial secondary charge production was needed to model the payload rotational effects on the grid impact currents. The effect of secondary charging has since been mapped in several other rocket flights (Havnes et al., 2009, 2014; Kassa et al., 2012; Antonsen and Havnes, 2015; Antonsen et al., 2017). One result of the analysis of the secondary impact effects of NLC particles on the main grids of DUSTY-type probes was that it had to be much more efficient than what has been found for impact of ice particles in laboratory experiments. A probable reason for this difference is most likely connected to the fact that pure laboratory ice particles below ca 7 nm have a tendency to stick to the impact surface and evaporate (Tomsic, 2001). Conversely, the NLC and PMSE icy particles, containing a substantial number of embedded MSPs (Hervig et al., 2012; Havnes and Næsheim, 2007), will partly fragment on impact and MSPs that are released will not evaporate but survive to carry away rubbed-off electrons. With a MSP volume filling factor of up to 3 % in a NLC or PMSE particle (Hervig et al., 2012), even a 7 nm NLC or PMSE icy particle can contain up to 10 to 30 MSPs if the MSP sizes are in the range of 0.7 to 1 nm.

The secondary production, the number of charged fragments produced by one impacting NLC or PMSE particle of radius r_d, varies with the cross section of the impacting particle as

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathit{\eta }}_{\mathrm{S}}\left(r_{\mathrm{d}}\right)={\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}(r_{\mathrm{d}}/r_{\mathrm{d},\mathrm{ref}}{)}^{\mathrm{2}}.\end{array}$$

Havnes and Næsheim (2007) found that for a reference icy dust particle, of radius $r_{\mathrm{d},\mathrm{ref}}=\mathrm{50}$ nm a number of ${\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}=\mathrm{50}$ to 100 negative unit charges would be released. With 3 % MSP volume filling factor (Hervig et al., 2012) this corresponds to that ∼1 % of the embedded MSPs become charged fragments, if we set the embedded MSP radius to 1 nm.

We can now express the secondary current I_S by using Eq. (6) and with knowledge of how large the fraction of the grid wires that contribute to the secondary charge production is. In the modeling by Havnes and Næsheim (2007) they found that secondary charges are produced on a fraction σ_2,sec ∼0.28 of the G2 grid diameter, where the total area of G2 in MXD-1 covers a fraction σ₂=0.235 of the total probe cross section ${\mathit{\sigma }}_{\mathrm{P}}=\mathit{\pi }{R}_{\mathrm{P}}^{\mathrm{2}}$. The probe radius is R_P=0.04 m. From this we can express the secondary charge current as

$$\begin{array}{}\text{(7)}& {\displaystyle }{I}_{\mathrm{S}}=e{N}_{\mathrm{D}}{V}_{\mathrm{R}}{A}_{\sec }{\mathit{\eta }}_{\mathrm{S}}\left(r_{\mathrm{d}}\right).\end{array}$$

Here N_D=ΣN_Z, the total dust number density, and $A_{\sec }={\mathit{\sigma }}_{\mathrm{2},\sec }{\mathit{\sigma }}_{\mathrm{2}}{\mathit{\sigma }}_{\mathrm{P}}$ is the effective area of the probe for secondary charge production. This is only ∼7 % of the total probe cross section σ_P. The observed secondary charge current I_S is also found from Eqs. (1) and (2) as

$$\begin{array}{}\text{(8)}& {\displaystyle }{I}_{\mathrm{S}}=(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{2}})I_{\mathrm{G}\mathrm{2}}-{\mathit{\sigma }}_{\mathrm{2}}{I}_{\mathrm{BP}}.\end{array}$$

Inserting Eq. (6) into Eq. (7) we can solve Eqs. (7) and (8) for the dust radius.

$$\begin{array}{}\text{(9)}& {\displaystyle }{\left({\displaystyle \frac{r_{\mathrm{d}}}{r_{\mathrm{d},\mathrm{ref}}}}\right)}^{\mathrm{2}}={\displaystyle \frac{\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{2}}\right)I_{\mathrm{G}\mathrm{2}}-{\mathit{\sigma }}_{\mathrm{2}}{I}_{\mathrm{BP}}}{A_{\sec }{\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}e{N}_{\mathrm{D}}{V}_{\mathrm{R}}}}\end{array}$$

Fixing the values for η_S,ref and r_d,ref, the only unknown parameter on the right-hand side is the total dust number density N_D. If this is also known, we can find the dust radius from Eq. (9). However, the value of N_D is not directly available but can be found in an iteration process that includes a charging model for the dust. One should be aware that our charging model, in which we use monodisperse dust sizes at each height, will most likely result in the inferred (average) dust radius r_d being larger than the true average size for a distribution of dust sizes. We will address this in more detail in the discussion.

The charging model computes the equilibrium charge distribution of the ambient dust particles. The electron density n_e (Fig. 9) is measured by various probes on the payload. We require charge neutrality and find the ion density n_i from

$$\begin{array}{}\text{(10)}& n_{\mathrm{i}}-n_{\mathrm{e}}+\sum N_Z{Z}_{\mathrm{D}}=\mathrm{0}.\end{array}$$

The plasma temperature is equal to the neutral temperature and we will use a temperature of 150 K. For our equilibrium charging model we require that the rate at which dust particles of charge Z are given the charge number (Z−1) by an electron colliding with it and sticking to it is equal to the rate by which dust with charge number (Z−1) is given charge number Z by ions colliding and sticking to it:

$$\begin{array}{}\text{(11)}& N_Z{J}_{\mathrm{e}}\left(Z\right)=N_{Z-\mathrm{1}}{J}_{\mathrm{i}}(Z-\mathrm{1}).\end{array}$$

Here J_e(Z) and J_i(Z) are the rates at which charged particles (electrons or ions) arrive at the surface of a dust particle with charge number Z and stick to it. We have used the expressions for J_e and J_i from Draine and Sutin (1987), which include the short range polarization forces, and refer to that paper for the full expressions.

The iteration procedure to extract values for dust radius r_d, dust total density N_D, and also the dust charge distribution N_Z, together with other relevant parameters dependent on r_d and N_D, starts with a guess for the average dust charge number Z_av. A good guess is normally $Z_{\mathrm{av}}=-\mathrm{1}$. This will give an initial value for the total dust number density $N_{\mathrm{D}}=\sum \left(N_Z{Z}_{\mathrm{D}}\right)/Z_{\mathrm{av}}$. Here ∑(N_ZZ_D) is the observed dust charge density found from Eq. (4). From this value of N_D we calculate a value for the dust radius from Eq. (9). These approximations to N_D and r_d are now used in the charging model, together with known values for the plasma parameters, to calculate a new total dust number density and a new average dust charge number, which is used to find a new value for r_d. This process is repeatedly run through the charging code until it converges to a solution.

3 Measurements by the DUSTY probe on MAXIDUSTY-1, analyzed with the extended method

We now use the observations by the DUSTY probe on MXD-1 and the new extended method to find the basic dust parameters: radius r_d, total density N_D, and average dust charge number Z_av throughout the observed NLC and PMSE clouds. The electron data are taken from the results by the onboard Faraday instrument (Friedrich and Rapp, 2009). In Fig. 3 we show smoothed raw currents I_G2 and I_BP and the adopted background that will be subtracted from the raw currents to give the net currents. The curves show that the main cloud system extends from ∼81.3 to ∼86.8 km with a clear but weak additional dust cloud layer between ∼88.5 and ∼89.9 km, which is also shown in Fig. 3b, multiplied by a factor of 10. We are unable to say if this consists of icy dust particles or MSPs. We see indications that a weak structure also extends below 81.3 km, possibly down to ∼80 km. This is apparent mainly in Fig. 3a in which there is a weak I_G2 in this interval and the payload rotation effect is different above and below 80 km, possibly indicating the presence of small MSPs in the size range of up to several nanometers. They may have been released by melting of the larger icy particles and may be affected by the airstream around the payload and by the payload rotation.

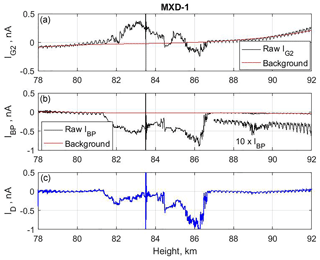
Figure 3 The smoothed currents I_G2 and I_BP and the assumed background currents are shown in panels (a) and (b). In panel (c) we show the I_D current based on the currents I_G2 and I_BP, corrected for background. The “event” at ∼83.5 km is due to a squib being fired to open another instrument on the payload. In panel (b) we have also plotted a current 10×I_BP to emphasize that there is a clear but weak dust structure at least spanning the altitude region from ∼88.5 to ∼89.9 km.

In Fig. 4 we show the inferred values for dust radius r_d and N_D for three values of the secondary charge efficiency ${\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}=\mathrm{50}$, 100, and 150. The large noise signals around ∼83.5 km in Figs. 2 and 3, which were caused by a squib being fired, have been removed. The other four narrow and strong features in the middle of the cloud region (∼83.3 to ∼84.5 km) indicate the presence of dust layers, or “dust voids”, with much larger dust sizes than just outside these layers.

In our calculations we have focused on the value ${\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}=\mathrm{100}$ and find uncertainties in r_d and N_D based on changes in secondary production efficiency, as shown in Fig. 4. The results are in best accordance with the lidar results for high values of η_S,ref.

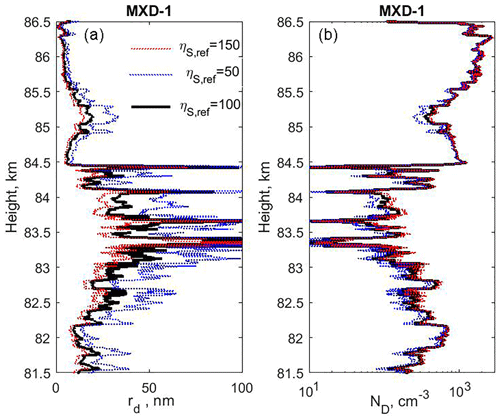
Figure 4 The inferred dust radius r_d and dust density N_D within the main cloud for the three values of the secondary charge efficiency as given in panel (a). We have applied a moderate sliding mean smoothing over 100 data points, changing the altitude resolution from 0.1 m in the observed data points to 10 m. We have also removed the signals in the altitude region of 83.5 to 83.55 km, which is dominated by strong noise from the squib firing, shown in Figs. 2 and 3.

The dust sizes just outside the narrow layers range from ∼10 to ∼40 nm for η_S,ref > 100. The values for r_d in these four narrow layers with large dust particles are probably considerably more uncertain than in most other parts of the NLC and PMSE cloud. The reason for this is that these four layers (voids) have a very low dust density N_D, much lower than in the regions just outside the layers. We can see this from Figs. 2 and 3 in which the current I_D is very low within the four layers and therefore the dust density N_D will also be low. This is directly evident from Fig. 4, which shows both r_d and N_D. The narrow layers with the large increase in dust sizes r_d also have low dust densities, for which N_D can be down to ∼10 cm⁻³. At such low values for the dust density, the dust radius r_d computed by Eq. (9) can be much affected by noise fluctuations in the signals, payload rotational effects, and uncertainties in the assumed background currents. This will lead to relatively large uncertainties in N_D and therefore also in r_d when computed with Eq. (9). The narrow layers or voids in NLC and PMSE clouds will probably still exist (see also Havnes et al., 1996b) and contain large dust particles but their peak values may be questionable.

4 Comparison of the extended DUSTY method results with lidar and photometer results

As a test on the values of r_d and N_D found by the extended method, we compare with corresponding values found from the ALOMAR RMR lidar observations (von Zahn et al., 2000; Baumgarten et al., 2007) and the onboard MISU photometer (Gumbel et al., 2001; Hedin et al., 2008; Megner et al., 2009).

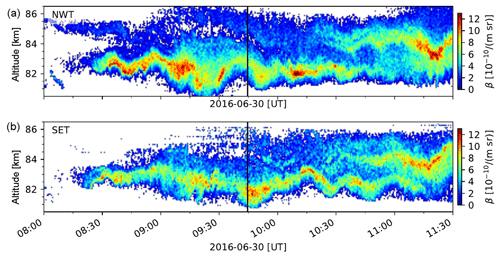
Figure 5 Backscatter coefficient (532 nm) measured by the RMR lidar along the payload trajectory of MXD-1 (a) and about 18 km to the southeast of the trajectory (b). The time of the rocket penetrating through the NLC layer is marked by the vertical black line.

The ALOMAR RMR lidar is a twin-lidar system with two power lasers simultaneously emitting at the 1064, 532, and 355 nm wavelengths and with two receiving telescopes each with a 1.8 m primary mirror. The lidar can be operated all year and under daylight conditions. During the MAXIDUSTY-1 launch, one beam was pointed along the predicted payload trajectory at 85 km and one in the vertical direction. In Fig. 5 we show the RMR observations close to the payload trajectory where the separation of the lidar and rocket measurements was less than 2 km. The second lidar performed measurements above the lidar station at about 18 km separated from MXD-1 measurements. At both locations a double layer was observed and both layers show up and downward motion indicating small-scale perturbations of the atmosphere. The size of the particles is calculated from the signal of three wavelengths assuming a distribution of needle- and plate-like particles of multiple sizes (Baumgarten et al., 2007). The size values given here are radii of a volume-equivalent sphere and give the mode of a Gaussian distribution of particle sizes.

The side-looking MISU NLC photometer on board the payload also detected a two-layer NLC with an altitude profile very similar to the one in Fig. 5 at the time of the rocket measurement. Comparing the angle dependence of the scattering of sunlight on the NLC particles to theoretical Mie scattering phase functions, one can find an effective optical scattering radius, r_Eff, of the particles in the NLC using a monodisperse size distribution. This method is biased towards the largest particles due to the very strong dependence of scattering on dust radius. Below the layer, measuring the entire vertical extent of the NLC, the effective radius r_Eff=46 (±4) nm. As we ascend through the NLC, the retrieved particle radius decreases with increasing altitude and the effective optical scattering radius in the top layer is 40(±8) nm.

The two extended layers in Fig. 5, centered on ∼83 and ∼85 km, also coincide with two layers at the same altitudes at which layers were detected with DUSTY. For DUSTY each of the two layers is characterized by containing large dust particles of low number density. This demonstrates again the strong dependence of scattering of light on the dust radius, increasing very rapidly with size so that layers of low density but containing large dust particles can dominate the scattering.

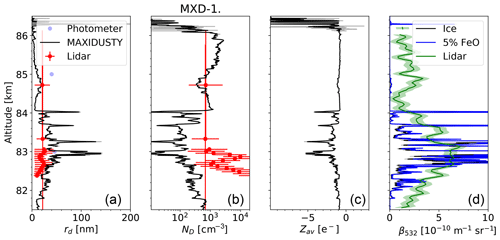
Figure 6 Panels (a)–(c) show results for r_d, N_D, and Z_av for an assumed value of ${\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}=\mathrm{100}$. RMR lidar results are marked by red dots while the two blue dots at 83 and 85 km are for the MISU photometer. Panel (d) shows the observed lidar altitude profile in which the black curve shows model results computed based on the MAXIDUSTY data of panels 1 and 2 and the assumption of pure ice particles, and the blue curve shows results based on the assumption that the ice particles contain 5 % FeO. The green shaded area indicates the measurement uncertainty.

In Fig. 6 we show the DUSTY results, for one set of secondary charging parameters, dust radius r_d, total dust number density N_D, and average dust charge number Z_av. We also show RMR lidar results for 5 min centered on the MXD-1 measurements (09:44:36 UT) as well as the photometer measurements. The average dust particle size indicated by the lidar measurements through the layer is 22 nm with a standard deviation of 5 nm. The average width of the Gaussian size distribution is 8 nm. In the last panel we show the RMR lidar observations of NLC brightness for 30 s around 09:44:36 UT compared with two model lidar profiles computed for dust parameters inferred from the DUSTY observations and for the assumptions that the particles are pure ice or ice contaminated with 5 % FeO, which is the upper limit used by Hervig et al. (2012). We find it surprising that the two cases are practically identical. The refractive index for mixture with FeO was calculated using the effective medium approximation (Garnett, 1904). We have excluded the data in the altitude region from ∼83.5 to ∼83.7 km that were affected by the squib event.

The variations in the DUSTY results for r_d,N_D, and Z_av seem qualitatively reasonable. At the top of the cloud above ∼84 km, we find the smallest dust particles with sizes r_d generally below ∼20 nm, sometimes down to a few nanometers. The one measurement by the lidar in this height region is taken at the height at which the dust particles in this layer have their maximum size. The lidar and DUSTY results for the dust radius and dust number density agree very well. The MISU photometer indicates larger dust particles than DUSTY. The dust particles in this upper layer have presumably been created recently and now grow by deposition of water vapor that freezes out on their surface. They also contain embedded MSPs (Havnes and Næsheim, 2007; Hervig et al., 2012). The highest dust number density, close to 2×10³ cm⁻³, is found in this region. In the middle of the cloud the dust sizes, outside the narrow dust voids, have increased to a maximum value of around 40 nm and a number density of around 10² cm⁻³. The lidar and DUSTY values for the dust radius agree well at one point, at ∼83.3 km, but the dust number density N_D found by DUSTY is a factor of roughly ∼2 to ∼4 lower than the lidar values. The dust radius becomes smaller further down into the bottom parts of the cloud with values of r_d down to ∼20 nm and number densities up to $\sim \mathrm{6}\times {\mathrm{10}}^{\mathrm{2}}$ cm⁻³. The dust radius r_d from DUSTY is roughly a factor of 2 larger than the corresponding lidar radius while the dust number density N_D from DUSTY can be lower by a factor of 10 or more.

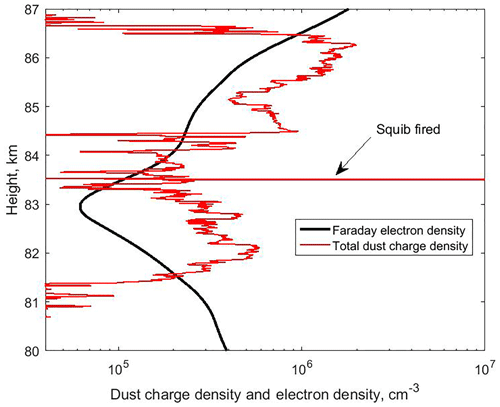
Figure 7 Electron density measured with the Faraday instrument, and the total dust charge density as observed by DUSTY, on MXD-1.

The average dust charge number is close to $Z_{\mathrm{av}}=-\mathrm{1}$ in the lower and upper parts of the cloud while in the middle part it is around Z_av $\sim -\mathrm{2}$ to −3. That the comparatively large grains in the middle part do not have larger negative charge numbers is due to a paucity of electrons, which is demonstrated by the electron bite-out from ∼82 to 84 km, shown in Fig. 7. In this figure we also show the dust charge density ∑(N_ZZ_D) and note that the dust particles are the dominant negative charge carriers in practically the whole extent of the cloud.

5 Discussion and conclusion

The extended method with its unsurpassed altitude resolution gives, in our opinion, reasonable results that compare well with the RMR lidar and MISU photometer results (Fig. 6). It is noteworthy that the parameters for the secondary charging model in the present work have been taken from earlier modeling not aimed at finding r_d, N_D, and Z_av but to demonstrate that secondary charging was essential in reproducing the currents to BP and G2 and their variation with payload rotation (Havnes and Næsheim, 2007; Havnes et al., 2009; Kassa et al., 2012).

If we compare the various results in Fig. 6, in which DUSTY results are based on ${\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}=\mathrm{100}$, there are some significant differences between DUSTY results and the RMR lidar or MISU photometer results. The first is that the RMR lidar in the region at and slightly below 83 km finds particles of half of or less than the size that DUSTY finds. This is probably to some degree influenced by the analysis of the DUSTY data being based on a monodisperse dust size distribution at a specific height. The monodisperse values are related to the true dust size distribution weighted by the individual charges and also their ability to produce secondary charges. Since the dust charges in general increase with the dust size, and the secondary production is proportional to the cross section of the dust particle, an average of the weighted dust number density observed by DUSTY should normally lead to larger values for the monodisperse dust size than for a simple average of the unweighted true dust size distribution. The lidar analysis is based on the assumption of a Gaussian size distribution. The MISU photometer values are closer to the DUSTY values. Also, the lidar total dust densities in the same altitude region are in general more than an order of magnitude larger than what DUSTY finds.

We should bear in mind that some of the differences may result from the lidar and DUSTY probe sampling very different volumes. The sounding volumes are separated horizontally by about 2 km and differ in size. With an altitude resolution of 475 m and integration time of 300 s the lidar samples a volume of about 10⁵ m³ while DUSTY, with some smoothing of the data, samples 0.5 m³ ($\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ m³ with unsmoothed data). These differences may be important, taking into account small-scale dynamics (Baumgarten and Fritts, 2014; Fritts et al., 2017). The time evolution shown in Fig. 5 indicates that such small-scale variations were indeed likely during the time of the measurement.

For DUSTY we could lower the computed r_d and increase the N_D by increasing the secondary efficiency η_S,ref in Eq. (9) from its “accepted” values between 50 and 100. This may require that the embedded MSPs occupy an exceptionally large volume of the icy NLC and PMSE particles. However, we see from Fig. 6d that the lidar profile, computed on the basis of the DUSTY results for a ${\mathit{\eta }}_{\mathrm{S},\mathrm{ref}}=\mathrm{100}$, compares reasonably with the observed lidar profile while an increase in η_S,ref to 150 will lead to the computed DUSTY lidar profile becoming very weak compared the observed one. The best fit of the model DUSTY lidar profile to the observed results is obtained for a value of η_S,ref of around 70 to 80.

The values of r_d, N_D, and Z_av from the DUSTY data will also be affected by the electron density within the dust cloud. This can be critical if the dust density is large enough to create an electron bite-out with locally large reductions in the electron density. In such cases the dust charges can be reduced significantly compared to those that would occur if no bite-out were present. In Fig. 7 we see a significant electron bite-out with a minimum electron density of 60 cm⁻³ at an altitude of 83 km. At such low electron densities the Faraday method to determine the electron density is uncertain. We examine the consequences of reducing the electron density within the bite-out compared to the Faraday results shown in Fig. 7. Arbitrarily reducing the electron density by a factor of 10 will lead to a reduction of r_d by a factor of ∼2 and an increase in N_D by a factor of ∼3 within the bite-out.

The charge model we have used does not include the photodetachment effect (Havnes and Kassa, 2009; Rapp, 2009) and it does not include any photoelectric effect. Inclusion of a photodetachment effect will have some – but not serious – effect on dust particles less than ∼5 nm. It will lead to a moderate increase in dust number density and a decrease in the dust radius. In our model, using values of the photodetachment effect taken from Havnes and Kassa (2009), we obtain a moderate reduction of the dust radius r_d in the altitude region above ∼85.5 km.

Another uncertainty, caused by the design of the DUSTY probe, is that small dust particles (less than ∼2 nm at an altitude of ∼85 km), which may be carrying a non-negligible part of the charge density, will be swept away from the probe by the airstream around the payload and its probes (Horányi et al., 1999; Hedin et al., 2007). Observations by the MASS instrument (Robertson et al., 2009, 2014; Knappmiller, 2008) indicate that considerable numbers of small charged dust particles, possibly MSPs, have a tendency to be present in the upper layers of NLC and PMSE clouds, together with larger NLC and PMSE cloud particles. We cannot exclude that this is also the case for the clouds observed by MXD-1. To evaluate the consequences of small charged particles potentially not being registered by DUSTY, we will need a charging model with more than one dust size. Such models should also improve the comparison to lidar measurements, as these take the effect of different sizes into account and show that the ensemble of particles often has a width of the size distribution of about half the mode radius (Baumgarten et al., 2010).

We find that the development of the new extended method to analyze the DUSTY measurements has given this probe a power that is astounding considering its simplicity. It can in principle be used to measure the radius, total number density, charge density, and charge of icy and non-icy dust particles – with an unsurpassed altitude resolution down to scales of 10 cm or smaller if the plasma probes on the payload have the same or better height resolution. This will also open up for a mapping of the distribution of dust size, dust density, and dust charges within small-scale dust structures (Havnes et al., 1996b). To achieve the best foundation for the extended method and future use of DUSTY-like probes, we plan to refine the analysis with a more complete charging model and to map the effects of changes in the various parameters involved in the method. A comparison with the RMR lidar and MISU photometer observations during the MXD-1 flight will continue to be essential in refining the method. This may also lead to a fine-tuning of the construction of the DUSTY probe for which the basic structure should be retained though modifications of G2 might be advantageous. For future campaigns we intend to improve the collocation of the measurement volumes and use the high-resolution DUSTY measurements to derive the actual size distribution within the lidar sounding volume.