A new approach to estimate supersaturation fluctuations in stratocumulus cloud using ground-based remote-sensing measurements

Supersaturation, crucial for cloud droplet activation and condensational growth, varies in clouds at different spatial and temporal scales. In-cloud supersaturation is poorly known and rarely measured directly. On the scale of a few tens of meters, supersaturation in clouds has been estimated from in situ measurements assuming quasi-steady-state supersaturation. Here, we provide a new method to estimate supersaturation using ground-based remote-sensing measurements, and results are compared with those estimated from aircraft in situ measurements in a marine stratocumulus cloud during the Aerosol and Cloud Experiment (ACE-ENA) field campaign. Our method agrees reasonably well with in situ estimations, and it has three advantages: (1) it does not rely on the quasi-steady-state assumption, which is questionable in clean or turbulent clouds, (2) it can provide a supersaturation profile, rather than just point values from in situ measurements, and (3) it enables building statistics of supersaturation in stratocumulus clouds for various meteorological conditions from multi-year ground-based measurements. The uncertainties, limitations, and possible applications of our method are discussed.

1 Introduction

Cloud forms under supersaturated conditions when the air contains more water vapor than it can retain. Supersaturation (s), which plays a crucial role in cloud droplet formation and growth, depends on air vertical velocity and can also be adjusted by cloud microphysical composition (e.g., Lamb and Verlinde, 2011; Grabowski and Wang, 2013). s in atmospheric clouds fluctuates on a wide range of temporal and spatial scales because of turbulence. Previous studies show that the average value of s as well as its fluctuation are important for cloud microphysical processes. For example, the variation in supersaturation in a vertically oscillating cloud parcel can cause droplet deactivation and reactivation (see Yang et al., 2018a, and references therein). Additionally, results from recent laboratory experiments and direct numerical simulations show that stochastic diffusional growth due to supersaturation fluctuations in a turbulent environment can broaden the cloud droplet size distribution, which might be important for drizzle formation in warm clouds (e.g., Sardina et al., 2015; Chandrakar et al., 2016; Li et al., 2019).

Despite its importance, s is barely known and poorly measured in atmospheric clouds. If we can simultaneously measure water vapor pressure (e) and temperature (T) at the same location, we can directly calculate s based on its definition,

$$\begin{array}{}\text{(1)}& s={\displaystyle \frac{e}{e_{\mathrm{sat}}}}-\mathrm{1},\end{array}$$

where e_sat is the saturated water vapor pressure which depends only on T. However, it is extremely difficult to measure e and T precisely in clouds due to the influence of liquid droplets on the measurements (Siebert and Shaw, 2017). For example, fast-response measurements of the water vapor mixing ratio usually rely on the absorption of infrared light, which can be affected by the presence of liquid droplets or the accumulation of a liquid film on the instrument. Temperature measurements can be biased by latent heat of condensation, evaporation, and also ram heating caused by the deceleration of air on the aircraft body (Wendisch and Brenguier, 2013).

Because of the difficulties in using direct measurements, s is usually estimated indirectly based on either (1) cloud condensation nuclei (CCN), cloud droplet number concentration (CDNC) closure or (2) the quasi-steady-state assumption. For the CDNC closure method, s in the CCN counter is used to describe the maximum s at the cloud base if the number of activated CCN in the counter is similar to the number of cloud droplets (e.g., Yum et al., 1998). s estimated based on this method indicates the maximum supersaturation at the cloud base for droplet activation and does not represent real-time in-cloud supersaturation fluctuations. Additionally, the maximum s for cloud droplet activation can only be positive, whereas the s of interest here can be either positive or negative due to turbulence. The second method is to estimate s in clouds based on the quasi-steady-state assumption through the following formula (e.g., Politovich and Cooper, 1988):

$$\begin{array}{}\text{(2)}& s\approx s_{\mathrm{qs}}=A{\displaystyle \frac{w}{N_{\mathrm{d}}\stackrel{\mathrm{‾}}{r}}},\end{array}$$

where s_qs is the quasi-steady-state supersaturation, A is a parameter that depends on temperature and pressure (see Eq. A1 in Appendix), w is vertical air velocity, N_d is the cloud droplet number concentration, and $\stackrel{\mathrm{‾}}{r}$ is the mean cloud droplet radius. This method relies on the quasi-steady-state assumption in which the source or sink of water vapor in an adiabatic air parcel due to vertical motion is roughly balanced with the source or sink of water vapor due to condensation or evaporation. However, this assumption might not be valid in clean (low N_d) and/or vigorous (large w) clouds for which clouds need a longer time to return to the quasi-steady state for the change in environmental conditions. Additionally, since all of these methods need in situ measurements, they have limited scope, owing to the difficulties of building statistics from short-term aircraft flights.

Here we develop a new method to estimate s in clouds using ground-based remote-sensing measurements. A non-drizzling marine stratocumulus cloud is chosen to evaluate the estimation of in-cloud s based on our method (Eq. 11), and results are compared with s estimated based on in situ measurements (Eq. 2). The uncertainties, limitations, and applications of our method are discussed.

2 In-cloud supersaturation equation for ground-based measurements

Our remote-sensing method is adapted from McGraw (1997), in which aerosol dynamics is represented by the method of moments and equations describing moment evolution. Here, we apply the method of moments to derive the in-cloud supersaturation equation, starting with the definition of the kth radial moment (μ_k) of the cloud droplet size distribution (f(r)),

$$\begin{array}{}\text{(3)}& {\mathit{\mu }}_k=\int r^{k}f\left(r\right)\mathrm{d}r.\end{array}$$

Differentiating the moments with respect to time gives (McGraw, 1997)

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{d}{\mathit{\mu }}_k}{\mathrm{d}t}}=k\int r^{k-\mathrm{1}}\left({\displaystyle \frac{\mathrm{d}r}{\mathrm{d}t}}\right)f\left(r\right)\mathrm{d}r.\end{array}$$

It should be mentioned that Eq. (4) follows from the continuity equation for particle number, which is conserved for condensation or evaporation, for which an integration by parts uses the fact that f(r) vanishes at the limits of integration (McGraw and Wright, 2003). Meanwhile, the change of droplet radius due to condensation or evaporation is governed by the diffusional growth equation (Lamb and Verlinde, 2011),

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}{r}^{\mathrm{2}}}{\mathrm{d}t}}=\mathrm{2}Gs,\end{array}$$

where G is the growth factor depending on temperature and pressure, and s is supersaturation. Combining Eqs. (4) and (5) results in

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{d}{\mathit{\mu }}_k}{\mathrm{d}t}}=kGs{\mathit{\mu }}_{k-\mathrm{2}}.\end{array}$$

It should be noted that the moments of f(r) are related to several physical variables, such as cloud droplet number concentration (N_d=μ₀) and liquid water content (LWC; $\mathrm{LWC}=\frac{\mathrm{4}\mathit{\pi }}{\mathrm{3}}{\mathit{\rho }}_{\mathrm{l}}{\mathit{\mu }}_{\mathrm{3}}$, where ρ_l is the density of liquid water).

Now consider the logarithmic change of LWC with time for a rising parcel. The relationship between LWC and μ₃ leads to

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\mathrm{d}\ln \mathrm{LWC}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{3}}}}{\displaystyle \frac{\mathrm{d}{\mathit{\mu }}_{\mathrm{3}}}{\mathrm{d}t}}.\end{array}$$

If the lateral entrainment and mixing are not the main processes affecting supersaturation, which is likely to be true for stratocumulus clouds, the change in LWC with time can also be linked to the change of LWC in altitude,

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\mathrm{d}\ln \mathrm{LWC}}{\mathrm{d}t}}={\displaystyle \frac{\partial \ln \mathrm{LWC}}{\partial z}}{\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}}=w{\displaystyle \frac{\partial \ln \mathrm{LWC}}{\partial z}}.\end{array}$$

By substituting $\frac{\mathrm{d}{\mathit{\mu }}_{\mathrm{3}}}{\mathrm{d}t}$ from Eq. (6) into Eq. (7) and adding in Eq. (8), we get

$$\begin{array}{}\text{(9)}& s={\displaystyle \frac{w}{\mathrm{3}G}}{\displaystyle \frac{\partial \ln \mathrm{LWC}}{\partial z}}{\displaystyle \frac{{\mathit{\mu }}_{\mathrm{3}}}{{\mathit{\mu }}_{\mathrm{1}}}}.\end{array}$$

Note that $\frac{\partial \ln \mathrm{LWC}}{\partial z}$ is the gradient of LWC which can be retrieved from the ground-based measurements (explained in the following section).

If the cloud droplet size distribution is assumed to be represented by a Weibull distribution,

$$\begin{array}{}\text{(10)}& f\left(r\right)=\mathrm{2}\mathit{\pi }{N}_{\mathrm{d}}{\left({\displaystyle \frac{{\mathit{\rho }}_{\mathrm{l}}{N}_{\mathrm{d}}}{\mathrm{LWC}}}\right)}^{\mathrm{2}/\mathrm{3}}r\exp \left[-\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\rho }}_{\mathrm{l}}{N}_{\mathrm{d}}}{\mathrm{LWC}}}\right)}^{\mathrm{2}/\mathrm{3}}{r}^{\mathrm{2}}\right],\end{array}$$

substituting the first and third moments of Eq. (10) into Eq. (9) leads to the final equation of s,

$$\begin{array}{}\text{(11)}& s={\displaystyle \frac{w}{\mathrm{2}\mathit{\pi }G}}{\displaystyle \frac{\partial \ln \mathrm{LWC}}{\partial z}}{\left({\displaystyle \frac{\mathrm{LWC}}{{\mathit{\rho }}_{\mathrm{l}}{N}_{\mathrm{d}}}}\right)}^{\mathrm{2}/\mathrm{3}}.\end{array}$$

We note that assuming a different functional shape for the cloud droplet size distribution (f(r)) can change the expression of s. However, it is unclear whether there is a unified f(r) for atmospheric clouds applicable for different conditions. This is a general question for cloud retrievals that is worth investigation, but it is beyond the scope of this study. We choose the Weibull distribution (Eq. 10) because it shows good agreement with previous in situ measurements (e.g., Costa et al., 2000). Additionally, it has a theoretical basis, as it can be derived analytically by using a Brownian drift-diffusion model (McGraw and Liu, 2006), using the maximum entropy approach constrained by surface area (Zhang and Zheng, 1994; Liu and Hallett, 1998; Wu and McFarquhar, 2018), or solving the Fokker–Planck equation (Saito et al., 2019). Recent lab experiments also show that Eq. (10) fits reasonably well with the cloud droplet size distribution in a turbulent cloud chamber (Chandrakar et al., 2019). The effect and limitation of the assumed f(r) on s will be discussed in Sect. 6.

Our method requires LWC for two adjacent layers to estimate s (i.e., the LWC vertical gradient). This is the major difference compared with the quasi-steady supersaturation (Eq. 2), where LWC is only needed for one layer. In fact, s estimated based on our method represents the mean s between two layers and does not rely on the quasi-steady-state assumption. However, if the cloud is adiabatic, meaning that LWC increases linearly with height, Eq. (11) is dimensionally similar to Eq. (2): $w(\partial \ln \mathrm{LWC}/\partial z)(\mathrm{LWC}/N_{\mathrm{d}}{)}^{\mathrm{2}/\mathrm{3}}\sim (\partial \mathrm{LWC}/\partial z\left)\right(w/{\mathrm{LWC}}^{\mathrm{1}/\mathrm{3}}{N}_{\mathrm{d}}^{\mathrm{2}/\mathrm{3}})\sim w/(\stackrel{\mathrm{‾}}{r}{N}_{\mathrm{d}})$.

3 Data and methods

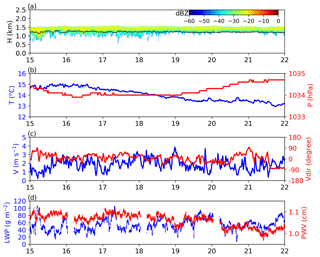
Figure 1 Cloud- and environmental-property time series observed at the eastern North Atlantic (ENA) site on Graciosa Island (39^∘5^′ N, 28^∘1^′ W) on 7 February 2018. Shown are (a) cloud-base height (black line) and Ka-band radar reflectively (colored shading), (b) surface temperature (blue line) and pressure (red line), (c) surface horizontal wind speed (blue line) and direction (red line), and (d) liquid water path (blue line) and precipitable water vapor (red line).

We use data for a marine stratocumulus cloud observed over the Department of Energy (DOE) Atmospheric Radiation Measurement (ARM) Eastern North Atlantic (ENA) facility on 7 February 2018 during the Aerosol and Cloud Experiments (ACE-ENA) field campaign (Wang et al., 2016). The stratocumulus cloud was precipitating in the morning, but between 15:00 and 22:00 UTC it had little to no precipitation, as shown in Fig. 1a. The cloud is very stable during this period, with a base height of 1.23±0.03 km and a top height of 1.52±0.02 km. The stable cloud is also consistent with the steady meteorological conditions during that time: surface pressure varies less than 1 hPa within 7 h (red line in Fig. 1b), and surface temperature decreases only slightly, from about 15 to 13 ^∘C (blue line in Fig. 1b), mainly due to the decrease in shortwave radiation (sunset at 19:00 UTC). The wind is from the north and is very light near the surface, with a mean value of 1.84±0.65 m s⁻¹ (Fig. 1c). The liquid water path and precipitable water vapor retrieved from the microwave radiometer (MWRRet; Turner et al., 2007) are 54±16 g m⁻² and 1.06±0.03 cm, respectively (Fig. 1d).

Ground-based remote sensing is used to retrieve all the variables needed to estimate in-cloud s based on Eq. (11). The site's zenith-pointing Ka-band cloud radar (KAZR), ceilometer, micropulse lidar (MPL), and microwave radiometer were used to derive the information on vertical air velocity, liquid water content, and cloud droplet number concentration. The vertical resolution of the KAZR is 30 m (one range gate), and for the ceilometer and MPL, it is 15 m. The temporal resolutions of the KAZR, ceilometer, and MPL are 2, 16, and 10 s, respectively. At the distance of the observed targets, the radar and lidar beams are, respectively, about 3 m and 2 mm wide. The microwave radiometer employs three receiver channels operating at 23.84, 31.4, and 90 GHz, providing liquid water path estimates at a temporal resolution of 3 s. Specifically, w, LWC, and N_d at each radar height are computed by taking the difference between the estimated radar reflectivity-weighted particle sedimentation speed and measured mean Doppler velocity (Kalesse and Kollias, 2013). The estimate of particle sedimentation speed at each radar time sample (every 2 s) is obtained by mapping measured reflectivity to velocity using a two-parameter Z–V power law model computed from the data within a 30 min moving window centered on the sample. The retrieval of LWC is a two-step process. The first step is to identify cloud columns in which drizzle does not dominate the reflectivity by applying two criteria. The majority of the samples in a cloud column must either have a negative Doppler spectral skewness (Luke and Kollias, 2013), assuming a positive velocity sign convention, or have a reflectivity of less than −25 dBZ. The skewness and reflectivity fields used for this determination are first smoothed by a 2 m wide box-car filter. For the columns identified, the second step is to partition the measured integrated liquid water path over the cloud vertical extent in accordance with measured radar reflectivity (Frisch et al., 1998).

Retrieving N_d remains a challenge and presents larger uncertainties compared with LWC and w retrievals, as recently discussed in a review (Grosvenor et al., 2018). Here, N_d is retrieved using ground-based micropulse lidar (MPL) measurements following Snider et al. (2017). In summary, N_d, the cloud extinction coefficient (σ), and LWC can be expressed as the zeroth, second, and third moments of cloud droplet size distributions. N_d can be estimated from the lidar-derived σ profile by assuming that the cloud droplet size distribution follows a log-normal distribution with a constant geometric standard deviation (σ_g=1.4) and that the cloud LWC profile follows an adiabatic model. In this study, cloud σ profiles are obtained through inversion of the lidar attenuated backscatter measurements using the Fernald (1984) method and assuming that the extinction-to-backscatter ratio for liquid droplets is 18.8 (O'Connor et al., 2004). The retrievals can be affected at the cloud base by turbulent mixing and higher above the cloud base by the lidar signal's quick attenuation, so we use the mean σ and LWC over the range between 30 and 120 m above the cloud base. Additionally, stratocumulus may have a subadiabatic LWC profile, which would adversely affect the retrievals. Thus, we reduce the bias caused by subadiabatic LWC profiles by scaling the liquid water path (LWP) from the adiabatic LWC profile to the LWP retrieved by MWRRET.

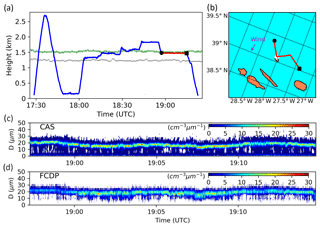
Figure 2 Time series of flight patterns and cloud droplet size distributions for our study period. (a) Time series of flight altitude, where gray and green lines represent, respectively, the cloud-base and top heights from the ground-based measurements. The red line indicates the in-cloud flight leg used in this study, and black dots represent the beginning and ending points of the selected flight leg. (b) Top view of the flight path for the selected in-cloud flight leg in (a). Ocean is bluish green, land is coral, and the ENA facility is marked by a white dot. Measured cloud droplet size distributions in the red flight leg are obtained from the (c) Cloud Aerosol Spectrometer (CAS) and (d) Fast Cloud Droplet Probe (FCDP).

In situ measurements from ARM's Gulfstream-159 (G-1) aircraft on that day (Fig. 2a) enable evaluating our retrieved variables and estimate of quasi-steady supersaturation (Eq. 2). Air vertical velocity is measured at 20 Hz by the Aircraft Integrated Meteorological Measurement System (AIMMS-20) with an uncertainty of ±0.75 m s⁻¹. N_d and $\stackrel{\mathrm{‾}}{r}$, used to estimate s, are obtained from cloud droplet size distributions measured by the Cloud Aerosol Spectrometer (CAS, DMT, Inc.) and the Fast Cloud Droplet Probe (FCDP, SPEC, Inc.). The CAS measures small particles ranging from 0.5 to 50 µm in 30 size bins at 1 Hz, while the FCDP measures cloud droplets ranging from 1 to 50 µm with a resolution of about 3 µm at a frequency of 10 Hz. Because in situ measurements from AIMMS-20, CAS, and FCDP have different sampling frequencies, we average them to the lowest frequency (1 Hz) to calculate s, which represents the mean value over 100 m (aircraft speed 100 m s⁻¹).

4 Results and discussions

We use probability density functions (PDFs) of w, LWC, and N_d to compare the ground-based retrievals with in situ aircraft observations. Otherwise, it is difficult to make an apples-to-apples comparison between the two because they never sample the same cloud volume at the same time. PDFs are compared from the 105 km in-cloud flight leg (from the 17.5 min period highlighted in Fig. 2a and b) with those retrieved at the flight level from 7 h of ground-based measurements, between 15:00 and 22:00 UTC. We choose that horizontal flight leg rather than all in-cloud measurements because (1) LWC depends on the height above the cloud base and because (2) that flight leg was the longest, providing reliable statistics from the in situ measurements. Note that although the flight height is very steady during the 17.5 min (1.471±0.004 km a.s.l.; see Fig. 2a), the G-1 does not fly in one direction, as is shown in Fig. 2b. The flight leg is initially 37 km from the ENA site, heading toward the site from the northwest and then turning to the northeast. The nearest horizontal distance between the G-1 and the site is more than 1 km away, which is also why we use a statistical rather than point-to-point comparison. We assume that the stratocumulus cloud has sufficient statistical spatiotemporal homogeneity during the chosen flight period for the statistical properties to fall within a relatively narrow range. This assumption is supported by the ground-based measurements, e.g., the stable cloud-base and top heights as shown in Fig. 1a. A stable cloud layer also increases confidence in the determination of how far above the cloud base the in situ measurements are obtained. Additionally, cloud droplet size distributions measured by CAS and FCDP do not significantly change during the flight leg (Fig. 2c, d), suggesting that the cloud is spatially homogeneous within ∼56 km of the site (Fig. 2b).

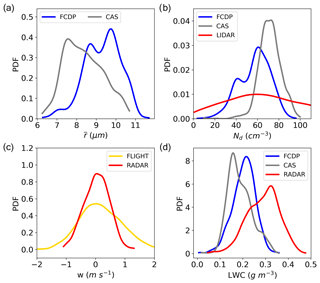
Figure 3 PDFs of four key variables used to estimate s. Shown are (a) mean droplet radius ($\stackrel{\mathrm{‾}}{r}$), (b) droplet number concentration (N_d), (c) air vertical velocity (w), and (d) liquid water content (LWC). In situ measured cloud microphysical properties and air vertical velocity are collected during the flight leg highlighted in Fig. 2. The measurements are from the FCDP (blue), CAS (gray), and AIMMS-20 (gold). Red lines represent the variables retrieved from ground-based measurements between 15:00 and 22:00 UTC. Retrieval methods are explained in the text.

Figure 3 shows the PDFs of four key variables used to estimate s. The in situ values for $\stackrel{\mathrm{‾}}{r}$, N_d, and LWC are calculated from the cloud droplet size distributions measured by the CAS and FCDP. Because the CAS has the ability to measure sub-micron-sized particles (see Fig. 2c), we only use droplet diameters larger than 1.5 µm from the CAS to match the observational range of the FCDP. Results show that mean $\stackrel{\mathrm{‾}}{r}$ from the CAS (8.4±1.0 µm) is about 1 µm smaller than that from the FCDP (9.3±0.9 µm; Fig. 3a), and the mean N_d from the CAS (72 cm⁻³) is about 15 cm⁻³ larger than that from the FCDP (57 cm⁻³; Fig. 3b). These differences might be due to the shattering of large cloud droplets for the CAS, resulting in reduced $\stackrel{\mathrm{‾}}{r}$ and enhanced N_d. The retrieved N_d (71±43 cm⁻³) is significantly broader than the in situ measurements, but it is gratifying to see that their modes are similar (Fig. 3b). The mean w from in situ measurements is 0.2 m s⁻¹, with a standard deviation of about 0.7 m s⁻¹. For ground-based measurements, the retrieved w at the flight level is smaller (0.04 m s⁻¹) with a smaller standard deviation (0.4 m s⁻¹; Fig. 3c). The mean LWC from the CAS (0.19±0.05 g m⁻³) and the FCDP (0.20±0.05 g m⁻³) are similar; however, the retrieved LWC is about 0.1 g m⁻³ larger and with a broader PDF (Fig. 3d). Note that our new method primarily depends on the vertical gradient of LWC and, to a lesser degree, on its absolute value.

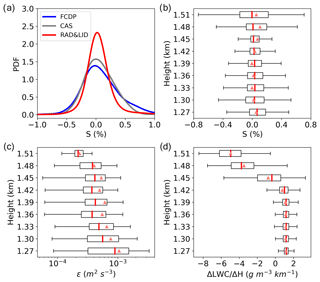
Figure 4 PDF of estimated s and profiles of energy dissipation rate and of the vertical gradients of liquid water content. (a) PDF of estimated s from the quasi-steady-state assumption (Eq. 2) based on the in situ measurements from the CAS (gray) and FCDP (blue) during the flight leg highlighted in Fig. 2a. PDF of estimated s from remote-sensing measurements (Eq. 11; red) is given for the flight level between 15:00 and 22:00 UTC. Box-and-whisker plots are provided for the profiles of (b) s based on Eq. (11), (c) the energy dissipation rate (ϵ) on a log scale, and (d) liquid water content gradients (ΔLWC∕Δz) in the stratocumulus cloud between 15:00 and 22:00 UTC. The box and whiskers indicate the 5th, 25th, 50th, 75th, and 95th percentiles, and the means are indicated by triangles.

With the measured or retrieved variables in Fig. 3, we estimate s during the flight leg using the quasi-steady-state assumption (Eq. 2) for the in situ measurements and s at the flight level using Eq. (11) for the ground-based remote-sensing measurements. The PDFs of s are shown in Fig. 4a with two noticeable features. First, although the $\stackrel{\mathrm{‾}}{r}$ and N_d measured by the CAS and FCDP are somewhat different (Fig. 3), the PDFs of the estimated s based on these two instruments are similar. This is because $s\sim (\stackrel{\mathrm{‾}}{r}{N}_{\mathrm{d}}{)}^{-\mathrm{1}}$ based on Eq. (2) and $\stackrel{\mathrm{‾}}{r}{N}_{\mathrm{d}}$ is similar for the CAS (smaller $\stackrel{\mathrm{‾}}{r}$ and larger N_d) and FCDP (larger $\stackrel{\mathrm{‾}}{r}$ and smaller N_d). Second, the PDF of s (i.e., supersaturation fluctuation) estimated from the retrieved variables based on the radar and lidar measurements (Fig. 4a) is of the same order of magnitude as the in situ measurements, although its full width at half maximum (FWHM) of 0.3 is narrower than that of the in situ measurements (0.6).

With our new method, we can also estimate the profile of in-cloud supersaturation fluctuations based on the retrieved LWC and w profiles. Figure 4b shows box-and-whisker plots of the estimated s based on Eq. (11) at different heights. It is interesting to see that the s fluctuations are larger either close to the cloud base or at the cloud top. The main reason for the larger s fluctuations in these two regions likely has different root causes. Close to the cloud base, s fluctuations are mainly driven by stronger turbulence. This is supported by the energy dissipation rate (ϵ) profile shown in Fig. 4c, which is retrieved by relating the power spectrum of mean Doppler velocity computed over a 25 min moving window to the $-\mathrm{5}/\mathrm{3}$ slope line of the Kolmogorov law of energy dissipation (Borque et al., 2016). Note that turbulence with a maximum at the cloud base on this day is inconsistent with the general statistical properties of ϵ in marine stratocumulus clouds, in which ϵ typically reaches a maximum close to the cloud top where turbulence is mainly driven by wind shear or radiative cooling, especially at nighttime (Wood, 2012; Borque et al., 2018). This inconsistency is believed to be because, for our particular case, the daytime cloud is thin and the wind is light; thus, turbulence in the cloud may be mainly driven by surface forcing (Borque et al., 2018). At cloud top, the large s fluctuations are mainly controlled by the large gradient of LWC and spread therein (Fig. 4d), where the large reduction of LWC is likely due to the cloud-top entrainment and mixing (Mellado, 2017). It should be mentioned that a larger fluctuation in s at the cloud base could also arise from changes in cloud-base height. However, this thermodynamic effect is unlikely the main cause because the gradient of LWC close to the cloud base is relatively small, as shown in Fig. 4d.

5 Uncertainties of our supersaturation estimation

Our method relies on several retrieved variables (w, LWC, and N_d). Although efforts have been made to improve the retrieval quality for decades, these retrieved variables still have large uncertainties that could impact the estimated supersaturation. The retrieved LWC and w can be affected by the existence of large drizzle or raindrops which are frequently observed in marine stratocumulus clouds (Yang et al., 2018b). Minimizing the influence of drizzle on the retrieved LWC and w would be helpful for the estimation of supersaturation in drizzling stratocumulus clouds using our method. The retrieved N_d is usually extracted from higher moments of the droplet size distribution, such as radar reflectively (sixth moment) or lidar back scattering (second moment), such that droplet size uncertainty can cause large uncertainties in N_d. The uncertainty of the retrieved N_d can be up to 100 %, which is much greater than that for the LWC and w retrieval (Grosvenor et al., 2018).

In this section, we will explore uncertainties of our estimated supersaturation fluctuations due to the uncertainties of w, LWC, and N_d. Specifically, we will assume that the “true” values of those variables, respectively, are 0.5, 0.8, 1.2, and 2.0 times our original retrieved values. Also, two additional retrieval methods of N_d are used. While a careful investigation of the retrieval method that agrees best with N_d in situ measurements is under investigation (Zhang et al., 2019), here we only focus on the influence of different retrieval methods of N_d on supersaturation estimation.

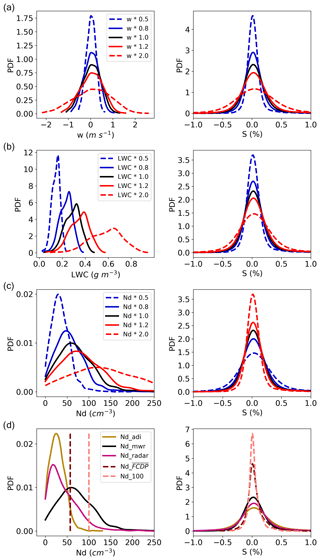
Figure 5 Various retrieved and modified PDFs of input properties and their corresponding PDFs of estimated s: (a) w, (b) LWC, (c) N_d, and (d) N_d from three different retrieval methods and two constant N_d values. Details of the modified variables and retrieval methods are described in the text.

PDFs of retrieved or modified variables (w, LWC, and N_d) and the corresponding estimated supersaturation are shown in Fig. 5a–c. The truth value of each retrieved variable is assumed to be systematically either smaller by 0.5 or 0.8 times or larger by 1.2 or 2.0 times the original retrieval, while keeping other retrieved variables unchanged. It can be seen that an underestimation of w and LWC will lead to a larger estimated s and with a broader PDF (Fig. 5a, b), while an underestimation of N_d will cause a smaller estimated supersaturation. This is because s is proportional to w and LWC^2∕3 but inversely proportional to $N_{\mathrm{d}}^{\mathrm{2}/\mathrm{3}}$.

Of course, all retrieved variables have uncertainties that can propagate to the estimated s. The total error budget of s can be expressed as

$$\begin{array}{}\text{(12)}& {\left({\displaystyle \frac{\partial s}{s}}\right)}^{\mathrm{2}}={\left({\displaystyle \frac{\partial w}{w}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{\partial \mathrm{LWC}}{\mathrm{LWC}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{\partial N_{\mathrm{d}}}{N_{\mathrm{d}}}}\right)}^{\mathrm{2}}.\end{array}$$

Thus, our estimated s uncertainties are more sensitive to the relative changes of w compared with those for LWC and N_d. Specifically, 20 % uncertainties of w, LWC, and N_d will cause a total of $\left[\right(\mathrm{20}\mathit{\%}{)}^{\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{9}}(\mathrm{20}\mathit{\%}{)}^{\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{9}}(\mathrm{20}\mathit{\%}{)}^{\mathrm{2}}{]}^{\mathrm{1}/\mathrm{2}}=\mathrm{27}\mathit{\%}$ uncertainty of s. If we assume the in situ measurements to represent the truth, the standard deviation of the retrieved w is about 43 % smaller, the mean retrieved LWC is about 50 % larger, and the uncertainty in retrieved N_d can be up to 100 %. So if we assume the uncertainties of the retrieved w, LWC, and N_d to be 43 %, 50 %, and 100 %, respectively, the total uncertainty of the estimated s is about 86 %. However, we do not see such large fluctuations ($\mathit{\sigma }\left(s\right)/\stackrel{\mathrm{‾}}{\left|s\right|}$) in Fig. 4a. The reason is probably because this uncertainty assumes no correlations among the retrieved variables, and it represents a systematic bias rather than a random bias. Although such uncertainty exists in the estimated s, the location of the regions of larger supersaturation fluctuations should not change in Fig. 4b.

The retrieved N_d in the previous section uses LWC profiles by scaling the integrated LWP from the adiabatic LWC profile to the LWP retrieved by MWRRET (labeled as N_{d_mwr} in Fig. 5d). Two additional retrieval methods of N_d are applied here: N_d is retrieved by assuming an adiabatic LWC profile without the constraint of LWP (labeled as N_{d_adi} in Fig. 5d), and N_d is retrieved using LWC profiles derived from the combined radar and microwave radiometer measurements following Frisch et al. (1998) (labeled as N_{d_radar}). In addition, two constant values of N_d are tested: mean N_d from FCDP (labeled as $N_{\mathrm{d}\mathrm{\_}\stackrel{\mathrm{‾}}{\mathrm{FCDP}}}$) and 100 cm⁻³ (labeled as N_{d_100}). The PDFs of N_d and the corresponding PDFs of s are shown in Fig. 5d. It can be seen that the FWHMs of the estimated s are similar for three retrieval methods of N_d, with a value of 0.49 for N_{d_adi}, 0.40 for N_{d_radar}, and 0.37 for N_{d_mwr}. But the PDFs of the estimated s are much narrower for a constant N_d, with the FWHM of 0.15 for $N_{\mathrm{d}\mathrm{\_}\stackrel{\mathrm{‾}}{\mathrm{FCDP}}}$ and 0.10 for N_{d_100}.

It should be mentioned that the method we use to retrieve cloud droplet number concentration is based on Snider et al. (2017), in which a log-normal size distribution is assumed. If we use a Weibull distribution, the retrieved cloud droplet number concentration will be 25 % larger (detailed in the Appendix B). Such a difference is smaller than using different retrieval methods, as shown in Fig. 5d. Using the exact same method and size distribution used in Snider et al. (2017) is helpful in comparing the retrieved cloud droplet number concentration with other studies, and it will be easier to extend the application of Eq. (11) for people who only use retrieval products.

6 Conclusions

In this study, we provide a new method to estimate in-cloud supersaturation from ground-based remote-sensing measurements. Our analytical formula (Eq. 11) relies on the retrieved values of w, LWC, and N_d. The fundamental idea is that the difference in LWC between two cloud layers is the result of condensation or evaporation of cloud droplets; thus, the gradient of LWC together with w can be used to estimate the mean supersaturation between the two layers. We evaluate our method using a stable, non-drizzling stratocumulus cloud observed over the ARM ENA Facility on 7 February 2018 during the ACE-ENA field campaign. In situ measurements from a 105 km (17.5 min) flight leg are compared to values and supersaturation estimates retrieved from ground-based measurements for the aircraft flight level. Results show that PDFs of the retrieved w agree reasonably well with the in situ measurements, while the retrieved N_d has larger fluctuations, and the retrieved LWC is about 0.1 g m⁻³ larger and has a broader distribution. The FWHM of the PDF of supersaturation fluctuations based on Eq. (11) is about half that for the quasi-steady supersaturation estimated from Eq. (2). We also investigate the profile of supersaturation in the stratocumulus cloud. Results show that supersaturation fluctuations are larger either at the cloud base, where, for this case, the eddy dissipation rate is largest due to strong turbulence, or close to the cloud top, where the reduction of LWC is largest due to entrainment and mixing.

Note that our analytical expression for supersaturation (Eq. 11) assumes that cloud droplet distribution follows a Weibull distribution (Eq. 10). The formula will change if a different shape is assumed for cloud droplet size distribution. We choose a Weibull distribution because it has a theoretical basis and is consistent with previous observational and laboratory studies (Costa et al., 2000; McGraw and Liu, 2006; Chandrakar et al., 2016). However, it is still unclear what the best shape is for representing the cloud droplet distribution in atmospheric clouds over a broader range of conditions. This topic is beyond the scope of this paper but is worth investigation in the future. The uncertainty of the estimated s based on our method strongly depends on the uncertainties of three retrieved variables (w, LWC, and N_d). Improving retrieval accuracy can increase the confidence level of the estimated s as well as support other model evaluations.

The good agreement between the supersaturation estimated from ground-based measurements and from the quasi-steady supersaturation obtained from in situ measurements suggests that Eq. (11) is a suitable tool to estimate in-cloud supersaturation, which has several advantages over the quasi-steady method. First, our method does not rely on the quasi-steady-state assumption, which is questionable in clean (low N_d) or vigorous (large w) clouds. In fact, supersaturation based on our method is not as sensitive to N_d ($\sim N_{\mathrm{d}}^{-\mathrm{2}/\mathrm{3}}$ in Eq. 11) compared with quasi-steady supersaturation ($\sim N_{\mathrm{d}}^{-\mathrm{1}}$ in Eq. 2), but it is sensitive to w and the vertical gradient in LWC. Also note that retrieved w is more reliable compared with retrieved N_d, which is good for the estimation of s. Second, our method can provide profiles of supersaturation in clouds (Fig. 4b) rather than point values from the in situ measurements. Last, our method enables building statistics of supersaturation in stratocumulus clouds for various meteorological conditions from multi-year ground-based measurements.

It should be mentioned that our approach of estimating s cannot obtain the true supersaturation at the current stage due to (1) the difficulty of directly measuring s for evaluation and (2) the uncertainty in retrieved variables used in our method, but it still can be very useful for getting a relative measure of in-cloud supersaturation. For example, for the profiles in Fig. 4b, the most important and useful information is to say where there are relatively narrower or broader regions of s fluctuation, not whether the s fluctuation is 0.3 % vs. 0.4 %, as the latter would require exact accuracy in the retrieved variables. It is interesting and useful to investigate the s distribution for different clouds in the future.

Our method might be helpful in improving understanding of drizzle initiation in marine stratocumulus clouds. Ground-based observations at the ENA facility show that 83 % of marine stratocumulus clouds are drizzling (Yang et al., 2018b). A long-standing problem in drizzle initiation is the requirement of a mechanism to increase cloud droplet size 10-fold to become drizzle-sized. Recent laboratory and theoretical studies suggest that stochastic condensational growth due to supersaturation fluctuations could provide the link, where some lucky cloud droplets stay longer in high-supersaturation regions and form drizzle drops (e.g., McGraw and Liu, 2003, 2004; Sardina et al., 2015; Chandrakar et al., 2016). Equation (11) can be used to estimate supersaturation fluctuations in atmospheric clouds for different conditions, which may be helpful to assess the notion that drizzle formation is due to stochastic condensational growth. Finally, it should be mentioned that supersaturation fluctuation varies on spatial and temporal scales (Siebert and Shaw, 2017). If all measurements are perfect, we expect that s estimated from 1 Hz in situ measurements represents the mean over about 100 m, while s estimated from ground-based measurements can represent the value in one radar sampling volume, about 10 m×10 m×30 m. It is interesting to note that the radar sampling volume for one range gate is close in size to one grid box in a large-eddy simulation (LES) model. This provides an opportunity to further compare estimated and simulated supersaturation fluctuations in the future.

Appendix A: Parameter A in Equation 2

The parameter A in Eq. (2) follows Lamb and Verlinde (2011):

$$\begin{array}{}\text{(A1)}& A={\displaystyle \frac{Q_{\mathrm{1}}G}{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{l}}{Q}_{\mathrm{2}}}},\end{array}$$

where

$$\begin{array}{}\text{(A2)}& {\displaystyle }& {\displaystyle }{Q}_{\mathrm{1}}=\left({\displaystyle \frac{l_{\mathrm{v}}}{c_{\mathrm{p}}T}}-\mathrm{1}\right){\displaystyle \frac{M_{\mathrm{a}}g}{RT}},\text{(A3)}& {\displaystyle }& {\displaystyle }{Q}_{\mathrm{2}}={\displaystyle \frac{l_{\mathrm{v}}^{\mathrm{2}}}{M_{\mathrm{w}}{c}_{\mathrm{p}}pT}}+{\displaystyle \frac{RT}{M_{\mathrm{w}}{e}_{\mathrm{s}}}},\text{(A4)}& {\displaystyle }& {\displaystyle }G={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{l}}RT}{M_{\mathrm{w}}{D}_v{e}_{\mathrm{s}}}}+{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{l}}{l}_{\mathrm{v}}}{M_{\mathrm{w}}{k}_{v}T}}\left({\displaystyle \frac{l_{\mathrm{v}}}{RT}}-\mathrm{1}\right).\end{array}$$

Here l_v is the latent heat of vaporization, c_p is the specific heat of air at constant pressure, M_a is the molar mass of air, M_w is the molar mass of water, R is the universal gas constant, D_v is the molecular diffusion coefficient, k_v is the coefficient of thermal conductivity of air, and e_s is the saturated water vapor pressure at temperature T. Note that the unit here is mole-based (i.e., the unit for l_v is J mol⁻¹ and not J kg⁻¹).

Appendix B: Retrieving cloud droplet number concentration

Based on Snider et al. (2017), the cloud droplet number concentration can be retrieved from the lidar backscatter coefficient (σ) and liquid water content (q_l),

$$\begin{array}{}\text{(B1)}& N_{\mathrm{d}}={\displaystyle \frac{\mathrm{2}{e}^{\mathrm{3}{\mathit{\sigma }}_x^{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{l}}^{\mathrm{2}}}{\mathrm{9}\mathit{\pi }}}{\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{3}}}{q_{\mathrm{l}}^{\mathrm{2}}}},\end{array}$$

where the cloud droplet size distribution is assumed to be log-normal and have a standard deviation of σ_x=ln 1.4. If we assume that the cloud droplet sizes follow a Weibull distribution (Eq. 10), the cloud droplet number concentration has a similar relationship between σ and q_l but a different prefactor,

$$\begin{array}{}\text{(B2)}& N_{\mathrm{d}}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{l}}^{\mathrm{2}}}{\mathrm{8}}}{\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{3}}}{q_{\mathrm{l}}^{\mathrm{2}}}}.\end{array}$$

Specifically, the retrieved cloud droplet number concentration using a Weibull distribution is 25 % larger than if a log-normal distribution was used.