the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
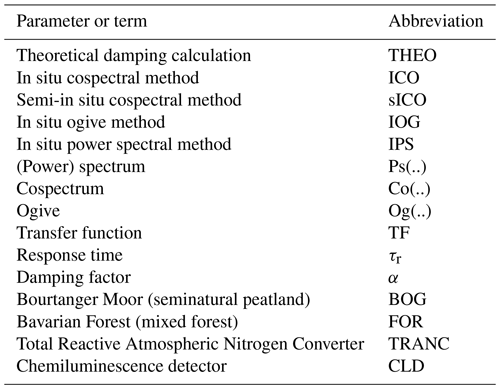
Correcting high-frequency losses of reactive nitrogen flux measurements
Pascal Wintjen
Christof Ammann
Frederik Schrader
Christian Brümmer
Flux measurements of reactive nitrogen compounds are of increasing importance to assess the impact of unintended emissions on sensitive ecosystems and to evaluate the efficiency of mitigation strategies. Therefore, it is necessary to determine the exchange of reactive nitrogen gases with the highest possible accuracy. This study gives insight into the performance of flux correction methods and their usability for reactive nitrogen gases. The eddy-covariance (EC) technique is today widely used in experimental field studies to measure land surface–atmosphere exchange of a variety of trace gases. In recent years, applying the EC technique to reactive nitrogen compounds has become more important since atmospheric nitrogen deposition influences the productivity and biodiversity of (semi)natural ecosystems and their carbon dioxide (CO2) exchange. Fluxes, which are calculated by EC, have to be corrected for setup-specific effects like attenuation in the high-frequency range. However, common methods for correcting such flux losses are mainly optimized for inert greenhouse gases like CO2 and methane or water vapor. In this study, we applied a selection of correction methods to measurements of total reactive nitrogen (ΣNr) conducted in different ecosystems using the Total Reactive Atmospheric Nitrogen Converter (TRANC) coupled to a chemiluminescence detector (CLD). Average flux losses calculated by methods using measured cospectra and ogives were approximately 26 %–38 % for a seminatural peatland and about 16 %–22 % for a mixed forest. The investigation of the different methods showed that damping factors calculated with measured heat and gas flux cospectra using an empirical spectral transfer function were most reliable. Flux losses of ΣNr with this method were on the upper end of the median damping range, i.e., 38 % for the peatland site and 22 % for the forest site. Using modified Kaimal cospectra for damping estimation worked well for the forest site but underestimated damping for the peatland site by about 12 %. Correction factors of methods based on power spectra or on site-specific and instrumental parameters were mostly below 10 %. Power spectra of ΣNr were heavily affected – likely by white noise – and deviated substantially at lower frequencies from the respective temperature (power) spectra. Our study supports the use of an empirical method for estimating flux losses of ΣNr or any reactive nitrogen compound and the use of locally measured cospectra.
- Article
(2758 KB) - Full-text XML
- BibTeX
- EndNote
The eddy-covariance (EC) method is widely applied for determining turbulent exchange of trace gases and energy between the biosphere and atmosphere (Aubinet et al., 2012; Burba, 2013). EC is mainly used for long-lived, stable gases like carbon dioxide (CO2), water vapor (H2O), and methane (CH4). Only a few studies concentrated on reactive, short-lived gases like reactive nitrogen compounds (Nr). In our study, Nr covers species like nitrogen monoxide (NO), nitrogen dioxide (NO2), nitric acid (HNO3), nitrous acid (HONO), peroxyacetyl nitrate (PAN), ammonia (NH3), and particulate ammonium nitrate (NH4NO3). The sum of these species is called total reactive nitrogen (ΣNr). Nitrous oxide (N2O), sometimes also considered to be a reactive N compound, is not detected with our system (see Sect. 2.1) and is excluded from ΣNr here and not taken into account.
Application of the EC technique to Nr or NH3 is challenging, because most Nr compounds are highly reactive and water soluble, and background concentrations are typically low. In close proximity to sources like stables, managed fields (Sutton et al., 2011; Flechard et al., 2013), traffic, or industry (Sutton et al., 2011; Fowler et al., 2013), compounds of Nr like NH3 or NO2 can reach high concentrations. In the past, low-cost measurement devices like passive samplers (Tang et al., 2009), DELTA samplers (DEnuder for Long-Term Atmospheric sampling) (Sutton et al., 2001), or wet chemistry analyzers (von Bobrutzki et al., 2010) were mainly used in Nr measurement studies. However, these instruments typically have a low time resolution and require inferential modeling for estimating fluxes (e.g., Hurkuck et al., 2014). Recently, new measurement techniques for Nr compounds were developed, such as quantum cascade lasers (QCLs) using tunable-infrared-laser differential absorption spectroscopy (TILDAS), mainly for NH3 (Ferrara et al., 2012; Zöll et al., 2016; Moravek et al., 2019), or the total reactive nitrogen converter (TRANC) (Marx et al., 2012; Ammann et al., 2012; Brümmer et al., 2013; Zöll et al., 2019) coupled to a fast-response chemiluminescence detector (CLD). Both measurement systems have a certain robustness and a high sampling frequency and are sensitive enough to allow EC measurements of NH3 or ΣNr.
Evaluating fluxes with these closed-path EC systems leads to underestimation of fluxes due to damping in the high- and low-frequency ranges. An EC setup, like any measurement setup, is comparable with a filter which removes high- and low-frequency parts from measured signals. High-frequency losses are, for example, related to sensor separation (Lee and Black, 1994), air transport through tubes in closed-path systems (Leuning and Moncrieff, 1990; Massman, 1991; Lenschow and Raupach, 1991; Leuning and Judd, 1996), different response characteristics of the instruments, and phase-shift mismatching (Ammann, 1999). These processes inducing flux losses are usually described by spectral transfer functions (Moore, 1986; Zeller et al., 1988; Aubinet et al., 1999).
The magnitude of the high-frequency flux loss depends on the trace gas of interest, the experimental setup, wind speed, and atmospheric stability. In recent literature, different estimates of flux losses due to high-frequency damping have been reported. For example Zöll et al. (2016) found flux losses of 33 % for NH3 at an ombrotrophic, moderately drained peatland site. Ferrara et al. (2012) used the same QCL instrument and estimated flux losses from 23 % to 43 % depending on the correction method. Moravek et al. (2019) proposed a new approach for correcting high-frequency flux losses of NH3 measured by a QCL. The method is based on frequently measuring the analyzer's time response. The application of this method resulted in 46 % flux loss. Ammann et al. (2012) measured ΣNr with a TRANC–CLD system at an intensively managed grassland site and estimated flux losses between 19 % and 26 %. Brümmer et al. (2013) operated a TRANC–CLD system at a managed agricultural site and calculated flux losses of roughly 10 %. Stella et al. (2013) calculated flux losses of 12 %–20 % for NO and 16 %–25 % for NO2. Evidently, the range and magnitude of flux losses of ΣNr and several compounds is quite large. Correction factors for CO2 and H2O are usually lower. CO2 shows attenuation factors from 2 % up to 15 % for a closed-path EC setup (Su et al., 2004; Ibrom et al., 2007; Mammarella et al., 2009; Burba et al., 2010; Butterworth and Else, 2018). H2O shows a stronger damping than CO2 that depends on humidity and age of intake tube due to interactions of sample air water vapor with the inner tube surfaces. The corresponding flux loss varies from 10 % to 42 % (Su et al., 2004; Ibrom et al., 2007; Mammarella et al., 2009; Burba et al., 2010). Mammarella et al. (2009) reported that strong damping (up to 40 %) of H2O occurs in wintertime and during the night due to high relative humidity and only 10 % to 15 % during summertime.
In the past decades, several methods for calculating spectral correction factors have been proposed based on theoretical cospectra (Kaimal et al., 1972; Moore, 1986; Moncrieff et al., 1997), measured power spectra (Ibrom et al., 2007; Fratini et al., 2012), and measured cospectra or ogives (Ammann et al., 2006). Some of these methods are implemented in ready-to-use eddy-covariance post-processing packages like EddyPro (LI-COR Biosciences, Lincoln, USA). In principle, it is possible to calculate flux losses without measuring trace gas concentrations, if all physical parameters of the setup and process losses are known. Such a method does not consider gas-specific properties and may not be suitable for highly reactive gases. In general, all these methods are optimized for inert greenhouse gases and not for Nr species. It is therefore questionable if common methods for spectral correction are applicable for Nr given the high reactivity and chemical characteristics of single compounds. Recently, Polonik et al. (2019) found that the applied correction method depends strongly on the gas of interest (CO2 and H2O) and the type of gas analyzer used. They suggest that high-frequency attenuation of closed and enclosed devices measuring H2O should be corrected empirically. Consequently, common methods are not perfectly suited for dealing with specific EC setups. In this study, we test five different spectral damping correction methods for EC fluxes of ΣNr that were measured at two different sites using a TRANC–CLD system. We investigate (1) quantitative differences between the methods, (2) their sensitivity to the input data, and (3) dependencies on meteorological conditions (wind speed, atmospheric stability, etc.) and measurement height.
2.1 Sites and experimental setup
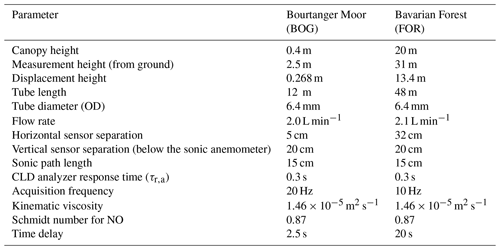
We analyzed data from two measurement sites. At both sites we installed a custom-built ΣNr converter (total reactive atmospheric nitrogen converter, TRANC) after Marx et al. (2012), a 3-D ultrasonic anemometer (GILL-R3, Gill Instruments, Lymington, UK), a fast-response chemiluminescence detector (CLD 780 TR, ECO PHYSICS AG, Dürnten, Switzerland), and a dry vacuum scroll pump (BOC Edwards XDS10, Sussex, UK).
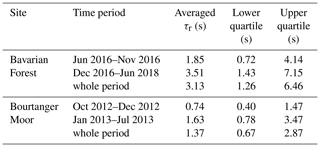
The first site (52∘39′ N, 7∘11′ E, 19 m a.s.l.) is a seminatural peatland in northwest Germany, called “Bourtanger Moor” (BOG). It is an ombrotrophic, moderately drained bog with high ambient NH3 concentrations (Zöll et al., 2016) dominating the local deposition of ΣNr (Hurkuck et al., 2014). Average NH3 concentrations ranged from 8 to 22 ppb, HONO was mostly below 0.1 ppb, HNO3 had an average concentration of 0.04 ppb, NO was approximately 3.6 ppb, and NO2 was 8.6 ppb on average (Hurkuck et al., 2014; Zöll et al., 2016). Averaged values refer to the entire measurement campaign of the cited publications. Concentrations of NO and NO2 were requested from the “Air Quality Monitoring Lower Saxony” (Lower Saxony Ministry of Environment, Energy and Climate Protection) (for data availability please see https://www.umwelt.niedersachsen.de/startseite/themen/luftqualitat/lufthygienische_uberwachung_niedersachsen/aktuelle_messwerte_messwertarchiv/, last access: 4 May 2020). A detailed description of the site is given in Hurkuck et al. (2014, 2016). The EC system was operated from October 2012 to the middle of July 2013.
The TRANC and sonic anemometer were installed at 2.50 m above ground. The sampling inlet was designed after Marx et al. (2012) and Ammann et al. (2012). The inlet tube was 15 cm long, consisted of FeNiCr, had an outer diameter of 0.25 in., and was actively heated from the edge of the tube. Inner temperatures were higher than 100 ∘C. While passing through the TRANC, air samples undergo two conversion steps. The first one is a thermal pathway inside an iron–nickel–chrome (FeNiCr) alloy tube at approximately 870 ∘C. Inside the FeNiCr tube, NH4NO3 is thermally split up into gaseous NH3 and HNO3. HNO3 is thermally converted to NO2, H2O, and O2. NH3 reacts at a platinum gauze with O2 to NO and H2O. HONO is thermally split up to NO and a hydroxyl radical. In a passively heated gold tube (approx. 300 ∘C) a catalytic conversion follows. Before reaching the gold tube, carbon monoxide (CO) is applied as a reducing agent resulting in a reduction of the remaining nitrogen compounds, NO2 and other higher nitrogen oxides, to NO inside the gold tube. To sum it up, all ΣNr (except for N2O and N2) are converted to NO. At the end of the converter a critical orifice was mounted, which ensured a pressure reduction at a constant flow rate of ∼2.0 L min−1. After passing through a 12 m opaque polytetrafluoroethylene (PTFE) tube, the sample air was analyzed in the CLD with a sampling frequency of 20 Hz. The GILL-R3 was installed next to the inlet of the TRANC (Table 1). The CLD and pump were located in an air-conditioned box. For further details of converter and field applications, we refer to Marx et al. (2012), Ammann et al. (2012), and Brümmer et al. (2013). It was shown that concentrations measured by the CLD are affected by water vapor due to quantum mechanical quenching. To compensate for this effect, calculated fluxes were corrected following the approach by Ammann et al. (2012) and Brümmer et al. (2013). Another EC system for CO2 and H2O measurements was placed next to the ΣNr setup (Hurkuck et al., 2016) using a GILL-R3 and a fast-response, open-path infrared gas analyzer (IRGA, LI-7500, LI-COR Biosciences, Lincoln, USA).
Our second site (48∘56′ N, 13∘25′ E, 807 m a.s.l.) was located in the Bavarian Forest (FOR) National Park, Germany. The same TRANC and sonic anemometer were mounted on different booms next to each other at a height of 30 m above ground and approximately 10 m above the forest canopy. Next to the sonic anemometer, an open-path LI-7500 infrared gas analyzer (IRGA) for measuring CO2 and H2O concentrations was installed. The CLD and pump were placed in an air-conditioned box at the bottom of the tower. A 45 m long, opaque PTFE tube connected the TRANC with the CLD. A critical orifice at the end of the TRANC restricted the flow to 2.1 L min−1 and assured low pressure along the tube. Air temperature and relative humidity sensors (HC2S3, Campbell Scientific, Logan, Utah, USA) were mounted at four different heights along a vertical gradient (10, 20, 40, and 50 m). The site was located in a remote area, next to the Czech border, with no local industrial and agricultural emission hot spots (Beudert et al., 2018). Therefore, concentrations of Nr species such as NH3 (1.3 ppb), NO (0.4–1.5 ppb), and NO2 (1.9–4.4 ppb) were very low (Beudert and Breit, 2010). A detailed description of the forest site can be found in Zöll et al. (2019). For the attenuation analysis, data from June 2016 to the end of June 2018 were selected. Important site-specific parameters of both measurement sites are listed in Table 1. Table 2 gives an overview about abbreviations used in this study.
2.2 Calculation and quality selection of fluxes and spectra
Data were collected with the software EddyMeas, included in the software EddySoft (Kolle and Rebmann, 2007), with time resolutions of 20 Hz at BOG and 10 Hz at FOR. Analog signals from CLD and LI-7500 were sampled by the interface of the anemometer and combined with the ultrasonic wind components and temperature data to a common data stream. Periods of maintenance and insufficient instrument performance were removed from damping analysis based on manual screening and monitoring performance parameters such as TRANC heating temperature or flow rate. The software EddyPro 6.2.1 (LI-COR Biosciences, 2017) was used for raw data processing and flux calculation. A 2-D coordinate rotation of the wind vector was selected (Wilczak et al., 2001), spikes were detected and removed after Vickers and Mahrt (1997), and block averaging was applied.
The recorded datasets show a time lag between the measurements of the sonic anemometer and the gas analyzers due to sampling of air through the inlet system (converter, tube, analyzer cell), the processing of signals within the analyzers, and the distance between the two instruments. The time lag was estimated with the covariance maximization method (Aubinet et al., 2012; Burba, 2013), which is based on shifting the time series of vertical wind and concentration against each other to determine the lag time, at which the covariance between the two is maximized. At BOG the time lag was around 2.5 s, and at FOR the time lag was around 20 s. Accordingly, the time lag computation method in EddyPro was set to covariance maximization with the default. Based on theoretical considerations, we restricted the range for time lag computation from 15 to 25 s for the FOR data and from 0 to 5 s for the BOG data. The default value was set to 20 s for FOR and to 2.5 s for BOG. The windows for the time lag compensation were chosen in such a way because estimated lags were broadly distributed around the physical (default) lag. The chosen range for the time lag computation coincides with the range of the highest time lag density. The variation in time lags around the physical lag was almost constant for both measurement campaigns and not correlated to the temporal variation in the damping factors. The difference in ranges may be related to different site characteristics, different mixing ratio fluctuations of ΣNr compounds at the sites, and performance of the TRANC–CLD setup. Time lags, estimated with a stand-alone script, are used as filtering criteria for the damping analysis. For the CO2 and H2O measurements, time lags were mostly negligible.
For the high-frequency damping analysis, we selected time series of vertical wind, temperature, and ΣNr concentrations. These raw data were corrected for several effects in the following order: despiking (Vickers and Mahrt, 1997), cross-wind correction (Liu et al., 2001), angle of attack correction (Nakai et al., 2006), tilt correction (Wilczak et al., 2001), time lag compensation, and block averaging. As the next step, the time series were subject to a fast Fourier transformation (FFT) that yielded the power spectra of individual quantities like the temperature (power) spectrum Ps(T) and the cospectra of two quantities like the heat flux cospectrum Co(w, T) (Aubinet et al., 2012). The same was done for CO2, H2O, and ΣNr, resulting in Co(w, CO2), Co(w, H2O), and Co(w, ΣNr) and Ps(CO2), Ps(H2O), and Ps(ΣNr), respectively. From the cospectra, flux-normalized ogives (Og) were calculated (Ammann et al., 2006) as the cumulative cospectrum (Desjardins et al., 1989; Oncley et al., 1996). The ogives and cospectra consisted of 40 log-spaced frequency bins.
For a quantitative evaluation of the high-frequency damping from the half-hourly flux (co)spectra, a quality flagging has to be applied. Flagging of (co)spectra is done automatically in EddyPro. However, the criteria are usually optimized for inert gases like CO2 and H2O that show characteristic daily flux cycles and magnitudes. They are much less specific and were not very successful for filtering ΣNr fluxes and spectra. Therefore, we performed a two-stage quality selection. First, common criteria were applied: discarding cases with (i) insufficient turbulence ( m s−1), (ii) low flux quality (flag =2) after Mauder and Foken (2006), (iii) variances of T and ΣNr exceeding a threshold of 1.96 σ, and (iv) a time lag outside the predefined range (see above). Next, we checked with manual screening whether the shapes of ogives and cospectra were relatively smooth and not influenced by considerable noise or outliers. A total of 821 cospectra passed the flagging criteria at BOG, and 872 cospectra passed the flagging criteria at FOR. With common selection criteria, 3232 cases at BOG and 9889 at FOR would have been retrieved.
Another possibility for the characterization of the quality or influence of noise on power spectra and cospectra is the determination of the decline in the inertial subrange following the power law. Therefore, the slope of the decrease was evaluated on a double logarithmic scale by a linear regression. The theoretical slope for power spectra of temperature and inert trace gas concentrations is .
2.3 High-frequency damping and determination of correction factor
We used four different cospectral approaches for the computation of high-frequency losses. The fifth approach of Ibrom et al. (2007) is based on power spectral analysis and implemented in EddyPro. The majority of the approaches determine the damping factor of a trace gas flux as an integral of the frequency-dependent attenuation of the corresponding cospectrum. With Co(f) being the true undamped cospectrum, the flux damping factor(s) α, or its inverse, the correction factor α−1 can be described in the following way, e.g., (Moore, 1986):
The flux attenuation factor is the ratio of the measured flux covariance of vertical wind w′ and scalar s′ to the true covariance , where the prime denotes fluctuations of the scalars. is evaluated by the integral of Co(f) over the frequency. Also, can be expressed by the integral of Co(f) over the frequency, but it has to consider a transfer function. TF is the overall spectral transfer function of the EC setup and is usually a product of several individual damping processes with specific transfer functions TFi. In the following subsections we describe the methods in detail.
2.3.1 Theoretical damping calculation (THEO)
The theoretical damping calculation (THEO) is the most commonly applied method (Spank and Bernhofer, 2008). It is independent of any measured data and works for open-path as well as closed-path EC systems (Leuning and Moncrieff, 1990; Lenschow and Raupach, 1991; Massman, 1991; Leuning and Judd, 1996; Moncrieff et al., 1997). It is based on the assumption that all relevant attenuation processes are known and can be quantitatively described by spectral transfer functions TFi. Detailed descriptions of the TFi are given in Moore (1986), Moncrieff et al. (1997), Ammann (1999), and Aubinet et al. (1999, 2012). The TFi and physical parameters for the EC setups used here, like the analyzer response time τr, a, flow rate, tube length, and sensor separation, are listed in Tables A1 and 1. All TFi functions were merged into a single total transfer function (TFtheo), which was applied to theoretical (modified) Kaimal cospectra (from the original Kaimal et al., 1972). Subsequently, α was calculated after Eq. (1) for every quality-selected flux averaging interval. Kaimal cospectra exclusively depend on stability, wind speed, and measurement height above canopy (Moore, 1986; Ammann, 1999). Further in situ measurements were not used for this approach.
In order to prevent a misunderstanding between τr, a and the later introduced parameter τr, we state their differences here. Physically, the analyzer response time τr, a represents the time at which the difference between the measured quantity and the analyzer output signal is reduced by 1∕e after a step change. Thus, it is also called e-folding time. If it is zero, changes will be recognized instantaneously. This is mostly not possible for common gas analyzers. Our TRANC–CLD system, which has proven to be suitable for EC measurements (Marx et al., 2012; Brümmer et al., 2013), has an e-folding time of about 0.3–0.35 s. τr, a is used for the first-order filter transfer function (Table A1) in the THEO approach. In this paper τr, which is also called response time, is a fitting parameter used in Eq. (2). It is linked to the cutoff frequency , at which the cospectrum is damped to or the power spectrum to 50 %.
2.3.2 In situ cospectral method (ICO)
Theoretical cospectra could deviate from site-specific characteristics of the turbulent transfer, while theoretical transfer functions could miss important chemical or microphysical processes, which are more important for ΣNr than for inert gases like CO2, H2O, CH4, or N2O. In the exemplary case of Fig. 1, the prescribed cospectrum of Kaimal corresponds generally well with Co(w, T), but a systematic deviation may exist in the low-frequency range for BOG. At both sites, differences to Co(w, Nr) are also visible in the high-frequency range right of the cospectral maximum, which is around 0.2 Hz for BOG and around 0.02 Hz for FOR in the present example.
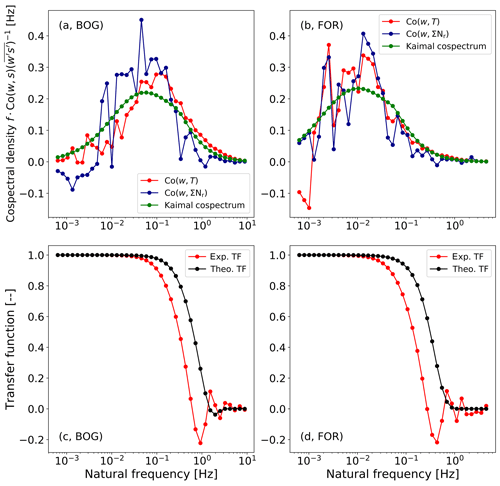
Figure 1Comparison of observed normalized cospectra with modified Kaimal cospectra (green) for similar wind speed and stability and their theoretical and experimental transfer functions at BOG (a, c) (, m s−1) and FOR (b, d) (ζ=0.17, m s−1). Panels (c, d) show the theoretical cospectral transfer function (TFtheo) (black) and the experimental transfer function (TFexp) (red). The experimental transfer functions were determined with the cospectra in (a, b). The displayed cospectra of heat (red) and ΣNr mass flux (blue) are averaged over half-hourly measurements on 10 October 2012 between 09:30 and 14:00 CET and on 28 October 2016 between 10:00 and 15:30 CET for BOG and FOR, respectively. The choice of different days was caused by data gaps in the measurements.
Cospectra of FOR are shifted to the left due to the larger measurement height above canopy and the increased contribution of low-frequency, large-scale eddies with height (Burba, 2013). The wind speed and stability values of the shown example are in close agreement with long-term, daytime averages of the corresponding sites. On average, wind speed and stability were approximately 1.65 m s−1 and −0.22 at BOG during daytime. At FOR, the average wind speed and stability were 1.91 m s−1 and −0.44 during daytime. Wind speed conditions of the cospectra displayed in Fig. 1 are similar to the average values during daytime for the entire period. Stability values of the displayed case are in agreement with the daytime average for BOG. At FOR, the shown example refers to stable conditions, whereas an unstable average is exhibited during daytime. In general, daytime stability values of both sites are rather low and close to neutral conditions. At both sites, approximately 10 % of the analyzed cospectra were in the range of ±0.5 m s−1 for the average wind speed and ±0.15 for the average stability. Using only the wind speed restriction resulted in 40 % agreement at FOR and 55 % at BOG. It seems that the stability is more diverse and not correlated to wind speed. The correlation between wind speed and stability for the analyzed cospectra used for the damping analysis is rather low for both sites (0.26 for BOG and 0.15 for FOR). In conclusion, the shown example represents a common case of the selected cospectra, which were used for the empirical approaches, especially for wind speed.
The in situ cospectra method (ICO) utilizes Co(w, T) instead of the Kaimal cospectrum in Eq. (1). Co(w, T) is used as the reference cospectrum because it is almost unaffected by damping processes. Assuming spectral similarity between Co(w, T) and Co(w, ΣNr), we can derive TFexp as follows (Aubinet et al., 1999; Su et al., 2004):
In principle, this equation compares the ratio of the cospectra, which corresponds to the cospectral transfer function, to the empirical transfer function TFexp. Equation (2) allows us to determine τr. TFexp consists of a first-order filter TFR combined with a mismatching phase-shift TFΔR for first-order systems (Ammann, 1999) (Table A1):
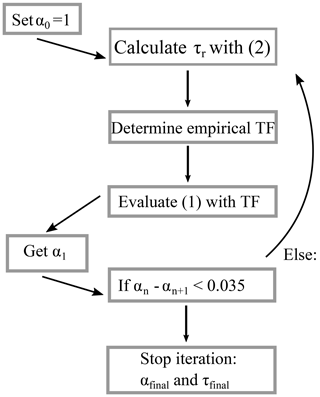
The approach used in this study is somewhat different to other methods that are also based on using measured cospectra of heat and gas flux, for example the method of Aubinet et al. (1999). The latter uses a normalization factor, which corresponds to the ratio of the heat flux cospectrum to gas flux cospectrum. Both cospectra are integrated until frequency fo, which should not be affected by high-frequency damping but is high enough to allow an accurate calculation of the normalization factor. However, the definition of fo is rather imprecise, and thus an incorrect setting of fo can lead to significant uncertainties in the damping analysis. In our approach cospectra are normalized by their corresponding total covariance. In order to consider the damping of the gas flux cospectrum and its covariance, the damping factor is introduced in Eq. (2). Thus, we assume that both approaches give similar results, since both approaches cover the damping of the gas flux cospectrum. The procedure of solving Eq. (2) is not straightforward. Thus, a flow chart of the important calculation steps is shown in Fig. 2.
The iteration was started with α0=1. Afterwards, a nonlinear least-square fit of Eq. (2) was performed. For minimizing both sides of Eq. (2), τr was used as the optimization parameter. After τr was calculated, TFexp(f) could be determined and inserted into Eq. (1). α1 was estimated by Eq. (1) using Co(w, T) as the reference. Finally, the process was terminated if the difference between the first guess and α1 was sufficiently low (<0.035). Otherwise, the whole process was repeated. Equation (2) was solved iteratively until α converged. Our experience was that three iteration steps were mostly enough to fulfill the termination criterion. The nonlinear fit (Eq. 2) was performed for frequencies larger than 0.055 Hz for the BOG campaign. This frequency range is assumed to be affected by damping effects. A similar frequency limit had been used in the damping analysis of Zöll et al. (2016) for the same site. For the FOR campaign the lower frequency limit was set to 0.025 Hz. The decision of the lower frequency limits was further proven by the examination of the ogives ratio, which shows constant values in a certain frequency range. The position exhibits the frequency at which high-frequency attenuation mostly starts to increase. Figure 1c, d show examples of the theoretical and experimentally determined transfer functions for the two measurement sites. In both cases the experimental transfer function drops earlier than the theoretical transfer function and reveals a significant variation in the high-frequency range.
2.3.3 Semi-in-situ cospectra method (sICO)
The semi-in-situ cospectra approach is similar to the one described in Sect. 2.3.2. The determination of τr follows the same procedure as for ICO, but, instead of using Co(w, T) in Eq. (1), this approach uses Kaimal cospectra (Eqs. A1 and A2) as the reference. This method is useful if the quality of Co(w, T) is not sufficient for estimating the damping factors, especially in the low-frequency range.
2.3.4 In situ ogive method (IOG)
The in situ ogive method (IOG) is based on Ammann et al. (2006) and Ferrara et al. (2012). An ogive is defined as the cumulative integral of the cospectrum from the lowest frequency f0, which is given by the averaging interval, to the highest frequency, the Nyquist frequency fN. The Nyquist frequency is half of the sampling frequency.
This method is similar to ICO, but does not rely on a specific form for the spectral transfer functions or cospectra and only requires Og(w, T) and Og(w, ΣNr). Again, spectral similarity between Og(w, T) and Og(w, ΣNr) is assumed. For estimating the damping, a linear regression between Og(w, T) and Og(w, ΣNr) was performed in a specific frequency range. The range was constrained by frequencies for which and were fulfilled. Frequencies lower than 0.002 Hz were excluded. The difference between the regression line and Og(w, ΣNr) was calculated, and points exceeding a difference of 0.1 or frequencies above which the signal is totally damped were not considered for a linear least-square fit of Og(w, ΣNr) and Og(w, T). The former criterion was applied for discarding spikes. Finally, the optimization factor, which minimizes the difference between Og(w, ΣNr) against Og(w, T), is the result of the least-squares problem and corresponds to the damping factor.
2.3.5 In situ power spectral method (IPS)
Application of the in situ power spectral method (IPS) after Ibrom et al. (2007) was executed using EddyPro. It uses measured power spectra of a reference scalar and of the trace gas of interest, here Ps(T) and Ps(ΣNr). The first step – the estimation of τr or the cutoff frequency fc – is similar to the in situ cospectra method (Eq. 2), but the transfer function is different.
For estimating fc EddyPro uses quality-selected and averaged power spectra. We set 0.4 Hz as the lowest noise frequency in the option “removal of high frequency noise” and adjusted the threshold values for removing power spectra and cospectra from the analysis accordingly. The value for the “lowest noise frequency”, which was set in EddyPro for running IPS, was a subjective decision based on visual screening through power spectra. Therefore, we calculated slopes of ΣNr power spectra in the inertial subrange and estimated the frequency at which noise started to increase and slopes became positive. Additionally, we forced EddyPro to filter the spectra after statistical (Vickers and Mahrt, 1997) and micrometeorological (Mauder and Foken, 2004) quality criteria. We applied the correction of instrument separation after Horst and Lenshow (2009) for crosswind and vertical wind and took the suggested lowest and highest frequencies (0.006 and 5 Hz) as the fitting range for Ps(T) and Ps(ΣNr) for FOR. Applying the IPS through EddyPro for ΣNr at BOG requires CO2 and H2O measurements. Since both inert gases were not measured at the ΣNr tower, we used high-frequency CO2 and H2O data from the EC setup described in Hurkuck et al. (2016), which was placed next to the ΣNr setup. Then, the application of IPS to ΣNr at BOG was performed, thereby inducing additional uncertainty. We changed the highest frequency to 8 Hz and took the lowest frequency from standard settings (0.006 Hz). For comparing the results of IPS to our cospectral methods, we chose the same half hours which passed the automatic selection criteria and the manual screening (see Sect. 2.2). In general, the idea of IPS is that the EC system can be simulated by a recursive filter. Thereby, α−1 is determined by the ratio of the unfiltered covariance to the filtered covariance and applying the recursive filter to degrade the time series of sonic temperature (Ibrom et al., 2007). However, Ibrom et al. (2007) argued that this ratio gives erroneous results for small fluxes. Therefore, they parameterized α by the mean horizontal wind speed (), stability, and fc. Ibrom et al. (2007) investigated a proportionality between α−1 and . By introducing a proportionality constant A1 and a second constant A2, which should account for spectral properties of the time series, the following equation for calculating the correction factor was proposed (for details see Ibrom et al., 2007, Sect. 2.4):
A1 and A2 were estimated for stable and unstable stratification using degraded time series of sonic temperature. The degradation was carried out using a varying low-pass recursive filter (Ibrom et al., 2007; Sabbatini et al., 2018). A general summary of processing eddy-covariance data including high-frequency spectral correction methods is given in Sabbatini et al. (2018).
3.1 Characterization of power spectra and cospectra
Figure 3 shows exemplary cospectra and power spectra of the two measurement sites. We compare cospectra which were measured during unstable daytime conditions and at similar wind speeds. All in all, the cospectral densities of the gas and heat fluxes are quite similar. This indicates that the chosen sampling interval and frequency were sufficient to capture flux-carrying eddies. However, Co(w, ΣNr) shows a stronger variation than the other cospectra. The effect of different measurement heights is quite obvious. It results in a shift of all cospectra to the left for the FOR site. The stronger drop of Co(w, ΣNr) compared to Co(w, CO2) and Co(w, H2O) in the high-frequency range is likely related to damping by the ΣNr inlet tubes, which did not affect the CO2 and H2O open-path measurements. It also appears that the damping (difference of cospectra in the high-frequency range) at BOG is higher than that at FOR for the selected averaging interval.
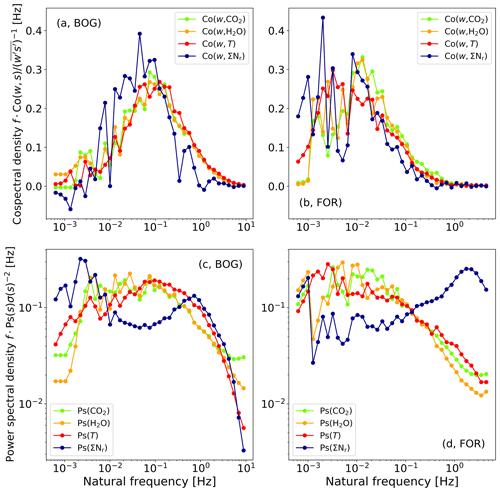
Figure 3Normalized cospectra and power spectra of T (red), ΣNr (blue), CO2 (green), and H2O (orange) at BOG (a, c) and FOR (b, d). (Co)spectra were averaged at BOG from 11 October 2012 09:00 CET to 11 October 2012 16:30 CET (, m s−1) and at FOR from 16 October 2016 10:00 CET to 16 October 2016 15:30 CET (, m s−1). CO2 and H2O (co)spectra of BOG were adjusted to the aerodynamic measurement height of the ΣNr setup. Note that the time period used for averaging is different from the periods of Fig. 1.
The shapes of the power spectra for T, CO2, and H2O are comparable to those found in other studies (e.g., Ammann, 1999; Ibrom et al., 2007; Rummel et al., 2002; Aubinet et al., 2012; Ferrara et al., 2012; Fratini et al., 2012; Min et al., 2014). For Ps(T) a slope of −0.62 (BOG) and −0.63 (FOR) was determined in the inertial subrange. The fitting range used for the derivation of the slopes is smaller than the inertial subrange, for example, to exclude slightly positive slopes of the inert trace gases at the very high frequencies. Differences to the theoretical shape, for power spectra, may be related to slight damping of Ps(T) in the high-frequency range. A slight high-frequency damping of Ps(T) can be caused by the path averaging of the sonic anemometer (e.g., Moore, 1986). In addition, the observed shape of the spectrum (slope) can deviate from the theoretical shape due to nonideal environmental conditions (e.g., nonhomogeneous turbulence, influence of roughness sublayer). The stronger drop of Co(w, ΣNr), compared to Co(w, CO2) and Co(w, H2O) in the high-frequency range, is likely related to damping by the tubes, which is not relevant for open-path instruments. Ps(CO2) and Ps(H2O) have nearly the same slope in the inertial subrange and exhibit the excepted shape. In contrast, Ps(ΣNr) is lower than Ps(CO2), and Ps(H2O) at lower frequencies (<0.1 Hz) starts to rise afterwards and reaches a maximum around 1 Hz. This phenomenon was found in almost all Ps(ΣNr) spectra at the measurement sites, for which we estimated the slope of Ps(ΣNr) in the high-frequency range. However, the number of Ps(CO2) measurements that were affected by this phenomenon was rather small compared to Ps(ΣNr). For an in-depth investigation of slope we applied a variance filter of w, T, and ΣNr and excluded Ps if the variance was higher than 1.96σ, which corresponds to a confidence limit of 95 %. Additionally, we excluded low-quality fluxes (flag =2) of sensible heat and ΣNr after Mauder and Foken (2006) and applied the time lag filtering criteria. These criteria were used to exclude periods of rather low fluxes, instrument performance issues, and conditions of insufficient turbulence. We used equivalent filtering criteria for CO2 and additionally applied a precipitation filter due to the open-path characteristics of the LI-7500. The precipitation filter was also applied for filtering the lower-quality cases of CO2 and H2O shown in Fig. 3. Figure 4 shows a distribution of the estimated slopes at both measurement sites.
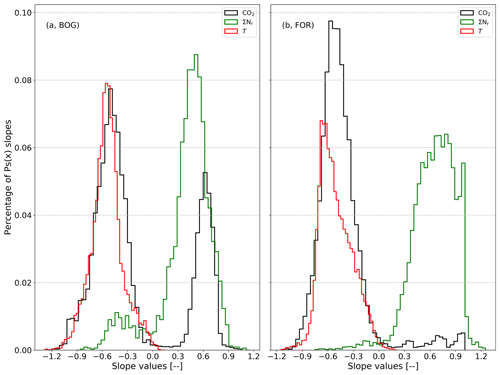
Figure 4Distribution of spectral slopes in the high-frequency range (>0.1 Hz) of Ps(ΣNr) (green), Ps(CO2) (black), and Ps(T) (red) for the BOG site (a) and for the FOR site (b). Slopes were estimated for half-hourly power spectra from 2 October 2012 to 17 July 2013 and from 1 June 2016 to 28 June 2018 at BOG and FOR, respectively.
The slopes of Ps(T) are between −0.5 and −0.7, which is close to the theoretical value, and the shape of the histogram seems to be narrower around the theoretical value at BOG than at FOR. The distribution of the Ps(CO2) slopes is rather bimodal at BOG but coincides well with the slope shape of the Ps(T) slopes at FOR. In volume terms, most slopes of Ps(CO2) are negative at both sites (70 % for BOG and nearly all for BOG, 95 %), but their maximum is slightly higher than (−0.53 for BOG and −0.58 for FOR). More Ps(CO2) slopes of BOG exhibit a positive slope between 0.50 and 0.75 (24 %) than the Ps(CO2) slopes of FOR (2 %) in the same range. In contrast, the slopes of Ps(ΣNr) are mostly positive at both sites (88 % at BOG and 97 % at FOR). Also at BOG, the slopes of Ps(ΣNr) exhibit a slight bimodal distribution. The second maximum is observed at around −0.45. The number of Ps(ΣNr) slopes around is rather small at BOG (fewer than 10 % are lower than −0.25) and even negligible at FOR (fewer than 1 % are lower than −0.25). A positive slope for nearly all power spectra value of a certain trace gas is rather unexpected.
3.2 Comparison of different damping correction methods
In the following, we present the results of the damping correction methods introduced in Sect. 2.3. Firstly, we describe the results of the in situ power spectral method (IPS) and the four cospectral methods. Secondly, we demonstrate findings of dependencies on meteorological variables. Figures 5 and 6 show statistical analyses of α which were calculated by each method on a monthly (BOG) or bimonthly (FOR) basis depicted as box plots. It was possible to estimate α with all methods for 816 half hours for BOG and 811 half hours for FOR. All damping correction methods were evaluated for the same half hours.
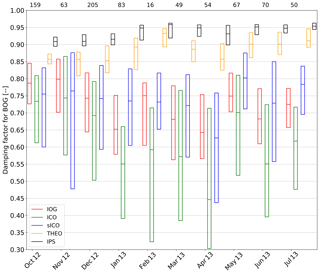
Figure 5Boxplots of the flux damping factor (α) for BOG without whiskers and outliers (the box frame is the 25 % to 75 % interquartile ranges (IQR); the bold line is the median). The number of observations which are displayed at the top of the plot is the same for every method.
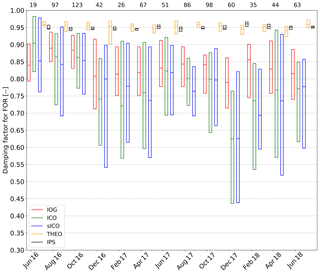
Figure 6Box plots of the flux damping factor (α) for FOR without whiskers and outliers (the box frame is the 25 % to 75 % interquartile ranges (IQR); the bold line is the median). The number of observations displayed at the top of the plot is the same for every method.
Monthly α values calculated with the IPS method show no temporal drift at FOR (Fig. 6). The median α is around 0.95 for nearly every month. Additionally, the interquartile range (IQR; 25 % to 75 % quartiles) is very small (0.01 to 0.02). At BOG, monthly median α values calculated with IPS were also mostly around 0.95; only the first 3 months were sightly lower by ∼0.04. Their IQR is around 0.04 on average. It is obvious that α of IPS is the highest compared to the cospectral methods, and it exhibits the lowest IQR during the measurement period.
At both sites, the median α of the in situ cospectral methods ICO, sICO, and IOG show only moderate temporal variations during the entire measurement campaign. While slightly higher values in summer and lower values in winter were found at the FOR site (Fig. 6), the opposite pattern was observed at the BOG site (Fig. 5). Their IQR is more variable and ranges from 0.13 to 0.26 at BOG and from 0.16 to 0.31 at FOR. Changes in the range of the IQR and fluctuations of the medians may be related to different meteorological conditions, to changes in composition of ΣNr, or to a degeneration of instrumental response. During field visits for maintenance, parts of the TRANC like the heating tube or platinum gauze were exchanged or cleaned, which could influence the results. At both sites, α values by THEO were always higher than those from in situ cospectral methods (IOG, ICO, sICO), and their medians were about 0.90 at BOG and about 0.95 at FOR. Their IQR is smaller than those of IOG, ICO, and sICO, too.
At FOR, the median α values of ICO and sICO are similar for every month, showing a difference of 0.03 on average, and their IQRs cover mostly the same range (Table 3 and Fig. 6). Values for α by IOG are mostly higher and exhibit a difference of 0.06 on average to sICO and ICO. The IQR by IOG is roughly half of the IQR of ICO and sICO (Table 3). During the month of December in 2016 and 2017, as well as January in 2017 and 2018, and April to May in 2018, IQR of ICO and sICO is relatively large. Common to both periods, the average vertical wind was quite low in January 2017 and 2018 (less than 0.01 m s−1). Additionally, we had some instrumental performance problems (exchange of the pump and heating tube, power failure) with the TRANC in the mentioned months. As mentioned in Sect. 2.2, these periods were not considered in the flux analysis. As a matter of fact, not all affected fluxes can be excluded by the selection criteria. Thus, an influence on the quality of the cospectra and ogives can not be excluded. Consequently, IOG, ICO, and sICO exhibit a wide IQR from 0.15 to 0.40 and differences in the median from 0.06 to 0.16, which could be related to the low number of valid cospectra and ogives. Therefore, classifying α at FOR bimonthly (Fig. 6) was a necessary approach to enhance the quality when the number of valid cospectra is not enough for a robust estimation of α. Overall, a good agreement of IOG, ICO, and sICO was found.
At BOG, the median α values of ICO are the lowest, and the median α values of sICO and IOG are nearly the same for every month (Table 3 and Fig. 5). The difference of ICO to IOG varies by 0.05 and 0.20 and to sICO by 0.02 and 0.18. A systematic difference in α between ICO and sICO was not observed for FOR. At the beginning of the measurements the difference was rather small, but it started increasing after December 2012. The range of the quartiles is similar for IOG and sICO for certain months (see Table 3 and Fig. 5), but their IQR is lower than the IQR of ICO. Again, the IQR of IOG is roughly half of ICO IQR. It seems that theoretical cospectra could not reproduce the shape of Co(w, T) well under certain site conditions, although τr values of sICO and ICO were quite similar. They show a correlation of 0.75 and an average absolute difference of 0.48. Comparing α between the sites shows that the damping is stronger at BOG than at FOR. Table 3 shows the averaged α at FOR and BOG.
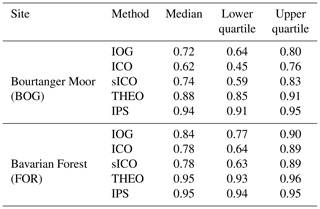
By subtracting α from an ideal, unattenuated system, which has a damping factor of 1, the result will be the flux loss value (). This loss value shows how much of the signal is lost from the inlet to the analysis of the signal by the instrument. Thus, flux losses calculated by IPS for our TRANC–CLD setup are around 6 % at BOG and around 5 % at FOR. The flux loss after THEO was approximately 12 % at BOG and about 5 % at FOR. The methods using measured cospectra or ogives (ICO, sICO, and IOG) showed a flux loss of roughly 16 %–22 % for FOR and around 26 %–38 % for BOG. ICO shows the strongest damping at both sites. These values are in common with other EC studies conducted on ΣNr and other reactive nitrogen compounds (Ammann et al., 2012; Ferrara et al., 2012; Brümmer et al., 2013; Stella et al., 2013; Zöll et al., 2016; Moravek et al., 2019).
Table 3Averages of monthly medians and lower and upper quartiles of α over the whole measurement period for all applied methods at both sites.
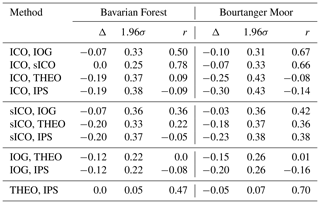
For investigating deviations of the different methods more precisely, we computed correlation, bias, and precision as the standard deviation of the difference for each pair of methods. The results are summarized in Table B1. IOG exhibits a bias of not more than 0.10 to ICO and sICO and is rather small at BOG (0.03). The bias and precision between sICO and ICO is lowest at FOR. Additionally, the scattering of sICO α is more pronounced, which results in a lower precision of sICO compared with the IOG α. Common to both sites, the correlation of IOG with sICO was inferior to ICO. Checking ICO α against sICO α demonstrates a high correlation at both sites (0.78 for FOR and 0.66 for BOG). This is excepted since theoretical cospectra are based on Co(w, T). IOG, ICO, and sICO show a strong bias, low precision, and nearly no correlation to THEO. The correlation between sICO and THEO is somewhat higher because of utilizing Kaimal cospectra for both methods. IPS shows a negative bias and high precision against IOG, ICO, and sICO at FOR. At BOG, IPS exhibits a negative bias against THEO of approximately -0.05. The correlation of IPS with THEO is quite high at both sites, which is reasonable since bias and precision are quite low. Both methods give almost equal α.
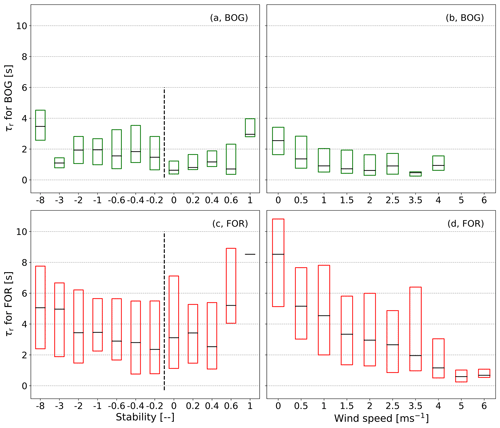
For investigating a trend in meteorological variables such as temperature, relative humidity, stability, and wind speed, we classified them into bins, calculated α for each bin, and display them as box plots (Fig. 7). In the following figure, only wind speed and stability are shown. These are two variables for which we except a dependence, since the shape and position of a Kaimal cospectrum varies with wind speed and stability. We checked for dependencies on the other variables such as global radiation, temperature, and humidity, but no significant influence was found.
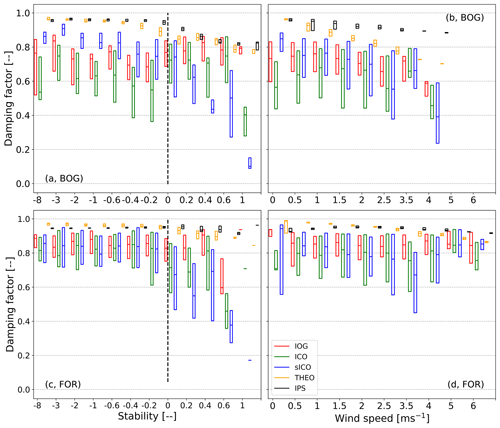
Figure 7Dependency of the flux damping factor (α) on stability and wind speed classes as box plots without whiskers and outliers (box frame is the 25 % to 75 % interquartile ranges (IQR); the bold line is the median). Each damping estimation method is assigned a different color (red: IOG, green: ICO, blue: sICO, orange: THEO, black: IPS). Panels (a, b) refer to the BOG site and (c, d) to the FOR site.
A slight dependence on wind speed for BOG α is starting to be relevant at wind speeds above 1 m s−1, which is confirmed by IOG, ICO, and sICO. The influence on wind speed predicted by THEO already begins at low wind speed, which means that stronger damping was found at higher wind speed values. It shows a (linear) decrease from the beginning. A bias of IOG, ICO, and sICO to THEO (Fig. 7) exists for all wind speed classes. Considering the medians, we observe an increase in attenuation from 0.15 till 0.20 over the whole wind speed regime. The bias of IOG and ICO with sICO (Fig. 7) is mostly visible for wind speeds up to 1.5 m s−1 and becomes negligible afterwards.
α values of IOG, ICO, and sICO are nearly invariant to changes in wind speed at FOR. The predicted drop due to wind speed by THEO is roughly 0.10 at FOR. The difference of the empirical cospectral methods with THEO diminished for wind speeds larger than 4 m s−1. IPS shows the weakest α for all wind speed classes at both sites. The decrease in α with wind speed is less than 0.10 at BOG and hence lower than the cospectral methods. IPS exhibits no significant drop in α with wind speed at FOR.
Values of α estimated by THEO are almost equal for unstable conditions and decline for stable situations. As before, the theoretical drop in attenuation is stronger at BOG (up to 0.20) than at FOR (not exceeding 0.10). At FOR, α values of IOG, ICO, and sICO are nearly equal (∼0.85) for unstable cases. ICO, IOG, and sICO exhibit no distinct trend through all positive stability classes. Only for stability values above 0.4 is a decrease in α visible. However, this decline in α is rather uncertain since the IQR is relatively large compared to the unstable classes, and the number of cospectra that are attributed to stable conditions is relatively small.
At BOG, the linear decline in α is given for sICO but does not exist for IOG and ICO. α values of IOG and ICO are similar for unstable cases but show no clear decrease with increasing stability. The IQR of the sICO increases for positive stability and is smaller than IOG and ICO for negative values. The bias of sICO to IOG and ICO is obvious for the negative stability values. Similar to THEO, IPS shows a drop of α with increasing stability at BOG, but values are higher than for the cospectral methods. As observed for wind speed at FOR, no significant drop in α for IPS occurs under stable conditions.
3.3 Analysis of response time
After comparing α of the individual methods, we focus on variation in τr in time. Therefore, we show statistical analyses of τr of both measurement sites. Figure 8 shows statistical analyses of τr, which were calculated by ICO on a bimonthly basis depicted as box plots.
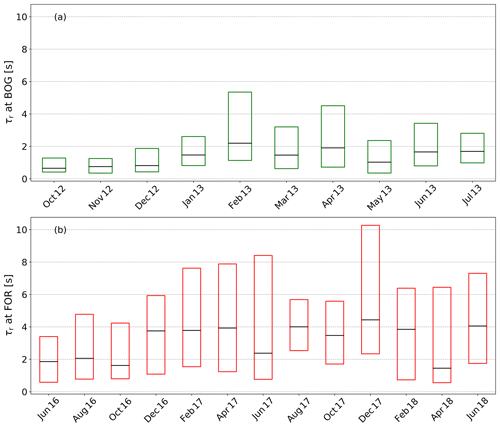
Figure 8Statistical analysis of the response time (τr) depicted as a box plot without whiskers and outliers (the box frame is the 25 % to 75 % interquartile ranges (IQR); the bold line is the median) for the BOG site (a) and the FOR site (b).
It is obvious that medians of τr of FOR are generally larger than medians of τr of BOG. The averaged median τr is 1.37 s for BOG and 3.13 s for FOR (Table B2). Common to both sites, τr was sightly lower at the start of the measurements and the medians were quite constant until December 2012 at BOG and October–November 2016 at FOR. Afterwards τr and its IQR increased significantly, especially at FOR. The variation in τr follows no trend and seems to be rather random. The IQR of FOR was larger, indicating that scattering of τr was enhanced at FOR. On average, τr increased from 0.74 to 1.63 s at BOG and from 1.85 to 3.51 s at FOR (Table B2).
We further determined the correlation between monthly averaged τr and α. Correlations of −0.83 for BOG and −0.72 for FOR show that there is a significant inverse relation between both parameters, which is expected due to the inverse dependency of τr in the empirical transfer function. The analysis of τr stratified by meteorological variables can be useful in order to investigate whether the scattering in α is related either to the variability in cospectra or to the instrument performance. τr is mostly a device-specific parameter. It should have a higher affinity to instrument or measurement setup parameters such as measurement height, pump and heating efficiency, altering of the inlet, and sensitivity of the analyzer than to turbulent atmospheric variations. Changes in gas concentrations may also affect τr. Therefore, we classified the meteorological parameters into bins, calculated τr for each bin, and display them as box plots (Fig. B1). τr is mostly constant for medium and high wind speed at BOG and exhibits slightly higher values at low wind speeds (0–0.5 m s−1). During highly stable and unstable conditions τr reaches up to 3.50 s. It seems rather constant during medium unstable conditions but increases under stable conditions. The same is valid for τr at FOR. τr exhibits the highest values under both highly unstable and stable conditions. However, τr is strongly affected by wind speed at FOR. It decreases with wind speed and seems to follow a nonlinear relationship.
4.1 Noise effects on power spectra and cospectra
4.1.1 Sources of spectral noise
Measured fluxes of ΣNr are heavily affected by white and red noise. They are caused by low and nonstationary ambient trace gas concentrations and fluxes, typically low fluxes due to weak sources and inhomogeneously distributed N sources, limited resolution and precision of the CLD, and varying proportions of different Nr compounds. This leads to a high rejection rate of cospectra and power spectra during quality screening, which is challenging for every spectral analysis using in situ measurements. While the influence on cospectra is mainly limited to the low-frequency range, power spectra show systematic deviations in the low- and high-frequency ranges. The positive slope (Figs. 3 and 4) is related to white noise which compromises the Ps(ΣNr) in the high-frequency domain. White and red noise are more present at FOR, because the site was located in a remote area with no nearby anthropogenic sources of ΣNr (Zöll et al., 2019), resulting in low concentrations of Nr compounds (see Sect. 2.1). At BOG white noise is weaker since more sources of ΣNr were next to the EC station. As shown by Hurkuck et al. (2014), Nr concentrations at BOG were relatively high and showed a distinct diurnal cycle due to intensive livestock and crop production in the surrounding region. The disturbance due to red noise is also visible in Fig. 3. The variability (scattering) of cospectra and power spectra is more pronounced at FOR than at BOG in the low-frequency range as visible in the shown example.
Some Ps(ΣNr) measurements in Fig. 4, mainly at BOG, show a slope near the theoretical value of and were not affected by white noise. Therefore, we examined the environmental conditions such as wind speed, friction velocity, concentration, and flux values at that site during half hours, which were attributed to slopes less than −0.25, and compared them to half hours with a slope greater than −0.25. Only the distribution of concentration was different for the two regimes: most Ps(ΣNr) measurements with a slope less than −0.25 were associated with concentration values between 25 and 40 ppb, whereas Ps(ΣNr) power spectra with a slope greater than −0.25 were associated with concentration values between 10 and 25 ppb, which is in common with the background concentration level of ΣNr at BOG. It was about 21 ppb, whereas only 5 ppb on average was measured at FOR. Thus, it seems that the concentration is an important factor for regulating the quality of Ps(ΣNr). The slope of Ps(T) shows a clear peak between −0.5 and −0.7 for both sites, which is close to the theoretical value of . The differences in the distribution may be related to different site characteristics like surface roughness length, inhomogeneous canopy height, or turbulence or to large-scale eddies which gain more influence on the fluxes at higher aerodynamic measurement height. Before, we argued that concentration of ΣNr leads to differences in the slope distribution (Fig. 4). Concentrations of CO2 were not significantly different between the sites. As a consequence, there has to be another parameter responsible for discrepancy in the contribution of positive Ps(CO2) slopes at the measurement sites. We suppose that the discrepancy of positive Ps(CO2) slopes corresponds to different levels of humidity at the measurement sites. Humid conditions could reduce the sensitivity of the open-path instrument and introduce noise in power spectra. Above the forest the air was less humid and consequentially fewer Ps(CO2) measurements were affected by white noise.
4.1.2 Impact of noise on power spectra and cospectra
Removing high-frequency variations which consist mainly of white noise is easier for Ps(CO2) measurements because their signal is higher than those of Ps(ΣNr) in the low-frequency domain, and the observed noise is limited to the highest frequencies (>2 Hz at FOR and >5 Hz at BOG). Additionally, the noise is strictly linear and exhibits no parabolic structure like for Ps(ΣNr) (Fig. 3). The observed parabolic shape in Ps(ΣNr), which occurs around 1 Hz, is most likely caused by uncorrelated noise, which is induced by some components of the setup like pump, air-conditioning system, or electrical components, and decreased towards the highest frequencies. Handling the impact of unknown noise on power spectra is challenging for common linear noise compensation methods. Thus, it is probably not possible to remove the uncorrelated noise from Ps(ΣNr) completely.
Wolfe et al. (2018) installed an EC setup in an aircraft and measured CO2, H2O, and CH4 with Los Gatos Research analyzers and H2O with an open-path infrared absorption spectrometer. They found a slope of ∼1 in Ps(CO2), Ps(H2O), and Ps(CH4) above 0.4 Hz but not in the Ps(H2O) of the open-path analyzer. They concluded that the white noise was related to insufficient precision of the closed-path analyzers at higher frequencies. No white noise was detected in the corresponding cospectra, because it does not correlate with w. Kondo and Tsukamoto (2007) performed CO2 flux measurements above the equatorial Indian Ocean. They concluded that white noise was related to a lack of sensitivity to small CO2 density fluctuations. Density fluctuations of CO2 above open-ocean surfaces are much smaller than over vegetation. Similar to the present study, they detected no white noise in Co(w, CO2). Their site characteristics and related low fluctuations of trace gas are comparable to those of the forest site. The latter was located in a remote area and therefore far away from potential (anthropogenic) nitrogen sources. This led to low concentrations and less variability in concentrations and deposition fluxes. Very small fluctuations of ΣNr are probably not detectable by the instrument. This is further confirmed by the time lag analysis we did before flux estimation. The broad shape of the empirical lag distribution around the physical lag (not shown) and the random time lag scattering demonstrated that most of the fluxes were near or below the detection limit, and thus quality of (co)spectra suffered from noise. Instrumental noise also affects the shape of the covariance function. It can lead to a broadening of the covariance peak and generally enhances the scattering of the covariance values. Both effects are already enlarged in the case of small mixing ratio fluctuations. Thus, instrumental noise further compromises the time lag estimation and leads to additional noise in cospectra. Due to the applied time lag criterion, the effect of instrumental noise is mostly canceled out. The position of the cospectral peak is less impacted, and thus instrumental noise can only lead to an enhancement of scattering of cospectral values, preferentially in the low-frequency range of the cospectrum. In other words, instrumental noise mostly contributes to the low-frequency noise, the red noise. Additionally, physical reasons, such as an inhomogeneous surface roughness length, canopy height in the footprint of the tower, and different range of relevant eddy sizes, may have been reasons for fewer valid high-quality (co)spectra compared to the BOG site.
4.1.3 Impact of noise on IPS
The findings indicate that using Ps for estimating correction factors of gases with low turbulent fluctuations, which are measured by a closed-path instrument, can be problematic. Therefore, we recommend using cospectra to estimate τr and α of reactive gases, since these gases normally exhibit low-density fluctuations. However, Fig. 3 reveals that Ps(ΣNr) shows a steep decline in the high-frequency range after the peak at BOG, which is similar to the decline of Ps(T). ΣNr concentration was 24.4 ppb on average and exhibits a standard deviation of 9.6 ppb for the averaging period in Fig. 3, suggesting significant differences in concentration levels. It confirms the statement that the concentration is an important driver for the quality of Ps(ΣNr). This leads us to the assumption that the instrument was in principle able to capture differences in concentration levels in the high-frequency range if mixing ratio fluctuations are relatively high.
White noise was observed in power spectra of CO2 and H2O, too. Both gases were measured with an open-path analyzer, but their concentrations are higher and the variability in concentrations of these gases is much larger than for ΣNr. It indicates that Ps(CO2) values are clearly less affected by white noise, and the instrument is able to capture the high-frequency variability of CO2 well. The assumption of spectral similarity, which is a critical assumption for all in situ methods, was valid for Ps(CO2) but was not fulfilled for Ps(ΣNr) due to the influence of red and white noise. Consequentially, an optimization fit with an infinite impulse response function gives unrealistic results for τr. Most likely, automatic filtering criteria are not sufficient enough to extract good quality (co)spectra of ΣNr efficiently, and thereby the averaged Ps(ΣNr) used for the fitting procedure is dominated by low-quality and invalid cases. However, using more restrictive quality selection criteria or narrowing the frequency range for the fitting of the transfer function produced rapidly changing values or even negative values for τr. This demonstrates that the estimation of τr with Ps(ΣNr) via IPS is very uncertain, and the number of Ps(ΣNr) measurement with sufficient quality was not high enough for a robust fitting. Consequently, for estimating damping factors with IPS certain conditions seem to be fulfilled. For example, (i) instruments need a low detection limit and (ii) influence of noise on (co)spectra has to be reduced to a minimum, for instance by optimizing the positions of the sonic anemometer and gas analyzer. In addition, (iii) strategies for the elimination of noise have to be aligned with the design of the instrument and trace gas of interest. The latter should be (iv) rather inert, i.e., little interaction with surfaces or other chemical compounds, and, in the case of IPS, (v) trace gases should exhibit a wind speed dependency on damping factors. Similar to cospectral methods, IPS will also benefit from a well-defined footprint, equal canopy height, and sufficient turbulence. Satisfying these aspects is quite difficult for a custom-built EC system, for which not all attenuation processes are identified yet. In addition, measuring and analyzing ΣNr is challenging since the concentrations of the several compounds contributing to ΣNr are unknown, and the compounds exhibit complex reaction pathways and generally low fluctuations.
The number of good quality (co)spectra for CO2 and H2O was at least 1 order of magnitude higher than for ΣNr. Monthly averaged α values for CO2 and H2O by IPS were in the range of 0.95 and 0.90, which is quite reasonable for an open-path instrument and in agreement with studies dealing with the same instrument (Burba et al., 2010; Butterworth and Else, 2018).
4.2 Assessment of cospectral approaches
4.2.1 THEO vs. (semi)empirical approaches
In general, α values determined by the (semi)empirical cospectral methods (sICO, ICO, and IOG) were considerably lower than the results of THEO. The difference indicates a strong additional damping effect whose impact on ΣNr fluxes is not detected by the fluid-dynamics-related transfer functions used in THEO. This additional damping must be caused by adsorption processes at the inner surfaces of the inlet system, for example in the converter or the sample lines or the CLD. Studies from Aubinet et al. (1999), Bernhofer et al. (2003), Ammann et al. (2006), and Spank and Bernhofer (2008) have also shown that the damping factor by the THEO approach is often too high. Besides disregarded damping processes, this could have also been caused by deviations of the site-specific cospectra from theoretical cases. Therefore, it is advisable to apply empirical methods to measurements of gases with unknown properties or to setups and instrument devices with flux loss sources which are difficult to quantify. Empirical methods take the sum of all potential flux losses into account and do not take care of an individual or specific flux loss. The difference between THEO and empirical methods in total flux losses at the two study sites can be explained by the different aerodynamic measurement heights. With increasing measurement height, turbulence cospectra are shifted to lower frequencies (Figs. 1 and 3), and hence a weaker high-frequency damping is expected. Vertical sensor separation was not considered by the spectral transfer function in the THEO approach. However, the impact of vertical sensor separation on the flux loss is very low if the gas analyzer is placed below the anemometer as in the present study. Kristensen et al. (1997) determined a flux loss of only 2 % at the vertical separation of 20 cm and measurement height of 1 m. This effect becomes even smaller with increasing measurement height. Besides the measurement height, the wind speed and stability are also expected to have an influence on the position and shape of the cospectrum and thus on the damping factor. Yet, no clear systematic dependencies of (s)ICO and IOG results on these parameters were found. At BOG, the dependency on wind speed is only valid for medium- and high-wind-speed classes. α values of IOG and ICO appear to be invariant to changes in stability at BOG, whereas α values of the cospectral empirical approaches are quite constant under unstable conditions at FOR. In contrast, sICO follows the expected drop at stable conditions as observed for THEO at both sites. The reason for the difference between sICO and ICO is discussed in Sect. 4.2.2.
There could be other effects which superpose the wind speed and stability dependencies, for example, (chemical) damping processes occurring inside the TRANC–CLD system. Humidity and ΣNr could affect the aging of the tube and consequentially the adsorption at inner tube walls. However, we found no dependency of these parameters on damping factor and time response. Interactions with tube walls is probably less important, especially for the tube connecting the end of the TRANC to the CLD, because the main trace gas within the line is NO, which acts rather inertly in the absence of ozone and NO2. Because NO2 and O3 are converted in the TRANC, it can be assumed that the influence of interaction with tube walls on time response and high-frequency flux losses is mostly negligible compared to effects that happen in the CLD and TRANC. The CLD contributes more to the total attenuation than the tubing, but supposedly not as much as the TRANC. Rummel et al. (2002) also used the CLD 780 TR as a device for measuring NO fluxes. High-frequency flux losses were rather low and ranged between 21 % (close to the ground) and 5 % (11 m above ground). Also, Wang et al. (2020) observed low flux losses of NO by approximately 12 % by measuring with a QCL (1.7 m above ground).
Consequently, the strongest contributor to the overall damping has to be the TRANC. NH3 is, considering all possible convertible compounds, the most abundant in certain ecosystems, highly reactive, and rather “sticky”. In absolute terms it has the highest influence on the damping of ΣNr. QCL devices, which may be used for the detection of NH3 (Ferrara et al., 2012; Zöll et al., 2016; Moravek et al., 2019), were equipped with a special designed, heated, and opaque inlet to avoid sticking of NH3 at tube walls and water molecules and preventing unwanted molecules entering the analyzer cell. Thus, NH3 has high flux loss factors ranging from 33 % to 46 % (Ferrara et al., 2012; Zöll et al., 2016; Moravek et al., 2019). These damping factors are closer to the damping factors of ΣNr, in particular for BOG, at which high NH3 concentrations were measured, and most of ΣNr can be attributed to NH3 (Hurkuck et al., 2014; Zöll et al., 2016). At FOR, flux losses were lower due to physical reasons and due to a lower contribution of NH3 to ΣNr at FOR. According to DELTA-Denuder measurements presented in Zöll et al. (2019), NH3 concentrations were relatively low at the FOR site (Beudert and Breit, 2010). A fraction of 33 % of ΣNr was NH3 and 32 % NO2. NH3 is converted inside the TRANC at the platinum gauze after passing through the actively heated inlet and iron–nickel–chrome (FeNiCr) alloy tube. Since the main part of the pathway is heated and isolated against environmental impacts, the inlet of the TRANC and the distance to the sonic anemometer seem to be critical for the detection and attenuation of NH3. Finally, we suppose that the response time and attenuation of our TRANC–CLD system is more similar to that of an NH3 analyzer under a high ambient NH3 load.
4.2.2 ICO vs. sICO approach
The difference between the ICO and sICO method is the usage of Kaimal cospectra for determining α after Eq. (1). One reason for using theoretical cospectra is that it lowers the computation time for estimation of α. Moreover, due to site or experimental setup reasons, the Co(w, T) may be influenced by noise in the low-frequency range, which compromises the determination of α. In such cases, using Kaimal cospectra can be a good alternative. The usage of standard Kaimal cospectra leads to a loss of site-specific information. Differences to measured Co(w, T) can lead to uncertainties in the damping estimation of sICO. The consequence is an observed bias of unstable α between sICO and ICO at BOG (Fig. 7) or wind speed and stability dependencies induced by the usage of Kaimal cospectra, which are not confirmed by ICO or IOG. Mamadou et al. (2016) computed α of CO2 with locally measured cospectra and Kansas cospectra (Kaimal et al., 1972), which are slightly different from the theoretical cospectra used in this study. They found that theoretical and measured Co(w, T) differ significantly in shape, which resulted in large differences of correction factors during stable conditions, although their investigated site exhibited no complex terrain or vegetation. This led to an overestimation of nighttime fluxes of 14 %–28 % if Kansas cospectra were used. Therefore, we selected α of ICO and sICO estimated at stable conditions during day and nighttime. Comparing stable (ζ>0.05) nighttime–dawn (Rg<20 W m−2) α with stable daytime half-hourly α showed that stable nighttime α had a higher variability and were mostly overestimated by 0.14–0.35, whereas stable daytime α values were overestimated by 0.10–0.20 if Kaimal cospectra (sICO) were used. Some α values were underestimated by sICO, but the discrepancy was about 0.15 on average. Using Kaimal cospectra can be problematic for estimating α under stable conditions. If typical wind speed or stability dependencies are not approved by other cospectral methods, we do not recommend the usage of theoretical methods such as Kaimal cospectra since it may lead to a bias or unproven dependency.
4.2.3 ICO vs. IOG approach
The main difference between ICO and the IOG method is that IOG utilizes the low-frequency part and (s)ICO the high-frequency part of the cospectrum. The low-frequency part is much more variable than the high-frequency one, especially on a half-hourly basis. As a consequence, the ratio between Og(w, ΣNr) and Og(w, T) is often not well-defined in the fitting range and hence the linear regression between Og(w, ΣNr) and Og(w, T) gives erroneous results. Strong attenuation is possibly underestimated by IOG because damping can extend into the fit range. IOG may perform better for averaged cospectra since the impact of scattering in the low-frequency part of the spectrum would be reduced. The variability (scattering) of cospectra in the high-frequency part is comparatively small, and differences in the decay of Co(w, ΣNr) and Co(w, T) are easier to identify than differences in the low-frequency part. The transfer function used in the ICO fitting routine has to consider the relevant damping processes. While the transfer functions for physical damping effects are relatively well defined (see Mamadou et al., 2016; Table A1), chemical damping effects are rather unknown, although they can be very important for reactive gases such as NH3 or ΣNr. The empirical transfer function was chosen with regard to different response times of the individual sensors. Since both sensors are first-order system filters, the dynamic frequency response can be described by the first-order filter transfer function (Eq. A1). Additionally, the TRANC–CLD has a slower response than the sonic anemometer. The mismatch in the response times introduces a phase shift in the time series, which is accounted for by applying the phase-shift mismatch function (Table A1) after Zeller et al. (1988), and Ammann (1999). The inclusion of the shift mismatch in Eq. (3) leads to a steeper slope in the empirical transfer function and variations around zero at higher frequencies (see Fig. 1) compared to a first-order function alone (not shown). If α is calculated without including the phase-shift effect, we get an overestimation of the damping of up to 10 % for both sites. This could be expected and indicates that most of the damping is related to a time shift. Until now, there is no ideal transfer function which can capture all damping processes. The transfer function can differ depending on trace gas and site setup. Our empirical transfer function was chosen especially for reactive gases such as ΣNr or NH3 measured with a closed-path instrument. The usage of Eq. (3) for other gases like CO2 or H2O is not recommended without knowing any spectral characteristics. In the case of CO2 and H2O measured with Li-7500 at FOR and BOG, we have to modify Eq. (3). We would leave out the phase-shift mismatch since the Li-7500 has a faster response and consider using the sensor separation and/or path-averaging transfer function (Moore, 1986).
4.3 Recommendations for correcting high-frequency flux losses of Nr compounds
ΣNr is a complex trace gas signal since it consists of many reactive N gases, which have various reaction pathways, and concentrations of the single compounds are unknown. We have shown that very low concentration differences of ΣNr are difficult to detect for the CLD. This has an influence on the variability of (co)spectra, strengthens their susceptibility to noise, and reduces the number of high-quality (co)spectra. Since power spectra had a strong affinity to white noise and exhibited no spectral similarity to temperature spectrum due to red noise, we recommend using cospectra for estimating α. We found that flux loss is rather chemical driven, in particular determined by the dimensions of the inlet and ambient NH3 load. It could lead to an invariance in wind speed and stability. As a consequence, common approaches, which are based on theoretical, physical assumptions or established dependencies on environmental dependencies, are not suitable for our EC system. Specifying the flux loss of the different compounds is rather difficult due to the measurement of the sum of individual Nr compounds. Thus, we can only roughly estimate the contribution of individual species to the flux and its high-frequency loss. At BOG, mostly NH3 seems to influence the damping of ΣNr. At FOR, NH3 as well as NO2 were the main ΣNr flux contributors, thereby playing an important role in the detected flux loss at the forest site (see Sect. 4.2.1). Due to the unknown physical and chemical characteristics of ΣNr, an empirical approach seems to be the best solution for capturing attenuation processes of ΣNr and its complex compounds. Having carefully considered all pros and cons of the used approaches, our method of choice will be ICO.
A general or site-specific parameterization of the damping as a function of wind speed and stability was not possible for the entire wind speed and stability range. A parameterization would be possible only for certain wind speed and stability ranges. For example, a parameterization can be performed for unstable conditions and for wind speeds above 1.5 m s−1 at BOG. As mentioned in Sect. 3.2, other parameters such as global radiation showed no clear dependency on α. No significant difference between day and nighttime α values was found. The exchange pattern of ΣNr is rather bidirectional during the entire day. The exchange pattern of inert gases like CO2 is largely related to photosynthesis and respiration. During daytime CO2 also exhibits bidirectional exchange characteristics. During nighttime the exchange of CO2 is mostly unidirectional. Thus, we would expect a diurnal variation in the CO2 attenuation. The influence of global radiation on the biosphere–atmosphere exchange of ΣNr and CO2 was explicitly shown by Zöll et al. (2019) for FOR. They also investigated drivers of ΣNr. However, global radiation explained only 22 % of the variability in ΣNr fluxes, whereas 66 % of the variability in CO2 fluxes was related to global radiation. ΣNr had the concentration as a second driver, which was approximately 24 %. Consequently, there are additional factors controlling the biosphere–atmosphere exchange of total reactive nitrogen, which may be of a chemical nature and challenging to quantify. Thus, a flux loss correction of ΣNr after meteorologically classified parameters is not provided.
For an aspired correction of the determined fluxes, half-hourly estimated α values of the empirical methods will not be used due to their variation with time and to the limited number of high-quality ΣNr cospectra. Therefore, it is advisable to use averages over certain time periods. We decided to use monthly median values for correcting fluxes at BOG. A bimonthly classification was conducted for FOR because the rejection rate was higher due to higher uncertainty of cospectra in the low-frequency range. For estimating α, a reliable determination of τr is needed. Using a constant τr is possible but not recommended for our ΣNr setup since τr varied with time and started to increase after a few months. It seems that the variation in α in time was mainly driven by the change in τr. The increase in τr and the enhanced variation in τr after a few months could be related to instrumental performance problems caused by aging of the inlet, tubes, and filters, reducing pump performance; problems with the CO supply and TRANC temperature; or a sensitivity loss of the CLD. The variability in τr also has an influence on the meteorological classification of α. Generally, it is not known how much the variability in τr contributes to the scattering in α for certain wind speeds or stability values. Thus, usage of τr and the corresponding α classified by meteorological parameters is only recommended for medium or high wind speeds at BOG or near-neutral and unstable atmospheric conditions at both sites. Finally, it seems that the attenuation of the TRANC–CLD system is mainly driven by the performance of the EC setup and by changes in the composition of ΣNr.
We investigated flux losses of total reactive nitrogen (ΣNr) measured with a custom-built converter (TRANC) coupled to a fast-response CLD above a mixed forest and a seminatural peatland. We compared five different methods for the quantification and correction of high-frequency attenuation: the first is adapted from Moore (1986) (THEO), the second uses measured cospectra of sensible heat and trace gas flux (ICO), the third uses response time calculated from measured cospectra and estimate damping with modified Kaimal cospectra (Ammann, 1999) (sICO), the fourth uses the measured ogives (IOG), and the fifth method is the power spectral method by Ibrom et al. (2007) (IPS). The flux losses by IPS for our closed-path eddy-covariance setups were around 6 % at the peatland site (BOG) and around 5 % at the forest site (FOR). The attenuation after THEO was about 12 % at BOG and about 5 % at FOR. The methods using measured cospectra or ogives (ICO, sICO, and IOG) showed a flux loss of roughly 16 %–22 % for the forest measurements and around 26 %–38 % for the peatland measurements, with ICO showing the strongest damping at both sites. Flux losses of the empirical approaches are comparable to other EC studies on ΣNr and other reactive nitrogen compounds.
We found that Ps(ΣNr) was heavily affected by white and red noise. No robust estimation of the response time (τr) by using measured power spectra was possible. THEO could not capture strong damping processes of ΣNr fluxes, which are likely caused by adsorption processes occurring at inner surfaces of the inlet system or missing information about the contribution of specific gases to ΣNr. Consequently, THEO and IPS are not recommended for estimating reliable flux losses of ΣNr.
Differences in flux losses are related to measurement height and hence to the variable contribution of small- and large-scale eddies to the flux. No systematic or only partly significant dependencies of the empirical methods (ICO, sICO, and IOG) on parameters such as atmospheric stability and wind speed, which have an influence on the shape and position of cospectrum, were observed. In the case of the empirical methods, we found a wind speed dependency on damping factors (α), apparently a linear decrease in α with increasing wind speed at BOG. However, the trend is limited to wind speeds higher than 1.5 m s−1. At FOR, α values of IOG, sICO, and ICO seem to be invariant to changes in wind speed. For unstable cases, α values are rather constant at FOR (∼0.85). At BOG, α values of IOG and ICO were similar and vary between 0.60 and 0.80 at unstable conditions, whereas sICO values were higher by approximately 0.05–0.15. The expected decline of α with increasing stability was only observed in sICO at both sites, probably related to the usage of Kaimal cospectra. IOG and ICO showed no clear trend for stable cases. We suppose that other factors like varying atmospheric concentration, distribution, and strength of sources and sinks; enhanced chemical activity of ΣNr compared to CO2 and H2O; aging of the TRANC inlet; varying CLD performance; and vegetation could influence α more strongly and may superpose slight effects of wind speed and stability. Thus, a general or site-specific parameterization of the damping for the complete wind speed and stability range was not possible.
The empirical methods perform well at both sites and median α values are in the range of former studies about reactive nitrogen compounds. However, we detected significant discrepancies to ICO which were related to site-specific problems or to using different frequency ranges of the cospectrum for the assessment. We discovered a bias between α computed with ICO and sICO for the BOG measurements. No significant bias for ICO and sICO was detected at the FOR site. We supposed that Kaimal cospectra may underestimate the attenuation of fluxes under certain site conditions (see Mamadou et al., 2016). Differences in α to IOG are induced by utilizing the low-frequency part of the cospectrum. The low-frequency part is more variable than the high-frequency part on a half-hourly basis. Strong attenuation cases could be underestimated by IOG since damping already occurs in the fit range.
Our investigation of different spectral correction methods showed that ICO is most suitable for capturing damping processes of ΣNr. However, not all damping processes of reactive gases are fully understood yet, and current correction methods have to be improved with regard to quality selection of cospectra. Power spectral and purely theoretical methods which are established in flux calculation software worked well for inert gases, but they are not suitable for reactive nitrogen compounds. Estimating damping of EC setups designed for highly reactive gases with an empirical method may be a considerable and reliable option. For further correction of fluxes, we will use monthly median α since half-hourly values will lead to significant uncertainties in fluxes. Using a constant τr is not recommended as we noticed variation in τr with time, which is caused by altering the inlet system. Correcting fluxes after meteorologically classified α is possible if dependencies are exhibited by the EC setup.
A1 Transfer functions of the ΣNr setup
Transfer functions used for validation of α after THEO, ICO, and sICO are listed in Table A1. A detailed description is given in the mentioned literature. Table 1 contains physical parameters of the setup which are necessary to estimate α.
(Moore, 1986; Moncrieff et al., 1997)(Moore, 1986; Aubinet et al., 2012)(Moore, 1986; Moncrieff et al., 1997; Aubinet et al., 2012)(Ammann, 1999; Aubinet et al., 1999, 2012)(Zeller et al., 1988; Ammann, 1999)A2 Kaimal cospectrum used in THEO and sICO
The cospectrum for stable conditions after Ammann (1999) has the following form:
where a is the aerodynamic measurement height and is given by the difference of measurement height z and the zero-plane displacement height d with (Spank and Bernhofer, 2008). ζ is the stability parameter and is defined by . L is the Obukhov length. The cospectrum for unstable conditions is determined by two parts:
B1 Results of different damping correction methods
B2 Analysis of the response time estimated by ICO
All data are available upon request from the first author of this study (pascal.wintjen@thuenen.de). Also, Python 3.7 code for damping factor calculation as well as the data analysis code can be requested from the first author. All necessary equations for determining the damping factors are given in this paper.
PW wrote the manuscript, carried out the measurements at the forest site, and performed data analysis and interpretation. CA gave scientific advice. FS helped with coding and evaluated meteorological measurements. CB conducted the measurements at the peatland site and gave scientific advice. All authors discussed the results, and FS, CA, and CB reviewed the manuscript.
The authors declare that they have no conflict of interest.
We thank Undine Zöll for scientific and logistical help; Jeremy Rüffer and Jean-Pierre Delorme for excellent technical support, particularly during the field campaigns; and the Bavarian Forest National Park Administration, namely Burkhard Beudert, Wilhelm Breit, and Ludwig Höcker, for technical and logistical support at the site. We further thank the two anonymous reviewers for valuable comments that helped improve the quality of the manuscript.
This research has been supported by the German Environment Agency (UBA) (FORESTFLUX project, support code FKZ 3715512110) and the German Federal Ministry of Education and Research (BMBF) (Junior Research Group NITROSPHERE, support code FKZ 01LN1308A).
This paper was edited by Thomas F. Hanisco and reviewed by two anonymous referees.
Ammann, C.: On the applicability of relaxed eddy accumulation and common methods for measuring trace gas fluxes, PhD thesis, ETH Zurich, https://doi.org/10.3929/ethz-a-002031554, 1999 a, b, c, d, e, f, g, h, i, j
Ammann, C., Brunner, A., Spirig, C., and Neftel, A.: Technical note: Water vapour concentration and flux measurements with PTR-MS, Atmos. Chem. Phys., 6, 4643–4651, https://doi.org/10.5194/acp-6-4643-2006, 2006. a, b, c, d
Ammann, C., Wolff, V., Marx, O., Brümmer, C., and Neftel, A.: Measuring the biosphere-atmosphere exchange of total reactive nitrogen by eddy covariance, Biogeosciences, 9, 4247–4261, https://doi.org/10.5194/bg-9-4247-2012, 2012. a, b, c, d, e, f
Aubinet, M., Grelle, A., Ibrom, A., Rannik, U., Moncrieff, J., Foken, T., Kowalski, A. S., Martin, P. H., Berbigier, P., Bernhofer, C., Clement, R., Elbers, J., Granier, A., Grünwald, T., Morgenstern, K., Pilegaard, K., Rebmann, C., Snijders, W., Valentini, R., and Vesala, T.: Estimates of the Annual Net Carbon and Water Exchange of Forests: The EUROFLUX Methodology, Adv. Ecol. Res., 30 113–175, https://doi.org/10.1016/S0065-2504(08)60018-5, 1999. a, b, c, d, e, f
Aubinet, M., Vesala, T., and Papale, D. (Eds.): Eddy Covariance: A Practical Guide to Measurement and Data Analysis, Springer Science+Business Media B.V., Dordrecht, The Netherlands, 2012. a, b, c, d, e, f, g, h
Bernhofer, C., Feigenwinter, C., Grünwald, T., and Vogt, R.: Spectral Correction of Water and Carbon Flux for EC Measurements at the Anchor Station Tharandt, in: Flussbestimmung an komplexen Standorten, edited by: Bernhofer, C., Tharandter Klimaprotokolle Band 8, 1–13, 2003. a
Beudert, B. and Breit, W.: Integrated Monitoring Programm an der Meßstelle Forellenbach im Nationalpark Bayerischer Wald, Untersuchungen zum Stickstoffeintrag und zum wassergebundenen Stickstoffhaushalt des Forellenbachgebiets, Förderkennzeichen 351 01 012, Nationalparkverwaltung Bayerischer Wald, Sachgebiet IV, techreport, Umweltbundesamt, available at: https://www.umweltbundesamt.de/sites/default/files/medien/370/dokumente/ece_im_forellenbach_berichtsjahr_2009.pdf (last access: 4 May 2020), 2010. a, b
Beudert, B., Bernsteinová, J., Premier, J., and Bässler, C.: Natural disturbance by bark beetle offsets climate change effects on streamflow in headwater catchments of the Bohemian Forest, Silva Gabreta, 24, 21–45, available at: https://www.npsumava.cz/wp-content/uploads/2019/06/2_sg_24_beudertetal.pdf, (last access: 4 May 2020), 2018. a
Brümmer, C., Marx, O., Kutsch, W., Ammann, C., Wolff, V., Flechard, C. R., and Freibauer, A.: Fluxes of total reactive atmospheric nitrogen (ΣNr) using eddy covariance above arable land, Tellus B, 65, 19770, https://doi.org/10.3402/tellusb.v65i0.19770, 2013. a, b, c, d, e, f
Burba, G.: Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates, LI-COR Biosciences, Lincoln, Nebraska, USA, 2013. a, b, c
Burba, G. G., Mcdermitt, D. K., Anderson, D. J., Furtaw, M. D., and Eckles, R. D.: Novel design of an enclosed CO2/H2O gas analyser for eddy covariance flux measurements, Tellus B, 62, 743–748, https://doi.org/10.1111/j.1600-0889.2010.00468.x, 2010. a, b, c
Butterworth, B. J. and Else, B. G. T.: Dried, closed-path eddy covariance method for measuring carbon dioxide flux over sea ice, Atmos. Meas. Tech., 11, 6075–6090, https://doi.org/10.5194/amt-11-6075-2018, 2018. a, b
Desjardins, R. L., MacPherson, J. I., Schuepp, P. H., and Karanja, F.: An evaluation of aircraft flux measurements of CO2, water vapor and sensible heat, Bound.-Lay. Meteorol., 47, 55–69, https://doi.org/10.1007/BF00122322, 1989. a
Ferrara, R. M., Loubet, B., Di Tommasi, P., Bertolini, T., Magliulo, V., Cellier, P., Eugster, W., and Rana, G.: Eddy covariance measurement of ammonia fluxes: Comparison of high frequency correction methodologies, Agr. Forest Meteorol., 158-159, 30–42, https://doi.org/10.1016/j.agrformet.2012.02.001, 2012. a, b, c, d, e, f, g
Flechard, C. R., Massad, R.-S., Loubet, B., Personne, E., Simpson, D., Bash, J. O., Cooter, E. J., Nemitz, E., and Sutton, M. A.: Advances in understanding, models and parameterizations of biosphere-atmosphere ammonia exchange, Biogeosciences, 10, 5183–5225, https://doi.org/10.5194/bg-10-5183-2013, 2013. a
Fowler, D., Coyle, M., Skiba, U., Sutton, M. A., Cape, J. N., Reis, S., Sheppard, L. J., Jenkins, A., Grizzetti, B., Galloway, J. N., Vitousek, P., Leach, A., Bouwman, A. F., Butterbach-Bahl, K., Dentener, F., Stevenson, D., Amann, M., and Voss, M.: The global nitrogen cycle in the twenty-first century, Philos. T. Roy. Soc. B, 368, 20130164, https://doi.org/10.1098/rstb.2013.0164, 2013. a
Fratini, G., Ibrom, A., Arriga, N., Burba, G., and Papale, D.: Relative humidity effects on water vapour fluxes measured with closed-path eddy-covariance systems with short sampling lines, Agr. Forest Meteorol., 165, 53–63, https://doi.org/10.1016/j.agrformet.2012.05.018, 2012. a, b
Horst, T. W. and Lenshow, D. H.: Attenuation of Scalar Fluxes Measured with Spatially-displaced Sensors, Bound.-Lay. Meteorol., 130, 275–300, https://doi.org/10.1007/s10546-008-9348-0, 2009. a
Hurkuck, M., Brümmer, C., Mohr, K., Grünhage, L., Flessa, H., and Kutsch, W. L.: Determination of atmospheric nitrogen deposition to a semi-natural peat bog site in an intensively managed agricultural landscape, Atmos. Environ., 97, 296–309, https://doi.org/10.1016/j.atmosenv.2014.08.034, 2014. a, b, c, d, e, f
Hurkuck, M., Brümmer, C., and Kutsch, W. L.: Near-neutral carbon dioxide balance at a seminatural, temperate bog ecosystem, J. Geophys. Res.-Biogeo., 121, 370–384, https://doi.org/10.1002/2015jg003195, 2016. a, b, c
Ibrom, A., Dellwick, E., Flyvbjerg, H., Jensen, N. O., and Pilegaard, K.: Strong low-pass filtering effects on water vapour flux measurements with closed-path eddy correlation systems, Agr. Forest Meteorol., 147, 140–156, https://doi.org/10.1016/j.agrformet.2007.07.007, 2007. a, b, c, d, e, f, g, h, i, j, k, l
Kaimal, J. C., Wyngaard, J. C., Izumi, Y., and Coté, O. R.: Spectral characteristics of surface-layer turbulence, Q. J. Roy. Meteor. Soc., 98, 563–589, https://doi.org/10.1002/qj.49709841707, 1972. a, b, c
Kolle, O. and Rebmann, C.: EddySoft Documentation of a Software Package to Acquire and Process Eddy Covariance Data, techreport, MPI-BGC, available at: https://repository.publisso.de/resource/frl:4414276-1/data (last access: 4 May 2020), 2007. a
Kondo, F. and Tsukamoto, O.: Air-Sea CO2 Flux by Eddy Covariance Technique in the Equatorial Technique in the Equatorial, J. Oceanogr., 63, 449–456, available at: https://www.terrapub.co.jp/journals/JO/pdf/6303/63030449.pdf (last access: 4 May 2020), 2007. a
Kristensen, L., Mann, J., Oncley, S. P., and Wyngaard, J. C.: How Close is Close Enough When Measuring Scalar Fluxes with Displaced Sensors?, J. Atmos. Ocean. Tech., 14, 814–821, https://doi.org/10.1175/1520-0426(1997)014<0814:HCICEW>2.0.CO;2, 1997. a
Lee, X. and Black, T. A.: Relating eddy correlation sensible heat flux to horizontal sensor separation in the unstable atmospheric surface layer, J. Geophys. Res., 99, 18545–18553, https://doi.org/10.1029/94JD00942, 1994. a
Lenschow, D. H. and Raupach, M. R.: The attenuation of fluctuations in scalar concentrations through sampling tubes, J. Geophys. Res., 96, 15259–15268, https://doi.org/10.1029/91JD01437, 1991. a, b
Leuning, R. and Judd, M. J.: The relative merits of open- and closed-path analysers for measurement of eddy fluxes, Glob. Change Biol., 2, 241–253, https://doi.org/10.1111/j.1365-2486.1996.tb00076.x, 1996. a, b
Leuning, R. and Moncrieff, J.: Eddy-covariance CO2 flux measurements using open- and closed-path CO2 analysers: Corrections for analysers water vapour sensitivity and damping of fluctuations in air sampling tubes, Bound.-Lay. Meteorol., 53, 63–76, https://doi.org/10.1007/BF00122463, 1990. a, b
Liu, H., Peters, G., and Foken, T.: New equations for sonic temperature variance and buoyancy heat flux with an omnidirectional sonic anemometer, Bound.-Lay. Meteorol., 100, 459–468, https://doi.org/10.1023/A:1019207031397, 2001. a
Mamadou, O., de la Motte, L. G., De Ligne, A., Heinisch, B., and Aubinet, M.: Sensitivity of the annual net ecosystem exchange to the cospectralmodel used for high frequency loss corrections at a grazed grassland site, Agr. Forest Meteorol., 228–229, 360–369, https://doi.org/10.1016/j.agrformet.2016.06.008, 2016. a, b, c
Mammarella, I., Launiainen, S., Gronholm, T., Keronen, P., Pumpanen, J., Rannik, U., and Vesala, T.: Relative Humidity Effect on the High-Frequency Attenuation of Water Vapor Flux Measured by a Closed-Path Eddy Covariance System, J. Atmos. Ocean. Tech., 26, 1856–1866, https://doi.org/10.1175/2009JTECHA1179.1, 2009. a, b, c
Marx, O., Brümmer, C., Ammann, C., Wolff, V., and Freibauer, A.: TRANC – a novel fast-response converter to measure total reactive atmospheric nitrogen, Atmos. Meas. Tech., 5, 1045–1057, https://doi.org/10.5194/amt-5-1045-2012, 2012. a, b, c, d, e
Massman, W. J.: The attenuation of concentration fluctuations in turbulent flow through a tube, J. Geophys. Res., 96, 15269–15274, https://doi.org/10.1029/91JD01514, 1991. a, b
Mauder, M. and Foken, T.: Documentation and instruction manual of the eddy covariance software package TK2, 26, Arbeitsergebnisse, Universität Bayreuth, Abt. Mikrometeorologie, Bayreuth, Germany, 2004. a
Mauder, M. and Foken, T.: Impact of post-field data processing on eddy covariance flux estimates and energy balance closure, Meteorol. Z., 15, 597–609, https://doi.org/10.1127/0941-2948/2006/0167, 2006. a, b
Min, K.-E., Pusede, S. E., Browne, E. C., LaFranchi, B. W., and Cohen, R. C.: Eddy covariance fluxes and vertical concentration gradient measurements of NO and NO2 over a ponderosa pine ecosystem: observational evidence for within-canopy chemical removal of NOx, Atmos. Chem. Phys., 14, 5495–5512, https://doi.org/10.5194/acp-14-5495-2014, 2014. a
Moncrieff, J. B., Massheder, J. M., deBruin, H., Elbers, J., Friborg, T., Heusinkveld, B., Kabat, P., Scott, S., Soegaard, H., and Verhoef, A.: A system to measure surface fluxes of momentum, sensible heat, water vapour and carbon dioxide, J. Hydrol., 188, 589–611, https://doi.org/10.1016/S0022-1694(96)03194-0, 1997. a, b, c, d, e
Moore, C. J.: Frequency response corrections for eddy correlation systems, Bound.-Lay. Meteorol., 37, 17–35, https://doi.org/10.1007/BF00122754, 1986. a, b, c, d, e, f, g, h, i, j, k
Moravek, A., Singh, S., Pattey, E., Pelletier, L., and Murphy, J. G.: Measurements and quality control of ammonia eddy covariance fluxes: a new strategy for high-frequency attenuation correction, Atmos. Meas. Tech., 12, 6059–6078, https://doi.org/10.5194/amt-12-6059-2019, 2019. a, b, c, d, e
Nakai, T., van der Molen, M. K., Gash, J. H. C., and Kodama, Y.: Correction of sonic anemometer angle of attack errors, Agr. Forest Meteorol., 136, 19–30, https://doi.org/10.1016/j.agrformet.2006.01.006, 2006. a
Oncley, S. P., F. C. A., Larue, J. C., Businger, J. A., Itsweire, E. C., and Chang, S. S.: Surface-Layer Fluxes, Profiles, and Turbulence Measurements over Uniform Terrain under Near-Neutral Conditions, J. Atmos. Sci., 53, 1029–1044, https://doi.org/10.1175/1520-0469(1996)053<1029:SLFPAT>2.0.CO;2, 1996. a
Polonik, P., Chan, W. S., Billesbach, D. P., Burba, G., Nottrott, A., Bogoev, I., Conrad, B., and Biraud, S. C.: Comparison of gas analyzers for eddy covariance: Effects of analyzer type and spectral corrections on fluxes, Agr. Forest Meteorol., 272–273, 128–142, https://doi.org/10.1016/j.agrformet.2019.02.010, 2019. a
Rummel, U., Ammann, C., Gut, A., Meixner, F. X., and Andreae, M. O.: Eddy covariance measurements of nitric oxide flux within an Amazonian rain forest, J. Geophys. Res., 107, 8050, https://doi.org/10.1029/2001JD000520, 2002. a, b
Sabbatini, S., Mammarella, I., Arriga, N., Fratini, G., Graf, A., Hörtnagel, L., Ibrom, A., Longdoz, B., Mauder, M., Merbold, L., Metzger, S., Montagnani, L., Pitacco, A., Rebmann, C., Sedlák, P., Sigut, L., Vitale, D., and Papale, D.: Eddy covariance raw data processing for CO2 and energy fluxes calculation at ICOS ecosystem stations, Int. Agrophys., 32, 495–515, https://doi.org/10.1515/intag-2017-0043, 2018. a, b
Spank, U. and Bernhofer, C.: Another Simple Method of Spectral Correction to Obtain Robust Eddy-Covariance Results, Bound.-Lay. Meteorol., 128, 403–422, https://doi.org/10.1007/s10546-008-9295-9, 2008. a, b, c
Stella, P., Kortner, M., Ammann, C., Foken, T., Meixner, F. X., and Trebs, I.: Measurements of nitrogen oxides and ozone fluxes by eddy covariance at a meadow: evidence for an internal leaf resistance to NO2, Biogeosciences, 10, 5997–6017, https://doi.org/10.5194/bg-10-5997-2013, 2013. a, b
Su, H.-B., Schmid, H. P., Grimmond, C. S. B., Vogel, C. S., and Oliphant, A. J.: Spectral characteristics and correction of long-term eddy-covariance measurements over two mixed hardwood forests in non-flat terrain, Bound.-Lay. Meteorol., 110, 213–253, https://doi.org/10.1023/A:1026099523505, 2004. a, b, c
Sutton, M. A., Tang, Y. S., Miners, B., and Fowler, D.: A New Diffusion Denuder System for Long-Term, Regional Monitoring of Atmospheric Ammonia and Ammonium, Water, Air and Soil Pollution: Focus, 1, 145–156, https://doi.org/10.1023/a:1013138601753, 2001. a
Sutton, M. A., Howard, C. M., Erisman, J. W., Billen, G., Bleeker, A., Grennfelt, P., van Grinsven, H., and Grizzetti, B. (Eds.): The European Nitrogen Assessment: sources, effects and policy perspectives, Cambridge University Press, Cambridge, UK, 2011. a, b
Tang, Y. S., Simmons, I., van Dijk, N., Di Marco, C., Nemitz, E., Dämmgen, U., Gilke, K., Djuricic, V., Vidic, S., Gliha, Z., Borovecki, D., Mitosinkova, M., Hanssen, J. E., Uggerud, T. H., Sanz, M. J., Sanz, P., Chorda, J. V., Flechard, C. R., Fauvel, Y., Ferm, M., Perrino, C., and Sutton, M. A.: European scale application of atmospheric reactive nitrogen measurements in a low-cost approach to infer dry deposition fluxes, Agr. Ecosyst. Environ., 133, 183–195, https://doi.org/10.1016/j.agee.2009.04.027, 2009. a
Vickers, D. and Mahrt, L.: Quality Control and Flux Sampling Problems for Tower and Aircraft Data, J. Atmos. Ocean. Tech., 14, 512–526, https://doi.org/10.1175/1520-0426(1997)014<0512:QCAFSP>2.0.CO;2, 1997. a, b, c
von Bobrutzki, K., Braban, C. F., Famulari, D., Jones, S. K., Blackall, T., Smith, T. E. L., Blom, M., Coe, H., Gallagher, M., Ghalaieny, M., McGillen, M. R., Percival, C. J., Whitehead, J. D., Ellis, R., Murphy, J., Mohacsi, A., Pogany, A., Junninen, H., Rantanen, S., Sutton, M. A., and Nemitz, E.: Field inter-comparison of eleven atmospheric ammonia measurement techniques, Atmos. Meas. Tech., 3, 91–112, https://doi.org/10.5194/amt-3-91-2010, 2010. a
Wang, K., Wang, D., Zheng, X., and Nelson, D. D.: Applicability of a closed-path quantum cascade laser spectrometer for eddy covariance (EC) flux measurements of nitric oxide (NO) over a cropland during a low emission period, Agr. Forest Meteorol., 282–283, 107855, https://doi.org/10.1016/j.agrformet.2019.107855, 2020. a
Wilczak, J. M., Oncley, S. P., and Stage, S. A.: Sonic Anemometer Tilt Correction Algorithms, Bound.-Lay. Meteorol., 99, 127–150, https://doi.org/10.1023/A:1018966204465, 2001. a, b
Wolfe, G. M., Kawa, S. R., Hanisco, T. F., Hannun, R. A., Newman, P. A., Swanson, A., Bailey, S., Barrick, J., Thornhill, K. L., Diskin, G., DiGangi, J., Nowak, J. B., Sorenson, C., Bland, G., Yungel, J. K., and Swenson, C. A.: The NASA Carbon Airborne Flux Experiment (CARAFE): instrumentation and methodology, Atmos. Meas. Tech., 11, 1757–1776, https://doi.org/10.5194/amt-11-1757-2018, 2018. a
Zeller, K. F., Massman, W. J., Stocker, D. W., Fox, D. A., and Stedman, D. H.: Initial results from the Pawnee Eddy Correlation system for dry acid-deposition research, United States Department of Agriculture, Forest Service, Rocky Mountain Forest and Range Experiment Station Fort Collins, CO, Forest Service research paper, Report No., RM-282, 30 pp., 1988. a, b, c
Zöll, U., Brümmer, C., Schrader, F., Ammann, C., Ibrom, A., Flechard, C. R., Nelson, D. D., Zahniser, M., and Kutsch, W. L.: Surface–atmosphere exchange of ammonia over peatland using QCL-based eddy-covariance measurements and inferential modeling, Atmos. Chem. Phys., 16, 11283–11299, https://doi.org/10.5194/acp-16-11283-2016, 2016. a, b, c, d, e, f, g, h, i
Zöll, U., Lucas-Moffat, A. M., Wintjen, P., Schrader, F., Beudert, B., and Brümmer, C.: Is the biosphere-atmosphere exchange of total reactive nitrogen above forest driven by the same factors as carbon dioxide? An analysis using artificial neural networks, Atmos. Environ., 206, 108–118, https://doi.org/10.1016/j.atmosenv.2019.02.042, 2019. a, b, c, d, e