A GPS water vapour tomography method based on a genetic algorithm

Water vapour is an important substituent of the atmosphere but its spatial and temporal distribution is difficult to detect. Global Positioning System (GPS) water vapour tomography, which can sense three-dimensional water vapour distribution, has been developed as a research area in the field of GPS meteorology. In this paper, a new water vapour tomography method based on a genetic algorithm (GA) is proposed to overcome the ill-conditioned problem. The proposed approach does not need to perform matrix inversion, and it does not rely on excessive constraints, a priori information or external data. Experiments in Hong Kong under rainy and rainless conditions using this approach show that there is a serious ill-conditioned problem in the tomographic matrix by grayscale and condition numbers. Numerical results show that the average root mean square error (RMSE) and mean absolute error (MAE) for internal and external accuracy are 1.52∕0.94 and 10.07∕8.44 mm, respectively, with the GAMIT-estimated slant water vapour (SWV) as a reference. Comparative results of water vapour density (WVD) derived from radiosonde data reveal that the tomographic results based on GA with a total RMSE ∕ MAE of 1.43∕1.19 mm are in good agreement with that of radiosonde measurements. In comparison to the traditional least squares method, the GA can achieve a reliable tomographic result with high accuracy without the restrictions mentioned above. Furthermore, the tomographic results in a rainless scenario are better than those of a rainy scenario, and the reasons are discussed in detail in this paper.

1 Introduction

Water vapour is a major component of the atmosphere, and its distribution and dynamics are the main driving force of weather and climate change. A good understanding of water vapour is crucially important for meteorological applications and research such as severe weather forecasting and warnings (Liu et al., 2005). Nevertheless, the variation of water vapour is affected by many factors, including temperature, topography and seasons with characteristics of changing fast with time and changing strongly in vertical and horizontal directions, which makes it difficult to monitor with high temporal and spatial resolutions (Rocken et al., 1993).

Thanks to the development of GPS station networks providing atmospheric information under all weather conditions, GPS is considered a powerful technique to retrieve water vapour. Since Bevis et al. (1992) first envisioned the potential of tomography to be applied in GPS meteorology, water vapour tomography has become a promising method to improve the restitution of the spatio-temporal variations of this parameter (Braun et al., 1999; Nilsson et al., 2004; Song et al., 2006; Perler et al., 2011; Rohm, 2012; Dong and Jin, 2018).

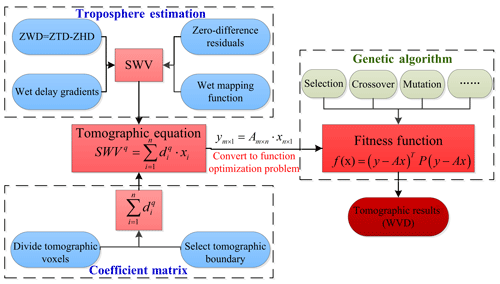
In GPS water vapour tomography, the research area should be covered by ground-based GPS receivers and discretized into a number of cubic closed voxels by latitude, longitude and altitude, each of which has a fixed amount of water vapour at a particular time (Guo et al., 2016). The observations are GPS-derived slant water vapour data, the precipitable water in the direction of the signal ray path, which travels through the troposphere from its top (Zhao and Yao, 2017). After obtaining the precise measurement of the signal ray distance in each voxel by ray tracing its path from receiver to satellite, we can achieve the basic equation for water vapour tomography, which can be expressed in linear form (Flores et al., 2000; Yang et al., 2018):

$$\begin{array}{}\text{(1)}& {\text{SWV}}^q=\sum _{i=\mathrm{1}}^n{d}_i^q\cdot {\mathit{x}}_i,\end{array}$$

where the superscript q is the satellite signal index, SWV^q denotes the qth slant water vapour achieved by GPS tropospheric estimation and n is the total number of tomographic voxels discretized. $d_i^q$ denotes the distance of the qth signal ray inside voxel i, which can be obtained by the satellite and station coordinates, and x_i is the water vapour density of voxel i. Using all suitable SWV observations, we can form the tomographic observation equation:

$$\begin{array}{}\text{(2)}& {\mathit{y}}_{\mathrm{m}\times \mathrm{1}}={\mathbf{A}}_{\mathrm{m}\times \mathrm{n}}\cdot {\mathit{x}}_{n\times \mathrm{1}},\end{array}$$

where y is a column vector of SWV, m is the total number of SWV measurements in tomography, A denotes the intercept matrix containing the distance of the signal ray in each of the voxels, n is the number of voxels in the study area and x denotes the vector of the unknown water vapour density.

Since a GPS signal ray can only pass through a small part of the voxels in the study area, the elements of matrix A are likely to be equal to zero, making it a large, sparse matrix. In addition, the effective signal rays will concentrate around the zenith due to the unfavourable geometry of the GPS stations and the special structures of the satellites. These all make Eq. (2) ill conditioned, and it is difficult to obtain the unknowns by performing the inversion of Eq. (2) in the form of $\mathit{x}={\mathbf{A}}^{-\mathrm{1}}\cdot \mathit{y}$.

To circumvent the ill-conditioned problem, many methods are explored in the literature. Flores et al. (2000) added constraints on the vertical and horizontal variability of tomography with additional top constraints to the model. Most constraints are based on experience and difficult to match to the actual water vapour distribution, resulting in the deviation of tomographic results. Moreover, singular value decomposition (SVD) is required to perform matrix inversion. Bender et al. (2011) utilized an iterative algorithm called the algebraic reconstruction technique (ART) to solve the observation equation. Several reconstruction algorithms of the ART family were also implemented, e.g. the multiplicative algebraic reconstruction techniques (MART) and the simultaneous iterations reconstruction technique (SIRT) (Stolle et al., 2006; Liu et al., 2010). The ART techniques are iterative algorithms that proceed observation by observation. Only two vectors, y and x, and a data structure containing the slant sub-paths in each voxel are required to solve the observation equations. The algorithms consist of two loops: The inner loop processes SWV by SWV and applies an adequate correction to each voxel. SWVs that execute the next iteration start in the outer loop (Bender et al., 2011). Performing the matrix inversion is not necessary, thus avoiding the ill-conditioned problem. However, only the results of the voxels that travelled through via signal rays are updated, and the tomographic results heavily depend on the exact initial field, the data quality and relaxation parameter (Wang et al., 2014). Nilsson and Gradinarsky (2004) adapted a Kalman filter approach to estimate tomographic results without adding constraints and performing inversion. This approach assumes that the water vapour density in each voxel meets the Gauss–Markov random walk pattern for a certain period of time, and it establishes the corresponding state equation of the Kalman filter. The observation vector used is based on the mathematical model to perform the optimal estimation of the state vector, which is a process of continuous prediction and correction. In this method, initializing the filter with an informed estimation of the water vapour field and providing the initial covariance of state equation are based on external data. Other approaches that enrich the information of the observation equation were exploited in recent years, including the Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC) occultation data by Xia et al. (2013), Interferometric Synthetic Aperture Radar (InSAR) by Benevides et al. (2015), and water vapour radiometer (WVR) and numerical weather prediction by Chen and Liu (2016).

In the above-mentioned tomographic methods, excessive constraints on the matrix inversion, exact priori information or external data are commonly used to overcome the ill-conditioned problem. The mandatory usage of excessive constraints in tomographic experiments with poor voxel structure will induce limitations, while reliance on exact priori information will make the tomographic solutions too similar to the priori data and decrease the role of the tomography technique. External data cannot be used in all tomographic experiments. Therefore, this paper proposes a new tomography method based on a genetic algorithm (Sect. 2). The tomography experiments and results of the analysis are presented in Sect. 3. Section 4 summarizes the conclusions.

2 Methodology

2.1 Troposphere estimation

In water vapour tomography, the observation is slant water vapour, which can be converted from slant wet delay (SWD) by the following formula (Adavi and Mashhadi, 2015):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& \text{SWV}=\mathrm{\Pi }\times \text{SWD}\\ & ={\displaystyle \frac{{\mathrm{10}}^{\mathrm{6}}}{{\mathit{\rho }}_{\mathrm{w}}\times \frac{R}{m_{\mathrm{w}}}\left(\frac{k_{\mathrm{3}}}{T_{\mathrm{m}}}+k_{\mathrm{2}}-\frac{m_{\mathrm{w}}}{m_{\mathrm{d}}}\times k_{\mathrm{1}}\right)}}\times \text{SWD},\end{array}\end{array}$$

where Π denotes a conversion factor. k₁=77.604K hPa⁻¹, k₂=70.4K hPa⁻¹ and $k_{\mathrm{3}}=\mathrm{3.775}\times {\mathrm{10}}^{\mathrm{5}}$K² hPa⁻¹; ρ_w is the liquid water density (unit: g m⁻³), R=8314 Pa m³ K⁻¹ kmol⁻¹ represents the universal gas constant, and m_w=18.02 kg kmol⁻¹ and m_d=28.96 kg kmol⁻¹ indicate the molar mass of water and the dry atmosphere, respectively. T_m denotes the weighted mean temperature, which is the ratio of two vertical integrals though the atmosphere (Davis et al., 1985). In practice, an empirical formula is used to achieve approximate T_m by surface temperature T_s in kelvin ($T_{\mathrm{m}}=\mathrm{85.63}+\mathrm{0.668}$ T_s) (Liu et al., 2001; Astudillo et al., 2018). SWD can be obtained as follows (Zhang et al., 2017):

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& \text{SWD}=f\left(\text{ele}\right)\times \text{ZWD}+f\left(\text{ele}\right)\times \cot \left(\text{ele}\right)\\ & \times \left(G_{\text{NS}}^{\mathrm{w}}\times \cos \left(\text{azi}\right)+G_{\text{WE}}^{\mathrm{w}}\times \sin \left(\text{azi}\right)\right)+R_e,\end{array}\end{array}$$

where ele and azi are the satellite elevation and azimuth, respectively. f denotes the wet mapping function, $G_{\text{NS}}^{\mathrm{w}}$ and $G_{\text{WE}}^{\mathrm{w}}$ refer to the wet delay gradient parameters in the north–south and east–west directions, respectively. R_e is the un-modelled atmospheric slant delay, which is included in the zero-difference residuals. ZWD represents zenith wet delay, which is the wet component of zenith total delay (ZTD) affected by water vapour along the satellite signal ray. It can be separated from ZTD by subtracting the zenith hydrostatic delay (ZHD). The ZTD is the primary parameter retrieved with GPS, and it is a spatially averaged parameter. If pressure measurements are available, the ZHD is calculated by the Saastamoinen model as follows (Saastamoinen, 1972):

$$\begin{array}{}\text{(5)}& \text{ZHD}={\displaystyle \frac{\mathrm{0.002277}\times P_{\mathrm{s}}}{\mathrm{1}-\mathrm{0.00266}\times \cos \left(\mathrm{2}\mathit{\phi }\right)-\mathrm{0.00028}\times H}},\end{array}$$

where P_s refers to the surface pressure, and φ and H represent the latitude and the geodetic height of the station, respectively.

2.1.1 Water vapour tomography based on the least squares method

After obtaining the observation equation (Eq. 2), three types of constraints are usually added:

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathrm{0}=\mathbf{H}\cdot \mathit{x},\text{(7)}& {\displaystyle }\mathrm{0}=\mathbf{V}\cdot \mathit{x},\text{(8)}& {\displaystyle }\mathrm{0}=\mathbf{T}\cdot \mathit{x}.\end{array}$$

Equations (6)–(8) are the vertical, horizontal and top constraints, respectively. The horizontal constraint equation assumes that the distribution of water vapour density is relatively stable in the horizontal direction within a small region. Thus, the water vapour density within a certain voxel can be represented by the weighted average of its neighbouring voxels in the same layers. The vertical constraint equation is a relationship established for the voxels between two adjacent layers based on the analysis of meteorological data for many years. The top constraint is obtained by setting the water vapour density of the top boundary to a small constant. Based on the principle of least squares, the tomographic results can be achieved by the following formula:

$$\begin{array}{}\text{(9)}& \mathit{x}={\left({\mathbf{A}}^T\mathbf{A}+H^{T}H+V^{T}V+T^{T}T\right)}^{-\mathrm{1}}\times \left({\mathbf{A}}^{T}y\right).\end{array}$$

To obtain the inverse matrix in Eq. (9), the singular value decomposition is required. More details on this technique can be found in Flores et al. (2000).

Figure 1 Flowchart of the water vapour tomography based on the genetic algorithm.

2.2 Water vapour tomography based on the genetic algorithm

For water vapour tomography based on the genetic algorithm, the first procedure is to construct the tomographic equation. The idea of function optimization is then used to solve Eq. (2) (Guo and Hu, 2009; Olinsky et al., 2004), which is similar to the principle of least squares, $V^T\text{PV}=min$ (Flores et al., 2000). Equation (2) can be converted into the following form:

$$\begin{array}{}\text{(10)}& minf\left(x\right)={\left(\mathit{y}-\mathbf{A}\mathit{x}\right)}^T\mathbf{P}\left(\mathit{y}-\mathbf{A}\mathit{x}\right),\mathit{x}\in R+,\end{array}$$

where the terms are the same as in Eq. (2). In this equation, the values of x that minimize function f(x) are the result of tomography. To achieve the best values of x, the traditional method adopts a derivative method which needs matrix inversion in the follow-up. The genetic algorithm, which was first introduced by Holland (1992), provides an adaptive search method to achieve the tomographic results. It is designed to simulate the evolutionary processes in nature, in which the principle of survival of the fittest is applied to produce better and better approximates to the function. Equation (10) is regarded as the fitness function that is used to measure the performance of the searched values of x by computing the fitness value (Goldberg, 1989; Venkatesan et al., 2004). Through searching generation after generation, the water vapour result that best fits the function can be found. The specific steps of water vapour tomography based on the genetic algorithm are as follows:

1. construct the fitness function which is converted from the tomographic equation.

2. generate some groups representing approximates of x (water vapour density) stochastically, which form the initial population,

3. select groups from the last generation of the population as parents according to a lower-to-higher order of the groups of x corresponding to their fitness values;

4. produce offspring groups from parents by crossover and mutation to make up a new set of approximated solutions (new generation);

5. compute the fitness values of the new generation, go back to step 3 and produce the next generation of the population;

6. terminate the search when a group of approximates meets the requirements of the fitness value. (Generally, we set the stopping criteria for generation or calculation time.)

The parameters of genetic algorithm are listed in Table 1 (Wang et al., 2010). Roulette is a function used for selection in step 3, referring to the concept of a roulette wheel in which the area of each segment is proportional to its expected value, and one of the sections is selected with a random number whose probability equals its area. For the crossover function, “Intermediate” in Table 1 is intended to create offspring groups by a random weighted average of the parents. The mutation process forces the individuals in the population to undergo small random changes that enable the genetic algorithm to search a wider space. Adaptive feasibility is chosen for the mutation function, which means that the adaptive direction is generated randomly with respect to the last successful or unsuccessful generation (Dwivedi and Dikshit, 2013). Based on these steps, the optimal solution of Eq. (10) is derived; that is, the value of x that gives f(x) the minimum value, and also the value of water vapour density in the tomographic equations. To more clearly show the process of water vapour tomography based on a genetic algorithm, a flowchart is shown in Fig. 1.

Table 1 Parameters of the genetic algorithm.

Figure 2 Geographic distribution of GPS, radiosonde stations and the horizontal structure of the voxels used in water vapour tomography. Map data ©2018 Google.

3 Experiment and analysis

3.1 Experiment description

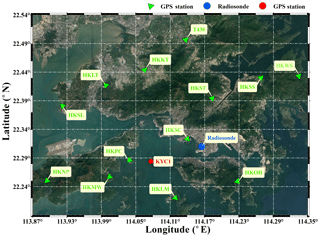
In order to conduct the tomographic experiment based on a genetic algorithm, Hong Kong was selected as the research region. The boundary and resolution in west–east and south–north directions were 113.87–114.35^∘ and 0.06^∘ and 22.19–22.54^∘ and 0.05^∘, respectively; for the altitude direction, 0–8.0 km and 800 m were chosen. A total of $\mathrm{8}\times \mathrm{7}\times \mathrm{10}$ voxels in the tomography grid was obtained. As shown in Fig. 2, 13 GPS stations of the Hong Kong Satellite Positioning Reference Station Network (green triangle) were selected in the tomography modelling to provide SWV measurements. Another GPS station (KYC1, red spot) and radiosonde station (45 005, blue spot) were used to check the result of tomography. Each GPS station recorded temperature, pressure and relative humidity by an automatic meteorological device, by which the hydrostatic parts of the troposphere delay can be accurately achieved. All the stations are under 400 m and located in the first layer of the tomographic grids.

Figure 3 Grayscale graph of number of signal rays passing through each voxel and distribution of voxel with sufficient signal rays (a, b stand for a rainless and a rainy day, respectively).

The GPS tropospheric parameters (zenith tropospheric delay and gradient parameters) were estimated by the GAMIT 10.61 software based on a double-differenced model. In order to reduce the strong correlation of tropospheric parameters caused by the short baseline between GPS receivers in the tomographic area, three International GNSS Service (IGS) stations (GJFS, LHAZ and SHAO) were incorporated into the solution model. In the processing, the sampling rate of observations was 30 s, a cut-off elevation angle of 10^∘ was selected, and the IGS precise ephemeris was adopted. The LC_AUTCLN and BASELINE modes were selected as the processing strategies, meaning that the GPS observation was the ionosphere-free linear combination and the orbital parameters were fixed, respectively. The tropospheric parameters, including troposphere delay gradients and ZTD at 4 and 2 h intervals, are estimated and interpolated to a 30 s sampling rate in the GAMIT software. Note that the outputs of GAMIT are double-differenced residuals and troposphere delay gradients. To obtain the R in Eq. (4), double-differenced residuals should be converted to zero-difference residuals, and multipath effects should be considered by the method proposed by Alber et al. (2000). To achieve the wet delay gradients, Bar-Sever et al. (1998) considered the average of troposphere gradients within 12 h as the dry delay gradients and subtracted it from the troposphere delay gradients. Then all the necessary parameters are available for Eq. (4) to build SWD, and SWV was obtained by Eq. (3).

To verify the proposed method, two periods of GPS observation data, with a sampling rate of 30 s, were used in the tomography experiment. One from 13 to 19 August 2017 (day of year (DOY) of 225 to 231, 2017), during which a spell of fine weather prevailed in Hong Kong with a ridge of high pressure extending westwards from the Pacific to cover south-eastern China on 16–18 August. In that period of time, the daily rainfall was 0 mm. Moreover, the relative humidity and SWV produced in the selected stations on average are 75 % and 79.1 mm, respectively. This period is defined as rainless days. Hence, fine weather occurs without any rainfall. In addition, the relative humidity and SWV are small. The other period is from 12 to 18 June 2017 (DOY of 163 to 169, 2017), which covers the rainy days. During the selected rainy period, the weather of Hong Kong was first affected by the approach and the passage of a severe tropical storm, named Merbok, with more than 150 mm of rainfall recorded on 13–14 June. Thereafter, from 15 and 16 June, the influence of an enhanced southwest monsoon and the development of a lingering through of low pressure made the remaining weather unstable and rainy till 21 June. In this period of time, the maximum daily rainfall is up to 203.7 mm, and the average daily rainfall is 66.8 mm. The average relative humidity and SWV produced in the selected stations are 89 % and 112.9 mm, respectively. This period represents rainy days, indicating that continuous rainfall occurs, and the relative humidity and SWV are high. The period covered is 0.5 h for each tomographic solution. The radiosonde data, collected twice daily at 00:00 and 12:00 UTC in these two periods, were treated as reference data.

According to the flowchart presented in Fig. 1, the above GPS observation data were processed to construct the tomographic equation and further converted into the fitness function for the optimization algorithm. Population size is chosen based on the total number of unknown parameters (water vapour density). The value of 200 is the default option of the algorithm when the number of unknowns exceeds a certain amount. The reproduction of elite count is chosen to be 10 to specify the number of individuals that are guaranteed to survive to the next generation because it is based on population size (0.05 × population size). The crossover fraction is set to the default value of 0.8 to specify the fraction of the next generation that crossover produces. In this study, generation is chosen as the stopping criteria and “100 × number of variables” is the default. Other parameters, including roulette, intermediate and adaptive feasibility, are selected because they are the most commonly used settings for genetic algorithms. Other selection functions as well as crossover and mutation functions can be adopted in the genetic algorithm. In addition, population size, crossover fraction, elite count and stopping criteria can also be set to other values which may slightly affect solution time and results. The specific impact can be explored in depth in future research.

Figure 4 Scatter diagram of the SWV residuals in different weather conditions for internal accuracy testing.

3.2 Analysis of matrix ill condition

In a tomographic solution, the structure of the coefficient matrix in the observation equation depends on which voxels are crossed by SWV and the number of signal rays penetrating each voxel. Figure 3 illustrates this in the form of a grayscale graph for two different days: 13 August 2017 at 00:00 UTC, a rainless day (a), and 13 June 2017 at 12:00 UTC, a rainy day (b). In the upper panels of each sub-figure, the deepening of the grayscale refers to an increase in the number of signal rays crossing through the voxel. The closer the layer is to the ground, the more voxels are not crossed by any signal rays. Although there are few voxels with no signal rays passing through in the upper layers, many of the voxels have a lighter grayscale, which means that the voxels are crossed by fewer signal rays.

Note that when the signal ray passes vertically through the tomographic region, the ray crossed a minimum number of voxels; that is, 10 in the tomographic area. Therefore, the minimum probability that a voxel will be crossed by a ray is 1.79 % (10∕560; 560 is the total number of voxels in this tomographic experiment). Thus 1.79 % of the total SWV is taken as a criteria to further illustrate the structure of the coefficient matrix. If the number is greater than the threshold, the voxel is considered to be crossed by sufficient rays, otherwise the voxel is defined as an insufficient one. For the two examples shown, the number of total SWV and the criteria are 4930∕4569 and 88∕81, respectively. The lower panels of each sub-figure display the distribution of sufficient (black rectangle) and insufficient (white rectangle) ones. Obviously, many voxels are not crossed by enough satellite rays, both for the upper layers or the lower layers.

To better analyse the ill-conditioned nature of the observation equation in tomography modelling, the number of zero elements in matrix A is counted. We found that the proportion of zero element is over 97 % in all tomographic solutions. In addition, the concept of matrix condition number is introduced to measure the degree of dispersion of the eigenvalues of the coefficient matrix (Edelman, 1989). The larger the value of the condition number, the more ill-conditioned the matrix is. The results show that the condition number in every tomographic solution is infinite, which means a serious ill-conditioned problem.

Figure 5 Comparison of SWV residuals in zenith direction: circles for RMSE and diamonds for MAE; blue for rainy days and red for rainless days.

3.3 Internal accuracy testing

To evaluate the performance of water vapour tomography based on a genetic algorithm, slant water vapour of GPS stations for the data of 13 to 19 August and 12 to 18 June 2017 were computed using the tomographic results based on the water vapour tomographic observation equation established in Eq. (1). In this process, the parameters on the right side of Eq. (1) (the distance of the signal ray in each of the voxels and the water vapour density calculated by the tomographic modelling) are taken as known quantities. Moreover, the SWV on the left is the parameter to be determined, i.e. the tomography-computed SWV. The differences against the GAMIT-estimated SWV (as a reference) were also identified.

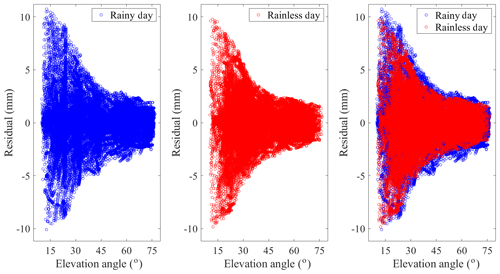
For internal accuracy testing, 13 GPS stations used in the tomographic modelling were adopted. The change of tomography computed vs. GAMIT-estimated slant water vapour residuals with elevation angle is shown in Fig. 4, where the blue and red dots represent the rainy and rainless days, respectively. The maximum residuals for rainy and rainless scenarios are 10.74 and −9.84 mm, respectively. The root mean square error (RMSE) and mean absolute error (MAE) for rainy and rainless days are 1.56∕0.98 and 1.48∕0.89 mm, respectively. Figure 4 shows that most of the residuals are concentrated between −2.0 and 2.0 mm, which indicates good internal accuracy.

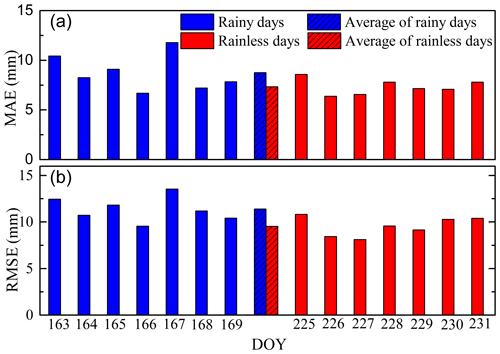
Figure 6 Histogram for MAE (a) and RMSE (b) of SWV residuals (differences between the tomography-computed SWV and GAMIT-estimated SWV) for the KYC1 station, which has not been used in the tomographic modelling (blue for rainy days, red for rainless days).

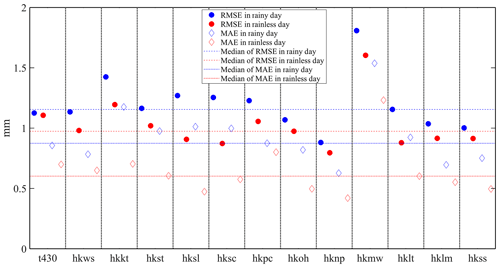
To normalize SWV residuals for their evaluation in a single unit, we mapped the tomography-computed SWVs back to the zenith direction using the 1∕sin (e) formula and computed their differences with the GAMIT-estimated SWV (Michal et al., 2017). Figure 5 shows the statistical results of the residuals in the zenith direction. In the figure, the colours indicate the weather conditions (blue for rainy days and red for rainless days), and the 13 stations were arranged in the order in which they were added to the tomographic model. The maximum and minimum RMSE in the two periods are 0.79 and 1.81 mm, respectively, whereas the maximum and the minimum values for MAE are 0.43 and 1.54 mm, respectively. The RMSE and MAE of rainless days are better than those of rainy days in each station. The medians of RMSE and MAE are displayed for 13 stations to highlight differences among the stations. A particular outlier is the HKMW station, with RMSE and MAE values of 1.81∕1.53 and 1.60∕1.23 mm in rainy and rainless days, respectively. The reason for the divergent behaviour may be that two stations (HKPC and HKMW) exist in the same voxel, which may result in the station (HKPC) data first introduced into the tomographic model affecting the subsequent station (HKMW) data. This hypothesis will be further investigated in future research. However, plots with RMSE and MAE are consistent within 2.0 mm among all the stations (1.5 mm except for HKMW).

Figure 7 Comparison of SWV residuals (differences between the tomography-computed SWV and GAMIT-estimated SWV) for the KYC1 station in each elevation bin; (a,b) for RMSE ∕ MAE; (c, d) for normalized RMSE ∕ MAE.

3.4 External accuracy testing

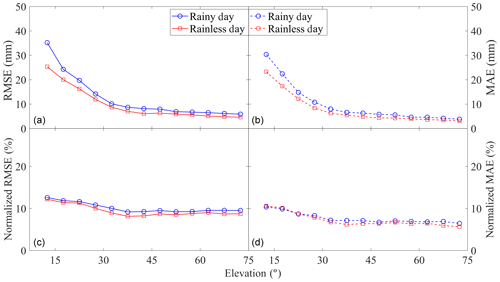
For external accuracy testing, the data from KYC1 station, which was not included in the tomographic modelling, were used. Figure 6 shows the histogram for MAE (upper) and RMSE (lower) of SWV residuals (differences between the tomography-computed SWV and GAMIT-estimated SWV), in which the blue and red bars represent rainy and rainless days, respectively. The dashed bars are the averages for those different weather conditions. From this figure, it can be noted that all MAE and RMSE values are below 15 mm, with average values lower for rainless days than for rainy days, respectively 8.75∕7.33 and 11.38∕9.54 mm for RMSE ∕ MAE. Therefore, a good external accuracy is achieved by tomographic solutions, considering the low RMSE and MAE of rainy and rainless days.

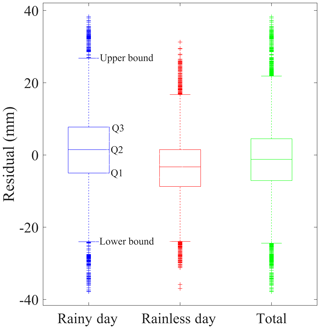
Figure 8 Box plots of the SWV residuals (differences between the tomography-computed SWV and the GAMIT-estimated SWV) for the KYC1 station.

To further assess external accuracy, slant water vapour outputs were grouped into individual elevation bins of 5^∘, i.e. all SWVs with an elevation angle between 10 and 15^∘ were evaluated as a single unit. The RMSE and MAE of each elevation bin were calculated. To examine the dependence of relative errors in SWVs at different elevations, normalized RMSE and MAE were computed. For this computation, residuals of SWV were divided by the GAMIT-estimated SWV and multiplied by 100 to obtain the percentages. Figure 7 shows the variation of RMSE, MAE, normalized RMSE and normalized MAE as the elevation angle changes in different weather conditions. For Fig. 7a and b, the RMSE and MAE reduction of SWV residuals are clearly visible as the increasing elevation angle, which is consistent with the trend shown in Fig. 4. The colours in the figure indicate that better RMSE and MAE results can be achieved on a rainless day than on a rainy day in each elevation bin. In terms of normalized RMSE and MAE, we note that they remain almost constant over all elevation angles, indicating a consistent relative performance of computing SWV in each type of weather condition. It is noted that the normalized RMSE and MAE of rainless days are close to those of rainy days which may be due to the large SWV during rainy days that introduced a large denominator in the normalized calculation. Therefore, the good performance on relative error in SWVs at different elevations with a low normalized RMSE ∕ MAE (<0.125 for normalized RMSE and <0.106 for normalized MAE) points to good external accuracy.

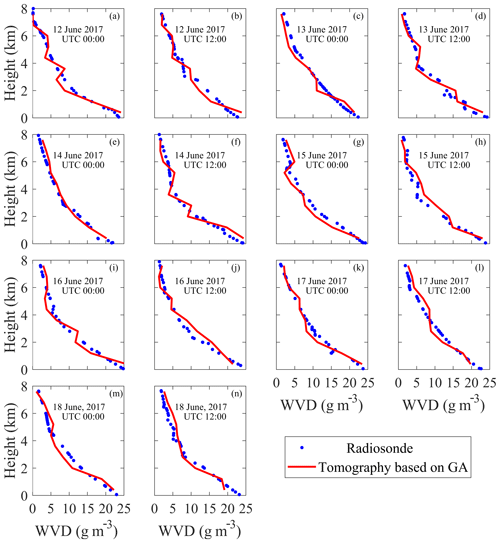
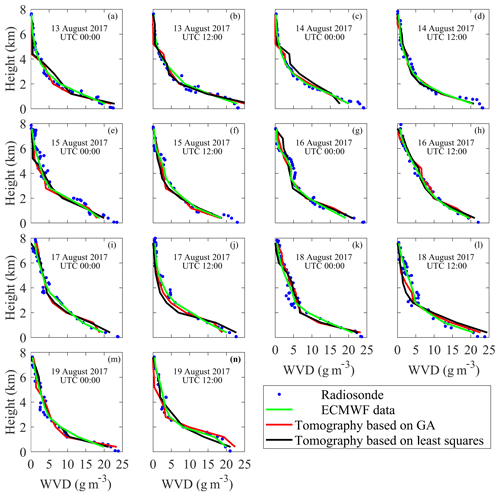
Figure 9 Panels (a)–(n) represent water vapour density comparisons between radiosonde and tomography based on the genetic algorithm at 00:00 and 12:00 UTC from 12 to 18 June 2017 (rainy days).

In the above analysis, RMSE and MAE were used for the external accuracy testing of the tomographic results based on the GA. Box plots are used to explore the statistical characteristics of SWV residuals and to detect the outliers in the tomographic errors. Five characteristic values are shown in the box plots. Q1 and Q3 located at the bottom and top of the box represent the first and third quartiles; the second quartile (Q2) is located inside the box; the ends of the whiskers refer to the upper and lower bounds, which are located at Q1 − 1.5 (IQR) and Q3 + 1.5 (IQR), respectively. IQR is the interquartile range, defined as the difference between Q3 and Q1, and it reflects the discreteness of a set of data. In Fig. 8 the length of the box and the range of bound in rainless days (in red) are smaller than those in rainy days (in blue), indicating better residual distribution in rainless days than in rainy days. The right plot (in green) denotes the result of the combination of rainless and rainy days, representing the overall distribution of SWV residuals of tomography based on a genetic algorithm. In our experiments, 50 % of the residuals are concentrated between −7.08 and 4.47 mm and only 3.24 % of the residuals are outliers when combining the data of rainy and rainless days.

Figure 10 Linear regression of the water vapour density from radiosonde and tomography based on the genetic algorithm. Panels (a), (b) and (c) represent rainy days, rainless days and their combination, respectively.

3.5 Comparison with radiosonde data

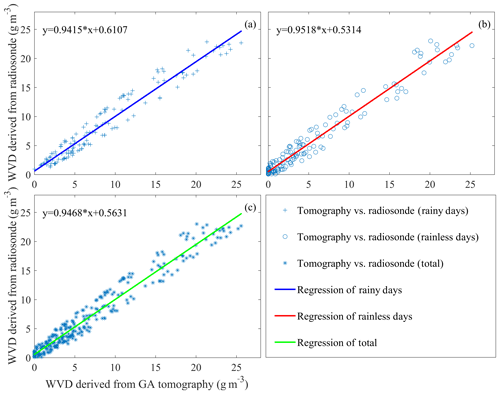
The water vapour density profile derived from the radiosonde data can be used as a reference value, which is well suited to evaluate the accuracy of the tomographic results based on a genetic algorithm. As the radiosondes are launched daily at 00:00 and 12:00 UTC, the tomographic results of 12 to 18 June (rainy days) and 13 to 19 August 2017 (rainless days) at these times were compared. Figure 9 shows the water vapour density comparisons between radiosonde data and tomographic results for different altitudes at individual dates (rainy period). It is clear from the profiles that the water vapour density (WVD) decreases with increasing height. The WVD profiles reconstructed by the GA tomographic solutions conform with those derived from the radiosonde data, especially in the upper troposphere in absolute terms. With respect to the relative error, the values of the voxels higher than 5 km and lower than 5 km are 31 % and 15 %, respectively. The reason for this phenomenon is that the value of water vapour in the upper layers is relatively low. Even a small difference between the radiosonde and tomographic result can also lead to a large relative error, whereas the water vapour content resides for more than 90 % below 5 km near the Earth's surface. In certain cases, a relatively good consistency can also be seen in the lower atmosphere. This may be because a GPS station (HKSC) for tomography modelling is located at the voxel where the radiosonde station is situated, resulting in the low atmosphere with sufficient signal rays passing through.

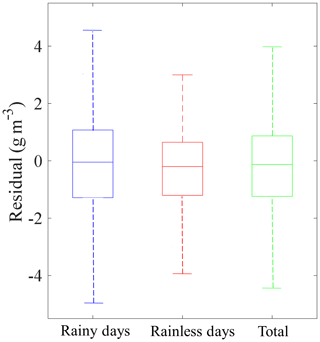
Figure 11 Box plots of the WVD residuals, which are computed between the GA tomographic approach and radiosondes.

Table 2 RMSE and MAE of the water vapour density comparison between radiosonde and tomography based on the genetic algorithm for different weather conditions (g m⁻³).

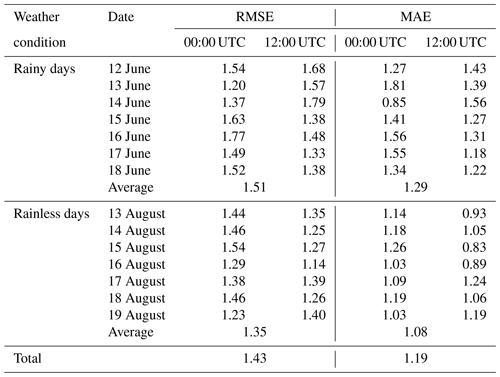
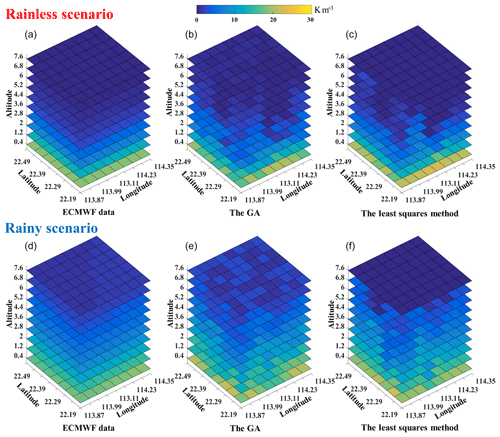
Figure 12 The three-dimensional distribution of water vapour density derived from ECMWF data, the GA method and the least squares method (upper for rainless scenario and lower for rainy scenario).

To further illustrate the comparison with the radiosonde data, Table 2 lists RMSE and MAE of the WVD. In the table, the WVD in the voxels above the radiosonde station computed by tomography and those derived from radiosonde are counted to calculate their RMSE and MAE in each solution. Thus, the average RMSE ∕ MAE of rainless days are 1.35/1.08 g m⁻³, which is smaller than 1.51∕1.29 g m⁻³ in rainy days. This finding is consistent with the comparison of SWV above. We compare those values with the results obtained from other Hong Kong tomographic experiments. For example, Xia et al. (2013) obtained an RMSE of 1.01 g m⁻³ by adding the COSMIC profiles as external data based on a two-step reconstruction. Using the least squares method with horizontal and vertical constraints, Yao et al. (2016) obtained an RMSE of 1.23 g m⁻³ by maximally using GPS observations and an RMSE of 1.60 g m⁻³ without the operation. Zhao et al. (2017) achieved an RMSE of 1.19 and 1.61 g m⁻³ considering the signal rays crossing from the side of the research area and an RMSE of 1.79 g m⁻³ without this consideration. Yao et al. (2017) achieved an RMSE from 1.48 to 1.80 g m⁻³ using different voxel division approaches. Ding et al. (2017) obtained an RMSE of 1.23 g m⁻³ by utilizing the new parametric methods based on inverse-distance-weighted (IDW) interpolation and an RMSE of 1.45 g m⁻³ using the traditional methods, respectively. Note that the RMSE values calculated in the above experiments are based on the radiosonde data. Therefore, the total RMSE of 1.43 g m⁻³ for the two time periods in this paper can be considered to be in good agreement with the radiosonde data regardless of the weather conditions. Moreover, many different settings are applied in tomographic experiments by different groups, such as the selection of tomographic boundary, differences in experimental period and weather conditions, division rule of horizontal and vertical voxel, and addition of other observations.

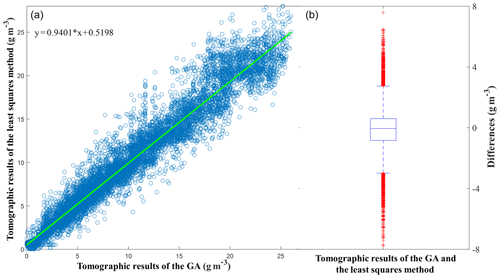
Figure 13 Regression (a) and boxplot (b) for tomographic results (WVD) of the GA and the least squares method.

To explore the overall accuracy of water vapour density reconstructed by the GA tomography, the linear regression analysis and box plot were adopted for different weather conditions. Figure 10 shows the linear regression of the water vapour density for rainy days (Fig. 10a), rainless days (Fig. 10b) and their combination (Fig. 10c), in which the scatter points of three graphs are close to the 1:1 lines. In comparison with the coefficients of regression equations, the results from rainless days are slightly better than those of rainy days. When combining the data of two periods, the starting point of the regression equation is 0.5631 and the slope is 0.9468; water vapour density can be achieved with high accuracy by tomography based on the GA. The corresponding box plots are shown in Fig. 11. It can be noted that the WVD residuals are concentrated in the range of −2 to 2 mm, and the rainless scenario is better than the rainy scenario. The Q1 ∕ Q3 values are $-\mathrm{1.28}/\mathrm{1.08}$, $-\mathrm{1.20}/\mathrm{0.65}$ and $-\mathrm{1.24}/\mathrm{0.87}$ mm for rainy days, rainless days and their combination, respectively. The upper and lower boundaries are located near 4 and −4 mm. No outlier is present in this box plots, probably due to few WVD residuals.

Figure 14 Water vapour density comparisons between GA and the least squares method in the selected voxels at 00:00 and 12:00 UTC from 13 to 19 August 2017 (rainless days); radiosonde and ECMWF data are used as reference.

3.6 Comparison with tomographic results of the least squares method

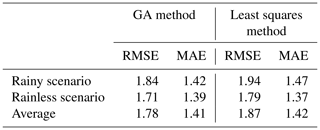
The least squares method is most commonly used in water vapour tomography, and numerous experiments prove that water vapour density with high accuracy can be obtained with this method (Flores, et al., 2000; Zhang et al., 2017; Zhao et at., 2017). To verify the accuracy of the genetic algorithm, we compared the tomographic results between the genetic algorithm and the least squares method in this section. The specific process and introduction to the least squares method can be found in detail in Flores et al. (2000), Guo et al. (2016) and Yang et al. (2018). Figure 12 shows the three-dimensional distribution of water vapour density derived from tomography based on the GA and the least squares method. The water vapour computed by the European Centre for Medium-Range Weather Forecasts (ECMWF) data, which provides various meteorological parameters at different pressure levels with a spatial resolution of $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$, is displayed in the figure as a reference. Here both the GA and the least squares method give a reasonable tomographic result. In certain voxels, the GA achieves the closer results to the ECMWF data, whereas for other voxels, the least squares method performs better. Both methods (the GA and the least squares) generally have a good consistency with ECMWF data regardless of the weather conditions, and they can accurately describe the spatial distribution of water vapour. Additionally, a larger variation of water vapour with altitude occurs in a rainy scenario than in a rainless scenario, especially in the upper atmosphere, which is well captured by the GA and the least squares method. Numerical results including RMSE and MAE during the whole experimental period are listed in Table 3 to show the comparison of the GA and the least squares method, in which the water vapour density derived from ECMWF data is regarded as the true value. It indicates that the result of the GA is a little better than that of the least squares method.

Table 3 Statistical results of the GA and the least squares method comparison; ECMWF data are shown as a reference (g m⁻³).

To further analyse the tomographic results of the GA and the least squares method, regression and boxplot analyses are conducted and displayed in Fig. 13, which covers all solutions, each of them containing 560 voxel results. In Fig. 13a, a good linear regression relationship is shown by the distribution of scatter points and the straight line of regression. Specifically, the starting points of the regression equation and the slope are 0.5198 and 0.9401, respectively. The right panel shows the distribution of differences between the two types of tomographic results. The Q1 and Q3 are −0.84 and 0.60 g m⁻³, respectively, which means that more than 50 % of the differences between the two methods are within 1 g m⁻³. The upper and lower bounds are 2.75 and −2.98 g m⁻³, respectively, and outliers only account for 3.11 %. Consequently, the tomographic results based on the GA are in agreement with those of the least squares method for this experiment. A reliable tomographic result can be achieved by the GA without being restricted by constraint equations and matrix inversion like the traditional least squares method.

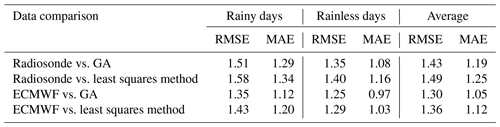
Moreover, a detailed comparison between GA and the least squares method is conducted using the voxels above the radiosonde station. Figure 14 shows the changes in water vapour density derived from GA and the least squares method with altitudes in different days (rainless days), in which the radiosonde data and ECMWF data are considered reference data. All the profiles derived from the two methods decrease with increasing height and show good consistency with the reference data. The statistical values are computed and listed in Table 4 to illustrate the comparison of GA and the least squares method. The RMSE and MAE indicate that both the GA and the least squares method can achieve good tomographic results compared with the reference values (radiosonde and ECMWF data) whether in the rainy or rainless scenario. The GA which has an average RMSE ∕ MAE of 1.43∕1.19 and 1.30∕1.05 g m⁻³ compared with radiosonde and ECMWF data, respectively, performs slightly better than the least squares method, of which the average RMSE ∕ MAE are 1.49∕1.23 and 1.36∕1.12 g m⁻³.

Table 4 Statistical results of the GA and the least squares method using radiosonde and ECMWF data as reference in the selected voxels (g m⁻³).

Figure 15 Changes in water vapour density with altitude in different weather conditions; data are from radiosonde measurements (blue for rainy days from 12 to 18 June 2017 and red for rainless days from 13 to 19 August 2017).

3.7 Analysis of results in different weather conditions

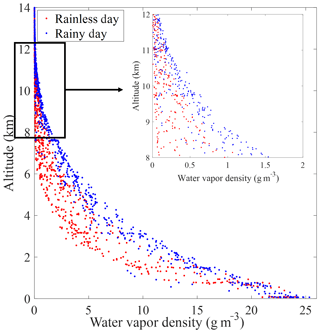
In our experiments, the comparisons under various weather conditions illustrate that the tomographic result of rainless scenarios was better than rainy scenarios, which is also concluded in other studies (Yao et al., 2016; Zhao et al., 2017; Ding et al., 2017). This result is because the spatial structure of atmospheric water vapour is relatively stable in rainless weather, whereas its spatial distribution changes faster in rainy weather. Thus, certain limitations are imposed on tomography to obtain accurate water vapour during unstable weather conditions. Additionally, all the water vapour densities along the radiosonde path were collected during the experiments. Their changes with altitude are shown in Fig. 15, in which the rainy and rainless weather are represented by blue and red dots, respectively. The situation of 8–12 km is magnified to show the water vapour information outside the tomographic region. In the figure, the larger value of WVD can be observed above 8 km in rainy days compared with that of rainless days. For the rainless situation, the value of WVD within 8–12 km is small and near to zero. By contrast, the value is basically not close to zero in the rainy situation, especially in the range of 8–10 km, which is substantially greater than 0.5 g m⁻³. Referring to the selection of the tomographic heights in other articles, considering the long-term statistics of water vapour in Hong Kong, and taking into account the drawbacks of the excessive number of tomographic voxels, we selected 8 km as the top boundary of the research area in this paper, which ignores the water vapour information above 8 km in our tomographic model. Obviously, it has limited influence on the accuracy of the tomographic result in rainless weather condition. For the rainy weather condition, the effect could be slightly larger, which is one reason why the tomographic results of rainy days were worse than those of rainless days in our experiments.

4 Conclusions

In this paper, a new tomography approach based on the genetic algorithm was proposed to reconstruct a three-dimensional water vapour field in Hong Kong under rainy and rainless weather conditions. The inversion problem was transformed into an optimization problem that no longer depends on excessive constraints, a priori information or external data. Thus, many problems do not need to be considered, including the difficulty of inverting the sparse matrix, the limitation and irrationality of constraints, the weakening of tomographic technique by prior information, and the restriction of obtaining external data. Based on the fitness function established by the tomographic equation, the water vapour tomographic solution could be achieved by the genetic algorithm through the process of selection, crossover and mutation.

Our new approach is validated by tomographic experiments using GPS data collected over Hong Kong from 12 to 18 June (rainy days) and 13 to 19 August 2017 (rainless days). The problem of matrix ill condition was discussed and analysed by the grayscale graph and condition number. In a comparison of the SWV residuals, internal and external accuracy testing were used for the GA tomography. The internal accuracy testing refers to computing the differences between the tomography-computed SWV and GAMIT-estimated SWV for the 13 GPS stations used in the tomographic modelling, whereas the external accuracy testing denotes the differences for the KYC1 station which is not included in the tomographic modelling. The RMSE ∕ MAE of SWV residuals are 1.52∕0.94 and 10.07∕8.44 mm for the internal and external accuracy testing, respectively. Thus, a good tomographic result is achieved. In addition, the water vapour density of the proposed method agreed with that of radiosonde. The RMSE and MAE are 1.43 and 1.19 g m⁻³, whereas the starting point and the slope of the regression equation are 0.5631 and 0.9468, respectively. ECMWF data are utilized to display the three-dimensional distribution of tomographic results. The least squares method is selected as the representative of the traditional tomographic method to compare with the GA. A good consistency is demonstrated in terms of RMSE, MAE, linear regression and boxplot. Thus, a reliable tomographic result can be achieved by the GA without being restricted by constraint equations and matrix inversion like the traditional least squares method. Moreover, the comparison under various weather conditions illustrated that the tomographic result of the rainless scenario was better than that of the rainy scenario, and the reasons were discussed. In a future study, the tomography approach based on the genetic algorithm, which is not dependent on constraints, a priori data and external data, could provide potential interest for the establishment of a real-time or near-real-time water vapour tomographic system.