Advanced hodograph-based analysis technique to derive gravity-wave parameters from lidar observations

An advanced hodograph-based analysis technique to derive gravity-wave (GW) parameters from observations of temperature and winds is developed and presented as a step-by-step recipe with justification for every step in such an analysis. As the most adequate background removal technique the 2-D FFT is suggested. For an unbiased analysis of fluctuation whose amplitude grows with height exponentially, we propose applying a scaling function of the form exp (z∕(ςH)), where H is scale height, z is altitude, and the constant ς can be derived by a linear fit to the fluctuation profile and should be in the range 1–10. The most essential part of the proposed analysis technique consists of fitting cosine waves to simultaneously measured profiles of zonal and meridional winds and temperature and subsequent hodograph analysis of these fitted waves. The linear wave theory applied in this analysis is extended by introducing a wave packet envelope term $\exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})$ that accounts for limited extent of GWs in the observational data set. The novelty of our approach is that its robustness ultimately allows for automation of the hodograph analysis and resolves many more GWs than can be inferred by the manually applied hodograph technique. This technique allows us to unambiguously identify upward- and downward-propagating GWs and their parameters. This technique is applied to unique lidar measurements of temperature and horizontal winds measured in an altitude range of 30 to 70 km.

1 Introduction

It is generally accepted that atmospheric gravity waves (GWs) produce global effects on the atmospheric circulation from the surface up to the mesosphere and lower thermosphere (MLT) region (e.g., Fritts and Alexander, 2003; Alexander et al., 2010; Becker, 2017). Well-known tropospheric sources for these waves are the orography (flows over mountains), convection and jet imbalance (e.g., Subba Reddy et al., 2005; Alexander et al., 2010; Mehta et al., 2017). When propagating upwards, GWs dissipate and thereby deposit their momentum starting from the troposphere and reaching all the way up to the MLT. This process is referred to as GW forcing and plays a key role in the global circulation. Most of the climate models are not able to resolve these small-scale waves (i.e., waves with horizontal wavelengths typically shorter than 1000 km; e.g., Kim et al., 2003; Geller et al., 2013). That is why these waves and their dissipation (and also their interaction with each other and with the background flow) are often called “sub-grid-scale processes” (e.g., Shaw and Shepherd, 2009; Lott and Millet, 2009). In order to account for the influence of GWs, these models need to rely on various parameterizations. To construct a proper parametrization one has to describe GW frequencies, wavelengths and momentum flux over the model coverage zone (e.g., Alexander et al., 2010; Bölöni et al., 2016).

Our knowledge about gravity-wave parameters can be improved by means of high-resolution measurements of atmospheric GWs. Ideally, the measurement range should cover the entire path of the waves, starting from their sources in the troposphere to the level of their dissipation that is up to the MLT region. This type of measurement ultimately faces high experimental challenges, which explains why we still do not have satisfactory and conclusive observational data on these processes.

In the altitude range of the mesosphere only a few observation techniques exist. In the last decades the only source of high-resolution GW observations based on both temperatures and winds in the stratosphere and mesosphere region were rocket soundings (see, e.g., Schmidlin, 1984; Eckermann and Vincent, 1989; Lübken, 1999; Rapp et al., 2002, and references therein). Rocket measurements with falling spheres, for example, can provide vertical profiles of horizontal winds and atmospheric temperatures and densities with an altitude resolution of about 1–10 km.

Satellite-borne remote-sensing techniques can provide excellent global coverage; their observations deliver unique horizontal information about GWs (see, e.g., Alexander et al., 2010; Alexander, 2015; Ern et al., 2018), but they are based solely on temperature observations.

Ground-based radar systems are able to measure winds at heights of 0–30 and 60–100 km. From the altitudes between 30 and 60 km radars do not receive sufficient backscatter and, therefore, cannot provide wind measurements in this region. While the vertical wave structure can be resolved from rocket profiles, the long and irregular time intervals between successive launches prevent the study of temporal gravity-wave fluctuations over a larger time span (Eckermann et al., 1995; Goldberg et al., 2004).

Recent developments in lidar technology give us new possibilities to study GWs experimentally on a more or less regular basis and resolve spatial sales of 150 m on vertical and temporal scales of 5 min (e.g. Chanin and Hauchecorne, 1981). In particular, the daylight lidar capabilities allow for long-term wave observations (e.g., Baumgarten et al., 2015, 2018). The new Doppler Rayleigh Iodine Spectrometer (DoRIS) in addition to the established lidar temperature measurements yields simultaneous, common-volume measurements of winds (Baumgarten, 2010; Lübken et al., 2016). This combination of capabilities makes the lidar data unique.

All those quantities, i.e. winds and temperature, when measured with high temporal and spatial resolution, reveal structuring at scales down to minutes and hundreds of meters. In our analysis technique we focus solely on such fluctuations which are generated by GWs. By applying a proper data analysis technique, one can extract several important parameters of GWs from the advanced lidar measurements.

In this paper we describe a newly developed analysis technique which allows for derivation of GW parameters such as vertical wavelength, the direction of propagation, phase speed, kinetic and potential energy, and momentum flux from the advanced lidar measurements. We aim at presenting a step-by-step recipe with justification of every step in such an analysis. Every single step, if considered independently, is in general well known. The strength and novelty of our work is their combination and some justification on their importance and how they affect analysis results. The paper is structured as follows. In the next section a short description of the lidar measurement technique is given. The theoretical basis used by the data analysis technique is shortly summarized in Sect. 3 and extended in Appendix A. Section 4 describes the new methodology in detail. Finally, in Sect. 5 geophysically meaningful quantities are deduced from the analyzed data, which also demonstrates the capabilities of the introduced analysis technique.

2 Instrumentation

The ALOMAR Rayleigh–Mie–Raman lidar in northern Norway (69.3^∘ N, 16.0^∘ E) is a Doppler lidar that allows for simultaneous temperature and wind measurements in the altitude range of about 30 to 80 km. The lidar is based on two separate pulsed lasers and two telescopes (von Zahn et al., 2000). Measurements are performed simultaneously in two different directions, typically 20^∘ off zenith towards the north and the east by pointing the telescopes and the outgoing laser pulses in this direction. The diameter of each telescope is about 1.8 m, and the average power of each laser is ∼14 W at the wavelength of 532 nm. Both pulsed lasers operate with a repetition rate of 30 Hz and are injection seeded by one single continuous-wave laser that is locked to an iodine absorption line. The light received by both telescopes is coupled alternatingly into one single polychromatic detection system. Temperatures and winds are derived using the Doppler Rayleigh Iodine Spectrometer (Baumgarten, 2010). As the measurements discussed below are performed also under daytime conditions, we process the data as described in Baumgarten et al. (2015). Measurements by the lidar were extensively compared to other instruments, showing the good performance of the lidar system (Hildebrand et al., 2012; Lübken et al., 2016; Hildebrand et al., 2017; Rüfenacht et al., 2018). The lidar data are recorded with an integration time of 30 s and a range resolution of 50 m. The data are then integrated to a resolution of 5 min and 150 m and afterwards smoothed with a Gaussian window with a full width at half maximum of 15 min and 0.5 km. For calculation of horizontal winds from the measured line-of-sight winds we assume that the vertical wind component is equal to zero. Importantly, the estimated uncertainty imposed by this assumption is negligible and does not affect final results of our analysis. The hydrostatic temperature calculations were seeded using measurements from the IAP mobile Fe resonance lidar, and the temperatures from both lidar systems were then combined by calculating an error-weighted mean (Lautenbach and Höffner, 2004).

3 Brief theoretical basis

A GW field consists of various waves with different characteristics. An attempt to describe this system as a whole is made, for example, by Stokes analysis (e.g., Vincent and Fritts, 1987; Eckermann, 1996). In this work we do not try to describe bulk fluctuations but rather to extract the single most dominant quasi-monochromatic gravity waves (QMGWs) from the set of the observed fluctuations. The advantage of this approach is that it allows us to describe these selected waves as precisely as possible by the linear theory of GWs. Moreover, the main idea of our retrieval is finding GW packets where fluctuations of the both wind components, i.e. where zonal and meridional wind (u^′ and v^′), as well as temperature fluctuations T^′, show the same characteristics, i.e., belonging to the same wave packet. This requirement ensures that our analysis only accounts for wave structures and not for those created by accompanying dynamical processes like turbulence or other wave-like structures created by, for example, temperature inversion layers (e.g., Szewczyk et al., 2013).

For this analysis we use the assumption that a wave packet at a fixed time point and in a limited altitude range can be considered to be QMGWs, i.e., dispersion within one wave packet is neglected. Also we assume that all the observed parameters ($T,u,v$) reveal fluctuations ($T^{\prime },u^{\prime },v^{\prime }$) at the same wavelength. Mathematically it can be written in the following form (see Appendix A for more details):

$$\begin{array}{}\text{(1)}& {\mathit{\vartheta }}^{\prime }=\left|\widehat{\mathit{\vartheta }}\right|\cdot \cos \left(m\right(z-z_{\mathrm{0}})+{\mathit{\phi }}_{\mathit{\vartheta }})\cdot \exp (z/\mathrm{2}H),\end{array}$$

where ϑ refers to either temperature (ϑ≡T), zonal or meridional wind components (ϑ≡u or ϑ≡v); prime variables describe fluctuations (T^′, u^′, v^′) and $\widehat{\mathit{\vartheta }}$ is the amplitude of those fluctuations; φ_ϑ is the phase shift; m is the vertical wave number (${\mathit{\lambda }}_z=\mathrm{2}\mathit{\pi }/m$ is vertical wavelength); and H is the scale height.

Equation (1) is an ansatz which describes an ideal monochromatic GW under the conditions of conservative propagation in a constant background. A similar description of GW propagation is widely used in the literature (see, e.g., Gavrilov et al., 1996). Since most GWs propagate oblique through the field of view of the ground-based instruments, they appear in the observations as waves of a limited vertical extent, i.e., as wave packets. Hence any vertically propagating waves might appear in nature in the form of wave packets rather than continuous waves of quasi-infinite length. Therefore we extend the Eq. (1) by introducing a wave packet envelope term $\exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})$ that accounts for the limited presence of the GW packet in observations:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathit{\vartheta }}^{\prime }=& \left|\widehat{\mathit{\vartheta }}\right|\cdot \exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})\cdot \cos (m(z-z_{\mathrm{0}})\\ +& {\mathit{\phi }}_{\mathit{\vartheta }})\cdot \exp (z/\mathrm{2}H),\end{array}\end{array}$$

where σ is a factor that describes the width of wave packet and z₀ is the altitude of maximum of wave envelope (its central altitude).

Following Cot and Barat (1986) or Gavrilov et al. (1996), for example, the horizontal propagation angle of a QMGW can be defined as

$$\begin{array}{}\text{(3)}& \mathit{\xi }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathit{\pi }n+\arctan ({\displaystyle \frac{\mathrm{2}{\mathrm{\Phi }}_{uv}}{{\widehat{v}}^{\mathrm{2}}-{\widehat{u}}^{\mathrm{2}}}}\left)\right),\end{array}$$

where ξ is the azimuth angle of the wave propagation direction and ${\mathrm{\Phi }}_{uv}=\widehat{u}\cdot \widehat{v}\cdot \cos ({\mathit{\phi }}_u-{\mathit{\phi }}_v)$. The integer n is 1 when $\widehat{v}<\widehat{u}$. When $\widehat{v}>\widehat{u}$, n=0 and 2 for Φ_uv>0 and Φ_uv<0, respectively. This implies that for ${\mathit{\phi }}_u-{\mathit{\phi }}_v=\mathit{\pi }/\mathrm{2}$ the propagation direction can be 0 or 180^∘, i.e. northward or southward if $\widehat{v}>\widehat{u}$ and eastward or westward if $\widehat{v}<\widehat{u}$. The sign of m in Eqs. (1) and (2) shows the vertical propagation direction: m<0 for upward-propagating and m>0 for downward-propagating GWs.

This theoretical basis allows us to describe the main GW parameters and to derive them from observations. However, in practice, noisy data and/or insufficient resolution of measurements may lead to large uncertainties when applying these equations directly to the measured time series. Therefore, the most common technique, based on linear theory of gravity waves to derive the propagation direction, intrinsic frequency and phase velocity of GWs from ground-based observations, is the hodograph method (e.g., Sawyer, 1961; Cot and Barat, 1986; Wang and Geller, 2003; Zhang et al., 2004; Baumgarten et al., 2015). The hodograph technique explicitly utilizes the following polarization relations of GWs for winds and temperature.

For mid- and low-frequency GWs the velocity perturbations in the propagation direction and perpendicular to this direction are related by the polarization relation (e.g. Gavrilov et al., 1996; Fritts and Alexander, 2003; Holton, 2004):

$$\begin{array}{}\text{(4)}& {\widehat{v}}_{\perp }=-i(f/\widehat{\mathit{\omega }}){\widehat{u}}_{\Vert },\end{array}$$

where ${\widehat{v}}_{\perp }$ is the complex amplitude of wind fluctuations in the direction perpendicular to the direction of propagation and ${\widehat{u}}_{\Vert }$ is amplitude of wind fluctuations along the propagation direction. f=2Ωsin Φ is the Coriolis parameter, and $\widehat{\mathit{\omega }}$ is the intrinsic frequency – that is, for a zonally propagating wave, ${\widehat{v}}_{\perp }$ is the meridional velocity amplitude.

If we assume that $\widehat{\mathit{\theta }}/\stackrel{\mathrm{‾}}{\mathit{\theta }}=\widehat{T}/T_{\mathrm{0}}$ (Fritts and Rastogi, 1985; Eckermann et al., 1998), the temperature amplitude is related to the parallel wind amplitude for a wave propagating in the zonal direction ((e.g.,; Hu et al., 2002; Geller and Gong, 2010)):

$$\begin{array}{}\text{(5)}& \widehat{T}={\displaystyle \frac{im{T}_{\mathrm{0}}}{g}}{\displaystyle \frac{{\widehat{\mathit{\omega }}}^{\mathrm{2}}-f^{\mathrm{2}}}{\widehat{\mathit{\omega }}{k}_h}}\cdot {\widehat{u}}_{\Vert }={\displaystyle \frac{i{T}_{\mathrm{0}}}{g}}{\displaystyle \frac{\sqrt{{\widehat{\mathit{\omega }}}^{\mathrm{2}}-f^{\mathrm{2}}}}{\widehat{\mathit{\omega }}}}\sqrt{N^{\mathrm{2}}-{\widehat{\mathit{\omega }}}^{\mathrm{2}}}\cdot {\widehat{u}}_{\Vert },\end{array}$$

where $k_h=\mathrm{2}\mathit{\pi }/{\mathit{\lambda }}_h$ is the horizontal wave number and λ_h is the horizontal wavelength of the QMGW, $\widehat{\mathit{\theta }}/\stackrel{\mathrm{‾}}{\mathit{\theta }}$ is potential temperature perturbations, T₀ and g are the background temperature and the acceleration due to gravity averaged over the altitude range of the QMGW, and N is the buoyancy frequency of background atmosphere estimated from T₀.

To summarize, the basic theory, briefly described in this section, allows us to derive the main GW parameters: intrinsic frequency, amplitude and the direction of propagation. From these parameters one can derive a more extended set of GW parameters: horizontal and vertical phase speed, group velocity, kinetic and potential energy, and vertical flux of horizontal momentum, as summarized in Appendix A.

4 Retrieval algorithm

In this section we describe the procedure for deriving wave parameters from the measured lidar data. For our analysis we need simultaneously measured wind and temperature profiles. Technically we can extract wave parameters from a single measurement – that is, using two wind and one temperature profile. However, for a robust estimation of the atmospheric background we need an observational data set that is several hours long.

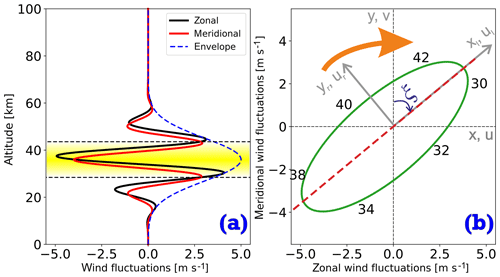
Figure 1 Schematics of the method. (a) Altitude profile of horizontal velocity fluctuations. Blue dashed line demonstrates an envelope. Colored area marks altitude range of one wavelength where wave amplitude is most significant ($[z_{\mathrm{0}}-{\mathit{\lambda }}_z/\mathrm{2},z_{\mathrm{0}}+{\mathit{\lambda }}_z/\mathrm{2}]$). (b) Hodograph ellipse of GW horizontal velocity variations taken from altitude range marked in plot (a). Dashed line shows major axis of ellipse, which is a propagation direction of the wave. Numbers around ellipse are altitudes. These schematics have a clockwise rotation.

4.1 Separation of GWs and background

The first step is to remove the background from the measured data. The background removal procedure plays a key role in GW analysis techniques and may even lead to strongly biased results. This is because most analysis techniques rely on fluctuation's amplitudes remaining after subtraction of the background to infer wave energy (e.g., Rauthe et al., 2008; Ehard et al., 2015; Baumgarten et al., 2017; Cai et al., 2017, and others). Since the GW energy is proportional to the amplitude squared, any uncertainty in the background definition ultimately leads to large biases in estimation of GW energy.

We define the background as fluctuations with periods and vertical wavelengths longer that typical GW parameters. This means that tidal fluctuations and planetary waves are attributed to the background. Tidal periods are integer fractions of a solar day. Semidiurnal tides have period of 12 h, and the Coriolis period (2π∕f) at 69^∘ N is 12.8 h. On the other hand, typical vertical wavelengths of GWs were summarized in Table 2 of Chane-Ming et al. (2000) and do not exceed 17 km.

Thus, we define the background as wind or temperature fluctuations with periods longer than 12 h and vertical wavelengths larger than 15 km. Fluctuations with periods shorter than 12 h, which have any vertical wavelength (also greater than 15 km), are attributed to GWs and are the subject of further analysis.

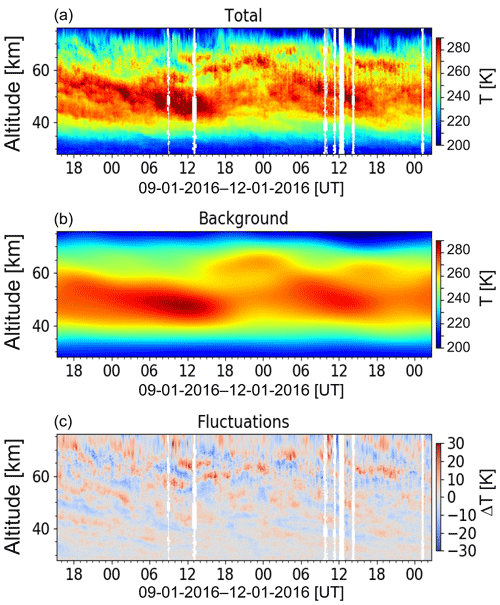
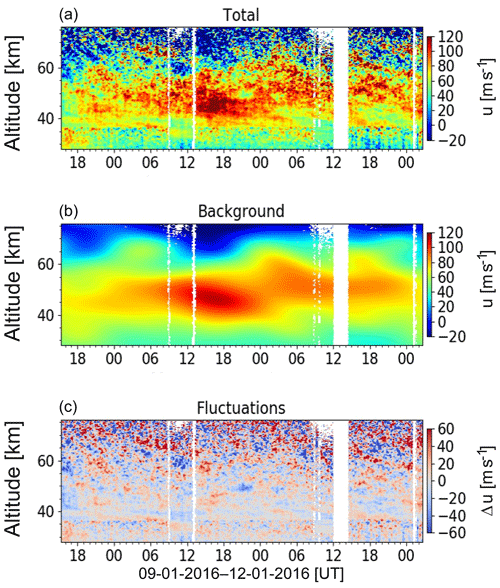
Figure 2 Temperature observations. (a) demonstrates temperature observations obtained from 9–12 January 2016. In (b) background obtained by 2-D FFT is demonstrated. (c) shows remaining small-scale fluctuations used for GW analysis. White vertical lines represent gaps in the measured data.

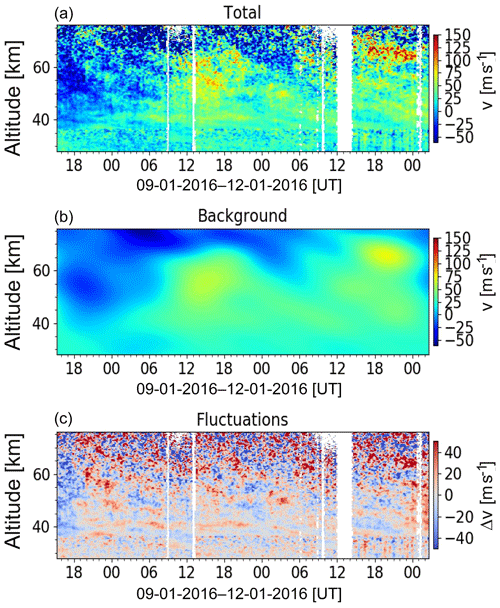
To extract such a background from measurements, we apply a low-pass filter to the altitude vs. time data. Specifically, we use the two-dimensional fast Fourier transform ((2-D FFT; e.g., González and Woods, 2002), and, after blocking the specified high frequencies and short wavelengths and applying the inverse 2-D FFT, we finally construct the background. The advantage of this method is that it simultaneously accounts for both variability in space and time. After subtracting the derived background from the original measurements we obtain the wind and temperature fluctuations which have periods shorter than 12 h or wavelengths smaller than 15 km and are supposedly produced by gravity waves. This procedure is demonstrated in Figs. 2, 3 and 4 for temperature, zonal and meridional wind, respectively. The upper, middle and lower panels represent the original measured quantities, estimated background and the resultant fluctuations, respectively. These time–altitude plots consist of many single-time (“instant”) altitude profiles which are further analyzed individually. More specifically, fluctuations T^′, u^′ and v^′ are analyzed with our automated hodograph method.

Figure 3 The same as Fig. 2 but for zonal wind observations.

We also performed a robustness test to check how different background removals influence our advanced hodograph-based method. To derive the background (for both wind and temperature data) we additionally made use of (a) a running mean with different smoothing window lengths, (b) different splines and (c) constant values in time. It turned out that our analysis results were near identical for all these different backgrounds. The new technique is not sensitive to the background derivation schemes and may even allow us to skip this step from the analysis or to apply simple methods. A more in-depth analysis showed that the robustness to the background removal is a consequence of the analysis approach. We only search for waves which are prominent simultaneously in temperature and both wind components. Even though we are confident in the robustness of our GW analysis technique to the various background derivation methods, we need a well-defined and well-behaved (i.e. continuous and smooth) background (1) to derive the basic parameters of atmosphere like buoyancy frequency and wind shear and (2) to find out how the background wind and temperature fields affect (or at least correlate with) the GW field. Thus, we consider the 2-D-FFT-based approach to be the one most adequate for this purpose.

Figure 4 The same as Fig. 3 but for meridional wind observations.

4.2 Scaling of fluctuations

Under the assumptions of conservative propagation (i.e., without wave breaking and dissipations) in the isothermal atmosphere without background winds, the amplitude of fluctuations increases with altitude as exp (z∕(2H)). In the real observations, since waves cannot freely propagate throughout the atmosphere, the amplitude of the fluctuations increases with altitude as exp (z∕(ςH)), where the coefficient ς≥2 is derived from the observed data. The exponential growth, however, also affects any analysis, in particular wavelet analysis, since normalization is always applied. The growing amplitude works as a weighting function, and, therefore, the largest amplitudes will dominate the analysis (e.g., spectrum), thereby hiding the small-amplitude waves (see also Wright et al., 2017, who pointed out a similar effect in the satellite data). This effect, in particular, prohibits analysis of small-scale features at lower altitudes. Scaling the fluctuations by $\mathrm{1.0}/\exp (z/(\mathit{\varsigma }H\left)\right)$ yields fluctuations with comparable amplitudes over the whole altitude range. For the observations presented here, we derived ς=2.15. Note, however, if further analysis requires treatment of fluctuation amplitudes, this scaling must be either taken somehow into account (e.g., by appropriate normalization) or removed (by applying inverse scaling) as we do in Sect. 4.7.

Figure 5 Wavelet transform of zonal and meridional wind and temperature fluctuations at 02:07 UT on 10 January 2016.

4.3 Detection of wave packets

Starting from this point we only analyze the altitude profiles at every time step. At every time step we have measured profiles of wind and temperature, which are split into fluctuations and background profiles.

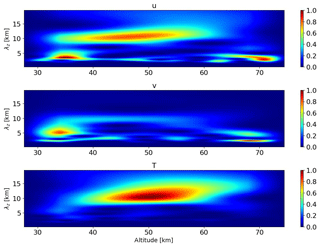
First, we search for dominant waves in both altitude and wave-number domains. For this purpose we apply the continuous wavelet transform (CWT) to every profile of the extracted fluctuations. We use a Morlet wavelet of the sixth order (Torrence and Compo, 1998) and apply it to the vertical profiles of wind and temperature fluctuations. Similar procedure was also applied by Zink and Vincent (2001) and Murphy et al. (2014). By applying wavelet analysis they define regions from which the Stokes analysis (e.g., Vincent and Fritts, 1987; Eckermann, 1996) is further evaluated with better precision. We note here that their results rely on the accuracy of wavelet transform and on the assumption that wave signatures are well separated from each other and clearly resolved by the CWT.

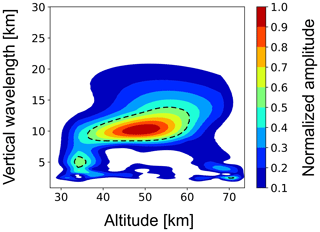
An example of the resulting scalograms for one time step is shown in Fig. 5. These scalograms are normalized to unity to make spectral signatures comparable between the different fluctuations. In zonal wind and temperature fluctuations, a clear peak between ∼40 and ∼55 km with a vertical wavelength of approximately 10 to 15 km can be seen. Both wind components reveal peaks below ∼40 and above ∼60 km, with wavelengths of about 5 km. As a next step we combine these wavelet spectra and construct a single scalogram that reflects the features common for all three components. We calculate the product of all three spectra and define this as the combined spectrum. Note that Zink and Vincent (2001) and Murphy et al. (2014) used the sum of scalograms of both wind components. The combined scalogram in Fig. 6 reveals one large (around 10 km wavelength) and two smaller (near 35 and 70 km altitude) regions with weaker wave amplitudes. The larger region is relatively broad and reveals a vertical wavelength increase with increasing altitude. This can be due to two reasons: (1) it is one wave packet with changing vertical wavelength due to variable background or (2) it is a sum of two wave packets with overlap at around 50 km altitude. This uncertainty is difficult to resolve by just using the information from wavelet transform. To resolve this ambiguity we developed a sequence of further analysis steps and only use these CWT results as an input (zero guess) for further analysis.

Figure 6 Combined wavelet transform of profiles shown in Fig. 5.

4.4 Fitting of linear wave theory

In this step we fit a wave function to all three measured profiles, i.e., $u^{\prime }\left(z\right),v^{\prime }\left(z\right)$ and T^′(z). The wave function was derived from the linear wave theory as summarized in Sect. 3 and in Appendix A. Note that the wave function described by Eq. (1) includes the scaling factor exp (z∕(2H)). After applying the scaling $\mathrm{1}/\exp (z/(\mathit{\varsigma }H\left)\right)$ to fluctuation profiles as described in Sect. 4.2, we get rid of exponential growth in those profiles. Therefore, we have to exclude this scaling factor from the wave equation. The wave function that we fit to the profiles $u^{\prime }\left(z\right),v^{\prime }\left(z\right)$ and T^′(z) reads

$$\begin{array}{}\text{(6)}& {\mathit{\vartheta }}^{\prime }=\left|\widehat{\mathit{\vartheta }}\right|\cdot \exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})\cdot \cos (m(z-z_{\mathrm{0}})+{\mathit{\phi }}_{\mathit{\vartheta }}),\end{array}$$

where ϑ refers to u,v and T.

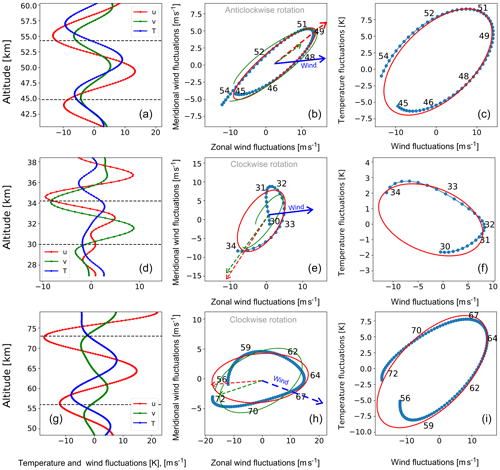
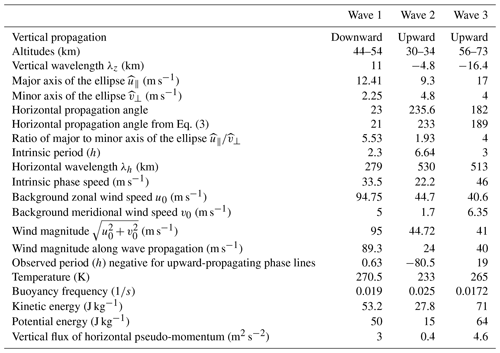
Figure 7 (a), (d) and (g) are vertical profiles of observed fluctuations of both wind components and temperature observed at 02:07 UT on 10 January 2016, and dashed lines mark the altitude range used for the hodographs. Hodographs of (b), (e) and (h) are the zonal wind versus meridional wind fluctuations, and (c), (f) and (i) are the parallel wind fluctuations ($u_{\Vert }^{\prime }$) versus temperature fluctuations. Further quantities of the GW, and the background are listed in Table 1.

The fit can be performed using a least-squares regression algorithm implemented in numerous routines. The data (measurements) to which the wave function is to be fitted are the three profiles $u^{\prime }\left(z\right),v^{\prime }\left(z\right)$ and T^′(z). The fit must converge for all three profiles to be qualified as successful. The free fitting parameters are the central altitude of the wave packet z₀, width of the wave packet σ, wavelength of oscillations in this wave packet λ_z, amplitude of fluctuations in the wave packet $\left|\widehat{\mathit{\vartheta }}\right|$ and the phase shift φ_ϑ. The initial guess for parameters λ_z,z₀ and σ is estimated from the wavelet scalogram derived in the previous step. The zero guess for the amplitude $\left|\widehat{\mathit{\vartheta }}\right|$ is directly derived from the fluctuation profile as the maximum amplitude in the height range $z_{\mathrm{0}}\pm {\mathit{\lambda }}_z/\mathrm{2}$. The initial value for the phase shift φ_ϑ is taken randomly.

Thus, to derive the first set of initial parameters λ_z,z₀ and σ, we start with the larger area encircled by the dashed lines in Fig. 6 and pick up the values λ_z=12 km, z₀=45 km and σ=15 km. The initial amplitude for zonal wind fluctuations estimated from the red profile in Fig. 7a $\left|\widehat{u}\right|$ is 10 m s⁻¹. The fit of Eq. (1) to the temperature and two wind profiles will yield a set of parameters that describe a wave packet: λ_z, z₀, σ, $\left|\widehat{u}\right|$, $\left|\widehat{v}\right|$, $\left|\widehat{T}\right|$, φ_u, φ_v and φ_T.

Thus, the updated values for this demonstration case are z₀=49 km and λ_z=11 km.

We recall that the vertical extend of wave packet $\exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})$ introduced in Sect. 3 is essential for analysis of observations which cover an altitude range of approximately 50 km and are thus much longer than a wavelength and the expected scale of amplitude variations.

A similar way of deriving initial guess parameters was implemented by Hu et al. (2002), for example, who used the power spectrum to define the dominant waves. However, since their observations only cover 20 km altitude, they do not need to consider the thickness of the wave packet. Hu et al. (2002) simply assumed that the wave packet covers the entire altitude range of their observations. Obviously, such an assumption is not valid if observations cover an extended altitude range like that in our study. Section 4.3, and in particular Fig. 6, clearly support this statement.

Generally speaking, intrinsic frequency and the propagation direction can be estimated from the obtained fitting results by applying Eqs. (3) and (A5), respectively. However, by testing different simulated and measured data we concluded that for GWs with intrinsic periods larger than ∼1 h the hodograph analysis yields more accurate results than those based on the fitting of Eq. (6). Therefore, the described fitting procedure is only used to precisely derive the altitude z₀ and the vertical wavelength ${\mathit{\lambda }}_z=\mathrm{2}\mathit{\pi }/m$ of the wave packet, which are smeared in the spectrogram (Fig. 6). Thus, we continue analysis using the hodograph technique.

4.5 Hodograph method

According to the theory (see Appendix A and e.g.,  Sawyer, 1961; Cot and Barat, 1986; Wang and Geller, 2003; Zhang et al., 2004; Baumgarten et al., 2015) the u^′ and v^′ fluctuations form an ellipse if the intrinsic period is between ∼1 and ∼12 h. For higher-frequency GWs, i.e. with periods below ∼1 h, the fluctuations form a line, as the influence of the Coriolis force is negligible. For low-frequency GWs, i.e., those with periods close to the Coriolis period (2π∕f), the fluctuations' hodograph closely resembles a circle.

To extract the essential parameters of the wave packet found in the previous steps we apply the hodograph analysis around the center of the wave packet (e.g. Baumgarten et al., 2015). Figure 1 schematically illustrates this method. In the center of the wave packet the QMGW produces fluctuations in zonal and meridional wind components with equal vertical wavelengths but different phases and amplitudes, which is described by Eq. (1). Figure 1a shows the u^′ and v^′ wind fluctuations as a function of altitude. One can see several oscillation periods centered around ∼40 km altitude. If we select one full wave period around the center altitude of the QMGW, i.e. from $z_{\mathrm{0}}-{\mathit{\lambda }}_z/\mathrm{2}$ to $z_{\mathrm{0}}+{\mathit{\lambda }}_z/\mathrm{2}$, and plot u^′ versus v^′, we get an ellipse as shown in Fig. 1b. The selected height range with one wave period is marked in Fig. 1a by the shaded area. The major axis of the ellipse is oriented along the wave propagation direction.

In order to minimize an error in the hodograph analysis due to the presence of other waves (Zhang et al., 2004), we apply a vertical band-pass filter to all three profiles and thereby remove the waves with wavelengths shorter than λ_z∕2 and longer than 2λ_z. For example, if the vertical wavelength obtained in the previous step is 10 km, we remove waves with wavelengths shorter (longer) than 5 km (20 km). Such filtering (and especially its high-frequency part) works to denoise the profiles and improves the robustness of the subsequent fitting. The choice of the filter width (λ_z∕2, 2λ_z) is rather arbitrary and can be inferred, for example, from the e-folding time of the wavelet function around the detected peak. Using a two-dimensional least-square fitting software we find the best fit parameters that satisfy the ellipse equation (Fitzgibbon et al., 1996). The fitting procedure is sensitive to the data quality, and if, for example, the data are far away from an elliptical shape, the fitting procedure does not converge. Only if the ellipse was successfully fitted do we extract further wave characteristics from this data set.

The vertical propagation direction of the wave is unambiguously determined by the rotation direction of the zonal wind versus meridional wind hodograph. In the Northern Hemisphere the (anti-clockwise) clockwise rotation of the hodograph indicates a (downward-propagating) upward-propagating wave.

The rotation direction of the hodograph is defined as a phase angle change of either u^′ or v^′ from the bottom level to the top level over the height region $[z_{\mathrm{0}}-{\mathit{\lambda }}_z/\mathrm{2},z_{\mathrm{0}}+{\mathit{\lambda }}_z/\mathrm{2}]$.

An additional hodograph of the parallel wind fluctuations versus temperature fluctuations is used to resolve an ambiguity in the horizontal propagation direction that arises from the orientation of the ellipse in Fig. 1b.

4.6 Optimization of results

If, in the previous step, the rotation of the hodograph does not make a full 360^∘ cycle, this suggests either an inconsistency in the hodograph results (Sect. 4.5) and the wave fit (Sect. 4.4) or that the vertical extent of the wave packet is smaller than its vertical wavelength. In such a case we apply a correction to the vertical wavelength derived in Sect. 4.4. This correction to the vertical wavelength is found by forcing the hodograph to close the full 360^∘ cycle and calculating the additional vertical length resulting from this extra rotation. If the new (corrected) wavelength λ_z differs significantly from λ_z obtained before (Sect. 4.4), we repeat the hodograph analysis using the new (corrected) wavelength.

4.7 Calculation of GW parameters

The ratio of the major and minor ellipse axes is further used to derive the intrinsic frequency of GWs (Appendix A). The analysis presented so far allows us to derive the intrinsic wave frequency, vertical wavelength, and upward or downward propagation. The horizontal direction of propagation is along the major axis of the ellipse, with a remaining uncertainty of 180^∘. To resolve this ambiguity we further use the temperature fluctuation profile as described in Sect. 3. Specifically, we construct a hodograph from the temperature fluctuations and wind fluctuations along the wave propagation direction, i.e., parallel to the derived wave vector. The rotation direction of this new hodograph finally defines the direction of the wave vector: for upward-propagating GWs clockwise or counterclockwise rotation indicates an eastward or westward direction, respectively. For downward-propagating GWs the opposite direction has to be used (Hu et al., 2002).

Knowing all these wave parameters and applying the linear wave theory we derive further wave characteristics as summarized in Sect. 3 and described in Appendix A in more detail. Note that as mentioned in Sect. 4.2, at this point the fluctuation amplitudes must be rescaled back to their original growth rate with altitude using the derived scaling parameter ς to legitimate their use for the estimation of wave energy, for example.

Figure 7a–c show the fluctuations and two hodographs defined from the two maxima shown in Fig. 6. Results obtained from this example are summarized in Table 1 (first column).

4.8 Iteration process

After the first QMGW is identified in all three profiles, it is subtracted from those data. We repeat the procedure described above for all of the maxima seen in the combined spectrogram (Fig. 6). In order to avoid overfitting, we limit our analysis to maximum of 20 waves per time step. As will be demonstrated in the next section, we never reach this limit. In the given example five waves were detected. The first three waves are demonstrated in Fig. 7, and the obtained parameters are summarized in Table 1. In this example we found that a wave with a vertical wavelength of 16.4 km propagates upward and against the background wind in the altitude range from 56 to 73 km. In the altitude range from 44 to 54 km a wave with 11 km vertical wavelength propagates downward and with nearly the same direction as the background wind. The analysis indicates that the broad maximum in the combined spectrogram (Fig. 6) was produced by the sum of the two wave packets with different characteristics.

Figure 8 Total number of waves obtained per altitude profile for the entire data set.

4.9 Reconstruction of 2-D fields

Finally, this algorithm for a single point in time is subsequently applied to all time points of the entire data set shown in Figs. 2, 3 and 4. Thereby, two-dimensional time–altitude fields of GW parameters can be reconstructed, which is demonstrated in the next section.

Table 1 Examples of hodograph results from 10 January 2016 at 02:07:30 UT.

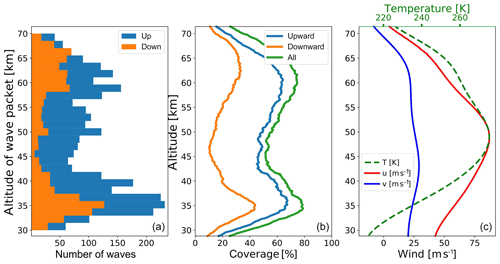
Figure 9 (a) Number of waves detected per 1.5 km altitude range bin. Blue (orange) bars mark upward-propagating (downward-propagating) GWs. (b) Mean coverage by detected waves when taking the altitude extent of the waves into account. The green profile indicates whether a wave was found, whereas blue and orange lines are for upward- and downward-propagating waves, respectively. (c) Background mean wind and temperature.

5 Results and discussion

In this section we demonstrate, on a real data set, how our analysis works, and results are summarized in the form of different statistics.

The data used in this study were obtained from 9 to 12 January 2016. During this time period a strong jet with wind speeds of more than 100 m s⁻¹ was observed at an altitude range of 45 to 55 km (Figs. 3 and 4). During this period, maps of the horizontal winds extracted from the ECMWF IFS (European Centre for Medium-Range Weather Forecasts – Integrated Forecasting System) showed a strong polar vortex with wind speeds of more than 160 m s⁻¹ at the vortex edge. The vortex was elongated towards Canada and Siberia and its center displaced towards Europe. ALOMAR was located roughly below the vortex edge, and the polar night jet was located to the south of the ALOMAR, at about 60^∘ N, with wind speeds of more than 160 m s⁻¹.

After applying the new analysis technique to the ∼60 h measurements shown in Figs. 2, 3 and 4 we obtain the following results.

First, a short discussion about the exponential scaling factor $\mathrm{1}/\exp (z/(\mathit{\varsigma }H\left)\right)$ applied to the fluctuation profiles as described in Sect. 4.2 is necessary. This factor should compensate for the exponential growth of GW amplitude due to the exponential decrease in atmospheric density. It is commonly accepted to use ς=2. However, since the exact value of ς depends on the particular state of the atmosphere during the observations, it has to be directly estimated from the measurements. Thus, Fritts and VanZandt (1993), for example, theoretically derived ς=2.3, consistent with number of observations revised in, for example, Fritts and Alexander (2003). Lu et al. (2015) incorporate this factor into the “observed” scale height, which implies that ς=2.5 to 2.8 for different observations over the McMurdo Station (77.8^∘ S, 166.7^∘ E). We derived ς=2.15 as a mean value over the entire time series, which is as an average of ς of all the individual profiles. We assume that ς does not change significantly during the observational time period of approximately 3 d. However, if observations last longer, this assumption will not hold. In such a case the scaling function has to be optimized to reveal some time dependence (not addressed in this work).

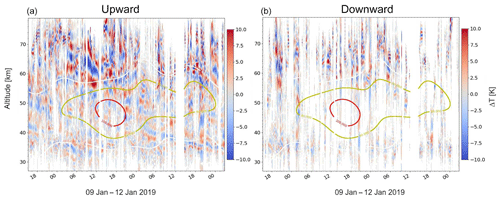
Figure 10 Reconstructed temperature fluctuations of upward-propagating GWs (a) and downward-propagating GWs (b). Contour lines show the background zonal wind, and the numbers on the contour lines are given in meters per second.

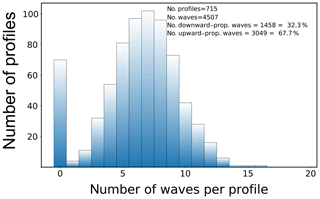
The number of detected waves per altitude profile is summarized in the histogram in Fig. 8. In 645 out of 715 altitude profiles, we find at least one height range with a dominant GW where the hodograph analysis provides a reliable result. We recall that the analysis technique allows for up to 20 waves in a single profile. The total number of the detected waves amounts to 4507. It is seen that the majority of the profiles yield 5 to 10 waves, and none of them reach the 20-wave limit. From the rotation direction of the velocity hodographs, we derive that 32.3 % of all the detected waves propagate downwards.

Figure 9 shows details of the wave packets as functions of altitude and separated for upward- and downward-propagating GWs. The first plot (Fig. 9a) shows the number of wave center altitudes (z₀) and does not consider the vertical extent of the wave packets (vertical wavelengths). The latter is taken into account in Fig. 9b, which shows the mean fraction of the profile where a wave packet is present (any part of the wave, center or tail). We find that the most active regions (in terms of number of GWs) are ∼32 to 40 km and 58–64 km. The altitude region between ∼40 and 55 km contains the smallest number of the detected waves.

It is interesting to compare these results with the mean background wind shown in Fig. 9c. It is obvious that the minimum in the wave activity as deduced by our analysis technique is co-located with the maximum of the mean zonal wind as well as the background temperature.

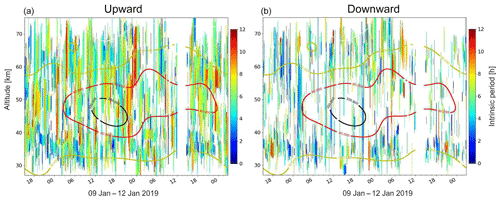
Figure 11 Color-coded bars show the intrinsic period of upward-propagating (a) and downward-propagating (b) waves. The length of the bar is given by the extend of the waves. Contour lines show the background total wind, and the numbers on the contour lines are given in meters per second.

The existence of the downward-propagating waves was reported earlier from observations by different methods (e.g., Hirota and Niki, 1985; Gavrilov et al., 1996; Wang et al., 2005) and also from model simulations (e.g., Holton and Alexander, 1999; Becker and Vadas, 2018). However, the reported number of downward-propagating GWs is very variable, since most of the observations were done at different altitudes or latitudes. Hu et al. (2002) found 223 (71 %) waves propagating upwards and 91 (29 %) downwards in the altitude range 84–104 km, which is in accord with our results. Gavrilov et al. (1996) reported that up to 50 % of the detected waves propagate downwards in the altitude range 70 to 80 km. In the troposphere and lower stratosphere (below 20 km) Sato (1994) reported less than 10 % downward-propagating GWs, and Mihalikova et al. (2016) reported 18.4 % during wintertime and 10.7 % during summertime. From rocket observations of zonal and meridional wind components with a vertical resolution of 1 km in the altitude range 30 to 60 km, Hirota and Niki (1985) found, in middle and high latitudes, about 20 % downward-propagating GWs and 30 %–40 % in low latitudes at Northern Hemisphere stations. At the only Southern Hemisphere station (Ascension Island) 36 % downward-propagating GWs were observed (Hirota and Niki, 1985). Hamilton (1991) found, from rocketsonde observations of wind and temperature in the 28–57 km height range at 12 stations (spanning 8^∘ S to 76^∘ N), different fractions of downward-propagating GWs spanning from 2 % to 46 %, depending on latitude and season. Wang et al. (2005) reported that approximately 50 % of the tropospheric gravity waves show upward energy propagation, whereas there is about 75 % upward energy propagation in the lower stratosphere. From their radiosonde observations the authors demonstrate that the lower-stratospheric fraction of the upward energy propagation is generally smaller in winter than in summer, especially at middle and high latitudes. Thus, our finding of 32.3 % downward-propagating GWs reasonably agrees with the other experimental data. We note that the observed downward- or upward-propagating GWs are instantaneous observations, which means that we have no information about the fate of the observed waves; i.e., we cannot estimate the percentage of waves which ultimately reach the ground.

To investigate the time and altitude dependence of the GWs detected by our hodograph technique, we reconstructed the temperature and the wind fluctuation fields from the derived waves parameters using Eq. (1). Figure 10 shows the result of this reconstruction for the temperature fluctuations separated for upward- and downward-propagating GWs. Contour lines show the background zonal wind velocity. We recall that the analysis technique treats every single altitude profile independently, and therefore the influence of neighboring profiles is only due to time averaging. It is therefore remarkable that the joint field of the reconstructed GWs shown in Fig. 10 build a consistent picture. Thus, one can recognize, for instance, wave packets with a duration of several hours. In some cases phase lines of waves follow the background wind. For example, on 11 January, after 18:00 UT at altitudes between 54 and 63 km, a maximum of temperature fluctuations of upward-propagating waves follows the contour line of the zonal wind of 60 m s⁻¹.

We use similar representations to investigate the temporal variability in any of the other derived GW properties. For example, Fig. 11 summarizes the obtained intrinsic periods of GWs throughout the measurement. On the one hand, these figures demonstrate high variability, but on the other hand, they also show regions of a consistent picture. For example, on 11 January after 21:00 UT at altitudes between 54 and 62 km, one can see a wave period of about 7 h for ∼2 h. The analysis allows studying the temporal and altitude variation in the wave periods; e.g., upward-propagating low period waves with large vertical wavelengths are often found above the jet maximum.

Figure 12 Histograms of different GW properties separated for upward- and downward-propagating waves. (a–d) vertical wavelength, intrinsic period, horizontal wavelength and horizontal phase speed, estimated from Eqs. (1), (A5), (A9) and (a), respectively.

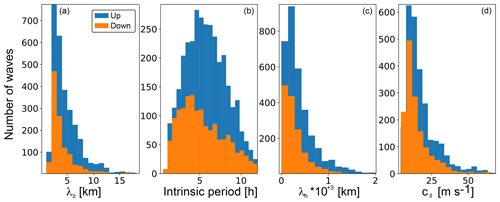
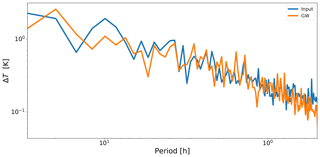
Figure 13 Fourier power spectra of measured temperature fluctuations (blue) and of the reconstructed GWs (orange).

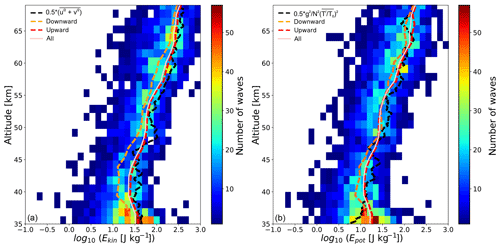
Figure 14 Kinetic (a) and potential (b) energy of waves. Colored boxes show 2-D histograms (number of waves per 1.5 km altitude and 0.15 log(energy) bin). Lines show mean values of whole distribution (pink) and upward- or downward-propagating waves (red and orange dashed), and black dashed lines are energy estimated from the variance in the temperature (a) and wind (b) fluctuations throughout the measurement.

In Fig. 12 we show distributions of the derived GW parameters for all identified waves. One remarkable feature seen in these histograms is that the distributions of wavelengths and phase velocities reveal very similar shapes for upward- and downward-propagating waves. The distributions of intrinsic periods show quite different shapes, i.e. dissimilar kurtosis and skewness, for upward- and downward-propagating GWs. These histograms also demonstrate limitations of the presented analysis. Only a few waves with intrinsic periods smaller than 1 h or with vertical wavelengths below 1 km are detected. This is likely caused by the smoothing of the lidar data with a Gaussian window of 15 min and 0.5 km rather than by the hodograph method itself. Waves with vertical wavelengths above ∼15 km were likely associated with the background fluctuations when applying the 2-D FFT.

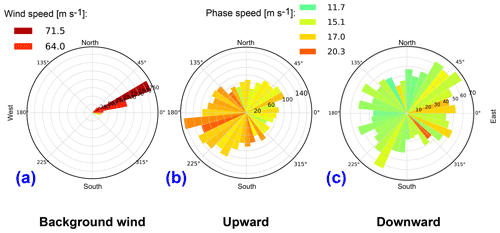
Figure 15 Polar histograms of the direction of the background wind (a) and waves for upward-propagating (b) and downward-propagating (c) waves. Length of the bars represents the number of waves per 10^∘ horizontal direction. The color represents the average wind (a) or average intrinsic phase speeds (b, c) or the respective directions.

The distribution of phase velocities in Fig. 12 demonstrates that the velocities are below 60 m s⁻¹, with a maximum of occurrence at ∼10 m s⁻¹. Matsuda et al. (2014) estimated horizontal GW phase velocities from airglow images. Their waves had periods below ∼1 h and revealed phase speeds between 0 and 150 m s⁻¹. Among those waves, ∼70 % showed phase speeds between 0 and 60 m s⁻¹. In our case, the observed wave periods have a maximum in the range 4 to 5 h, and, as expected from Eq. (), the horizontal phase velocity is also lower than those reported by Matsuda et al. (2014).

Another way to check the consistency of our technique is to look at the spectrum of fluctuations before and after analysis. As an example, Fig. 13 shows the Fourier spectra of the temperature fluctuations calculated in the time domain. The measurements and the analysis results are represented by the blue and orange lines, respectively. We recall that the analysis is made in the spatial domain – that is, it only deals with altitude profiles of fluctuations. Close similarity in both spectra, which were calculated in the time domain that is across the analyzed profiles, suggests that the reconstructed two-dimensional (time vs. altitude) GW field does not significantly deviate from the observed one. The reconstructed field indeed reflects the main GW content, and, therefore, in this respect it may be qualified as lossless algorithm.

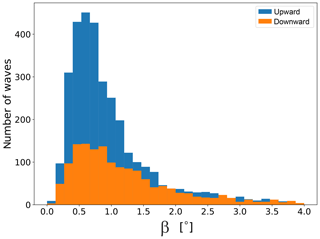
Figure 16 Histogram of the absolute value of the angle between the group velocity vector and the horizon, separated for upward- and downward-propagating waves.

Next, we analyze and sum up the wave energetics. Figure 14 shows the derived kinetic (E_kin) and potential (E_pot) energy densities as well as their statistical basis. The altitude dependence of the energy distribution is shown as a color-coded two-dimensional histogram (color bar on the right-hand side defines number of waves). For these histograms all waves were used, i.e. both propagating upwards and downwards. Figure 14 also shows the mean energy separated for the upward- and downward-propagating waves. We find that E_kin of the downward-propagating GWs is lower than E_kin of the upward-propagating waves, and E_pot is nearly identical for the upward- and downward-propagating GWs. The standard method to derive E_kin and E_pot from ground-based observations is to average bulk wind and temperature fluctuations and apply Eqs. (A13) and (A15). Figure 14 shows that the fluctuation-based method reveals a good agreement with mean profiles derived from our new retrievals. Obtained results for averaged E_kin and E_pot are also in agreement with the mean winter profiles measured at the ALOMAR observatory, summarized by Hildebrand et al. (2017).

The directions of background wind and wave propagation are summarized in Fig. 15 as polar histograms. Figure 15a shows a histogram of the background wind at the time and altitude of every hodograph. The analysis shows that, in almost all cases, the wind in the vicinity of the detected waves blows towards the east–north-east with a mean speed of about 70 m s⁻¹.

Figure 15b and c show polar histograms of the detected upward- and downward-propagating waves. From the color code we see that the horizontal phase speed of the upward-propagating waves is in general larger than that of the downward-propagating waves. Downward-propagating waves reveal a rather uniform spatial distribution, whereas the upward-propagating waves prefer to propagate against the background wind.

To find the vertical angles at which the GWs propagate, we show histograms of the angle between the group velocity vector and the horizon (β; Eq. A12) separated for the upward- and downward-propagating waves in Fig. 16. In the beginning of this section we noted that our analysis reveals that ∼30 % of all the detected waves propagate downwards. From the histograms we note that this difference of the upward- and downward-propagating waves is mostly due to waves propagating at shallow angles of less than $\sim \mathrm{1}{}^{\circ }$. GWs with larger vertical angles are found in same numbers for the upward- and downward-propagating waves.

The vertical group velocities c_gz estimated using Eq. (A11) are summarized in Fig. 17 for the upward- and downward-propagating waves. Since the vertical group velocity depends on the wave periods, we split the histograms into two groups of histograms that are longer and shorter than 8 h. These results show, for instance, that all low-frequency waves (in the range of frequencies considered in our study) reveal small vertical group velocities. Waves with periods shorter than 8 h show a somewhat more complicated picture. The vertical group velocities of the downward-propagating waves exceed those of the upward-propagating GWs for waves that propagate in the direction of the background wind. In turn, upward-propagating GWs reveal the highest vertical group velocities if they propagate against the background wind. The vertical group velocities c_gz are at least 2 times lower than vertical phase speeds (c_z; not shown here). The values of the vertical group velocity imply that if waves propagate from the ground to the altitude where they were observed, they need 6 to 14 d (2 to 4 d) if they have periods longer (shorter) than 8 h. Somewhat similar timescales for GWs to reach the lower stratosphere were reported by Sato et al. (1997), whose group velocity for waves with a period of 17 h was 1.7 km d⁻¹.

Finally, in Fig. 18 we show vertical fluxes of horizontal momentum (see Eq. A18) averaged over periods from 2 to 12 h, which is a key quantity for atmospheric coupling by waves. This plot demonstrates that, for these measurements, the vertical flux of horizontal momentum rapidly decreases with altitudes up to ∼45 km. Above ∼42 km it remains rather constant up to ∼70 km. In the altitude range from 42 to 70 km, where we find low variability in the momentum flux, we analyzed its dependence on the horizontal propagation direction of the waves. The result is shown as polar histograms in Fig. 19. We see that the momentum flux of the downward-propagating waves is lower than that of the upward-propagating GWs. Figure 19 also shows that the waves propagating nearly perpendicular to the mean wind carry the smallest flux for both the upward- and downward-propagating GWs. Note that the direction of the momentum flux is not necessarily along the major axis of the ellipse. The angle between the directions of momentum flux and GW propagation was estimated by Eq. (13) from Gavrilov et al. (1996) and does not exceed 2.8^∘, which is much lower than the width of the bins in the histograms.

6 Summary and conclusion

In this paper, a detailed step-by-step description of a new algorithm for derivation of GW parameters with justification for every step is presented. Most of these steps, if considered independently, are well known and validated in numerous experimental works. The advantage and novelty of this work are their combination and some justifications of their importance and how they affect GW analysis results.

Thus the very first action normally performed on the measured time series is background removal. Since most conventional techniques based on smoothing or averaging in time or altitude ultimately introduce artifacts, we justify that application of the 2-D FFT for background removal is the most appropriate. The advantage of this method is that it simultaneously accounts for both variability in space and time.

A specific feature of our algorithm for GW analysis is that it is insensitive to the particular background removal scheme. Therefore, to avoid any degree of arbitrariness, the background removal can be excluded from fluctuation analysis when applying further steps of the analysis technique described in the paper.

As a next step we proposed applying a scaling function of the form $\mathrm{1}/\exp (z/(\mathit{\varsigma }H\left)\right)$, where H is scale height, z is altitude, and the constant ς can be derived by a linear fit to fluctuation profiles and should be in the range 1–10 (we derived ς=2.15 for our data). This, to our knowledge, is a new technique which is not explicitly described in the literature. The advantage of this approach is to suppress exponential growth of GW amplitudes to allow for equally weighted detection of wave signatures within the entire altitude range. This is clearly seen in the wavelet scalograms, for example, which would otherwise be predominantly sensitive to the strongest amplitudes, hiding waves at lower altitudes.

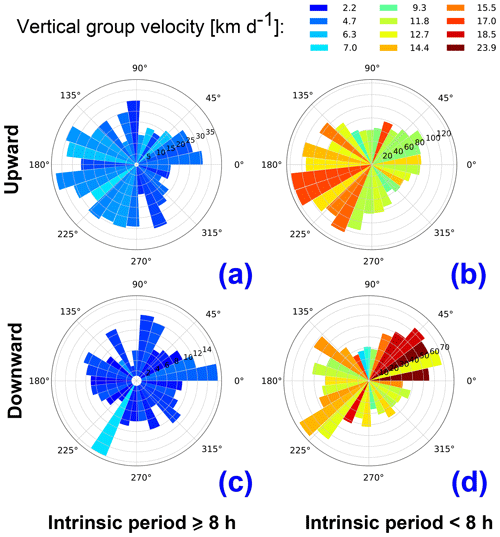
Figure 17 Polar histogram of the upward (a, b) and downward-propagating (c, d) GWs separated for waves with intrinsic periods ≥8 h (a, c) and <8 h (b, d). The length of the bars represents the number of waves per given horizontal direction. The colors represent the vertical group velocity (in km d⁻¹).

The most essential part of the proposed analysis technique consists of fitting cosine waves to simultaneously measured profiles of winds and temperature and subsequent hodograph analysis of these fitted waves. We emphasize that this fit must be applied to all three quantities, i.e., zonal and meridional wind and temperature (u, v and T), simultaneously. This ensures that we deal with a real GW which leaves its signature in all the physical quantities that were measured simultaneously in the same volume. The main difficulty in application of the hodograph analysis to real measurements is finding the wavelengths and altitude regions where a certain GW dominates all measured quantities (u, v and T). Since very often the measured data represent a mixture of vast different GWs, it is generally very difficult to find them automatically in the frame of hodograph analysis. Therefore, such work was always accomplished manually, by applying a visual check of data and analysis quality. This was also done in particular by Baumgarten et al. (2015). The novelty of our approach is that its robustness ultimately allows for automation of the hodograph analysis. Also, our algorithm resolves many more GWs than can be inferred by the manually applied hodograph technique.

All these advantages are especially important, since modern advanced measurement techniques (e.g., our lidar system described in Sect. 4) are capable of taking long-term measurements that cover the large altitude range ∼30 to 80 km. This large number of data requires a robust and stable automatic analysis technique, which we developed and presented in this work.

One obvious advantage of the proposed algorithm is that it allows for simultaneous detection of any kind of waves presented in the measurements. This includes not only GWs but also tides. Since the new analysis algorithm allows us to apply the simplest background removal techniques like subtraction of a mean, the necessity of the removal of tidal components a priori, which cannot be done unambiguously, is eliminated. All the detected waves can be sorted out on a statistical basis after the observational database is analyzed by using the proposed algorithm.

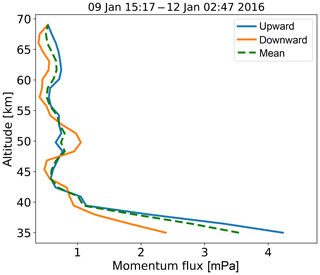
Figure 18 Vertical flux of horizontal momentum averaged through all observed hodographs (dashed) and upward-propagating (blue) and downward-propagating (orange) waves.

Another specific feature of our analysis technique is the extension to the linear wave theory introduced in Sect. 3, the wave packet envelope term $\exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})$ that accounts for limited presence of the GW packet in observations. This, however, only works in spatial domain, i.e., vertically. At the current stage of development, our analysis technique is not capable of detecting the lifetime of gravity waves in an observational data set. This capability is currently under development, as well as an additional robust algorithm, to pick out wave packets in the time domain automatically.

By applying this new methodology to real data obtained by lidar during about 60 h of observations in January 2016 we found 4507 single hodographs. In general, 5 to 10 waves were detected from every vertical profile. This allowed identifying and analyzing quasi-monochromatic waves in about ∼80 % of the observations. The measurements were performed while a jet at the stratopause (45–55 km) of more than 100 m s⁻¹ was located above the lidar station. We found a strong decrease in vertical flux of horizontal momentum up to ∼42 km altitude. Due to the strong wind above ∼40 km, it is likely that waves break, are absorbed and are reflected below this altitude region. The new method allows studying waves separated for the upward and downward propagation according to their group velocities.

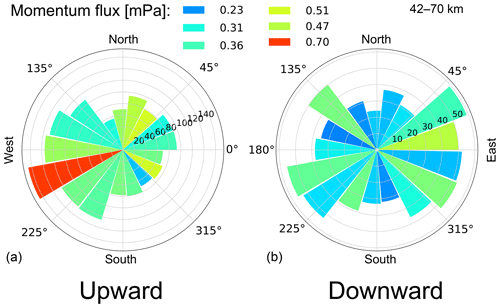
Figure 19 Polar histogram of upward-propagating (a) and downward-propagating (b) waves limited to the altitude range from 42 to 70 km. The length of the bars represents the number of waves per given horizontal direction. The average momentum flux per 20^∘ directional bin (in mPa) is color-coded.

The main characteristics of the upward- and downward-propagating GWs were investigated statistically. We find that the downward-propagating GWs reveal shorter intrinsic periods and lower phase speeds than the upward-propagating GWs. Downward waves propagate at steeper angles than the upward-propagating ones. Currently, our analysis does not allow us to distinguish between primary and secondary GWs. The next step will be to look for similar wave characteristics (horizontal, vertical wavelengths and propagation direction) in the upward- and downward-propagating waves. The nearby occurrence of similar waves with an opposite vertical propagation direction is an indication of secondary GWs (e.g., Vadas et al., 2018).

Appendix A: Theoretical basis and formulary

A monochromatic gravity-wave (GW) perturbation in Cartesian coordinates (x, y, z) with wave number components (k, l, m) and ground-relative (Eulerian) frequency ω can be written in the following form (e.g.; Gill, 1982; Fritts and Alexander, 2003; Holton, 2004):

$$\begin{array}{}\text{(A1a)}& {\displaystyle }& {\displaystyle }{T}^{\prime }=Re\mathit{\{}\widehat{T}\cdot \exp (i(kx+ly+mz-\mathit{\omega }t)\left)\mathit{\right\}}\cdot \exp (z/\mathrm{2}H),\text{(A1b)}& {\displaystyle }& {\displaystyle }{u}^{\prime }=Re\mathit{\{}\widehat{u}\cdot \exp (i(kx+ly+mz-\mathit{\omega }t)\left)\mathit{\right\}}\cdot \exp (z/\mathrm{2}H),\text{(A1c)}& {\displaystyle }& {\displaystyle }{v}^{\prime }=Re\mathit{\{}\widehat{v}\cdot \exp (i(kx+ly+mz-\mathit{\omega }t)\left)\mathit{\right\}}\cdot \exp (z/\mathrm{2}H),\end{array}$$

where $\widehat{T}$, $\widehat{u}$ and $\widehat{v}$ are complex amplitudes of temperature, zonal and meridional wind fluctuations and H is scale height.

Alternatively, these equations can be rewritten in the form

$$\begin{array}{}\text{(A2a)}& {\displaystyle }\begin{array}{rl}{T}^{\prime }=& \left|\widehat{T}\right|\cdot \cos (kx+ly+mz-\mathit{\omega }t+{\mathit{\phi }}_{T\mathrm{0}})\cdot \exp (z/\mathrm{2}H)\\ =& \left|\widehat{T}\right|\cdot \cos (mz+{\mathit{\phi }}_T)\cdot \exp (z/\mathrm{2}H),\end{array}\text{(A2b)}& {\displaystyle }\begin{array}{rl}{u}^{\prime }=& \left|\widehat{u}\right|\cdot \cos (kx+ly+mz-\mathit{\omega }t+{\mathit{\phi }}_{u\mathrm{0}})\cdot \exp (z/\mathrm{2}H)\\ =& \left|\widehat{u}\right|\cdot \cos (mz+{\mathit{\phi }}_u)\cdot \exp (z/\mathrm{2}H),\end{array}\text{(A2c)}& {\displaystyle }\begin{array}{rl}{v}^{\prime }=& \left|\widehat{v}\right|\cdot \cos (kx+ly+mz-\mathit{\omega }t+{\mathit{\phi }}_{v\mathrm{0}})\cdot \exp (z/\mathrm{2}H)\\ =& \left|\widehat{v}\right|\cdot \cos (mz+{\mathit{\phi }}_v)\cdot \exp (z/\mathrm{2}H),\end{array}\end{array}$$

where the general phase shift in the form of ${\mathit{\phi }}_i=kx+ly-\mathit{\omega }t+{\mathit{\phi }}_{i\mathrm{0}}$ (subscript i refers to T,u or v) was introduced. For observations of one vertical profile, the quantity $(kx+ly-\mathit{\omega }t)$ contributes to the fluctuations as a phase shift.

Finally, we take into account that the quasi-monochromatic gravity wave (QMGW) is limited in space; i.e. it appears in our observations within a limited altitude range:

$$\begin{array}{}\text{(A3a)}& {\displaystyle }\begin{array}{rl}{T}^{\prime }=& \left|\widehat{T}\right|\cdot \exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})\cdot \cos (m(z-z_{\mathrm{0}})\\ +& {\mathit{\phi }}_T)\cdot \exp (z/\mathrm{2}H),\end{array}\text{(A3b)}& {\displaystyle }\begin{array}{rl}{u}^{\prime }=& \left|\widehat{u}\right|\cdot \exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})\cdot \cos (m(z-z_{\mathrm{0}})\\ +& {\mathit{\phi }}_u)\cdot \exp (z/\mathrm{2}H),\end{array}\text{(A3c)}& {\displaystyle }\begin{array}{rl}{v}^{\prime }=& \left|\widehat{v}\right|\cdot \exp (-(z-z_{\mathrm{0}}{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}})\cdot \cos (m(z-z_{\mathrm{0}})\\ +& {\mathit{\phi }}_v)\cdot \exp (z/\mathrm{2}H),\end{array}\end{array}$$

where σ is a factor describing the width of wave packet, and z₀ is the altitude of the maximum wave amplitude. Following Cot and Barat (1986) and Gavrilov et al. (1996), the horizontal propagation angle of QMGWs can be defined as follows:

$$\begin{array}{}\text{(A4)}& \mathit{\xi }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathit{\pi }n+\arctan ({\displaystyle \frac{\mathrm{2}{\mathrm{\Phi }}_{uv}}{{\widehat{v}}^{\mathrm{2}}-{\widehat{u}}^{\mathrm{2}}}}\left)\right),\end{array}$$

where ξ is the azimuth angle of the wave propagation direction and ${\mathrm{\Phi }}_{uv}=\widehat{u}\cdot \widehat{v}\cdot \cos ({\mathit{\phi }}_u-{\mathit{\phi }}_v)$. The integer n is 1 when $\widehat{v}<\widehat{u}$. When $\widehat{v}>\widehat{u}$, n=0 and 2 for Φ_uv > 0 and Φ_uv < 0, respectively. This implies that for ${\mathit{\phi }}_u-{\mathit{\phi }}_v=\mathit{\pi }/\mathrm{2}$ the propagation direction can be 0 or 180^∘, i.e., northward or southward if $\widehat{v}>\widehat{u}$ and eastward or westward if $\widehat{v}<\widehat{u}$. The sign of m in Eq. (1) shows the vertical propagation direction: m<0 for upward-propagating and m>0 for downward-propagating GWs. This theoretical basis allows us to describe the main GW parameters and to derive them from observations. However, in practice, noisy data and/or insufficient resolution of measurements may lead to large uncertainties when applying these equations directly to the measured time series.

The most common technique, based on the linear theory of gravity waves to derive the propagation direction, intrinsic frequency and phase velocity of GW from ground-based observations, is the hodograph method (e.g., Cot and Barat, 1986; Sawyer, 1961; Wang and Geller, 2003; Zhang et al., 2004; Baumgarten et al., 2015).

In order to keep the polarization relation as simple as Eq. (4), we can rotate the coordinate system (x, y) with wave wind fluctuations u^′ and v^′ to (x_∥, y_⟂) – a Cartesian coordinate system in which the origin is kept fixed and the x_∥ and y_⟂ axes are obtained by rotating the x and y counterclockwise through an angle $\mathit{\pi }/\mathrm{2}-\mathit{\xi }$. In new coordinate system, waves propagate along the x_l axis, and the amplitude ratio in the new coordinate system is

$$\begin{array}{}\text{(A5)}& \left|\widehat{u_{\parallel }}\right|/\left|\widehat{u_{⟂}}\right|=\widehat{\mathit{\omega }}/f.\end{array}$$

The relationship between fluctuations in new (x_∥, y_⟂) and standard coordinate systems (x, y) are

$$\begin{array}{}\text{(A6a)}& {\displaystyle }& {\displaystyle }{u}^{\prime }=u_{\parallel }^{\prime }\cdot \sin \left(\mathit{\xi }\right)-v_{⟂}^{\prime }\cdot \cos \left(\mathit{\xi }\right),\text{(A6b)}& {\displaystyle }& {\displaystyle }{v}^{\prime }=u_{\parallel }^{\prime }\cdot \cos \left(\mathit{\xi }\right)+v_{⟂}^{\prime }\cdot \sin \left(\mathit{\xi }\right),\text{(A6c)}& {\displaystyle }& {\displaystyle }{u}_{\parallel }^{\prime }=u^{\prime }\cdot \sin \left(\mathit{\xi }\right)+v^{\prime }\cdot \cos \left(\mathit{\xi }\right),\text{(A6d)}& {\displaystyle }& {\displaystyle }{u}_{⟂}^{\prime }=-u^{\prime }\cdot \cos \left(\mathit{\xi }\right)+v^{\prime }\cdot \sin \left(\mathit{\xi }\right).\end{array}$$

Amplitudes of the ellipse in the new coordinate system (Gavrilov et al., 1996) are

$$\begin{array}{}\text{(A7a)}& {\displaystyle }\mathrm{2}{\widehat{u_{\parallel }}}^{\mathrm{2}}={\widehat{u}}^{\mathrm{2}}+{\widehat{v}}^{\mathrm{2}}+\sqrt{({\widehat{u}}^{\mathrm{2}}-{\widehat{v}}^{\mathrm{2}}{)}^{\mathrm{2}}+\mathrm{4}{\mathrm{\Phi }}_{uv}^{\mathrm{2}}},\text{(A7b)}& {\displaystyle }\mathrm{2}{\widehat{u_{⟂}}}^{\mathrm{2}}={\widehat{u}}^{\mathrm{2}}+{\widehat{v}}^{\mathrm{2}}-\sqrt{({\widehat{u}}^{\mathrm{2}}-{\widehat{v}}^{\mathrm{2}}{)}^{\mathrm{2}}+\mathrm{4}{\mathrm{\Phi }}_{uv}^{\mathrm{2}}}.\end{array}$$

Thus, $\widehat{u_{\parallel }}$ and $\widehat{u_{⟂}}$ can be derived from fitting the ellipse to a wind vector or by fitting Eq. () to the data and applying Eq. (). Afterwards Eq. (A5) is used to derive the intrinsic frequency $\widehat{\mathit{\omega }}$ of the wave.

On the other hand the intrinsic frequency is a function of the buoyancy frequency (N), Coriolis parameter f and angle α, which is the angle between phase lines and the vertical (Holton, 2004, Eq. 7.56):

$$\begin{array}{}\text{(A8)}& {\widehat{\mathit{\omega }}}^{\mathrm{2}}=N^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\alpha }+f^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\alpha }.\end{array}$$

From this equation the horizontal wave number along the propagation direction can be derived (Fritts and Alexander, 2003; Vaughan and Worthington, 2007):

$$\begin{array}{}\text{(A9)}& k_{\Vert }^{\mathrm{2}}=m^{\mathrm{2}}\left({\displaystyle \frac{{\widehat{\mathit{\omega }}}^{\mathrm{2}}-f^{\mathrm{2}}}{N^{\mathrm{2}}-{\widehat{\mathit{\omega }}}^{\mathrm{2}}}}\right).\end{array}$$

The horizontal–vertical phase speed is the ratio of intrinsic frequency to the horizontal–vertical wave number (e.g., Nappo, 2002):

$$\begin{array}{}\text{(A10a)}& {\displaystyle }{c}_{\Vert }=\widehat{\mathit{\omega }}/k_{\Vert },\text{(A10b)}& {\displaystyle }{c}_z=\widehat{\mathit{\omega }}/m.\end{array}$$

The vertical component of the group velocity c_gz of the hydrostatic inertia–gravity waves is given by (Gill, 1982; Sato et al., 1997)

$$\begin{array}{}\text{(A11)}& c_{\text{gz}}\equiv {\displaystyle \frac{\partial \widehat{\mathit{\omega }}}{\partial m}}=-{\displaystyle \frac{(N^{\mathrm{2}}-f^{\mathrm{2}})k_{\Vert }^{\mathrm{2}}m}{\widehat{\mathit{\omega }}(k_{\Vert }^{\mathrm{2}}+m^{\mathrm{2}}{)}^{\mathrm{2}}}}\simeq -{\displaystyle \frac{N^{\mathrm{2}}{k}_{\Vert }^{\mathrm{2}}}{\widehat{\mathit{\omega }}{m}^{\mathrm{3}}}}.\end{array}$$

The angle between the group velocity vector and the horizon can be estimated from α as

$$\begin{array}{}\text{(A12)}& \mathit{\beta }=\mathit{\pi }/\mathrm{2}-\mathit{\alpha }.\end{array}$$

The kinetic energy density of GWs estimated from observed fluctuations (e.g., Gill, 1982; Holton, 2004; Placke et al., 2013) is

$$\begin{array}{}\text{(A13)}& E_{\text{kin}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\stackrel{\mathrm{‾}}{\left({v^{\prime }}^{\mathrm{2}}+{u^{\prime }}^{\mathrm{2}}\right)}.\end{array}$$

Thus, the kinetic energy density as a function of fitted amplitudes of the wind hodograph is

$$\begin{array}{}\text{(A14)}& E_{\text{kin}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left({\widehat{v}}_{\parallel }^{\mathrm{2}}+{\widehat{u}}_{⟂}^{\mathrm{2}}\right).\end{array}$$

The potential energy density of GWs estimated from observed fluctuations is (e.g., Holton, 2004; Geller and Gong, 2010; Placke et al., 2013)

$$\begin{array}{}\text{(A15)}& E_{\text{pot}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{g^{\mathrm{2}}}{N^{\mathrm{2}}}}\stackrel{\mathrm{‾}}{{\displaystyle \frac{{T^{\prime }}^{\mathrm{2}}}{T_{\mathrm{0}}^{\mathrm{2}}}}}.\end{array}$$

E_pot from amplitudes of temperature fluctuations is

$$\begin{array}{}\text{(A16)}& E_{\text{pot}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}{\displaystyle \frac{g^{\mathrm{2}}}{N^{\mathrm{2}}}}{\displaystyle \frac{{\widehat{T}}^{\mathrm{2}}}{T_{\mathrm{0}}^{\mathrm{2}}}}.\end{array}$$

The vertical flux of horizontal momentum in the wave propagation direction can be written as (e.g., Fritts and Alexander, 2003)

$$\begin{array}{}\text{(A17)}& F_{P\Vert }=\stackrel{\mathrm{‾}}{\mathit{\rho }}\left(\mathrm{1}-{\displaystyle \frac{f^{\mathrm{2}}}{{\widehat{\mathit{\omega }}}^{\mathrm{2}}}}\right)\stackrel{\mathrm{‾}}{u_l^{\prime }{w}^{\prime }},\end{array}$$

where w^′ is vertical wind fluctuations and $\stackrel{\mathrm{‾}}{\mathit{\rho }}$ is the atmospheric density. From the continuity equation, we get $w^{\prime }=-(k_{\Vert }/m)\cdot u_l^{\prime }$, and the vertical momentum flux is transformed into (e.g., Réchou et al., 2014)

$$\begin{array}{}\text{(A18)}& F_{P\Vert }={\displaystyle \frac{\stackrel{\mathrm{‾}}{\mathit{\rho }}}{\mathrm{2}}}\left(\mathrm{1}-{\displaystyle \frac{f^{\mathrm{2}}}{{\widehat{\mathit{\omega }}}^{\mathrm{2}}}}\right){\displaystyle \frac{k_{\Vert }}{m}}{\widehat{u}}_l^{\mathrm{2}}.\end{array}$$