Estimation of the height of the turbulent mixing layer from data of Doppler lidar measurements using conical scanning by a probe beam

A method is proposed for determining the height of the turbulent mixing layer on the basis of the vertical profiles of the dissipation rate of turbulent energy, which is estimated from lidar measurements of the radial wind velocity using conical scanning by a probe beam around the vertical axis. The accuracy of the proposed method is discussed in detail. It is shown that for the estimation of the mixing layer height (MLH) with the acceptable relative error not exceeding 20 %, the signal-to-noise ratio should be no less than −16 dB, when the relative error of lidar estimation of the dissipation rate does not exceed 30 %. The method was tested in a 6 d experiment in which the wind velocity turbulence was estimated in smog conditions due to forest fires in Siberia in summer 2019. The results of the experiment reveal that the relative error of determination of the MLH time series obtained by this method does not exceed 10 % in the period of turbulence development. The estimates of the turbulent mixing layer height by the proposed method are in a qualitative agreement with the MLH estimated from the distributions of the Richardson number in height and time obtained during the comparison experiment in spring 2020.

1 Introduction

The turbulent mixing layer in the lower part of the Earth's atmosphere has an important role in the vertical transport of moisture, small gas constituents, pollutants, and heat from the surface to the upper layers of the atmosphere. The turbulent mixing layer height is usually understood to be the thickness of the layer adjacent to the ground, in which incoming substances become completely vertically distributed throughout the layer owing to convection or turbulence for an hour (Stull, 1988; Garratt, 1994; Bonin et al., 2018). Among other factors (Garratt, 1994), the mixing layer height strongly depends on the intensity of wind turbulence.

There are different technical facilities that are widely used for turbulent parameter estimation in the atmospheric boundary layer (ABL) and determining the mixing layer height. Doppler sodars, radio acoustic systems, and Doppler lidars are the most suitable for this task, as they allow for meteorological data to be measured in real time with the required space and time resolution (Bonin et al., 2018; Emeis et al., 2008; Hogan et al., 2009; Tucker et al., 2009; Pichugina and Banta, 2010; Barlow et al., 2011; Helmis et al., 2012; Schween et al., 2014; Vakkari et al., 2015; Huang et al., 2017; Petenko et al., 2019). From the data of lidar measurements, the variance of radial velocity ${\mathit{\sigma }}_r^{\mathrm{2}}\left(h\right)$, variances of vertical ${\mathit{\sigma }}_w^{\mathrm{2}}\left(h\right)$ and horizontal ${\mathit{\sigma }}_u^{\mathrm{2}}\left(h\right)$ and ${\mathit{\sigma }}_v^{\mathrm{2}}\left(h\right)$ wind vector components, turbulence kinetic energy (TKE) E(h), and turbulent energy dissipation rate ε(h) can be estimated at different heights h.

In Bonin et al. (2018), Hogan et al. (2009), Tucker et al. (2009), Pichugina and Banta (2010), Barlow et al. (2011), Schween et al. (2014), Vakkari et al. (2015), and Huang et al. (2017), the mixing layer height (MLH) h_mix was determined from the decrease in the variance ${\mathit{\sigma }}_{\mathit{\alpha }}^{\mathrm{2}}\left(h\right)$ ($\mathit{\alpha }=r,w,u,v$ are indexes for designating the radial, vertical, and two horizontal components of wind velocity vector, respectively) with height h down to some minimum threshold value ${\mathit{\sigma }}_{\mathit{\alpha }}^{\mathrm{2}}\left(h_{\mathrm{mix}}\right)={\mathrm{Thr}}_{\mathit{\alpha }}$, at which the turbulence intensity becomes insufficient for efficient air mixing. The variances and MLH were estimated from pulsed coherent Doppler lidar (PCDL) data through the use of various measurement strategies and data processing algorithms (Bonin et al., 2018; Hogan et al., 2009; Tucker et al., 2009; Pichugina and Banta, 2010; Barlow et al., 2011; Schween et al., 2014; Vakkari et al., 2015; Huang et al., 2017; Manninen et al., 2018): (i) in the fixed strictly vertical direction of the probing beam (vertical stare mode), (ii) by scanning in vertical plane, and (iii) by conical scanning by a beam around the vertical axis at a certain elevation angle φ. In Bonin et al. (2018), the “composite fuzzy logic approach” based on the use of all three measurement geometries was applied to determine h_mix.

According to analysis (Tucker et al., 2009), lidar measurements of the vertical profile of the variance of vertical velocity ${\mathit{\sigma }}_w^{\mathrm{2}}\left(h\right)$ in the fixed vertical probing direction provide the best accuracy of estimation of the mixing layer height h_mix. However, it was shown (Bonin et al., 2018) that this is not always the case. In particular, during the propagation of internal gravity waves (IGWs), this method may significantly overestimate h_mix, and it becomes necessary to perform high-frequency filtering of the data.

The turbulence energy dissipation rate, as well as variances of the fluctuations of wind vector components, characterizes the turbulence (air mixing) intensity and can also be used for the estimation of h_mix. This was done for the first time in Vakkari et al. (2015), in which the diurnal profile of h_mix(t), where t is time, was determined from the space–time distributions of the dissipation rate ε(h,t). The dissipation rate ε(h,t) was estimated from temporal spectra of the vertical velocity measured by lidar in the fixed strictly vertical direction of the probing beam with the use of the Taylor “frozen turbulence” hypothesis (O'Connor et al., 2010).

A method for estimating the turbulence energy dissipation rate ε(h,t) from lidar data obtained with the use of conical scanning by a lidar probing beam around the vertical axis was developed in Banakh and Smalikho (2013) and Smalikho and Banakh (2017). This measurement geometry does not require invoking the frozen turbulence hypothesis. In contrast to O'Connor et al. (2010), this method (Banakh and Smalikho, 2013; Smalikho and Banakh, 2017) takes into account the spatial averaging of the radial velocity over probing volume. The algorithm for calculating the error of the lidar estimation of the dissipation rate by this method (Banakh and Smalikho, 2013; Smalikho and Banakh, 2017) can be found in Banakh et al. (2017). It was shown in Smalikho and Banakh (2017) that, in the case of moderate and strong turbulence and a sufficiently high signal-to-noise ratio SNR(h), when a relative error in estimating ε does not exceed 30 %, the accuracy of lidar estimates of the turbulence energy dissipation rate is, as a rule, markedly higher than the accuracy of estimation of the variances of different wind vector components from lidar data. The estimate of ε(h) remains reliable even during the appearance of IGWs with quite a high amplitude of harmonic oscillations of wind vector components (Banakh and Smalikho, 2018; Banakh et al., 2020).

In this paper, we report the results of estimating the turbulent mixing layer height from measurement data of the pulsed coherent Doppler lidar StreamLine obtained with the use of conically scanning by a probing beam. The mixing layer height h_mix(t) is determined from the height–temporal distributions of lidar estimates of the turbulence energy dissipation rate. The data used were obtained during smog conditions due to forest fires in Siberia in summer 2019. In this period the signal-to-noise ratio (SNR) was abnormally high for micropulse low-energy lidars such as StreamLine (pulse energy about 10 µJ). This gave us the opportunity to obtain vertical profiles of turbulence in the entire mixing layer. In contrast to previous works on this subject, the accuracy of estimation of the turbulent mixing layer height from lidar data is analyzed. The examples of comparison of the estimates of the turbulent mixing layer height from the dissipation rate and from the height–temporal distributions of the Richardson number obtained during an experiment in spring 2020 are listed in the paper as well.

2 Method for determination of the turbulent mixing layer height from PCDL data obtained by conical scanning

It was shown in Smalikho and Banakh (2017) that PCDL data obtained with the use of conical scanning by a probing beam around the vertical axis under the elevation angle φ could be used to estimate not only wind speed and direction but also space–time distributions of estimates of wind turbulence parameters. These parameters are the dissipation rate ε(h,t), the variance of the radial velocity ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}(h,t)$, and the integral scale of longitudinal correlation of turbulent fluctuations of radial velocity L_V(h,t). If the angle is φ=35.3^∘, then, with an allowance made for the relation $E=(\mathrm{3}/\mathrm{2}){\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}$ (Eberhard et al., 1989), two-dimensional TKE distributions E(h,t) can be assessed as well.

The method for obtaining the time series of the turbulent mixing layer height h_mix(t) from PCDL data measured by conical scanning by a probing beam consists of the following. A probing beam is rotated around the vertical axis z at the angle φ to the horizontal with a constant angular rate and the azimuth angle θ (the angle between the projection of the beam axis on the horizontal plane and the axis x), varying from 0 to 360^∘. During the scanning, the probing volume moves at the height h=Rsin φ along the circle of the base of the probing cone at a distance R from the lidar.

After the primary processing of coherently detected echo signals of PCDL, we obtained arrays of estimates of the signal-to-noise ratio $\mathrm{SNR}(R_k,{\mathit{\theta }}_m;n)$ and the radial velocity $V_L(R_k,{\mathit{\theta }}_m;n)$. Here, SNR is the ratio of the average heterodyne signal power to the noise power in a 50 MHz bandwidth, and the radial velocity is a projection of the wind vector onto the optical axis of the probing beam. The estimates of SNR and radial velocity V_L are functions of the distance from the lidar to the center of probing volume $R_k=R_{\mathrm{0}}+k\mathrm{\Delta }R$, azimuth angle θ_m=mΔθ, and the scan (full azimuth scan of 360^∘ at a certain elevation angle) number n. Here, $k=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },K-\mathrm{1}$; ΔR is the range gate length; $m=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },M-\mathrm{1}$; $\mathrm{\Delta }\mathit{\theta }=\mathrm{360}/M$ is the resolution in the azimuth angle, $n=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{\dots },N$.

The method (Smalikho and Banakh, 2017) for determining wind turbulence parameters from the array of lidar estimates of the radial velocity obtained with conical scanning is applicable if the probability P_b of a bad (false) estimate of the radial velocity is close to zero (for example, at $P_{\mathrm{b}}\le {\mathrm{10}}^{-\mathrm{4}}$). The instrumental error σ_e of a good estimate of the radial velocity (Frehlich and Yadlowsky, 1994; Banakh and Smalikho, 2013) and the probability P_b depend on the signal-to-noise ratio (SNR), which decreases with distance. The smaller the SNR, the larger σ_e and P_b. Thus, the maximum range for the probing of wind turbulence R_K−1 is determined by the value of SNR. The distances R_k correspond to heights h_k=R_ksin φ.

On the assumption that the wind field is a stationary process (within 1 h) and statistically homogeneous along the horizontal (within the circle of the base of the scanning cone), the array $V_L(R_k,{\mathit{\theta }}_m;n)$ was used to estimate the vector of the mean wind velocity $\langle \mathit{V}\left(h_k\right)\rangle =\mathit{\{}\langle V_z\rangle ,\langle V_x\rangle ,\langle V_y\rangle \mathit{\}}$, where V_z is the vertical component and V_x and V_y are the horizontal components of the wind vector $\mathit{V}=\mathit{\{}{V}_z,V_x,V_y\mathit{\}}$, by the sine wave fitting method (Banakh and Smalikho, 2013). Angular brackets indicate the average of an ensemble of realizations. Then, the array of random components of estimates of radial velocities is calculated as

$$\begin{array}{}\text{(1)}& V_L^{\prime }(R_k,{\mathit{\theta }}_m;n)=V_L(R_k,{\mathit{\theta }}_m;n)-\mathit{S}\left({\mathit{\theta }}_m\right)\langle \mathit{V}\left(h_k\right){\rangle }_N,\end{array}$$

where $\mathit{S}\left({\mathit{\theta }}_m\right)=\mathit{\{}\sin \mathit{\phi },\cos \mathit{\phi }\cos {\mathit{\theta }}_m,\cos \mathit{\phi }\sin {\mathit{\theta }}_m\mathit{\}}$ is the unit vector along the optical axis of the probing beam, and $\langle f\left(n\right){\rangle }_N=\frac{\mathrm{1}}{N}\sum _{n^{\prime }=n-N/\mathrm{2}}^{n+N/\mathrm{2}-\mathrm{1}}f(n+n^{\prime })$ is the average of N scans. The averaged (over all azimuth angles θ_m) variance ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_L^{\mathrm{2}}$ and the azimuthal structure function ${\stackrel{\mathrm{‾}}{D}}_L\left({\mathit{\psi }}_l\right)$ of the fluctuations of radial velocity measured by the lidar are calculated from this array for every height h_k by the following equations:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_L^{\mathrm{2}}=\langle {\displaystyle \frac{\mathrm{1}}{M}}\sum _{m=\mathrm{0}}^{M-\mathrm{1}}\left[V_L^{\prime }\right(R_k,{\mathit{\theta }}_m;n){]}^{\mathrm{2}}{\rangle }_N,\text{(3)}& {\displaystyle }\begin{array}{rl}{\stackrel{\mathrm{‾}}{D}}_L\left({\mathit{\psi }}_l\right)& =\langle {\displaystyle \frac{\mathrm{1}}{M-l}}\sum _{m=\mathrm{0}}^{M-l-\mathrm{1}}\left[V_L^{\prime }\right(R_k,{\mathit{\theta }}_m+{\mathit{\psi }}_l;n)\\ & -V_L^{\prime }(R_k,{\mathit{\theta }}_m;n){]}^{\mathrm{2}}{\rangle }_N,\end{array}\end{array}$$

where ψ_l=lΔθ and $l=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{\dots }$

According to Smalikho and Banakh (2017), the turbulence energy dissipation rate ε is determined by the azimuthal structure function ${\stackrel{\mathrm{‾}}{D}}_L\left({\mathit{\psi }}_l\right)$, which is calculated from the lidar data measured within the inertial subrange of turbulence by the following equation:

$$\begin{array}{}\text{(4)}& \mathit{\epsilon }={\left[{\displaystyle \frac{{\stackrel{\mathrm{‾}}{D}}_L\left({\mathit{\psi }}_l\right)-{\stackrel{\mathrm{‾}}{D}}_L\left({\mathit{\psi }}_{\mathrm{1}}\right)}{A\left(l\mathrm{\Delta }{y}_k\right)-A\left(\mathrm{\Delta }{y}_k\right)}}\right]}^{\mathrm{3}/\mathrm{2}},\end{array}$$

where A(y) is the theoretically calculated function, the equation for which can be found in Smalikho and Banakh (2017), Δy_k=ΔθR_kcos φ (Δθ is in radians), and l≥2. Then, the variance of radial velocity fluctuations ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}$ averaged over all azimuth angles θ_m is estimated as (Smalikho and Banakh, 2017)

$$\begin{array}{}\text{(5)}& {\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}={\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_L^{\mathrm{2}}-{\stackrel{\mathrm{‾}}{D}}_L\left({\mathit{\psi }}_{\mathrm{1}}\right)/\mathrm{2}+{\mathit{\epsilon }}^{\mathrm{2}/\mathrm{3}}\left[F\right(\mathrm{\Delta }{y}_k)+A(\mathrm{\Delta }{y}_k)/\mathrm{2}].\end{array}$$

The function F(y) in Eq. (5) is defined in Smalikho and Banakh (2017).

Equations (4) and (5) are used to obtain estimates of ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}$ and ε at different heights h_k and at different instants $t_{n^{\prime }}=n^{\prime }\mathrm{\Delta }t$, where $n^{\prime }=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },N^{\prime }$, Δt is defined by the duration of the scan Δt≈T_scan, and N^′ depends on the duration of measurements. For 24 h measurements, N^′ can be found from the equation $N^{\prime }\mathrm{\Delta }t=\mathrm{24}$ h. The mixing layer height h_mix for every instant $t_{n^{\prime }}$ is determined from the vertical profiles of ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}$ or ε obtained for this instant as the height, where ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}$ or ε decrease with height h_k down to the corresponding minimum threshold values ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}\left(h_{\mathrm{mix}}\right)={\mathrm{Thr}}_{\mathit{\sigma }}$ or ε(h_mix)=Thr_ε, at which the turbulence intensity is already insufficient for efficient mixing of air.

The algorithm for the evaluation of the mixing layer height is based on the serial search of values of ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}\left(h_k\right)$ or ε(h_k) at different heights h_k, starting from the minimum height h₀ up to the height at which the velocity variance or the dissipation rate decreases to the threshold Thr_σ or Thr_ε, respectively. When assessing the time series of the mixing layer height $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ from the height–temporal distributions $\mathit{\epsilon }(h_k,t_{n^{\prime }})$, we use Thr${}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³, which corresponds to the lower boundary of moderate turbulence. With weak turbulence $\mathit{\epsilon }<{\mathrm{10}}^{-\mathrm{4}}$ m²/s³, the turbulent mixing of air may be considered to be insignificant. The same threshold was used in Vakkari et al. (2015). For estimation of the MLH from the radial velocity variance profiles, we use the threshold Thr_σ=0.1 m²/s². According to the calculation using Eq. (1) in the paper by Banakh and Smalikho (2019), at such threshold values ($\mathit{\epsilon }={\mathrm{10}}^{-\mathrm{4}}$ m²/s³ and ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}=\mathrm{0.1}$ m²/s²), the integral scale of turbulence L_V is approximately 200 m in the case of lidar measurement at an elevation angle of 60^∘. Such L_V is quite consistent with the results of our measurements in the daytime at heights of 200–600 m. Therefore, we used this threshold (0.1 m²/s²) for the radial velocity variance.

3 Experiment during forest fires in Siberia in 2019

To study the atmospheric boundary layer in the air with intense smoke due to forest fires in Siberia in 2019, we conducted a lidar experiment on the measurement of wind turbulence parameters and determination of diurnal variations of the mixing layer height. Continuous measurements by the StreamLine lidar (Halo Photonics, Brockamin, Worcester, United Kingdom) were carried out from 20 to 29 July 2019 in the territory of the Basic Experimental Observatory (BEO) of the Institute of Atmospheric Optics SB RAS in the Tomsk suburbs (56.481430^∘ N, 85.099624^∘ E). During the experiment, the probing beam was focused to a distance of 500 m. Conical scanning by the probing beam around the vertical axis at the alternating elevation angles 35.3 and 60^∘ was used. For the accumulation of raw lidar data, N_a=7500 (until 12:30 UTC/GMT+7 on 22 July 2019) and N_a=3000 (after 12:30 UTC/GMT+7 on 22 July 2019) laser shots were used. The pulse repetition frequency was f_p=15 kHz. Thus, the duration of the measurements of an array of radial velocities $V_L(R_k,{\mathit{\theta }}_m;n)$ for each azimuth angle θ_m was, respectively, $\mathit{\delta }t=N_{\mathrm{a}}/f_{\mathrm{p}}=\mathrm{0.5}$ and 0.2 s. The time for one scan was T_scan=60 s. The azimuth resolution was $\mathrm{\Delta }\mathit{\theta }=\mathrm{360}{}^{\circ }/M=\mathrm{3}$^∘, where $M=T_{\mathrm{scan}}/\mathit{\delta }t=\mathrm{120}$ is the number of rays per scan at N_a=7500, and Δθ=1.2^∘, M=300 at N_a=3000. The range gate length was ΔR=18 m. At the beginning of the experiment, we set the maximum range R_K−1 equal to 2100 m (maximum measurement heights h_K−1 of 1213 and 1818 m at elevation angles of 35.3 and 60^∘, respectively), but after 12:30 UTC/GMT+7 on 22 July 2019 the maximum range R_K−1 was increased to 3000 m (h_K−1 of 1734 and 2600 m at elevation angles of 35.3 and 60^∘, respectively).

During the experiment, the optical characteristics of the atmosphere varied considerably. Most of the time, the aerosol backscatter coefficient far exceeded the background level owing to the smog from the forest fires. The signal-to-noise ratio (SNR) was abnormally high for lidars such as StreamLine and sometimes achieved 0 dB in the cloudless atmosphere at a height of 500 m when scanning at an elevation angle of 60^∘. This can be seen from the data for SNR on 20 and 21 July 2019 in Fig. 5a. Under these conditions, with the method of filtered sine wave fitting (FSWF) (Smalikho, 2003), we succeeded in retrieving the vertical profiles of wind speed and direction up to a height of 2.5 km. Unfortunately, during the lidar measurements on 26 and 27 July, there was a series of technical failures (rather lengthy), which made the obtained data unusable. In the last 2 d of the experiment, the smog disappeared, and the atmosphere became so clear that the echo from distances exceeding 500 m was very weak: $\mathrm{SNR}<-\mathrm{16}$ dB. Estimates of wind turbulence parameters from the data obtained at this SNR have a relative error exceeding 30 % (the method for calculating the error is described in papers by Banakh et al., 2017, 2020). In some time intervals of 20, 22, 24, and 25 July (white areas in Fig. 5a for SNR), the lidar measurements were carried out under conditions of dense fog or low cloudiness, which were serious obstacles to obtaining information about wind and turbulence in the entire atmospheric boundary layer and, correspondingly, to accurately determining the mixing layer height from lidar measurements. Thus, we have data measured by the lidar for 6 d (from 20 to 25 July 2019) and which can be used to determine the height of the mixing layer.

Each of the obtained arrays of estimates of the signal-to-noise ratio $\mathrm{SNR}(R_k,{\mathit{\theta }}_m;n)$ and the radial velocity $V_L(R_k,{\mathit{\theta }}_m;n)$ contained two sub-arrays, ${\mathrm{SNR}}_i(R_k,{\mathit{\theta }}_m;n)$ and $V_{Li}(R_k,{\mathit{\theta }}_m;n)$, where the subscript i=1 corresponds to measurements at the elevation angle $\mathit{\phi }={\mathit{\phi }}_{\mathrm{1}}=\mathrm{35.3}$^∘ (odd scan numbers n), and i=2 corresponds to measurements at $\mathit{\phi }={\mathit{\phi }}_{\mathrm{2}}=\mathrm{60}$^∘ (even n). The elevation angle φ was alternated from 60^∘ on 35.3^∘ or vice versa during the time interval Δτ≈1.5 s. The height–temporal distributions of the absolute value of the speed $U_i(h_{ki},t_{n^{\prime }})$ and direction angle ${\mathit{\theta }}_{Vi}(h_{ki},t_{n^{\prime }})$ of the horizontal wind and the vertical wind velocity $W_i(h_{ki},t_{n^{\prime }})$, where h_ki=R_ksin φ_i, $t_{n^{\prime }}=t_{\mathrm{0}i}+n^{\prime }\mathrm{2}(T_{\mathrm{scan}}+\mathrm{\Delta }\mathit{\tau })$, $n^{\prime }=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots }$, were calculated from the arrays $V_{Li}(R_k,{\mathit{\theta }}_m;n)$ through the methods of direct and filtered sine wave fitting (Banakh and Smalikho, 2013). The height–temporal distributions of the signal-to-noise ratio ${\mathrm{SNR}}_i(h_{ki},t_{n^{\prime }})$ for every nth scan were found as a result of averaging ${\mathrm{SNR}}_i(R_k,{\mathit{\theta }}_m;n)$ over all the azimuth angles θ_m.

4 Results of the experiment

First, we will consider the results of lidar measurements in a cloudless atmosphere (at least up to height of 1800 m) and at the highest signal-to-noise ratio. Figure 1 shows the height–temporal distributions ${\mathrm{SNR}}_i(h_{ki},t_{n^{\prime }})$, $U_i(h_{ki},t_{n^{\prime }})$, ${\mathit{\theta }}_{Vi}(h_{ki},t_{n^{\prime }})$, and $W_i(h_{ki},t_{n^{\prime }})$ obtained from measurements on 21 July 2019. Owing to the smog, the signal-to-noise ratio was high, and at an elevation angle of 60^∘, it exceeded −10 dB for the entire day in the 1 km atmospheric layer adjacent to the ground. Most of the time, in the layer above 500 m, SNR₁(h)<SNR₂(h) at the same height h since the echo signal travels a longer distance at smaller elevation angles. The analysis of wind data for this day shows that for the 30 min moving average of lidar estimates of wind velocity vector components, there are practically no differences between U₁(h,t) and U₂(h,t) or between θ_V1(h,t) and θ_V2(h,t) up to a height of 1200 m.

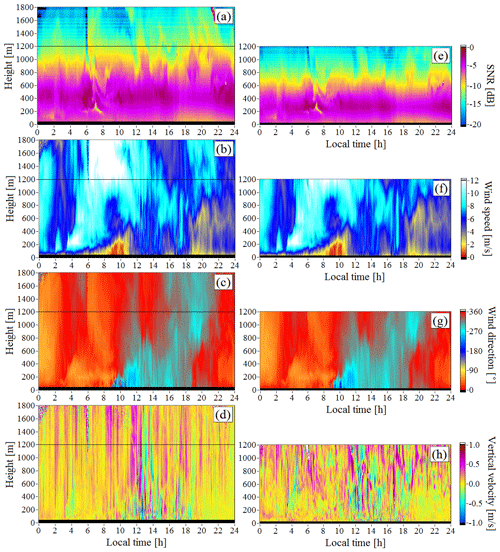
Figure 1 Height–temporal distributions of the signal-to-noise ratio (a, e), wind speed (b, f), wind direction angle (c, g), and vertical component of the wind vector (d, h) for elevation angles of 60^∘ (a–d) and 35.3^∘ (e–h) on 21 July 2019.

From the obtained arrays of lidar estimates of the radial velocity $V_{L\mathrm{1}}(R_k,{\mathit{\theta }}_m;n)$ and $V_{L\mathrm{2}}(R_k,{\mathit{\theta }}_m;n)$, the height–temporal distributions of the turbulence energy dissipation rate ${\mathit{\epsilon }}_i(h_{ki},t_{n^{\prime }})$ and the variance of radial velocity ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{ri}^{\mathrm{2}}(h_{ki},t_{n^{\prime }})$ up to heights of 1200 m (i=1, elevation angle φ=35.3^∘) and 1800 m (i=2, φ=60^∘) were calculated by Eqs. (1)–(5). In the calculations with Eqs. (2) and (3), we took N=15. For scanning at two angles at T_scan=60 s, this corresponds to the approximately 30 min average of measured data. The calculated results are shown in Figs. 2 and 3. The black color in these figures and in Fig. 5 represents a lack of data because of their low quality owing to an insufficiently high signal-to-noise ratio (Banakh et al., 2017).

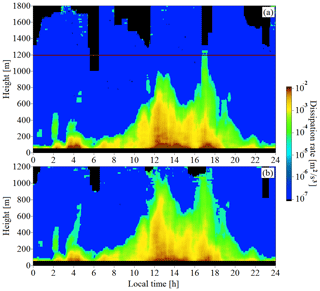
Figure 2 Height and time distributions of the turbulence energy dissipation rate at elevation angles of 60^∘ (a) and 35.3^∘ (b). Measurements were taken on 21 July 2019.

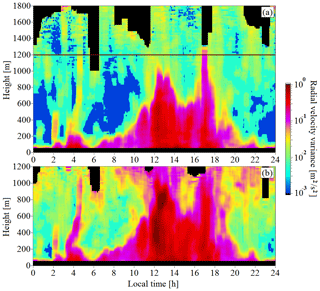
Figure 3 Height and time distributions of the variance of radial velocity at elevation angles of 60^∘ (a) and 35.3^∘ (b). Measurements were taken on 21 July 2019.

A comparison of the data in Fig. 2a and b for the lower 1 km layer of the atmosphere demonstrates the closeness of the estimates ε₁(h,t) and ε₂(h,t) obtained from measurements at different elevation angles, which is in agreement with the results of Banakh and Smalikho (2019) and confirms the assumption of horizontal homogeneity of the turbulent wind field. The difference in the estimates of the radial velocity ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{r\mathrm{1}}^{\mathrm{2}}(h,t)$ and ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{r\mathrm{2}}^{\mathrm{2}}(h,t)$ measured at different elevation angles (see Fig. 3a and b) is more significant than that for the dissipation rate and is caused by the anisotropy of wind turbulence (Banakh and Smalikho, 2019).

The mixing layer height h_mix was determined from the obtained height–temporal distributions of ${\mathit{\epsilon }}_i(h_k,t_{n^{\prime }})$ and ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{ri}^{\mathrm{2}}(h_k,t_{n^{\prime }})$ for every instant $t_{n^{\prime }}$ with the use of the relations ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}\left(h_{\mathrm{mix}}\right)={\mathrm{Thr}}_{\mathit{\sigma }}=\mathrm{0.1}$ m²/s² and $\mathit{\epsilon }\left(h_{\mathrm{mix}}\right)={\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³. The maximum height of the estimation of the temporal MLH series was 1.2 km for the measurements at an elevation angle of 35.3^∘ and 1.8 km for the measurements at an angle of 60^∘. The minimum height was h₀=60 m. If the estimates of ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}(h_{\mathrm{0}},t_{n^{\prime }})$ or $\mathit{\epsilon }(h_{\mathrm{0}},t_{n^{\prime }})$ at a height of 60 m were smaller than the corresponding threshold, we did not estimate the mixing layer height for such cases. If the estimates of ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_r^{\mathrm{2}}(h_{\mathrm{0}},t_{n^{\prime }})$ or $\mathit{\epsilon }(h_{\mathrm{0}},t_{n^{\prime }})$ at the maximum height exceeded the threshold, we took h_mix to be equal to the maximum height of retrieval of the vertical profiles of turbulence parameters.

Figure 4 shows the diurnal time series of $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ obtained from the height–temporal distributions of the dissipation rate and the variance of radial velocity shown in Figs. 2 and 3. One can see that for the diurnal series of the turbulent mixing layer height retrieved from measurements of the dissipation rate at elevation angles of 35.3 and 60^∘, we have, with rare exceptions, rather close results. The temporal series $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ calculated from the variances differ more widely as a result of turbulence anisotropy (Banakh and Smalikho, 2019).

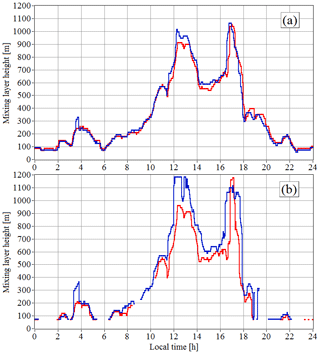
Figure 4 Temporal series of the turbulent mixing layer height (thickness) obtained from spatiotemporal distributions of the turbulence energy dissipation rate (a) and the variance of radial velocity (b). Scanning at elevation angles of 60^∘ (red curves) and 35.3^∘ (blue curves). Measurements were taken on 21 July 2019. The data of Figs. 2 and 3 are used.

Since the temporal MLH series found from estimates of the dissipation rate at different elevation angles differ insignificantly, for other days of the experiment, we calculated $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ from the estimates of the dissipation rate obtained by scanning at an elevation angle 60^∘. The signal-to-noise ratio (SNR) at heights above 500 m is markedly higher at an elevation angle of 60^∘ than at φ=35.3^∘ (Fig. 1a and e). Thus, measurements at 60^∘ provide an estimation of turbulence intensity at higher levels.

Figure 5 shows the height–temporal distributions over of the signal-to-noise ratio, wind velocity, wind direction angle, and turbulent energy dissipation rate, retrieved from lidar measurements during 6 d of the considered experiment. From the data for the SNR, it can be seen that in the morning hours of 20, 22, and 25 July, there was cloudiness at low heights, which rose over time due to convection. During the first 3 d of the experiment, the wind was predominantly northerly. From 11:00 to 19:00 UTC/GMT+7 on 21 July (see Fig. 1c and g, as well), the wind direction changed to the west, and there were significant changes in the wind direction with height, which is apparently the reason for the local minimum of the mixing layer height at about 15:00 UTC/GMT+7 (see Fig. 4). From about 12:00 UTC/GMT+7 on 23 July to 18:00 UTC/GMT+7 on 24 July the wind was predominantly southerly.

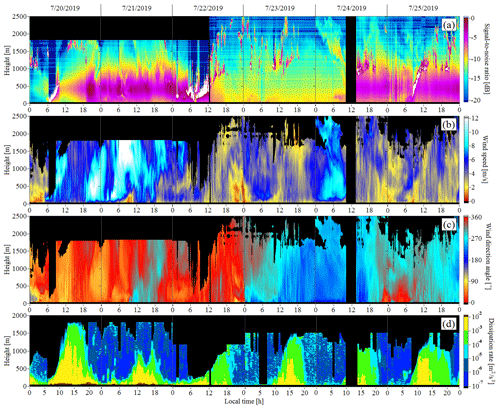
Figure 5 Height and time distributions of SNR (a), wind speed (b), wind direction angle (c), and turbulent energy dissipation rate (d) retrieved from StreamLine lidar measurements at elevation angles of 60^∘.

Using the data in Fig. 5 for the dissipation rate $\mathit{\epsilon }(h_k,t_{n^{\prime }})$ and the threshold $\mathit{\epsilon }\left(h_{\mathrm{mix}}\right)={\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³, we obtained the dependence of the height of the mixing layer on time $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ during 6 d of the experiment (from 20 to 25 July 2019). The time series $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ are shown in Fig. 6. One can see from Fig. 6 that on 20 and 25 July the time series of MLH are practically identical during the period from 08:00 to almost 12:00 UTC/GMT+7. In both cases, the increase in h_mix was accompanied by the rise of the cloud base due to convection (see Fig. 5a for SNR). It follows from Fig. 6 that between 12:00 and 18:00 UTC/GMT+7 in the daytime, the mixing layer height varied widely between 400 and 1800 m.

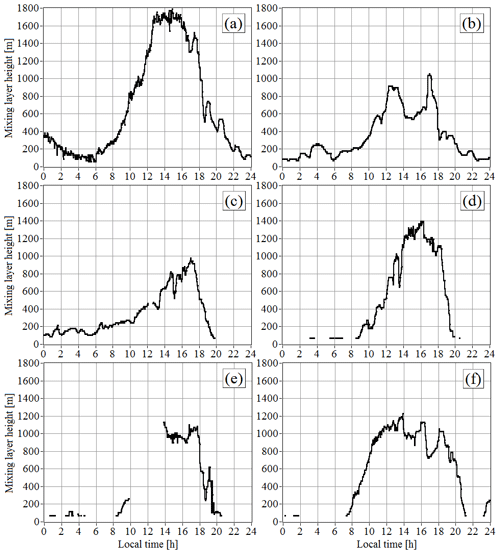
Figure 6 Time series of the turbulent mixing layer height (thickness) obtained from lidar data on 20 July (a), 21 July (b), 22 July (c), 23 July (d), 24 July (e), and 25 July (f) of 2019.

From 00:00 to 07:00 UTC/GMT+7 in the morning and 21:00 to 24:00 UTC/GMT+7 in the evening, when the temperature stratification, according to data of sonic anemometers employed in this experiment, was stable, approximately in half of the cases the MLH could not been estimated, since the values of the dissipation rate at the lowest height (h₀=60 m) were less than the threshold of 10⁻⁴ m²/s³. The choice of the minimum height h₀=60 m in the measurements at the elevation angle φ=60^∘ is explained by the fact that the minimum range of the pulsed coherent Doppler lidar should be no smaller than the two lengths of the probing volume (Smalikho et al., 2015). Used in the experiment range gate length ΔR=18 m corresponds to a 120 ns time window. Hence, according to calculations by Eq. (2.34) in Banakh and Smalikho (2013), the StreamLine lidar emitting 170 ns pulses formed a probing volume with a longitudinal dimension of 30 m.

The results shown in Fig. 6 do not contradict the known experimental data relative to estimates of the absolute values of the mixing layer height at different times of the day and night (Tucker et al., 2009; Barlow et al., 2011; Vakkari et al., 2015; Huang et al., 2017; Bonin et al., 2018; Manninen et al., 2018). Nevertheless, we made an attempt to determine the accuracy of the lidar estimate of the mixing layer height for conditions of this experiment.

5 Error of MLH estimation

The accuracy of MLH estimation from the PCDL data obtained with the use of conical scanning is determined by the error of estimation of the turbulence energy dissipation rate in the relatively thin atmospheric layer centered at the height h_mix. To determine this error, we calculated not only height–temporal distributions of the dissipation rate $\mathit{\epsilon }(h_k,t_{n^{\prime }})$ but also instrumental errors of lidar estimation of the radial velocity ${\mathit{\sigma }}_{\mathrm{e}}(h_k,t_{n^{\prime }})$ by Eq. (23) from Smalikho and Banakh (2017). Then, the relative errors of lidar estimation of the turbulence energy dissipation rate $E_{\mathit{\epsilon }}(h_k,t_{n^{\prime }})(E_{\mathit{\epsilon }}={\left[\langle (\widehat{\mathit{\epsilon }}/\mathit{\epsilon }-\mathrm{1}{)}^{\mathrm{2}}\rangle \right]}^{\mathrm{1}/\mathrm{2}}\times \mathrm{100}$ %, where $\widehat{\mathit{\epsilon }}$ is the estimate and ε is true dissipation rate) were calculated with the use of the distributions of the dissipation rate $\mathit{\epsilon }(h_k,t_{n^{\prime }})$ and the instrumental error ${\mathit{\sigma }}_{\mathrm{e}}(h_k,t_{n^{\prime }})$ by Eqs. (6)–(11) from Banakh et al. (2017), and the time series of this error $E_{\mathit{\epsilon }}\left(h_{\mathrm{mix}}\right(t_{n^{\prime }}\left)\right)$ at heights $h_{\mathrm{mix}}\left(t_{n^{\prime }}\right)$ were determined.

Figure 7 illustrates the behavior of the relative error $E_{\mathit{\epsilon }}\left(h_{\mathrm{mix}}\right(t_{n^{\prime }}\left)\right)$ for the diurnal time series of MLH shown in Fig. 6. It follows from Fig. 7a that the relative errors $E_{\mathit{\epsilon }}\left(h_{\mathrm{mix}}\right(t_{n^{\prime }}\left)\right)$ exceed 30 % for measurements on 20 July in the period between 00:00 and 06:00 UTC/GMT+7. This is explained by the relatively large instrumental error of estimation of the radial velocity due to the low signal-to-noise ratio ($\mathrm{SNR}<-\mathrm{15}$ dB, see Fig. 5a). On the same day, in the period between 11:00 and 18:00 UTC/GMT+7, the signal-to-noise ratio at heights above 1 km did not exceed −10 dB (Fig. 5a) and sometimes decreased to the lowest threshold $\mathrm{SNR}=-\mathrm{16}$ dB, at which the probability of a bad (false) estimate of the radial velocity P_b can still be considered close to zero. As a result, the instrumental error of estimation of the radial velocity σ_e is much larger than that at heights below 1 km. As the mixing layer height increases, SNR decreases, and the error σ_e increases too (and vice versa for a decrease in h_mix). This explains the initial increase in the relative error of estimation of the dissipation rate E_ε and its subsequent decrease in the considered period between 11:00 and 18:00 UTC/GMT+7. In the other periods, as can be seen from Fig. 7a, the error E_ε is about 10 %, which provides high accuracy of the determination of the mixing layer height.

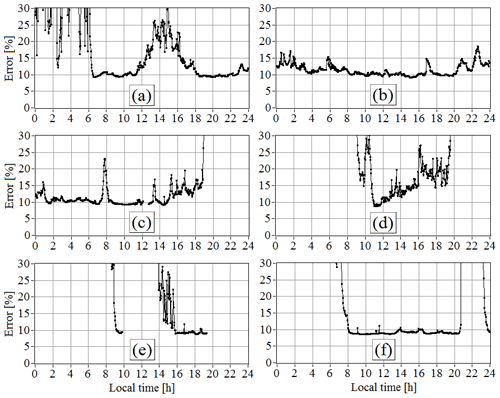
Figure 7 Relative error of estimation of the turbulent energy dissipation rate at the mixing layer heights determined from measurements on 20 July (a), 21 July (b), 22 July (c), 23 July (d), 24 July (e), and 25 July (f) of 2019.

On 21 July, the signal-to-noise ratio in the 1 km layer adjacent to the Earth's surface was very high most of the time (see Figs. 1a or 5a). Correspondingly, the instrumental error of estimation of the radial velocity σ_e within the mixing layer did not exceed 0.1 m/s. Therefore, according to the data in Fig. 7b, the error of estimation of the dissipation rate E_ε(h_mix) was low (mostly about 10 %) and did not exceed 18 %.

According to the data in Fig. 7c, the relative error of the dissipation rate estimates in the period 00:00 to 18:00 UTC/GMT+7 on 22 July did not exceed 25 %. This is due to the rather high signal-to-noise ratio at the top of the mixing layer (see Figs. 5a and 6c). On 23 July, the signal-to-noise ratio was low. Within the mixing layer, SNR is $\sim -\mathrm{10}$ dB at a height of 100 m and $\sim -\mathrm{15}$ dB at a height of 1 km (see Fig. 5a). As a result, the relative error E_ε(h_mix) varied widely from 10 % to 30 % (mostly larger than 15 %), as is indicated by Fig. 7d.

Due to the lack of measurement data on 24 July from about 10:00 to 13:30 UTC/GMT+7, and very weak turbulence on this day at night and in the evening, we calculated the relative errors in estimating the dissipation rate in a short period of time, as can be seen in Fig. 7e.

In the period between 08:00 and 20:40 UTC/GMT+7 on 25 July, as is seen in Fig. 7f, the dissipation rate was determined with very high accuracy. The relative error E_ε(h_mix) did not exceed 15 %, mostly 9 %, which is explained by the very high signal-to-noise ratio (see Fig. 5a). Despite the fact that the SNR was also rather high for the rest of the time, the accuracy of the dissipation rate estimation in the periods from 00:00 to 07:00 and from 21:00 to 23:00 UTC/GMT+7 on 25 July was low, and the relative error E_ε(h_mix) exceeded 30 %. The reason for this is that the dissipation rate at the height $h_{\mathrm{mix}}=h_{\mathrm{0}}=\mathrm{60}$ m during this time, according to Fig. 5a, was smaller by approximately an order of magnitude than the threshold value ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³.

With the use of the algorithm in Smalikho and Banakh (2013), we conducted a series of closed numerical experiments on the retrieval of vertical profiles of the turbulence energy dissipation rate ε(h_k) from simulated lidar data. The purpose of these experiments is to reveal the degree of impact of the signal-to-noise ratio and the vertical gradient of the dissipation rate on the accuracy of estimating h_mix by the proposed method. The simulation was performed for different values of the signal-to-noise ratio (SNR) and the vertical gradient of the dissipation rate $\mathit{\gamma }=-\mathrm{d}\mathit{\epsilon }/\mathrm{d}h>\mathrm{0}$ at the height h, where the dissipation rate was set equal to $\mathit{\epsilon }={\mathrm{10}}^{-\mathrm{4}}$ m²/s³. The turbulent mixing layer height was estimated from the profiles of ε(h_k) obtained in the numerical experiments with the use of the threshold ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³. The obtained estimates ${\widehat{h}}_{\mathrm{mix}}$ were compared with the preset values h_mix. The analysis of results of the numerical experiments shows that the accuracy of estimates ${\widehat{h}}_{\mathrm{mix}}$ depends significantly not only on SNR but also on the vertical gradient of the dissipation rate γ. The smaller the value of γ (the slower the decrease in the dissipation rate with height), the larger the error ${\mathit{\sigma }}_h=\sqrt{\langle ({\widehat{h}}_{\mathrm{mix}}-h_{\mathrm{mix}}{)}^{\mathrm{2}}\rangle }$.

Calculation of the error σ_h, using the data of the above experiment, with the algorithm in Smalikho and Banakh (2013), would require very computationally expensive simulation. The error of MLH estimation was determined in another way. To this end, on the assumption that E_ε(h_k)<30 %, the random estimate of the dissipation rate $\widehat{\mathit{\epsilon }}\left(h_k\right)$ at the height h_k was taken as

$$\begin{array}{}\text{(6)}& \widehat{\mathit{\epsilon }}\left(h_k\right)=\mathit{\epsilon }\left(h_k\right)\left[\mathrm{1}+{\displaystyle \frac{E_{\mathit{\epsilon }}\left(h_k\right)}{\mathrm{100}\mathit{\%}}}\mathit{\xi }\left(h_k\right)\right],\end{array}$$

where ε(h_k) and E_ε(h_k) are respectively the estimate of the dissipation rate and its relative error obtained from the data of the lidar experiment, and ξ(h_k) is a pseudo-random number obeying the Gaussian statistics with zero mean 〈ξ〉=0 and unit variance 〈ξ²〉=1. To construct the vertical profile $\widehat{\mathit{\epsilon }}\left(h_k\right)$, random numbers ξ(h_k) for different heights h_k were generated in accordance with the correlation function $C_{\mathit{\xi }}\left(l\mathrm{\Delta }h\right)=\langle \mathit{\xi }(h_{\mathrm{mix}}+l\mathrm{\Delta }h/\mathrm{2})\mathit{\xi }(h_{\mathrm{mix}}-l\mathrm{\Delta }h/\mathrm{2})\rangle$, where h_mix is the turbulent mixing layer height determined from the atmospheric experiment, $l=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{\dots }$, and Δh=15.6 m is a step in height at ΔR=18 m and φ=60^∘. The correlation function C_ξ(lΔh) was found from averaging of random realizations of $\mathit{\xi }(h_{\mathrm{mix}}+l\mathrm{\Delta }h/\mathrm{2})\mathit{\xi }(h_{\mathrm{mix}}-l\mathrm{\Delta }h/\mathrm{2})$ at the values of h_mix and SNR observed in the experiment (Figs. 5a, d, 6). For the error E_ε(h_k)<30 % and ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³, the correlation function C_ξ(lΔh) weakly depends on SNR and h_mix, which considerably simplifies the procedure of numerical simulation of $\widehat{\mathit{\epsilon }}\left(h_k\right)$ by Eq. (6).

Let us consider an example of calculating the error in estimating the height of the mixing layer from the lidar data of an atmospheric experiment. Figure 8 shows the altitude profiles of the signal-to-noise ratio, the instrumental error in estimating the radial velocity, the relative error in estimating the rate of dissipation, and the dissipation rate itself. Data were taken from lidar measurements from 17:40 to 18:20 UTC/GMT+7 on 20 July 2019. It can be seen that in a layer up to 1400 m the signal-to-noise ratio is so high that the instrumental error in estimating the radial velocity and the relative error in estimating the dissipation rate do not exceed 0.3 m/s (Fig. 8b) and 30 % (Fig. 8c), respectively. According to Fig. 8d, the point of intersection of the vertical profile ε(h_k) of the threshold ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³ is at a height h_mix=976 m. At this height, the vertical gradient of the dissipation rate $\mathit{\gamma }=\mathrm{2.7}\times {\mathrm{10}}^{-\mathrm{7}}$ m/s³.

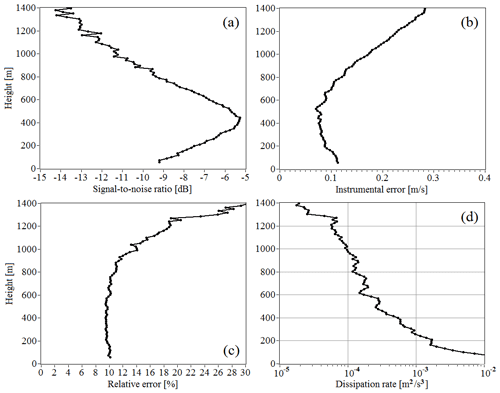
Figure 8 Vertical profiles of signal-to-noise ratio (a), instrumental error of radial velocity estimate (b), relative error of estimation of the turbulent energy dissipation rate (c), and turbulent energy dissipation rate (d) retrieved from measurements from 17:40 to 18:20 on 20 July 2019.

Figure 9 shows (as red curves) statistically independent random realizations of vertical profiles of the dissipation rate $\widehat{\mathit{\epsilon }}\left(h_k\right)$ simulated by Eq. (6) using the data in Fig. 8c (E_ε(h_k)) and Fig. 8d (ε(h_k)). The estimates of the mixing layer height ${\widehat{h}}_{\mathrm{mix}}$ determined from each of the simulated profiles $\widehat{\mathit{\epsilon }}\left(h_k\right)$ are given in Fig. 9 as well. Using 100 000 independent estimates ${\widehat{h}}_{\mathrm{mix}}$, we found that the error in estimating the height of the mixing layer σ_h=69 m.

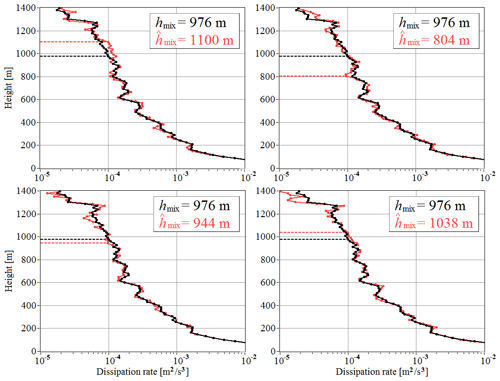
Figure 9 Measured (black curve taken from Fig. 8d) and four examples of random realizations of simulated (red curves obtained with the use of Eq. 6 and data of Fig. 8c and d) vertical profiles of the turbulent energy dissipation rate.

Figure 10 shows the errors in the estimates of the mixing layer height ${\mathit{\sigma }}_h\left(t_{n^{\prime }}\right)$ obtained from lidar measurements during 6 d of the experiment (from 20 to 25 July 2019). The figure shows that, depending on the atmospheric conditions (signal-to-noise ratio and the vertical gradient of the dissipation rate), the error in the lidar estimate of the mixing layer height varies from 10 to 100 m or more. Even with a very high SNR and small error of estimation of the dissipation rate, the error ${\mathit{\sigma }}_h\left(t_{n^{\prime }}\right)$ can exceed 100 m due to the small value of the vertical gradient of the dissipation rate γ (see data in Figs. 5a and d, 7f, and 10f for the time interval 19:00–20:00 UTC/GMT+7 on 25 July 2019).

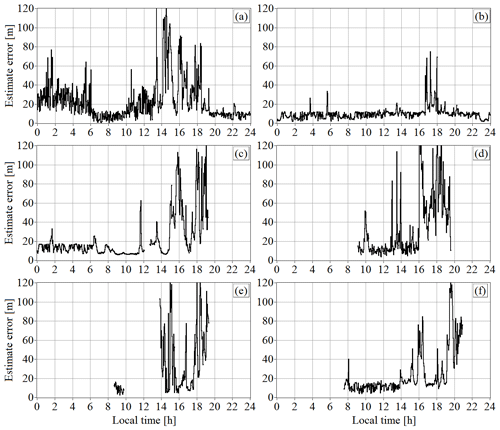
Figure 10 Error of estimation of the mixing layer heights determined from measurements on 20 July (a), 21 July (b), 22 July (c), 23 July (d), 24 July (e), and 25 July (f) of 2019.

Calculations of the relative error $E_h=({\mathit{\sigma }}_h/h_{\mathrm{mix}})\times \mathrm{100}$ % of lidar estimation of the turbulent mixing layer height, carried out using the data in Figs. 6 and 10, showed that, with rare exceptions, E_h does not exceed 30 %, and for data measured from 12:00 to 18:00 UTC/GMT+7, E_h varies from 2 % to 10 %. It should be noted that the relative error E_h does not exceed 20 % if the estimate of the mixing layer height is obtained from lidar measurements with SNR of at least −16 dB.

6 Comparison with the Richardson number

One of the parameters characterizing the stability of the atmospheric boundary layer is the gradient Richardson number,

$$\begin{array}{}\text{(7)}& \mathit{Ri}=N^{\mathrm{2}}{\left({\displaystyle \frac{\partial U}{\partial h}}\right)}^{-\mathrm{2}},\end{array}$$

where

$$\begin{array}{}\text{(8)}& N^{\mathrm{2}}={\displaystyle \frac{g}{T_{\mathrm{p}}}}{\displaystyle \frac{\partial T_{\mathrm{p}}}{\partial h}},\end{array}$$

$T_{\mathrm{p}}(h,t)=T(h,t)+{\mathit{\gamma }}_{\mathrm{a}}h$ is the potential temperature, T(h,t) is the temperature of the air, γ_a=0.0098 ^∘/m is the dry-adiabatic lapse rate, and $\partial T_{\mathrm{p}}(h,t)/\partial h=\partial T(h,t)/\partial h+{\mathit{\gamma }}_{\mathrm{a}}$. The gradient Richardson number can be used to estimate the turbulent mixing layer height (Helmis et al., 2012; Petenko et al., 2019; Gibert et al., 2011).

For additional proof of the suitability of the method for estimating the turbulent mixing layer height from lidar data obtained with the use of conical scanning, we conducted a lidar experiment with concurrent measurement of the temperature. The experiment was conducted from 8 April to 6 May 2020. The temperature was measured by the MTP-5 microwave temperature profiler (Atmospheric Technology, Dolgoprudny, Moscow, Russia). This profiler is widely used in atmospheric research currently. The accuracy of temperature measurement and experience of the use of this device in the atmospheric boundary layer research is discussed in references 51–58 cited in Banakh et al. (2020). The temperature profiler and the wind lidar StreamLine were installed on the roof of the Institute of Atmospheric Optics (IAO) building in Tomsk (56.475504^∘ N, 85.048225^∘ E) 4 km from the Basic Experimental Observatory. The profiler provided measurements of the vertical temperature profiles every 5 min, with a resolution of 25 m for heights from 0 to 100 m and a resolution of 50 m for heights from 100 to 1000 m with respect to the height of its installation. As a result, we obtained the height–temporal distributions of the air temperature T(h,t). In calculating the derivative $\partial T_{\mathrm{p}}(h,t)/\partial h$ and the parameter N² (Eq. 8), we used the temperature measurement data averaged over a 10 min period. Then, the Richardson number Ri was calculated by Eq. (7). The mean horizontal wind velocity U and its derivative $\partial U/\partial h$ in Eq. (7) were assessed from the lidar data averaged, as with the temperature, over a 10 min period (10 scans). The parameters and geometry of the lidar measurements were the same as those in July 2019. The scanning was carried out at an elevation angle of 60^∘.

In contrast to uniquely high SNR for lidar StreamLine in July 2019, during this experiment the signal-to-noise ratio was rather low. It did not allow us to obtain estimates of the wind velocity with an acceptable error at heights above 800 m–1 km. The conditionSNR $>-\mathrm{16}$ dB, which provides an acceptable error in estimating the dissipation rate by the method used (Smalikho and Banakh, 2017), was violated at heights above 400 m. As a consequence, the relative errors of estimation of the turbulence energy dissipation rate and the turbulent mixing layer height could exceed 30 % starting from heights of 400 m. Moreover, the weather was rainy and snowy during the experiment often, and not all the measurement data could be used in processing. Nevertheless, the height–temporal distributions of the dissipation rate obtained in the experiment allowed us to monitor the turbulent mixing layer height by the threshold ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³ in many cases.

Figure 11 shows the daily height–temporal distributions of the turbulence energy dissipation rate and the Richardson number assessed from the data of wind velocity and temperature measurements on 10, 12, 15, 21, 22, 26, and 27 April and on 1 May 2020. The distributions illustrate typical stratification regimes which were observed in the atmospheric boundary layer during the experiment. White curves in Fig. 11 show the diurnal time series of the turbulent mixing layer height, as estimated from the threshold value ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³ for the turbulence energy dissipation rate. Red curves in Fig. 11 show the diurnal time series of the SNR at the level −16 dB. Black color on the Richardson number distributions in Fig. 11 shows the zones where Ri<0.5.

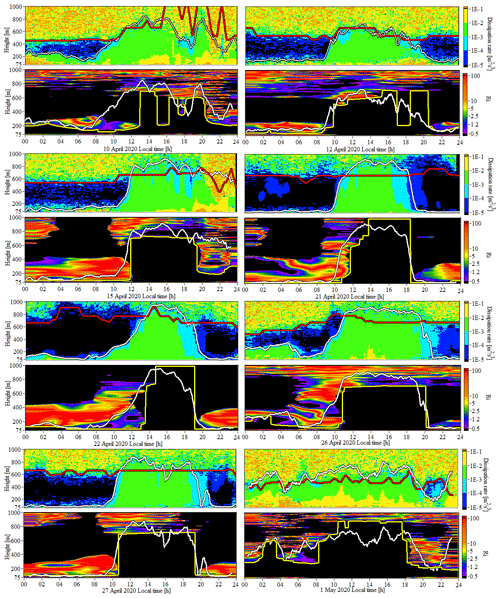
Figure 11 Height–temporal distributions of the turbulence energy dissipation rate and the Richardson number as obtained from measurements on 10, 12, 15, 21, 22, 26, and 27 April and on 1 May 2020. White curves reproduce the diurnal time series of the turbulent mixing layer height, as estimated from the turbulence energy dissipation rate. Red curves show the diurnal time series of the SNR at the level −16 dB. Black color on the Richardson number distributions shows the zones where Ri<0.5. Yellow curves show the diurnal time series of the turbulent mixing layer height, estimated as a minimum height, above which the Richardson number exceeds 0.5.

When estimating the daily variations in the height of the turbulent mixing layer from the height–temporal distributions of the Richardson number, we considered the following. According to the classification of the atmospheric turbulent regimes based on the Richardson number (Baumert and Peters, 2009; Grachev et al., 2013), the small-scale turbulence becomes weak at gradient Richardson numbers more than 0.5. Therefore, it is natural to believe that the turbulent mixing occurs at the time and heights at which the Richardson number Ri<0.5. Thus, the minimum height, above which the Richardson number exceeds 0.5, can be taken as the height of the turbulent mixing layer at the current time moment. Yellow curves show the diurnal time series of the turbulent mixing layer height h_mixR, as estimated from the distributions of the Richardson number using this criterion.

The temporal variations of the MLH estimated from the dissipation rate of turbulence energy reproduce the development of the turbulence in the daytime observed from the height–temporal distributions of the Richardson number on 15, 21, 26, and 27 April 2020 with good accuracy. For these days in the period between 12:00 and 18:00 UTC/GMT+7 the estimates of the MLH based on the dissipation rate h_mix (white curves) differ from the MLH estimates calculated based on the Richardson number h_mixR (yellow curves) insignificantly. The relative divergence of the heights h_mix and h_mixR, determined as ${\mathit{\sigma }}_{\mathrm{hR}}=\left|h_{\mathrm{mix}}-h_{\mathrm{mixR}}\right|/\left(\right(h_{\mathrm{mix}}+h_{\mathrm{mixR}})/\mathrm{2})$, is less than 25 % on average in these periods.

The criterion used for determining h_mixR is sensitive to the small spots with Ri>0.5 against the background areas with Ri<0.5, while the estimates of the MLH based on the dissipation rate do not “notice” them. It is the reason for the strong divergence of h_mix and h_mixR in the morning hours on 10, 12, 21, 22, and 26 April and on the 1 May. This is also a reason for the strong divergence of h_mix and h_mixR in the afternoon on 10 and 12 April.

Thus, from Fig. 11 it follows that the estimates of the turbulent mixing layer height as a height at which the dissipation rate becomes less than the threshold value ${\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³, and as a height above which the Richardson number exceeds 0.5, are in a qualitative agreement.

7 Summary

In this paper, we propose a method for estimating the turbulent mixing layer height on the basis of the height–temporal distributions of the turbulence energy dissipation rate obtained from PCDL measurement data with conical scanning by a probing beam around the vertical axis. The method was tested in the experiments in summer 2019 in strong smog due to forest fires and in spring 2020.

The optical characteristics of the atmosphere varied significantly during the experiment in 2019. Most of the time, the aerosol backscatter coefficient far exceeded the background level because of the smog. Under these conditions, the signal-to-noise ratio (SNR) was abnormally high for lidars in the class of the StreamLine lidar with a pulse energy of about 10 µJ. As a result, in the experiment, we succeeded in retrieving the vertical profiles of the wind speed and direction up to a height of 2.5 km and wind turbulence parameters up to a height of 1.8 km.

The raw data of the lidar experiments conducted on 20–25 July 2019 were used to find the diurnal time series of MLH under conditions of intense smog from the height–temporal distributions of the dissipation rate with the use of the inequality $\mathit{\epsilon }<{\mathrm{Thr}}_{\mathit{\epsilon }}={\mathrm{10}}^{-\mathrm{4}}$ m²/s³ as a criterion that indicates the absence of turbulent mixing. According to the results obtained, on these days, the MLH was at its maximum between 11:00 and 18:00 UTC/GMT+7 and varied from 400 to 1800 m. It was shown in the experiment that the estimation of the turbulent mixing layer height from the height–temporal distributions of the turbulence energy dissipation rate has some advantages in comparison with the estimation from the height–temporal distributions of the variance of radial velocity. Because of the anisotropy of wind turbulence, the variance of radial velocity depends significantly on the elevation angle of the scanning.

The accuracy of the method for estimating the turbulent mixing layer height from the lidar data obtained with the use of conical scanning is discussed in detail in this paper. We developed a method for calculating the experimental error of estimation of the turbulent mixing layer height from the height–temporal distributions of the turbulence energy dissipation rate. The analysis of the errors calculated by this method shows that the accuracy of MLH estimation depends decisively on the error of estimation of the dissipation rate and on the vertical gradient of the dissipation rate at heights near the top of the mixing layer. In turn, the accuracy of estimation of the dissipation rate depends strongly on the lidar signal-to-noise ratio (SNR). For the estimation of MLH with the acceptable relative error not exceeding 20 %, SNR should be no less than −16 dB, when the relative error of lidar estimation of the dissipation rate does not exceed 30 %. With the data obtained in the experiments, we demonstrate that the relative error of determination of the MLH time series from lidar measurements of the dissipation rate with the use of conical scanning does not exceed 10 % in the period of turbulence development, from 06:00 to 22:00 UTC/GMT+7. Most of the time in this period, it is less 5 %. The method described here can be applied to data measured by a high-power pulsed coherent Doppler lidar at a background aerosol concentration, which will enable a full-edged statistical analysis.

To prove the suitability of the method for estimating the turbulent mixing layer height from lidar data obtained with the use of conical scanning, we conducted a lidar experiment with concurrent measurement of the temperature in April–May 2020. From the obtained data, we calculated the height–temporal distributions of the gradient Richardson number and determined the MLH from these distributions. A comparison shows that the estimates of the turbulent mixing layer height from the dissipation rate distributions and from the Richardson number distributions using the criterion Ri<0.5 are in a qualitative agreement.