An approach to minimize aircraft motion bias in multi-hole probe wind measurements made by small unmanned aerial systems

A multi-hole probe mounted on an aircraft provides the air velocity vector relative to the aircraft, requiring knowledge of the aircraft spatial orientation (e.g., Euler angles), translational velocity and angular velocity to translate this information to an Earth-based reference frame and determine the wind vector. As the relative velocity of the aircraft is typically an order of magnitude higher than the wind velocity, the extracted wind velocity is very sensitive to multiple sources of error including misalignment of the probe and aircraft coordinate system axes, sensor error and misalignment in time of the probe and aircraft orientation measurements in addition to aerodynamic distortion of the velocity field by the aircraft. Here, we present an approach which can be applied after a flight to identify and correct biases which may be introduced into the final wind measurement. The approach was validated using a ground reference, different aircraft and the same aircraft at different times. The results indicate a significant reduction in wind velocity variance at frequencies which correspond to aircraft motion.

1 Introduction

The past few decades have witnessed a significant increase in the utilization of small unmanned aerial systems (sUASs) in a wide range of atmospheric research areas, such as the evolution and structure of the atmospheric boundary layer (see, for example, van den Kroonenberg et al., 2007, 2008; Cassano et al., 2010; Bonin et al., 2013; Lothon et al., 2014; Wildmann et al., 2015; Bärfuss et al., 2018; de Boer et al., 2018; Kral et al., 2018; Bailey et al., 2019), turbulence (Balsley et al., 2013; Witte et al., 2017; Bailey et al., 2019; Mansour et al., 2011; Calmer et al., 2018; Båserud et al., 2016), analysis of aerosols and gas concentrations in the atmosphere (Bärfuss et al., 2018; Platis et al., 2016; Corrigan et al., 2008; Schuyler and Guzman, 2017; Illingworth et al., 2014; Zhou et al., 2018), cloud microphysics (Ramanathan et al., 2007; Roberts et al., 2008), and observation and analysis of extreme weather events such as hurricanes (Cione et al., 2016). This increasing interest in sUASs is motivated in part by the rapid increase in their commercial development and use combined with advantages of sUASs over traditional ground-based measurement systems utilizing either remote sensing or in situ approaches. Specifically, sUASs can acquire high-spatial- and temporal-resolution measurements in a relatively low-cost package that provides flexibility in measurement location and flight path. In addition, when compared to manned aircraft measurements, their operation mitigates risks associated with measurement at lower altitudes and during hazardous conditions or events (Elston et al., 2015; Bärfuss et al., 2018; Barbieri et al., 2019) such as erupted volcanoes with ash covers (Pieri et al., 2017), near thunderstorms (Elston et al., 2011) and over contaminated regions (Bärfuss et al., 2018).

The most common atmospheric properties sampled using sUASs are pressure, temperature, humidity and wind (e.g., Egger et al., 2002; Hobbs et al., 2002; Balsley et al., 2013; Witte et al., 2017; Bärfuss et al., 2018; Rautenberg et al., 2018; Jacob et al., 2018; Barbieri et al., 2019; Bailey et al., 2019). Although these scalar quantities are relatively straightforward to acquire, obtaining all three components of the wind velocity vector is complicated by the presence of the continual translation and rotation of the measurement platform, resulting in different approaches developed to determine the wind vector (Rautenberg et al., 2018; Suomi and Vihma, 2018; Laurence and Argrow, 2018; Shevchenko et al., 2016). Wind velocity measurements can typically be partitioned into several approaches: directly by using the instrumentation employing an onboard wind sensor and subtracting the aircraft kinematics (Suomi and Vihma, 2018; Cassano et al., 2016); indirectly using the attitude and position data recorded by the inertial measurement unit (IMU) and GPS, respectively (Suomi and Vihma, 2018); using both techniques (Rautenberg et al., 2018); or through calibration of the aircraft's kinematic and dynamic response to the wind (González-Rocha et al., 2020).

Broadly speaking, wind measurements taken by sensors like sonic anemometers, single- and multi-hole pressure probes, and hot wires tend to have higher temporal (and hence spatial) response (Suomi and Vihma, 2018). Multi-hole pressure probes have been frequently used for sUAS-based wind velocity measurements (van den Kroonenberg et al., 2008; Elston et al., 2015; Spiess et al., 2007; Thomas et al., 2012) due to their high sampling frequency, light weight, simplicity, accuracy and almost linear relation between pressure and velocity at large flow velocities (Suomi and Vihma, 2018). More importantly, multi-hole probes are able to resolve all three wind velocity components. The simplest multi-hole probe capable of resolving all three velocity components is the five-hole probe, composed of five holes arranged symmetrically on a semi-spherical or conical tip. When the wind velocity is oriented in different directions relative to the probe axis, each hole converts a different proportion of the dynamic pressure to stagnation pressure, allowing the dynamic pressure and direction to be determined using laboratory or in-flight calibration of the probe's directional response.

The use of five-hole probes in sUAS measurements has evolved from their employment in manned aircraft measurements (Lenschow, 1970, 1972). Such measurements frequently employ in-flight calibration procedures. For instance, Parameswaran and Jategaonkar (2004) presented a calibration procedure for five-hole probes using flight recorder data with an optimization algorithm to estimate the time delay, biases and scale factors in the pressure measurements. Afterwards, the corrected five-hole probe measurements were compared with the measurements from the inertial measurement unit to check their compatibility. Drüe and Heinemann (2013) present a comprehensive review of in-flight calibration of several atmospheric measurement instruments, including five-hole probes. They identified five-hole probe in-flight calibration maneuvers to determine the sideslip angle, angle of attack, static pressure and position errors. Moreover, they highlighted the need for in-flight calibration in the experiment location under favorable atmospheric conditions and following removal of the sensors from the aircraft.

The simplicity and compact nature of multi-hole probes also make it particularly useful for fixed-wing sUASs. However, as with manned aircraft, these aircraft have the ability to fly at velocities up to an order of magnitude greater than the wind velocity, and their usage can be very sensitive to small errors in calibration and probe alignment (Suomi and Vihma, 2018; Laurence and Argrow, 2018). Furthermore, accurate position and orientation determination usually requires very accurate orientation information (e.g., obtained through the use of dual-antenna combination GPS–IMU), and accurate time stamping of the data is critical to align sensor and flight data. Here, we present an approach which can be implemented a posteriori to minimize the impact of unidentified and unquantified biases introduced during wind velocity measurement which result in contamination of the wind signal by the aircraft velocity. This contamination results in overestimation or underestimation of the wind vector and, in particular, errors in estimation of turbulence statistics (e.g., momentum fluxes, dissipation rate, turbulence kinetic energy) measured by the sUAS. Hence, it is vital to minimize errors in the wind components measured by sUASs. In the following sections we overview a multi-hole probe implementation and discuss the potential sources of bias within the approach. We then present a simple automated optimization which is designed to identify and remove these biases and demonstrate that this approach improves the wind estimate of an existing dataset.

2 Multi-hole probe implementation

Multi-hole probes are an adaptation of the common Pitot static probe to allow the determination of relative wind direction and magnitude. Widely used in laboratory wind tunnel studies of three-dimensional flow fields, they found use in manned aircraft studies of atmospheric wind (Treaster and Yocum, 1978; Axford, 1968; Lenschow, 1972) before being adopted for sUAS use. Five-hole probes, being the simplest form of multi-hole probes, are most common. The arrangement of the normal vector of each plane of the holes on the probe tip typically consists of a central hole with normal vector in line with the probe axis, measuring pressure P₁, and with the normal vector of the remaining holes at an angle to the probe axis. Two holes measure the pressure at opposing directions on the horizontal plane, e.g., P₂ and P₃, with the remaining two in opposite directions on the vertical plane, e.g., P₄ and P₅. Static pressure, P_s, is also measured, either through a ring of holes oriented perpendicular to the probe axis or through an alternate pressure port. Wind tunnel calibrations are used to determine calibration coefficients, for example

$$\begin{array}{}\text{(1)}& {\displaystyle }{C}_{P_{\mathrm{yaw}}}=(P_{\mathrm{2}}-P_{\mathrm{3}})/(P_{\mathrm{1}}-\stackrel{\mathrm{‾}}{P}),\text{(2)}& {\displaystyle }{C}_{P_{\mathrm{pitch}}}=(P_{\mathrm{2}}-P_{\mathrm{5}})/(P_{\mathrm{1}}-\stackrel{\mathrm{‾}}{P}),\text{(3)}& {\displaystyle }{C}_{P_{\mathrm{total}}}=(P_{\mathrm{1}}-P_{\mathrm{0}})/(P_{\mathrm{1}}-\stackrel{\mathrm{‾}}{P}),\text{(4)}& {\displaystyle }\stackrel{\mathrm{‾}}{P}=(P_{\mathrm{2}}+P_{\mathrm{3}}+P_{\mathrm{4}}+P_{\mathrm{5}})/\mathrm{4},\end{array}$$

where $P_{\mathrm{0}}=\mathrm{0.5}\mathit{\rho }|{\mathit{U}}_{\mathrm{m}}{|}^{\mathrm{2}}+P_{\mathrm{s}}$ is the total pressure, ρ the density of the air and $\left|{\mathit{U}}_{\mathrm{m}}\right|$ the magnitude of the relative air velocity vector U_m. During calibration P₁, P₂, P₃, P₄, P₅ and P_s are measured at different sideslip, β, and angle of attack, α, at known P₀. Depending on the specifics of the probe geometry, a unique set of coefficients is recovered for each α and β combination up to some limit (referred to as the cone angle) typically between 25 and 45^∘ depending on the specifics of the probe geometry. During measurement P₁, P₂, P₃, P₄, P₅ and P_s are simultaneously sampled and $C_{P_{\mathrm{yaw}}}$ and $C_{P_{\mathrm{pitch}}}$ calculated for each sample. The known dependence of α, β and $C_{P_{\mathrm{total}}}$ on $C_{P_{\mathrm{yaw}}}$ and $C_{P_{\mathrm{pitch}}}$ from the calibration is then applied to determine α, β and P₀, which, when combined with a known ρ, provide the air velocity and direction relative to the probe axis. Additional calibration is also possible to account for an imprecise frequency response of the probes caused by resonance and viscous damping in the pressure tubing and sensors (e.g., as described in Gerstoft and Hansen, 1987), which can potentially require additional corrections (e.g., Yang et al., 2006). These additional corrections are not addressed here.

When implemented on a moving platform such as an aircraft, U_m is no longer the wind velocity but is instead a combination of the aircraft and wind velocity vectors:

$$\begin{array}{}\text{(5)}& [{\mathit{U}}_{\mathrm{m}}{]}_{\mathrm{B}}=[\mathit{U}{]}_{\mathrm{B}}-[{\mathit{U}}_{\mathrm{s}}{]}_{\mathrm{B}},\end{array}$$

where U_s is the velocity vector of the sensor and U is the desired wind velocity vector. We have also introduced the subscript B to indicate that these velocities are in a body-fixed frame of reference, i.e., a coordinate system attached to the aircraft. Due to the pitch, roll and yaw angles of the aircraft, Ω=[θ ϕ γ], or more specifically their time rate of change $\dot{\mathbf{\Omega }}$, U_s can experience additional velocity relative to the aircraft velocity U_ac=[U_ac V_ac W_ac] (Lenschow and Johnson, 1968) such that

$$\begin{array}{}\text{(6)}& [{\mathit{U}}_{\mathrm{s}}{]}_{\mathrm{B}}=[{\mathit{U}}_{\mathrm{ac}}{]}_{\mathrm{B}}+[\dot{\mathbf{\Omega }}\times \mathit{r}{]}_{\mathrm{B}},\end{array}$$

where r is the distance vector between the aircraft center of gravity and the measurement volume on the probe.

Note that the desired quantity is [U]_I=[U V W], the wind velocity vector in the Earth-fixed inertial frame of reference. Furthermore, U_ac is also typically measured in the Earth-fixed inertial frame (e.g., through a global positioning system), and therefore a transformation matrix L_BI must be determined using the aircraft's pitch (θ), roll (ϕ) and yaw (γ) angles in the inertial frame. The velocity vector [U_ac]_I, along with θ, ϕ, γ and their rates as required to build Ω and L_BI, can be measured by an onboard inertial measurement unit and GPS, and they are commonly provided by most autopilots used for sUAS operation, thus providing enough information to determine [U]_I from [U_m]_B.

However, as noted earlier, U_s is often an order of magnitude larger than the desired U, making the process sensitive to an abundance of small biases. For example, the procedure above assumes perfect alignment between the probe's coordinate system and the aircraft's coordinate system. It also assumes that Ω and L_BI are measured at the aircraft's center of gravity, that r is precisely known, that there are negligible flow blockage effects in the wind tunnel calibration or from the aircraft fuselage, and that all sensors are free of error. Although every effort can be made to minimize these biases, it is unlikely that they can be removed completely. The result is that U is often contaminated by U_s. This is most evident when L_BI, U_ac and Ω are changing rapidly. The following section describes a procedure developed to determine additional calibration coefficients and implement them following an in-flight calibration or measurement to minimize these biases.

3 Correction procedure

The net effect of the majority of biases can be summarized as influencing four parameters. Misalignment of probe and aircraft axes, calibration errors, and aerodynamic distortion of the flow around the probe will introduce bias errors into the time-dependent pitch, roll and yaw angles θ(t), ϕ(t) and γ(t), which relate the measured velocity vector in body-frame coordinates to the aircraft velocity vector. In addition, calibration errors, transducer errors and airframe aerodynamic effects (e.g., airframe blockage and streamline deflection due to the generation of lift) can also influence the direction of airflow relative to the probe and the magnitude of the measured dynamic pressure $Q\left(t\right)=\mathrm{0.5}\mathit{\rho }\left(t\right)\left|{\mathit{U}}_{\mathrm{m}}\right(t){|}^{\mathrm{2}}$ relative to the true dynamic pressure. Note that the distortion of the flow may also depend on lift production of the aircraft and therefore Q(t) may also include dependence on the lift coefficient, which is not considered in the version of the corrections described here. Finally, it is also important for all sensor readings to precisely correspond to orientation readings in time to allow precise removal of aircraft motion from measured relative air velocity. However, implementation of software and differences in sensor time response can cause a delay between when probe-measured velocity and aircraft-measured velocity occur; e.g., the values of U_m(t) and U_s(t) may not correspond to the same t. The proposed correction procedure assumes that these values are biased in a way such that

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathit{\theta }\left(t\right)={\mathit{\theta }}_{\mathrm{m}}\left(t\right)+\mathrm{\Delta }\mathit{\theta },\text{(8)}& {\displaystyle }\mathit{\varphi }\left(t\right)={\mathit{\varphi }}_{\mathrm{m}}\left(t\right)+\mathrm{\Delta }\mathit{\varphi },\text{(9)}& {\displaystyle }\mathit{\gamma }\left(t\right)={\mathit{\gamma }}_{\mathrm{m}}\left(t\right)+\mathrm{\Delta }\mathit{\gamma },\text{(10)}& {\displaystyle }Q\left(t\right)=\mathit{\zeta }{Q}_{\mathrm{m}}\left(t\right),\text{(11)}& {\displaystyle }{\mathit{U}}_{\mathrm{m}}\left(t\right)={\mathit{U}}_{\mathrm{m}}(t_{\mathrm{m}}+\mathrm{\Delta }t),\end{array}$$

where the subscripted m indicates the measured value. The objective is then to find $\mathrm{\Delta }\mathit{ϵ}=\left\{\mathrm{\Delta }\mathit{\theta },\mathrm{\Delta }\mathit{\varphi },\mathrm{\Delta }\mathit{\gamma },\mathit{\zeta },\mathrm{\Delta }t\right\}$. Using assumptions about how these biases will impact U(t) allows the determination of optimal values for Δϵ which minimize this negative behavior. With Δϵ known, we are able to remove its influence on the final time series of U(t).

The assumptions used here are relatively straightforward, the first being that any biasing of U(t) by U_s will result in U(t) having a dependence on the direction of travel of the aircraft. The second assumption we make is that the vertical component of U(t) will be approximately zero in the mean. This assumption may not hold in flight over sloped terrain and/or for relatively short flight domains (both spatial and temporal), in which case an alternative assumption may be needed. Moreover, we assume that the sensors have an adequate response and that the greatest error is due to the specific configuration which logs IMU–GPS, pressure transducers, and local pressure, temperature and humidity (PTU) on three separate systems.

The correction procedure, as implemented, follows a multistage approach used to optimize Δϵ. This multistage approach was implemented to allow different objective functions to be used for different components of Δϵ. However, in practice, it is likely that a well-implemented single-stage optimization will achieve the same results.

The first step is to identify a portion of the flight which will be used to determine Δϵ. This portion should not include any significant acceleration or deceleration of the aircraft's horizontal ground speed (e.g., as experienced during takeoff or landing) and should include multiple changes of direction of the aircraft. In addition, the portion should be long enough to ensure that unsteadiness in the mean winds, e.g., as introduced by thermals, are averaged out. Ideally, devoting a portion of the flight after takeoff to conducting calibration orbits for later use in this process would be desired. With this portion of the flight identified, the determination of Δϵ is found by an optimization process seeking to minimize an objective function, δ, through iterative calculation of [U]_I (as described in Sect. 2).

Through perturbing Δϵ and examining its influence on U(t) it was found that the standard deviation of the horizontal components of [U(t)]_I, specifically U(t) and V(t), were most sensitive to Δt (due to the aircraft flight being predominantly in the horizontal plane), with values of Δt as low as tenths or hundredths of a second contributing to large biases of the horizontal components of [U(t)]_I. We thus first use a Nelder–Mead multidimensional unconstrained nonlinear minimization approach, implemented using the MATLAB fminsearch command, to identify the value of Δt which minimizes the objective function δ, defined as

$$\begin{array}{}\text{(12)}& {\displaystyle }{\mathit{\delta }}_U=\langle U\rangle {|}_{U_{\mathrm{ac}}>\mathrm{0}}-\langle U\rangle {|}_{U_{\mathrm{ac}}<\mathrm{0}},\text{(13)}& {\displaystyle }{\mathit{\delta }}_V=\langle V\rangle {|}_{U_{\mathrm{ac}}>\mathrm{0}}-\langle V\rangle {|}_{U_{\mathrm{ac}}<\mathrm{0}},\text{(14)}& {\displaystyle }\mathit{\delta }={\mathit{\delta }}_U^{\mathrm{2}}+{\mathit{\delta }}_V^{\mathrm{2}}.\end{array}$$

Note that $\langle \rangle {|}_{U_{\mathrm{ac}}>\mathrm{0}}$ indicates an average conditioned on when the aircraft is flying with a positive inertial velocity component U_ac. Likewise, $\langle \rangle {|}_{U_{\mathrm{ac}}<\mathrm{0}}$ indicates an average of all values obtained when the aircraft inertial U_ac velocity component is negative. The selection of U_ac vs. V_ac for conditioning is arbitrary and should be selected based on the actual flight trajectory. For flight trajectories without many trajectory changes, it was also found that the objective function

$$\begin{array}{}\text{(15)}& \mathit{\delta }=\langle (U-\langle U\rangle {)}^{\mathrm{2}}\rangle +\langle (V-\langle V\rangle {)}^{\mathrm{2}}\rangle \end{array}$$

was equally effective, but it relies on the assumption that the biases will act only to increase the fluctuations of the velocity signal at the probe. Here 〈 〉 indicates an average over the entire portion of the flight used to find Δϵ. The resulting value of Δt which minimizes δ is then implemented in the remaining optimization stages.

The second stage follows a similar approach. Noting that the mean value of the vertical component of [U(t)]_I, i.e., W(t), is most sensitive to Δθ, we then find the value of Δθ that minimizes

$$\begin{array}{}\text{(16)}& \mathit{\delta }=\langle W\rangle \end{array}$$

using ${\mathit{U}}_{\mathrm{m}}\left(t\right)={\mathit{U}}_{\mathrm{m}}(t_{\mathrm{m}}+\mathrm{\Delta }t)$ as found above.

The remaining elements of Δϵ, specifically ζ, Δϕ and Δγ, are then found by minimizing δ as defined in Eq. (14) using ${\mathit{U}}_{\mathrm{m}}\left(t\right)={\mathit{U}}_{\mathrm{m}}(t_{\mathrm{m}}+\mathrm{\Delta }t)$ and $\mathit{\theta }={\mathit{\theta }}_{\mathrm{m}}+\mathrm{\Delta }\mathit{\theta }$ as found in the preceding two stages.

Finally, to ensure that the values of Δϵ determined using the latter optimization stages do not influence the values found during the earlier stages, Δϵ is further refined by repeating the above three stages once again. In practice, this last step only influenced Δϵ by 1 % or less and can likely be omitted without loss of confidence in the final values of Δϵ.

4 Results

With Δϵ known, the biases described by Δϵ can be removed following Eqs. (7) to (11) prior to a final determination of [U(t)]_I. To validate this correction procedure, we applied it to measurement data acquired during the LAPSE-RATE campaign described in de Boer et al. (2018). The data were acquired using two different five-hole-probe-equipped fixed-wing aircraft, with the aircraft, probe and data reduction procedures described in detail in Witte et al. (2017). We first demonstrate the correction procedure in flights compared to a ground reference, followed by a demonstration of the improvements made to vertical profiles of the wind velocity and direction.

4.1 Comparison to ground reference

A key part of the LAPSE-RATE campaign was an intercomparison study between numerous sUASs measuring pressure, temperature, humidity, wind speed and wind direction. As detailed in Barbieri et al. (2019), the intercomparison was conducted by flying the sUASs near the Mobile UAS Research Collaboratory (MURC) vehicle, which was equipped with a 15 m mast supporting reference instruments, including a sonic anemometer. For the fixed-wing aircraft used here, this comparison was performed by having the aircraft orbit the mast at 20 m above ground level with an orbit radius of 80 m. This orbit was performed for approximately 5 min before the aircraft ascended to 120 m to perform similar orbits for 2 min, then descending back to 20 m to resume the orbits around the tower for another 2 min before starting its landing pattern.

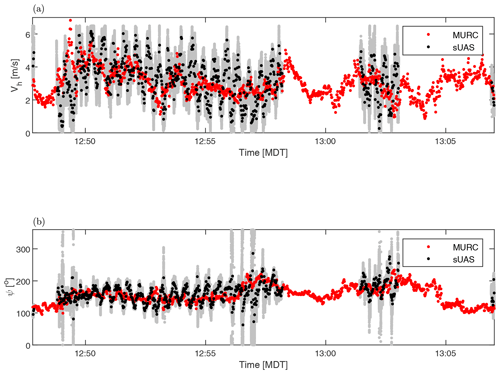
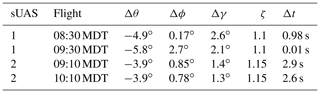
Figure 1 Comparison between uncorrected (a) horizontal wind speed and (b) wind direction measured by the sUAS to the reference signal measured by MURC. Gray lines indicate full signal from the sUAS, whereas black lines indicate the same signal downsampled to the same data rate as that of the MURC by plotting every 200th data point.

Figure 2 The sUAS-based wind measurements from Fig. 1 following correction compared to the reference signal measured by MURC: (a) horizontal wind speed and (b) wind direction. Gray lines indicate full signal from the sUAS, whereas black lines indicate the same signal downsampled to the same data rate as that of the MURC by plotting every 200th data point.

This circular flight pattern introduced a periodic variation in θ, γ and ϕ, with the period corresponding to the time to complete an orbit (approximately 25 s). Although convenient for the measurement of atmospheric parameters at a single geographic location, these types of orbits consist of the worst-case scenario for the contamination of the measured wind direction by the biases discussed in Sect. 2.

The periodicity is clearly evident in the estimated horizontal wind speed, $V_{\mathrm{h}}=(U^{\mathrm{2}}+V^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}$, and direction, ψ, prior to implementing the corrections, as shown in Fig. 1a and b, respectively. Although the general trends of the measured wind velocity and direction time series follow that of the reference velocity and direction, the magnitude of the fluctuations is clearly contaminated by the aircraft velocity and direction. The period in the wind signal is consistent with the time required to orbit the fixed mast at 25 s. Note that in Fig. 1 only the two portions of the flight during which the sUAS is at the same altitude as the reference sensors are presented.

The same time series are shown in Fig. 2a and b corrected following the procedure described in Sect. 3. The 10 min of flight between 12:49 and 12:58 MDT were selected to conduct the optimization of Δϵ. The result of optimization was $\mathrm{\Delta }\mathit{ϵ}=\mathit{\{}\mathrm{\Delta }\mathit{\theta }=-\mathrm{6.4}{}^{\circ },\mathrm{\Delta }\mathit{\varphi }=\mathrm{0.9}{}^{\circ },\mathrm{\Delta }\mathit{\gamma }=\mathrm{2.1}{}^{\circ },\mathit{\zeta }=\mathrm{1.07},\mathrm{\Delta }t=-\mathrm{0.045}\mathrm{s}\mathit{\}}$, which highlights the sensitivity of the estimated wind velocity and direction to even small deviations from ideal orientations. As shown in Fig. 2, the corrected signals are now largely free of the 25 s periodicity, although there is some evidence of contamination between 12:56 and 12:58 MDT. When the aircraft returns to 18 m of altitude for the second set of orbits (which were not included in the optimization) there is little evidence of aircraft velocity contamination in the wind estimates.

The periodicity described above is more clearly evident in the difference between the power spectrum of horizontal wind speed calculated for both the corrected and uncorrected cases. These spectra are presented in Fig. 3. The influence of the periodic orbits of the aircraft is apparent in the uncorrected measurements as a spike at 0.035 Hz (consistent with an orbital period of 28 s). This spike is greatly reduced by the correction. Importantly, besides what appears to be a harmonic peak at 0.07 Hz which is also reduced, the remainder of the spectrum appears largely unaffected by the correction.

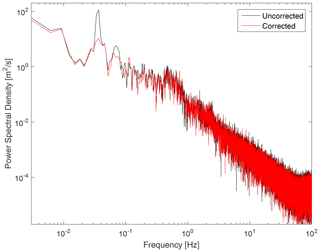
Figure 3 Power spectrum of horizontal wind magnitude calculated from uncorrected and corrected time series.

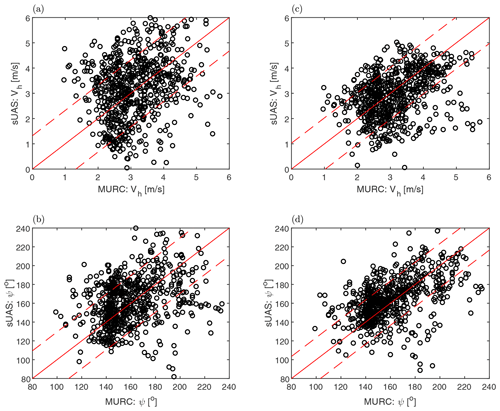
Figure 4 Direct comparison between (a) uncorrected and (c) corrected horizontal wind speed measured simultaneously by the sUAS and MURC. Similar comparison shown for (b) uncorrected and (d) corrected wind direction. The solid red line indicates where both measurements are identical, and dashed lines indicate 2 standard deviations of the difference between the sUAS- and MURC-measured values.

To provide a more quantitative comparison between the sUAS and reference measurement, we directly compare the velocity magnitude and direction measured at each instant a sample was made by the ground reference. This comparison is presented in Fig. 4 in which a perfect comparison would result in the straight line as indicated in the figure. Note that, a perfect correlation should not be expected as the sUAS and reference sensor were not collocated. Also shown as a dashed line in the figure are the bounds described by 2 standard deviations of the difference between the sUAS- and MURC-measured values.

For the uncorrected velocity magnitude and direction, the comparison shown in Figs. 4a and b reveals a broad spread about the reference line. This spread decreases significantly when the corrections are applied, as shown by comparison to Figs. 4c and d. The mean difference between the two measurements decreases by approximately 35 % in magnitude and direction with correction, corresponding to an increase in the correlation coefficient from 0.13 to 0.19 in magnitude and 0.22 to 0.32 in direction. This increased correlation is reflected in the statistics. The correction brings the standard deviation of the sUAS-measured velocity much closer to the reference signal. The standard deviation in magnitude measured by the sUAS decreases from 1.2 to 0.90 m s⁻¹, very close to the value of 0.86 m s⁻¹ measured by the reference. For direction the standard deviation decreases with correction from 27 to 22^∘, whereas it is 24^∘ for the reference.

4.2 Implementation in profiling measurements

The results of the comparison to the ground reference provide confidence in the success of the correction. To demonstrate the improvement offered by application of these corrections to vertical profiling by fixed-wing aircraft, we now examine their impact on profiles of wind speed and direction measured by two separate aircraft at different locations. These two fixed-wing aircraft were essentially identical in configuration to that described in Witte et al. (2017) and were flown at measurement sites separated by 16 km. Each aircraft measured an atmospheric profile every hour, with the two aircraft staggered in time by 30 min.

Each profile consisted of a 20 min flight, with the aircraft performing a spiralling ascent to 900 m followed by a spiralling descent, with this pattern repeated until the 10Ah battery was depleted. In the following discussion the times are those corresponding to when the profile measuring flight initiates with the X, Y and Z coordinate system origin at the takeoff location. These particular profiles were selected for discussion as they were measured during the boundary layer transition and represent different behaviors, including the presence of turbulence and variability in the wind direction. The wind speeds during these profiles were also low, producing a large ratio of aircraft velocity to wind velocity and therefore a challenging case to accurately extract the wind components from the five-hole probe signal.

As previously mentioned, the orbital flight patterns also represented a challenge for extracting the wind data due to the periodic variation in θ, γ and ϕ introducing a corresponding periodic variation in [U(t)]_I. This bias can be clearly illustrated by comparing γ to ψ, as done for an example flight in Fig. 5a. For this flight, the aircraft completed a full 360^∘ turn in approximately 30 s, introducing a corresponding period in both the wind speed and direction before correction. Once the corrections have been applied, as shown in Fig. 5b, there is a distinct reduction of periodicity in the direction of the wind measured by the sUAS.

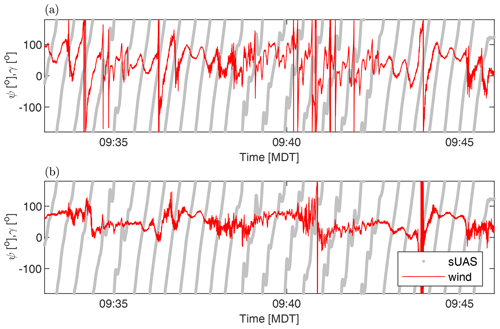
Figure 5 Comparison between measured wind direction and aircraft yaw direction for (a) uncorrected and (b) corrected signals as a function of time for a single flight.

The means of the corresponding wind speed and direction profiles are presented in Fig. 6 for sUAS 1 and Fig. 7 for sUAS 2. In these figures both the uncorrected and corrected mean profiles are displayed in order to show the relative improvement offered by application of the bias correction. For all profiling flights, the correction coefficients were determined by optimizing the entire flight once the aircraft was in its flight pattern. Before correction, the bias introduced by the aircraft trajectory is apparent as large coherent deviations from the general trend, mostly evident in the velocity magnitude but also present in the direction. When the corrections were applied, these large deviations were greatly reduced, better representing the structure of the boundary layer throughout the profiles. In the wind velocity profiles presented in Fig. 6 for sUAS 1 there were still high velocity deviations, even in the corrected profiles near the surface corresponding to when the aircraft was being manually controlled and experiencing strong acceleration. It has been found that the corrections presented here cannot completely remove the bias due to aircraft acceleration, suggesting a potential time response lag between the five-hole probe and the inertial measurement unit, which agrees with what was reported in Båserud et al. (2016).

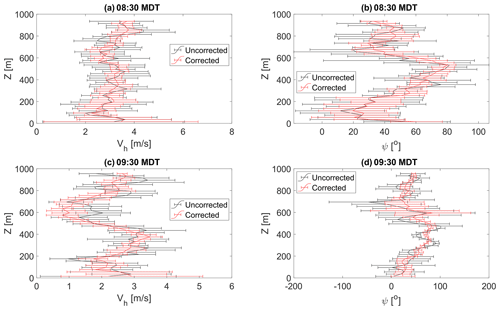
Figure 6 Comparison of mean (a) horizontal wind magnitude and (b) wind direction profiles measured by sUAS 1 at 08:30 MDT with and without correction applied. Horizontal mean magnitude and direction profiles measured at 09:30 MDT are shown in (c, d), respectively.

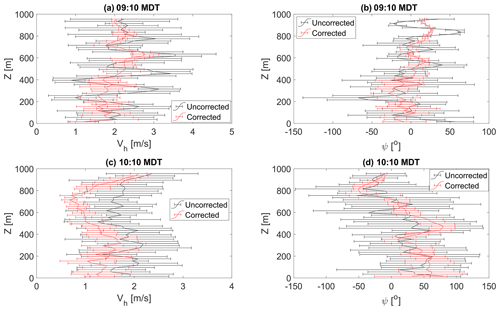
Figure 7 Comparison of mean (a) horizontal wind speed and (b) direction profiles measured by sUAS 2 at 09:10 MDT with and without correction applied. Horizontal wind speed and direction profiles measured at 10:10 MDT are shown in (c, d), respectively.

The corrected profiles show very different wind behaviors for the different sites and times. At the site measured by sUAS 1, the profiles measured at 08:30 MDT shown in Fig. 6a and b reflect the correspondence between the stable thermodynamic conditions throughout the boundary layer and the horizontal wind magnitude, with winds increasing from 2 m s⁻¹ near the ground to 4 m s⁻¹ at Z=900 m and staying consistently between ψ=0^∘ and 100^∘. There was noticeably stronger velocity and direction fluctuations measured for Z<200 m, indicating the presence of turbulence near the surface. This turbulence appears to still have been present at 09:30 MDT, as shown in Fig. 6c and d, but at this time there was a region of calm air centered at Z=600 m, coinciding with a significant deviation in measured wind direction. For Z>200 m, the corrected profile of wind direction was consistent with the one measured at 08:30 MDT, except the region of calm air at Z=600 m.

At the site measured by sUAS 2, the corrected mean wind speed and direction profiles measured at 09:10 MDT shown in Fig. 7a and b reflect a boundary layer undergoing transition, with evidence of turbulence for Z<500 m. At 10:10 MDT, as shown in Fig. 7c and d, a multi-layer structure was also evident in the wind profiles in the form of significant changes in the wind direction throughout the profile. The horizontal wind speed was relatively consistent between 1 and 2 m s⁻¹ for Z<800 m, but there was evidence of stronger turbulence for Z<500 m and moderate wind shear for Z>700 m. As noted, the wind direction exhibited significant variation in the range 400 m $<Z<\mathrm{500}$ m, with continual backing within 500 m $<Z<\mathrm{900}$ m and veering for Z<900 m. These different altitudes of behavior were consistent with the measured potential temperature changes (not included for conciseness) and became much easier to identify in the corrected profiles than they were before correction.

Table 1 Components of Δϵ determined by optimization for each sUAS for both flights.

It is clear through comparison of the corrected and uncorrected profiles in Figs. 6 and 7 that the corrections reduce fluctuations about the mean profile under different conditions and for different aircraft. Similar improvements have been observed for other profiles measured with these and other sUASs. The coefficients determined by the optimization routine for these profiles are presented in Table 1. Comparing each flight for the same sUAS demonstrates that the automated optimization converged on nearly identical coefficients for the same sUAS, with only one coefficient changing by more than 1^∘ between each flight. Indeed, the correction coefficients were found to be remarkably similar for each sUAS used throughout the LAPSE-RATE campaign. This similarity between the coefficients reinforces the assumption that the biases are caused by physical misalignment between the coordinate systems of the aircraft and the five-hole probe. Note that bias corrected by Δt should not be expected to be consistent for the systems used here, as the time series of U_m, U_ac and Ω are measured by separate acquisition systems at different rates and aligned using post-processing software. Thus, the Δt bias is most likely introduced by errors in this alignment process and can be expected to be random.

5 Conclusions

Small unmanned aerial systems have been increasingly used in atmospheric research. Frequently, this research requires the acquisition of the wind velocity vector. Multi-hole probe measurements are among the more common and reliable techniques used for this purpose. However, when implemented on sUASs there is significant potential to introduce bias due to the large ratio of aircraft velocity to the wind velocity. Therefore, the measured wind velocities are very sensitive to these small biases. Furthermore, when conducting vertical profiles at a fixed location, these profiles typically require circular flight patterns, which increase the probability of small misalignment between the probe and the aircraft axes, introducing a time-dependent periodic error in the wind velocity measurement that can propagate into post-flight analysis such as the calculation of energy spectra and Reynolds stresses.

An approach was presented that can be applied in post-processing of the flight data to automatically estimate the biases in axis misalignment and errors in their alignment in time. Once estimated, these biases can be removed, improving the quality of the wind estimate.

These corrections were validated using data acquired as part of the LAPSE-RATE field campaign. Measurements flown near a ground-based reference system revealed a significant reduction in measured oscillations of both wind magnitude and direction, which corresponded to the aircraft flight pattern. Additional verification was conducted by comparing profiles of wind speed and direction measured by two different aircraft at two different times. The estimated biases were within ±1^∘ for each aircraft, and successful minimization of aircraft-induced oscillations in the measured profiles was observed for both aircraft. These results confirm that the biases are most likely due to physical misalignment of the aircraft and probe axes, as well as demonstrating that the same correction procedures can be applied to multiple aircraft.