the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Application of the Complete Data Fusion algorithm to the ozone profiles measured by geostationary and low-Earth-orbit satellites: a feasibility study
Simone Ceccherini
Bruno Carli
Samuele Del Bianco
Marco Gai
Cecilia Tirelli
Flavio Barbara
Rossana Dragani
Antti Arola
Jukka Kujanpää
Jacob C. A. van Peet
Ronald van der A
Ugo Cortesi
The new platforms for Earth observation from space are characterized by measurements made at great spatial and temporal resolutions. While this abundance of information makes it possible to detect and study localized phenomena, it may be difficult to manage this large amount of data for the study of global and large-scale phenomena.
A particularly significant example is the use by assimilation systems of Level 2 products that represent gas profiles in the atmosphere. The models on which assimilation systems are based are discretized on spatial grids with horizontal dimensions of the order of tens of kilometres in which tens or hundreds of measurements may fall in the future.
A simple procedure to overcome this problem is to extract a subset of the original measurements, but this involves a loss of information. Another option is the use of simple averages of the profiles, but this approach also has some limitations that we will discuss in the paper. A more advanced solution is to resort to the so-called fusion algorithms, capable of compressing the size of the dataset while limiting the information loss. A novel data fusion method, the Complete Data Fusion algorithm, was recently developed to merge a set of retrieved products in a single product a posteriori. In the present paper, we apply the Complete Data Fusion method to ozone profile measurements simulated in the thermal infrared and ultraviolet bands in a realistic scenario. Following this, the fused products are compared with the input profiles; comparisons show that the output products of data fusion have smaller total errors and higher information contents in general. The comparisons of the fused products with the fusing products are presented both at single fusion grid box scale and with a statistical analysis of the results obtained on large sets of fusion grid boxes of the same size. We also evaluate the grid box size impact, showing that the Complete Data Fusion method can be used with different grid box sizes even if this possibility is connected to the natural variability of the considered atmospheric molecule.
- Article
(2914 KB) - Full-text XML
-
Supplement
(1277 KB) - BibTeX
- EndNote
In the context of the Copernicus programme (https://www.copernicus.eu, last access: 29 December 2020) coordinated by the European Commission, the European Space Agency is responsible for the Space Component, consisting of a novel set of Earth Observation (EO) satellite missions for environmental monitoring applications: the Sentinel missions (https://sentinel.esa.int/web/sentinel/missions, last access: 29 December 2020). Each mission focuses on a specific aspect of EO. In particular, the geostationary (GEO) mission Sentinel-4 and the two low-Earth-orbit (LEO) missions (Sentinel-5p and Sentinel-5), referred to as the atmospheric Sentinels, are dedicated to monitoring air quality, stratospheric ozone, ultraviolet surface radiation and climate.
The atmospheric Sentinels will provide an enormous amount of data with unprecedented accuracy and spatio-temporal resolution. In this scenario, a central challenge is to enable a generic data user (for example, an assimilation system) to exploit such a large amount of data.
A variety of approaches can serve the purpose of conveying, in a single product, the information associated with remote sensing observations of the vertical distribution of a given atmospheric target from multiple independent sources. Strategies for the combined use of multiple atmospheric profile datasets include a posteriori data fusion techniques, synergistic inversion processes (Aires et al., 2012 and references therein; Natraj et al., 2011; Cuesta et al., 2013; Cortesi et al., 2016; Sato et al., 2018) and, in broader terms, might include assimilation systems (Lahoz and Schneider, 2014).
The three approaches differ in the accepted inputs and in the involved models. In the synergistic inversion, the inputs consist of the radiance observations (Level 1 products) of all the measurements, and the output profiles are obtained by a simultaneous retrieval of these observations. A posteriori fusion techniques consist of sophisticated averaging processes in which the inputs are profiles (Level 2 products) retrieved from the single measurements. The assimilation techniques, in their more general implementations, can accept both radiances and profiles as inputs and use the information of the measurements as inputs of an atmospheric model. Each of these strategies implies different advantages and drawbacks, ultimately assessing the cost-to-benefit ratio that drives the selection of the option of choice for the specific case under investigation.
In particular, data fusion algorithms, such as the Complete Data Fusion (CDF) algorithm (Ceccherini et al., 2015), can be well suited to reducing the data volume that users need to access and handle while retaining the information content of the whole Level 2 (L2) product.
The CDF inputs are any number of L2 profiles retrieved with the optimal estimation technique and characterized by their a priori information, covariance matrix (CM) and averaging kernel (AK) matrix. The output of the CDF is a single product (also characterized by a priori, CM and AK matrices) in which the vertical sensitivity increases and the error reduces with respect to the inputs (Ceccherini et al., 2015).
This work is based on the simulated data produced in the context of the Advanced Ultraviolet Radiation and Ozone Retrieval for Applications project (AURORA; Cortesi et al., 2018), funded by the European Commission in the framework of the Horizon 2020 programme. The project regards the sequential application of fusion and assimilation algorithms to ozone profiles simulated according to specifications similar to those of the atmospheric Sentinels.
The use of synthetic data allows for evaluating the performances of the algorithms in terms of differences between the products and a reference truth, represented by the atmospheric scenario used in the L2 simulation procedure. On the other hand, the absence of systematic errors in the simulated measurements limits the study to ideal measurement conditions. However, the CDF algorithm intrinsically provides a mechanism to include different kinds of errors in the analysis. For instance, Ceccherini et al. (2018) discussed how to treat interpolation and coincidence errors, while Ceccherini et al. (2019) explicitly introduce the treatment of systematic errors.
This work is divided into two parts. In the first part, we describe the datasets and methodologies (the L2 simulation procedure and the CDF) and discuss the differences between CDF and mere averaging. In the second part, the quality of the fused products obtained from L2 profiles that are not perfectly co-located in space and in time is analysed. To account for the geo-temporal differences in the L2 profiles, a coincidence error is added to the fused product error budget. The fused and standard L2 products are compared and assessed in terms of their information content, highlighting the better data quality provided by the fusion. Finally, we also show that the CDF can be applied with different coincidence grid box sizes, allowing for different compression factors of the Level 2 input data volume.
Some of the characteristics of the products used in this work differ from what they will be in reality: in particular, the spatial sampling (spacing between pixels and shape) and in some cases the signal-to-noise ratio (GEO-TIR instrument) of the instruments used in the present paper (both GEO and LEO) are different from those of that will be onboard the Sentinel 4/MTG-S and EPS-SG. Nevertheless, this work focuses on a comparison of the fused and L2 products and, in particular, on the ability of the CDF to induce quality improvements that are, in some sense, independent from precise instrumental characteristics.
The application of CDF to L2 products simulated with the characteristics that are even only similar to the ones expected from the atmospheric Sentinel 4 and 5 products allows for establishing the possible benefits in the case of real Sentinel data.
2.1 Atmospheric scenario and ozone climatology
In this work, we used two basic external sources to generate the database of the standard L2 ozone products: the ozone climatology and the atmospheric scenario.
We used the ozone climatology as a priori information in both the simulation of L2 products and the CDF. The atmospheric scenario represents the true state of the atmosphere, and we used it in both the simulation of L2 products and the quality assessment of the fused ones.
In particular, the ozone climatology was derived from McPeters and Labow (McPeters and Labow, 2012) and directly provided the a priori profile xa used either in the simulation equations (Eq. 1) or in the fusion equation (see Eq. 6). We calculate the diagonal terms of the a priori CM Sa as the square of the SD of McPeters and Labow climatology, putting an inferior limit to this diagonal value equal to the square of 20 % of the a priori profile. The off-diagonal elements are calculated using a correlation length of 6 km. The correlation length is used to reduce oscillations in the simulated profiles, and 6 km is the typical value used for nadir ozone profile retrieval (Liu et al., 2010; Miles et al., 2015). The a priori CM is used in the equation of the L2 AK matrix (Eq. 2) and in Eqs. (4) and (5) of the next paragraph. The a priori CM Sa also plays an important role in the CDF equations (see Eq. 6).
The atmospheric scenario is taken from the Modern Era-Retrospective analysis for Research and Applications version 2 (MERRA-2) reanalysis (Gelaro et al., 2017). The MERRA-2 data are provided by the Global Modelling and Assimilation Office (GMAO) at NASA Goddard Space Flight Center. This reanalysis covers the recent time of remotely sensed data, from 1979 through the present. The atmospheric scenario is the source of true profile xt used in Eq. (1) to synthesize the simulated L2 products and represents the main reference for the comparison of the quality of L2 and fused products.
2.2 L2 product simulation algorithm
The simulation algorithm was originally formalized in the context of the AURORA project, aiming at an efficient computational process. The L2 retrieved state is simulated on a fixed vertical grid with a 3 km step by the linear approximation given in Eq. (1):
In Eq. (1), xt is the true state of the atmosphere represented by the atmospheric scenarios, xa is the a priori estimate of the state vector provided by the ozone climatology, δ is the uncertainty in the retrieved value due to measurement noise and is the AK matrix (Rodgers, 2000) calculated according to Eq. (2).
In Eq. (2), K is the Jacobian matrix of the forward model, the superscript T is the transpose operator, Sy is the CM of the observations and Sa is the CM of the a priori profile. The retrieval error δ is calculated by applying the gain matrix G (Rodgers, 2000) to an error ε on the observations randomly taken from a Gaussian distribution with average equal to zero and CM given by Sy:
The CM S associated with the retrieval error δ (introduced in Eq. 3) is given by Eq. (4) (Rodgers, 2000):
The CM Stotal associated with the total error δtotal (i.e. the difference between the simulated and the true profiles, equal to the random δ plus the so-called smoothing error, caused by the limited vertical resolution of the measurement; see Eq. 7), is given by Eq. (5) (Rodgers, 2000):
It should be noted that through the term δ it is possible to simulate additional error components with respect to the random one considered in this study, and this fact adds flexibility to the simulation method.
In this study, we use the above formulation to simulate ozone profiles in two spectral bands (UV1 and TIR) for both GEO and LEO, after considering the instrument specifications and accounting for the differences in the two spectral bands. In particular, considering a fixed geolocation, true profile and a priori information, we obtain the L2 products of the different instruments by choice of K and Sy, that have been synthesized using the technical requirements of the considered platforms and their foreseen performances.
2.3 L2 product technical specifications
In the context of Sentinel missions, the ozone profiles derived from measurements in the UV region will be retrieved from spectral radiances acquired by the UVNS/Sentinel-5 spectrometer onboard the Meteorological Operational satellite–Second Generation (MetOp-SG) and by the UVN/Sentinel-4 spectrometer onboard the Meteosat Third-Generation Sounder (MTG-S). For ozone and other targets observed in the TIR, the atmospheric Sentinel missions will use the operational products of IASI-NG on MetOp-SG and IRS on MTG.
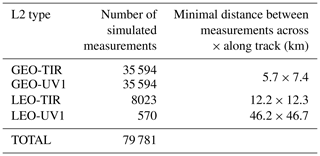
In the framework of the AURORA project, we simulated ozone products from the instruments mentioned above by using the information available at the beginning of 2016 (ESA, 2011, 2012; EUMETSAT, 2010; Crevoisier et al., 2014). We applied some simplifications to these specifications: for example, we considered only the UV1 band (neglecting UV2, 300–320 nm), simplified spatial sampling (spacing between pixels and shape) and in some cases a different signal-to-noise ratio (GEO-TIR L2 type, see Table 1). Consequently, the dataset of simulated L2 products is not exactly in line with the specifications currently foreseen for the instruments of interest. Table 1 reports some of the more relevant characteristics of the simulated measurements. It is worth noting that when an instrumental parameter has both a goal value (the value in case the instrument performs at its best) and a threshold value (the value that we expect to reach anyhow), the latter is used for the simulation.
Table 1Instrument characterization relevant for the simulation process. Goal (G) and threshold (T) values correspond, respectively, to estimates of the parameters in the case that the instrument performs at its best and to limit values that we expect to reach anyhow. AURORA will be using threshold values for the generation of simulated data.
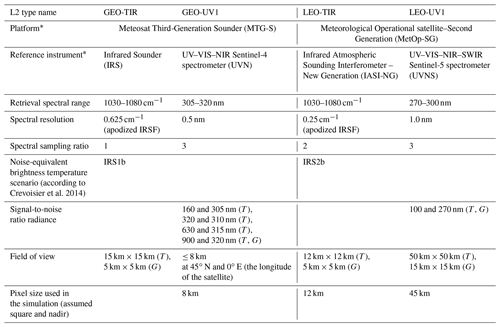
* The table entries in these rows are not meant to suggest that the specifications listed in this table refer directly to these instruments. Instead, the listed instruments are examples of instruments that are actually planned with similar (but slightly different) specifications.
A more detailed description of the instrumental and observational features goes beyond the scope of this article. All the relevant information was reported in the Technical Note on L2 data simulations (AURORA, 2017) and can also be found in Cortesi et al. (2018). In the following sections of this paper, we do not directly refer to the reference instruments names, but we use an alternative nomenclature: specifically, we refer to UVNS/MetOp-SG as LEO-UV1, to UVN/MTG as GEO-UV1, to IASI-NG/MetOp-SG as LEO-TIR and IR/MTG as GEO-TIR. Since we simulated instruments with characteristics that differ from the real specifications, we think it is appropriate to also use an independent terminology to avoid misunderstandings.
2.4 The CDF method
In this section, we briefly recall the formulas of the CDF method (Ceccherini et al., 2015). We assume N independent simultaneous measurements of the vertical profile of an atmospheric species that refer to the same geolocation. Performing the retrieval of the N measurements, we obtain N vectors () that provide independent estimates of the profile, here assumed to be represented on a common vertical grid. Using these N measurements as inputs, the CDF produces a single product characterized by a profile xf, an AK matrix Af and a CM matrix Sf as output, with the procedure summarized by Eq. (6). These three quantities are dependent on the input products, Ai and Si, hereafter referred to as fusing products, and depend on the a priori information (xa, Sa) used as a constraint for the fused product.
Concerning the profile and the error, we can consider the CDF as a “smart average” in which the a priori information is removed from the L2 profiles and CMs before they are put together in the average. The total error of the L2 product without a priori is higher than the original one, and the effect of the average only partially compensates this error increase. Consequently, even if the total error of the fused product is generally lower than the one of the single L2 fusing product, it is in general higher than the error of the average. The behaviour of the AK matrix is less intuitive, and we will thoroughly analyse it in the presentation of the results.
If the input products are not coincident in time and space, the CDF introduces a coincidence error characterized by a CM Scoinc. In this work, we calculated the diagonal elements of Scoinc as the square of 5 % of the a priori profile xa, where we choose this value considering the size of the coincidence grid cells used in this study. We calculate the off-diagonal elements of Scoinc, applying an exponential decay with a correlation length of 6 km (Ceccherini et al., 2018). The 5 % choice matured in a heuristic way by varying the percentage value, observing the quality of the fused product in single reference cells, and by looking at the entire dataset in representations similar to Figs. 6 and 7.
The dynamical choice of Scoinc is presented in Ceccherini et al. (2019). Specifically, the a priori error (coincident with the climatological variability) is used as the reference for the diagonal elements and a fixed exponential decay is applied as well. However, the multiplicative factor is calculated by imposing the requirement the cost function of the retrieval be equal to its expected value. That study, which is based on simulated products similar to the ones of this work, shows that even if the coincidence error is strictly needed for the correct behaviour of the CDF product, this is not strongly dependent on its exact amount until it is smaller than the errors of the individual L2 products.
The formulae of Eq. (6) refer to cases of measurements made on the same vertical grid. In general, an interpolation error may also be needed, considering that the retrievals of the products to be fused can be defined on different vertical grids. In Ceccherini et al. (2018) the general equations of CDF in the case of the fusion of products characterized by different vertical grids are presented and discussed together with the equation of the interpolation error that depends on the involved grids and the AK matrices of the fusing products. However, since the interpolation error does not apply to the present study (we simulated all the L2 products on the same vertical grid), it has not been considered in Eq. (6) or in the following discussion.
2.5 Arithmetical average and biases
Before proceeding, it is necessary to clarify why the arithmetic average of the profiles cannot be considered as a good option to represent a set of products retrieved with optimal estimation techniques.
To do this, we consider N coincident L2 measurements () referring to the same true profile, the same AK matrix and the same CM but having different (noise) errors δi randomly generated according to Eq. (3). The total error equation for the ith measurement is given in Eq. (7) and can be easily derived from Eq. (1).
Considering that the individual measurements are co-located in space and time, they thus refer to the same truth, the same a priori profile and the same AK matrix A; the mean total error is equal to
It follows that the averaging process reduces the random component of the total error but does not reduce the bias due to the a priori information. This bias is equal to the term of Eq. (8), which therefore becomes a dominant component as the number N increases. The existence of this bias is one of the reasons why the arithmetic average cannot be considered as a reference algorithm to collect the information of several products into one. Further reasons concern the choice of a suitable AK matrix to be assigned to the average (see also von Clarmann and Glatthor, 2019) and the management of possible coincidence and interpolation errors. An explicative comparison of the application of CDF and standard averages in the case of 1000 coincident L2 products is reported in the Supplement.
3.1 Fusion in realistic spatial and temporal resolution conditions: the L2 datasets
To analyse the behaviour of CDF in realistic spatial and temporal resolution conditions, we consider four sets of measurements. These measurements correspond to the cloud-free observations that were possible between 09:00 and 10:00 UTC on 1 April 2012. Table 2 lists the L2 product types, namely GEO-TIR, GEO-UV1, LEO-TIR and LEO-UV1, used in this article. The L2 datasets have been generated according to the Eqs. (1)–(5) described in Sect. 2.2. The details of the simulation process are explored in the Technical Note (AURORA, 2017), considering that here we simulated all the pixels corresponding to a clear sky line of sight in the atmospheric scenario, without applying any additional selection criteria. In the AURORA project's main work stream, we considered 4 months of data; however, we simulated only a subset of the clear-sky pixels to reduce the computational cost of the simulations (Tirelli et al., 2020). In this AURORA side study, we consider 1 h of data, and we simulate all the clear-sky pixels without additional filters, choosing the orbits so that GEO-LEO coincidences occur. Figure 5a indirectly represents the spatial distribution of the products simulated for this study.
3.2 Single grid box analysis (0.5∘ × 0.625∘)
We consider the case of a single grid box (Fig. 1). In the selected grid box, 118 measurements were available (55 of GEO-TIR, 55 of GEO-UV1, 8 of LEO-TIR and no LEO-UV1). The cell is 0.5∘ in latitude and 0.625∘ in longitude, centred on Aegina in the Aegean Sea. The cell size has been chosen to be comparable with the assimilation grid used in the AURORA project. We assign the geolocation of the fused product to be the barycentre of the horizontal coordinates of the L2 measurements in the grid box. In this particular case, since the horizontal distribution of the 118 L2 profiles is quite homogeneous, the barycentre is placed at the centre of the grid cell.
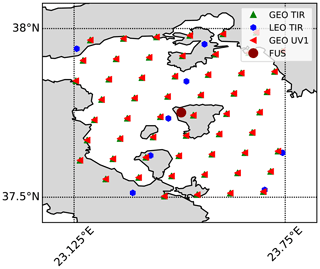
Figure 1Geographical distribution of the simulated L2 measurements and geolocation of the fused product. The dashed and dotted black lines represent the borders of the 0.5∘ × 0.625∘ grid cells.
Figure 2 shows with green lines the absolute (Fig. 2a) and relative (Fig. 2b) differences between each L2 profile and the corresponding true profile, with a red line showing the difference between the fused (FUS) profile and the mean truth (computed as the average of the 118 true profiles), a dashed and dotted black line showing the average of the estimated SD of the total error of the individual L2 measurements σtotal, and with a dashed and dotted red line showing the estimated SD of the total error of the fused profile σf total. The last two quantities have been calculated as the square root of the diagonals of the Stotal and Sf total CMs given by Eqs. (5) and (6), respectively. Figure 2 shows that the fused product is in better agreement with its truth than the individual profiles with their own, and presents a smaller estimated total error than the individual L2 products. In particular, the Fig. 2b allows for seeing the performances of CDF in the tropospheric region in detail.
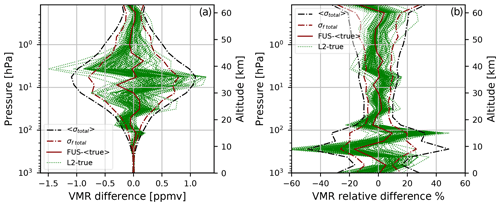
Figure 2(a) The absolute differences between L2 profiles and their true profiles (green lines), the absolute difference between the fused profile and the average of the true profiles (continuous dark red line), and the average of σtotal of L2 simulations (dashed and dotted black lines) and σf total (dashed and dotted dark red lines). (b) The relative percentage differences between L2 profiles and their true profiles (green lines), the relative percentage difference between the fused profile and the average of the true profiles (continuous dark red line), the average of σtotal of L2 simulations normalized with respect to the true profile and expressed in percentage (dashed and dotted black lines), and σf total normalized with respect to the true profile and expressed in percentage (dashed and dotted dark red lines).
The retrieved profile representation is always a compromise between the amplitude of the errors and the vertical resolution. The latter can be quantified by the AKs, which ideally would be equal to the identity matrix in the case of a profile that has a vertical resolution equal to that defined by the sampling grid. Diagonal elements with values smaller than 1 correspond to a loss of vertical resolution. In Fig. 3b, we compare the diagonal elements of the AKs of the L2 products with the AK diagonal of the fused product. Here we have also computed the number of degrees of freedom (DOF), given by the sum of the diagonal elements of the AK matrix (Rodgers, 2000), for both L2 and fused products and reported the values in the text box in Fig. 3a. Note that the number of DOF of the fused product is about twice the number of DOF of the best L2 product. In Fig. 3b, we compare the vertical resolution profiles of L2 and fusion products. We calculate the vertical resolution starting from AK matrices according to the full-width-at-half-maximum (FWHM) approach (Rodgers, 2000) and specifically with the algorithm defined in Ridolfi and Sgheri (2009).
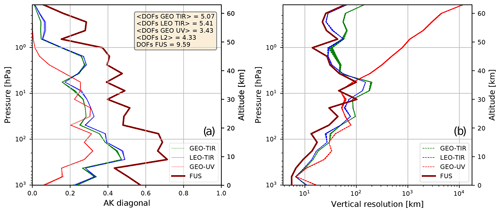
Figure 3(a) AK diagonals for the GEO-TIR products (red lines), LEO-TIR products (blue lines), GEO-UV products (red lines) and the FUS product (dark red line). In the text box, the average number of DOF for each type of L2 product, the average number of DOF for all L2 products and the number of DOF of the FUS product are reported. (b) Vertical resolution (FWHM) profiles for the GEO-TIR products (red lines), LEO-TIR products (blue lines), GEO-UV products (red lines) and the FUS product (dark red line). In each panel, while the solid dark red line is a single one, the red and green lines are both 55 overlapped lines, and the blue lines are eight overlapped lines (one for each L2 product).
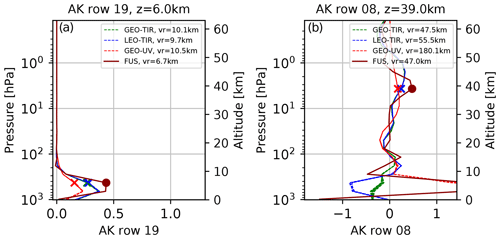
Figure 4(a) Rows of AK matrices at 6 km. (b) Rows of AK matrices at 39 km GEO-TIR products (red lines), LEO-TIR products (blue lines), GEO-UV products (red lines) and the FUS product (dark red line).
From the comparison of the Fig. 3a and b, it can be noted that the increase of the AK matrix diagonal values of FUS product, and consequently the increase of the number of DOF, implies an improved vertical resolution only in a subset of the vertical levels. To better understand the effect of the fusion on the AK matrices, it is useful to analyse the behaviour of their rows. In Fig. 4, two rows are represented, one that refers to the troposphere (Fig. 4a, 6 km) and one the middle stratosphere (Fig. 4b, 39 km), where the reference altitude is corresponding to the diagonal value of the row. The value of the vertical resolution at the considered altitude is reported in the legend (the minimum vertical resolution at the considered vertical level for each type of L2 product), and the diagonal value of each row is evidenced in the graphs with cross (L2) and dot markers (FUS). At lower altitudes (Fig. 4a), the DOF increase can be attributed to three distinct phenomena. The first is the constriction of the main FUS AK lobe and the consequent improvement (of more than 30 %) of the vertical resolution with respect to L2 products. The second phenomenon is linked to the fact that while for the FUS product the maximum value of the AK row corresponds to its diagonal element, for the L2 products these maxima are shifted with respect to the reference altitude of the rows. The last phenomenon is a stronger contribution of the (simulated) measurements with respect to the a priori values in the FUS product, where the latter effect can be evidenced by considering the sum of all the elements of the rows that assume 0.913 as the maximum value for the L2 products and 0.956 for the FUS product. In this particular case, all these three effects go in such a direction that they can be considered benefits of CDF application. The results at higher altitudes (39 km, Fig. 4b) are primarily influenced by the shape of the AK rows that exhibit large secondary lobes that degrade the vertical resolution.
Table 3Types and characteristics of the fused product when a coincidence grid cell size of 0.5∘ × 0.625∘ is used. Ncells is the number of grid boxes characterized by the considered FUS type, < NL2 > is the mean number of individual L2 fusing profiles per grid box and maxNL2 is the maximum number of individual L2 fusing products per grid box.

3.3 Statistical analysis for a large domain
While the analysis of the previous paragraph focuses on a particular grid box, here an analysis of the CDF behaviour is presented, referring to all the 1939 fusion grid boxes in which more than one of the 79 781 L2 simulated products considered in Table 2 is placed. The fused products can be classified depending on the types of L2 measurements falling inside the coincidence grid cell. Since GEO-TIR and GEO-UV1 products are in perfect coincidence and LEO-UV1 products have a horizontal spacing larger than the cell size, only six fused product types (FUS type), listed in Table 3, effectively occur. In this table, the FUS type and its description are reported together with the following complementary data:
-
N cells, i.e. the number of grid boxes characterized by the considered FUS type.
-
< NL2 >, i.e. the mean number of individual L2 fusing profiles per grid box.
-
Max NL2, i.e. the maximum number of individual L2 fusing products per grid box.
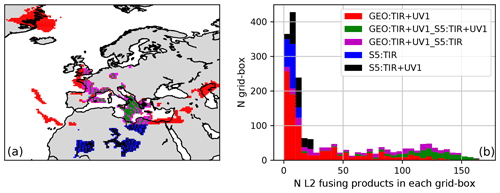
Figure 5(a) Geographical distribution of FUS products differentiated by FUS type where the effect of the lower resolution of LEO-UV1 with respect to the other L2 products is the cause of the periodic FUS type transitions in the Mediterranean area. (b) Histogram of the number of cells with a given number of L2 measurements differentiated by FUS type.
Figure 5a shows the geographical distribution of the FUS products. Different colours have been used to classify the fused data according to their provenance type. The irregular geographical coverage is due to the realistic distribution of the cloud-free measurements. The histogram in the Fig. 5b shows the number of cells that contain a given number of measurements, divided into different colours depending on the FUS type. The FUS cells in which only LEO products fall are characterized by a small number of L2 measurements, while when GEO products are present, many L2 measurements can be present.
With the selected grid box size and the multitude of different products that are present in each cell, the question is which product can be used in alternative to the fusion process in those operations in which a single product is requested in each grid box. Since the averaging process is affected by a large bias error, a viable alternative is the use of the best fusing product present in the cell, and we want to compare the CDF result with this product. This comparison is the so-called Synergy Factor (SF), introduced by Aires et al. (2012). Although Aires introduces SF only for errors (Eq. 11), we extend their definition to include other quantities because they constitute a useful tool to synthetically represent the performances of fusion algorithms.
The SF DOF, defined by Eq. (9), is the ratio between the number of DOF of the FUS product, and the maximum number of DOF of L2 fusing products. In this equation, the index l enumerates the vertical levels and the index i enumerates the L2 products fused in each grid box.
When SF DOF is larger than 1.0, the FUS product carries more information than the individual L2 measurements. Figure 6 shows that the SF DOF computed for all the fused products (and plotted as a function of the number of L2 profiles in each grid box) is always larger than 1.0. It is also worth noticing that SF DOF increases approximately linearly with the logarithm of the number of fusing products, although the proportionality depends on the FUS type. The two different clusters of red symbols (GEO:TIR + UV1) are caused by the different latitude bands in which these products are distributed (see also Fig. 5a). It is important to underline that the improvement in vertical resolution is the most demanding requirement in remote sensing observations and, considering the significant gain obtained relative to the single product selection, is the most important feature of fused products.
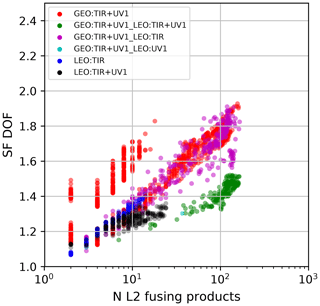
Figure 6Scatter plot of SF DOF as a function of the number of L2 measurements fused in each coincidence grid cell; different colours represent different FUS types.
While SF DOF is a scalar quantity, both SF AK and SF ERR, defined by Eqs. (10) and (11), respectively, are vertical profiles of pure numbers. SF AK represents an expansion on the vertical dimension of SF DOF and, in particular, is calculated level by level as the ratio between the diagonal elements of the AK matrix of the FUS product and the maximum of the corresponding elements of the AK matrices of the fusing L2 measurements.
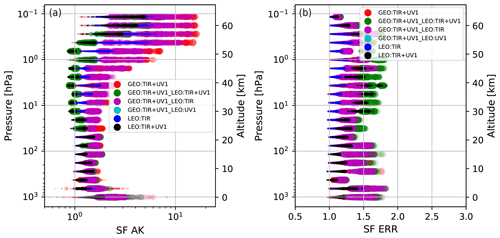
Figure 7(a) SF AK vs. vertical level. (b) SF ERR vs. vertical level. In both panels, the different colours of the symbols represent the FUS type, and the different sizes of the symbols represent the number of measurements that have been fused. The maximum symbol size shown in the legend corresponds to N=160.
A value of SF AK larger than 1.0 at a specific vertical level (indicated by the index l) means that at that level the diagonal value of the AK matrix of the FUS product has a larger value than that of all the individual products. As we have seen in Figs. 3 and 4, the increase of the AK diagonal values at a specific level can happen for different reasons, but all of them can be considered as an improvement in the product quality.
The SF ERR (Eq. 11) at a given level is the ratio between the minimum total error of the L2 measurements that have been fused and the total error of the FUS product. A value of SF ERR larger than 1.0 means that at a specific level the error of the FUS product is smaller than that of all the individual products.
The SFs defined by Eqs. (10) and (11) provide a conservative comparison because the fused product is compared with the L2 product that at that level has the largest diagonal value in its AK matrix and with the one that has the smallest total error at the same level (generally, these are two distinct L2 products).
Figure 7 shows the SF AK (Fig. 7a) and SF ERR (Fig. 7b) profiles for the 1939 FUS products considered in Table 3. We have used different colours to denote the provenance of the L2 data contributing to the fused products and different symbol sizes to infer the number of L2 fusing measurements (the larger the symbol size, the larger the number of L2 fusing profiles). The significant improvement obtained with the fused products is confirmed by Fig. 6. In Fig. 7, considering symbols of the same colour, the size (N) increases moving horizontally in the graph (same vertical level) from left to right (SF increasing). This fact denotes that for each FUS type, SF increases with N. This is not in contradiction with the fact that symbols with different colours (FUS types) and different sizes (N) can share the same position (SF, vertical level) on the graph. Some SF AK values, both in the troposphere and in the middle to upper atmosphere are smaller than 1; in the troposphere, this happens in 20 cells out of 1939 while in the middle to upper atmosphere this happens in almost 500 cells for two possible and sometimes simultaneous circumstances. The first circumstance occurs when the introduction of the coincidence error provokes a sensible degradation of the quality of the FUS AK matrix. The second circumstance occurs, for example, when one of the L2 products is characterized by a vertical resolution that is much better than all the other fusing products and, in particular, the peaks of their AK rows tend to not coincide with the nominal vertical level of the row itself.
3.4 Statistical analysis on a coarse horizontal resolution
We have seen that starting from 79 781 L2 measurements (Table 2), when a coincidence grid box with size 0.5∘ × 0.625∘ is used, the number of fused profiles is 1939 (Table 3), with a reduction of the data volume of more than a factor 40.
Table 4 provides a summary of the number of fused profiles and the provenance of the L2 profiles that contribute to them for a fusion grid resolution of 1∘ × 1∘. In this case, the total number of FUS products is 775, with a reduction of the data volume of more than a factor 100.
Table 4Like in Table 2 but with a grid box size of 1∘ × 1∘. Ncells is the number of grid boxes characterized by the considered FUS type. < NL2 > is the mean number of individual L2 fusing profiles per grid box and maxNL2 is the maximum number of individual L2 fusing products per grid box.

The synergy factors SF DOF, SF AK and SF ERR, in this case have also been considered, and the resulting figures (similar to Figs. 6 and 7) are reported in the Supplement. In summary, the greater number of fusing observations in each fusion cell produces a further improvement for both the vertical resolution and the total error. This observation confirms that the CDF method can be used with a wide range of grid box sizes and data compressions and that the quality of the products generally improves with larger cells. An upper limit to the grid box size is caused by the coincidence error amplitude, which increases with the geographical variability, degrading the quality of the fused product. The study of this aspect will be of crucial importance if the CDF is to be applied to species with greater spatial and temporal variability than ozone or in any cases with very large spatial and temporal domains.
This paper presents a feasibility study of the CDF technique applied to L2 products simulated according to the characteristics of the atmospheric Sentinel missions. Despite the approximations that characterize the simulated L2 products (technical specifications that are not exactly in line with the ones of the atmospherics Sentinels with no systematic errors added), this analysis allows for the evaluation of the performances of the CDF algorithm in a realistic scenario.
In particular, we show the application of CDF to a single cell with a size of 0.5∘ in latitude and 0.625∘ in longitude in which more than 100 L2 products are fused. Results show that the fused product is characterized by higher information content, smaller errors and smaller residuals (i.e. smaller anomalies from the true profiles) compared to individual L2 products. The information content being, with its improvement of the vertical resolution, the most important achievement.
This analysis is then extended to a larger domain consisting of 79 781 L2 products subdivided into 1939 grid boxes of 0.5∘ × 0.625∘ size. In this case, the comparison of L2 products and CDF output are carried on in terms of synergy factors. This analysis shows that the CDF can be applied to a wide range of situations and that the benefits of the fusion strongly depend on the number of measurements that are fused and on their characteristics. It is also shown that CDF can be run by customizing grid resolutions, e.g. to match the resolution requirements of the process that will ingest the products, with full exploitation of all the available measurements.
As the fused products are traced back to a regular, fixed horizontal grid and, as shown here, are not affected by the bias introduced by the a priori information, they can be considered a new type of Level 3 product with improved quality (reduced bias) and the same characteristics (AK included) with respect to L2 products, even if further analysis is needed, especially concerning the coincidence error to be applied to fuse data on large spatial and temporal domains.
The data of the simulations presented in the paper are available from the authors upon request.
MERRA-2 data (atmospheric scenario) are available at https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/ (last access: 29 December 2020, NASA GMAO, 2020).
The ML climatology is available at https://acd-ext.gsfc.nasa.gov/anonftp/toms/ML_climatology/ (last access: 17 February 2021, NASA GSFC, 2021). The ML climatology is available as ASCII tables of ozone mixing ratios (ML_ppmv_table.dat), the associated standard deviations (ML_ppmv_stats.dat), and a table of ozone layer amounts (ML_du_table.dat).
The supplement related to this article is available online at: https://doi.org/10.5194/amt-14-2041-2021-supplement.
NZ wrote the Python code that implemented the CDF, applied it to simulated data, collaborated with the study planning and the interpretation of the results, created all of the figures, and wrote the paper's draft version. SC deduced the CDF expressions, wrote the first version of the CDF code, and collaborated on the study planning and the interpretation of the results. FB maintained and organized the calculus resources used for this work. BC supervised the study, promoted the insights into the vertical resolution, and collaborated on the study planning and the interpretation of the results. RvdA led the work package regarding the simulation of synthetic data. JCAvP generated the orbit data for all of the simulated L2 datasets. MG, CT, and SDB performed the simulation of the infrared measurements. AA and JK performed the simulation of the ultraviolet measurements. RD was responsible for choosing the atmospheric scenario and the ozone climatology. SdB and CT acted in the role of project manager for the first and the second and third year of AURORA, respectively. UC collaborated on the study planning and was the principal investigator of the AURORA project. All of the authors revised the paper.
The authors declare that they have no conflict of interest.
The results presented in this paper arise from research activities conducted in the framework of the AURORA project (http://www.aurora-copernicus.eu/, last access: 29 December 2020) supported by the Horizon 2020 research and innovation programme of the European Union (Call H2020-EO-2015; Topic EO-2-2015) under grant agreement no. 687428.
This research has been supported by the Horizon 2020 research and innovation programme of the European Union (Call H2020-EO-2015; Topic EO-2-2015) under grant agreement no. 687428, research activities conducted in the framework of the AURORA project (http://www.aurora-copernicus.eu/, last access: 29 December 2020).
This paper was edited by Thomas von Clarmann and reviewed by two anonymous referees.
Aires, F., Aznay, O., Prigent, C., Paul, M., and Bernardo, F.: Synergistic multi-wavelength remote sensing versus a posterior combination of retrieved products: Application for the retrieval of atmospheric profiles using MetOp-A, J. Geophys. Res., 117, D18304, https://doi.org/10.1029/2011JD017188, 2012.
AURORA consortium (Advanced Ultraviolet Radiation and Ozone Retrieval for Applications, grant no. 687428): Technical Note On L2 Data Simulations [D3.4], 35 pp., available at: https://cordis.europa.eu/project/id/687428/results (last access: 29 December 2020), 2017.
Ceccherini, S., Carli, B., and Raspollini, P.: Equivalence of data fusion and simultaneous retrieval, Opt. Express, 23, 8476–8488, https://doi.org/10.1364/OE.23.008476, 2015.
Ceccherini, S., Carli, B., Tirelli, C., Zoppetti, N., Del Bianco, S., Cortesi, U., Kujanpää, J., and Dragani, R.: Importance of interpolation and coincidence errors in data fusion, Atmos. Meas. Tech., 11, 1009–1017, https://doi.org/10.5194/amt-11-1009-2018, 2018.
Ceccherini, S., Zoppetti, N., Carli, B., Cortesi, U., Del Bianco, S., and Tirelli, C.: The cost function of the data fusion process and its application, Atmos. Meas. Tech., 12, 2967–2977, https://doi.org/10.5194/amt-12-2967-2019, 2019.
Cortesi, U., Del Bianco, S., Ceccherini, S., Gai, M., Dinelli, B. M., Castelli, E., Oelhaf, H., Woiwode, W., Höpfner, M., and Gerber, D.: Synergy between middle infrared and millimeter-wave limb sounding of atmospheric temperature and minor constituents, Atmos. Meas. Tech., 9, 2267–2289, https://doi.org/10.5194/amt-9-2267-2016, 2016.
Cortesi, U., Ceccherini, S., Del Bianco, S., Gai, M., Tirelli, C., Zoppetti, N., Barbara, F., Bonazountas, M., Argyridis, A., Bós, A., Loenen, E., Arola, A., Kujanpää, J., Lipponen, A., Nyamsi, W. W., van der A, R., van Peet, J., Tuinder, O., Farruggia, V., Masini, A., Simeone, E., Dragani, R., Keppens, A., Lambert, J.-C., van Roozendael, M., Lerot, C., Yu, H., and Verberne, K.: Advanced Ultraviolet Radiation and Ozone Retrieval for Applications (AURORA): A Project Overview, Atmosphere, 9, 454, https://doi.org/10.3390/atmos9110454, 2018.
Crevoisier, C., Clerbaux, C., Guidard, V., Phulpin, T., Armante, R., Barret, B., Camy-Peyret, C., Chaboureau, J.-P., Coheur, P.-F., Crépeau, L., Dufour, G., Labonnote, L., Lavanant, L., Hadji-Lazaro, J., Herbin, H., Jacquinet-Husson, N., Payan, S., Péquignot, E., Pierangelo, C., Sellitto, P., and Stubenrauch, C.: Towards IASI-New Generation (IASI-NG): impact of improved spectral resolution and radiometric noise on the retrieval of thermodynamic, chemistry and climate variables, Atmos. Meas. Tech., 7, 4367–4385, https://doi.org/10.5194/amt-7-4367-2014, 2014.
Cuesta, J., Eremenko, M., Liu, X., Dufour, G., Cai, Z., Höpfner, M., von Clarmann, T., Sellitto, P., Foret, G., Gaubert, B., Beekmann, M., Orphal, J., Chance, K., Spurr, R., and Flaud, J.-M.: Satellite observation of lowermost tropospheric ozone by multispectral synergism of IASI thermal infrared and GOME-2 ultraviolet measurements over Europe, Atmos. Chem. Phys., 13, 9675–9693, https://doi.org/10.5194/acp-13-9675-2013, 2013.
ESA, Mission Science Division: GMES Sentinels 4 and 5 Mission Requirements Document (MRD), EOP-SM/2413, issue 1 rev. 0, available at: http://aurora.ifac.cnr.it/utils/personaldocs/see/93/ (last access: 29 December 2020), 2011.
ESA, Mission Science Division: GMES Sentinels 4 and 5 Mission Requirements Traceability Document (MRTD), EOP-SM/2413/BV-bv, issue 1 rev. 0, available at: http://aurora.ifac.cnr.it/utils/personaldocs/see/96/ (last access: 29 December 2020), 2012.
EUMETSAT: MTG End-User Requirements Document, EUM/MTG/SPE/07/0036, v3C, available at: https://www.ncdc.noaa.gov/sites/default/files/attachments/PDF_MTG_EURD.pdf (last access: 29 December 2020), 2010.
Gelaro, R., McCarty, W., Max J. Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G. K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017.
Lahoz, W. A. and Schneider, P.: Data assimilation: making sense of Earth Observation, Frontiers in Environmental Science, 2, 16, https://doi.org/10.3389/fenvs.2014.00016, 2014.
Liu, X., Bhartia, P. K., Chance, K., Spurr, R. J. D., and Kurosu, T. P.: Ozone profile retrievals from the Ozone Monitoring Instrument, Atmos. Chem. Phys., 10, 2521–2537, https://doi.org/10.5194/acp-10-2521-2010, 2010.
McPeters, R. D. and Labow, G. J.: Climatology 2011: An MLS and sonde derived ozone climatology for satellite retrieval algorithms, J. Geophys. Res., 117, D10303, https://doi.org/10.1029/2011JD017006, 2012.
Miles, G. M., Siddans, R., Kerridge, B. J., Latter, B. G., and Richards, N. A. D.: Tropospheric ozone and ozone profiles retrieved from GOME-2 and their validation, Atmos. Meas. Tech., 8, 385–398, https://doi.org/10.5194/amt-8-385-2015, 2015.
NASA GMAO (Global Modeling and Assimilation Office): Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-2), NASA GES DISC, available at: https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/, last access: 29 December 2020.
NASA GSFC (Goddard Space Flight Center): Atmospheric Chemistry and Dynamics Laboratory: McPeters and Labow Climatology, available at: https://acd-ext.gsfc.nasa.gov/anonftp/toms/ML_climatology/, last access: 17 February 2021.
Natraj, V., Liu, X., Kulawik, S., Chance, K., Chatfield, R., Edwards, D. P., Eldering, A., Francis, G., Kurosu, T., Pickering, K., Spurr, R., and Worden, H.: Multi-spectral sensitivity studies for the retrieval of tropospheric and lowermost tropospheric ozone from simulated clear-sky GEO-CAPE measurements, Atmos. Environ., 45, 7151–7165, 2011
Ridolfi, M. and Sgheri, L.: A self-adapting and altitude-dependent regularization method for atmospheric profile retrievals, Atmos. Chem. Phys., 9, 1883–1897, https://doi.org/10.5194/acp-9-1883-2009, 2009.
Rodgers, C. D.: Inverse Methods for Atmospheric Sounding: Theory and Practice, Vol. 2 of Series on Atmospheric, Oceanic and Planetary Physics, World Scientific, Singapore, 2000.
Sato, T. O., Sato, T. M., Sagawa, H., Noguchi, K., Saitoh, N., Irie, H., Kita, K., Mahani, M. E., Zettsu, K., Imasu, R., Hayashida, S., and Kasai, Y.: Vertical profile of tropospheric ozone derived from synergetic retrieval using three different wavelength ranges, UV, IR, and microwave: sensitivity study for satellite observation, Atmos. Meas. Tech., 11, 1653–1668, https://doi.org/10.5194/amt-11-1653-2018, 2018.
Tirelli, C., Ceccherini, S., Zoppetti, N., Del Bianco, S., Gai, M., Barbara, F., Cortesi, U., Kujanpää, J., Huan, Y., and Dragani, R.: Data fusion analysis of Sentinel-4 and Sentinel-5 simulated ozone data, J. Atmos. Ocean. Tech., 37, 573–587, https://doi.org/10.1175/JTECH-D-19-0063.1, 2020.
von Clarmann, T. and Glatthor, N.: The application of mean averaging kernels to mean trace gas distributions, Atmos. Meas. Tech., 12, 5155–5160, https://doi.org/10.5194/amt-12-5155-2019, 2019.