the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Model-enforced post-process correction of satellite aerosol retrievals
Ville Kolehmainen
Pekka Kolmonen
Antti Kukkurainen
Tero Mielonen
Neus Sabater
Larisa Sogacheva
Timo H. Virtanen
Antti Arola
Satellite-based aerosol retrievals provide a timely view of atmospheric aerosol properties, having a crucial role in the subsequent estimation of air quality indicators, atmospherically corrected satellite data products, and climate applications. However, current aerosol data products based on satellite data often have relatively large biases compared to accurate ground-based measurements and distinct uncertainty levels associated with them. These biases and uncertainties are often caused by oversimplified assumptions and approximations used in the retrieval algorithms due to unknown surface reflectance or fixed aerosol models. Moreover, the retrieval algorithms do not usually take advantage of all the possible observational data collected by the satellite instruments and may, for example, leave some spectral bands unused. The improvement and the re-processing of the past and current operational satellite data retrieval algorithms would become tedious and computationally expensive. To overcome this burden, we have developed a model-enforced post-process correction approach to correct the existing operational satellite aerosol data products. Our approach combines the existing satellite aerosol retrievals and a post-processing step carried out with a machine-learning-based correction model for the approximation error in the retrieval. The developed approach allows for the utilization of auxiliary data sources, such as meteorological information, or additional observations such as spectral bands unused by the original retrieval algorithm. The post-process correction model can learn to correct for the biases and uncertainties in the original retrieval algorithms. As the correction is carried out as a post-processing step, it allows for computationally efficient re-processing of existing satellite aerosol datasets without fully re-processing the much larger original radiance data. We demonstrate with over-land aerosol optical depth (AOD) and Ångström exponent (AE) data from the Moderate Imaging Spectroradiometer (MODIS) of the Aqua satellite that our approach can significantly improve the accuracy of the satellite aerosol data products and reduce the associated uncertainties. For instance, in our evaluation, the number of AOD samples within the MODIS Dark Target expected error envelope increased from 63 % to 85 % when the post-process correction was applied. In addition to method description and accuracy results, we also give recommendations for validating machine-learning-based satellite data products.
- Article
(2863 KB) - Full-text XML
- BibTeX
- EndNote
Climate change is one of the most serious problems humankind is facing today. Despite the long and active research, the future climate projections still contain significant uncertainties, and anthropogenic aerosol forcing currently comprises the largest source of this uncertainty (IPCC, 2014). More accurate information about the anthropogenic aerosols would help us improve our understanding of anthropogenic aerosol forcing, leading to a significant reduction of the uncertainties in future climate projections. Kaufman et al. (2005) and Yu et al. (2009) developed an algorithm to estimate the anthropogenic aerosol component utilizing MODIS fine-mode aerosol optical depth (AOD) fraction and corrections to exclude fine-mode natural dust and marine aerosols. The algorithm was only applicable over oceans due to the low accuracy of the fine-mode fraction over land, directly linked to an inaccurate Ångström exponent (AE). Therefore, any prospects to improve the satellite-based AE, particularly over land, could bring fundamental advances in measurement-based estimates of the global aerosol anthropogenic fraction. Another major global problem is air quality. In 2017, 2 %–25 % of all deaths globally were attributable to ambient particulate matter pollution (GBD 2017 Risk Factor Collaborators, 2018). To better monitor and understand air quality and pollution sources, near-real-time global observations of aerosols are needed. In this respect, the only way to get wide coverage and near-real-time information about atmospheric aerosols is to use satellite aerosol retrievals.
Satellite aerosol retrieval algorithms retrieve the aerosol optical properties such as AOD given the satellite observed top-of-atmosphere radiances or reflectances and the measurement geometry information. Other aerosol optical-property-related quantities, such as the AE, are often derived from the retrieved aerosol optical properties. Currently, satellite retrieval algorithms for multiple satellite instruments have been developed and the satellite aerosol data records span time series that are over 40 years long (Sogacheva et al., 2020). One of the most widely used satellite aerosol data products is based on the Moderate Imaging Spectroradiometer (MODIS) data (Salomonson et al., 1989) and the Dark Target algorithm (Levy et al., 2013). The MODIS Dark Target data start from the year 2000 and global data are available from two satellites: Terra and Aqua. The expected error (EE) envelope for AOD in Dark Target data over land is estimated to be , resulting in relatively large uncertainties, especially in regions with relatively low AOD. For more information about the concept of the EE envelope, see, for example, Sayer et al. (2015).
To improve the existing aerosol datasets, machine-learning-based solutions have been used in many studies. Most of the approaches that utilize machine learning employ a fully learned approach for the solution of a satellite retrieval. In the fully learned approach, a machine-learning-based model is trained to predict the values of the unknown aerosol parameters such as AOD given the measurement data (top-of-atmosphere radiances or reflectances) and observation geometry as the inputs. Neural-network-based fully learned aerosol retrievals are assimilated into NASA's MERRA-2 re-analysis model (Randles et al., 2017). In Di Noia et al. (2017), a fully learned AOD retrieval neural network model is used to retrieve the initial AOD for an iterative retrieval algorithm. In Lary et al. (2009), a fully learned approach with MODIS-retrieved AOD and the surface type as an additional input was used for the satellite AOD retrieval with MODIS data. The results of Lary et al. (2009) were evaluated using the accurate ground-based Aerosol Robotic Network (AERONET) data (Holben et al., 1998). With neural networks the authors were able to reduce the bias of the MODIS AOD data from 0.03 to 0.01, while with support vector machines even better improvement was reported – AOD bias was less than 0.001, and the correlation coefficient with AERONET was larger than 0.99. In the abovementioned work, the validation was performed using all the available AERONET stations both for training and validation. The split between the training and validation datasets was carried out using random splits of the pixels. With the random split of all pixels, the data samples from the same AERONET station were present in both training and evaluation datasets. This may lead to overly optimistic results as the model learns, for example, the surface properties at the locations of the AERONET stations and can thus predict the aerosol properties very accurately at these locations but may not generalize the results to other regions very well. In Albayrak et al. (2013), a neural-network-based fully learned MODIS AOD retrieval model was trained and evaluated. In their model, in addition to MODIS reflectances and measurement geometry information, they used MODIS-retrieved AOD and its quality flag as additional auxiliary inputs. The output of their model was AOD. They found their model to produce more accurate AOD retrievals than the operational MODIS Dark Target algorithm. In Lanzaco et al. (2017), a slightly different type of machine-learning-based approach was used to improve satellite AOD retrievals. The authors used MODIS AOD retrievals and local meteorology information as inputs to predict the AOD in South America. This approach that combines the conventional AOD retrievals and local meteorology information was reported to improve the AOD accuracy over the operational MODIS AOD. A problem in fully learned approaches is that they fully rely on trained data and do not employ physics-based models in the retrievals. This may cause problems in the capability of the model to generalize to cases in which the inputs are far outside the input space spanned by the training dataset.
Following the philosophy of a post-processing correction strategy, we have developed a new model-enforced machine learning approach in which we also exploit the models and the physics-based satellite-derived aerosol retrieval product. More specifically, we train the machine learning model for post-process correction of the approximation error in the result of the conventional retrieval algorithm. While the post-process correction approach is new to satellite retrievals, it has been found to perform better and produce more stable and accurate results than a fully learned approach in generation of surrogate simulation models (Lipponen et al., 2013, 2018) and in medical imaging, where many of the inverse imaging problems are mathematically highly similar to the satellite retrieval problems; see for example Hamilton et al. (2019). The key advantages of the new model-enforced post-process correction approach are (1) the improved accuracy over the existing data products and existing fully learned satellite data approaches and (2) the possibility to post-process-correct existing (past) satellite data products with no need for full re-processing of the enormous satellite datasets. A reason why our approach outperforms the current state-of-the-art fully learned machine learning retrievals is that the approximation error is a less complicated function for machine learning regression than the full physics-based retrieval. In our proposed correction approach, we combine the best aspects of the conventional retrievals and machine learning to get the full information content out of the satellite data. Our approach is not limited to aerosols and is generally applicable to different types of satellite data products as long as suitable training data for the model are available.
The manuscript is organized as follows. The proposed post-process correction of satellite aerosol retrievals is presented in Sect. 2. In Sect. 3, the data and models used to test our approach are shown. Evaluation of the models is presented in Sect. 4, and results are shown in Sect. 5. The conclusions are given in Sect. 6.
Let y be an accurate satellite aerosol retrieval (e.g., AOD) so that
where f is an accurate retrieval algorithm and x contains all the algorithm inputs including the observation geometry and satellite observations such as the top-of-atmosphere reflectances. An approximative retrieval algorithm is denoted by . In reality, due to uncertainties in the atmospheric properties and computational limitations among other reasons, it is not possible to construct an accurate retrieval algorithm f, which is why an approximative algorithm is used instead. The discrepancy between the accurate and approximative algorithm retrievals, that is the approximation error corresponding to , is denoted by
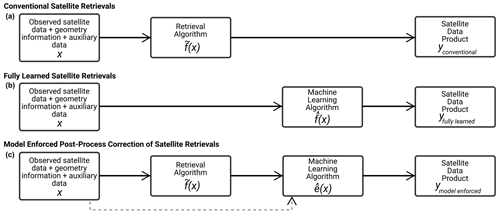
To compute the corrected retrieval in the model-enforced post-process correction of satellite aerosol retrievals, we use both the conventional retrieval algorithm and a machine-learning-based model to predict the realization of the approximation error e(x), and Eq. (1). Note that this is different from the fully learned model in which the aim is to emulate the accurate retrieval algorithm f(x) with a machine learning model . The approximation error e(x) is a typically less complicated function for machine learning regression than the full physics-based retrieval f(x), thus resulting in more accurate and reliable results with the model-enforced correction than with a fully learned approach. For a chart of conventional retrieval, fully learned machine learning, and model-enforced post-process correction approaches, see Fig. 1. Remark that as the training of the post-process correction is based on existing satellite data and retrievals, the implementation can be done in a straightforward manner, for example, using black-box machine learning code packages. In addition, the post-process correction model is also flexible with respect to the choice of the statistical regression model, and the choice of the regression model can be tailored to different retrieval problems separately.
For testing the model-enforced post-process correction, we use MODIS satellite aerosol retrieval data (AOD and AE) over land from the Aqua satellite. Both the proposed model enforced correction model and a fully learned model as a reference are trained and tested using data from the ground-based AERONET measurements.
3.1 MODIS Dark Target
MODIS instruments are flying on board NASA's Terra and Aqua satellites. Terra was launched in the year 1999, and the MODIS aerosol products currently span a relatively long time series of about 20 years. MODIS Dark Target aerosol data products are among the most widely used satellite aerosol data. In this study, we use the 10 km resolution MODIS Dark Target over land level 2 Collection 6.1 data of the Aqua satellite (MYD04_L2) from the years 2014–2018 (Levy et al., 2013). MODIS Dark Target aerosol data are also available with a spatial resolution of 3 km, but as the 10 km data product is the most widely used we chose to use this data product in our study. We use the AOD retrievals at wavelengths 440, 550, and 660 nm to compute the AE with a least-squares linear fit on a log-log scale. We accept all pixels with all quality flags in our datasets in this study. In addition to aerosol quantities, we use the observation (satellite acquisition and illumination) geometry, land surface altitude, and retrieval quality flags as inputs for our models from the aerosol data products in our study.
3.2 AERONET
AERONET is a global network of sun photometers (Holben et al., 1998). AERONET has a Direct Sun data product which contains both the AOD and Ångström exponent data that we will use in our study. AERONET data are most commonly used as an independent data source for aerosol retrieval validation, and all the data are publicly available at the AERONET website (http://aeronet.gsfc.nasa.gov/, last access: 16 May 2020). An extensive description of the AERONET sites, procedures, and data provided is available from this website. Ground-based sun photometers provide accurate measurements of AOD, because they directly observe the attenuation of the solar radiation without interference from land surface reflections. The AOD estimated uncertainty varies spectrally from ±0.01 to ±0.02 with the highest error in the ultraviolet wavelengths (Eck et al., 1999). In this study, we will use the AERONET Version 3, Level 2.0 Direct Sun data for both model training and validation purposes. The AERONET data are divided in cross-validation to sets of training stations and validation stations for good generalization of the machine learning model.
3.3 Fully learned and model-enforced post-process correction models for aerosol retrievals
In this study, in addition to the model enforced post-process correction model, we also train a fully learned model for the aerosol retrieval to be used as a reference. We use the random forest (RF) regressor (Breiman, 2001) as our machine learning method to train all the machine-learning-based models. RF is an ensemble learning algorithm that uses regression trees as base learners. RFs can learn non-linear functions, and they are relatively tolerant against overfitting. RFs have been shown to provide highly accurate results in many applications, and they are relatively straightforward to train with a low number of hyperparameters to tune in the training. Training of the RFs can also be done with relatively low computational costs, and the trained models are fast to evaluate. We use Python Scikit-Learn library implementation for the RFs (Pedregosa et al., 2011). During our work we also carried out preliminary tests with neural-network-based models trained with the same data as RFs but due to worse performance did not use them in the final evaluation.
Before training the final models, we carried out a hyperparameter optimization for each of the models. In the hyperparameter optimization, we used an exhaustive 3D grid search and tested all possible combinations of hyperparameters in our candidate sets using twofold cross validation with our training data. In the candidate set, we had three hyperparameters to be optimized.
-
The number of trees was 100, 200, and 400.
-
The maximum depth of a single tree was 30, 40, 50, and 60.
-
The maximum number of features to consider when building the regression trees (as fraction of number of features) was 100 %, 80 %, 60 %, and 40 %.
For other hyperparameters, the default values of the Scikit-Learn library were used. Based on the exhaustive grid search results, we averaged the hyperparameter values of the 10 best performing models measured with the explained variance metric. The hyperparameter values obtained by the averaging were used for the training of the final models. See derived values of the optimized hyperparameters in Table 1.
3.3.1 Fully learned model
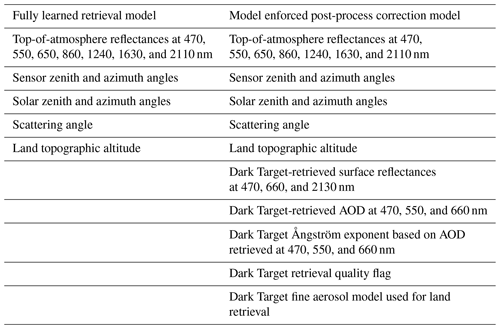
The fully learned machine learning model takes the MODIS observation geometry information and the top-of-atmosphere reflectance information as inputs and directly predicts the AOD at 550 nm and AE. The input variables in the fully learned models for both AOD and AE are the same, and they are listed in Table 2. Top-of-atmosphere reflectances include the mean values and standard deviations of the native MODIS pixels inside the 10 km MODIS aerosol pixel. The optimal hyperparameter values found in the hyperparameter optimization are listed in Table 1.
3.3.2 Model-enforced correction model
The model-enforced correction approach takes the same set of input variables as the fully learned model together with some additional Dark Target-related variables to predict the approximation errors for the AOD at 550 nm and AE. In the evaluation of the trained model-enforced post-process correction model, an estimate of the approximation error e(x) is first computed, and Eq. (1) is used to compute the corrected satellite AOD or AE as , where is the machine-learning-based estimate of the approximation error e(x). The input variables in the model-enforced models for both AOD and AE are the same, and they are listed in Table 2. Top-of-atmosphere reflectance inputs include the mean values and standard deviations of the native MODIS pixels inside the 10 km MODIS aerosol pixel. The wavelengths used for the Dark Target-related variables are those that are delivered in the operational data product files. More information on the specific details of the Dark Target-related variables can be found from the Algorithm Theoretical Basis Document (ATBD) (Levy et al., 2009). The optimal hyperparameter values found in the hyperparameter optimization are listed in Table 1.
To evaluate the model-derived aerosol data products, we first collocate the MODIS and AERONET observations. In the MODIS–AERONET collocation, we follow a similar comparison protocol as in Petrenko et al. (2012). For collocated MODIS pixel and AERONET observation we require
-
the distance from the center of a MODIS pixel to an AERONET stations to be less than 25 km.
-
each MODIS pixel to correspond to at least three AERONET observations within ±30 min from the satellite overpass.
We use the AERONET AOD at 500 nm and the AE 440–870 nm to compute the median AERONET AOD at 550 nm corresponding to the collocated satellite pixels. In the construction of the training dataset, all MODIS pixels fulfilling the above criteria are used. In the construction of the validation dataset, we compute spatial median values for the MODIS and temporal median values for the AERONET AOD and AE values corresponding to a single satellite overpass and fulfilling the above criteria. We use medians instead of averages as recommended in Sayer and Knobelspiesse (2019) to obtain more representative and outlier-tolerant results.
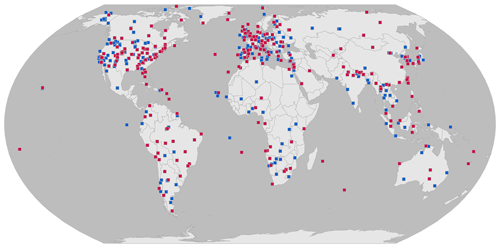
Figure 2Locations of AERONET stations used in training and testing of the models. Red and blue colors indicate the random grouping of the stations used in the cross-validation.
To get realistic estimates for the accuracy of the models, validation is carried out with cross-validation. In our two-fold cross-validation, we randomly divide AERONET stations into two groups and use one group of AERONET stations for training and the other group for validation. To take full advantage of the data and get a global estimate for the accuracies of the models, the training and testing are carried out two times with both combinations of the two groups. The AERONET stations and their groups used in this study are shown in Fig. 2. We also considered using a conventional cross-validation in which the full dataset would have been randomly divided into training and validation groups as is done for example in Lary et al. (2009). In the conventional cross-validation approach, however, the validation dataset pixels would have almost always contained remarkably similar pixels in the training dataset corresponding to the same AERONET station (e.g., two adjacent pixels). This would have resulted in overly optimistic results. We tested the conventional cross-validation approach and obtained almost perfect retrievals with the coefficient of determination R2=0.99 for both the fully learned and model-enforced models. This is a similar result as reported in Lary et al. (2009). However, to get realistic estimates for the model accuracies, we decided to divide the training and validation datasets based on AERONET stations so that an AERONET station is only present in either training or validation datasets but not in both.
Our goal is to get globally applicable results, and we use the coefficient of determination R2 based on correlation coefficient, root-mean-squared error (RMSE), and median bias as the metrics to compare the datasets. For AOD datasets, we also compute the ratio of samples that are inside the Dark Target over a land EE envelope of . In addition to AOD and AE, we will also evaluate the aerosol index (AI) that is defined as
AI has been considered a better proxy for cloud condensation nuclei (CCN) than AOD (e.g., Gryspeerdt et al., 2017), since AI is more sensitive than AOD to the accumulation mode aerosol concentration. However, as the AE has not been reliable over the land regions (Levy et al., 2010), the AI over land has not been properly usable either in satellite-based studies of aerosol–cloud interactions.
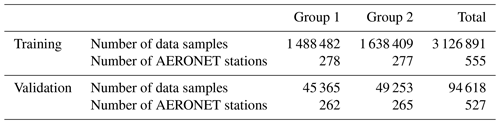
The developed model-enforced post-process correction method was tested with MODIS Aqua satellite data over land. We compare the post-process-corrected datasets to the operational Dark Target data over land and to a conventional fully learned machine learning retrieval. The number of samples and AERONET stations in training and validation datasets are shown in Table 3.
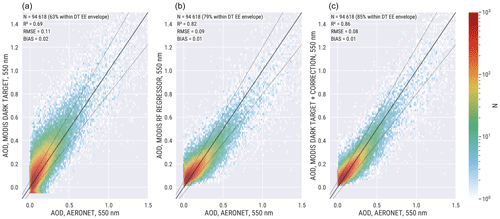
Figure 3Comparison of AERONET and MODIS AOD at 550 nm. (a) MODIS Dark Target over land. (b) MODIS fully learned random forest (RF) regression model. (c) MODIS Dark Target with RF regression-based model-enforced post-process correction. The solid black line indicates the 1:1 line. The dashed black lines show the MODIS Dark Target expected error (EE) envelope.
Figure 3 shows the MODIS–AERONET AOD comparison for the MODIS Dark Target, fully learned regression-based MODIS data and model-enforced post-process-corrected Dark Target AOD. The model-enforced correction model is clearly the most accurate dataset measured with the samples inside the Dark Target EE envelope (85 %), R2=0.87, and RMSE = 0.08. With both machine-learning-based datasets, a similar median AOD bias of about 0.01 is obtained while in the MODIS Dark Target, the median AOD bias is 0.02. The MODIS Dark Target data also show the non-physical negative AOD retrievals whereas the fully learned and model-enforced machine-learning-based datasets do not have samples with negative AOD. In the fully learned model with a RF regressor that cannot extrapolate values outside the training set, the non-negativity of retrieved AOD was expected as AERONET AOD is always non-negative. As the model-enforced correction model, however, uses the MODIS Dark Target AOD as a starting point, this is a very good result as the model regardless of the negative Dark Target AOD values learns to predict only non-negative AOD values.
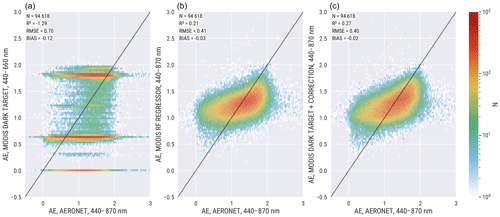
Figure 4Comparison of AERONET and MODIS Ångström exponent (AE). (a) MODIS Dark Target over land AE 440–660 nm. (b) MODIS fully learned random forest (RF) regression model AE 440–870 nm. (c) MODIS Dark Target AE 440–660 nm with RF regression-based model-enforced post-process correction. The solid black line indicates the 1:1 line.
Figure 4 shows the AE validation results. The results show that the satellite-based AE over land is clearly a less accurate quantity than the AOD. MODIS Dark Target is clearly the worst performing retrieval with a low information content and high uncertainty. Furthermore, the Dark Target AE values are mostly concentrated around three different values. This is a clear indication of relatively poor performance of the Dark Target mixing of fine and coarse aerosol models over land, which is the reason why there is no operational Dark Target AE product (Mielonen et al., 2011). Both of the machine-learning-based models result in a relatively similar performance. The model-enforced post-process correction has the best performance in all the metrics we use.
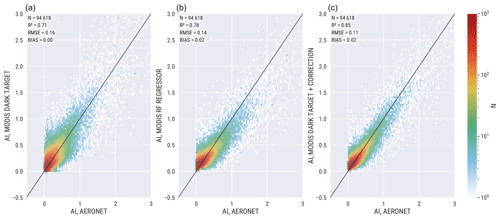
Figure 5Comparison of AERONET and MODIS aerosol index (AI). (a) MODIS Dark Target over land. (b) MODIS fully learned random forest (RF) regression model. (c) MODIS Dark Target with RF regression-based model-enforced post-process correction. The solid black line indicates the 1:1 line.
Figure 5 shows the results for the AI datasets. The accuracy of the AI datasets is generally similar to AOD datasets. Measured with R2 and RMSE the post-process-corrected dataset has the best accuracy. The machine-learning-based models have a median bias of 0.02, and the MODIS Dark Target is free of bias. The MODIS Dark Target AOD has a positive bias and AE a negative bias, thus resulting in bias-free AI.
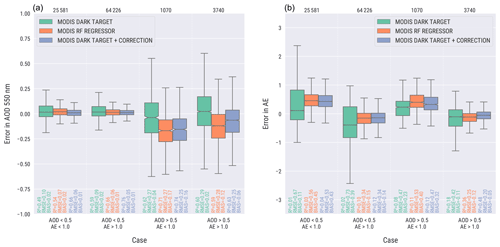
Figure 6Error distribution in AOD at 550 nm (a) and Ångström exponent (AE) (b) in different validation datasets. The data are grouped to four different groups based on AERONET AOD and AE. The numbers at the top of the figure indicate the number of validation samples in each group. The box shows the 25 %–75 % quartiles of the datasets. The whiskers extend to display the rest of the distribution, except for points that are determined to be outliers. The notch in the box shows the 95 % confidence interval around the median.
Figure 6 shows the AOD and AE error distributions for each dataset for four different AOD and AE ranges. For AOD, the model-enforced post-process-corrected model is clearly the best performing model for AOD < 0.5. For AOD larger than 0.5, the machine-learning-based models have negative bias, but the range of error values is clearly smaller than in the Dark Target. The samples with AOD > 0.5, however, represent only about 5 % of all data samples, so more data are needed for more accurate assessment of the accuracy of the models with large AOD. For AE, AE > 1.0 that corresponds to fine particles clearly results in smaller bias for machine-learning-based datasets than AE < 1.0. Generally, the error distribution is certainly narrower with machine-learning-based datasets than with Dark Target. With AE < 1.0, Dark Target results in a smaller median bias than the other datasets.
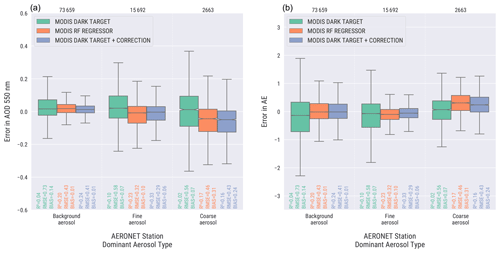
Figure 7Error distribution in AOD at 550 nm (a) and Ångström exponent (AE) (b) in different validation datasets. The data are grouped based on dominant aerosol type of AERONET stations based on Sogacheva et al. (2020). The numbers at the top of the figure indicate the number of validation samples in each group. The box shows the 25 %–75 % quartiles of the datasets. The whiskers extend to display the rest of the distribution, except for points that are determined to be outliers. The notch in the box shows the 95 % confidence interval around the median.
We also evaluate our datasets by comparing the AOD and AE with a grouping based on the dominant aerosol types of the AERONET stations (Sogacheva et al., 2020). Figure 7 shows the error distributions for AOD and AE for AERONET stations dominated by background aerosol, fine aerosol, and coarse aerosol. The seasonal classification from Sogacheva et al. (2020) is used for the classification of the AERONET stations according to the prevailing aerosol type. The results for both AOD and AE show that for aerosol stations dominated by background aerosol and fine aerosol the machine-learning-based datasets clearly perform better than the Dark Target. The background-aerosol-dominated data form the clear majority of the data (80 % of all samples), and the model-enforced post-process-corrected dataset is clearly the best performing dataset for these AERONET stations. For coarse-aerosol-dominated AERONET stations, the Dark Target has a smaller bias in the data than other datasets. Coarse-aerosol-dominated AERONET station data, however, have only about 3 % of all the samples in both training and validation, and thus more data are needed for further assessment of the results with coarse aerosol data and for better training of the machine learning methods.
To analyze the possible reasons for the improvements in the AOD accuracy, we also examined the correlations between the improvement in the AOD accuracy and some post-process correction model inputs and training parameters. In this analysis, we used seasonal averages of the improvements in the mean absolute error of AOD from each AERONET station. The input variables used for the AOD improvement correlation test included the measurement-geometry-related variables such as solar zenith angle, sensor zenith angle, and relative azimuth angle, AERONET AOD, AERONET station elevation, Dark Target fine aerosol model, and the number of training data samples used to train the post-process correction model. We also analyzed the geographic locations of the AERONET stations for which the post-process correction model performed best and worst by visual inspection. In these correlation analyses, we did not find a clear pattern to explain AOD accuracy improvements.
The results of the post-process-corrected aerosol dataset show that it is highly beneficial to combine both the physics-based retrieval algorithm and machine-learning-based post-process correction.
A model-enforced post-process correction method for the satellite aerosol retrievals was developed. In the correction method, a machine-learning-based model is trained to predict the approximation error in the conventional aerosol retrievals, and the estimate of the error is used to correct the retrievals. The proposed post-process correction approach is computationally efficient and processing of the existing satellite aerosol datasets does not require the much larger radiance datasets. The proposed approach is also generic in the sense that it does not require modifications to the original retrieval algorithm. The approach is also flexible with respect to the machine learning model (e.g., neural network, random forest), which can be chosen case specifically for each satellite dataset.
We found that the post-processing correction method resulted in significantly improved accuracy of the MODIS AOD and AE retrievals over land. With the proposed correction we obtained AOD bias smaller than the accuracy of the accurate ground-based AERONET AOD. Furthermore, the correction approach resulted in better accuracy retrievals than the conventional fully learned machine-learning-based models in which the satellite observations are used to directly predict the accurate retrievals. In many applications, even a small improvement in the aerosol characterization accuracy and precision could be translated into a significant gain, e.g., in remote sensing of land-surface-derived products such as solar-induced fluorescence or surface-reflectance-based indices within the visible and near-infrared parts of the spectrum. However, due to the small number of cases available with high AOD values, further studies would be required to better assess the post-process correction method's accuracy in high-AOD scenarios.
Compared to the Dark Target algorithm performance, the improved AOD and AE retrievals derived from the post-processing correction lead to a significant gain in the computation of the aerosol index (AI) over land. The accurate AI retrievals, especially for the small AI values, are highly important, for example, for the aerosol–cloud interaction studies in which AI is commonly used as a proxy for the CCN concentration. Here we observe that with the machine-learning-based retrievals there are a significantly lower number of highly biased AI retrievals, especially corresponding to small AI values. Improvement of small AI retrievals is highly beneficial, especially for the aerosol–cloud interaction studies. For the land satellite remote sensing community, any improvement in the aerosol characterization is translated into an important gain in terms of the achieved satellite-derived surface reflectance accuracy. In this regard, the use of the post-processing approach opens up the possibility to easily re-correct the long satellite-based land surface property time series.
We also found that the conventional cross-validation, in which the pixels of the full dataset are randomly divided into training and validation datasets, may lead to overly optimistic results in machine-learning-based algorithms for satellite retrievals. This is because too similar pixels corresponding to the same AERONET station are in both training and validation datasets. In our study, if we carried out this conventional cross-validation we would have obtained almost perfect retrievals with coefficient of determination R2=0.99. This is a similar result that can be found in some publications evaluating machine-learning-based approaches for satellite retrievals. We tackled the cross-validation issue by dividing the data into training and validation datasets by AERONET station.
Even though we tested the proposed approach with satellite aerosol data, our approach is not limited to aerosols only and is generally applicable to different types of satellite data products as long as suitable training data are available. In addition to observational data, simulated data could be suitable for training the post-process correction models in some applications. As we use an ensemble method random forest for the correction, it could be possible to use the spread of the ensemble members outputs to obtain pixel-based uncertainty estimates for the corrected retrievals. Furthermore, a sensitivity study for the post-process correction models could provide us valuable information on the weak parts of the conventional retrieval algorithms, and they could be used as a tool to assess the retrieval sensitivity.
The code and data to reproduce the results are available from the corresponding author on request.
AL and VK developed the methodology presented. AL collected and processed the data. AL, VK, PK, AK, TM, NS, LS, THV, and AA analyzed the results. AL wrote the original manuscript. VK, PK, AK, TM, NS, LS, THV, and AA reviewed and edited the manuscript.
The authors declare that they have no conflict of interest.
We thank the AERONET PIs and their staff for establishing and maintaining the AERONET sites used in this investigation. We thank the NASA MODIS and Dark Target teams for kindly making the MODIS data publicly available. Ville Kolehmainen acknowledges the Academy of Finland, Centre of Excellence in Inverse Modelling and Imaging (projects 312343 and 336791). The authors wish to acknowledge CSC – IT Center for Science, Finland, for computational resources.
This research has been supported by the Academy of Finland (grant nos. 312343 and 336791).
This paper was edited by Hiren Jethva and reviewed by two anonymous referees.
Albayrak, A., Wei, J., Petrenko, M., Lynnes, C. S., and Levy, R. C.: Global bias adjustment for MODIS aerosol optical thickness using neural network, J. Appl. Remote Sens., 7, 073514, https://doi.org/10.1117/1.JRS.7.073514, 2013. a
Breiman, L.: Random forests, Mach. Learn., 45, 5–32, 2001. a
Di Noia, A., Hasekamp, O. P., Wu, L., van Diedenhoven, B., Cairns, B., and Yorks, J. E.: Combined neural network/Phillips–Tikhonov approach to aerosol retrievals over land from the NASA Research Scanning Polarimeter, Atmos. Meas. Tech., 10, 4235–4252, https://doi.org/10.5194/amt-10-4235-2017, 2017. a
Eck, T. F., Holben, B., Reid, J., Dubovik, O., Smirnov, A., O'neill, N., Slutsker, I., and Kinne, S.: Wavelength dependence of the optical depth of biomass burning, urban, and desert dust aerosols, J. Geophys. Res.-Atmos., 104, 31333–31349, 1999. a
GBD 2017 Risk Factor Collaborators: Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks for 195 countries and territories, 1990–2017: a systematic analysis for the Global Burden of Disease Study 2017, Lancet, 392, 1923–1994, https://doi.org/10.1016/S0140-6736(18)32225-6, 2018. a
Gryspeerdt, E., Quaas, J., Ferrachat, S., Gettelman, A., Ghan, S., Lohmann, U., Morrison, H., Neubauer, D., Partridge, D. G., Stier, P., Takemura, T., Wang, H., Wang, M., and Zhang, K.: Constraining the instantaneous aerosol influence on cloud albedo, P. Natl. Acad. Sci. USA, 114, 4899–4904, https://doi.org/10.1073/pnas.1617765114, 2017. a
Hamilton, S. J., Hänninen, A., Hauptmann, A., and Kolehmainen, V.: Beltrami-net: domain-independent deep D-bar learning for absolute imaging with electrical impedance tomography (a-EIT), Physiol. Meas., 40, 074002, https://doi.org/10.1088/1361-6579/ab21b2, 2019. a
Holben, B. N., Eck, T., Slutsker, I., Tanre, D., Buis, J. P., Setzer, A., Vermote, E., Reagan, J. A., Kaufman, Y. J., Nakajima, T., Lavenu, F., Jankowiak, I., and Smirnov, A.: AERONET – A federated instrument network and data archive for aerosol characterization, Remote Sens. Environ., 66, 1–16, https://doi.org/10.1016/S0034-4257(98)00031-5, 1998. a, b
IPCC: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Core Writing Team, Pachauri, R. K. and Meyer, L. A.,IPCC, Geneva, Switzerland, 151 pp., 2014. a
Kaufman, Y. J., Boucher, O., Tanré, D., Chin, M., Remer, L., and Takemura, T.: Aerosol anthropogenic component estimated from satellite data, Geophys. Res. Lett., 32, L17804, https://doi.org/10.1029/2005GL023125, 2005. a
Lanzaco, B. L., Olcese, L. E., Palancar, G. G., and Toselli, B. M.: An Improved Aerosol Optical Depth Map Based on Machine-Learning and MODIS Data: Development and Application in South America, Aerosol Air Qual. Res., 17, 1523–1536, 2017. a
Lary, D. J., Remer, L., MacNeill, D., Roscoe, B., and Paradise, S.: Machine learning and bias correction of MODIS aerosol optical depth, IEEE Geosci. Remote S., 6, 694–698, 2009. a, b, c, d
Levy, R., Remer, L., Tanre, D., Mattoo, S., and Kaufman, Y.: Algorithm for remote sensing of tropospheric aerosol over dark targets from MODIS: Collections 005 and 051: Revision 2; Feb 2009, MODIS Algorithm Theoretical Basis Document, 2009. a
Levy, R. C., Remer, L. A., Kleidman, R. G., Mattoo, S., Ichoku, C., Kahn, R., and Eck, T. F.: Global evaluation of the Collection 5 MODIS dark-target aerosol products over land, Atmos. Chem. Phys., 10, 10399–10420, https://doi.org/10.5194/acp-10-10399-2010, 2010. a
Levy, R. C., Mattoo, S., Munchak, L. A., Remer, L. A., Sayer, A. M., Patadia, F., and Hsu, N. C.: The Collection 6 MODIS aerosol products over land and ocean, Atmos. Meas. Tech., 6, 2989–3034, https://doi.org/10.5194/amt-6-2989-2013, 2013. a, b
Lipponen, A., Kolehmainen, V., Romakkaniemi, S., and Kokkola, H.: Correction of approximation errors with Random Forests applied to modelling of cloud droplet formation, Geosci. Model Dev., 6, 2087–2098, https://doi.org/10.5194/gmd-6-2087-2013, 2013. a
Lipponen, A., Huttunen, J. M. J., Romakkaniemi, S., Kokkola, H., and Kolehmainen, V.: Correction of model reduction errors in simulations, SIAM J. Sci. Comput., 40, B305–B327, 2018. a
Mielonen, T., Levy, R. C., Aaltonen, V., Komppula, M., de Leeuw, G., Huttunen, J., Lihavainen, H., Kolmonen, P., Lehtinen, K. E. J., and Arola, A.: Evaluating the assumptions of surface reflectance and aerosol type selection within the MODIS aerosol retrieval over land: the problem of dust type selection, Atmos. Meas. Tech., 4, 201–214, https://doi.org/10.5194/amt-4-201-2011, 2011. a
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E.: Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 12, 2825–2830, 2011. a
Petrenko, M., Ichoku, C., and Leptoukh, G.: Multi-sensor Aerosol Products Sampling System (MAPSS), Atmos. Meas. Tech., 5, 913–926, https://doi.org/10.5194/amt-5-913-2012, 2012. a
Randles, C. A., da Silva, A. M., Buchard, V., Colarco, P. R., Darmenov, A., Govindaraju, R., Smirnov, A., Holben, B., Ferrare, R., Hair, J., Shinozuka, Y., and Flynn, C. J.: The MERRA-2 aerosol reanalysis, 1980 onward. Part I: System description and data assimilation evaluation, J. Climate, 30, 6823–6850, https://doi.org/10.1175/JCLI-D-16-0609.1, 2017. a
Salomonson, V. V., Barnes, W., Maymon, P. W., Montgomery, H. E., and Ostrow, H.: MODIS: Advanced facility instrument for studies of the Earth as a system, IEEE T. Geosci. Remote, 27, 145–153, 1989. a
Sayer, A., Hsu, N., Bettenhausen, C., Jeong, M.-J., and Meister, G.: Effect of MODIS Terra radiometric calibration improvements on Collection 6 Deep Blue aerosol products: Validation and Terra/Aqua consistency, J. Geophys. Res.-Atmos., 120, 12–157, 2015. a
Sayer, A. M. and Knobelspiesse, K. D.: How should we aggregate data? Methods accounting for the numerical distributions, with an assessment of aerosol optical depth, Atmos. Chem. Phys., 19, 15023–15048, https://doi.org/10.5194/acp-19-15023-2019, 2019. a
Sogacheva, L., Popp, T., Sayer, A. M., Dubovik, O., Garay, M. J., Heckel, A., Hsu, N. C., Jethva, H., Kahn, R. A., Kolmonen, P., Kosmale, M., de Leeuw, G., Levy, R. C., Litvinov, P., Lyapustin, A., North, P., Torres, O., and Arola, A.: Merging regional and global aerosol optical depth records from major available satellite products, Atmos. Chem. Phys., 20, 2031–2056, https://doi.org/10.5194/acp-20-2031-2020, 2020. a, b, c, d
Yu, H., Chin, M., Remer, L. A., Kleidman, R. G., Bellouin, N., Bian, H., and Diehl, T.: Variability of marine aerosol fine-mode fraction and estimates of anthropogenic aerosol component over cloud-free oceans from the Moderate Resolution Imaging Spectroradiometer (MODIS), J. Geophys. Res.-Atmos., 114, D10206, https://doi.org/10.1029/2008JD010648, 2009. a